Immersion and Invariance Adaptive Control for Unmanned Helicopter Under Maneuvering Flight
Abstract
Highlights
- A low-dimensional immersive system design approach is employed with the I&I (immersion and invariance) theory.
- To meet the requirements of I&I theory for asymptotic stability points in the system, in the constructed equivalent system, the first two state variables of the error system are artificially set with positive definite conditions to ensure stability.
- The non-cascade controller is constructed, which solely utilizes the velocity value as feedback.
- The control performance of the control law is influenced by the equivalent system as well as three parameters in its construction. However, the impact of these three parameters on the control effectiveness is positively correlated and mutually independent, resulting in very low difficulty in parameter tuning.
Abstract
1. Introduction
2. Modeling Method
2.1. Flight Dynamics Modeling of a UH-60A Helicopter
2.2. Implicit Model
3. Adaptive Controller Design Taking Advantage of Immersion and Invariance Theory
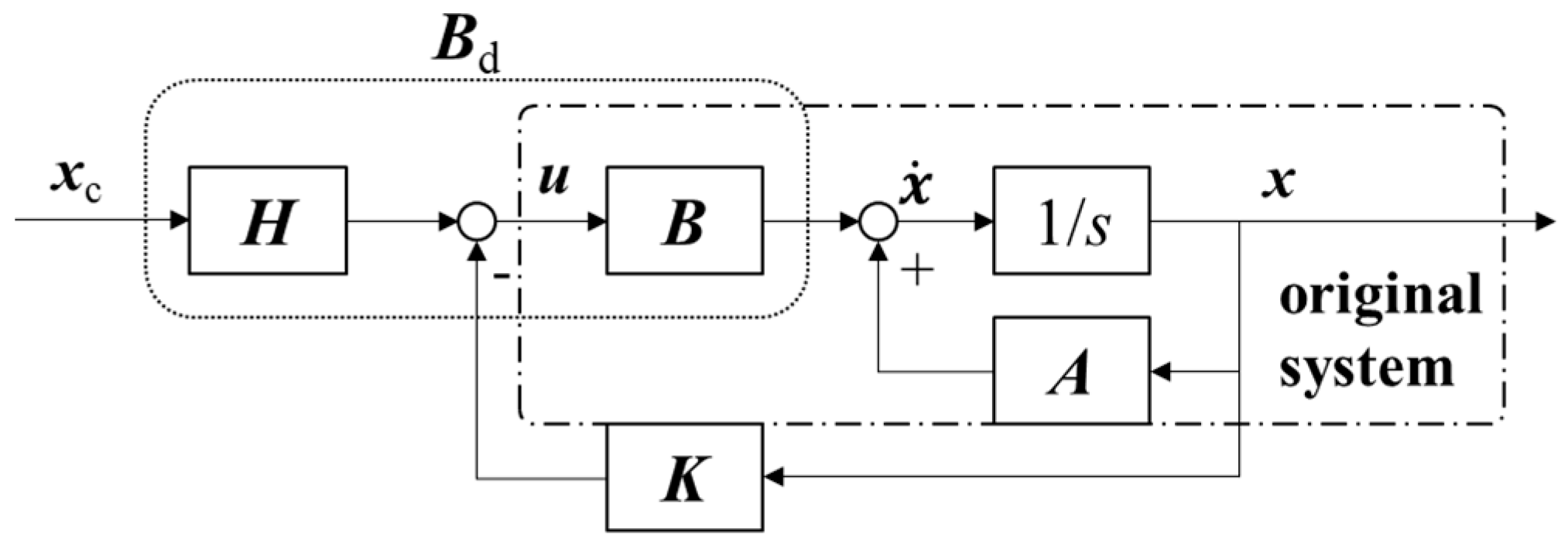
3.1. The Immersion and Invariance Theory
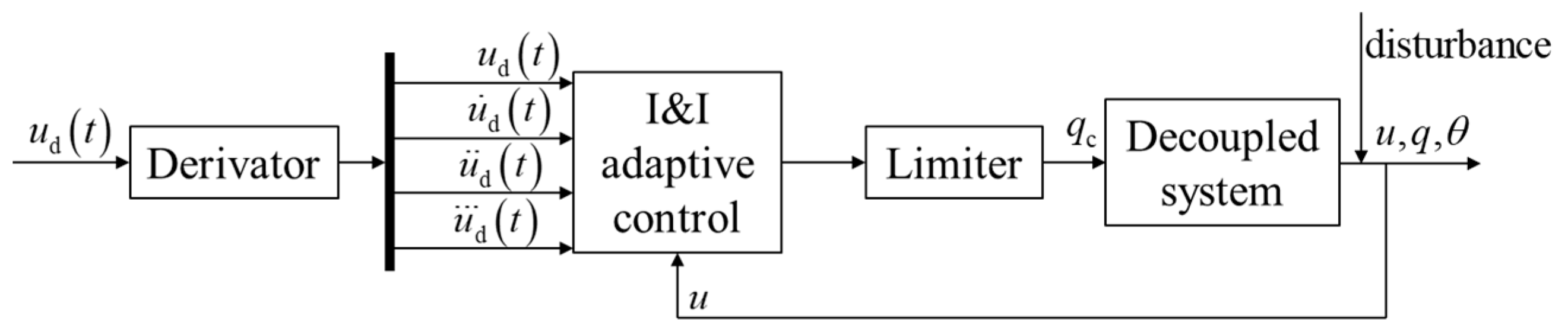
3.2. The Design of the Controller
4. Results
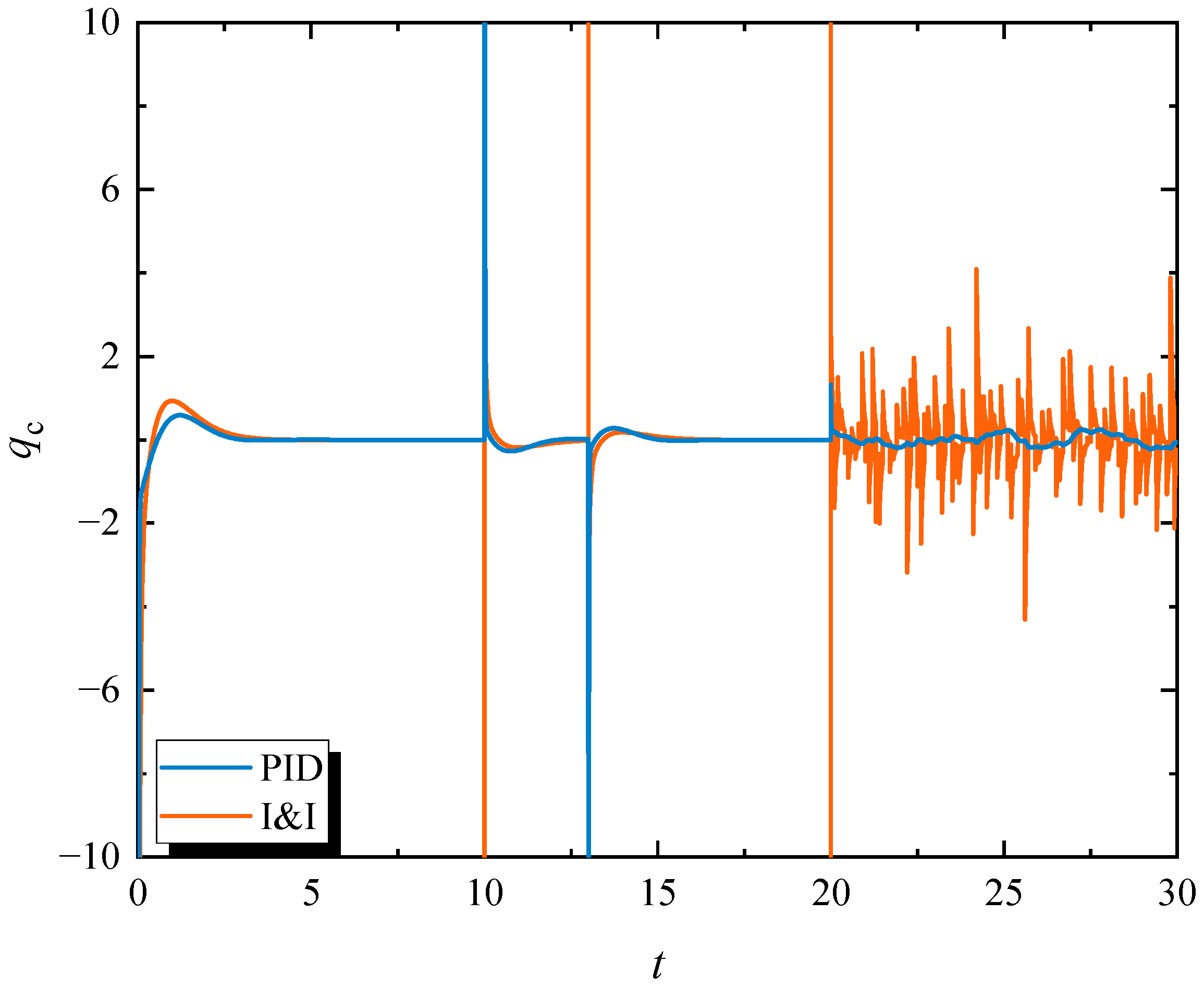
4.1. The Simulation of Step Signals
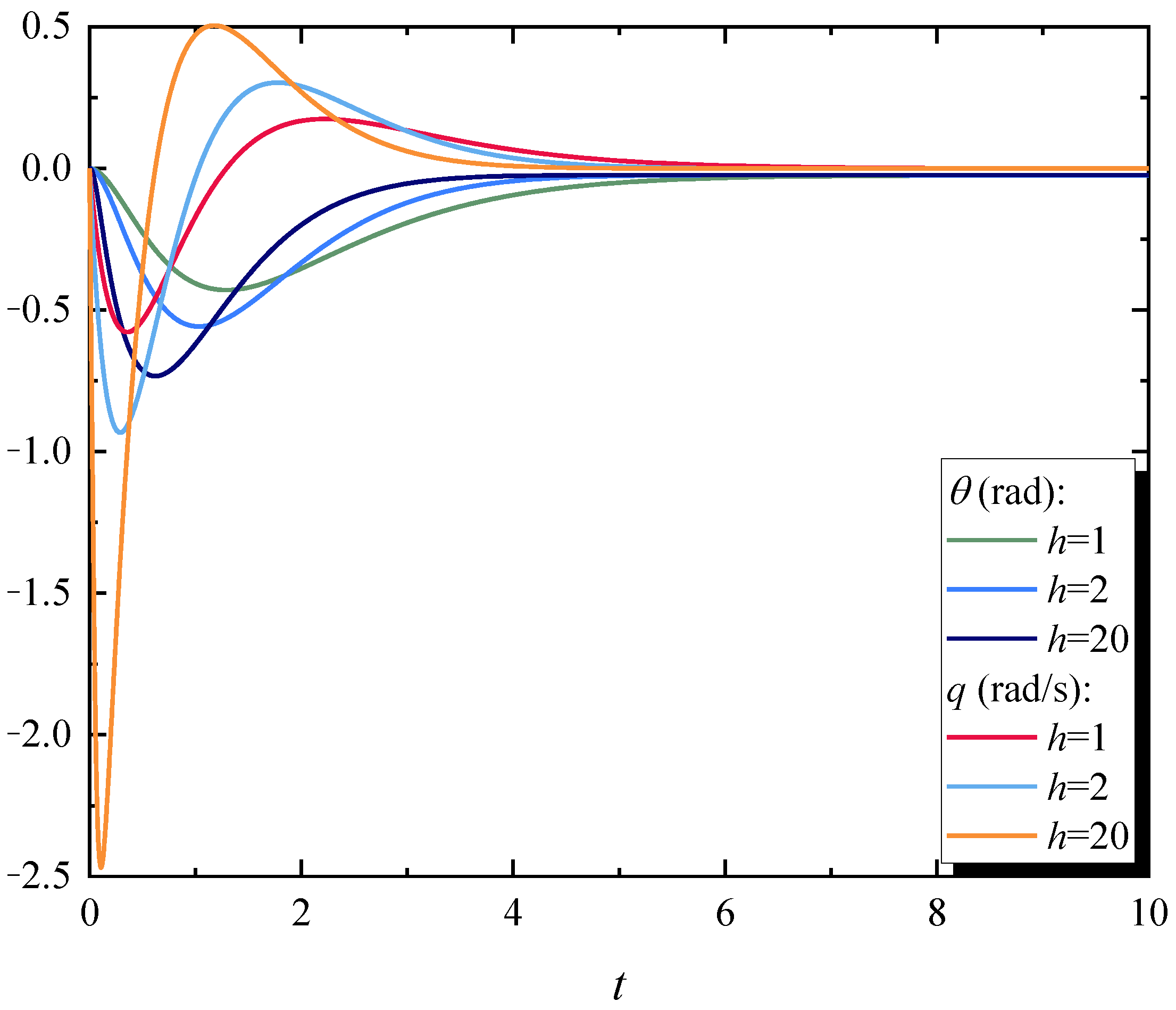
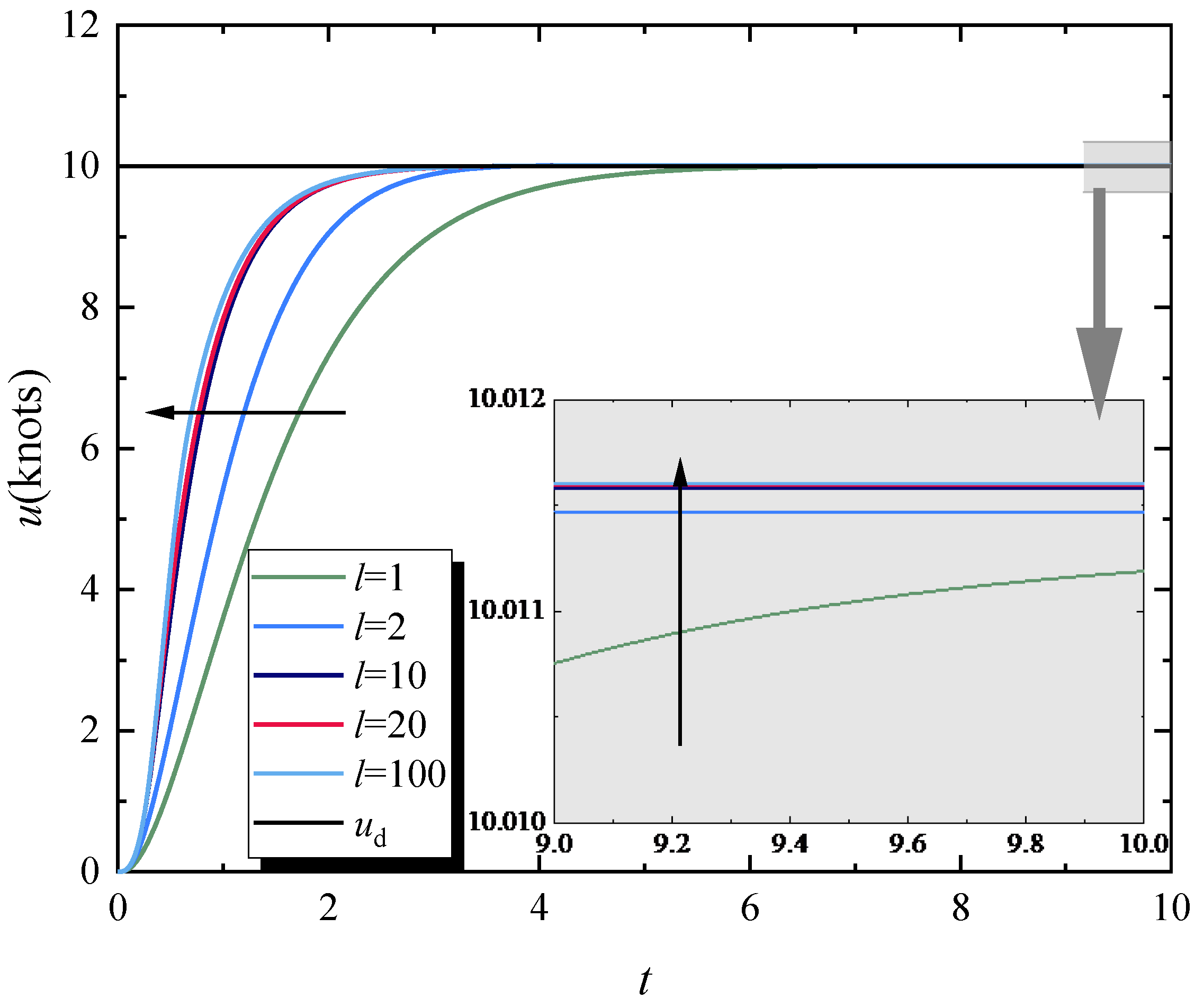
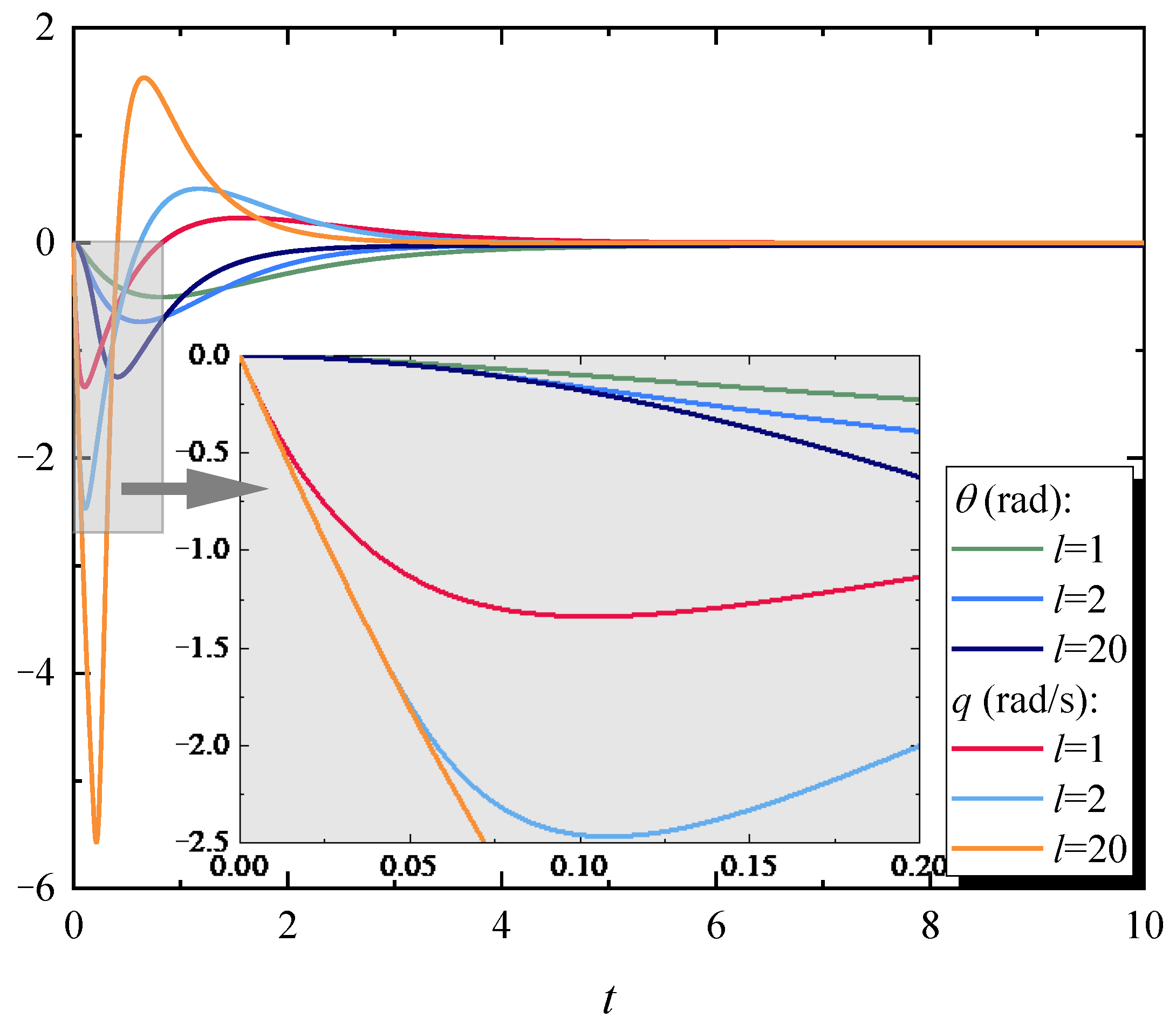
4.2. Analysis of System Parameters
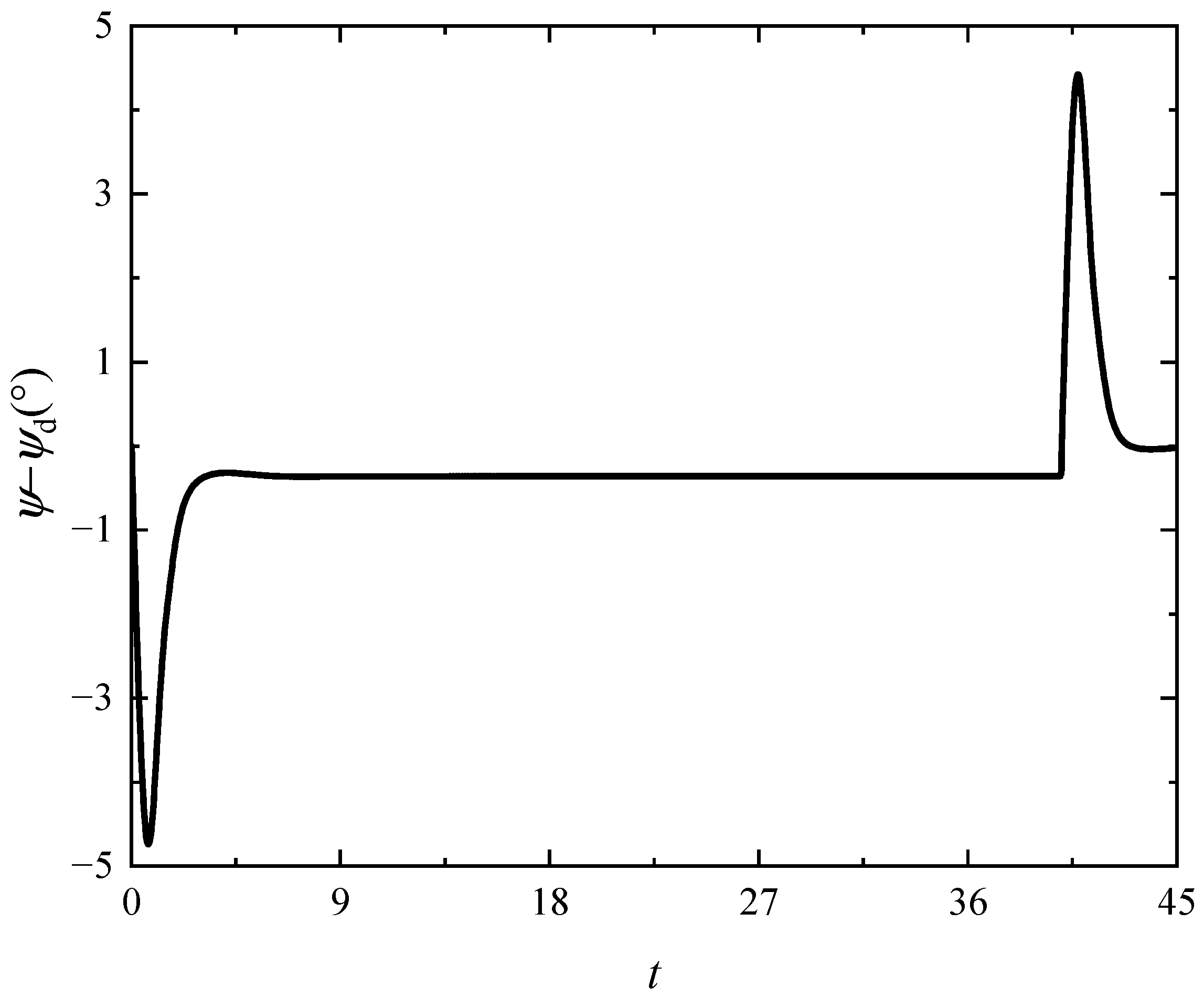
4.3. Sidestep and Pirouette
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, X. The Small-drone Revolution is Coming—Scientists Need to Ensure it Will be Safe. Nature 2025, 637, 29–30. [Google Scholar] [CrossRef]
- Grip, H.F.; Lam, J.N.; Bayard, D.; Conway, D.T.; Singh, G.; Brockers, R.; Delaune, J.; Matthies, L.; Malpica, C.; Brown, T.; et al. Flight Control System for NASA’s Mars Helicopter. In Proceedings of the AIAA Scitech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Takahashi, M.D.; Fujizawa, B.T.; Lusardi, J.A.; Whalley, M.S.; Goerzen, C.L.; Schulein, G.J.; Mielcarek, N.L.; Cleary, M.J.; Carr IV, J.P. Autonomous Guidance and Flight Control on a Partial-authority Black Hawk Helicopter. J. Aerosp. Inf. Syst. 2021, 18, 686–692. [Google Scholar] [CrossRef]
- Takahashi, M.D.; Fujizawa, B.T.; Lusardi, J.A.; Goerzen, C.L.; Cleary, M.J.; Carr IV, J.P.; Waldman, D.W. Comparison of Autonomous Flight Control Performance Between Partial- and Full-Authority Helicopters. J. Guid. Control Dyn. 2022, 45, 885–892. [Google Scholar] [CrossRef]
- Santoso, F.; Garratt, M.A.; Anavatti, S.G. State-of-the-Art Intelligent Flight Control Systems in Unmanned Aerial Vehicles. IEEE Trans. Autom. Sci. Eng. 2018, 15, 613–625. [Google Scholar] [CrossRef]
- Abdelmaksoud, S.I.; Mailah, M.; Abdallah, A.M. Control Strategies and Novel Techniques for Autonomous Rotorcraft Unmanned Aerial Vehicles: A Review. IEEE Access 2020, 8, 195142–195169. [Google Scholar] [CrossRef]
- Yan, K.; Wu, Q. Adaptive Tracking Flight Control for Unmanned Autonomous Helicopter with Full State Constraints and Actuator Faults. ISA Trans. 2022, 128 Pt B, 32–46. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Wu, Q.; Jiang, B.; Tao, G. A Reconfiguration Scheme for Quadrotor Helicopter via Simple Adaptive Control and Quantum Logic. IEEE Trans. Ind. Electron. 2015, 62, 4328–4339. [Google Scholar] [CrossRef]
- Chen, M.; Shi, P.; Lim, C.C. Adaptive Neural Fault-tolerant Control of a 3-DOF Model Helicopter System. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 260–269. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–910. [Google Scholar] [CrossRef]
- Feng, H.; Guo, B. Active Disturbance Rejection Control: Old and New Results. Annu. Rev. Control 2017, 44, 238–248. [Google Scholar] [CrossRef]
- Ren, B.; Du, S.; Cui, Z.; Xu, Y.; Zhao, Q. High-precision Trajectory Tracking Control of Helicopter Based on Ant Colony Optimization-slime Mould Algorithm. Chin. J. Aeronaut. 2025, 38, 103172. [Google Scholar] [CrossRef]
- Precup, R.E.; Nguyen, A.T.; Blažič, S. A Survey on Fuzzy Control for Mechatronics Applications. Int. J. Syst. Sci. 2024, 55, 771–813. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy Control Systems: Past, Present and Future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, Y.; Li, S.; Zhou, Y. Fuzzy Controller Design of Micro-unmanned Helicopter Relying on Improved Genetic Optimization Algorithm. Aerosp. Sci. Technol. 2020, 98, 105685. [Google Scholar] [CrossRef]
- Ma, H.; Chen, M.; Feng, G.; Wu, Q. Disturbance-Observer-Based Adaptive Fuzzy Tracking Control for Unmanned Autonomous Helicopter with Flight Boundary Constraints. IEEE Trans. Fuzzy Syst. 2023, 31, 184–198. [Google Scholar] [CrossRef]
- Zhang, X.; Zhuang, Y.; Zhang, X.; Fang, Y. A Novel Asymptotic Robust Tracking Control Strategy for Rotorcraft UAVs. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2338–2349. [Google Scholar] [CrossRef]
- ADS-33E-PRF; Aeronautical Design Standard, Handling Qualities Criteria for Military Rotorcraft. US Army: Washington, DC, USA, 2000.
- Ferguson, K.; Thomson, D. Maneuverability Assessment of a Compound Helicopter Configuration. J. Am. Helicopter Soc. 2016, 61, 012008. [Google Scholar] [CrossRef]
- Herbst, G.; Madonski, R. Tuning and Implementation Variants of Discrete-time ADRC. Control Theory Technol. 2023, 21, 72–88. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Tuning of Linear ADRC with Known Plant Information. ISA Trans. 2016, 65, 384–393. [Google Scholar] [CrossRef]
- Bai, Y.; Zhuang, H.; Wang, D. Fundamentals of Fuzzy Logic Control—Fuzzy Sets, Fuzzy Rules and Defuzzifications. In Advanced Fuzzy Logic Technologies in Industrial Applications; Springer: London, UK, 2006. [Google Scholar]
- Guerra, T.M.; Vermeiren, L. Control Laws for Takagi-Sugeno Fuzzy Models. Fuzzy Sets Syst. 2001, 120, 95–108. [Google Scholar] [CrossRef]
- Astolfi, A.; Ortega, R. Immersion and Invariance: A New Tool for Stabilization and Adaptive Control of Nonlinear Systems. IEEE Trans. Autom. Control 2003, 48, 590–606. [Google Scholar] [CrossRef]
- Zhao, B.; Xian, B.; Zhang, Y.; Zhang, X. Nonlinear Robust Adaptive Tracking Control of a Quadrotor UAV via Immersion and Invariance Methodology. IEEE Trans. Ind. Electron. 2015, 62, 2891–2902. [Google Scholar] [CrossRef]
- Zou, Y.; Meng, Z. Immersion and Invariance-based Adaptive Controller for Quadrotor Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2288–2297. [Google Scholar] [CrossRef]
- Saetti, U. Rotorcraft Simulations with Coupled Flight Dynamics, Free Wake, and Acoustics. Master’s Thesis, The Pennsylvania State University, University Park, PA, USA, 2016. [Google Scholar]
- Farrokhfal, H.; Pishevar, A.R. A New Coupled Free Wake-CFD Method for Calculation of Helicopter Rotor Flow-Field in Hover. J. Aerosp. Technol. Manag. 2014, 6, 129–147. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X.; Wang, B.; Zhao, Q. Aerodynamic and Structural Characteristics of Helicopter Rotor in Circling Flight. Chin. J. Aeronaut. 2023, 36, 282–296. [Google Scholar] [CrossRef]
- Hilbert, K.B. A Mathematical Model of the UH-60 Helicopter; NASA-TM-85890; National Aeronautics and Space Administration (NASA): Washington, DC, USA, April 1984. [Google Scholar]



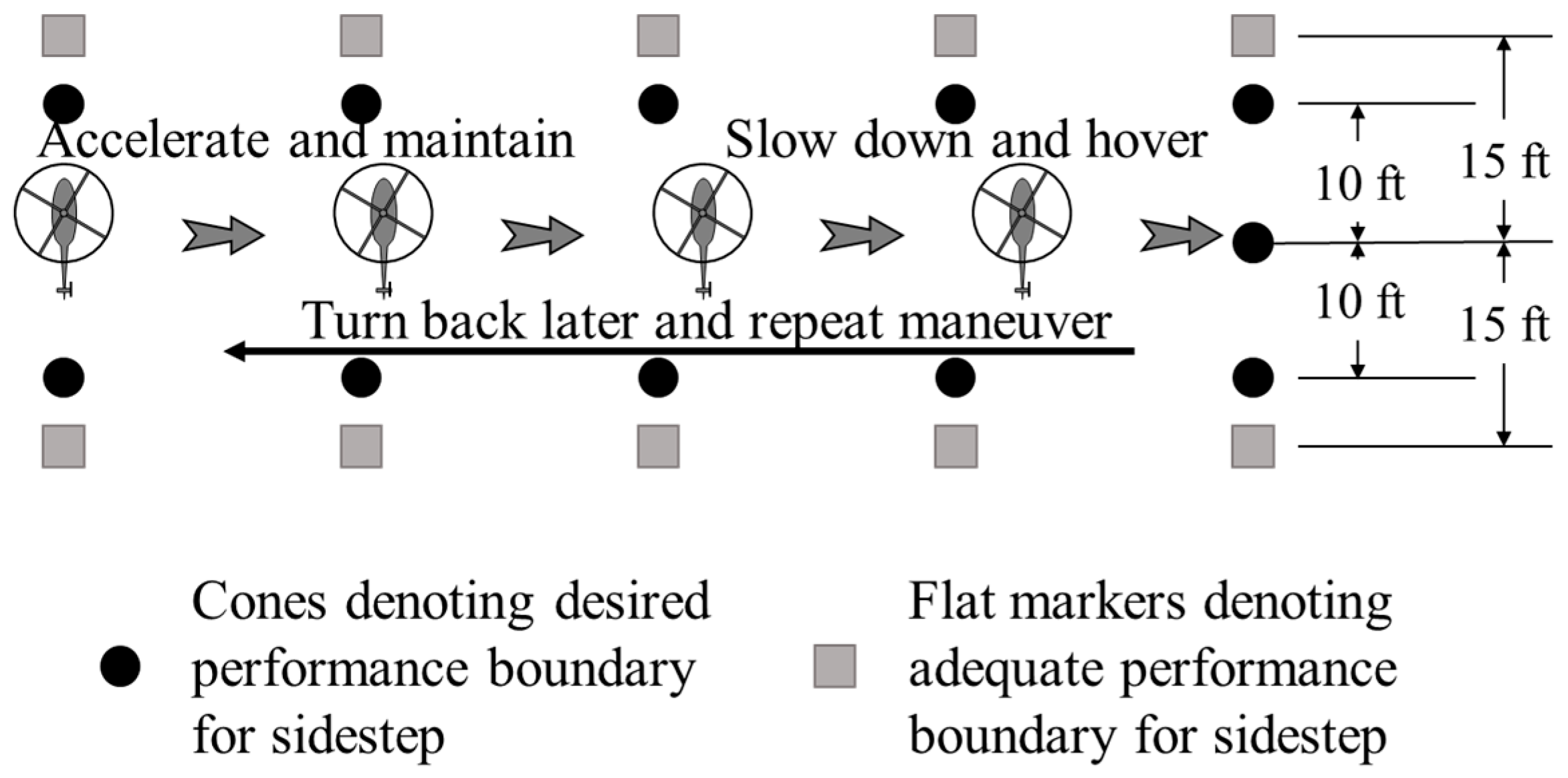


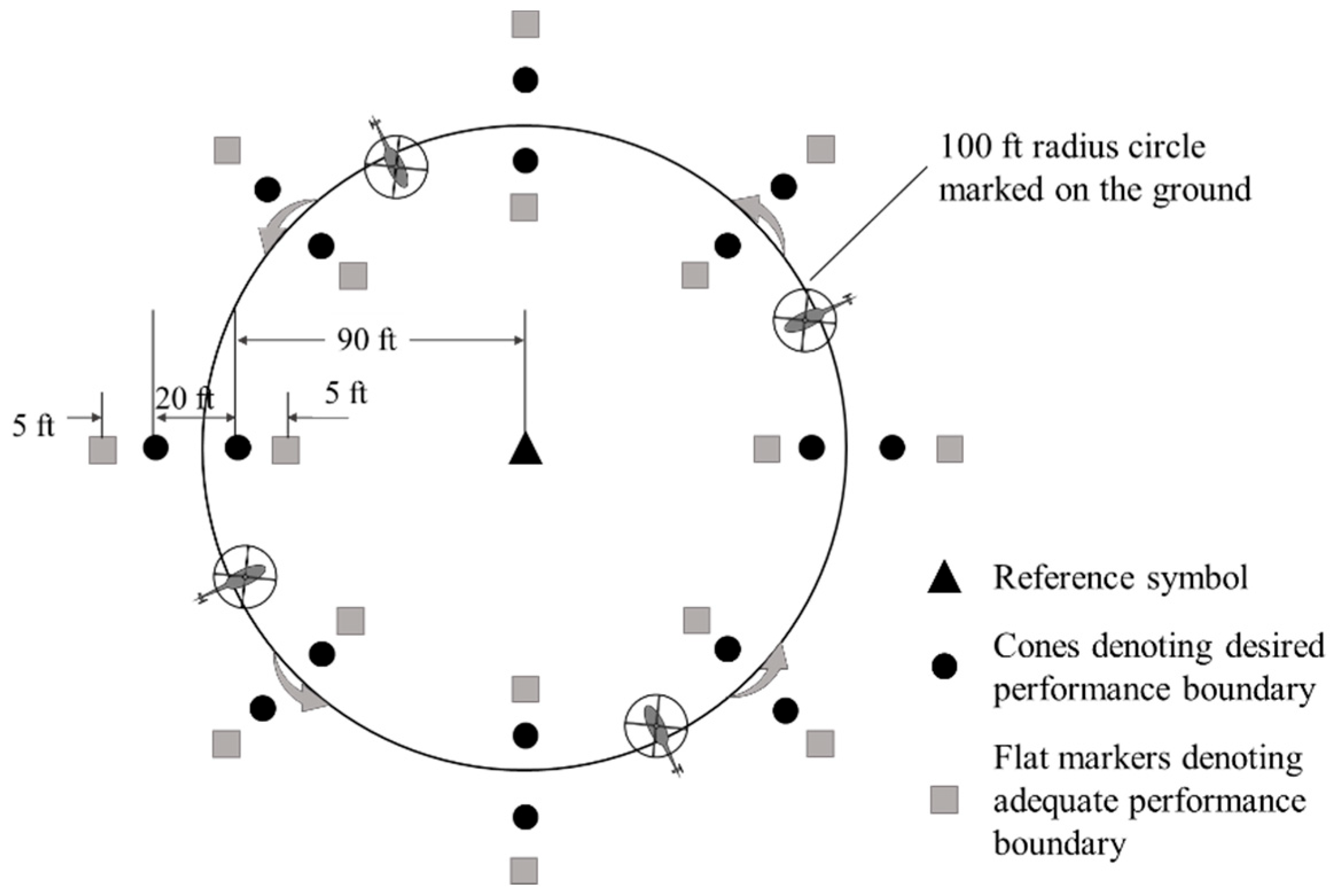

| Desired Performance | Good Visual Environments [18] | Actual Response |
|---|---|---|
| Upon initiating the maneuver, a roll angle change of at least X degrees must be achieved within 1.5 s | 25° | 41.11°/41.08° |
| Achieve a target airspeed of X knots | 40 knots | 40 knots |
| Upon commencing deceleration, a roll angle change of at least X degrees must be achieved within 1.5 s | 30° | 41.09°/41.09° |
| Maintain a selected reference point on the rotorcraft within ±X ft of the ground reference line | 10 ft | 0 |
| Maintain altitude within ±X ft at a selected altitude below 30 ft | 10 ft | 0 |
| Maintain heading within ±X deg | 10° | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Xu, Y.; Du, S.; Zhao, Q. Immersion and Invariance Adaptive Control for Unmanned Helicopter Under Maneuvering Flight. Drones 2025, 9, 565. https://doi.org/10.3390/drones9080565
Zhou X, Xu Y, Du S, Zhao Q. Immersion and Invariance Adaptive Control for Unmanned Helicopter Under Maneuvering Flight. Drones. 2025; 9(8):565. https://doi.org/10.3390/drones9080565
Chicago/Turabian StyleZhou, Xu, Yousong Xu, Siliang Du, and Qijun Zhao. 2025. "Immersion and Invariance Adaptive Control for Unmanned Helicopter Under Maneuvering Flight" Drones 9, no. 8: 565. https://doi.org/10.3390/drones9080565
APA StyleZhou, X., Xu, Y., Du, S., & Zhao, Q. (2025). Immersion and Invariance Adaptive Control for Unmanned Helicopter Under Maneuvering Flight. Drones, 9(8), 565. https://doi.org/10.3390/drones9080565







