Dynamic Obstacle Perception Technology for UAVs Based on LiDAR
Abstract
1. Introduction
2. LiDAR Point Cloud Preprocessing
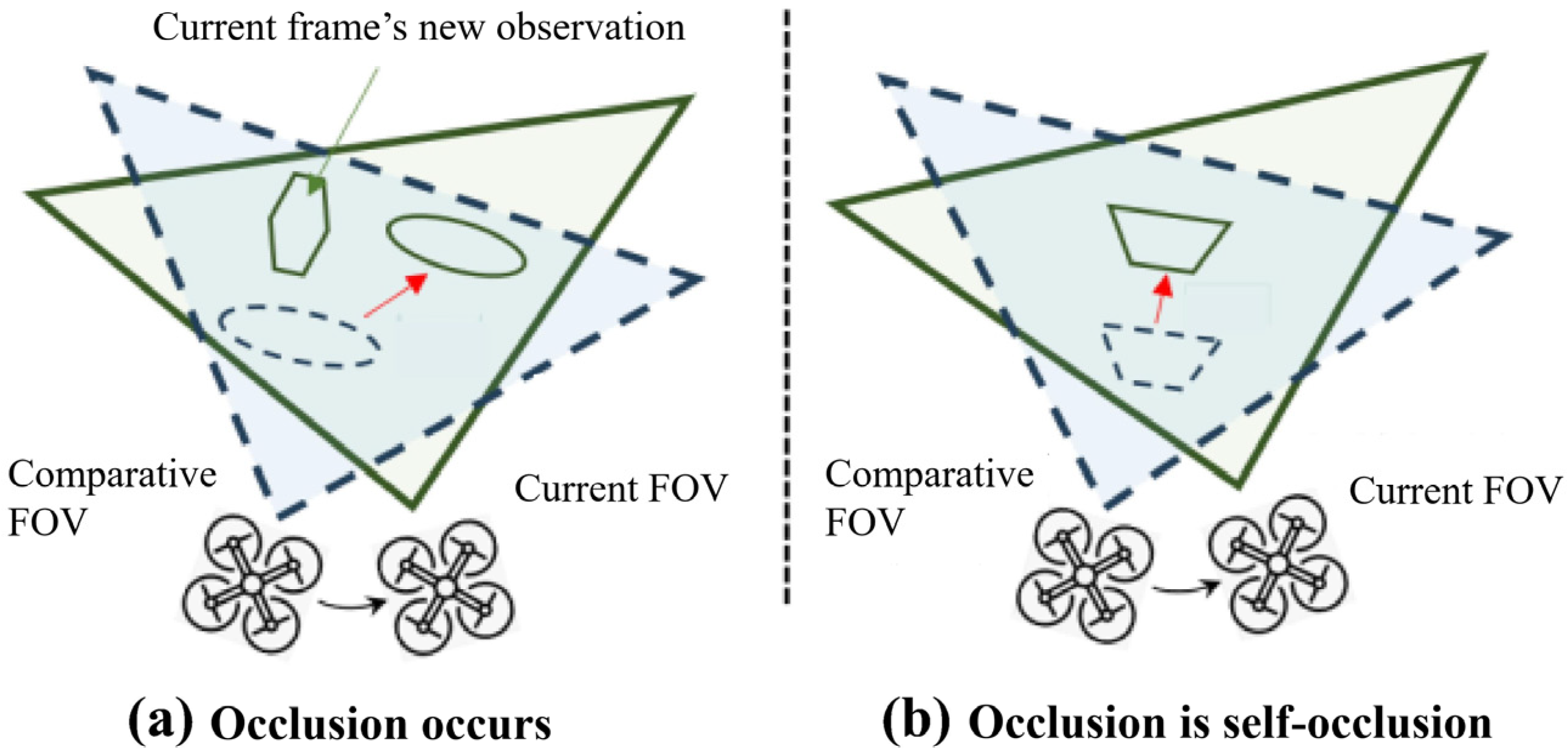
2.1. LiDAR Point Cloud Accumulation
2.2. LiDAR Point Cloud Filtering and Segmentation
3. Construction of LiDAR-Based Perception Algorithms
3.1. Point Cloud Clustering
| Algorithm 1: Point cloud clustering algorithm process |
| Input: point cloud pcl, search radius minimum number of points minPts |
| Output: clustering results 1: Foreach p in pcl do 2: if p.cluster_id undefined then continue 3: Neighbor N RangeQuery(pcl, p, ) 4: if |N| < minPts then 5: p.cluster_id Noise 6: continue 7: id next cluster id 8: p.cluster_id id 9: Seed set S N/{p} 10: Foreach q in S do 11: if q.cluster_id = Noise then q.cluster_id id 12: if q.cluster_id undefined then continue 13: Neighbors N RangeQuery(pcl, q, ) 14: q.cluster_id id 15: if |N| < minPts then continue 16: S S N |
3.2. Generation of Grids
| Algorithm 2: Dynamic point cloud cluster identification strategy based on point motion properties |
| Input: point cloud cluster , point cloud at seconds Input: point velocity threshold , absolute threshold , relative threshold |
| Output: clustering results 1: Foreach cluster c in do 2: Count dyn, total reset 3: Foreach point p in c do 4: if not Is_valid(p) then continue 5: total total + 1 6: Velocity Distance 7: if then dyn dyn + 1 8: if dyn or dyn then 9: label(c) dynamic 10: if not Is_consistent(c) then 11: label(c) uncertain |
3.3. Representation and Tracking of Dynamic Point Cloud
4. Experiments and Analysis
4.1. Simulation Platform and Flight Condition Settings
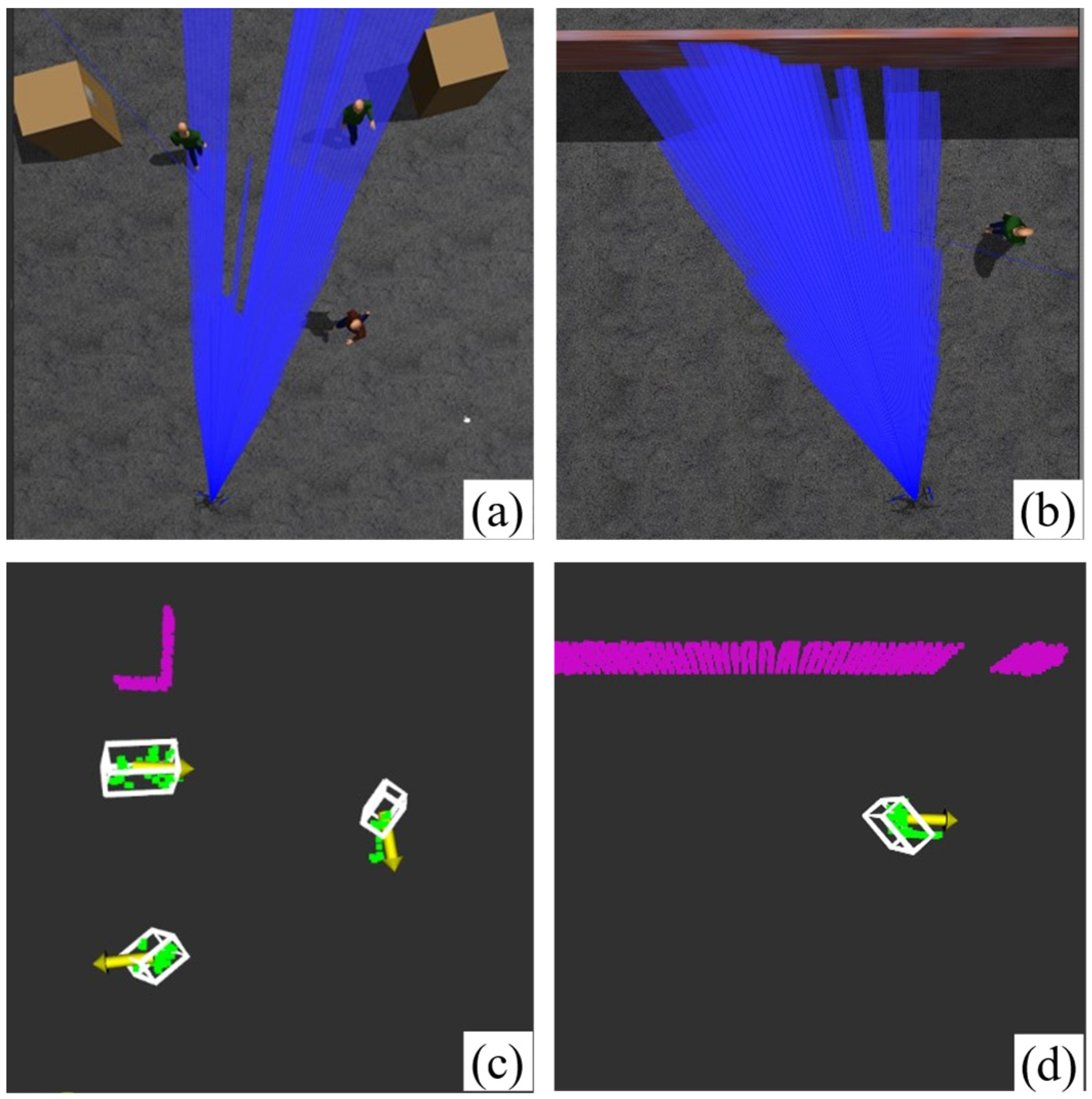
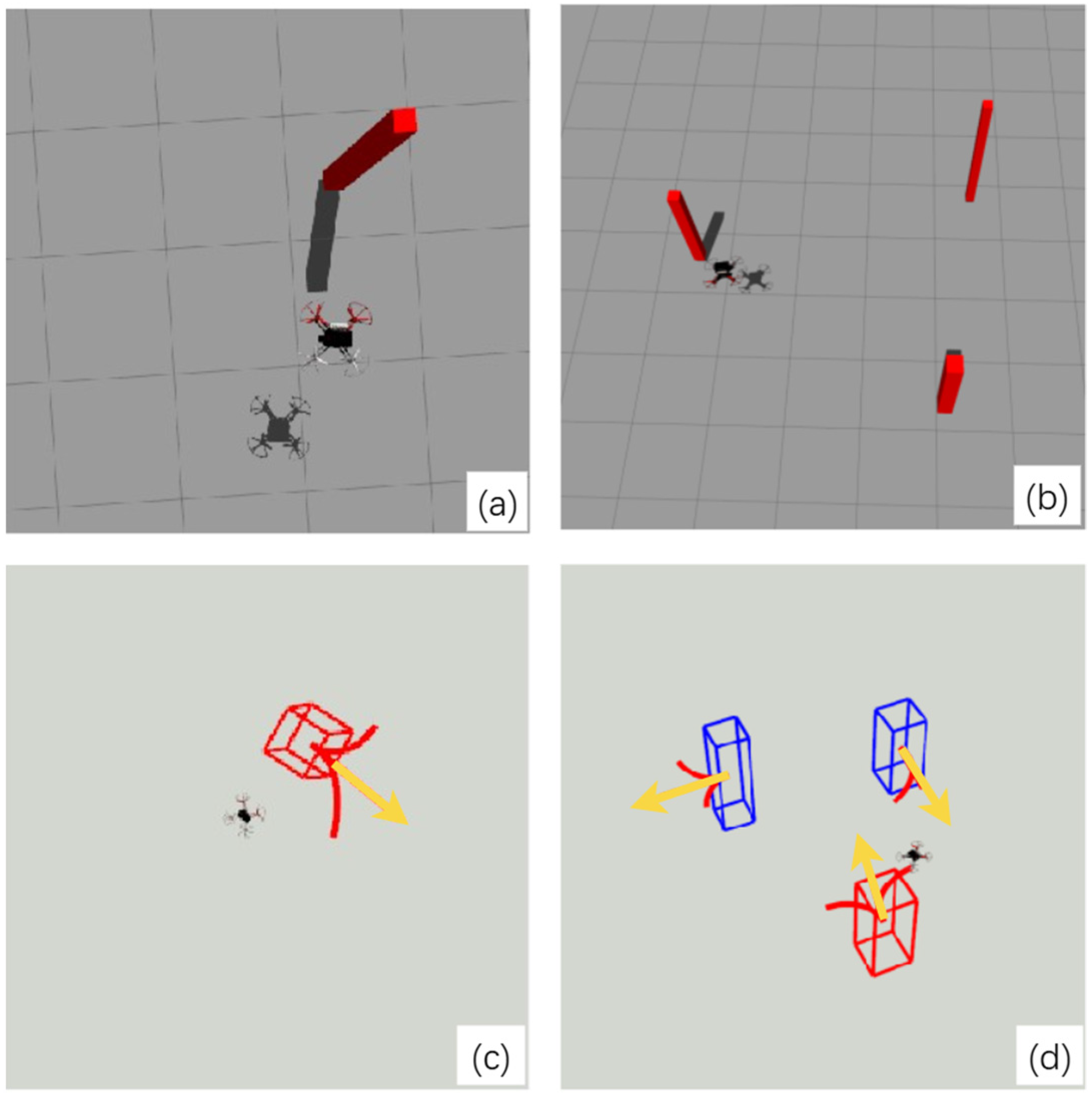
4.2. Comparison of Dynamic Obstacle Detection Results
4.3. Comparison of Motion Estimation Accuracy
4.4. Flight Test Validation
5. Conclusions
- (1)
- The proposed method achieves good dynamic obstacle perception results in simulation environments, demonstrating an improvement of approximately 15–20% in dynamic obstacle detection and motion estimation compared to previously proposed methods.
- (2)
- Flight tests demonstrate the effectiveness and practicality of the proposed LiDAR-based dynamic obstacle perception algorithm, which maintains robust perception capabilities in complex outdoor dynamic scenes, including random pedestrian movements and multiple moving pedestrians.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, L.; Fasano, G.; Carrio, A.; Lei, M.; Bavle, H.; Campoy, P. A comprehensive survey on non-cooperative collision avoidance for micro aerial vehicles: Sensing and obstacle detection. J. Field Robot. 2023, 40, 1697–1720. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Z.; Ye, H.; Xu, C.; Gao, F. Ego-planner: An esdf-free gradient-based local planner for quadrotors. IEEE Robot. Autom. Lett. 2020, 6, 478–485. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and efficient quadrotor trajectory generation for fast autonomous flight. IEEE Robot. Autom. Lett. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Yu, Q.; Qin, C.; Luo, L.; Liu, H.; Hu, S. CPA-Planner: Motion Planner with Complete Perception Awareness for Sensing-Limited Quadrotors. IEEE Robot. Autom. Lett. 2022, 8, 720–727. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Hui, Y.; Shen, H.; Xu, L.; Tian, B. Rapa-planner: Robust and efficient motion planning for quadrotors based on parallel ra-mppi. IEEE Trans. Ind. Electron. 2024, 72, 7149–7159. [Google Scholar] [CrossRef]
- Davide, F.; Kevin, K.; Davide, S. Dynamic obstacle avoidance for quadrotors with event cameras. Sci. Robot. 2020, 5, 13–27. [Google Scholar] [CrossRef]
- He, B.; Li, H.; Wu, S.; Wang, D.; Zhang, Z.; Dong, Q.; Xu, C.; Gao, F. Fast-dynamic-vision: Detection and tracking dynamic objects with event and depth sensing. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 3071–3078. [Google Scholar][Green Version]
- Iddrisu, K.; Shariff, W.; Corcoran, P.; O’Connor, N.E.; Lemley, J.; Little, S. Event camera based eye motion analysis: A survey. IEEE Access 2024, 12, 136783–136804. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, H.; Alonso-Mora, J. Robust vision-based obstacle avoidance for micro aerial vehicles in dynamic environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE Press: Piscataway, NJ, USA, 2020; pp. 2682–2688. [Google Scholar][Green Version]
- Oleynikova, H.; Honegger, D.; Pollefeys, M. Reactive avoidance using embedded stereo vision for MAV flight. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, DC, USA, 26–30 May 2015; IEEE Press: Piscataway, NJ, USA, 2015; pp. 50–56. [Google Scholar][Green Version]
- Tai, L.; Li, S.; Liu, M. A deep-network solution towards model-less obstacle avoidance. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE Press: Piscataway, NJ, USA, 2016; pp. 2759–2764. [Google Scholar][Green Version]
- Xu, Z.; Shi, H.; Li, N.; Xiang, C.; Zhou, H. Vehicle detection under UAV based on optimal dense YOLO method. In Proceedings of the 2018 5th International Conference on Systems and Informatics (ICSAI), Nanjing, China, 10–12 November 2018; IEEE Press: Piscataway, NJ, USA, 2018; pp. 407–411. [Google Scholar][Green Version]
- Mori, T.; Scherer, S. First results in detecting and avoiding frontal obstacles from a monocular camera for micro unmanned aerial vehicles. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE Press: Piscataway, NJ, USA, 2013; pp. 1750–1757. [Google Scholar][Green Version]
- Xu, Z.; Zhan, X.; Chen, B.; Xiu, Y.; Yang, C.; Shimada, K. A real-time dynamic obstacle tracking and mapping system for UAV navigation and collision avoidance with an RGB-D camera. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE Press: Piscataway, NJ, USA, 2023; pp. 10645–10651. [Google Scholar][Green Version]
- Li, J.; Li, Y.; Zhang, S.; Chen, Y. Image-point cloud embedding network for simultaneous image-based farmland instance extraction and point cloud-based semantic segmentation. Int. J. Appl. Earth Obs. Geoinf. 2025, 136, 104361. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. Lvi-sam: Tightly-coupled lidar-visual-inertial odometry via smoothing and mapping. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 5692–5698. [Google Scholar][Green Version]
- Ren, Y.; Zhu, F.; Liu, W.; Wang, Z.; Lin, Y.; Gao, F. Bubble planner: Planning high-speed smooth quadrotor trajectories using receding corridor. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE Press: Piscataway, NJ, USA, 2022; pp. 6332–6339. [Google Scholar][Green Version]
- Kong, F.; Xu, W.; Cai, Y.; Zhang, F. Avoiding dynamic small obstacles with onboard sensing and computation on aerial robots. IEEE Robot. Autom. Lett. 2021, 6, 7869–7876. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, J.; Wang, Q.; Xu, C.; Gao, F. Autonomous flights in dynamic environments with onboard vision. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; IEEE Press: Piscataway, NJ, USA, 2021; pp. 1966–1973. [Google Scholar][Green Version]
- Tordesillas, J.; How, J.P. PANTHER: Perception-aware trajectory planner in dynamic environments. IEEE Access 2022, 10, 22662–22677. [Google Scholar] [CrossRef]
- Eppenberger, T.; Cesari, G.; Dymczyk, M.; Siegwart, R.; Dubé, R. Leveraging stereo-camera data for real-time dynamic obstacle detection and tracking. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; IEEE Press: Piscataway, NJ, USA, 2020; pp. 10528–10535. [Google Scholar][Green Version]
- Chen, H.; Lu, P. Real-time identification and avoidance of simultaneous static and dynamic obstacles on point cloud for UAVs navigation. Robot. Auton. Syst. 2022, 154, 104124. [Google Scholar] [CrossRef]
- Chen, X.; Mersch, B.; Nunes, L.; Marcuzzi, R. Automatic labeling to generate training data for online LiDAR-based moving object segmentation. IEEE Robot. Autom. Lett. 2022, 7, 6107–6114. [Google Scholar] [CrossRef]
- Mersch, B.; Chen, X.; Vizzo, I.; Nunes, L.; Behley, J.; Stachniss, C. Receding moving object segmentation in 3d lidar data using sparse 4d convolutions. IEEE Robot. Autom. Lett. 2022, 7, 7503–7510. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar][Green Version]
- Bernardin, K.; Elbs, A.; Stiefelhagen, R. Multiple object tracking performance metrics and evaluation in a smart room environment. In Proceedings of the Sixth IEEE International Workshop on Visual Surveillance, in Conjunction with ECCV, Graz, Austria, 13 May 2006; Citeseer Press: Princeton, NJ, USA, 2006; p. 90. [Google Scholar][Green Version]
- Cheng, H.; Zhang, X.T.; Fang, Y.Q. Target tracking estimation based on diffusion Kalman filtering algorithm. Comput. Appl. Softw. 2021, 38, 191–197+238. (In Chinese) [Google Scholar]






| Parameter | Value | Description of Influence on Detection Quality |
|---|---|---|
| Maximum Effective Range | 12 m | Limits the perception distance; affects the ability to detect distant obstacles. |
| Minimum Effective Range | 0.2 m | Affects the system’s ability to perceive nearby objects, which is critical for short-range collision avoidance. |
| Horizontal Samples | 300 | Determines the density of horizontal point cloud; higher values improve object contour resolution. |
| Vertical Samples | 40 | Affects vertical resolution of the point cloud, crucial for detecting obstacles of varying height. |
| Range Data Resolution | 0.002 m | Defines the precision of distance measurement, influencing localization accuracy. |
| Dynamic Obstacle Detection | Miss Rate (%) | False Positive Rate (%) | Mismatch Rate (%) | MOTA (%) |
|---|---|---|---|---|
| Reference 16 | 5.4 | 9.2 | 10.6 | 74.8 |
| Reference 18 | 7.7 | 8.3 | 8.6 | 75.4 |
| Our method | 3.5 | 5.0 | 4.2 | 87.3 |
| Motion Estimation Method | Position Estimation Errors (m) | Speed Estimation Errors (m/s) |
|---|---|---|
| [28] | 0.45 | 0.55 |
| Our method | 0.32 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, W.; Song, F.; Peng, Z. Dynamic Obstacle Perception Technology for UAVs Based on LiDAR. Drones 2025, 9, 540. https://doi.org/10.3390/drones9080540
Xia W, Song F, Peng Z. Dynamic Obstacle Perception Technology for UAVs Based on LiDAR. Drones. 2025; 9(8):540. https://doi.org/10.3390/drones9080540
Chicago/Turabian StyleXia, Wei, Feifei Song, and Zimeng Peng. 2025. "Dynamic Obstacle Perception Technology for UAVs Based on LiDAR" Drones 9, no. 8: 540. https://doi.org/10.3390/drones9080540
APA StyleXia, W., Song, F., & Peng, Z. (2025). Dynamic Obstacle Perception Technology for UAVs Based on LiDAR. Drones, 9(8), 540. https://doi.org/10.3390/drones9080540






