Abstract
The reliability of unmanned aerial vehicle (UAV) energy storage battery systems is critical for ensuring their safe operation and efficient mission execution, and has the potential to significantly advance applications in logistics, monitoring, and emergency response. This paper reviews theoretical and technical advancements in UAV battery reliability, covering definitions and metrics, modeling approaches, state estimation, fault diagnosis, and battery management system (BMS) technologies. Based on international standards, reliability encompasses performance stability, environmental adaptability, and safety redundancy, encompassing metrics such as the capacity retention rate, mean time between failures (MTBF), and thermal runaway warning time. Modeling methods for reliability include mathematical, data-driven, and hybrid models, which are evaluated for accuracy and efficiency under dynamic conditions. State estimation focuses on five key battery parameters and compares neural network, regression, and optimization algorithms in complex flight scenarios. Fault diagnosis involves feature extraction, time-series modeling, and probabilistic inference, with multimodal fusion strategies being proposed for faults like overcharge and thermal runaway. BMS technologies include state monitoring, protection, and optimization, and balancing strategies and the potential of intelligent algorithms are being explored. Challenges in this field include non-unified standards, limited model generalization, and complexity in diagnosing concurrent faults. Future research should prioritize multi-physics-coupled modeling, AI-driven predictive techniques, and cybersecurity to enhance the reliability and intelligence of battery systems in order to support the sustainable development of unmanned systems.
1. Introduction
Amid the global transition toward low-carbon and intelligent energy systems, unmanned aerial systems (UASs) have emerged as critical enablers for smart cities, logistics, emergency response, and environmental monitoring [1]. The International Civil Aviation Organization (ICAO) forecasts a 10-fold increase in the number of global civilian UAVs by 2030, with electric multirotor drones dominating the market [2]. However, as UAVs are increasingly deployed in complex environments, the reliability of their battery systems has become a critical concern, as it directly impacts flight safety and mission success rates and poses stringent demands on the safety, stability, and consistency of UAVs [3]. Developing a systematic theoretical and engineering framework for assessing UAV battery reliability is essential for ensuring low-altitude airspace safety and enhancing the operational efficiency of unmanned systems.
Diverse application scenarios impose varied and stringent requirements on UAV battery reliability. For instance, logistics drones like the Amazon Prime Air drone require their batteries to retain over 80% capacity after 500 charge–discharge cycles and withstand mechanical shocks from 20 takeoffs and landings per hour [4]. Military drones, such as the MQ-9 Reaper, demand batteries that support 5C high-rate discharge in extreme temperatures ranging from −40 °C to 65 °C to ensure rapid mission response [5]. A 2022 commercial UAV crash highlighted the consequences of reliability failures, where localized overheating in a battery pack under a temperature differential exceeding 15 °C led to state-of-charge (SOC) misestimation, triggering erroneous battery management system (BMS) protection mechanisms and resulting in flight control loss. This incident underscores deficiencies in thermal management, cell consistency, and BMS integration strategies.
International and industry standards provide fundamental guidance for battery reliability. For example, the United Nations Manual of Tests and Criteria (Part III, Sub-Section 38.3) requires lithium batteries to undergo laboratory tests such as high- and low-temperature cycling, vibration, and short circuiting prior to transportation, with a focus on verifying their physical safety during transit. The Airworthiness Standards for Medium Civil Unmanned Aircraft Systems (MH/T 6043-2021) [6] issued by the Civil Aviation Administration of China mandates endurance flight tests under real operational conditions to assess the long-term stability and reliability of batteries. Additionally, the Technical Requirements for Electric Multirotor Unmanned Aircraft Systems for Urban Logistics Scenarios (T/CAAC 002—2022) [7] stipulates that batteries must possess a power redundancy capacity of 25% to ensure emergency capabilities in complex urban environments.
These three standards exhibit significant differences in their testing environments, validation methods, and performance criteria. For instance, UN 38.3 emphasizes individual physical tests conducted under standardized laboratory conditions; MH/T 6043-2021 focuses on a comprehensive evaluation of battery degradation during flight missions; and T/CAAC 002—2022 introduces scenario-specific requirements for performance redundancy. Such disparities necessitate that manufacturers develop and adapt distinct battery system testing and certification processes depending on the target country or application scenario, thereby complicating efforts to meet multi-regional regulatory requirements in a unified manner [8]. Therefore, it is imperative to establish a reliability evaluation framework for battery systems that is applicable across multiple operating conditions, performance metrics, and regions to support the globally consistent deployment and regulatory compliance of unmanned aerial vehicle battery management systems.
Quantifying the reliability of UAV batteries requires a multilevel, multidimensional metric system. At the cell level, the cycle life and capacity retention rate are core indicators. At the system level, the availability (mean time between failures, MTBF) and mission completion rate are more practical, with commercial UAVs often requiring a battery system availability that exceeds 98% annually [9]. Recent advancements in artificial intelligence have driven the development of predictive metrics, such as state-of-health (SOH) and remaining useful life (RUL), with advanced algorithms reducing estimation errors to within 3% and enabling a shift from reactive to proactive maintenance [10]. Nevertheless, most metrics are derived from controlled laboratory conditions, which results in researchers struggling to address complex real-world scenarios that involve high temperatures, high altitudes, and strong electromagnetic interference. A dynamic adaptability evaluation framework remains a critical research gap.
Reliability modeling underpins the state assessment of UAV battery systems. Electrochemical models that couple the Butler–Volmer equation with diffusion theory accurately simulate internal reactions, which makes them suitable for extreme condition analysis. However, their computational intensity, requiring hours for a single simulation, limits real-time applications [11]. Equivalent circuit models (ECMs) offer millisecond-level responses, which supports embedded flight control systems, but their depiction of aging mechanisms is limited [12]. Data-driven models that leverage superior temporal learning capabilities achieve high accuracy in state-of-health and remaining useful life predictions, yet rely heavily on high-quality training data [13]. Multiscale coupled models, which integrate electrochemical mechanisms with data-driven approaches, enhance SOH assessment accuracy [14]. Nonetheless, model generalization across operating conditions and online deployment capabilities require further improvement.
The accurate estimation of battery state parameters is central to UAV battery reliability. The use of traditional ampere-hour integration for state-of-charge estimation yields errors up to 10%, whereas extended Kalman filtering (EKF) significantly reduces the amount of errors when it is adapted to dynamic flight scenarios [15]. In fault diagnosis, acoustic emission sensing can predict lithium plating faults 30 min in advance, with a sensitivity that is five times higher than that of voltage monitoring [16]. Infrared thermography combined with convolutional neural networks (CNNs) detects micron-scale separator defects [17]. However, concurrent fault scenarios, such as overcharge and thermal runaway, result in feature overlap, causing misclassification rates up to 15% and necessitating multimodal fusion algorithms to improve their diagnostic specificity [18].
The battery management system serves as a critical safeguard for UAV battery reliability. Hardware-wise, active balancing circuits enhance pack capacity utilization [19]. Algorithmically, distributed BMSs with machine learning improve the SOH prediction accuracy while preserving data privacy. Cutting-edge digital twin technology, which synchronizes physical and virtual models in real time, significantly reduces fault response times [20]. However, BMS cybersecurity is increasingly critical, with a rising number of network attacks targeting battery systems, which underscores the need for robust intrinsic security mechanisms.
Current research on UAV battery reliability faces multiple challenges:
- Fragmented reliability standards with varying definitions and the lack of a unified framework;
- Disjointed modeling approaches, with electrochemical, ECM, and data-driven models failing to achieve effective integration, which limits their generalization;
- Fault diagnosis being largely confined to single-fault scenarios, and struggling with complex features of concurrent faults like overcharge and thermal runaway as a result;
- Underdeveloped BMS research in edge computing, cybersecurity, and real-time balancing strategies that inadequately addresses highly dynamic flight demands.
This paper systematically elucidates key technologies for UAV battery reliability, with the following contributions:
- A comprehensive review of reliability modeling methods, including mathematical, data-driven, and hybrid models, and an analysis of their applicability and limitations under complex conditions;
- An in-depth exploration of state estimation techniques for five key battery parameters and fault diagnosis methods;
- A systematic analysis of UAV BMS architecture and active balancing strategies, with trends toward intelligent management being envisioned, which provides theoretical guidance and practical references for safe and efficient UAV battery operation.
This paper is organized as follows: Section 2 defines UAV battery reliability and metrics. Section 3 reviews the state of reliability modeling. Section 4 discusses state estimation, fault diagnosis, and early warning. Section 5 addresses BMS architecture and balancing strategies. Figure 1 details the UAV battery reliability review in this paper. Finally, Section 6 summarizes the findings and outlines future research directions.
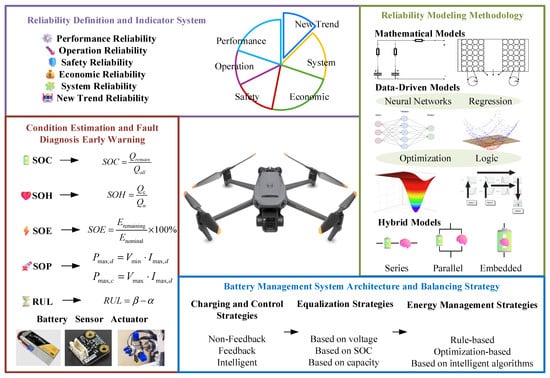
Figure 1.
A review of UAV battery reliability.
2. Definition and Metrics of Unmanned Aerial Vehicle Battery Reliability
2.1. Definition of Drone Battery Reliability by International Organizations
The definition of reliability for unmanned aerial vehicle battery systems has evolved with the diversification of application scenarios. The International Electrotechnical Commission (IEC) standard IEC 62619 [21] indirectly supports battery system reliability through safety requirements, focusing on performance under extreme conditions such as short circuits, overcharging, and thermal abuse to prevent explosions or fires, which aligns with UAV safety and stability needs [22]. The International Civil Aviation Organization (ICAO) [23], in its Technical Specifications for Unmanned Aircraft Systems, emphasizes dynamic reliability in high-altitude and vibrational environments, which requires a stable performance output under complex flight conditions [24]. The Institute of Electrical and Electronics Engineers (IEEE) explores mission reliability, modeling the relationship between battery failure rates and mission success rates to ensure high completion rates. These varied definitions reflect multidimensional evaluations of UAV battery performance across standards.
Differences in safety redundancy requirements significantly influence UAV battery design specifications. IEC 62619 mandates multiple protection mechanisms, such as overcharging and overheating safeguards, to address sudden failures, reflecting a conservative design approach. In contrast, IEEE 1625 [25] favors risk-based, system-level safety designs without mandating specific protection levels, offering greater flexibility. These differences manifest in market applications: European markets typically adopt IEC’s stringent safety standards, while U.S. markets prefer IEEE’s adaptable frameworks. Additionally, China’s GB/T 34131-2023 Technical [26] Requirements for Civil UAV Batteries impose strict criteria for cycle life and fast charging, requiring batteries to maintain a specified capacity after a defined number of cycles and complete rapid charging within set times, and addresses reliability demands for high-frequency mission scenarios.
The reliability of unmanned aerial vehicle battery systems is defined as the system’s ability to maintain the expected performance levels throughout its lifecycle under specified environmental conditions and flight scenarios. This comprehensive concept encompasses five core dimensions. Additionally, a six-dimensional radar chart that integrates emerging trends in reliability metrics for evaluating UAV battery reliability is presented in Figure 2.
- Performance reliability: The battery must achieve a cycle life of at least 500 charge–discharge cycles while maintaining the designed capacity, retaining ≥80% of its initial capacity after 500 cycles. Power output fluctuations should be constrained within ±5% under rated conditions, and the calendar life should exceed 5 years;
- Operational reliability: The battery must exhibit environmental adaptability, operating effectively within a temperature range from −20 °C to 50 °C and from 20% to 95% relative humidity (non-condensing). For its dynamic response, it should maintain ≥90% power output during load transitions from 2C to 5C discharge. Continuous operation is reflected by a single-flight availability of ≥95% and a mean time between failures (MTBF) of ≥5000 h;
- Safety reliability: The system must incorporate fault tolerance and ensure that single-cell failures do not compromise the system’s overall operation through an N + 1 redundancy design. For thermal runaway protection, a warning time of ≥5 min and a propagation suppression time of ≥15 min are required. Electromagnetic interference resistance must ensure no performance degradation under a 10 kV/m field strength;
- Economic reliability: The lifecycle cost per flight should be ≤0.05 USD/Wh, and the maintenance costs should not exceed 10% of the total costs. The recycling rate should reach ≥80%;
- System-level reliability: The battery system must comply with communication protocols such as ISO 21895 [27] to ensure interoperability. Mission support requires a power response time of ≤100 ms to meet rapid takeoff and landing demands. Module consistency means a voltage deviation of ≤50 mV and a temperature difference of ≤3 °C.
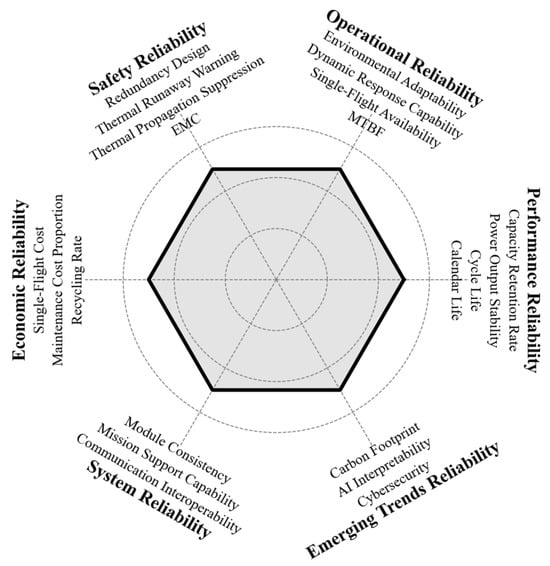
Figure 2.
Six-dimensional radar chart for unmanned aerial vehicle battery reliability evaluation.
In summary, the reliability of unmanned aerial vehicle battery systems is defined as the system’s ability to consistently maintain the designed performance, safe operation, and economic viability throughout its lifecycle under specified environmental conditions and flight scenarios. This multifaceted concept encompasses five core dimensions: performance reliability, covering capacity, power, and lifespan metrics; operational reliability, which includes environmental adaptability, dynamic response, and availability; safety reliability, which includes redundancy design, thermal runaway protection, and electromagnetic compatibility; economic reliability, which is reflected in the flight costs, maintenance expenses, and recycling efficiency; and system-level reliability, which involves interoperability, mission support, and module consistency. Furthermore, reliability distinctions include inherent reliability, operational reliability, and environmental reliability, extending to emerging aspects such as cybersecurity, the interpretability of state prediction models, and sustainability. Together, these form an integrated assurance system that balances performance, safety, and economic considerations.
2.2. Indicators of UAV Battery Reliability
To comprehensively evaluate the stability and availability of unmanned aerial vehicle battery systems across diverse flight scenarios, the multidimensional reliability metrics framework is essential. As shown in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, this framework encompasses five core dimensions—performance reliability, operational reliability, safety reliability, economic reliability, and system-level reliability—while extending to emerging requirements such as cybersecurity, artificial intelligence interpretability, and sustainability. The performance dimension reflects the battery’s sustained capabilities in terms of its capacity, power output, cycle life, and calendar life. The operational dimension addresses its adaptability to external conditions, including temperature, humidity, high altitudes, and vibration, as well as its stability in high-frequency missions. The safety dimension emphasizes fault tolerance, thermal runaway protection, and electromagnetic compatibility to ensure safe operation under extreme conditions. The economic dimension evaluates the lifecycle cost-effectiveness through metrics such as the per-flight cost, maintenance expenses, and material recycling rate. The system-level dimension focuses on inter-module communication compatibility, mission support capabilities, and cell consistency to ensure efficient system coordination. This comprehensive metrics system aligns with standards such as IEC 62619, IEEE P2836 [28], and China’s GB/T 34131, providing quantitative benchmarks and decision-making support for UAV battery design optimization, reliability assessment, and lifecycle management.

Table 1.
Performance reliability indicators.

Table 2.
Operational Reliability Indicators.

Table 3.
Safety Reliability Indicators.

Table 4.
Economic Reliability Indicators.

Table 5.
System Reliability Indicators.

Table 6.
Emerging Trends in Reliability Indicators.
3. Reliability Modeling Methods for UAV Batteries
As UAV batteries are the core component responsible for ensuring endurance and flight safety, their performance, lifespan, and safety status require accurate prediction and control, which depend critically on appropriate modeling and simulation. Battery modeling aims to describe dynamic processes such as electrochemical reactions, thermal behavior, and degradation mechanisms through mathematical or physical representations. With the rapid expansion of UAV applications in fields such as logistics, surveying, and emergency response, battery models are required to simultaneously achieve high accuracy, low computational complexity, and scalability so that they can adapt to dynamic flight scenarios. As illustrated in Figure 3, which is based on modeling principles and levels of fidelity, the mainstream battery modeling approaches can be broadly classified into three categories: mathematical models (white-box models), data-driven models (black-box models), and hybrid models (grey-box models).
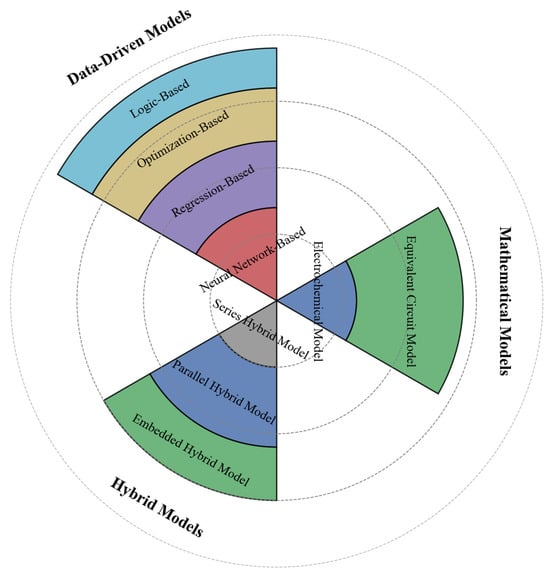
Figure 3.
Comparison of drone battery reliability modeling methods.
3.1. Mathematical Models
Mathematical models are constructed based on the multi-physical processes that occur within UAV energy storage batteries, including electrochemical reactions, thermal conduction, mechanical stress, and aging mechanisms. These models aim to accurately capture the intrinsic behavior of batteries during UAV operations. Mathematical models offer strong interpretability and predictive capability, playing a critical role in battery structural design, flight performance evaluation, safety analysis, and lifespan prediction. According to modeling approaches and levels of data dependence, battery models can be classified into three main types:
- Mathematical models, such as the Newman electrochemical model, equivalent circuit models, and thermal models, which are based on physical mechanisms and emphasize mechanistic interpretability;
- Data-driven models, which rely on extensive operational data (e.g., voltage, current, and temperature) collected during flight missions and are constructed using machine learning or statistical methods, which makes them suitable for complex, nonlinear scenarios;
- Hybrid models, which integrate the mechanistic foundation of mathematical models with the adaptability of data-driven models and thereby balance interpretability and predictive accuracy.
These models can be employed individually or coupled together to form multi-physics or multi-method frameworks, which enables their adaptation to varying precision and computational complexity requirements for UAV applications across different flight missions.
3.1.1. Electrochemical Models
- Pseudo-Two-Dimensional Model
For unmanned aerial vehicle systems that operate under highly dynamic flight conditions, the pseudo-two-dimensional (P2D) model enables the detailed simulation of internal electrochemical processes within the battery and thereby provides a theoretical foundation for optimizing battery performance under high-rate discharge and frequent load fluctuations.
The pseudo-two-dimensional model of lithium-ion batteries, as illustrated in Figure 4, was proposed by Newman, M. Doyle, and co-workers. This model describes key physical and chemical processes, including lithium-ion diffusion in the electrolyte, electrode reaction kinetics, ohmic behavior, charge conservation, and mass conservation [30].
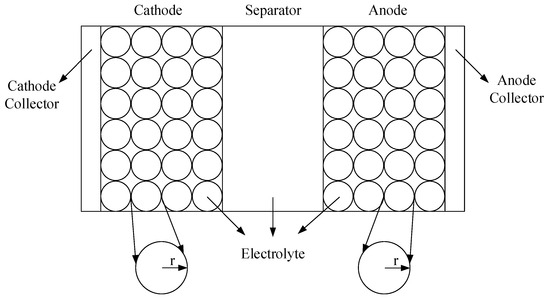
Figure 4.
Pseudo-two-dimensional (P2D) model.
The P2D model is capable of simultaneously describing both the internal and external characteristics of lithium-ion batteries. M. Rosas et al. developed a P2D model for lithium manganese oxide (LMO) batteries and validated it under dynamic conditions [31]. Zhang Q. et al. employed the P2D model to simulate the charge distribution in lithium cobalt oxide (LCO) electrodes and introduced a semi-empirical treatment of the symmetry factor in the reaction kinetics equations, demonstrating the model’s applicability for the electrode analysis of LCO materials [32]. T. T. Sara et al. proposed a model based on the particle radii of both the anode and cathode, and established a P2D model for 18650-format lithium iron phosphate (LFP) batteries [33]. The parameters in the P2D model have clear physical significance, allowing the model to capture the internal states of lithium-ion batteries during charge and discharge processes. Therefore, the P2D model is particularly well-suited for the micro-scale investigation of lithium-ion battery behavior.
In unmanned aerial vehicle systems, the pseudo-two-dimensional model can be employed to thoroughly analyze the impacts of dynamic variations on internal battery reactions, such as lithium-ion concentration gradients, intensified polarization, and thermal accumulation. By simulating the electrochemical behavior of batteries during acceleration, hovering, and prolonged flight, the P2D model facilitates the optimization of thermal management and state-of-health assessment, thereby providing theoretical support for the enhancement of UAV endurance and flight safety.
- 2.
- SP Model
The P2D model consists of partial differential equations and nonlinear parameters, and results in a high number of iterations, lengthy computation times, and numerous parameters. Due to differences in computational efficiency and parameter identification, the application of the P2D model is limited. As a result, many researchers have been continuously exploring reasonable and effective simplification methods for the P2D model, among which the most widely used is the single particle (SP) model. The SP model was proposed by B. S. Haran et al. [34]. In this model, it is assumed that the lithium-ion concentration in the liquid phase is uniform throughout the battery, and the electromotive force of the solid phase is uniform within the electrode. The SP model neglects the non-uniform distribution of the lithium-ion diffusion potential in the liquid phase and, therefore, the entire electrode can be represented by a single active particle.
Based on the P2D model, the SP model introduces the following assumptions, which significantly simplify the computational process of the model.
Compared to the P2D model, the SP model has fewer equations, fewer parameters, and higher computational efficiency. Therefore, it is an electrochemical model that is applicable to real-time systems and has been employed by some researchers for the real-time monitoring of lithium-ion concentrations in lithium-ion batteries [35].
To meet the real-time control requirements of unmanned aerial vehicle systems, the single particle model is particularly well-suited for embedded battery management systems due to its simplified structure and computational efficiency. By employing a reduced-order particle-based representation, the SP model enables the rapid prediction of batteries’ state of charge and voltage variations during flight, and thereby provides low-latency support for energy scheduling and remaining range estimation during mission execution.
- 3.
- Extended SP Model
Due to its excessive simplification of electrochemical processes, the SP model suffers from reduced accuracy and is only suitable for low-rate charge and discharge conditions. To address the limitations of the SP model, many researchers have proposed extended SP models. To address the challenges of high-rate charge–discharge and rapid operational transitions in unmanned aerial vehicles (UAVs), the extended single particle (SP) model was developed, which enhances the SP model’s capability to capture battery dynamic behavior by incorporating electrolyte-phase diffusion and heterogeneous reactions. This improvement makes the model more suitable for meeting the demands of flight safety and performance optimization. Luo W, Lyu C, and others introduced the effects of liquid-phase diffusion and heterogeneous reaction distribution into the SP model, proposing an extended SP model capable of charge and discharge modelling at 4C rates [36]. Han X and Ouyang M, among others, approximated the solid-phase diffusion of lithium ions using multiple first-order processes and used parabolic fitting to handle liquid-phase concentration distribution, which resulted in an extended SP model that is applicable to battery management systems [37]. S. K. Rahimian and S. Rayman incorporated a liquid-phase potential and material balance into the SP model [38]. I. Goto and H. Ohkuma included the concentration distribution of lithium electrolyte ions into the SP model [39]. In the extended SP model, the electrode is simplified to a single active particle, and the electrochemical processes omitted in the SP model are approximated and solved.
The extended single particle model offers enhanced electrochemical modeling accuracy, enabling the more precise representation of phenomena such as lithium-ion concentration polarization and potential hysteresis. By coupling the extended SP model with flight control data, it becomes possible to dynamically predict battery performance degradation and thermal accumulation during flight, and thereby to provide critical decision-making support for safe UAV landing and an early warning of battery degradation.
3.1.2. Equivalent Circuit Model
In UAV battery management, equivalent circuit models have become a core tool for battery state estimation and energy management within flight control systems, owing to their computational simplicity and fast real-time response. The equivalent circuit model of a battery is developed based on its operational principles, in which a circuit network is utilized to characterize the performance of lithium-ion batteries. These models are thus applicable to a broader range of battery types. To meet the demands of simulation techniques, various equivalent circuit models for lithium-ion batteries have been developed. Reference [40] categorizes the existing methods for constructing equivalent circuit models into two types: time-domain and frequency-domain analysis models. Time-domain analysis models primarily utilize voltage and current data of lithium-ion batteries, whereas frequency-domain analysis models rely on impedance measurements, such as Nyquist and Bode plots. The most commonly used equivalent circuit models are established through time-domain analysis. This review primarily focuses on the RC, PNGV, Thevenin, and modified Thevenin models [41].
- RC Model
The RC model consists of two capacitors and three resistors, as illustrated in Figure 5. The large capacitor represents the charge storage capacity of the lithium-ion battery, while the small capacitor accounts for the surface capacitance and diffusion effects of the battery. Resistor denotes the terminal resistance, represents the surface resistance, and corresponds to the terminal resistance.
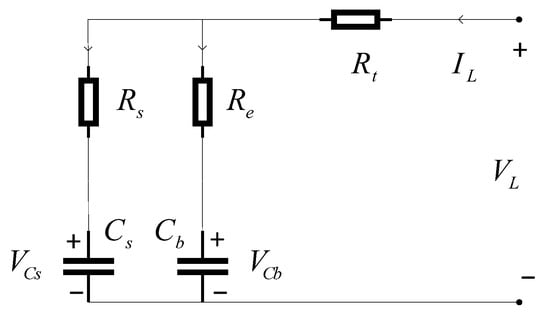
Figure 5.
RC model.
The voltages across the two capacitors, and , serve as state variables, the terminal current as the input variable, and the terminal voltage as the output variable. Equation (2) is formulated based on Kirchhoff’s laws, from which the state-space equations of the RC model can be derived.
The RC model features a simple structure and parameters with clear physical interpretations, which makes it suitable for rapid state estimation in embedded systems. In UAV applications, this model can be integrated into the flight control system to enable real-time battery voltage prediction and health state estimation during flight, which ensures energy continuity throughout the execution of missions.
- 2.
- Thevenin Model
The Thevenin model, as shown in Figure 6, is a widely used model. This model employs an ideal voltage source to represent the open-circuit voltage of a lithium-ion battery and incorporates a series resistor and a parallel RC network to predict the battery’s response to transient loads at a specific state of charge.
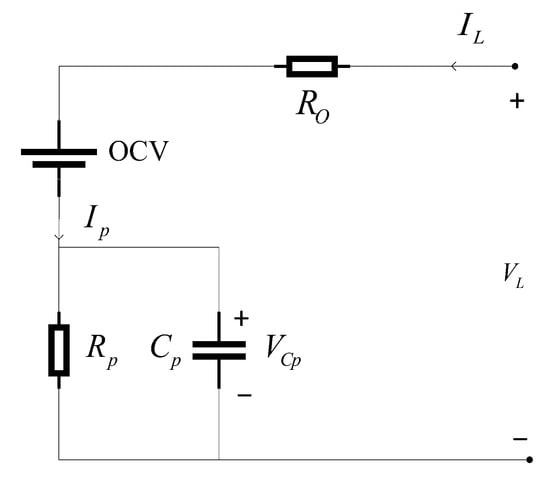
Figure 6.
Thevenin model.
The voltage across capacitor , denoted as , serves as the state variable, the terminal current as the input variable, and the terminal voltage as the output variable. Equations (4) and (5) are formulated based on Kirchhoff’s laws, from which the state-space equations of the Thevenin model are derived.
Due to its simplicity and ability to meet the basic requirements of lithium-ion batteries, the Thevenin model has been widely adopted. However, if the open-circuit voltage does not vary with the state of charge, this model is limited to describing the transient response of lithium-ion batteries at a specific SOC. Consequently, it is incapable of capturing steady-state voltage variations or predicting the runtime of the battery. Additionally, the model cannot describe the relationship between the OCV and SOC, nor can it predict the battery’s runtime or manage its charge–discharge processes.
In sudden high-current scenarios that are commonly encountered during UAV flights, such as takeoff or emergency obstacle avoidance, the Thevenin model enables the efficient evaluation of voltage drop and transient response characteristics with a low computational cost. It is widely used in flight control systems to support decision-making for energy-performance trade-offs.
- 3.
- PNGV Model
As depicted in Figure 7, the PNGV model is derived by incorporating an additional capacitor into the Thevenin model. The PNGV model enhances the dynamic tracking capability between the battery voltage and state of charge by introducing a polarization capacitor and thereby enabling more accurate endurance prediction during long-duration flight missions in unmanned aerial vehicles. This model possesses clear physical significance, with the ideal voltage source representing the OCV of the lithium-ion battery. Resistor denotes the battery’s ohmic internal resistance, resistor represents the polarization internal resistance, and capacitor corresponds to the polarization capacitance. denotes the load current, represents the polarization current, is the terminal voltage, and capacitor accounts for the OCV variation caused by the time integral of the load current . When the lithium-ion battery is in a charging or discharging state, the accumulation of current over time alters the SOC, which further modifies the battery’s OCV and is manifested as a voltage change across capacitor . In this model, capacitor not only represents the capacity of the lithium-ion battery but also its DC response, and thereby addresses the limitations of the Thevenin model.
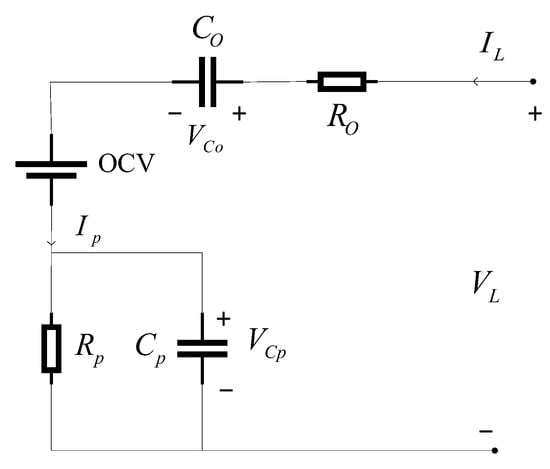
Figure 7.
PNGV model.
The voltages across capacitors and , denoted as and , serve as state variables, the terminal current as the input variable, and the terminal voltage as the output variable. Equations (6) and (7) are developed based on Kirchhoff’s laws, from which the state-space equations of the PNGV model are derived.
The PNGV model, proposed by the Partnership for a New Generation of Vehicles in the United States, is significantly influenced by the Freedom CAR hybrid electric vehicle initiative. Owing to its systematic parameter identification methods and relatively high model accuracy, the PNGV model facilitates straightforward parameter identification experiments. Consequently, it is one of the most commonly adopted models.
Additionally, for medium- to high-power UAV platforms, the PNGV model can accurately characterize the evolution of the state of charge and voltage during long-endurance flights. This facilitates the development of mission-oriented endurance prediction systems and thereby enhances the robustness of flight mission planning and improves energy utilization efficiency.
- 4.
- Modified Thevenin Model
Single-pole models of lithium-ion batteries do not always meet the requirements for dynamic performance. Consequently, researchers have introduced various bipolar and multipolar models [42]. Among these, the modified Thevenin model, as depicted in Figure 8, is frequently utilized. In this model, an ideal voltage source represents the open-circuit voltage of the lithium-ion battery. Resistor denotes the ohmic internal resistance, resistor represents the electrochemical polarization internal resistance, and capacitor corresponds to the electrochemical polarization capacitance. Resistor is associated with the concentration polarization capacitance, capacitor represents the concentration polarization capacitance, denotes the electrochemical polarization voltage, represents the concentration polarization voltage, is the load current, and is the terminal voltage.
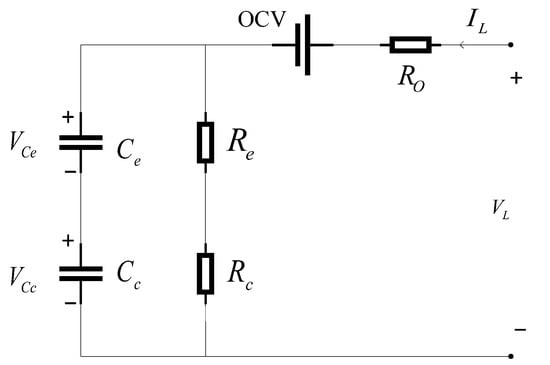
Figure 8.
Modified Thevenin model.
The electrochemical polarization voltage and the concentration polarization voltage serve as state variables, the terminal current as the input variable, and the terminal voltage as the output variable. Equations (8) and (9) are derived based on Kirchhoff’s laws, from which the state-space equations of the modified Thevenin model are obtained.
The polarization in the modified Thevenin model enables a precise representation of the battery’s dynamic characteristics. As the performance requirements for lithium-ion batteries continue to increase, the application of this model has become increasingly widespread. The frequent dynamic load variations encountered during UAV missions impose higher demands on battery performance evaluation. The modified Thevenin model incorporates concentration polarization processes to more accurately characterize the dynamic voltage response of the battery, which aids in voltage drop risk prediction and the dynamic correction of the remaining energy during flight state transitions. However, similar to its original version, the modified Thevenin model cannot account for OCV variations caused by the time integration of the load current . If the OCV in the Thevenin model is treated as a variable, the equivalent relationship between the lithium-ion battery’s OCV and its SOC can replace the capacitor in the PNGV model. Despite its limitations, the modified Thevenin model retains significant practical importance.
3.2. Data-Driven Models
Data-driven models represent an approach that leverages extensive operational data to model and predict the dynamic behavior of energy storage battery systems using methods such as statistical learning, machine learning, or deep learning. In contrast to white-box modeling, which relies on the physicochemical mechanisms within the battery, data-driven models fall into the “black-box” or “gray-box” category. Their core principle is to forego explicit physical model construction and instead utilize the inherent relationships within the data to map and predict battery performance metrics. This approach is particularly suitable for scenarios where physical processes cannot be accurately modeled or where abundant data are available but the structural information is incomplete. Data-driven models offer advantages such as low modeling costs, high deployment efficiency, and strong adaptability.
In real-world operational environments, unmanned aerial vehicle battery systems are exposed to complex and dynamic working conditions such as frequent takeoffs and landings, rapid load switching, strong electromagnetic interference, and pressure fluctuations at high altitudes. Data-driven approaches can leverage historical flight data—such as data on the voltage, current, temperature, and load power—to rapidly adapt to variations in flight missions and environmental conditions. This enables the real-time, online estimation of key indicators such as the state of charge, state of health, and remaining useful life within complex urban airspace, and thereby enhances flight safety and mission success rates.
As illustrated in Figure 9, data-driven models are primarily categorized into four types: neural network-based, regression-based, optimization-based, and logic-based models, with the classification being based on the core algorithms and data processing methods used by the model. Neural network-based models rely on artificial neural networks, employing multilayer nonlinear mapping to learn complex data relationships, which makes them suitable for high-dimensional nonlinear problems. Regression-based models utilize statistical regression techniques to focus on fitting mathematical relationships between inputs and outputs and are applicable to scenarios with clear data patterns. Optimization-based models employ optimization algorithms to identify optimal parameters or structures and are commonly used for system parameter identification or control strategy optimization. Logic-based models, which are grounded in logical reasoning or rules, emphasize rule-driven decision-making and are well-suited for systems with discrete or well-defined conditions. These four types of data-driven models reflect the differences in modeling objectives, complexity, and applicable scenarios among various algorithms.

Figure 9.
Classification of data-driven models for UAV batteries.
3.2.1. Neural Network-Based Models
Neural network-based models represent a significant branch of data-driven models for unmanned aerial vehicle battery systems, being constructed using artificial neural networks (ANNs) and excelling in handling complex nonlinear relationships and high-dimensional data. Their core mechanism involves simulating the dynamic characteristics of UAV batteries—such as their capacity degradation, voltage response, and internal resistance variations—through a multilayer structure comprising input, hidden, and output layers. During training, the model adjusts weights using experimental or flight data, including current, voltage, and temperature data, to optimize its prediction accuracy. Common types include feedforward neural networks, recurrent neural networks (RNNs), and long short-term memory (LSTM) networks, with LSTM networks being particularly suitable for UAV battery state estimation due to their ability to capture long-term dependencies in time-series data. Neural network-based models do not require in-depth knowledge of internal battery mechanisms, offering strong generalization capabilities. However, they demand substantial high-quality data and computational resources, which results in longer training times. In recent years, the integration of deep learning and transfer learning has expanded their applications in UAV battery life prediction and fault diagnosis, significantly enhancing flight safety and the precision and robustness of battery management.
Artificial neural networks were among the earliest neural networks to be applied to battery modeling [43]. Utilizing a multilayer perceptron (MLP) structure with fully connected layers, ANNs fit nonlinear relationships between battery operational data and state metrics. Their training typically employs the backpropagation algorithm with a mean squared error (MSE) loss function, which makes ANNs suitable for static mapping tasks such as capacity degradation prediction or voltage–current relationship modeling. ANNs achieve high accuracy without requiring a detailed understanding of battery mechanisms, outperforming methods like open-circuit voltage estimation in lead-acid battery state-of-charge applications. Their advantages include their structural simplicity and ease of implementation. However, ANNs struggle to handle time-series data, which limits their ability to capture dynamic behaviors in charge–discharge cycles, and their generalization to complex datasets is constrained, often requiring extensive feature engineering. Although enhanced by deep networks and optimization algorithms (e.g., Adam), ANNs remain valuable in simple scenarios but are gradually being supplanted by more sophisticated models.
Recurrent neural networks (RNNs) [44] are applied to battery modeling due to their ability to process time-series data. By retaining historical information through a recurrent structure, RNNs take sequential inputs such as the voltage and current to predict battery states. They are well-suited for capturing short-term dynamic behaviors, such as changes during charge–discharge processes. However, RNNs suffer from the vanishing gradient problem, which limits their ability to model long-term dependencies and results in reduced accuracy under complex operating conditions. Their strength lies in sequence modeling, but their training is sensitive to hyperparameters and their computational costs are high. Due to gradient-related limitations, traditional RNNs have gradually faded from mainstream application, although they laid the foundation for dynamic system modeling.
Long short-term memory networks [45], an advanced variant of RNNs, incorporate memory cells and gating mechanisms (input, forget, and output gates) to retain long-term historical information, which makes them particularly suitable for modeling slow battery degradation processes. LSTMs excel in online SOC estimation and their combination with Kalman filtering further enhances their accuracy. Compared to traditional RNNs, LSTMs effectively capture long-term dependencies and adapt to dynamic changes in complex operating conditions. However, they require substantial data for training, have a high computational complexity, and involve intricate hyperparameter tuning. LSTMs offer high accuracy and robustness, which makes them widely used in battery life prediction, although they may be limited in scenarios that require strong real-time performance.
Gated recurrent units (GRUs) [46], another RNN variant, feature a simpler structure than LSTMs, merging the input and forget gates into an update gate, which reduces the number of parameters and the computational complexity. With inputs and outputs similar to LSTMs, GRUs are suitable for SOC, state-of-health (SOH), or remaining useful life (RUL) predictions. GRUs enable faster SOC estimation on embedded devices, which makes them ideal for real-time applications while still allowing them to retain their long-term dependency modeling capabilities. They offer higher training efficiency and simpler hyperparameter tuning. However, their modeling capacity for extremely long sequences is slightly inferior to that of LSTMs, and they still require substantial data support. Due to their balance of efficiency and accuracy, GRUs have become a popular choice for battery modeling, particularly in resource-constrained scenarios, and there is potential for their future integration with lightweight techniques for edge computing applications.
Inspired by computer vision, convolutional neural networks (CNNs) [47] have been adapted for battery modeling. Battery data, such as voltage curves and impedance spectra, exhibit local patterns that are suitable for feature extraction using convolutional kernels. CNNs capture temporal or spatial correlations through convolution operations, with pooling layers reducing the dimensionality of the output SOC, SOH, or RUL predictions. One-dimensional CNNs process time-series data, while two-dimensional CNNs analyze impedance spectra. CNNs are robust to noise, parameter-efficient, and well-suited for large-scale data processing. However, their ability to model long-term temporal dependencies is limited, which makes it challenging to capture slow changes in battery cycles. To address this, CNNs are often combined with LSTMs or GRUs to form hybrid models with enhanced dynamic modeling capabilities. The efficiency of CNNs in feature extraction makes them a valuable tool for complex battery modeling.
Autoencoders (AEs) [48] are employed in battery modeling due to their unsupervised learning capabilities. AEs consist of an encoder that compresses input data into a low-dimensional representation and a decoder that reconstructs the data, which makes them suitable for tasks such as dimensionality reduction, denoising, or anomaly detection. Variational autoencoders (VAEs) model data distributions, excelling in scenarios with scarce fault data. Denoising autoencoders (DAEs) enhance models’ robustness by handling noisy data. The primary advantage of AEs is their ability to operate without labeled data, which makes them ideal for preprocessing or feature extraction. However, their direct modeling capacity for high-dimensional time-series data is limited, and they often require integration with networks like LSTMs. AEs typically serve as auxiliary tools in battery modeling, but their potential in multimodal data fusion is significant, particularly in data-scarce scenarios.
Generative adversarial networks (GANs) [49] are utilized in battery modeling for their data augmentation capabilities. Comprising a generator that produces realistic battery data and a discriminator that distinguishes between real and synthetic data, GANs are effective for expanding training datasets or detecting anomalies. Conditional GANs (CGANs) generate data for specific operating conditions and have found wide applications in SOC estimation and fault detection. The strength of GANs lies in their mitigating data scarcity and enhancing models’ generalization. However, their training is often unstable, requiring carefully designed loss functions. GANs that incorporate physical constraints are emerging as a research focus, promising to improve the authenticity of generated data. GANs hold substantial potential for small-sample learning and fault diagnosis, with their future applications likely extending to full-lifecycle data simulation.
Transformer models, known for their powerful sequence modeling capabilities, have been applied to battery modeling [50]. Their self-attention mechanism assigns weights to each time step, capturing both short- and long-term dependencies. With multidimensional time-series inputs, the encoder extracts features, and the decoder generates predictions for the SOC or RUL. Transformers achieve high accuracy in life prediction under complex operating conditions, benefiting from their ability to process long sequences in parallel, which makes them suitable for large-scale datasets. However, their high computational complexity demands substantial data and computational resources. Lightweight transformers (e.g., Informer) and pre-training techniques are being explored to reduce costs. Transformers show immense potential in multi-battery collaborative management and full-lifecycle modeling. Although their application is still in the early stages, their parallel processing and accuracy advantages position them as a future mainstream direction.
From simple artificial neural networks to complex transformer models, neural networks have significantly advanced battery modeling techniques. ANNs established a foundation for static modeling through nonlinear mapping, while RNNs, LSTMs, and GRUs addressed dynamic sequence modeling challenges. CNNs and AEs optimized feature extraction, and GANs and transformers overcame limitations in data scarcity and long-sequence modeling. The primary strength of neural networks lies in their robust nonlinear fitting capabilities and adaptability to complex operating conditions, which enable the precise prediction of battery state parameters such as the SOC, SOH, and RUL. However, their training requires substantial data and computational resources, and their interpretability is limited, which constrains real-time applications. Recent developments in hybrid modeling and lightweight designs have improved the real-time performance of battery modelling, while transfer learning has reduced data requirements. In the future, hybrid models that integrate physical knowledge, multimodal data fusion, and enhanced interpretability will be key research directions that offer new opportunities for efficient battery management.
3.2.2. Regression-Based Models
Regression-based, data-driven models rely on statistical regression techniques to model battery behavior by fitting mathematical relationships between inputs (e.g., voltage, current, temperature) and outputs (e.g., battery state parameters). Their core premise assumes that battery behavior can be described by parameterized functions. Common methods include linear regression, polynomial regression, support vector regression (SVR), random forest regression (RFR), gradient boosting regression (GBR), and kernel adaptive filtering regression (KAF). These models typically aim to minimize prediction errors, optimizing parameters through algorithms such as gradient descent or least squares. In battery modeling, regression-based models excel in scenarios with clear data patterns, such as capacity degradation trend prediction or state parameter estimation under static conditions. Their advantages include algorithmic simplicity, high computational efficiency, and strong interpretability, which make them suitable for use with small-scale datasets or real-time applications. However, their limitations lie in their restricted ability to model nonlinear, high-dimensional, or dynamic data, as they struggle to capture long-term temporal dependencies or complex degradation patterns. Recent advancements that have combined feature selection and ensemble learning have kept regression-based models competitive in specific scenarios, although they often require integration with neural networks or other methods to enhance their accuracy.
Linear regression [51], rooted in statistics, is the most fundamental regression method. It assumes a linear relationship between battery operational data (e.g., voltage, current) and state metrics, optimizing parameters via the least squares method. Widely applied in simple conditions, such as open-circuit voltage (OCV)-SOC estimation for lead-acid batteries, it is valued for its computational simplicity. Its strengths include its ease of implementation, strong interpretability, and suitability for small-scale datasets and rapid deployment, particularly for beginners. Linear regression serves as a baseline model, providing a reference for more complex methods. However, its capacity to model nonlinear relationships is limited, which makes it inadequate for capturing dynamic behaviors like nonlinear capacity loss during cycling, and it is sensitive to noise, requiring high-quality data. In modern complex scenarios, linear regression is often used as a component of hybrid models or for validating simple hypotheses.
Polynomial regression [52] extends linear regression by incorporating higher-order terms to fit nonlinear relationships. Commonly used for fitting voltage–current curves or predicting capacity degradation trends, it is prevalent in lithium-ion battery research. Polynomial regression retains the simplicity and interpretability of linear regression while capturing moderately nonlinear patterns, has low computational costs, and is suitable for small-to-medium-scale datasets. Its limitations include the risk of overfitting with higher-order terms, particularly with limited data, which leads to poor generalization. Additionally, it struggles with dynamic time-series modeling, failing to address long-term dependencies in battery cycling. When combined with regularization techniques, polynomial regression remains valuable in simple scenarios but typically requires integration with other methods to improve its accuracy.
Support vector regression (SVR) [53], based on support vector machine principles, maps data to a high-dimensional space using kernel functions to fit nonlinear relationships, with the aim of minimizing the structural risk. SVR performs exceptionally in lithium-ion battery state parameter estimation. Its strengths include robustness to noise and outliers, suitability for small-to-medium-scale datasets, and flexibility in adapting to various nonlinear patterns through kernel functions. However, SVR is sensitive to kernel and regularization parameters, requiring complex tuning, and its computational cost escalates with the use of large-scale data. While effective for static state predictions, SVR requires enhancements for dynamic sequence modeling and is often combined with sequential models. SVR’s strong generalization capabilities ensure its continued importance in battery modeling.
Random forest regression (RFR) [54], an ensemble method based on decision trees, constructs multiple trees through random sampling and feature selection, averaging its predictions to enhance its accuracy. Widely applied in battery life prediction, such as estimating the SOH from voltage curves, RFR achieves accuracy comparable to that of neural networks. Its advantages include robustness to noise, a low risk of overfitting, and the ability to assess feature importance, and it is often used to guide feature engineering. However, its predictions are discrete averages, and the training time increases with the number of trees. RFR excels in complex condition state estimation but requires improvements for dynamic sequence modeling, often being paired with sequential models to enhance its dynamic capabilities. RFR’s potential in multivariable scenarios remains significant.
Gradient boosting regression (GBR) [55] iteratively optimizes weak learners to fit residuals, constructing high-accuracy models. In battery life prediction, GBR achieves superior precision, effectively capturing complex nonlinear patterns. It is highly adaptable to imbalanced or noisy data, which makes it suitable for multivariable battery state parameter estimation. GBR’s strengths include high accuracy and flexibility, with a performance that is tunable through learning rate and tree depth adjustments. However, it is sensitive to hyperparameters, has long training times, and risks overfitting due to its complexity. GBR is commonly used for high-precision state predictions, and its efficiency can be further improved with automated hyperparameter tuning. GBR’s potential to rival deep learning models in complex conditions makes it a key choice for high-accuracy modeling.
Kernel adaptive filtering regression (KAF) [56] integrates kernel methods with adaptive filtering, allowing the dynamic adjustment of parameters through online learning to adapt to changing battery data. It is well-suited for real-time applications and resource-constrained scenarios, such as state estimation under dynamic conditions. KAF’s advantages include a low computational cost and online learning capabilities, which enable it to rapidly adapt to condition changes, and it has significant potential in battery management systems (BMSs). However, KAF is sensitive to initial parameters, and its long-term prediction accuracy may lag behind that of deep learning models. KAF offers a novel approach for real-time scenarios, with future integration with edge computing likely to expand its applications, particularly in high-response-demand environments.
Regression-based methods have evolved from the simple linear fitting of linear regression to the nonlinear modeling of polynomial regression, SVR, and RFR, and further to the high-precision dynamic predictions of GBR and KAF. Linear and polynomial regression provide straightforward baselines, SVR and RFR enhance robustness, while GBR, KAF, and advanced methods address complex scenarios. The strengths of regression-based models lie in their simplicity, computational efficiency, and interpretability, with SVR and RFR offering noise robustness and KAF enabling online learning. Their limitations include restricted nonlinear modeling capabilities and weak dynamic sequence processing. Recent advancements in ensemble learning and online optimization have improved the performance of these models. In the future, integrating physical constraints, multimodal data fusion, and lightweight designs will address interpretability challenges, enabling reliable battery management.
3.2.3. Optimization-Based Models
Optimization-based data-driven models address parameter identification and control strategy design by seeking optimal solutions to target functions, such as minimizing prediction errors or maximizing system efficiency. Their core approach involves using global or local search algorithms to fit complex relationships between battery operational data and state parameters. Common methods include particle filtering (PF), genetic algorithms (GAs), particle swarm optimization (PSO), differential evolution (DE), grey wolf optimization (GWO), deep reinforcement learning (DRL), and hybrid optimization. These models do not require in-depth knowledge of battery mechanisms and excel in handling nonlinear, high-dimensional problems, which makes them widely used for equivalent circuit model parameter estimation and charging strategy optimization. Their strengths include robust global search capabilities and adaptability to complex operating conditions, particularly in dynamic scenarios.
Particle filtering (PF) [57], based on Monte Carlo sampling, estimates the posterior distribution of battery states by generating numerous particles, which makes it suitable for nonlinear, non-G MSM systems. PF uses data such as the voltage and current to approximate the SOC or SOH, excelling in handling dynamic uncertainties and commonly being applied in real-time state tracking. Its advantages include strong adaptability to nonlinear systems and the ability to integrate multi-source information (e.g., temperature, cycle counts) to enhance its accuracy, which make it ideal for online battery state estimation. However, PF suffers from particle degradation, which can lead to bias, and its computational complexity increases with the number of particles, which reduces its efficiency in large-scale systems. Improved resampling strategies are critical to mitigate these issues. PF performs reliably on small-scale datasets and is often combined with Kalman filtering to form hybrid methods, which enhances its robustness and accuracy, with this combination serving as a benchmark for battery state estimation.
Genetic algorithms (GAs) [58] emulate biological evolution, using selection, crossover, and mutation operations to search for optimal solutions in the parameter space and thus optimize battery model parameters. With the objective of minimizing errors, GAs are well-suited for parameter identification in ECMs, as they are capable of handling complex nonlinear optimization problems. Their strengths include robust global search capabilities, the ability to escape local optima, and a low dependence on initial conditions, which ensure broad adaptability. However, GAs converge slowly and incurs high computational costs, particularly in high-dimensional parameter spaces. To improve their convergence, GAs are often combined with local optimization algorithms to form more efficient search strategies. While their standalone use has decreased, GAs remain a cornerstone of hybrid optimization frameworks, being applicable to parameter estimation and multi-objective optimization scenarios, such as balancing energy efficiency and battery lifespan.
Particle swarm optimization (PSO) [59], inspired by collective behaviors, optimizes target functions through collaborative particle searches, and is commonly used for ECM parameter estimation or control strategy design. PSO offers advantages such as minimal parameters, ease of implementation, and superior global search capabilities compared to traditional gradient-based methods, which makes it suitable for small-to-medium-scale optimization problems. Its limitations include the risk of converging to local optima in high-dimensional or multimodal problems and its sensitivity to velocity update parameters, which necessitate careful tuning. To enhance its performance, PSO is often integrated with deep models to improve its adaptability in complex conditions. Widely applied in SOH prediction and charging optimization, PSO’s efficiency and flexibility make it a classic method in battery modeling.
Differential evolution (DE) [60] optimizes parameters through differential mutation, crossover, and selection operations, which makes it suitable for parameter identification in complex battery models, such as electrochemical models. DE offers strong exploration capabilities and faster convergence than GAs, with a low dependence on initial conditions. Its advantages include a simple algorithmic structure, suitability for high-dimensional nonlinear optimization, and efficiency in handling multi-objective tasks, such as balancing accuracy and efficiency. However, DE is sensitive to mutation factors and crossover rates, and improper tuning can degrade its performance. Adaptive parameter adjustment strategies are increasingly explored to address this issue. DE excels in SOC estimation and lifespan prediction, and its recent use in multivariable optimization scenarios, coupled with dynamic tuning, enhances its potential for real-time modeling applications.
Grey wolf optimization (GWO) [61], inspired by wolf pack hunting behaviors, optimizes target functions by simulating leadership and collaboration mechanisms, which makes it suitable for battery model or control parameter adjustments. GWO is simple, gradient-free, and converges quickly. Its strengths include a hierarchical structure that balances exploration and exploitation, offering superior robustness compared to traditional swarm intelligence algorithms. This makes it suitable for small-to-medium-scale optimization tasks. However, GWO may converge prematurely in ultra-high-dimensional problems, in which case it requires improved diversity mechanisms to maintain its search capabilities. With an accuracy surpassing that of PSO and GWO, when combined with multi-objective optimization, its applicability in complex conditions is broad, and this method is emerging as a promising choice for efficient modeling.
Deep reinforcement learning (DRL) [62], integrating deep learning and reinforcement learning, optimizes BMS control or parameter adjustments by enabling agents to learn optimal strategies. Targeting long-term reward maximization, DRL adapts to high-dimensional dynamic systems. Its strengths include leveraging deep networks to extract features and handle nonlinear behaviors in complex conditions, which make it suitable for adaptive SOC estimation or charging optimization. However, DRL requires substantial data and computational resources for training, and its strategy convergence may be unstable, with limited interpretability. Transfer learning, to reduce costs, is a growing research focus. DRL holds immense potential in dynamic optimization scenarios, such as designing strategies to extend batteries’ lifespan.
Hybrid optimization methods integrate multiple algorithms, combining the strengths of global and local searching to optimize complex battery model parameters or control strategies. For instance, combining GAs with PSO significantly improves their accuracy [63]. Targeting multi-objective optimization (e.g., balancing accuracy and efficiency), hybrid optimization overcomes the limitations of single methods, offering strong robustness. Its advantages include balancing convergence speed and global search capabilities, which allows it to adapt to multivariable optimization in complex conditions. However, its design complexity requires tailored algorithm combinations for specific problems. Hybrid optimization excels in full-lifecycle parameter identification and can further improve models’ performance through adaptive mechanisms.
Optimization-based methods have evolved from the probabilistic estimation of particle filtering to the swarm intelligence searches of genetic algorithms, particle swarm optimization, and differential evolution, and further to the dynamic modeling of grey wolf optimization, deep reinforcement learning, and hybrid optimization. PF excels in nonlinear state estimation, GAs and PSO provide global search capabilities, DE and GWO offer faster convergence, and DRL adapts to dynamic control. The strengths of optimization-based models lie in escaping local optima, handling high-dimensional nonlinear problems, and supporting parameter identification and strategy optimization. However, they incur high computational costs, involve complex parameter tuning, and, for DRL, involve lengthy training times. Recent advancements in adaptive strategies and multi-objective optimization have improved the efficiency of these models. In the future, reducing computational demands through physical knowledge integration, multimodal data fusion, and algorithmic lightweighting will drive BMSs toward efficient, intelligent development.
3.2.4. Logic-Based Models
Logic-based models rely on rule-based reasoning or logical relationships to model battery behavior by defining explicit state transitions or decision rules. Their core approach involves utilizing logical frameworks, such as fuzzy logic, decision trees, or Markov models, to map the relationship between unmanned aerial vehicle battery operational data and states. These models are commonly applied in fault diagnosis, state classification, and flight control strategy development, particularly in scenarios with discrete or well-defined conditions. Typical methods include fuzzy logic control, decision tree classification, hidden Markov models (HMMs), Bayesian networks, fuzzy neural networks (FNNs), and dynamic Bayesian networks (DBNs). The strengths of logic-based models lie in their clear rules, strong interpretability, ability to incorporate expert knowledge, and high computational efficiency, which make them suitable for real-time UAV applications. In recent years, logic-based models have increasingly been combined with neural networks to enhance their flexibility. In the future, logic-based models that incorporate adaptive rules and multimodal data will play a greater role in intelligent decision-making and safety management for UAV battery systems.
Fuzzy logic (FL) [64] employs fuzzy sets and membership functions to model uncertainty, using expert-defined rules to infer battery states, which makes it suitable for control and diagnostic scenarios. FL maps data such as voltage and current data to fuzzy rules, generating outputs like the SOC or fault states, and is often used for tasks like overcharge detection. Its advantages include intuitive rules, strong interpretability, no requirement for precise mathematical models, and high computational efficiency, and it is ideal for real-time applications. FL effectively handles nonlinear relationships through fuzzy inference, performing reliably in simple conditions. However, its rule design relies heavily on expert experience, which limits its ability to handle high-dimensional data or dynamic sequence modeling. To enhance its flexibility, FL is often combined with adaptive algorithms to optimize its rule generation. FL is widely applied in BMSs for state classification and preliminary control strategies, as it is suitable for rapid deployment in low-complexity scenarios.
Decision trees (DTs) [65] use a tree-like structure to perform classification or regression based on feature conditions, and are used in optimizing battery state predictions. With operational data as the input, DTs split nodes based on information gain, outputting SOH or fault categories, and are commonly used in health classification tasks. Their advantages include clear logic, low computational cost, and the rapid processing of discrete data, which make them suitable for fault diagnosis. DTs reveal key variables through feature selection, offering strong interpretability and facilitating the analysis of influencing factors. However, DTs are prone to overfitting, exhibit poor generalization on small datasets, and have limited effectiveness in continuous dynamic modeling. To improve their performance, DTs are often used as components in ensemble models. DTs perform reliably in preliminary classification tasks, and combining them with automated feature engineering can enhance their applicability in complex conditions.
Hidden Markov models (HMMs) [66] model time-series data based on state transition probabilities, assuming battery states as hidden variables and inferring the SOC or SOH from observed data. They are suitable for cycle degradation prediction. Their strengths include capturing temporal dependencies, which makes them appropriate for sequential state estimation in nonlinear systems with moderate computational efficiency. HMMs handle uncertainty through probabilistic inference, meeting dynamic modeling needs. However, their assumption of Markovian state transitions limits their ability to model complex long-term dependencies, and their training requires substantial data. To improve their accuracy, HMMs are often combined with particle filtering. HMMs perform reliably in SOC estimation and fault detection, and expanding the state space can further enhance their modeling capabilities in multi-condition scenarios.
Bayesian networks (BNs) [67] model probabilistic dependencies between variables using directed graphs, optimizing the conditional distribution of battery states and generating SOH or fault probabilities. They are commonly used for anomaly detection. Their advantages include the ability to integrate multi-source data (e.g., temperature, cycle counts), handle uncertainty through probabilistic inference, and offer strong interpretability, which make them suitable for static or semi-dynamic scenarios with moderate computational complexity. BNs facilitate causal analysis but require careful network structure design, and their inference costs increase in complex scenarios, which limits their dynamic modeling capabilities. To enhance their performance, BNs are often combined with temporal models. BNs are widely applied in fault diagnosis and state classification, and automated structure learning can improve their adaptability across diverse conditions.
Fuzzy neural networks (FNNs) [68] integrate fuzzy logic and neural networks, optimizing state predictions through adaptive rules to generate SOC or RUL predictions, and are suitable for fault diagnosis. Their strengths include leveraging neural networks to automatically adjust membership functions, which reduces their reliance on expert experience and allows them to adapt to complex nonlinear relationships. FNNs combine inference and learning, offering superior accuracy and generalization compared to FL, which makes them suitable for dynamic conditions. However, their training requires substantial data, their hyperparameter tuning is complex, and their computational costs are high. For real-time applications, FNNs often adopt lightweight structures. FNNs excel in state estimation and health management, and integrating online learning can further enhance their dynamic modeling potential in BMSs.
Dynamic Bayesian networks (DBN) [69] extend BNs to time-series data, modeling battery dynamic behavior through temporal probabilities for state parameter estimation. They are suitable for full-lifecycle prediction. Their strengths include capturing long-term dependencies, integrating multisource data to improve their accuracy, and adapting to nonlinear systems in complex conditions. DBNs handle dynamic uncertainty through temporal inference, offering greater flexibility than static BNs. However, they require careful structure and parameter design, their performance is limited with insufficient data, and their computational costs are significant. To enhance their robustness, DBNs are often combined with deep models. DBNs show significant potential in dynamic state estimation, and adaptive structure design can further improve their performance in multi-scenario modeling.
Logic-based methods have evolved from the rule-based inference of fuzzy logic and decision trees to the probabilistic modeling of hidden Markov models and Bayesian networks, and further to the dynamic predictions of fuzzy neural networks and dynamic Bayesian networks. FL and DTs provide intuitive rules, HMMs and BNs excel in sequential and probabilistic inference, while FNNs and DBNs have an enhanced accuracy in complex scenarios. The strengths of logic-based models include strong interpretability, clear rules, suitability for fault diagnosis and state classification, and high computational efficiency. However, their rule design relies on experience, their dynamic modeling capabilities are limited, and FNNs and DBNs require substantial data. Recent advancements in adaptive rules and model integration have improved their flexibility. In the future, simplifying rules, integrating physical knowledge, and adopting online learning will drive the broader application of logic-based models in intelligent battery management.
3.3. Hybrid Models
Hybrid modeling integrates the interpretability of physics-based mechanistic models with the robust fitting capabilities of data-driven models, aiming to address the limitations of both pure white-box models, which heavily rely on mechanistic understanding and exhibit low inference efficiency, and black-box models, which are sensitive to data quality and lack interpretability. By achieving the complementary coupling of physical and data-driven approaches at different modeling levels, hybrid models construct high-accuracy, highly generalizable, and robust frameworks for battery behavior prediction and health assessment. These models have emerged as a research hotspot in energy storage battery system modeling.
In UAV application scenarios, it is challenging for a single modeling approach to simultaneously achieve high computational efficiency and predictive accuracy. Hybrid modeling improves the stability and responsiveness of flight state awareness by combining the real-time capabilities of mathematical models with the pattern recognition strengths of data-driven models. For example, in urban logistics drones, integrating heat conduction equations with long short-term memory networks enables the early warning of thermal runaway risks. In fixed-wing UAVs that are used for emergency rescue missions, incorporating physical priors with transformer networks enhances the robustness of remaining useful life predictions during high-altitude, long-endurance flights. Moreover, hybrid modeling supports lightweight deployment on edge computing platforms, meeting the dual requirements of real-time performance and safety in embedded battery management systems. This provides critical support for high-reliability flight missions.
3.3.1. Series Hybrid Modeling
Series hybrid modeling establishes a sequential connection between physics-based and data-driven models, with the core concept of this method being employing these models in a “pre-processing–post-learning” or “coarse prediction–fine correction” framework. Typically, the physics-based model is positioned at the front end of the system and is responsible for preliminary feature extraction or intermediate variable estimation, while the data-driven model serves as a subsequent module to compensate for errors, refine predictions, or enhance accuracy. This approach preserves the strong interpretability of physics-based models while leveraging the powerful fitting capabilities of data-driven models to improve their prediction accuracy, which makes it particularly suitable for complex system scenarios with incomplete information or features that are difficult to extract directly.
In practical applications, series hybrid modeling is commonly used for state estimation in UAV battery systems. For state-of-charge estimation, researchers often first employ an equivalent circuit model to model the battery’s voltage–current response, generating an initial SOC estimate. However, ECMs are highly condition-dependent and prone to deviations under dynamic loads. To address this, deep learning models, such as long short-term memory networks, can be introduced to model the error sequence between the initial estimate and the true value, dynamically correcting the prediction. Similarly, state-of-health estimation can adopt this structure, using electrochemical impedance characteristics or equivalent parameters to provide physical priors for neural networks and thereby enhance their generalization and interpretability.
Beyond correcting target variables, series hybrid modeling can also improve the performance of data-driven models through feature enhancement. Specifically, physics-based models can extract intermediate variables with clear physical significance—such as voltage slopes, time constants, open-circuit voltage, polarization voltage, or thermal resistance-capacitance—from raw sensor data. These variables offer higher information density and stability, effectively reducing the data-driven model’s reliance on large-scale training data and mitigating overfitting. In battery thermal management modeling, one-dimensional or three-dimensional heat conduction models are often used to estimate temperature trends, with their outputs serving as features for machine learning models to further identify potential thermal runaway precursors [70].
Compared to parallel or embedded hybrid models, the primary advantage of the series structure lies in its relative simplicity, clear architecture, and modular design, which facilitate the system’s deployment and phased training. The distinct boundary between the physics-based and data-driven models allows independent design and optimization, which are connected through standard interfaces, which is particularly valuable for engineering implementation. Additionally, the series structure offers fault tolerance; even if the physics-based model is imperfect, the data-driven model can compensate at the back end, enhancing the overall system robustness.
However, series hybrid modeling has certain limitations. Due to its shallow coupling depth, the data-driven model typically cannot directly intervene in the physics-based modeling process, which limits dynamic feedback and the optimization of internal system states. Furthermore, this approach remains dependent on the accuracy of the front-end physics-based model. If the physics-based model produces systematic biases or fails to adequately reflect changes in boundary conditions, the back-end data-driven model may struggle to achieve effective corrections. Additionally, the misalignment of training objectives between the physics-based and data-driven models can impact overall their performance, necessitating the careful design of joint optimization mechanisms in practical applications.
Overall, series hybrid modeling is a highly adaptable and easily implementable strategy, and is particularly suited for typical battery system modeling scenarios characterized by “insufficient data but known physics” or “imperfect physics with available priors.” By rationally delineating the functional boundaries between physics-based and data-driven models and designing efficient interfaces and error feedback mechanisms, this approach demonstrates broad application prospects in improving modeling accuracy, reducing training complexity, and enhancing model interpretability. With the advancement of the Internet of Things, big data, and edge computing, series hybrid modeling will further drive the intelligent upgrading of state awareness and management in energy storage systems across a wider range of applications.
3.3.2. Parallel Hybrid Modeling
Parallel hybrid modeling is a strategy that operates physics-based and data-driven models concurrently, with each producing independent outputs. The core concept involves both models independently predicting the same target variable, such as the battery SOC, SOH, or RUL, with their outputs subsequently being integrated through a fusion mechanism to generate the final prediction. This structure emphasizes redundancy and complementarity between models, leveraging the relative strengths of each under varying operating conditions to enhance the overall robustness, adaptability, and accuracy of the system.
In battery system modeling, parallel hybrid modeling is widely applied to state estimation and lifespan prediction tasks [71]. Specifically, the physics-based model, constructed using first-order or higher-order equivalent circuits, heat conduction equations, or electrochemical mechanisms, effectively characterizes the mid-to-low-frequency or steady-state performance of the battery system. In contrast, the data-driven model, utilizing algorithms such as neural networks, random forests, or support vector machines, learns dynamic nonlinear features embedded in large datasets, compensating for the limitations of physics-based models under non-standard conditions or degradation states. The complementary nature of their structures, input variables, and response speeds ensures that the fused prediction results are typically more accurate and reliable than those from a single model.
A common fusion strategy in parallel hybrid modeling is weighted linear combination, where the final output is a weighted average of the physics-based and data-driven model results:
where represents the fusion weight. This weight can be fixed or dynamically adjusted, for instance, based on current model errors, confidence levels, or external operating condition metrics such as the temperature or current amplitude. In certain applications, Bayesian methods are employed, with model outputs being treated as likelihood functions for fusion, which is a more effective method of handling uncertainty. In practical deployment, a well-designed fusion mechanism significantly enhances the model’s generalization across diverse scenarios, particularly in boundary conditions, complex tasks, and multimodal input contexts.
Moreover, the parallel structure naturally lends itself to extensions of ensemble learning principles. For example, multiple data-driven models can be constructed and fused with the physics-based model to form a more robust ensemble prediction framework. This structure also facilitates integration with fault-tolerance mechanisms: if one model fails due to sensor malfunctions or anomalous data, the system can rely on the remaining models to maintain functionality, which thereby improves the system’s safety and robustness. In UAV battery management systems, particularly for SOC estimation and rapid RUL assessment, parallel hybrid models have been widely adopted, demonstrating superior real-time performance and stability in dynamic scenarios.
However, parallel hybrid modeling presents certain challenges. First, the outputs of physics-based and data-driven models often differ in their physical significance, numerical scale, and temporal response characteristics, which necessitates normalization and time synchronization during fusion. Second, discrepancies or mutual interference between models may lead to cumulative biases, and improperly set fusion weights could result in combined outputs that underperform in comparison to those of individual models. Thus, designing a scientifically sound fusion mechanism that ensures complementary model strengths, rather than mutual degradation, is critical to the success of the parallel structure. Recent studies have introduced methods such as reinforcement learning and adaptive filtering to dynamically adjust fusion strategies, addressing temporal variations and uncertainties in models’ performance.
From an engineering perspective, parallel hybrid modeling offers high modularity and scalability. Physics-based and data-driven models can be independently trained and deployed, which facilitates their maintenance and iterative updates. Additionally, the parallel structure aids in model interpretability: the physics-based model provides deterministic causal explanations, while the data-driven model uncovers latent correlations and trends, which enables a multilevel, multifaceted understanding of system states.
Overall, parallel hybrid modeling, as a strategy that balances robustness and flexibility, is particularly well-suited for battery system modeling scenarios where high accuracy is required, physical modeling is incomplete, and data features are complex yet not fully comprehensive. With advancements in multisource sensor fusion, edge AI computing, and digital twin systems, parallel hybrid modeling is poised to play an increasingly vital role in intelligent energy systems.
3.3.3. Embedded Hybrid Modeling
Embedded hybrid modeling represents the most deeply integrated modeling approach, with its core principle being the direct incorporation of physical knowledge into the structural design, training objectives, or representational framework of data-driven models to achieve precise system behavior modeling. This method seeks to transcend the traditional boundaries between physics-based and data-driven models, moving beyond merely combining them as independent components. Instead, it employs coupling mechanisms to endow models with both “physical consistency” and “data adaptability.” This deeply fused approach provides a novel solution for complex system modeling, particularly in scenarios that involve multi-physics coupling, strong nonlinearity, and high dynamism.
In battery system modeling, embedded hybrid modeling manifests primarily in three forms: physical regularization, structural embedding, and physics-informed neural network construction. The first and most common approach involves incorporating physical laws as regularization terms in the loss function of data-driven models. For instance, when predicting variables such as the SOC, SOH, or temperature, constraints like conservation laws (e.g., charge or energy conservation), system stability conditions, or boundary conditions can be added to ensure physical consistency. These constraints guide the model to maintain reasonable physical behavior while optimizing its data-fitting accuracy, effectively mitigating issues such as overfitting, unreasonable predictions, or poor generalization.
The second form is structural embedding, where prior physical model information is integrated into the architectural design of neural networks. For example, the structure of an equivalent circuit model can be directly embedded into a neural network, ensuring that certain layers’ connections, activation functions, or output features carry explicit physical meaning. A typical approach involves outputting RC parameters from the network while constraining their value ranges to align with real battery response behaviors. Alternatively, some studies embed discretized forms of heat conduction differential equations into networks or use neural ordinary differential equation (ODE) frameworks to simulate the temporal evolution of battery states. This method enhances models’ interpretability and robustness, which has made it more readily accepted in industrial applications.
The third approach involves constructing neural networks based on physical differential equations, which are commonly referred to as physics-informed neural networks (PINNs) [72]. PINNs use governing equations—such as heat conduction equations, Fourier’s law, Newton’s law of cooling, or Poisson’s equation—as training objectives, leveraging automatic differentiation to compute physical derivative terms. This enables comprehensive learning of the system’s state space. In UAV battery modeling, PINNs have been applied to predict temperature fields, electric field distributions, and aging behaviors under varying flight conditions and charge–discharge rates. Notably, PINNs demonstrate robust reconstruction and inference capabilities in scenarios with incomplete boundary conditions or sparse sensor data, providing reliable support for flight safety and battery management.
The primary advantage of embedded hybrid modeling lies in its ability to fully leverage existing physical knowledge, which enhances the credibility and constraint adherence of data-driven models. Compared to series and parallel hybrid models, embedded approaches more closely align with the true behavior of physical systems, which makes them particularly suitable for high-precision, safety-critical tasks such as thermal runaway prediction, thermo-electro-mechanical coupled modeling, and degradation mechanism diagnosis. Additionally, the transparent and physically consistent internal structure facilitates the causal analysis and mechanistic interpretation of predictions.
However, embedded hybrid modeling faces significant challenges. On one hand, the design and training processes are highly complex, requiring a deep integration of mathematical physics and deep learning expertise, and thus demanding interdisciplinary knowledge from modelers. On the other hand, the inclusion of physical constraints may reduce models’ flexibility and fitting capacity. If the physical knowledge is inaccurate or overly simplified, it could inadvertently limit the performance of the data-driven model. Furthermore, the difficulty of hyperparameter tuning and the elevated demands on computational resources and optimization algorithms pose additional hurdles.
Overall, embedded hybrid modeling represents a cutting-edge direction in the fusion of physical modeling and artificial intelligence. Its high-fidelity, strongly constrained, and highly interpretable characteristics make it particularly well-suited for complex, high-risk, and high-dimensional energy storage systems. With the development of emerging technologies such as symbolic regression, graph neural networks, and neural differential equations, the construction and optimization of embedded models will become increasingly flexible and powerful. In the future, embedded hybrid modeling is poised to become a cornerstone for intelligent battery management, digital twins, and adaptive control in energy systems.
4. UAV Battery State Estimation and Fault Diagnosis Early Warning
4.1. State Estimation of UAV Batteries
As UAV batteries are the core component of unmanned aerial systems, their performance directly affects UAVs’ flight endurance, safety, and task efficiency. State estimation is a key task of the battery management system, covering the state of charge (SOC), state of health (SOH), state of power (SOP), state of energy (SOE), and remaining useful life (RUL), providing a basis for optimizing flight control, extending the battery life, and ensuring safe operation.
The SOC reflects the current available capacity of the battery and is the core of real-time flight management; the SOH quantifies the aging degree of the battery, guiding maintenance and replacement decisions; the SOP describes the instantaneous power capability, ensuring stability during highly dynamic flights; the SOE measures the remaining available energy, allowing for the optimization of task planning; the RUL predicts the battery life, supporting long-term operation.
Traditional state estimation relies on physical models, requiring accurate mechanism descriptions and complex calculations, and exhibiting difficulty in adapting to the variable working conditions of UAVs. In recent years, data-driven methods, including neural networks, regression, optimization, and logic-based models, have become a research hotspot due to their nonlinear fitting and generalization capabilities. These methods use voltage, current, temperature, and other data to achieve high-precision estimation through rule reasoning, probabilistic modeling, or optimization algorithms.
However, data-driven methods face challenges such as high data requirements and a lack of interpretability. By explaining the applications of neural networks, regression, optimization, and logic-based methods in SOC, SOH, SOP, SOE, and RUL estimation, analyzing their advantages and limitations, and looking forward to hybrid modeling and intelligent trends, this paper provides a reference for efficient battery management.
4.1.1. Introduction to State Parameters
The state of charge is one of the most widely used parameters for estimating battery capacity. Estimating the battery SOC is a challenging process, as the chemical energy stored in a battery is not readily accessible, and the presence of nonlinear parameters further complicates the estimation [73]. The remaining stored energy in a battery represents its SOC [74]. Periodically determining the SOC helps extend the battery life, improves control strategies, and provides protection against overcharging and undercharging.
The SOC generally refers to the ratio of the remaining capacity to the total available capacity , indicating the current level of stored electrical energy in the battery. An SOC value of 0% indicates that the battery is fully discharged, whereas an SOC of 100% indicates that the battery is fully charged.
The state of health (SOH) plays a critical role in assessing the performance of a battery over time and significantly influences the efficiency, cost, and reliability of associated systems. Understanding the SOH helps predict battery degradation and optimize maintenance strategies, and thereby improves the reliability and cost-effectiveness in various applications such as electric vehicles and renewable energy storage systems. Accurate SOH estimation can also identify potential risks associated with battery aging and degradation, and thereby contributes to improved safety.
The SOH is a subjective indicator that is affected by various factors, including the temperature, current rate, and cutoff voltage. During charge and discharge cycles, the SOH tends to decline gradually. Due to the diverse characteristics of power batteries, definitions of SOH vary across countries and institutions, which has resulted in a lack of consensus on its exact meaning. Currently, SOH estimation is primarily expressed in terms of factors such as the capacity, energy, internal resistance, and remaining number of charge–discharge cycles [75,76]. Although the SOH depends on these parameters, it is essentially defined as a comparison between the health and performance of an aged battery and those of a brand-new battery of the same type [77]. The SOH is typically determined by the ratio of the battery’s current actual capacity to its rated (nominal) capacity , as shown in Equation (12).
Accurate estimation of the state of energy is crucial for the rational energy allocation of lithium-ion battery energy storage systems. A precise and effective SOE estimation can better address the issue of battery energy distribution and ensure the safe operation of the battery. Compared with the SOC, the SOE provides a more accurate representation of the battery’s state in terms of its remaining energy, shareable charge, and health. The SOE cannot be directly measured; instead, it must be indirectly estimated using measurable variables such as the voltage, current, and temperature [78]. The formula for the SOE is given as follows:
where represents the remaining energy of the battery and denotes the nominal total energy. The remaining energy can be estimated by integrating the voltage, current, and time.
Here, represents the battery voltage, is the battery current (positive during charging and negative during discharging), and denotes the initial energy.
The state of power is defined as the ratio of the peak power to the nominal power. Under the constraints of the voltage, current, SOC, and power limits, the peak power refers to the maximum power the battery can continuously deliver over a specific period of time [79]. The SOP represents the maximum available power that can be drawn from or delivered to the battery within a given future time frame.
In unmanned aerial systems, the SOP is a critical parameter in ensuring flight capabilities such as takeoff, rapid speed changes, hovering, and executing high-load missions [80]. Any estimation error in the SOP may result in abnormal power distribution, which would negatively impact the flight performance and potentially cause mission failure. The SOP is typically divided into maximum charging power and maximum discharging power, which can be estimated using the following equations.
Here, denotes the maximum discharge power, represents the maximum charge power, and is the open-circuit voltage.
As an internal state parameter, the SOP is influenced by a variety of factors. It is constrained not only by design parameters such as the cut-off current, cut-off voltage, cut-off SOC, and temperature, but also by battery characteristics such as the capacity, internal resistance, and polarization parameters. For instance, as the battery undergoes aging, a reduction in capacity or an increase in internal resistance will lead to a gradual decline in the SOP [81].
The main challenges in SOP estimation arise from two aspects. First, battery operation is a highly nonlinear and dynamic process that is subject to multiple constraints. Second, the key influencing parameters for SOP estimation—such as the SOC, capacity, and resistance—are themselves subject to parameter uncertainties. Accurately estimating these parameters is a complex task in itself. Therefore, compared to the SOC and SOH, the research on SOP estimation remains relatively underdeveloped.
Accurate estimation of the remaining useful life (RUL) of lithium-ion batteries is essential for the widespread deployment of these batteries as energy sources in unmanned aerial vehicles. In general, the RUL of a battery is defined as the number of cycles at which its capacity degrades to 80% of the initial value, which is known as the end of life (EOL) [82]. denotes the cycle at the battery’s end of life, and is the current cycle.
In addition to improving battery efficiency, accurate lifetime prediction techniques can significantly reduce the likelihood of unexpected failures. Determining the remaining useful life of lithium-ion batteries is critical for maintaining their performance and enhancing battery management systems. The RUL refers to the number of charge–discharge cycles from the beginning of life to the end-of-life (EOL) of a battery under specific operating conditions, with a typical degradation threshold being 20% capacity loss at EOL [83].
Several variables influence battery capacity degradation, including charge–discharge profiles, the ambient temperature, the electrode materials, and the capacity regeneration behavior. A fundamental understanding of the factors that affect the RUL is essential for advancing battery technologies. However, accurately predicting the RUL remains a significant challenge due to the complexity and nonlinearity of internal degradation mechanisms, as well as the dynamic operating conditions encountered in real-world applications.
4.1.2. State Estimation Methods
Current research methods can generally be classified into four categories. The UAV battery state estimation parameters and methods are shown in Figure 10:
- Battery characteristic-based methods: these include table look-up methods, the open-circuit voltage method (OCV-SOC), and the ampere-hour integration method;
- Model-based methods: These include electrochemical models, equivalent circuit models, electrochemical impedance spectroscopy models, and fractional-order models;
- Data-driven methods: these include machine learning methods such as support vector machines, artificial neural networks, fuzzy logic, and deep learning methods such as genetic algorithms, particle swarm optimization, extended Kalman filter algorithms, and unscented Kalman filter algorithms;
- Hybrid methods: these include combinations of model-based and data-driven approaches, as well as data-driven and data-driven combinations, such as LSTM combined with extended Kalman filtering, equivalent circuit models combined with extreme learning machines, equivalent circuit models combined with Kalman filtering, and simplified electrochemical models combined with deep learning.
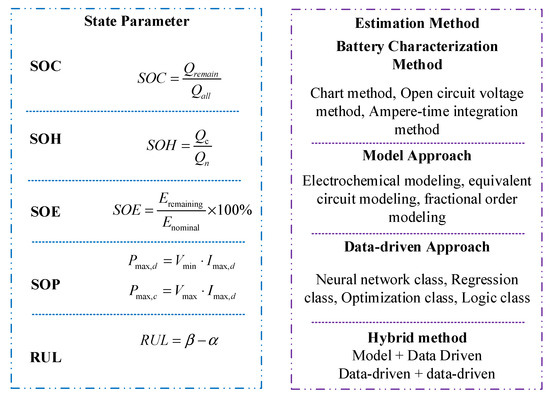
Figure 10.
The UAV battery state estimation parameters and methods.
The lookup table method is simple, with fast computation speed, which makes it suitable for real-time applications. By pre-measuring and recording the voltage–capacity characteristic curve of the battery, the SOC can be estimated based on the current battery voltage. However, its accuracy is limited and significantly influenced by factors such as the battery’s lifespan and temperature. To ensure accuracy, frequent calibration and updating of the lookup table are required, which poses a challenge for practical implementation [84].
Experimental methods include both direct measurement and indirect analysis approaches. Direct measurement involves techniques such as impedance, capacity testing, internal resistance, and AC/DC testing, while indirect analysis includes methods such as ICA, DVA, charging curves, and ultrasonic methods. The ampere-hour integration method is based on the principle of integrating the current, which can accurately estimate the SOC and is characterized by simplicity and efficiency. However, it suffers from integration errors that accumulate over time. Accurate estimates require a long-term, stable charge–discharge process. For short-term or unstable charging/discharging processes, the estimation accuracy is lower. This method is highly sensitive to initial values and often exhibits significant errors. It relies on electrochemical microcell models that describe the terminal behavior. Additionally, it monitors internal physical factors, such as the temperature, potential, and ion flow. However, balancing computational complexity and SOC prediction accuracy is difficult for such models [85].
The open-circuit voltage (OCV) method is simple and easy to implement. The relationship between the OCV and SOC is derived from extensive tests in controlled environments (e.g., laboratories) to characterize battery’s behavior. While the OCV-SOC method is easy to use and yields accurate results, although it requires a long settling time after each charge or discharge to reach equilibrium, which makes it unsuitable for real-time estimation in lithium-ion batteries.
Mechanism-based methods evaluate the SOH by considering the impact of various factors during battery aging based on the battery’s chemical reaction mechanism. This includes models such as RC equivalent circuit models [86], Thevenin equivalent circuit models [87], and electrochemical models. State observers are designed based on these models, where the SOH is treated as a state variable and health-related parameters are iteratively identified to estimate it. This method is accurate, but the model-building process is complex and involves numerous parameters. Despite maintaining high estimation accuracy, such models suffer from sensitivity and vulnerability to disturbances, which limits their application in real scenarios. Equivalent circuit models are typically combined with Kalman filters (KF) to estimate the SOE [88,89]. For instance, Lai et al. [90] proposed a novel SOE method using particle filters (PFs) and extended Kalman filters (EKFs) to handle uncertain total usable energy loss and environmental temperature insensitivity, achieving a maximum error of less than 3%. Although the use of ECM-based methods improves the SOE estimation accuracy, the precision of the ECM model directly impacts the estimation results, requiring substantial time for model construction. Neural network models [91], which do not require ECM construction, exhibit strong generalization ability across different battery types. The mainstream approach for estimating battery SOP is based on the dynamic estimation of the SOP using equivalent circuit models, but electrochemical models offer higher accuracy as they can comprehensively describe internal processes and characteristics.
Battery SOC and SOE are two primary states that represent real-time battery status. Various SOC and SOE estimation methods have emerged in recent years. In reference [92], two independent H-infinity algorithms were used to estimate the SOC and SOE. The results showed high accuracy under dynamic operating conditions, but the overall method is highly complex, as the algorithm’s complexity is proportional to the computational load of the battery management system (BMS). There remains a need to balance the accuracy and complexity of combined SOC and SOE estimation methods. As discussed in [93], a positive correlation exists between the SOC and SOE, with claims that this relationship remains unaffected under dynamic working conditions. Leveraging this feature, a simpler combined estimation method for the SOC and SOE was developed, in contrast to using two separate estimation algorithms.
Electrochemical models use partial differential equations (PDEs) to describe physical and chemical phenomena such as diffusion, electrochemical kinetics, and intercalation occurring within the battery. Due to the coupled time-varying PDEs, these models are computationally challenging. Common electrochemical models include one-dimensional models [94], pseudo-two-dimensional models [95], quasi-three-dimensional full-order physical models [96], and first-principles models [97]. To reduce the computational time, a single-particle model has been proposed. Compared to electrochemical models, equivalent circuit models achieve a better balance between model complexity and estimation accuracy. While the second-order RC equivalent circuit model is widely used, it exhibits simulation distortion in high-SOC and low-SOC regions [98]. Considering the fractional characteristics inherent in capacitors within equivalent circuits, fractional-order modeling methods more accurately represent the dynamic characteristics of batteries. A physical data fusion framework was proposed for accurate SOC estimation of lithium-ion batteries which combines fractional-order Kalman filters (FOEKFs) with error models established by long-short-term memory (LSTM) to improve the estimation accuracy by compensating for errors [99]. Model-based SOC algorithms, such as extended Kalman filters (EKFs) and unscented Kalman filters (UKFs), are common methods for SOC estimation. EKFs and UKFs are based on equivalent circuits, where the parameter identification results directly affect the prediction accuracy.
Data-driven models primarily include four categories: neural networks, regression, optimization, and logic-based methods. For data-driven SOC and SOH estimation, large amounts of battery test data are collected, and various data analysis methods, including support vector machines (SVMs), neural networks (NNs), and particle filters (PFs), are used to predict and estimate the SOH of lithium batteries. These methods do not require the construction of complex battery equivalent models; however, the accuracy of SOC and SOH estimation often depends on the depth and breadth of data collection [100].
Data-driven methods do not rely on specific battery models but instead utilize statistical techniques to establish the relationship between the battery input-output behavior and SOC. These methods typically use large input-output datasets to train machine learning or artificial neural network models. The trained models are then used to estimate the SOC based on battery input signals (e.g., current, voltage, and temperature). Data-driven methods are flexible and adaptable to different battery chemistries and operating conditions. A non-parameterized SOC simplification modeling and non-parameter estimation method was proposed in [101]. Zhang et al. developed a kernel-based extreme learning machine for SOC estimation [102]. However, these data-driven methods may require a substantial amount of training data and may be sensitive to variations in operating conditions. While deep learning models can effectively train nonlinear models using inputs and the SOC, their estimation accuracy still needs improvement. In some cases, large discrepancies exist between the estimated and actual values. To improve SOC estimation accuracy, training options for learning models were systematically compared, and an optimal model was proposed by optimizing network parameters using GRU models for accurate SOC estimation [103].
In reference [104], fuzzy entropy (FE) was proposed as a feature for SOH estimation. FE is a powerful feature for accurately estimating the SOH of lithium-ion batteries independently of aging conditions and battery chemistry. A SVM was used to establish an FE-SOH mapping. The model’s high performance was validated under various calendar and cycle aging conditions using LFP chemistry.
For the issue of SOH imbalance, a technique for lifespan extension balancing based on the internal resistance, capacity, and SOC was proposed. The method uses equivalent circuit models to represent internal chemical behaviors, and its accuracy depends on the speed of parameterization. These methods exhibit nonlinearity during battery aging and show limitations in their dynamic capability and adaptability when considering aging and failure. A novel SOH module balancing algorithm was proposed using degradation parameters which derives the SOH from the most effective health degradation parameters based on the DOD and charging rate. A power-sharing control algorithm to achieve SOH balance was also developed [105].
Zhang et al. [106] proposed a deep belief network (DBN)-based model, aiming for differentiation and accuracy, using multi-objective genetic algorithms to construct an ensemble model. However, due to the high sensitivity of deep learning to structural complexity, existing ensemble frameworks struggle to balance accuracy while maintaining the independence of base models. For key diversity generation methods, researchers tend to use a single disturbance scheme, which leads to insufficient model diversity and redundancy and thus affects the enhancement of deep learning by ensemble learning.
To address these issues, a two-stage selective deep neural network ensemble-based RUL prediction method was proposed [107]. Using high-dimensional, multi-type battery status monitoring data as the input, hierarchical multi-method joint disturbances were adopted to ensure the diversity of the candidate set during deep neural network construction.
For hybrid methods, Xu et al. [108] proposed Coulomb counting and first-order RC models to estimate the SOC of lithium-ion batteries. GAs were used to optimize battery parameters, and the verification results showed that the proposed method could estimate the online SOC using various driving cycles. Five different ECM parameters for SOC estimation were optimized using classic GAs [109]. A GA was used for weight optimization, with a single hidden layer BPNN and an output that was only for SOC. The Thevenin ECM was used to calculate the OCV, and the decay KF was used to estimate the SOC. PSO technology was used in [110] to determine unknown parameters in the second-order ECM and to determine the OCV. SOC estimation was iteratively updated, and particle positions were adjusted until the stopping conditions were met. PSO was also applied for optimal parameter search, with a SVM being used for SOC estimation [111]. The results showed faster convergence and better precision compared to traditional SVMs, with an error limit of 1.3%. Other model-based approaches used in conjunction with data-driven models for lithium battery SOC estimation include RBFNN and EKF. SOC estimation is accomplished using EKFs, while RBFNN training is performed offline using a lithium battery dataset, yielding an RMSE of less than 3%.
Although convolutional neural networks (CNNs) and long short-term memory models (LSTMs) have been used for the RUL prediction of LIBs [112,113], previous evaluations often faced overfitting issues due to small datasets. Some researchers have developed models using expanded datasets and their parameters to improve generalization, further enhancing these models by incorporating Bayesian optimization in the hyperparameter tuning process to boost the performance of CNNs and LSTMs [114].
Following data-driven approaches, a convolutional and LSTM neural network with attention mechanisms was proposed in [115]. Unlike the previous work, our focus is on improving the accuracy of final lifecycle estimation by adopting data augmentation and customized loss functions. This is crucial because accurate RUL estimation becomes more critical as the end of life of the battery approaches, a concern that is often overlooked in other works.
Battery status estimation for drones is crucial to ensuring their flight performance and safety, and involves precise predictions of the SOC, SOH, SOP, SOE, and RUL. Neural networks excel in capturing complex nonlinear relationships, which makes them suitable for dynamic conditions, but they require large amounts of data and have high computational costs. Regression methods provide simple and efficient fitting with strong interpretability but limited dynamic modeling ability. Optimization methods use global searching to optimize parameters, fitting high-dimensional problems but facing challenges in parameter tuning and real-time performance. Logic-based methods excel in rule-based reasoning, offering interpretability, but their flexibility is limited by the need for human expert involvement.
4.2. UAV Fault Diagnosis and Early Warning
The widespread use of unmanned aerial vehicles in fields such as aerial photography, logistics, disaster monitoring, and defense has made them a pillar of modern technology. As UAV batteries are the core power source of UAVs, their reliability is directly related to flight safety and mission success. Battery failures, such as internal short circuits, thermal runaway, or electrode degradation, can lead to a sudden reduction in flight time, system failure, or even crashing. Therefore, fault diagnosis and early warning technologies, through real-time monitoring, anomaly detection, and risk prediction, ensure the stable operation of UAVs. This paper provides a comprehensive review of fault diagnosis and early warning methods based on feature extraction, time-series modeling, and probabilistic reasoning in UAV battery systems. It analyzes the technical advantages, limitations, and future trends of these methods, offering insights for improving the reliability of UAV battery management.
UAV battery systems exhibit a range of fault modes, and the failure mechanisms are typically very complex. From a control perspective, these fault modes can be categorized into battery faults, sensor faults, and actuator faults. Battery faults include overcharging, over-discharging, overheating, external short circuits (ESCs), internal short circuits (ISC), electrolyte leakage, swelling, accelerated degradation, and thermal runaway (TR), which are the most critical failures in UAV battery systems. These failures are often interrelated. Overcharging and over-discharging can lead to various adverse side reactions in the battery, accelerating its degradation. The gases generated during side reactions and thermal runaway can eventually cause battery swelling. This swelling, along with mechanical damage, can further lead to electrolyte leakage.
In addition to battery faults, sensor faults can also severely impact the operation of UAV battery systems, as all feedback-based algorithms in the battery management system (BMS) heavily rely on sensor measurements. Sensor faults in UAV battery systems primarily involve voltage sensor faults, current sensor faults, and temperature sensor faults. Current sensor faults can affect the estimation of battery state parameters and the accuracy of multi-state estimation [116]. The estimated state parameters and temperature measurements are used to update battery model parameters in real-time, which enables high-precision predictions. Lithium-ion batteries must operate within safe voltage and temperature ranges [117]. Exceeding these ranges can degrade batteries’ performance and even cause accidents. Voltage and temperature sensor faults may also lead to balancing errors and thermal management issues in the BMS.
Compared to battery and sensor faults, actuator faults have a more direct impact on the control system’s performance. The literature [118] summarizes potential actuator faults in battery systems, including terminal connector faults, cooling system faults, controller area network bus faults, high-voltage contactor faults, and fuse faults. A cooling system failure may prevent the battery from maintaining an appropriate operating temperature range, which can potentially trigger thermal runaway. Battery connection faults not only result in insufficient power supply but also increase the risk of accidents [119]. Poor connections between battery cells can lead to increased resistance and result in excessive abnormal heat generation and subsequent rises in temperature [120]. As the charge and discharge processes continue, arcing or sparking may occur, causing battery terminals to melt.
Currently, the fault diagnosis of UAV battery systems still faces numerous challenges. There is limited research on the fault diagnosis of UAV battery systems in the existing literature. To provide a clear and systematic understanding of the current state of fault diagnosis technologies for UAV battery systems, this paper comprehensively reviews the fault mechanisms, fault features, and fault diagnosis technologies of lithium-ion batteries, sensors, and actuators in UAV battery systems, as shown in Figure 11.
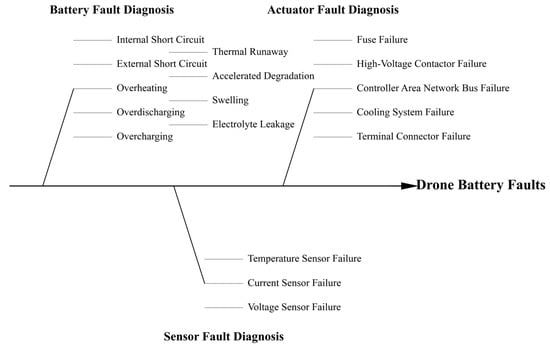
Figure 11.
UAV battery failure fishbone diagram.
4.2.1. Lithium-Ion Battery Fault Diagnosis
Fault diagnosis methods for batteries generally include model-based approaches, data-driven approaches, knowledge-based approaches, and hybrid methods that integrate multiple techniques.
The model-based approach relies on battery models and measurement data, using state estimation and parameter estimation techniques to generate residuals for fault detection. Fault isolation can be achieved by constructing fault feature tables. Due to its simplicity and intuitiveness, the model-based approach is widely used for the fault diagnosis of both individual battery cells and battery packs. Alavi et al. [121] used electromagnetism as a foundation and applied the particle filter (PF) algorithm to estimate the lithium ion transport rates in the positive and negative electrodes, then compared the estimated data with boundary conditions to detect lithium plating. Since overcharging and over-discharging can cause changes in model parameters, Sidhu et al. [122] utilized electrochemical impedance spectroscopy theory to guide and improve equivalent circuit models. Based on the analysis of impedance spectra in the high- and mid-frequency ranges as functions of the battery’s state of charge and temperature, they proposed a variable-order equivalent model using the Arrhenius equation and Bayesian information criterion. Additionally, the autoregressive equations were employed to refine the state and observation equations of the variable-order ECM. Song et al. [123] developed a fault diagnosis algorithm based on a lithium-ion battery equivalent circuit model integrated within a neural network framework. This method embeds the deterministic structural components directly into the ECM, while the uncertain components are modeled by the neural network, which allows for leveraging the high accuracy of the physical model alongside the powerful nonlinear processing capability of neural networks to enhance fault diagnosis performance.
Li et al. [124] proposed a framework that combines electrical and thermal models, employing particle swarm optimization to identify optimal thermal model parameters using real-time open-circuit voltage and terminal voltage data. The framework also integrates an unscented Kalman filter estimator to predict the core temperature based on real-time surface temperature measurements and diagnoses faults by analyzing the rate of change in the estimated temperature. In reference [125], Yun et al. introduced a backstepping-based fault localization filter that is capable of localizing faults without requiring full-state temperature measurements. The method ensures reliable thermal fault detection through FLF design, distributed residual evaluation, and threshold computation. Furthermore, in [126], they used a partial differential equation (PDE)-based model to detect and estimate the magnitude of thermal faults.
Phenomenological models are also capable of capturing correlations due to overcharging and abnormal heating in ISC (internal short circuit) batteries, which affect their voltage and temperature responses. Shrivastava et al. [127] employed a recursive least squares method with a forgetting factor to estimate model parameters. Their model incorporates parallel resistance, capacitance, ohmic resistance, and the temperature derivative of the equilibrium potential within the energy conservation equation. Based on the variations in these key parameters, internal short circuit (ISC) fault detection is performed. Yang et al. [128] proposed an ISC detection method based on a transformation matrix and an improved state-space model for ISC resistance calculation. By capturing the characteristic voltage slope decline of ISC cells within the battery pack through shear elements in the matrix and designing an online detection procedure that leverages the inverse variation relationship of shear elements between adjacent cells, the method significantly enhances the effectiveness and superiority of ISC detection.
The model-based approach combines the related information of adjacent cells in a battery pack. Fault diagnosis can be achieved by analyzing the differences in state parameters and model parameters between the faulty and healthy batteries. For example, Zhang et al. [129] combined a physics-based observer with a bidirectional long short-term memory neural network, enabling the observer to learn uncertainties and effectively distinguish soft fault information from uncertainties within residuals. Moreover, by leveraging the memory capabilities of the bidirectional long short-term memory neural network and optimizing training data and input features, the robustness of the detection system was significantly enhanced.
Data-driven approaches extract fundamental patterns from large datasets of battery samples. However, due to the difficulty in obtaining large amounts of battery fault data, these methods are currently less commonly applied in battery fault diagnosis. For example, Chen et al. [130] proposed a hybrid neural network fault diagnosis model that integrates a deep learning system with a convolutional neural network. The deep learning system eliminates temporal features from raw current signals and captures more comprehensive and representative sample features within a broad feature space. Subsequently, the CNN is employed for feature extraction and classification tasks. This current-signal-based fault diagnosis approach for UAV motors addresses the challenge of limited training samples in fault data, overcoming the difficulty of traditional machine learning and deep learning methods in identifying representative features from small datasets.
Cabahug et al. [131] developed a fast and accurate fault detection system utilizing the unsupervised learning k-means clustering algorithm. The system was validated during experimental flights of a UAV using an LED subsystem to visually represent the proposed algorithm, and its effectiveness in rapidly and accurately detecting faults was demonstrated. Kim et al. [132,133] proposed a distance-based outlier detection method and used Z-score normalization preprocessing for battery fault diagnosis. They performed cluster analysis on estimated capacity and resistance parameters to detect healthy, short-circuited, and aging faulty batteries.
Knowledge-based fault diagnosis relies on understanding battery mechanisms and long-term accumulated knowledge and experience. Xiong et al. [134] proposed a rule-based method for detecting over-discharge in lithium-ion batteries. Temperature rise and voltage drop during over-discharge were used to establish temperature and voltage rules, and faults were detected and warned about using Boolean expressions. However, determining appropriate fixed or time-varying thresholds for the rules is challenging in practical applications.
Guo et al. [135] proposed an uncertainty-aware LSTM-based fault detection method for unmanned aerial vehicles. Initially, a prediction-based fault detection model was established using LSTM, wherein time-series features that were indicative of model prediction uncertainty were constructed on selected inputs to more accurately characterize dynamic flight conditions. An adaptive threshold estimation space was then developed based on an enhanced distribution-based conditional clustering approach to obtain fault detection thresholds under various flight conditions, which were further smoothed to mitigate interference effects. Experimental results from simulations and real flight data demonstrated that the proposed method achieves superior fault detection performance under dynamic flight conditions through the incorporation of a fault detection model with progressively adaptive thresholds. Huber et al. [136] proposed a method for classifying separator defects in batteries using optical detection and integrated expert knowledge, machine learning, and machine vision during the diagnostic process. This hybrid approach, which combines multiple diagnostic technologies, typically offers high accuracy and robustness, although it does so at the cost of increased computational complexity.
4.2.2. Sensor Fault Diagnosis
The sensor fault diagnosis methods used in unmanned aerial vehicle battery systems can be classified into three types: sensor topology-based methods, model-based methods, and fusion methods. Sensor topology-based methods primarily rely on the configuration of the sensors and the redundancy of sensor functions, which makes them easy to implement. Xia et al. [137] proposed a redundant voltage measurement topology for series battery packs which replaces individual cell measurements with total voltage measurements and employs matrix-based structural analysis to isolate faults in voltage sensors and individual cells. Building upon this, Yang et al. [138] introduced a correlation coefficient method to establish bidirectional redundancy relationships between sensors and connection resistances, enabling the effective separation of voltage sensor faults, short-circuit faults, and connection faults.
Kang et al. [139] proposed a multi-fault diagnostic scheme that combines voltage measurement topology and correlation coefficient methods, where the correlation coefficient is used to detect fault features. In this sensor topology, each unit and connecting resistor is associated with two sensors, which thereby enables the isolation of voltage sensor faults, short-circuit faults, and connection faults.
Model-based methods use sensor measurement data and prior information or constraints expressed by models to generate residuals. By analyzing and evaluating these residuals, the degree, type, and location of faults can be determined. Typical battery models used for sensor fault diagnosis include electrical models, equivalent circuit models, superimposed parameter thermal models, and dual-state superimposed parameter thermal models.
Lombardi et al. [140] tested the electrical relationship between current and voltage sensor measurements based on Kirchhoff’s laws to generate residuals, and implemented fault detection and isolation (FDI) for voltage and current sensors using the residual sets associated with each sensor and the battery pack structure. Zhang et al. [141] proposed a systematic approach that applies structural analysis theory to detect and isolate faults in voltage, current, and temperature sensors. Specifically, they identified the structurally overdetermined parts of the system model, which was followed by analyzing the fault detectability and isolability. Subsequently, diagnostic tests were developed by selecting minimal overdetermined sets. Residuals were generated by examining analytical redundancy relations within each test. Structural analysis theory [142,143] can effectively reduce the effort involved in selecting residual generators; however, such analyses are susceptible to noise and model uncertainties.
Due to inaccurate initial values, unknown disturbances, and noise, the residuals directly generated by the model’s constraint relations may contain errors. Observers and filters can reduce the impact of these factors. Sensor fault diagnosis methods based on various observers follow a similar process, as shown in Figure 12. These methods first estimate the battery states based on the battery model and the measurements from current, voltage, and temperature sensors. Then, by comparing the measured outputs with the estimated outputs, residuals containing sensor fault information are generated. Finally, sensor FDI is achieved through residual evaluation, and alarms and fault flags are set. Mukherjee et al. [144] modeled current sensor faults as bias signals in the system input and employed a proportional-integral observer (PIO) to achieve fault detection and estimation. While this method is accurate and easy to implement, improper PIO parameter settings may lead to instability in the diagnostic system.
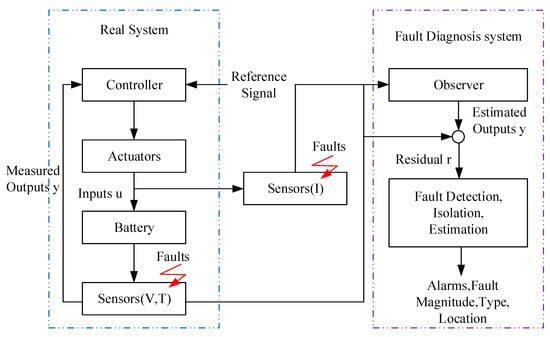
Figure 12.
Observer-based sensor fault diagnosis.
Zhang et al. [145] proposed a novel fault diagnosis framework based on multiple performance indices of closed-loop control systems, providing standards for quantification, SAR residual normalization, and explicit mapping between thresholds and the desired performance. By monitoring the length and direction of normalized residual vectors in the SAR performance residual space, simultaneous fault detection and isolation can be easily achieved. This method assumes that a subset of inputs and outputs is fault-free. Under this assumption, the system’s forward and inverse models generate residuals, but the minimum detectable fault magnitude is limited by observer errors. Shahzad et al. [146] employed a sliding mode observer for sensor fault diagnosis and fault-tolerant control by reconstructing sensor faults with the SMO, which are then fed to the control block post-compensation. Simulation-based analyses were conducted by presenting results of state/output estimation, estimation errors, fault reconstruction, estimated disturbances, and fault-tolerant control performance. Vafamand et al. [147] proposed a model-based diagnosis scheme using an adaptive extended Kalman filter to estimate the state of individual batteries for detecting current or voltage sensor faults. The method shows robustness to inaccurate initial values and noise; however, precise determination of the process noise covariance matrix in EKF remains challenging in practice. Tudoroiu et al. [148] implemented the FDI of current and voltage sensors in series battery packs using AEKF, which adaptively tunes process and measurement noise covariance matrices [149] and thereby exhibits improved noise robustness.
Strategies that combine multiple model-based methods can compensate for the inherent limitations of individual approaches. For example, diagnostic tests based on structural analysis theory were constructed [150], and EKF-generated residuals were obtained for each test. The generated residuals were further evaluated through statistical cumulative sum tests to detect sensor faults. This fusion approach reduces the effort needed to find suitable residual generators and enhances models’ robustness against noise and inaccurate initial values, but it also increases the system complexity and computational cost.
4.2.3. Actuator Fault Diagnosis
Actuators with different functionalities exhibit diverse fault mechanisms and characteristics. As such, there is no universal diagnostic method that is applicable to all actuator faults. Two typical approaches for actuator fault diagnosis are model-based techniques and signal processing methods. Model-based approaches can be directly applied to fault diagnosis in cooling systems. In battery systems, the cooling subsystem—which includes cooling fans and drive motors—serves to enhance heat dissipation. The effective heat transfer coefficient is a parameter in thermal models and varies with the type of convection. Therefore, faults in the cooling system can be considered as deviations in thermal model parameters and can be detected using conventional model-based methods. Liu et al. [151] implemented the fault detection and isolation (FDI) of cooling systems based on a block thermal model using structural analysis theory. Fan et al. proposed a battery fault diagnosis method that combines relative entropy with state estimation sliding windows, enabling the rapid detection of SOC shifts caused by sudden connection anomalies. This approach demonstrated strong adaptability and timeliness within UAV power systems [152]. Furthermore, by integrating the cumulative sum detection algorithm, the dynamic identification of various short-circuit faults—including contact faults—was achieved, which is suitable for health management under multiple actuator operating conditions.
In signal processing methods, Hu et al. employed variational mode decomposition combined with Shannon entropy to construct a multiscale diagnostic model for current signals, effectively identifying nonlinear disturbances due to poor connections and demonstrating feasibility for real-time operation during UAV flights [153]. Zhang et al. introduced a hybrid approach that fuses entropy measures with the local outlier factor for actuator fault detection in highly dynamic UAV scenarios. Validation with onboard measured data confirmed the model’s robustness under high-frequency vibration interference [154].
Meanwhile, advancements in information entropy have further promoted the development of multi-source information fusion diagnostic strategies. Liu et al. compared Shannon entropy and fuzzy entropy in terms of their sensitivity to voltage fluctuations under real flight conditions, noting that fuzzy entropy offers superior performance in handling non-stationary states and is thus more suitable for the health assessment of highly dynamic platforms such as UAV actuators [155].
Moreover, Liu et al. proposed a multi-source information fusion model based on structural analysis and Bayesian networks which can be extended to jointly model battery voltage and actuator vibration data. This model enables the refined differentiation of connection faults and intrinsic degradation within UAV systems, providing fault localization and risk level assessment capabilities for UAV battery management systems [156].
Currently, the challenges in fault diagnosis for UAV battery systems can be categorized into two types: those related to the diagnostic target and those related to diagnostic or control methods. Issues associated with the diagnostic target include the following:
- Many battery fault mechanisms remain poorly understood, and there is no unified consensus on fault mechanisms in the existing literature;
- Standardized surrogate testing methods for battery faults have not yet been developed. Destructive methods often suffer from poor controllability and reproducibility and tend to trigger catastrophic faults instantaneously, which makes it difficult to simulate fault incubation phases;
- There is a lack of mature mathematical models that are capable of accurately describing certain fault behaviors—e.g., the modeling of lithium dendrite growth remains a significant challenge;
- The relationship between external symptoms and internal mechanisms is often unclear. Similar fault phenomena may arise from different causes, yet most existing studies focus on single fault mechanisms without accounting for interactions among multiple fault processes.
5. UAV Battery Management System Architecture and Balancing Strategies
The battery management system of unmanned aerial vehicles plays a critical role in ensuring flight endurance, operational safety, and mission efficiency. It is responsible for monitoring, protecting, and optimizing the battery’s performance. Due to the high dynamic load, space constraints, and lightweight design requirements of UAVs, the architecture and balancing strategies of the BMS directly affect the system’s reliability and the battery’s lifespan. The design of a UAV BMSs must integrate state monitoring, fault diagnosis, and optimal control, while balancing strategies are essential for mitigating inconsistencies among individual cells to extend the overall battery life. Based on functional modules, the UAV BMS architecture and balancing strategies can be categorized into three main components: battery charging and control, battery balancing strategies, and battery energy management strategies. Each of these components is reviewed with respect to their technical features, current applications, and development trends, which provides insights for improving the performance of UAV battery management.
5.1. Battery Charging and Control
UAV batteries typically consist of multiple cells connected in series. However, variations caused by manufacturing, handling, or environmental factors may lead to inconsistencies among individual cells, resulting in overcharging, over-discharging, and reduced energy efficiency. Overcharging can cause battery degradation, thermal runaway, or even explosions, whereas over-discharging significantly reduces the energy conversion efficiency, compromising flight endurance. Therefore, managing the balance between charging and discharging is crucial.
Currently, the endurance of most commercial electric UAVs is limited by their battery capacity, which generally does not exceed one hour [157]. To address this limitation, battery replacement remains the most common charging approach, done either manually or through automated operations enabled by BMS–ground station communication. Additionally, wireless power transfer (WPT) has emerged as a promising alternative [158]. WPT transfers energy via electromagnetic induction or magnetic resonance, yet its practical implementation faces technical challenges, such as high-precision landing and efficient energy transfer between the UAV and the ground station. These operations typically rely on real-time battery state information from the BMS, flight control system positioning, and coordinated efforts of the ground station [159].
The charging control strategies for BMSs can be broadly categorized into non-feedback, feedback, and intelligent control techniques [160]. Non-feedback methods include constant current (CC), constant voltage (CV), and constant current–constant voltage (CC-CV) schemes. These techniques, when combined with fast-charging algorithms, can improve the charging efficiency to some extent. However, their inability to respond to real-time battery dynamics limits their adaptability under complex operating conditions. Feedback-based techniques utilize battery models—such as equivalent circuit models or electrochemical models—to estimate the battery state and optimize charging. By monitoring the voltage, current, and temperature in real time, they dynamically adjust the charging profile to enhance safety and efficiency. Intelligent techniques incorporate machine learning, fuzzy logic, and big data analysis to adaptively optimize the charging process, which makes them particularly well suited for scenarios with highly dynamic loads.
Despite the progress of these charging strategies in UAV BMSs, several challenges remain. Non-feedback techniques are too simplistic to account for battery aging or extreme environmental conditions. Feedback-based methods depend heavily on the model accuracy, and complex electrochemical models may exceed the computational capacity of embedded systems. Intelligent methods, while flexible, require extensive training data and may increase the system’s complexity and cost. Therefore, future research should focus on hybrid strategies that combine lightweight modeling with efficient algorithms to develop more adaptive and computationally efficient charging techniques. Moreover, the advancement and integration of WPT technologies with BMSs could further enhance UAVs’ endurance. Through the comprehensive optimization of charging control and hardware design, UAV BMSs are expected to achieve a better balance between safety and efficiency, laying a solid foundation for long-endurance and high-reliability UAV applications.
5.2. Battery Balancing Strategies
In drone battery systems, discrepancies in the electrochemical characteristics among individual cells—stemming from manufacturing variances, transportation conditions, and environmental factors—can lead to imbalances during charging and discharging processes. Such inconsistencies may result in overcharging or over-discharging, accelerating battery degradation, inducing thermal runaway, and potentially causing fires or explosions. Therefore, implementing effective battery balancing strategies is crucial for ensuring operational safety and prolonging batteries’ lifespan.
Battery balancing techniques are primarily categorized into passive and active methods. Passive balancing employs shunt resistors to dissipate excess energy from higher state-of-charge cells as heat and align them with lower SOC cells. While this approach is straightforward and cost-effective [161], it is inherently inefficient due to energy loss and is typically limited to the charging phase. Conversely, active balancing redistributes energy from higher- to lower-SOC cells using components such as inductors, capacitors, or transformers. This method enhances the energy efficiency and can operate during both charging and discharging cycles; however, it involves more complex circuitry and higher costs, which may constrain its widespread adoption in drone applications.
Balancing strategies can also be differentiated based on the parameters that they monitor: into voltage-based, SOC-based, and capacity-based methods [162]. Voltage-based balancing is simple to implement but may overlook internal cell disparities, potentially leading to suboptimal balancing outcomes. SOC-based balancing offers more precise energy distribution by estimating each cell’s charge state in real-time. For instance, a study proposed an SOC-based active balancing technique utilizing Internet of Things technologies [163], which resulted in a cost-effective and reliable battery management system for drones. Capacity-based balancing considers cell aging and degradation, which makes it suitable for long-term applications, albeit with increased computational complexity.
To further enhance the balancing speed and accuracy of these systems, intelligent algorithms such as genetic algorithms, fuzzy logic, and neural networks have been explored [164,165,166,167]. These methods dynamically adjust balancing parameters based on real-time battery conditions, improving the system’s efficiency and adaptability. However, their high computational demands pose challenges for integration into the resource-constrained embedded systems typical of drones. Consequently, developing lightweight algorithms that balance performance with resource consumption is essential.
Given the wide variability in UAV mission profiles, payload capacities, flight durations, and power system architectures, the adaptability of battery balancing strategies has become increasingly critical. Different types of UAVs exhibit diverse requirements for their energy management, and a single balancing strategy is unlikely to achieve optimal performance across all application scenarios. Therefore, it is necessary to formulate principled guidelines for selecting appropriate strategies based on specific operational contexts.
For lightweight, consumer-grade UAVs with limited mission durations, passive balancing strategies remain the mainstream solution due to their low cost and simple circuitry. In contrast, for industrial-grade UAVs that require extended flight times or perform frequent missions, active balancing strategies offer superior performance in managing capacity inconsistencies and mitigating cell aging, owing to their higher energy utilization efficiency and dynamic adjustment capabilities. Moreover, for military or special-purpose UAV platforms with stringent reliability demands, intelligent algorithm-driven active balancing schemes that combine state-of-charge and capacity considerations can provide robust support throughout the mission lifecycle.
Therefore, future UAV battery management system designs should incorporate a standardized selection framework for balancing strategies that is tailored to platform-specific features and task requirements. By introducing task-oriented evaluation metrics, this framework can enable the comprehensive optimization of the cost, energy efficiency, and safety and ultimately deliver customized and highly adaptive energy balancing solutions for various UAV categories.
The future trajectory of drone battery balancing strategies is expected to focus on multi-objective optimization and technological integration. Hybrid approaches that combine active and passive balancing aim to strike a balance between efficiency and cost. Composite methods that integrate SOC and capacity considerations can enhance reliability over prolonged operations. Moreover, advancements in IoT and edge computing facilitate real-time data acquisition and cloud-based collaborative control, offering more precise balancing support. Designing application-specific integrated circuits (ASICs) tailored for drones’ lightweight requirements will also be pivotal in achieving efficient and compact balancing systems, thereby laying the groundwork for extended endurance and heightened safety in drone operations.
5.3. Battery Energy Management Strategies
As previously mentioned, to fully exploit the advantages of various types of batteries, the application of hybrid batteries in unmanned aerial vehicles has become a research hotspot. A typical example is the combination of fuel cells and supercapacitors. The appropriate selection of energy management strategies can ensure that the output power meets the demands of UAVs under different flight conditions, while simultaneously maximizing the flight time and battery lifespan. Therefore, the study of energy management strategies is at the core of hybrid battery development. The common energy management strategies can be categorized into three types: rule-based, optimization-based, and intelligent algorithm-based approaches [168], as shown in Table 7.

Table 7.
Summary of advantages and disadvantages of battery energy management strategies.
Rule-based strategies operate by comparing control variables with predefined thresholds to switch battery packs among different operating modes. This method is easy to implement and suitable for online applications [169]; however, it is highly dependent on manually set parameters and may encounter uncertainties in real-world scenarios [170]. In references [171,172], the power and state of charge were used as control variables to design rule-based strategies for hybrid fuel cell–lithium battery UAVs, and the simulation results validated the effectiveness of these strategies. Nevertheless, the absence of actual flight experiments makes it difficult to assess whether the strategies fulfill real-flight requirements, which thereby limits further exploration of their endurance performance.
Model predictive control (MPC) has emerged as a popular optimization-based strategy. Reference [173] proposed a two-layer fuzzy nonlinear MPC approach to simultaneously manage energy distribution and flight trajectory in UAVs powered by solar cells, fuel cells, and lithium batteries. Further, [174] introduced a hierarchical model in which the upper layer optimizes flight paths based on economic cost and battery lifespan, while the lower layer predicts the battery output power using a grey Markov chain. This model significantly extended the flight endurance, reduced the energy consumption, and demonstrated excellent robustness under complex flight conditions.
Among intelligent algorithms, fuzzy logic has found the widest application. FL relies on predefined rules and employs fuzzy inference to offer more robust control than deterministic rules. In reference [175], a comparison among online FL, passive control, and state-machine strategies revealed that online FL effectively balances the use of fuel cells and lithium batteries. Moreover, applied the particle swarm optimization algorithm to tune the threshold values of FL membership functions, thereby improving the energy distribution efficiency and reducing the hydrogen consumption of UAV batteries.
Despite notable progress in energy management strategies for hybrid battery UAVs, several challenges remain. Rule-based strategies have advantages in real-time performance due to their simplicity, but their limited adaptability to dynamic operating conditions constrains their application in complex flight scenarios. MPC enhances the accuracy of energy management through prediction and optimization, but its computational complexity imposes high demands on the processing capabilities of UAV-embedded systems, especially on resource-constrained lightweight platforms. Intelligent algorithms such as FL and PSO offer excellent adaptability and robustness but rely heavily on high-quality training data and rule design. Moreover, their real-time performance must be further optimized to meet the dynamic requirements of UAV operations.
The development of hybrid battery energy management strategies is expected to focus on multi-technology integration and real-time optimization. By combining the simplicity of rule-based strategies with the predictive capabilities of optimization-based methods, lightweight control frameworks that are suitable for complex flight scenarios can be constructed to enhanced the flexibility and efficiency of the energy allocation in these systems. Meanwhile, intelligent algorithms such as reinforcement learning have shown strong adaptability in dynamic environments, enabling real-time power allocation optimization based on flight demands and thereby improving the endurance and reducing the energy consumption of these systems. With the advancement of edge computing and Internet of Things (IoT) technologies, real-time data acquisition and cloud-based cooperative processing will greatly improve the accuracy and responsiveness of energy management, providing stable support for UAVs under diverse operating conditions. Furthermore, in response to the lightweight requirements of UAVs, low-power dedicated hardware designs, such as high-efficiency energy management chips, will become a key research focus. Through multi-source data fusion, algorithm optimization, and hardware-software co-design, future energy management strategies are expected to achieve high efficiency, intelligence, and reliability, which will lay a solid foundation for the widespread application of long-endurance, high-performance hybrid-powered UAVs.
6. Conclusions and Future Perspectives
6.1. Core Contributions and Research Significance
This study addresses the reliability challenges of UAV battery systems by developing a systematic and scalable analytical framework. It provides a comprehensive review and integrated evaluation that covers multi-dimensional indicator systems, modeling approaches, state estimation, fault diagnosis, and energy management strategies. By introducing a six-dimensional reliability metric—performance–operation–safety–economy–system–emerging Trends—this study proposes a quantitative assessment mechanism that is suitable for complex flight missions, offering theoretical support for future standardization and engineering applications. In terms of modeling, the research clarifies the applicable boundaries of physical models, data-driven models, and hybrid approaches, enhancing the adaptability of models to various flight scenarios. Furthermore, multi-modal fusion and temporal modeling strategies are incorporated into state estimation and fault prediction, which significantly improves the ability to perceive battery status and identify risks under complex operating conditions. In addition, through a comparative analysis of passive and active balancing strategies, this work provides a theoretical foundation and decision-making reference for selecting management strategies in different types of UAV battery management systems.
6.2. Limitations of the Current Study
Despite the systematic advances made in establishing a theoretical framework and summarizing key technologies, this study still faces several limitations concerning engineering feasibility and cross-platform deployment. First, although the proposed multi-dimensional reliability metric system offers strong adaptability and scalability, practical application in UAV missions is challenged by incomplete data acquisition, label scarcity, and the high complexity of scenario modeling. Second, while the current state estimation and fault diagnosis algorithms demonstrate high accuracy in experimental simulations, they generally rely on large-scale, high-quality datasets and significant computational resources, which limits their stable operation on resource-constrained embedded platforms or real-time flight control systems. Moreover, although hybrid modeling methods offer significant advantages in robustness and generalization, their engineering deployment remains hindered by complex model structures, high parameter tuning costs, tight coupling between algorithm modules, and a lack of standardized interfaces—factors that restrict real-time deployment and online learning capabilities.
Finally, most current mainstream BMS architectures remain at the distributed or hierarchical passive management stage. As these systems evolve toward highly integrated, intelligent, and networked architectures, they still lack unified communication protocols, security authentication mechanisms, and remote coordination capabilities. These factors collectively form major barriers in transitioning UAV battery systems from theoretical research to practical engineering applications.
6.3. Future Research Challenges and Open Issues
Future research on UAV battery system reliability must overcome several key challenges: At the standards level, it is necessary to develop a cross-scenario, dynamically evolving reliability evaluation framework that incorporates emerging dimensions such as mission specificity, cybersecurity, and carbon emissions; in modeling, the stronger integration of multi-physics coupling and physics-informed neural networks is needed to enable the edge deployment of high-accuracy, low-power prediction models; for complex flight environments, adaptive state estimation algorithms under uncertainty should be advanced, along with the exploration of causal diagnosis mechanisms for multi-fault coexistence; in system integration, the evolution of BMSs toward highly integrated and intelligent architectures must be promoted, with the development of self-learning management systems supporting dynamic control, cloud coordination, and remote maintenance. Particularly in hybrid battery systems and multi-energy platforms, achieving optimal energy allocation and coordinated scheduling will become a crucial research direction.
6.4. Potential Impact and Application Prospects
The theoretical framework and technical roadmap proposed in this study not only provide valuable insights for enhancing the reliability of UAV battery systems but also demonstrate transferable potential to other energy storage applications such as electric aircrafts, mobile robots, and intelligent IoT nodes. Emphasizing multi-source data fusion, hybrid modeling, and edge deployment methods, this research supports the development of battery system architectures that are capable of high autonomy, task diversity, and full lifecycle management. These capabilities will be critical for advancing the intelligence, safety, and sustainability of unmanned systems. As the low-altitude economy, green aviation, and urban air mobility sectors continue to evolve, this work lays a theoretical foundation and methodological pathway for constructing a future-oriented battery reliability technology system.
Table 8 provides a comprehensive summary of the advantages and disadvantages associated with the principal methodologies across each research domain covered in this study. By systematically comparing modeling approaches, state estimation techniques, fault diagnosis strategies, and energy management methods, the table highlights the respective strengths—such as accuracy, adaptability, and real-time performance—and the limitations—including computational cost, data dependency, and scalability constraints—of these systems. This comparative analysis not only facilitates a clearer understanding of methodological trade-offs but also serves as a practical reference for researchers and engineers in selecting suitable approaches that are tailored to specific UAV battery system applications.

Table 8.
Summary of advantages and disadvantages of main methods in each research area.
Author Contributions
All authors of this paper acknowledge that we have jointly contributed to the preparation of this manuscript. Each author has significantly contributed to the research and writing of this work, providing valuable intellectual content and assisting in the development of the manuscript. T.Z. was responsible for Conceptualization and Software, with major contributions in the development and design of methodology, including the creation of models. He also was responsible for the programming and software development, including designing computer programs, implementing code and supporting algorithms, and testing existing code components. Y.Z. contributed to Investigation and Resources, primarily responsible for conducting the research process, including experiments and data collection, and providing research materials, instrumentation, and computing resources. M.W. contributed to Conceptualization and Validation, formulating the overarching research goals and verifying the reproducibility and reliability of the results. W.F. was responsible for Supervision and Visualization, providing oversight and leadership throughout the research process and preparing the visual presentation of the published work. S.C. contributed to Formal analysis and Writing—original draft, applying formal computational and statistical techniques to analyze the data and drafting the initial version of the manuscript. G.W. was responsible for Project administration and Writing—review & editing, managing and coordinating the planning and execution of the research activities, and contributing to the critical review and revision of the manuscript. Finally, we assert that this manuscript is original and has not been plagiarized. Each of us has endeavored to attribute properly the ideas and words of others and to acknowledge any material used or quoted. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported mainly by the Key Project of Shenzhen Science and Technology Plan Grant No. JCYJ20220818103416035 and Technology Program under grant JCYJ20220530150005011 and Guangdong Basic and Applied Basic Research Foundation under grant 2023B0909050006.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Yanhui Zhang reports financial support was provided by the key project of Shenzhen science and technology plan. Yanhui Zhang reports a relationship with the key project of Shenzhen science and technology plan that includes: funding grants. If there are other authors, they declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| BMS | Battery Management System |
| UAS | Unmanned Aerial Systems |
| SOC | State of Charge |
| SOH | State of Health |
| SOE | State of Energy |
| SOP | State of Power |
| RUL | Remaining Useful Life |
| MTBF | Mean Time Between Failures |
| EKF | Extended Kalman Filter |
| P2D | Pseudo-Two-Dimensional Model |
| SP | Single Particle Model |
| ECM | Equivalent Circuit Model |
| OCV | Open Circuit Voltage |
| ANN | Artificial Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| CNN | Convolutional Neural Network |
| AE | Autoencoder |
| GAN | Generative Adversarial Network |
| LR | Linear Regression |
| PR | Polynomial Regression |
| SVR | Support Vector Regression |
| RFR | Random Forest Regression |
| GBR | Gradient Boosting Regression |
| KAF | Kernel Adaptive Filtering |
| PF | Particle Filtering |
| GA | Particle Filtering |
| PSO | Particle Swarm Optimization |
| DE | Differential Evolution |
| GWO | Grey Wolf Optimizer |
| DRL | Deep Reinforcement Learning |
| FLC | Fuzzy Logic Control |
| DTC | Decision Tree Classification |
| HMM | Hidden Markov Model |
| BN | Bayesian Network |
| FNN | Fuzzy Neural Network |
| DBN | Dynamic Bayesian Network |
| OCV-SOC | Open-Circuit Voltage-State of Charge |
| Ah | Ampere-hour |
| EM | Electrochemical Model |
| EIM | Electrochemical Impedance Model |
| FOM | Fractional Order Model |
| UKF | Unscented Kalman Filter |
| FE | Fuzzy Entropy |
| DOD | Depth of Discharge |
| LIB | Lithium-ion Battery |
| RBFNN | Radial Basis Function Neural Network |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| ESC | External Short Circuit |
| ISC | Internal Short Circuit |
| TR | Thermal Runaway |
| PDE | Partial Differential Equation |
| MSS | Multi-level Screening Strategy |
| AEKF | Adaptive Extended Kalman Filter |
| CC | Constant Current |
| CV | Constant Voltage |
| CC-CV | Constant Current-Constant Voltage |
| MPC | Model Predictive Control |
| PINN | Physics-Informed Neural Network |
| EOL | End of Life |
| DVA | Dynamic Voltage Adjustment |
| KF | Kalman Filter |
| FOEKF | Fractional Order Extended Kalman Filter |
| ICAO | International Civil Aviation Organization |
References
- Telli, K.; Kraa, O.; Himeur, Y. A comprehensive review of recent research trends on unmanned aerial vehicles (uavs). Systems 2023, 11, 400. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F. Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- Onggowidjojo, V.; Ellitan, L. Strategies for Achieving Competitive Advantage: The Case of Amazon. Int. J. Res. 2023, 10, 249–265. [Google Scholar]
- Butcher, G.B. In the Eye of the Reaper: Drone Pilots, Remote War, and Resistance in the United States. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2024. [Google Scholar]
- MH/T 6043-2021; Airworthiness Standards for Medium Civil Unmanned Aircraft Systems. Civil Aviation Administration of China (CAAC): Beijing, China, 2021.
- T/CAAC 002–2022; Electric Multirotor Unmanned Aircraft Systems for Urban Logistics Scenarios. Civil Aviation Administration of China (CAAC): Beijing, China, 2022.
- Wanner, D.; Hashim, H.A.; Srivastava, S. UAV avionics safety, certification, accidents, redundancy, integrity, and reliability: A comprehensive review and future trends. Drone Syst. Appl. 2024, 12, 1–23. [Google Scholar] [CrossRef]
- Rajabi, M.S.; Beigi, P.; Aghakhani, S. Drone delivery systems and energy management: A review and future trends. In Handbook of Smart Energy Systems; Springer: Cham, Switzerland, 2023; pp. 1–19. [Google Scholar]
- Shibl, M.M.; Ismail, L.S.; Massoud, A.M. A machine learning-based battery management system for state-of-charge prediction and state-of-health estimation for unmanned aerial vehicles. J. Energy Storage 2023, 66, 107380. [Google Scholar] [CrossRef]
- Tian, A.; Dong, K.; Yang, X.G.; Wang, Y.; He, L.; Gao, Y.; Jiang, J. Physics-based parameter identification of an electrochemical model for lithium-ion batteries with two-population optimization method. Appl. Energy 2025, 378, 124748. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O. Dynamic equivalent circuit model to estimate state-of-health of lithium-ion batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
- Yao, L.; Xu, S.; Tang, A. A review of lithium-ion battery state of health estimation and prediction methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Qin, D.; Li, L.; Wu, H. A composite progressive approach alternating between electrochemical model and data-driven model for the state of health assessment of lithium-ion batteries. J. Energy Storage 2024, 97, 112921. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Kalman filtering techniques for the online model parameters and state of charge estimation of the Li-ion batteries: A comparative analysis. J. Energy Storage 2022, 51, 104174. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.; Zhang, H. Active acoustic emission sensing for fast co-estimation of state of charge and state of health of the lithium-ion battery. J. Energy Storage 2023, 64, 107192. [Google Scholar] [CrossRef]
- Mellit, A. An embedded solution for fault detection and diagnosis of photovoltaic modules using thermographic images and deep convolutional neural networks. Eng. Appl. Artif. Intell. 2022, 116, 105459. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Ma, X. SOC estimation and fault diagnosis framework of battery based on multi-model fusion modeling. J. Energy Storage 2023, 65, 107296. [Google Scholar] [CrossRef]
- Dinh, M.C.; Le, T.T.; Park, M. A low-cost and high-efficiency active cell-balancing circuit for the reuse of EV batteries. Batteries 2024, 10, 61. [Google Scholar] [CrossRef]
- Li, H.; Kaleem, M.B.; Chiu, I.J. An intelligent digital twin model for the battery management systems of electric vehicles. Int. J. Green Energy 2024, 21, 461–475. [Google Scholar] [CrossRef]
- IEC 62619; Secondary Cells and Batteries Containing Alkaline or Other Non-Acid Electrolytes—Safety Requirements for Secondary Lithium Cells and Batteries, for Use in Industrial Applications. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2017.
- Hildebrand, S.; Eddarir, A.; Lebedeva, N. Overview of Battery Safety Tests in Standards for Stationary Battery Energy Storage Systems; Publications Office of the European Union: Luxembourg, 2024. [Google Scholar]
- International Civil Aviation Organization. Technical Specifications for Unmanned Aircraft Systems (UAS); ICAO: Montreal, QC, Canada, 2020. [Google Scholar]
- Laghari, A.A.; Jumani, A.K.; Laghari, R.A. Unmanned aerial vehicles: A review. Cogn. Robot. 2023, 3, 8–22. [Google Scholar] [CrossRef]
- IEEE 1625; Standard for Rechargeable Batteries for Multi-Cell Mobile Computing Devices. Institute of Electrical and Electronics Engineers (IEEE) Standards Association: New York, NY, USA, 2004.
- GB/T 34131-2023; Technical Requirements for Civil Unmanned Aerial Vehicle Batteries. Standardization Administration of China (SAC): Beijing, China, 2023.
- ISO 21895; Unmanned Aircraft System Battery Communication Protocol. International Organization for Standardization (ISO): Geneva, Switzerland, 2021.
- IEEE P2836; Standard for Battery Management System Requirements for Unmanned Aerial Vehicles. Institute of Electrical and Electronics Engineers (IEEE) Standards Association: New York, NY, USA, 2024.
- IEC 62443-1-1; Industrial Communication Networks—Network and System Security—Part 1-1: Terminology, Concepts and Models. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2009.
- Hussain, A.; Mao, Z.; Li, M. A Comprehensive Review of the Pseudo-Two-Dimensional (P2D) Model: Model Development, Solutions Methods, and Applications. Adv. Theory Simul. 2025, 8, 2401016. [Google Scholar] [CrossRef]
- Martínez-Rosas, E.; Vasquez-Medrano, R.; Flores-Tlacuahuac, A. Modeling and simulation of lithium-ion batteries. Comput. Chem. Eng. 2011, 35, 1937–1948. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, Q.; White, R.E. Semiempirical modeling of charge and discharge profiles for a LiCoO2 electrode. J. Power Sources 2007, 165, 427–435. [Google Scholar] [CrossRef]
- Sara, T.T.; Bernard, M.; Lantagne, G. Modeling and simulation of a commercial graphiteLiFePO4 cell in a full range of C-rates. J. Appl. Electrochem. 2018, 48, 1389–1400. [Google Scholar]
- Hussein, H.M.; Aghmadi, A.; Abdelrahman, M.S. A review of battery state of charge estimation and management systems: Models and future prospective. Wiley Interdiscip. Rev. Energy Environ. 2024, 13, e507. [Google Scholar]
- Wang, Y.; Zhang, X.; Li, K. Perspectives and challenges for future lithium-ion battery control and management. eTransportation 2023, 18, 100260. [Google Scholar] [CrossRef]
- Luo, W.; Lyu, C.; Wang, L. A new extension of physics-based single particle model for higher charge–discharge rates. J. Power Sources 2013, 241, 295–310. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Rahimian, S.K.; Rayman, S.; White, R.E. Extension of physics-based single particle model for higher charge–discharge rates. J. Power Sources 2013, 224, 180–194. [Google Scholar] [CrossRef]
- Goto, I.; Ohkuma, H.; Hongo, H. Feasibility Study of Modified Single-Particle Model for Composite Cathode at High-Rate Discharge. Electrochemistry 2016, 84, 432–437. [Google Scholar] [CrossRef]
- Graule, A.; Oehler, F.F.; Schmitt, J. Development and evaluation of a physicochemical equivalent circuit model for lithium-ion batteries. J. Electrochem. Soc. 2024, 171, 020503. [Google Scholar] [CrossRef]
- Tao, Z.; Zhao, Z.; Wang, C. State of charge estimation of lithium batteries: Review for equivalent circuit model methods. Measurement 2024, 236, 115148. [Google Scholar] [CrossRef]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N. A review on battery modelling techniques. Sustainability 2021, 13, 10042. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelghafar, A.A.; Soudan, B. Artificial neural network driven prognosis and estimation of Lithium-Ion battery states: Current insights and future perspectives. Ain Shams Eng. J. 2024, 15, 102429. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Cao, Y. An RNN with small sequence trained by multi-level optimization for SOC estimation in Li-ion battery applications. IEEE Trans. Veh. Technol. 2023, 72, 11469–11481. [Google Scholar] [CrossRef]
- Chung, D.W.; Ko, J.H.; Yoon, K.Y. State-of-charge estimation of lithium-ion batteries using LSTM deep learning method. J. Electr. Eng. Technol. 2022, 17, 1931–1945. [Google Scholar] [CrossRef]
- Cui, S.; Joe, I. A dynamic spatial-temporal attention-based GRU model with healthy features for state-of-health estimation of lithium-ion batteries. IEEE Access 2021, 9, 27374–27388. [Google Scholar] [CrossRef]
- Xu, H.; Wu, L.; Xiong, S. An improved CNN-LSTM model-based state-of-health estimation approach for lithium-ion batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- Hong, S.; Kang, M.; Kim, J. Investigation of denoising autoencoder-based deep learning model in noise-riding experimental data for reliable state-of-charge estimation. J. Energy Storage 2023, 72, 108421. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Liu, Y. A time-series Wasserstein GAN method for state-of-charge estimation of lithium-ion batteries. J. Power Sources 2023, 581, 233472. [Google Scholar] [CrossRef]
- Zequera, R.A.G.; Rassõlkin, A.; Vaimann, T. Charge diagnostics and state estimation of Battery Energy Storage Systems through Transformer models. IEEE Access 2025, 13, 17733–17744. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D.I. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Yüksek, G.; Alkaya, A. A novel state of health estimation approach based on polynomial model for lithium-ion batteries. Int. J. Electrochem. Sci. 2023, 18, 100111. [Google Scholar] [CrossRef]
- Bianchi, V.; Stighezza, M.; Toscani, A. An improved method based on support vector regression with application independent training for state of charge estimation. IEEE Trans. Instrum. Meas. 2023, 72, 2524811. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A. Real-time state of charge estimation of lithium-ion batteries using optimized random forest regression algorithm. IEEE Trans. Intell. Veh. 2022, 8, 639–648. [Google Scholar] [CrossRef]
- Li, G.; Li, B.; Li, C. Battery state of charge probabilistic estimation using natural gradient boosting. IEEE Trans. Ind. Electron. 2023, 71, 10636–10646. [Google Scholar] [CrossRef]
- Shi, H.; Liang, Y.; Wu, B. Time-Varying Non-parametric Remaining Useful Life of Systems Based on Adaptive Kernel Auxiliary Particle Filter. IEEE Trans. Instrum. Meas. 2025, 74, 3519414. [Google Scholar]
- Ahwiadi, M.; Wang, W. An enhanced particle filter technology for battery system state estimation and RUL prediction. Measurement 2022, 191, 110817. [Google Scholar] [CrossRef]
- Ma, Q.; Zou, C.; Wang, S. The state of charge estimation of lithium-ions battery using combined multi-population genetic algorithm-BP and Kalman filter methods. Int. J. Electrochem. Sci. 2022, 17, 220214. [Google Scholar] [CrossRef]
- He, M.; Wang, S.; Fernandez, C. A novel adaptive particle swarm optimization algorithm based high precision parameter identification and state estimation of lithium-ion battery. Int. J. Electrochem. Sci. 2021, 16, 21054. [Google Scholar] [CrossRef]
- Wang, C.; Xu, M.; Zhang, Q. Cooperative co-evolutionary differential evolution algorithm applied for parameters identification of lithium-ion batteries. Expert Syst. Appl. 2022, 200, 117192. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, C.; Gu, Y. Research on SOC estimation method of hybrid electric vehicles battery based on the grey wolf optimized particle filter. Comput. Electr. Eng. 2023, 110, 108907. [Google Scholar] [CrossRef]
- Saba, I.; Tariq, M.; Ullah, M. Deep reinforcement learning based state of charge estimation and management of electric vehicle batteries. IET Smart Grid 2023, 6, 422–431. [Google Scholar] [CrossRef]
- Zhi, Y.; Wang, H.; Wang, L. A state of health estimation method for electric vehicle Li-ion batteries using GA-PSO-SVR. Complex Intell. Syst. 2022, 8, 2167–2182. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y.; Feng, X. Optimal fuzzy logic control of energy storage systems for V/f support in distribution networks considering battery degradation. Int. J. Electr. Power Energy Syst. 2022, 139, 107867. [Google Scholar] [CrossRef]
- Roman, D.; Saxena, S.; Robu, V. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
- Lin, M.; You, Y.; Wang, W. Battery health prognosis with gated recurrent unit neural networks and hidden Markov model considering uncertainty quantification. Reliab. Eng. Syst. Saf. 2023, 230, 108978. [Google Scholar] [CrossRef]
- Huo, Q.; Ma, Z.; Zhao, X. Bayesian network based state-of-health estimation for battery on electric vehicle application and its validation through real-world data. IEEE Access 2021, 9, 11328–11341. [Google Scholar] [CrossRef]
- Ghosh, N.; Garg, A.; Panigrahi, B.K. An evolving quantum fuzzy neural network for online state-of-health estimation of Li-ion cell. Appl. Soft Comput. 2023, 143, 110263. [Google Scholar] [CrossRef]
- Zeng, L.; Zheng, J.; Yao, L. Dynamic Bayesian networks for feature learning and transfer applications in remaining useful life estimation. IEEE Trans. Instrum. Meas. 2022, 72, 108881. [Google Scholar] [CrossRef]
- Feng, X.; He, X.; Ouyang, M. A coupled electrochemical-thermal failure model for predicting the thermal runaway behavior of lithium-ion batteries. J. Electrochem. Soc. 2018, 165, A3748–A3765. [Google Scholar] [CrossRef]
- Xu, L.; Deng, Z.; Xie, Y. A novel hybrid physics-based and data-driven approach for degradation trajectory prediction in Li-ion batteries. IEEE Trans. Transp. Electrif. 2022, 9, 2628–2644. [Google Scholar] [CrossRef]
- Singh, S.; Ebongue, Y.E.; Rezaei, S. Hybrid modeling of lithium-ion battery: Physics-informed neural network for battery state estimation. Batteries 2023, 9, 301. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z. Review on the battery model and SOC estimation method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Espedal, I.B.; Jinasena, A.; Burheim, O.S. Current trends for state-of-charge (SoC) estimation in lithium-ion battery electric vehicles. Energies 2021, 14, 3284. [Google Scholar] [CrossRef]
- Li, X.; Wang, P.; Wang, J.; Xiu, F.; Xia, Y. State of health estimation and prediction of electric vehicle power battery based on operational vehicle data. J. Energy Storage 2023, 72, 108247. [Google Scholar] [CrossRef]
- Liu, Z.M. Research on SOH Estimation Algorithm of Power Battery Based on LSTM-RNN; Guilin University of Electronic Science and Technology: Guilin, China, 2020. [Google Scholar]
- Vignesh, S.; Che, H.S.; Selvaraj, J. State of Health (SoH) estimation methods for second life lithium-ion battery—Review and challenges. Appl. Energy 2024, 369, 123542. [Google Scholar]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B. Model-based state of X estimation of lithium-ion battery for electric vehicle applications. Int. J. Energy Res. 2022, 46, 10704–10723. [Google Scholar] [CrossRef]
- Reshma, P.; Manohar, V.J. Collaborative evaluation of SoC, SoP and SoH of lithium-ion battery in an electric bus through improved remora optimization algorithm and dual adaptive Kalman filtering algorithm. J. Energy Storage 2023, 68, 107573. [Google Scholar] [CrossRef]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2021, 8, 2205–2232. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, L.; Zhang, Y. Aging behavior and mechanisms of lithium-ion battery under multi-aging path. J. Clean. Prod. 2023, 423, 138678. [Google Scholar] [CrossRef]
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.J.; She, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef]
- Ni, Z.; Yang, Y. A Combined Data-Model Method for State-of Charge Estimation of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 2022, 71, 2503611. [Google Scholar] [CrossRef]
- Lee, J.; Won, J. Enhanced Coulomb Counting Method for SoC and SoH Estimation Based on Coulombic Efficiency. IEEE Access 2023, 11, 15449–15459. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z. Study of SOC estimation by the ampere-hour integral method with capacity correction based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Tran, M.-K. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Hou, G.; Liu, X.; He, W. An equivalent circuit model for battery thermal management system using phase change material and liquid cooling coupling. J. Energy Storage 2022, 55, 105834. [Google Scholar] [CrossRef]
- Maheshwari, A.; Nageswari, S. Effect of Noise Covariance Matrices on State of Charge Estimation Using Extended Kalman Filter. IETE J. Res. 2022, 69, 8130–8141. [Google Scholar] [CrossRef]
- Peng, X.B. Real-Time State of Charge Estimation of the Extended Kalman Filter and Unscented Kalman Filter Algorithms Under Different Working Conditions. J. Electrochem. Energy Convers. Storage 2021, 18, 041007. [Google Scholar] [CrossRef]
- Lai, X. A novel method for state of energy estimation of lithiumion batteries using particle filter and extended Kalman filter. J. Energy Storage 2021, 43, 103269. [Google Scholar] [CrossRef]
- Lin, B. An Adversarial Network-based Multi-model Black-box Attack. Intell. Autom. Soft Comput. 2021, 30, 641649. [Google Scholar] [CrossRef]
- Chen, Y.; Li, R.; Sun, Z. SOC estimation of retired lithium-ion batteries for electric vehicle with improved particle filter by H-infinity filter. Energy Rep. 2023, 9, 1937–1947. [Google Scholar] [CrossRef]
- Laadjal, K.; Marques Cardoso, A.J. A review of supercapacitors modeling, SoH, and SoE estimation methods: Issues and challenges. Int. J. Energy Res. 2021, 45, 18424–18440. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Zhu, C.; Li, K.; Fei, M.; Peng, C.; Zhang, X.; Han, Q.-L. Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control Eng. Pract. 2022, 124, 105176. [Google Scholar] [CrossRef]
- Kim, J.; Chun, H.; Baek, J. Parameter identification of lithium-ion battery pseudo-2-dimensional models using genetic algorithm and neural network cooperative optimization. J. Energy Storage 2022, 45, 103571. [Google Scholar] [CrossRef]
- Li, H.; Saini, A.; Liu, C. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Lim, K.; Bastawrous, H.A.; Duong, V.H.; See, K.W.; Zhang, P.; Dou, S.X. Fading kalman filter-based real-time state of charge estimation in lifepo4 battery-powered electric vehicles. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- Fu, B.; Li, Y.; Liu, K. A Physical-Data Fusion Framework for Lithium-ion Battery SOC Estimation. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Chen, T.; Guo, J.W.; Zhang, R. Lithium battery soc-soh joint estimation method based on dual UKF filter Marine power technology. Mar. Electr. Electron. Eng. 2020, 40, 95–100. [Google Scholar] [CrossRef]
- Ipek, E.; Yilmaz, M. A novel method for SOC estimation of Li-ion batteries using a hybrid machine learning technique. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 18–31. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Chen, J.; Liao, C. The adaptive kernel-based extreme learning machine for state of charge estimation. Ionics 2023, 29, 1863–1872. [Google Scholar] [CrossRef]
- Li, Y.; Ding, P.; Zheng, L. Optimized Training Options of a Deep Learning Model for Lithium-Ion Battery State of Charge Estimation. In Proceedings of the 2023 IEEE International Future Energy Electronics Conference (IFEEC), Sydney, Australia, 20–23 November 2023; pp. 267–270. [Google Scholar]
- Sui, X. Robust State of Health Estimation for Lithium-Ion Batteries Using Machine Learning. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 2022. [Google Scholar]
- Reddy, M.S.; Padhy, N.P. SOH Based Power Sharing Algorithm for Second-life Batteries Using Health Factors. In Proceedings of the 2024 Third International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 18–20 January 2024; pp. 663–668. [Google Scholar]
- Hein, W.Y.; Narang, A.; Tafti, H.D.; Farivar, G.; Ceballos, S.; Pou, J. Minimizing energy storage utilization in a stand-alone dc microgrid using photovoltaic flexible power control. IEEE Trans. Smart Grid 2021, 12, 3755–3764. [Google Scholar] [CrossRef]
- Li, Y.; Luan, J.; Yang, Y. Remaining Lifetime Estimation of Retired Batteries Based on Multiple Deep Neural Network Ensembles. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1942–1944. [Google Scholar]
- Yan, Q.; Wang, Y. Predicting for power battery SOC based on neural network. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 4140–4143. [Google Scholar]
- Demirci, O.; Taskin, S.; Schaltz, E. Review of battery state estimation methods for electric vehicles-Part I: SOC estimation. J. Energy Storage 2024, 87, 111435. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An overview on thermal safety issues of lithium-ion batteries for electric vehicle application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Hafizhahullah, H. A Hybrid CNN-LSTM for Battery Remaining Useful Life Prediction with Charging Profiles Data. In Proceedings of the ACM International Conference Proceeding Series, New York, NY, USA, 22–23 November 2022; pp. 106–110. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Wang, Y.; Stolkin, R. Predicting the Remaining Life of Lithium-ion Batteries Using a CNN-LSTM Model. In Proceedings of the 2022 8th International Conference on Mechatronics and Robotics Engineering, ICMRE 2022, Munich, Germany, 10–12 February 2022; pp. 73–78. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Contreras, C.A.; Stolkin, R. Hyperparameter-optimized CNN and CNN-LSTM for Predicting the Remaining Useful Life of Lithium-Ion Batteries. In Proceedings of the 2023 Eleventh International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 21–23 November 2023; pp. 110–115. [Google Scholar]
- Martiri, L.; Azzalini, D.; Flammini, B. Improving Remaining Useful Life Estimation of Lithium-Ion Batteries when Nearing End of Life. In Proceedings of the 2023 IEEE International Conference on Metrology for eXtended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Milano, Italy, 25–27 October 2023; pp. 317–322. [Google Scholar]
- Hwang, J.H.; Lee, J.H.; Lee, I.S. Analysis and Diagnosis of the Effect of Voltage and Current Sensor Faults on the State of Charge Estimation of Lithium-ion Batteries Based on Neural Networks. Int. J. Control. Autom. Syst. 2024, 22, 1691–1706. [Google Scholar] [CrossRef]
- Arshad, F.; Lin, J.; Manurkar, N. Life cycle assessment of lithium-ion batteries: A critical review. Resour. Conserv. Recycl. 2022, 180, 106164. [Google Scholar] [CrossRef]
- Hong, J.; Liang, F.; Yang, J. An exhaustive review of battery faults and diagnostic techniques for real-world electric vehicle safety. J. Energy Storage 2024, 99, 113234. [Google Scholar] [CrossRef]
- Kaliaperumal, M.; Dharanendrakumar, M.S.; Prasanna, S. Cause and mitigation of lithium-ion battery failure—A review. Materials 2021, 14, 5676. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, Y.; Hu, X. Thermal state monitoring of lithium-ion batteries: Progress, challenges, and opportunities. Prog. Energy Combust. Sci. 2024, 100, 101120. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, S.; Tang, N. Research progress in fault detection of battery systems: A review. J. Energy Storage 2024, 98, 113079. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Liu, Y. Variable-order equivalent circuit modeling and state of charge estimation of lithium-ion battery based on electrochemical impedance spectroscopy. Energies 2021, 14, 769. [Google Scholar] [CrossRef]
- Song, Y.; Yu, J.; Zhou, J. Detection of voltage fault in lithium-ion battery based on equivalent circuit model-informed neural network. IEEE Trans. Instrum. Meas. 2024, 73, 3508010. [Google Scholar] [CrossRef]
- Li, X.; Lyu, M.; Gao, X. An adaptive threshold method for multi-faults diagnosis of lithium-ion batteries based on electro-thermal model. Measurement 2023, 222, 113671. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, X.; Wang, Y. PDE model-based on-line cell-level thermal fault localization framework for batteries. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2507–2516. [Google Scholar] [CrossRef]
- Niu, G. Data-Driven Technology for Engineering Systems Health Management; Springer: Singapore, 2017. [Google Scholar]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.B. Lithium-ion battery model parameter identification using modified adaptive forgetting factor-based recursive least square algorithm. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2169–2174. [Google Scholar]
- Yang, Q.; Sun, J.; Kang, Y. Internal short circuit detection and evaluation in battery packs based on transformation matrix and an improved state-space model. Energy 2023, 276, 127555. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, B.; Zhang, F. Adaptive fault detection for lithium-ion battery combining physical model-based observer and BiLSTMNN learning approach. J. Energy Storage 2024, 91, 112067. [Google Scholar] [CrossRef]
- Chen, G.; Li, S.; He, Q. Fault diagnosis of drone motors driven by current signal data with few samples. Meas. Sci. Technol. 2024, 35, 086202. [Google Scholar] [CrossRef]
- Cabahug, J.; Eslamiat, H. Failure detection in quadcopter UAVs using K-means clustering. Sensors 2022, 22, 6037. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Kim, T. Outlier mining-based fault diagnosis for multicell lithium-ion batteries using a low-priced microcontroller. In Proceedings of the 2018 IEEE Applied Power Electronics Conf. and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; p. 33653369. [Google Scholar] [CrossRef]
- Kim, T.; Makwana, D.; Adhikaree, A.; Vagdoda, J.; Lee, Y. Cloud-based battery condition monitoring and fault diagnosis platform for large-scale lithium-ion battery energy storage systems. Energies 2018, 11, 125. [Google Scholar] [CrossRef]
- Guo, K.; Wang, N.; Liu, D. Uncertainty-aware LSTM based dynamic flight fault detection for UAV actuator. IEEE Trans. Instrum. Meas. 2022, 72, 1–13. [Google Scholar] [CrossRef]
- Muddappa, V.K.; Anwar, S. Electrochemical model based fault diagnosis of li-ion battery using fuzzy logic. ASME 2014 Int. Mech. Eng. Congr. Expo. 2014, 37134, V04BT04A048. [Google Scholar] [CrossRef]
- Gan, W.; Li, X.; Wei, D. Real-Time Multi-Sensor Joint Fault Diagnosis Method for Permanent Magnet Traction Drive Systems Based on Structural Analysis. Sensors 2024, 24, 2878. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Jung, J.; Ghorbanpour, S. Data–Driven Fault Diagnosis and Cause Analysis of Battery Pack with Real Data. Energies 2022, 15, 1647. [Google Scholar] [CrossRef]
- Xia, B.; Nguyen, T.; Yang, J.; Mi, C. The improved interleaved voltage measurement method for series connected battery packs. J. Power Sources 2016, 334, 12–22. [Google Scholar] [CrossRef]
- Kang, Y.; Duan, B.; Zhou, Z.; Shang, Y.; Zhang, C. A multi-fault diagnostic method based on an interleaved voltage measurement topology for series connected battery packs. J. Power Sources 2019, 417, 132–144. [Google Scholar] [CrossRef]
- Zhang, K.; Hu, X.; Liu, Y. Multi-fault detection and isolation for lithium-ion battery systems. IEEE Trans. Power Electron. 2021, 37, 971–989. [Google Scholar] [CrossRef]
- Yan, Y.; Luo, W.; Wang, Z. Fault diagnosis of lithium-ion battery sensors based on multi-method fusion. J. Energy Storage 2024, 85, 110969. [Google Scholar] [CrossRef]
- Mercorelli, P. Recent advances in intelligent algorithms for fault detection and diagnosis. Sensors 2024, 24, 2656. [Google Scholar] [CrossRef]
- Mukherjee, S.; Chowdhury, K. State of charge estimation techniques for battery management system used in electric vehicles: A review. Energy Syst. 2023, 6, 100328. [Google Scholar] [CrossRef]
- Zhang, Y.; Shaoping, W.; Jian, S.H.I. SAR performance-based fault diagnosis for electro-hydraulic control system: A novel FDI framework for closed-loop system. Chin. J. Aeronaut. 2022, 35, 381–392. [Google Scholar] [CrossRef]
- Shahzad, E.; Khan, A.U.; Iqbal, M. Sensor fault-tolerant control of microgrid using robust sliding-mode observer. Sensors 2022, 22, 2524. [Google Scholar] [CrossRef]
- Vafamand, N.; Arefi, M.M.; Asemani, M.H. Dual-EKF-based fault-tolerant predictive control of nonlinear DC microgrids with actuator and sensor faults. IEEE Trans. Ind. Appl. 2022, 58, 5438–5446. [Google Scholar] [CrossRef]
- Tudoroiu, N.; Zaheeruddin, M.; Tudoroiu, R.E. Investigations on using intelligent learning techniques for anomaly detection and diagnosis in sensors signals in Li-ion battery—Case study. Inventions 2023, 8, 74. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Li, L. Progress on the Fault Diagnosis Approach for Lithium-ion Battery Systems: Advances, Challenges, and Prospects. Prot. Control. Mod. Power Syst. 2024, 9, 16–41. [Google Scholar] [CrossRef]
- Puchalski, R.; Giernacki, W. UAV fault detection methods, state-of-the-art. Drones 2022, 6, 330. [Google Scholar] [CrossRef]
- Liu, Z.; He, H.; Ahmed, Q.; Rizzoni, G. Structural analysis based fault detection and isolation applied for a lithium-ion battery pack. IFAC-Pap. 2015, 48, 1465–1470. [Google Scholar] [CrossRef]
- Fan, T.E.; Chen, F.; Lei, H.R. Fault diagnosis for lithium-ion battery pack based on relative entropy and state of charge estimation. Batteries 2024, 10, 217. [Google Scholar] [CrossRef]
- Hu, J.; Cheng, Y.; Yu, H. Research on Early Fault Diagnosis of Lithium Batteries Based on WOA-VMD and Shannon Entropy. Automot. Eng. 2024, 46, 1189–1196. [Google Scholar]
- Zhang, F.; Zheng, X.; Xing, Z. Fault Diagnosis Method for Lithium-Ion Power Battery Incorporating Multidimensional Fault Features. Energies 2024, 17, 1568. [Google Scholar] [CrossRef]
- Liu, R.; Li, Z.; Deng, Y. Performance evaluation of information fusion systems based on belief entropy. Eng. Appl. Artif. Intell. 2024, 127, 107262. [Google Scholar] [CrossRef]
- Liu, B.; Bi, X.; Gu, L. Application of a Bayesian network based on multi-source information fusion in the fault diagnosis of a radar receiver. Sensors 2022, 22, 6396. [Google Scholar] [CrossRef]
- Bdour, J.; Sababha, B.H. A hybrid thrusting system for increasing the endurance time of multirotor unmanned aerial vehicles. Int. J. Adv. Robot. Syst. 2023, 20, 17298806231172335. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Khan, M.A.; Amjad, H.; Żywiołek, J. A comprehensive review of micro UAV charging techniques. Micromachines 2022, 13, 977. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Nie, H.; Zhang, P.; Lin, Z.; Zhou, Y.-G. Effectiveconfiguration WPT systems for drones charging area extension featuring quasi-uniform magnetic coupling. IEEE Trans. Transport. Electrif. 2020, 6, 920–934. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Monfared, M. Charging control strategies for lithium-ion battery packs: Review and recent developments. IET Power Electron. 2022, 15, 349–367. [Google Scholar] [CrossRef]
- Kıvrak, S.; Özer, T.; Og, Y.; Kelek, M.M. Novel active and passive balancing method-based battery management system design and implementation. J. Power Electron. 2021, 21, 1855–1865. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, J.; Lin, X.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Battery management system of UAV based on IoT. Front. Comput. Intell. Syst. 2022, 1, 41–43. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, W.W.; Su, M. Optimizing fuel economy and durability of hybrid fuel cell electric vehicles using deep reinforcement learning-based energy management systems. Energy Convers. Manag. 2023, 291, 117288. [Google Scholar] [CrossRef]
- Dong, G.; Yang, F.; Tsui, K.-L.; Zou, C. Active balancing of lithiumion batteries using graph theory and A-star search algorithm. IEEE Trans. Ind. Inform. 2021, 17, 2587–2599. [Google Scholar] [CrossRef]
- Jinlei, S.; Wei, L.; Chuanyu, T.; Tianru, W.; Tao, J.; Yong, T. A novel active equalization method for series-connected battery packs based on clustering analysis with genetic algorithm. IEEE Trans. Power Electron. 2021, 36, 7853–7865. [Google Scholar] [CrossRef]
- Aghajan-Eshkevari, S.; Azad, S.; Nazari-Heris, M. Charging and discharging of electric vehicles in power systems: An updated and detailed review of methods, control structures, objectives, and optimization methodologies. Sustainability 2022, 14, 2137. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhou, Y. Energy management strategies for fuel cell hybrid electric vehicles: Classification, comparison, and outlook. Energy Convers. Manag. 2022, 270, 116179. [Google Scholar] [CrossRef]
- Chen, X.; Li, M.; Chen, Z. Meta rule-based energy management strategy for battery/supercapacitor hybrid electric vehicles. Energy 2023, 285, 129365. [Google Scholar] [CrossRef]
- Ding, N.; Prasad, K.; Lie, T.T. Design of a hybrid energy management system using designed rule-based control strategy and genetic algorithm for the series-parallel plug-in hybrid electric vehicle. Int. J. Energy Res. 2021, 45, 1627–1644. [Google Scholar] [CrossRef]
- Lei, T.; Wang, Y.; Jin, X.; Min, Z.; Zhang, X.; Zhang, X. An optimal fuzzy logic-based energy management strategy for a fuel cell/battery hybrid power unmanned aerial vehicle. Aerospace 2022, 9, 115. [Google Scholar] [CrossRef]
- Marqués, R.; Montero, Á.; Sánchez-Diaz, C. Design methodology and simulation analysis of hybrid fuel cell and battery systems for powering unmanned aircraft systems. Energy Convers. Manag. 2024, 306, 118303. [Google Scholar] [CrossRef]
- Tian, W.; Liu, L.; Zhang, X.; Yang, D. Double-layer fuzzy adaptive NMPC coordinated control method of energy management and trajectory tracking for hybrid electric fixed wing UAVs. Int. J. Hydrogen Energy 2022, 47, 39239–39254. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, J.; Zhou, Z.; Li, H.; Liu, H.; Li, T. Grey Markov prediction-based hierarchical model predictive control energy management for fuel cell/battery hybrid unmanned aerial vehicles. Energy 2023, 262, 125405. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, G.; Zhou, M. A comprehensive review of research hotspots on battery management systems for UAVs. IEEE Access 2023, 11, 84636–84650. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).