1. Introduction
Smart farming refers to agriculture that utilizes various information technologies (ITs) to maximize productivity, efficiency, and sustainability. To optimize crop growth, data on soil moisture, light, temperature, and humidity are collected and analyzed through IT-based systems, which are then used to build an automated system that allows real-time farm management. In recent years, smart farming has gained global attention as a potential solution to various challenges of the 21st century, including rapid climate change, population growth, and limitations in agricultural infrastructure [
1].
The adoption of Internet of Things (IoT) technologies and Unmanned Aerial Vehicles (UAVs) plays a crucial role in the effective management of smart farming systems. IoT sensor nodes distributed throughout the farm continuously collect environmental data and transmit them to a central server for analysis. Based on the analyzed result, UAVs are used to precisely deliver water or pesticides only to areas in need, thereby enabling efficient management of large-scale farmland. The integration of IoT and UAV technologies significantly enhances operational efficiency in farm management [
2,
3,
4].
Although various studies have been conducted on the optimization of smart farm operations in recent years, there remain significant areas for improvement. In order to determine where irrigation should be applied based on collected data, it is not sufficient to consider only soil moisture levels; a comprehensive analysis involving additional factors such as light, atmospheric humidity, and temperature are also required. Furthermore, UAVs are typically used to visit areas that require water, but their flight distance is significantly limited. Due to the nature of UAV propulsion systems, carrying water increases the payload weight, which in turn substantially reduces the flight distance. Therefore, it is necessary to minimize the energy that UAVs must travel in order to visit more areas at once.
Several related studies have been actively conducted on each component of the smart farm system. For the analysis of the environment data, the continued advancement of artificial intelligence has led to extensive research on Recurrent Neural Networks (RNNs), which are capable of inferring meaningful patterns from time-series, multi-dimensional datasets [
5,
6,
7]. In addition, numerous studies have explored the use of UAVs for various tasks, including optimal path planning for area detection, path optimization considering battery constraints, and delivery of supplies to designated locations [
3,
8,
9]. Despite the progress made in each of these individual domains, a comprehensive solution that effectively integrates them to address the operational challenges of smart farming remains largely unexplored.
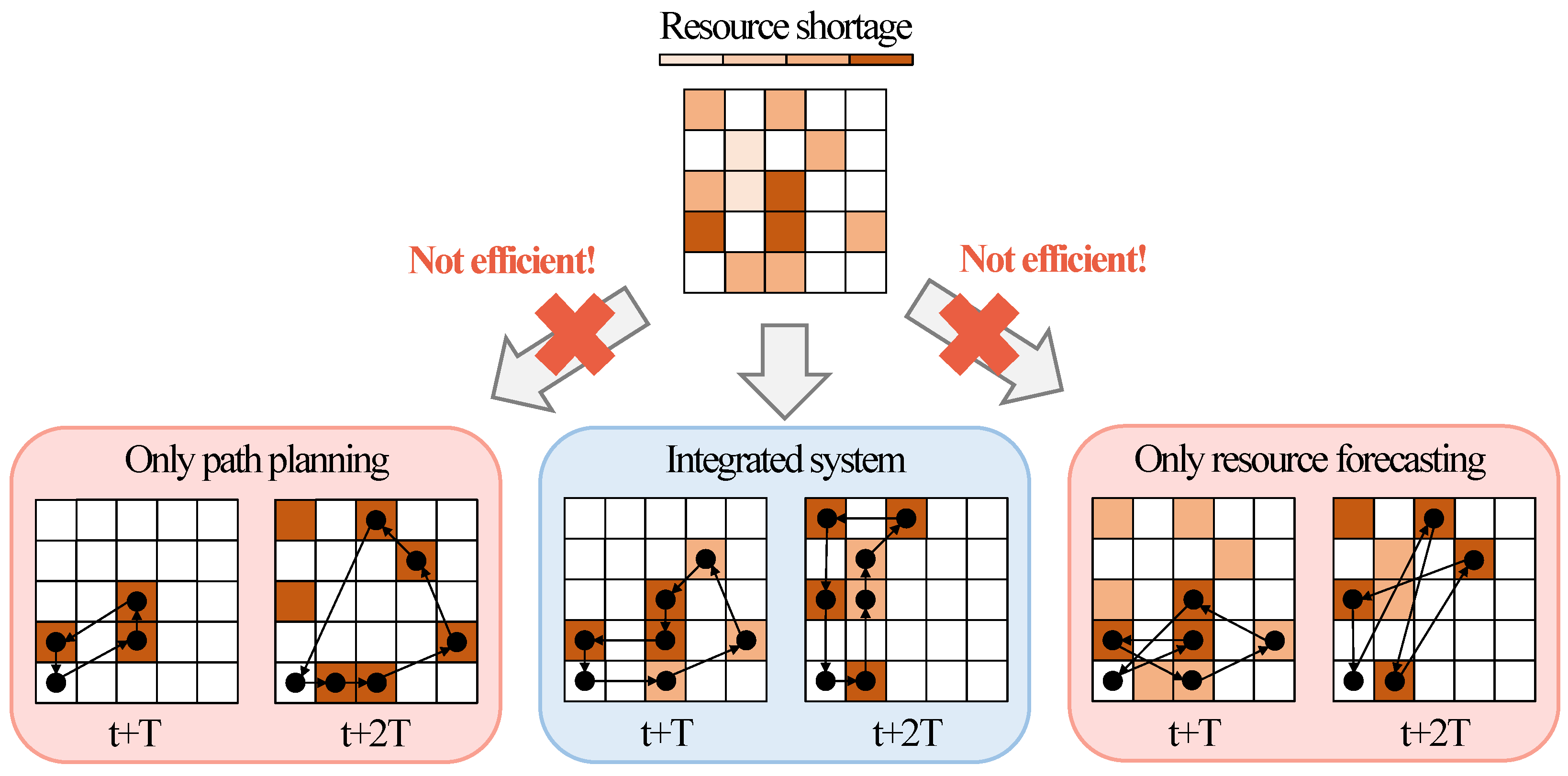
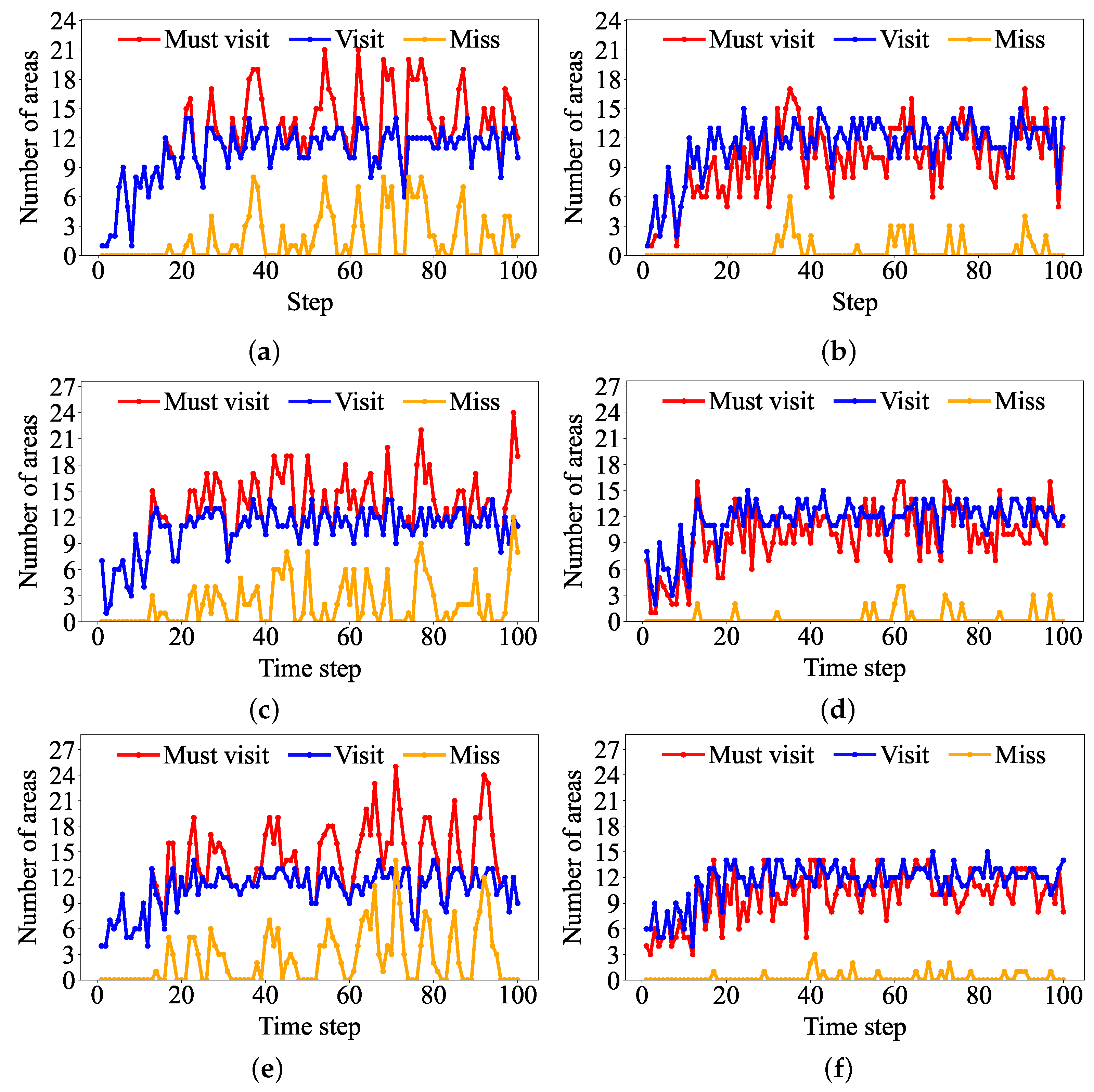
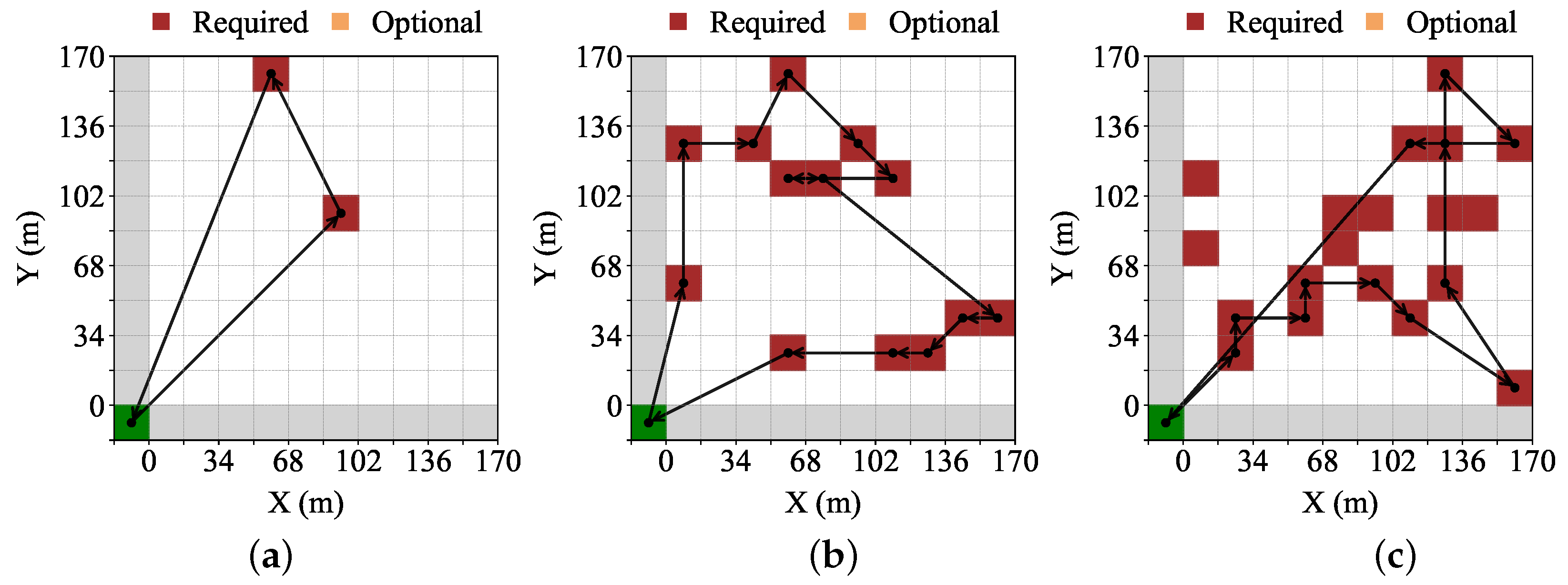
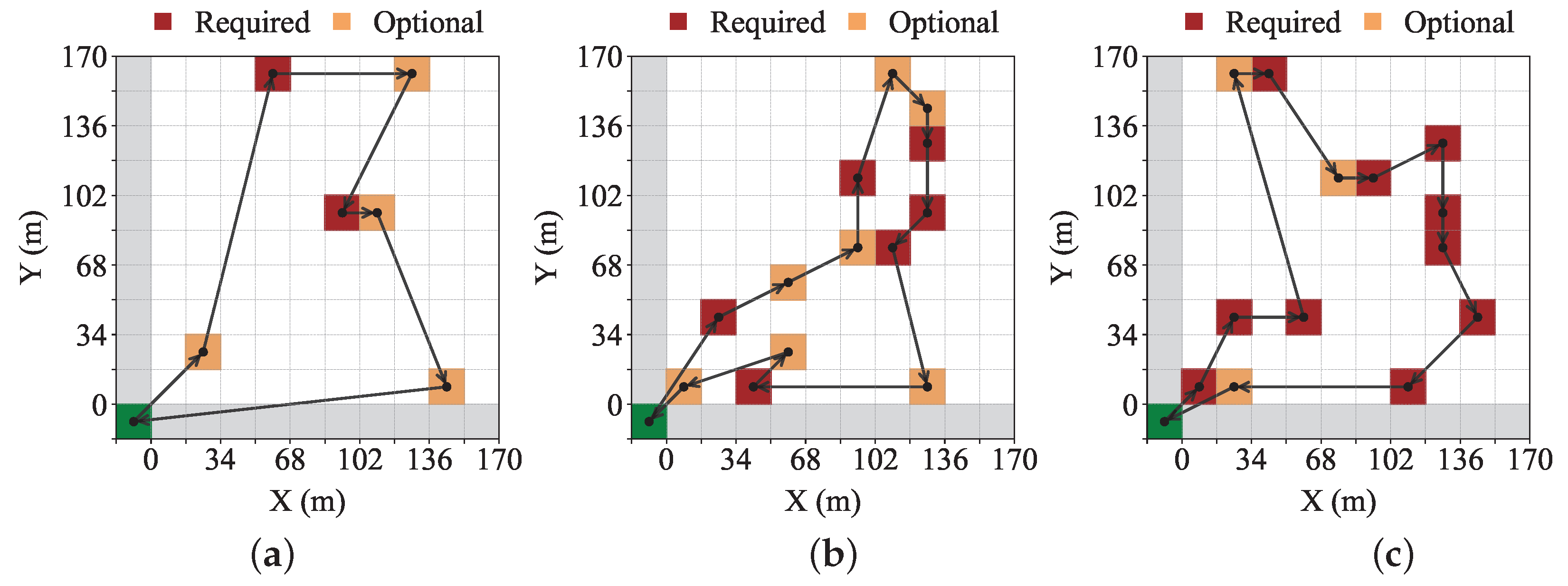
When only one of the two methods, path planning or resource forecasting, is applied in real environments, situations such as the one illustrated in
Figure 1 may occur. When applying a path planning method, more areas can be covered under operational constraints. However, the number of required areas varies over time, being low during certain times and concentrated at specific times, with multiple areas requiring visitation simultaneously. If multiple areas that require visitation at the same time, it may be impossible to visit all areas due to operational constraints. Conversely, resource forecasting allows the UAV to utilize residual capacity after visiting required areas to handle additional areas in advance, thereby reducing future concentration of areas that require visitation. Nevertheless, due to inefficient movement in path planning, it may be impossible to visit a large number of areas. To address this issue, resource forecasting is used to prioritize areas for visitation, and a path planning method is applied to maximize the number of high-priority areas visited. This approach ensures that high-priority areas are visited as needed, improving overall mission efficiency.
In this paper, we propose an integrated resource supply framework that forecasts future resources such as soil moisture using an RNN model, schedules the resource supply according to forecast-based priority, and derives the dynamic energy-aware UAV path to support.
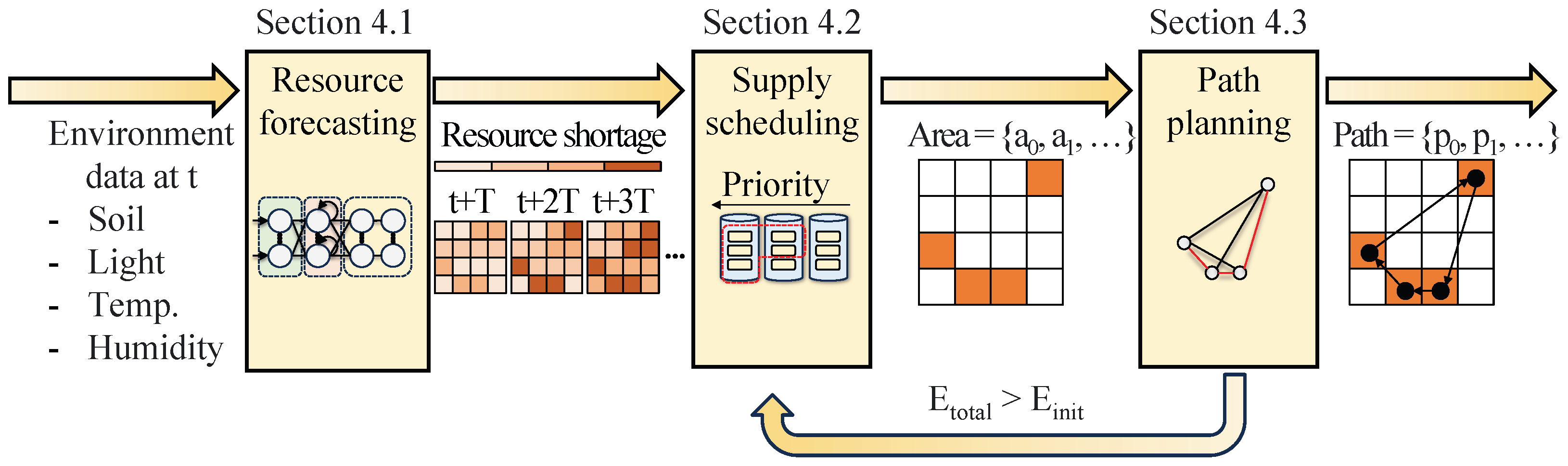
Figure 2 illustrates the proposed integrated smart farm framework. First, various environmental data such as soil moisture, light intensity, temperature, and humidity are collected at interval
T. Using the collected data, an RNN model forecasts temporal patterns of potential water shortages in each area. Details of the model are discussed in
Section 4.1. Once potential resource shortages in each area are identified, they are prioritized based on urgency—ranging from areas requiring immediate support to areas that will experience resource shortages in the near future. Based on this prioritization, the target areas to be supported by the UAV are determined. This is described in
Section 4.2.
After determining the target areas for resource supply, we derive the UAV flight path required to visit those areas. To address this NP-hard Traveling Salesman Problem (TSP), we propose a hybrid heuristic algorithm that combines the Genetic Algorithm (GA) with the Christofides algorithm, thereby achieving efficient path planning within a short computation time. If the total energy consumption
exceeds the UAV’s maximum allowable energy
, a rescheduling is performed to reduce the number of destinations. The detailed methodology for path planning is described in
Section 4.3.
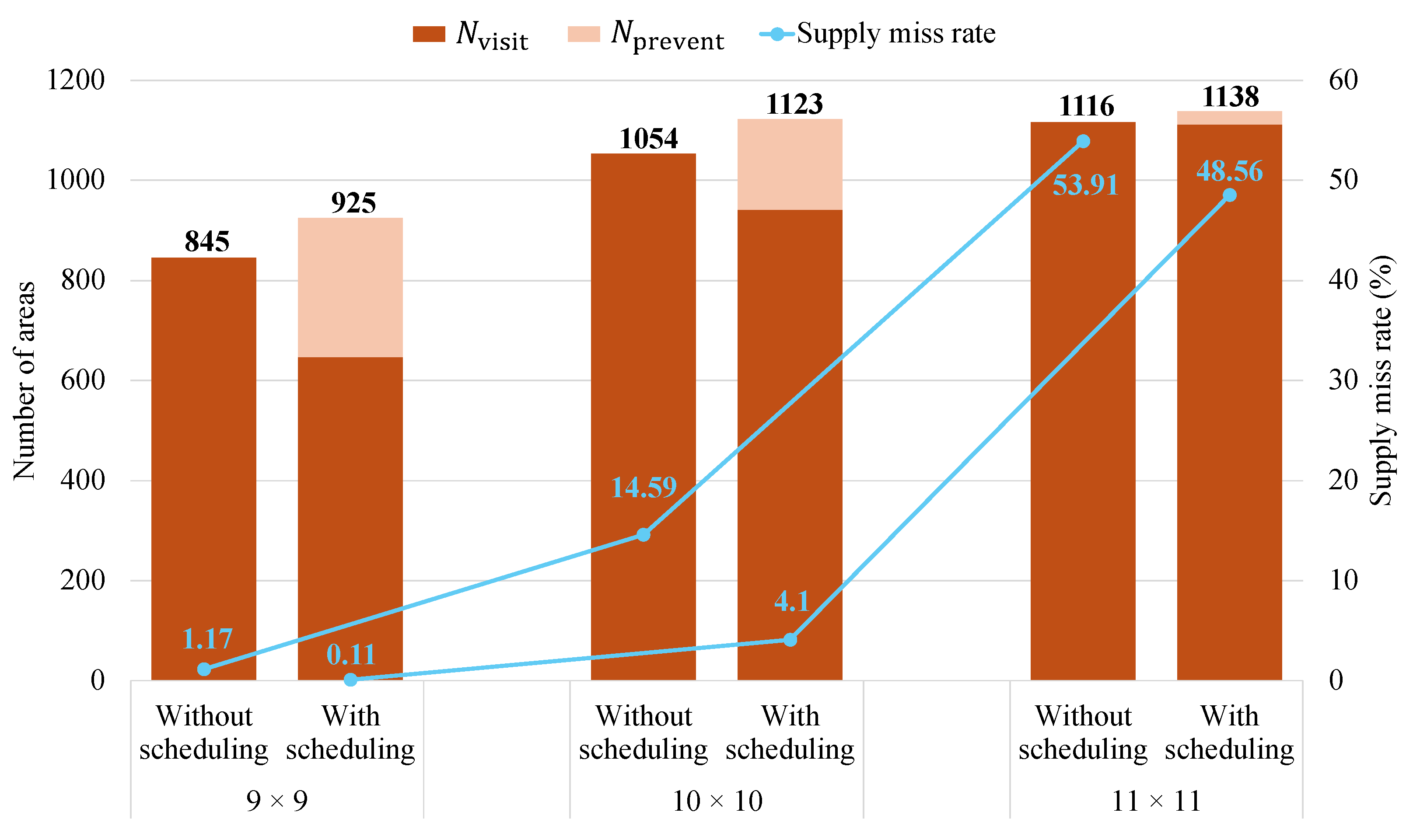
To evaluate the proposed system, we implemented the system shown in
Figure 2, including resource forecasting, supply scheduling, and path planning. In this paper, we evaluate how effectively the proposed approach addresses resource shortage issues under different scheduling. For the open irrigation environment data, we confirmed that the proposed framework achieved an average reduction of 81.08% in the supply miss rate. The main contributions of this paper are summarized as follows:
Introduction to the integrated resource forecasting, scheduling, and path planning smart farm framework;
Implementation of an RNN-based resource forecast model using open environment data;
Development of the hybrid UAV path planning method for the resource supply under a given maximum energy;
Analysis of the impact of the proposed method on the resource supply result through simulation.
The remainder of this paper is organized as follows:
Section 2 reviews existing smart farming operations, the UAV path planning method, the use of UAVs in agriculture, and studies that integrate prediction models into various systems.
Section 3 introduces system models, such as the mobility model, the delay model, and the energy model.
Section 4 introduces the RNN-based resource forecasting, supply scheduling method, and UAV path planning to maximize the number of resource shortage areas.
Section 5 validates the proposed integrated smart farm framework. Finally,
Section 6 concludes the paper and discusses potential future applications.
2. Related Work
Effective management methodology of water resources is becoming increasingly necessary in various fields with the increasing utilization of limited water resources [
10]. In response to this need, machine learning-based smart irrigation systems have been conducted in recent years [
11]. Some smart irrigation systems were proposed to determine whether irrigation is needed [
12,
13]. The systems in question have been integrated with IoT sensors where environmental data are gathered. Then, the data are classified based on similarity in characteristics. Based on the classification model, the operation of sprinklers or pumps is determined.
A comprehensive summary of the recurrent models, including their features and application fields, is provided in the review [
14].
Table 1 summarizes the features and application fields of various recurrent models, such as RNN, Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU), which are presented in [
14].
Among the various application fields of recurrent models, some research has been conducted to forecast future soil moisture based on past environmental data that have been used for irrigation scheduling [
5,
6,
7]. A LSTM model uses temperature, humidity, and soil moisture data as inputs and generates individual forecasts for each parameter [
5]. The LSTM model and a scheduler were used for precise irrigation planning [
6]. In addition, a research study proposed a deep bidirectional LSTM model to forecast soil moisture and electrical conductivity using IoT-sensed environmental data [
7].
Such forecasts of soil moisture can be effectively integrated with UAV-based irrigation systems. However, due to the limited flight distance of UAVs, optimizing the UAV path is essential for efficient irrigation systems. In smart farming environments, UAVs are used for various purposes such as crop monitoring, pesticide spraying, and data collection. There are several research studies on UAV path optimization to solve the Coverage Path Planning (CPP) problem, which aims to design paths that enable UAVs to visit some points within the area of interest. One research study suggests the
algorithm to optimize the UAV flight path for pesticide spraying [
3]. Other researchers optimized the UAV flight path with a reinforcement learning method for collecting data measured by IoT sensors [
8]. The method minimizes overlapping paths to cover the whole IoT devices. Furthermore, as an approach to solve the energy supply issues of IoT sensor nodes in a wide farm area, a path optimization system has been proposed that utilizes the UAV for wireless charging [
9]. Some research studies tried to solve complex problems such as the fusion of TSP and CPP [
15,
16]. They redefined the path planning problem and used the Double Deep Q-Network to solve the problem. One research study proposed a task allocation and path optimization method for UAV operations in dynamically changing mission environments, incorporating energy constraints and cooperation among multiple UAVs [
17]. In addition, another research study established a dynamic energy consumption model based on payload variation and derived the optimal UAV path using the heuristic search method [
18].
Several research studies have also been actively conducted on integrating predictive models such as LSTM and RNN into systems to enhance overall efficiency. One research study proposed a dynamic UAV deployment algorithm that maximizes communication coverage by predicting ship trajectories using LSTM [
19]. Another research study predicted the travel time between customers using LSTM and applied a hybrid GA to optimize delivery routes under real-time traffic conditions [
20]. In addition, to address inefficiencies arising from the separation of procurement and production scheduling, an integrated planning method was proposed by combining LSTM-based procurement cost prediction with GA-based production scheduling optimization [
21].
Although various studies have been conducted in the fields of resource forecasting and UAV path optimization, most research studies have only focused on individual fields. In addition, various studies have integrated prediction-based models with different applications to improve overall system efficiency. However, there have been few attempts that integrate both a method for forecasting the priority of resource supply areas and a UAV path planning method that considers both area priority and dynamic energy changes due to payload variation.
4. Resource Supply Planning
In this section, we propose an integrated method for resource supply planning.
Section 4.1 describes the RNN-based resource forecast model. This model forecasts the future resource trend from recent environmental information. The forecast results are used for supply scheduling.
Section 4.2 describes how to plan the the order of the supply based on the resource forecast. Based on the forecast results, resource supplying is scheduled with priority given to areas with low current resources or areas where resources are depleting quickly.
Section 4.3 presents the path planning method for supplying the scheduled areas. If
is larger than
, the supply plan must be adjusted accordingly.
4.1. RNN-Based Resource Forecasting
Soil moisture, one of the important resources for agriculture, is determined by various parameters, such as air temperature, air humidity, and light intensity [
22]. Forecasting the trend of this key resource is essential for improving irrigation efficiency, and it requires past environmental data over a specific period. The required environmental data take the form of sequence data, specifically time-series data. Sequence data are highly correlated with both current and previous states, and due to this characteristic, they are difficult to model using standard feedforward networks. In contrast, RNNs include hidden layers that extract features, allowing them to perform better in modeling sequence data compared to standard feedforward networks [
23]. The RNN-based Sequence-to-Sequence model is widely applied in various fields, such as machine translation, text summarization, headline generation, and sequence data analysis [
24].
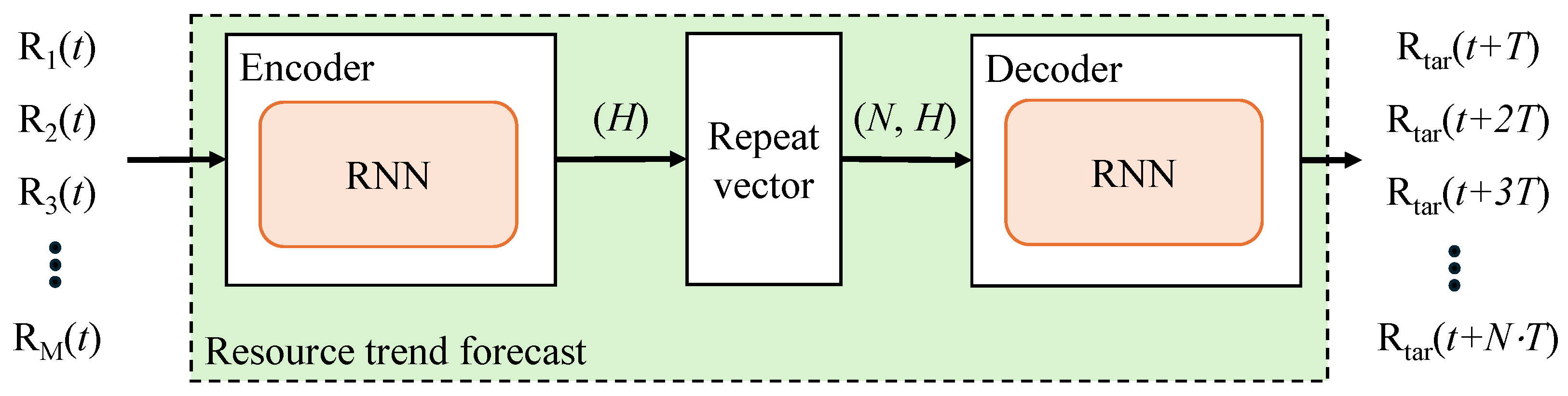
Figure 4 illustrates the model for forecasting resource trends
.
M and
N represents the number of inputs and outputs of the model, respectively. The inputs of the model are
to
at time
t, and the outputs of the model are
to
, where
T means the period for the forecast. These inputs take the form of sequential data, and the encoder compresses them to represent the features of the data. These data are used by the decoder for forecasting. The output of the encoder, which has a hidden state size
H, is transformed into a shape of
using a repeat vector. This operation replicates the encoder output into
N copies, because the decoder requires
N inputs, whereas the encoder generates only one output. The decoder transforms the compressed data into different sequence data, allowing
forecast from
to
. These outputs are used as inputs for resource supply scheduling in
Section 4.2. During training, the model learns to minimize the mean squared error between the forecasted outputs and the actual values. The entire model is trained end-to-end using Backpropagation Through Time, and detailed hyperparameter settings are described in
Section 5.2.
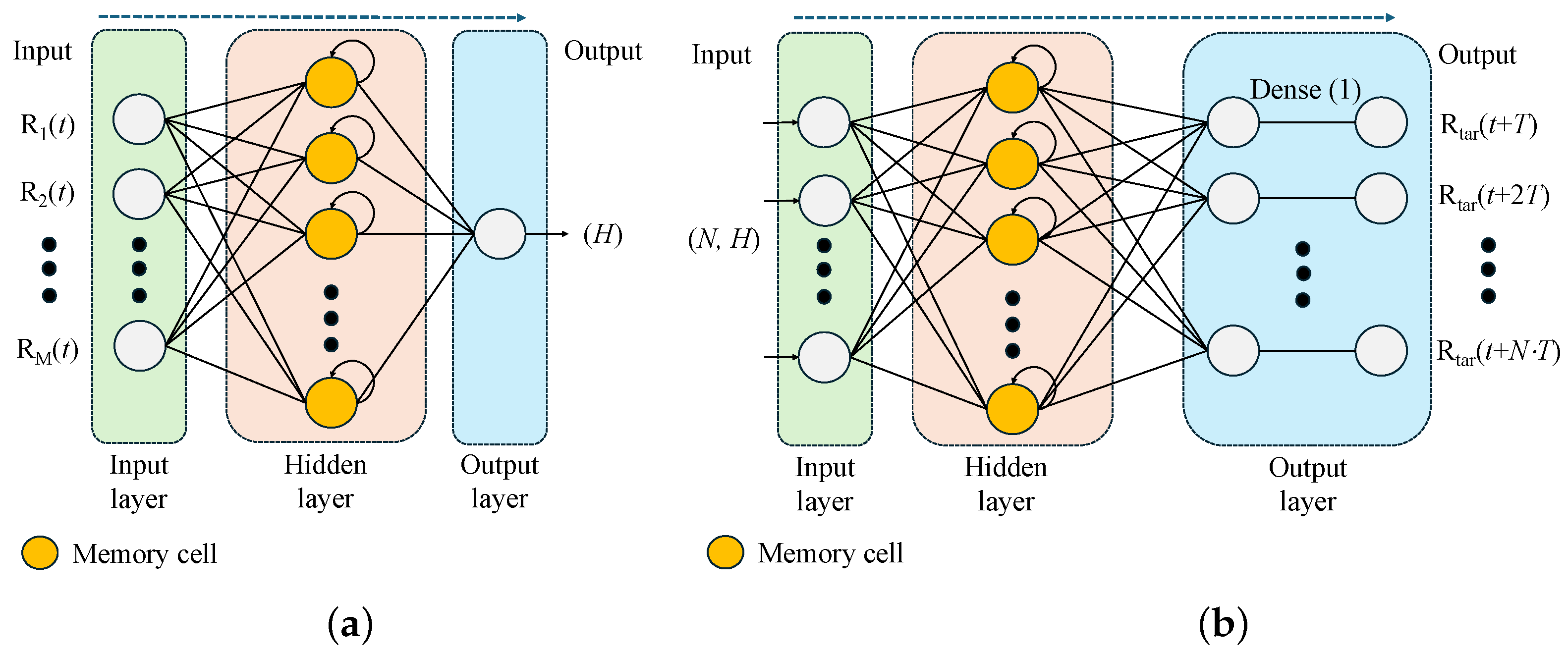
Figure 5 illustrates the RNN structures of the encoder and decoder, respectively. As illustrated in
Figure 5a, the encoder receives
M inputs and generates one output, which has a hidden state size of
H. As illustrated in
Figure 5b, the decoder receives
N inputs replicated by the repeat vector and generates
N outputs. The hidden layers of both the encoder and decoder consist of memory cells, where each cell generates an output based on the current input and hidden state. The hidden state is the output generated from the previous input and is a compressed summary of all the data from previous inputs. As illustrated in
Figure 4, the proposed model generates output using
N steps of input data. Therefore, the hidden layers of both the encoder and the decoder perform
N iterations of computation before producing the final output. The use of memory cells in both the encoder and decoder plays a critical role in preserving and leveraging temporal dependencies. In particular, the final hidden state of the encoder acts as a compact summary of the dynamic information from the input time series, which the decoder then expands to generate predictions over multiple future time steps. This memory-based architecture is essential for capturing temporal trends in resource data and serves as a foundational component of the proposed resource operation planning system.
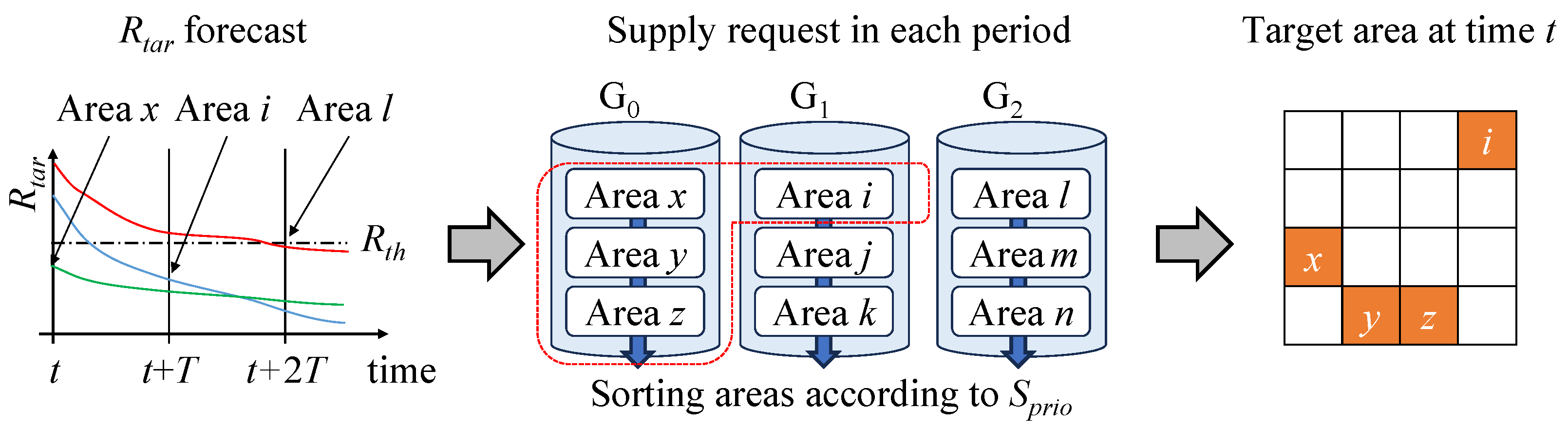
4.2. Supply Scheduling
Resource supply scheduling plays a key role in efficient resource management. Based on the forecasted data of resources,
in
Section 4.1, we proposes a resource supply scheduling method based on forecasted data.
Figure 6 illustrates the proposed supply scheduling process, which is performed according to the follow steps. First, based on the resource forecast model, we obtain the measured resource data
and forecasted resource data
. In this case,
is normalized between 0 and 1. Then, we detect the time at which
drops below the resource threshold
. Based on each detected time step
T, each area is assigned to one of the groups
. For example,
at area
x is lower than
. So, area
x is assigned to
. Also, area
i is assigned to
because the
of area
i is lower than the
.
In the next step, within each group, areas are sorted according to a given priority score
at time
, which is derived as
For the first term
, fewer resources mean higher priorities.
is the gradient score at time
that indicates the degree of variability in the forecasted data. A higher
means a rapid decline in
.
is the adjustment coefficient. A smaller
focuses more on
shortage, whereas a larger
gives more weight to the trend of
.
is specified as
where
means the variation of
at time
. By setting the weight to
, sudden fluctuations in the near future are more strongly reflected in
.
After sorting the areas based on in each group, we select the target areas to be supported by the UAV at time t. First, select the area in the group with the smaller i value, and then select in order of priority if the area is in the same group. The number of areas that can be selected depends on the flight distance of the UAV. If the UAV maximum flight distance is long enough, more areas can be supplied via the UAV. However, if the UAV flight path, which will be covered in the next section, is not sufficiently optimized, the number of areas is limited.
We introduce some terms to evaluate the supply miss rate as a metric. The number of required resource supply areas visited by the UAVs is
, and the number of areas visited before resource shortage occurs is
. The number of areas requiring resource supply is
, and the supply misses is
. The areas that are not supported remains in
and are given the highest supply priority in the next round
. To evaluate the performance of the resource supply system, we define the supply miss rate as follows:
where the supply miss rate represents the total number of supply misses of the total number of shortages over the total
K times of supply.
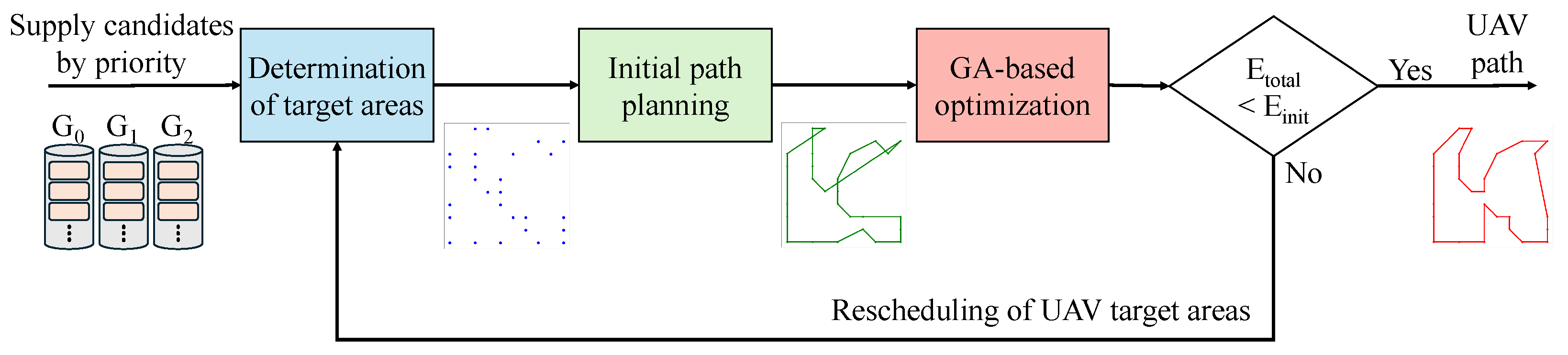
4.3. UAV Path Planning
In various applications of UAVs, their limited flight distance acts as a significant constraint. To overcome this limitation, the battery capacity can be expanded; however, the resulting increase in battery weight causes higher power consumption during UAV flight. Our objective is solve this problem by deriving the UAV flight path that considers both visit priorities and dynamic energy consumption in order to visit the target areas. To address this, we propose a hybrid heuristic algorithm that combines the Christofides algorithm with the GA.
Figure 7 illustrates the path planning process applying the proposed hybrid heuristic algorithm. First, target areas are determined through the resource supply scheduling method. Then, an initial solution for visiting these target areas is derived by applying the Christofides algorithm. The Christofides algorithm is an algorithm for deriving an approximate solution to the TSP, providing an approximation with a guaranteed performance bound [
25]. However, since it does not always guarantee the optimal solution, the solution to the Christofides algorithm is used as the initial path for the proposed UAV path planner.
The GA is a metaheuristic algorithm based on the concept of genetic evolution, which explores a diverse set of solutions through genetic operations such as selection, crossover, and mutation [
26]. In this work, path planning is performed in each iteration by applying crossover, mutation, and selection to solutions selected based on either the initial path or the one with the lowest
. If the
of the path derived by the proposed path planning method exceeds
, the target areas for resource supply are rescheduled. The proposed hybrid heuristic algorithm addresses the approximation limitations of the Christofides algorithm while reducing the computation time of the GA.
Algorithm 1 shows the proposed resource-forecasting-based path planning method. The inputs of the method are the area groups
,
, …,
, which are classified based on priority in
Section 4.2, and
. The output of method is a UAV flight path that considers both the priority of the areas and dynamic energy consumption. First, the areas in two highest-priority groups are assigned to
, while the remaining areas are assigned to
(lines 4–5). Subsequently, the Christofides algorithm is applied to generate an initial approximate optimal path
that visits the
(line 6). If the value of
I is 1, the
is refined using genetic operations, including mutation, crossover, and selection, to initialize
. The
for this path is calculated based on the number of visited areas and energy efficiency metric, which is the total energy consumption divided by the number of visited areas (lines 9–10). If
I is not 1, the proposed algorithm iteratively explores paths based on
, which is the number of combinations within
(line 12). A subset of areas from
is added to
to expand the path, followed by genetic operations. The
of the temporary path
is calculated using Equation (
5). If the
satisfies the energy constraint and
exceeds
, then both
and
are updated (lines 13–18). If
exceeds
, meaning the UAV cannot execute the path, the areas in
and
are reconfigured to reschedule the visiting area set and explore the path (lines 19–21). If even the areas in
cannot be visited within the energy constraints, the proposed algorithm attempts to find an available combination of areas from
that satisfies the energy constraints. The overall time complexity of the Algorithm 1 depends on three main factors:
I,
, and the total number of candidate areas
. Genetic operations and energy evaluations are performed on each candidate path. In the worst case, each path may include up to
points; the proposed Algorithm 1 has a time complexity of
.
| Algorithm 1: Resource-forecasting-based path planning method |
- 1:
Input: , , …, , - 2:
Output: - 3:
- 4:
- 5:
- 6:
- 7:
for I iterations do - 8:
if I == 1 then - 9:
- 10:
- 11:
else - 12:
for iterations do - 13:
- 14:
- 15:
- 16:
if < then - 17:
- 18:
- 19:
else if > then - 20:
- 21:
- 22:
end if - 23:
end for - 24:
end if - 25:
end for
|
While static energy models are relatively easy to apply because they can be modeled in advance of the path planning, dynamic energy models are more challenging to incorporate in standard GAs, as energy consumption continuously changes depending on the UAV’s flight path. To address this limitation, the proposed method applies the dynamic energy model to each candidate path during evaluation to determine its feasibility and iteratively improves the path using selection, crossover, and mutation operations. However, this approach requires recalculating the energy consumption for every candidate route, leading to a significant increase in computational load as the number of target areas increases. To address this issue, the proposed hybrid algorithm initializes the search with a near-optimal path generated based on flight distance, thereby reducing the number of iterations and effectively narrowing the search space. As a result, it can significantly reduce the computation time while still ensuring a satisfactory level of path quality compared to the GA-based path planning method that begins with random paths.
6. Conclusions
In this paper, we proposed an integrated smart farming framework that combines AI-based resource forecasting and UAV-assisted resource supply to enhance operational efficiency. By leveraging the RNN, the system effectively forecasts resource shortages using time-series environmental data. Based on these forecasts, supply scheduling prioritizes areas with the highest urgency, and UAVs are deployed accordingly. To further optimize the resource supply process, we introduced a hybrid UAV path planning method, which maximizes the number of areas that receive resource supply. If the total energy consumption exceeds the UAV’s maximum allowable energy, the system reschedules the resource supply tasks to maintain feasibility. Experimental evaluation demonstrates that the proposed method improves the effectiveness of resource supply, confirming its applicability in real-world smart farming environments. Future work will focus on utilizing multiple UAVs to enhance the system’s applicability in real-world environments. Also, we will aim to solve other problems, such as UAV operational constraints in adverse weather, UAV collision probability, and robustness to sensor failure, using deep reinforcement learning.