Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm
Abstract
1. Introduction
- (1)
- The trajectory planning features and constraints of typical types of UAV in complex environments are classified and introduced.
- (2)
- The growth trends, development processes, and specific applications of different intelligent algorithms in complex environments are reviewed and compared.
- (3)
- The limitations of current UAV trajectory planning algorithms in complex environments and potential future research directions are proposed and discussed.
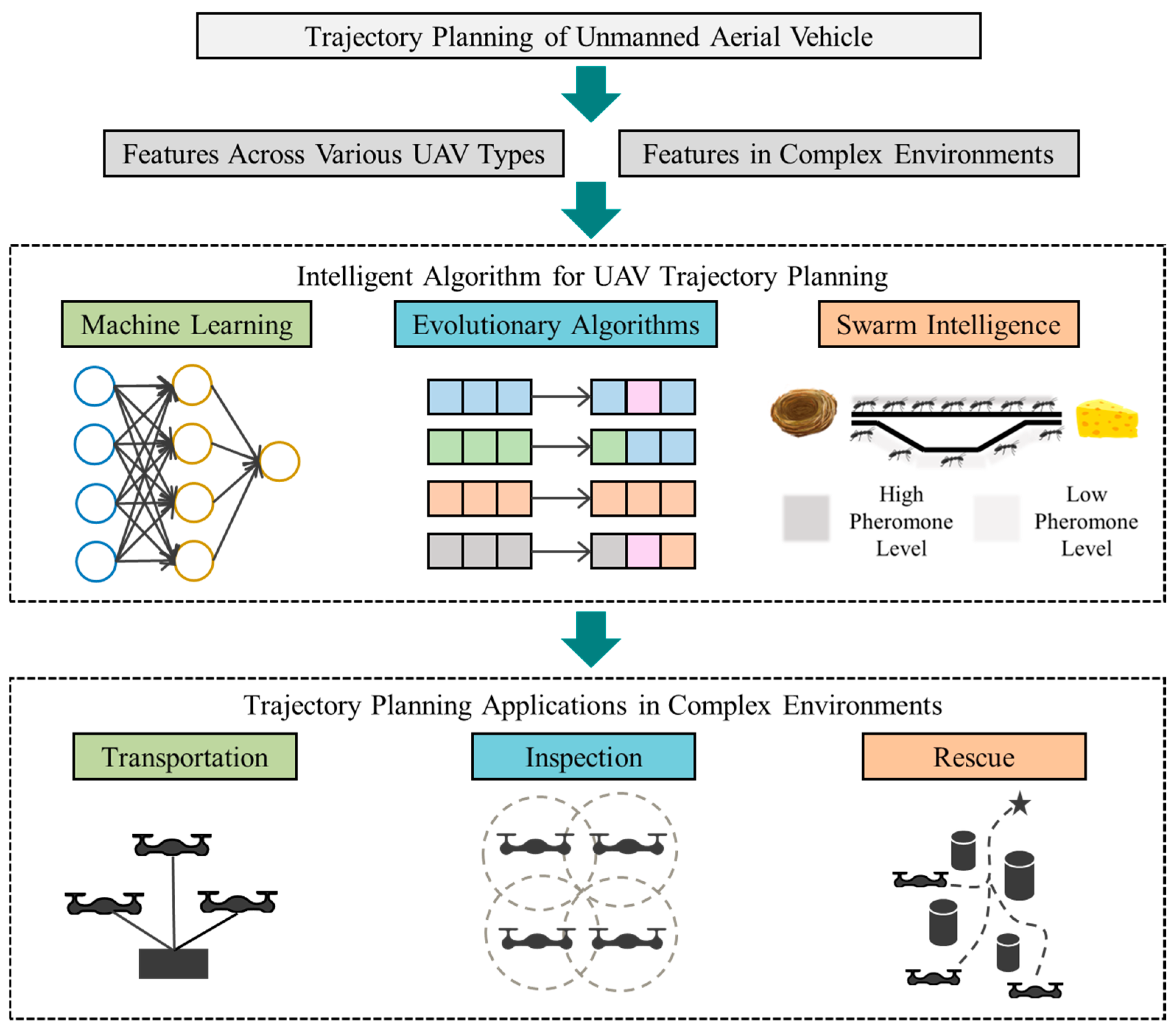
2. Trajectory Planning Features
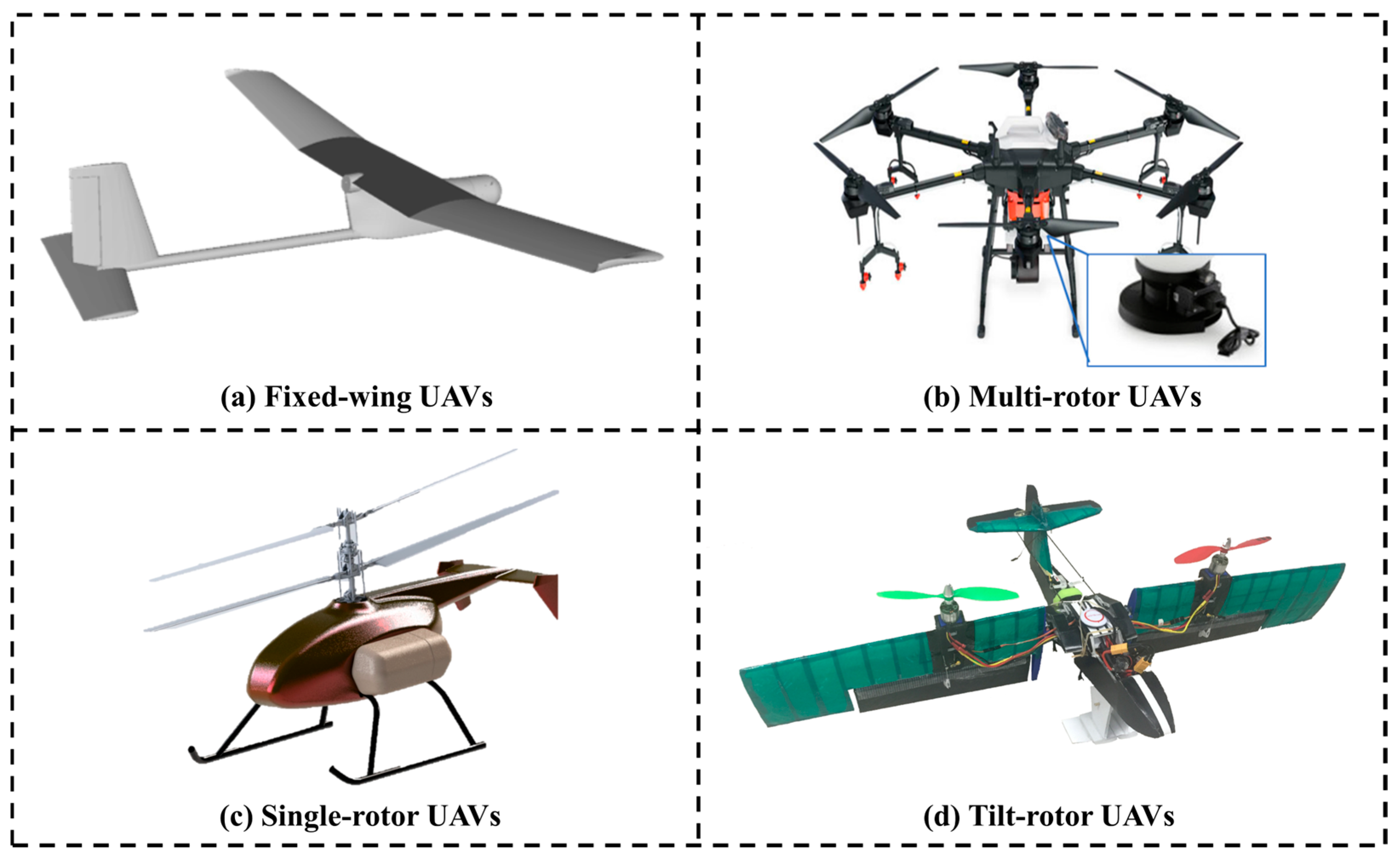
2.1. Trajectory Planning Features Across Various UAV Types
2.2. Trajectory Planning Features in Complex Environments
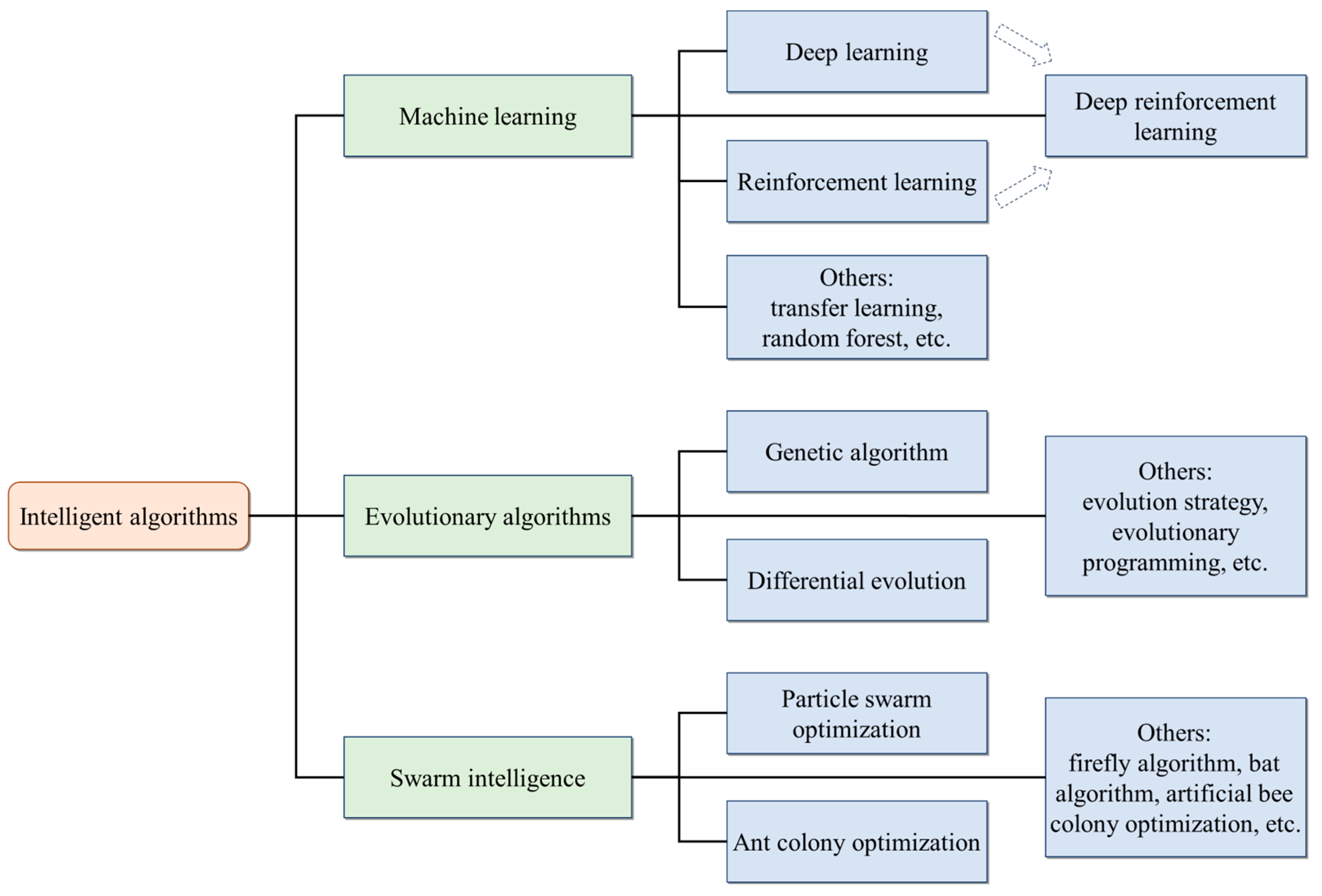
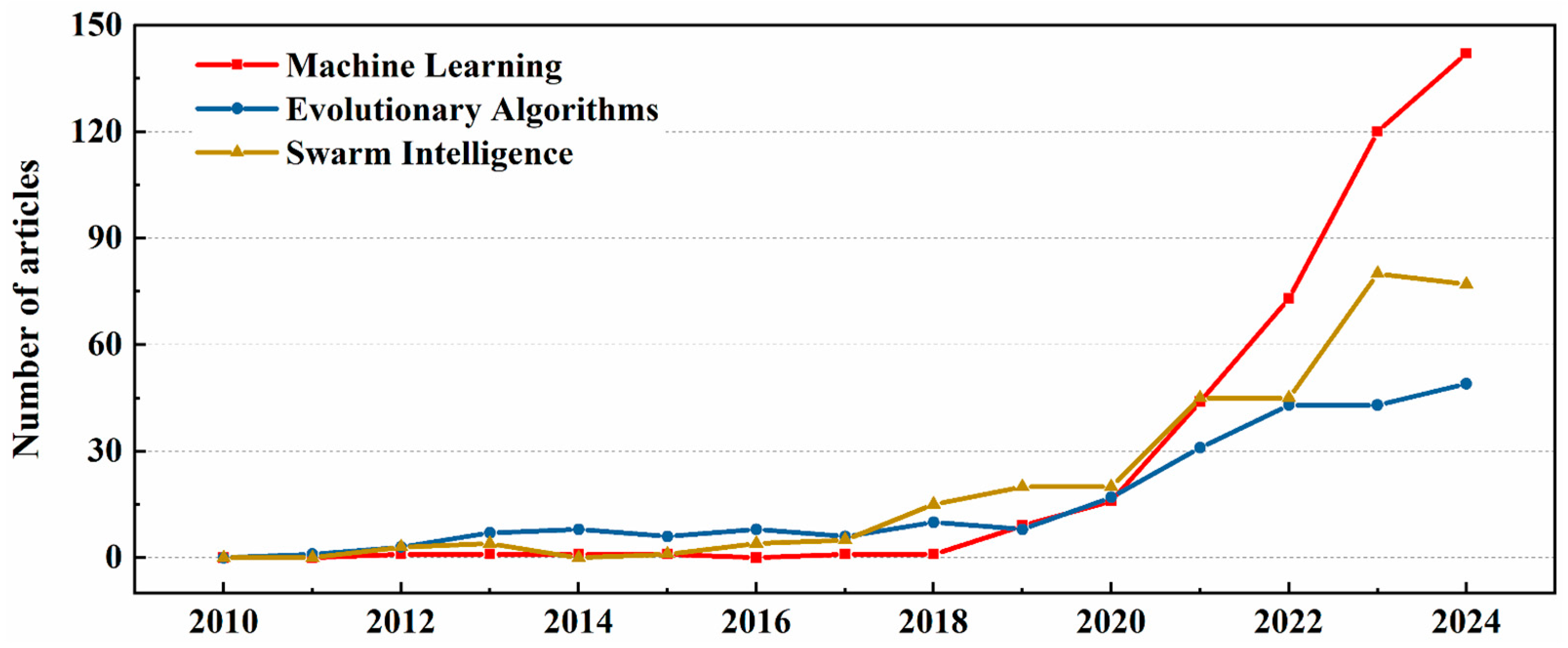
3. Intelligent Algorithms for UAV Trajectory Planning
3.1. Machine Learning
3.1.1. Deep Learning
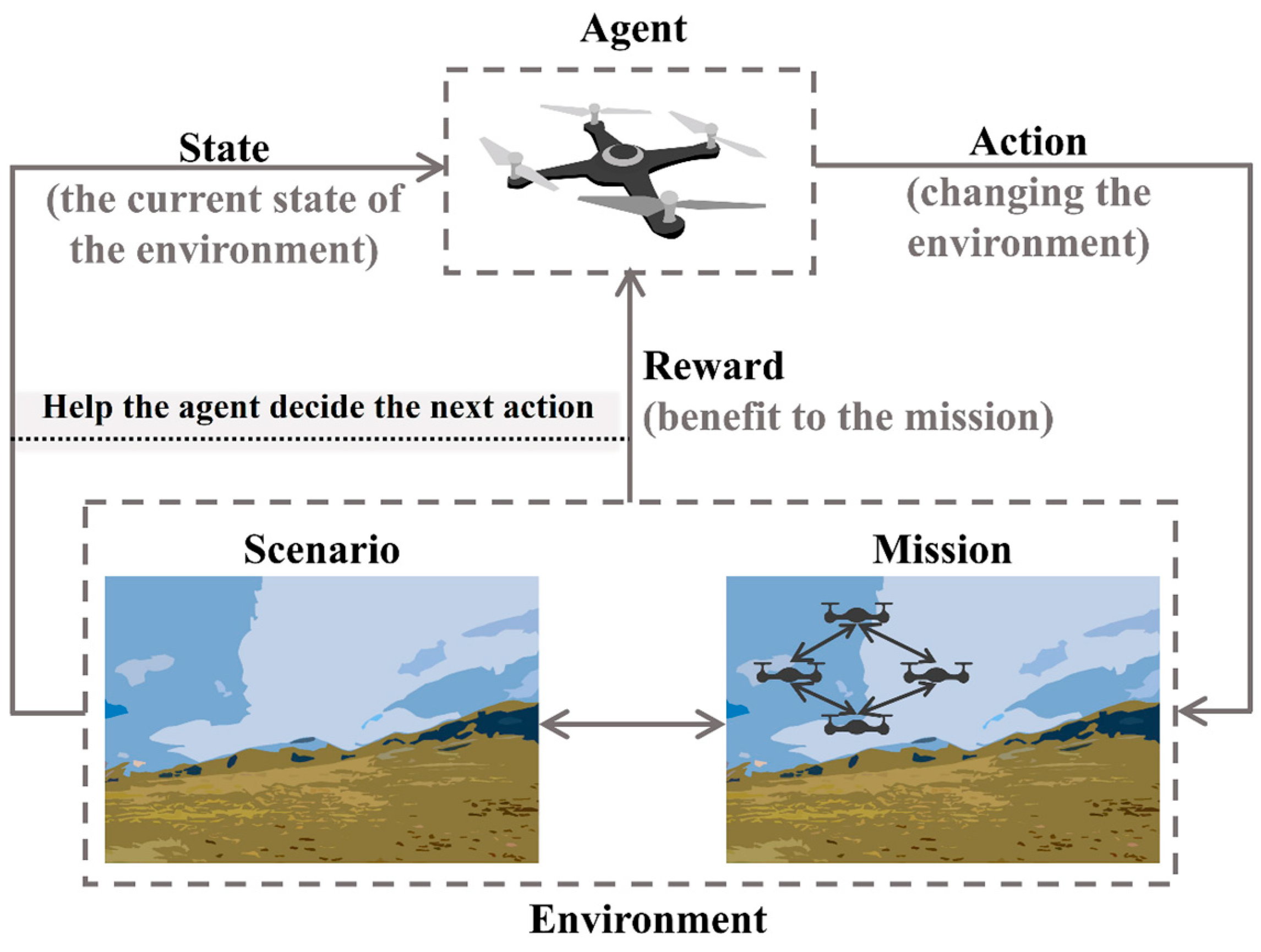
3.1.2. Reinforcement Learning
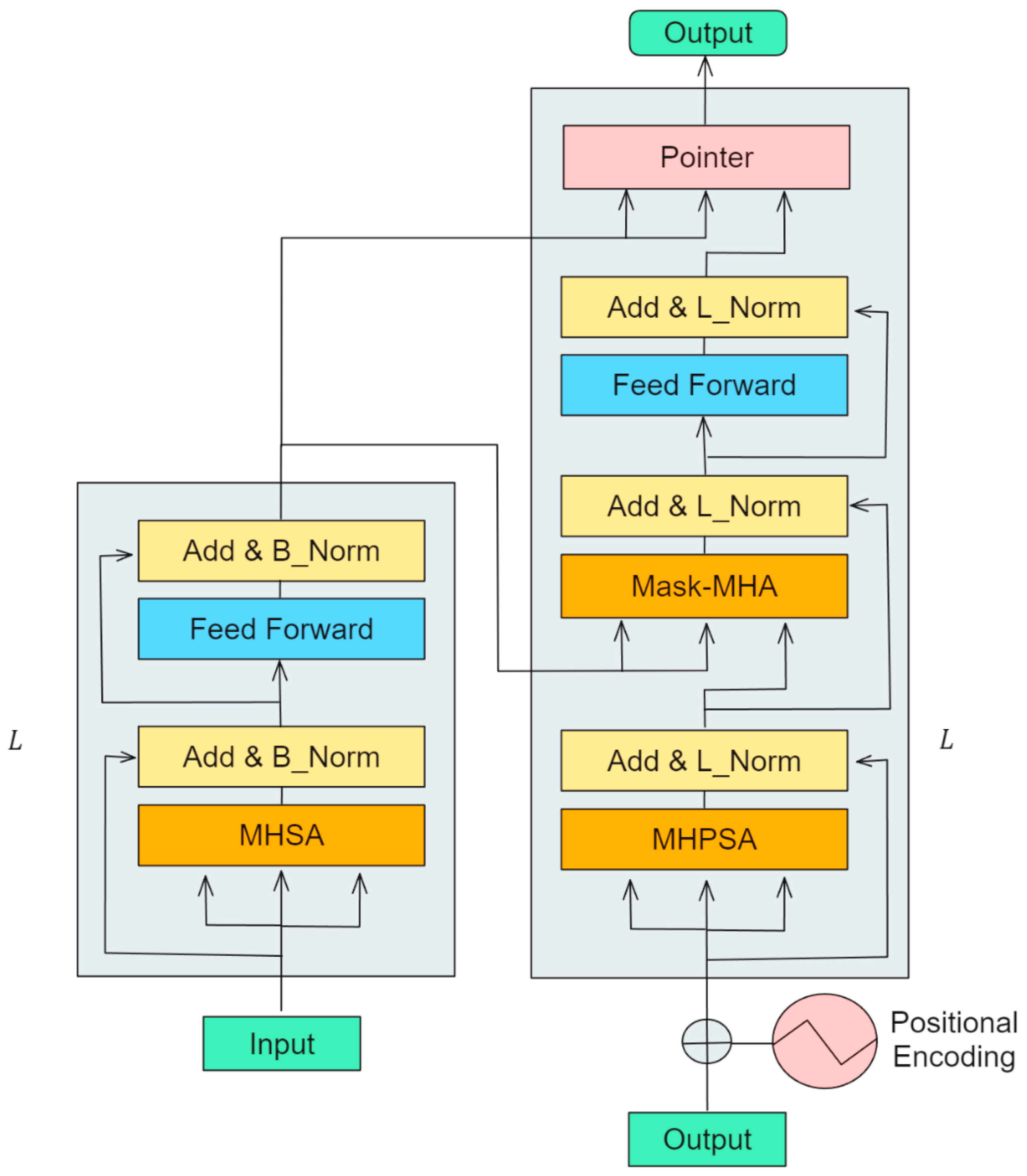
3.1.3. Deep Reinforcement Learning
3.1.4. Other Machine Learning Methods
3.2. Evolutionary Algorithms
3.2.1. Genetic Algorithm
3.2.2. Differential Evolution
3.2.3. Other Evolutionary Algorithms
3.3. Swarm Intelligence
3.3.1. Particle Swarm Optimization
3.3.2. Ant Colony Optimization
3.3.3. Other Swarm Intelligence Algorithms
4. Trajectory Planning Applications in Complex Environments
4.1. Transportation
4.1.1. Slung-Load Transportation
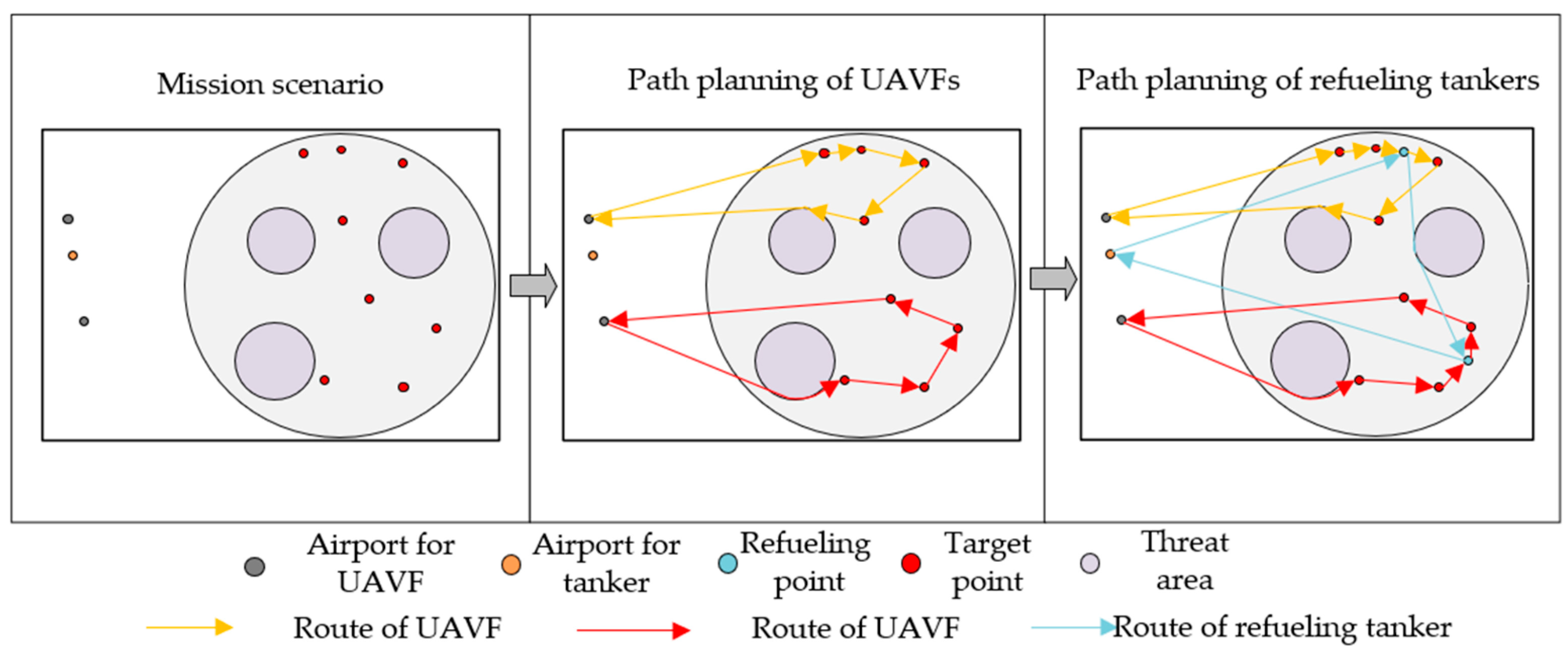
4.1.2. Multi-Destination Transport
4.2. Inspection
4.2.1. Predetermined Checkpoints
4.2.2. Minimum Time Search
4.2.3. Sweep Coverage
4.3. Others
5. Trends and Challenges
- In many cases, the environmental information used for trajectory planning is incomplete or uncertain, containing many unpredictable dynamic factors that evolve. One common approach is to plan the trajectory for UAVs online, which has become a current research trend. The update rate is one of the important requirements for online trajectory planning, which will affect the quality of the planned trajectory and even flight safety. To address this challenge, finding more efficient intelligent algorithms or representing the trajectory with fewer parameters is necessary, thereby reducing the computational time required for planning the trajectory.
- Intelligent algorithms are one of the novel solutions to plan trajectories for UAVs, and they have unique advantages in complex environments. However, significant challenges persist and cannot be overlooked. EAs and SI algorithms have the advantages of strong adaptability, good robustness, and strong parallelism, but they may face the challenge of falling into local optima, which may mislead the trajectory planning of the UAV. Despite numerous attempts to address this issue, further research is required to ensure global convergence throughout the optimization process. The characteristics of DL make it highly adaptable in complex environments, while its unpredictability and the potential for erroneous decisions may result in safety and reliability issues. Furthermore, when applying RL- or DRL-based trajectory planning methods in practical scenarios, the environment rarely provides useful reward feedback, typically indicating either partial or full task completion. The sparse reward problem may significantly slow the convergence of the algorithm or even fail to find a feasible trajectory within an acceptable time.
- To cope with complex environments, UAV trajectory planning methods based on intelligent algorithms are often expected to balance coordination, accuracy, collision avoidance, and efficiency. Current research usually focuses on developing UAV trajectory planning methods tailored to specific scenarios or requirements. In transportation applications, factors such as terrain and obstacles are generally considered. Coordinated delivery between UAVs and ground vehicles and multi-UAV cable-suspended load transportation are gradually becoming a research trend. Still, the current related research based on intelligent algorithms usually models the load as a point mass, which lacks general applicability. The main research objectives of UAV trajectory planning in inspection applications include minimizing search time and maximizing information collection. Consequently, developing real-time trajectory planning methods capable of processing large volumes of information is a direction that warrants further research. Existing UAV trajectory planning methods based on intelligent algorithms each demonstrate unique advantages. However, approaches that achieve a balance across multiple scenarios may be more practical for real-world applications.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nayeem, G.M.; Fan, M.; Daiyan, G.M. Adaptive Q-Learning Grey Wolf Optimizer for UAV Path Planning. Drones 2025, 9, 246. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Ahn, C.K.; Gong, W. Optimized Intelligent Tracking Control for a Quadrotor Unmanned Aerial Vehicle with Actuator Failures. Aerosp. Sci. Technol. 2024, 144, 108803. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Dong, Q.; Wang, Z.; Xi, H.; Yuan, J. Fsmp: A Frontier-Sampling-Mixed Planner for Fast Autonomous Exploration of Complex and Large 3-D Environments. IEEE Trans. Instrum. Meas. 2025, 74, 1–14. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, D.; Wang, B.; Li, L. Dynamic Trajectory Planning for Multi-UAV Multi-Mission Operations Using a Hybrid Strategy. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 7369–7386. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Z.; Yao, M.; Fan, G. A Self-Adaptive Improved Slime Mold Algorithm for Multi-UAV Path Planning. Drones 2025, 9, 219. [Google Scholar] [CrossRef]
- Xie, R.; Meng, Z.; Wang, L.; Li, H.; Wang, K.; Wu, Z. Unmanned Aerial Vehicle Path Planning Algorithm Based on Deep Reinforcement Learning in Large-Scale and Dynamic Environments. IEEE Access 2021, 9, 24884–24900. [Google Scholar] [CrossRef]
- Dentler, J.; Rosalie, M.; Danoy, G.; Bouvry, P.; Kannan, S.; Olivares-Mendez, M.A.; Voos, H. Collision Avoidance Effects on the Mobility of a UAV Swarm Using Chaotic Ant Colony with Model Predictive Control. J. Intell. Robot. Syst. 2019, 93, 227–243. [Google Scholar] [CrossRef]
- Sushma, M.B.; Mashhoodi, B.; Tan, W.; Liujiang, K.; Xu, Q. Spatial Drone Path Planning: A Systematic Review of Parameters and Algorithms. J. Transp. Geogr. 2025, 125, 104209. [Google Scholar]
- Merei, A.; McHeick, H.; Ghaddar, A.; Rebaine, D. A Survey on Obstacle Detection and Avoidance Methods for UAVs. Drones 2025, 9, 203. [Google Scholar] [CrossRef]
- Tang, Y.; Huang, K.; Tan, Z.; Fang, M.; Huang, H. Multi-Subswarm Cooperative Particle Swarm Optimization Algorithm and Its Application. Inf. Sci. 2024, 677, 120887. [Google Scholar] [CrossRef]
- Xing, X.; Zhou, Z.; Li, Y.; Xiao, B.; Xun, Y. Multi-UAV Adaptive Cooperative Formation Trajectory Planning Based on an Improved Matd3 Algorithm of Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 12484–12499. [Google Scholar] [CrossRef]
- Shao, J.; Cheng, J.; Xia, B.; Yang, K.; Wei, H. A Novel Service System for Long-Distance Drone Delivery Using the “Ant Colony+ A*” Algorithm. IEEE Syst. J. 2020, 15, 3348–3359. [Google Scholar] [CrossRef]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.A.; de la Cruz, J.M. Ant Colony Optimization for Multi-UAV Minimum Time Search in Uncertain Domains. Appl. Soft Comput. 2018, 62, 789–806. [Google Scholar] [CrossRef]
- Zhang, H.; Xin, B.; Dou, L.-H.; Chen, J.; Hirota, K. A Review of Cooperative Path Planning of an Unmanned Aerial Vehicle Group. Front. Inf. Technol. Electron. Eng. 2020, 21, 1671–1694. [Google Scholar]
- Falomir, E.; Chaumette, S.; Guerrini, G. A Mobility Model Based on Improved Artificial Potential Fields for Swarms of UAVs. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 8499–8504. [Google Scholar]
- Natarajan, R.; Choset, H.; Likhachev, M. Interleaving Graph Search and Trajectory Optimization for Aggressive Quadrotor Flight. IEEE Robot. Autom. Lett. 2021, 6, 5357–5364. [Google Scholar] [CrossRef]
- Chamseddine, A.; Zhang, Y.; Rabbath, C.A.; Join, C.; Theilliol, D. Flatness-Based Trajectory Planning/Replanning for a Quadrotor Unmanned Aerial Vehicle. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2832–2848. [Google Scholar] [CrossRef]
- Tarjan, R. Depth-First Search and Linear Graph Algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Mansard, N.; DelPrete, A.; Geisert, M.; Tonneau, S.; Stasse, O. Using a Memory of Motion to Efficiently Warm-Start a Nonlinear Predictive Controller. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 2986–2993. [Google Scholar]
- Kuwata, Y.; How, J.P. Cooperative Distributed Robust Trajectory Optimization Using Receding Horizon Milp. IEEE Trans. Control Syst. Technol. 2010, 19, 423–431. [Google Scholar] [CrossRef]
- Maldonado-Romo, J.; Aldape-Pérez, M. Interoperability between Real and Virtual Environments Connected by a Gan for the Path-Planning Problem. Appl. Sci. 2021, 11, 10445. [Google Scholar] [CrossRef]
- Zhou, Y.; Rao, B.; Wang, W. UAV Swarm Intelligence: Recent Advances and Future Trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Glasius, R.; Komoda, A.; Gielen, S.C. Neural Network Dynamics for Path Planning and Obstacle Avoidance. Neural Netw. 1995, 8, 125–133. [Google Scholar] [CrossRef]
- Oreski, S.; Oreski, G. Genetic Algorithm-Based Heuristic for Feature Selection in Credit Risk Assessment. Expert Syst. Appl. 2014, 41, 2052–2064. [Google Scholar] [CrossRef]
- Xu, X.; Rong, H.; Trovati, M.; Liptrott, M.; Bessis, N. Cs-Pso: Chaotic Particle Swarm Optimization Algorithm for Solving Combinatorial Optimization Problems. Soft Comput. 2018, 22, 783–795. [Google Scholar] [CrossRef]
- Lin, N.; Tang, J.; Li, X.; Zhao, L. A Novel Improved Bat Algorithm in UAV Path Planning. Comput. Mater. Contin. 2019, 61, 323–344. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Yang, H. Path Planning for Solar-Powered UAV in Urban Environment. Neurocomputing 2018, 275, 2055–2065. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yan, Y. UAV Formation Trajectory Planning Algorithms: A Review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Chai, S.; Yang, Z.; Huang, J.; Li, X.; Zhao, Y.; Zhou, D. Cooperative UAV Search Strategy Based on Dmpc-Aaco Algorithm in Restricted Communication Scenarios. Def. Technol. 2024, 31, 295–311. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, Y.; Ren, J. Dynamic Mission Planning Algorithm for UAV Formation in Battlefield Environment. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3750–3765. [Google Scholar] [CrossRef]
- Liu, X.; Li, G.; Yang, H.; Zhang, N.; Wang, L.; Shao, P. Agricultural UAV Trajectory Planning by Incorporating Multi-Mechanism Improved Grey Wolf Optimization Algorithm. Expert Syst. Appl. 2023, 233, 120946. [Google Scholar] [CrossRef]
- Basiri, A.; Mariani, V.; Silano, G.; Aatif, M.; Iannelli, L.; Glielmo, L. A Survey on the Application of Path-Planning Algorithms for Multi-Rotor UAVs in Precision Agriculture. J. Navig. 2022, 75, 364–383. [Google Scholar] [CrossRef]
- Luo, Y.; Yu, X.; Yang, D.; Zhou, B. A Survey of Intelligent Transmission Line Inspection Based on Unmanned Aerial Vehicle. Artif. Intell. Rev. 2023, 56, 173–201. [Google Scholar]
- Li, X.; Lu, X.; Chen, W.; Ge, D.; Zhu, J. Research on UAVs Reconnaissance Task Allocation Method Based on Communication Preservation. IEEE Trans. Consum. Electron. 2024, 70, 684–695. [Google Scholar] [CrossRef]
- Wan, Y.; Zhong, Y.; Ma, A.; Zhang, L. An Accurate UAV 3-D Path Planning Method for Disaster Emergency Response Based on an Improved Multiobjective Swarm Intelligence Algorithm. IEEE Trans. Cybern. 2022, 53, 2658–2671. [Google Scholar] [CrossRef]
- Puente-Castro, A.; Rivero, D.; Pazos, A.; Fernandez-Blanco, E. A Review of Artificial Intelligence Applied to Path Planning in UAV Swarms. Neural Comput. Appl. 2022, 34, 153–170. [Google Scholar] [CrossRef]
- Yahia, H.S.; Mohammed, A.S. Path Planning Optimization in Unmanned Aerial Vehicles Using Meta-Heuristic Algorithms: A Systematic Review. Environ. Monit. Assess. 2023, 195, 30. [Google Scholar] [CrossRef] [PubMed]
- Hooshyar, M.; Huang, Y.-M. Meta-Heuristic Algorithms in UAV Path Planning Optimization: A Systematic Review (2018–2022). Drones 2023, 7, 687. [Google Scholar] [CrossRef]
- Poudel, S.; Arafat, M.Y.; Moh, S. Bio-Inspired Optimization-Based Path Planning Algorithms in Unmanned Aerial Vehicles: A Survey. Sensors 2023, 23, 3051. [Google Scholar] [CrossRef]
- Sharma, A.; Shoval, S.; Sharma, A.; Pandey, J.K. Path Planning for Multiple Targets Interception by the Swarm of UAVs Based on Swarm Intelligence Algorithms: A Review. IETE Tech. Rev. 2022, 39, 675–697. [Google Scholar] [CrossRef]
- Tang, J.; Duan, H.; Lao, S. Swarm Intelligence Algorithms for Multiple Unmanned Aerial Vehicles Collaboration: A Comprehensive Review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Pessanha Santos, N. Fixed-Wing UAV Pose Estimation Using a Self-Organizing Map and Deep Learning. Robotics 2024, 13, 114. [Google Scholar] [CrossRef]
- Song, C.; Liu, L.; Wang, G.; Han, J.; Zhang, T.; Lan, Y. Particle Deposition Distribution of Multi-Rotor UAV-Based Fertilizer Spreader under Different Height and Speed Parameters. Drones 2023, 7, 425. [Google Scholar] [CrossRef]
- Dudnik, V. Determination of the Tail Unit Parameters of Ultralight Manned and Unmanned Helicopters at the Preliminary Design Stage. Aerospace 2025, 12, 33. [Google Scholar] [CrossRef]
- Sanchez-Rivera, L.M.; Lozano, R.; Arias-Montano, A. Development, Modeling and Control of a Dual Tilt-Wing UAV in Vertical Flight. Drones 2020, 4, 71. [Google Scholar] [CrossRef]
- Ma, Y.; Luo, R.; Meng, X.; Cao, Y.; Yu, S.; Sun, H.; Ding, W. Path Planning for Searching Submarine with Cooperative Coverage of Fixed-Wing UAVs Cluster in Complex Boundary Sea Area. IEEE Sens. J. 2023, 23, 30070–30083. [Google Scholar] [CrossRef]
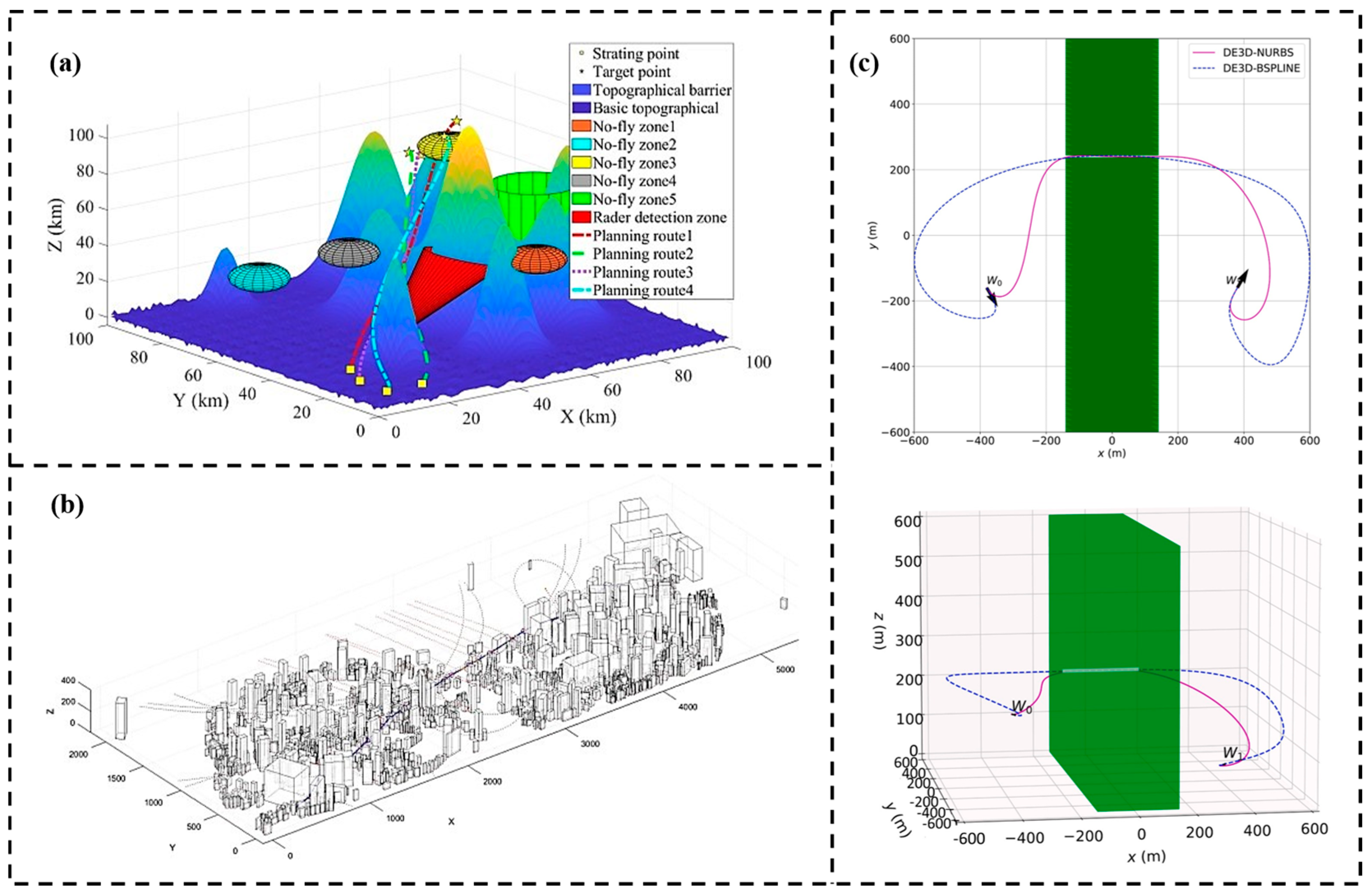
- Freitas, E.J.R.; Cohen, M.W.; Neto, A.A.; Guimarães, F.G.; Pimenta, L.C.A. DE3D-NURBS: A Differential Evolution-Based 3D Path-Planner Integrating Kinematic Constraints and Obstacle Avoidance. Knowl.-Based Syst. 2024, 300, 112084. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Kanth Hari, S.K.; Rathinam, S.; Darbha, S.; Kalyanam, K.; Manyam, S.G.; Casbeer, D. Optimal UAV Route Planning for Persistent Monitoring Missions. IEEE Trans. Robot. 2021, 37, 550–566. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Y.; Li, H.; Fang, R.; Liu, Y.; Zhao, R. Spatio-Temporal Coding-Based Helicopter Trajectory Planning for Pulsed Neural Membrane System. Comput. Intell. Neurosci. 2022, 2022, 1787013. [Google Scholar] [CrossRef]
- Choudhury, S.; Scherer, S.; Singh, S. RRT*-AR: Sampling-Based Alternate Routes Planning with Applications to Autonomous Emergency Landing of a Helicopter. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3947–3952. [Google Scholar]
- Han, Z.; Chen, M.; Shao, S.; Zhou, T.; Wu, Q. Path Planning of Unmanned Autonomous Helicopter Based on Hybrid Satisficing Decision-Enhanced Swarm Intelligence Algorithm. IEEE Trans. Cogn. Dev. Syst. 2023, 15, 1371–1385. [Google Scholar] [CrossRef]
- Ren, B.W.; Wang, B.; Zhang, X.Y.; Zhao, Q.J. Trajectory Planning of Tilt-Rotor UAV Based on Hybrid Algorithm. In Proceedings of the Asia-Pacific International Symposium on Aerospace Technology (APISAT), Jeju, Republic of Korea, 15–17 November 2021; pp. 619–631. [Google Scholar]
- Valente, J.; Del Cerro, J.; Barrientos, A.; Sanz, D. Aerial Coverage Optimization in Precision Agriculture Management: A Musical Harmony Inspired Approach. Comput. Electron. Agric. 2013, 99, 153–159. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, X.; Ma, S.; Tang, R. Research on Global Trajectory Planning for UAV Based on the Information Interaction and Aging Mechanism Wolfpack Algorithm. Expert Syst. Appl. 2025, 273, 126867. [Google Scholar] [CrossRef]
- Lin, X.; Wang, C.; Wang, K.; Li, M.; Yu, X. Trajectory Planning for Unmanned Aerial Vehicles in Complicated Urban Environments: A Control Network Approach. Transp. Res. Part C Emerg. Technol. 2021, 128, 103120. [Google Scholar] [CrossRef]
- Li, B.; Yang, Z.-p.; Chen, D.-q.; Liang, S.-y.; Ma, H. Maneuvering Target Tracking of UAV Based on Mn-Ddpg and Transfer Learning. Def. Technol. 2021, 17, 457–466. [Google Scholar] [CrossRef]
- Li, R.; Xin, B. Autonomous Navigation of Quadrotors in Dynamic Complex Environments. IEEE Trans. Ind. Electron. 2025, 72, 2790–2800. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Yao, P. Energy-Optimal Path Planning for Solar-Powered UAV with Tracking Moving Ground Target. Aerosp. Sci. Technol. 2016, 53, 241–251. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, Q.; Zou, Z. Threat-Oriented Collaborative Path Planning of Unmanned Reconnaissance Mission for the Target Group. Aerospace 2022, 9, 577. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Antsaklis, P.J. Neural Networks for Control Systems. IEEE Trans. Neural Netw. 1990, 1, 242–244. [Google Scholar] [CrossRef]
- Pandey, A.; Jain, K. An Intelligent System for Crop Identification and Classification from UAV Images Using Conjugated Dense Convolutional Neural Network. Comput. Electron. Agric. 2022, 192, 106543. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Fan, J.; Wu, J.; Wu, T. Control-Oriented UAV Highly Feasible Trajectory Planning: A Deep Learning Method. Aerosp. Sci. Technol. 2021, 110, 106435. [Google Scholar] [CrossRef]
- Shaffer, J.A.; Xu, H. Centralized and Decentralized Application of Neural Networks Learning Optimized Solutions of Distributed Agents. In Proceedings of the Micro- and Nanotechnology Sensors, Systems, and Applications XI, Baltimore, MD, USA, 14–18 April 2019; pp. 395–408. [Google Scholar]
- Khan, A.; Kumar, V.; Ribeiro, A. Large Scale Distributed Collaborative Unlabeled Motion Planning with Graph Policy Gradients. IEEE Robot. Autom. Lett. 2021, 6, 5340–5347. [Google Scholar] [CrossRef]
- Tsubaki, M.; Tomii, K.; Sese, J. Compound–Protein Interaction Prediction with End-to-End Learning of Neural Networks for Graphs and Sequences. Bioinformatics 2019, 35, 309–318. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Lin, W.; Liu, Z.; Prorok, A. Message-Aware Graph Attention Networks for Large-Scale Multi-Robot Path Planning. IEEE Robot. Autom. Lett. 2021, 6, 5533–5540. [Google Scholar] [CrossRef]
- Palossi, D.; Conti, F.; Benini, L. An Open Source and Open Hardware Deep Learning-Powered Visual Navigation Engine for Autonomous Nano-UAVs. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini Island, Greece, 29–31 May 2019; pp. 604–611. [Google Scholar]
- Dai, X.; Mao, Y.; Huang, T.; Qin, N.; Huang, D.; Li, Y. Automatic Obstacle Avoidance of Quadrotor UAV Via CNN-Based Learning. Neurocomputing 2020, 402, 346–358. [Google Scholar] [CrossRef]
- Kalinov, I.; Petrovsky, A.; Ilin, V.; Pristanskiy, E.; Kurenkov, M.; Ramzhaev, V.; Idrisov, I.; Tsetserukou, D. Warevision: CNN Barcode Detection-Based UAV Trajectory Optimization for Autonomous Warehouse Stocktaking. IEEE Robot. Autom. Lett. 2020, 5, 6647–6653. [Google Scholar] [CrossRef]
- Chen, N.; Fan, J.; Yuan, J.; Zheng, E. Obtpn: A Vision-Based Network for UAV Geo-Localization in Multi-Altitude Environments. Drones 2025, 9, 33. [Google Scholar] [CrossRef]
- Wang, J.; Guan, X.; Sun, Z.; Shen, T.; Huang, D.; Liu, F.; Cui, H. Omega: Efficient Occlusion-Aware Navigation for Air-Ground Robots in Dynamic Environments Via State Space Model. IEEE Robot. Autom. Lett. 2025, 10, 1066–1073. [Google Scholar] [CrossRef]
- Wang, H.; Tan, A.H.; Nejat, G. Navformer: A Transformer Architecture for Robot Target-Driven Navigation in Unknown and Dynamic Environments. IEEE Robot. Autom. Lett. 2024, 9, 6808–6815. [Google Scholar] [CrossRef]
- Zhu, B.; Bedeer, E.; Nguyen, H.H.; Barton, R.; Gao, Z. UAV Trajectory Planning for Aoi-Minimal Data Collection in UAV-Aided Iot Networks by Transformer. IEEE Trans. Wirel. Commun. 2023, 22, 1343–1358. [Google Scholar] [CrossRef]
- Yu, C.-H.; Tsai, J.; Chang, Y.-T. Intelligent Path Planning for UAV Patrolling in Dynamic Environments Based on the Transformer Architecture. Electronics 2024, 13, 4716. [Google Scholar] [CrossRef]
- Dong, L.; Jiang, F.; Peng, Y. Attention-Based UAV Trajectory Optimization for Wireless Power Transfer-Assisted Iot Systems. IEEE Trans. Ind. Electron. 2025, 72, 8463–8471. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.H.; Yang, H.; Wang, G.; Leung, K.K. Ensuring Threshold Aoi for UAV-Assisted Mobile Crowdsensing by Multi-Agent Deep Reinforcement Learning with Transformer. IEEE/ACM Trans. Netw. 2024, 32, 566–581. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning That Matters. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zhao, X.; Ding, S.; An, Y.; Jia, W. Asynchronous Reinforcement Learning Algorithms for Solving Discrete Space Path Planning Problems. Appl. Intell. 2018, 48, 4889–4904. [Google Scholar] [CrossRef]
- Zhang, B.; Mao, Z.; Liu, W.; Liu, J. Geometric Reinforcement Learning for Path Planning of UAVs. J. Intell. Robot. Syst. 2015, 77, 391–409. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Y. UAV Path Planning Based on Multi-Layer Reinforcement Learning Technique. IEEE Access 2021, 9, 59486–59497. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- He, L.; Aouf, N.; Song, B. Explainable Deep Reinforcement Learning for UAV Autonomous Path Planning. Aerosp. Sci. Technol. 2021, 118, 107052. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Towards Real-Time Path Planning through Deep Reinforcement Learning for a UAV in Dynamic Environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Wang, X.; Gursoy, M.C.; Erpek, T.; Sagduyu, Y.E. Learning-Based UAV Path Planning for Data Collection with Integrated Collision Avoidance. IEEE Internet Things J. 2022, 9, 16663–16676. [Google Scholar] [CrossRef]
- Bo, L.; Zhang, T.; Zhang, H.; Hong, J.; Liu, M.; Zhang, C.; Liu, B. 3D UAV Path Planning in Unknown Environment: A Transfer Reinforcement Learning Method Based on Low-Rank Adaption. Adv. Eng. Inform. 2024, 62, 102920. [Google Scholar] [CrossRef]
- Fontanesi, G.; Zhu, A.; Arvaneh, M.; Ahmadi, H. A Transfer Learning Approach for UAV Path Design with Connectivity Outage Constraint. IEEE Internet Things J. 2023, 10, 4998–5012. [Google Scholar] [CrossRef]
- Pérez-Cutiño, M.A.; Rodríguez, F.; Pascual, L.D.; Díaz-Báñez, J.M. Ornithopter Trajectory Optimization with Neural Networks and Random Forest. J. Intell. Robot. Syst. 2022, 105, 17. [Google Scholar] [CrossRef]
- Hönig, W.; Preiss, J.A.; Kumar, T.K.S.; Sukhatme, G.S.; Ayanian, N. Trajectory Planning for Quadrotor Swarms. IEEE Trans. Robot. 2018, 34, 856–869. [Google Scholar] [CrossRef]
- Pan, H.; Zahmatkesh, M.; Rekabi-Bana, F.; Arvin, F.; Hu, J. T-Star: Time-Optimal Swarm Trajectory Planning for Quadrotor Unmanned Aerial Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 1–16. [Google Scholar] [CrossRef]
- Bäck, T.; Schwefel, H.-P. An Overview of Evolutionary Algorithms for Parameter Optimization. Evol. Comput. 1993, 1, 1–23. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonté, G. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning. IEEE Trans. Ind. Inform. 2012, 9, 132–141. [Google Scholar] [CrossRef]
- Cao, Y.; Wei, W.; Bai, Y.; Qiao, H. Multi-Base Multi-UAV Cooperative Reconnaissance Path Planning with Genetic Algorithm. Clust. Comput. 2019, 22, 5175–5184. [Google Scholar] [CrossRef]
- Ergezer, H.; Leblebicioglu, K. Path Planning for UAVs for Maximum Information Collection. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 502–520. [Google Scholar] [CrossRef]
- Sahingoz, O.K. Generation of Bezier Curve-Based Flyable Trajectories for Multi-UAV Systems with Parallel Genetic Algorithm. J. Intell. Robot. Syst. 2014, 74, 499–511. [Google Scholar] [CrossRef]
- Shorakaei, H.; Vahdani, M.; Imani, B.; Gholami, A. Optimal Cooperative Path Planning of Unmanned Aerial Vehicles by a Parallel Genetic Algorithm. Robotica 2016, 34, 823–836. [Google Scholar] [CrossRef]
- Volkan Pehlivanoglu, Y.; Baysal, O.; Hacioglu, A. Path Planning for Autonomous UAV Via Vibrational Genetic Algorithm. Aircr. Eng. Aerosp. Technol. 2007, 79, 352–359. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V. A New Vibrational Genetic Algorithm Enhanced with a Voronoi Diagram for Path Planning of Autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution–a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Slowik, A. Application of an Adaptive Differential Evolution Algorithm with Multiple Trial Vectors to Artificial Neural Network Training. IEEE Trans. Ind. Electron. 2010, 58, 3160–3167. [Google Scholar] [CrossRef]
- Brintaki, A.N.; Nikolos, I.K. Coordinated UAV Path Planning Using Differential Evolution. Oper. Res. 2005, 5, 487–502. [Google Scholar] [CrossRef]
- Adhikari, D.; Kim, E.; Reza, H. A Fuzzy Adaptive Differential Evolution for Multi-Objective 3D UAV Path Optimization. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia-San Sebastian, Spain, 5–8 June 2017; pp. 2258–2265. [Google Scholar]
- Yu, X.; Li, C.; Zhou, J. A Constrained Differential Evolution Algorithm to Solve UAV Path Planning in Disaster Scenarios. Knowl.-Based Syst. 2020, 204, 106209. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N.; Wang, R.; Chen, H. Differential Evolution with Multi-Population Based Ensemble of Mutation Strategies. Inf. Sci. 2016, 329, 329–345. [Google Scholar] [CrossRef]
- Wu, G.; Shen, X.; Li, H.; Chen, H.; Lin, A.; Suganthan, P.N. Ensemble of Differential Evolution Variants. Inf. Sci. 2018, 423, 172–186. [Google Scholar] [CrossRef]
- Gui, L.; Xia, X.; Yu, F.; Wu, H.; Wu, R.; Wei, B.; Zhang, Y.; Li, X.; He, G. A Multi-Role Based Differential Evolution. Swarm Evol. Comput. 2019, 50, 100508. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-Strategy Fusion Differential Evolution Algorithm for UAV Path Planning in Complex Environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection (Complex Adaptive Systems); MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Yang, X.; Cai, M.; Li, J. Path Planning for Unmanned Aerial Vehicles Based on Genetic Programming. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 717–722. [Google Scholar]
- Hohmann, N.; Bujny, M.; Adamy, J.; Olhofer, M. Hybrid Evolutionary Approach to Multi-Objective Path Planning for UAVs. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–8. [Google Scholar]
- Hohmann, N.; Bujny, M.; Adamy, J.; Olhofer, M. Multi-Objective 3D Path Planning for UAVs in Large-Scale Urban Scenarios. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022; pp. 1–8. [Google Scholar]
- Duan, H.; Zhang, X. Phase Transition of Vortexlike Self-Propelled Particles Induced by a Hostile Particle. Phys. Rev. E 2015, 92, 012701. [Google Scholar] [CrossRef]
- Long, N.K.; Sammut, K.; Sgarioto, D.; Garratt, M.; Abbass, H.A. A Comprehensive Review of Shepherding as a Bio-Inspired Swarm-Robotics Guidance Approach. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 523–537. [Google Scholar] [CrossRef]
- Shi, Y. Particle Swarm Optimization: Developments, Applications and Resources. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; pp. 81–86. [Google Scholar]
- Liu, Y.; Zhang, X.; Guan, X.; Delahaye, D. Adaptive Sensitivity Decision Based Path Planning Algorithm for Unmanned Aerial Vehicle with Improved Particle Swarm Optimization. Aerosp. Sci. Technol. 2016, 58, 92–102. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-Enhanced UAV Path Planning with Spherical Vector-Based Particle Swarm Optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Pérez-Carabaza, S.; Scherer, J.; Rinner, B.; López-Orozco, J.A.; Besada-Portas, E. UAV Trajectory Optimization for Minimum Time Search with Communication Constraints and Collision Avoidance. Eng. Appl. Artif. Intell. 2019, 85, 357–371. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, C.; Feng, J.; Liu, Z.; Zhou, Y.; Zhang, Z. A Self-Heuristic Ant-Based Method for Path Planning of Unmanned Aerial Vehicle in Complex 3-D Space with Dense U-Type Obstacles. IEEE Access 2019, 7, 150775–150791. [Google Scholar] [CrossRef]
- Hunter III, J.E.; Gannon, T.W.; Richardson, R.J.; Yelverton, F.H.; Leon, R.G. Integration of Remote-Weed Mapping and an Autonomous Spraying Unmanned Aerial Vehicle for Site-Specific Weed Management. Pest Manag. Sci. 2020, 76, 1386–1392. [Google Scholar] [CrossRef]
- Akshya, J.; Priyadarsini, P. Graph-Based Path Planning for Intelligent UAVs in Area Coverage Applications. J. Intell. Fuzzy Syst. 2020, 39, 8191–8203. [Google Scholar] [CrossRef]
- Rosalie, M.; Danoy, G.; Chaumette, S.; Bouvry, P. Chaos-Enhanced Mobility Models for Multilevel Swarms of UAVs. Swarm Evol. Comput. 2018, 41, 36–48. [Google Scholar] [CrossRef]
- Li, F.; Fan, X.; Hou, Z. A Firefly Algorithm with Self-Adaptive Population Size for Global Path Planning of Mobile Robot. IEEE Access 2020, 8, 168951–168964. [Google Scholar] [CrossRef]
- Cheng, L.; Zhong, L.; Zhang, X.; Xing, J. A Staged Adaptive Firefly Algorithm for UAV Charging Planning in Wireless Sensor Networks. Comput. Commun. 2020, 161, 132–141. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chu, H.E.; Mirjalili, S. Three-Dimensional Path Planning for Ucav Using an Improved Bat Algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Han, Z.; Chen, M.; Shao, S.; Wu, Q. Improved Artificial Bee Colony Algorithm-Based Path Planning of Unmanned Autonomous Helicopter Using Multi-Strategy Evolutionary Learning. Aerosp. Sci. Technol. 2022, 122, 107374. [Google Scholar] [CrossRef]
- Wang, B.H.; Wang, D.B.; Ali, Z.A. A Cauchy Mutant Pigeon-Inspired Optimization–Based Multi-Unmanned Aerial Vehicle Path Planning Method. Meas. Control 2020, 53, 83–92. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, J.; Zhang, C.; Zhan, B.; Zheng, X. A Novel Whale Optimization Algorithm of Path Planning Strategy for Mobile Robots. Appl. Intell. 2023, 53, 10843–10857. [Google Scholar] [CrossRef]
- Jamshidi, V.; Nekoukar, V.; Refan, M.H. Real Time UAV Path Planning by Parallel Grey Wolf Optimization with Align Coefficient on Can Bus. Clust. Comput. 2021, 24, 2495–2509. [Google Scholar] [CrossRef]
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three Dimensional Path Planning Using Grey Wolf Optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Marinaki, M.; Taxidou, A.; Marinakis, Y. A Hybrid Dragonfly Algorithm for the Vehicle Routing Problem with Stochastic Demands. Intell. Syst. Appl. 2023, 18, 200225. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, P.; Liang, D.; Dong, J. A Learning-Based Anti-Swing Trajectory Refinement Approach for UAVs with Cable-Suspended Payload without Offline Training. IEEE Trans. Intell. Veh. 2024, 9, 6950–6959. [Google Scholar] [CrossRef]
- Li, R.; Yang, F.; Xu, Y.; Yuan, W.; Lu, Q. Deep Reinforcement Learning-Based Swing-Free Trajectories Planning Algorithm for UAV with a Suspended Load. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 6149–6154. [Google Scholar]
- Hua, H.; Fang, Y.; Zhang, X.; Qian, C. A Time-Optimal Trajectory Planning Strategy for an Aircraft with a Suspended Payload Via Optimization and Learning Approaches. IEEE Trans. Control Syst. Technol. 2022, 30, 2333–2343. [Google Scholar] [CrossRef]
- Faust, A.; Palunko, I.; Cruz, P.; Fierro, R.; Tapia, L. Automated Aerial Suspended Cargo Delivery through Reinforcement Learning. Artif. Intell. 2017, 247, 381–398. [Google Scholar] [CrossRef]
- Ergezer, H. Multi-Objective Trajectory Planning for Slung-Load Quadrotor System. IEEE Access 2021, 9, 155003–155017. [Google Scholar] [CrossRef]
- Hegde, A.; Ghose, D. Multi-UAV Collaborative Transportation of Payloads with Obstacle Avoidance. IEEE Control Syst. Lett. 2021, 6, 926–931. [Google Scholar] [CrossRef]
- Jackson, B.E.; Howell, T.A.; Shah, K.; Schwager, M.; Manchester, Z. Scalable Cooperative Transport of Cable-Suspended Loads with UAVs Using Distributed Trajectory Optimization. IEEE Robot. Autom. Lett. 2020, 5, 3368–3374. [Google Scholar] [CrossRef]
- Duan, D.; Zu, R.; Yu, T.; Zhang, C.; Li, J. Differential Flatness-Based Real-Time Trajectory Planning for Multihelicopter Cooperative Transportation in Crowded Environments. AIAA J. 2023, 61, 4079–4095. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Han, J. Trajectory Planning of Load Transportation with Multi-Quadrotors Based on Reinforcement Learning Algorithm. Aerosp. Sci. Technol. 2021, 116, 106887. [Google Scholar] [CrossRef]
- Du, P.; He, X.; Cao, H.; Garg, S.; Kaddoum, G.; Hassan, M.M. AI-Based Energy-Efficient Path Planning of Multiple Logistics UAVs in Intelligent Transportation Systems. Comput. Commun. 2023, 207, 46–55. [Google Scholar] [CrossRef]
- Stodola, P.; Kutěj, L. Multi-Depot Vehicle Routing Problem with Drones: Mathematical Formulation, Solution Algorithm and Experiments. Expert Syst. Appl. 2024, 241, 122483. [Google Scholar] [CrossRef]
- Tsourdos, A.; White, B.; Shanmugavel, M. Cooperative Path Planning of Unmanned Aerial Vehicles; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cheng, Z.; Yang, J.; Sun, Y.; Zhao, L.; Zhao, L. State Predictor-Based Deep Model Reference Adaptive Control for Quadrotor Trajectory Tracking. Aerosp. Sci. Technol. 2025, 157, 109868. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V.; Pehlivanoglu, P. An Enhanced Genetic Algorithm for Path Planning of Autonomous UAV in Target Coverage Problems. Appl. Soft Comput. 2021, 112, 107796. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Y.; She, J.; Wu, M. A Path Planning Method for Sweep Coverage with Multiple UAVs. IEEE Internet Things J. 2020, 7, 8967–8978. [Google Scholar] [CrossRef]
- Çakıcı, F.; Ergezer, H.; Irmak, U.; Leblebicioğlu, M.K. Coordinated Guidance for Multiple UAVs. Trans. Inst. Meas. Control 2016, 38, 593–601. [Google Scholar] [CrossRef]
- Xie, J.; Chen, J. Multiregional Coverage Path Planning for Multiple Energy Constrained UAVs. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17366–17381. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, P.; Liang, X.; Wang, W.; Zhang, J.; Fu, Q. Reconnaissance Mission Conducted by UAV Swarms Based on Distributed Pso Path Planning Algorithms. IEEE Access 2019, 7, 105086–105099. [Google Scholar] [CrossRef]
- Mou, Z.; Zhang, Y.; Gao, F.; Wang, H.; Zhang, T.; Han, Z. Deep Reinforcement Learning Based Three-Dimensional Area Coverage with UAV Swarm. IEEE J. Sel. Areas Commun. 2021, 39, 3160–3176. [Google Scholar] [CrossRef]
- Hu, W.; Yu, Y.; Liu, S.; She, C.; Guo, L.; Vucetic, B.; Li, Y. Multi-UAV Coverage Path Planning: A Distributed Online Cooperation Method. IEEE Trans. Veh. Technol. 2023, 72, 11727–11740. [Google Scholar] [CrossRef]
- Aslan, S. An Immune Plasma Algorithm with a Modified Treatment Schema for Ucav Path Planning. Eng. Appl. Artif. Intell. 2022, 112, 104789. [Google Scholar] [CrossRef]
- Duan, H.; Huang, L. Imperialist Competitive Algorithm Optimized Artificial Neural Networks for Ucav Global Path Planning. Neurocomputing 2014, 125, 166–171. [Google Scholar] [CrossRef]
- Duan, H.; Yu, Y.; Zhang, X.; Shao, S. Three-Dimension Path Planning for Ucav Using Hybrid Meta-Heuristic ACO-DE Algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Niu, Y.; Yan, X.; Wang, Y.; Niu, Y. An Adaptive Neighborhood-Based Search Enhanced Artificial Ecosystem Optimizer for UCAV Path Planning. Expert Syst. Appl. 2022, 208, 118047. [Google Scholar] [CrossRef]
- Chen, Q.-y.; Lu, Y.-f.; Jia, G.-w.; Li, Y.; Zhu, B.-j.; Lin, J.-c. Path Planning for UAVs Formation Reconfiguration Based on Dubins Trajectory. J. Cent. South Univ. 2018, 25, 2664–2676. [Google Scholar] [CrossRef]
- Huang, L.; Qu, H.; Ji, P.; Liu, X.; Fan, Z. A Novel Coordinated Path Planning Method Using K-Degree Smoothing for Multi-UAVs. Appl. Soft Comput. 2016, 48, 182–192. [Google Scholar] [CrossRef]
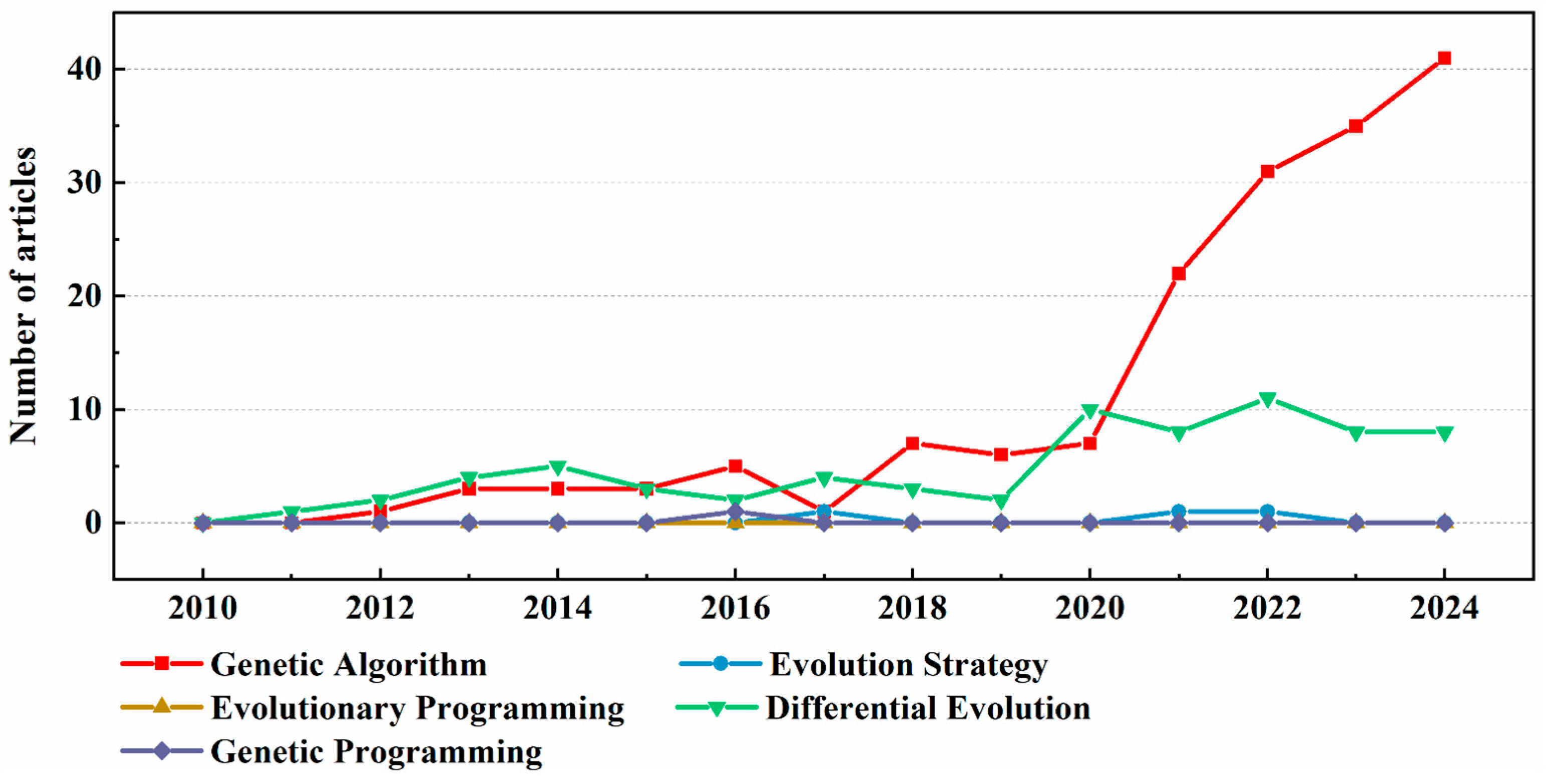


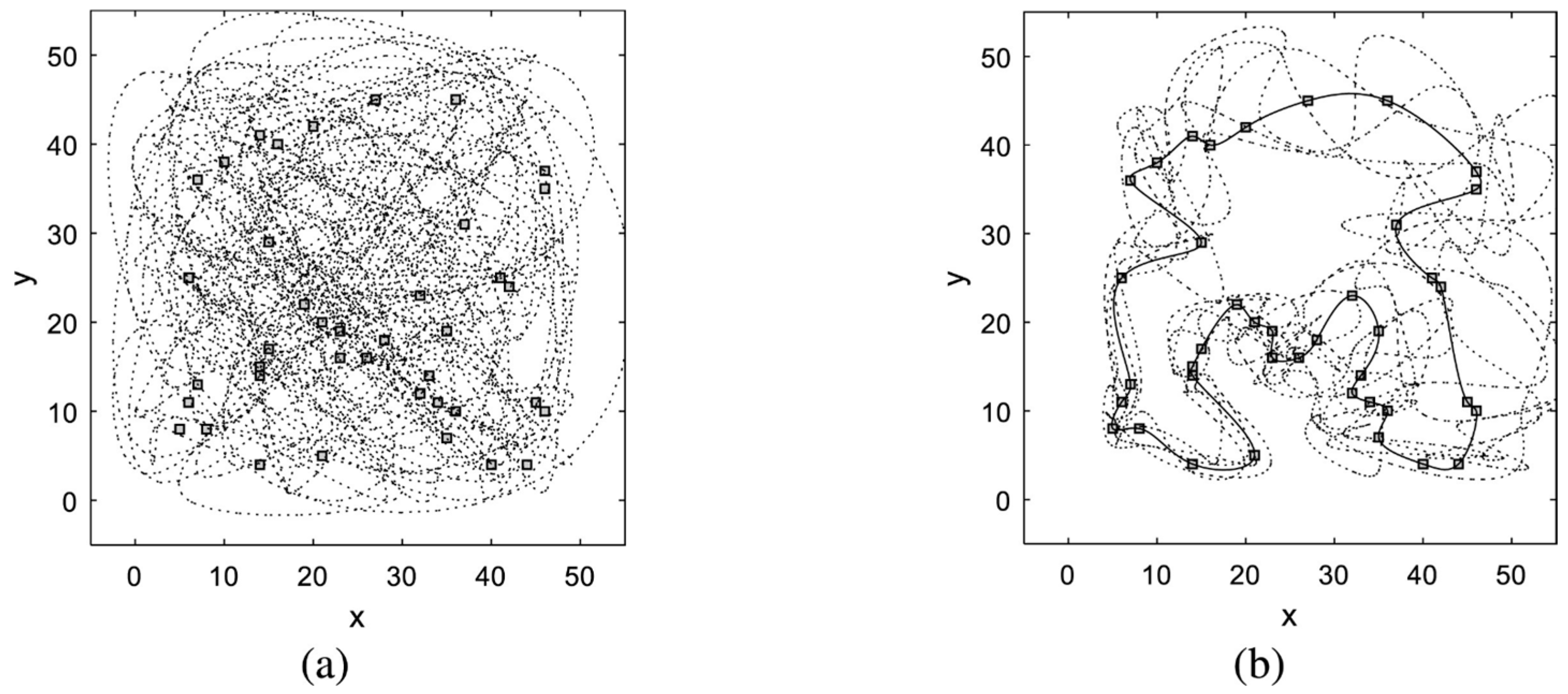
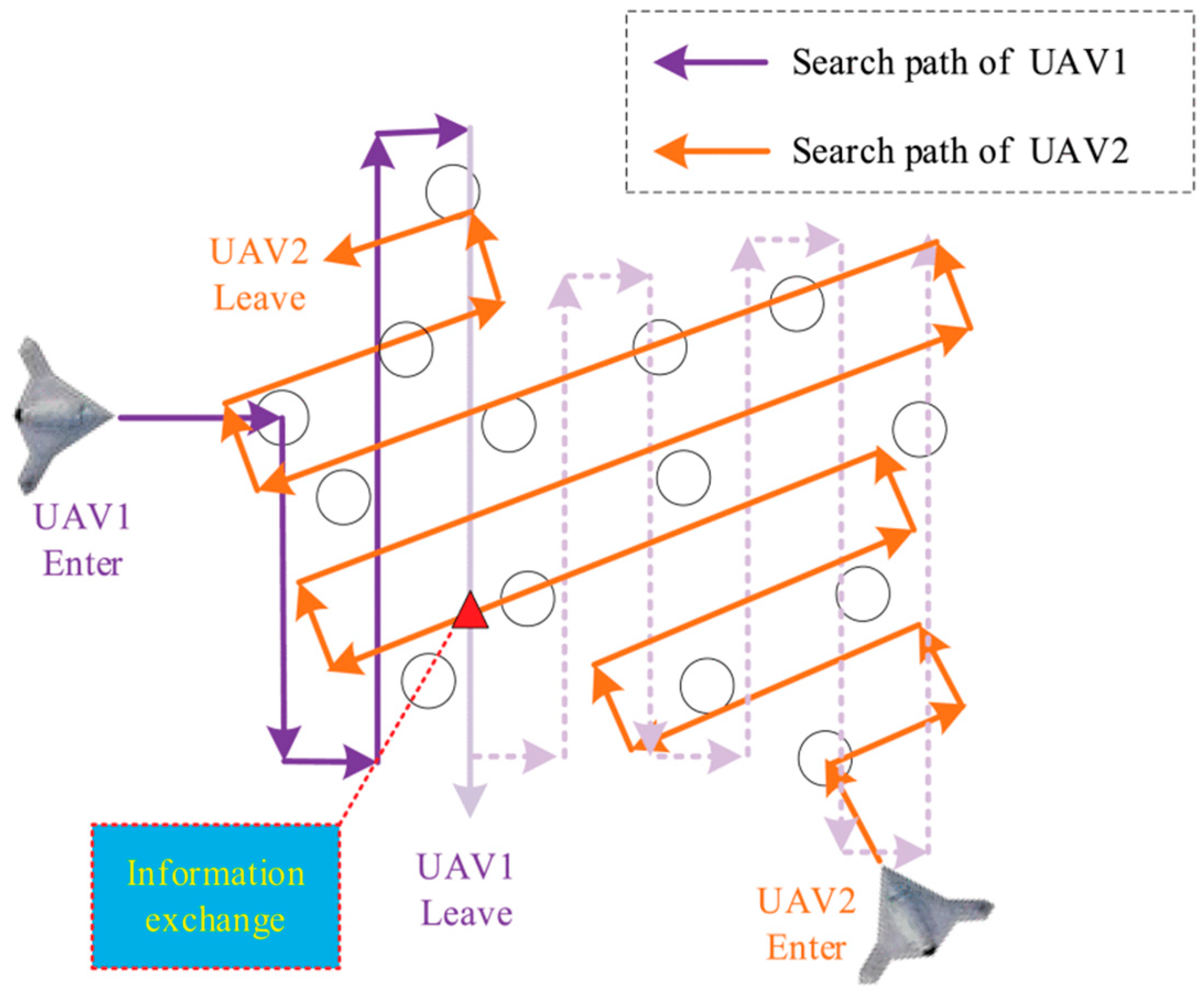
| Publication | Algorithms | Planning Features | Applications |
|---|---|---|---|
| Puente-Castro et al. [36] | Machine learning, evolutionary algorithms, and swarm intelligence algorithms | \ | \ |
| Yahia and Mohammed [37] | Metaheuristic algorithms | Complex environment | \ |
| Hooshyar and Huang [38] | Metaheuristic algorithms | Complex environment | \ |
| Poudel et al. [39] | Bio-inspired algorithms | \ | \ |
| Sharma et al. [40] | Swarm intelligence algorithms | \ | Multiple target interception |
| Tang et al. [41] | Swarm intelligence algorithms | \ | \ |
| This work | Machine learning, evolutionary algorithms, and swarm intelligence algorithms | Complex environment, UAV Types | Transportation, inspection, show, etc. |
| Characteristic | Multi-Rotor UAV | Single-Rotor UAV | Tilt-Rotor UAV | Fixed-Wing UAV |
|---|---|---|---|---|
| Propulsion | Multiple fixed motors with propellers | One main rotor and anti-torque mechanism | Tiltable rotors with fixed wings | Propeller or jet engine with fixed wings |
| Lift Generation | Rotors | Rotors | Rotors/fixed wings | Fixed wings |
| Thrust-Attitude Coupling | Strong coupling | Strong coupling | Strong in rotor mode, weak in fixed-wing mode | Weak coupling |
| Endurance | <1 h | About 1–3 h | About 3–8 h | About 5–30 h |
| Speed | About 0–20 m/s | About 0–50 m/s | About 0–100 m/s | About 15–100 m/s |
| Maneuverability | High | High | Medium (weak in transition) | Low (large turn radius) |
| Category | Algorithm | Contributions | Reference |
|---|---|---|---|
| DL | CNN | Adding time-series properties to CNN to adapt to time-series prediction problems | [65] |
| RNN | Solving multi-agent trajectory planning problems together with a decentralized version | [66] | |
| GNN | Combining a mechanism that allows message-dependent attention and a message-aware graph attention network | [69] | |
| Transformer | Powerful representation capabilities and parallel computing characteristics | [77] | |
| RL | Asynchronous RL | Combining asynchronous methods with the tabular Q-learning algorithm alleviates the slow convergence of classical RL. | [81] |
| GRL | Adaptively updating the reward matrix based on geometric distance and risk information when only partial information about the map is available | [82] | |
| multi-layer RL | Collecting both global and local information | [83] | |
| DRL | TD3 | Proposing a model explanation method based on feature attribution to achieve model explainability | [85] |
| D3QN | Combining the greedy strategy with heuristic search rules to improve the learning efficiency of the D3QN during the training phase | [86] | |
| MATD3 | Introducing LSTM RNN into the environment perception end of the MATD3 network and developing an improved potential field-based dense reward function | [11] | |
| Others | TL | Integrating prior knowledge, improving the effect of formal training | [88] |
| RF | Improving accuracy and stability in the case of a few samples | [90] | |
| SVM | Establishing safe flight corridors for trajectory planning | [91] |
| Category | Algorithm | Contributions | Reference |
|---|---|---|---|
| GA | GA | Solving complex combinatorial optimization problems | [96] |
| GA | Proposing new mutation operators for specific problems | [97] | |
| parallel GA | Developing a parallel implementation of GA to find a solution faster. | [98] | |
| parallel GA | Trajectory planning based on probability graph and parallel GA | [99] | |
| mVGA | Using the vibrational mutation operators to solve the premature convergence of GA | [101] | |
| DE | DE | Designing an offline UAV trajectory planner based on DE | [104] |
| FA-DE | Introducing a fuzzy logic controller to automatically adjust parameters | [105] | |
| CDE | Designing an adaptive selection mutation operator | [106] | |
| MSFDE | Integrating multi-population strategy, adaptive strategy, and interactive mutation strategy | [110] | |
| Others | GP | Designing special function and symbol operators for GP | [112] |
| ES | Combining ES with the exact Dijkstra algorithm | [113] | |
| MO-CMA-ES | Proposing an energy model and a noise model for a UAV | [114] |
| Category | Algorithm | Contributions | Reference |
|---|---|---|---|
| PSO | PSO | Proposing an adaptive sensitivity decision operator to address the limitations of local optimal and premature | [118] |
| SPSO | SPSO searches for solutions within the configuration space rather than the Cartesian space to improve the chances of identifying quality solutions. | [119] | |
| ACO | ACO | Using ACO to provide an approximate solution | [123] |
| CACOC | Using chaotic dynamics to replace the random part of ACO to improve performance on the coverage problem | [124] | |
| CACOC | Extending CACOC by a collision avoidance mechanism | [7] | |
| Others | BA | Using the artificial potential field method to speed up the convergence of bat position updates | [26] |
| WOA | Introducing an adaptive chaos-Gaussian switching method coupled with a coordinated decision-making framework to overcome the defect of local minima | [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Yang, J.; Sun, J.; Zhao, L. Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm. Drones 2025, 9, 468. https://doi.org/10.3390/drones9070468
Cheng Z, Yang J, Sun J, Zhao L. Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm. Drones. 2025; 9(7):468. https://doi.org/10.3390/drones9070468
Chicago/Turabian StyleCheng, Zhekun, Jueying Yang, Jinfeng Sun, and Liangyu Zhao. 2025. "Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm" Drones 9, no. 7: 468. https://doi.org/10.3390/drones9070468
APA StyleCheng, Z., Yang, J., Sun, J., & Zhao, L. (2025). Trajectory Planning of Unmanned Aerial Vehicles in Complex Environments Based on Intelligent Algorithm. Drones, 9(7), 468. https://doi.org/10.3390/drones9070468






