Abstract
This work investigates multi-UAV navigation tasks where multiple drones need to reach initially unassigned goals in a limited time. Reinforcement learning (RL) has recently become a popular approach for such tasks. However, RL struggles with low sample efficiency when directly exploring (nearly) optimal policies in a large exploration space, especially with an increased number of drones (e.g., 10+ drones) or in complex environments (e.g., a 3D quadrotor simulator). To address these challenges, this paper proposes Multi-UAV Scalable Graph-based Planner (MASP), a goal-conditioned hierarchical planner that reduces space complexity by decomposing the large exploration space into multiple goal-conditioned subspaces. MASP consists of a high-level policy that optimizes goal assignment and a low-level policy that promotes goal navigation. MASP uses a graph-based representation and introduces an attention-based mechanism as well as a group division mechanism to enhance cooperation between drones and adaptability to varying team sizes. The results demonstrate that MASP outperforms RL and planning-based baselines in task and execution efficiency. Compared to planning-based competitors, MASP improves task efficiency by over 27.92% in a 3D continuous quadrotor environment with 20 drones.
1. Introduction
Navigation is a fundamental task for drones, with broad applications in areas such as object detection and tracking [1,2], logistics and transportation [3,4], and disaster rescue [5,6]. This work focuses on a multi-UAV navigation problem, where multiple drones simultaneously navigate toward a set of initially unassigned goals. In this case, goal assignment and navigation can be jointly optimized, leading to more efficient and effective multi-UAV navigation.
Planning-based approaches have been widely applied in multi-UAV navigation tasks [7,8,9]. However, these methods struggle with complex coordination strategies and require intricate hyperparameter tuning for each specific scenario. Moreover, frequent re-planning at each decision step can be computationally expensive and time-consuming. Conversely, reinforcement learning (RL) demonstrates strong representational capabilities for complex strategies while maintaining low inference overhead once policies are well-trained [10,11]. However, directly learning an end-to-end policy [12,13] in a large exploration space suffers from low sample efficiency, which is more severe as the number of drones or the environmental complexity increases. Therefore, existing methods [14,15] mainly focus on simple scenarios with a few drones.
This paper proposes an RL-based hierarchical framework, Multi-UAV Scalable Graph-based Planner (MASP), to solve this challenge. MASP decomposes a large exploration space into multiple goal-conditioned subspaces by integrating a high-level policy that assigns goals to drones at each high-level step and a low-level policy that navigates drones toward the designated goals at each timestep. The reward function for the high-level policy, Goal Matcher, is designed to encourage each drone to select a goal distinct from those of other drones while minimizing the overall assignment cost. For the low-level policy, Coordinated Action Executor, the reward function promotes efficient navigation and collision avoidance. To ensure scalability to arbitrary numbers of drones, the drones and the goals are represented as two dynamic graphs, where nodes can expand as needed. Goal Matcher leverages an attention-based mechanism over these graphs to optimize goal assignment, as the attention mechanism is well-suited for solving long and variable-length sequences [16]. Recent studies [17,18,19] have also demonstrated its effectiveness in modeling interactions among varying numbers of agents. Coordinated Action Executor employs a group division mechanism that extracts features from only a small subset of drones at a time, significantly reducing the input dimension of drones’ state information while maintaining effective cooperation between drones during action execution.
MASP is compared with planning-based methods and RL-based competitors in two continuous testbeds: multi-agent particle environments (MPE) [20], where drones are abstracted as two-dimensional (2D) particles, and a complex three-dimensional (3D) quadrotor environment (OmniDrones) [21]. Empirical results demonstrate that MASP significantly outperforms its competitors in task and execution efficiency. MASP is applicable to tasks that require effective goal assignment and navigation. It serves as a policy enabling UAVs to rapidly and continuously make decisions based on current states. MASP can also be extended to vision-based applications by integrating it with a visual perception module. More information can be found at the website: https://sites.google.com/view/masp-drones (accessed on 20 June 2025).
The main contributions of this paper include:
- Proposing a hierarchical multi-UAV navigation planner, Multi-UAV Scalable Graph-based Planner (MASP), to decompose a large exploration space into multiple goal-conditioned subspaces, enhancing sample efficiency in a large exploration space.
- Representing drones and goals as graphs and applying an attention-based mechanism and a group division mechanism to ensure scalability to arbitrary numbers of drones and promote effective cooperation.
- Compared to planning-based competitors, enhancing task efficiency by over 19.12% in MPE with 50 drones and 27.92% in OmniDrones with 20 drones (referred to Section 5.5.1), and achieving at least a 47.87% enhancement across varying team sizes (referred to Section 5.5.2).
2. Related Work
2.1. Multi-UAV Navigation
Multi-UAV navigation [10,14,22,23] is a fundamental cooperative task. Existing approaches can be broadly categorized into two types: (1) navigation toward preassigned goals and (2) navigation toward a set of initially unassigned goals. This paper focuses on the latter, as jointly optimizing goal assignment and navigation improves task efficiency. As the number of drones increases, the exploration space grows significantly, making it challenging to find a (nearly) optimal navigation strategy. Some works address this challenge for universal use: Ref. [24] employs imitation learning to constrain the exploration space based on the expert trajectories, while DARL1N [25] restricts the exploration space by only perceiving adjacent neighbors. For multi-UAV navigation, [26,27] adopts independent learning with parameter sharing to cope with the large joint exploration space issue. However, these approaches neglect global information and may diminish the final performance. This work proposes a hierarchical framework that explicitly divides the process into two stages: goal assignment and goal navigation, which is based on prior knowledge of multi-UAV navigation. This method breaks down the exploration space into multiple goal-conditioned subspaces, enabling the search for (nearly) globally optimal strategies in each subspace.
For goal assignment, the Hungarian algorithm [28] uses a weighted bipartite graph to find a minimum-cost match. [29] allocates goals to minimize the longest individual trajectory. However, this method suffers from high computational overhead, making it unsuitable for large-scale multi-UAV systems. M* [30] mitigates this issue by reassigning targets only when potential collisions are detected, but it struggles when multiple drones simultaneously require reassignment. For goal navigation, effectively modeling drone interactions is crucial for collision avoidance and cooperative behavior. Recent works leverage transformer-based architectures [27,31,32] and graph-based methods [14,22] to capture these interactions in dynamic drone populations. Inspired by these advances, a graph-based method is introduced that adapts to large-scale and dynamic drone populations.
2.2. Goal-Conditioned HRL
Goal-conditioned hierarchical reinforcement learning (HRL) is effective across various tasks [33,34], typically using a high-level policy to select subgoals and a low-level policy to predict actions to achieve them. However, existing approaches [35,36,37] struggle in multi-target scenarios, as they fail to establish clear connections between subgoals and multiple targets. HTAMP [38] addresses this challenge for general multi-agent tasks, where the high-level policy directly assigns tasks to agents, and the low-level policy yields actions based on the assigned tasks. This hierarchical paradigm can be extended to multi-UAV scenarios [14,39,40], decomposing the whole navigation task into two stages: goal assignment and goal navigation. Inspired by [14,38], goal-conditioned HRL is employed for multi-UAV navigation.
2.3. Graph Neural Networks
Graph neural networks (GNNs) [41] excel at modeling complex relationships among diverse entities and have been widely applied in various domains, including social networks [42] and molecular structure [43]. In multi-UAV systems [44,45,46], GNNs are effective in capturing interactions among drones. DRGN [22] obtains extra spatial information through graph-convolution-based inter-UAV communication. [47] introduces a two-stream graph multi-agent proximal policy optimization (two-stream GMAPPO) algorithm that models UAVs and other entities as graph-structured data, aggregates the node information, and extracts relevant features. In this paper, MASP adopts graph-based representations to model the relationships between drones and goals.
3. Problem Formulation
This paper considers a multi-UAV navigation task where N drones reach M initially unassigned goals with B obstacles. The objective is to minimize the execution time required for goal assignment and goal navigation. This problem could be formulated as a goal-conditioned Markov Decision Process (MDP) . is the set of N drones. is a goal set. is the joint state space. is the joint action space. P is the transition function. R is the reward function. is the discount factor. Under MDP, the objective is transformed into maximizing the cumulative reward for efficient navigation.
4. Methodology
4.1. Overview
As the joint state and action spaces grow exponentially with the number of drones, multi-UAV navigation tasks face a critical challenge of low sample efficiency in policy learning. To address this challenge, this paper proposes Multi-UAV Scalable Graph-based Planner (MASP), a goal-conditioned HRL framework. MASP consists of a high-level policy for goal assignment and a low-level policy for goal navigation. Both policies are parameterized by neural networks with parameters and , respectively. As each drone perceives an assigned goal rather than all possible goals, the hierarchical framework decomposes the state and action space into multiple goal-conditioned subspaces, effectively improving sample efficiency.
This work adopts the centralized training with decentralized execution (CTDE) paradigm, where each drone is equipped with its own MASP, ensuring scalability to an arbitrary number of drones. Take drone k as an example. The high-level policy, referred as Goal Matcher (GM), assigns a goal, , to drone k at every high-level step . To achieve scalability in the number of drones, the drones and the goals are modeled as two dynamically expanding graphs. Attention-based mechanisms [48] are then applied to compute matching scores between drone k and goals in these graphs, effectively extracting meaningful features from the variable-sized and high-dimensional graph representation. Once drone k receives its assigned goal, the low-level policy, termed Coordinated Action Executor (CAE), outputs its environmental action at each timestep t, denoted as . CAE proposes a group division mechanism to extract relationships among varying drone numbers while reducing the input dimension by focusing only on drones within the same group at a time. Notably, this mechanism is not applicable to GM, as goal assignment requires a global matching across all drones and goals. Incorporating the extracted drone relationships and goal positional information, drone k navigates toward its designated goal while maintaining cooperative behavior.
4.2. The High-Level Policy: Goal Matcher
The Workflow. The high-level policy focuses on goal assignment, a well-known NP-hard maximum matching problem [29,49]. To solve this challenge, this work introduces an RL-based solution, Goal Matcher, which operates in a discrete action space consisting of goal candidates. Its state space includes the positional information of all drones and goals. To ensure scalable representation, MASP constructs two dynamically expandable fully connected graphs: the drone graph, , and the goal graph, . The node set represents drones or goals, where each node feature encodes positional information with L dimensions. All edge connections are initially set to 1.
As illustrated in Figure 1, a Self-Encoder is used to update node features in or , by capturing the spatial relationship among drones or goals. Inspired by the effectiveness of self-attention mechanisms in handling long and variable-length sequences [16,50], GM applies self-attention [48] over graphs to compute , in or . The updated node features are obtained by adding to X, allowing each node to encode spatial information with its neighbors. Then, GM introduces a Cross-Encoder to capture the relationship between drone k and goals, computing a matching score for goal assignment. The navigation distance is a key factor in multi-UAV navigation. Since obstacle avoidance is handled by the low-level policy, the simple L2 distance between drone k and each goal is adopted as the navigation distance, denoted as . The features , , and D are passed through a multi-layer perceptron (MLP) layer to extract spatial relationships between drone k and goals. A softmax operation is then applied to the MLP output, yielding the matching score, . This matching score represents the probability of assigning each goal to drone k. Finally, drone k selects the goal with the highest matching score at each high-level step. More details are provided on the website.
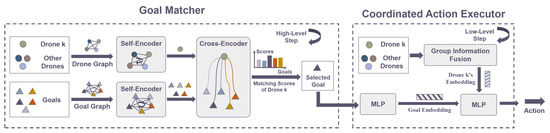
Figure 1.
Overview of Multi-UAV Scalable Graph-based Planner. Here, Drone k is taken as an example here.
Reward Design. The reward for drone k, is formulated as follows:
To encourage selecting a goal that differs from other drones, a repeated penalty is introduced, where signifies the number of other drones assigned the same goal as drone k. Additionally, a distance-based reward is employed to minimize the total travel distance. Specifically, the Hungarian algorithm [28] is used as an expert. represents the predicted goal from GM for drone k, and denotes the goal assigned by the Hungarian algorithm. denotes the total distance cost from the predicted goals to agents, and denotes the total distance cost from the Hungarian-assigned goals to agents. If MASP has a lower distance cost than the Hungarian algorithm, is positive, incentivizing GM to learn a better goal assignment strategy.
4.3. The Low-Level Policy: Coordinated Action Executor
Coordinated Action Executor takes the goal assigned by GM and navigates drone k toward this goal while minimizing collisions. In CAE, the action space consists of the environmental actions available to drone k, while the state space includes the locations and velocities of all drones, along with the location of the designated goal.
Group Division. During goal navigation, it is essential to extract drone relationships to ensure cooperation and collision avoidance. However, as the number of drones increases, directly using the state information of all drones results in high input dimensionality, making training inefficient. To solve this, MASP introduces a group division mechanism by focusing only on drones within the same group at a time. Each group is assumed to contain drones. As illustrated in Figure 2, all drones, excluding drone k, are first divided into groups of drones. If the drones cannot be evenly divided, some drones are randomly assigned to multiple groups to ensure group formation. Then, drone k is added to each group repeatedly, maintaining connections with all drones across groups.
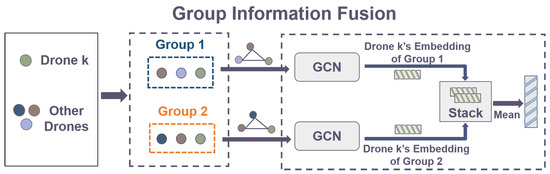
Figure 2.
The workflow of Group Information Fusion in Coordinated Action Executor. Take Drone k as an example.
The Workflow. CAE partitions drones into groups and represents each group as a fully connected subgraph, . In each subgraph, the node set encodes the positions and velocities of the drones, while the edges E are set to 1. Notably, each subgraph is newly constructed and distinct from the graphs used in GM. To capture drone relationships efficiently, CAE introduces Group Information Fusion that applies graph convolutional networks (GCNs) to each subgraph and then aggregates the node features of drone k across all subgraphs using a mean operation over the graph–number dimension. This process yields an updated node feature of drone k, denoted as , which encodes the relationships between drone k and all other drones. Next, an MLP layer is fed into the positional embedding of the designated goal and the updated node feature of drone k, extracting the relationship between drone k and its assigned goal. Finally, based on the MLP output, , where represents the action dimension, CAE generates an environmental action to guide drone k toward its goal. More details are provided on the website.
Reward Design. The reward, , for drone k in CAE encourages goal-conditioned navigation while minimizing collisions. is a linear combination of three components:
- A complete bonus for successfully reaching the assigned goal, , which is 1 if agent k reaches its assigned goal, otherwise 0.
- A distance penalty for task efficiency, , which is the negative L2 distance between agent k and its assigned goal.
- A collision penalty for collision avoidance, , computed based on the number of collisions at each time step.
The formulation is as follows:
where , and are the coefficients of , and , respectively.
4.4. Multi-UAV Scalable Graph-Based Planner Training
MASP, following the goal-conditioned MARL framework, trains two policy networks for Goal Matcher and Coordinated Action Executor separately, which are optimized by maximizing the accumulated reward in the entire episode via RL. Both GM and CAE are optimized using multi-agent proximal policy optimization (MAPPO) [12], an extension of proximal policy optimization (PPO) [51] specifically designed for multi-agent settings.
As shown in Algorithm 1, MASP takes in the drone graph , the goal graph , and the joint state s of all agents. Then, it produces the final policy for GM and for CAE. First, MASP initializes the number of agents along with several training parameters, including maximal steps, the high-level step, parameters in GM, parameters in CAE, GM reply buffer , and CAE reply buffer (Line 1). GM assigns the goals to each agent k every high-level step (Lines 7–10) and receives the reward and the subsequent state , where represents the step-count in (Line 11 and 12). Thereafter, for the policy network and for the value network in GM are updated. Regarding CAE, it outputs the action for each agent k, and stores a group of data in at each timestep (Line 15–18). Similarly, for the policy network , and for the value network are updated in CAE.
| Algorithm 1 Training Procedure of MASP |
|
5. Experiments
5.1. Testbeds
To assess the effectiveness of this approach, two continuous testbeds are selected as shown in Figure 3: a 2D environment, MPE [20], and a 3D environment, OmniDrones [21], with a substantial number of drones.
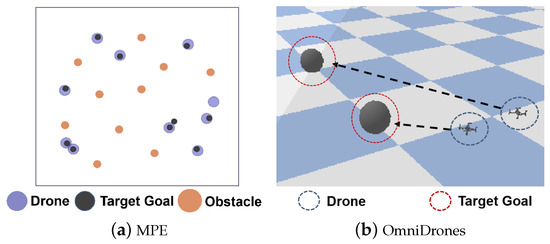
Figure 3.
The chosen testbeds.
MPE is a classical 2D environment where drones are abstracted as particles to enable fast verification of this method. The available environmental actions are discrete, including Up, Down, Left, and Right. Each action corresponds to a force with a fixed value in a specific direction. Therefore, the movement of the drones is continuous. The collision between drones causes a disruptive bounce-off, reducing navigation efficiency. The experiment is conducted with randomized spawn locations for N drones, N landmarks, and B obstacles. The drones, the obstacles, and the landmarks are circular with a radius of 0.1 m, 0.1 m, and 0.05 m, respectively. Experiments consider and on the maps of 4 m2, 64 m2, and 400 m2, with the horizons of the environmental steps of 18, 45, and 90, respectively.
OmniDrones is an efficient and flexible 3D simulator for drone control, incorporating precise aerodynamic models and increasing the exploration space. The continuous action space of each drone is the throttle for each motor. Collisions directly lead to crashes and task failures, increasing task difficulty. The drones are modeled based on [52], which offers very high-fidelity simulation of sensors, actuators, and built-in controllers. This enables more efficient sim-to-real transfer of control policies. Specifically, the drones used are hummingbird models, each with a mass of 0.716 kg and an arm length of 0.17 m. Each drone is equipped with four motors. The moments of inertia are 0.007 kg·m2 for the xx and yy axes, 0.012 kg·m2 for the zz axis, and zero for all other components. The thrust coefficient is , and the maximum rotational velocity is 838 revolutions per second (rps). The landmarks are virtual balls of 0.05 m radius. Experiments consider drones, where the spawn locations for both drones and landmarks are randomly distributed on the maps sized at 36 m2 and 256 m2, respectively. In addition, the horizons of the environmental steps are 300 for 5 drones and 500 for 20 drones.
5.2. Implementation Details
Each RL training is performed over three random seeds for a fair comparison. Each evaluation score is expressed in the format of “mean (standard deviation)”, averaged over a total of 300 testing episodes, i.e., 100 episodes per random seed. The high-level step is set to 3 timesteps, and the low-level step is set to 1 timestep. Experiments consider and (The sensitivity analysis is detailed in Section 5.8).
5.3. Evaluation Metrics
There are six statistical metrics to capture different characteristics of the navigation strategy.
- Success Rate (SR): This metric measures the average ratio of goals reached by the drones to the total goals per episode.
- Steps: This metric represents the average timesteps required to reach 100% Success Rate per episode.
- Collisions: This metric denotes the average number of collisions per step.
- Execution Time: This metric represents the time required for evaluation, measured in milliseconds (ms).
- Memory Usage: This metric represents the memory size required for evaluation, measured in Gigabyte (GB).
- Network Parameters: This metric refers to the number of network parameters needed for each RL-based method.
Steps is taken as the primary metric for measuring task efficiency. In tables, the value in bold signifies that this method earns the highest performance among all competitors in terms of this metric. The backslash in Steps denotes that the drones can not reach the target 100% Success Rate in any episode. An upward arrow (↑) signifies that higher values indicate better performance, while a downward arrow (↓) indicates that lower values are preferable.
5.4. Baselines
MASP is compared with three representative planning-based approaches (ORCA, RRT*, Voronoi) and four prominent RL-based solutions (MAPPO, DARL1N, HTAMP, MAGE-X). In planning-based approaches, the Hungarian algorithm, denoted (H), is utilized for goal assignment.
- ORCA [7]: ORCA is an obstacle avoidance algorithm that excels in multi-UAV scenarios. It predicts the movements of surrounding obstacles and other drones, and then infers a collision-free velocity for each drone.
- RRT* [8]: RRT* is a sample-based planning algorithm that builds upon the RRT algorithm [53]. It first finds a feasible path by sampling points in the scenario and then iteratively refines the path to achieve an asymptotically optimal solution.
- Voronoi [9]: A Voronoi diagram comprises a set of continuous polygons, with a vertical bisector of lines connecting two adjacent points. By partitioning the map into Voronoi units, a safe path can be planned from the starting point to the destination.
- MAPPO [12]: MAPPO is a straightforward extension of PPO in the multi-agent setting, where each agent is equipped with a policy with a shared set of parameters. MAPPO is updated based on the aggregated trajectories from all drones. Additionally, an attention mechanism is applied to enhance the model’s performance.
- (H)MAPPO [12]: (H)MAPPO adopts a hierarchical framework, with the Hungarian algorithm as the high-level policy for goal assignment and MAPPO as the low-level policy for goal achievement.
- DARL1N [25]: DARL1N is under an independent decision-making setting for large-scale agent scenarios. It breaks the curse of dimensionality by restricting the agent interactions to one-hop neighborhoods. This method is extended to multi-UAV navigation tasks.
- HTAMP [38]: This is a hierarchical method for task and motion planning via reinforcement learning, integrating high-level task generation with low-level action execution.
- MAGE-X [14]: This is a hierarchical approach applied in multi-UAV navigation tasks. It first centrally allocates target goals to the drones at the beginning of the episode and then utilizes GNNs to construct a subgraph only with important neighbors for higher cooperation.
5.5. Main Results
5.5.1. Training with a Fixed Team Size
MPE. The training curves is represented in Figure 4 and the evaluation performance is represented in Table 1. MASP outperforms all methods with the least training data. Its advantage in Steps, Success Rate, and Collisions becomes more evident as drone numbers increase. Especially in scenarios with 50 drones, MASP achieves a nearly 100% Success Rate, while other RL baselines fail to complete the task in any episode. Among RL baselines, except (H)MAPPO, DARL1N shows the best performance at with a 49% Success Rate, while it loses its advantage at . This implies that when the scenario only has a few drones, DARL1N may lead to the absence of one-hop neighbors, thereby being harmful to the drones’ decisions. MAPPO has only a 0.01% Success Rate at , showing that a single policy has difficulty in being optimized in a large exploration space. (H)MAPPO has comparable performance with MASP but requires 8.52% more Steps at . MAGE-X has a 23% Success Rate at , suggesting its MLP-based goal assignment encounters challenges in preventing collisions between a large number of drones. Although HTAMP is also in a hierarchical manner, its MLP backbone fails to perceive the relationship between drones and targets, exhibiting inferior performance.
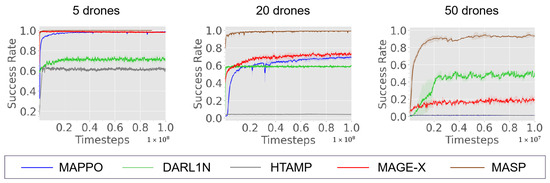
Figure 4.
Comparison between MASP and other baselines in MPE with , 20, 50.

Table 1.
Performance of MASP, planning-based baselines and RL-based baselines with drones in MPE.
Regarding planning-based methods, (H)RRT* and (H)Voronoi have comparable performance and require approximately 19.12% more Steps than MASP at . This indicates that although (H)RRT* and (H)Voronoi can handle obstacle-rich scenarios, their cooperation strategies remain less effective than MASP. (H)ORCA performs the worst, requiring at least 21.76% more Steps than MASP, highlighting its difficulty in finding shorter navigational paths.
OmniDrones. The training performance is represented in Figure 5 and the evaluation results are represented in Table 2. MASP is superior to all competitors, achieving a 100% Success Rate at and 96% at in this complex 3D environment. Most RL baselines, except MAGE-X and (H)MAPPO, achieve only around 50% Success Rate at , failing to address the navigation problem in complex exploration space. MAGE-X drops to a 15% Success Rate at . This reveals that its MLP-based goal assignment struggles with complex environments with increased drone numbers.
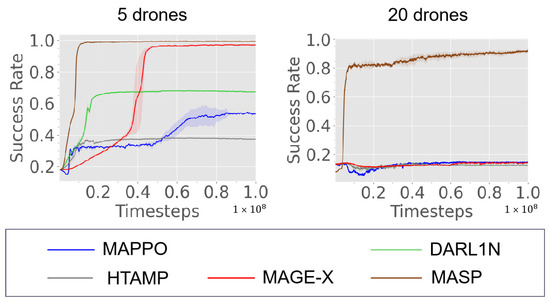
Figure 5.
Comparison between MASP and other baselines in Omnidrones with , 20.

Table 2.
Performance of MASP, planning-based baselines and RL-based baselines with drones in OmniDrones.
In contrast to RL baselines, most planning-based baselines achieve over 90% Success Rate. This is primarily owing to the Hungarian algorithm, ensuring that drones are assigned different goals. For Steps metric, the planning-based baselines require at least 27.92% more Steps than MASP at . Among planning-based baselines, (H)Voronoi performs best at but shows comparable performance at . This indicates that its partitioning strategy struggles to figure out efficient navigation paths in complex 3D environments as the number of drones increases.
5.5.2. Varying Team Sizes Within an Episode
Due to unstable communication or drone loss, the experiments further consider scenarios where the team size decreases during an episode. With more goals than drones, some drones may need to first reach some goals and then adjust their plans to navigate toward the remaining goals. The Success Rate is defined as the ratio of the goals reached during the navigation to the total number of goals. “” is used to denote that an episode starts with drones and switches to after one-third of the total timesteps. The number of goals is . Since MASP is trained with a fixed team size, this setup presents a zero-shot generalization challenge. Experiments adopt MASP model trained with drones. As RL baselines lack generalization in both network architecture and evaluation performance, MASP is only compared with planning-based methods. In addition, the Hungarian algorithm is originally designed for scenarios with equal numbers of drones and goals; therefore, it is applied on a subset of unreached goals that matches the drone count at each high-level step.
As shown in Table 3, the advantage of MASP becomes more apparent in the setting of varying drone numbers. In the scenario in MPE, MASP consumes around 47.87% fewer Steps than (H)RRT* and (H)Voronoi. Table 4 presents the evaluation results for zero-shot generalization in OmniDrones. The planning-based baselines fail to reach a 100% Success Rate in any episode, whereas MASP maintains an average Success Rate of 94%. This highlights the superior flexibility and adaptability of the goal assignment strategy compared to the Hungarian algorithm.

Table 3.
Performance of MASP and planning-based baselines with a varying team size in MPE.

Table 4.
Performance of MASP and planning-based baselines with a varying team size in OmniDrones.
5.6. Robustness Evaluation in Noisy and Realistic Environments
To evaluate MASP’s applicability to real drones, experiments are conducted in environments with sensor noise and time delay. Concretely, experiments are conducted on Omnidrones with 5 and 20 drones, as well as with varying drone numbers from 20 to 10. The position of each drone is perturbed by uniform noise in the range [−0.1 m, 0.1 m], and a time delay of two timesteps is introduced. As RL-based baselines show inferior performance compared to planning-based competitors in Omnidrones, MASP is only compared with planning-based methods in this setting. MASP is trained and tested in these scenarios, with randomized initial states.
The evaluation results are presented in Table 5. Although sensor noise and time delay affect the overall performance of all methods, MASP consistently outperforms planning-based baselines, requiring at least 28.12% fewer Steps with 5 drones and 18.01% fewer Steps with 20 drones. In scenarios with varying drone numbers, planning-based baselines fail to complete the navigation in any episode, leaving Steps metric without value. For Success Rate, MASP achieves 90%, compared to 57∼85% for planning-based baselines. It indicates that the reward design for MASP promotes collision avoidance, enabling it to better handle positional disturbances. Additionally, the goal assignment of MASP encourages diverse target allocation, further mitigating the effects of noise and delay.

Table 5.
Robustness evaluation in Noisy and realistic environments of MASP and planning-based baselines with drones and a varying team size in OmniDrones.
5.7. Computational Cost
Computational cost experiments in terms of time and memory are conducted in MPE with 100 drones to verify MASP’s feasibility for large-scale UAV scenarios. As shown in Table 6, a single inference of MASP requires approximately 2 GB memory size, comprising 1.28 GB for GM and 0.72 GB for CAE. GM uses an attention-based graph mechanism that considers all agent and goal positions for global matching, while CAE employs a group division mechanism. Therefore, the memory usage of GM is relatively larger than that of CAE. Notably, 2 GB memory usage is far less than 8∼16 GB capacity of Jetson Xavier NX, commonly used in real drones. For inference time, experiments consider the time that MASP costs for inferring an action at a time. MASP takes around 18 ms, comprising 11 ms for GM and 7 ms for CAE. This is affordable for a normal drone at a speed of 0∼5 m/s.

Table 6.
Performance of MASP on memory usage and execution time with N = 100 drones in MPE.
As most baselines struggle with 100-drone scenarios, execution time comparisons between MASP and the baselines are conducted in MPE with 50 drones. In Table 7, MASP is at least 3× more efficient than planning-based competitors. Compared to the best planning-based competitor, (H)RRT*, MASP’s computation time is 32× faster than it. While MASP has a comparable execution efficiency to RL-based methods, it outperforms them in task performance.

Table 7.
Average performance of MASP and baselines on the execution time.
5.8. Sensitivity Analysis
Group Size. Table 8 shows a sensitivity analysis of the group size, , for group division in MPE with 20 drones. When is too small, it hinders capturing the correlations between drones. A larger improves the performance but increases required network parameters (i.g., the results of metric ‘Network Parameters’ in Table 8), depreciating the training efficiency. The performance improvement of MASP is negligible when exceeds 3. Thus, is selected to balance the final performance and the training efficiency.

Table 8.
Performance of = 2, 3, and 5. P denotes required network parameters when = 2.
The High-level Step. Evaluation performance is reported in Table 9 to assess the sensitivity to high-level steps in MPE with 20 drones. Fewer high-level steps lead to more frequent goal assignment adjustments, improving the evaluation performance. However, it also increases execution time. The results indicate that the performance remains comparable when high-level steps are fewer than 3. To balance evaluation performance and execution time, the high-level step is set to 3.

Table 9.
Performance of High-level Steps = 1, 3, and 10.
Feature Embeddings. The evaluation results in Table 10 analyze the sensitivity of feature embedding dimensions, L, in MPE with 20 drones. As L decreases, training efficiency improves due to fewer required network parameters (i.g., the results of the metric ‘Network Parameters’ in Table 10). However, lower-dimensional embeddings may struggle to capture the complex features of drones and goals. The results suggest that choosing achieves a balance between evaluation performance and training efficiency.

Table 10.
Performance of L = 8, 32, and 64. P denotes required network parameters when L = 8.
5.9. Ablation Studies
To illustrate the effectiveness of each component of MASP, five variants of the method are evaluated in MPE with 20 drones:
- MASP w. RG: GM is replaced by random sampling, assigning each drone a random yet distinct goal.
- GM w.o. Graph: An MLP layer is adopted as an alternative to GM for assigning goals to drones at each high-level step. For drone k, the MLP layer takes in the concatenated position information of all drones and goals, with the position information of drone k listed first.
- CAE w.o. Graph: An MLP layer is employed as an alternative to CAE to capture the correlation between drones and goals. The input for drone k comprises the position of all drones and the assigned goal for drone k.
- MASP w. GraphSAGE: GM and Group Information Fusion module in CAE are replaced with GraphSAGE [54]. GraphSAGE generates embeddings by sampling and aggregating features from a node’s local neighborhood.
- MASP w. GATv2: GM and Group Information Fusion module in CAE are replaced with GATv2 [55]. GATv2 is a dynamic graph attention variant of GAT [56].
To demonstrate the performance of MASP and its variants, the training curves are reported in Figure 6 and the evaluation results are shown in Table 11. MASP outperforms its counterparts with a 100% Success Rate and the fewest Steps. GM w.o. Graph degrades the most, indicating difficulties in perceiving the correlations between drones and goals without the graph-based Self-Encoder and Cross-Encoder. MASP w. RG consistently assigns different goals to drones and only trains the low-level policy, leading to the fastest training convergence. However, as shown in the evaluation performance in Table 11, it requires 32.02% more Steps due to random goal assignment. CAE w.o. Graph is slightly inferior to MASP with slower training convergence and 13.59% more Steps in the evaluation. This suggests that GCN in CAE better captures the relationships between drones and assigned goals than the MLP layer. MASP w. GATv2 and MASP show comparable training performance, but MASP achieves 13.35% fewer Steps during evaluation. Although MASP w. GATv2 is able to perceive all agents with different attentions, it lacks a specific design like MASP that first models the interaction of nodes in the same graph and then the interaction of nodes in different graphs. MASP w. GraphSAGE reduces computational complexity by only interacting with a fixed number of neighbors. However, due to its limited perception, MASP w. GraphSAGE may fail to achieve global goal assignment, sometimes assigning multiple agents the same goal. Therefore, it requires 37.36% more Steps than MASP.
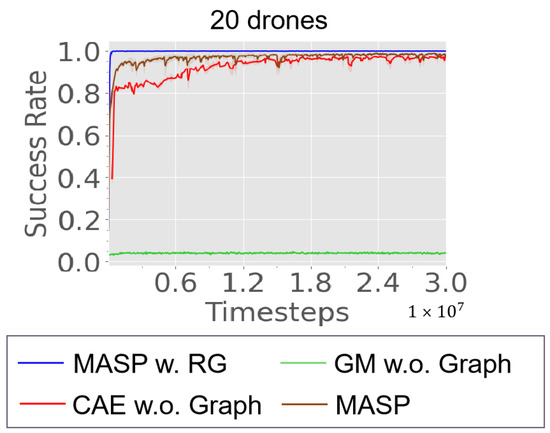
Figure 6.
Ablation study on MASP in MPE with 20 drones. Note that ‘w.’ stands for ‘with’ and ‘w.o.’ stands for ‘without’.

Table 11.
Performance of MASP and RL variants with drones in MPE.
5.10. Strategies Analysis
As depicted in Figure 7, the learned strategies of DARL1N and MASP are visualized to showcase high cooperation among MASP drones. In some cases, drones initially select the same goal (e.g., the drone in the red hexagon and the drone in the yellow hexagon). In Figure 7a, two DARL1N drones fail to adjust their strategies and finally stay at the same goal. In contrast, Figure 7b illustrates that when the red MASP drone notices the yellow MASP drone moving toward the same goal, it quickly adjusts its strategy to navigate toward another unreached goal. This cooperation strategy allows MASP drones to occupy different goals, achieving a 100% Success Rate.
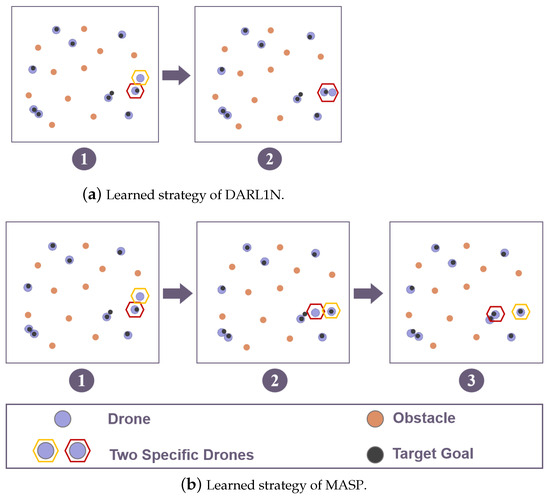
Figure 7.
The compariso in learned strategies of DARL1N and MASP in MPE. The blue circles represent drones, the orange circles represent obstacles, and the black circles represent target goals. The drones highlighted by the yellow and red hexagons exhibit different behaviors under DARL1N and MASP.
6. Conclusions
This paper proposes a goal-conditioned hierarchical planner, Multi-UAV Scalable Graph-based Planner, to improve data efficiency and cooperation in navigation tasks with a varying and substantial number of drones. Thorough experiments demonstrate that MASP achieves higher task and execution efficiency than planning-based baselines and RL competitors in MPE and Omnidrones. Concretely, MASP increases execution efficiency by at least 3× (see Section 5.7). It also enhances task efficiency by over 19.12% in MPE with 50 drones and 27.92% in OmniDrones with 20 drones (see Section 5.5.1), achieving at least a 47.87% enhancement across varying team sizes (see Section 5.5.2).
7. Limitation
Although this method proposes a scalable and promising way for varying numbers of agents in multi-agent navigation, there still remains some limitations. First, this work focuses on multi-agent navigation where agents move toward initially unassigned goals. Leveraging prior knowledge, the task is naturally decomposed into goal assignment and goal navigation. To this end, a hierarchical framework is proposed with a high-level policy for assigning goals and a low-level policy for navigating to them. This intuitive decomposition avoids significant suboptimality. It is acknowledged that not all tasks can be heuristically decomposed based on prior knowledge. In complex multi-agent scenarios, tasks may lack clearly defined subtasks for each agent. A possible solution is to learn latent subtask representations [57,58], allowing the high-level policy to assign them for coordinated execution. Second, this approach assumes that every agent can receive global pose. In real deployments, communication among agents may meet challenges of delayed or missing data. This results in task failure or reduced task efficiency. To mitigate this, MASP needs an adaptive bandwidth allocator [59], and integrates a robust state estimator [60]. Finally, this method currently lacks vision-based mapping and dynamic perception modules. MASP intends to integrate lightweight vision sensors and adopt incremental vision-based mapping techniques [61,62].
Author Contributions
Conceptualization, X.Y. (Xinyi Yang) and C.Y.; methodology, X.Y. (Xinyi Yang); software, X.Y. (Xinting Yang); validation, X.Y. (Xinyi Yang) and X.Y. (Xinting Yang); formal analysis, J.C.; data curation, X.Y. (Xinting Yang); writing—original draft preparation, J.C.; writing—review and editing, C.Y.; visualization, X.Y. (Xinyi Yang) and W.D.; supervision, Y.W. and H.Y.; project administration, Y.W. and J.C. and C.Y.; funding acquisition, C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (No. 62406159, 62325405), Postdoctoral Fellowship Program of CPSF under Grant Number (GZC20240830, 2024M761676), China Postdoctoral Science Special Foundation 2024T170496.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Du, D.; Qi, Y.; Yu, H.; Yang, Y.; Duan, K.; Li, G.; Zhang, W.; Huang, Q.; Tian, Q. The unmanned aerial vehicle benchmark: Object detection and tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September. 2018; pp. 370–386. [Google Scholar]
- Wu, X.; Li, W.; Hong, D.; Tao, R.; Du, Q. Deep learning for unmanned aerial vehicle-based object detection and tracking: A survey. IEEE Geosci. Remote. Sens. Mag. 2021, 10, 91–124. [Google Scholar] [CrossRef]
- Menouar, H.; Guvenc, I.; Akkaya, K.; Uluagac, A.S.; Kadri, A.; Tuncer, A. UAV-enabled intelligent transportation systems for the smart city: Applications and challenges. IEEE Commun. Mag. 2017, 55, 22–28. [Google Scholar] [CrossRef]
- Maza, I.; Kondak, K.; Bernard, M.; Ollero, A. Multi-UAV cooperation and control for load transportation and deployment. In Proceedings of the Selected Papers from the 2nd International Symposium on UAVs, Reno, NE, USA, 8–10 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 417–449. [Google Scholar]
- Alotaibi, E.T.; Alqefari, S.S.; Koubaa, A. Lsar: Multi-uav collaboration for search and rescue missions. IEEE Access 2019, 7, 55817–55832. [Google Scholar] [CrossRef]
- Scherer, J.; Yahyanejad, S.; Hayat, S.; Yanmaz, E.; Andre, T.; Khan, A.; Vukadinovic, V.; Bettstetter, C.; Hellwagner, H.; Rinner, B. An autonomous multi-UAV system for search and rescue. In Proceedings of the First Workshop on Micro Aerial Vehicle Networks, Systems, and Applications for Civilian Use, Florence, Italy, 18 May 2015; pp. 33–38. [Google Scholar]
- Chang, X.; Wang, J.; Li, K.; Zhang, X.; Tang, Q. Research on multi-UAV autonomous obstacle avoidance algorithm integrating improved dynamic window approach and ORCA. Sci. Rep. 2025, 15, 14646. [Google Scholar] [CrossRef]
- Wang, L.; Huang, W.; Li, H.; Li, W.; Chen, J.; Wu, W. A review of collaborative trajectory planning for multiple unmanned aerial vehicles. Processes 2024, 12, 1272. [Google Scholar] [CrossRef]
- Dong, Q.; Xi, H.; Zhang, S.; Bi, Q.; Li, T.; Wang, Z.; Zhang, X. Fast and Communication-Efficient Multi-UAV Exploration Via Voronoi Partition on Dynamic Topological Graph. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 14063–14070. [Google Scholar]
- Liu, C.H.; Ma, X.; Gao, X.; Tang, J. Distributed energy-efficient multi-UAV navigation for long-term communication coverage by deep reinforcement learning. IEEE Trans. Mob. Comput. 2019, 19, 1274–1285. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, W. Multi-agent deep reinforcement learning for UAVs navigation in unknown complex environment. IEEE Trans. Intell. Veh. 2023, 9, 2290–2303. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Wang, Y.; Bayen, A.; Wu, Y. The Surprising Effectiveness of PPO in Cooperative, Multi-Agent Games. arXiv 2021, arXiv:2103.01955. [Google Scholar]
- Wen, M.; Kuba, J.G.; Lin, R.; Zhang, W.; Wen, Y.; Wang, J.; Yang, Y. Multi-Agent Reinforcement Learning is a Sequence Modeling Problem. arXiv 2022, arXiv:2205.14953. [Google Scholar]
- Yang, X.; Huang, S.; Sun, Y.; Yang, Y.; Yu, C.; Tu, W.W.; Yang, H.; Wang, Y. Learning Graph-Enhanced Commander-Executor for Multi-Agent Navigation. In Proceedings of the 2023 International Conference on Autonomous Agents and Multiagent Systems, London, UK, 29 May–2 June 2023; pp. 1652–1660. [Google Scholar]
- Zhao, X.; Yang, R.; Zhong, L.; Hou, Z. Multi-UAV path planning and following based on multi-agent reinforcement learning. Drones 2024, 8, 18. [Google Scholar] [CrossRef]
- Hofstätter, S.; Zamani, H.; Mitra, B.; Craswell, N.; Hanbury, A. Local self-attention over long text for efficient document retrieval. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020; pp. 2021–2024. [Google Scholar]
- Yu, C.; Yang, X.; Gao, J.; Yang, H.; Wang, Y.; Wu, Y. Learning efficient multi-agent cooperative visual exploration. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 497–515. [Google Scholar]
- Yang, X.; Yang, Y.; Yu, C.; Chen, J.; Yu, J.; Ren, H.; Yang, H.; Wang, Y. Active neural topological mapping for multi-agent exploration. IEEE Robot. Autom. Lett. 2023, 9, 303–310. [Google Scholar] [CrossRef]
- Hu, S.; Zhu, F.; Chang, X.; Liang, X. UPDeT: Universal Multi-agent RL via Policy Decoupling with Transformers. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Xu, B.; Gao, F.; Yu, C.; Zhang, R.; Wu, Y.; Wang, Y. OmniDrones: An Efficient and Flexible Platform for Reinforcement Learning in Drone Control. arXiv 2023, arXiv:2309.12825. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, K.; Chen, Y.; Jiang, X.; Song, G. Multi-UAV navigation for partially observable communication coverage by graph reinforcement learning. IEEE Trans. Mob. Comput. 2022, 22, 4056–4069. [Google Scholar] [CrossRef]
- Causa, F.; Vetrella, A.R.; Fasano, G.; Accardo, D. Multi-UAV formation geometries for cooperative navigation in GNSS-challenging environments. In Proceedings of the 2018 IEEE/ION position, location and navigation symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 775–785. [Google Scholar]
- Li, Q.; Gama, F.; Ribeiro, A.; Prorok, A. Graph neural networks for decentralized multi-robot path planning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NE, USA, 25–29 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 11785–11792. [Google Scholar]
- Wang, B.; Xie, J.; Atanasov, N. Darl1n: Distributed multi-agent reinforcement learning with one-hop neighbors. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 9003–9010. [Google Scholar]
- Wang, W.; Wang, L.; Wu, J.; Tao, X.; Wu, H. Oracle-guided deep reinforcement learning for large-scale multi-UAVs flocking and navigation. IEEE Trans. Veh. Technol. 2022, 71, 10280–10292. [Google Scholar] [CrossRef]
- Cheng, J.; Li, N.; Wang, B.; Bu, S.; Zhou, M. High-Sample-Efficient Multiagent Reinforcement Learning for Navigation and Collision Avoidance of UAV Swarms in Multitask Environments. IEEE Internet Things J. 2024, 11, 36420–36437. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Turpin, M.; Mohta, K.; Michael, N.; Kumar, V. Goal assignment and trajectory planning for large teams of interchangeable robots. Auton. Robot. 2014, 37, 401–415. [Google Scholar] [CrossRef]
- Wagner, G.; Choset, H. M*: A complete multirobot path planning algorithm with performance bounds. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 3260–3267. [Google Scholar]
- Chen, D.; Qi, Q.; Fu, Q.; Wang, J.; Liao, J.; Han, Z. Transformer-based reinforcement learning for scalable multi-UAV area coverage. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10062–10077. [Google Scholar] [CrossRef]
- Wei, A.; Liang, J.; Lin, K.; Li, Z.; Zhao, R. DTPPO: Dual-Transformer Encoder-Based Proximal Policy Optimization for Multi-UAV Navigation in Unseen Complex Environments. arXiv 2024, arXiv:2410.15205. [Google Scholar]
- Ji, Y.; Li, Z.; Sun, Y.; Peng, X.B.; Levine, S.; Berseth, G.; Sreenath, K. Hierarchical reinforcement learning for precise soccer shooting skills using a quadrupedal robot. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1479–1486. [Google Scholar]
- Nasiriany, S.; Liu, H.; Zhu, Y. Augmenting reinforcement learning with behavior primitives for diverse manipulation tasks. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 7477–7484. [Google Scholar]
- Takubo, Y.; Chen, H.; Ho, K. Hierarchical reinforcement learning framework for stochastic spaceflight campaign design. J. Spacecr. Rocket. 2022, 59, 421–433. [Google Scholar] [CrossRef]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Rosenbluth, D.; Ritholtz, L.; Twedt, J.C.; Walker, T.T.; Alcedo, K.; Javorsek, D. Hierarchical reinforcement learning for air-to-air combat. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 275–284. [Google Scholar]
- Hafner, D.; Lee, K.H.; Fischer, I.; Abbeel, P. Deep hierarchical planning from pixels. Adv. Neural Inf. Process. Syst. 2022, 35, 26091–26104. [Google Scholar]
- Newaz, A.A.R.; Alam, T. Hierarchical Task and Motion Planning through Deep Reinforcement Learning. In Proceedings of the 2021 Fifth IEEE International Conference on Robotic Computing (IRC), Taichung, Taiwan, 15–17 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 100–105. [Google Scholar]
- Cheng, Y.; Li, D.; Wong, W.E.; Zhao, M.; Mo, D. Multi-UAV collaborative path planning using hierarchical reinforcement learning and simulated annealing. Int. J. Perform. Eng. 2022, 18, 463. [Google Scholar]
- Yuan, Y.; Yang, J.; Yu, Z.L.; Cheng, Y.; Jiao, P.; Hua, L. Hierarchical goal-guided learning for the evasive maneuver of fixed-wing uavs based on deep reinforcement learning. J. Intell. Robot. Syst. 2023, 109, 43. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, K.; Wang, H.; Song, X.; Zhou, B. Content matters: A GNN-based model combined with text semantics for social network cascade prediction. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Virtual Event, 11–14 May 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 728–740. [Google Scholar]
- Zhang, S.; Liu, Y.; Xie, L. Molecular mechanics-driven graph neural network with multiplex graph for molecular structures. arXiv 2020, arXiv:2011.07457. [Google Scholar]
- Jiang, Z.; Chen, Y.; Wang, K.; Yang, B.; Song, G. A Graph-Based PPO Approach in Multi-UAV Navigation for Communication Coverage. Int. J. Comput. Commun. Control. 2023, 18, 5505. [Google Scholar] [CrossRef]
- Du, Y.; Qi, N.; Li, X.; Xiao, M.; Boulogeorgos, A.A.A.; Tsiftsis, T.A.; Wu, Q. Distributed multi-UAV trajectory planning for downlink transmission: A GNN-enhanced DRL approach. IEEE Wirel. Commun. Lett. 2024, 13, 3578–3582. [Google Scholar] [CrossRef]
- Zhao, B.; Huo, M.; Li, Z.; Yu, Z.; Qi, N. Graph-based multi-agent reinforcement learning for large-scale UAVs swarm system control. Aerosp. Sci. Technol. 2024, 150, 109166. [Google Scholar] [CrossRef]
- Wu, D.; Cao, Z.; Lin, X.; Shu, F.; Feng, Z. A Learning-based Cooperative Navigation Approach for Multi-UAV Systems Under Communication Coverage. IEEE Trans. Netw. Sci. Eng. 2024, 12, 763–773. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.Z.; Kaiser, L. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Zhao, H.; Jia, J.; Koltun, V. Exploring self-attention for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10076–10085. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Rotors—A modular gazebo mav simulator framework. In Robot Operating System (ROS) The Complete Reference (Volume 1); Springer: Berlin/Heidelberg, Germany, 2016; pp. 595–625. [Google Scholar]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the Proceedings 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065); IEEE: Piscataway, NJ, USA, 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Brody, S.; Alon, U.; Yahav, E. How Attentive are Graph Attention Networks? In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022.
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Na, H.; Moon, I.C. LAGMA: Latent goal-guided multi-agent reinforcement learning. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 37122–37140. [Google Scholar]
- Zhang, Q.; Zhang, H.; Xing, D.; Xu, B. Latent Landmark Graph for Efficient Exploration-exploitation Balance in Hierarchical Reinforcement Learning. In Machine Intelligence Research; Springer: Berlin/Heidelberg, Germany, 2025; pp. 1–22. [Google Scholar]
- Tan, D.M.S.; Ma, Y.; Liang, J.; Chng, Y.C.; Cao, Y.; Sartoretti, G. IR 2: Implicit Rendezvous for Robotic Exploration Teams under Sparse Intermittent Connectivity. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 13245–13252. [Google Scholar]
- Alvarez, J.; Belbachir, A. Dynamic Position Estimation and Flocking Control in Multi-Robot Systems. In Proceedings of the 21st International Conference on Informatics in Control, Automation and Robotics, SCITEPRESS-Science and Technology Publications, Porto, Portugal, 18–20 November 2024; pp. 269–276. [Google Scholar]
- Deng, T.; Shen, G.; Xun, C.; Yuan, S.; Jin, T.; Shen, H.; Wang, Y.; Wang, J.; Wang, H.; Wang, D.; et al. MNE-SLAM: Multi-Agent Neural SLAM for Mobile Robots. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 1485–1494. [Google Scholar]
- Blumenkamp, J.; Morad, S.; Gielis, J.; Prorok, A. CoViS-Net: A Cooperative Visual Spatial Foundation Model for Multi-Robot Applications. In Proceedings of the 8th Annual Conference on Robot Learning, Munich, Germany, 6–9 November 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).