Joint Caching and Computation in UAV-Assisted Vehicle Networks via Multi-Agent Deep Reinforcement Learning

Abstract

Intelligent Connected Vehicles (ICVs) impose stringent requirements on real-time computational services. However, limited onboard resources and the high latency of remote cloud servers restrict traditional solutions. Unmanned Aerial Vehicle (UAV)-assisted Mobile Edge Computing (MEC), which deploys computing and storage resources at the network edge, offers a promising solution. In UAV-assisted vehicular networks, jointly optimizing content and service caching, computation offloading, and UAV trajectories to maximize system performance is a critical challenge. This requires balancing system energy consumption and resource allocation fairness while maximizing cache hit rate and minimizing task latency. To this end, we introduce system efficiency as a unified metric, aiming to maximize overall system performance through joint optimization. This metric comprehensively considers cache hit rate, task computation latency, system energy consumption, and resource allocation fairness. The problem involves discrete decisions (caching, offloading) and continuous variables (UAV trajectories), exhibiting high dynamism and non-convexity, making it challenging for traditional optimization methods. Concurrently, existing multi-agent deep reinforcement learning (MADRL) methods often encounter training instability and convergence issues in such dynamic and non-stationary environments. To address these challenges, this paper proposes a MADRL-based joint optimization approach. We precisely model the problem as a Decentralized Partially Observable Markov Decision Process (Dec-POMDP) and adopt the Multi-Agent Proximal Policy Optimization (MAPPO) algorithm, which follows the Centralized Training Decentralized Execution (CTDE) paradigm. Our method aims to maximize system efficiency by achieving a judicious balance among multiple performance metrics, such as cache hit rate, task delay, energy consumption, and fairness. Simulation results demonstrate that, compared to various representative baseline methods, the proposed MAPPO algorithm exhibits significant superiority in achieving higher cumulative rewards and an approximately 82% cache hit rate.

1. Introduction

As a core component of future transportation systems, Intelligent Connected Vehicles (ICVs) are driving rapid advancements in onboard intelligent services, including advanced driver assistance systems, real-time route planning, and in-vehicle infotainment [1]. While these services enhance driving safety and user experience, they also impose stringent computational demands on vehicles. Due to limited onboard computing resources and energy constraints, processing computation-intensive tasks locally often leads to severe computational overload and excessive power consumption, making it difficult to meet real-time requirements. Although offloading tasks to remote cloud servers presents a potential solution, the long-distance deployment of cloud infrastructure introduces significant transmission delays and backhaul energy consumption, particularly unsuitable for latency-sensitive vehicular applications [2]. MEC technology, which brings computing and storage resources closer to the network edge, offers a promising alternative [3]. In this context, UAV-assisted vehicular MEC systems leverage their high mobility, flexible coverage, and Line-of-Sight (LoS) communication advantages to provide on-demand edge services for high-speed vehicles, effectively addressing the limitations of traditional ground-based MEC infrastructure, such as high deployment costs and restricted coverage [4].

In UAV-assisted vehicular MEC systems, content caching plays a crucial role in reducing service latency and improving user experience. Existing research primarily focuses on optimizing caching strategies based on content popularity or user mobility to maximize cache hit rates or minimize content delivery delays [5,6]. For instance, in [7], Choi Y and Lim Y utilized deep reinforcement learning (DRL) to optimize edge caching in vehicular networks by predicting user mobility, aiming to minimize content delivery delays. However, most of these works consider content caching in isolation, overlooking the dependencies between computational service caching and task offloading decisions. For example, works like [7] primarily focus on caching optimization, while studies such as [8] by S Yu et al. concentrate on developing task offloading strategies for connected vehicles, often considering these aspects in isolation and thus overlooking their inherent dependencies [9]. In practice, vehicles not only require access to content data but also rely on specific computational services for task execution [10]. Successful task processing necessitates that edge nodes cache both the required service programs and relevant data, necessitating a co-optimization of caching and offloading strategies [11,12]. To address this, recent efforts, including [13] by K Xue et al., have begun to explore co-optimization of task offloading and multi-cache placement in UAV-assisted MEC networks, recognizing the joint requirement for service programs and data. Similarly, Ref. [14] by X Wang proposed a joint task offloading and resource allocation framework in medical vehicular networks, demonstrating the trend towards integrated solutions. Meanwhile, a common limitation in many existing task offloading studies, such as [15] by M Hong et al., which focuses on energy-efficient data offloading in high-mobility vehicular MEC environments, is the implicit assumption that necessary services are always pre-deployed at edge nodes, thereby overlooking the critical impact of service availability on offloading feasibility. Such fragmented optimization approaches struggle to achieve optimal performance.

Furthermore, UAV flight trajectories directly influence communication quality, coverage range, and energy consumption, significantly affecting caching efficiency and offloading performance [16]. For instance, in [17], Bi X and Zhao L designed a two-layer edge intelligence framework for UAV-assisted vehicular networks, explicitly considering how UAV trajectories impact task offloading and computing capacity allocation. Moreover, studies like [18] by F Shen et al. have focused on TD3-based trajectory optimization for energy consumption minimization in UAV-assisted MEC systems, and [19] by E Pei et al. optimized resource and trajectory for UAV-assisted MEC communication, underscoring the direct link between UAV movement and system performance. Beyond these, recent works have also explored UAV trajectory optimization for specific objectives in diverse scenarios. For example, Ref. [20] focused on ordered submodularity-based value maximization for UAV data collection in earthquake areas, while [21] investigated reward maximization for disaster zone monitoring with heterogeneous UAVs. These studies highlight the critical role of UAV trajectory planning in achieving various system goals. Therefore, to fully exploit the potential of UAV-assisted vehicular MEC, a joint optimization of caching strategies, task offloading, and UAV trajectory planning is essential. Acknowledging this complexity, a holistic approach is warranted, necessitating a joint optimization of caching strategies, task offloading, and UAV trajectory planning. For example, Ref. [4] by M Abdel-Basset et al. proposed an intelligent joint optimization of deployment (implying trajectory) and task scheduling for multi-UAV-assisted MEC systems, and [22] by MF Dehkordi et al. explored efficient and sustainable task offloading in UAV-assisted MEC systems using meta deep reinforcement learning, implicitly integrating aspects of trajectory and resource management. This joint optimization problem exhibits high dynamism and complexity, involving discrete caching and offloading decisions alongside continuous trajectory variables. Traditional optimization methods, such as convex optimization or integer programming, face substantial challenges due to the non-convexity and high dimensionality of the problem, making real-time decision-making in dynamic environments difficult. For instance, while methods like those in [23] by L Shao apply optimization techniques to UAV-assisted MEC systems for security and resource allocation, the inherent non-convexity and dynamic nature of jointly optimizing caching, offloading, and trajectory often render classical approaches computationally intractable for real-time scenarios.

DRL, leveraging its adaptability to dynamic environments and capability to handle high-dimensional decision spaces, provides a novel approach to solving such complex optimization problems. Multi-Agent DRL (MADRL) extends this capability further, making it suitable for collaborative optimization scenarios involving multiple UAVs and vehicles [6]. Recent advancements have seen MADRL effectively applied to various aspects of UAV-aided MEC and resource management. For instance, Li et al. [24,25] extensively investigated the energy-efficient computation offloading problem in multi-UAV-assisted Internet of Things (IoT) networks over the Terahertz (THz) band. They jointly optimized UAV trajectories, user equipment (UE), local central processing unit (CPU) clock speeds, UAV–UE associations, time slot slicing, and UE offloading powers through a tailored MADRL solution, DSPAC-MN. Their work notably focused on maximizing energy efficiency in THz communications and ensuring safe UAV flights, even incorporating a more practical ITU-suggested building distribution model [24] into their channel modeling.

However, existing MADRL methods still exhibit notable limitations when addressing joint optimization in vehicular networks: most studies focus on optimizing only one or two aspects among offloading [26], caching [27], and trajectory planning [28], failing to achieve comprehensive joint optimization [29], and widely used algorithms (such as Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [6], Deep Q-Learning Network (DQN) [30], Actor Critic (AC) [31], and Deep Deterministic Policy Gradient (DDPG) [32]) suffer from training instability and hyperparameter sensitivity, limiting their effectiveness in complex vehicular environments. Particularly, in scenarios where task execution depends on cached services, existing algorithms struggle to manage multi-agent coordination and non-stationarity effectively.

To address the aforementioned challenges, particularly the fragmented optimization of existing approaches and the inherent instability of current MADRL algorithms in dynamic vehicular environments where task execution depends on cached services, this paper proposes a MADRL problem tailored for joint optimization in UAV-assisted vehicular networks. Unlike existing studies that often overlook the strong interdependencies or optimize only one or two aspects among offloading, caching, and trajectory planning, our problem achieves comprehensive joint optimization of content and service caching, computation offloading decisions, and UAV trajectories, explicitly accounting for task dependencies on cached services. We precisely model this highly dynamic and complex problem as a Dec-POMDP, which effectively captures system dynamics and multi-agent interactions. Furthermore, to overcome the training instability and hyperparameter sensitivity observed in widely used MADRL algorithms like MADDPG, we employ a MAPPO algorithm. This algorithm operates under a CTDE paradigm, balancing efficient learning with robust real-world deployment. Table 1 summarizes and compares our contributions in the field of UAV-assisted MEC with the current state-of-the-art in this domain. The key contributions of this work include the following:

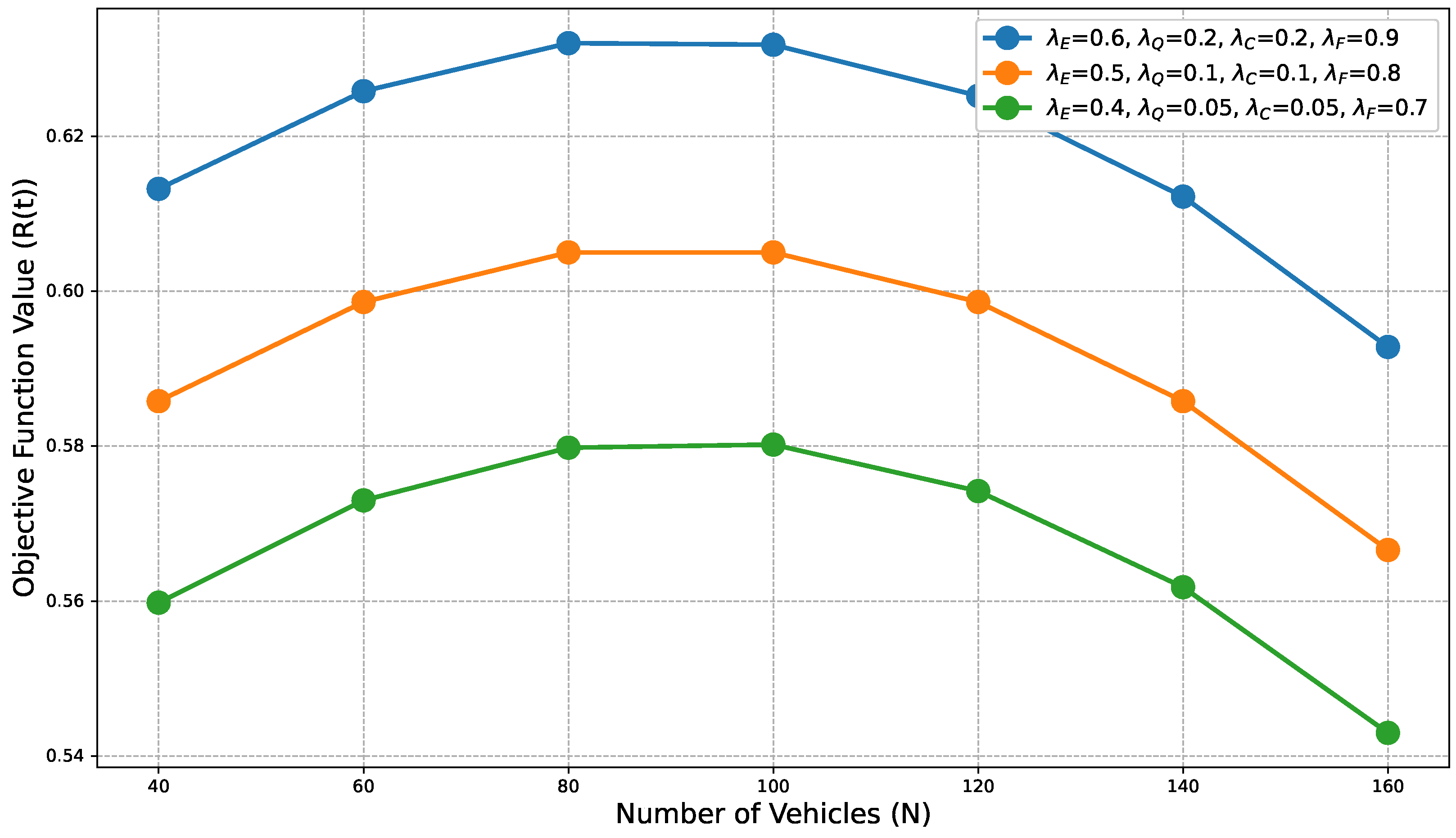
• We propose a comprehensive joint optimization problem for UAV-assisted vehicular networks, precisely modeled as a Dec-POMDP to capture dynamic environments and complex agent interactions. The model thoroughly considers UAVs’ roles in service and content caching and vehicular computation offloading, while simultaneously accounting for cache hit rate, computation delay, and system energy consumption. To balance these conflicting metrics and ensure fairness, we innovatively introduce “system efficiency” as a holistic and unified performance indicator. This metric comprehensively considers cache hit rate, task computation latency, system energy consumption, and resource allocation fairness, and is balanced through appropriate weighting. The ultimate objective is to maximize overall system efficiency by jointly optimizing UAV caching strategies, vehicular computation offloading decisions, and UAV flight trajectories within the Dec-POMDP framework.
• To address the complex Dec-POMDP model, we propose a MAPPO reinforcement learning algorithm. It efficiently solves the problem through innovative state space design and refined reward shaping mechanisms. The state space comprehensively includes UAV locations, caching states, vehicular service requests, network resource status, and real-time channel quality, providing agents with complete environmental awareness. Beyond positive rewards for service efficiency, the reward mechanism meticulously designs various penalty terms for exceeding UAV flight areas, excessive energy consumption, latency, and unfair resource allocation. These designs effectively constrain agent behavior, ensuring learning stability, accelerating convergence, and enabling optimal decisions in dynamic environments, significantly improving system performance.
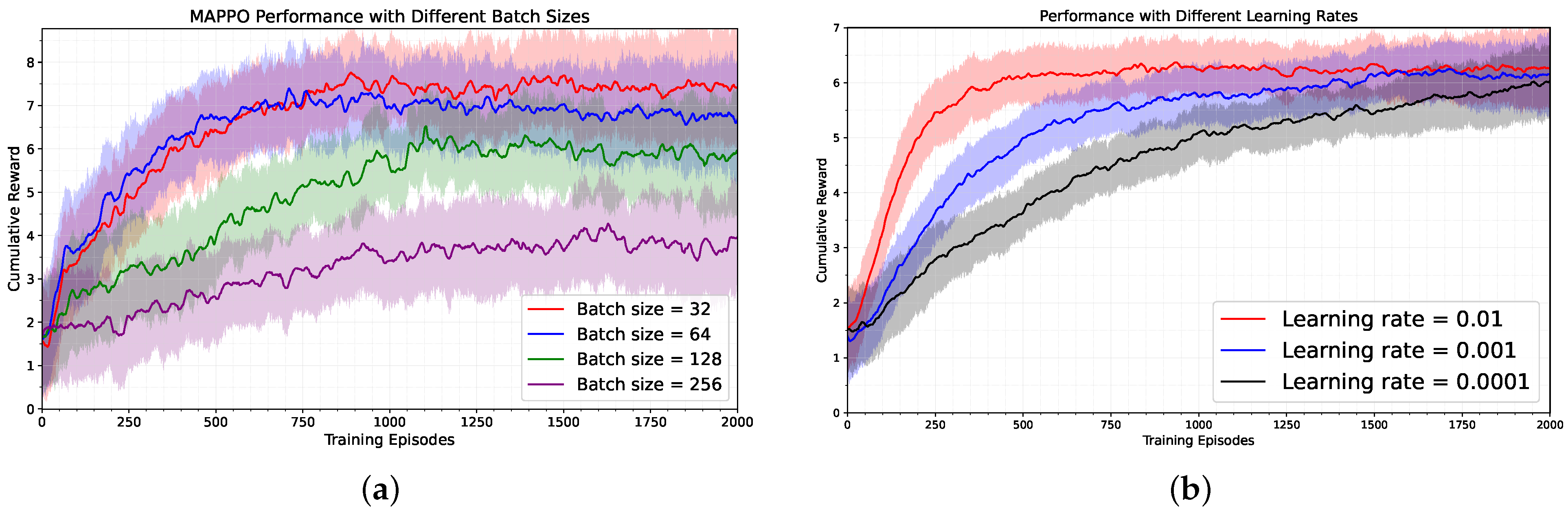
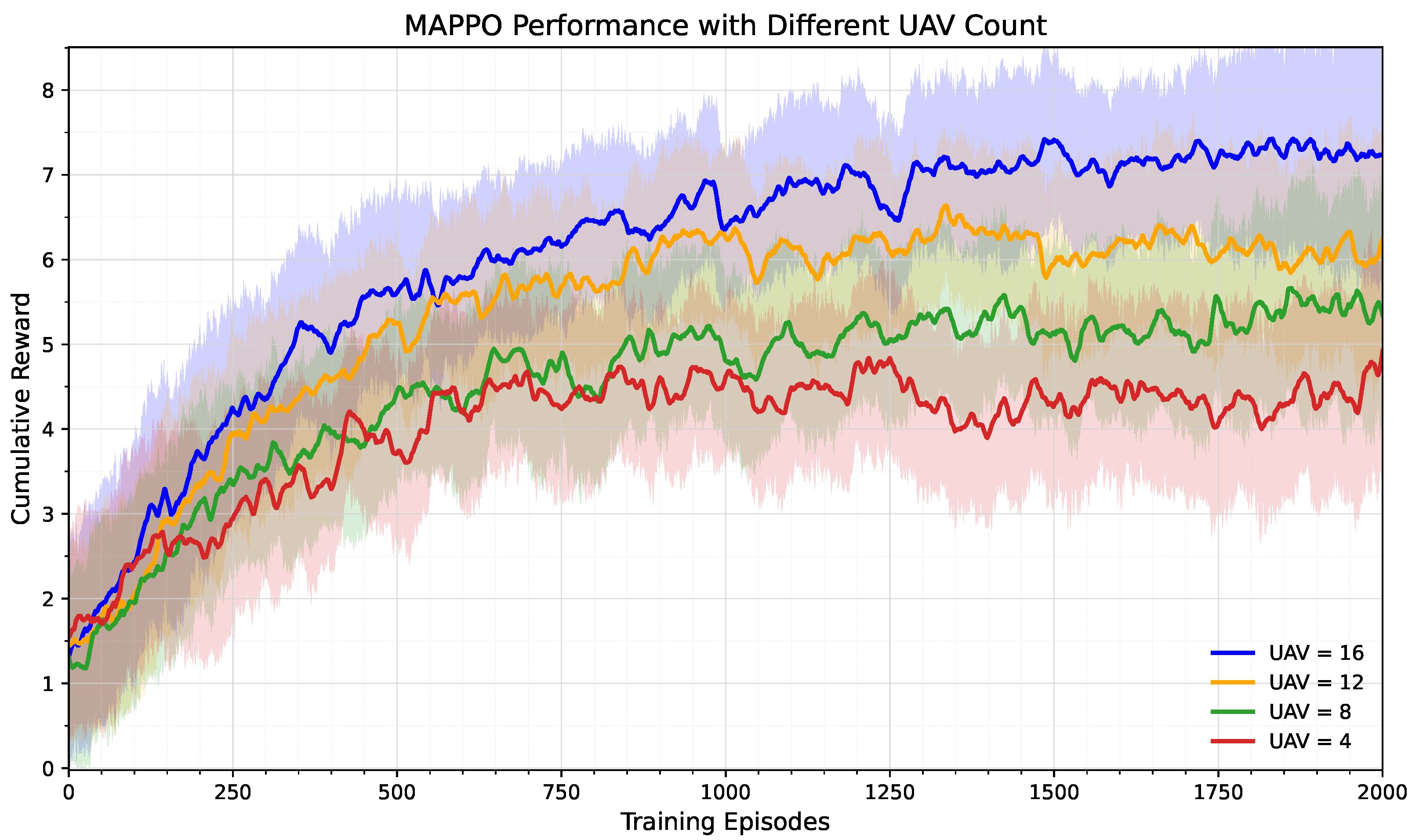
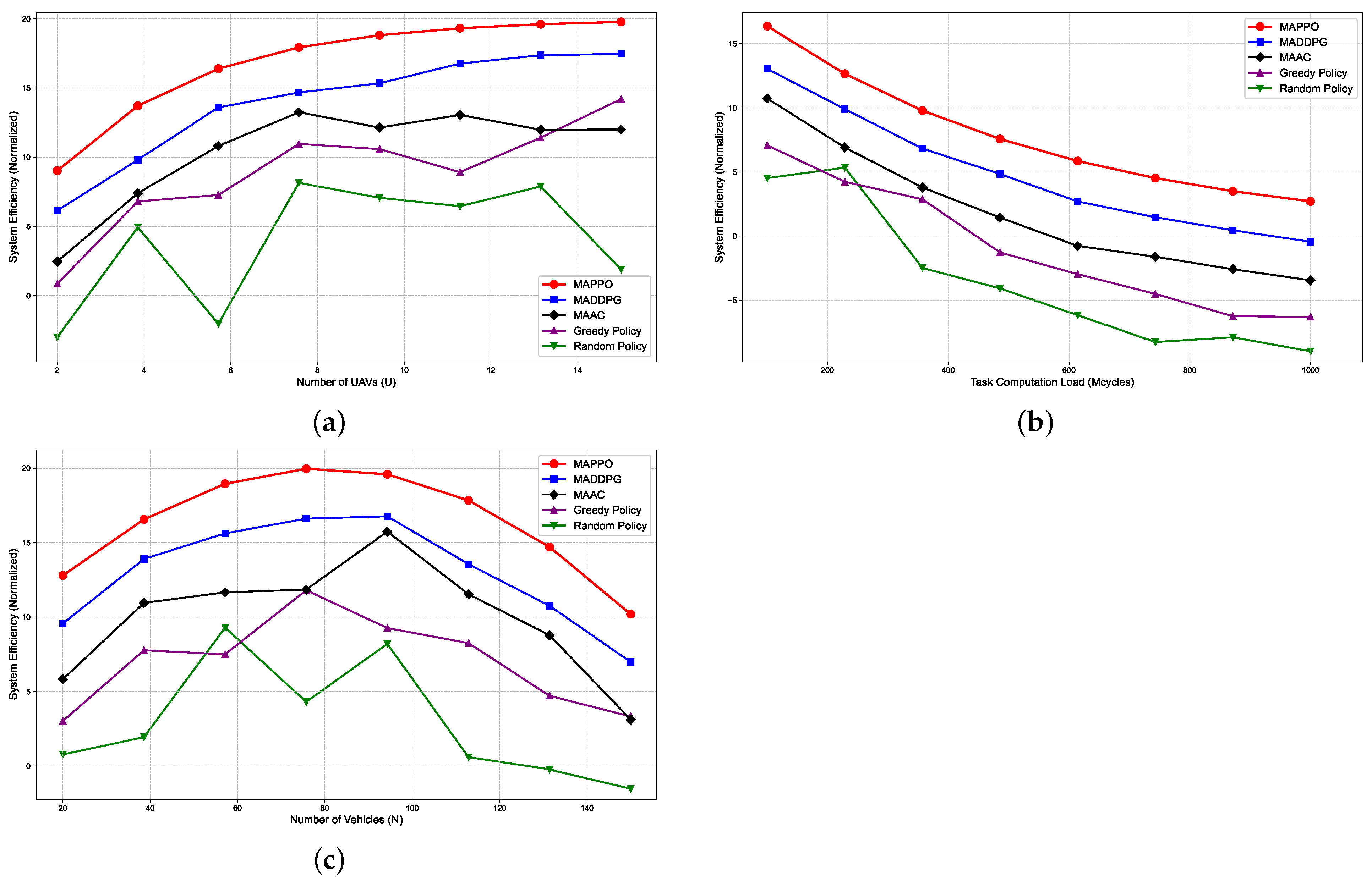
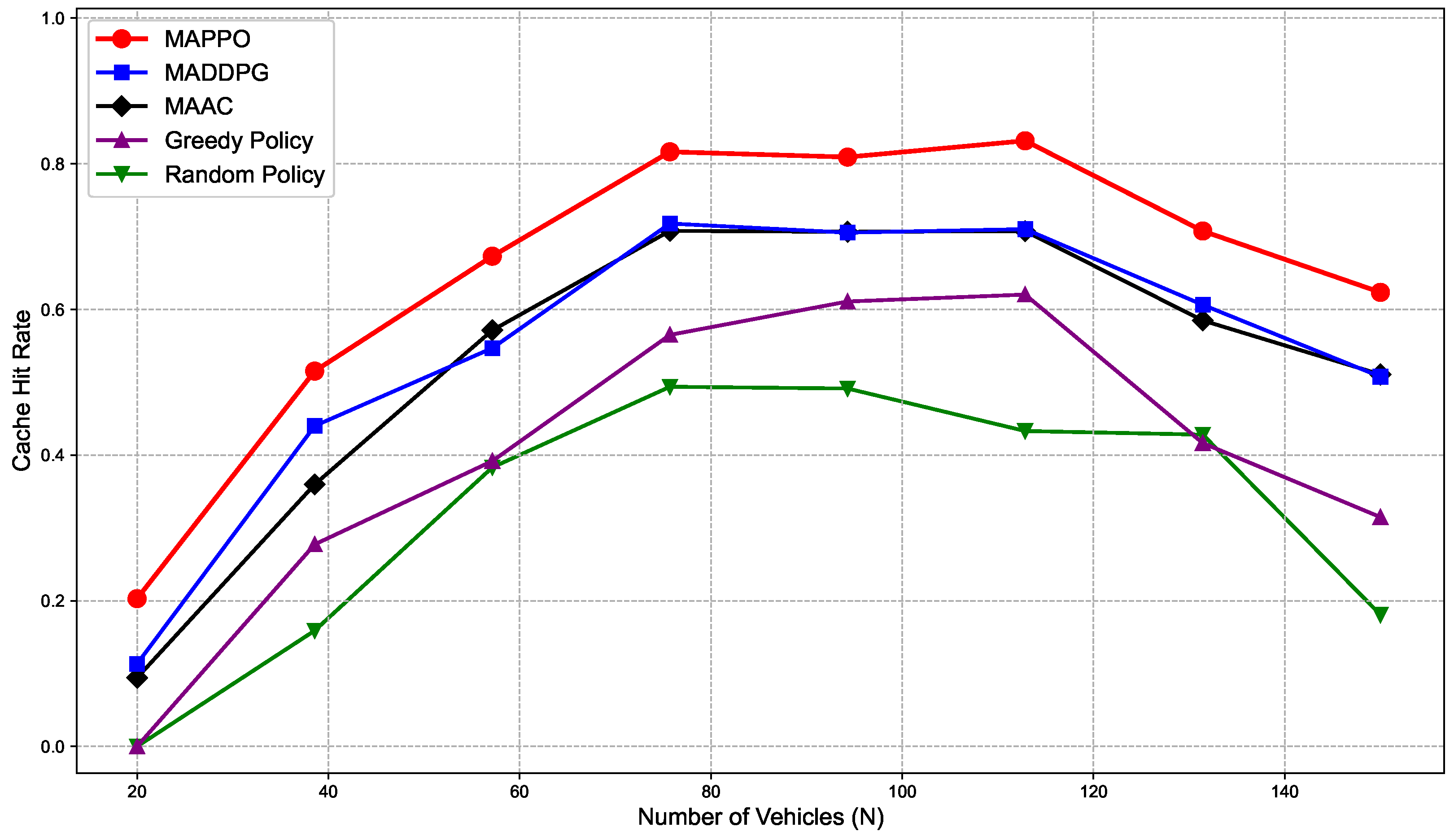
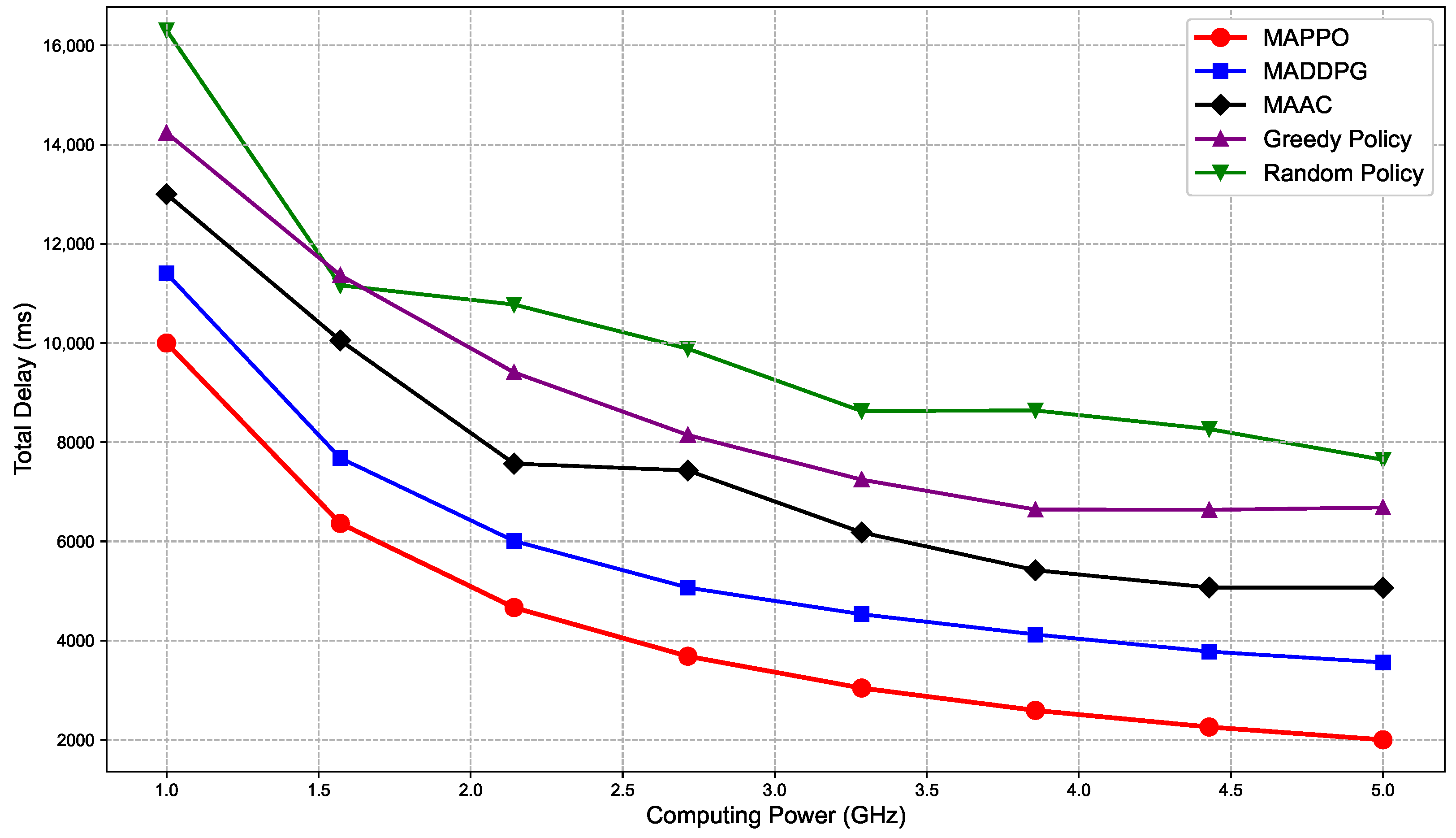
• To comprehensively validate the effectiveness, robustness, and practical feasibility of the proposed joint optimization problem and reinforcement learning algorithm, extensive system simulations were conducted. The simulation results clearly demonstrate our method’s significant advantages in improving the service efficiency of UAV-assisted vehicular networks, specifically in reducing user task computation delay, decreasing overall system energy consumption, increasing content and service hit rates, and ensuring fair resource allocation. Comparative analysis across different network scenarios, vehicle densities, and UAV configurations further validates the crucial role of the innovative state space design and reward shaping mechanisms in training stability and algorithm convergence speed. These detailed results provide strong quantitative support for our solution’s practicality and superiority.

Table 1. Comparison of our contributions to the state-of-the-art related literature.

	[4]	[9]	[22]	[23]	[24]	[25]	[27]	[28]	[31]	[32]	Ours
UAV-Assisted Vehicle Networks			✔	✔					✔	✔	✔
Multi-UAV Cooperation	✔	✔					✔	✔	✔	✔	✔
Service Caching			✔	✔					✔	✔	✔
Content Caching			✔	✔					✔	✔	✔
Computation Offloading	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔
UAV Trajectory Optimization	✔	✔			✔	✔	✔	✔	✔	✔	✔
DRL-based Solution	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔

Table 1. Comparison of our contributions to the state-of-the-art related literature.

	[4]	[9]	[22]	[23]	[24]	[25]	[27]	[28]	[31]	[32]	Ours
UAV-Assisted Vehicle Networks			✔	✔					✔	✔	✔
Multi-UAV Cooperation	✔	✔					✔	✔	✔	✔	✔
Service Caching			✔	✔					✔	✔	✔
Content Caching			✔	✔					✔	✔	✔
Computation Offloading	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔
UAV Trajectory Optimization	✔	✔			✔	✔	✔	✔	✔	✔	✔
DRL-based Solution	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔

The remainder of this paper is organized as follows: Section 2 details the system model and problem formulation. Section 3 presents the MAPPO-based joint optimization algorithm. Section 4 evaluates performance through experiments, and Section 5 concludes the paper and discusses future directions.

2. System Model and Problem Formulation

In this section, we first introduce the UAV-assisted Internet of Vehicles (IoV) system, followed by a detailed description of the system model, including the caching model, the computation model, and the communication model. Then, we propose a joint data caching and computation offloading optimization problem for UAV-assisted IoV. To quickly clarify some variables, we summarize the key symbols used in

Table 2. Summary of key notations.

Notation	Description
$\mathcal{U}$	Set of UAVs
$\mathcal{N}$	Set of vehicles
$\mathcal{T}$	Set of time slots
${\mathbf{l}}_{\mathbf{u}}\left(t\right)$	UAV u’s location at time t
${\mathbf{l}}_{\mathbf{n}}\left(t\right)$	Vehicle n’s location at time t
V	UAV u’s instantaneous speed at time t
$d_{\min }$	Minimum safe distance between UAVs
$H_{\min }$	Minimum flight altitude
$H_{\max }$	Maximum flight altitude
$s_n^d\left(t\right)$	Task size of vehicle n
$c_n^d\left(t\right)$	CPU cycles for task n
$f_n$	Computation resource of vehicle n
$f_u$	Computation resource of UAV u
$a_{u,n}^d\left(t\right)$	Offloading decision (V2U)
$x_{u,d}\left(t\right)$	Caching decision for program d
$x_{u,k}\left(t\right)$	Caching decision for content k
$R_{n,u}\left(t\right)$	Data transmission rate (V2U)
$T_n\left(t\right)$	Total task delay of vehicle n
$E_u^{\mathrm{fly}}$	Flight energy consumption of UAV u
$E_u^{\mathrm{comp}}$	Computation energy consumption of UAV u
$E^{\max }$	UAV u’s max energy budget
$P\left(V\right)$	Propulsion power at speed V
$L_{n,u}\left(t\right)$	Distance between vehicle n and UAV u

.

2.1. Network Model

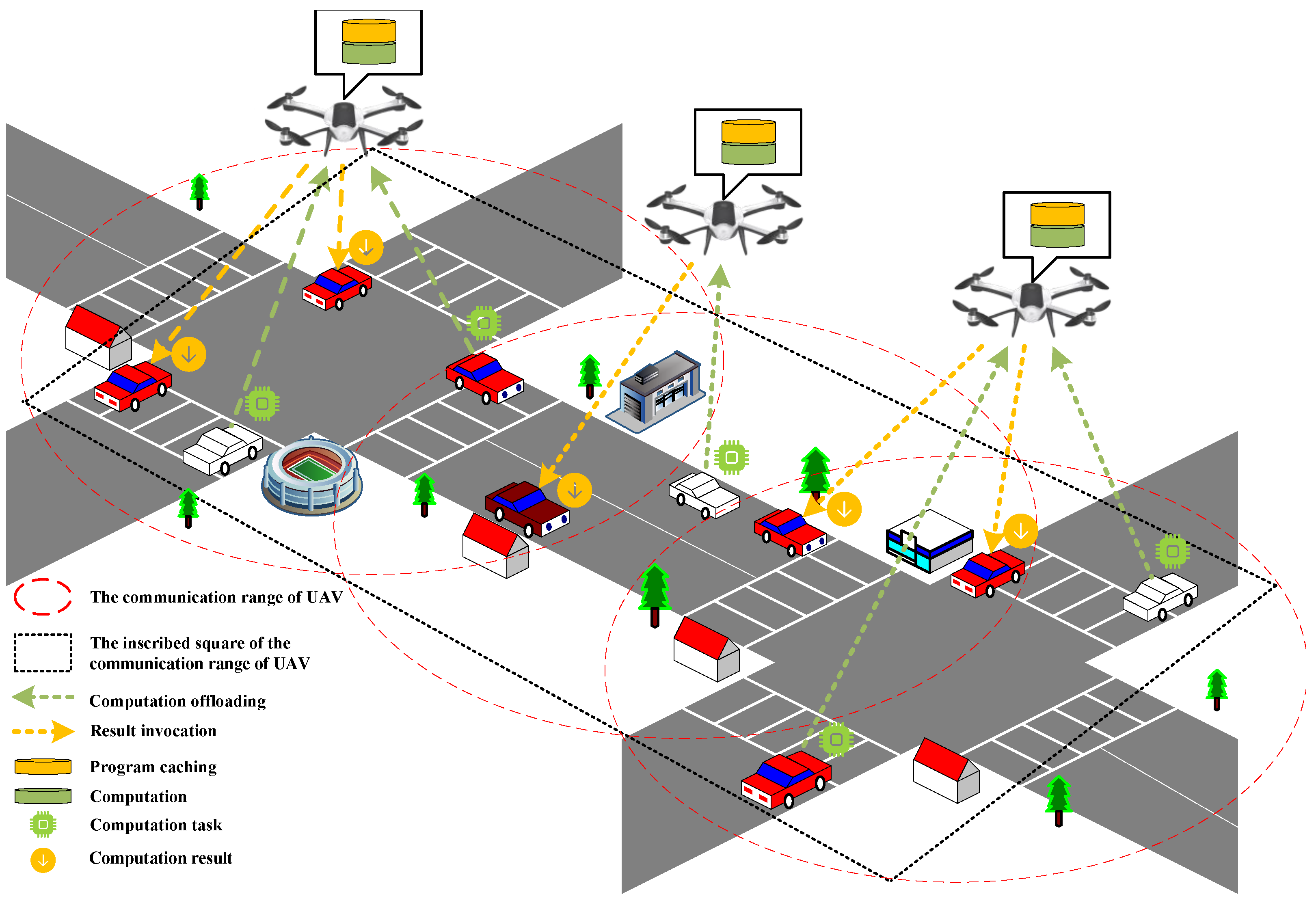
As shown in Figure 1, we consider a multi-UAV-enabled MEC scenario for the IoV [33]. UAVs can provide computing and caching services for vehicles on the ground. The set of UAVs and vehicles is represented as $\mathcal{U}=\left\{1,2,\dots ,u,\dots ,U\right\}$ and $\mathcal{N}=\left\{1,2,\dots ,n,\dots ,N\right\}$, respectively. Since the take-off and landing times of UAVs are very short, and the energy consumption during these processes is minimal, we can ignore both the time and energy consumption involved in the UAVs’ takeoff and landing. For simplicity, it is assumed that the capacity of the wireless backhaul link from the BS to each UAV is equal to $R_b$.

In our paper, we adopt the 3D Cartesian coordinate system to represent the positions of UAVs and vehicles. We divide time transmitted from the vehicle to the UAV into a set of discrete time slots $\mathcal{T}=\{1,2,\dots ,t,\dots ,T\}$, and the size of each time slot is $\tau$. Thus, the location of UAV u at time slot t is denoted as ${\mathbf{l}}_{\mathbf{u}}\left(t\right)=(X_u\left(t\right),Y_u\left(t\right),Z_u\left(t\right))$. The location of vehicle n at the time slot t is represented as ${\mathbf{l}}_{\mathbf{n}}\left(t\right)=(X_n\left(t\right),Y_n\left(t\right),0)$. We assume that the velocity of the u-th UAV at time slot t is denoted by V and each vehicle n, $n\in N$, in the system generates multiple tasks ${\pi }_n\left(t\right)$ during each time slot t, $t\in \mathcal{T}$. For UAVs, they are independent and identically distributed, follow the homogeneous Poisson point process (PPP) with density ${\lambda }_u$, and are represented by set ${\Phi }_s$. This modeling choice indicates that the initial position of the UAV is randomly and uniformly distributed within the service area.

In the scenario studied in this paper, vehicles move along straight paths only, without considering turns or complex road conditions. This setup simplifies the vehicle motion model, allowing us to focus on the communication, computation, and caching scheduling problems during straight-line driving. This is a common simplification in initial studies before considering more complex mobility models [34].

For the multi-UAV cooperative system architecture, we consider the following UAV location constraints to ensure proper system operation:

Safety Distance Constraint Between UAVs: The distance between each pair of UAVs u and v must be greater than or equal to the minimum safe distance dmin in all time slots:

$$∥{\mathbf{l}}_u\left(t\right)-{\mathbf{l}}_v\left(t\right)∥\ge d_{min},\forall u\ne v,\forall t\in \mathcal{T},\forall u,v\in \mathcal{U},$$

(1)

where ${\mathbf{l}}_u\left(t\right)$ and ${\mathbf{l}}_v\left(t\right)$ denote the positions of UAV u and UAV v at the t-th time slot, respectively. This constraint is essential for safety in multi-UAV systems [35].

UAV Flight Altitude Constraint: Each UAV u should maintain its altitude within the specified range:

$$H_{min}\le Z_u\left(t\right)\le H_{max},\forall u\in \mathcal{U},\forall t\in \mathcal{T},$$

(2)

These altitude limits are practical considerations for UAV deployment [36].

As stated in [24,37], for a UAV with speed V at time slot t, the propulsion energy consumption within that time slot can be calculated as follows:

$$\begin{array}{cc}\hfill P\left(V\right)=& {\left.P_0\left(1+{\displaystyle \frac{3V^2}{U_r^2}}\right)+P_1\left({\left(1+{\displaystyle \frac{V^4}{4v_r^4}}\right)}^{{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{V^2}{2v_r^2}}\right)\right)}^{{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{1}{2}}{d}_0\rho sA{V}^3,\hfill \end{array}$$

(3)

where $P_0$ represents the rotor blade profile power of a UAV in a hovering state, $P_1$ is the rotor blade induced power in hovering, $U_r$ denotes the tip speed of the blades, $v_r$ signifies the average rotor induced velocity during hover, $d_0$ is the drag ratio experienced by the UAV, $\rho$ represents air density, s denotes the rotor disc solidity, and A represents the blade disc area. The power consumption for the hovering state is $P_h=P(V=0)=P_0+P_1$.

Therefore, the UAV’s propulsion consumption at the time slot t is obtained by

$$E_u^{\mathrm{fly}}\left(t\right)=P\left(V\right)·{\displaystyle \frac{∥{\mathbf{l}}_{\mathbf{u}}\left(t\right)-{\mathbf{l}}_{\mathbf{u}}\left(t-1\right)∥}{V}}+P_h·max\left(0,\tau -{\displaystyle \frac{∥{\mathbf{l}}_{\mathbf{u}}\left(t\right)-{\mathbf{l}}_{\mathbf{u}}\left(t-1\right)∥}{V}}\right).$$

(4)

This energy model is commonly used in UAV trajectory optimization studies [38].

2.2. Caching Model

Let $\mathcal{D}=\{1,2,\dots ,d,\dots ,D\}$ and $\mathcal{K}=\{1,2,\dots ,k,\dots ,K\}$ denote the set of services and the set of contents, respectively. We use $s_d$ and $s_k$ to represent the size of service d and content k. Each UAV can cache some services that will be used by the associated vehicle to save the wireless backhaul time. Caching services at the edge is crucial for reducing latency in VEC systems [39].

Let $x_{u,d}\left(t\right)\in \{0,1\},u\in \mathcal{U},d\in \mathcal{D}$ ($x_{u,k}\left(t\right)\in \{0,1\},u\in \mathcal{U},k\in \mathcal{K}$) be the binary decision variable indicating whether the UAV u caches program d (content k). $x_{u,d}\left(t\right)=1$ ($x_{u,k}\left(t\right)=1$) indicates that program d (content k) is cached by UAV u; otherwise, $x_{u,d}\left(t\right)=0$ ($x_{u,k}\left(t\right)=0$).

Since the caching capacity of each UAV is limited, we have the following constraint:

$$\sum _{d=1}^D{x}_{u,d}\left(t\right)s_d+\sum _{k=1}^K{x}_{u,k}\left(t\right)s_k\le Q_u,\forall u\in \mathcal{U},t\in \mathcal{T}$$

(5)

where $Q_u$ is the total storage space of UAV u. This constraint is standard in caching problems [40].

2.3. Communication Model

In our work, we assume that the communication links between a vehicle and a UAV (V2U) are LoS. Due to that, the size of the processing result is in general much smaller than the size of the task, we ignore the transmission time of the downlink channel [24,25].

According to the Euclidean formula, the distance between vehicle n and UAV u at time slot t is given by

$$L_{n,u}\left(t\right)=\sqrt{{(X_u\left(t\right)-X_n\left(t\right))}^2+{(Y_u\left(t\right)-Y_n\left(t\right))}^2+Z_u{\left(t\right)}^2}.$$

(6)

We assume that the wireless channel from ground vehicles to the UAV is dominated by the LoS transmission link. It is noted that real-world scenarios, particularly in IoV, often utilize 3GPP Urban Macro (UMa) [41,42] or Urban Micro (UMi) [43] environments. In this case, the channel remains unchanged within each fading block and is subject to distance-dependent power attenuation. Therefore, at the t-th time slot, the channel power gain between the n-th vehicle and the u-th UAV can be formulated as

$$h_{n,u}\left(t\right)={\eta }_0{L}_{n,u}^{-\zeta }\left(t\right)={\displaystyle \frac{{\eta }_0}{{\left(∥{\mathbf{l}}_{\mathbf{u}}\left(t\right)-{\mathbf{l}}_{\mathbf{n}}\left(t\right)∥\right)}^{\zeta }}},$$

(7)

where ${\eta }_0$ is the channel power gain at a reference distance $L_0=1m$, and $\zeta \ge 2$ is the path-loss exponent [34].

The data transmission rate for offloading the task from vehicle n to UAV u can be calculated as:

$$R_{n,u}\left(t\right)=B_{n,u}{log}_2\left(1+{\displaystyle \frac{P_n{G}_0{h}_{n,u}\left(t\right)}{{\sigma }^2}}\right),$$

(8)

where $B_{n,u}$ is the spectrum bandwidth of the vehicle-to-UAV (V2U) communication channel, $P_n$ is the transmission power of vehicle n, $G_0\approx 2.2846$ [44], and ${\sigma }^2$ is the power of the white Gaussian noise. In this formula, we assume that all vehicles are connected to UAV u using Orthogonal Frequency-Division Multiple Access (OFDMA), which is allocated by the spectrum resource. Thus, different V2U links do not interfere with each other, and the coverage areas of the UAVs do not overlap, eliminating interference between UAVs [45]. Based on (8), the transmission delay from vehicle n to UAV u is given by:

$$T_{n,u}^{\mathrm{comm}}\left(t\right)={\displaystyle \frac{s_n^d\left(t\right)}{R_{n,u}\left(t\right)}}.$$

(9)

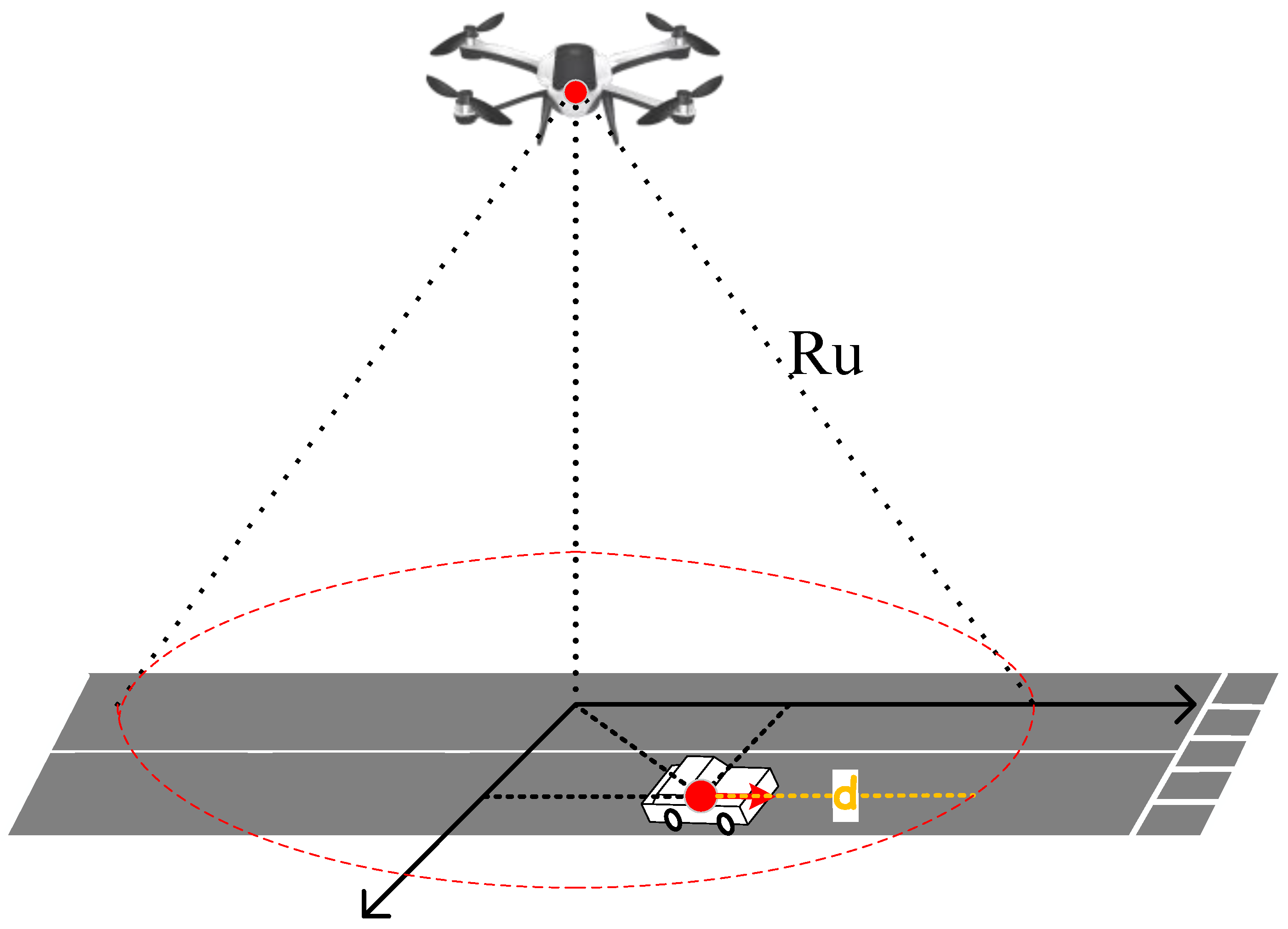
If a vehicle requests service from a UAV, the condition that must be satisfied is that the UAV is within the vehicle’s coverage range. This spatial condition is illustrated in Figure 2, which shows the geometric relationship between the UAV and the vehicle. Whether the vehicle is within the UAV’s coverage range is represented by a binary 0–1 indicator I, given by

$$I_{n,u}\left(t\right)=\left\{\begin{array}{cc}1,\hfill & \hfill if{R}_{n,u}\left(t\right)\ge R_{th}\\ 0,\hfill & \hfill else.\end{array}\right.$$

(10)

where $R_{th}$ represents the threshold of the communication rate.

2.4. Request Model

In this subsection, we consider ${\pi }_n\left(t\right)$ to represent the request generated by vehicle n at time slot t. We consider that ${\pi }_n\left(t\right)$ can either be a service request or a content request. By denoting $g_{n,d}\left(t\right)=(0, 1)(g_{n,k}\left(t\right)=(0, 1))$ as the indicator of whether service d (content k) is requested by vehicle n at time slot t, we express the constraint on vehicle n’s request as

$$\sum _{d=1}^D{g}_{n,d}\left(t\right)q_n\left(t\right)+\sum _{k=1}^K{g}_{n,k}\left(t\right)(1-q_n\left(t\right))\le 1,\forall n\in \mathcal{N},\forall t\in \mathcal{T},$$

(11)

where $q_n\left(t\right)\in \{0, 1\}$ denotes the indicator of the request type. If $q_n\left(t\right)=1$, ${\pi }_n\left(t\right)$ is a service request. Otherwise, ${\pi }_n\left(t\right)$ is a content request [46].

2.4.1. Content Request

When ${\pi }_n\left(t\right)$ is a content request, i.e., $q_n\left(t\right)=0$. If vehicle n can download the requested content k from a specific UAV u, we consider that the request ${\pi }_n\left(t\right)$ is satisfied. Meanwhile, vehicle n needs to be within the coverage of UAV u, i.e., $x_{u,k}=1$ and $I_{n,u}\left(t\right)=1$. Otherwise, ${\pi }_n\left(t\right)$ is not satisfied.

2.4.2. Service Request

When ${\pi }_n^d\left(t\right)$ is a service request, i.e., $q_n\left(t\right)=1$. To better show this request, we represent ${\pi }_n\left(t\right)$ using a parameter tuple, given by ${\pi }_n^d\left(t\right)=({\xi }_n^d\left(t\right),s_n^d\left(t\right),c_n^d\left(t\right))$, where ${\xi }_n^d\left(t\right)$ represents the d-th service required for computing ${\pi }_n^d\left(t\right)$, $s_n^d\left(t\right)$ represents the task data sizes (in bits), and $c_n^d\left(t\right)$ represents the total number of instructions (in CPU cycles).

Vehicle n can choose to either compute it locally or offload it to the associated UAV that cached the service ${\xi }_n^d\left(t\right)$. We note that vehicle n can offload the computation tasks to UAV u when UAV u is accessible and deployed with the service, i.e., $x_{u,d}\left(t\right)=1$ and $I_{n,u}=1$.

We use $a_{u,n}^d\left(t\right)=0, 1$ to represent whether the computation ${\pi }_n^d\left(t\right)$ is offloaded to UAV u. Therefore, we have

$$\sum _{u=1}^U{a}_{u,n}^d\left(t\right)\le 1,\forall t\in \mathcal{T}.$$

(12)

Note that ${\sum }_{u=1}^U{a}_{u,n}^d\left(t\right)=0$ indicates that task ${\pi }_n^d\left(t\right)$ is computed locally at vehicle n at time slot t. This models the binary offloading decision [38].

For UAV u, it can provide computation services to multiple vehicles satisfying the constraint on its computation capability, represented by the maximum number of services for UAVs, i.e., $Cor{e}^{UAV}$. So, we have the constraint

$$\sum _{n=1}^N\sum _{d=1}^D{a}_{u,n}^d\left(t\right)\le Cor{e}^{UAV},\forall u\in \mathcal{U},\forall t\in \mathcal{T}.$$

(13)

2.5. Performance Metrics

In this section, we will introduce the performance metrics used in this work. First, we define the UAV’s successful transmission probability and then calculate the content caching hit rate, which is defined as the ratio between the number of successfully responded content requests and the total number of content requests from all vehicles.

Let $P_U$ represent the signal transmission power utilized by the UAVs, under the assumption that these UAVs share the spectrum resources with other UAVs, which results in interference from neighboring devices. When a user retrieves cached content from the UAV, the Signal-to-Interference-plus-Noise Ratio (SINR) can be formulated as

$$SIN{R}_{u,n}\left(t\right)={\displaystyle \frac{P_U{h}_{n,u}\left(t\right){\left|g_{n,u}\right|}^2}{I_{other}^u\left(t\right)+{\sigma }^2}},$$

(14)

where ${\sigma }^2$ is the noise power, and $|g_{n,u}{|}^2$ represents the Rayleigh channel gain from UAV u to vehicle n. The interference from other UAVs is represented as

$$I_{other}^u\left(t\right)=\sum _{v=1,v\ne u}^U{P}_U{h}_{n,v}\left(t\right){\left|g_{n,v}\right|}^2.$$

(15)

The probability of successful transmission for vehicle n to receive the requested content through U2V communication is defined as the likelihood that the Signal-to-Interference-plus-Noise Ratio (SINR) of the received signal surpasses the decoding threshold. This is mathematically expressed as $P_{u,n}^{\mathrm{suc}}\left(t\right)=Pr[SIN{R}_{u,n}\ge \theta ]$, where $Pr\left[A\right]$ denotes the probability of event A [47]. When vehicle n successfully retrieves the desired content via U2V communication, the successful transmission probability can be derived as follows.

$$\begin{array}{cc}\hfill P_{u,n}^{suc}\left(t\right)& =Pr\left[SIN{R}_u\left(t\right)\ge \theta \right]\hfill \\ \hfill & =E\left[Pr\left[{\displaystyle \frac{P_U{h}_{n,u}\left(t\right){\left|g_{n,u}\right|}^2}{I_{other}^u\left(t\right)+{\sigma }^2}}\ge \theta \right]\right]\hfill \\ \hfill & \stackrel{\left(\mathrm{a}\right)}{=}{\int }_{Z_u\left(t\right)}^{R_u}Pr\left[{\displaystyle \frac{P_U{\left|g_{n,u}\right|}^2\eta L_{n,u}^{-\zeta }\left(t\right)}{I_{other}^u\left(t\right)+{\sigma }^2}}\ge \theta \right]f_{R_u}\left(r_u\right)d{L}_{n,u}\left(t\right)\hfill \\ \hfill & ={\int }_{Z_u\left(t\right)}^{R_u}Pr\left[|g_{n,u}{|}^2\ge {\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right)(I_{other}^u\left(t\right)+{\sigma }^2)}{P_U\eta }}\right]f_{R_u}\left(L_{n,u}\left(t\right)\right)d{L}_{n,u}\left(t\right)\hfill \\ \hfill & ={\int }_{Z_u\left(t\right)}^{R_u}exp\{-{\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right){\sigma }^2}{P_U\eta }}\}{E}_{I_{other}^u\left(t\right)}\left[exp\left\{-{\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right)I_{other}^u\left(t\right)}{P_U\eta }}\right\}\right]f_{R_u}\left(L_{n,u}\left(t\right)\right)d{L}_{n,u}\left(t\right)\hfill \\ \hfill & ={\int }_{Z_u\left(t\right)}^{R_u}exp\{-{\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right){\sigma }^2}{P_U\eta }}\}{L}_{I_{other}^u\left(t\right)}\left({\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right)}{P_U\eta }}\right)f_{R_u}\left(L_{n,u}\left(t\right)\right)d{L}_{n,u}\left(t\right)\hfill \end{array}$$

(16)

wherein step $\left(\mathrm{a}\right)$ is derived based on the formula $E\left[\chi \right]={\int }_0^{\infty }Pr(\chi >x)dx$. The power gain $|g_{n,u}{|}^2$ of a Rayleigh fading channel follows an exponential distribution. For an exponentially distributed random variable X with rate parameter ${\lambda }^{\prime }$, the probability $P(X\ge x)$ is given by $e^{-{\lambda }^{\prime }x}$. In this context, we assume a unit mean for $|g_{n,u}{|}^2$, which implies ${\lambda }^{\prime }=1$. Therefore, by letting $X_{\mathrm{threshold}}={\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right)(I_{other}^u\left(t\right)+{\sigma }^2)}{P_U{\eta }_0}}$, the probability $Pr\left[\right|g_{n,u}{|}^2\ge X_{\mathrm{threshold}}]$ is transformed to $exp\{-X_{\mathrm{threshold}}\}$. $R_u$ represents the max communication distance between the UAV and vehicle and $f_{R_u}\left(L_{n,u}\left(t\right)\right)$ is the probability density function (PDF) of the distance from the UAV to the requesting vehicle, expressed as

$$f_{R_u}\left(L_{n,u}\left(t\right)\right)=\left\{\begin{array}{cc}{\displaystyle \frac{L_{n,u}\left(t\right)}{R_u^2}},\hfill & L_{n,u}\left(t\right)\in \left[0,R_u\right],\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(17)

Let $z={\displaystyle \frac{\theta L_{n,u}^{\zeta }\left(t\right)}{P_U\eta }}$, then the Laplace transform $L_{I_{other}^u\left(t\right)}\left(z\right)$ of interference $I_{other}^u\left(t\right)$ is derived by using the properties of stochastic geometry as follows [48].

$$\begin{array}{cc}\hfill & L_{I_{other}^u\left(t\right)}\left(z\right)\hfill \\ \hfill & =exp\left\{-2\pi {\lambda }_u{\int }_0^{\infty }[1-\right.\hfill \\ \hfill & \left.\left.E_{|h_{n,u}{|}^2}\left(exp\left(-z{P}_u{\left|h_{n,u}\right|}^2{x}^{-\zeta }\right)\right)\right]xdx\right\}\hfill \\ \hfill & =exp\left\{-2\pi {\lambda }_u{\int }_0^{\infty }\left[1-{\displaystyle \frac{1}{1+\frac{\theta L_{n,u}{\left(t\right)}^{-\zeta }{P}_U{x}^{-\zeta }}{P_U\eta }}}\right]xdx\right\}\hfill \\ \hfill & =exp\left\{-2\pi {\lambda }_u{\int }_0^{\infty }\left[{\displaystyle \frac{\theta r_u^{\zeta }{P}_U}{\theta L_{n,u}^{-\zeta }\left(t\right)P_U+P_U\eta x^{\zeta }}}\right]xdx\right\}\hfill \\ \hfill & =exp\left\{-\pi {\lambda }_u{\int }_0^{\infty }\left[{\displaystyle \frac{1}{1+{\left(\frac{\theta }{\beta }\right)}^{-1}{L}_{n,u}^{-\zeta }\left(t\right)x^{\zeta }}}\right]d{x}^2\right\}\hfill \end{array}$$

(18)

Let $\delta ={\left({\displaystyle \frac{\theta }{\eta }}\right)}^{-1}{L}_{n,u}^{-\zeta }\left(t\right)x^{\zeta }$, then we have

$$\begin{array}{cc}\hfill & L_{I_{other}^u\left(t\right)}\left(z\right)\hfill \\ \hfill & =exp\left[-\pi {\lambda }_u{\left({\displaystyle \frac{\theta }{\eta }}\right)}^{{\displaystyle \frac{2}{\zeta }}}{L}_{n,u}^2\left(t\right){\int }_0^{\infty }\left[{\displaystyle \frac{1}{1+{\delta }^{\frac{\zeta }{2}}}}\right]dt\right]\hfill \\ \hfill & =exp\left[-\pi {\lambda }_s{\left({\displaystyle \frac{\theta }{\eta }}\right)}^{{\displaystyle \frac{2}{\zeta }}}{L}_{n,u}^2\left(t\right)G_{\zeta }\left(0\right)\right],\hfill \end{array}$$

(19)

where $G_{\zeta }\left(x\right)={\int }_x^{\infty }{\displaystyle \frac{1}{1+{\delta }^{\frac{\pi }{2}}}}dt$. Then, by substituting (24) and (26) into (23), the expression for the successful transmission probability can be obtained as follows

$$P_{u,n}^{suc}\left(t\right)={\int }_{Z_u\left(t\right)}^{R_u}exp\left[-\pi {\lambda }_u{\left({\displaystyle \frac{\theta }{\eta }}\right)}^{{\displaystyle \frac{2}{\zeta }}}{L}_{n,u}^2\left(t\right)G_{\zeta }\left(0\right)\right]{\displaystyle \frac{L_{n,u}\left(t\right)}{R_u^2}}d{L}_{n,u}\left(t\right)$$

(20)

Mathematically, the content cache hit ratio can be expressed as

$$P{r}_h\left(t\right)={\displaystyle \frac{{\sum }_{n=1}^{N}min\{1,{\sum }_{u=1}^U{\sum }_{k=1}^K{P}_{u,n}^{suc}\left(t\right)(1-q_n\left(t\right))g_{n,k}\left(t\right)x_{n,k}\left(t\right)\}}{{\sum }_{n=1}^N(1-q_n\left(t\right))}}$$

(21)

This metric quantifies the effectiveness of the caching strategy [49].

2.5.1. Local Computation

When ${\sum }_{u=1}^U{a}_{u,n}\left(t\right)=0$, tasks ${\pi }_n^d\left(t\right)$ will be computed locally at vehicle n. The computation delay of task ${\pi }_n\left(t\right)$ is expressed as

$$T_n^{\mathrm{comp}}\left(t\right)={\displaystyle \frac{c_n^d\left(t\right)}{f_n}},$$

(22)

where $f_n$ is the total computation resource of vehicle n. Local computation serves as a baseline option for task execution [50].

2.5.2. UAV’s Computation

When $a_{u,n}\left(t\right)=1$, tasks ${\pi }_n\left(t\right)$ will be offloaded to UAV u. At each time slot t, the UAV u needs to process multiple tasks from vehicles within its coverage area simultaneously. However, due to the limited computation resources of UAVs, UAVs must efficiently allocate a portion of their computation resources to each task. Then, the computation delay of task ${\pi }_n\left(t\right)$ processed by UAV u is expressed as

$$T_{n,u}^{\mathrm{comp}}\left(t\right)={\displaystyle \frac{c_n^d\left(t\right)}{f_u}},$$

(23)

where $f_u$ is the total computation resource of UAV u. This delay depends on the UAV’s processing capacity [38].

Employing the dynamic voltage and frequency scaling technique at the UAV, the energy consumption for computation at the u-th UAV at the time slot t is

$$E_u^{\mathrm{comp}}\left(t\right)=\sum _{n=1}^N{\beta }_u{f}_u^3{T}_{n,u}^{\mathrm{comp}}\left(t\right),$$

(24)

where ${\beta }_u$ represents the computation energy efficiency coefficient related to the processor’s chip of the u-th UAV [51].

In addition to minimizing task latency and energy consumption, we also want to achieve fair task allocation among multiple UAVs to avoid situations where some UAVs are overloaded while others are underloaded. Jain’s Fairness Index (JFI) is commonly used to measure the fairness of resource allocation, so we include it in our optimization objective. JFI is a standard metric for evaluating fairness in resource allocation problems [52]. $P_{Fair}\left(t\right)$ is Jain’s fairness index, which is calculated as follows:

$$P_{\mathrm{Fair}}\left(t\right)={\displaystyle \frac{{\left({\sum }_{u=1}^U{\sum }_{n=1}^N{a}_{u,n}\left(t\right)\right)}^2}{U{\sum }_{u=1}^U{\left({\sum }_{n=1}^N{a}_{u,n}\left(t\right)\right)}^2}},$$

(25)

2.6. Problem Formulation

In this section, an optimization problem is formulated to minimize the maximum task latency among all vehicles, subject to the constraints of communication rate, UAV energy consumption, and memory capacity.

Based on (9) and (23), if the task ${\pi }_n\left(t\right)$ of vehicle n is offloaded to UAV u at time slot t, its overall processing delay is given by:

$$\begin{array}{cc}\hfill T_n^{\mathrm{UAV}}\left(t\right)=& \sum _{u=1}^U{a}_{u,n}\left(t\right)(T_{n,u}^{\mathrm{comm}}\left(t\right)+T_{n,u}^{\mathrm{comp}}\left(t\right)),\forall n\in \mathcal{N},\hfill \end{array}$$

(26)

Therefore, based on (22) and (26), at the time slot t, the total delay of processing task ${\pi }_n\left(t\right)$ from vehicle n is expressed by:

$$\begin{array}{cc}\hfill T_n\left(t\right)=& T_n^{\mathrm{UAV}}\left(t\right)+(1-\sum _{u=1}^U{a}_{u,n}\left(t\right))T_n^{\mathrm{comp}}\left(t\right),\hfill \\ \hfill & \forall n\in \mathcal{N},\forall t\in \mathcal{T},\hfill \end{array}$$

(27)

This combines the local and offloaded computation delays [45].

Based on (4) and (24), the total energy consumption of the u-th UAV at the time slot t can be given as:

$$E_u^{\mathrm{UAV}}\left(t\right)=E_u^{\mathrm{comp}}\left(t\right)+\kappa E_u^{\mathrm{fly}}\left(t\right),$$

(28)

where $\kappa$ is the energy regulation factor balancing the magnitude disparity between computation and propulsion energy costs [25].

We define the system efficiency for the system at time slot t, denoted as $SE\left(t\right)$. This is a comprehensive metric designed to balance the content cache hit rate, task computation performance, system energy consumption, and resource allocation fairness. Its formula is as follows:

$$SE\left(t\right)={\displaystyle \frac{{\mathrm{Pr}}_h\left(t\right)}{{\sum }_{n=1}^N{T}_n\left(t\right)}}-w_1\sum _{u=1}^U{E}_u^{\mathrm{UAV}}\left(t\right)+w_2{P}_{Fair}\left(t\right)$$

(29)

We jointly optimize the service placement decision ${\mathbf{X}}_{\mathbf{d}}={\left[x_{u,d}\left(t\right)\right]}_{u\in \mathcal{U},d\in \mathcal{D}}$, the content cache decision ${\mathbf{X}}_{\mathbf{k}}={\left[x_{u,k}\left(t\right)\right]}_{u\in \mathcal{U},k\in \mathcal{K}}$, the vehicle task offloading decision $\mathbf{A}={\left[a_{u,n}\left(t\right)\right]}_{u\in \mathcal{U},n\in \mathcal{N}}$, and the locations of UAVs ${\mathbf{L}}_{\mathbf{u}}={\left[{\mathbf{l}}_{\mathbf{u}}\left(t\right)\right]}_{u\in \mathcal{U}}$.

To sum up, the optimization problem can be formulated as:

$$\begin{array}{cc}\hfill \underset{{\mathbf{X}}_{\mathbf{d}},{\mathbf{X}}_{\mathbf{k}},\mathbf{A},{\mathbf{L}}_{\mathbf{u}}}{max}& \sum _{t=1}^{T}SE\left(t\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\end{array}$$

(30)

$$\begin{array}{cc}\hfill \mathrm{C}1:& \sum _{d\in \mathcal{D}}{x}_{u,d}\left(t\right)s_d+\sum _{k\in \mathcal{K}}{x}_{u,k}\left(t\right)s_k\le Q_u,\forall u\in \mathcal{U},\forall t\in T,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \mathrm{C}2:& \begin{array}{cc}\hfill a_{u,n}\left(t\right)& \in \{0,1\},x_{u,d}\left(t\right)\in \{0,1\},x_{u,k}\left(t\right)\in \{0,1\},\hfill \\ \hfill & \forall n\in \mathcal{N},\forall u\in \mathcal{U},\forall d\in \mathcal{D},\forall k\in \mathcal{K},\forall t\in \mathcal{T}\hfill \end{array}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \mathrm{C}3:& \sum _{t=1}^T{E}_u^{\mathrm{UAV}}\left(t\right)\le E^{\max },\forall u\in \mathcal{U},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill \mathrm{C}4:& \parallel l_u\left(t\right)-l_v\left(t\right)\parallel \ge d_{\min },u\ne v,\forall u,v\in \mathcal{U},\forall t\in \mathcal{T},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \mathrm{C}5:& H_{\min }\le Z_u\left(t\right)\le H_{\max },\forall u\in \mathcal{U},\forall t\in \mathcal{T},\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill \mathrm{C}6:& \sum _{n=1}^N\sum _{d=1}^D{a}_{u,n}^d\left(t\right)\le Cor{e}^{UAV},\forall u\in \mathcal{U},\forall t\in \mathcal{T},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \mathrm{C}7:& \sum _{u=1}^U{a}_{u,n}^d\left(t\right)\le 1,\forall t\in \mathcal{T},\hfill \end{array}$$

(37)

where $w_1$ and $w_2$ are the weights for energy consumption and fairness, respectively.

C1 limits the total cached data size for UAV u at time t within its storage capacity $Q_u$. C2 enforces binary offloading and caching decisions for $a_{u,n}\left(t\right)$, $x_{u,d}\left(t\right)$, and $x_{u,k}\left(t\right)$. C3 restricts UAV u’s total energy consumption to not exceed $E^{\max }$. C4 ensures the minimum safe distance $d_{\min }$ between any two UAVs. Finally, C5 constrains UAV u’s flight altitude between $H_{\min }$ and $H_{\max }$. C6 limits the maximum number of tasks that can be processed by a single UAV u at time slot t to $Cor{e}^{UAV}$ [53]. C7 ensures that for each vehicle n, its task is offloaded to at most one UAV u at any given time slot t.

3. MAPPO-Based Joint Caching and Computation Offloading Scheme

To effectively address the joint caching and computation offloading optimization problem, this paper adopts a Multi-Agent Deep Reinforcement Learning (MADRL) algorithm. Traditional optimization methods face significant challenges when dealing with complex Mixed-Integer Nonlinear Programming (MINLP) problems, such as high computational complexity, lack of real-time applicability, and sensitivity to model parameters. Deep reinforcement learning, on the other hand, can significantly reduce online computation through offline training and adapt to dynamic environments with uncertainty [54]. Particularly for objectives that are difficult to model explicitly, such as minimizing system latency, MADRL enables efficient and robust optimization by learning the interactions and cooperation among multiple agents. To better implement the MADRL algorithm, we build it upon a Dec-POMDP framework, which will be described in detail below. Dec-POMDPs are suitable for modeling scenarios with multiple agents and partial observations [55].

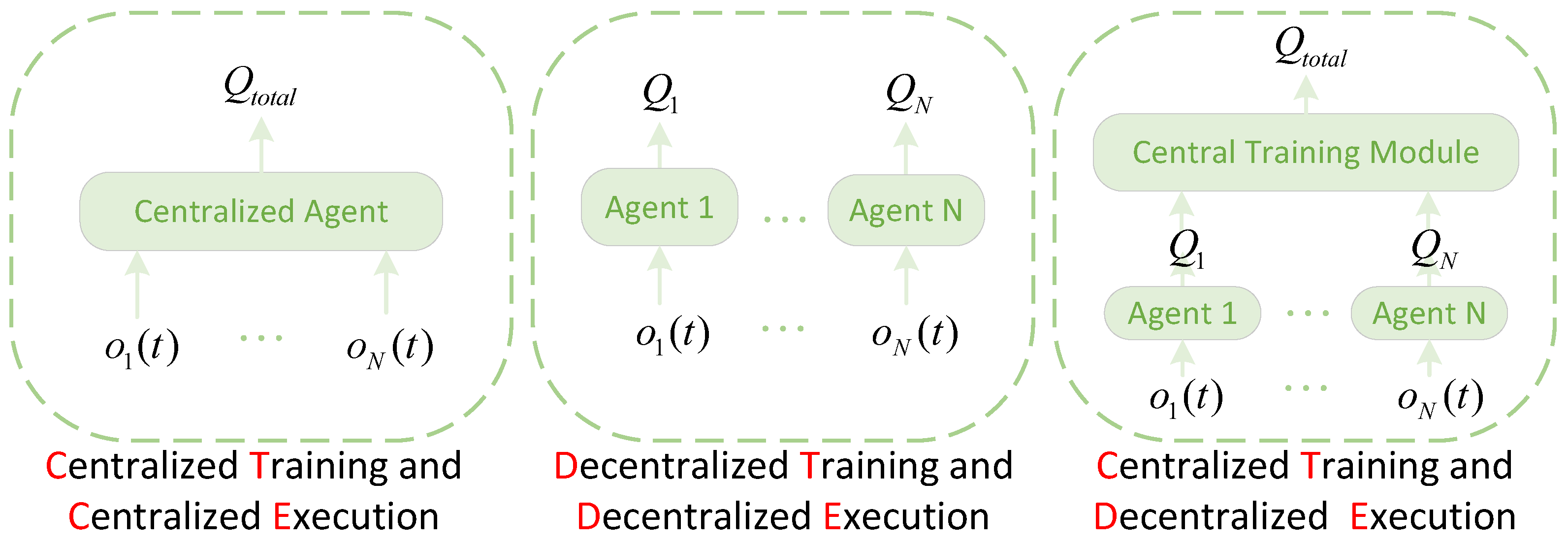
In Multi-Agent Reinforcement Learning (MADRL), various training and execution paradigms exist, as illustrated in Figure 3. These paradigms primarily differ in whether agents share information or have a centralized coordinator during the training phase, and whether agents act independently or are controlled by a central entity during the execution phase. Common paradigms include: Centralized Training Centralized Execution (CTCE), Decentralized Training Decentralized Execution (DTDE), and CTDE, which combines the advantages of both training and execution. CTCE is suitable for scenarios with high agent cooperation and fully observable environments, but centralized execution has poor robustness and is difficult to scale to large-scale systems. DTDE emphasizes agent independence, resulting in simple and robust execution, but agents face a non-stationary environment during training, making it difficult to guarantee convergence and optimality. The CTDE paradigm allows the use of global information or centralized coordination during the training phase to stabilize the learning process, while in the execution phase, each agent makes decisions independently based on its local observations. This approach balances training efficiency with the flexibility and robustness of decentralized execution, making it particularly suitable for dynamic and partially observable distributed environments like vehicular networks.

3.1. Dec-POMDP Framework

Based on the MADRL algorithm introduced earlier, we build it upon a Dec-POMDP framework to address the joint caching and computation offloading optimization problem. This framework empowers individual agents (UAVs and vehicles) to make decentralized decisions in a dynamic IoV environment with partial state observability. Agents learn through interactions with the environment, adapting their actions to optimize collective behavior and maximize service efficiency, defined as the ratio of the cache hit rate to the total task processing delay.

The Dec-POMDP framework is formally defined as a tuple $\langle \mathcal{S},\mathcal{A},\mathcal{R},\mathcal{P},\mathcal{O},\mathcal{Z},\gamma \rangle$, where $\mathcal{S}$ is the global state space; $\mathcal{O}$ is the observation space; $\mathcal{Z}\left(o\left(t\right)\right|s\left(t\right)):S\to O$ denotes the mapping from global state $s\left(t\right)\in S$ to observation $o\left(t\right)\in O$; $\mathcal{A}$ is the action space; $\mathcal{P}$ is the transition probability distribution of the global state transition $P\left(s\right(t+1\left)\right|s\left(t\right),a\left(t\right))$: $\mathcal{S}\times \mathcal{A}\to \mathcal{S}$ and $a\left(t\right)\in \mathcal{A}$; $\mathcal{R}$ is the instantaneous reward $\mathcal{R}\left(r\right(t\left)\right|s\left(t\right),a\left(t\right))$: $\mathcal{S}\times \mathcal{A}\to \mathcal{R}$; and $\mathcal{S}\times \mathcal{A}\to \mathcal{S}$ is the discount factor.

Assume that there is no global information exchange and each unit (UAV and vehicle) can only obtain its direct information. Then, we can obtain the state space, action space, and reward as follows.

Observation (O):

$$\begin{array}{cc}\hfill \mathcal{O}=\{& o_1^{UAV}\left(t\right),o_2^{UAV}\left(t\right),\dots ,o_u^{UAV}\left(t\right),\dots ,o_U^{UAV}\left(t\right),\hfill \\ \hfill & o_1^{Vehicle}\left(t\right),o_2^{Vehicle}\left(t\right),\dots ,o_n^{Vehicle}\left(t\right),\dots ,o_N^{Vehicle}\left(t\right)\}\hfill \end{array}$$

(38)

The observation of UAV u, $o_u^U\left(t\right)$, contains the location of the UAV u, the coverage range of the UAV u, the remaining energy of the UAV u, and the remaining caching space, i.e.,

$$o_u^U\left(t\right)=\{{\mathbf{l}}_{\mathbf{u}}\left(t\right),{\mathbf{I}}_u\left(t\right),E_u\left(t\right),C_u\left(t\right)\},u\in \mathcal{U}$$

(39)

where ${\mathbf{I}}_u\left(t\right)=\{I_{1,u}\left(t\right),\dots ,I_{n,u}\left(t\right),\dots ,I_{N,u}\left(t\right)\}$, $C_u\left(t\right)=Q_u-({\sum }_{d\in D}{x}_{u,d}\left(t\right)s_d+{\sum }_{k\in K}{x}_{u,k}\left(t\right)s_k)$, and $E_u\left(t\right)=E^{\max }-{\sum }_{t^{\prime }=1}^t{E}_u^{\mathrm{UAV}}\left(t^{\prime }\right)$. Partial observations are typical in decentralized MADRL [56].

The observation of vehicle n, $o_n^N\left(t\right)$, contains its location, i.e.,

$$o_n^N\left(t\right)=\left\{{\mathbf{l}}_{\mathbf{n}}\left(t\right)\right\},n\in \mathcal{N}$$

(40)

Action Space ($\mathcal{A}$): The action space of the UAV u contains the cache decision of the UAV u and the location of the UAV u, i.e.,

$$a_u\left(t\right)=\{{\mathbf{X}}_u\left(t\right),{\mathbf{l}}_{\mathbf{u}}\left(t\right)\}$$

(41)

where ${\mathbf{X}}_u\left(t\right)={\left[{\mathbf{x}}_{u,d}\left(t\right),{\mathbf{x}}_{u,k}\left(t\right)\right]}_{d\in \mathcal{D},k\in \mathcal{K}}$ denotes the caching decision vector of UAV u, and ${\mathbf{l}}_{\mathbf{u}}\left(t\right)=(X_u\left(t\right),Y_u\left(t\right),Z_u\left(t\right))$ represents the location of UAV u at time slot t, and to satisfy the altitude constraint (35), the vertical coordinate must obey $H_{min}\le Z_u\left(t\right)\le H_{max}$.

The action space of vehicle n contains its offloading decision, i.e.,

$$a_n\left(t\right)=\left\{{\mathbf{A}}_n\left(t\right)\right\}$$

(42)

where ${\mathbf{A}}_n\left(t\right)={\left\{a_{u,n}\left(t\right)\right\}}_{u\in \mathcal{U}}$.

Reward Function ($\mathcal{R}$): The reward function $R(s,a)$ quantifies the immediate reward obtained by all agents after taking joint action a in state s. We aim to maximize the system efficiency, defined as below.

The service coefficient related reward $r_1\left(t\right)$ is defined as

$$r_1\left(t\right)={\displaystyle \frac{P{r}_h\left(t\right)}{{\sum }_{n=1}^N{T}_n\left(t\right)}}$$

(43)

The UAV energy consumption and minimum safe distance related reward $r_{2,u}\left(t\right)$ is defined as

$$r_{2,u}\left(t\right)=\left\{\begin{array}{cc}-E_u^{\mathrm{UAV}}\left(t\right),\hfill & \hfill \mathrm{if}\left(33\right)\mathrm{and}\left(34\right)\mathrm{is}\mathrm{satisfied},\\ -\infty ,\hfill & \hfill \mathrm{else}\end{array}\right.$$

(44)

The total energy consumption related reward $r_2\left(t\right)$ is the sum of these individual rewards across all UAVs U.

$$r_2\left(t\right)=\sum _{u=1}^U{r}_{2,u}\left(t\right)$$

(45)

The remaining caching space-related reward $r_{3,u}\left(t\right)$ is defined as

$$r_{3,u}\left(t\right)=\left\{\begin{array}{cc}\sum _{d\in \mathcal{D}}{x}_{u,d}\left(t\right)s_d+\sum _{k\in \mathcal{K}}{x}_{u,k}\left(t\right)s_k,\hfill & \hfill \mathrm{if}\left(31\right)\mathrm{is}\mathrm{satisfied},\\ -\infty ,\hfill & \hfill \mathrm{else}\end{array}\right.$$

(46)

The total remaining caching space reward $r_3\left(t\right)$ is the sum of $r_{3,u}\left(t\right)$ over all UAVs U.

$$r_3\left(t\right)=\sum _{u=1}^U{r}_{3,u}\left(t\right)$$

(47)

The remaining computation core-related reward $r_{4,u}\left(t\right)$ is defined as

$$r_{4,u}\left(t\right)=\left\{\begin{array}{cc}\sum _{n=1}^N\sum _{d=1}^D{a}_{u,n}\left(t\right),\hfill & \hfill \mathrm{if}\left(37\right)\mathrm{is}\mathrm{satisfied},\\ -\infty ,\hfill & \hfill \mathrm{else}\end{array}\right.$$

(48)

The total remaining cores reward $r_4\left(t\right)$ is the sum of $r_{4,u}\left(t\right)$ over all UAVs U.

$$r_4\left(t\right)=\sum _{u=1}^U{r}_{4,u}\left(t\right)$$

(49)

The fairness related reward is defined as

$$r_5\left(t\right)={\displaystyle \frac{{\left({\sum }_{u=1}^U{\sum }_{n=1}^N{a}_{u,n}\left(t\right)\right)}^2}{U{\sum }_{u=1}^U{\left({\sum }_{n=1}^N{a}_{u,n}\left(t\right)\right)}^2}}$$

(50)

The overall reward function $R\left(t\right)$ at time slot t is a composite value that combines the aforementioned components. It is defined as

$$R\left(t\right)=r_1\left(t\right)+{\lambda }_E{r}_2\left(t\right)+{\lambda }_Q{r}_3\left(t\right)+{\lambda }_C{r}_4\left(t\right)+{\lambda }_F{r}_5\left(t\right)$$

(51)

where ${\lambda }_E$, ${\lambda }_Q$, ${\lambda }_C$, and ${\lambda }_F$ are positive weighting coefficients that balance the relative importance of UAV energy consumption, remaining cache capacity, available computation cores, and task allocation fairness in the overall optimization objective, respectively. These weights are hyperparameters tuned to achieve the desired trade-offs among the different performance metrics [54].

3.2. MAPPO-Based DRL Training Framework

The Dec-POMDP structure is realized through a multi-agent deep reinforcement learning (MADRL) methodology. Within this framework, each agent independently learns its operational policy aiming to maximize its expected cumulative return based on its own partial observations. Agents engage with the environment, carry out actions derived from their acquired policies, receive feedback in the form of rewards, and iteratively refine their strategies via a learning algorithm. This centralized learning approach facilitates the agents’ ability to adapt effectively to dynamic environmental shifts and to optimize their collective performance collaboratively. MAPPO is a popular on-policy MADRL algorithm known for its stability [6].

The proposed MAPPO-based joint optimization strategy utilizes a CTDE paradigm, whose comprehensive diagram is depicted in Figure 4. Under this paradigm, agents (comprising UAVs and vehicles) transmit their respective local observed data to a central training entity during the learning phase. This entity is tasked with aggregating observations and actions from all participating agents, calculating the global reward signal, and coordinating the policy adjustment process for the agents. Specifically, each agent possesses its distinct Actor network and Critic network. The Actor network generates potential action distributions based on the agent’s specific local observations, serving to guide agent behavior during the operational phase. The Critic network functions as a centralized value estimator that accepts the local observations of all agents (which are first processed by state encoders and multi-head attention modules) to evaluate the utility of the collective actions taken by the agents within the current global state, thereby supplying a value-based corrective signal for the Actor network’s training. State encoders are employed to transform raw observational inputs into condensed, low-dimensional feature representations, while multi-head attention mechanisms are utilized to capture the intricate interdependencies and interactive dynamics among agents, assisting the Critic network in forming a more precise assessment of the global state’s value. During the training period, the central module leverages comprehensive global information (like the positions, caching statuses, and task states of all agents) to train the Critic network; it then uses the advantage measure derived from the Critic network to direct the policy gradient updates of the individual, decentralized Actor networks. During the actual deployment phase, each agent relies solely on its local observations and its trained Actor network to make decisions, eliminating the need for centralized coordination, which boosts the system’s responsiveness and resilience. The detailed steps of the proposed MAPPO-based training framework are outlined in Algorithm 1.

Algorithm 1: MAPPO-based joint caching and computation offloading training framework

We advocate employing the MAPPO algorithm to refine the policies within our established framework. In this setup, the actor network, parameterized by ${\theta }_v$, produces action choices guided by the policy ${\pi }_v\left(a\left(t\right)\right|s\left(t\right);{\theta }_v)$; this policy corresponds to the v-th agent type and can be shared across agents of the same category. The critic network, parameterized by ${\omega }_v$, appraises the merit of these actions based on the received reward $R\left(t\right)$ and the state $s\left(t\right)$ [55].

To facilitate implementation in distributed network environments, we adopt a framework involving centralized training and decentralized execution, as illustrated in Figure 4. This architecture is designed to ensure robust overall system performance while preserving the decision-making autonomy of each individual agent. It is important to note that during the centralized training procedure, calculating rewards independently at each vehicle or UAV is challenging. Consequently, the involvement of a training hub is necessary; this hub centrally collects all observations and actions to compute the rewards. Concurrently, this training hub integrates the collected observations into a unified global state representation, which is then conveyed to the critic network associated with each agent. Subsequently, the critic network formulates the state–value function, formally defined as:

$$\begin{array}{cc}\hfill V_v{\left(t\right)}^{\pi }(s\left(t\right),{\theta }_v)& ={\mathbb{E}}_{a\left(t\right)\sim {\pi }_v\left(a\left(t\right)\right|s\left(t\right);{\theta }_v)}[R\left(s\left(t\right)\right|a\left(t\right)),{\pi }_v]\hfill \\ \hfill & ={\mathbb{E}}_{a\left(t\right)\sim {\pi }_v\left(a\left(t\right)\right|s\left(t\right);{\theta }_v)}\left[\sum _{i=0}^{\infty }{\gamma }_v^{i}R\left(s(t+i)\right|a(t+i))|s\left(t\right),{\pi }_v\right],\hfill \end{array}$$

(52)

Here, $\mathbb{E}[·]$ signifies the expectation operator, $R\left(s\right(t\left)\right|a\left(t\right))$ represents the reward function for agent i belonging to the u-th agent type, ${\gamma }_v$ serves as the reward discount factor, and ${\pi }_v\left(a\left(t\right)\right|s\left(t\right);{\theta }_v)$ denotes the collective policy employed by all agents.

As derived from (52), the state–value function $V_v{\left(t\right)}^{\pi }(s\left(t\right),{\theta }_v)$ is influenced by both the prevailing state $s\left(t\right)$ and the parameters ${\theta }_v$ of the policy network ${\pi }_v$. Specifically, as the state $s\left(t\right)$ improves or becomes more favorable, the value $V_v{\left(t\right)}^{\pi }$ increases, signaling higher anticipated future returns. Similarly, when the policy ${\pi }_v$, characterized by parameters ${\theta }_v$, demonstrates enhanced performance, the value $V_v{\left(t\right)}^{\pi }$ also rises. If a policy ${\pi }_v$ consistently achieves exceptional outcomes across all relevant states $s\left(t\right)$ within the same time step, the averaged value of the state–value function $V_v{\left(t\right)}^{\pi }$ is expected to be notably elevated. Consequently, we define the optimization objective for the actor network as:

$$P\left({\theta }_v\right)={\mathbb{E}}_{s\left(t\right)}\left[V_v{\left(t\right)}^{\pi }(s\left(t\right),{\theta }_v)\right],$$

(53)

This objective function is independent of the specific state $s\left(t\right)$ and depends solely on the parameter set ${\theta }_v$.

We modify the parameters ${\theta }_v$ of the policy network using a gradient ascent approach, seeking to maximize the objective function. Let ${\theta }_v^{\mathrm{now}}$ indicate the current parameter values of the policy network; following a gradient ascent update step, the refined parameters ${\theta }_v^{\mathrm{new}}$ are obtained via:

$${\theta }_v^{\mathrm{new}}\leftarrow {\theta }_v^{\mathrm{now}}+\psi {\nabla }_{{\theta }_v}P\left({\theta }_v^{\mathrm{now}}\right),$$

(54)

where $\psi$ is the learning rate for the actor network, and the gradient ${\nabla }_{{\theta }_v}P\left({\theta }_v^{\mathrm{now}}\right)$ can be expressed as:

$$\begin{array}{cc}\hfill {\nabla }_{{\theta }_v}P\left({\theta }_v^{\mathrm{now}}\right)=& {\left.{\displaystyle \frac{\partial P\left(\theta \right)}{\partial \theta }}\right|}_{\theta ={\theta }_v^{\mathrm{now}}}\hfill \\ \hfill & ={\mathbb{E}}_{s\left(t\right),a\left(t\right)\sim {\pi }_v\left(a\left(t\right)\mid s\left(t\right);{\theta }_v\right)}\left[{\nabla }_{{\theta }_v}ln\left({\pi }_v\left(a\left(t\right)\mid s\left(t\right);{\theta }_v\right)\right)\right.\hfill \\ \hfill & \left.\sum _{l=1}^{\infty }{\left({\gamma }_v\lambda \right)}^l\left(Q_{v,u}^{\pi }\left(s\left(t\right);a\left(t\right)\right)-V_{v,u}^{\pi }\left(s\left(t\right),{\theta }_v\right)\right)\right]\hfill \end{array}$$

(55)

Here, $\lambda$ is a coefficient that balances the trade-off between bias and variance in the estimation. The action–value function is defined as $Q_{v,u}^{\pi }\left(s\left(t\right);a\left(t\right)\right)$, formulated as:

$$Q_{v,u}^{\pi }\left(s\left(t\right);a\left(t\right)\right)=\mathbb{E}\left[\sum _{i=1}^{\infty }{\gamma }_v^i{\mathcal{R}}_{v,u}\left(s_{t+i},a_{t+i}\right)\mid s\left(t\right)=s,a\left(t\right)=a,{\pi }_v\right]$$

(56)

To effectively gauge the comparative advantage of a specific action and concurrently mitigate variance and bias during the learning phase, we employ generalized advantage estimation (GAE) as a substitute for the advantage function-like term appearing in (53), in a manner that preserves generality. This approach bears resemblance to the use of surrogate objective functions and importance sampling techniques in conventional policy optimization methods. The policy gradient can thus be reformulated as:

$$\begin{array}{cc}\hfill {\nabla }_{{\theta }_v}P\left({\theta }_v^{\mathrm{now}}\right)=& {\mathbb{E}}_{s\left(t\right),a\left(t\right)\sim {\pi }_v\left(a\left(t\right)\mid s\left(t\right);{\theta }_v\right)}\left[{\displaystyle \frac{{\pi }_{{\theta }_v^{mov}}\left(a\left(t\right)\mid s\left(t\right)\right)}{{\pi }_{{\theta }_{v}error}\left(a\left(t\right)\mid s\left(t\right)\right)}}\right.\hfill \\ \hfill & \left.{\nabla }_{{\theta }_v}ln\left({\pi }_v\left(a\left(t\right)\mid s\left(t\right);{\theta }_v\right)\right)\widehat{A}\left(s\left(t\right)\right)\right]\hfill \end{array}$$

(57)

where $\widehat{A}\left(s\left(t\right)\right)={\sum }_{l=1}^{\infty }{\left({\gamma }_v\lambda \right)}^l\left(r_n+{\gamma }_v{V}_v\left(s_{t+i+1}\right)-V_v\left(s\left(t\right)\right)\right)$.

Furthermore, to constrain the magnitude of policy updates and thereby preclude excessive optimization steps that could compromise stability [57], we incorporate a clipping mechanism. The clip function serves to bind the ratio between the probabilities assigned by the new and old policies, ensuring that policy adjustments remain within an acceptable range. The definition of the clip function is given by:

$$clip(x,1-\varsigma ,1+\varsigma )=\left\{\begin{array}{cc}1+\varsigma ,\hfill & \hfill \mathrm{if}x>1+\varsigma \\ x,\hfill & \hfill \mathrm{if}1-\varsigma \le x\le 1+\varsigma \\ 1-\varsigma ,\hfill & \hfill \mathrm{if}x<1-\varsigma \end{array}\right.$$

(58)

Here, $\varsigma$ acts as a regularization parameter. Drawing upon concepts from (51), (55), and (56), we introduce $\psi S_{t,u}$ to represent the policy entropy of the state. Consequently, the objective function for the actor network, which now incorporates the clip function, can be formulated as:

$$\begin{array}{cc}\hfill P\left({\theta }_v\right)={\mathbb{E}}_{s\left(t\right)}& \left[min\left[clip\left({\displaystyle \frac{{\pi }_{{\theta }_v^{mov}}\left(a\left(t\right)\mid s\left(t\right)\right)}{{\pi }_{{\theta }_v^{now}}\left(a\left(t\right)\mid s\left(t\right)\right)}},1-ϵ,1+ϵ\right)\widehat{A}\left(s\left(t\right)\right),\right.\right.\hfill \\ \hfill & \left.\left.{\displaystyle \frac{{\pi }_{{\theta }_v^{mow}}\left(a\left(t\right)\mid s\left(t\right)\right)}{{\pi }_{{\theta }_v^{mow}}\left(a\left(t\right)\mid s\left(t\right)\right)}}\widehat{A}\left(s\left(t\right)\right)\right]+\psi S_{t,v}\right].\hfill \end{array}$$

(59)

In parallel, to update the critic network, which functions as a value estimator employed to evaluate the effectiveness of the actor network’s policies, we specify its loss function as:

$$P\left({\omega }_v\right)={\mathbb{E}}_{s\left(t\right),a\left(t\right)}\left[{\left((1-\gamma )\mathcal{R}\left(s\left(t\right)\mid a\left(t\right)\right)+\gamma {\widehat{V}}_{{\omega }_v}\left(s(t+1)\right)-V_{{\omega }_v}\left(s\left(t\right)\right)\right)}^2\right]$$

(60)

Here, $V_{{\omega }_v}\left(s\left(t\right)\right)$ denotes the approximation of the state–value function produced by the value network with parameters ${\omega }_v$, and ${\widehat{V}}_{{\omega }_v}\left(s(t+1)\right)$ represents the estimated value of the subsequent state after the agent performs an action in the current state. Subsequently, we execute gradient descent to adjust the parameters ${\omega }_v$ under the influence of the learning rate $\phi$, yielding the updated parameters:

$${\omega }_v^{\mathrm{new}}\leftarrow {\omega }_v^{\mathrm{now}}-\phi {\nabla }_{{\omega }_v}P\left({\omega }_v^{\mathrm{now}}\right)$$

(61)

3.3. Complexity Analysis

The computational complexity, associated with the MAPPO algorithm, primarily consists of two parts. On the one hand, the computational complexity generated by the i-th layer of the MLP can be expressed as $\mathcal{O}(C_{i-1}{C}_i+C_i{C}_{i+1})$, where $C_i$ represents the number of neurons in the i-th layer. Denoting the number of layers of one MLP as I, we can calculate the computational complexity of an MLP as $\mathcal{O}({\sum }_{i=2}^{I-1}{C}_{i-1}{C}_i+C_i{C}_{i+1})$. On the other hand, the complexity generated by the attention module can be expressed as $\mathcal{O}\left(I^{2}W\right)$, in which W denotes the length of feature values output from the state encoders [54]. In our framework, the actor networks are composed of a single MLP, while the critic networks consist of one MLP for value output and two encoders designed for distinct agent types. Therefore, the computational complexity of the training algorithm for all Mte episodes is calculated as

$$\mathcal{O}\left(Mte\left(Pec·I^{2}W+Epl\sum _{i=2}^{I-1}\left(C_{i-1}{C}_i+C_i{C}_{i+1}\right)\right)\right)$$

(62)

3.4. Scalability Analysis and the Role of the Attention Mechanism

The multi-agent joint optimization strategy based on MAPPO proposed in this paper, under the CTDE paradigm, effectively enhances the algorithm’s scalability when dealing with high-dimensional observation and action spaces through a carefully designed neural network architecture. Specifically, a state encoder transforms high-dimensional raw local observations into compact feature representations, thereby reducing the input dimension for the core network. Building upon this, the centralized Critic network creatively integrates a multi-head attention mechanism, enabling it to dynamically focus on and selectively weight the most relevant and critical information within the observation space. This mechanism efficiently captures complex correlations and interaction dynamics between agents, as well as between agents and the environment. Regardless of changes in the number of agents in the system, it avoids the inefficiencies that traditional fully connected networks might suffer due to dimensionality explosion, significantly enhancing the algorithm’s learning efficiency and evaluation accuracy when dealing with increasing dimensions.

4. Numerical Results

In this section, we evaluate the performance of the proposed MAPPO-based joint caching and computation offloading scheme in UAV-assisted vehicular networks. We conduct simulation experiments to compare the proposed scheme with several baseline strategies and analyze the impact of key system parameters on the scheme’s performance.

4.1. Simulation Settings

Based on the relevant research literature, we set the following simulation parameters. These parameters are divided into environment parameters and reinforcement learning parameters. Parameter selection often draws from related studies to ensure comparability and realism [6].

4.1.1. Environment Parameters

The environment parameters define the physical characteristics, resource configuration, communication model, and task load of the simulated scenario. The specific parameter settings are shown in

Table 3. Environment parameter settings.

Parameter	Symbol	Value	Unit
System Scale and Deployment
Number of UAVs	$\left|U\right|$	5	-
Number of Vehicles	$\left|N\right|$	50	-
Area Size	-	$1000\times 1000$	m2
UAV Height Range	$[H_{min},H_{max}]$	$[50,200]$	m
UAV Minimum Safe Distance	$d_{min}$	10	m
Resource Configuration
UAV Cache Size	$Q_u$	$1\times {10}^9$	Bytes (1 GB)
Vehicle Computation Capacity	$f_n$	$5\times {10}^9$	Cycles/s (5 G cycles/s)
UAV Computation Capacity	$f_u$	$15\times {10}^9$	Cycles/s (15 G cycles/s)
UAV Core Limit	$Cor{e}_{UAV}$	4	-
Communication Model
Bandwidth	$B_{n,u}$	$20\times {10}^6$	Hz (20 MHz)
Vehicle Transmission Power	$P_n$	0.5	W
Noise Power	${\sigma }^2$	$1\times {10}^{-13}$	W
Path Loss Exponent	$\zeta$	2.7	-
Reference Path Gain at 1 m	${\eta }_0$	1.0	-
Communication Rate Threshold	$R_{th}$	$1\times {10}^6$	bps (1 Mbps)
Backhaul Capacity	$R_b$	$1\times {10}^8$	bps (100 Mbps)
Tasks and Content
Number of Service Types	$\left|D\right|$	5	-
Number of Content Types	$\left|K\right|$	5	-
Service Size	$s_d$	$1\times {10}^6$	Bytes (1 MB)
Content Size	$s_k$	$1\times {10}^6$	Bytes (1 MB)
Computation Cycles per Task	$c_n$	$1\times {10}^9$	Cycles (1 G cycles)
Task Request Probability	-	0.3	-
Energy Consumption Model
Compute Efficiency Coefficient	${\beta }_u$	$1\times {10}^{-27}$	J/(Cycles/s)3·s
Hovering Power Parameter	$P_0$	79.86	W
Flight Power Parameter	$P_1$	88.63	W
Blade Tip Speed	$U_r$	120.0	m/s
Average Rotor Induced Velocity	$v_r$	4.03	m/s
Fuselage Drag Ratio	$d_0$	0.6	-
Air Density	$\rho$	1.225	kg/m3
Rotor Solidity	s	0.05	-
Rotor Disc Area	A	0.503	m2
Simulation Duration
Time Slot	$\tau$	0.1	s

.

4.1.2. Reinforcement Learning Parameters

The reinforcement learning parameters are mainly used to configure the training process, including reward function weights and training step limits. The specific parameter settings are shown in

Table 4. Reinforcement learning parameter settings.

Parameter	Symbol	Value
Reward Function Weights
Weight for Energy Penalty	${\lambda }_E$	0.5
Weight for Remaining Cache	${\lambda }_Q$	0.1
Weight for Remaining Cores	${\lambda }_C$	0.1
Weight for Fairness	${\lambda }_F$	0.8
Energy Budget	$E_{max}$	1000.0
Training Configuration
Max Steps per Episode	$\left|T\right|$	200
Warmup Steps	-	10000
UAV Maximum Velocity	$v_{max}$	30.0
Algorithm Hyperparameters
Actor Learning Rate	$\psi$	0.001
Critic Learning Rate	$\varphi$	0.001
Discount Factor	$\gamma$	0.99
Clip Parameter	$ϵ$	0.2
Entropy Coefficient	$\beta$	0.01
Batch Size	-	64

.

4.2. Algorithm Performance and Robustness Analysis

4.2.1. Convergence Performance Comparison

Cumulative Reward Convergence: Figure 5 shows the cumulative reward convergence curves of different algorithms during the training process. As shown in Figure 5, the proposed MAPPO algorithm demonstrates the fastest convergence speed and achieves the highest final cumulative reward. As shown in Figure 5, the cumulative reward of MAPPO stabilizes after approximately 750 training episodes, significantly outperforming other baseline algorithms. MADDPG and MAAC also learn and achieve higher cumulative rewards than the Greedy and Random policies, but their convergence is slower, and their final performance is lower than MAPPO. The cumulative rewards of the Greedy and Random policies remain at a low level with significant fluctuations, indicating that these simple strategies cannot effectively address the complex joint optimization problem. This validates the advantage of MAPPO in learning multi-agent cooperation and optimizing complex objectives.

4.2.2. Hyperparameter and System Scale Analysis

To further analyze the robustness and performance of the proposed MAPPO algorithm, we investigate the impact of different hyperparameters (Batch Size, Learning Rate) and system scale (Number of UAVs) on the cumulative reward convergence.

Figure 6a compares the cumulative reward convergence curves of the MAPPO algorithm under different Batch Size settings. As shown in Figure 6a, the choice of Batch Size has a significant impact on the training effectiveness of MAPPO. With Batch Sizes of 32 and 64, the algorithm converges fastest and achieves the highest final cumulative reward, showing optimal performance. With a Batch Size of 128, the convergence is slightly slower, and the final performance is marginally lower. With a Batch Size of 256, the convergence is significantly slower, and the final cumulative reward is the lowest, indicating the poorest performance among tested values. This suggests that in this simulation environment, smaller Batch Sizes (e.g., 32 or 64) are more conducive to the learning process and performance improvement of the MAPPO algorithm.

Impact of Learning Rate on Performance: Figure 6b compares the cumulative reward convergence curves of the MAPPO algorithm under different Learning Rate settings. As depicted in Figure 6b, the selection of the Learning Rate is crucial for the algorithm’s convergence speed and stability. With a Learning Rate of 0.001, the algorithm converges quickly and stably to a high cumulative reward, exhibiting the best performance. With a Learning Rate of 0.01, although the initial convergence is very fast, it shows fluctuations or premature saturation in the later stages, resulting in a slightly lower final cumulative reward than 0.001. With a Learning Rate of 0.0001, the convergence speed is very slow. While it might eventually reach a reward level similar to 0.001, it requires significantly more training episodes. This highlights that selecting an appropriate Learning Rate (0.001) is vital for balancing convergence speed and training stability.

Impact of Number of UAVs on Performance (Robustness Analysis): Figure 7 compares the cumulative reward convergence curves of the MAPPO algorithm with different numbers of UAVs. As shown in Figure 7, as the number of UAVs increases from 4 to 16, the final cumulative reward of the MAPPO algorithm shows a clear upward trend. This is consistent with the trend observed in Figure 8a, where system efficiency improves with an increasing number of UAVs. More UAVs provide richer computation, caching, and communication resources, allowing the system to better serve vehicle requests. The MAPPO algorithm is capable of effectively utilizing these additional resources and achieves good learning performance across different scales of UAV deployment, which indicates that the proposed algorithm exhibits a certain degree of robustness to changes in system scale.

4.2.3. Detailed Performance Metrics Comparison

System Efficiency: Figure 8a–c illustrate the system efficiency as a function of the number of UAVs, task computation load, and number of vehicles, respectively. Figure 8a shows the system efficiency as the number of UAVs $\left|U\right|$ changes. As the number of UAVs increases, system efficiency generally improves because more UAVs provide increased computation and caching resources. MAPPO achieves the highest system efficiency across different numbers of UAVs, and its advantage over other algorithms further widens as the number of UAVs increases. This validates MAPPO’s ability to effectively coordinate multiple UAV resources and enhance overall system performance. Figure 8b shows the system efficiency as the task computation load changes. A higher task computation load generally leads to decreased system efficiency, as limited computation resources struggle to handle heavy tasks. However, MAPPO consistently maintains the highest system efficiency under various computation loads. Especially under high load, its performance degradation is less significant than other algorithms, demonstrating good robustness. Figure 8c shows the system efficiency as the number of vehicles $\left|N\right|$ changes. Similar to the cache hit rate, the system efficiency shows an initial increase followed by a decrease with the number of vehicles, reflecting the utilization efficiency of system resources under different user scales. MAPPO consistently outperforms other algorithms and peaks when the number of vehicles is around 80–100, indicating its ability to effectively balance user demand and system resources to achieve optimal system efficiency.

These results consistently demonstrate that the proposed MAPPO algorithm significantly improves system efficiency across different system scales and load conditions, outperforming other baseline strategies.

Cache Hit Rate: Figure 9 compares the cache hit rate of different strategies as the number of vehicles changes. As shown in Figure 9, the cache hit rate shows a trend of initially increasing and then decreasing as the number of vehicles increases. This is because when the number of vehicles is small, the cache capacity is relatively sufficient, leading to a high hit rate. As the number of vehicles increases beyond a certain point, the limited cache capacity cannot satisfy all requests, causing the hit rate to decline. Across the entire range of vehicle numbers, the MAPPO algorithm consistently maintains the highest cache hit rate. Particularly when the number of vehicles is between 80 and 120, the advantage of MAPPO is more pronounced, reaching a hit rate of around 82%. The cache hit rates of MADDPG and MAAC are close but lower than MAPPO. The Greedy and Random policies exhibit the lowest cache hit rates, indicating their inefficiency in content caching decisions. This demonstrates the effectiveness of MAPPO in learning dynamic caching strategies to maximize the hit rate.

Total Delay: Figure 10 compares the total task delay of different strategies as computing power (GHz) changes. (Note: The x-axis is labeled “Computing Power (GHz)”. Given the trend of decreasing delay as this value increases, it should be interpreted as the effective computing capacity available to the system or relevant to task computation.) As shown in Figure 10, with the increase in computing power (i.e., the value on the x-axis increases), the total task delay of all strategies decreases significantly. This aligns with intuition, as more computing resources can process tasks faster. Across all levels of computing power, the total delay of the MAPPO algorithm is consistently the lowest. This implies that it can perform task offloading and resource allocation more effectively, thus minimizing the end-to-end task processing time. The delays of MADDPG and MAAC are higher than MAPPO but lower than the Greedy and Random policies. The Greedy and Random policies have the highest total delays. This further confirms the superior performance of MAPPO in optimizing task processing delay.

Energy Consumption: Figure 11 compares the energy consumption (mJ) of different strategies as the offloaded computation (Mcycles) changes. The total energy consumption of the system generally increases with the increase in offloaded computation. This is because processing more computation tasks requires more energy. The MAPPO algorithm typically exhibits the lowest energy consumption across different levels of offloaded computation, although it is close to MADDPG at lower offload amounts. This indicates that while optimizing task offloading decisions, MAPPO can also effectively control the computation and flight energy consumption of the UAVs. Lower energy consumption is an important component for improving overall system efficiency, which is also consistent with MAPPO achieving the highest cumulative reward.

4.2.4. Sensitivity Analysis of Objective Function to Reward Weights

The analysis of Figure 12 reveals that even with different settings of weight coefficients (${\lambda }_E,{\lambda }_Q,{\lambda }_C,{\lambda }_F$), the overall trend of the objective function value ($R\left(t\right)$) with respect to the number of vehicles (N) remains largely consistent. The objective function value gradually increases when the number of vehicles is small, reaches a peak in the intermediate range (approximately 80–120 vehicles), and then may slightly decrease or level off due to resource saturation. This demonstrates the robustness of the multi-agent deep reinforcement learning scheme proposed in this paper to changes in system scale under different weight configurations.

Differences in $\lambda$ group values lead to slight variations in the absolute magnitude of the objective function value: when the weight coefficients are generally higher (e.g., the group with ${\lambda }_E=0.6,{\lambda }_Q=0.2,{\lambda }_C=0.2,{\lambda }_F=0.9$), the total objective function value is typically slightly higher, as it places greater emphasis on various reward components, incentivizing agents to achieve higher overall performance. Conversely, when the weight coefficients are generally lower (e.g., the group with ${\lambda }_E=0.4,{\lambda }_Q=0.05,{\lambda }_C=0.05,{\lambda }_F=0.7$), the total objective function value is typically slightly lower. This consistent trend supports the rationality of the default $\lambda$ parameter configuration in this paper, indicating that the overall behavior pattern of system performance remains stable even under different performance trade-offs, and validating the model’s effectiveness in complex dynamic environments.

4.3. Research Insights

The simulation results demonstrate that the proposed MAPPO-based joint caching and computation offloading scheme performs excellently in UAV-assisted vehicular networks. Compared to baseline strategies such as MADDPG, MAAC, Greedy, and Random, the MAPPO algorithm achieves significant advantages in key performance metrics, including cumulative reward, cache hit rate, system efficiency, and total task delay, while also effectively controlling energy consumption. Furthermore, through the analysis of different Batch Sizes and Learning Rates, we identified suitable hyperparameter settings for this scheme. The analysis of different numbers of UAVs also validated the effectiveness and robustness of the proposed scheme to changes in system scale. These results fully demonstrate the feasibility and superiority of applying multi-agent deep reinforcement learning to the joint caching and computation offloading problem in UAV-assisted vehicular networks.

5. Conclusions

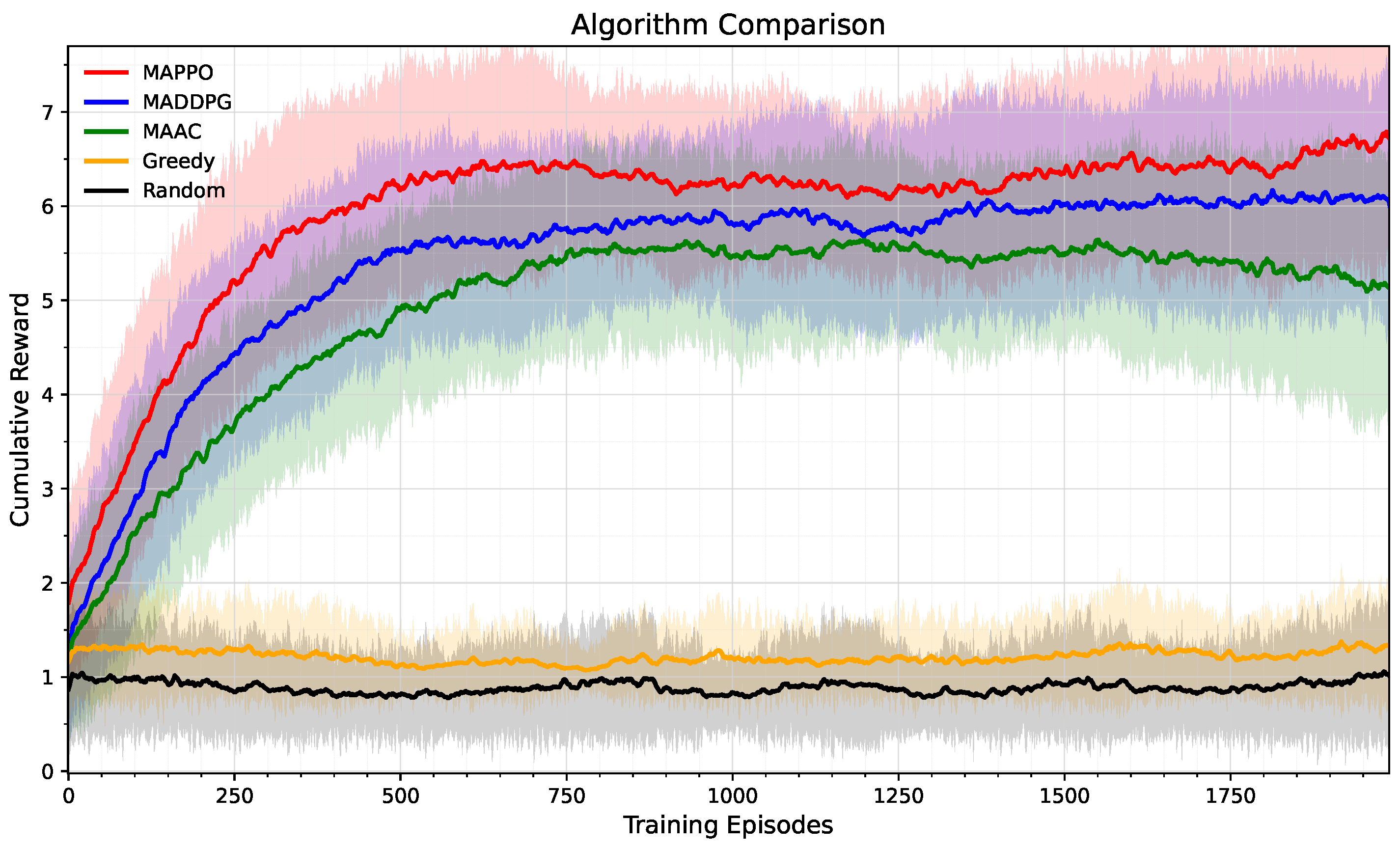
In this paper, we addressed the complex problem of jointly optimizing caching strategies, computation offloading, and UAV trajectories in dynamic UAV-assisted vehicular networks. Due to the problem’s coupled, distributed, and constrained nature, traditional optimization and existing multi-agent deep reinforcement learning (MARL) methods struggle with stability and convergence in such environments. To tackle this, we proposed a novel MARL framework by modeling the problem as a Dec-POMDP and developing a MAPPO algorithm that adheres to the CTDE paradigm. We innovatively introduce system efficiency as a unified performance metric, and with this as the primary optimization objective, we balance multiple performance indicators such as cache hit rate, task delay, energy consumption, and fairness. Extensive simulations demonstrated that our MAPPO-based approach outperforms baselines such as MADDPG, MAAC, Greedy, and Random, showing clear gains in cumulative rewards, cache hit rate, system efficiency, and task delay reduction, while effectively controlling UAV energy consumption. Sensitivity analysis across hyperparameters and system scales further confirmed its robustness. This work validates the potential of Dec-POMDP modeling and MAPPO enhanced by innovative state-space design and reward shaping mechanisms in solving dynamic, distributed resource management problems. Future directions include addressing realistic mobility patterns, large-scale scalability, and wireless interference, potentially incorporating predictive models to manage uncertainty.