Cooperative Networked Quadrotor UAV Formation and Prescribed Time Tracking Control with Speed and Input Saturation Constraints
Abstract
1. Introduction
- This study tackles the state coupling issue between the position outer loop and attitude inner loop in UAV formation control, which is exacerbated when the response frequencies of both loops are comparable. For the position outer loop, a distributed consensus protocol is designed to guarantee the position stability of the UAV formation. The attitude inner loop employs prescribed-time control strategy, which enables the arbitrary setting of the convergence speed of the inner loop, enhances the response speed of the inner loop relative to the outer loop, and reduces the spectral coupling effect between the inner and outer loops.
- To handle constraints on UAV velocity, attitude, torque, and other related control variables, a second-order consensus protocol is devised with velocity and input constraints, which is used to design a formation outer-loop controller that can impose constraints on the UAV speed and desired Euler angle. Furthermore, a continuous saturation function is introduced to design a PTSMAC with control input constraints, which can achieve prescribed-time convergent tracking control of attitude commands under constrained control inputs.
- For disturbance rejection against unmodeled errors, unknown wind disturbances, and other factors, an ESO is utilized in the outer-loop position control to ensure the robustness of disturbance estimation. In the attitude loop, a PTESO is adopted. By setting consistent convergence time parameters in both PTESO and PTSMAC, a less conservative control strategy is realized for the inner-loop attitude controller.
2. Preliminaries and Problem Formulation
2.1. Mathematical Model
- (1)
- The translational dynamics:
- (2)
- The rotational dynamics:
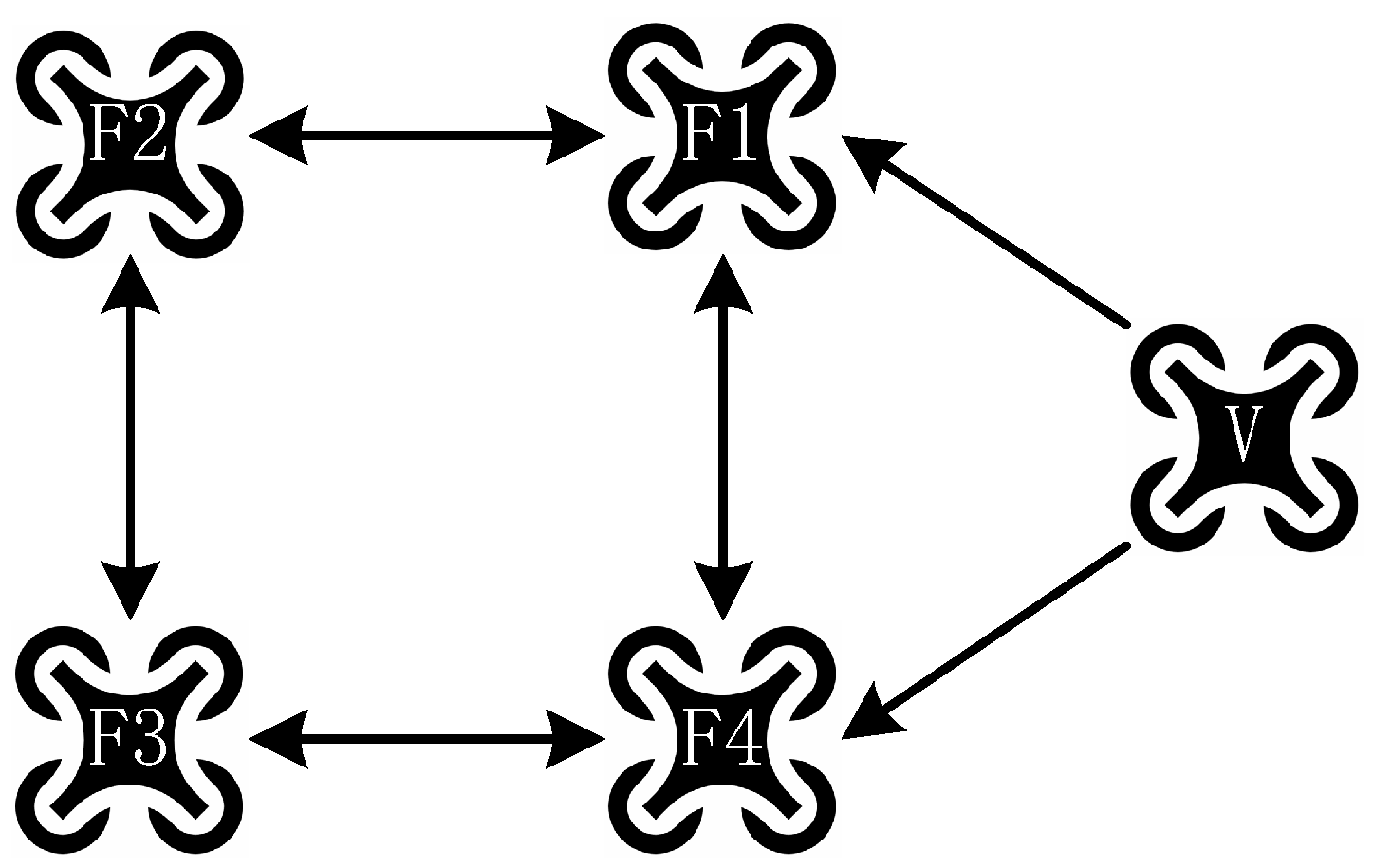
2.2. Graph Theory
2.3. Some Lemmas
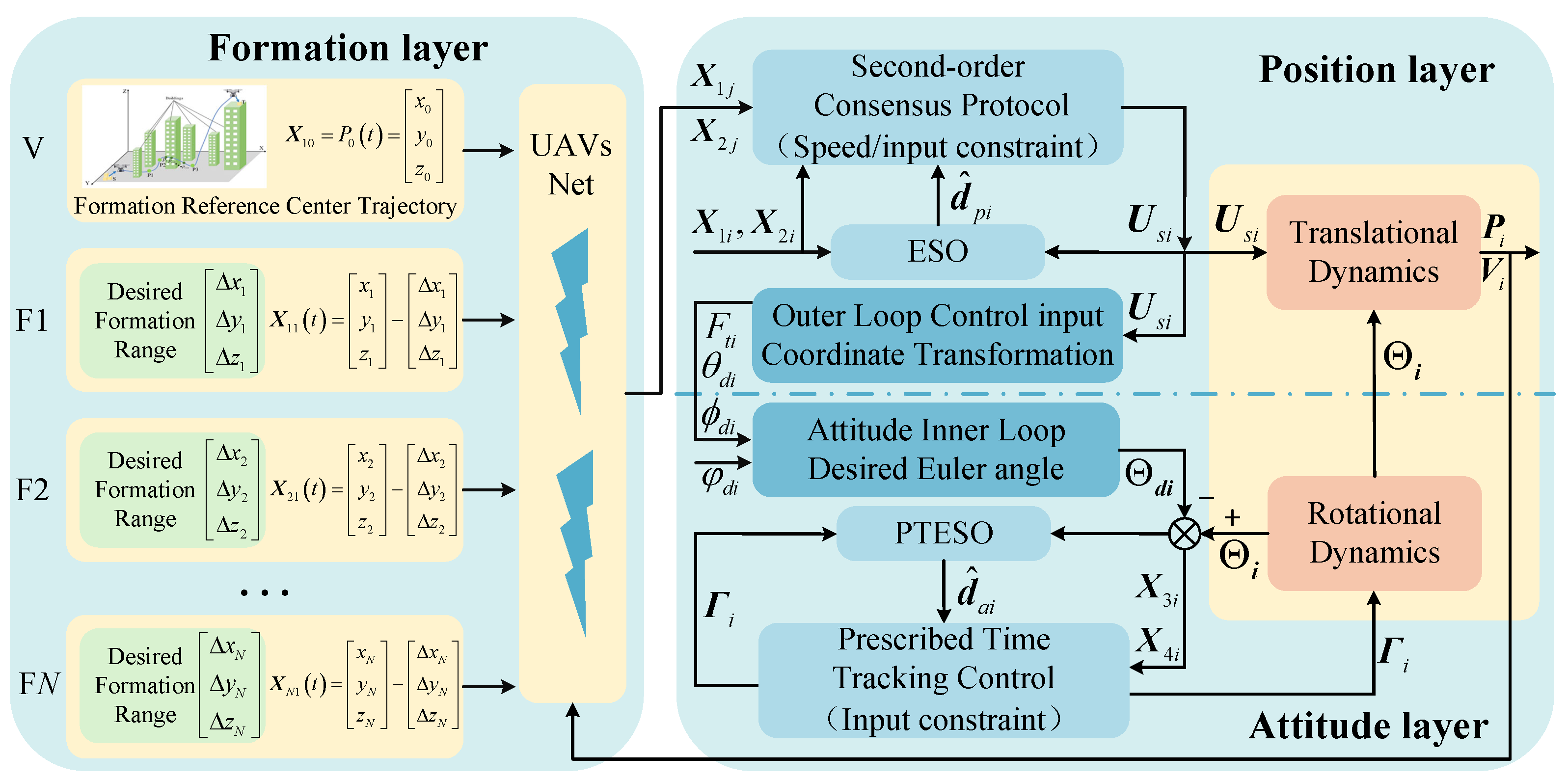
3. Main Results
- At the formation layer, the distance from each UAV to the reference trajectory is determined based on a predefined performance function, which yields the state variable of the multi-agent consensus protocol. This provides a foundational model for formation design.
- At the position layer, a distributed second-order multi-agent consensus protocol is utilized, which takes into account speed and input constraints. The reference trajectory acts as a virtual leader, allowing for consensus formation control among distributed, networked UAVs.
- At the attitude layer, the designed control input for the position loop is inversely computed to set the desired Euler angles for the attitude inner loop. A prescribed time sliding mode controller with input constraints ensures rapid and stable tracking control.
3.1. Formation Strategy
3.2. Distributed Formation Controller
- The trajectory of all UAVs should follow and navigate around the leader, with customizable formation spacing.
- The designed formation controller must be robust against model uncertainties and unknown disturbances.
- The convergence time of the controller should be as fast as possible to facilitate the rapid formation of UAV formation.
3.3. Attitude Controller
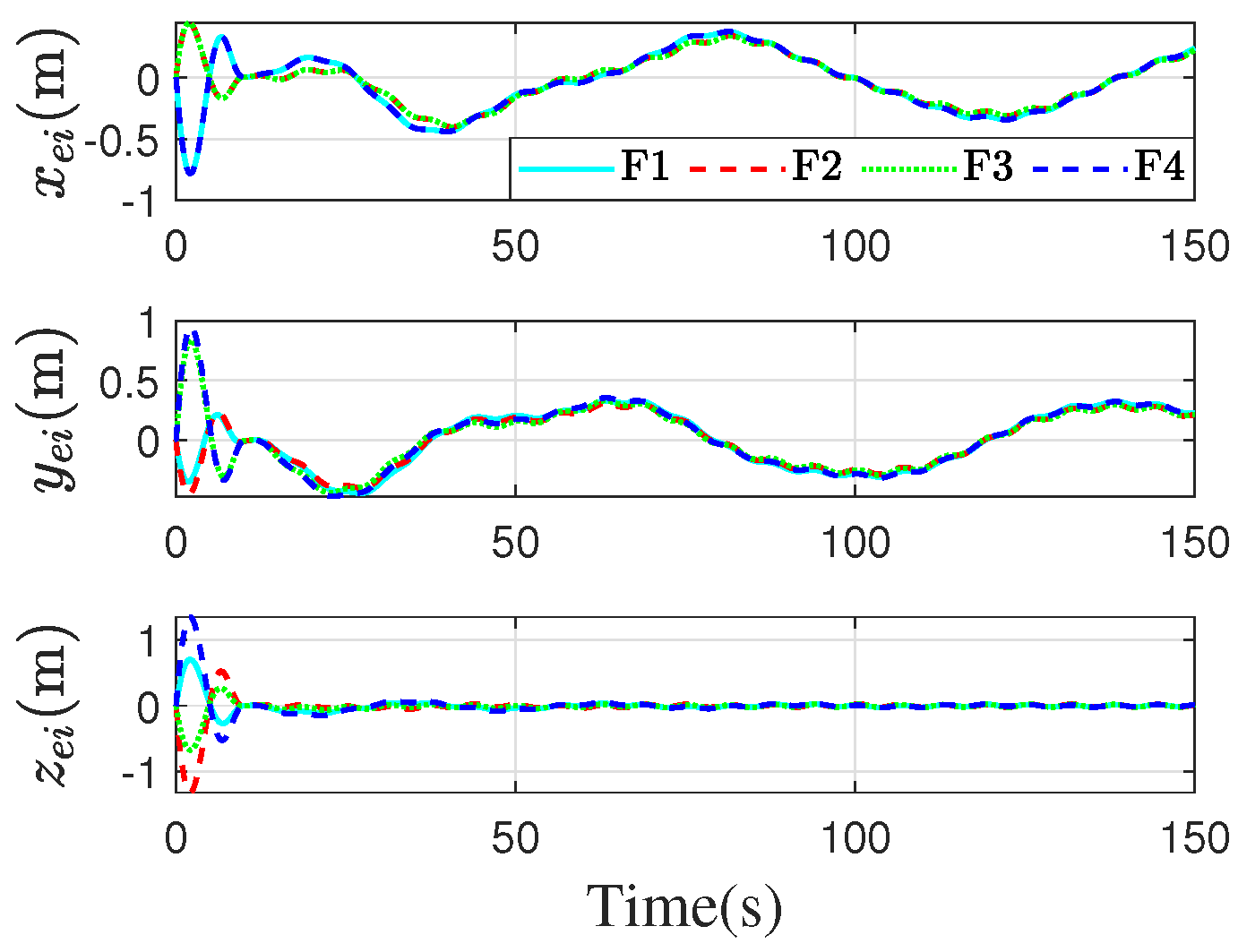
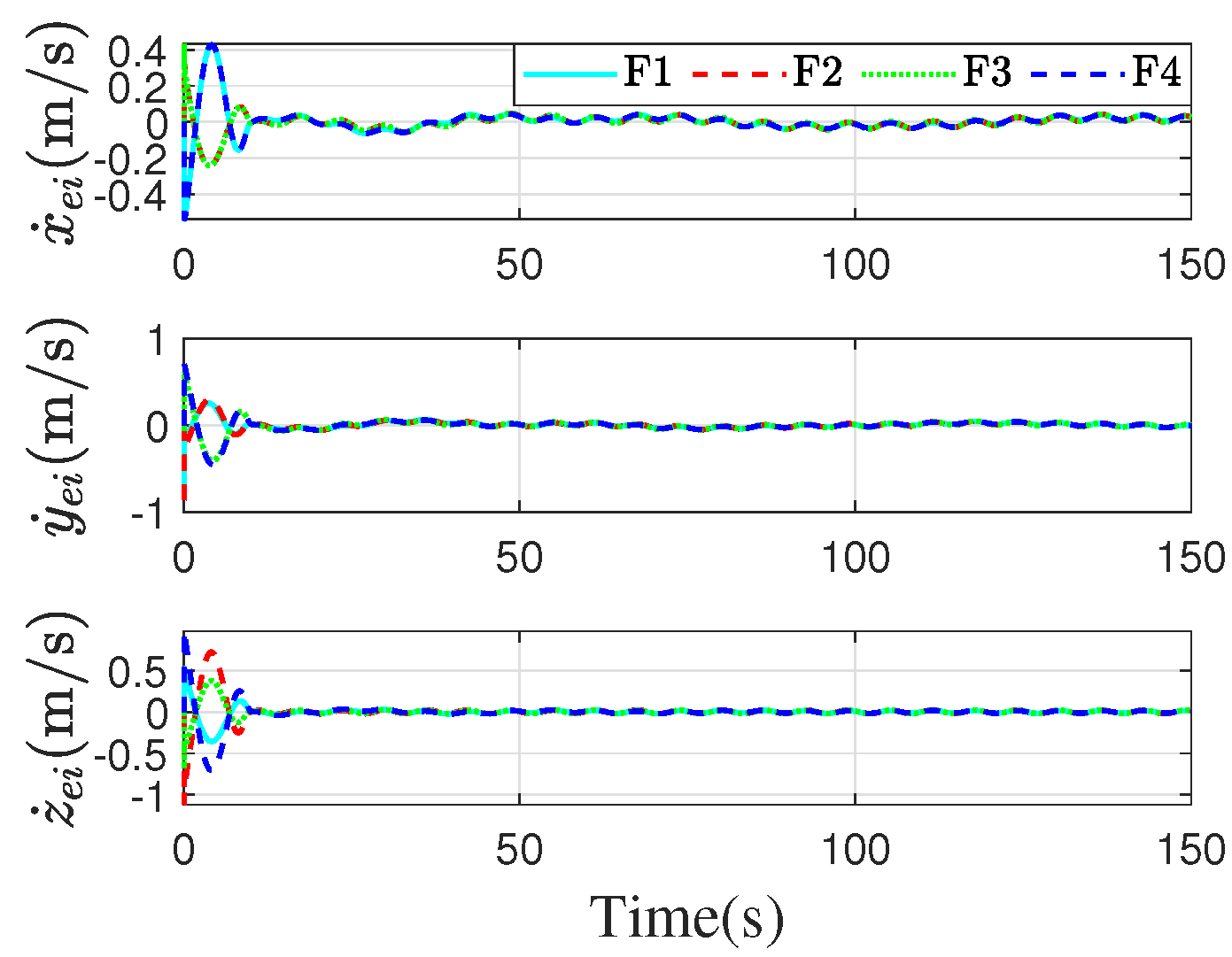
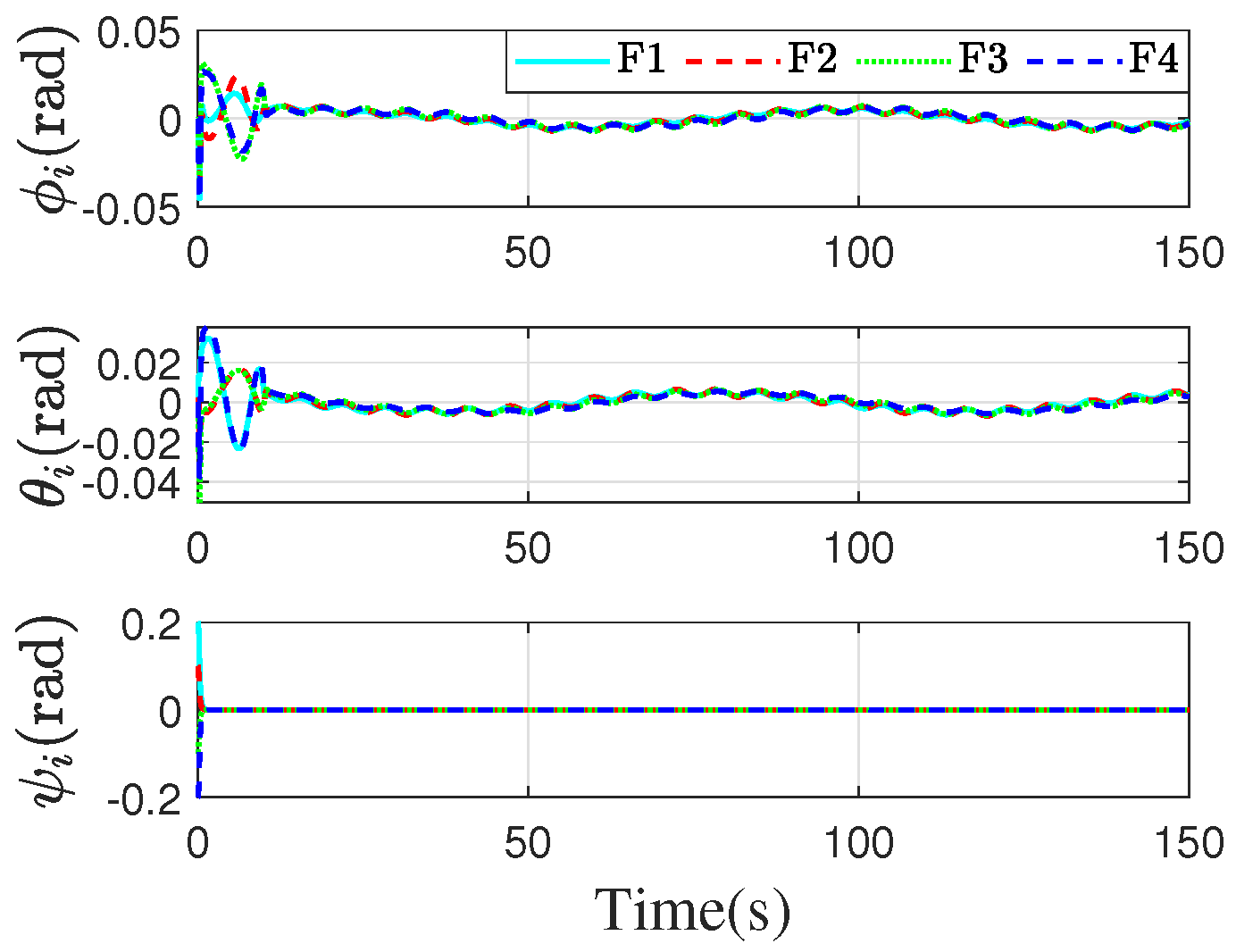
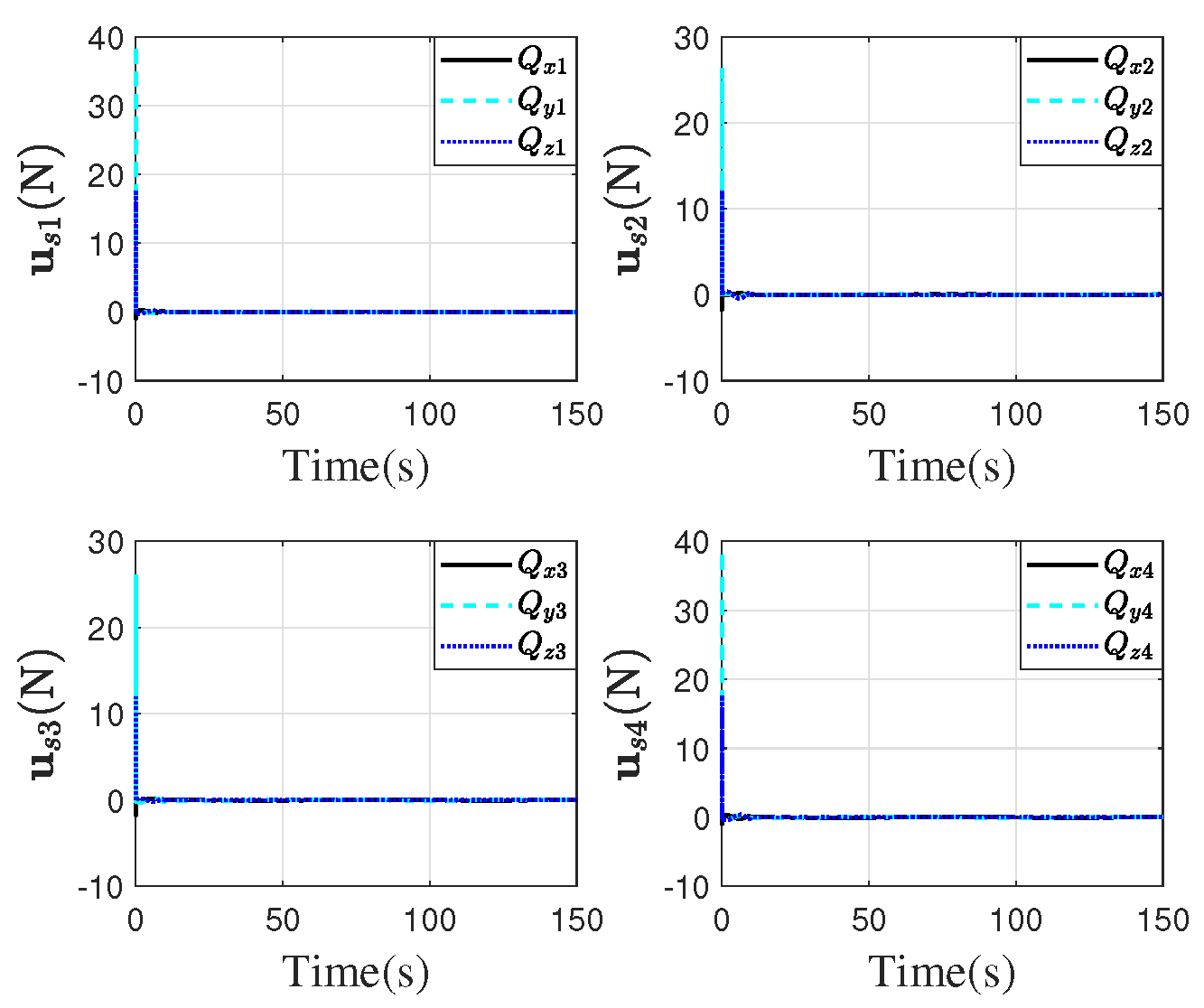
4. Simulation
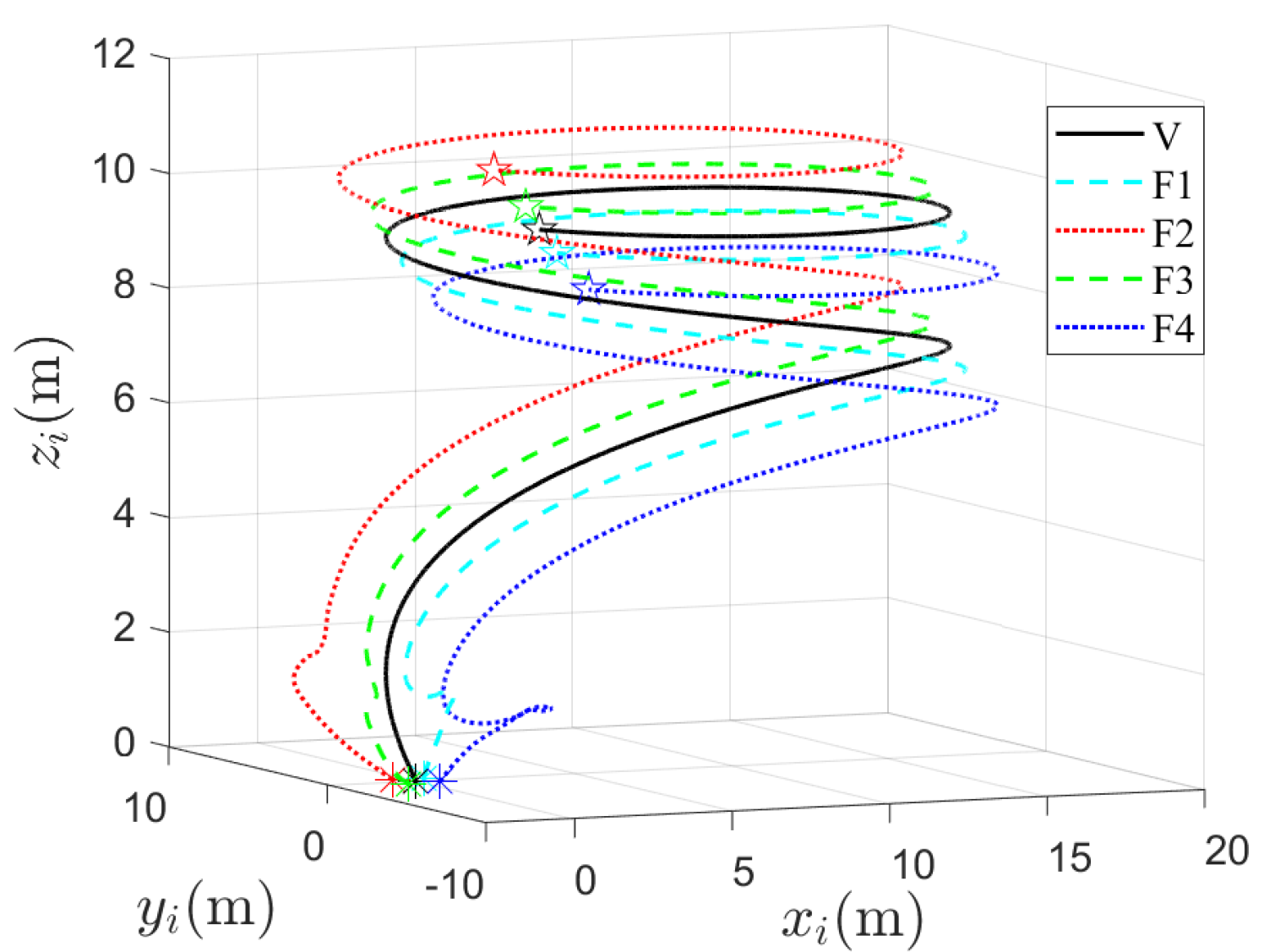
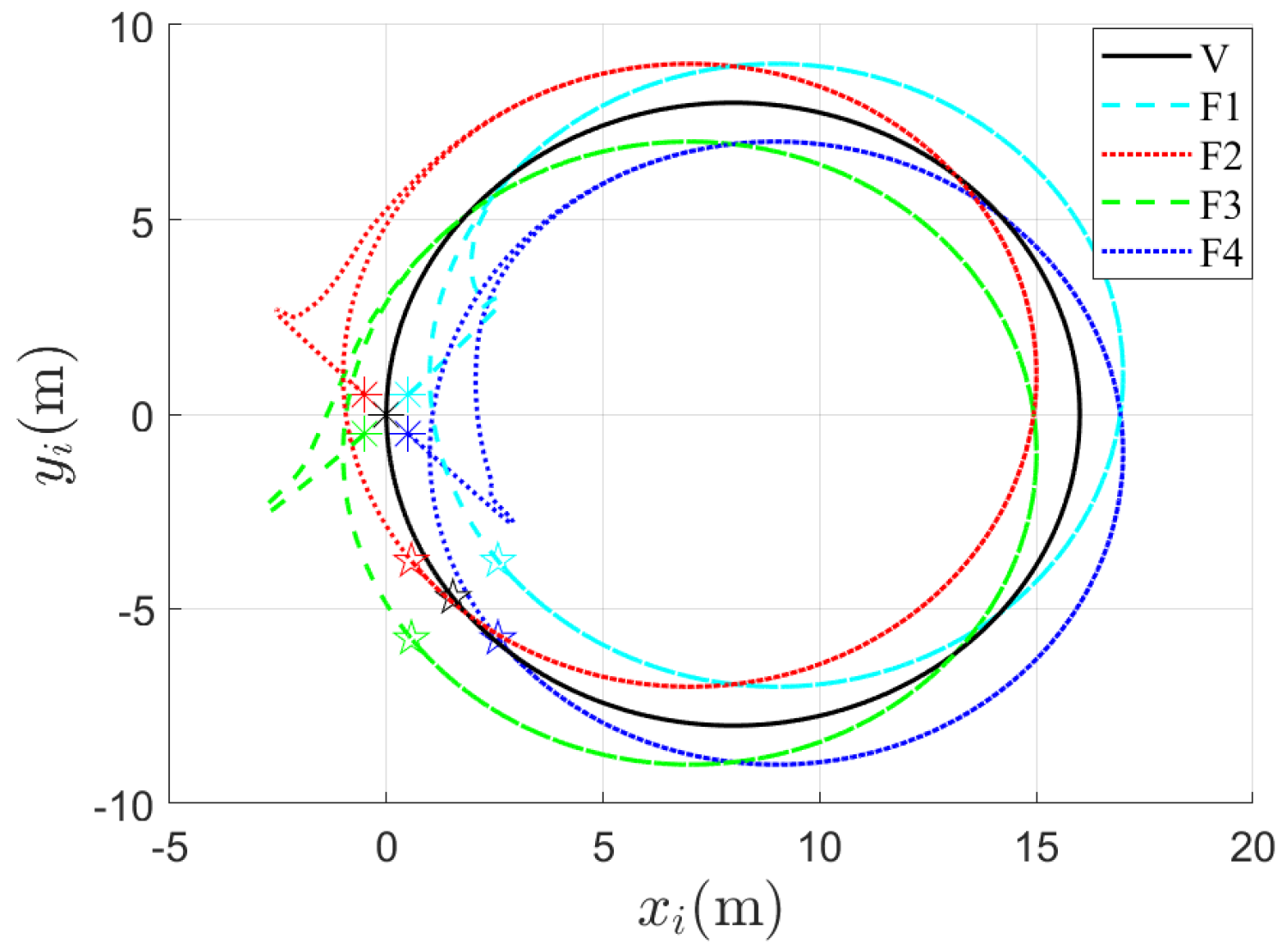
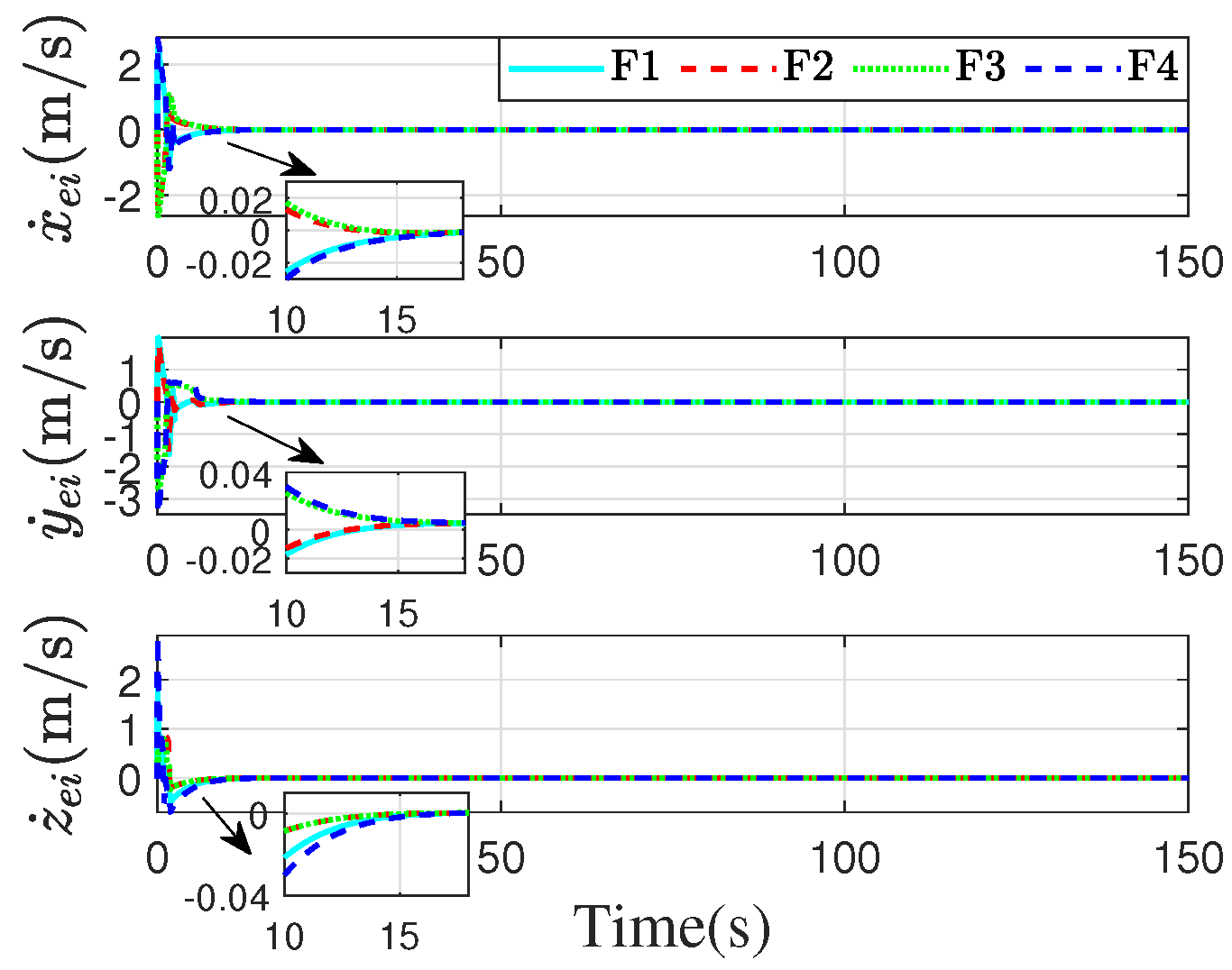
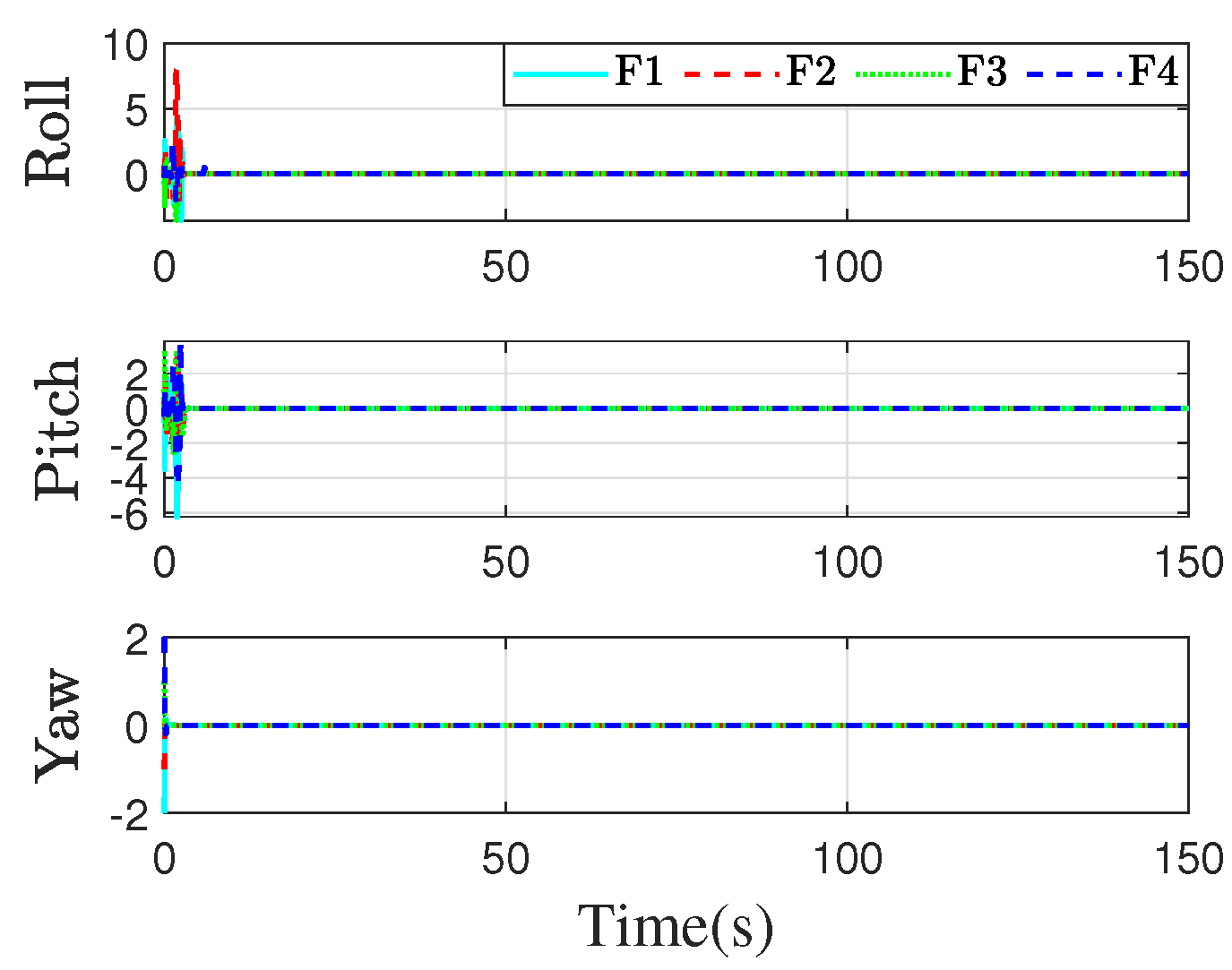
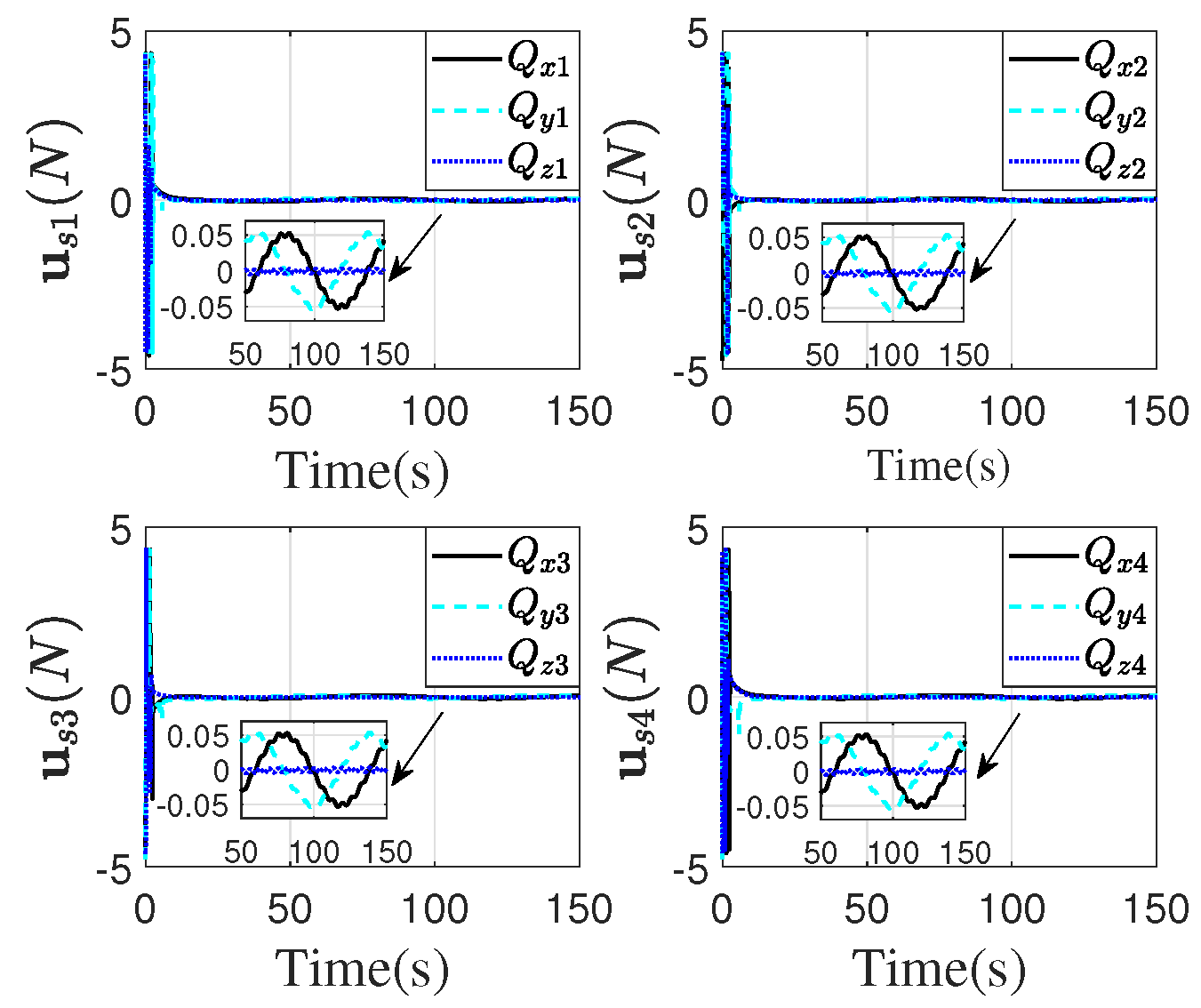
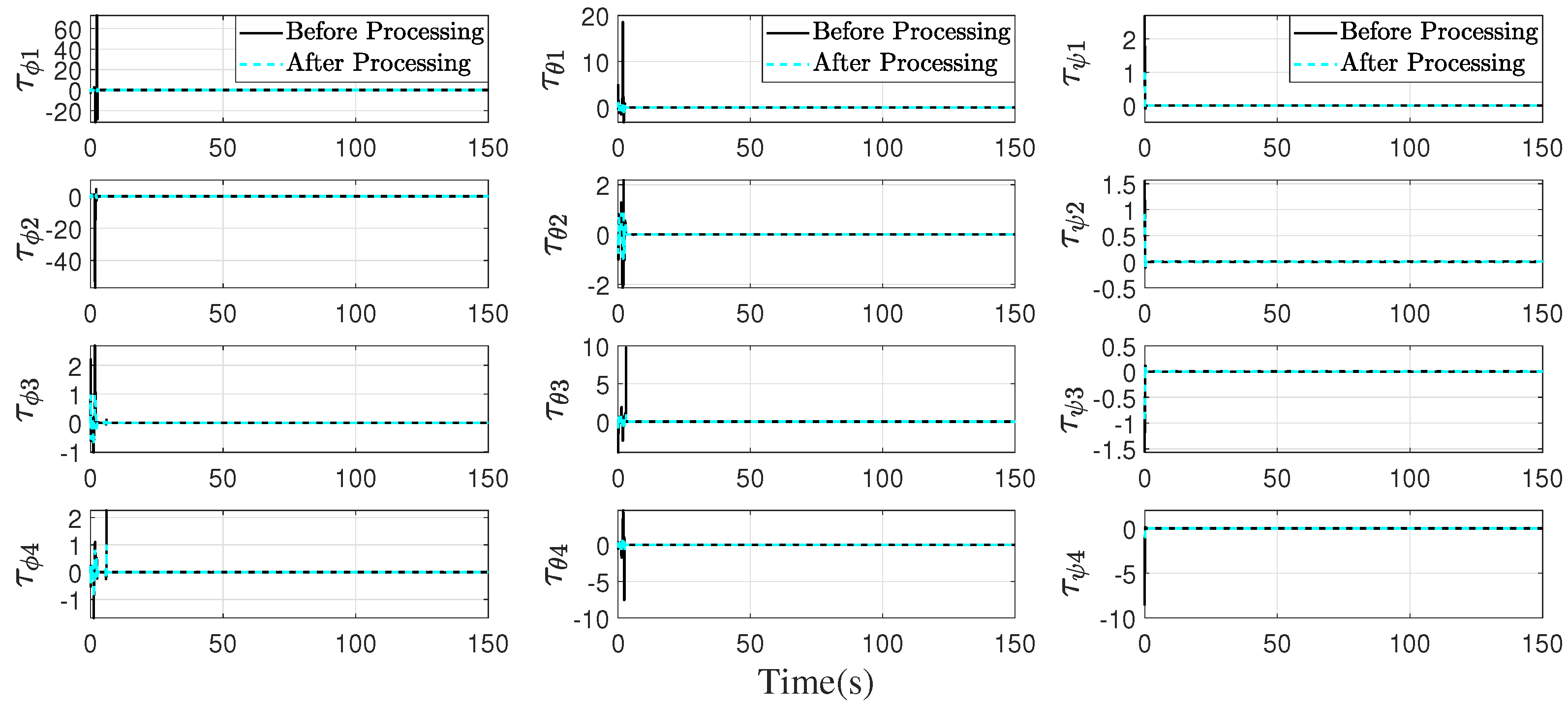
4.1. Simulation of the Proposed Method
4.2. Simulation of Comparison with the Other Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- (1)
- whenis the prescribed converge time for PTESO. Within this designated period, the system states have not yet attained the sliding mode surface, and estimation errors persist in the unknown disturbance vector , which are explicitly considered in the designed PTESO. Exponential convergence of the system is guaranteed if the maximum estimation errors fulfill the condition: . If this inequality does not hold, two alternative cases may occur.Case 1: if , one can obtain that and the system will converge to 0.Case 2: if , it can be obtained that , then it can be obtained that .It can be obtained that when t approaches , converges to the bounded neighbourhood of a positive number.
- (2)
- whenIn this time interval, the disturbance error can converge to 0 with the PTESO, which means . Then, one can obtain thatThen based on the Lemma 1, obtaining that converge to 0 at the prescribed time .
- (3)
- whenIn this time interval, it is clear that . According to the Lyapunov stability theory, it can obtain ; that is, . To analyze the motion of the system state after reaching the sliding surface, the following Lyapunov function is selected:Due to when ; combining Equation (31) the following equation can be obtained:According to Lemma 1, it can be obtained that can converge to 0 at the prescribed time . When , as well as ; that is, . In addition, according to the definition of the sliding surface, if satisfy, holds.This completes the proof. □
References
- Huang, J.; Luo, Y.; Quan, Q.; Wang, B.; Xue, X.; Zhang, Y. An autonomous task assignment and decision-making method for coverage path planning of multiple pesticide spraying UAVs. Comput. Electron. Agric. 2023, 212, 108128. [Google Scholar] [CrossRef]
- Muñoz, F.; Zúñiga-Peña, N.S.; Carrillo, L.R.G.; Espinoza, E.S.; Salazar, S.; Márquez, M.A. Adaptive fuzzy consensus control strategy for UAS-based load transportation tasks. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3844–3860. [Google Scholar] [CrossRef]
- Lu, L.; Dai, F. Accurate road user localization in aerial images captured by unmanned aerial vehicles. Autom. Constr. 2024, 158, 105257. [Google Scholar] [CrossRef]
- Fan, J.; Lei, L.; Cai, S.; Shen, G.; Cao, P.; Zhang, L. Area surveillance with low detection probability using UAV swarms. IEEE Trans. Veh. Technol. 2023, 73, 1736–1752. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, J.; Wang, F.; Chen, B.; Fan, C.; Yu, L.; Wang, Z. A dynamic parameters genetic algorithm for collaborative strike task allocation of unmanned aerial vehicle clusters towards heterogeneous targets. Appl. Soft Comput. 2025, 175, 113075. [Google Scholar] [CrossRef]
- Xu, L.X.; Wang, Y.L.; Wang, X.; Peng, C. Distributed active disturbance rejection formation tracking control for quadrotor UAVs. IEEE Trans. Cybern. 2023, 54, 4678–4689. [Google Scholar] [CrossRef]
- Meng, R.; Chen, S.; Hua, C.; Qian, J.; Sun, J. Disturbance observer-based output feedback control for uncertain QUAVs with input saturation. Neurocomputing 2020, 413, 96–106. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, J.; Ahn, C.K.; Xiang, Z. Neural adaptive distributed formation control of nonlinear multi-UAVs with unmodeled dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9555–9561. [Google Scholar] [CrossRef]
- Zou, Y.; Xia, K.; He, W. Adaptive fault-tolerant distributed formation control of clustered vertical takeoff and landing UAVs. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1069–1082. [Google Scholar] [CrossRef]
- Zheng, L.; Deng, F.; Yu, Z.; Luo, Y.; Zhang, Z. Multilayer neural dynamics-based adaptive control of multirotor UAVs for tracking time-varying tasks. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 52, 5889–5900. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, Y. Reinforcement learning-based formation-surrounding control for multiple quadrotor UAVs pursuit-evasion games. ISA Trans. 2024, 145, 205–224. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Chen, X.; Wang, W.; Wu, K.; Xie, M. Distributed observer-based finite-time control of moving target tracking for UAV formation. ISA Trans. 2023, 140, 1–17. [Google Scholar] [CrossRef]
- Yu, D.; Ma, S.; Liu, Y.J.; Wang, Z.; Chen, C.P. Finite-time adaptive fuzzy backstepping control for quadrotor UAV with stochastic disturbance. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1335–1345. [Google Scholar] [CrossRef]
- Su, Y.H.; Bhowmick, P.; Lanzon, A. A fixed-time formation-containment control scheme for multi-agent systems with motion planning: Applications to quadcopter UAVs. IEEE Trans. Veh. Technol. 2024, 73, 9495–9507. [Google Scholar] [CrossRef]
- Miao, Q.; Zhang, K.; Jiang, B. Fixed-time collision-free fault-tolerant formation control of multi-UAVs under actuator faults. IEEE Trans. Cybern. 2024, 54, 3679–3691. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.; Shen, H. Three-dimensional cooperative game guidance law for a leader–follower system with impact angles constraint. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 405–420. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Ahn, C.K.; Yang, Y. Prescribed-time extended state observer and prescribed performance control of quadrotor UAVs against actuator faults. Aerosp. Sci. Technol. 2023, 138, 108322. [Google Scholar] [CrossRef]
- Tian, M.; Wang, N.; Wang, Z.; Fu, Z.; Tao, F. Prescribed-time fault-tolerant tracking control for quadrotor UAV with guaranteed performance. Aerosp. Sci. Technol. 2025, 161, 110162. [Google Scholar] [CrossRef]
- Shao, X.; Sun, G.; Yao, W.; Liu, J.; Wu, L. Adaptive sliding mode control for quadrotor UAVs with input saturation. IEEE/ASME Trans. Mechatronics 2021, 27, 1498–1509. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Liang, M. Event-triggered finite-time adaptive neural network control for quadrotor UAV with input saturation and tracking error constraints. Aerosp. Sci. Technol. 2024, 155, 109658. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S. Adaptive finite-time backstepping global sliding mode tracker of quad-rotor UAVs under model uncertainty, wind perturbation, and input saturation. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 140–151. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.; Suzuki, S. UAV trajectory tracking under wind disturbance based on novel antidisturbance sliding mode control. Aerosp. Sci. Technol. 2024, 149, 109138. [Google Scholar] [CrossRef]
- Xing, Z.; Zhang, Y.; Su, C.Y. Active wind rejection control for a quadrotor UAV against unknown winds. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8956–8968. [Google Scholar] [CrossRef]
- Wang, G.; Zuo, Z.; Wang, C. Robust consensus control of second-order uncertain multiagent systems with velocity and input constraints. Automatica 2023, 157, 111226. [Google Scholar] [CrossRef]
- Geng, M.J.; Ding, H.F.; Yao, X.Y.; Liu, W.J.; Hua, M. Noncooperative Game of Distributed Quadrotor UAVs With Multiple Constraints. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4728–4739. [Google Scholar] [CrossRef]
- Teng, L.; Chuanjiang, L.; Yanning, G.; Guangfu, M. Three-dimensional finite-time cooperative guidance for multiple missiles without radial velocity measurements. Chin. J. Aeronaut. 2019, 32, 1294–1304. [Google Scholar]
- Ren, Y.H.; Zhou, W.N.; Li, Z.W.; Liu, L.; Sun, Y.Q. Prescribed-time cluster lag consensus control for second-order non-linear leader-following multiagent systems. ISA Trans. 2021, 109, 49–60. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Jin, N. Prescribed-time ESO-based prescribed-time control and its application to partial IGC design. Nonlinear Dyn. 2021, 106, 491–508. [Google Scholar] [CrossRef]
- Xu, Y.; Qu, Y.; Luo, D.; Duan, H. Distributed fixed-time time-varying formation-containment control for networked underactuated quadrotor UAVs with unknown disturbances. Aerosp. Sci. Technol. 2022, 130, 107909. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, Y.; Fu, W.; Ma, W.; Wang, M. Prescribed-time cooperative guidance law against manoeuvring target with input saturation. Int. J. Control 2023, 96, 1177–1189. [Google Scholar] [CrossRef]
- Chen, M.; Tao, G.; Jiang, B. Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 2086–2097. [Google Scholar] [CrossRef] [PubMed]

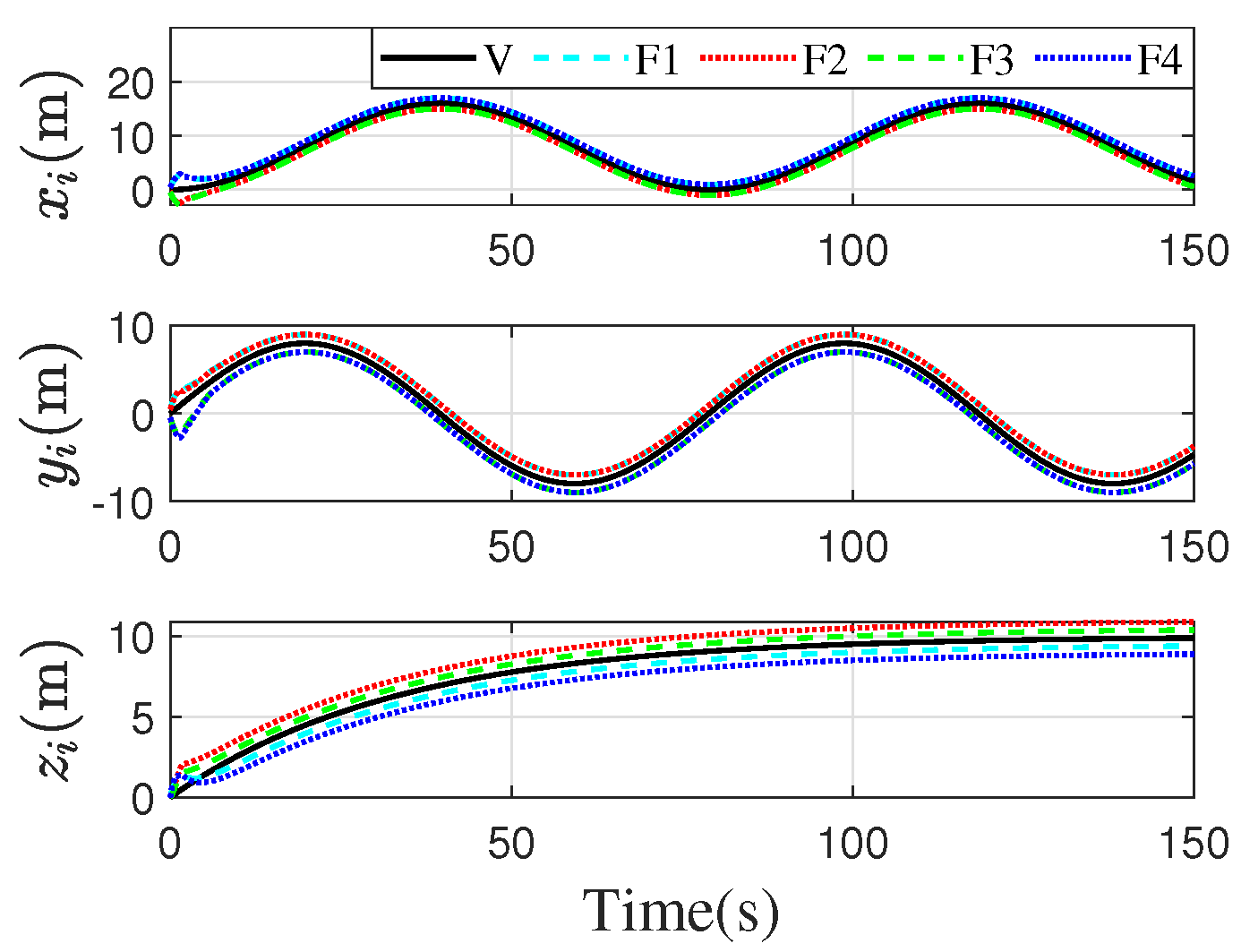
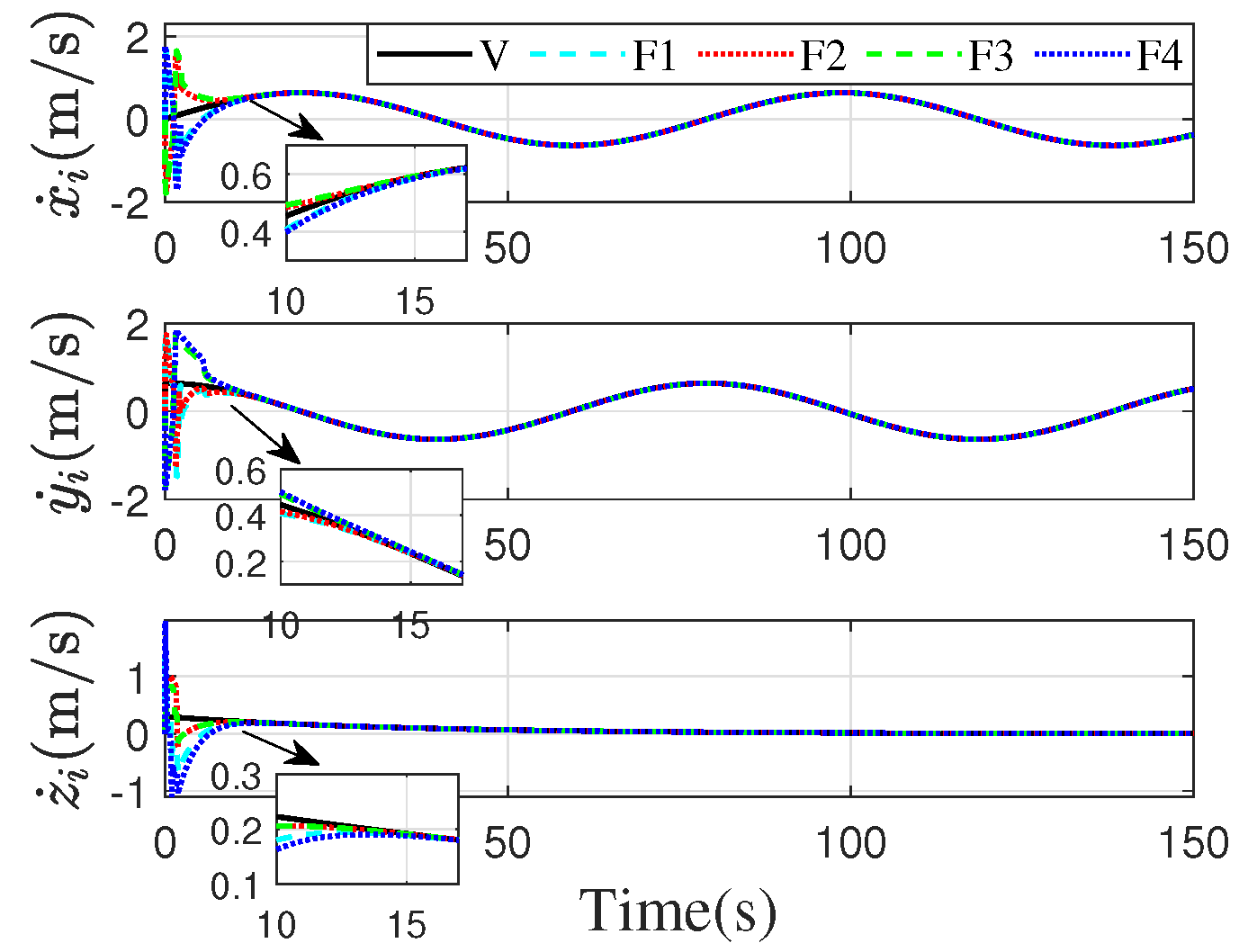
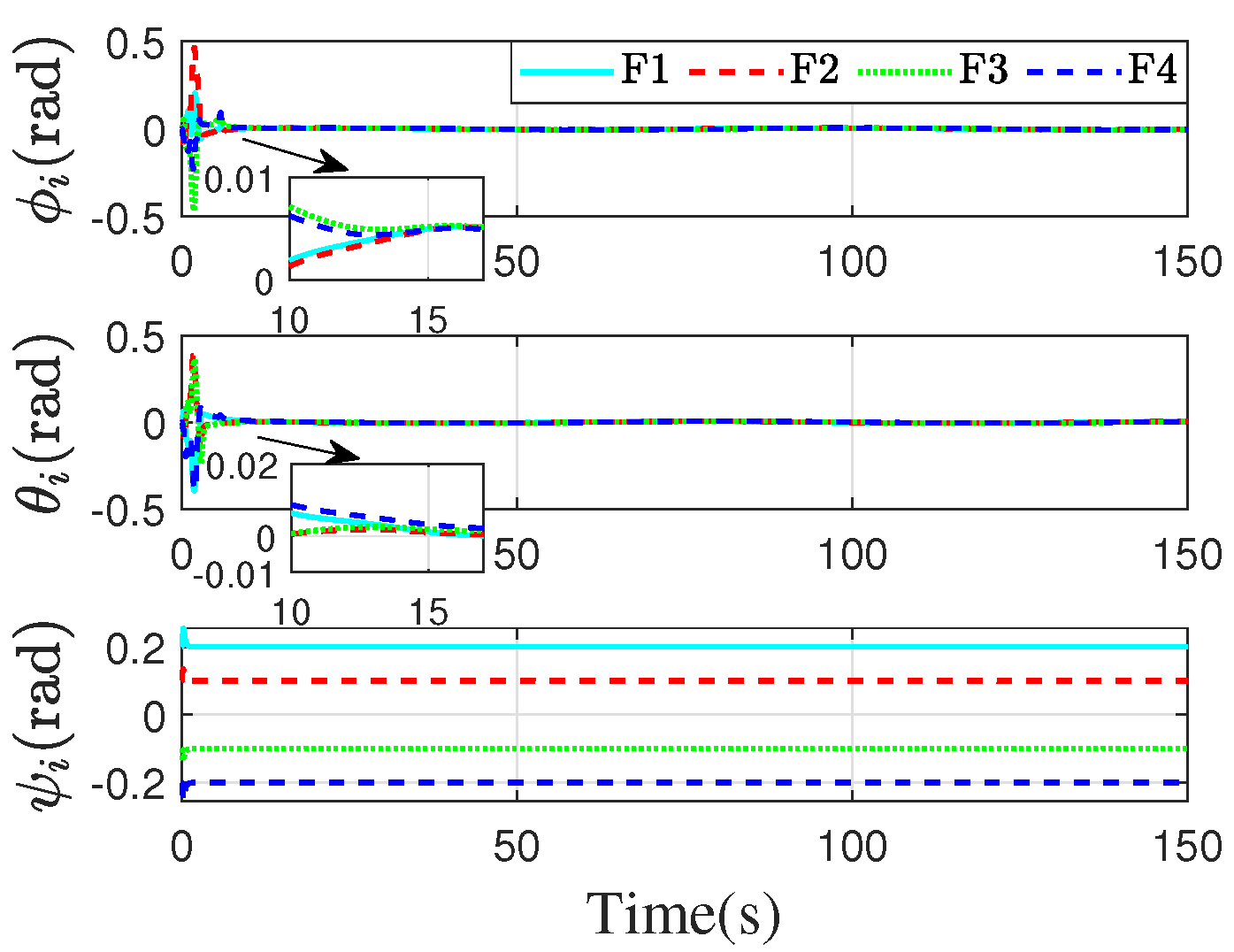

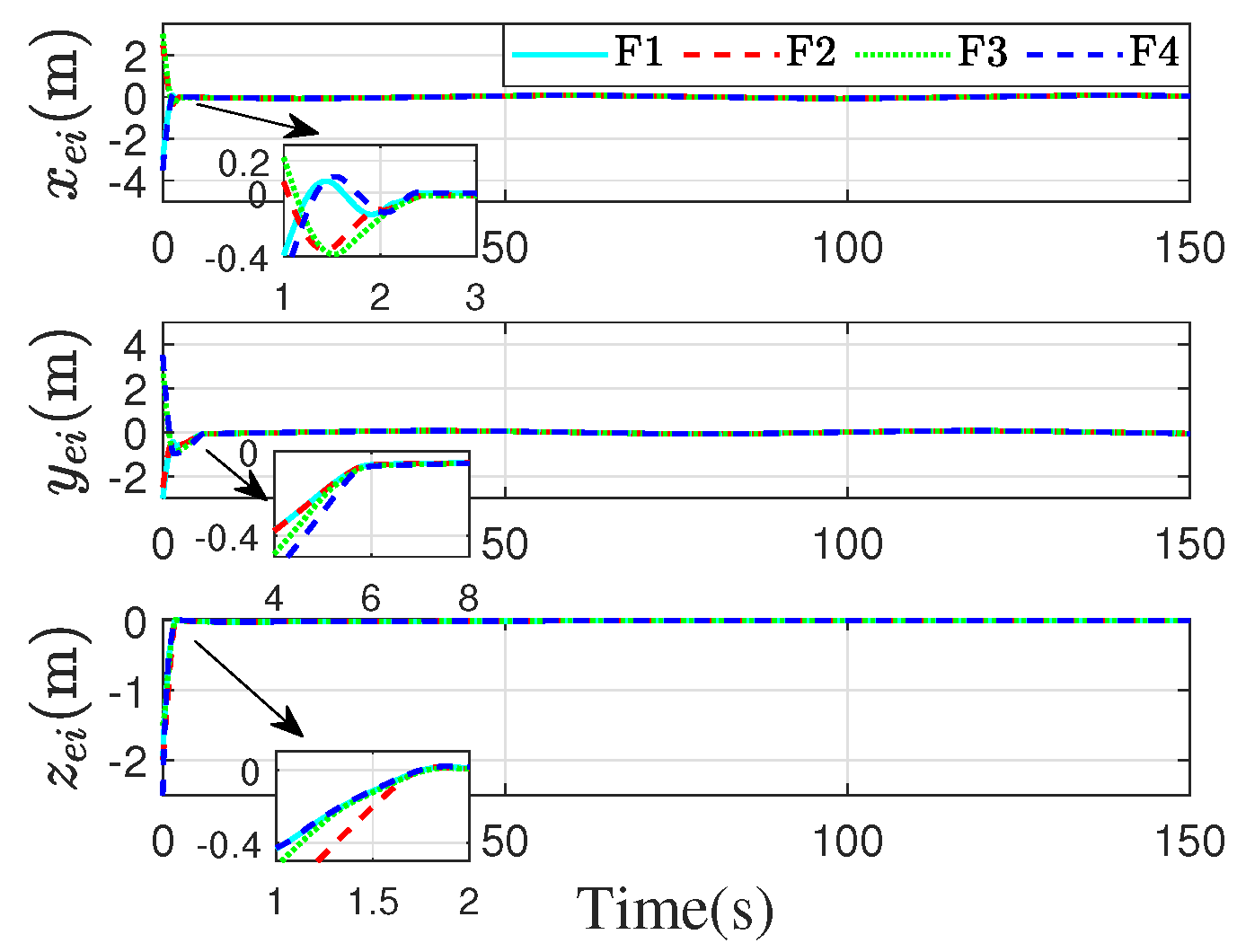




| Parameter | Values | Unit |
|---|---|---|
| m | 0.5 | kg |
| g | 9.8 | m/s2 |
| l | 0.225 | m |
| N/(rad/s)2 | ||
| N·m/(rad/s)2 | ||
| kg·m2 | ||
| kg·m2 | ||
| kg·m2 | ||
| kg·m2 | ||
| N·s/rad | ||
| N·s/rad |
| Parameter Category | Symbol | Value |
|---|---|---|
| ESO parameters | 200 | |
| 300 | ||
| 0.5 | ||
| 0.1 | ||
| PTESO parameters | 3.82 | |
| 6.94 | ||
| 1.5 | ||
| 1.2 | ||
| 0.6 | ||
| 0 | ||
| 0 | ||
| PTSMAC parameters | 4 | |
| 1 | ||
| 6 | ||
| 1 | ||
| 5 | ||
| 3 | ||
| 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Qin, Y.; Tao, F.; Wu, Z.; Gao, S. Cooperative Networked Quadrotor UAV Formation and Prescribed Time Tracking Control with Speed and Input Saturation Constraints. Drones 2025, 9, 417. https://doi.org/10.3390/drones9060417
Wang Z, Qin Y, Tao F, Wu Z, Gao S. Cooperative Networked Quadrotor UAV Formation and Prescribed Time Tracking Control with Speed and Input Saturation Constraints. Drones. 2025; 9(6):417. https://doi.org/10.3390/drones9060417
Chicago/Turabian StyleWang, Zhikai, Yifan Qin, Fazhan Tao, Zihao Wu, and Song Gao. 2025. "Cooperative Networked Quadrotor UAV Formation and Prescribed Time Tracking Control with Speed and Input Saturation Constraints" Drones 9, no. 6: 417. https://doi.org/10.3390/drones9060417
APA StyleWang, Z., Qin, Y., Tao, F., Wu, Z., & Gao, S. (2025). Cooperative Networked Quadrotor UAV Formation and Prescribed Time Tracking Control with Speed and Input Saturation Constraints. Drones, 9(6), 417. https://doi.org/10.3390/drones9060417








