Preliminary Design and Optimization Approach of Electric FW-VTOL UAV Based on Cell Discharge Characteristics
Abstract
1. Introduction
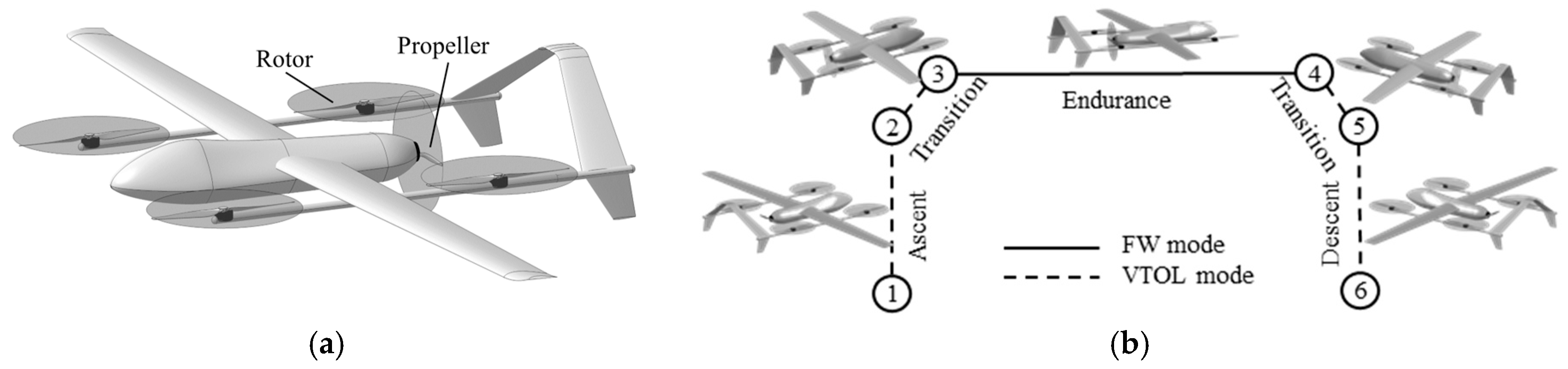
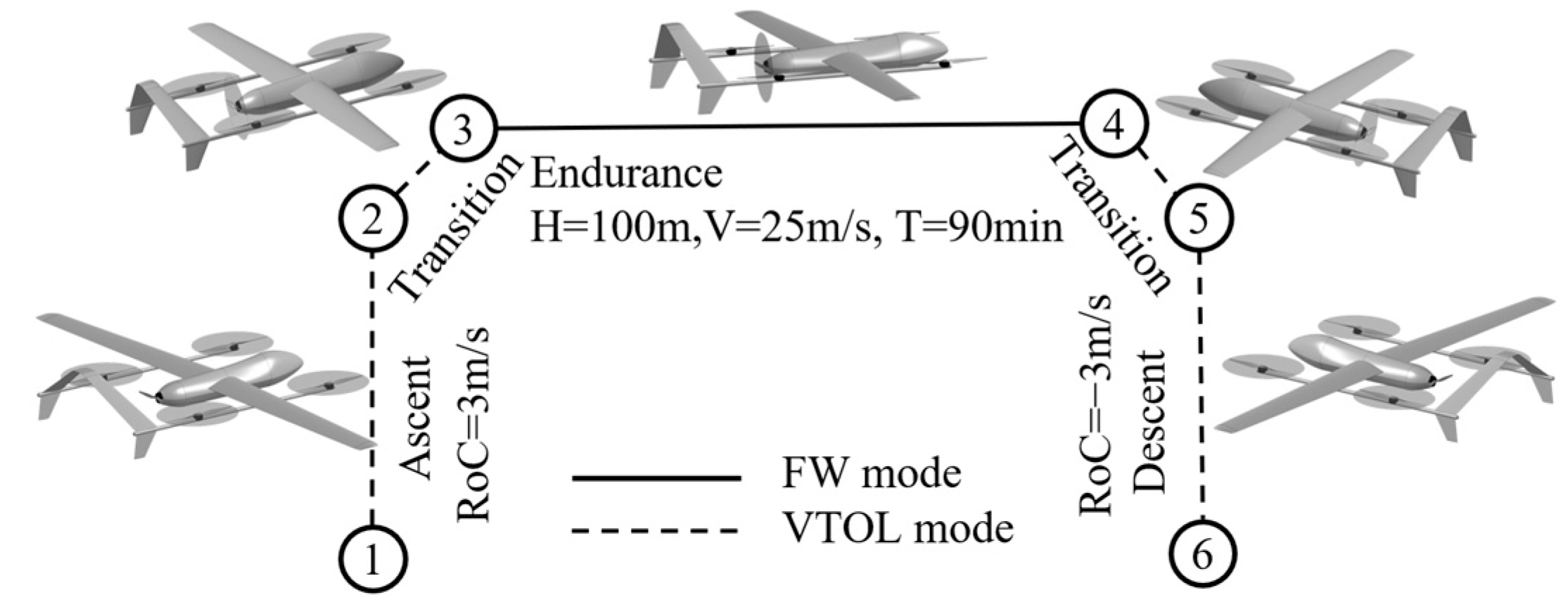
2. Multimodal Power and Energy Demand Analysis
2.1. Power and Energy Requirements in FW Mode
2.2. Power and Energy Requirements in VTOL Mode
2.3. Power and Energy Requirements in Transition Mode
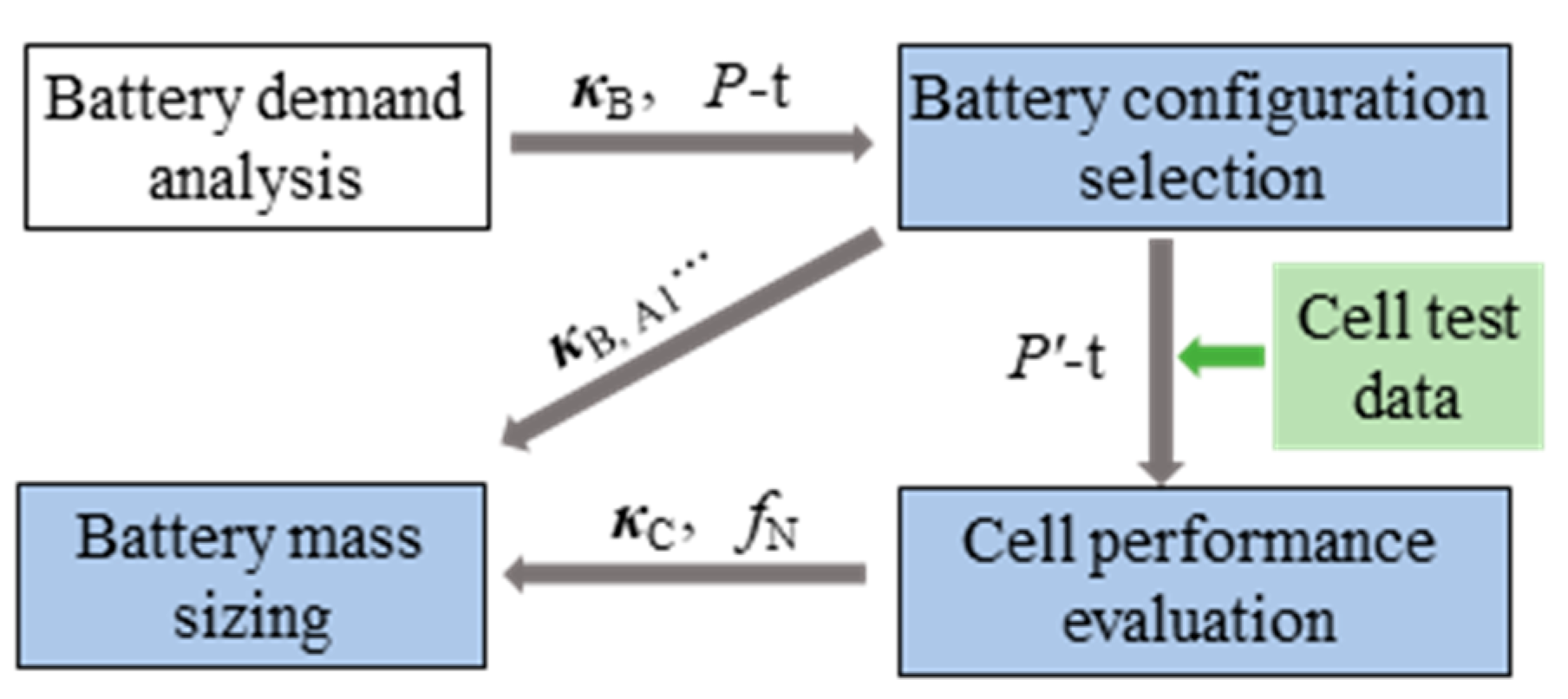
3. Power Battery Performance Model
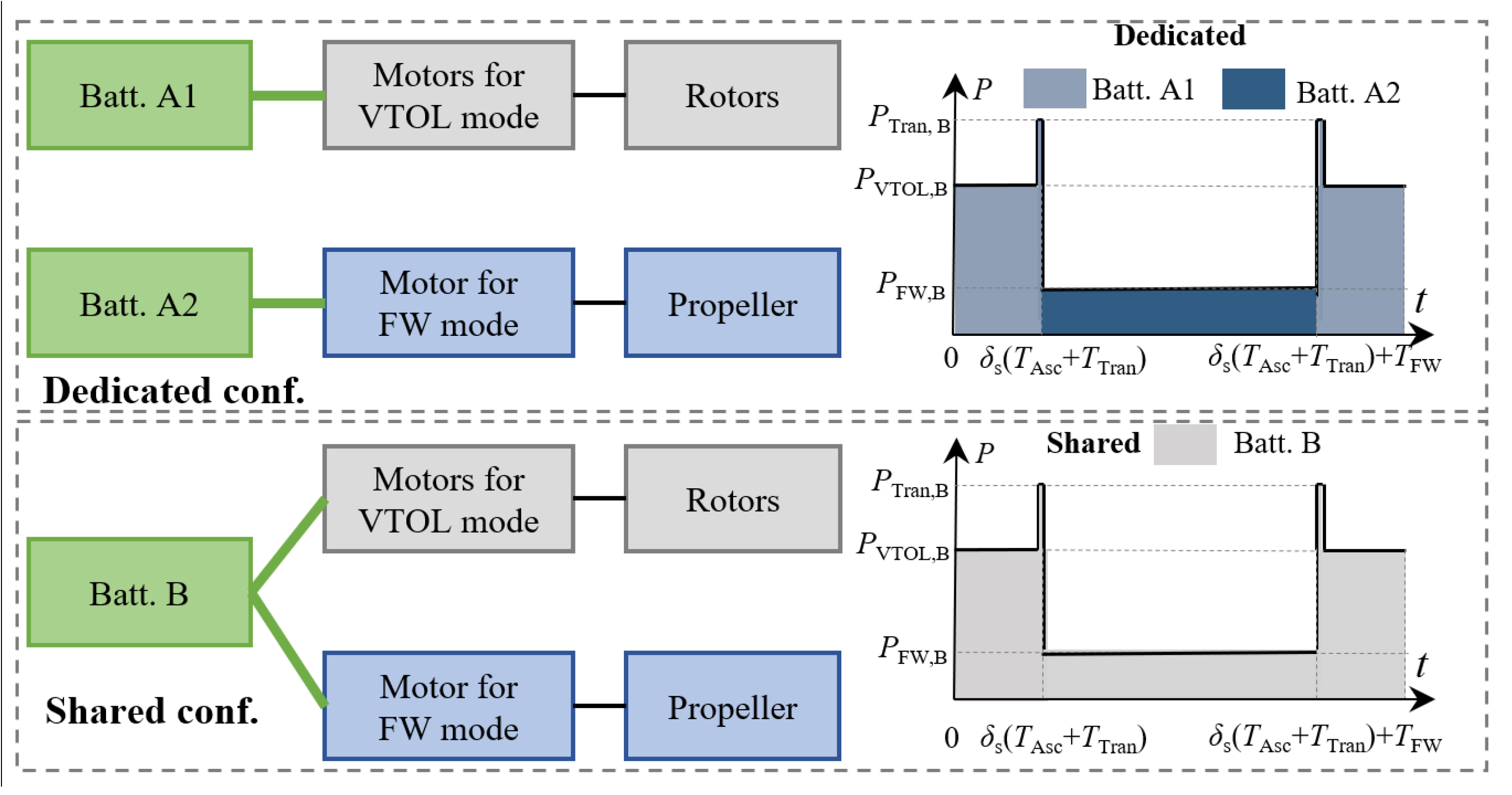
3.1. Battery Configuration Selection
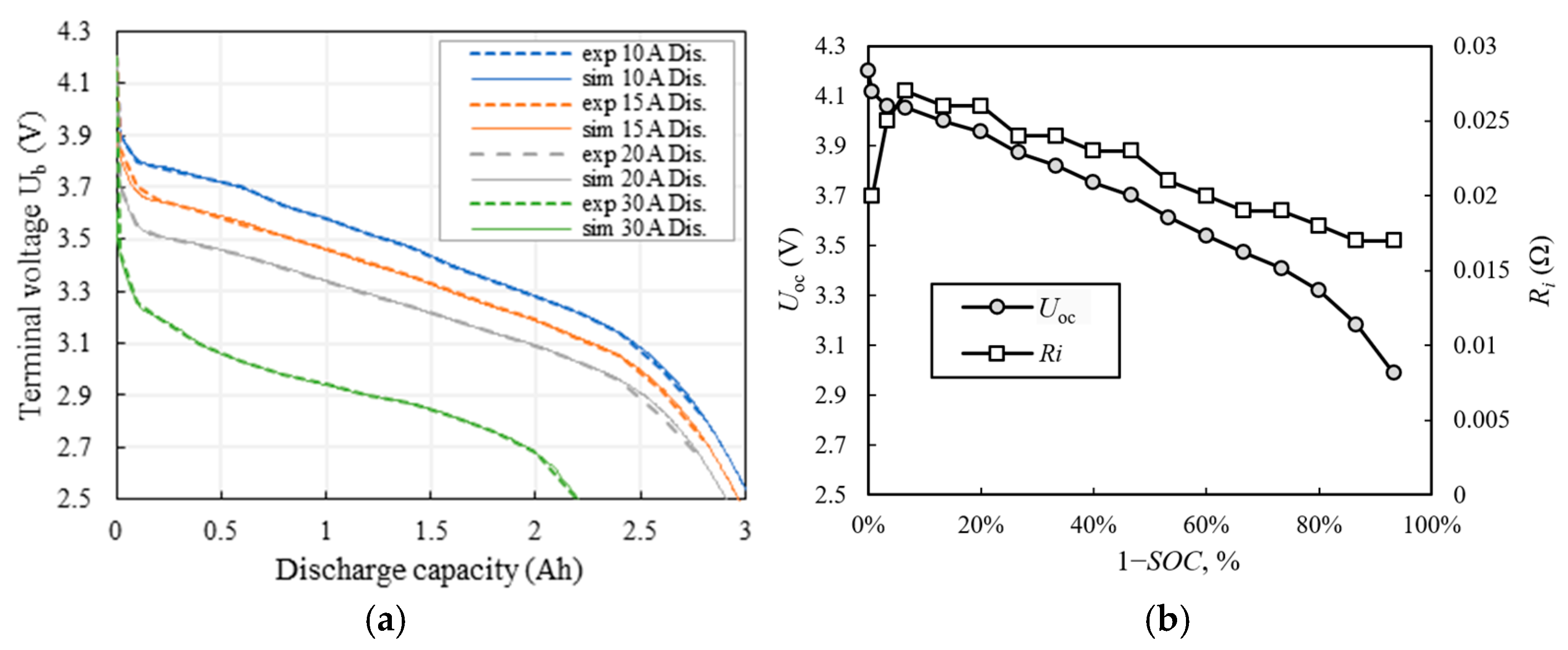
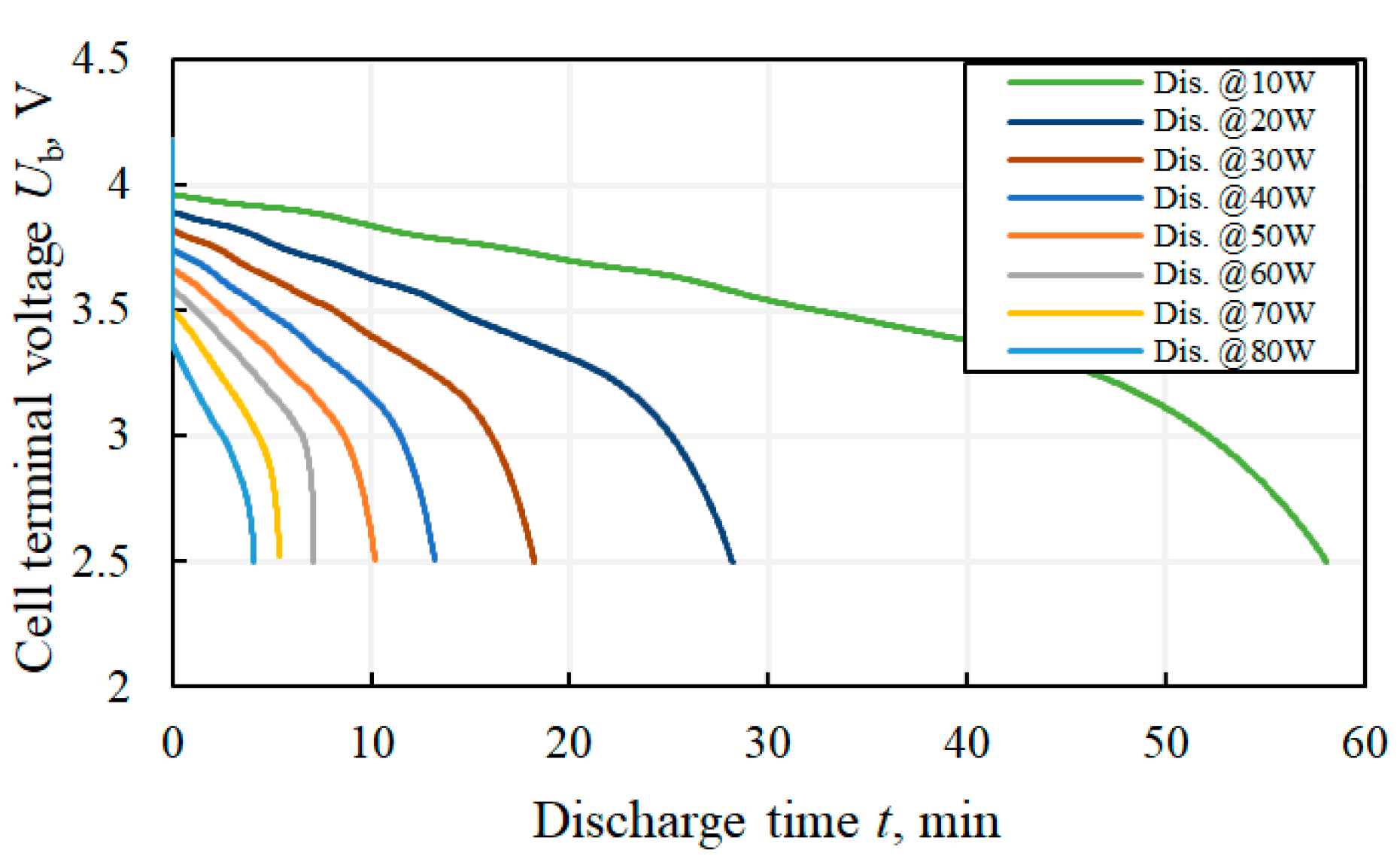
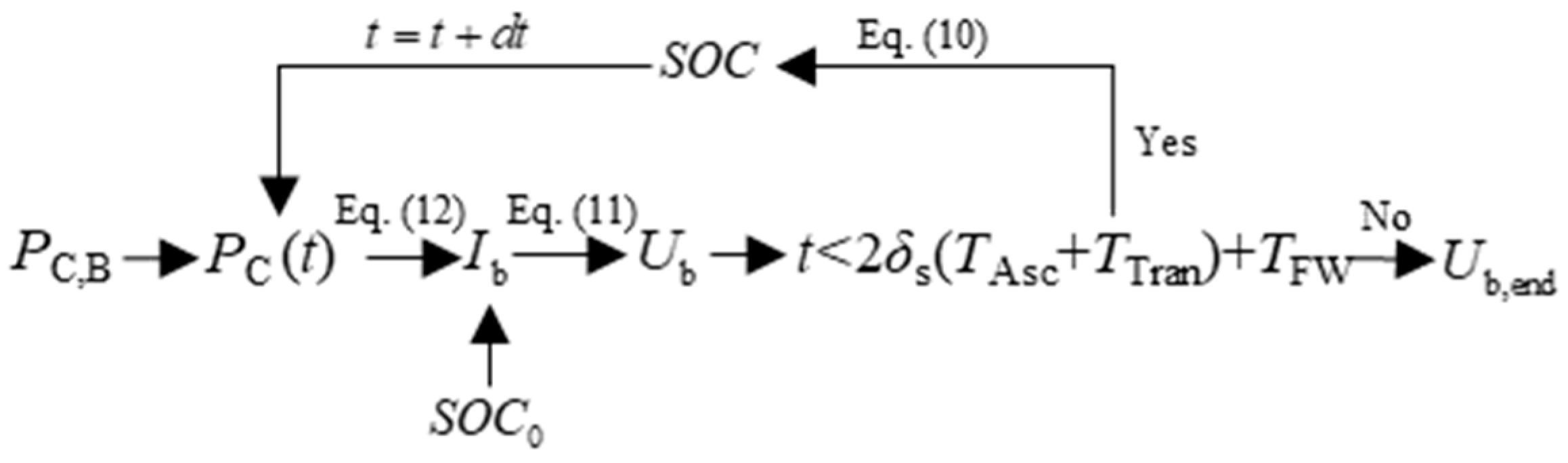
3.2. Cell Performance Assessment
3.2.1. Cell Maximum Available Energy Assessment
3.2.2. Cell Maximum Design Power Assessment
3.3. Battery Mass Sizing
4. Propulsion System Performance Analysis and Optimization Model
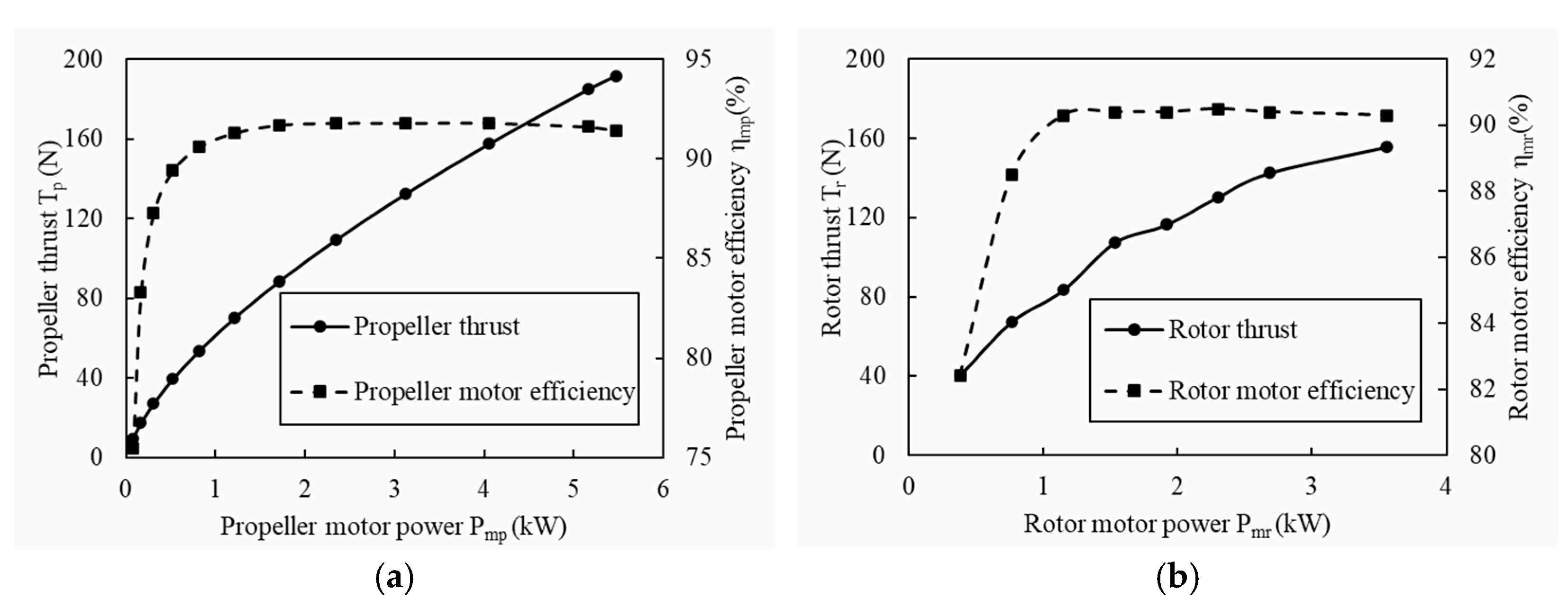
4.1. Motor Performance Model
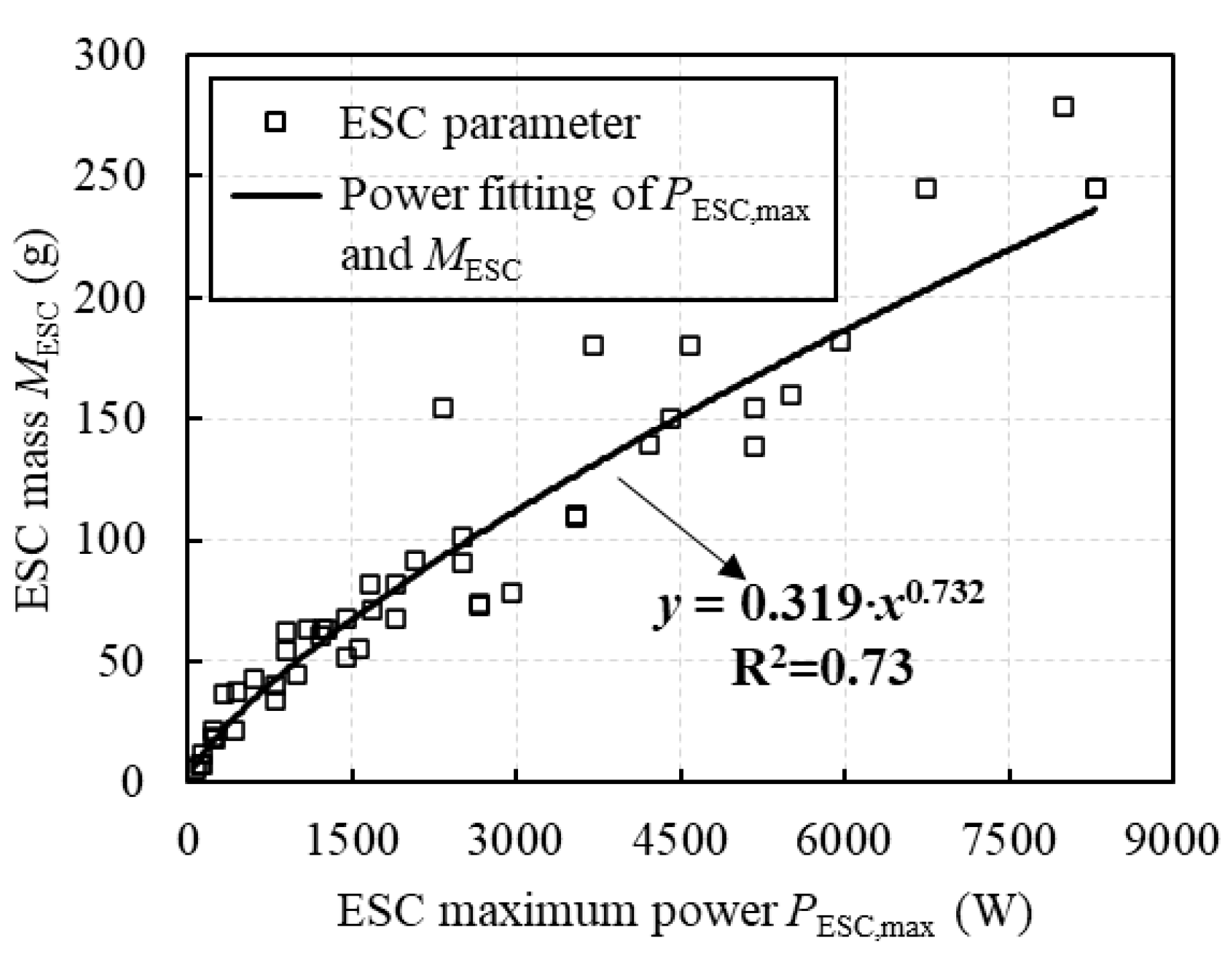
4.2. ESC Performance Model
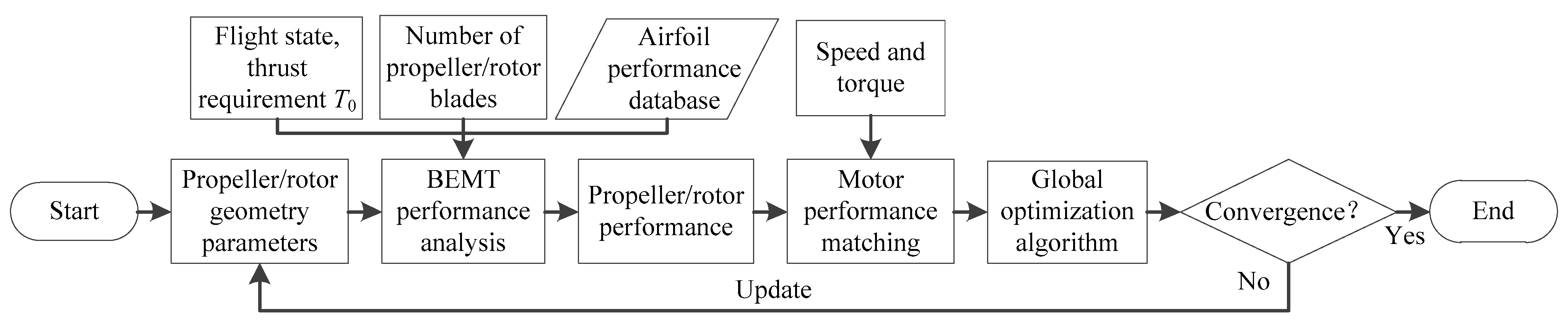
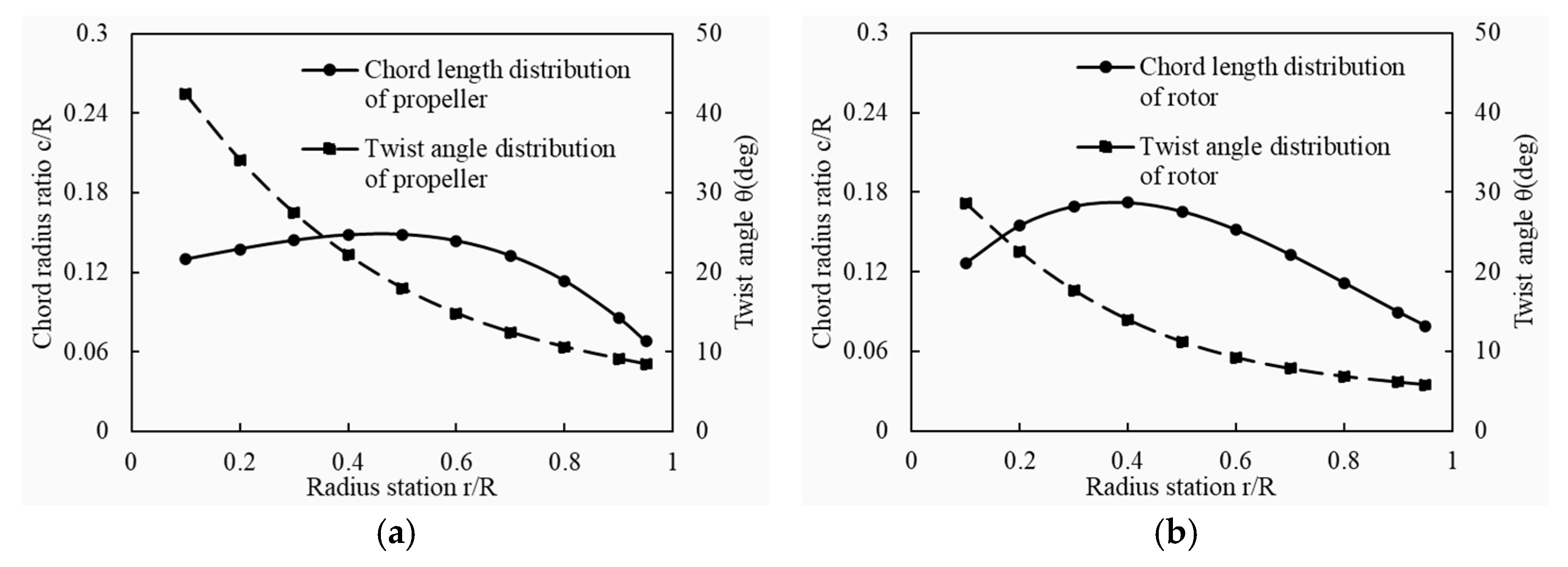
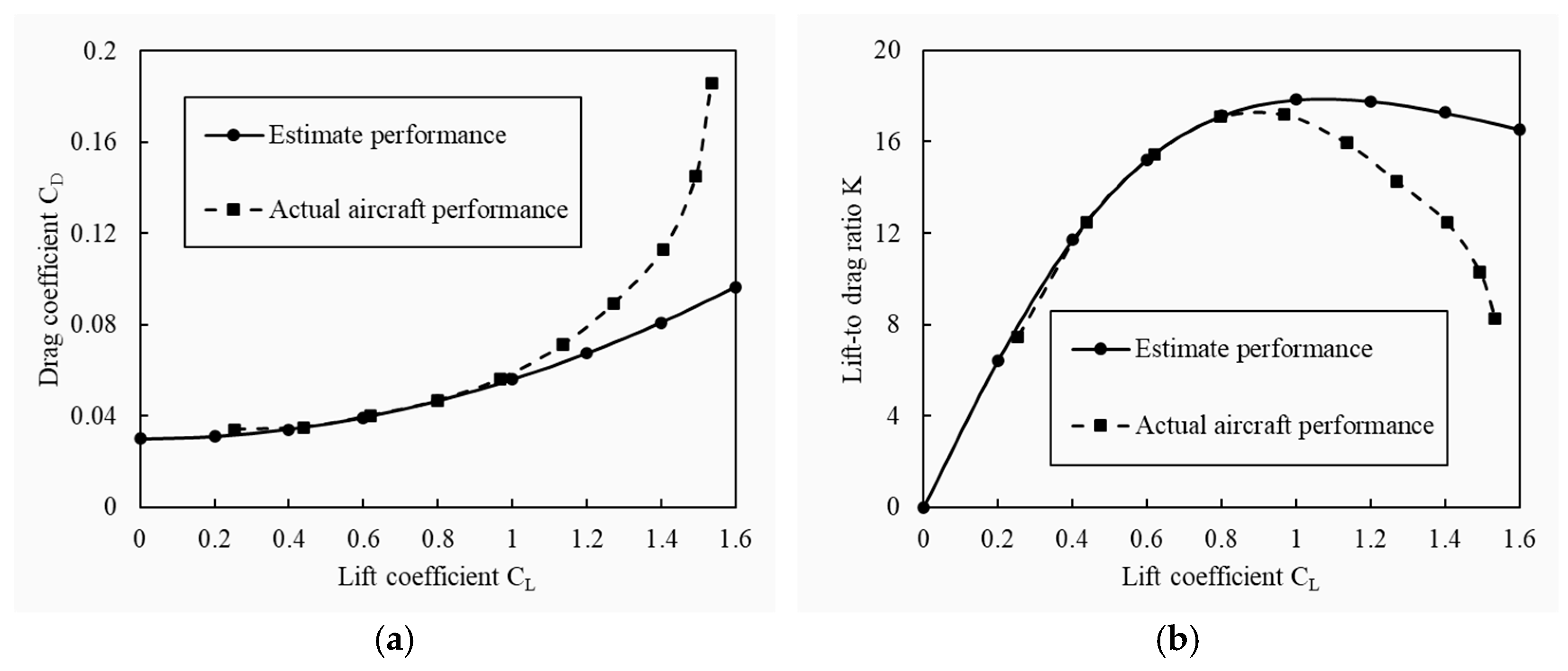
4.3. Propeller/Rotor Optimization Model
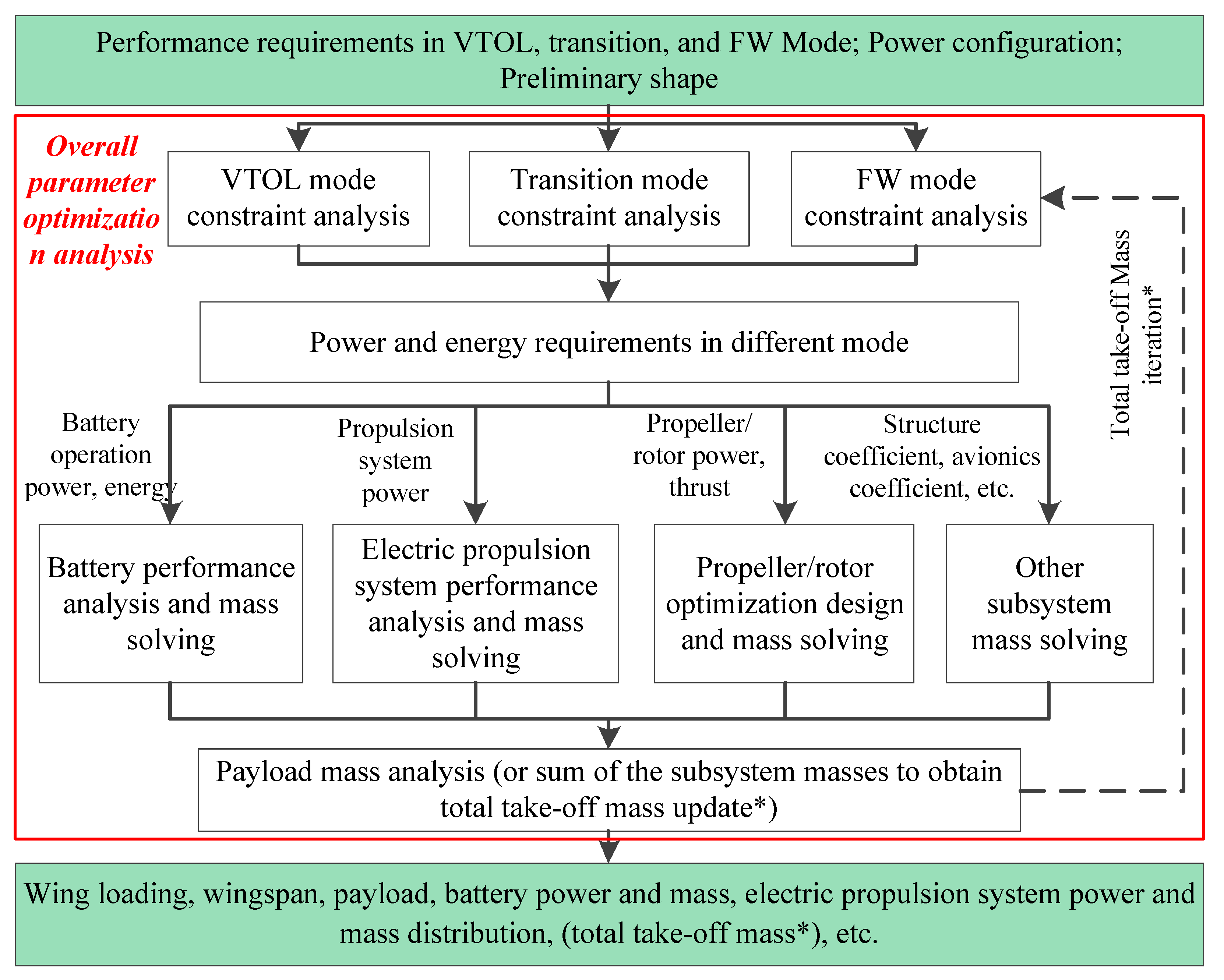
5. Preliminary Design and Optimization Process
6. Case Study
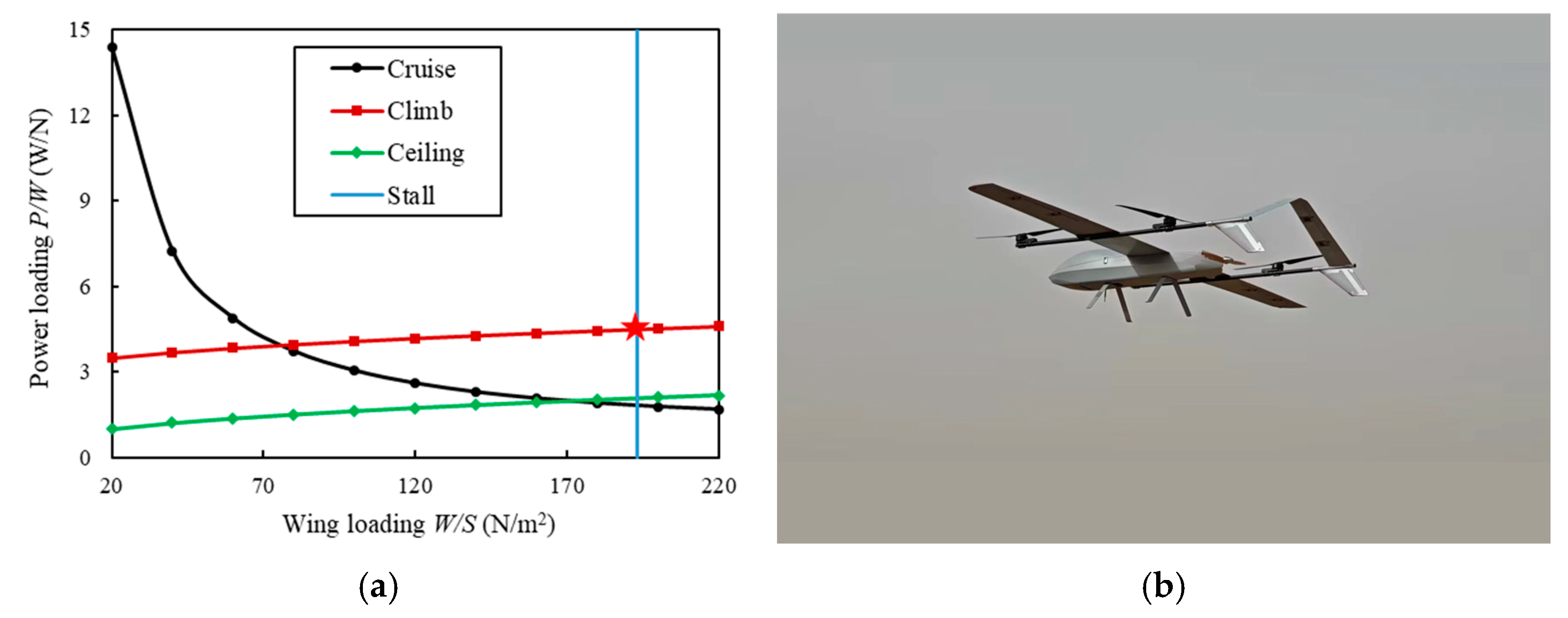
6.1. Design and Optimization Result
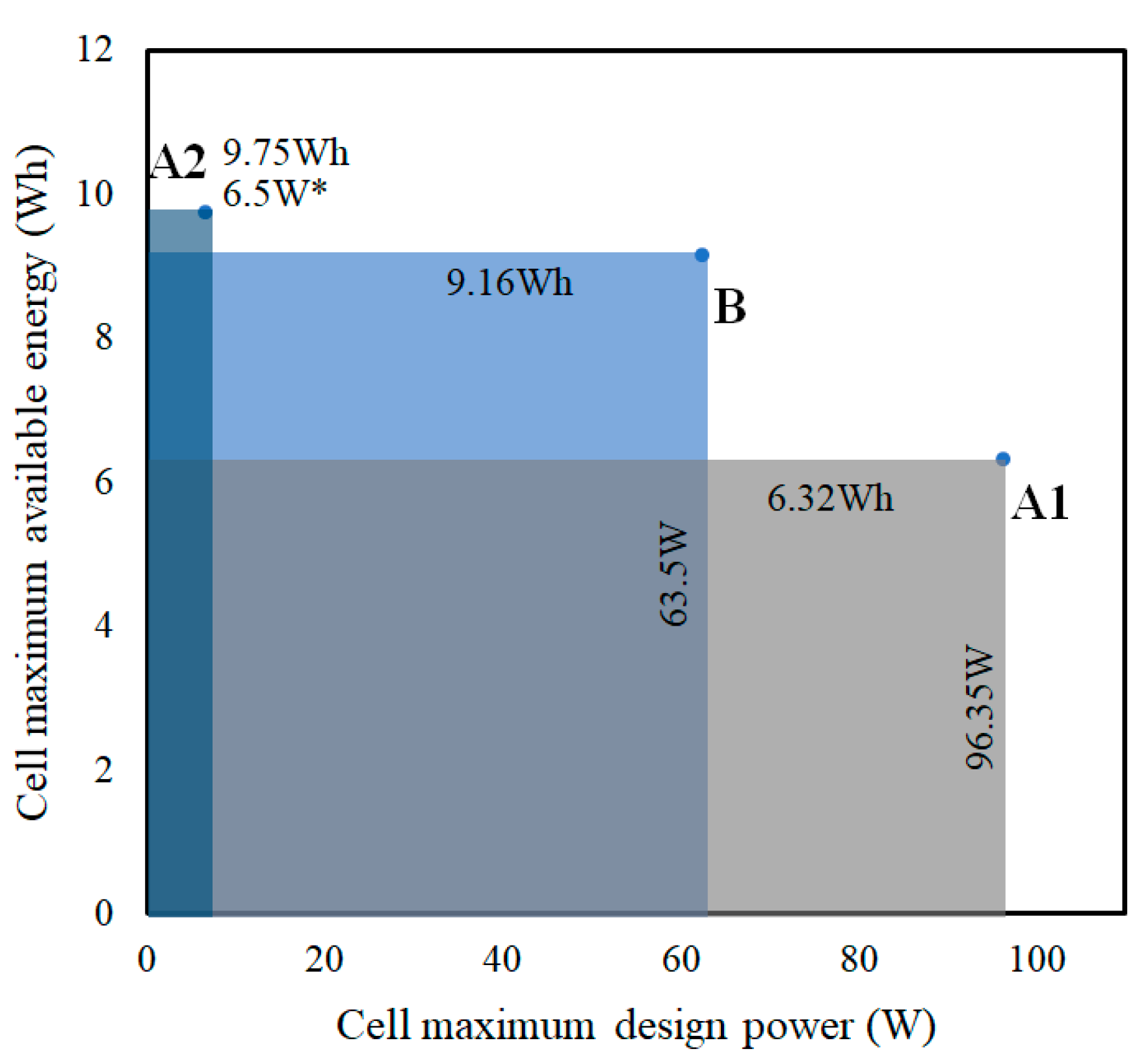
6.2. Cell Energy for Different Battery Configurations
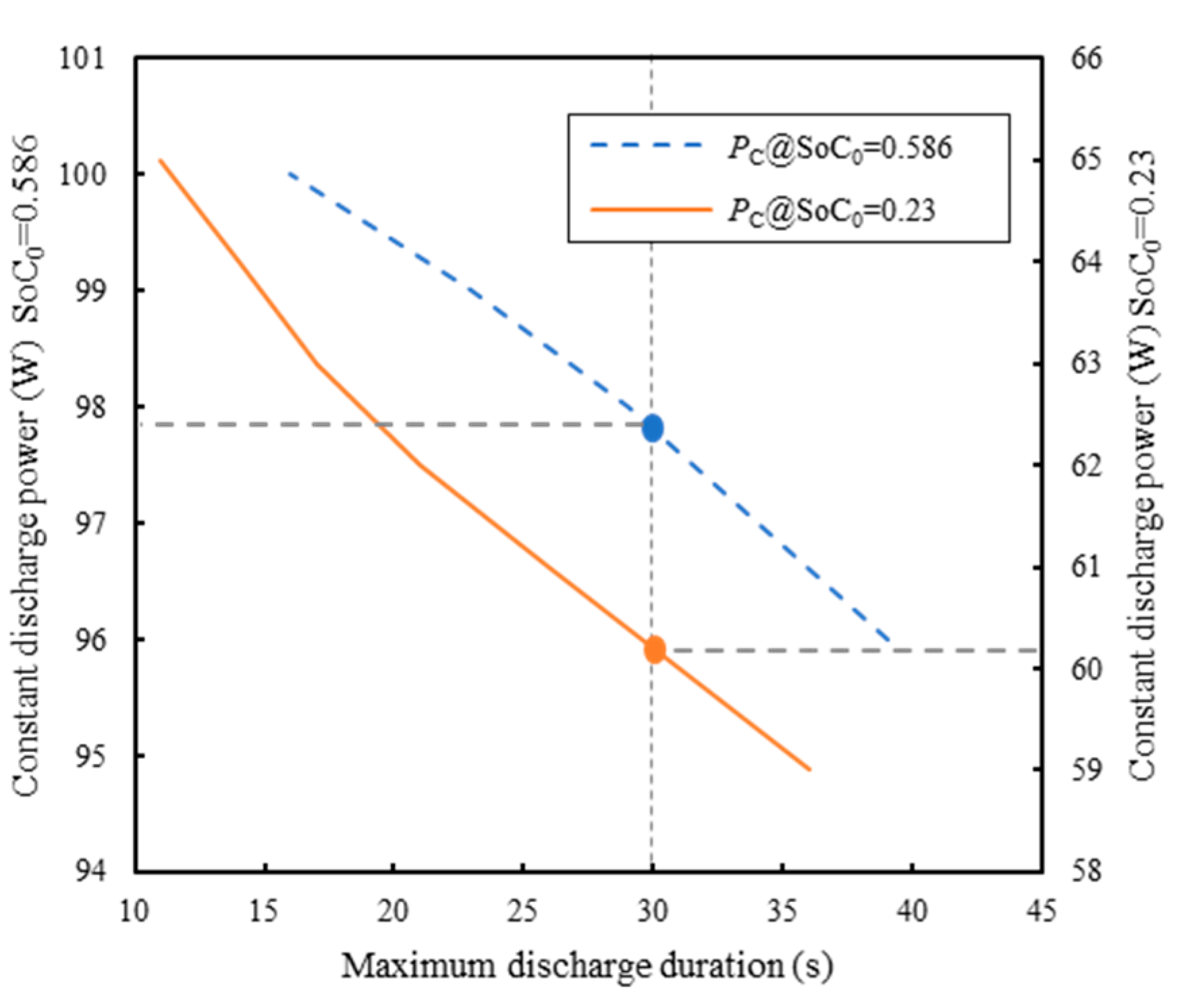
6.3. Cell Power for Different Battery Configurations
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cong, K.; Ma, D.; Xia, X.; Cheng, Y.; Guan, H.; Zhao, B. A Novel Sizing Methodology for Fixed-Wing VTOL UAVs Considering Constraint on Minimum Transition Time. Aerosp. Sci. Technol. 2025, 157, 109838. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Islam, S.; Dias, J.; Seneviratne, L.; Cai, G. A Review on the Platform Design, Dynamic Modeling and Control of Hybrid UAVs. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 806–815. [Google Scholar] [CrossRef]
- Ozdemir, U.; Aktas, Y.O.; Vuruskan, A.; Dereli, Y.; Tarhan, A.F.; Demirbag, K.; Erdem, A.; Kalaycioglu, G.D.; Ozkol, I.; Inalhan, G. Design of a Commercial Hybrid VTOL UAV System. J. Intell. Robot. Syst. Theory Appl. 2014, 74, 371–393. [Google Scholar] [CrossRef]
- Tyan, M.; Van Nguyen, N.; Kim, S.; Lee, J.W. Comprehensive Preliminary Sizing/Resizing Method for a Fixed Wing—VTOL Electric UAV. Aerosp. Sci. Technol. 2017, 71, 30–41. [Google Scholar] [CrossRef]
- Pornet, C.; Isikveren, A.T. Conceptual Design of Hybrid-Electric Transport Aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Frosina, E.; Caputo, C.; Marinaro, G.; Senatore, A.; Pascarella, C.; Di Lorenzo, G. Modelling of a Hybrid-Electric Light Aircraft. Energy Procedia 2017, 126, 1155–1162. [Google Scholar] [CrossRef]
- Mazzeo, F.; de Angelis, E.L.; Giulietti, F.; Talamelli, A.; Leali, F. Performance Analysis and Conceptual Design of Lightweight UAV for Urban Air Mobility. Drones 2024, 8, 507. [Google Scholar] [CrossRef]
- Sliwinski, J.; Gardi, A.; Marino, M.; Sabatini, R. Hybrid-Electric Propulsion Integration in Unmanned Aircraft. Energy 2017, 140, 1407–1416. [Google Scholar] [CrossRef]
- Abdilla, A.; Richards, A.; Burrow, S. Power and Endurance Modelling of Battery-Powered Rotorcraft. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 675–680. [Google Scholar] [CrossRef]
- Mulgaonkar, Y.; Kumar, V. Autonomous Charging to Enable Long-Endurance Missions for Small Aerial Robots. Micro-Nanotechnol. Sens. Syst. Appl. VI 2014, 9083, 90831S. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Quarta, A.A. Review of Hybrid-Electric Aircraft Technologies and Designs: Critical Analysis and Novel Solutions. Prog. Aerosp. Sci. 2023, 141, 100924. [Google Scholar] [CrossRef]
- Chang, T.; Yu, H. Improving Electric Powered UAVs’ Endurance by Incorporating Battery Dumping Concept. Procedia Eng. 2015, 99, 168–179. [Google Scholar] [CrossRef]
- Gatti, M.; Giulietti, F.; Turci, M. Maximum endurance for battery-powered rotary-wing aircraft. Aerosp. Sci. Technol. 2015, 45, 174–179. [Google Scholar] [CrossRef]
- Traub, L.W. Optimal Battery Weight Fraction for Maximum Aircraft Range and Endurance. J. Aircr. 2016, 53, 1176–1178. [Google Scholar] [CrossRef]
- Asli, M.; König, P.; Sharma, D.; Pontika, E.; Huete, J.; Konda, K.R.; Mathiazhagan, A.; Xie, T.; Höschler, K.; Laskaridis, P. Thermal Management Challenges in Hybrid-Electric Propulsion Aircraft. Prog. Aerosp. Sci. 2024, 144, 100967. [Google Scholar] [CrossRef]
- Omar, N.; Van den Bossche, P.; Coosemans, T.; Van Mierlo, J. Peukert Revisited-Critical Appraisal and Need for Modification for Lithium-Ion Batteries. Energies 2013, 6, 5625–5641. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Gualdoni, F.; Trainelli, L. Preliminary weight sizing of light pure-electric and hybrid-electric aircraft. Transp. Res. Procedia 2018, 29, 376–389. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Gualdoni, F. An Integrated Approach to the Preliminary Weight Sizing of Small Electric Aircraft. Aerosp. Sci. Technol. 2016, 58, 134–149. [Google Scholar] [CrossRef]
- Chen, G.; Ma, D.; Jia, Y.; Xia, X.; He, C. Comprehensive Sizing and Optimization Method for Series-Hybrid Unmanned Convertiplane. Chin. J. Aeronaut. 2021, 34, 387–402. [Google Scholar] [CrossRef]
- Magnussen, Ø.; Hovland, G.; Ottestad, M. Multicopter UAV Design Optimization. In Proceedings of the 2014 IEEE/ASME 10th International Conference on Mechatronic and Embedded Systems and Applications (MESA), Senigallia, Italy, 10–12 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Fuller, M.E. A Battery Model for Constant-Power Discharge Including Rate Effects. Energy Convers. Manag. 2014, 88, 199–205. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A Comparative Study of Equivalent Circuit Models for Li-Ion Batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- He, C.; Zhan, F.; Ma, L.; Chen, G.; Ma, J. Aero-Structural Design of Joined-Wing Aircraft Based on High-Fidelity Model. Chin. J. Aeronaut. 2024, 37, 363–377. [Google Scholar] [CrossRef]
- Serrano, A.R. Design Methodology for Hybrid (VTOL + Fixed Wing) Unmanned Aerial Vehicles. Aeronaut. Aerosp. Open Access J. 2018, 2, 165–176. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Y.; Li, L.; Huang, F.; Zhan, H.; Fu, Y.; Song, Y. Design and Flight Simulation Verification of the Dragonfly EVTOL Aircraft. Drones 2024, 8, 311. [Google Scholar] [CrossRef]
- He, C.; Jia, Y.; Ma, D. Optimization and Analysis of Hybrid Electric System for Distributed Propulsion Tilt-Wing UAV. IEEE Access 2020, 8, 224654–224667. [Google Scholar] [CrossRef]
- Bodlak, E. The Design Space Exploration and Preliminary Testing of a New Class of Tailsitting Quadrotor Aircraft. Ph.D. Thesis, University of Kansas, Lawrence, KS, USA, 2016. [Google Scholar]
- Donateo, T.; Spedicato, L. Fuel Economy of Hybrid Electric Flight. Appl. Energy 2017, 206, 723–738. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman Filtering for Battery Management Systems of LiPB-Based HEV Battery Packs—Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems: Introduction to Modeling and Optimization, 3rd ed.; Springer: Berlin, Germany, 2013; p. 96. [Google Scholar]
- Bershadsky, D.; Haviland, S.; Johnson, E.N. Electric Multirotor Propulsion System Sizing for Performance Prediction and Design Optimization. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; pp. 1–22. [Google Scholar] [CrossRef]
- Xia, X.; Ma, D.; Zhang, L.; Liu, X.; Cong, K. Blade Shape Optimization and Analysis of a Propeller for VTOL Based on an Inverse Method. Appl. Sci. 2022, 12, 3694. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; Li, J.; Zhuang, J. Aerodynamic Investigation for a Propeller-Induced Lift-Enhancing Vertical Take-Off and Landing (VTOL) Configuration. Drones 2025, 9, 20. [Google Scholar] [CrossRef]
- He, C.; Chen, G.; Sun, X.; Li, S.; Li, Y. Geometrically Compatible Integrated Design Method for Conformal Rotor and Nacelle of Distributed Propulsion Tilt-Wing UAV. Chin. J. Aeronaut. 2023, 36, 229–245. [Google Scholar] [CrossRef]
- Hicks, R.M.; Cliff, S.E. An Evaluation of Three Two-Dimensional Computational Fluid Dynamics Codes Including Low Reynolds Numbers and Transonic Mach Numbers; NASA: Washington, DC, USA, 1991. [Google Scholar]

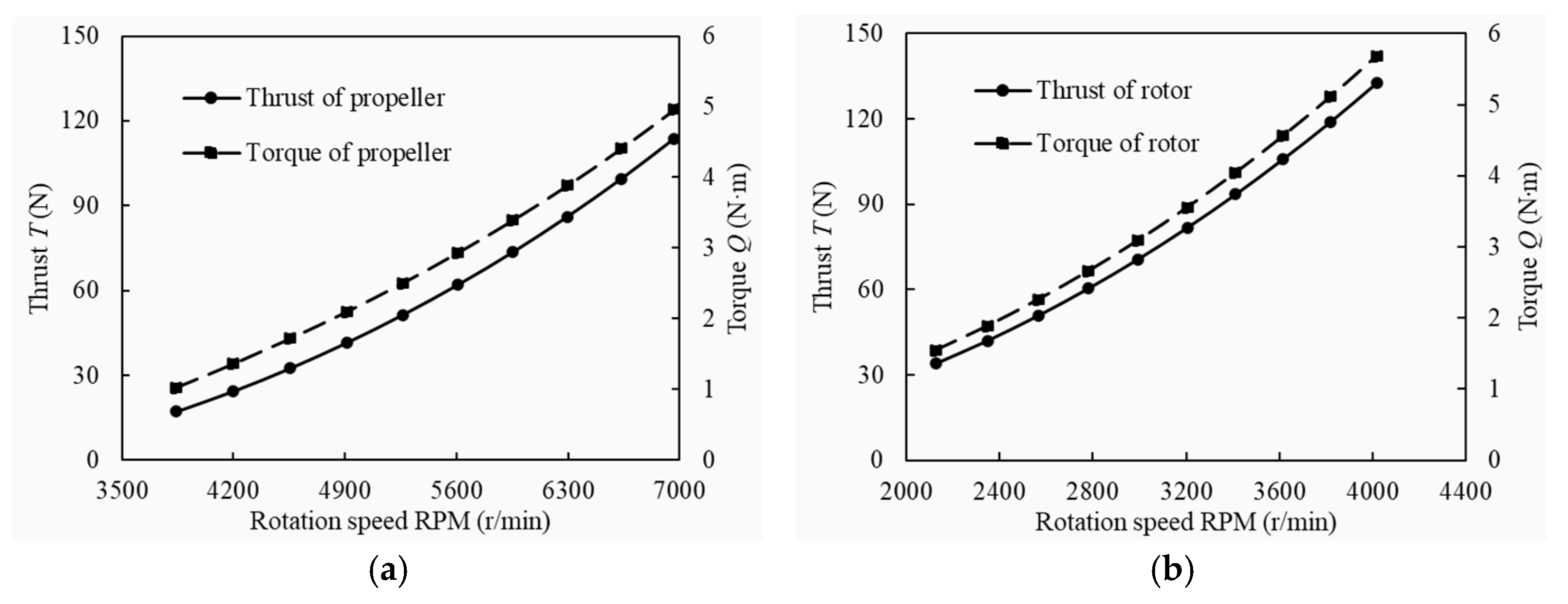
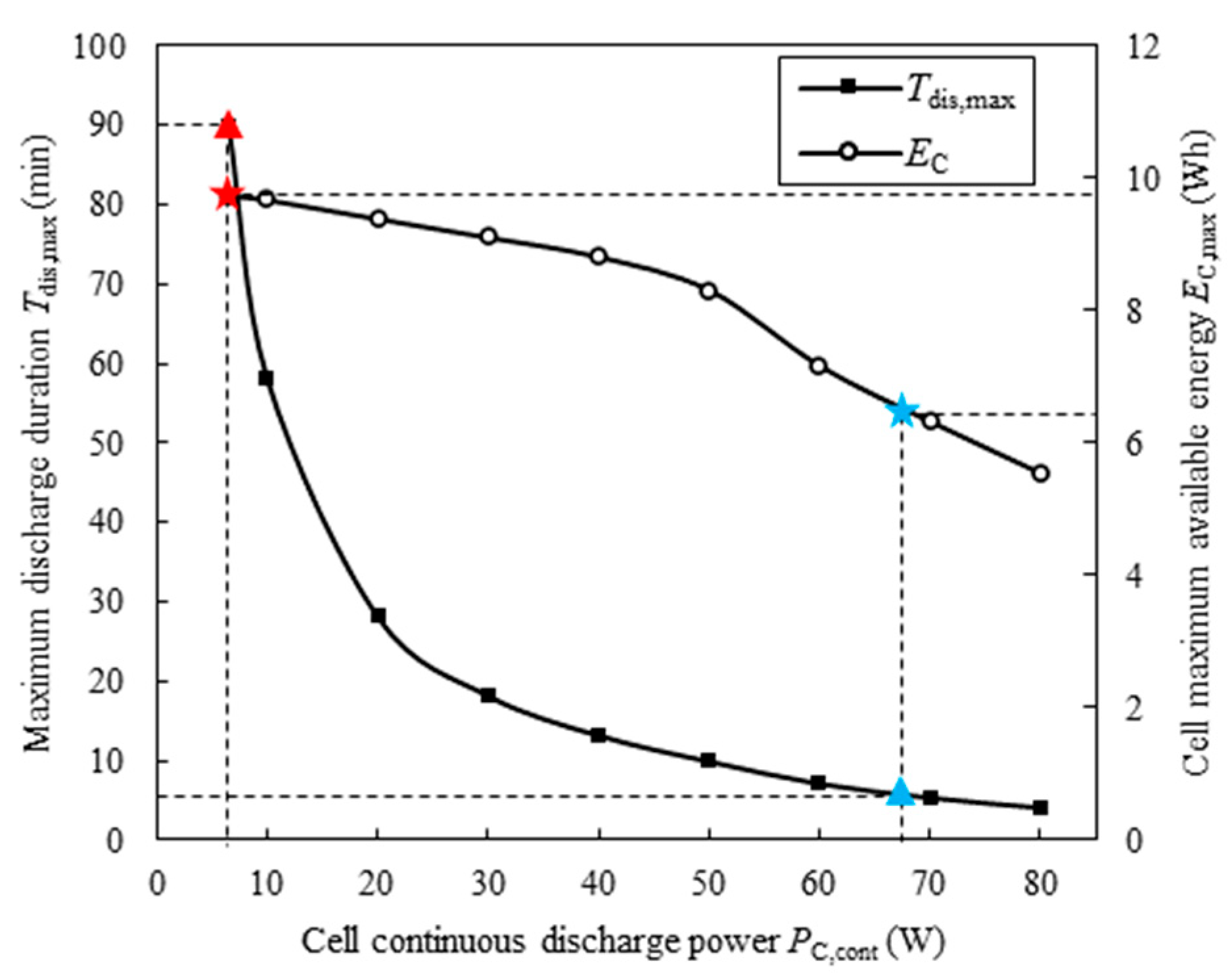
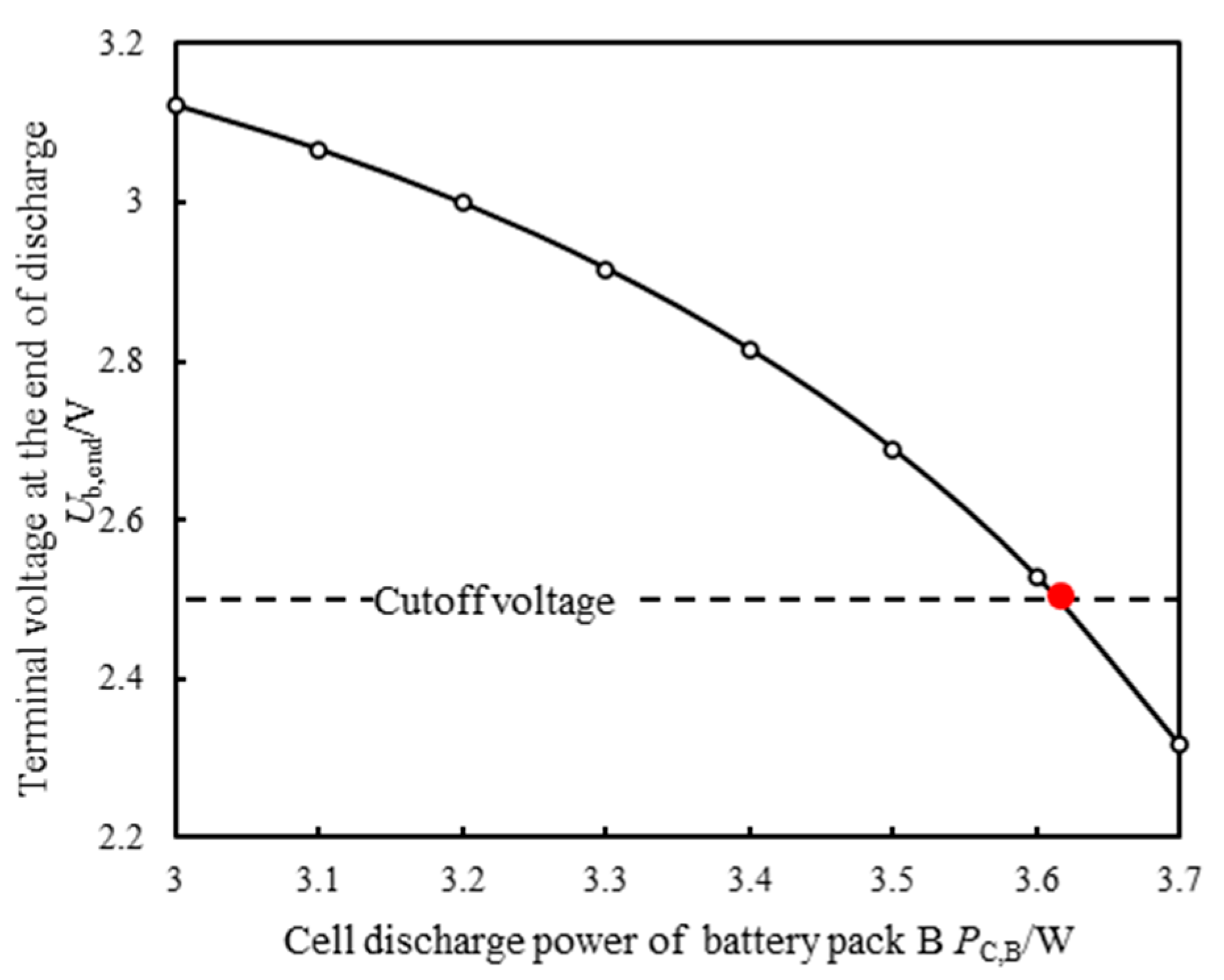
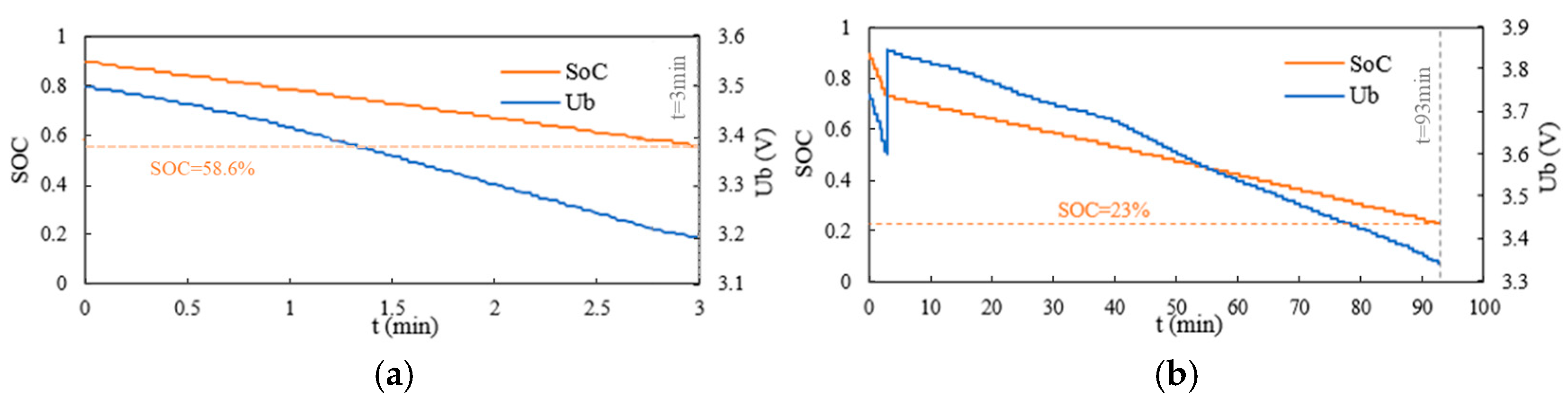
| Parameter | Value |
|---|---|
| Rated capacity | 3 Ah |
| Mass | 50 g |
| Maximum discharge voltage | 4.2 V |
| Cut off voltage | 2.5 V |
| Rated voltage | 3.6 V |
| Design Requirement | Value | Parameter | Value |
|---|---|---|---|
| Rate of climb dh/dt (m/s) | 3 | Aspect ratio AR | 18 |
| Transition altitude Htrans (m) | 100 | Zero-lift drag coefficient CD0 | 0.03 |
| Safety margin coefficient δS | 5 | Oswald’s span efficiency factor e | 0.68 |
| Static thrust coefficient δT | 1.3 | Drag coefficient (VTOL) CD,VTOL | 0.6 |
| Cruise speed V (m/s) | 25 | Battery-rated voltage UBatt (V) | 36 |
| Endurance in FW mode te (min) | 90 |
| Items | Dedicated Configuration | Shared Configuration | Actual Aircraft (Shared Configuration) |
|---|---|---|---|
| Takeoff mass (kg) | 30 | 30 | 30 |
| Wing loading (N/m2) | 192.5 | 192.5 | 196 |
| Wing area (m2) | 1.53 | 1.53 | 1.5 |
| Wing span (m) | 5.25 | 5.25 | 5 |
| Structural mass (kg) | 10.5 | 10.5 | 9.7 |
| Avionics mass (kg) | 1.5 | 1.5 | 1.25 |
| Payload mass (kg) | 1.56 | 3.36 | 3.67 |
| Battery mass (kg) | 12 | 10.2 | 10.7 |
| ESC mass (kg) | 0.56 | 0.56 | 0.64 |
| Motor mass (kg) | 3.35 | 3.35 | 3.58 |
| Propeller/rotor mass (kg) | 0.53 | 0.53 | 0.46 |
| Flight Stage | VTOL Ascent/Descent | VTOL Transition | FW Cruise |
|---|---|---|---|
| Power value (kW) | 6.35 | 10.03 | 0.57 |
| Energy value (Wh) | 582 | 83 | 855 |
| Duration (min) | 5.5 | 0.5 | 90 |
| Item | Dedicated Configuration | Shared Configuration | Constant Power/Energy Density 1 [4] | Constant Power/Energy Density 2 [17] | Actual (Shared Configuration) | |
|---|---|---|---|---|---|---|
| A1 | A2 | B | ||||
| NL × NS | 11 × 10 | 9 × 10 | 17 × 10 | - | - | 17 × 10 |
| MBatt, kg | 6.6 | 5.4 | 10.2 | 9.58 | 11.8 | 10.7 |
| Error | 12.1% | 4.6% | 10.5% | 10.3% | - | |
| Motor Type | Parameter | Speed Constant KV | Internal Resistance R0 (mΩ) | No-Load Current I0 (A) | Mass Mm (kg) |
|---|---|---|---|---|---|
| Rotor motor | Design result | 119 | 0.022 | 1.35 | 0.59 |
| Real-life rotor motor | 115 | 0.037 | 1.3 | 0.64 | |
| Fix-wing motor | Design result | 165 | 0.016 | 2.14 | 0.99 |
| Real-life fixed-wing motor | 160 | 0.017 | 1.8 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Tong, Y.; Liu, D.; Yang, S.; Zhan, F. Preliminary Design and Optimization Approach of Electric FW-VTOL UAV Based on Cell Discharge Characteristics. Drones 2025, 9, 415. https://doi.org/10.3390/drones9060415
He C, Tong Y, Liu D, Yang S, Zhan F. Preliminary Design and Optimization Approach of Electric FW-VTOL UAV Based on Cell Discharge Characteristics. Drones. 2025; 9(6):415. https://doi.org/10.3390/drones9060415
Chicago/Turabian StyleHe, Cheng, Yuqi Tong, Diyi Liu, Shipeng Yang, and Fengjiang Zhan. 2025. "Preliminary Design and Optimization Approach of Electric FW-VTOL UAV Based on Cell Discharge Characteristics" Drones 9, no. 6: 415. https://doi.org/10.3390/drones9060415
APA StyleHe, C., Tong, Y., Liu, D., Yang, S., & Zhan, F. (2025). Preliminary Design and Optimization Approach of Electric FW-VTOL UAV Based on Cell Discharge Characteristics. Drones, 9(6), 415. https://doi.org/10.3390/drones9060415







