Real-Time TECS Gain Tuning Using Steepest Descent Method for Post-Transition Stability in Unmanned Tilt-Rotor eVTOLs
Abstract
1. Introduction
- The development of a real-time adaptive TECS framework that dynamically tunes gains to improve post-transition stability in unmanned tilt-rotor eVTOLs.
- A simulation-based demonstration showing that SD-TECS outperforms PX4 TECS in altitude and airspeed control under various conditions.
- Validation of the proposed method’s practical applicability through sensitivity and computational complexity analyses, ensuring robustness and feasibility for real-world applications.
2. Preliminaries
2.1. PX4 VTOL Control Architecture Overview
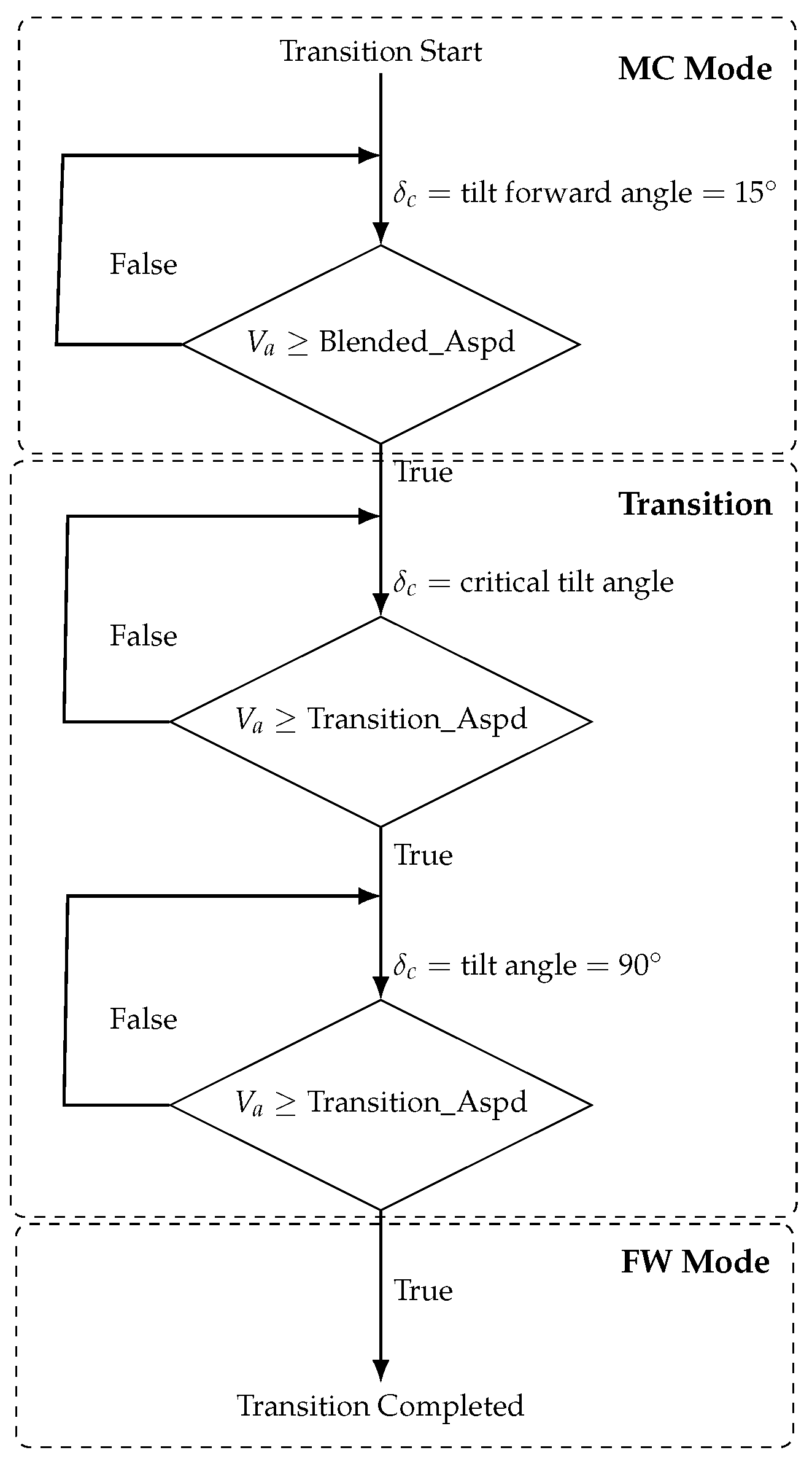
2.2. PX4 Transition Logic for Tilt-Rotor eVTOLs
- Open-loop tilt-angle control: Front rotors tilt incrementally based on fixed airspeed thresholds (e.g., BLENDED_ASPD for initiating control output blending, and TRANSITION_ASPD for full fixed-wing mode engagement).
- Linear control blending: PX4 linearly interpolates between multicopter and fixed-wing attitude controllers based on airspeed, ignoring aerodynamic nonlinearity.
2.3. Total Energy Control System (TECS)
Gain Nomenclature Clarification
3. Literature Review
3.1. Control Strategies for Urban Air Mobility (UAM)
3.2. PX4-Based Transition Control and Limitations
3.3. TECS and Energy-Based Control Advances
3.4. Gradient-Based Adaptive Control Techniques
3.5. Summary
4. Methodology
4.1. Adaptive Gain Tuning via Steepest Descent
4.1.1. Motivation for the Steepest Descent Method
4.1.2. Steepest Descent Gain-Update Formulation
4.2. Implementation and Validation
5. Simulation Model
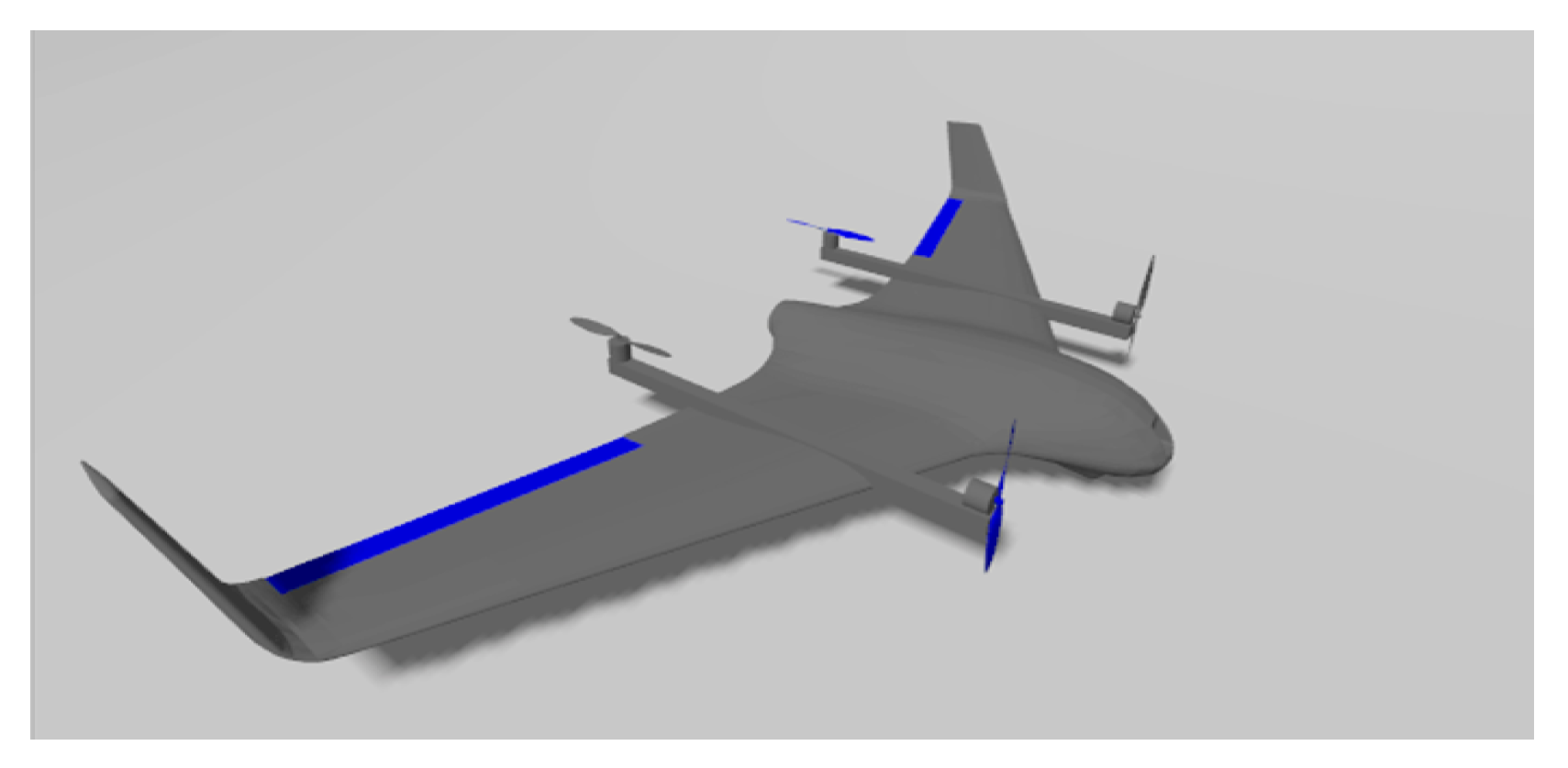
5.1. Aircraft Configuration and Longitudinal Dynamics
| Symbol | Value | Description |
|---|---|---|
| m | 5.22 kg | Total mass of the aircraft |
| 1.229 kg·m2 | Moment of inertia about the x-axis | |
| 0.1702 kg·m2 | Moment of inertia about the y-axis | |
| 0.8808 kg·m2 | Moment of inertia about the z-axis | |
| 0.9343 kg·m2 | Product of inertia | |
| 0.75 m2 | Wing surface area | |
| b | 2.10 m | Wingspan |
| 0.3571 m | Mean aerodynamic chord |
| Symbol | Value | Description |
|---|---|---|
| 0.0867 | Lift coefficient at zero angle of attack | |
| 4.02 | Lift coefficient per radian of angle of attack | |
| 3.8954 | Lift coefficient per unit pitch rate | |
| 0.278 | Lift coefficient per unit elevator deflection | |
| 0.0197 | Drag coefficient at zero angle of attack | |
| 0.0791 | Drag coefficient per radian of angle of attack | |
| 1.06 | Drag coefficient per radian squared of angle of attack | |
| 0.0 | Drag coefficient per unit pitch rate | |
| 0.0633 | Drag coefficient per unit elevator deflection | |
| 0.0302 | Moment coefficient at zero angle of attack | |
| −0.126 | Moment coefficient per radian of angle of attack | |
| −1.3047 | Moment coefficient per unit pitch rate | |
| −0.206 | Moment coefficient per unit elevator deflection |
5.2. Control Architecture
- Multicopter Flight Mode:
- –
- Attitude Stabilization: A cascaded PID controller regulates the roll, pitch, and yaw rates using angular rate feedback.
- –
- Altitude Hold: A proportional–integral (PI) controller tracks the desired altitude by modulating the vertical thrust.
- Fixed-Wing Flight Mode:
- –
- Attitude Control: A pitch attitude controller maintains longitudinal stability using elevator surface deflection.
- –
- Energy Management: TECS regulates the total and balanced energy rates by coordinating the throttle and pitch commands.
6. Simulation Results
6.1. Simulation Setup
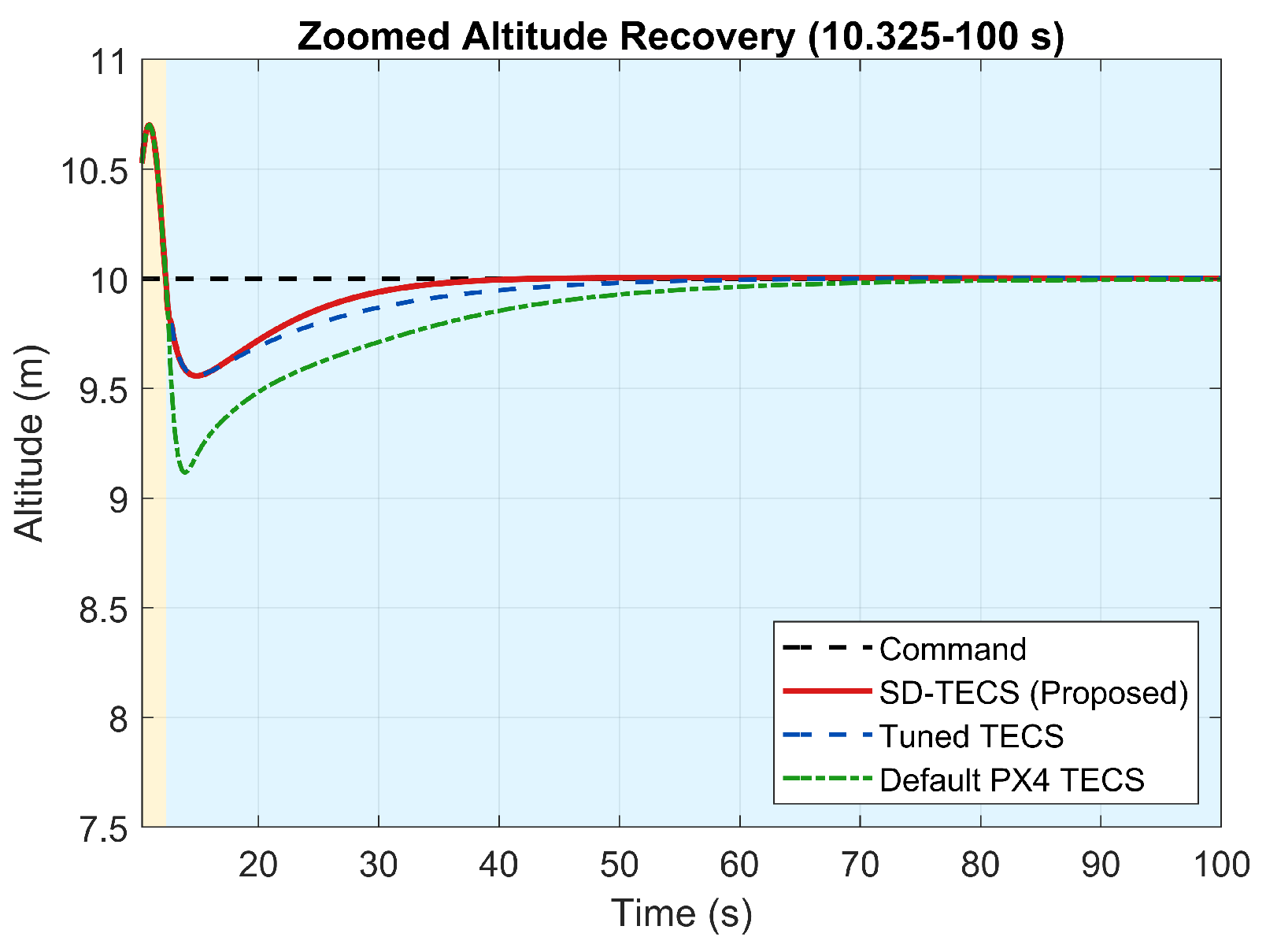
6.2. TECS State Response
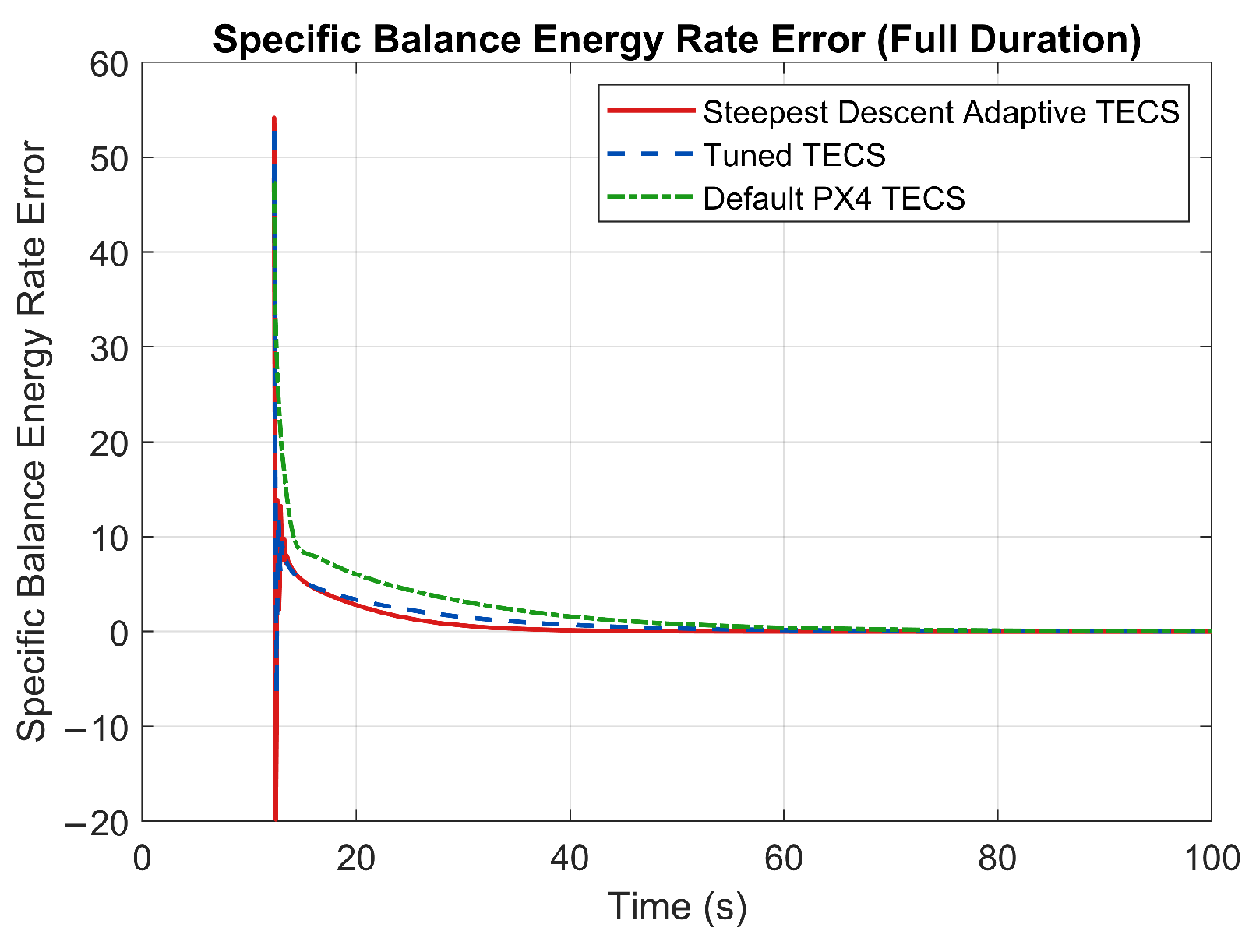
6.3. Energy-Rate Error Response
6.4. TECS Control Outputs
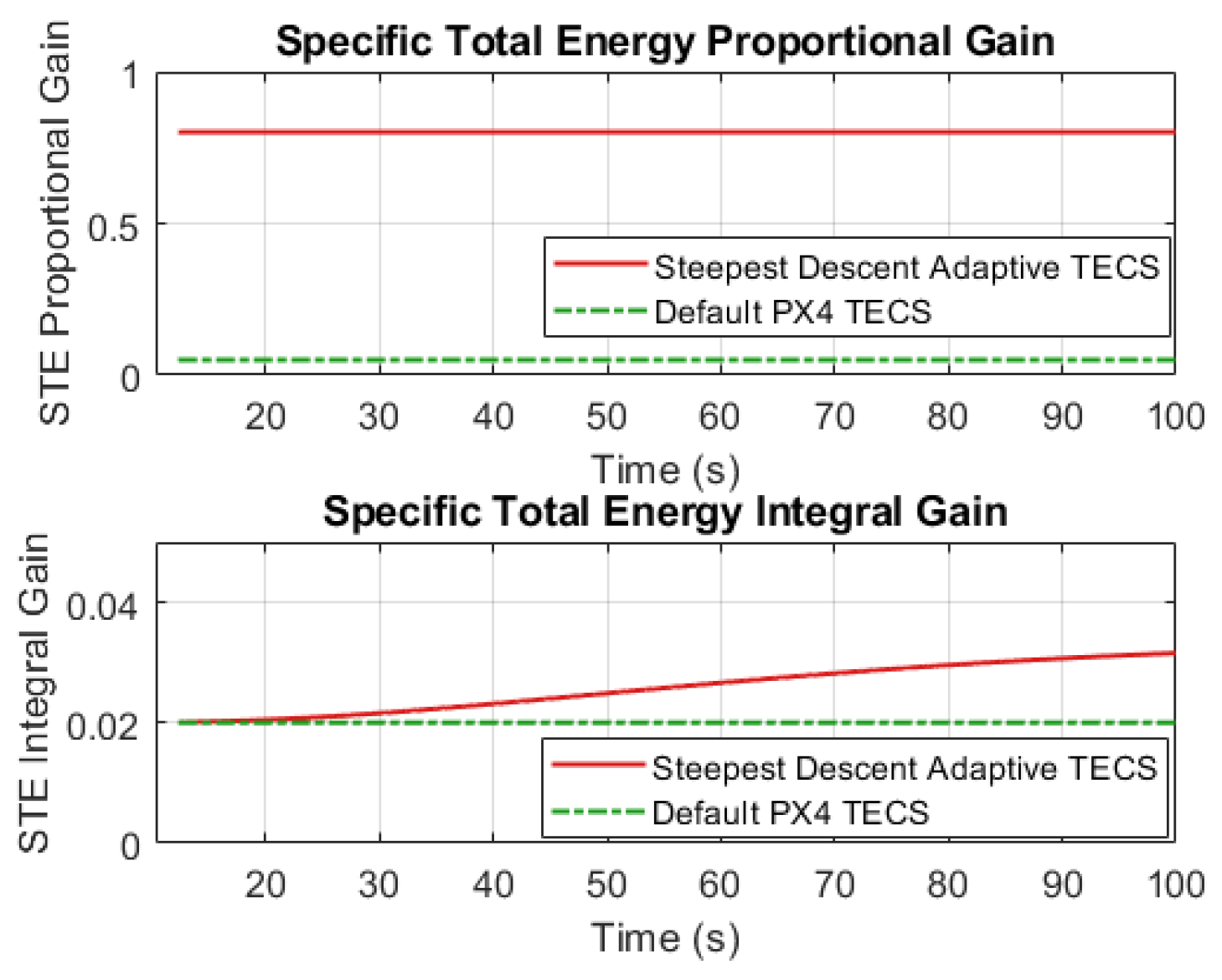
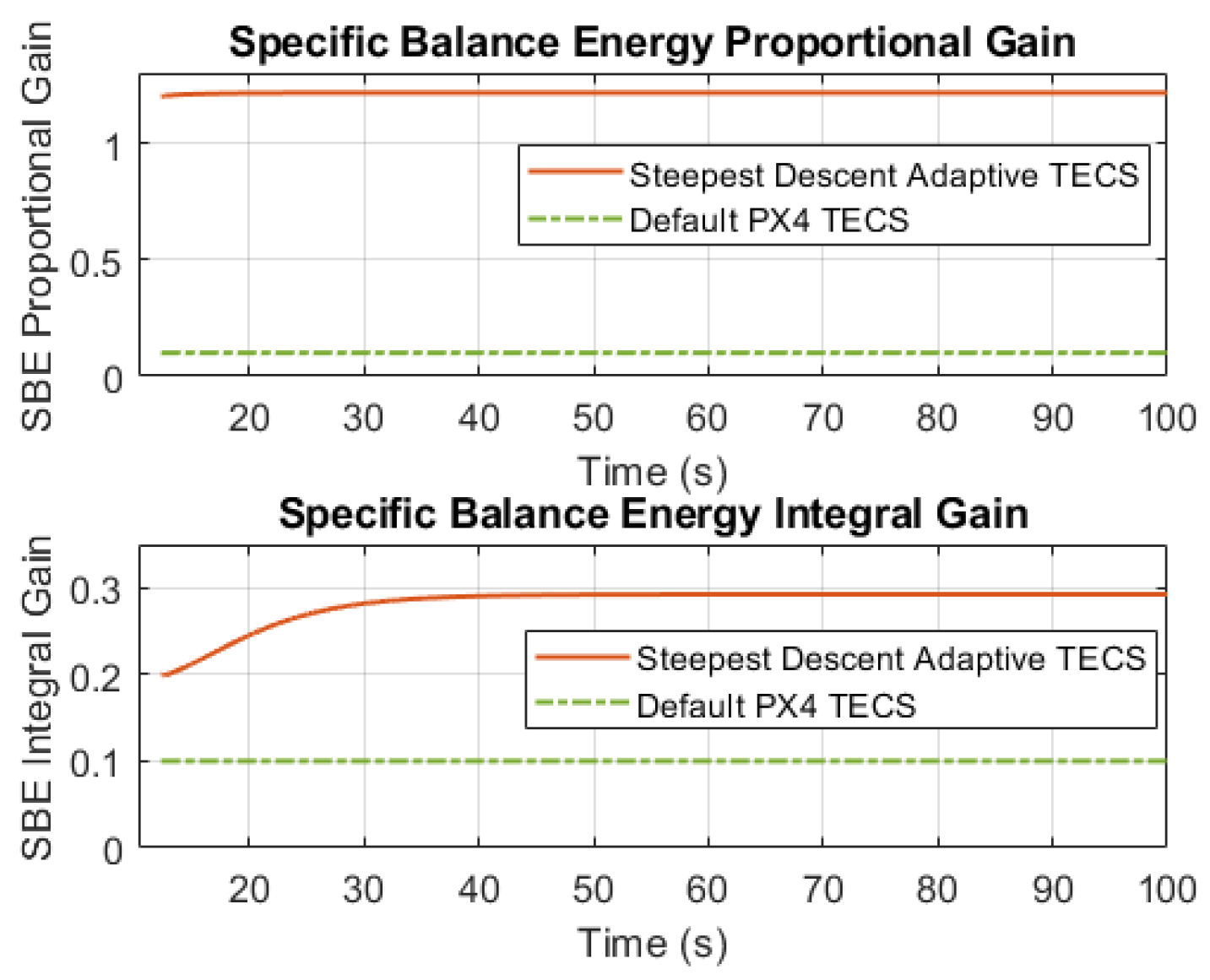
6.5. TECS Gain Tuning
6.6. Performance Analysis
6.6.1. Transient Response Metrics
6.6.2. Quantitative Evaluation: MAE, IAE, and ITAE
- MAE (Mean Absolute Error): ;
- IAE (Integral of Absolute Error): ;
- ITAE (Integral of Time-weighted Absolute Error): .
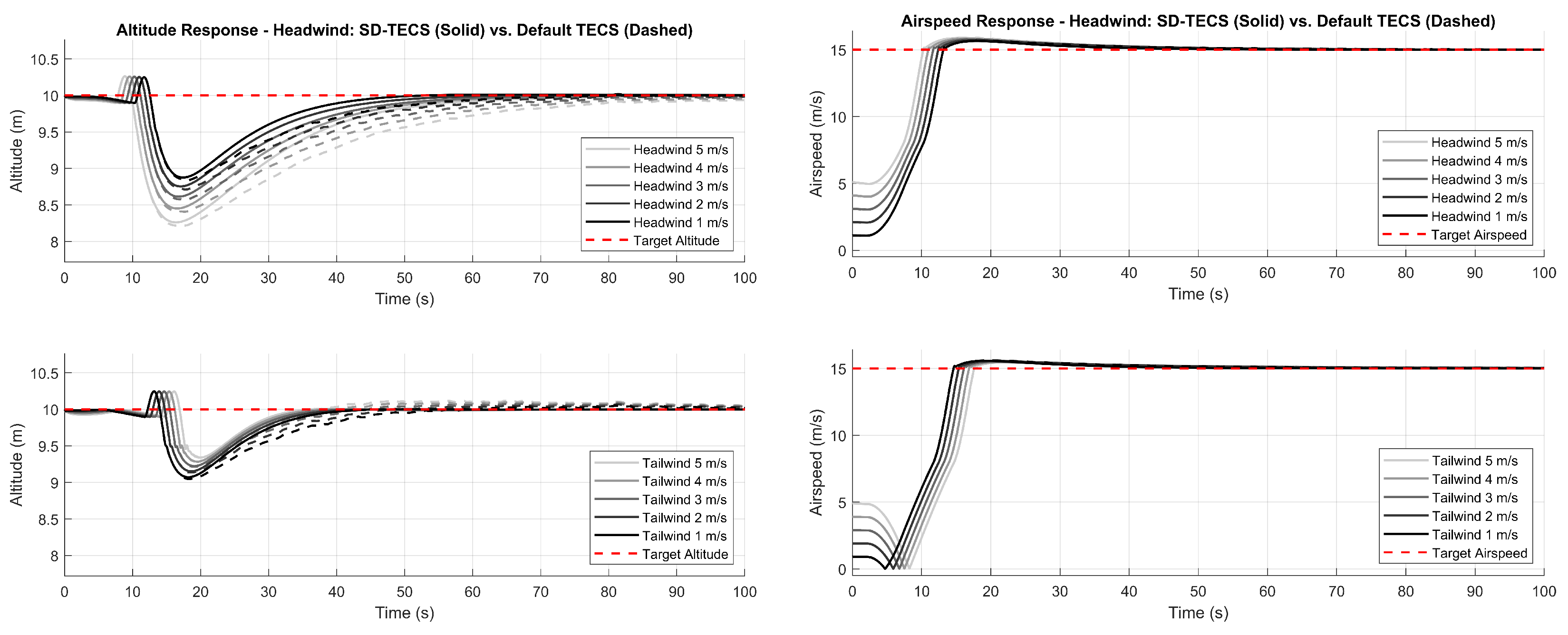
6.7. Robustness Analysis
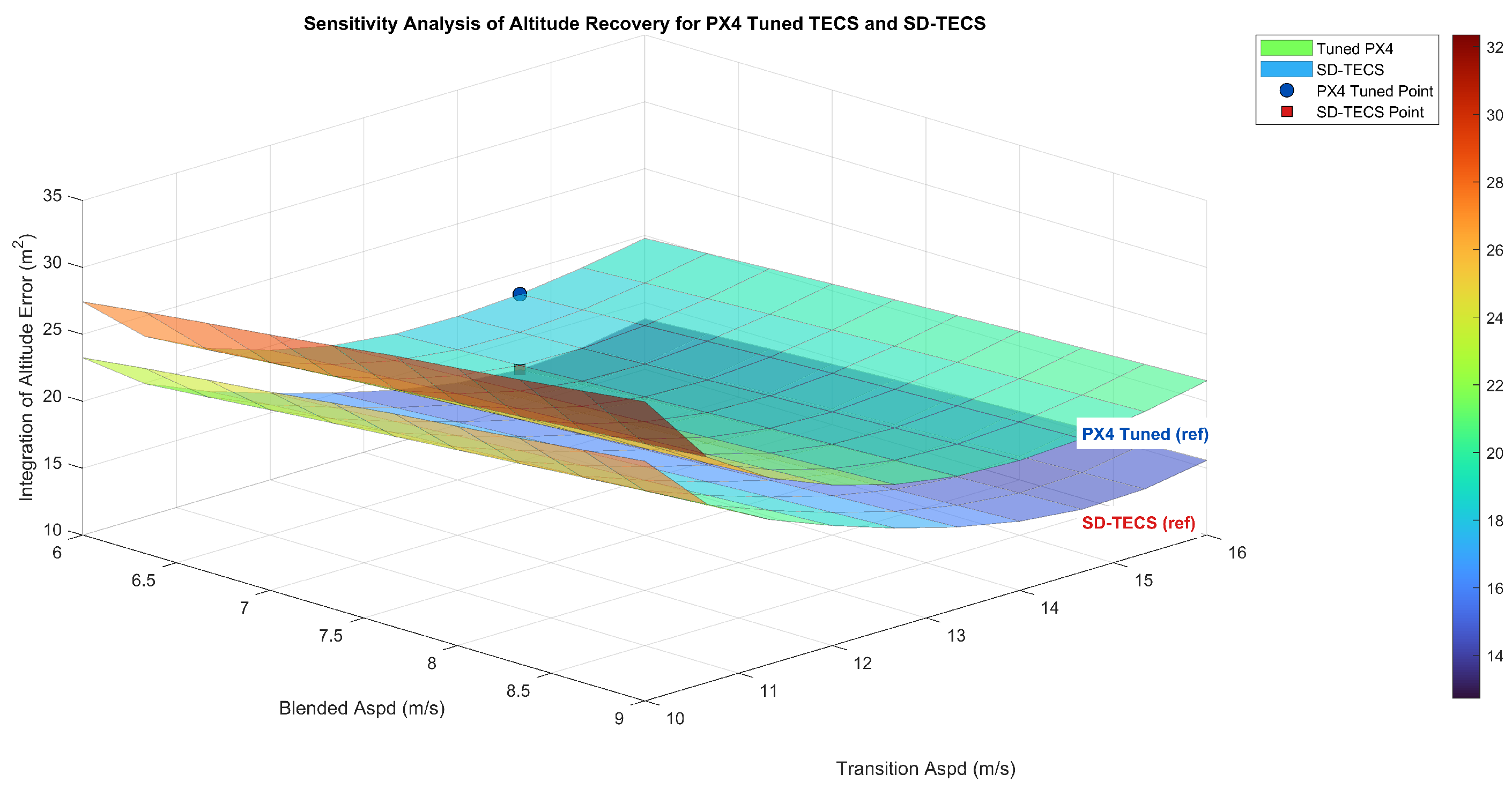
6.8. Sensitivity Analysis
6.9. Computational Complexity Analysis
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SD-TECS | Steepest Descent-based Total Energy Control System |
| TECS | Total Energy Control System |
| PX4 | PX4 Autopilot |
| eVTOL | Electric Vertical Take-Off and Landing |
| UAM | Urban Air Mobility |
| IAE | Integral of Absolute Error |
| ITAE | Integral of Time-weighted Absolute Error |
| MAE | Mean Absolute Error |
References
- Straubinger, A.; Rothfeld, R.; Shamiyeh, M.; Büchter, K.-D.; Kaiser, J.; Plötner, K.O. An overview of current research and developments in urban air mobility. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 417–441. [Google Scholar] [CrossRef]
- Saleem, O.; Kazim, M.; Iqbal, J. Robust position control of VTOL UAVs using a linear quadratic rate-varying integral tracker: Design and validation. Drones 2025, 9, 73. [Google Scholar] [CrossRef]
- Tutsoy, O.; Asadi, D.; Ahmadi, K.; Nabavi-Chashmi, S.Y.; Iqbal, J. Minimum distance and minimum time optimal path planning with bioinspired machine learning algorithms for faulty unmanned air vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9069–9077. [Google Scholar] [CrossRef]
- PX4 Autopilot. PX4 Open-Source Autopilot. Available online: https://px4.io/ (accessed on 3 June 2025).
- Meier, L.; Honegger, D.; Pollefeys, M. A Survey of Open-Source UAV Autopilots. Electronics 2024, 13, 4785. [Google Scholar] [CrossRef]
- Lambregts, A.A. Integrated System Design for Flight and Propulsion Control Using Total Energy Principles. In Proceedings of the AIAA Aircraft Design, Systems and Technology Meeting, Fort Worth, TX, USA, 17–19 October 1983. AIAA-83-2561. [Google Scholar] [CrossRef]
- PX4 Discussion Forum. Pitch up on Transitions to Fixed Wing. 2019. Available online: https://discuss.px4.io/t/pitch-up-on-transitions-to-fixed-wing/11287 (accessed on 3 June 2025).
- Brigido, D.; Rodriguez, H. Experimental Validation of an Adaptive Total Energy Control System Strategy for the Longitudinal Dynamics of a Fixed-Wing Aircraft. J. Aerosp. Eng. 2015, 28, 04014103. [Google Scholar] [CrossRef]
- Anandakumar, A.; Bernstein, D.S.; Goel, A. Adaptive Energy Control of Longitudinal Aircraft Dynamics. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- He, A.; Zhang, Y.; Zhao, H.; Wang, B.; Gao, Z. Adaptive Fault-Tolerant Control of a Hybrid VTOL UAV against Actuator Faults and Model Uncertainties under Fixed-Wing Mode. Int. J. Aerosp. Eng. 2022, 2022, 8191154. [Google Scholar] [CrossRef]
- Ahn, K.K.; Thanh, T.D.C. Nonlinear PID control to improve the control performance of the pneumatic artificial muscle manipulator using neural network. J. Mech. Sci. Technol. 2005, 19, 106–115. [Google Scholar] [CrossRef]
- Alagoz, B.B.; Tepljakov, A.; Kavuran, G.; Alisoy, H. Adaptive control of nonlinear TRMS model by using gradient descent optimizers. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Yağmur, N.; Alagoz, B.B. Comparison of solutions of numerical gradient descent method and continuous time gradient descent dynamics and Lyapunov stability. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 3897–3908. [Google Scholar]
- Lu, K.; Tian, H.; Zhen, P.; Lu, S.; Chen, R. Conversion Flight Control for Tiltrotor Aircraft via Active Disturbance Rejection Control. Aerospace 2022, 9, 155. [Google Scholar] [CrossRef]
- Chen, Q.; Hu, Z.; Geng, J.; Bai, D.; Mousaei, M.; Scherer, S. A Unified MPC Strategy for a Tilt-rotor VTOL UAV Towards Seamless Mode Transitioning. arXiv 2024, arXiv:2402.07375. Available online: https://arxiv.org/abs/2402.07375 (accessed on 3 June 2025).
- Garrow, L.A.; German, B.J.; Leonard, C.E. Urban air mobility: A comprehensive review and comparative analysis with autonomous and electric ground transportation for informing future research. Transp. Res. Part Emerg. Technol. 2021, 132, 103377. Available online: https://www.sciencedirect.com/science/article/pii/S0968090X21003788 (accessed on 3 June 2025). [CrossRef]
- Sengupta, R.; Bulusu, V.; Mballo, C.E.; Onat, E.B.; Cao, S.A. Urban Air Mobility Research Challenges and Opportunities. Annu. Rev. Control. Robot. Auton. Syst. 2025, 8, 407–431. [Google Scholar] [CrossRef]
- Schoser, J.J.; Cuadrat-Grzybowski, M.; Castro, S.G.P. Preliminary control and stability analysis of a long-range eVTOL aircraft. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Sobiesiak, L.; Topping, H.F. Modelling and control of transition flight of an eVTOL tandem tilt-wing aircraft. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain, 1–4 July 2019; Available online: https://www.eucass.eu/doi/EUCASS2019-0137.pdf (accessed on 3 June 2025).
- Salem, W.A.; Mohamady, O.; Draz, M.; El-bayoumi, G. Promoting the Maneuverability and Fault-Tolerant Control of Hybrid VTOL UAVs; Springer: Berlin/Heidelberg, Germany, 2023; Available online: https://link.springer.com/article/10.1007/s13369-023-08255-0 (accessed on 3 June 2025).
- Fixed-wing Altitude/Position Controller Tuning|PX4 Guide. PX4 Official Documentation. Available online: https://docs.px4.io/main/en/config_fw/position_tuning_guide_fixedwing.html (accessed on 3 June 2025).
- ArduPilot. QuadPlane Transition Control. Retrieved May 2025. Available online: https://ardupilot.org/plane/docs/quadplane-transitions.html (accessed on 3 June 2025).
- Choi, J.; Kim, H.M.; Hwang, H.J.; Kim, Y.-D.; Kim, C.O. Modular Reinforcement Learning for Autonomous UAV Flight Control. Drones 2023, 7, 418. [Google Scholar] [CrossRef]
- Jimenez, P.; Lichota, P.; Agudelo, D.; Rogowski, K. Experimental Validation of Total Energy Control System for UAVs. Energies 2020, 13, 14. [Google Scholar] [CrossRef]
- Spencer, J.; Lee, J.; Paredes, J.A.; Goel, A.; Bernstein, D.S. An Adaptive PID Autotuner for Multicopters with Experimental Results. University of Michigan, 2021. Available online: https://dsbaero.engin.umich.edu/wp-content/uploads/sites/441/2022/10/An_Adaptive_PID_Autotuner_for_Multicopters_with_Experimental_Results.pdf (accessed on 3 June 2025).
- Abdelkader, M.; Mabrok, M.; Koubaa, A. OCTUNE: Optimal Control Tuning Using Real-Time Data with Algorithm and Experimental Results. Sensors 2022, 22, 9240. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, X.; Zhang, B. Iterative learning control for path-following of ASV with the ice floes auto-select avoidance mechanism. IEEE Trans. Intell. Transp. Syst. 2025. [Google Scholar] [CrossRef]










| Parameter | Value |
|---|---|
| VTOL Parameters | |
| Critical Tilt Angle | 50 degrees |
| Transition Thrust | 0.35 |
| Blended Airspeed (BLENDED_ASPD) | 6 m/s |
| Transition Airspeed (TRANSITION_ASPD) | 15 m/s |
| TECS Parameters | |
| (STE Learning Rate) | 0.000001 |
| (SBE Learning Rate) | 0.000001 |
| (STE Sigmoid Parameter) | 0.3 |
| (SBE Sigmoid Parameter) | 0.2 |
| Initial (STE Proportional Gain) | 0.8 |
| Initial (STE Integral Gain) | 0.02 |
| Initial (SBE Proportional Gain) | 1.2 |
| Initial (SBE Integral Gain) | 0.20 |
| Default (Default STE Proportional Gain) | 0.8 |
| Default (Default STE Integral Gain) | 0.02 |
| Default (Default SBE Proportional Gain) | 1.2 |
| Default (Default SBE Integral Gain) | 0.20 |
| Default (Default SBE Feedforward Gain) | 1.0 |
| Initial Conditions | |
| Initial Altitude | 10 m |
| Initial Airspeed | 0.1 m/s |
| Metric | PX4 Default | Tuned TECS | SD-TECS (Proposed) |
|---|---|---|---|
| Settling Time | |||
| Altitude (s) | 44.31 | 35.31 | 28.56 |
| Improvement | - | 20.31% | 35.55% |
| Airspeed (s) | 40.20 | 26.75 | 23.14 |
| Improvement | - | 45.90% | 57.30% |
| Overshoot | |||
| Max Altitude Loss (m) | 1.62 | 0.87 | 0.83 |
| Improvement | - | 46.3% | 48.9% |
| Airspeed Overshoot (m/s) | 1.16 | 0.63 | 0.61 |
| Improvement | - | 33.46% | 42.44% |
| Metric | SD-TECS | TECS |
|---|---|---|
| Mean Total Time (s) | 0.7188 | 0.6500 |
| Standard Deviation (s) | 0.0062 | 0.0082 |
| Mean Time per Call (μs) | 6.95 | 6.29 |
| Increase in Simulation Time (%) | 10.58 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Nguyen, N.P.; Bae, S.; Hong, S.K. Real-Time TECS Gain Tuning Using Steepest Descent Method for Post-Transition Stability in Unmanned Tilt-Rotor eVTOLs. Drones 2025, 9, 414. https://doi.org/10.3390/drones9060414
Lee C, Nguyen NP, Bae S, Hong SK. Real-Time TECS Gain Tuning Using Steepest Descent Method for Post-Transition Stability in Unmanned Tilt-Rotor eVTOLs. Drones. 2025; 9(6):414. https://doi.org/10.3390/drones9060414
Chicago/Turabian StyleLee, Choonghyun, Ngoc Phi Nguyen, Sangjun Bae, and Sung Kyung Hong. 2025. "Real-Time TECS Gain Tuning Using Steepest Descent Method for Post-Transition Stability in Unmanned Tilt-Rotor eVTOLs" Drones 9, no. 6: 414. https://doi.org/10.3390/drones9060414
APA StyleLee, C., Nguyen, N. P., Bae, S., & Hong, S. K. (2025). Real-Time TECS Gain Tuning Using Steepest Descent Method for Post-Transition Stability in Unmanned Tilt-Rotor eVTOLs. Drones, 9(6), 414. https://doi.org/10.3390/drones9060414







