On the Flying Accuracy of Miniature Drones in Indoor Environments

Abstract

Micro drones are becoming more popular in many areas, because they are small and fast enough to fly in tight and complex spaces. But they still have some significant problems. Their batteries drain fast, they cannot carry much weight, and their sensors and computers are limited. These problems affect their flying performance and stability, which is very important for their missions. In this study, we evaluated the accuracy of mini drones in indoor environments. During hovering, the drones showed an average deviation of 77.9 cm, with a standard deviation of 26.4 cm, indicating moderate stability while stationary. In simple forward flights over 3 m, the average deviation increased to 92.6 cm, which showed slight drop in accuracy during movement. For more complex flight paths, such as L-shaped and square trajectories, the deviations increased to 141 cm and 245 cm, respectively.

1. Introduction

Recent advances in electronics and hardware technology have led to remarkable progress in the production of unmanned aerial vehicles. In the early 2000s, drones were large, expensive, and primarily used by the military or research institutions. Key innovations in electronics, such as tiny sensors, small and powerful processing units, and more efficient batteries, have reduced the size and weight of drones. The development of compact flight controllers and GPS modules has allowed controlled navigation and stability in smaller drones. Additionally, improvements in battery technology have extended the flight times of drones and made them more suitable for real-world applications.

In recent years, micro or miniature drones have become popular for many applications, including photography, delivery, search and rescue, entertainment, and even military operations [1,2]. These small drones can fly to places that are hard to reach, such as underground mining tunnels, subways, and sewage systems, and can perform many tasks efficiently. In emergencies, these drones can be used to find people who are lost or trapped. They can quickly cover large areas and access places that are difficult for humans to reach. They can also be used to monitor wildlife, forests, borders, and oceans. In the field of agriculture, small drones can be used to monitor crops, to check for signs of disease, pests, or water shortages [3]. This can help farmers take action quickly to protect their crops. Small drones are widely used to inspect infrastructure like bridges, buildings, and power lines [4]. They can safely reach high or dangerous places, helping to identify damage or wear. Small drones can also operate in swarms to cover larger areas or to maintain robust connectivity among ground-based devices [5,6].

While miniature drones have many benefits, they also face many challenges. Miniature drones are lightweight and can easily be disturbed by even slight winds. Maintaining a stable hover position or moving along planned paths can be challenging, especially in windy conditions. Small drones usually have a limited flight time due to small batteries. This limited energy source considerably restricts the tasks that these drones can complete. Small drones cannot carry heavy materials; hence, they usually have a limited number of sensors and hardware components, which reduces their sensing and processing abilities.

One of the most important aspects of using small drones is ensuring they fly accurately and know their exact location at all times. These problems are known as flying accuracy and localization. Flying accuracy means how well a drone can follow a planned path or reach a specific point in the air. Good flying accuracy is important because it helps drones avoid obstacles, stay on course, and complete their missions successfully. For example, if a drone is searching for a specific object, it needs to fly accurately to reach the correct location.

Localization, on the other hand, is about knowing where the drone is at any given moment. Drones use different technologies, like GPS, cameras, and sensors, to figure out their position. This information is crucial for navigating and making decisions while flying. Without accurate localization, a drone could get lost or crash. While GPS can provide location data, its accuracy can be limited, especially in indoor or densely populated areas. Miniature drones may need to rely on alternative localization methods, such as visual or inertial navigation. Achieving high flying accuracy requires precise control systems and high-quality sensors, which most small drones are unable to carry.

Drones come in various types and classifications, based on their size, purpose, and flight capabilities. This classification helps in understanding their applications, regulations, and technological requirements. Based on size and weight, drones can be classified into the following groups:

• Miniature Drones: These are the smallest drones, typically weighing less than 250 g. They are often used for indoor missions, hobby flying, and educational purposes.
• Micro Drones: Slightly larger than miniature drones, micro drones usually weigh between 250 g and 2 kg. They are commonly used for recreational flying, aerial photography, and short-range surveillance.
• Small Drones: Weighing between 2 and 25 kg, these drones are more robust and capable of carrying small payloads. They are used for commercial applications like agricultural monitoring, inspection, and medium-range surveillance.
• Medium Drones: These drones weigh between 25 and 150 kg. They are suitable for more demanding tasks, such as environmental monitoring, mapping, and industrial inspections.
• Large Drones: Weighing over 150 kg, large drones are capable of carrying significant payloads and flying longer distances. They are commonly used in military applications, large-scale cargo transport, and scientific research.

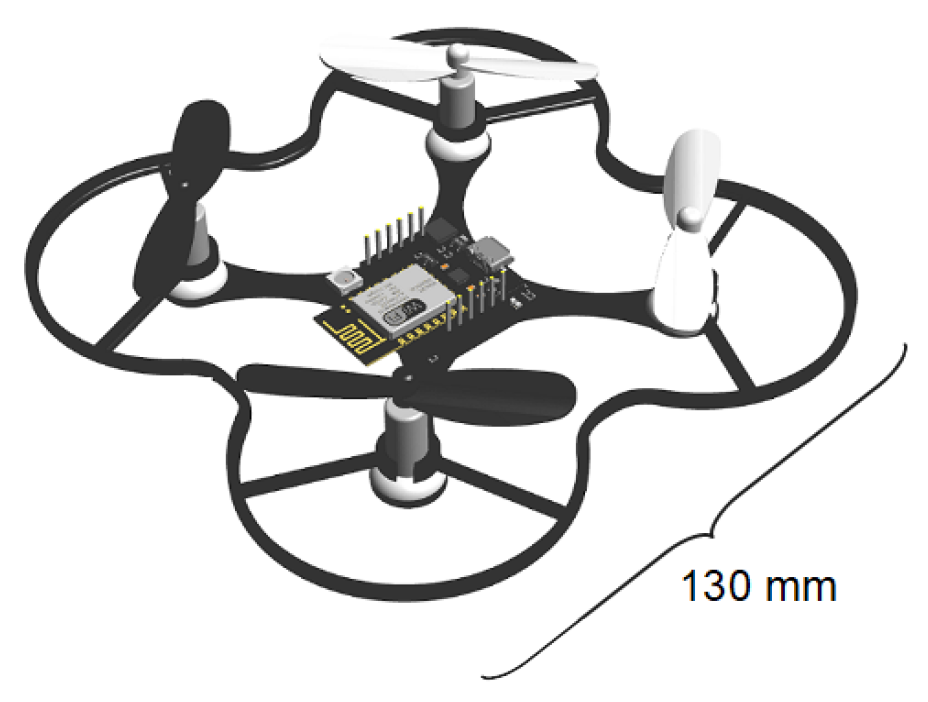
In this paper, we focused on the flying accuracy of miniature drones. We investigated a special kind of miniature drone called an ESPcopter (Figure 1) and performed different kinds of experimental evaluations to inspect the navigation accuracy of these drones. The ESPcopters (ESPcopter, İstanbul, Turkey) use an ESP8266-12E device (Espressif Systems, Shanghai, China) as the main processing and controlling unit. ESPcopters are equipped with a 300 mAh Li-Po battery as the power source. The drone automatically lands when the battery can no longer provide the required voltage for rotating the rotors. The weight of the drone is about 35 g and it has dimensions of $130\times 130$ mm. The length of the propellers is 55 mm, and it takes about 45 min via a standard micro-USB connection to fully charge the battery. Based on the datasheet, the nominal flight time of ESPcopters is up to 7 min. The ESP8266-12E has a 32-bit RISC CPU and can connect to the Internet through an IEEE 802.11 b/g/n Wi-Fi connection. The drone has a 3-axis accelerometer, 3-axis gyroscope, and 3-axis magnetometer to adjust the flying speed and direction. We investigated the flying accuracy of the drones in both hovering and flying modes.

The main contributions of this study are summarized as follows:

• A comprehensive experimental evaluation was conducted to assess the positional accuracy of miniature drones in various flight modes, including hovering, linear, L-shaped, and square trajectories within real-world indoor environments.
• A structured experimental methodology was established for evaluating the flight accuracy of miniature drones. We designed four different flying modes and measured the deviation between the expected and actual locations of the drone at each point.
• A quantitative analysis of flight deviations is presented, demonstrating how increasing trajectory complexity affects the navigation performance of miniature drones. This analysis highlights the limitations of existing low-cost control systems in maintaining stability during complex maneuvers.
• The insights derived from this study can serve as a benchmark for future improvements in control algorithms, sensor fusion strategies, and flight stability mechanisms in resource-constrained drone systems.

2. Related Works

The flying accuracy and indoor localization of drones have been extensively investigated from various perspectives [7]. While several studies have focused on evaluating existing tracking and localization methods for aerial systems [8,9], others have proposed novel localization frameworks tailored to specific environments [10,11]. For instance, Meissner et al. [12] introduced a deep-reinforcement-learning-based approach using ArUco markers, to allow drones to autonomously adjust their pose throughout takeoff, flight, and landing. Similarly, Tsai et al. [13] enhanced linear flight and landing precision through marker-based references, highlighting the effectiveness of vision-based localization.

Recent efforts have deepened the understanding of miniature drone navigation by exploring sophisticated trajectory planning and control techniques. Nieuwenhuisen and Behnke presented a visibility-constrained 3D path planning algorithm suited for sensor-limited environments, although its computational demands pose challenges for real-time use [14]. Zhou et al. proposed the RAPTOR framework for perception-aware fast-flight replanning, which enables high responsiveness but requires advanced sensing capabilities [15]. In their comparative study, Sun et al. showed that, while both nonlinear predictive control and differential flatness-based control performed well, the former offered superior precision for agile maneuvers [16]. Zhou et al. also developed rapid trajectory generation techniques that improve flight efficiency but rely heavily on accurate inertial measurements [17].

Navigating indoor environments without access to GPS remains a significant challenge for UAV systems. Alghamdi et al. explored this issue by examining the limitations of SLAM-based localization, noting that while effective in theory, such methods often suffer from real-world issues like sensor noise and accumulated drift [18]. Micro-UAVs, in particular, are prone to sudden collisions with obstacles, due to their lightweight design and limited sensing capabilities, which can severely impact flight stability. To address this, Battiston et al. [19] introduced a robust attitude recovery approach that leverages inertial data and model-based predictions to help quadcopters regain control after impacts. Enhancing localization accuracy through sensor fusion has also gained attention. Guo et al. [20] showed that combining IMU data with optical flow and environmental sensing can significantly improve performance in complex indoor settings. Another critical aspect is communication, especially in systems involving multiple UAVs. Lee et al. [21] tackled this by developing a secure and modular ROS-based framework that enables reliable telemetry exchange and coordinated control among drones. Meng et al. introduced trajectory conformity metrics to assess path deviations in real time [22], and Chen et al. demonstrated the effectiveness of bi-directional LSTM models for real-time trajectory prediction, achieving high accuracy with low latency, but requiring substantial training data [23]. In a related line of research, Jones et al. employed deep learning to detect hazardous regions, improving urban navigation but showing sensitivity to data quality [24]. Wang et al. proposed a conflict-free trajectory replanning method that accounts for uncertainty, enhancing decision-making under incomplete information, though dynamic environments remain a challenge [25]. Most of these approaches either rely on ideal sensing conditions or require computational and data resources that may not be feasible for real-time deployment on miniature UAV platforms.

Doroftei et al. developed a virtual testbed for drone pilot performance evaluation, offering behavioral insights but lacking physical feedback realism [26]. Guo et al. introduced a data-driven sensor fusion model to enhance flight measurement precision in structured indoor spaces [27]. Basil et al. employed hybrid fractional-order controllers to ensure smoother trajectories under noisy conditions [28], while Watanabe examined trajectory modeling in urban operations with limited experimental validation [29]. Johnson et al. reviewed autonomous UAV control architectures, identifying a growing trend toward modularity, though standardization across platforms remains limited [30]. Shuaibu et al. evaluated dynamic navigation strategies, concluding that hybrid models outperform rule-based systems in cluttered environments [31]. Most of these approaches were constrained by limited physical realism, insufficient standardization, or a lack of comprehensive experimental validation.

Swarm coordination and formation planning have attracted increased attention. Tang et al. proposed a deep-learning-based patrolling method for orchard monitoring [32], while Long et al. introduced a virtual navigator for decentralized coordination, though latency issues arose under high-density operation [33]. Yang et al. presented a comprehensive taxonomy of formation planning algorithms, highlighting the need for more real-time-capable solutions [34]. Shen et al. developed an inertial-data-driven aerodynamic model for small UAVs, enhancing simulation fidelity, but its accuracy depends on high-resolution IMU inputs [35]. Chen and Wong [36] explored decentralized frameworks for swarm coordination, while Spasojevic et al. [37] implemented collaborative positioning strategies in heterogeneous UAV fleets. Despite their scalability potential, such systems often assume ideal communication conditions, which are not always realistic. Casado and Bermúdez [38] proposed using onboard state machine model that enable real-time decision-making, although their work primarily remained within simulation environments.

Several survey studies have laid the foundational groundwork for drone localization and perception. Ullah et al. [39] categorized localization strategies for aerial robots, discussing their advantages and limitations. Fang et al. [40] reviewed SLAM techniques for constrained environments but lacked comprehensive comparisons across drone-specific datasets. Similarly, Sesyuk et al. [8] and Sandamini et al. [9] outlined indoor positioning methods, yet many of the proposed solutions lacked empirical validation, reducing their real-world applicability.

Sensor fusion remains a key strategy for improving localization accuracy. Gross et al. [41] analyzed Kalman and particle filters for integrating multi-sensor data, while You et al. [42] demonstrated that fusing Ultra-Wideband (UWB) and IMU data enables sub-meter accuracy in cluttered indoor spaces. Although effective, such methods often require significant computational resources, which can be a limitation for miniature drones. SLAM continues to be widely used for indoor navigation: for instance, Zhang et al. [43] applied LiDAR-based SLAM for obstacle-aware path planning, and Lee et al. [44] conducted a comparative study of SLAM and marker-based techniques. Nonetheless, scalability across multi-room or dynamic settings remains an unresolved issue.

Fiducial marker tracking has also proven effective. James et al. [45] and Pandey et al. [46] utilized RTABMap and AprilTag systems to enhance accuracy in short-range tasks like takeoff and landing. However, these approaches are susceptible to occlusion and changes in lighting. To address such challenges, Vrba et al. [47] and Ayyalasomayajula et al. [48] proposed markerless localization systems based on deep learning, which provide more flexibility but demand large, labeled datasets and high-performance onboard processing—often beyond the capability of lightweight drones.

Deep-learning-based pose estimation has also been widely explored. Chekakta et al. [49], Zhao et al. [50], and Minghu et al. [51] developed CNN-based models to extract 3D poses from raw sensor inputs. While these models show high accuracy, they also introduce challenges in inference speed, dataset dependency, and generalizability. zhang et al. [52] proposed a monocular vision approach that reduces computational requirements but sacrifices some precision for broader hardware compatibility.

Hybrid localization systems integrating alternative sensing modalities have also been proposed. Nie et al. [53] combined Wi-Fi fingerprinting with inertial sensors, but the spatial resolution remained limited. Stamatescu et al. [54] and Nguyen et al. [55] improved system robustness through the fusion of barometric, sonar, and RF data, though requiring custom infrastructure. Van et al. [56] analyzed the impact of environmental layout on localization error, though their methods showed limited adaptability in dynamically changing environments. These hybrid systems often depend on environment-specific infrastructure and exhibit limited adaptability in dynamic or unstructured indoor settings.

Despite the breadth of existing research, a lightweight and practical localization solution for miniature drones under real-world constraints remains an open challenge. Most prior studies have emphasized flying-mode localization; however, drones may also experience drift during hovering or deviate from intended paths during motion due to internal and external factors. Accurate measurement of such deviations in both hovering and flying conditions is crucial for improving the reliability of positioning and tracking systems. In this study, we experimentally analyzed the flight precision of miniature drones in indoor settings, aiming to estimate potential deviations under different operation modes and contribute to the development of more accurate navigation systems for lightweight UAVs.

3. Flying Accuracy

To evaluate the flying precision of drones, we measured the difference between the expected and actual location of a drone in hovering and different flight modes. In the evaluations, we used a special kind of miniature drone called ESPcopter and established different kinds of experimental evaluations to inspect the navigation accuracy of the drones. Each ESPcopter unit is powered by an ESP8266-12E microcontroller, which provides 32-bit processing capabilities and integrated Wi-Fi connectivity. The drone features a set of onboard sensors, including a 3-axis accelerometer, 3-axis gyroscope, and 3-axis magnetometer, which help real-time orientation and motion tracking.

All flight experiments were conducted in an indoor environment during daytime hours in a closed laboratory room with consistent ambient lighting and stable temperature conditions. The space was free of air currents, drafts, or ventilation effects. No external motion disturbances were introduced, and all windows and doors remained closed throughout the testing process. The floor of the testbed was flat and unobstructed, allowing the drones to operate within a predefined area without unexpected interference. The flight control of the ESPcopters used in this study was governed by an onboard PID (Proportional-Integral-Derivative) controller implemented on the embedded ESP8266 microcontroller. The control loop operated at a frequency of approximately 100 Hz, continuously adjusting motor speeds based on real-time sensor feedback. Figure 2 shows the drones that we used in the experiments.

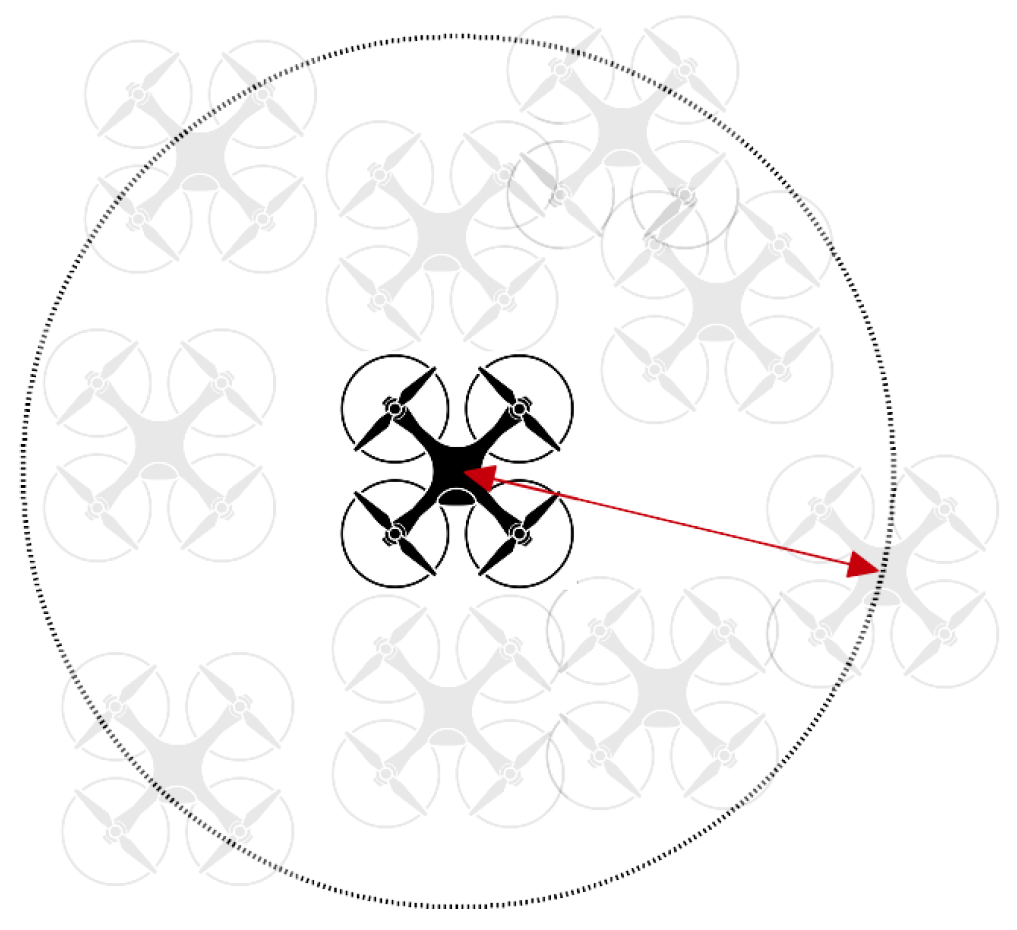
In hovering mode, the drone took off, flew up to 1 m, and stayed at the same position until it landed automatically due to a critical battery level. In these experiments, we expected the drone to remain in the same location without movement as much as possible. Before each experiment, we fully charged the battery of the drone. To measure the deviation, we measured the maximum distance that the drone moved from its take-off position in each experiment. Figure 3 shows how we measured the deviation in hovering mode using the ESPcopters.

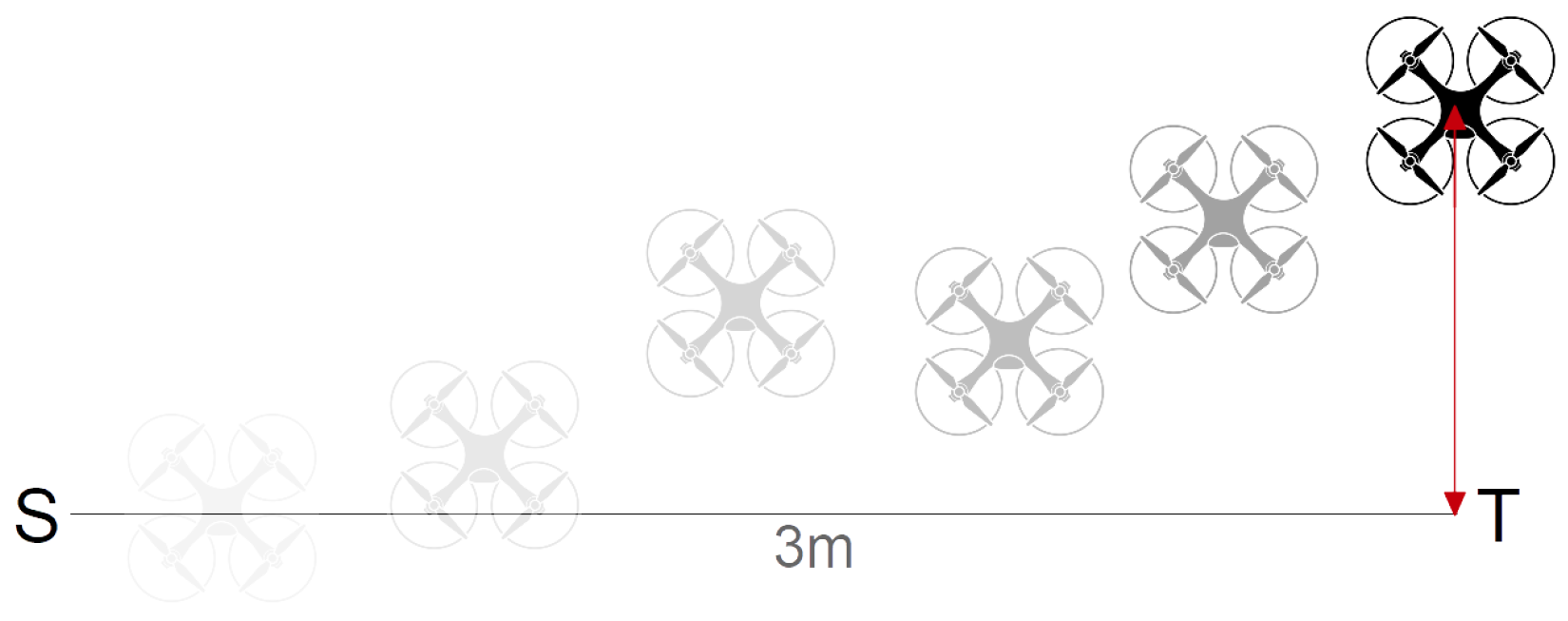
In flight mode, we designed three different flying paths and measured the difference between the expected and actual drone locations. In the first scenario, the drones took off up to 1 m and flew directly to a target position without any rotation. The distances between the start and target positions were 3 and 6 m. We kept the $y_{source}$ and $y_{target}$ coordinates of the start and target positions the same and set $x_{target}$ to $x_{source}+300$. When the drone arrived at the expected $x_{target}$ coordinate, we landed the drone and measured the distance between $y_{target}$ and $y_{source}$, considering this value as the deviation of the drone. Figure 4 shows how we measured the deviation in linear flight mode using the ESPcopters.

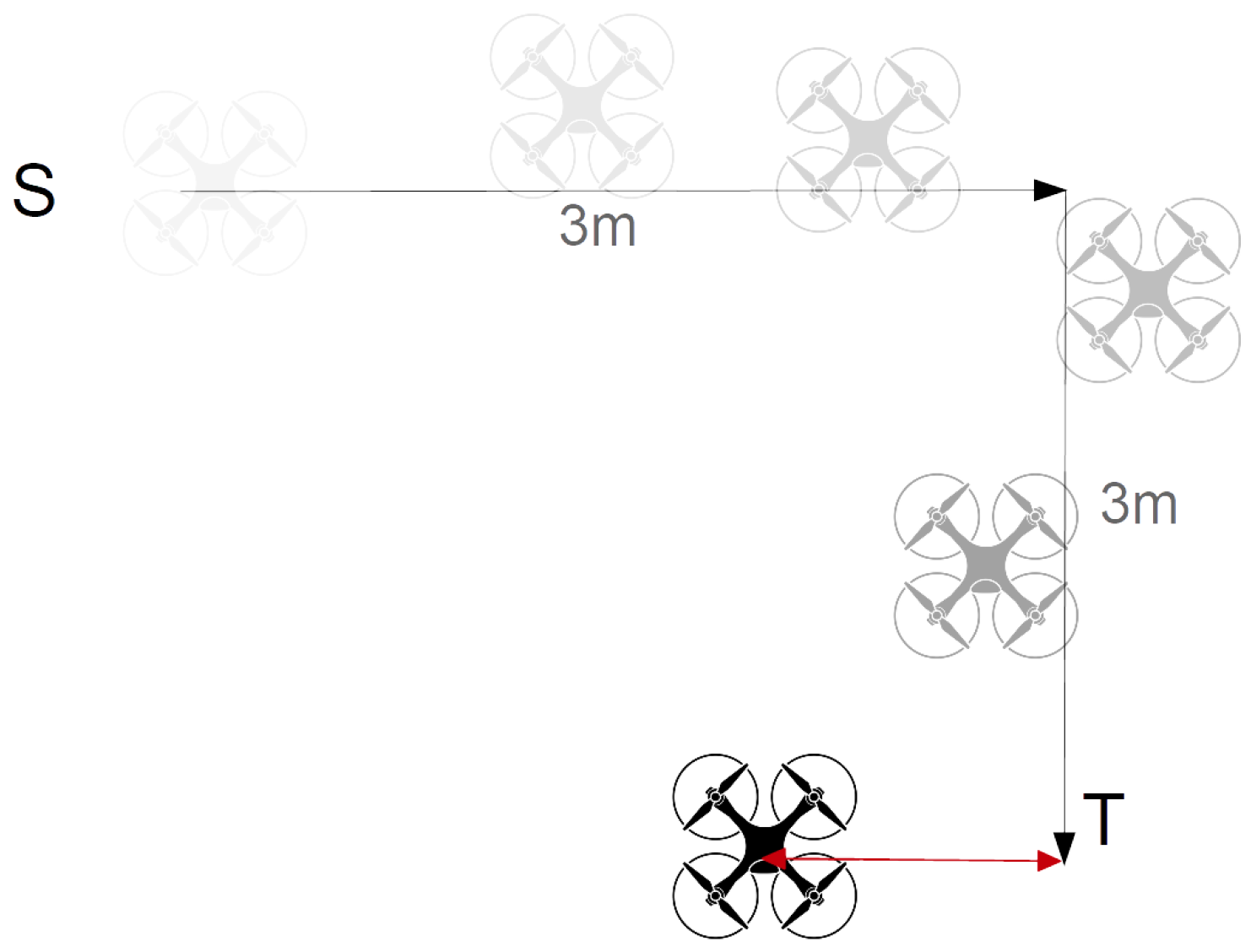
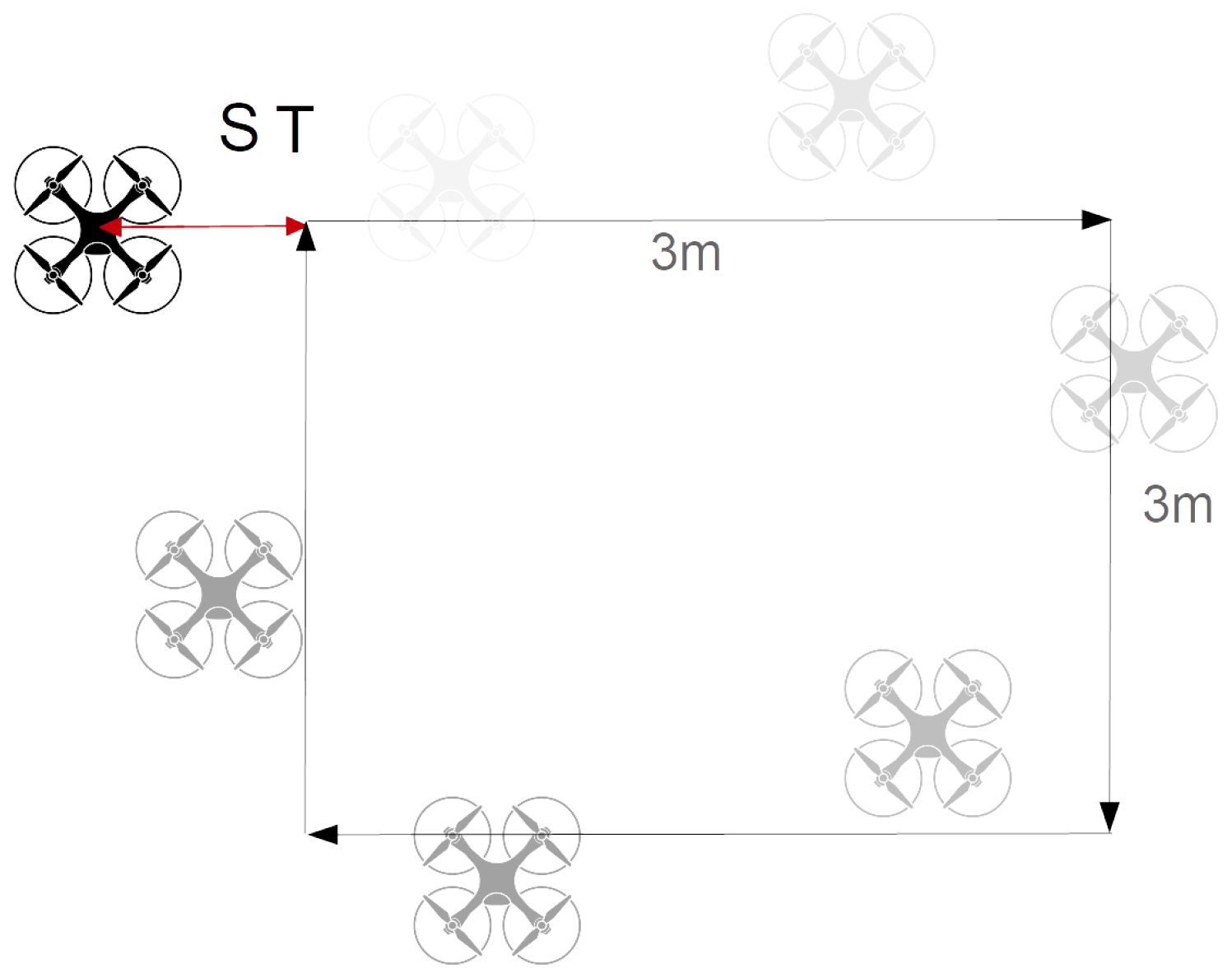
In the third scenario, the drone flew 3 m forward and 3 m right, making an L-shaped flying pattern. After reaching the target point, we measured the difference between the actual and expected locations of the drone. Figure 5 shows the flying pattern and measured distance as the deviation. In the last case, we designed a 3 × 3 square pattern where the robot returned back to the starting point after following a square-shaped path. Figure 6 shows the square flying pattern and measured distance as the deviation. In each mode, we repeated the experiments 100 times using the five available ESPcopters and measured the flying time after automatic landing and the deviation.

After take-off, in hovering mode, the drone slightly moved to the left or right. We measured the maximum distance that the drone moved from its starting position in hovering mode as the deviation. Figure 7a shows our testbed environment and three drones in the hovering mode and Figure 7b shows a drone flying along a linear path.

Figure 8 shows the observed deviations in 100 experiments in hovering mode. This figure shows that the drone slightly moved in hovering mode in all experiments. In most experiments, the maximum observed deviation was under 100 cm; however, there were a few exceptions, with up to 115 cm deviation. The maximum and minimum observed deviations in hovering mode were 115 cm and 20 cm, respectively. The average deviation over 100 experiments was 77.9 cm, and the standard deviation was 26.4 cm. Thus, in hovering mode, we can expect the drones to move around about 77.9 ± 26.4 cm.

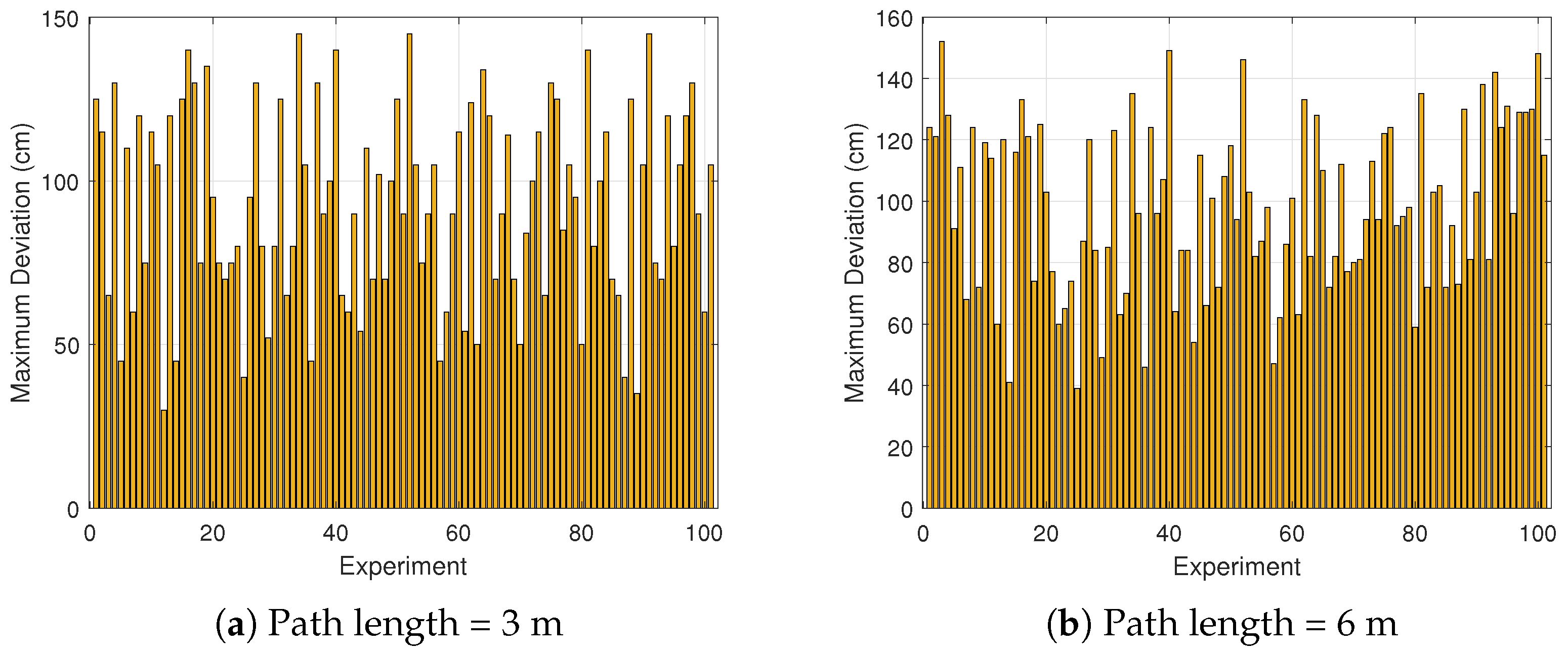
Figure 9 shows the observed deviations when the drones flew directly from the start position toward a target position. We performed the test with 3 m and 6 m path lengths, and their results have been presented in Figure 9a and Figure 9b, respectively. The maximum observed deviation in direct flight mode with the 3 m length was 145 cm; however, in most experiments, the observed deviation was less than 120 cm. The minimum observed deviation was 30 cm. The average deviation over 100 experiments was 92.6 cm, and the standard deviation was 30.8 cm. Thus, in linear flight mode, we can expect the drones to land about 92.6 ± 30.8 cm away from the expected location. For the 6 m flight path, the maximum deviation was 152 cm, while the minimum recorded deviation was 39 cm. The average deviation was 97.8 cm, with a standard deviation of 27.3 cm. These results indicate that in direct flight mode over a 6 m path, the drones typically landed approximately 97.8 ± 27.3 cm away from the intended target location. Although the average deviation slightly increased from 92.6 cm to 97.8 cm, and the maximum deviation also increased, the standard deviations (30.8 cm vs. 27.3 cm) showed a comparable variability in both cases. This may indicate that path length has a minor impact on the flight accuracy of micro drones.

To quantify the expected deviation more robustly, we calculated the 95% confidence interval for the mean deviation observed during the direct flight tests. The confidence interval of a sample set is given by

$$\overline{x}\pm z·{\displaystyle \frac{s}{\sqrt{n}}}$$

(1)

where $\overline{x}$ is the sample mean, s is the sample standard deviation, n is the number of observations, and z is the z-score corresponding to the desired confidence level. For a 95% confidence level, $z\approx 1.96$ and a higher z-score signifies more confidence. Considering $z=1.98$, for the 6 m path length ($n=100$, $\overline{x}=97.8$, $s=27.3$), the resulting 95% confidence interval will be

$$97.8\pm 1.98·{\displaystyle \frac{27.3}{\sqrt{100}}}=97.8\pm 5.42$$

(2)

$$\Rightarrow [92.38\mathrm{cm},103.22\mathrm{cm}]$$

(3)

This interval indicates that, with more than 95% confidence, the mean landing deviation for 6 m direct flights lies between 92.38 cm and 103.22 cm.

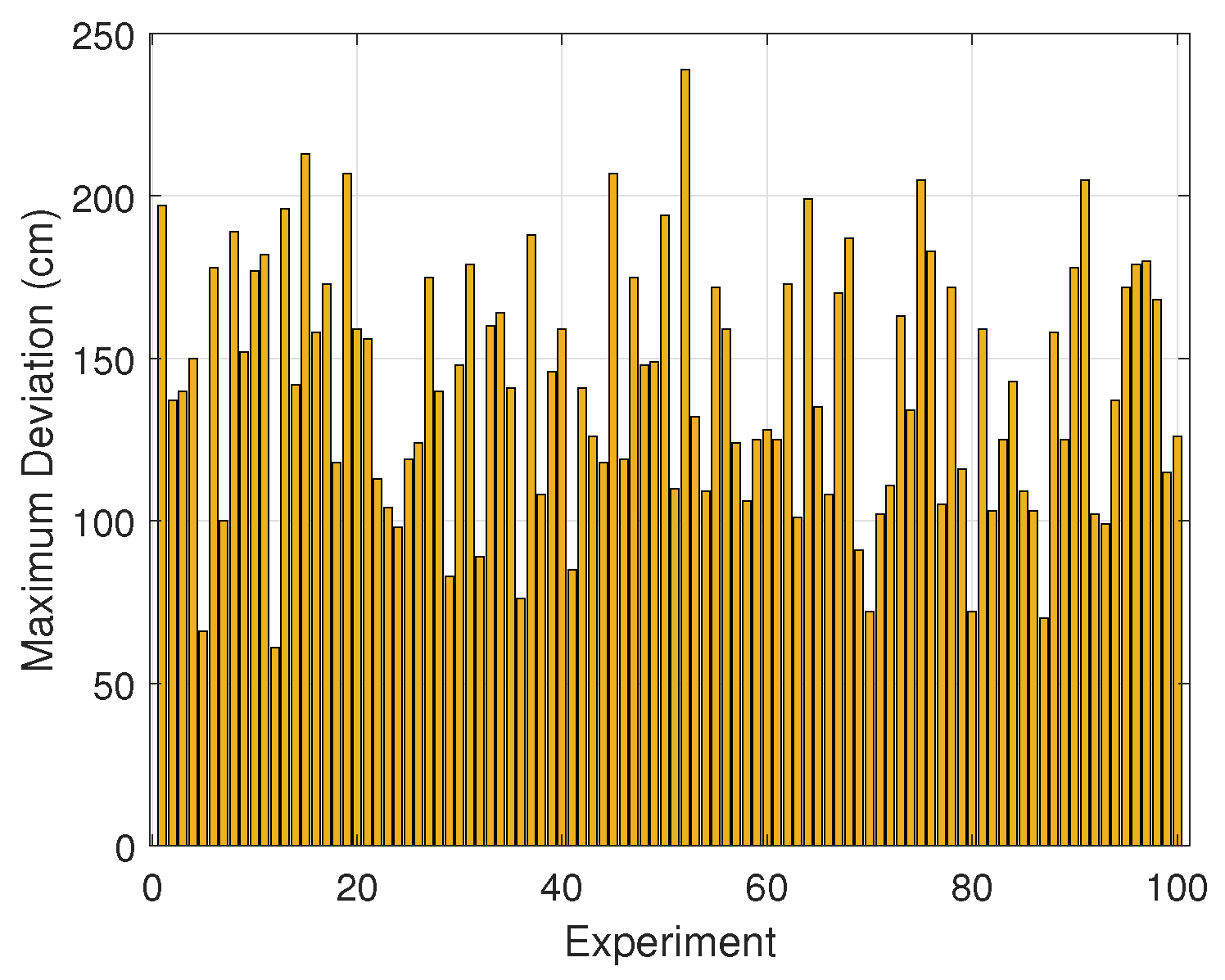
Figure 10 shows the observed deviations when the drones followed the L-shaped pattern. In all experiments, the drones flew 6 m between the start and target positions. The maximum observed deviation in this flight mode was 240 cm; however, in most experiments, the observed deviation was less than 200 cm. The minimum observed deviation was 65 cm. The average deviation over 100 experiments was 141 cm, and the standard deviation was 38.5 cm. Thus, in L-shaped flight mode, we may expect the drones to land about 141 ± 38.5 cm away from the expected location.

For the L-shaped pattern, the 95% confidence interval will be

$$141\pm 1.98·{\displaystyle \frac{38.5}{\sqrt{100}}}=141\pm 7.65$$

(4)

$$\Rightarrow [133.4\mathrm{cm},148.7\mathrm{cm}]$$

(5)

This interval indicates that, with 95% confidence, the mean landing deviation for the L-shaped pattern lies between 133.4 cm and 148.7 cm.

Figure 11 shows the observed deviations when the drones followed the square flying pattern. In all experiments, the drones flew 12 m between the start and target positions over a square pattern. The maximum observed deviation in this flight mode was 340 cm; however, in most experiments, the observed deviation was less than 300 cm. The minimum observed deviation was 135 cm. The average average deviation over 100 experiments was 245 cm, and the standard deviation was 45.4 cm. Thus, in square flight mode, we may expect the drones to land about 245 ± 45.4 cm away from the expected location.

For the square flying pattern, the 95% confidence interval will be

$$245\pm 1.98·{\displaystyle \frac{45.45}{\sqrt{100}}}=245\pm 9.02$$

(6)

$$\Rightarrow [236.5\mathrm{cm},254.6\mathrm{cm}]$$

(7)

This interval indicates that, with 95% confidence, the mean landing deviation for the square flying pattern lies between 236.5 cm and 254.6 cm.

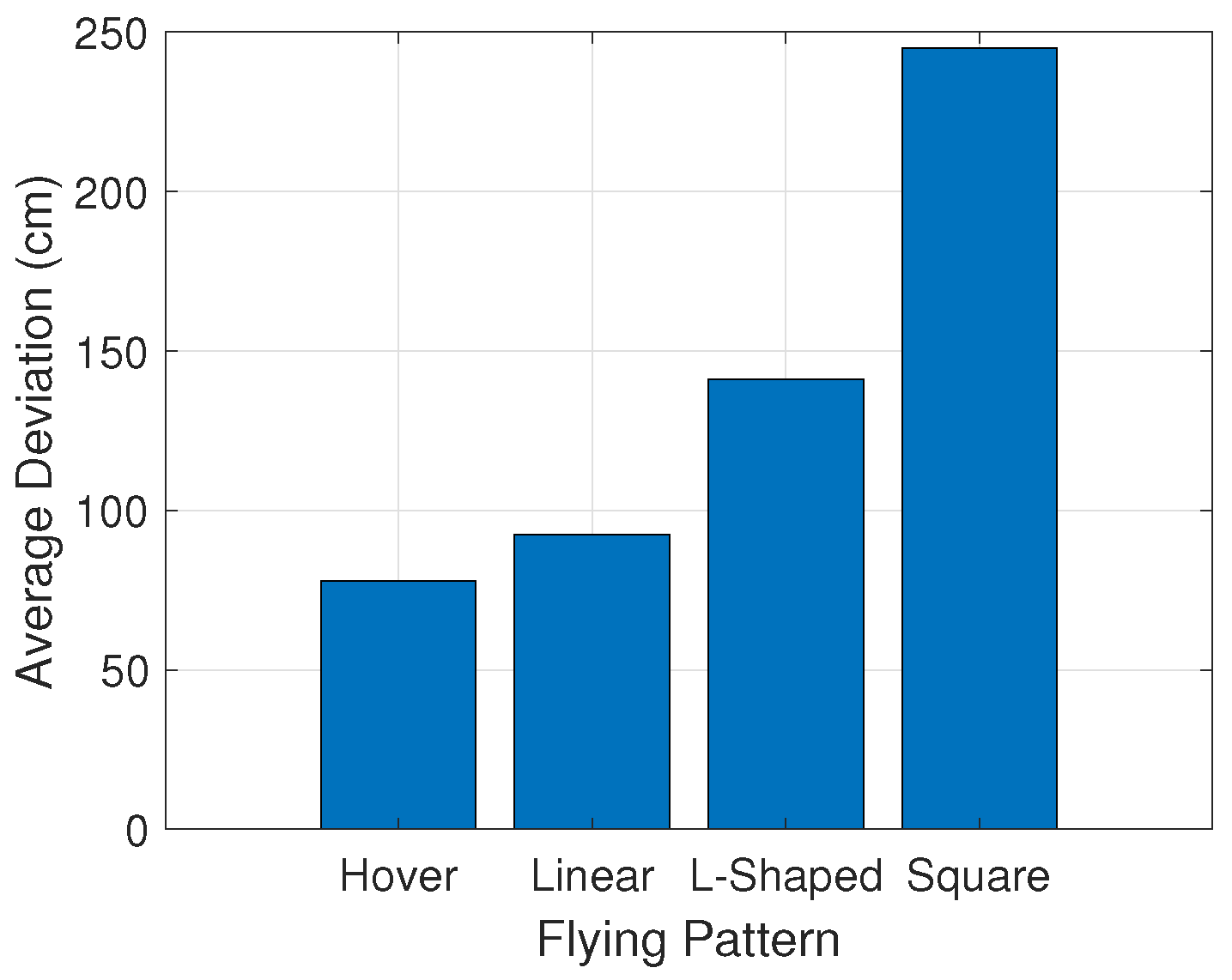
Figure 12 compares the observed deviations in the different flight modes. The figure clearly shows that the deviation of the drone in hovering mode was generally smaller than in all other modes. In almost all experiments, the deviation of the drone in hovering mode remained under 100 cm. The average deviation in this mode was 77.9 cm. This indicates that when the drone remained stationary, its error was relatively low, providing the most stable performance. In contrast, the deviation in 3 m linear mode was notably larger, with an average deviation of 92.6 cm, which was 19% higher than that of hovering. Despite this increase, the linear mode still maintained a moderate level of error, indicating that the drone’s movement along a straight path introduced some variability, but not extreme deviations. The L-shaped mode showed a significant increase in deviation, with an average of 141.11 cm, which was 52.4% higher than the linear mode. This increase can be attributed to the sharp turns in the L-shaped trajectory, leading to greater instability. The square mode exhibited a large deviation of 243.15 cm, reflecting a 212.7% higher deviation compared to hovering mode. The sharp changes in direction during square-shaped movements contributed to the increased error.

Figure 13 shows the average of observed deviations in all flight modes. The figure shows that increasing the path length and path complexity considerably reduced the accuracy of the drone.

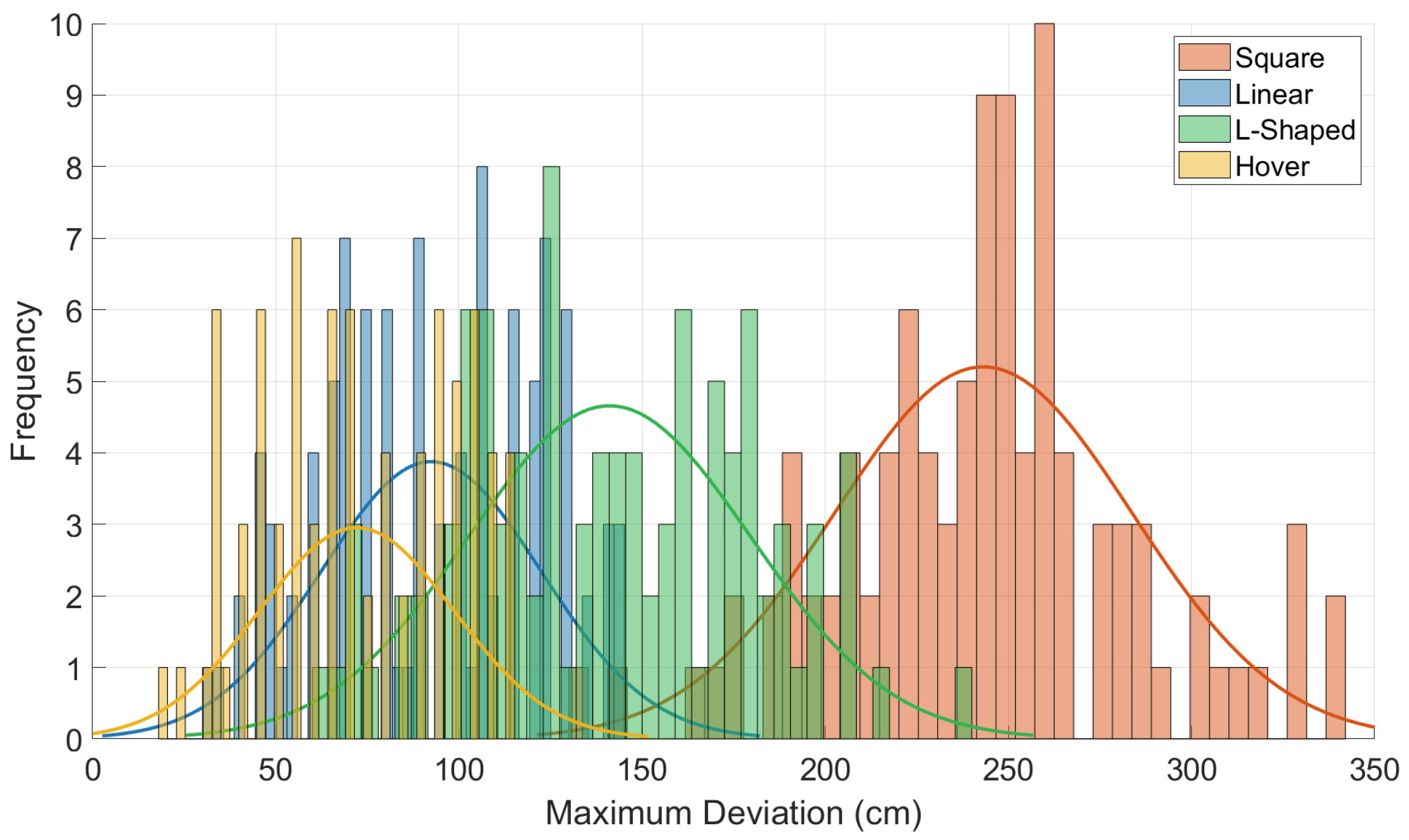
Figure 14 shows the distribution of the maximum deviation values in each flight mode. The figure shows that, in hovering mode (yellow line), the majority of errors fell in the range of 50 cm to 90 cm. This narrow distribution indicates a relatively consistent and stable behavior when the drone was stationary. Most of the deviations in hovering mode cluster around 65 cm. The standard deviation in this mode was also relatively low, showing minimal variability in the drone’s positioning.

In contrast, the L-shaped flight mode (green line) exhibited a broader distribution of deviation values. A significant number of values lie between 100 cm and 200 cm. This indicates that the drone experienced higher error rates during complex path maneuvers, especially around sharp corners. The presence of multiple peaks in this mode may suggest varying levels of stability across different segments of the L-shaped trajectory.

The linear mode (blue line) shows an intermediate pattern, where the deviations are mostly concentrated between 60 cm and 140 cm. The distribution is unimodal but more spread than in hovering mode. These error values indicate that straight-line flying is more stable than turns. The square mode (red line) shows the widest spread of all four distributions. Deviation values range from 130 cm up to 300 cm, with a pronounced peak near 250 cm. This large spread reflects the cumulative error introduced at each 90-degree rotation. The square trajectory likely exposed the drone to multiple disturbance conditions and increased the positional uncertainty.

Both the L-shaped and square modes had higher frequencies in the upper deviation range (above 200 cm), which may pose risks for applications requiring high accuracy. Conversely, the linear mode maintained a more centered distribution, with fewer extreme values. The overlapping regions of some histograms (especially between linear and L-shaped modes) suggest that there may be shared sources of error, such as control lag or sensor drift. Generally, this figure effectively demonstrates how path geometry affects flight stability. These insights can guide future path planning and control system improvements to minimize error accumulation in practical operations. One of the primary causes of the observed drifts was inertial sensor noise and bias, which accumulates over time due to the reliance on low-cost IMUs. As the ESPcopter lacks GPS or external correction mechanisms, even minor sensor inaccuracies can lead to significant cumulative positional errors during flight.

4. Conclusions

Miniature drones may have a wide range range of applications, including infrastructure inspection, precision agriculture, search and rescue missions, and underground exploration. Their compact size allows them to access environments that are often unreachable by larger aerial systems. However, this advantage comes with inherent trade-offs, such as limited battery life, reduced sensor accuracy, and constrained onboard computing power. These factors collectively impact their navigational precision and overall reliability in real-world scenarios.

In this study, we conducted an experimental evaluation of the flight accuracy of miniature drones across four distinct scenarios: hovering, straight-line motion, L-shaped paths, and square-shaped trajectories. The results demonstrated a correlation between flight path complexity and deviation from planned routes. On average, hovering resulted in a deviation of 77.9 cm, which increased to 92.6 cm during linear flights, 141 cm for L-shaped paths, and peaked at 245 cm for square trajectories.

Hovering flights exhibited narrow error distributions, indicating consistent and predictable behavior under static conditions. In contrast, the L-shaped and square trajectories produced broader distributions, reflecting increased instability during directional changes and more complex maneuvers. These observations are consistent with earlier research highlighting the difficulties miniature UAVs face when executing multi-directional paths with limited sensing and processing capabilities.

While techniques such as multi-sensor fusion, lightweight SLAM approaches, and adaptive feedback control have shown potential for improving navigation, they must be tailored to match the hardware constraints of miniature drones. The findings also highlight the importance of robust, real-time error correction strategies to minimize cumulative drift, particularly in longer or repetitive missions. This study provides a practical benchmark for evaluating the feasibility of deploying miniature drones in constrained or mission-critical environments. Ongoing advancements in battery efficiency, sensor miniaturization, and onboard computing can enhance both the accuracy and reliability of miniature drones.

The experiments conducted in this study were limited to a single drone model and a fixed indoor environment. Furthermore, the system’s behavior under dynamic conditions, such as the presence of moving obstacles, remains unexplored. Another important limitation was the inability to continuously track the drone’s ground-truth position throughout the flight. Due to payload constraints, the micro drones could not carry UWB tags, which ruled out UWB-based localization during airborne operation. As a result, flight performance was assessed based on a single manual measurement at landing.

Future work will include scenario-based evaluations in more realistic conditions, such as narrow tunnels, wind disturbances, and dynamic environments with moving obstacles. In addition, we plan to systematically log hardware-related factors, including pre and post flight battery voltage, IMU calibration offsets, and vibration characteristics. Flight performance differences among the five ESPcopter units will also be analyzed to identify potential hardware-induced variations. This study can be expanded to cover larger and more complex indoor environments, to evaluate the scalability and robustness of the drones. Visual odometry could be integrated to enhance localization redundancy and flight stability under real-time disturbances.

We also aim to expand the testbed to larger and more complex indoor environments, to evaluate scalability and robustness. Another important direction will be a comparative analysis of the ESPcopter platform against other miniature UAVs equipped with advanced localization systems, such as visual-inertial odometry, SLAM, or external tracking frameworks. To overcome the limitation of single-point landing-based measurements, we also plan to implement a camera-based localization system that provides continuous position tracking throughout the flight. This improvement will enable detailed observation of temporal error behavior while the drone follows the pattern.