Hierarchical Reinforcement Learning with Automatic Curriculum Generation for Unmanned Combat Aerial Vehicle Tactical Decision-Making in Autonomous Air Combat
Abstract
1. Introduction
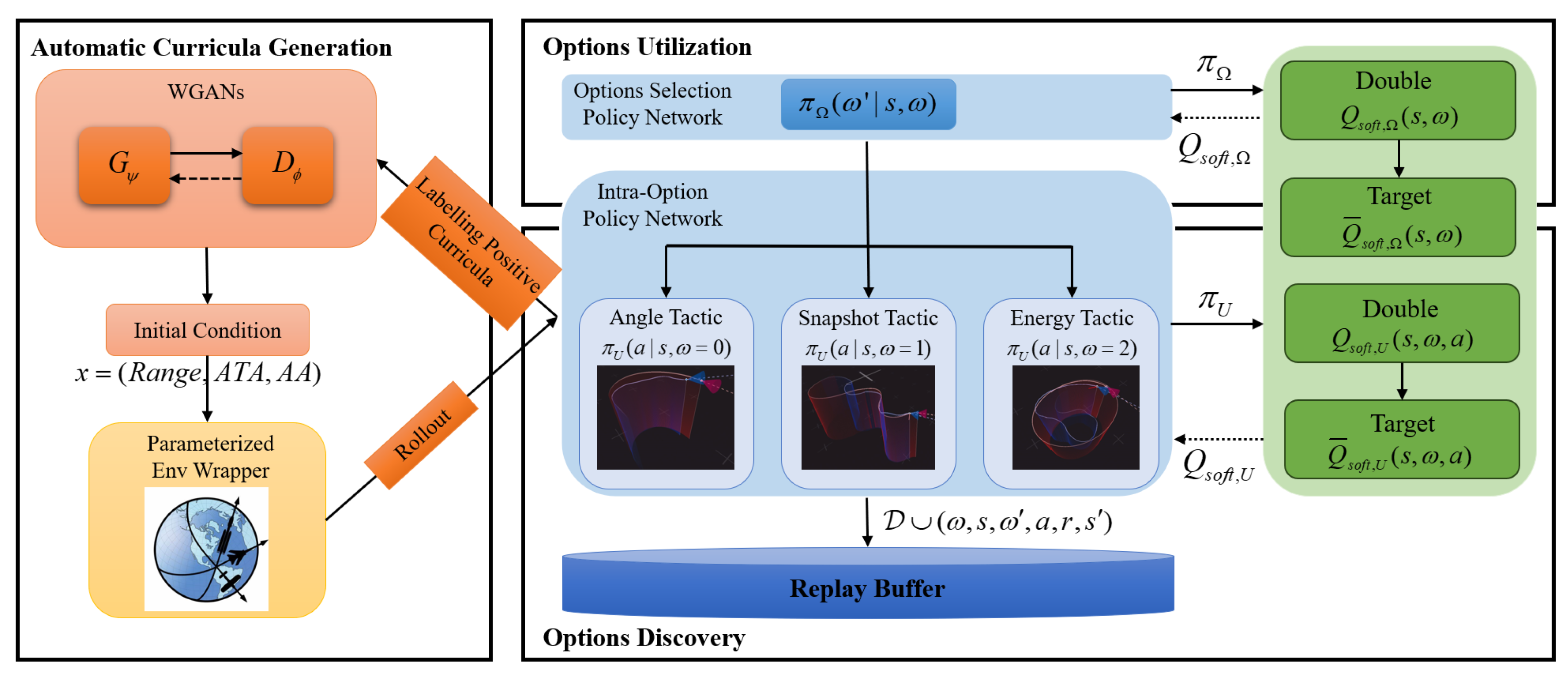
- The training of UCAV agents is conducted in accordance with a hierarchical structure within the MEOL framework. The option discovery enables the manoeuvring control of fighters with nonlinear flight dynamic models in a high-fidelity air combat simulation. The utilization of options extends beyond the selection of the most optimal option, but also extends the fixed duration of tactics [19,21,25] to a varied term.
- Propose an end-to-end automatic curriculum generation method that enhances learning efficiency in option discovery and adaptability to random initial situations. The WGANs is trained to propose feasible initial conditions for option discovery.
- The reward functions for the three types of tactical intra-options (angle, snapshot, and energy tactics) are shaped based on expert knowledge, and the tactical option-selection reward function is further designed. The final win rate against the rule-based adversary fighter is approximately 0.8, and the comparison test proves to be significantly better than the three types of tactical intra-option policies.
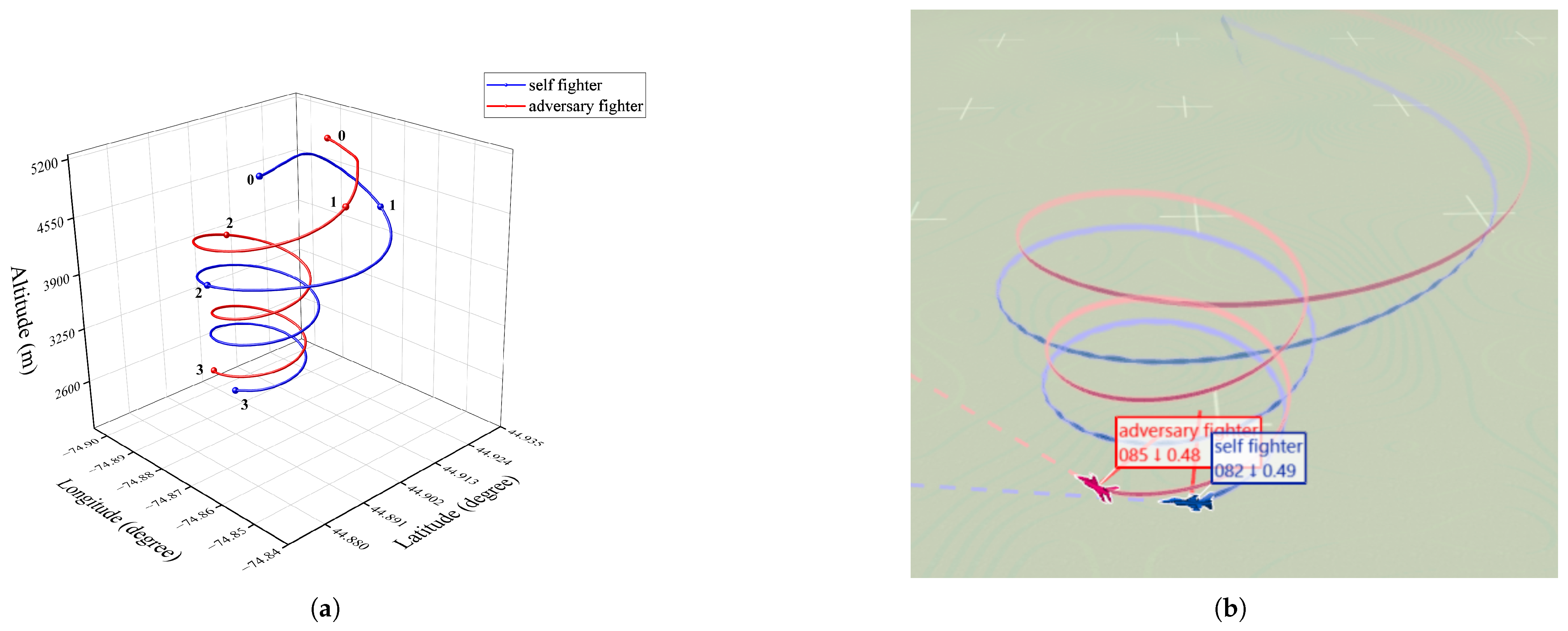
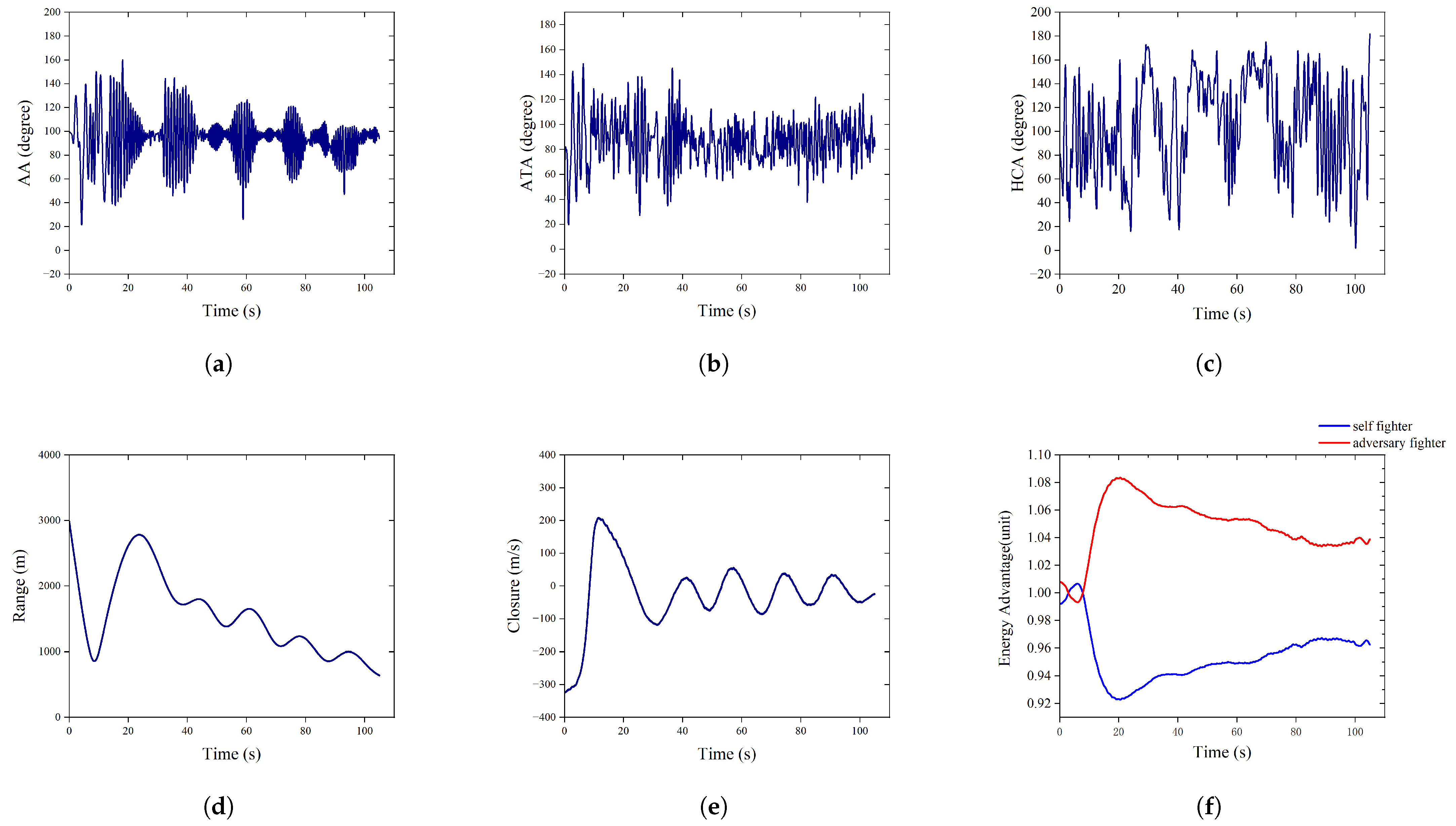
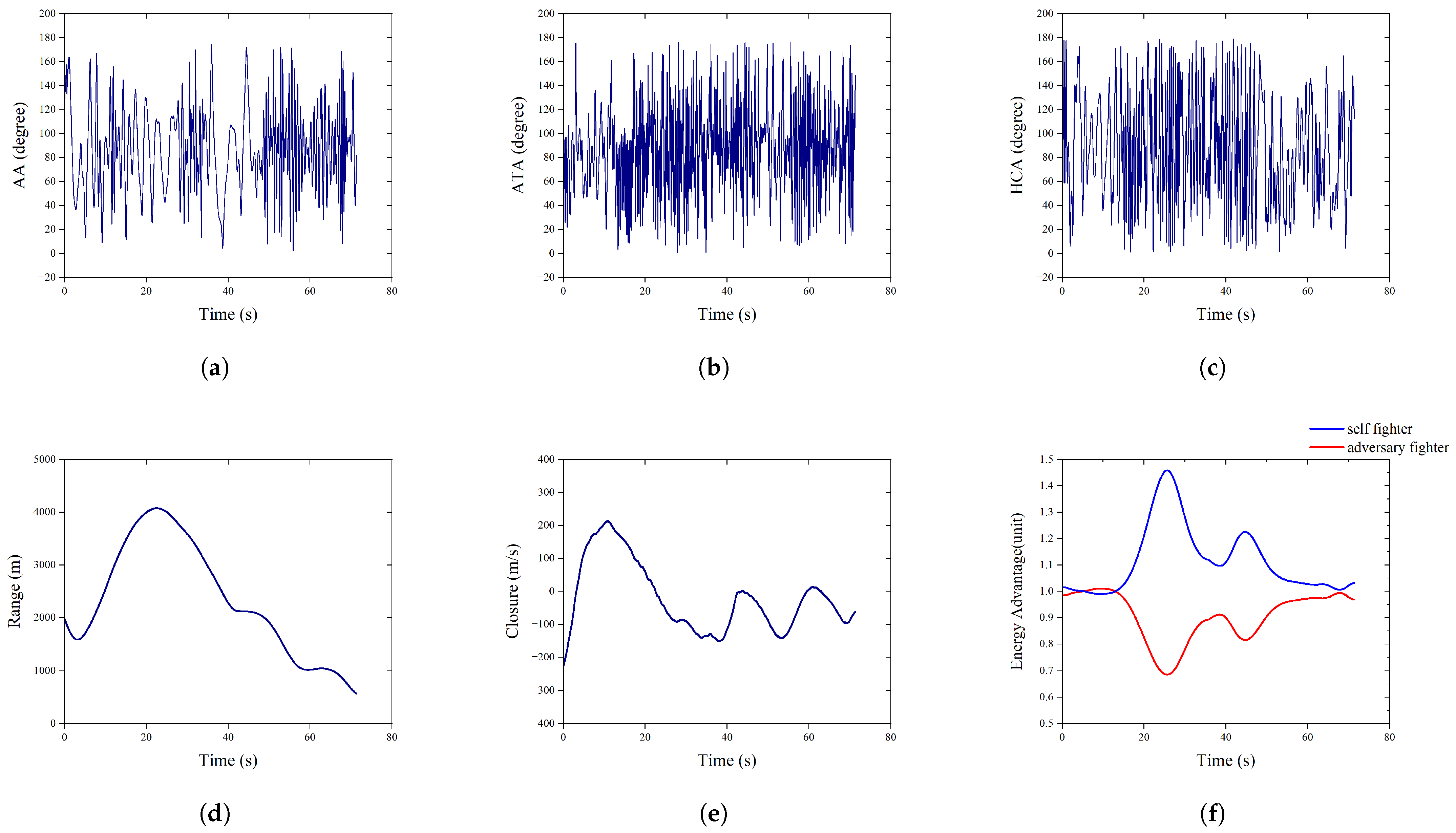
- The UCAVs’ flight logs are analysed in order to provide a visual representation of combat with a variety of adversaries, including an explanation of the skills that have been acquired and the manner in which these skills have been employed.
2. Preliminaries and Problem Formulation
2.1. Semi-Markov Decision Process with Options
2.2. Intra-Option Q-Learning
2.3. Within-Visual-Range Air Combat
2.4. Weapon Engagement Zone
3. Methods
3.1. Automatic Curriculum Generation with WGANs for Option Discovery
3.1.1. Labelling Positive Initial Condition
3.1.2. Wasserstein Generative Adversarial Networks
| Algorithm 1 Option discovery within MEOL framework for subpolicy |
|
| Algorithm 2 Wasserstein Curriculum Generation for Option Discovery |
|
3.2. Option Discovery Within MEOL Framework
3.3. Option Utilization Within MEOL Framework
| Algorithm 3 Option utilization within MEOL framework |
|
4. Hierarchical Training Architecture
4.1. Parameterized Environment of Air Combat Scenario
4.2. Construction of Tactical Intra-Option Policy
4.2.1. Reward Function for Angle Tactic
4.2.2. Reward Function for Snapshot Tactic
4.2.3. Reward Function for Energy Tactic
4.3. Construction of Tactical Option-Selection Policy
4.4. Observation Space and Action Space
5. Experiment
5.1. Air Combat Simulation Platform for HRL Training
5.2. Decoupled Training for Tactical Intra-Option Policies
5.2.1. Angle Tactic
5.2.2. Snapshot Tactic
5.2.3. Energy Tactic
5.3. Comparable Evaluation for Tactical Option-Selection Policies
5.3.1. Coupling Training for Option-Selection Policy
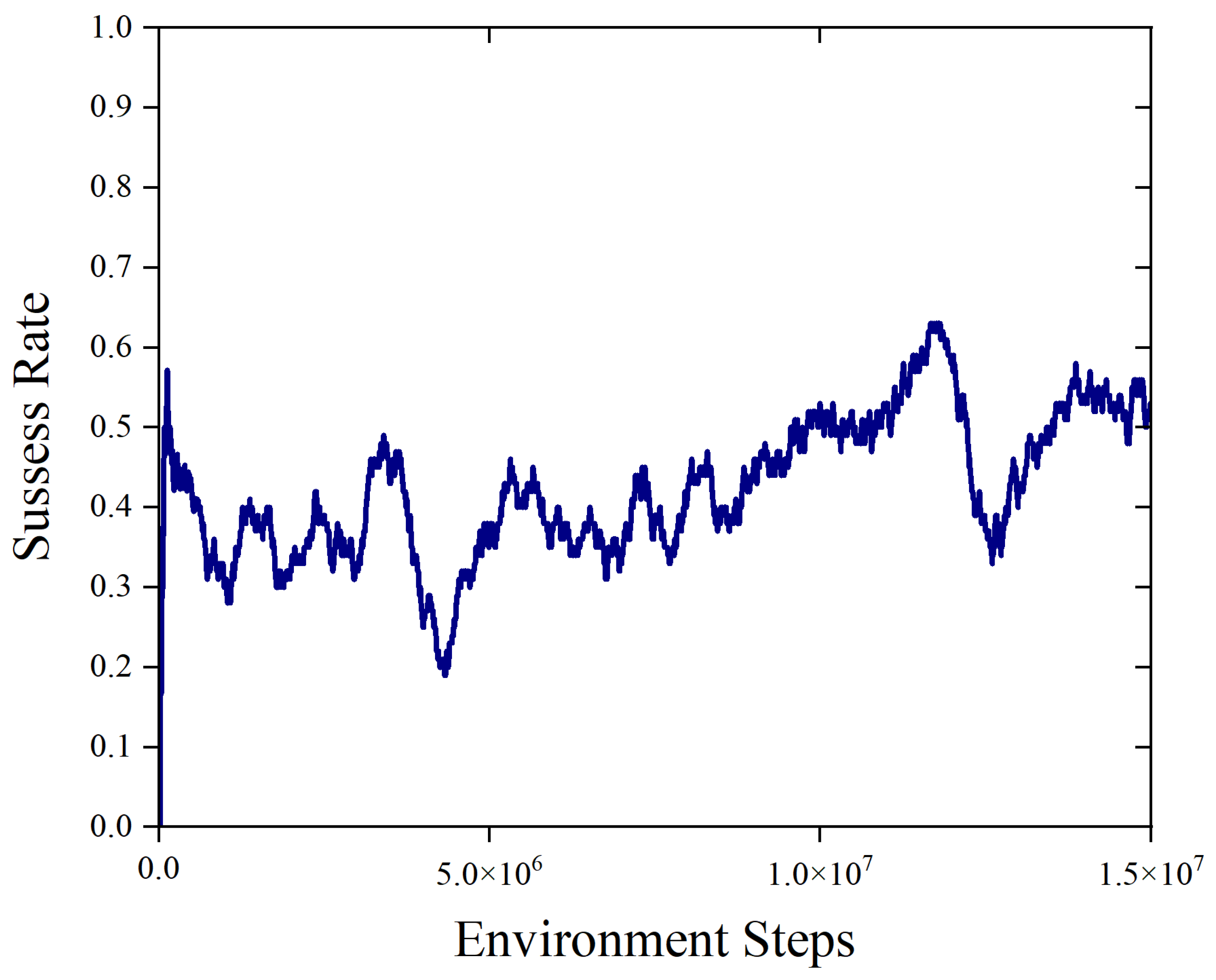
5.3.2. Confrontation Assessment
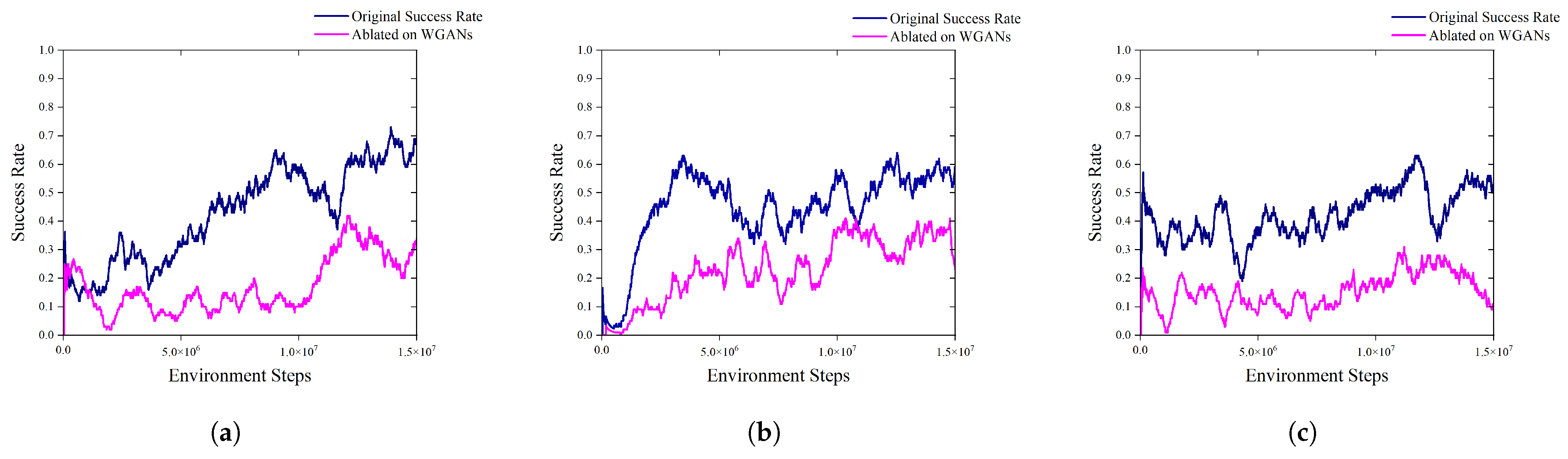
5.4. Ablation Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
DURC Statement
Conflicts of Interest
References
- Burgin, G.H.; Sidor, L. Rule-Based Air Combat Simulation; Technical Report; NASA: Washington, DC, USA, 1988.
- Austin, F.; Carbone, G.; Hinz, H.; Lewis, M.S.; Falco, M. Game theory for automated manoeuvring during air-to-air combat. J. Guid. Control Dyn. 1990, 13, 1143–1149. [Google Scholar] [CrossRef]
- Park, H.; Lee, B.; Tahk, M.; Yoo, D. Differential game based air combat manoeuvre generation using scoring function matrix. Int. J. Aeronaut. Space Sci. 2016, 17, 204–213. [Google Scholar] [CrossRef]
- Ernest, N.; Carroll, D.; Schumacher, C.; Clark, M.; Lee, G. Genetic fuzzy based artificial intelligence for unmanned combat aerialvehicle control in simulated air combat missions. J. Def. Manag. 2016, 1, 1000144. [Google Scholar] [CrossRef]
- McGrew, J.S.; How, J.P.; Williams, B.; Roy, N. Air-combat strategy using approximate dynamic programming. J. Guid. Control. Dyn. 2010, 33, 1641–1654. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, L.; Fang, W.; Xu, T. Approximate dynamic programming for CGF air combat maneuvering decision. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–16 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1386–1390. [Google Scholar] [CrossRef]
- Wang, M.; Wang, L.; Yue, T.; Liu, H. Influence of unmanned combat aerial vehicle agility on short-range aerial combat effectiveness. Aerosp. Sci. Technol. 2020, 96, 105534. [Google Scholar] [CrossRef]
- Crumpacker, J.B.; Robbins, M.J.; Jenkins, P.R. An approximate dynamic programming approach for solving an air combat manoeuvring problem. Expert Syst. Appl. 2022, 203, 117448. [Google Scholar] [CrossRef]
- Zhu, J.; Kuang, M.; Zhou, W.; Shi, H.; Zhu, J.; Han, X. Mastering air combat game with deep reinforcement learning. Def. Technol. 2023, 34, 295–312. [Google Scholar] [CrossRef]
- Bae, J.H.; Jung, H.; Kim, S.; Kim, S.; Kim, Y. Deep reinforcement learning-based air-to-air combat manoeuvre generation in a realistic environment. IEEE Access 2023, 11, 26427–26440. [Google Scholar] [CrossRef]
- Shaw, R.L. Fighter Combat: Tactics and Manoeuvring; Naval Institute Press: Annapolis, MD, USA, 1985. [Google Scholar]
- Dayan, P.; Hinton, G.E. Feudal reinforcement learning. In Proceedings of the 5th International Conference on Neural Information Processing Systems (NIPS’92), Denver, CO, USA, 30 November–3 December 1992; pp. 271–278. [Google Scholar]
- Dietterich, T.G. The maxq method for hierarchical reinforcement learning. In Proceedings of the Fifteenth International Conference on Machine Learning (ICML’98), Madison, WI, USA, 24–27 July 1998; pp. 118–126. [Google Scholar]
- Parr, R.; Russell, S. Reinforcement learning with hierarchies of machines. In Proceedings of the 10th International Conference on Neural Information Processing Systems (NIPS’97), Denver, CO, USA, 1–6 December 1997; pp. 1043–1049. [Google Scholar]
- Sutton, R.S.; Precup, D.; Singh, S. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Konidaris, G.; Barto, A. Skill discovery in continuous reinforcement learning domains using skill chaining. In Proceedings of the 22nd International Conference on Neural Information Processing Systems (NIPS’09), Vancouver, BC, Canada, 7–10 December 2009; pp. 1015–1023. [Google Scholar]
- Bradtke, S.J.; Duff, M.O. Reinforcement Learning Methods for Continuous-Time Markov Decision Problems. In Neural Information Processing Systems. 1994. Available online: https://api.semanticscholar.org/CorpusID:17149277 (accessed on 7 February 2025).
- Parr, R. Hierarchical Control and Learning for Markov Decision Processes. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 1998; 214p. Available online: https://api.semanticscholar.org/CorpusID:53939299 (accessed on 25 February 2025).
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Rosenbluth, D.; Ritholtz, L.; Twedt, J.C.; Walker, T.T.; Alcedo, K.; Javorsek, D. Hierarchical reinforcement learning for air-to-air combat. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 275–284. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; Volume 80, pp. 1861–1870. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Du, Y.; Zhou, Y.; Zhao, Y. Hierarchical multi-agent reinforcement learning for multi-aircraft close-range air combat. IET Control Theory Appl. 2023, 17, 1840–1862. [Google Scholar] [CrossRef]
- Selmonaj, A.; Szehr, O.; Del Rio, G.; Antonucci, A.; Schneider, A.; Rüegsegger, M. Hierarchical multi-agent reinforcement learning for air combat manoeuvring. In Proceedings of the 2023 International Conference on Machine Learning and Applications (ICMLA), Jacksonville, FL, USA, 15–17 December 2023; pp. 1031–1038. [Google Scholar] [CrossRef]
- Zhang, P.; Dong, W.; Cai, M.; Jia, S.; Wang, Z.-P. MEOL: A maximum-entropy framework for options learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 4834–4848. [Google Scholar] [CrossRef] [PubMed]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; PMLR: London, UK, 2017; pp. 214–223. [Google Scholar] [CrossRef]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Twedt, J.C.; Alcedo, K.; Walker, T.T.; Rosenbluth, D.; Ritholtz, L.; Javorsek, D. Hierarchical Reinforcement Learning for Air Combat at DARPA’s AlphaDogfight Trials. IEEE Trans. Artif. Intell. 2023, 4, 1371–1385. [Google Scholar] [CrossRef]
- Florensa, C.; Held, D.; Wulfmeier, M.; Zhang, M.; Abbeel, P. Reverse curriculum generation for reinforcement learning. In Proceedings of the 1st Annual Conference on Robot Learning (CoRL), Mountain View, CA, USA, 13–15 November 2017; Levine, S., Vanhoucke, V., Goldberg, K., Eds.; PMLR: London, UK, 2017; pp. 482–495. [Google Scholar]
- Florensa, C.; Held, D.; Geng, X.; Abbeel, P. Automatic goal generation for reinforcement learning agents. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: London, UK, 2018; pp. 1515–1528. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. 2014. Available online: https://arxiv.org/abs/1406.2661 (accessed on 1 March 2025).
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. 2017. Available online: https://arxiv.org/abs/1704.00028 (accessed on 5 March 2025).
- Ng, A.; Harada, D.; Russell, S.J. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999. [Google Scholar] [CrossRef]
- Dewey, D. Reinforcement learning and the reward engineering principle. In Proceedings of the AAAI Spring Symposium Series, Stanford, CA, USA, 24–26 March 2014; AAAI Press: Menlo Park, CA, USA, 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking deep reinforcement learning for continuous control. In Proceedings of the 33rd International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; PMLR: London, UK, 2016; pp. 1329–1338. [Google Scholar] [CrossRef]
- Berndt, J.S. JSBSim: An Open Source Flight Dynamics Model in C++. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; AIAA: Reston, VA, USA, 2004; pp. 1–12. [Google Scholar] [CrossRef]
- Garage Contributors Garage: A Toolkit for Reproducible Reinforcement Learning Research. Available online: https://github.com/rlworkgroup/garage (accessed on 12 October 2024).
- Zhang, S.; Whiteson, S. DAC: The Double Actor-Critic Architecture for Learning Options. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: Red Hook, NY, USA, 2019; p. 10112. [Google Scholar] [CrossRef]










| Initial Parameter | Value Domain |
|---|---|
| Range | |
| AA | |
| ATA |
| Hyperparameters | Value |
|---|---|
| Number of hidden layers | 2 |
| Dimensions of hidden layers | 256 |
| Nonlinearity of hidden layers | ReLU |
| Sample batch size | 5000 |
| Mini-batch size | 256 |
| Reward scale | 1 |
| Discount factor () | 0.99 |
| Target update interval | 1 |
| Gradient steps | 100 |
| Total environment steps | |
| Optimizer | Adam |
| Reward function parameter () | 10 |
| WGAN latent dimension () | 128 |
| WGAN gradient penalty coefficient () | 10 |
| Target action entropy () | −4 |
| Initial action entropy () | 0.1 |
| Target option entropy () | 1 |
| Initial option entropy () | 0.1 |
| Learning rate of WGAN generator () | |
| Learning rate of WGAN critic () | |
| Target Q-network soft update factor () | |
| Learning rate of option selection () | |
| Learning rate of intra-option selection () | |
| Learning rate of Q function () | |
| Learning rate of Sub-Q function () | |
| Learning rate of option alpha () | |
| Learning rate of action entropy () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Dong, W.; Zhang, P.; Zhai, H.; Li, G. Hierarchical Reinforcement Learning with Automatic Curriculum Generation for Unmanned Combat Aerial Vehicle Tactical Decision-Making in Autonomous Air Combat. Drones 2025, 9, 384. https://doi.org/10.3390/drones9050384
Li Y, Dong W, Zhang P, Zhai H, Li G. Hierarchical Reinforcement Learning with Automatic Curriculum Generation for Unmanned Combat Aerial Vehicle Tactical Decision-Making in Autonomous Air Combat. Drones. 2025; 9(5):384. https://doi.org/10.3390/drones9050384
Chicago/Turabian StyleLi, Yang, Wenhan Dong, Pin Zhang, Hengang Zhai, and Guangqi Li. 2025. "Hierarchical Reinforcement Learning with Automatic Curriculum Generation for Unmanned Combat Aerial Vehicle Tactical Decision-Making in Autonomous Air Combat" Drones 9, no. 5: 384. https://doi.org/10.3390/drones9050384
APA StyleLi, Y., Dong, W., Zhang, P., Zhai, H., & Li, G. (2025). Hierarchical Reinforcement Learning with Automatic Curriculum Generation for Unmanned Combat Aerial Vehicle Tactical Decision-Making in Autonomous Air Combat. Drones, 9(5), 384. https://doi.org/10.3390/drones9050384






