Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm
Abstract
1. Introduction
- The main contribution is establishing a multi-dimensional evaluation framework that integrates coordination, communication equilibrium, and safety metrics. The coordination metric explicitly considers the influence of the tracked UAV, communication equilibrium is evaluated based on channel capacity, and safety is quantified using a hierarchical scoring scheme. This framework offers a more comprehensive and systematic approach to evaluating the swarm’s cooperative capability.
- To validate the applicability of the proposed evaluation metrics, this paper introduces a formation control algorithm based on the synchronous DMPC method. This method allows each UAV to optimize its control strategy independently while maintaining the overall formation. Moreover, collision avoidance is incorporated into the cost function to ensure safe formation flight.
2. Preliminaries
2.1. Graph Theory
2.2. Model of UAV
2.3. Problem Formulation
3. Distributed Model Predictive Controller Design
3.1. Cost Function
3.2. Optimization Problem and Algorithm
| Algorithm 1 DMPC algorithm |
|
4. Cooperative Capability Evaluation Metrics of Swarm
4.1. Coordination
4.1.1. Velocity Consistency
4.1.2. Position Matching
4.2. Communication Equilibrium
4.3. Safety
5. Simulation Results
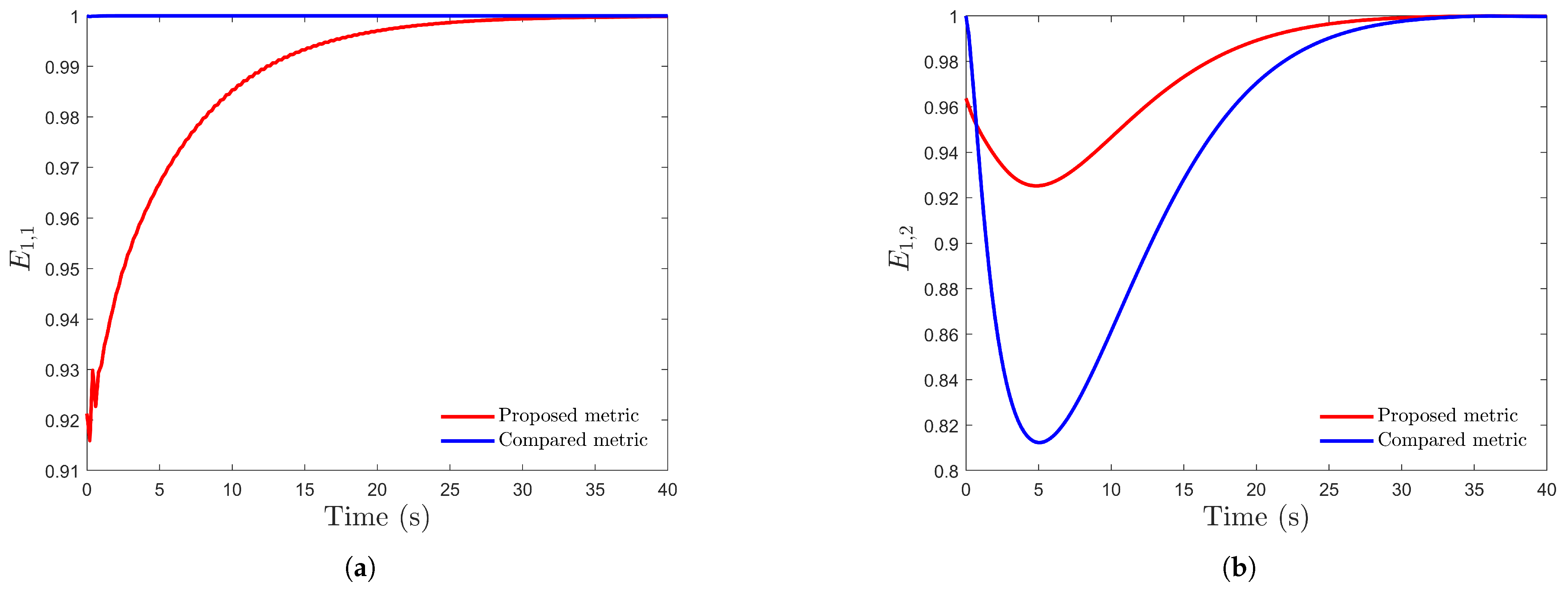
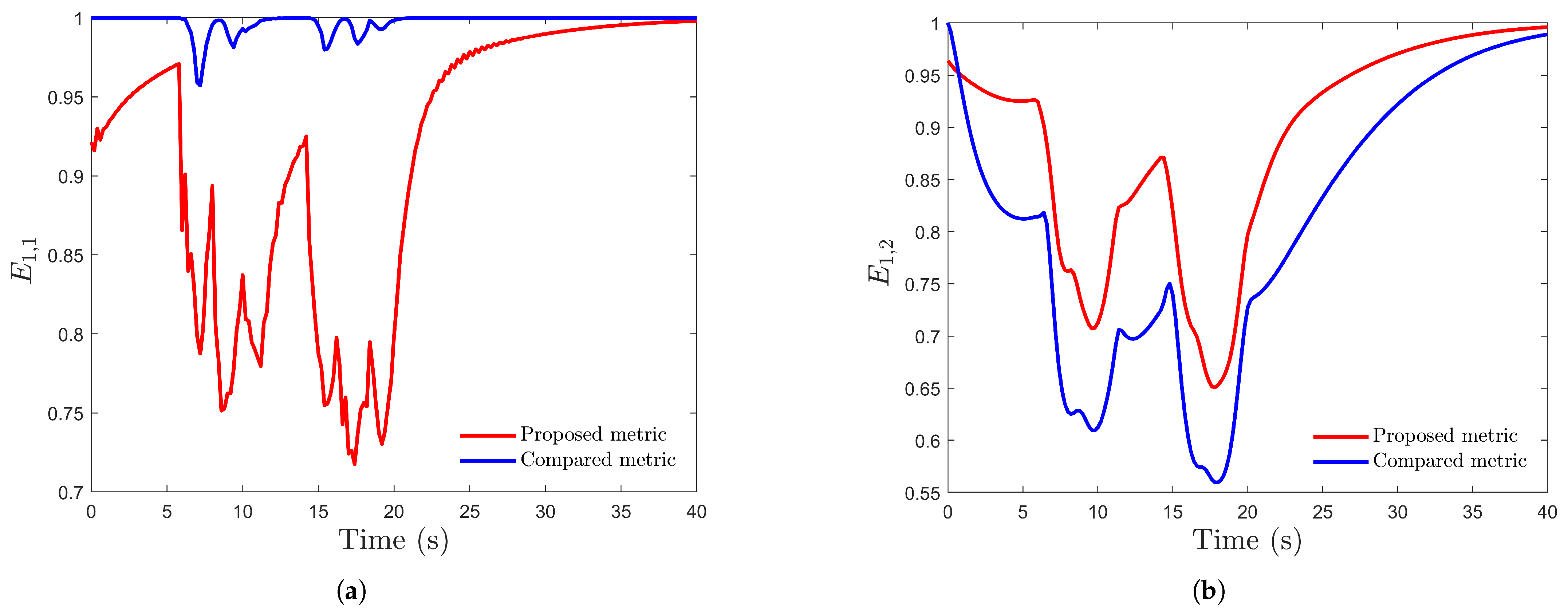
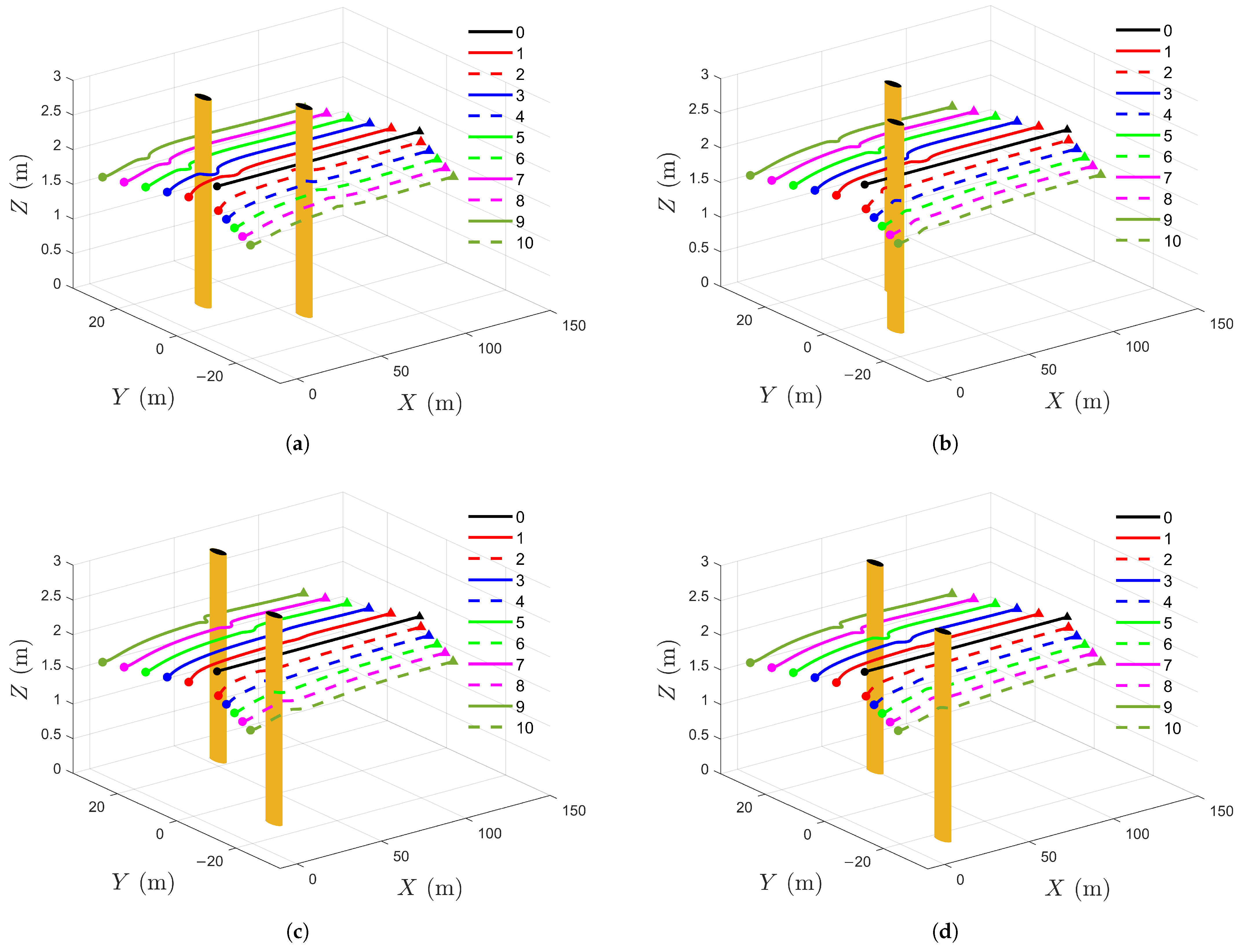
5.1. Formation Control for UAVs Without and with Obstacles
5.2. Formation Control for UAVs in Different Scenarios
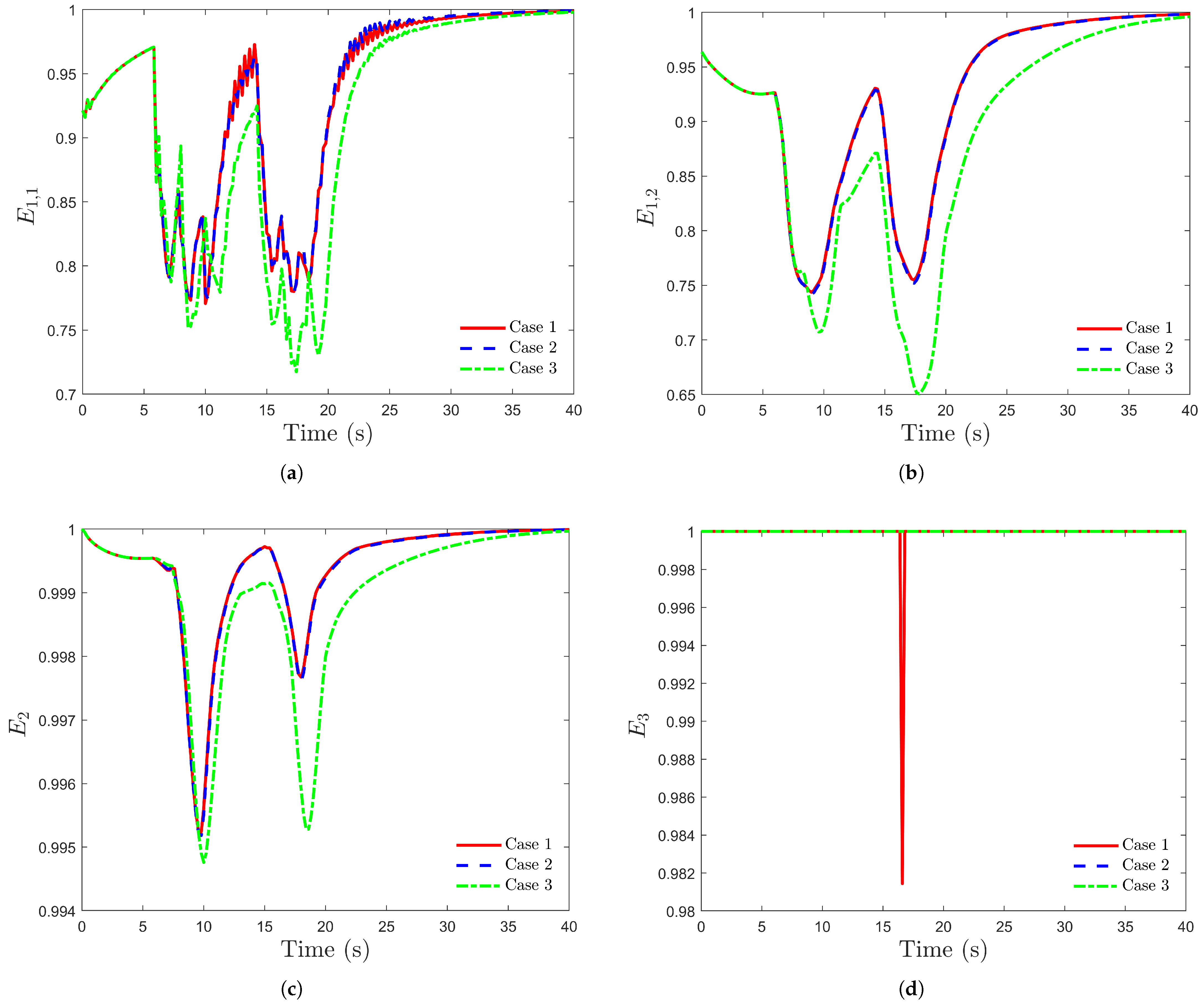
5.3. Cooperative Capability Evaluation Results Under Different Weighting Coefficients
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, Q.; Luan, T.H.; Shi, W.; Fan, P. Edge Computing Enabled Energy-Efficient Multi-UAV Cooperative Target Search. IEEE Trans. Veh. Technol. 2023, 72, 7757–7771. [Google Scholar] [CrossRef]
- Dai, J.; Pu, W.; Yan, J.; Shi, Q.; Liu, H. Multi-UAV Collaborative Trajectory Optimization for Asynchronous 3-D Passive Multitarget Tracking. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Sun, L.; Wang, J.; Wang, J.; Lin, L.; Gen, M. Efficient Joint Deployment of Multi-UAVs for Target Tracking in Traffic Big Data. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7780–7791. [Google Scholar] [CrossRef]
- Gu, J.; Su, T.; Wang, Q.; Du, X.; Guizani, M. Multiple Moving Targets Surveillance Based on a Cooperative Network for Multi-UAV. IEEE Commun. Mag. 2018, 56, 82–89. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, J.; Ahn, C.K.; Xiang, Z. Neural Adaptive Distributed Formation Control of Nonlinear Multi-UAVs With Unmodeled Dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9555–9561. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, Z.; Zhang, J. Dynamics Event-Triggered-Based Time-Varying Bearing Formation Control for UAVs. Drones 2024, 8, 185. [Google Scholar] [CrossRef]
- Zheng, R.; Lyu, Y. Nonlinear tight formation control of multiple UAVs based on model predictive control. Def. Technol. 2023, 25, 69–75. [Google Scholar] [CrossRef]
- Zhan, J.; Jiang, Z.P.; Wang, Y.; Li, X. Distributed Model Predictive Consensus With Self-Triggered Mechanism in General Linear Multiagent Systems. IEEE Trans. Ind. Inf. 2019, 15, 3987–3997. [Google Scholar] [CrossRef]
- Wang, J.; Li, S. Distributed Model Predictive Control for Consensus of Multi-Agent Systems With Connectivity Maintenance. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 71, 1299–1310. [Google Scholar] [CrossRef]
- Chen, Q.; Jin, Y.; Wang, T.; Wang, Y.; Yan, T.; Long, Y. UAV Formation Control Under Communication Constraints Based on Distributed Model Predictive Control. IEEE Access 2022, 10, 126494–126507. [Google Scholar] [CrossRef]
- Liu, S.S.; Ge, M.F.; Ding, T.F.; Liu, Z.W.; Dong, X.G.; Liang, C.D. Distributed Sensor-Tolerant MPC for Formation Tracking of Networked Multicopters With Input/State Constraints. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4429–4433. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, X. Distributed Model Predictive Formation Control for a Group of UAVs With Spatial Kinematics and Unidirectional Data Transmissions. IEEE Trans. Netw. Sci. Eng. 2023, 10, 3209–3222. [Google Scholar] [CrossRef]
- Xu, T.; Liu, J.; Zhang, Z.; Chen, G.; Cui, D.; Li, H. Distributed MPC for Trajectory Tracking and Formation Control of Multi-UAVs With Leader-Follower Structure. IEEE Access 2023, 11, 128762–128773. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, L.; Zhao, J.; Wu, K.; Wang, Y. Virtual target guidance-based distributed model predictive control for formation control of multiple UAVs. Chin. J. Aeronaut. 2020, 33, 1037–1056. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Adaptive differential evolution-based distributed model predictive control for multi-UAV formation flight. Int. J. Aeronaut. Space Sci. 2020, 21, 538–548. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, C.; Gong, H.; Zhang, S.; Wang, X. Formation Transformation Based on Improved Genetic Algorithm and Distributed Model Predictive Control. Drones 2023, 7, 527. [Google Scholar] [CrossRef]
- He, Y.; Shi, X.; Lu, J.; Zhao, C.; Zhao, G. Grouping Formation and Obstacle Avoidance Control of UAV Swarm Based on Synchronous DMPC. Int. J. Aerosp. Eng. 2024, 2024, 4934194. [Google Scholar] [CrossRef]
- Du, Z.; Zhang, H.; Wang, Z.; Yan, H. Model Predictive Formation Tracking-Containment Control for Multi-UAVs With Obstacle Avoidance. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3404–3414. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Virágh, C.; Somorjai, G.; Nepusz, T.; Eiben, A.E.; Vicsek, T. Optimized flocking of autonomous drones in confined environments. Sci. Robot. 2018, 3, eaat3536. [Google Scholar] [CrossRef]
- Cofta, P.; Ledziński, D.; Śmigiel, S.; Gackowska, M. Cross-entropy as a metric for the robustness of drone swarms. Entropy 2020, 22, 597. [Google Scholar] [CrossRef]
- Bahaidarah, M.; Rekabi-Bana, F.; Marjanovic, O.; Arvin, F. Swarm flocking using optimisation for a self-organised collective motion. Swarm Evol. Comput. 2024, 86, 101491. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Ding, W.; Wang, Q.; Zhang, Z.; Jia, J. Bio-Inspired Fission–Fusion Control and Planning of Unmanned Aerial Vehicles Swarm Systems via Reinforcement Learning. Appl. Sci. 2024, 14, 1192. [Google Scholar] [CrossRef]
- Rodríguez, I.; Rubio, D.; Rubio, F. Complexity of adaptive testing in scenarios defined extensionally. Front. Comput. Sci. 2023, 17, 173206. [Google Scholar] [CrossRef]

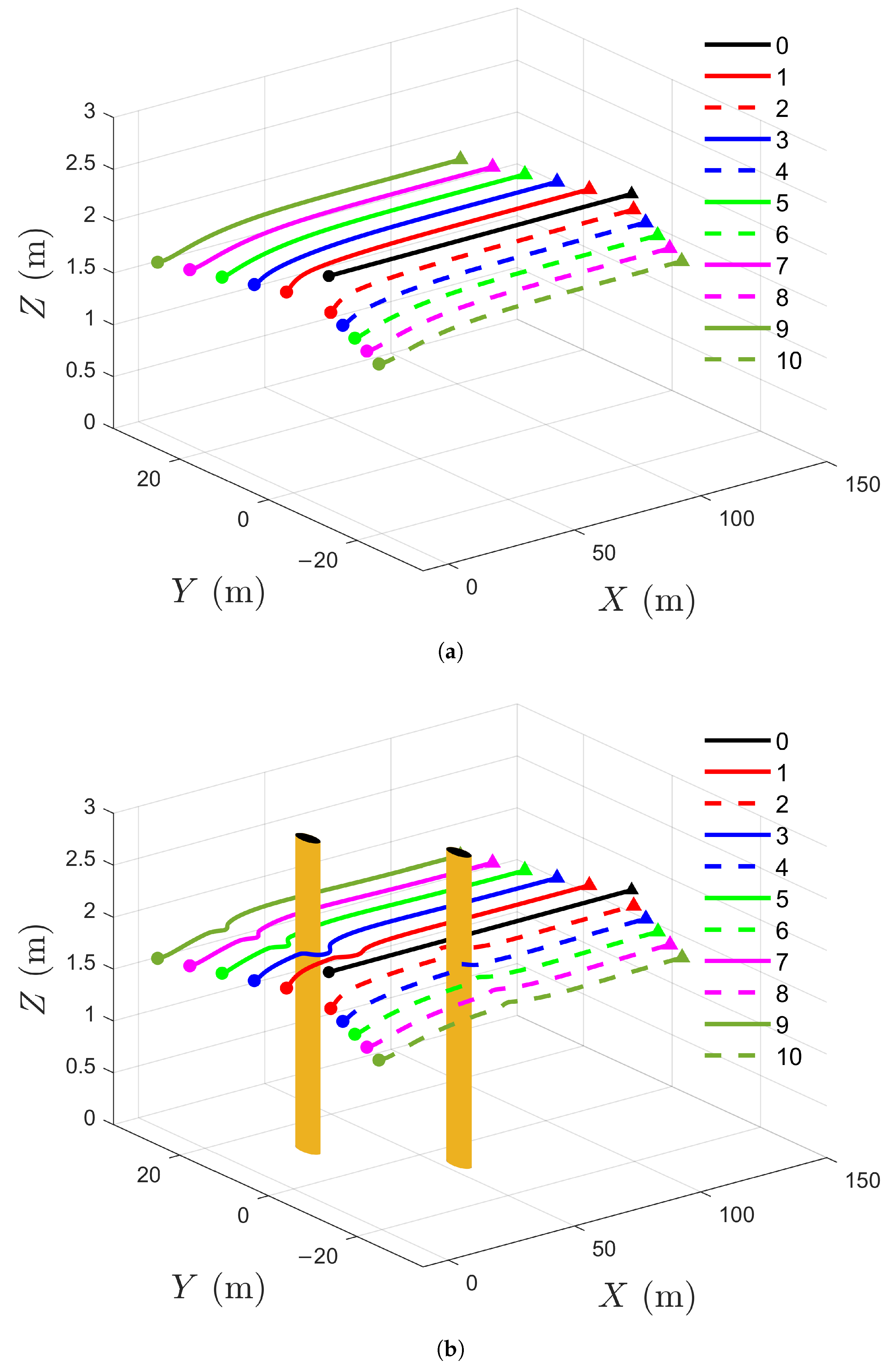
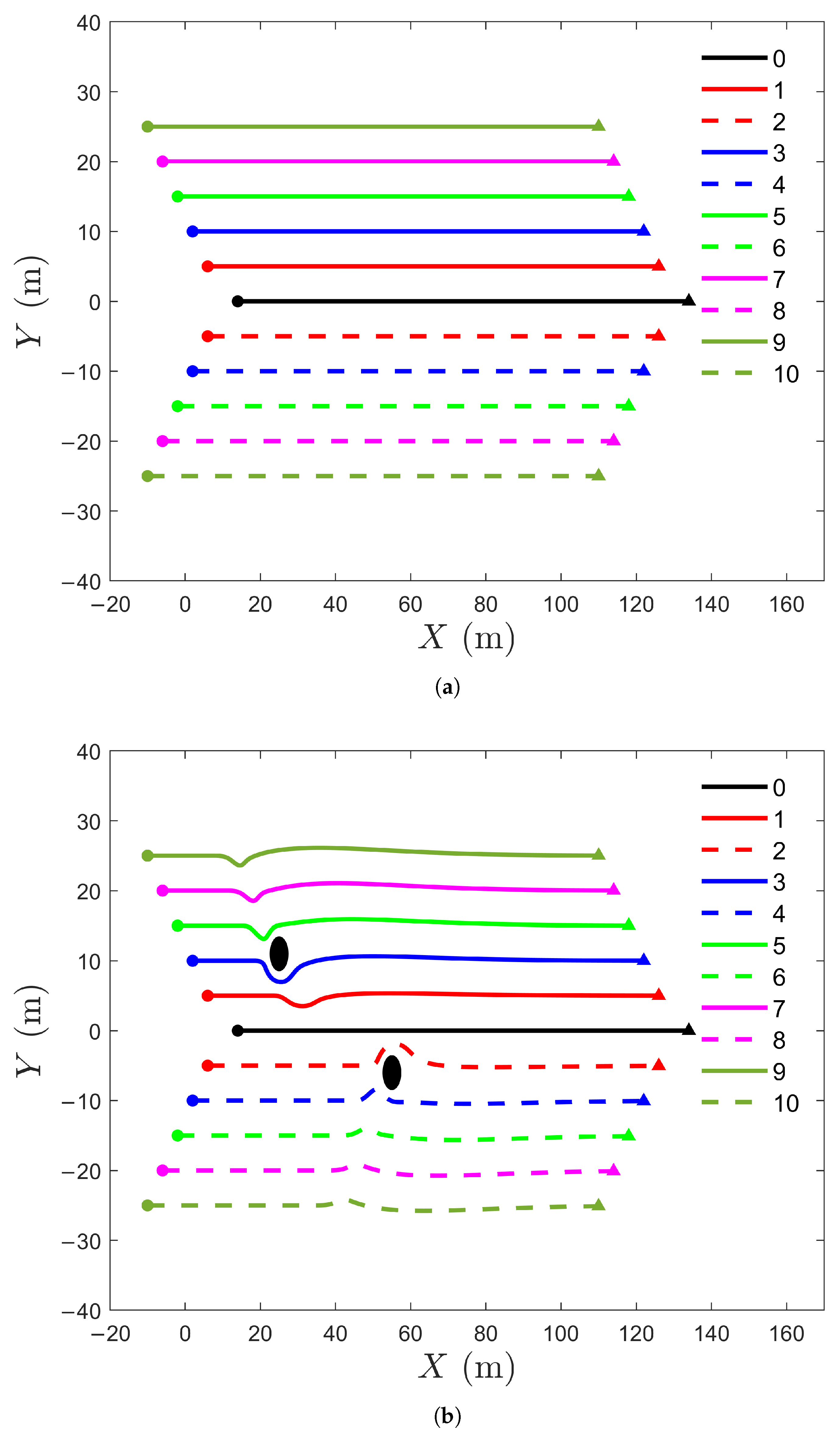
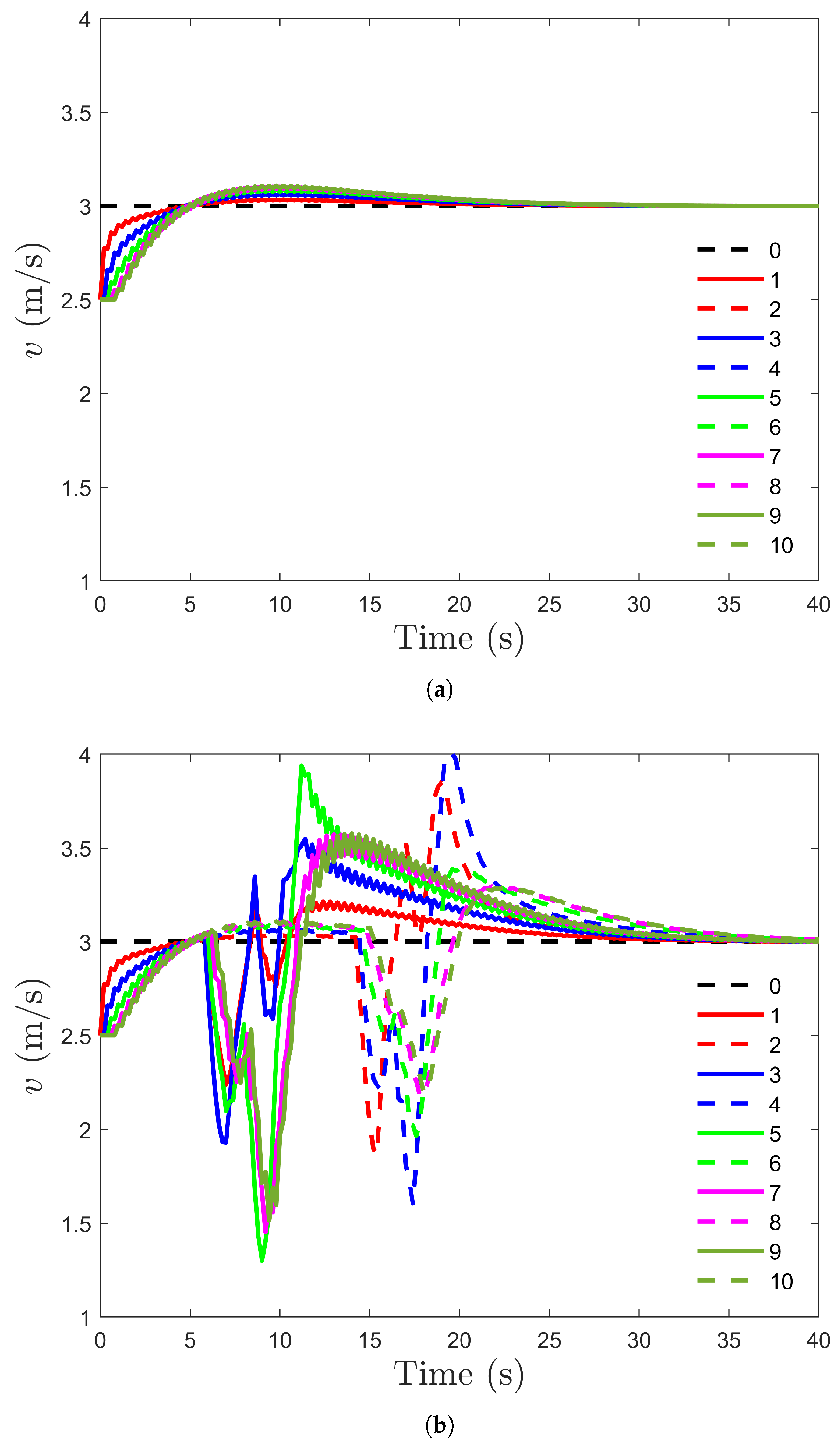
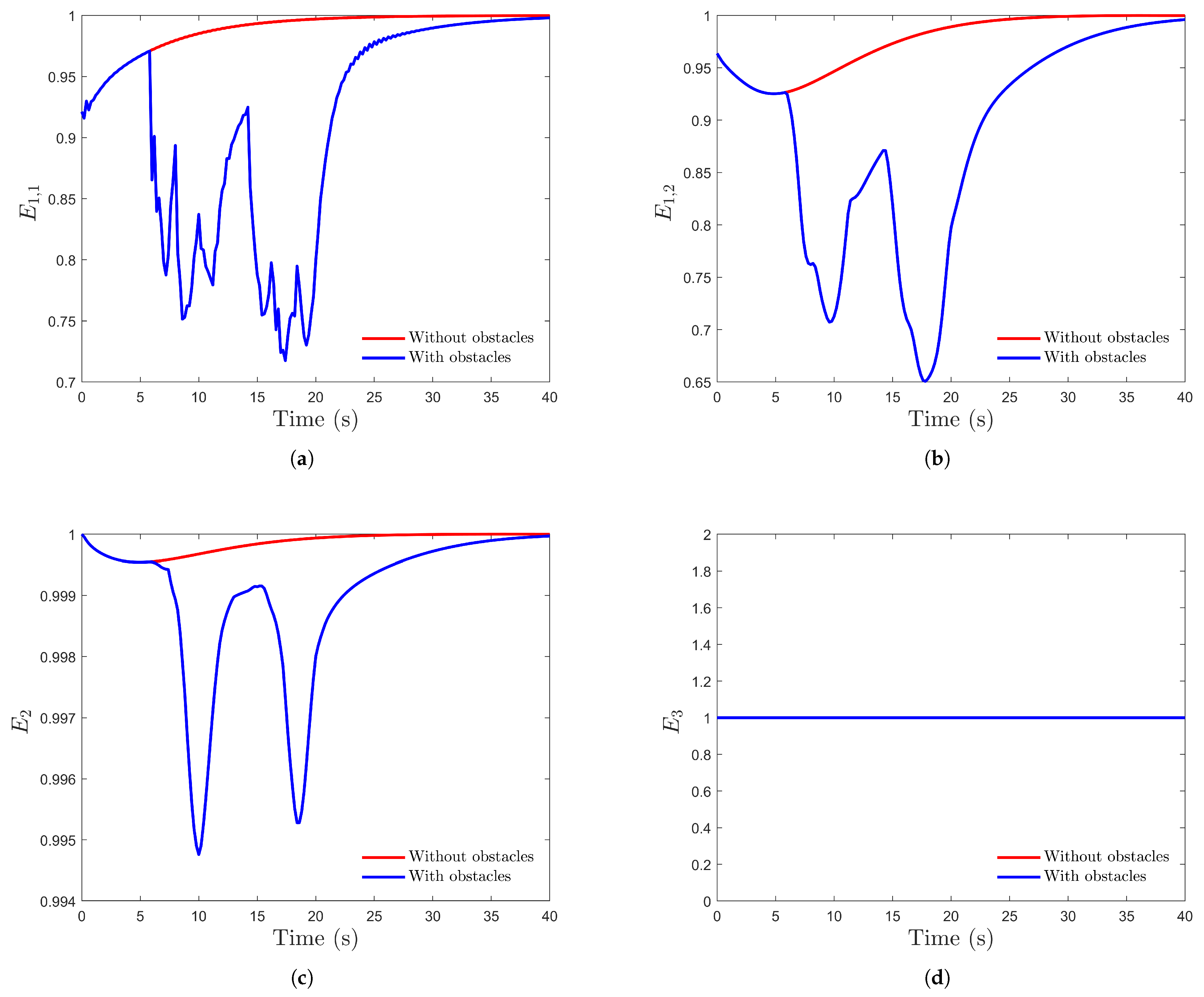


| ID | Initial State | Desired Relative State |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
| Parameter | Value |
|---|---|
| Weighting coefficient | 100 |
| Prediction horizon | 5 |
| Sampling period (s) | |
| Velocity range (m/s) | |
| Height range (m) | |
| Control input range | |
| Safety distances (m) and (m) | 1.2, 2.5 |
| UAV detection range (m) | 4 |
| Channel’s power gain (dB) | −20 |
| Noise power (dBm) | −80 |
| Communication bandwidth (MHz) | 1 |
| Transmitted power P (dBm) | 10 |
| Scenario | Coordinate for Obstacle 1 | Coordinate for Obstacle 2 |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Case | |
|---|---|
| 1 | 42 |
| 2 | 43 |
| 3 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Guan, X.; Shi, M.; Li, B.; Wei, C.; Yiu, K.-F.C. Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm. Drones 2025, 9, 366. https://doi.org/10.3390/drones9050366
Yang M, Guan X, Shi M, Li B, Wei C, Yiu K-FC. Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm. Drones. 2025; 9(5):366. https://doi.org/10.3390/drones9050366
Chicago/Turabian StyleYang, Ming, Xiaoyi Guan, Mingming Shi, Bin Li, Chen Wei, and Ka-Fai Cedric Yiu. 2025. "Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm" Drones 9, no. 5: 366. https://doi.org/10.3390/drones9050366
APA StyleYang, M., Guan, X., Shi, M., Li, B., Wei, C., & Yiu, K.-F. C. (2025). Distributed Model Predictive Formation Control for UAVs and Cooperative Capability Evaluation of Swarm. Drones, 9(5), 366. https://doi.org/10.3390/drones9050366






