The Equal-Time Waypoint Method: A Multi-AUV Path Planning Approach That Is Based on Velocity Variation
Abstract
1. Introduction
- 1.
- 2.
- Consideration of Ocean Current Effects: Compared to the underwater vehicle trajectory tracking methods presented in [10,11,16,25,26], the influence of ocean currents on AUV maneuverability and energy consumption is extensively considered, resulting in trajectories that are more adaptable to ocean currents.
- 3.
- NMPC Controller Adaptation: When designing the NMPC (Nonlinear Model Predictive Control) controller, waypoints are interpolated to allow the NMPC controller’s rolling optimization strategy to roll simultaneously with the reference positions at each time step, thereby enhancing the NMPC controller’s trajectory tracking capabilities.
2. Preparation Work
2.1. AUV Module
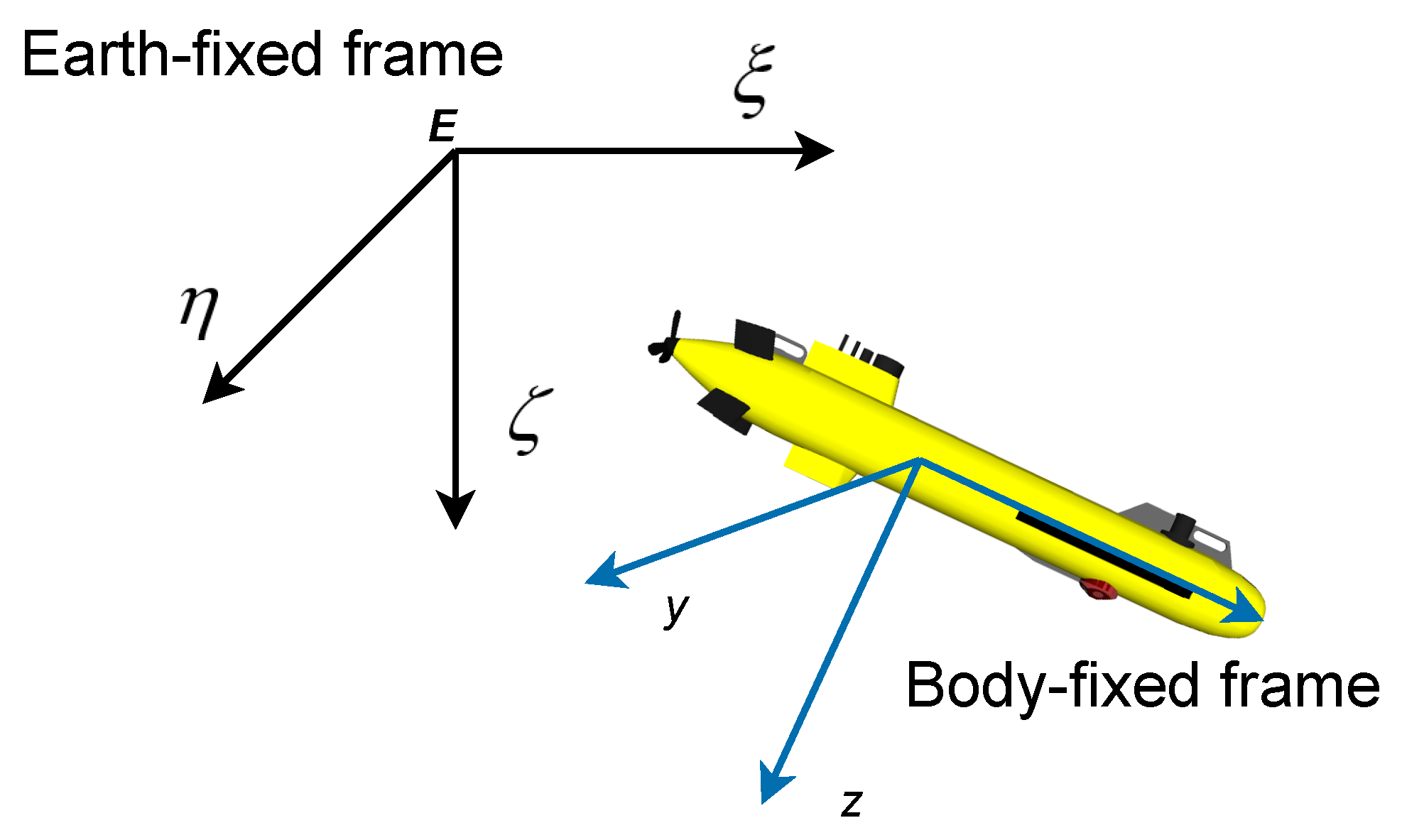
2.1.1. Coordinate Systems
2.1.2. Model of Motion
2.2. Ocean Current Modeling with Eddy
3. Path Planning Method Based on Equal-Time Waypoint
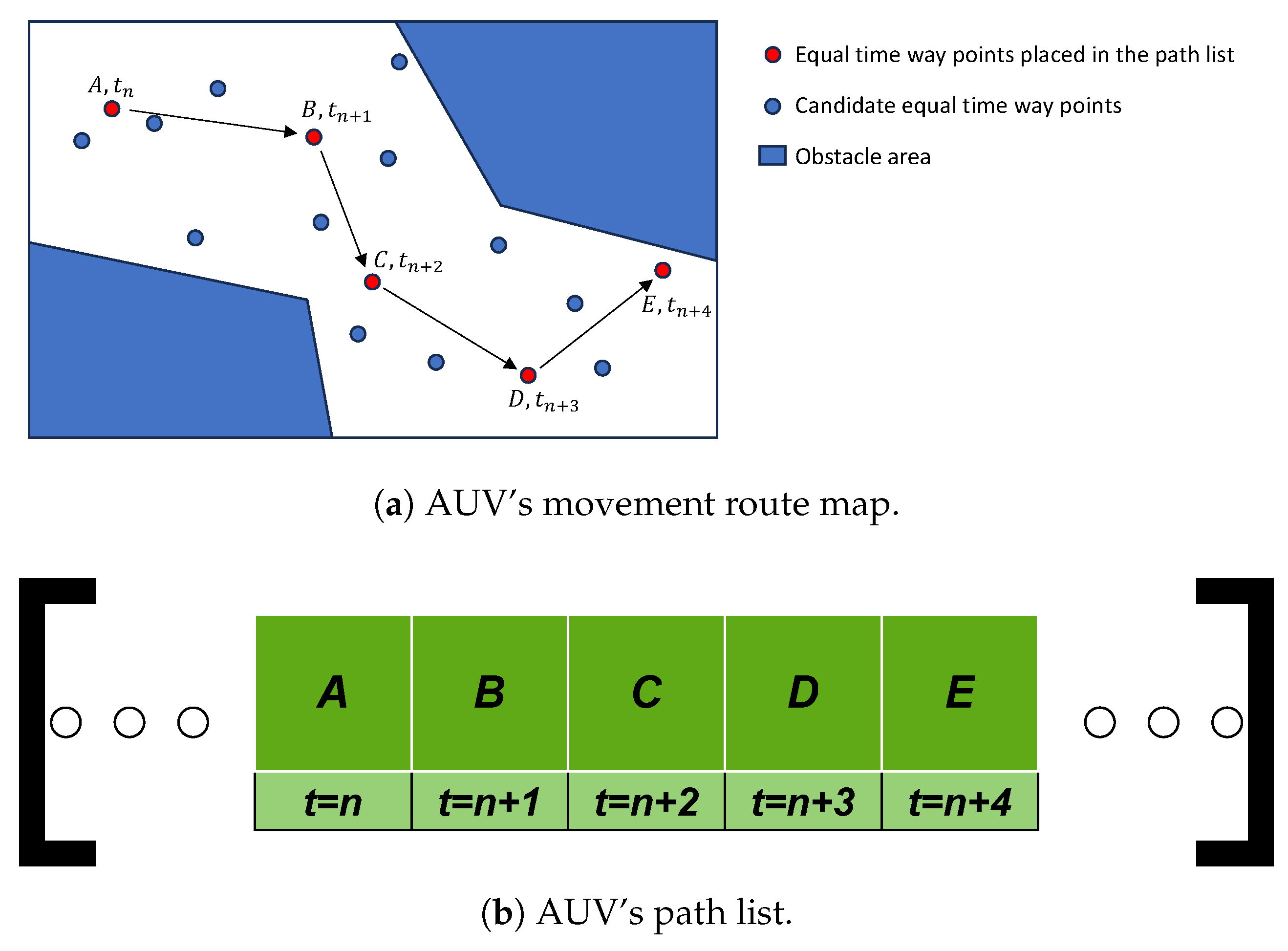
3.1. Equal-Time Waypoint
3.2. Optimization of Path List
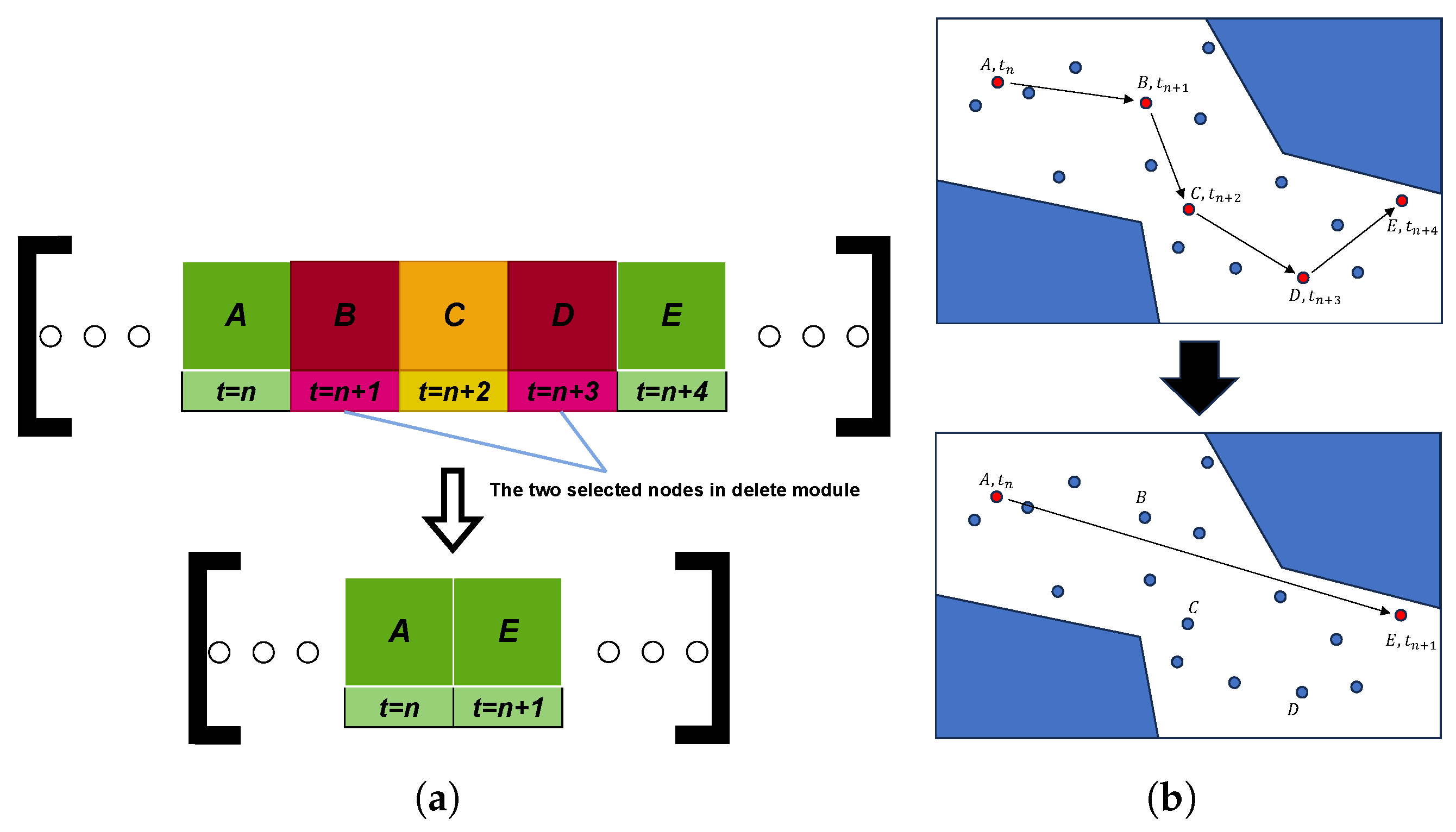
3.2.1. Delete Module
3.2.2. Replace Module
3.2.3. Exchange Module
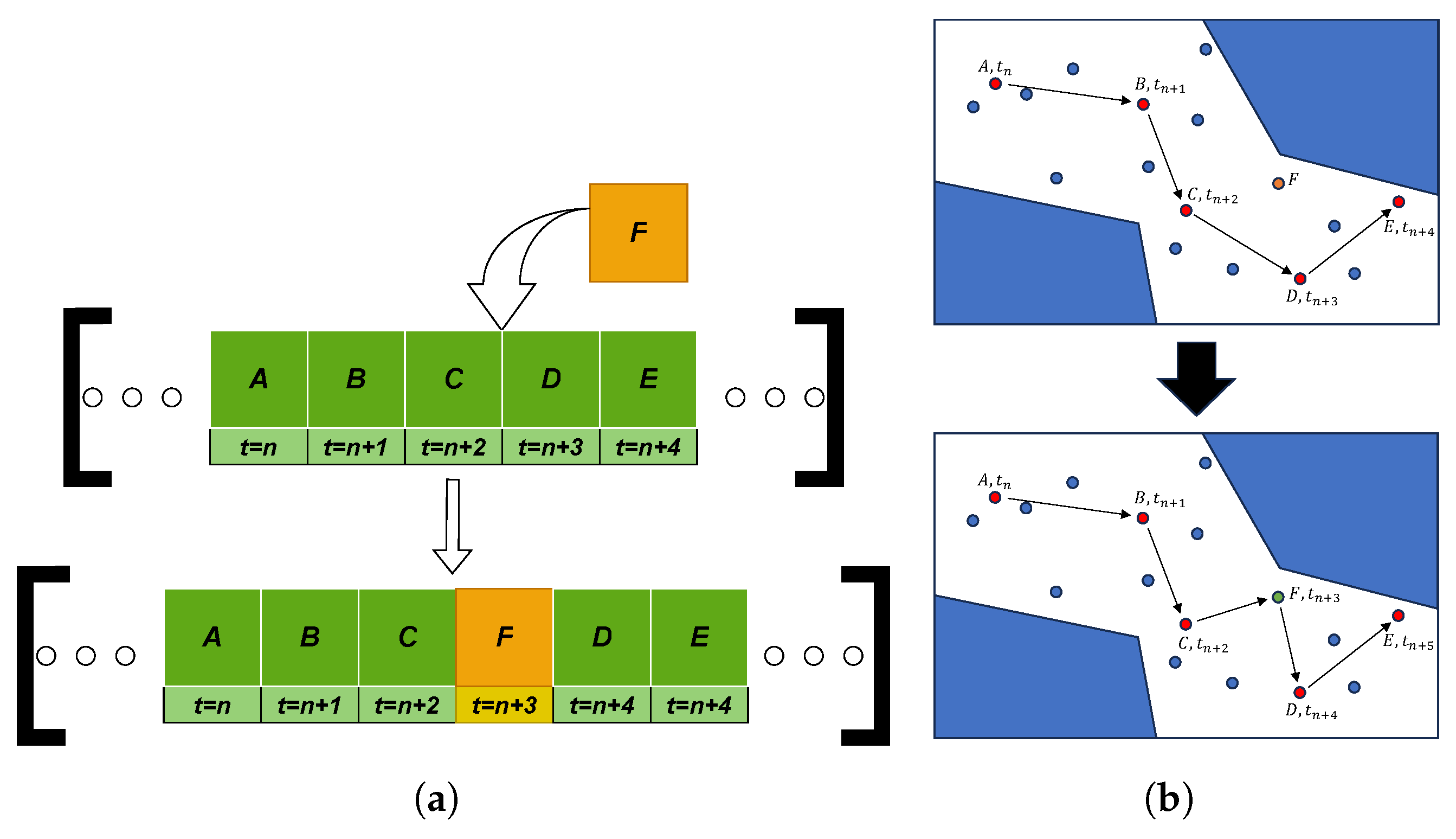
3.2.4. Add Module
3.3. Objective Function
3.3.1. The Total Path Length
3.3.2. Influence of Ocean Currents on Paths
3.3.3. Speed Offset
3.3.4. Smoothness of the Path
3.3.5. Multiple AUV Collisions
3.3.6. Fitness Function
3.4. Multi-AUV Path Planning Method Based on Equal-Time Waypoint
4. Simulation Results and Analysis
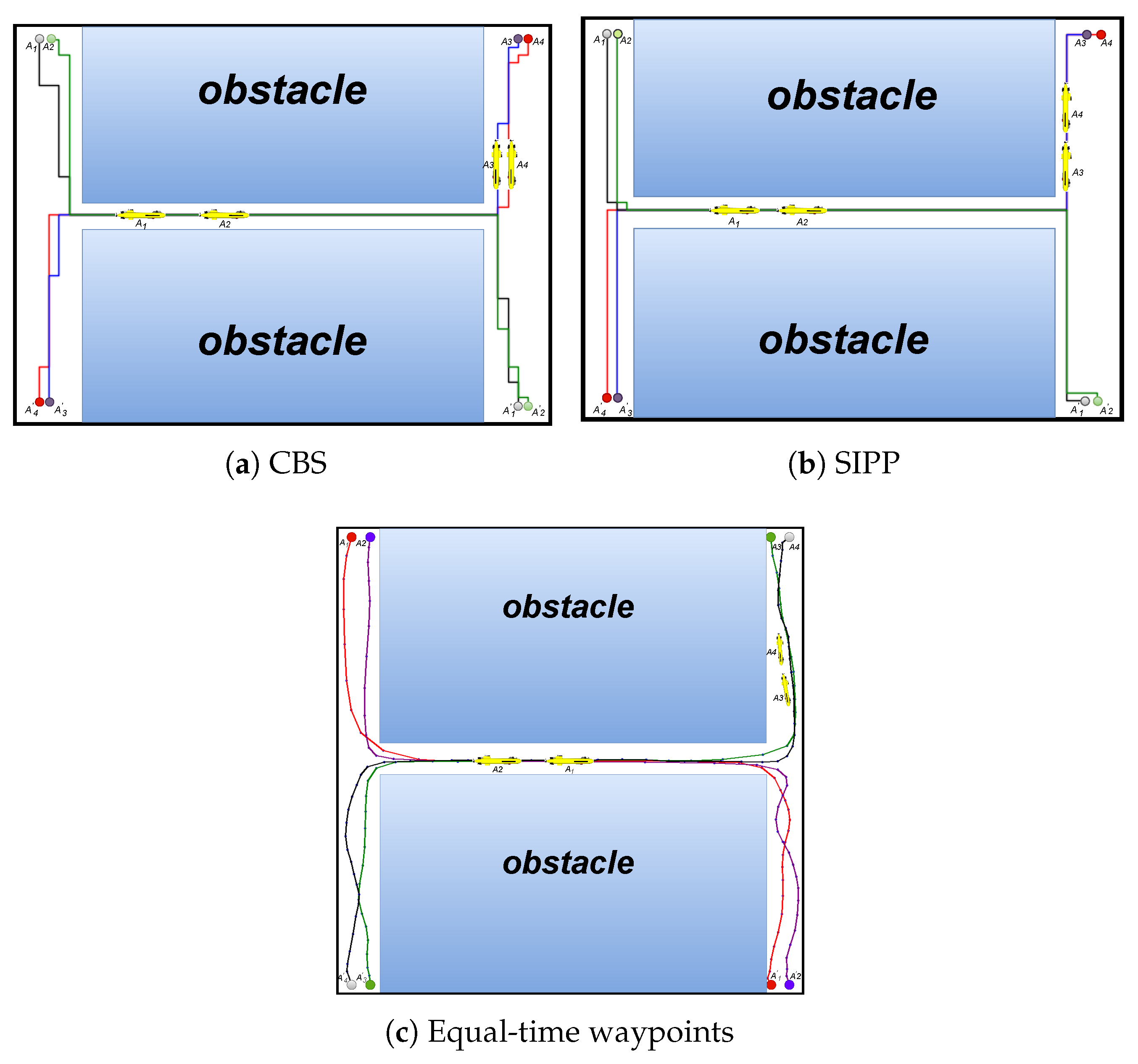
4.1. Comparative Experiments in Confined Spaces
4.2. The Impact of Ocean Currents on AUV Paths
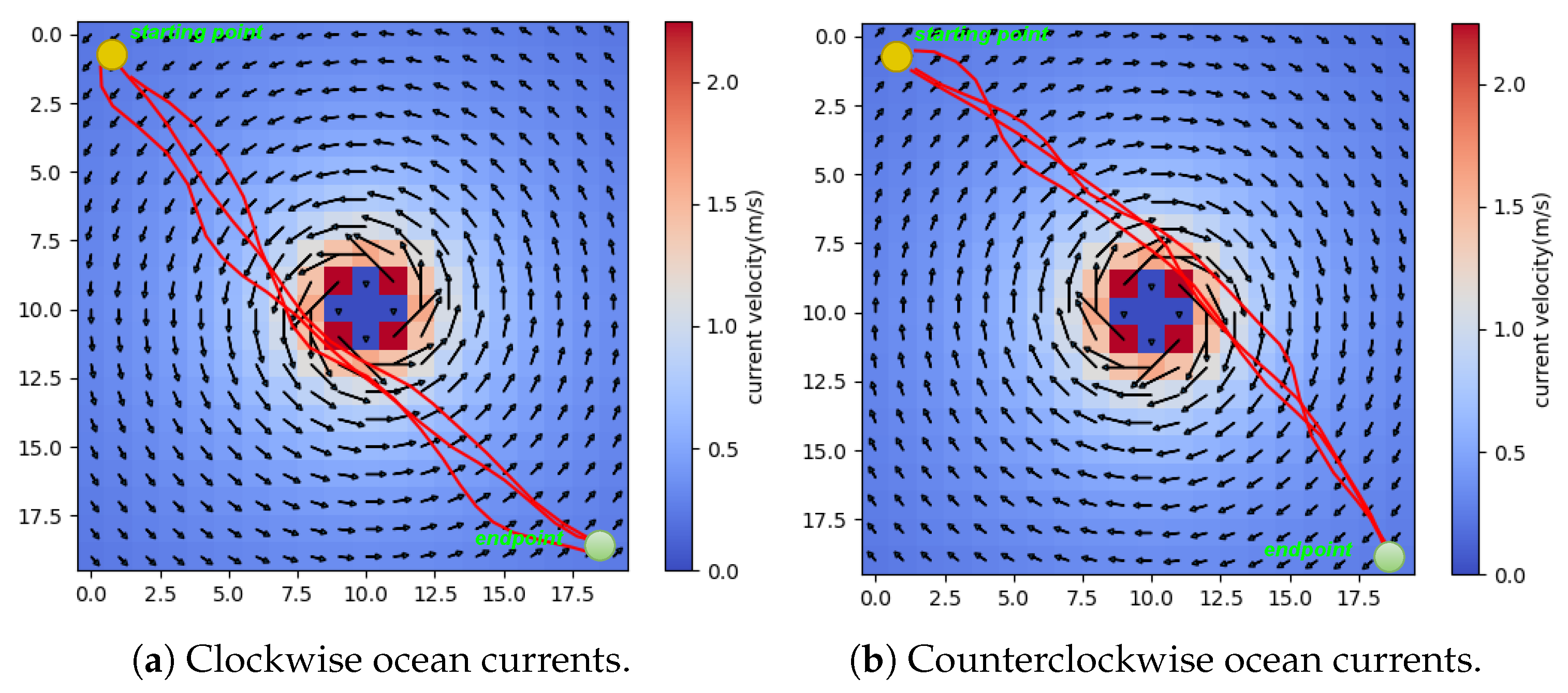
4.2.1. Selectivity of Ocean Currents on Paths
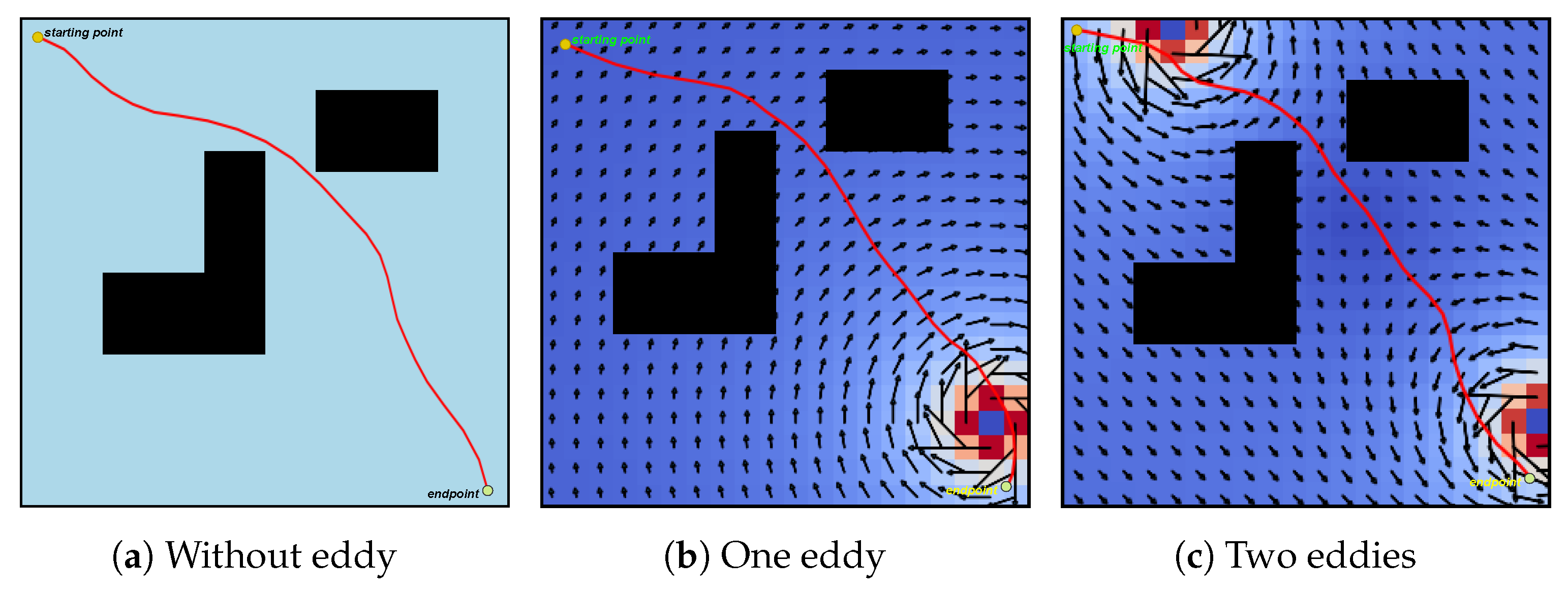
4.2.2. The Impact of Ocean Currents on Pathways
5. NMPC Control Simulation Results
6. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, L.; Wang, Y.; Hui, X.; Ma, X.; Bai, X.; Tan, M. Underwater Robots and Key Technologies for Operation Control. Cyborg Bionic Syst. 2024, 5, 0089. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhu, D.; Pang, W.; Zhang, Y. A survey of underwater search for multi-target using Multi-AUV: Task allocation, path planning, and formation control. Ocean. Eng. 2023, 278, 114393. [Google Scholar] [CrossRef]
- Gao, J.; Li, Y.; Li, X.; Yan, K.; Lin, K.; Wu, X. A review of graph-based multi-agent pathfinding solvers: From classical to beyond classical. Knowl.-Based Syst. 2024, 283, 111121. [Google Scholar] [CrossRef]
- Phillips, M.; Likhachev, M. SIPP: Safe interval path planning for dynamic environments. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5628–5635. [Google Scholar] [CrossRef]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Cheng, C.; Sha, Q.; He, B.; Li, G. Path planning and obstacle avoidance for AUV: A review. Ocean Eng. 2021, 235, 109355. [Google Scholar] [CrossRef]
- Zeng, Z.; Sammut, K.; Lian, L.; He, F.; Lammas, A.; Tang, Y. A comparison of optimization techniques for AUV path planning in environments with ocean currents. Robot. Auton. Syst. 2016, 82, 61–72. [Google Scholar] [CrossRef]
- Sun, B.; Zhu, D.; Tian, C.; Luo, C. Complete Coverage Autonomous Underwater Vehicles Path Planning Based on Glasius Bio-Inspired Neural Network Algorithm for Discrete and Centralized Programming. IEEE Trans. Cogn. Dev. Syst. 2019, 11, 73–84. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, B.; Yang, S.X. A Novel Algorithm of Multi-AUVs Task Assignment and Path Planning Based on Biologically Inspired Neural Network Map. IEEE Trans. Intell. Veh. 2021, 6, 333–342. [Google Scholar] [CrossRef]
- Chu, Z.; Wang, F.; Lei, T.; Luo, C. Path Planning Based on Deep Reinforcement Learning for Autonomous Underwater Vehicles Under Ocean Current Disturbance. IEEE Trans. Intell. Veh. 2023, 8, 108–120. [Google Scholar] [CrossRef]
- Wang, C.; Mei, D.; Wang, Y.; Yu, X.; Sun, W.; Wang, D.; Chen, J. Task allocation for Multi-AUV system: A review. Ocean Eng. 2022, 266, 112911. [Google Scholar] [CrossRef]
- Yin, L.; Yan, Z.; Tian, Q.; Li, H.; Xu, J. A novel robust algorithm for path planning of multiple autonomous underwater vehicles in the environment with ocean currents. Ocean Eng. 2024, 312, 119260. [Google Scholar] [CrossRef]
- Zhuang, Y.; Huang, H.; Sharma, S.; Xu, D.; Zhang, Q. Cooperative path planning of multiple autonomous underwater vehicles operating in dynamic ocean environment. ISA Trans. 2019, 94, 174–186. [Google Scholar] [CrossRef]
- Liu, X.F.; Fang, Y.; Zhan, Z.H.; Jiang, Y.L.; Zhang, J. A Cooperative Evolutionary Computation Algorithm for Dynamic Multiobjective Multi-AUV Path Planning. IEEE Trans. Ind. Inform. 2024, 20, 669–680. [Google Scholar] [CrossRef]
- Barer, M.; Sharon, G.; Stern, R.; Felner, A. Suboptimal variants of the conflict-based search algorithm for the multi-agent pathfinding problem. In Proceedings of the International Symposium on Combinatorial Search, Prague, Czech Republic, 15–17 August 2014; Volume 5, pp. 19–27. [Google Scholar]
- Li, J.; Ruml, W.; Koenig, S. EECBS: A Bounded-Suboptimal Search for Multi-Agent Path Finding. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, AAAI 2021, Virtual, 2–9 February 2021; Volume 14A, pp. 12353–12362. [Google Scholar]
- Mei, Y.; Li, S.; Chen, C.; Han, A. A Multi-robot Task Allocation and Path Planning Method for Warehouse System. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 1911–1916. [Google Scholar] [CrossRef]
- Feng, S.; Zeng, L.; Liu, J.; Yang, Y.; Song, W. Multi-UAVs Collaborative Path Planning in the Cramped Environment. IEEE/CAA J. Autom. Sin. 2024, 11, 529–538. [Google Scholar] [CrossRef]
- Yakovlev, K.; Andreychuk, A.; Vorobyev, V. Prioritized Multi-agent Path Finding for Differential Drive Robots. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- García, E.; Villar, J.R.; Tan, Q.; Sedano, J.; Chira, C. An efficient multi-robot path planning solution using A* and coevolutionary algorithms. Integr. Comput.-Aided Eng. 2023, 30, 41–52. [Google Scholar] [CrossRef]
- Kumar, S.; Sikander, A. A novel hybrid framework for single and multi-robot path planning in a complex industrial environment. J. Intell. Manuf. 2024, 35, 587–612. [Google Scholar] [CrossRef]
- Sandström, R.; Uwacu, D.; Denny, J.; Amato, N.M. Topology-Guided Roadmap Construction with Dynamic Region Sampling. IEEE Robot. Autom. Lett. 2020, 5, 6161–6168. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, H.; Cai, W. Hunting Task Allocation for Heterogeneous Multi-AUV Formation Target Hunting in IoUT: A Game Theoretic Approach. IEEE Internet Things J. 2024, 11, 9142–9152. [Google Scholar] [CrossRef]
- Xiong, M.; Xie, G. Swarm Game and Task Allocation for Autonomous Underwater Robots. J. Mar. Sci. Eng. 2023, 11, 148. [Google Scholar] [CrossRef]
- Li, J.H. 3D trajectory tracking of underactuated non-minimum phase underwater vehicles. Automatica 2023, 155, 111149. [Google Scholar] [CrossRef]
- Ebrahimpour, M.; Lungu, M. Finite-Time Path-Following Control of Underactuated AUVs with Actuator Limits Using Disturbance Observer-Based Backstepping Control. Drones 2025, 9, 70. [Google Scholar] [CrossRef]
- Patil, P.V.; Khan, M.K.; Korulla, M.; Nagarajan, V.; Sha, O.P. Design optimization of an AUV for performing depth control maneuver. Ocean Eng. 2022, 266, 112929. [Google Scholar] [CrossRef]
- Garau, B.; Alvarez, A.; Oliver, G. AUV navigation through turbulent ocean environments supported by onboard H-ADCP. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006, ICRA 2006, Orlando, FL, USA, 15–19 May; 2006; pp. 3556–3561. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Zhou, L. Optimal Path and Timetable Planning Method for Multi-Robot Optimal Trajectory. IEEE Robot. Autom. Lett. 2022, 7, 8130–8137. [Google Scholar] [CrossRef]
- Kavraki, L.; Svestka, P.; Latombe, J.C.; Overmars, M. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Smith, A.; Kitamura, Y.; Takemura, H.; Kishino, F. A simple and efficient method for accurate collision detection among deformable polyhedral objects in arbitrary motion. In Proceedings of the Virtual Reality Annual International Symposium ’95, Research Triangle Park, NC, USA, 11–15 March 1995; pp. 136–145. [Google Scholar] [CrossRef]
- Romeo, F.; Sangiovanni-Vincentelli, A. A theoretical framework for simulated annealing. Algorithmica 1991, 6, 302–345. [Google Scholar] [CrossRef]
- Sun, B.; Niu, N. Multi-AUVs cooperative path planning in 3D underwater terrain and vortex environments based on improved multi-objective particle swarm optimization algorithm. Ocean Eng. 2024, 311, 118944. [Google Scholar] [CrossRef]




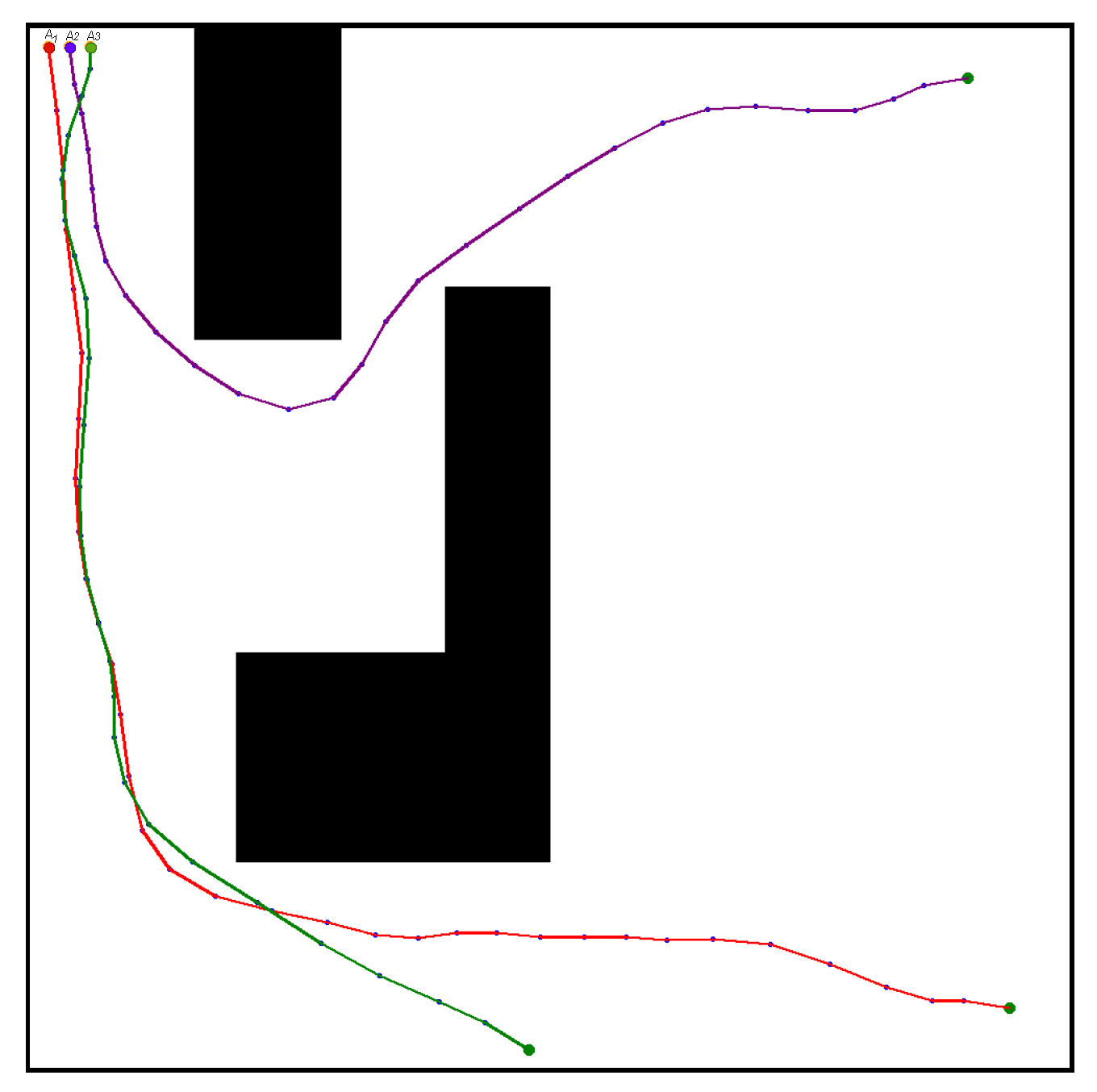

| AUV Number | Coordinate of Starting Point | Coordinate of Endpoint |
|---|---|---|
| (20, 20) | (940, 940) | |
| (40, 20) | (900, 50) | |
| (60, 20) | (480, 980) |
| Symbol | Parameter | Parameter Value |
|---|---|---|
| Number of random candidate equal-time waypoints | 1000 | |
| Equal interval | 50 s | |
| Optimal running speed | 1 m/s | |
| Safety distance | 5 m | |
| Temperature threshold | 3000 | |
| Over-speed-loss factor | 1 | |
| Below-speed-loss factor | 0.1 | |
| Path length influence factor | 1 | |
| Current influence factor | 2 | |
| Velocity offset influence factor | 1 | |
| Path smoothness influence factor | 1 | |
| Standard deviation of Gaussian function | 1 |
| AUV Number | Coordinate of Starting Point | Coordinate of Endpoint |
|---|---|---|
| (20, 20) | (980, 980) | |
| (40, 20) | (960, 980) | |
| (60, 20) | (40, 980) | |
| (60, 20) | (20, 980) |
| AUV Number | Coordinate of Starting Point | Coordinate of Endpoint |
|---|---|---|
| (20, 20) | (920, 920) | |
| (40, 40) | (940, 940) | |
| (60, 60) | (960, 960) |
| Experimental Scenario | Current Consideration | Mean | Max | Min | Std Dev |
|---|---|---|---|---|---|
| Single Vortex | Without Current | 5.13 | 11.95 | −5.35 | 4.92 |
| With Current | −3.78 | 2.46 | −11.78 | 5.07 | |
| Dual Vortices | Without Current | −29.62 | 95.27 | −99.35 | 73.69 |
| With Current | −530.02 | −97.42 | −1888.01 | 506.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Shi, K.; Wang, H. The Equal-Time Waypoint Method: A Multi-AUV Path Planning Approach That Is Based on Velocity Variation. Drones 2025, 9, 336. https://doi.org/10.3390/drones9050336
Yin C, Shi K, Wang H. The Equal-Time Waypoint Method: A Multi-AUV Path Planning Approach That Is Based on Velocity Variation. Drones. 2025; 9(5):336. https://doi.org/10.3390/drones9050336
Chicago/Turabian StyleYin, Chenxin, Kai Shi, and Hailong Wang. 2025. "The Equal-Time Waypoint Method: A Multi-AUV Path Planning Approach That Is Based on Velocity Variation" Drones 9, no. 5: 336. https://doi.org/10.3390/drones9050336
APA StyleYin, C., Shi, K., & Wang, H. (2025). The Equal-Time Waypoint Method: A Multi-AUV Path Planning Approach That Is Based on Velocity Variation. Drones, 9(5), 336. https://doi.org/10.3390/drones9050336









