Secure and Energy-Efficient Configuration Strategies for UAV-RIS System with Uplink NOMA
Abstract
1. Introduction
- A practical elevation-based A2G LoS link subject to Nakagami-m fading is established. This study specifically evaluates the effects of the phase estimation errors that arise from imperfect conditions such as UAV jitter, providing insights into how these errors influence the overall communication performance.
- The range of reflecting elements for simultaneously reliable and secure transmissions from an uplink NOMA UAV-RIS system is derived. The derivation serves as a theoretical reference for configuring RISs in UAV systems with heterogeneous service requirements, ensuring that the system can achieve both reliability and security.
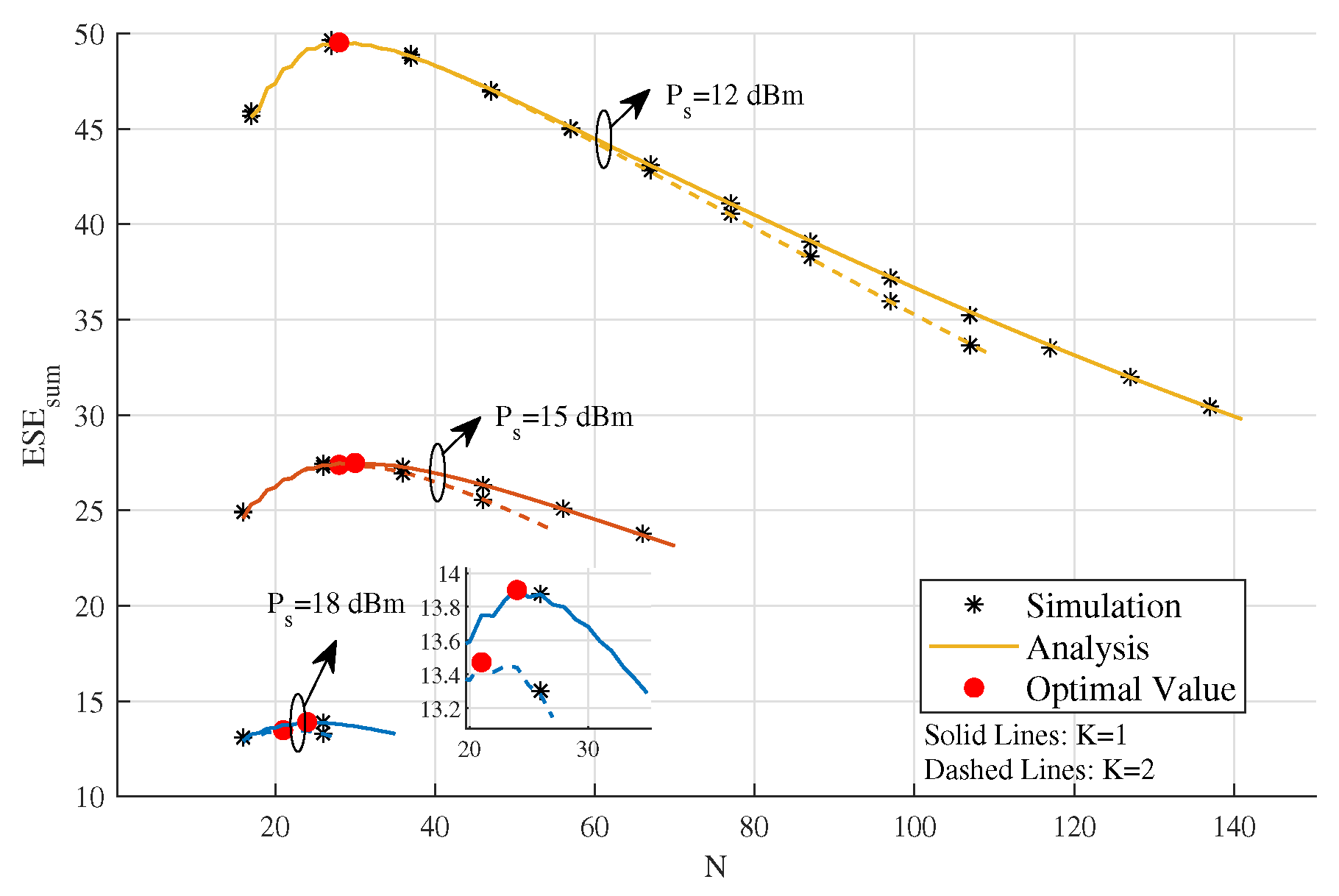
- To address the energy efficiency of the system, we define and utilize the indexed ESE metric to characterize the overall performance of the system. This metric comprehensively characterizes the system’s performance by balancing energy consumption and security. Under the constraints of reliability and security, the number of reflecting elements is optimized to maximize the ESE.
- Numerical results are presented to validate the accuracy of our theoretical analysis, revealing the impact of key system parameters on the system performance. These findings provide valuable guidance for the practical deployment and optimization of uplink NOMA UAV-RIS systems in future wireless communication networks.
2. System Model
2.1. The Channel Model
2.2. The Phase Shift Design and SNR Distribution
2.3. Statistical Characteristics of the Channels
3. Analysis of the Configuration of Reflecting Elements and Their Optimization
| Algorithm 1: Golden search iterative algorithm for |
| Initialization: , , and the maximum tolerance ; |
| Calculate and ; |
| While do; |
| , calculate using (27); |
| , calculate using (27) again; |
| if do; |
| , , ; |
| else do |
| , , ; |
| end if |
| end while |
| Obtain the optimal . |
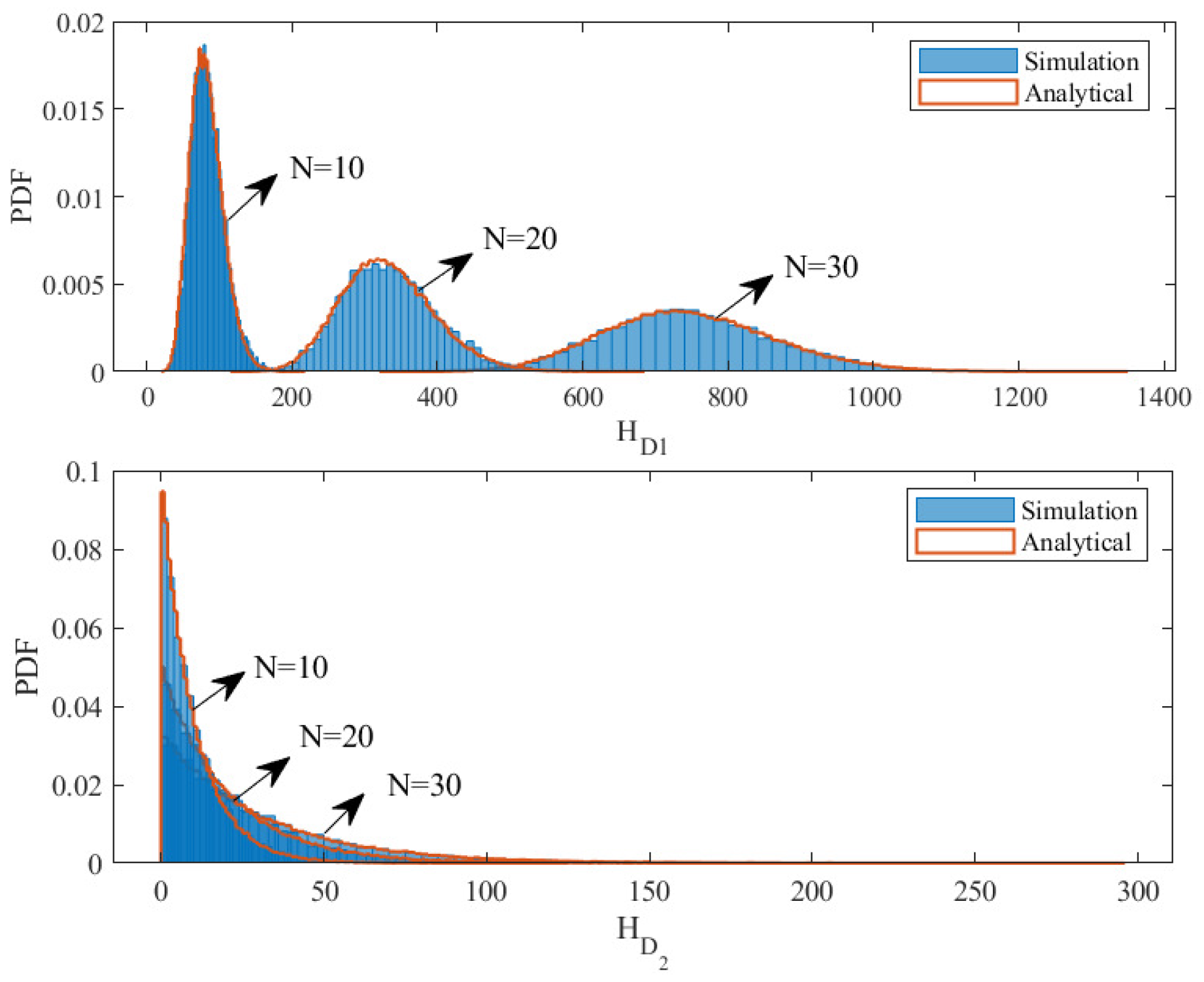
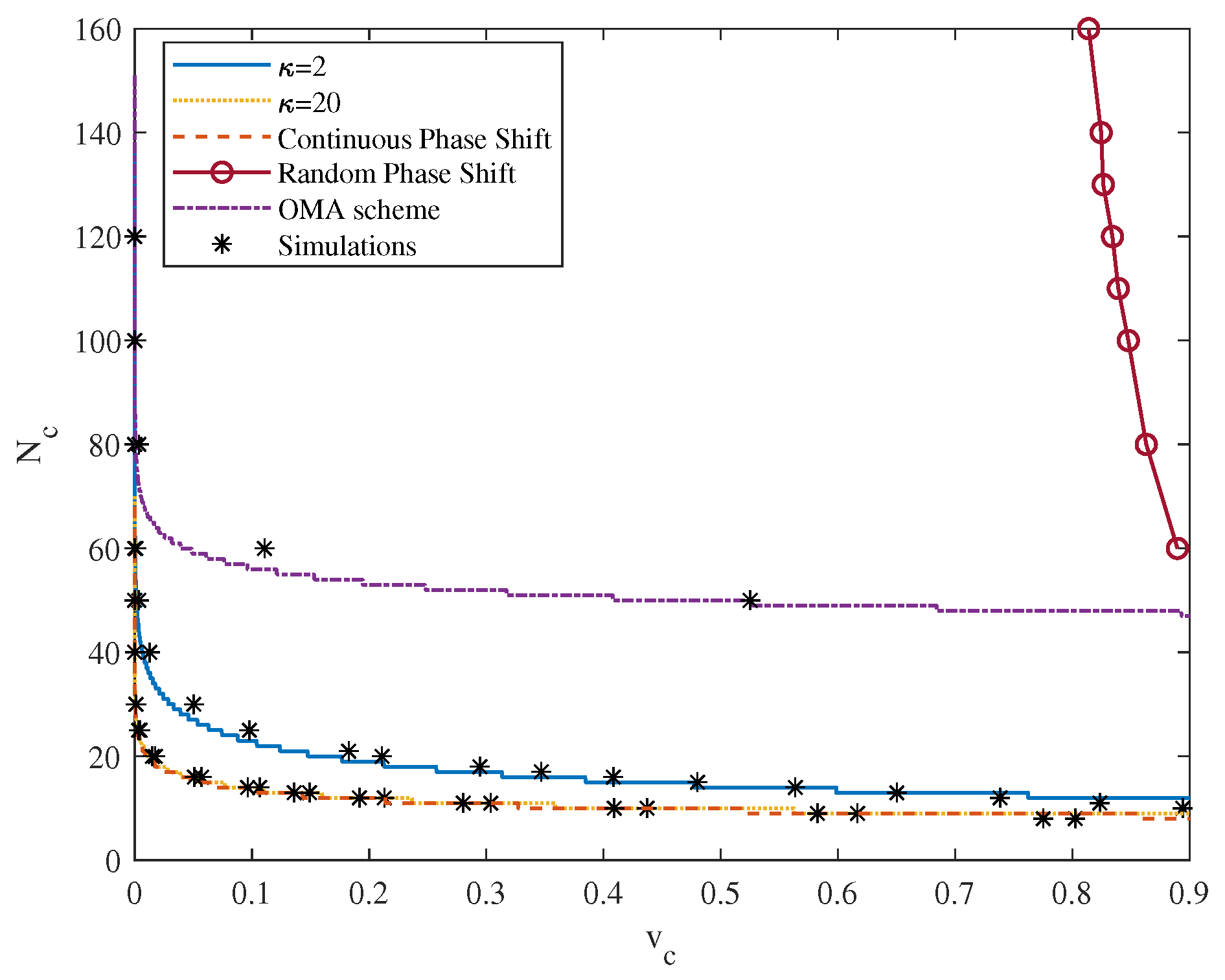
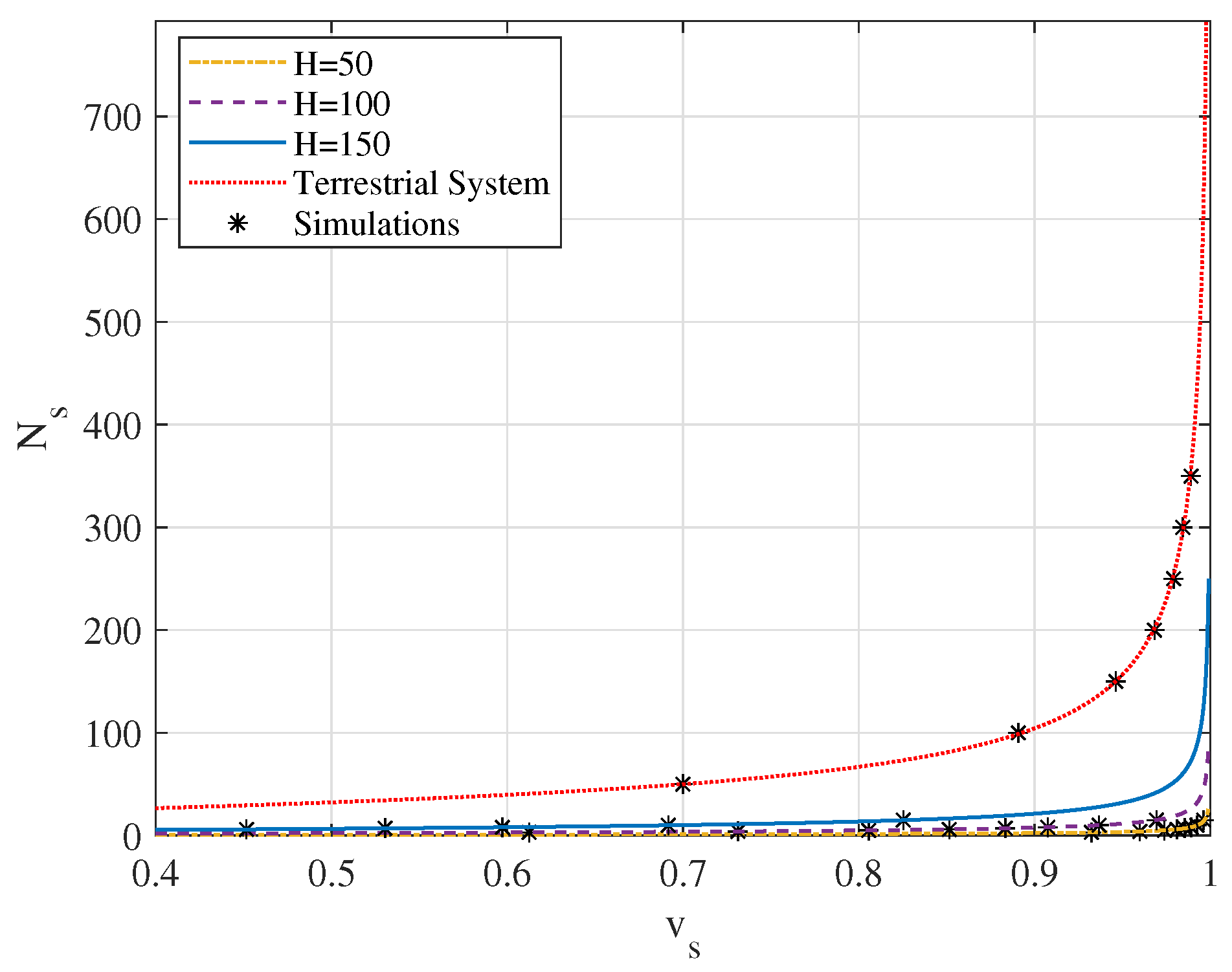
4. Simulation Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Li, B.; Fei, Z.; Zhang, Y.; Guizani, M. Secure UAV Communication Networks over 5G. IEEE Wirel. Commun. 2019, 26, 114–120. [Google Scholar] [CrossRef]
- Mu, J.; Zhang, R.; Cui, Y.; Gao, N.; Jing, X. UAV Meets Integrated Sensing and Communication: Challenges and Future Directions. IEEE Commun. Mag. 2023, 61, 62–67. [Google Scholar] [CrossRef]
- Cheng, X.; Jiang, R.; Sang, H.; Li, G.; He, B. Joint Optimization of Multi-UAV Deployment and User Association via Deep Reinforcement Learning for Long-Term Communication Coverage. IEEE Trans. Instrum. Meas. 2024, 73, 5503613. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Fotouhi, A.; Qiang, H.; Ding, M.; Hassan, M.; Giordano, L.G.; Garcia-Rodriguez, A.; Yuan, J. Survey on UAV Cellular Communications: Practical Aspects, Standardization Advancements, Regulation, and Security Challenges. IEEE Commun. Surv. Tutor. 2019, 21, 3417–3442. [Google Scholar] [CrossRef]
- Pan, Y.; Li, R.; Da, X.; Hu, H.; Zhang, M.; Zhai, D.; Cumanan, K.; Dobre, O.A. Cooperative Trajectory Planning and Resource Allocation for UAV-Enabled Integrated Sensing and Communication Systems. IEEE Trans. Veh. Technol. 2024, 73, 6502–6516. [Google Scholar] [CrossRef]
- Makki, B.; Chitti, K.; Behravan, A.; Alouini, M.S. A Survey of NOMA: Current Status and Open Research Challenges. IEEE Open J. Commun. Soc. 2020, 1, 179–189. [Google Scholar] [CrossRef]
- Ghous, M.; Hassan, A.K.; Abbas, Z.H.; Abbas, G.; Hussien, A.; Baker, T. Cooperative Power-Domain NOMA Systems: An Overview. Sensors 2022, 22, 9652. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-Domain Non-Orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef]
- Cao, K.; Wang, B.; Ding, H.; Lv, L.; Dong, R.; Cheng, T.; Gong, F. Improving Physical Layer Security of Uplink NOMA via Energy Harvesting Jammers. IEEE Trans. Inf. Forensics Secur. 2021, 16, 786–799. [Google Scholar] [CrossRef]
- Nimi, T.; Babu, A.V. Full-Duplex Cooperative NOMA Network with Multiple Eavesdroppers and Non-ideal System Imperfections: Analysis of Physical Layer Security and Validation Using Deep Learning. IEEE Trans. Veh. Technol. 2024, 73, 17192–17208. [Google Scholar] [CrossRef]
- Nguyen, A.N.; Nguyen, G.H.; Ngo, T.S.; Bui, N.A.; Le, P.C.; Hoang, M.D. Secrecy Offloading Performance Analysis for UAV Relay-assisted NOMA MEC System. In Proceedings of the 2024 28th International Computer Science and Engineering Conference (ICSEC), Khon Kaen, Thailand, 6–8 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Yu, K.; Feng, Z.; Yu, J.; Chen, T.; Peng, J.; Li, D. Secure Ultra-Reliable and Low Latency Communication in UAV-Enabled NOMA Wireless Networks. IEEE Trans. Veh. Technol. 2024, 73, 14908–14922. [Google Scholar] [CrossRef]
- Yang, X.; Han, B.; Zhang, G.; Zheng, P.; Bai, J.; Qin, D. NOMA-Assisted Routing Algorithm Design for UAV Ad Hoc Relay Networks. IEEE Sens. J. 2023, 23, 3296–3312. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Chen, H.; Han, C.; Li, L.; Do, D.T.; Mumtaz, S.; Nallanathan, A. UAV-Enabled Multi-Pair Massive MIMO-NOMA Relay Systems With Low-Resolution ADCs/DACs. IEEE Trans. Veh. Technol. 2024, 73, 2171–2186. [Google Scholar] [CrossRef]
- Liu, R.; Guo, K.; An, K.; Zhou, F.; Wu, Y.; Huang, Y.; Zheng, G. Resource Allocation for NOMA-Enabled Cognitive Satellite–UAV–Terrestrial Networks with Imperfect CSI. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 963–976. [Google Scholar] [CrossRef]
- Liu, Z.; Qi, J.; Shen, Y.; Ma, K.; Guan, X. Maximizing Energy Efficiency in UAV-Assisted NOMA–MEC Networks. IEEE Internet Things J. 2023, 10, 22208–22222. [Google Scholar] [CrossRef]
- Lu, W.; Ding, Y.; Gao, Y.; Chen, Y.; Zhao, N.; Ding, Z.; Nallanathan, A. Secure NOMA-Based UAV-MEC Network Towards a Flying Eavesdropper. IEEE Trans. Commun. 2022, 70, 3364–3376. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Leung, V.C.M.; Durrani, T.S. Energy-Efficient Resource Allocation for Dual-NOMA-UAV Assisted Internet of Things. IEEE Trans. Veh. Technol. 2023, 72, 3532–3543. [Google Scholar] [CrossRef]
- Hoang, T.M.; Dung, L.T.; Nguyen, B.C.; Kim, T. Outage and Throughput Analysis of UAV-Assisted NOMA Relay Systems with Indoor and Outdoor Users. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2633–2647. [Google Scholar] [CrossRef]
- Campion, M.; Ranganathan, P.; Faruque, S. UAV swarm communication and control architectures: A review. J. Unmanned Veh. Syst. 2019, 7, 93–106. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, C.; Yeoh, P.L.; Wang, K.; Elkashlan, M.; Vucetic, B.; Li, Y. Secure Communications for UAV-Enabled Mobile Edge Computing Systems. IEEE Trans. Commun. 2020, 68, 376–388. [Google Scholar] [CrossRef]
- Michailidis, E.T.; Maliatsos, K.; Skoutas, D.N.; Vouyioukas, D.; Skianis, C. Secure UAV-Aided Mobile Edge Computing for IoT: A Review. IEEE Access 2022, 10, 86353–86383. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, W.; Shikh-Bahaei, M. Energy Efficient UAV Communication with Energy Harvesting. IEEE Trans. Veh. Technol. 2020, 69, 1913–1927. [Google Scholar] [CrossRef]
- Cai, Y.; Wei, Z.; Li, R.; Ng, D.W.K.; Yuan, J. Joint Trajectory and Resource Allocation Design for Energy-Efficient Secure UAV Communication Systems. IEEE Trans. Commun. 2020, 68, 4536–4553. [Google Scholar] [CrossRef]
- Khoshafa, M.H.; Maraqa, O.; Moualeu, J.M.; Aboagye, S.; Ngatched, T.M.N.; Ahmed, M.H.; Gadallah, Y.; Renzo, M.D. RIS-Assisted Physical Layer Security in Emerging RF and Optical Wireless Communication Systems: A Comprehensive Survey. In IEEE Communications Surveys & Tutorials; IEEE: Piscataway, NJ, USA, 2024; p. 1. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, G.; Zhi, K.; Hong, S.; Wu, T.; Pan, Y.; Ren, H.; Renzo, M.D.; Lee Swindlehurst, A.; Zhang, R.; et al. An Overview of Signal Processing Techniques for RIS/IRS-Aided Wireless Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 883–917. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K.; Nallanathan, A. Exploring Sum Rate Maximization in UAV-Based Multi-IRS Networks: IRS Association, UAV Altitude, and Phase Shift Design. IEEE Trans. Commun. 2022, 70, 7764–7774. [Google Scholar] [CrossRef]
- Yuan, J.; Chen, G.; Wen, M.; Wan, D.; Cumanan, K. Security-Reliability Tradeoff in UAV-Carried Active RIS-Assisted Cooperative Networks. IEEE Commun. Lett. 2024, 28, 437–441. [Google Scholar] [CrossRef]
- You, C.; Kang, Z.; Zeng, Y.; Zhang, R. Enabling Smart Reflection in Integrated Air-Ground Wireless Network: IRS Meets UAV. IEEE Wirel. Commun. 2021, 28, 138–144. [Google Scholar] [CrossRef]
- Wei, W.; Pang, X.; Tang, J.; Zhao, N.; Wang, X.; Nallanathan, A. Secure Transmission Design for Aerial IRS Assisted Wireless Networks. IEEE Trans. Commun. 2023, 71, 3528–3540. [Google Scholar] [CrossRef]
- Qiao, T.; Cao, Y.; Tang, J.; Zhao, N.; Wong, K.K. IRS-Aided Uplink Security Enhancement via Energy-Harvesting Jammer. IEEE Trans. Commun. 2022, 70, 8286–8297. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Gao, R.; Lei, C.; Feng, W.; Ge, N.; Jin, S.; Quek, T.Q.S. Physical layer security for UAV communications: A comprehensive survey. China Commun. 2022, 19, 77–115. [Google Scholar] [CrossRef]
- Gu, X.; Duan, W.; Zhang, G.; Wen, M.; Choi, J.; Ho, P.H. Aerial Reconfigurable Intelligent Surface-Assisted Terrestrial Communications. IEEE Internet Things Mag. 2024, 7, 54–60. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Renzo, M.D.; Tao, M.; Yuan, X. Robust Secure UAV Communications with the Aid of Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- Solanki, S.; Park, J.; Lee, I. On the Performance of IRS-Aided UAV Networks with NOMA. IEEE Trans. Veh. Technol. 2022, 71, 9038–9043. [Google Scholar] [CrossRef]
- Ye, R.; Peng, Y.; Al-Hazemi, F.; Boutaba, R. A Robust Cooperative Jamming Scheme for Secure UAV Communication via Intelligent Reflecting Surface. IEEE Trans. Commun. 2024, 72, 1005–1019. [Google Scholar] [CrossRef]
- Diao, D.; Wang, B.; Cao, K.; Zheng, B.; Dong, R.; Cheng, T.; Chen, J. Reflecting Elements Analysis for Secure and Energy-Efficient UAV-RIS System with Phase Errors. IEEE Wirel. Commun. Lett. 2024, 13, 293–297. [Google Scholar] [CrossRef]
- Bor-Yaliniz, R.I.; El-Keyi, A.; Yanikomeroglu, H. Efficient 3-D placement of an aerial base station in next generation cellular networks. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Zaghdoud, N.; Mnaouer, A.B.; Alouane, W.H.; Boujemaa, H.; Touati, F. Secure Performance Analysis for Full-Duplex Cooperative NOMA System in the Presence of Multiple Eavesdroppers. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 1719–1725. [Google Scholar] [CrossRef]
- Al-Jarrah, M.; Al-Dweik, A.; Alsusa, E.; Iraqi, Y.; Alouini, M.S. On the Performance of IRS-Assisted Multi-Layer UAV Communications with Imperfect Phase Compensation. IEEE Trans. Commun. 2021, 69, 8551–8568. [Google Scholar] [CrossRef]
- Wyner, A.D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Yadav, S.; Vats, A.; Aggarwal, M.; Ahuja, S. Performance Analysis and Altitude Optimization of UAV-Enabled Dual-Hop Mixed RF-UWOC System. IEEE Trans. Veh. Technol. 2021, 70, 12651–12661. [Google Scholar] [CrossRef]
- Liu, H.; Luo, J.; Wang, S.; Ding, H. Effective Secrecy Capacity for RIS-Assisted NOMA Communication Networks. IEEE Trans. Veh. Technol. 2025, 74, 1379–1384. [Google Scholar] [CrossRef]
- Badiu, M.A.; Coon, J.P. Communication Through a Large Reflecting Surface with Phase Errors. IEEE Wirel. Commun. Lett. 2020, 9, 184–188. [Google Scholar] [CrossRef]
- Vega Sánchez, J.D.; Ramírez-Espinosa, P.; López-Martínez, F.J. Physical Layer Security of Large Reflecting Surface Aided Communications with Phase Errors. IEEE Wirel. Commun. Lett. 2021, 10, 325–329. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diao, D.; Wang, B.; Guo, R. Secure and Energy-Efficient Configuration Strategies for UAV-RIS System with Uplink NOMA. Drones 2025, 9, 289. https://doi.org/10.3390/drones9040289
Diao D, Wang B, Guo R. Secure and Energy-Efficient Configuration Strategies for UAV-RIS System with Uplink NOMA. Drones. 2025; 9(4):289. https://doi.org/10.3390/drones9040289
Chicago/Turabian StyleDiao, Danyu, Buhong Wang, and Rongxiao Guo. 2025. "Secure and Energy-Efficient Configuration Strategies for UAV-RIS System with Uplink NOMA" Drones 9, no. 4: 289. https://doi.org/10.3390/drones9040289
APA StyleDiao, D., Wang, B., & Guo, R. (2025). Secure and Energy-Efficient Configuration Strategies for UAV-RIS System with Uplink NOMA. Drones, 9(4), 289. https://doi.org/10.3390/drones9040289





