Abstract
The combination of Unmanned Aerial Vehicles (UAVs) and Mobile Edge Computing (MEC) effectively meets the demands of user equipments (UEs) for high-quality computing services, low energy consumption, and low latency. However, in complex environments such as disaster rescue scenarios, a single UAV is still constrained by limited transmission power and computing resources, making it difficult to efficiently complete computational tasks. To address this issue, we propose a UAV swarm-enabled MEC system that integrates data compression technology, in which the only swarm head UAV (USH) offloads the compressed computing tasks compressed by the UEs and partially distributes them to the swarm member UAV (USM) for collaborative processing. To minimize the total energy and time cost of the system, we utilize Markov Decision Process (MDP) for modeling and construct a deep deterministic policy gradient offloading algorithm with a prioritized experience replay mechanism (PER-DDPG) to jointly optimize compression ratio, task offloading rate, resource allocation and swarm positioning. Simulation results show that compared with deep Q-network (DQN) and deep deterministic policy gradient (DDPG) baseline algorithms, the proposed scheme performs excellently in terms of convergence and robustness, reducing system latency and energy consumption by about 32.7%.
1. Introduction
The rapid development of the Internet of Things (IoT) and new communication technologies has driven the explosive growth of mobile devices, which has been accompanied by a wide variety of computationally intensive and latency-sensitive applications [1,2]. In [3], Zhou et al. emphasize the significance of the convergence of communication, computing, and caching (3C) for future mobile networks, especially in the context of 6G. As an extension of cloud computing, Mobile Edge Computing (MEC) [4] offloads compute-intensive tasks to servers deployed at the edge of the wire access networks, meeting the demand for low-latency communication and computing in an energy-saving and efficient manner [5,6,7]. In [8], Cai et al. analyze the challenges in collaborating among different edge computing paradigms and propose solutions such as blockchain-based smart contracts and software-defined networking/network function virtualization (SDN/NFV) to tackle resource isolation. In the early stages, fixed base stations (BSs) were mainly used as an edge server to provide computational services for mobile users [9]. For example, in [10], Zhang et al. equipped a Macro Base Station (MBS) with an edge server with better processing capability, and optimized the offloading of computing tasks in fifth-generation (5G) heterogeneous networks while satisfying the latency constraints. However, in practical situations such as complex environments, remote areas or disaster relief sites, terrestrial MEC systems with fixed locations usually suffer from severe performance degradation or even inoperativity due to communication obstruction [11]. Fortunately, this dilemma is solved by unmanned aerial vehicle-enabled MEC. With the characteristics of high mobility, light weight, and no geographical constraints, we can utilize unmanned aerial vehicles (UAVs) as edge nodes to fulfill computational requirements across various scenarios [12]. Wang et al. [13] presented an iterative robust enhancement algorithm for a UAV-assisted ground–air cooperative MEC system, which minimized the system energy consumption by collectively optimizing the task offloading and flight trajectory of UAVs in a non-convex manner. To meet the low-latency demand for computational tasks in wireless sensor networks (WSNs), Yang et al. [14] constructed a framework where edge UAV nodes carry intelligent surfaces (STAR-RISs) for computing offloading and content caching. By cooperatively optimizing UAV position, offloading strategy and passive beam-forming, they reduced the energy consumption of the system while achieving good convergence.
Nevertheless, due to the shortcomings of limited transmission power, low load capacity and few computing resources, traditional single or multiple UAVs cannot efficiently complete numerous multifarious tasks [15]. In this case, UAV swarms are considered a viable solution. By managing and assigning tasks in cooperation under the leadership of the control unit, we can maximize energy utilization and minimize delay. With this advantage, UAV swarm-assisted MEC has become a popular trend in current research [16,17]. In [18], an MEC system composed solely of UAVs is presented, in which member UAVs generate tasks, helper UAVs offload computation, and a header UAV aggregates the processed results. To mitigate the total energy expenditure of the UAV swarm, the authors optimized the communication channels, offloading objects and offloading rate through a two-stage resource allocation algorithm. Seid et al. [19] considered a UAV cluster under an aerial-to-ground (A2G) network in response to emergencies, where member UAVs, under the coordination of header UCH, unload and compute independent tasks generated by Edge Internet of Things (EIoT) devices. Furthermore, a scheme based on deep reinforcement learning (DRL) for coordination computation offloading and resource allocation was proposed to control the total computation cost in terms of energy consumption and latency of EIoT, BSs, and UCH. In the research of Li et al. [20], UAVs are allowed to dynamically gather into multiple swarms to assist in completing MEC. In order to maximize the long-term energy efficiency of the system, a comprehensive optimization problem addressing dynamic clustering and scheduling was developed, and a UAV swarm dynamic coordination method based on reinforcement learning is developed to attain equilibrium. To match mobile devices and plan UAV trajectories, Miao et al. [21] put forward a global and local path planning algorithm based on ground station and onboard computer control in the framework of UAV swarm-assisted MEC task offloading, which minimizes the energy loss of global path planning for the UAV cluster while maximizing access and minimizing task completion delay. The issue of computational offloading and routing selection of UAV swarms under the UAV-Edge-Cloud computing architecture was highlighted in [22], in which the authors developed a polynomial near-optimal approximation algorithm using Markov approximation techniques [23], driven by the goal of maximizing the throughput while minimizing the routing and computational costs. To summarize, the research on UAV- or UAV swarm-assisted MEC for task offloading and resource allocation has been fully launched, but it is more reflected in scenario transformation and method update. In fact, the computational performance is related to the task size. Due to the temporal or spatial correlation of the tasks, the raw data generated by the user usually contain duplicates [24], which causes a waste of computational time and resources. Thus, it is necessary to perform preprocessing, such as data compression, before task offloading to reduce the burden of the MEC and speed up the task completion [25,26]. Cheng et al. in [26] investigated a scenario where a single UAV serves multiple wireless devices. The block coordinate descent (BCD) method is adopted to decompose the energy minimization problem into several subproblems for solution.
As an important field of modern information technology, data compression encodes data while retaining useful information, with the aim of reducing the size of data during storage and transmission [27,28,29]. Typically, data compression is categorized into lossless and loss compression. Lossless compression maintains the integrity of the data, i.e., the decompressed data match the original data exactly, and loss compression sacrifices tiny details that are difficult for the human brain to perceive in order to achieve a higher compression ratio [30,31]. In the practical application of MEC, research on data compression technology has already made some progress. Han et al. [32] considered introducing data compression to reduce offloading delay when using MEC to increase the computational energy of blockchain mining nodes, and then proposed a block coordinate descent (BCD) iterative algorithm to solve the problem of minimizing the total energy consumption of the system. In order to more accurately optimize the latency of the MEC system with multiple users and servers, Liang et al. [33] performed lossless compression before task offloading and associated the reliability of edge servers with delay and energy consumption [34], and then designed a distributed computational offloading strategy to make up for the shortcoming of centralized algorithms. Regarding the enhancement of data transmission efficiency in non-orthogonal multiple access (NOMA) MEC systems, Tu et al. [35] proposed a partial compression mechanism, which allows users to send tasks to the BS in two ways: lossless compression followed by offloading, and direct offloading without preprocessing. Ultimately, this approach achieved a good effect. Ding et al. [36] designed a multi-BS intelligent MEC system for the power grid, which utilizes two-level compression to ensure energy saving. Specifically, the small BSs receive information collected and losslessly compressed by MDs, and then transmit it to the micro-BS for processing after applying the same compression method. So far, it can be seen that MEC services benefit greatly from data compression strategies. Since the transmission of tasks typically consumes more energy than computation, data compression techniques are more advantageous in situations where the onboard energy budget is limited, especially in UAV swarm-supported MEC systems.
In this manuscript, we study the task offloading strategy of an MEC system that incorporates UAV swarms and data compression. The considered scenario focuses on the abnormal situation of BSs, mainly including one head UAV (USH), several member UAVs (USMs), and some randomly scattered user equipments (UEs). Since both the energy reserves and the processing capabilities of the edge servers carried are higher than those of the USMs, the USH can fly close to the UEs and offload tasks exceeding their capacity, then redistribute a small portion to the USM. In the process of data transmission, orthogonal frequency division multiple access (OFDMA) technology is employed to improve communication efficiency. To save communication bandwidth and maintain the value of the data, UEs first perform lossless compression on the calculated data, and the USH performs the corresponding decompression operation. Next, we formulate the task unloading strategy to the problem of minimizing the total energy and time expenditure, and adopt the Markov decision process model (MDP), the preferential experience playback mechanism (PER) and DRL to optimize the resource allocation, unloading rate and data compression ratio. Finally, simulation experiments are built to demonstrate the advantages of the proposed deep deterministic policy gradient offloading scheme with a prioritized experience replay mechanism (PER-DDPG) in saving system energy consumption, reducing latency and improving resource utilization efficiency. The main contributions are summarized as follows.
- An MEC system with multi-user and multi-auxiliary co-existence (e.g., UAV swarm, task offloading, and lossless data compression) is proposed, in which UAVs can be classified into USH and USM according to their functional differences. Through a detailed analysis of task transmission, USH movement, computation execute and onboard energy, etc., an optimization problem of collaborative task offloading and data compression was formulated.
- The optimization issue is modeled as MDP, and the action space, state space, and reward function are tailored to the specific requirements of the UAV swarm-enabled MEC system. Then, the deep deterministic strategy gradient (DDPG) algorithm in DRL is adopted to solve this issue, thus saving the delay and energy consumption during offloading. Furthermore, preferential experience replay is introduced into the DDPG algorithm to improve the efficiency of experience replay and speed up the training process, which increases the stability of the training process and is less sensitive to the changes of some hyperparameters.
- Extensive numerical simulations are carried out to verify the convergence, stability and effectiveness of the proposed algorithm. As the total number of tasks increases, the proposed algorithm can obtain a lower cumulative system reward than other baseline comparison algorithms. In addition, compared with the non-compressed scheme, the compressed scheme can better save system costs and reduce the system delay and energy consumption when there are more user tasks.
The remainder of this manuscript is structured as follows. Section 2 outlines the system model and formulates an optimization problem to minimize system energy usage and delay. Section 3 builds the MDP model and proposes the PER-DDPG offloading algorithm to solve the above problems. In Section 4, the performance of our proposed scheme is shown and compared with other schemes. Finally, we give the conclusion and future work in Section 5.
2. System Model
We consider an MEC network architecture enabled by a cluster of UAVs, as illustrated in Figure 1, which mainly comprises K UEs and N UAVs. The UEs are arbitrarily scattered throughout a rectangular area on the ground, and always generate computational tasks that are too large for them to handle. In this case, an aerial UAV swarm containing a USH and several USMs can provide support. The USMs are randomly distributed within a 300 m radius around the USH while maintaining a minimum separation distance to ensure collision avoidance, where the USH selects the nearest USM for task offloading based on the shortest-path principle. Compared to USM, USH has more processing power, so USH is responsible for establishing a communication link with the UE and offloading most of the computational task, then assigning a limited number of tasks to the USM and keeping the rest to itself. Moreover, to optimize network transmission, reducing both time delay and energy expenditure, and ensure the accuracy and completeness of the computation results, it is necessary to implement a lossless compression technique on UE and then decompress it accordingly at USM. Let and denotes the set of UEs and USMs. To facilitate the analysis of the dynamic changes of the system, we utilize quasistatic network scenarios to model and discretize an observation period D into T slots with equal length , indexed by .
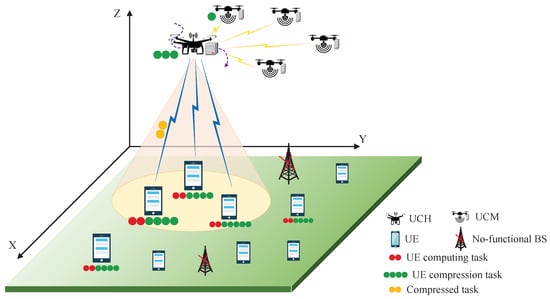
Figure 1.
System model of the UAV swarm-enabled mobile edge computing.
2.1. Data Compression
Assuming that the computational tasks generated by the UE k in time slot t are , where and represent the total amount of data to be processed and the CPU cycles consumed by , respectively, while the proportion of the local computation data to the total task is , then the amount of computation data that USH and USM must complete together is expressed as .
In order to prevent the loss of information contained in the computing tasks, and also to reduce the resources consumed by data transmission, it is necessary to use lossless compression technology on the UE side. Correspondingly, when the USH completes the offloading, the task reconstruction is performed first and then the computing is carried out. We use a continuous variable to represent the compression ratio of the lossless compression algorithm adopted by UE, where is the maximum compression ratio considering the network requirements, then the amount of data sent by the UE k to the USH is reduced to . As given in [26,37], the CPU cycles required to compress 1 bit of the original task can be approximated as
where is a positive constant hinge on the lossless compression technique. Let stand for the computing capability of UE k in time slot t, then the delay and energy expenditure due to the implementation of compression are derived by
where is the computational efficiency of , while we assume that each UE belonging to has the same . In addition, data decompression is much easier than compression, and the resulting latency is much smaller, so we can reasonably ignore it [26,38].
2.2. Task Transmission
Defining a 3D coordinate system with the ground as the reference plane, the location of UE k in time slot t is indicated by . At this point, the coordinates of USH and USM n are and , respectively, where and H is the current height of USH and USM relative to the ground.
2.2.1. Communication Between UEs and USH
Considering the impact of obstacles such as buildings, cars and terrain on radio propagation, we model the communication channel between UEs and USH as a superposition of the path loss of line of sight (LoS) and non-line of sight (NLoS) with different probabilities of occurrence. Let f and c represent the carrier frequency and the speed of light, while and denote the average additional attenuation, then the path loss and for LoS and NLoS at time slot t are expressed as
where is the distance from UE k to USH, and can be acquired by
Next, the probability of existing LoS and NLoS connections between UE k and USH can be calculated by
where a and b are variables that hinge on the operating environment. So far, the average path loss between UE and USH is formulated as
In order to avoid interference between channels, an orthogonal access scheme is used for both uplink and downlink communications. Assuming that the bandwidth resources allocated by USH for each UE are B, and the noise power of the communication link is and , respectively, the wireless transmission rate of data between USH and UE k at time slot t is denoted as
Notably, our proposed framework employs a large-scale fading model that achieves analytical tractability. For enhanced modeling precision, the system accommodates potential integration of small-scale fading components, particularly Rayleigh and Rician fading variants, as well as advanced path loss modeling techniques [39].
2.2.2. Communication Between USH and USMs
As part of the swarm, both USH and USMs communicate and compute in the air at height H, which can be approximated as the presence of only LoS components. If the communication bandwidth provided by the USH for each USM is B, the data transfer rate between USM n and the USH can be denoted as
as long as it satisfies , where and represent the data transmission power of the USH and the average channel power gain at a reference distance of 1m, respectively.
2.3. USH Movement
The location of USH at the current time slot t is known to be , , then after USH has flown a time slot of length with uniform speed , its location information is changed to , where is the angle formed by the projection of in the horizontal plane with the x-axis and satisfies . If we use to denote the maximum flight speed that USH can achieve, there is the following constraint:
It is important to note that the USH must avoid collisions with any USM during flight. To ensure safe operation within the same horizontal plane at a fixed altitude, we define a maximum distance threshold between the USH and USM. External obstacles (e.g., buildings) are not considered in this study, as UAVs are assumed to operate at a sufficient height to avoid interference from ground-based objects.
To ensure that USH can smoothly offload the computational tasks generated by UEs, the UEs must be within the coverage area of USH. Assuming that the coverage area of USH is a circle with radius , and using to denote the maximum coverage angle of USH at time slot t, then we have and . Meanwhile, the location of UE k must satisfy the constraints
2.4. Task Execution
In the MEC system proposed in this manuscript, UEs, USH and USMs jointly complete the computing task. For each , USH is preset to establish communication with only one UE or USM. Let indicate the connection status between the UE k and , and indicates that between the USH and USM n, respectively, specifically as follows:
and with the constraints:
2.4.1. UE Implementation
As previously set, represents the amount of CPU cycles needed for UE k to perform the entire task independently, is the proportion of computing tasks assigned to UE k in the total, is the computing capability of UE k, and is the computational efficiency of UE; we can obtain the time delay and energy consumption caused by local computing as follows:
In addition, the offloading of compressed data from the UE to the USH also generates time and energy consumption, which we represent as:
where is the transmitting power of the UE k.
2.4.2. USH Implementation
After the received task is decompressed, USH divides it into two parts; one is offloaded to USMs, and the other is left to calculate for itself. The corresponding delays of the former and the latter are expressed as
where is the proportion of the task assigned to the USM n by USH in the time slot t and satisfies , while represents the computing capability of USH. Let be the transmit power of USH in time slot t; USH unloading and the calculation of the energy consumption can be expressed as
The USH performs calculations and communication while flying, so the flight time has no effect on the system delay but the flight energy consumption is a factor worth adding. We utilize to denote the mass of the USH; the flight energy consumption of USH in time slot t is
2.4.3. USM Implementation
Compared with UEs and USH, which both transmit tasks and calculate, USM has a relatively simple work type and only needs to execute computing task offloading from USH. Let represent the computation capacity of USM; we can obtain the delay and energy usage of USM n in time slot t as
2.5. Problem Formulation
After determining the respective tasks, regardless of the UEs or USH, the modules used for computation and transmission are separated, which means that computation and transmission can be carried out simultaneously without interfering with each other; thus, the overall system delay is derived by
Regarding the overall energy usage of the system, it involves the components used by the UEs, USH and USMs for compression, communication and computation, expressed as
Our objective is to reduce the delay and energy usage of the entire system, which can be achieved by jointly optimizing parameters such as the compression ratio , the association status during task offloading and , the offloading rates and , and the USH flight trajectory M. Utilizing the wights and to indicate the degree of emphasis on delay and energy consumption, while , and represent the energy possessed by UE, USH and USM in the system cycle, the optimization problem of the UAV swarm-enabled MEC system is formulated as
where Equations (32b) and (32c) constrain the flight speed, safe distance, coverage area and communication status of the USH, while (32d), (32e) and (32f) limit the compression ratio and task offloading proportion. Moreover, the energy consumption requirements of UE, USH and USM are also specified by (32g), (32h) and (32i).
3. Computing Offloading Strategy
The optimization problem in (32) is non-convex and NP-hard. Moreover, it involves a dynamic model that jointly optimizes task compression ratios, power control, and resource allocation for multiple UEs. Since the decision-making scheme in each time slot depends on real-time system states, traditional optimization algorithms struggle to achieve the global optimal solution. To address this, we model the problem as an MDP and propose a computational offloading algorithm based on PER-DDPG, which seeks a more efficient and energy-saving strategy.
3.1. Construction of MDP
The optimization problem is formulated as an MDP defined by the quintuple (), where , , , and correspond to the state space, action space, state transition probability, reward function and discount factor, respectively. In an MDP, the decisions and actions of the agent are influenced by the environment, and also affect it own rewards. This interaction can be constructed as a time-slot-based sequence, in which in each time slot, the agent makes decisions based on its current state. Next, we describe the state, action, and reward function for the agent.
3.1.1. State Space
The energy loss and latency of the entire MEC system mainly involve three aspects. Firstly, the energy and time overhead of the UE k during compression and offloading are directly related to the initial task . Secondly, the location of USH and UE influences the transmission rate from UE to USH, thereby indirectly affecting the offloading delay and energy consumption of UE. In addition, the offloading decisions of UE k and USH must take into account their available energy and in the current time slot t. Therefore, the state space can be represented as:
3.1.2. Action Space
The task compression rate of the UE at time slot t, the communication connection between USH and UE k, the task offloading rate and of UE and USH, as well as the move angle and speed of USH together constitute the action space , that is,
3.1.3. Reward Design
According to the reward value, the agent carries out learning and action selection. Since the goal of this manuscript is to maximize the reward by minimizing the system energy consumption and delay, the reward function can be designed as follows:
3.2. Solution Based on PER-DDPG
In dynamic environments where UE positions and task requirements are constantly changing, DRL can continuously learn and adapt to these dynamic scenarios through the ongoing interactions between the agent and the environment, thereby obtaining the optimal solution to the optimization problem. Based on the Actor–Critic method, the DDPG algorithm combines the ideas of the deterministic policy gradient (DPG) and the deep Q-learning (DQN) algorithm, and adopts a dual neural network structure. As shown in the framework in Figure 2, the training data for the DDPG algorithm are generated during the interaction with the environment.
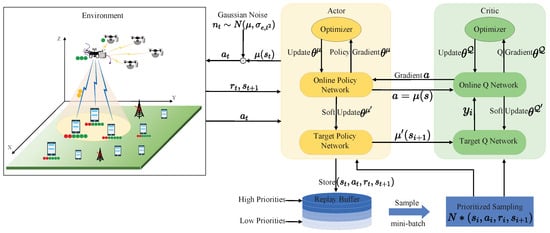
Figure 2.
UAV swarm-enabled MEC network framework based on PER-DDPG.
In view of the high continuity and dimensionality of state and action space, the PER mechanism is incorporated into the DDPG algorithm to improve sample efficiency, accelerate learning convergence, and mitigate overfitting risks. Let represent the random noise and decays with time slot t, then the DDPG algorithm selects the action according to the current state . Immediately afterwards, by interacting with the environment, the reward and the next state can be obtained. Next, the DDPG algorithm puts the tuple into the experience replay buffer, and randomly extracts a small batch of experience data for training during each learning iteration. After the Q-network outputs the Q-value for the current state–action pair, the target Q-network also obtains the target Q-value based on the state in the next time slot and the next action estimated by the target policy network. In order to make the estimated Q-value closer to the target Q-value, the Q-network compares their mean square error (MSE)and updates the network parameters. The loss function we applied is:
where M represents the number of mini-batch samples, and denotes the TD-error, which is used to evaluate the difference between the value of the current state and that of the next state. Let and represent the parameters of the Q-network and the target Q-network, respectively, then can be expressed as:
Combining the current state , the action and the Q-value output by the Q-network, we obtain the update gradient of the policy network as follows:
Assuming is a soft update parameter that controls the speed of network updates and influences the stability of the network, then through the soft update mechanism, upgrade the target policy network and target Q network parameters:
To ensure that high-value experiences can be retrieved with a higher probability, Prioritized Experience Replay (PER) assigns higher priority to particularly successful or unsuccessful experiences when extracting experience. However, this can lead to overfitting, so the PER mechanism usually also introduces a certain probability of low-value experience. By dynamically adjusting the probability of extracting experience, it not only helps the intelligent agent to understand the environment more comprehensively and avoid repeating mistakes, but can also help it utilize the learning potential of high-value experience to find better strategies in the process of exploration. The sampling probability of an experience sample can be expressed as:
where is the priority metric based on TD-error, and I represents the episode being carried out. As a priority adjustment parameter, is a random factor set when selecting experience, in order to give the opportunity to extract experience samples with small TD-error, thus maintaining sample diversity. If , the TD-error value is used directly; if , it corresponds to the original uniform random sampling. The priority metric is based on the following ranking method:
The agent prioritizes updating experience samples that have high TD-error values. However, this method introduces errors into the model, resulting in distortion of the traditional probability distribution, potentially hindering the convergence of the neural network during training. To alleviate this problem, importance sampling is used to correct the weight changes as follows:
where and R represent the degree of error correction and the capacity of the experience replay pool, respectively. So far, the data obtained from interacting with the environment successfully distinguish the importance of experience samples, thereby improving the learning efficiency of the experience samples. Moreover, the loss function is updated as:
With the above description as the cornerstone, we developed an algorithm based on PER-DDPG, which is suitable for computation offloading and resource allocation in UAV swarm-assisted MEC involving lossless data compression, as shown in Algorithm 1.
| Algorithm 1: Computation offloading algorithm based on PER-DDPG. |
 |
4. Numerical Simulation
In this section, the offloading efficiency of PER-DDPG in the UAV swarm-assisted MEC system is verified by numerical simulation, and its performance advantage in the data compression scenario is demonstrated. The experiments use Python 3.7 and the TensorFlow1 framework to simulate the system environment on the Pycharm platform.
4.1. Parameter Settings
This study assumes a collaborative computing network consisting of 50 UEs, 1 USH, and 4 USMs within a rectangular area of 400 m × 400 m. The USH dynamically adjusts its flight path based on Line-of-Sight (LoS) and Non-Line-of-Sight (NLoS) communication conditions with the UEs, while the USMs remain fixed in position. The UEs’ positions are randomly updated in each time slot, and their assigned tasks are synchronously refreshed across the network. These parameters are primarily configured based on references from the literature [26,40]. Additional communication, computational and other related simulation parameters are detailed in Table 1. The soft update coefficient of the PER-DDPG algorithm is , and the batch size for randomly sampled data is 64.

Table 1.
Main parameters and assumptions.
4.2. Convergence Analysis
To comprehensively evaluate the performance of the proposed PER-DDPG-based algorithm, this manuscript conducts a series of comparative experiments with three benchmark algorithms: the standard DDPG algorithm, the DQN algorithm, and the uncompressed PER-DDPG (PER-DDPG_Ncpr). The evaluation process in this manuscript consists of four main phases: (1) hyperparameter optimization for the PER-DDPG algorithm to identify the optimal configuration with superior convergence performance; (2) sensitivity analysis of delay and energy consumption metrics to determine the optimal weight coefficients; (3) performance comparison with the benchmark algorithms under identical experimental conditions; and (4) scalability analysis through varying data volumes and user numbers to assess the algorithm’s robustness.
The impact of learning rate () variations on algorithm performance is demonstrated in Figure 3. This study conducted systematic parameter tuning and comparative analysis, selecting a set of demonstrating distinct performance characteristics for detailed evaluation, specifically and . The selection of an appropriate significantly influences the training dynamics and ultimately determines the convergence behavior of the algorithm. As shown in Figure 3, when using of , , and , the algorithm exhibits substantial oscillation amplitudes, slower convergence rates, and difficulties in stabilizing at optimal values. This phenomenon occurs because excessively large learning rates cause the algorithm to overshoot the optimal solution, while overly small learning rates result in insufficient updates and slow progress. In contrast, the of results in faster convergence, reduced oscillation amplitude, and superior computational offloading strategy performance, achieving the optimal reward convergence value. Consequently, the in this study is established at .
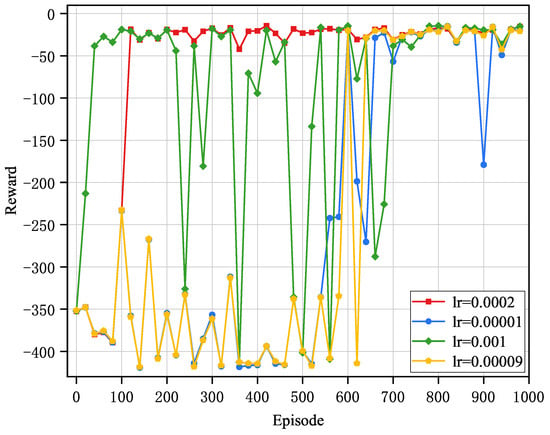
Figure 3.
Impact of learning rates on the convergence of PER-DDPG.
The appropriate configuration of the discount factor () significantly influences the algorithm’s convergence characteristics. A higher value emphasizes long-term returns, potentially leading to overly conservative strategies and unstable performance in certain states. Conversely, a lower value prioritizes immediate rewards, which may result in suboptimal long-term strategies and aggressive behavior, causing instability and fluctuations during training. Figure 4 demonstrates the impact of varying discount factors, specifically , , and , on algorithm performance. Experimental results indicate that when is set to or , the algorithm produces substantial oscillation amplitudes and difficulties in achieving stable convergence. In contrast, setting to significantly reduces oscillation amplitude, thus achieving optimal convergence performance. Consequently, the in this study is established at .
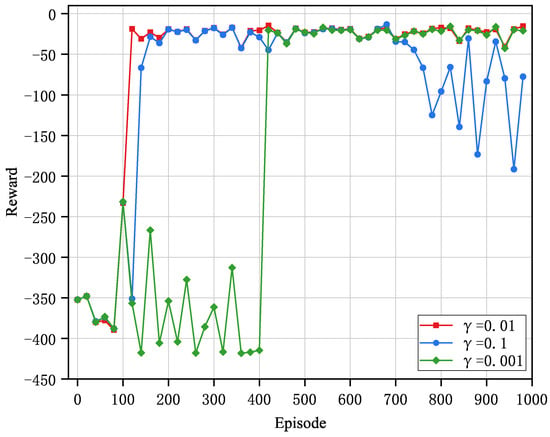
Figure 4.
Convergence performance of PER-DDPG with different .
The setting of weighting values in a multi-objective optimization problem should account for the sensitivity of both energy consumption and delay. The system delay weights and energy consumption weights are set within the range of . As shown in Figure 5, it can be seen that the convergence of this algorithm is poor when the weights are evenly distributed. When the sensitivity is skewed towards delay, the optimal strategy cannot be obtained. However, when , , the algorithm’s convergence is more stable, and the optimal strategy can be achieved.
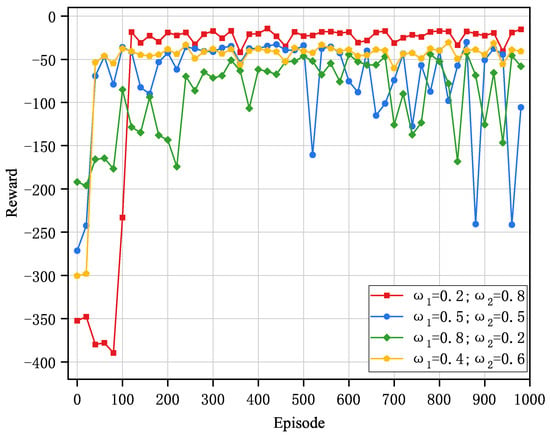
Figure 5.
Sensitivity analysis of weights in cumulative rewards.
Based on the comparative analysis of the above experiments, the PER-DDPG algorithm demonstrates optimal performance metrics when , , , . Therefore, we will adopt this set of optimized hyperparameter configurations in subsequent experiments.
Figure 6 shows the reward convergence comparison graph of different algorithms. It can be observed that as the amount of training steps grows, the rewards of the four algorithms demonstrate a consistent upward trajectory, and eventually converge to a stable reward value, which indicates that the reinforcement learning agents are able to learn better strategies to minimize the latency and energy consumption of the UEs through interaction with the environment. The fluctuations observed in the performance curves are primarily caused by the dynamic nature of the optimization process, including the exploration–exploitation trade-off in DRL, the varying complexity of tasks, and the real-time adjustments in resource allocation and task offloading. These factors collectively contribute to the non-monotonic behavior of the algorithm’s performance over time.
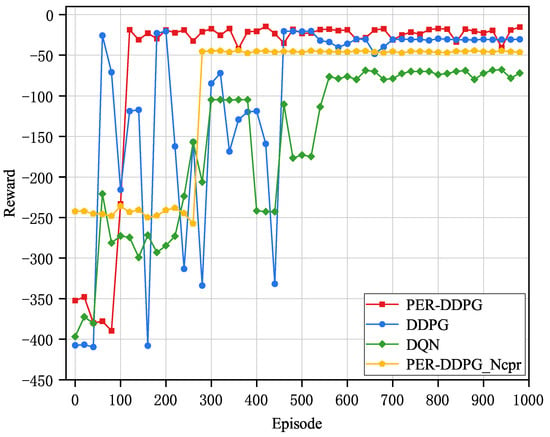
Figure 6.
Convergence performance of different algorithms.
Regarding convergence speed, the DDPG algorithm converges around 110 steps, while the other benchmark algorithms converge after 200 steps, which enables the proposed scheme to achieve superior convergence speed compared to the other algorithms. When considering convergence stability, the PER-DDPG_Ncpr algorithm exhibits the smoothest convergence, followed by the PER-DDPG algorithm. This is because the PER-DDPG_Ncpr algorithm has a smaller action space, which effectively reduces the policy search space and improves learning efficiency. Additionally, the DDPG algorithm solves the constraints of DQN in discrete action space through deterministic policy and policy gradient updates, and is suitable for solving continuous action space problems. In terms of overall performance, the PER-DDPG algorithm adopted in this manuscript achieves the highest reward and the smoothest convergence. This is attributed to the introduction of PER in PER-DDPG, which samples experiences based on their importance. This improves learning efficiency and sample utilization, further optimizing the algorithm’s performance in complex environments.
4.3. Performance Comparison
The performance of different algorithms under varying task volumes is compared in Figure 7. We can see that when the task data volume increases from Mb to Mb, the proposed algorithms result in the lowest total delay and energy usage in the system. Compared to PER-DDPG_Ncpr, DDPG, and DQN algorithms, there is a minimum reduction of , , and in total latency and energy consumption, respectively. This demonstrates that the approach explored by the proposed algorithm delivers better results than the other three baseline algorithms. Additionally, the adoption of the data compression technique significantly lowers the overall energy usage for users, and the benefits of data compression become more pronounced as the task data size increases.
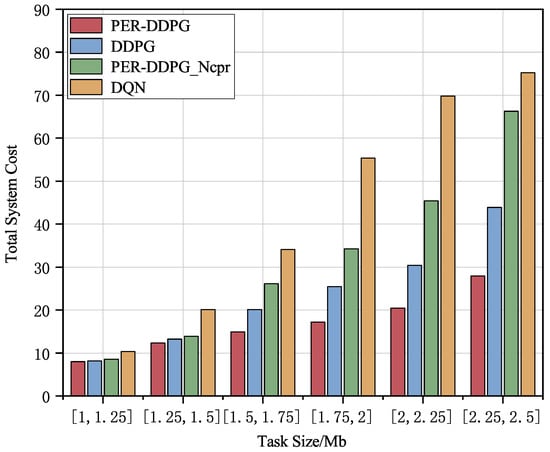
Figure 7.
Comparison of algorithm performance under different task sizes.
Figure 8 shows the system total cost and the relationship between the amount of UEs. With a growing number of UEs, the total energy usage exhibits a rising trend. This is primarily due to two factors: the increase in the total system cost caused by the growing number of UEs, combined with the limited communication resources of the system, which leads to resource competition among terminals and further increases the system cost. In contrast to the other three algorithms, the approach used in this article is able to allocate the system resources more rationally, and the total cost is always lower. For example, when the number of UEs is 50, the total system cost is reduced by at least , , and compared to PER-DDPG_Ncpr, DDPG, and DQN algorithms, respectively.
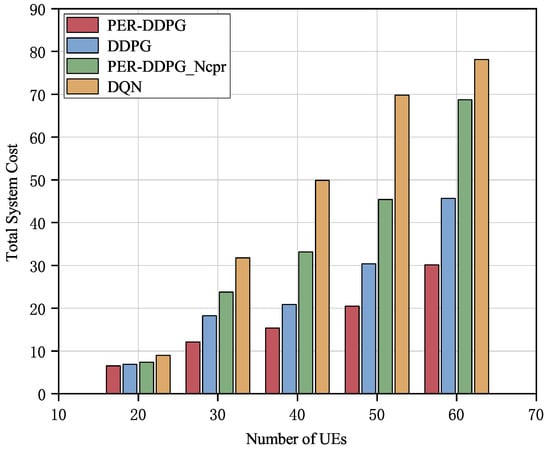
Figure 8.
Comparison of algorithm performance with different numbers of UEs.
Based on the above numerical analysis, the PER-DDPG algorithm introduced in this study demonstrates superior performance compared to the other three algorithms. By comprehensively optimizing task offloading, resource allocation, and data compression ratio, the algorithm can select the optimal strategy to achieve a relatively low maximum system processing cost.
5. Conclusions
In this manuscript, we study a coordination optimization scheme for task offloading and data compression enabled in UAV swarm-enabled mobile edge computing. First, we establish the system total delay and energy minimization problem by jointly considering the positional relationship between UAVs and UEs, the offloading ratio, the compression ratio, and the allocation of computational resources; second, we describe the problem as an MDP and solve it by using the PER-DDPG algorithm. Finally, we carried out extensive experiments to validate the validity of the proposed scheme. The numerical outcomes indicate that the scheme significantly lowers the overall system cost. Future work will consider the fairness problem of task offloading under multiple users, as well as the covertness of task transmission during task offloading to ensure security during communication.
Author Contributions
Conceptualization, Z.H. and S.L.; methodology, Z.H. and S.L.; software, S.L.; validation, S.L., D.Z. and C.S.; formal analysis, S.L. and D.Z.; investigation, Z.H. and S.L.; resources, Z.H. and S.L.; data curation, S.L. and D.Z.; writing—original draft preparation, Z.H. and S.L.; writing—review and editing, Z.H., D.Z. and T.W.; visualization, S.L. and D.Z.; supervision, Z.H.; project administration, Z.H. and T.W.; funding acquisition, Z.H. and C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China under Grant 52302505, the Shaanxi Key Research and Development Program of China under Grant 2023-YBGY-027.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, J.; Yi, C.; Chen, J.; Zhu, K.; Cai, J. Joint Trajectory Planning, Application Placement, and Energy Renewal for UAV-Assisted MEC: A Triple-Learner-Based Approach. IEEE Internet Things J. 2023, 10, 13622–13636. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, M.; Li, Z.; Hu, Y. Joint Allocations of Radio and Computational Resource for User Energy Consumption Minimization Under Latency Constraints in Multi-Cell MEC Systems. IEEE Trans. Veh. Technol. 2023, 72, 3304–3320. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, L.; Wang, L.; Hui, N.; Cui, X.; Wu, J.; Peng, Y.; Qi, Y.; Xing, C. Service-aware 6G: An intelligent and open network based on the convergence of communication, computing and caching. Digit. Commun. Netw. 2020, 6, 253–260. [Google Scholar] [CrossRef]
- Jeong, S.; Simeone, O.; Kang, J. Mobile Edge Computing via a UAV-Mounted Cloudlet: Optimization of Bit Allocation and Path Planning. IEEE Trans. Veh. Technol. 2018, 67, 2049–2063. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, M.; Bi, J.; Shi, S.; Yang, J.; Zhang, J.; Zhou, M.; Buyya, R. Cost-Efficient Task Offloading in Mobile Edge Computing With Layered Unmanned Aerial Vehicles. IEEE Internet Things J. 2024, 11, 30496–30509. [Google Scholar] [CrossRef]
- Trivisonno, R.; Guerzoni, R.; Vaishnavi, I.; Soldani, D. Towards zero latency Software Defined 5G Networks. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 2566–2571. [Google Scholar] [CrossRef]
- Liang, W.; Ma, S.; Yang, S.; Zhang, B.; Gao, A. Hierarchical Matching Algorithm for Relay Selection in MEC-Aided Ultra-Dense UAV Networks. Drones 2023, 7, 579. [Google Scholar] [CrossRef]
- Cai, Q.; Zhou, Y.; Liu, L.; Qi, Y.; Pan, Z.; Zhang, H. Collaboration of Heterogeneous Edge Computing Paradigms: How to Fill the Gap Between Theory and Practice. IEEE Wirel. Commun. 2024, 31, 110–117. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, C.; Wang, Y. Joint Computation Offloading and Trajectory Optimization for Edge Computing UAV: A KNN-DDPG Algorithm. Drones 2024, 8, 564. [Google Scholar] [CrossRef]
- Zhang, K.; Mao, Y.; Leng, S.; Zhao, Q.; Li, L.; Peng, X.; Pan, L.; Maharjan, S.; Zhang, Y. Energy-Efficient Offloading for Mobile Edge Computing in 5G Heterogeneous Networks. IEEE Access 2016, 4, 5896–5907. [Google Scholar] [CrossRef]
- Wang, M.; Li, R.; Jing, F.; Gao, M. Multi-UAV Assisted Air–Ground Collaborative MEC System: DRL-Based Joint Task Offloading and Resource Allocation and 3D UAV Trajectory Optimization. Drones 2024, 8, 510. [Google Scholar] [CrossRef]
- Wu, Z.; Yang, Z.; Yang, C.; Lin, J.; Liu, Y.; Chen, X. Joint deployment and trajectory optimization in UAV-assisted vehicular edge computing networks. J. Commun. Netw. 2022, 24, 47–58. [Google Scholar] [CrossRef]
- Wang, R.; Huang, Y.; Lu, Y.; Xie, P.; Wu, Q. Robust Task Offloading and Trajectory Optimization for UAV-Mounted Mobile Edge Computing. Drones 2024, 8, 757. [Google Scholar] [CrossRef]
- Yang, X.; Wang, Q.; Yang, B.; Cao, X. Energy-Efficient Aerial STAR-RIS-Aided Computing Offloading and Content Caching for Wireless Sensor Networks. Sensors 2025, 25, 393. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Li, W.; Yao, J. An Efficiency Framework for Task Allocation Based on Reinforcement Learning. In Proceedings of the 2023 International Conference on Image Processing, Computer Vision and Machine Learning (ICICML), Chengdu, China, 3–5 November 2023; pp. 928–933. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Xia, Z.; Zhao, Z.; Zhang, T.; Li, K.; Yin, X.; Shi, H.; Peng, T. Intelligent Resource Management and Optimization of Clustered UAV Airborne SAR System. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–May 2021; pp. 987–991. [Google Scholar] [CrossRef]
- Duan, H.; Luo, Q.; Shi, Y.; Ma, G. Hybrid Particle Swarm Optimization and Genetic Algorithm for Multi-UAV Formation Reconfiguration. IEEE Comput. Intell. Mag. 2013, 8, 16–27. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y.; Qi, N.; Yao, K.; Zhang, Y.; He, W. Joint Computation Offloading and Resource Allocation in UAV Swarms with Multi-access Edge Computing. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 280–285. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Yi, C.; Zhang, T.; Zhu, K.; Cai, J. Energy-Efficient UAV Swarm Assisted MEC With Dynamic Clustering and Scheduling. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Miao, Y.; Hwang, K.; Wu, D.; Hao, Y.; Chen, M. Drone Swarm Path Planning for Mobile Edge Computing in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2023, 19, 6836–6848. [Google Scholar] [CrossRef]
- Liu, B.; Huang, H.; Guo, S.; Chen, W.; Zheng, Z. Joint Computation Offloading and Routing Optimization for UAV-Edge-Cloud Computing Environments. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 1745–1752. [Google Scholar] [CrossRef]
- Chen, M.; Liew, S.C.; Shao, Z.; Kai, C. Markov Approximation for Combinatorial Network Optimization. IEEE Trans. Inf. Theory 2013, 59, 6301–6327. [Google Scholar] [CrossRef]
- Srisooksai, T.; Keamarungsi, K.; Lamsrichan, P.; Araki, K. Practical data compression in wireless sensor networks: A survey. J. Netw. Comput. Appl. 2012, 35, 37–59. [Google Scholar] [CrossRef]
- Lu, S.; Xia, Q.; Tang, X.; Zhang, X.; Lu, Y.; She, J. A Reliable Data Compression Scheme in Sensor-Cloud Systems Based on Edge Computing. IEEE Access 2021, 9, 49007–49015. [Google Scholar] [CrossRef]
- Cheng, K.; Fang, X.; Wang, X. Energy Efficient Edge Computing and Data Compression Collaboration Scheme for UAV-Assisted Network. IEEE Trans. Veh. Technol. 2023, 72, 16395–16408. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1996. [Google Scholar]
- Sharma, K.; Gupta, K. Lossless data compression techniques and their performance. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 256–261. [Google Scholar] [CrossRef]
- Rodríguez Marco, J.E.; Sánchez Rubio, M.; Martínez Herráiz, J.J.; González Armengod, R.; Del Pino, J.C.P. Contributions to Image Transmission in Icing Conditions on Unmanned Aerial Vehicles. Drones 2023, 7, 571. [Google Scholar] [CrossRef]
- Jayasankar, U.; Thirumal, V.; Ponnurangam, D. A survey on data compression techniques: From the perspective of data quality, coding schemes, data type and applications. J. King Saud Univ. Comput. Inf. Sci. 2021, 33, 119–140. [Google Scholar] [CrossRef]
- Dipti Mathpal, M.D.; Mehta, S. A Research Paper on Lossless Data Compression Techniques. Int. J. Innov. Res. Sci. Technol. 2017, 4, 190–194. [Google Scholar]
- Han, B.; Ye, Y.; Shi, L.; Xu, Y.; Lu, G. Energy-Efficient Computation Offloading for MEC-Enabled Blockchain by Data Compression. In Proceedings of the 2024 IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 7–9 August 2024; pp. 1970–1975. [Google Scholar] [CrossRef]
- Liang, J.; Ma, B.; Feng, Z.; Huang, J. Reliability-Aware Task Processing and Offloading for Data-Intensive Applications in Edge computing. IEEE Trans. Netw. Serv. Manag. 2023, 20, 4668–4680. [Google Scholar] [CrossRef]
- Qiu, X.; Dai, Y.; Xiang, Y.; Xing, L. Correlation Modeling and Resource Optimization for Cloud Service With Fault Recovery. IEEE Trans. Cloud Comput. 2019, 7, 693–704. [Google Scholar] [CrossRef]
- Tu, W.; Liu, X. Energy Consumption Minimization for a Data Compression Based NOMA-MEC System. In Proceedings of the 2024 5th Information Communication Technologies Conference (ICTC), Nanjing, China, 10–12 May 2024; pp. 337–343. [Google Scholar] [CrossRef]
- Ding, Z.; Lv, C.; Huang, Z.; Zhang, M.; Chang, M.; Liu, R. Joint Optimization of Transmission and Computing Resource in Mobile Edge Computing Systems with Multiple Base Stations. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 507–512. [Google Scholar] [CrossRef]
- Li, X.; You, C.; Andreev, S.; Gong, Y.; Huang, K. Wirelessly Powered Crowd Sensing: Joint Power Transfer, Sensing, Compression, and Transmission. IEEE J. Sel. Areas Commun. 2019, 37, 391–406. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; Cai, Y.; He, Y. Latency Optimization for Resource Allocation in Mobile-Edge Computation Offloading. IEEE Trans. Wirel. Commun. 2018, 17, 5506–5519. [Google Scholar] [CrossRef]
- Yang, Y.; Gong, Y.; Wu, Y.C. Intelligent-Reflecting-Surface-Aided Mobile Edge Computing with Binary Offloading: Energy Minimization for IoT Devices. IEEE Internet Things J. 2022, 9, 12973–12983. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Mareri, B.; Sun, G.; Jiang, W. Multi-Agent DRL for Task Offloading and Resource Allocation in Multi-UAV Enabled IoT Edge Network. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4531–4547. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).