Preassigned Fixed-Time Synergistic Constrained Control for Fixed-Wing Multi-UAVs with Actuator Faults
Abstract
1. Introduction
- To better align with practical scenarios, this study develops a distributed cooperative control scheme for multiple UAVs based on a more realistic six-DOF dynamic model. Additionally, a fault-tolerant mechanism is incorporated to address potential actuator failures that may occur during actual flight operations.
- In order to enforce full-state constraints on the UAV system, an improved segmented asymmetric tan-type BLF is introduced. This modification allows for the imposition of asymmetric constraints on the UAV system, which operates as a non-strict feedback system.
- To achieve fixed-time control for the multi-UAV system under full-state constraints, a novel fixed-time performance function (FTPF) is proposed. When combined with the improved segmented asymmetric tan-BLF, this approach overcomes the limitations of traditional fixed-time convergence methods, which are generally restricted to strict-feedback systems and impose rigid convergence conditions.
2. Problem Formulation and Preliminaries
2.1. UAV Kinematics and Dynamics
2.2. A Control-Based Model Incorporating Actuator Failures and Modeling Uncertainties
2.2.1. Translational Kinematics
- and . The system is fault-free.
- and . This represents a partial failure.
- and . A bias fault is present.
- and . A complete malfunction with a bias fault.
2.2.2. Rotational Kinematics
- and . The system is fault-free.
- and . This represents a partial failure.
- and . A bias fault is present.
- and . A complete malfunction with a bias fault.
2.3. Graph Theory
2.4. Neural Network Approximation
2.5. Control Objective
- All closed-loop signals are guaranteed to be SGUUB, and the synchronization tracking errors of both velocity and attitude are ensured to converge to a residual set around the origin within a fixed time.
- The velocity and attitude states remain within a set of time-varying asymmetric constraints. Specifically, for each UAV, both and satisfy the constraints and .
- For the convenience of derivation, the following definition and lemmas are needed.
3. Adaptive Fixed-Time Controller Design
3.1. Fixed-Time Performance Function
- is positive and decreasing over time for ;
- for all , where is a positive design parameter.
3.2. Controller Design and Stability Analysis
3.2.1. Translational Kinematics
- The closed-loop signals and are guaranteed to be SGUUB and the synchronization tracking errors of velocity converges to a residual set around origin within a fixed time.
- The state of velocity is consistently within a set of time-varying asymmetric constraints.
3.2.2. Rotational Kinematics
- The closed-loop signals are guaranteed to be SGUUB and the synchronization tracking errors of velocity converge to a residual set around origin within a fixed time.
- The state of attitude is consistently constrained within a set of time-varying asymmetric constraints.
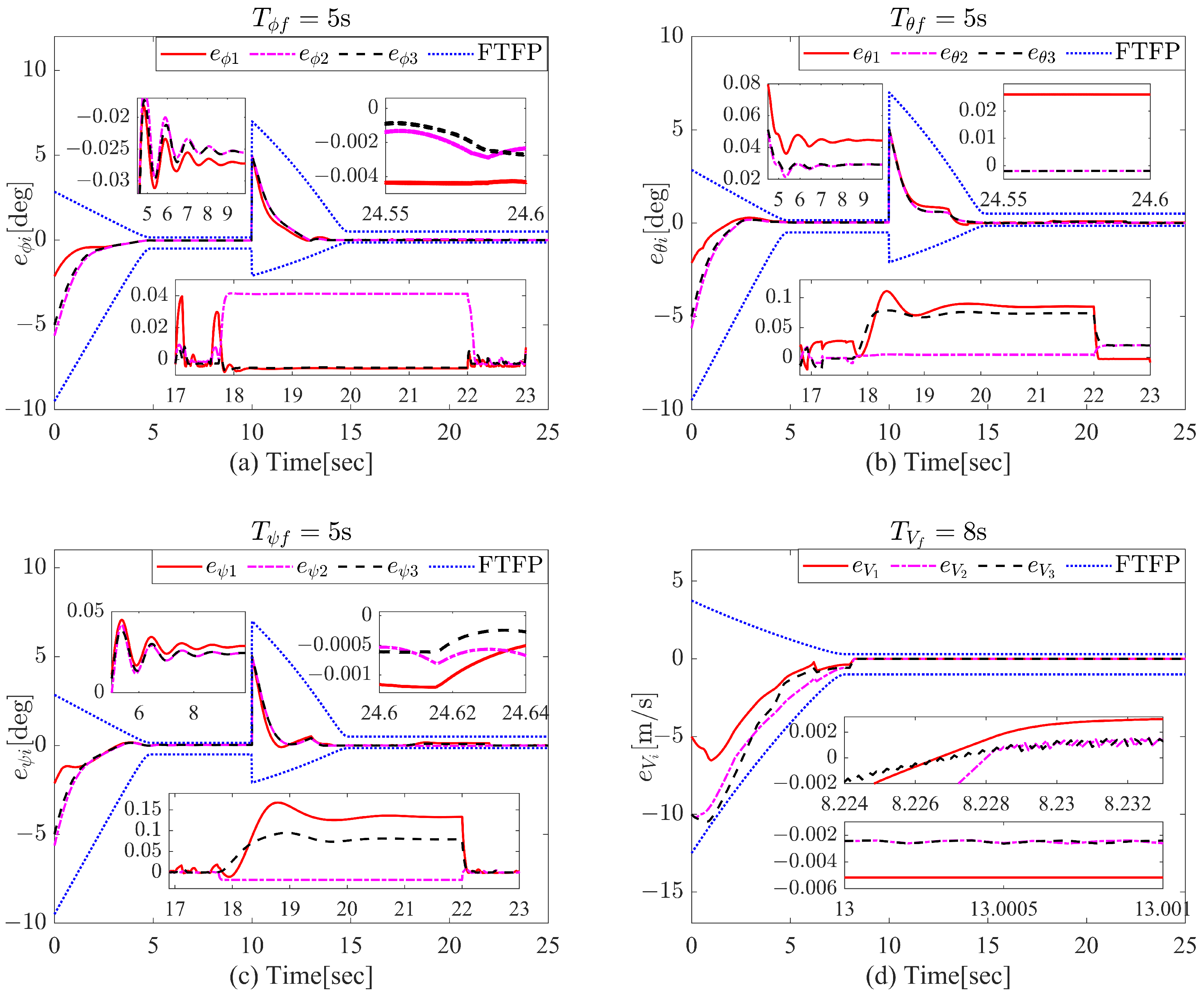
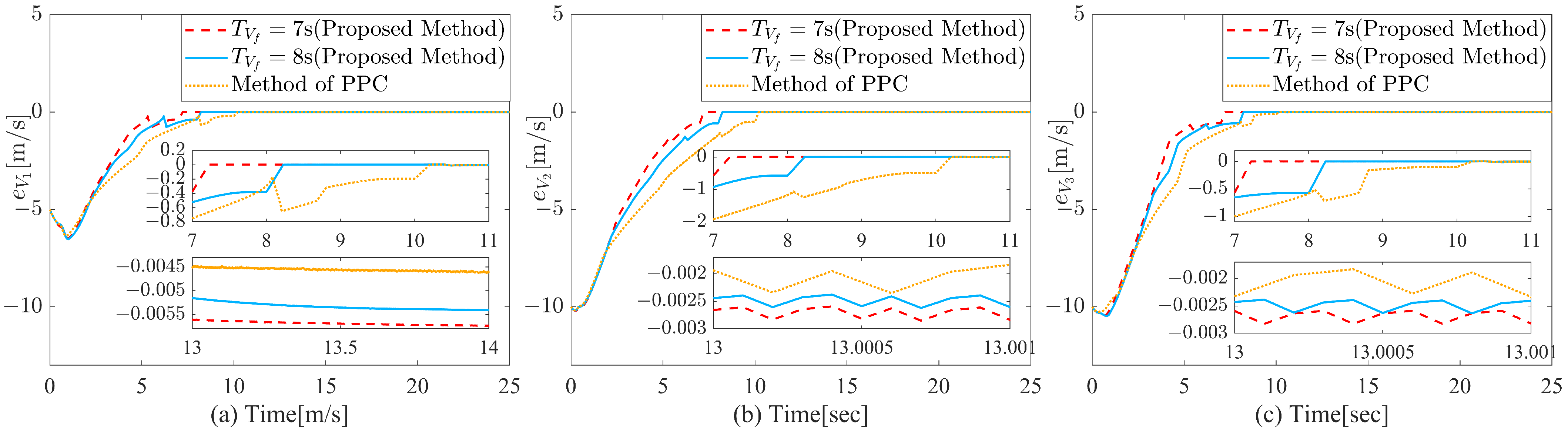
4. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.; Meng, Z. Bearing-based distributed formation control of multiple vertical take-off and landing unmanned aerial vehicles. IEEE Trans. Control Netw. Syst. 2021, 8, 1281–1292. [Google Scholar]
- Zou, Y.; Xia, K.; He, W. Adaptive fault-tolerant distributed formation control of clustered vertical takeoff and landing UAVs. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1069–1082. [Google Scholar] [CrossRef]
- Wang, R.; Lungu, M.; Zhou, Z.; Zhu, X.; Ding, Y.; Zhao, Q. Least global position information based control of fixed-wing unmanned aerial vehicles formation flight: Flight tests and experimental validation. Aerosp. Sci. Technol. 2023, 140, 108473. [Google Scholar]
- Xu, L.; Qi, G. Function observer based on model compensation control for a fixed-wing unmanned aerial vehicle. Aerosp. Sci. Technol. 2024, 152, 109325. [Google Scholar]
- Zhuang, X.; Li, D.; Wang, Y.; Liu, X.; Li, H. Optimization of high-speed fixed-wing unmanned aerial vehicle penetration strategy based on deep reinforcement learning. Aerosp. Sci. Technol. 2024, 148, 109089. [Google Scholar]
- Qian, M.; Wu, Z.; Jiang, B. Cerebellar model articulation neural network-based distributed fault tolerant tracking control with obstacle avoidance for fixed-wing unmanned aerial vehicles. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6841–6852. [Google Scholar]
- Yang, L.; Liu, Z.; Zhang, X.; Wang, X.; Shen, L. Image-based distributed predictive visual servo control for cooperative tracking of multiple fixed-wing unmanned aerial vehicles. IEEE Robot. Autom. Lett. 2024, 9, 7779–7786. [Google Scholar]
- Choi, J.; Seo, M.; Shin, H.-S.; Oh, H. Adversarial swarm defence using multiple fixed-wing unmanned aerial vehicles. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5204–5219. [Google Scholar]
- Zhang, B.; Sun, X.; Liu, S.; Lv, M.; Deng, X. Event-triggered adaptive fault-tolerant synchronization tracking control for multiple six-degree-of-freedom fixed-wing unmanned aerial vehicles. IEEE Trans. Veh. Technol. 2022, 71, 148–161. [Google Scholar]
- Wang, Y.; Wang, H.; Liu, Y.; Wu, J.; Lun, Y. Six-degree-of-freedom unmanned aerial vehicle path planning and tracking control for obstacle avoidance: A deep learning-based integrated approach. Aerosp. Sci. Technol. 2024, 151, 109320. [Google Scholar]
- Lv, M.; Ahn, C.K.; Zhang, B.; Fu, A. Fixed-time anti-saturation cooperative control for networked fixed-wing unmanned aerial vehicles considering actuator failures. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8812–8825. [Google Scholar] [CrossRef]
- Zhang, Q.; He, D. Adaptive fuzzy sliding exact tracking control based on high-order log-type time-varying barrier Lyapunov functions for high-order nonlinear systems. IEEE Trans. Fuzzy Syst. 2023, 31, 14–24. [Google Scholar] [CrossRef]
- Feng, Z.; Li, R.-B.; Zhang, N.; Wu, L. Event-based asymptotic tracking control for constrained multi-input-multioutput nonlinear systems via a single-parameter adaptation method. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 7758–7768. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Chen, Y.; Wang, R. Disturbance observer-based adaptive intelligent control of marine vessel with position and heading constraint condition related to desired output. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5870–5879. [Google Scholar] [CrossRef]
- Wang, L.; Dong, J. Integral concurrent learning control Lyapunov functions and high order control barrier functions and application to adaptive cruise control. IEEE Trans. Intell. Transp. Syst. 2024, 25, 3714–3723. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Xie, X.; Park, J.H.; Liu, Y.; Sun, J. Integral barrier Lyapunov function-based adaptive dynamic event-triggered boundary control for a flexible riser system. IEEE Trans. Cybern. 2024, 54, 5555–5564. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wang, X.; Jiao, R.; Dong, M. Asymmetric integral barrier Lyapunov function-based human–robot interaction control for human-compliant space-constrained muscle strength training. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 4305–4317. [Google Scholar] [CrossRef]
- Sun, W.; Su, S.-F.; Wu, Y.; Xia, J.; Nguyen, V.-T. Adaptive fuzzy control with high-order barrier Lyapunov functions for high-order uncertain nonlinear systems with full-state constraints. IEEE Trans. Cybern. 2020, 50, 3424–3432. [Google Scholar] [CrossRef]
- Chen, H.; Wang, P.; Tang, G. Prescribed-time control for hypersonic morphing vehicles with state error constraints and uncertainties. Aerosp. Sci. Technol. 2023, 142, 108671. [Google Scholar] [CrossRef]
- Liu, L.; Cui, Y.; Liu, Y.-J.; Tong, S. Adaptive event-triggered output feedback control for nonlinear switched systems based on full state constraints. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3779–3783. [Google Scholar] [CrossRef]
- Khadhraoui, A.; Zouaoui, A.; Saad, M. Barrier Lyapunov function and adaptive backstepping-based control of a quadrotor UAV. Robotica 2023, 41, 2941–2963. [Google Scholar]
- Habibi, H.; Safaei, A.; Voos, H.; Darouach, M.; Sanchez-Lopez, J.L. Safe navigation of a quadrotor UAV with uncertain dynamics and guaranteed collision avoidance using barrier Lyapunov function. Aerosp. Sci. Technol. 2023, 132, 108064. [Google Scholar]
- Wang, X.; Niu, B.; Zhang, J.; Wang, H.; Jiang, Y.; Wang, D. Adaptive event-triggered consensus tracking control schemes for uncertain constrained nonlinear multi-agent systems. IEEE Trans. Autom. Sci. Eng. 2023, 21, 7325–7335. [Google Scholar]
- Liu, M.; Wu, K.; Wu, Y. Event-triggered adaptive tracking control for disturbed nonholonomic systems with asymmetric state constraints. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3850–3854. [Google Scholar]
- Li, Z.; Li, S.; Liu, Y.-J.; Liu, L. Event-triggered neural control for time-varying delay switched systems with constraints related to historical states under average dwell time. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1427–1437. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Oh, H.; Moon, J.; Kim, Y. Multivariable disturbance observer-based finite-time sliding mode attitude control for fixed-wing unmanned aerial vehicles under matched and mismatched disturbances. IEEE Control Syst. Lett. 2023, 7, 1999–2004. [Google Scholar]
- Zhang, C.H.; Chang, L.; Xing, L.T.; Zhang, X.F. Fixed-time stabilization of a class of strict-feedback nonlinear systems via dynamic gain feedback control. IEEE/CAA J. Autom. Sin. 2023, 10, 403–410. [Google Scholar] [CrossRef]
- Sui, S.; Xu, H.; Chen, C.L.P.; Tong, S. Nonsingular fixed-time control of nonstrict feedback multi-input-multioutput nonlinear system with asymptotically convergent tracking error. IEEE Trans. Fuzzy Syst. 2023, 31, 1689–1702. [Google Scholar] [CrossRef]
- Hao, Z.; Peng, W.; Guojian, T.; Weimin, B. Fixed-time attitude control for hypersonic morphing vehicles: A dynamic memory event-triggering approach. Aerosp. Sci. Technol. 2024, 155, 109577. [Google Scholar]
- Baranwal, M.; Budhraja, P.; Raj, V.; Hota, A.R. Generalized gradient flows with provable fixed-time convergence and fast evasion of non-degenerate saddle points. IEEE Trans. Autom. Control 2024, 69, 2281–2293. [Google Scholar]
- Castaneda, H.; Salas-Pena, O.S.; Leon-Morales, J. Extended observer based on adaptive second order sliding mode control for a fixed wing unmanned aerial vehicle. ISA Trans. 2017, 66, 226–232. [Google Scholar] [PubMed]
- Drummond, R.; Turner, M.C.; Duncan, S.R. Reduced-order neural network synthesis with robustness guarantees. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 1182–1191. [Google Scholar]
- Xiao, W.-X.; Jiang, G.-R.; Mao, J.-K.; Xie, F.; Zhang, B.; Qiu, D.; Chen, Y.-F. Adaptive logarithmic state feedback control with quasi one-switching-cycle response characteristic for three-phase inverter. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3046–3050. [Google Scholar]
- Daubechies, I.; Devore, R.; Dym, N.; Faigenbaum-Golovin, S.; Kovalsky, S.Z.; Lin, K.C.; Park, J.; Petrova, G.; Sober, B. Neural network approximation of refinable functions. IEEE Trans. Inf. Theory 2023, 69, 482–495. [Google Scholar]
- Shao, S.; Chen, M.; Zhang, Y. Adaptive discrete-time flight control using disturbance observer and neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3708–3721. [Google Scholar] [PubMed]
- Hong, W.; Tao, G.; Wang, H.; Wang, C. Traffic signal control with adaptive online-learning scheme using multiple-model neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7838–7850. [Google Scholar]
- Xu, H.; Yu, D.; Sui, S.; Chen, C.L.P. An event-triggered predefined time decentralized output feedback fuzzy adaptive control method for interconnected systems. IEEE Trans. Fuzzy Syst. 2023, 31, 631–644. [Google Scholar]
- Wang, N.; Wang, Y. Fuzzy adaptive quantized tracking control of switched high-order nonlinear systems: A new fixed-time prescribed performance method. IEEE Trans. Circuits Syst. II: Express Briefs 2022, 69, 3279–3283. [Google Scholar]
- Sun, W.; Su, S.-F.; Wu, Y.; Xia, J. Adaptive fuzzy event-triggered control for high-order nonlinear systems with prescribed performance. IEEE Trans. Cybern. 2022, 52, 2885–2895. [Google Scholar]








| Parameter | Value/Unit | Parameter | Value/Unit | Parameter | Value/Unit |
|---|---|---|---|---|---|
| 20.64/kg | 1.96/m | 1.37/m2 | |||
| 0.76/m | 1.29/ | g | 9.8/ | ||
| 0.59/ | 0.1 (constant) | 0.25/ | |||
| 0.5 (constant) | −0.1/ | −0.001 (constant) | |||
| −0.038 (constant) | −0.213/ | 0.114/ | |||
| −0.056/ | 0.014/ | 0.022 (constant) | |||
| −0.473/ | −3.449/ | -0.364/ | |||
| 0.022 (constant) | 0.036/ | −0.151/ | |||
| −0.195/ | −0.036/ | −0.055/ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Yuan, Z.; Wang, N. Preassigned Fixed-Time Synergistic Constrained Control for Fixed-Wing Multi-UAVs with Actuator Faults. Drones 2025, 9, 268. https://doi.org/10.3390/drones9040268
Lu J, Yuan Z, Wang N. Preassigned Fixed-Time Synergistic Constrained Control for Fixed-Wing Multi-UAVs with Actuator Faults. Drones. 2025; 9(4):268. https://doi.org/10.3390/drones9040268
Chicago/Turabian StyleLu, Jianhua, Zehao Yuan, and Ning Wang. 2025. "Preassigned Fixed-Time Synergistic Constrained Control for Fixed-Wing Multi-UAVs with Actuator Faults" Drones 9, no. 4: 268. https://doi.org/10.3390/drones9040268
APA StyleLu, J., Yuan, Z., & Wang, N. (2025). Preassigned Fixed-Time Synergistic Constrained Control for Fixed-Wing Multi-UAVs with Actuator Faults. Drones, 9(4), 268. https://doi.org/10.3390/drones9040268






