Distributed Decision Making for Electromagnetic Radiation Source Localization Using Multi-Agent Deep Reinforcement Learning
Abstract
1. Introduction
- Advanced Multi-UAV Framework: We develop a distributed reinforcement learning framework that enables independent decision-making while facilitating collaborative positioning among multiple UAVs. This framework specifically addresses the challenges of radiation source detection and localization in complex urban environments.
- Innovative Algorithm Design: We propose the MURPPO algorithm, an innovative approach that features a dual-branch actor structure to reduce decision complexity and improve learning efficiency. The algorithm incorporates task-specific domain knowledge into its reward function design, enabling effective guidance for UAVs in their exploration tasks. Additionally, we develop a geometry-based three-point localization method that leverages the spatial distribution of multiple UAVs to achieve precise positioning of radiation sources.
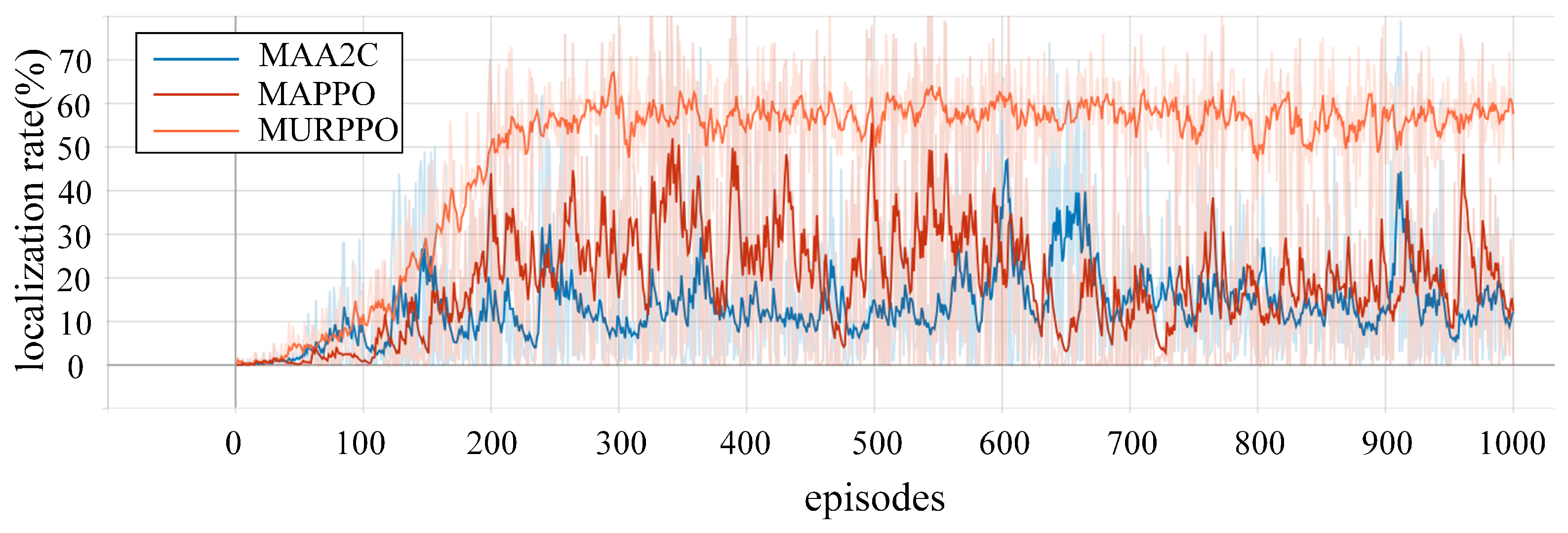
- Performance Validation: Our extensive simulations demonstrate that MURPPO achieves a 56.5% successful localization rate in later training stages, showing a 38.5% improvement over traditional multi-agent PPO algorithms with robust performance in complex urban electromagnetic environments.
2. Related Work
2.1. Traditional Heuristic Algorithms
2.2. Reinforcement Learning Algorithms
2.3. Research Gaps and Our Approach
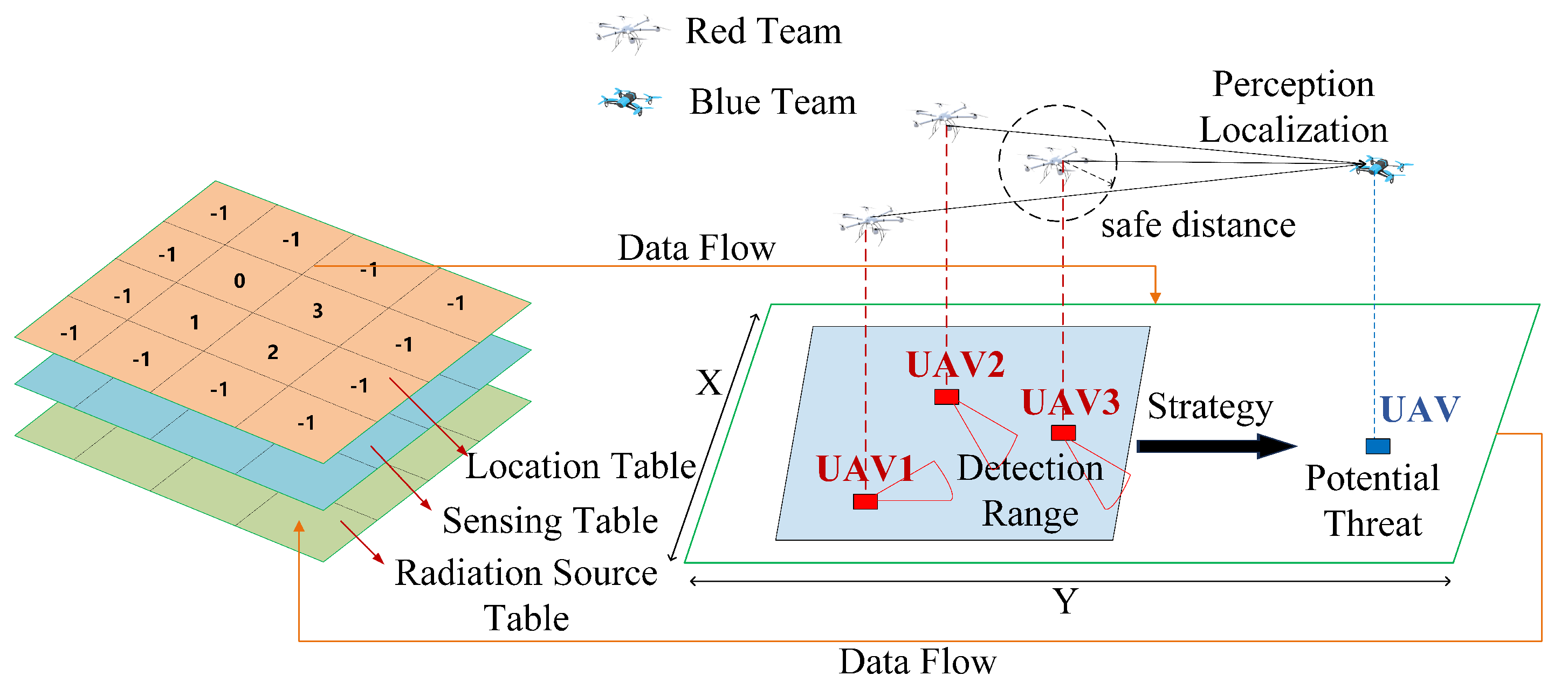
- It establishes a distributed multi-UAV collaborative perception and localization architecture to facilitate efficient cooperative operations.
- It integrates a branched actor network architecture for enhanced computational efficiency while utilizing trilateration methods to exploit the spatial distribution of UAVs for precise localization.
- it uses sophisticated reward mechanisms to ensure robust closed-loop perception and detection.
3. System Model
3.1. Environment Model
3.2. UAV Kinematic Model
4. Problem Definition and Analysis
4.1. Problem Formulation for Perception
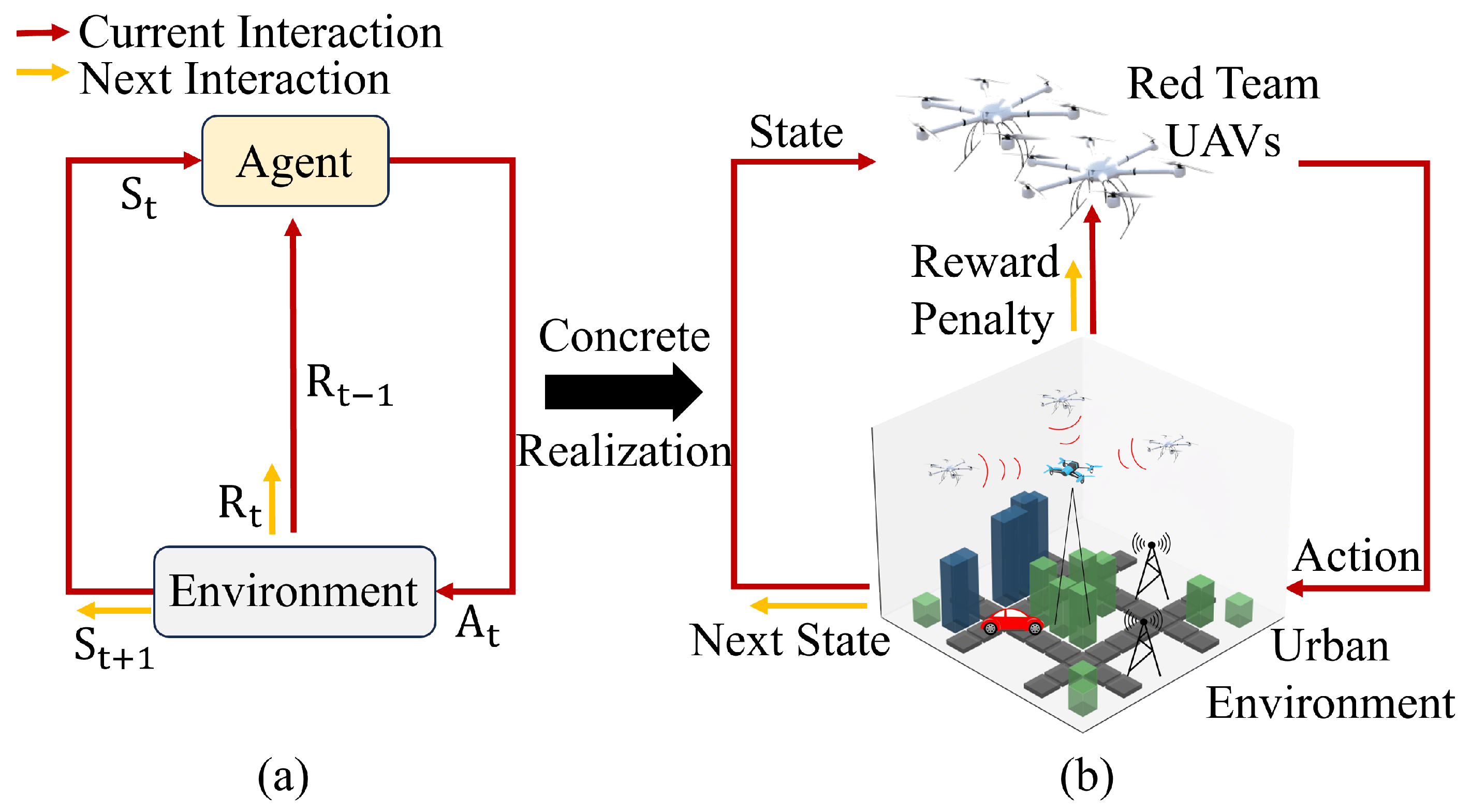
4.2. Markov Decision Process Modeling
- State: The state primarily focuses on the red team UAV’s current position , distance d, detection direction , current time step t, the number of successfully detected UAVs n, the anomalous radiation source position of the most recent effective scan , and its distance . The state space is constructed as a set . Different UAVs have varying attributes and represent different systems. Based on their specific characteristics, the state transitions for movement and detection are configured accordingly;
- Action: The red team UAV’s actions are primarily divided into movement direction and detection direction , where is determined by velocity and heading angle , while is determined by sensor orientation . For movement, the red team UAV has nine options: moving in cardinal and diagonal directions or staying. For detection, the red team UAV also has nine options: scanning or not scanning in 45-degree increments on the current plane. The action space is constructed as a set . The actual radiation detection depends on both sensor orientation and RSSI measurements. When three red team UAVs simultaneously detect the anomalous radiation source (i.e., ), it triggers the three-point localization function;
- Reward: The environment generates a scalar signal as reward feedback based on the state and actions taken by the red team UAV. In this paper, we design rewards from multiple aspects, providing rewards for individual UAV successful detection, first successful detection, and successful three-point localization. This multi-faceted reward design balances individual performance and team collaboration, while addressing both task speed and accuracy. The individual detection reward keeps all red team UAVs motivated, the first successful detection reward speeds up task completion through competition, and the three-point localization reward encourages cooperation, enhancing localization accuracy. To effectively guide the UAVs’ behavior, we design a distance-based reward function that provides continuous feedback during the detection process:where is the preset detection reward value, is the maximum cross-range distance of the key protection area (or the diagonal length if the area is square), is the minimum distance, and d is the distance calculated from RSSI using Equation (11). By using this method, we link the successful detection reward for an individual UAV to the distance, creating a dynamic reward mechanism. This guides the UAV to approach the anomalous radiation source for better detection results. The total reward for a corresponding action is then calculated. For the first successful detection and successful three-point localization, additional rewards are assigned to each UAV.
- Penalty: Due to the sparsity of rewards caused by the large spatial range, we implement penalties to encourage the red team UAVs to perform mobile detection behaviors. A penalty is applied at each step when a UAV fails to detect the anomalous radiation source. Additionally, a penalty is imposed if the UAV loses track of the detection target in the time step immediately following a successful detection, and when collisions occur between UAVs or with obstacles.
5. Multi-UAV Reconnaissance Proximal Policy Optimization Algorithm
5.1. Reinforcement Learning Algorithm
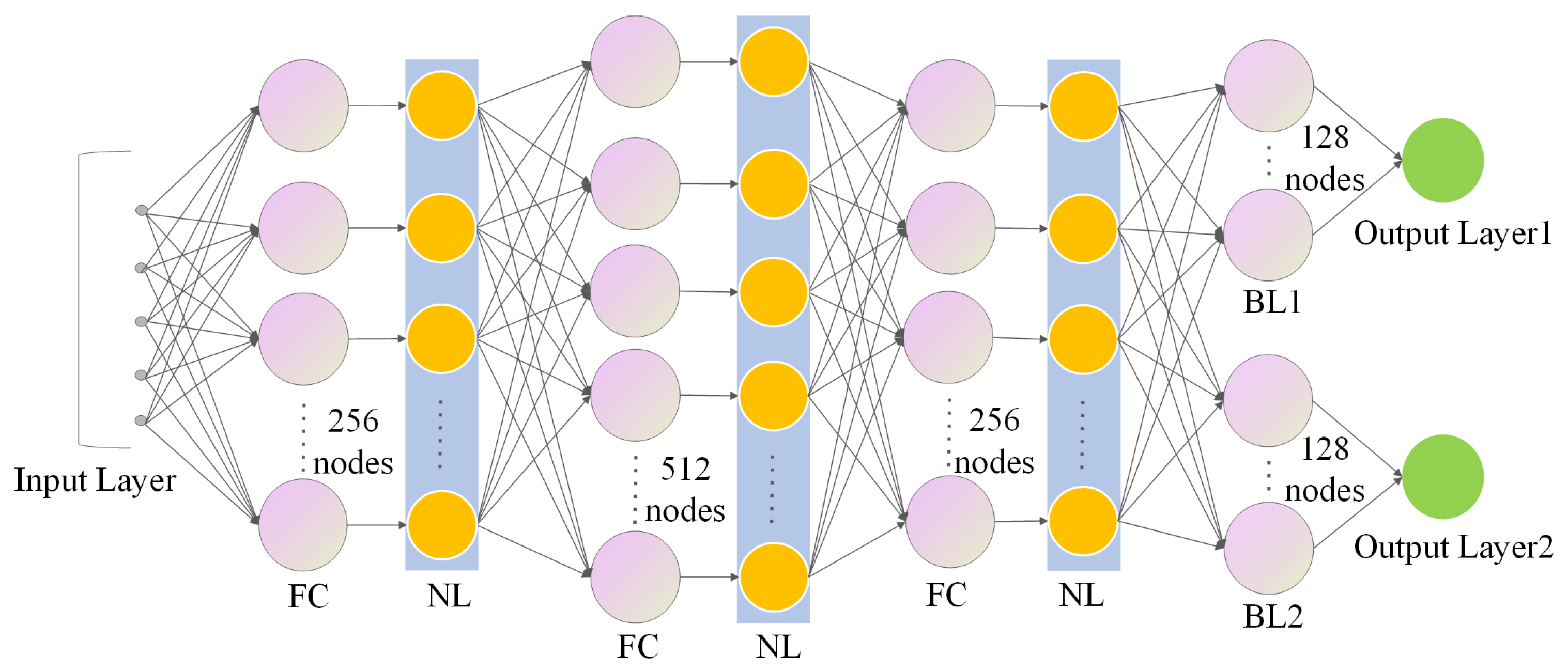
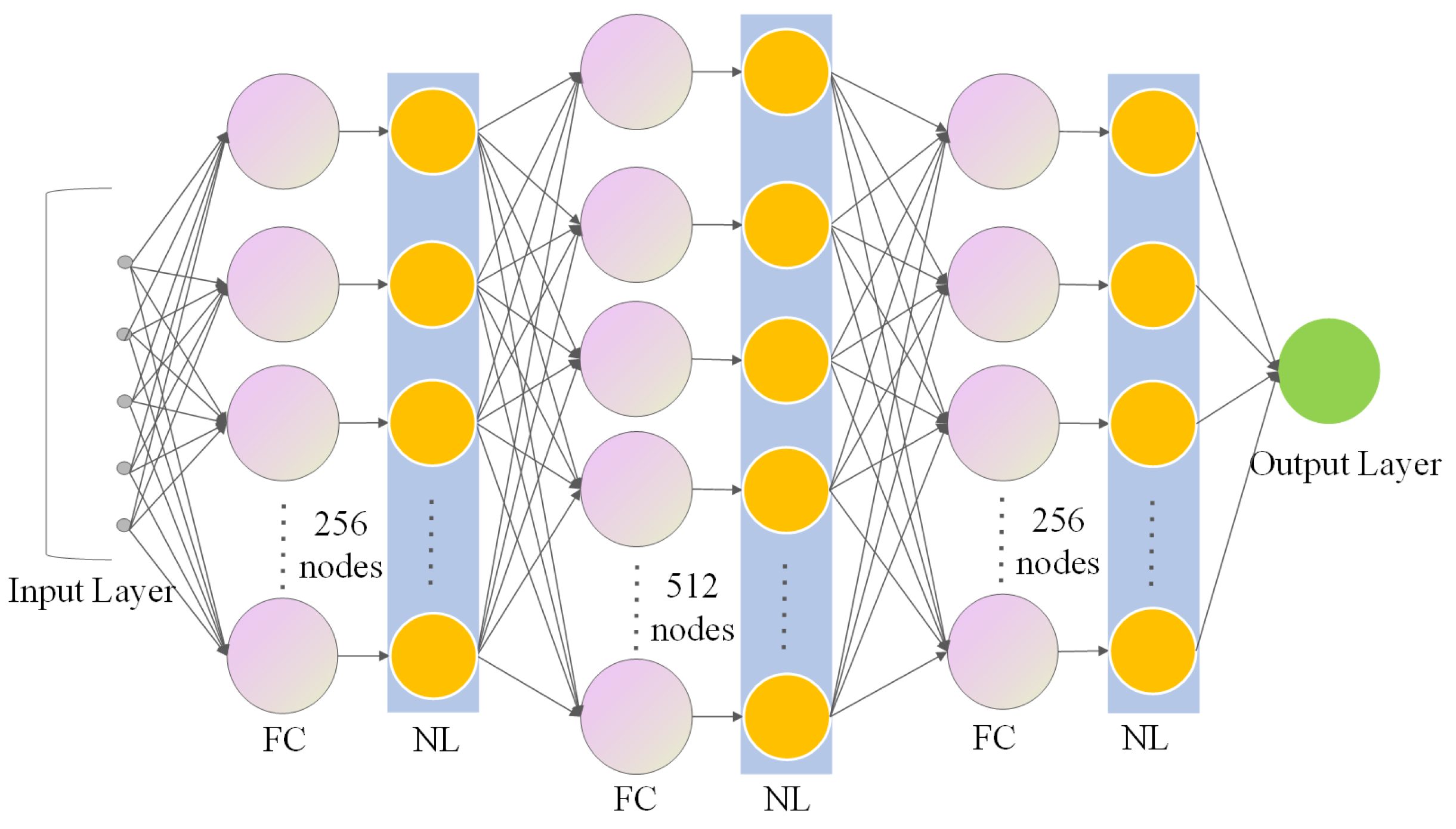
5.2. MURPPO Based on Branch Training
| Algorithm 1 MURPPO Algorithm Update Process |
|
| Algorithm 2 MURPPO Algorithm Execution Process |
|
6. Simulation Results
6.1. Experimental Configuration and Parameters
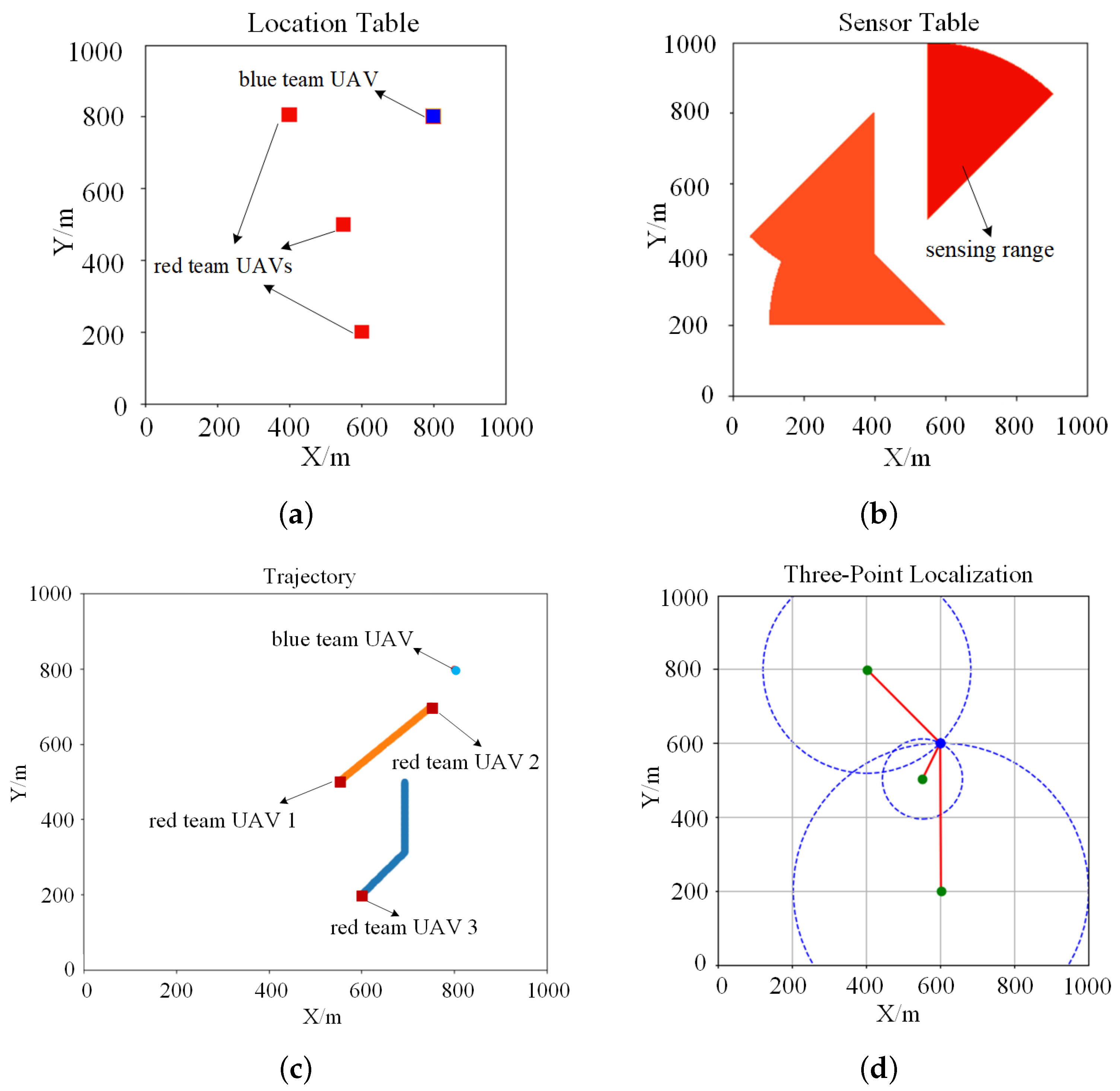
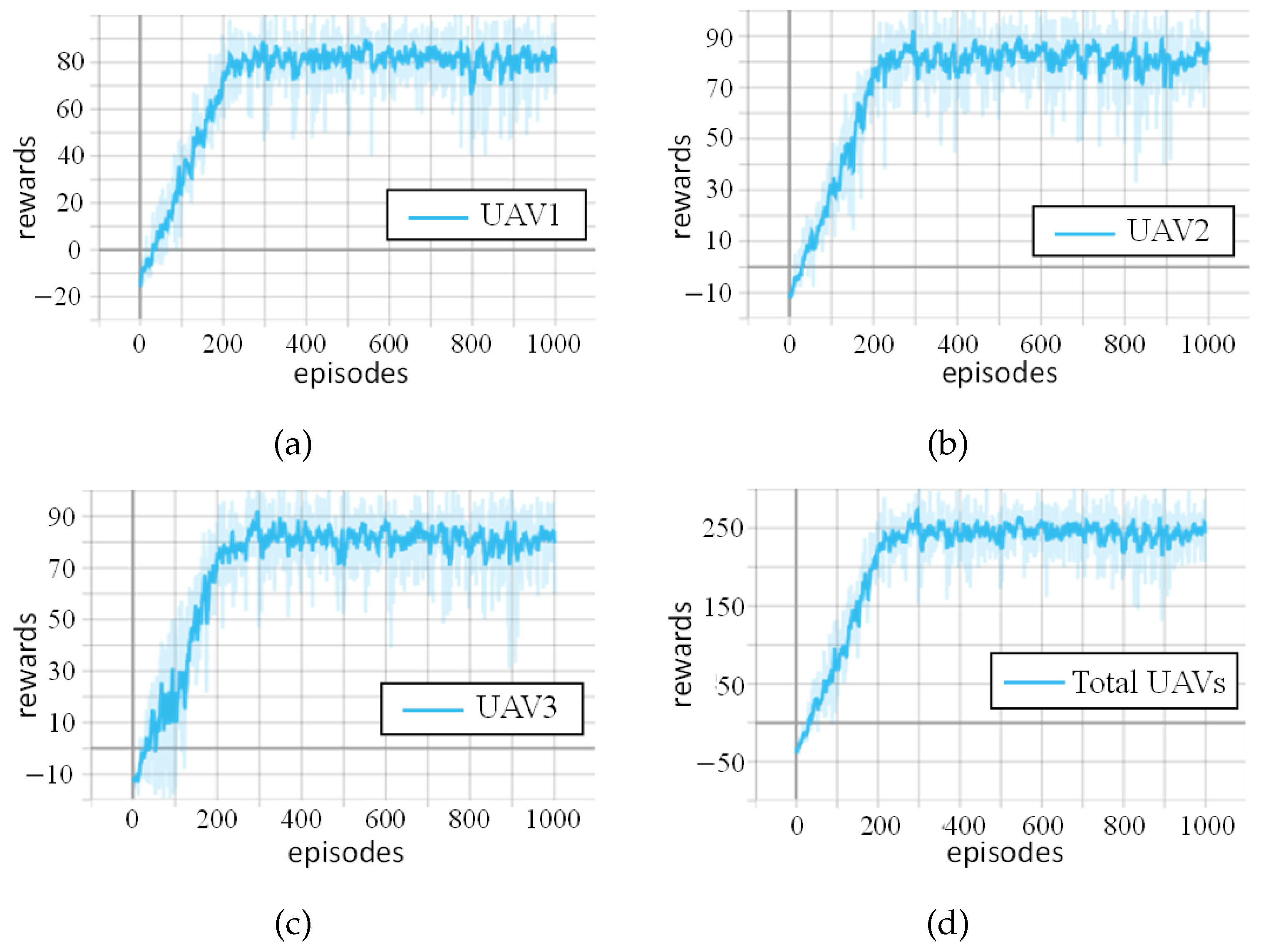
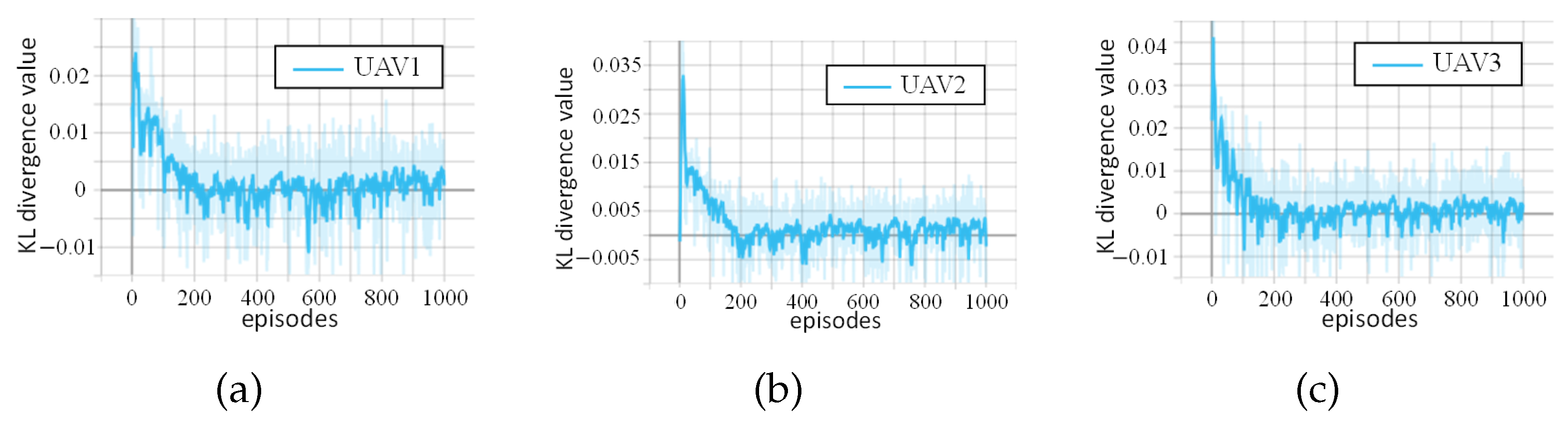
6.2. Experimental Results and Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| PPO | Proximal Policy Optimization |
| MURPPO | Multi-UAV Reconnaissance Proximal Policy Optimization |
| FFA | Firefly Algorithm |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| ABC | Artificial Bee Colony |
| IMUCS-BSAE | Improved Multi-UAV Collaborative Search Algorithm |
| based on Binary Search Algorithm | |
| MPSO | Motion-encoded Particle Swarm Optimization |
| DRL | Deep Reinforcement Learning |
| 2D | Two-Dimensional |
| MDP | Markov Decision Process |
| RSSI | Received Signal Strength Indication |
| FC | Fully Connected Layer |
| NL | Normalization Layer |
| BL | Branch Layer |
| MAA2C | Multi-Agent Advantage Actor-Critic |
| MAPPO | Multi-Agent Proximal Policy Optimization |
| KL divergence | Kullback–Leibler divergence |
References
- Meng, Y.; Qi, P.; Zhou, X.; Li, Z. Capability Analysis Method for Electromagnetic Spectrum. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China, 11–12 September 2021; pp. 739–740. [Google Scholar]
- Ye, N.; Miao, S.; Pan, J.; Xiang, Y.; Mumtaz, S. Dancing with Chains: Spaceborne Distributed Multi-User Detection under Inter-Satellite Link Constraints. IEEE J. Sel. Top. Signal Process. 2025. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Messer, H. Opportunistic Weather Sensing by Smart City Wireless Communication Networks. Sensors 2024, 24, 7901. [Google Scholar] [CrossRef] [PubMed]
- Alsarhan, A.; Al-Dubai, A.Y.; Min, G.; Zomaya, A.Y.; Bsoul, M. A New Spectrum Management Scheme for Road Safety in Smart Cities. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3496–3506. [Google Scholar] [CrossRef]
- Jasim, M.A.; Shakhatreh, H.; Siasi, N.; Sawalmeh, A.H.; Aldalbahi, A.; Al-Fuqaha, A. A Survey on Spectrum Management for Unmanned Aerial Vehicles (UAVs). IEEE Access 2022, 10, 11443–11499. [Google Scholar] [CrossRef]
- Zhou, L.; Leng, S.; Wang, Q.; Quek, T.Q.S.; Guizani, M. Cooperative Digital Twins for UAV-Based Scenarios. IEEE Commun. Mag. 2024, 62, 112–118. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned Aerial Vehicles (UAVs): Practical Aspects, Applications, Open Challenges, Security Issues, and Future Trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Xu, C.; Liao, X.; Tan, J.; Ye, H.; Lu, H. Recent Research Progress of Unmanned Aerial Vehicle Regulation Policies and Technologies in Urban Low Altitude. IEEE Access 2020, 8, 74175–74194. [Google Scholar] [CrossRef]
- Kang, H.; Joung, J.; Kim, J.; Kang, J.; Cho, Y.S. Protect Your Sky: A Survey of Counter Unmanned Aerial Vehicle Systems. IEEE Access 2020, 8, 168671–168710. [Google Scholar] [CrossRef]
- Kang, B.; Ye, N.; An, J. Achieving Positive Rate of Covert Communications Covered by Randomly Activated Overt Users. IEEE Trans. Inf. Forensics Secur. 2025, 20, 2480–2495. [Google Scholar] [CrossRef]
- Li, J.; Yang, L.; Wu, Q.; Lei, X.; Zhou, F.; Shu, F.; Mu, X.; Liu, Y.; Fan, P. Active RIS-Aided NOMA-Enabled Space-Air-Ground Integrated Networks with Cognitive Radio. IEEE J. Sel. Areas Commun. 2025, 43, 314–333. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, W. An Efficient UAV Localization Technique Based on Particle Swarm Optimization. IEEE Trans. Veh. Technol. 2022, 71, 9544–9557. [Google Scholar] [CrossRef]
- Abdelhakim, A. Heuristic techniques for maximum likelihood localization of radioactive sources via a sensor network. Nucl. Sci. Tech. 2023, 34, 127. [Google Scholar] [CrossRef]
- Yu, Y.; Lee, S. Efficient Multi-UAV Path Planning for Collaborative Area Search Operations. Appl. Sci. 2023, 13, 8728. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Motion-encoded Particle Swarm Optimization for Moving Target Search Using UAVs. Appl. Soft Comput. 2020, 97, 106705. [Google Scholar] [CrossRef]
- Chen, J.X. The Evolution of Computing: AlphaGo. Comput. Sci. Eng. 2016, 18, 4–7. [Google Scholar] [CrossRef]
- Wu, T.; He, S.; Liu, J.; Sun, S.; Liu, K.; Han, Q.-L.; Tang, Y. A Brief Overview of ChatGPT: The History, Status Quo and Potential Future Development. IEEE/CAA J. Autom. Sin. 2023, 10, 1122–1136. [Google Scholar] [CrossRef]
- Kortli, Y.; Jridi, M.; Al Falou, A.; Atri, M. Face Recognition Systems: A Survey. Sensors 2020, 20, 342. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Y.; Liu, J.; Liu, C. Multi-UAV Cooperative Task Offloading and Resource Allocation in 5G Advanced and Beyond. IEEE Trans. Wirel. Commun. 2024, 23, 347–359. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, X.; Wang, J.; Liu, J.; Benslimane, A. Intelligent Task Offloading and Resource Allocation in Digital Twin Based Aerial Computing Networks. IEEE J. Sel. Areas Commun. 2023, 41, 3095–3110. [Google Scholar] [CrossRef]
- Guo, H.; Chen, X.; Zhou, X.; Liu, J. Trusted and Efficient Task Offloading in Vehicular Edge Computing Networks. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 2370–2382. [Google Scholar] [CrossRef]
- Abdelhakim, A. Machine learning for localization of radioactive sources via a distributed sensor network. Soft Comput. 2023, 27, 10493–10508. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, T.; Zhao, Z.; Wang, Y.; Liu, F. An Intelligent Strategy Decision Method for Collaborative Jamming Based on Hierarchical Multi-Agent Reinforcement Learning. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 1467–1480. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Y.; Li, D.; Shi, J.; Li, X.; Gao, L.; Yu, L.; Han, G.; Wu, J. An Adaptive Conversion Speed Q-Learning Algorithm for Search and Rescue UAV Path Planning in Unknown Environments. IEEE Trans. Veh. Technol. 2023, 72, 15391–15404. [Google Scholar] [CrossRef]
- Moon, J.; Papaioannou, S.; Laoudias, C.; Kolios, P.; Kim, S. Deep Reinforcement Learning Multi-UAV Trajectory Control for Target Tracking. IEEE Internet Things J. 2021, 8, 15441–15455. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Y.; Fu, S.; Liu, X. Reduce UAV Coverage Energy Consumption through Actor-Critic Algorithm. In Proceedings of the 2019 15th International Conference on Mobile Ad-Hoc and Sensor Networks (MSN), Shenzhen, China, 11–13 December 2019; pp. 332–337. [Google Scholar]
- Hou, Y.; Zhao, J.; Zhang, R.; Cheng, X.; Yang, L. UAV Swarm Cooperative Target Search: A Multi-Agent Reinforcement Learning Approach. IEEE Trans. Intell. Veh. 2024, 9, 568–578. [Google Scholar] [CrossRef]
- Alagha, R.; Mizouni, R.; Singh, S.; Bentahar, J.; Otrok, H. Adaptive target localization under uncertainty using Multi-Agent Deep Reinforcement Learning with knowledge transfer. Internet Things 2025, 29, 101447. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Wang, Y.; Huang, W.; Yan, B.; Li, Y. Three-body cooperative active defense guidance law with overload constraints: A small speed ratio perspective. Chin. J. Aeronaut. 2025, 38, 103171. [Google Scholar] [CrossRef]
- Katircioglu, O.; Isel, H.; Ceylan, O.; Taraktas, F.; Yagci, H.B. Comparing Ray Tracing, Free Space Path Loss and Logarithmic Distance Path Loss Models in Success of Indoor Localization with RSSI. In Proceedings of the 19th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–24 November 2011; pp. 313–316. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1999; Volume 12. [Google Scholar]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2015, arXiv:1506.02438. [Google Scholar]
| Reference | Main Contributions | Key Limitations | Proposed Solutions |
|---|---|---|---|
| [24] |
|
|
|
| [25] |
|
|
|
| [26] |
|
|
|
| [27] |
|
|
|
| [28] |
|
|
|
| [29] |
|
|
|
| Symbol | Definition |
|---|---|
| Position information table | |
| Sensing information table | |
| Radiation propagation table | |
| Received radiation signal power | |
| Transmitted radiation signal power | |
| Directional sensing matrix of UAV i | |
| Sensing information table for UAV i | |
| Distance from UAV i to radiation source at time t | |
| Position coordinates of UAV i at time t | |
| Direction angle of UAV i at time t | |
| Speed of UAV i at time t | |
| Sensor heading angle of UAV i at time t | |
| M | Set of valid positions within map boundaries |
| Set of UAVs with valid measurements at time t | |
| Indicator function for successful localization at time t | |
| Normalized advantage function of UAV i at time t | |
| Clipped policy loss for movement actions of UAV i | |
| Clipped policy loss for scanning actions of UAV i | |
| Entropy of movement policy of UAV i | |
| Entropy of scanning policy of UAV i | |
| Overall MURPPO objective function of UAV i |
| System Parameters | Numerical Settings | Description |
|---|---|---|
| 1000 × 1000 () | map size | |
| the maximum angle change per step | ||
| 1 (m/step) | the maximum speed change per step | |
| m | 3 | number of red UAVs |
| n | 1 | number of blue UAVs |
| 1000 | number of training episodes | |
| T | 100 | time steps per round |
| 1.0 | greedy factor | |
| 0.1 | minimum greedy factor | |
| 0.99 | greedy factor decay rate | |
| 0.0001 | actor learning rate | |
| 0.0005 | critic learning rate | |
| 0.2 | clip ratio | |
| 200 (m) | maximum detection distance | |
| 0.9 | discount factor | |
| 0.5 | perception reward | |
| 0.5 | first perception reward | |
| 0.5 | three-point localization reward | |
| −0.2 | penalty for non-detection | |
| −0.2 | penalty for inconsistent action after detection | |
| −0.2 | collision penalty | |
| D | 1 (m) | safe distance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, Z.; Fan, D.; Hou, C.; Zhang, Y.; Hou, T.; Zou, X.; Zhao, J. Distributed Decision Making for Electromagnetic Radiation Source Localization Using Multi-Agent Deep Reinforcement Learning. Drones 2025, 9, 216. https://doi.org/10.3390/drones9030216
Chen J, Zhang Z, Fan D, Hou C, Zhang Y, Hou T, Zou X, Zhao J. Distributed Decision Making for Electromagnetic Radiation Source Localization Using Multi-Agent Deep Reinforcement Learning. Drones. 2025; 9(3):216. https://doi.org/10.3390/drones9030216
Chicago/Turabian StyleChen, Jiteng, Zehui Zhang, Dan Fan, Chaoqun Hou, Yue Zhang, Teng Hou, Xiangni Zou, and Jun Zhao. 2025. "Distributed Decision Making for Electromagnetic Radiation Source Localization Using Multi-Agent Deep Reinforcement Learning" Drones 9, no. 3: 216. https://doi.org/10.3390/drones9030216
APA StyleChen, J., Zhang, Z., Fan, D., Hou, C., Zhang, Y., Hou, T., Zou, X., & Zhao, J. (2025). Distributed Decision Making for Electromagnetic Radiation Source Localization Using Multi-Agent Deep Reinforcement Learning. Drones, 9(3), 216. https://doi.org/10.3390/drones9030216






