Enhancing Physical-Layer Security in UAV-Assisted Communications: A UAV-Mounted Reconfigurable Intelligent Surface Scheme for Secrecy Rate Optimization
Abstract
1. Introduction
- In this paper, we propose a flexible UAV-mounted reconfigurable intelligent surface secure design and attempt to investigate the assistance of the UAV-mounted reconfigurable intelligent surface in physical layer security. Specifically, we study a secure communication system consisting of a base station, a legitimate ground user, several passive eavesdroppers, and the dynamic UAV-mounted RIS. We jointly optimize the UAV trajectory, the RIS phase shifter, and transmit power, aiming to improve the average achievable secrecy rate in the multiple-eavesdroppers scenario.
- In order to maximize the average achievable secrecy rate, we formulate a joint RIS phase shifter, UAV trajectories, and base station transmit power optimization problem. To tackle the non-convexity of the formulated problem, we propose an iterative algorithm based on block coordinate descent and successive convex optimization techniques. The algorithm enables us to find an efficient solution to the optimization problem.
- To better present the superiority of our proposed secure design, we consider the conditions without the secure design, the proposed design in a static mode, and heuristic mode. Simulation results demonstrate that our proposed dynamic secure design outperforms other schemes in different channel and deployed height conditions in meliorating the secrecy rate. Besides, the numerical results also confirm the potential of using the proposed dynamic UAV-mounted RIS secure design to improve secrecy performance and save base station power.
2. System Model and Secure Design
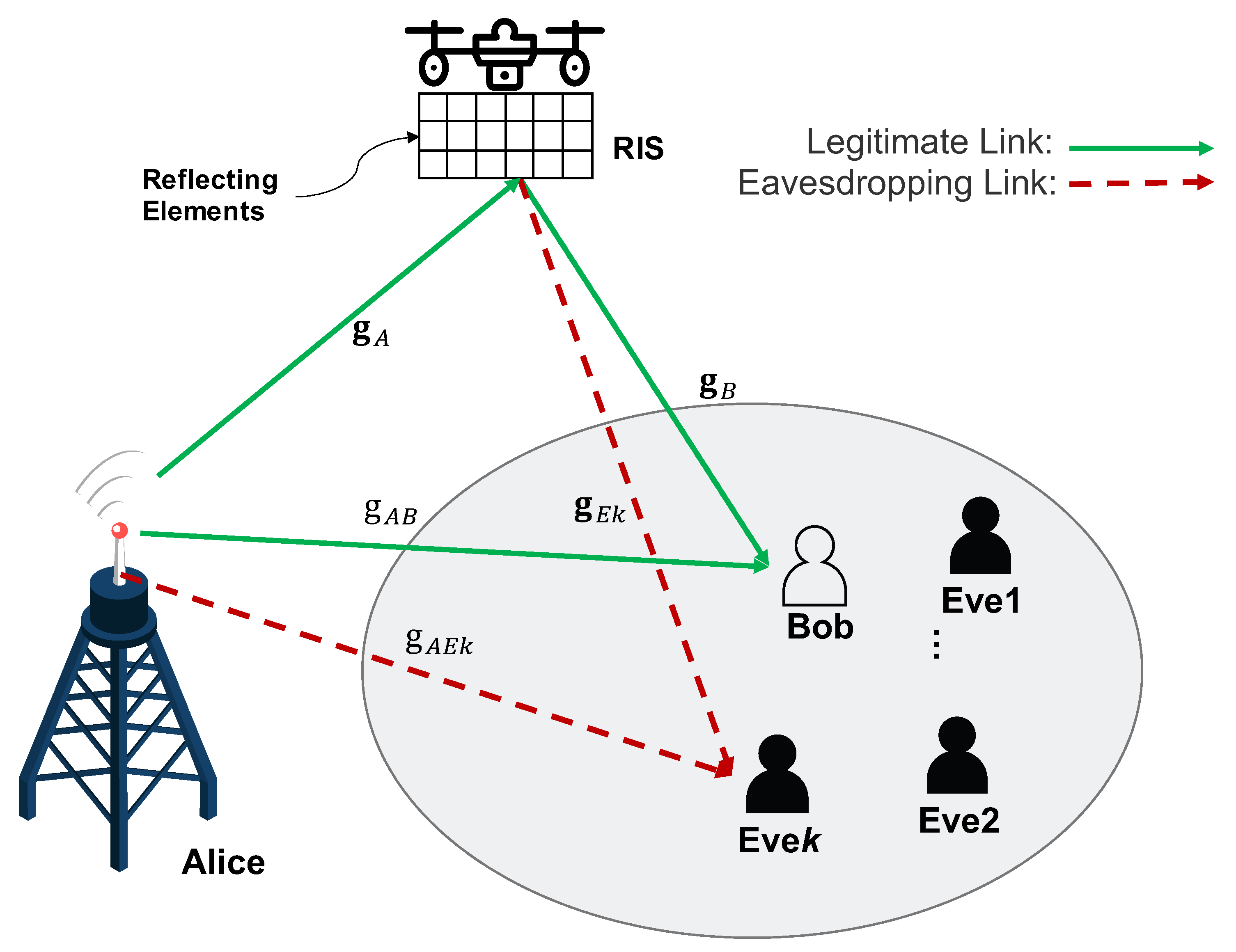
2.1. System Model
2.2. Dynamic UAV-RIS Secure Design
3. Problem Formulation
4. Proposed Algorithm
4.1. Phase Shifter Optimization
4.2. Trajectory Optimization
4.3. Transmit Power Optimization
4.4. Overall Algorithm
| Algorithm 1 Proposed Algorithm for Solving () |
Initialize: Set tolerance . Set initial variables , , , , , , , and iteration number . Use Equation (17) to get with . Solve (2) to get . Repeat: 1. Set . 2. Update with given through solving (). 3. With given , obtain by using Equation (17). 4. Update through solving () with given . 5. Calculate with given , , by solving (). Until: |
5. Numerical Results
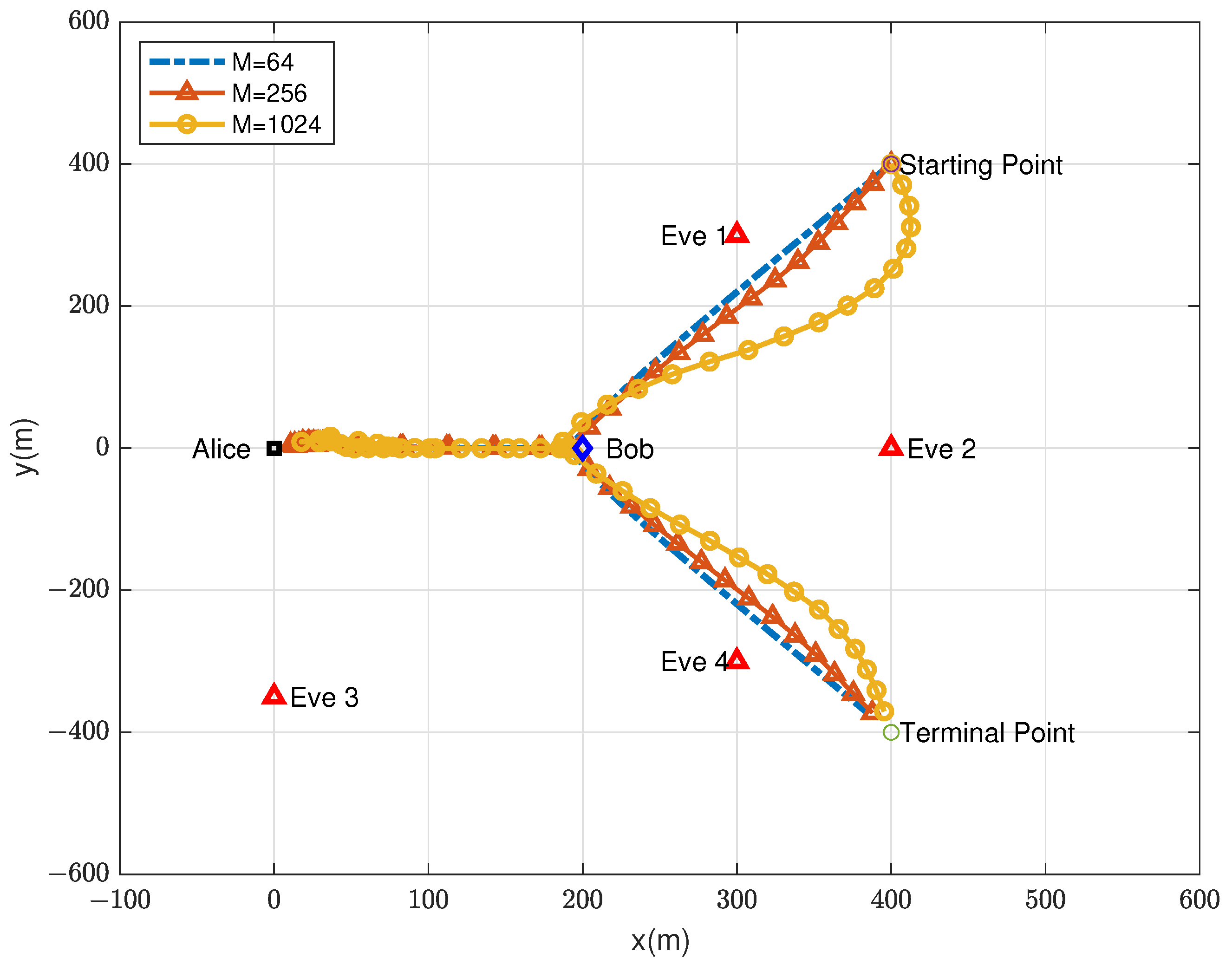
5.1. UAV Trajectories with Different RIS Elements
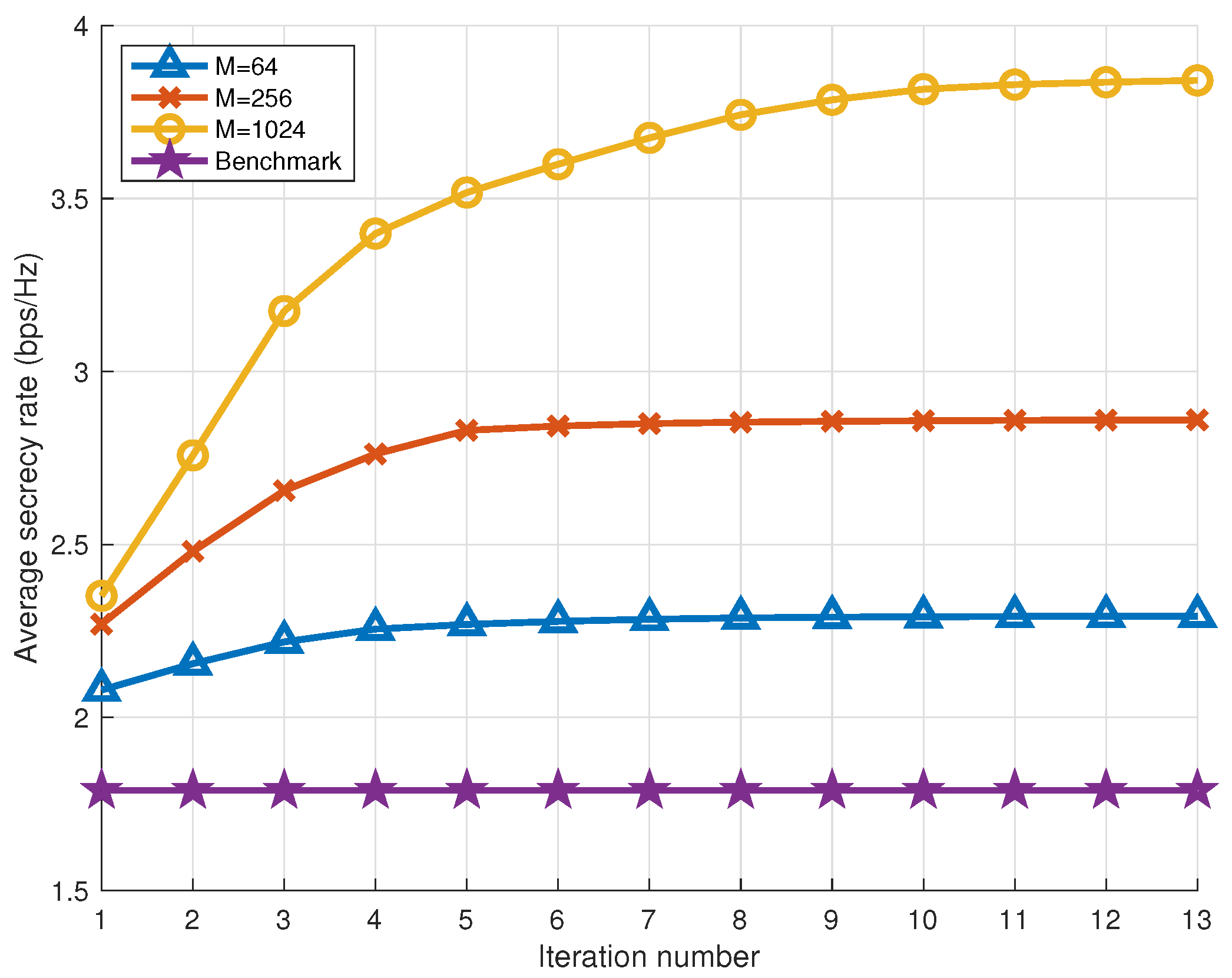
5.2. Convergence of the Proposed Algorithm
5.3. The Transmit Power P Throughout the Optimization Process
5.4. Average Secrecy Rate with Different Average Transmit Power
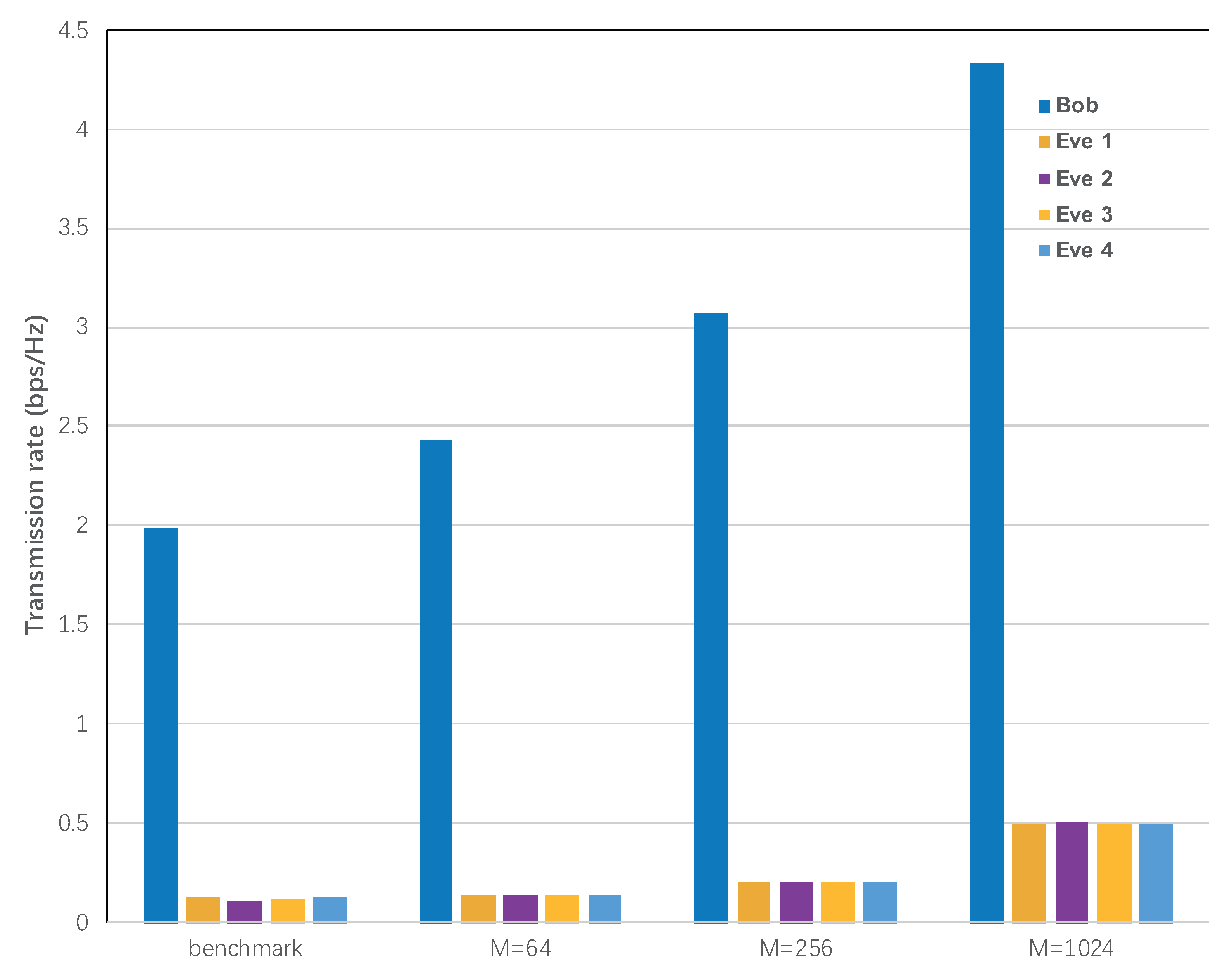
5.5. Transmission Rate with Different Number of RIS Elements
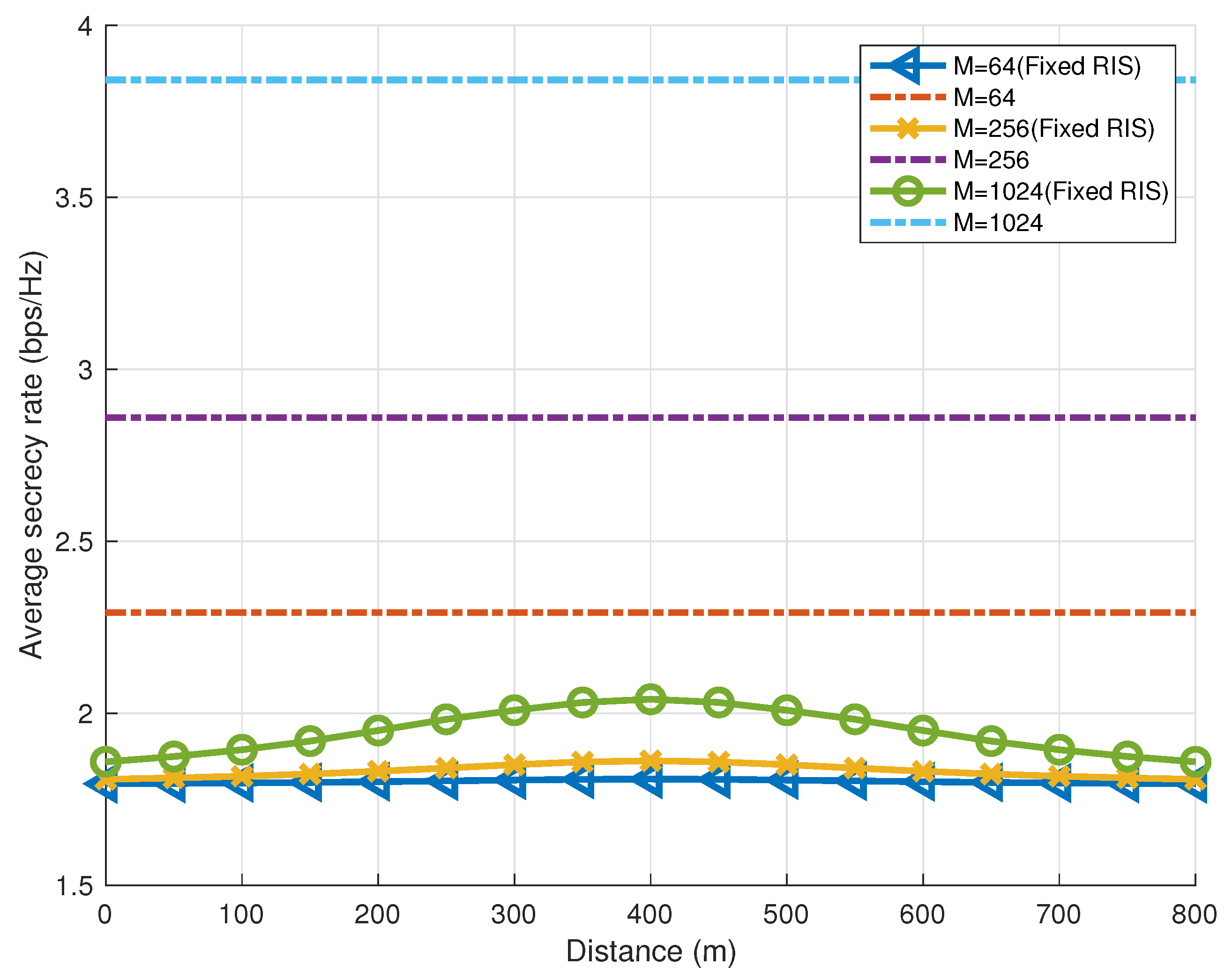
5.6. Comparisons of UAV-Mounted Mobile RIS and Static RIS
5.7. The Influence of Pathloss Exponent and UAV Deployment Height
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of Important Issues in UAV Communication Networks. IEEE Commun. Surv. Tutor. 2016, 18, 1123–1152. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV Communications for 5G and Beyond: Recent Advances and Future Trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Yan, C.; Fu, L.; Zhang, J.; Wang, J. A Comprehensive Survey on UAV Communication Channel Modeling. IEEE Access 2019, 7, 107769–107792. [Google Scholar] [CrossRef]
- Wu, B.; Guo, D.; Zhang, B.; Zhang, X.; Wang, H.; Wang, H.; Jiang, H. Completion time minimization for UAV enabled data collection with communication link constrained. IET Commun. 2022, 16, 1025–1040. [Google Scholar] [CrossRef]
- Liu, Y.; Han, F.; Zhao, S. Flexible and Reliable Multiuser SWIPT IoT Network Enhanced by UAV-Mounted Intelligent Reflecting Surface. IEEE Trans. Reliab. 2022, 71, 1092–1103. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, S.; Han, F.; Chai, M.; Jiang, H.; Zhang, H. Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks. Remote Sens. 2023, 15, 5126. [Google Scholar] [CrossRef]
- Mao, B.; Liu, J.; Wu, Y.; Kato, N. Security and Privacy on 6G Network Edge: A Survey. IEEE Commun. Surv. Tutor. 2023, 25, 1095–1127. [Google Scholar] [CrossRef]
- Lee, S.B.; Ahn, G.S.; Campbell, A. Improving UDP and TCP performance in mobile ad hoc networks with INSIGNIA. IEEE Commun. Mag. 2001, 39, 156–165. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.H.; Wang, L. Physical Layer Security for Next Generation Wireless Networks: Theories, Technologies, and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 347–376. [Google Scholar] [CrossRef]
- Jiang, H.; Xiong, B.; Zhang, H.; Basar, E. Physics-Based 3D End-to-End Modeling for Double-RIS Assisted Non-Stationary UAV-to-Ground Communication Channels. IEEE Trans. Commun. 2023, 71, 4247–4261. [Google Scholar] [CrossRef]
- Wang, H.M.; Zhang, X.; Jiang, J.C. UAV-Involved Wireless Physical-Layer Secure Communications: Overview and Research Directions. IEEE Wirel. Commun. 2019, 26, 32–39. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV Communications via Joint Trajectory and Power Control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Z.; Mei, W.; Fang, J. Improving Physical Layer Security Using UAV-Enabled Mobile Relaying. IEEE Wirel. Commun. Lett. 2017, 6, 310–313. [Google Scholar] [CrossRef]
- Nuradha, T.; Hemachandra, K.T.; Samarasinghe, T.; Atapattu, S. Physical-Layer Security for Untrusted UAV-Assisted Full-Duplex Wireless Networks. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Big Island, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Rao, B.; Hu, J.; Al-Nahari, A.; Yang, K.; Jäntti, R. On the Physical Layer Security of UAV-Aided Backscatter Communications. IEEE Wirel. Commun. Lett. 2024, 13, 274–278. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Zheng, Z.; Lin, R.; Wu, L.; Shu, F. Physical Layer Security Enhancement in UAV-Assisted Cooperative Jamming for Cognitive Radio Networks: A MAPPO-LSTM Deep Reinforcement Learning Approach. IEEE Trans. Veh. Technol. 2025, 74, 4713–4727. [Google Scholar] [CrossRef]
- Tang, Z.; Hou, T.; Liu, Y.; Zhang, J.; Zhong, C. A Novel Design of RIS for Enhancing the Physical Layer Security for RIS-Aided NOMA Networks. IEEE Wirel. Commun. Lett. 2021, 10, 2398–2401. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, R.; Han, Z. Passive Beamforming for Practical RIS-Assisted Communication Systems with Non-Ideal Hardware. IEEE Trans. Veh. Technol. 2024, 73, 17743–17748. [Google Scholar] [CrossRef]
- Tang, X.; Wang, D.; Zhang, R.; Chu, Z.; Han, Z. Jamming Mitigation via Aerial Reconfigurable Intelligent Surface: Passive Beamforming and Deployment Optimization. IEEE Trans. Veh. Technol. 2021, 70, 6232–6237. [Google Scholar] [CrossRef]
- Guo, H.; Liang, Y.C.; Xiao, S. Intelligent Reflecting Surface Configuration with Historical Channel Observations. IEEE Wirel. Commun. Lett. 2020, 9, 1821–1824. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Shen, H.; Xu, W.; Gong, S.; He, Z.; Zhao, C. Secrecy Rate Maximization for Intelligent Reflecting Surface Assisted Multi-Antenna Communications. IEEE Commun. Lett. 2019, 23, 1488–1492. [Google Scholar] [CrossRef]
- Chu, Z.; Hao, W.; Xiao, P.; Shi, J. Intelligent Reflecting Surface Aided Multi-Antenna Secure Transmission. IEEE Wirel. Commun. Lett. 2020, 9, 108–112. [Google Scholar] [CrossRef]
- Arzykulov, S.; Celik, A.; Nauryzbayev, G.; Eltawil, A.M. Artificial Noise and RIS-Aided Physical Layer Security: Optimal RIS Partitioning and Power Control. IEEE Wirel. Commun. Lett. 2023, 12, 992–996. [Google Scholar] [CrossRef]
- Khoshafa, M.H.; Ngatched, T.M.N.; Ahmed, M.H. Reconfigurable Intelligent Surfaces-Aided Physical Layer Security Enhancement in D2D Underlay Communications. IEEE Commun. Lett. 2021, 25, 1443–1447. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, S.; Shen, Y.; Jiang, X.; Shiratori, N. Enhancing the Physical Layer Security of Two-Way Relay Systems with RIS and Beamforming. IEEE Trans. Inf. Forensics Secur. 2024, 19, 5696–5711. [Google Scholar] [CrossRef]
- Pogaku, A.C.; Do, D.T.; Lee, B.M.; Nguyen, N.D. UAV-Assisted RIS for Future Wireless Communications: A Survey on Optimization and Performance Analysis. IEEE Access 2022, 10, 16320–16336. [Google Scholar] [CrossRef]
- Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. A New Wireless Communication Paradigm through Software-Controlled Metasurfaces. IEEE Commun. Mag. 2018, 56, 162–169. [Google Scholar] [CrossRef]
- Li, S.; Duo, B.; Renzo, M.D.; Tao, M.; Yuan, X. Robust Secure UAV Communications with the Aid of Reconfigurable Intelligent Surfaces. IEEE Trans. Wirel. Commun. 2021, 20, 6402–6417. [Google Scholar] [CrossRef]
- Shang, Y.; Peng, Y.; Ye, R.; Lee, J. RIS-Assisted Secure UAV Communication Scheme Against Active Jamming and Passive Eavesdropping. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16953–16963. [Google Scholar] [CrossRef]
- Qin, C.; Niu, M.; Zhang, P.; He, J. Exploiting Cascaded Channel Signature for PHY-Layer Authentication in RIS-Enabled UAV Communication Systems. Drones 2024, 8, 358. [Google Scholar] [CrossRef]
- Diao, D.; Wang, B.; Cao, K.; Zheng, B.; Weng, J.; Chen, J. Secure RIS Deployment Strategies for Wireless-Powered Multi-UAV Communication. IEEE Internet Things J. 2024, 11, 18154–18166. [Google Scholar] [CrossRef]
- Bithas, P.S.; Ropokis, G.A.; Karagiannidis, G.K.; Nistazakis, H.E. UAV-Assisted Communications with RIS: A Shadowing-Based Stochastic Analysis. IEEE Trans. Veh. Technol. 2024, 73, 10000–10010. [Google Scholar] [CrossRef]
- Mughal, U.A.; Alkhrijah, Y.; Almadhor, A.; Yuen, C. Deep Learning for Secure UAV-Assisted RIS Communication Networks. IEEE Internet Things Mag. 2024, 7, 38–44. [Google Scholar] [CrossRef]
- Yang, H.; Liu, S.; Xiao, L.; Zhang, Y.; Xiong, Z.; Zhuang, W. Learning-Based Reliable and Secure Transmission for UAV-RIS-Assisted Communication Systems. IEEE Trans. Wirel. Commun. 2024, 23, 6954–6967. [Google Scholar] [CrossRef]
- Qian, P.; Zhang, Y.; Yan, X.; Chen, Y.; Sun, Y. A Robust Scheme for RIS-Assisted UAV Secure Communication in IoT. Electronics 2023, 12, 2507. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Fang, S.; Chen, G.; Li, Y. Joint Optimization for Secure Intelligent Reflecting Surface Assisted UAV Networks. IEEE Wirel. Commun. Lett. 2021, 10, 276–280. [Google Scholar] [CrossRef]
- Hu, E.L.; Kwok, J.T. Scalable Nonparametric Low-Rank Kernel Learning Using Block Coordinate Descent. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1927–1938. [Google Scholar] [CrossRef]
- Gopala, P.K.; Lai, L.; El Gamal, H. On the Secrecy Capacity of Fading Channels. IEEE Trans. Inf. Theory 2008, 54, 4687–4698. [Google Scholar] [CrossRef]



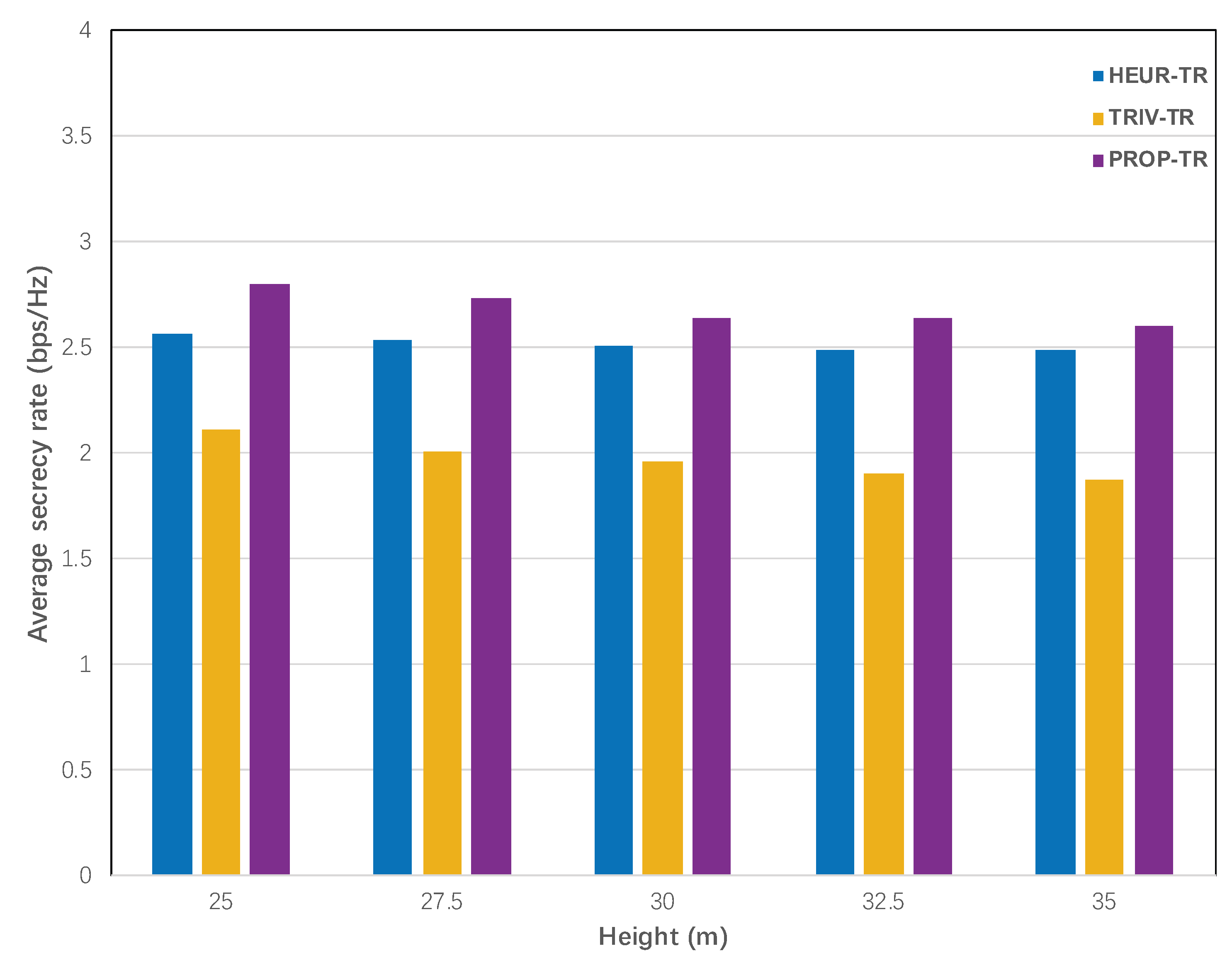
| Parameters | Values |
|---|---|
| Height of the UAV | 40 m |
| Height of the Alice | 20 m |
| Average transmit power | 10 mW |
| Peak transmit power | 40 mW |
| Tolerance | |
| Reference channel gain | −20 dB |
| AWGN power | −80 dBm |
| Defaule UAV flight period T | 150 s |
| Element separation distance at the RIS | |
| Pathloss exponent of RIS and Alice/Bob/Eves | 2.5 |
| Path loss exponent of AB and AE | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, M.; Liu, Y.; Zhao, S.; Deng, H. Enhancing Physical-Layer Security in UAV-Assisted Communications: A UAV-Mounted Reconfigurable Intelligent Surface Scheme for Secrecy Rate Optimization. Drones 2025, 9, 208. https://doi.org/10.3390/drones9030208
Chai M, Liu Y, Zhao S, Deng H. Enhancing Physical-Layer Security in UAV-Assisted Communications: A UAV-Mounted Reconfigurable Intelligent Surface Scheme for Secrecy Rate Optimization. Drones. 2025; 9(3):208. https://doi.org/10.3390/drones9030208
Chicago/Turabian StyleChai, Mengqiu, Yuan Liu, Shengjie Zhao, and Hao Deng. 2025. "Enhancing Physical-Layer Security in UAV-Assisted Communications: A UAV-Mounted Reconfigurable Intelligent Surface Scheme for Secrecy Rate Optimization" Drones 9, no. 3: 208. https://doi.org/10.3390/drones9030208
APA StyleChai, M., Liu, Y., Zhao, S., & Deng, H. (2025). Enhancing Physical-Layer Security in UAV-Assisted Communications: A UAV-Mounted Reconfigurable Intelligent Surface Scheme for Secrecy Rate Optimization. Drones, 9(3), 208. https://doi.org/10.3390/drones9030208






