Mutual Cooperation System for Task Execution Between Ground Robots and Drones Using Behavior Tree-Based Action Planning and Dynamic Occupancy Grid Mapping †
Abstract
1. Introduction
2. Related Work
2.1. Cooperative Systems with Multiple Robots Such as Drones and Ground Robots
2.2. Action Planner
3. Overview of BT-Based Multi-Robot Interaction System
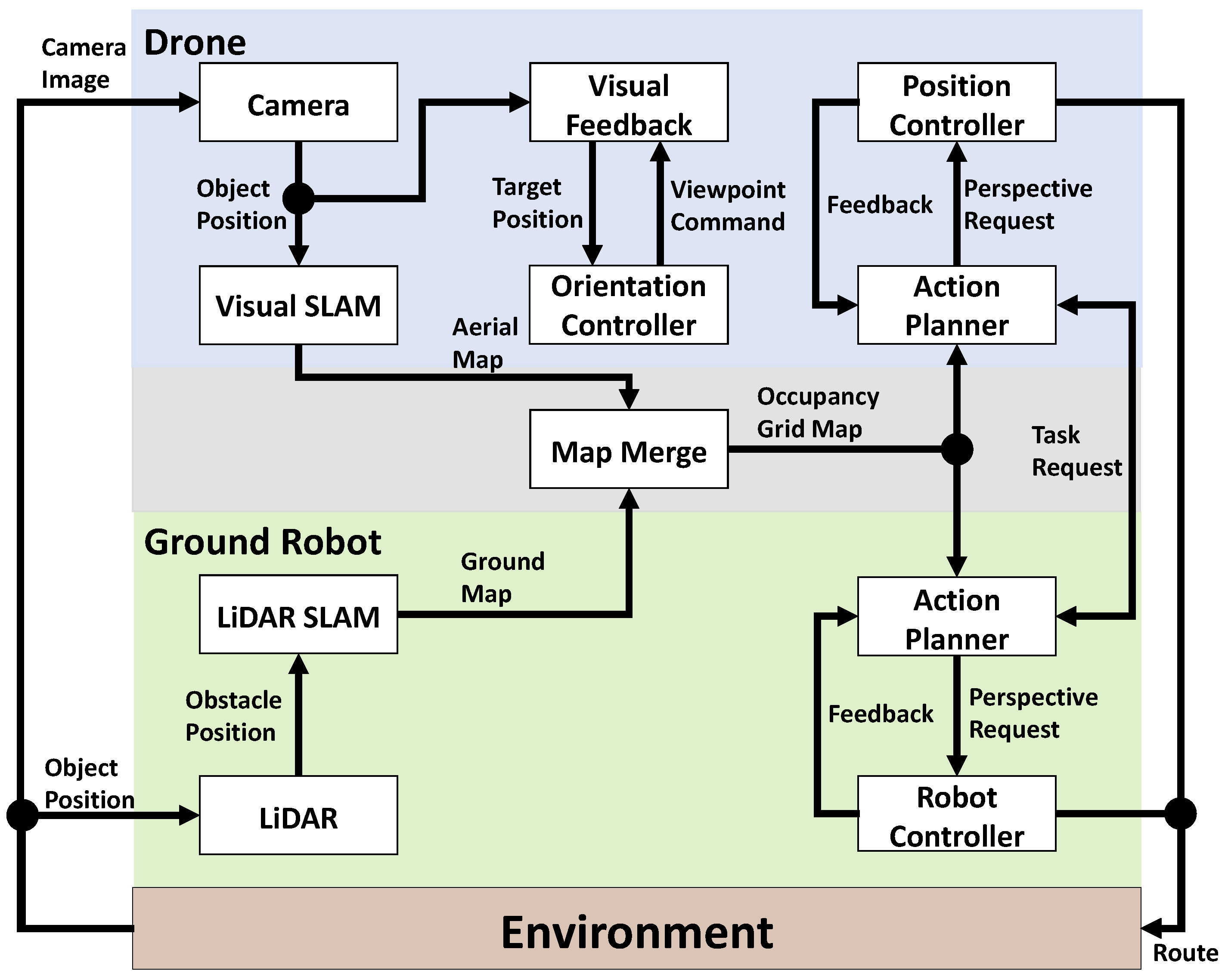
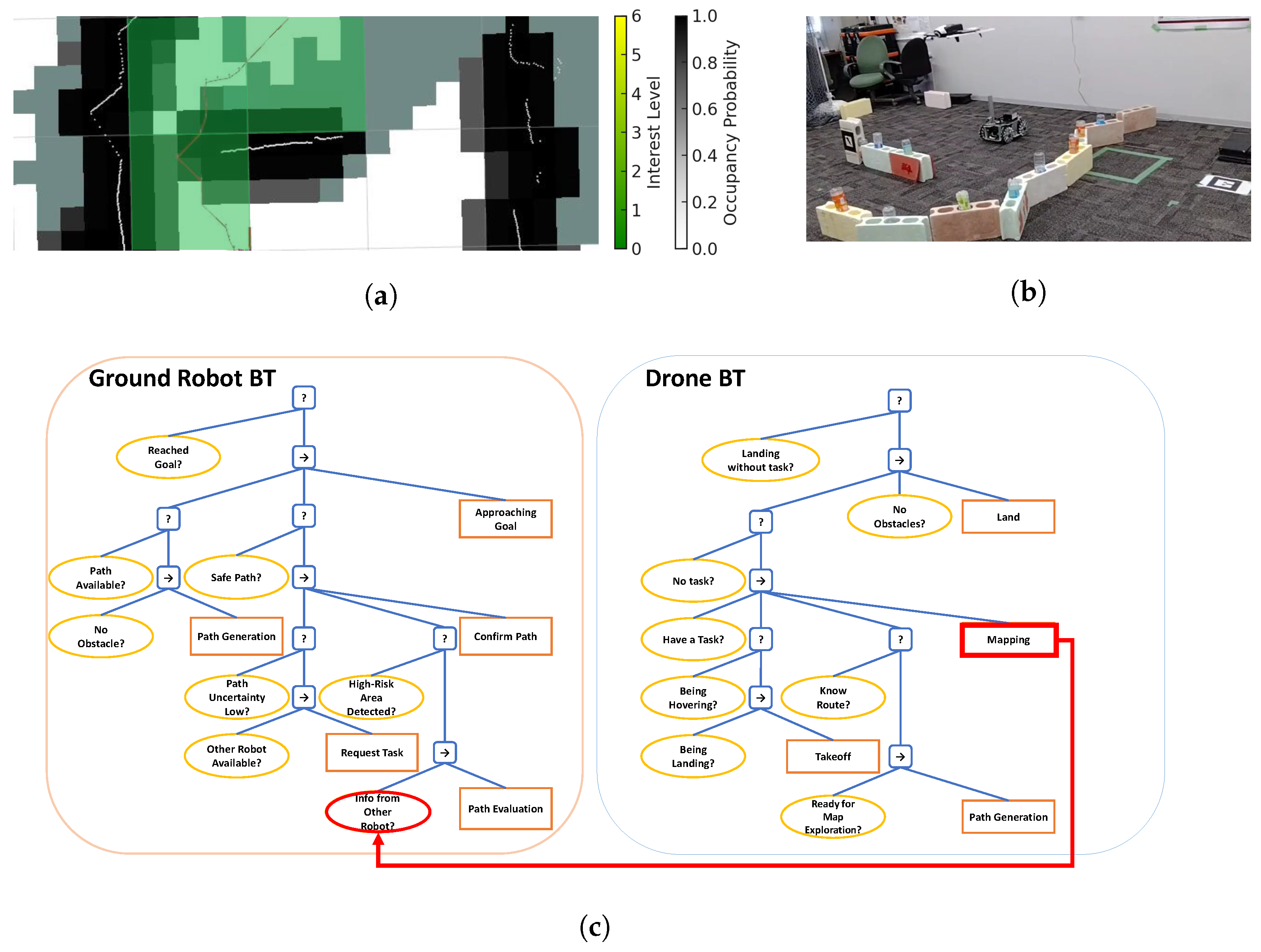
3.1. System Architecture for Coordinated Robot Task Execution
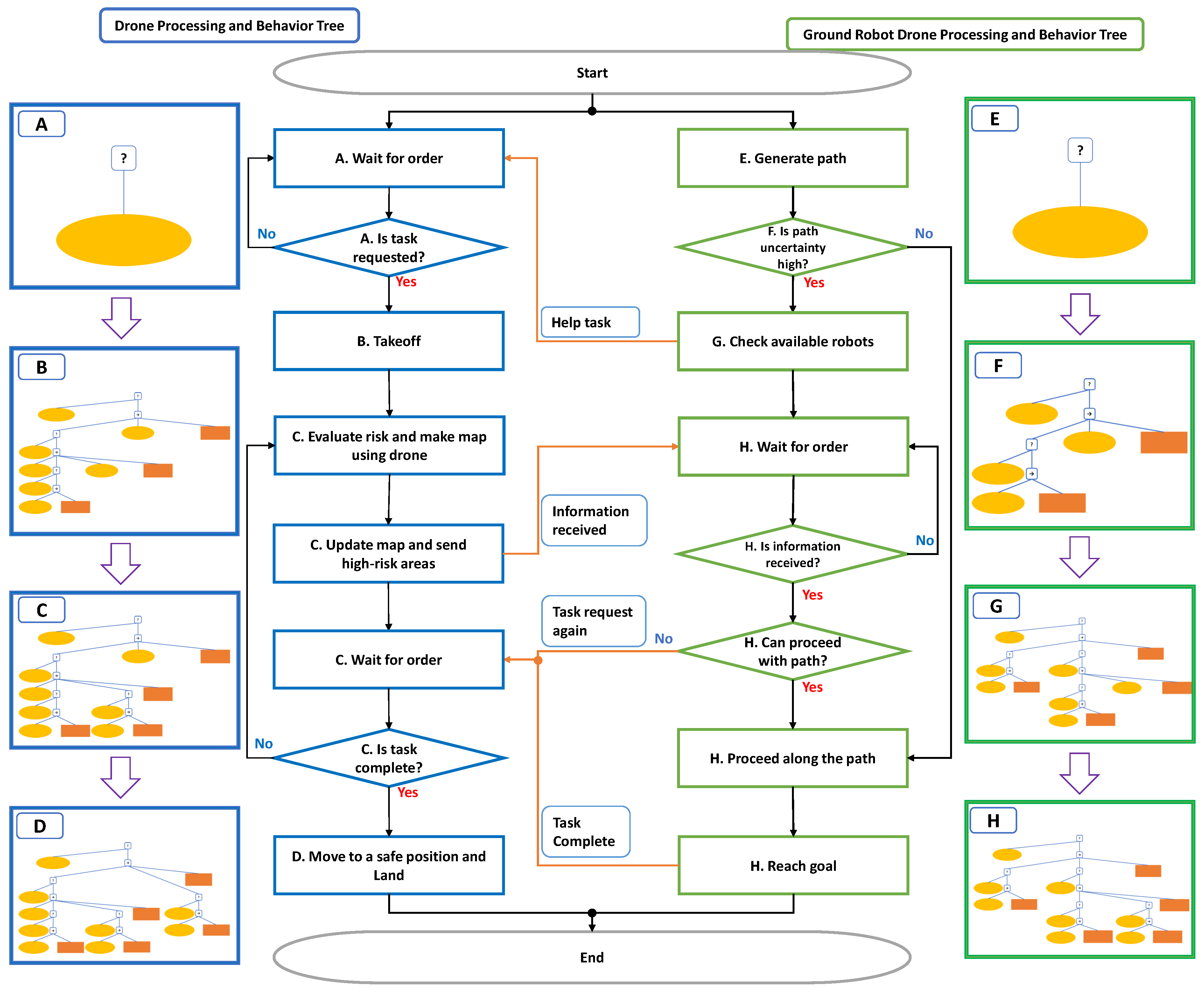
3.2. Flowchart of Coordinated Robot Tasks and Detailed Operation of Each Robot
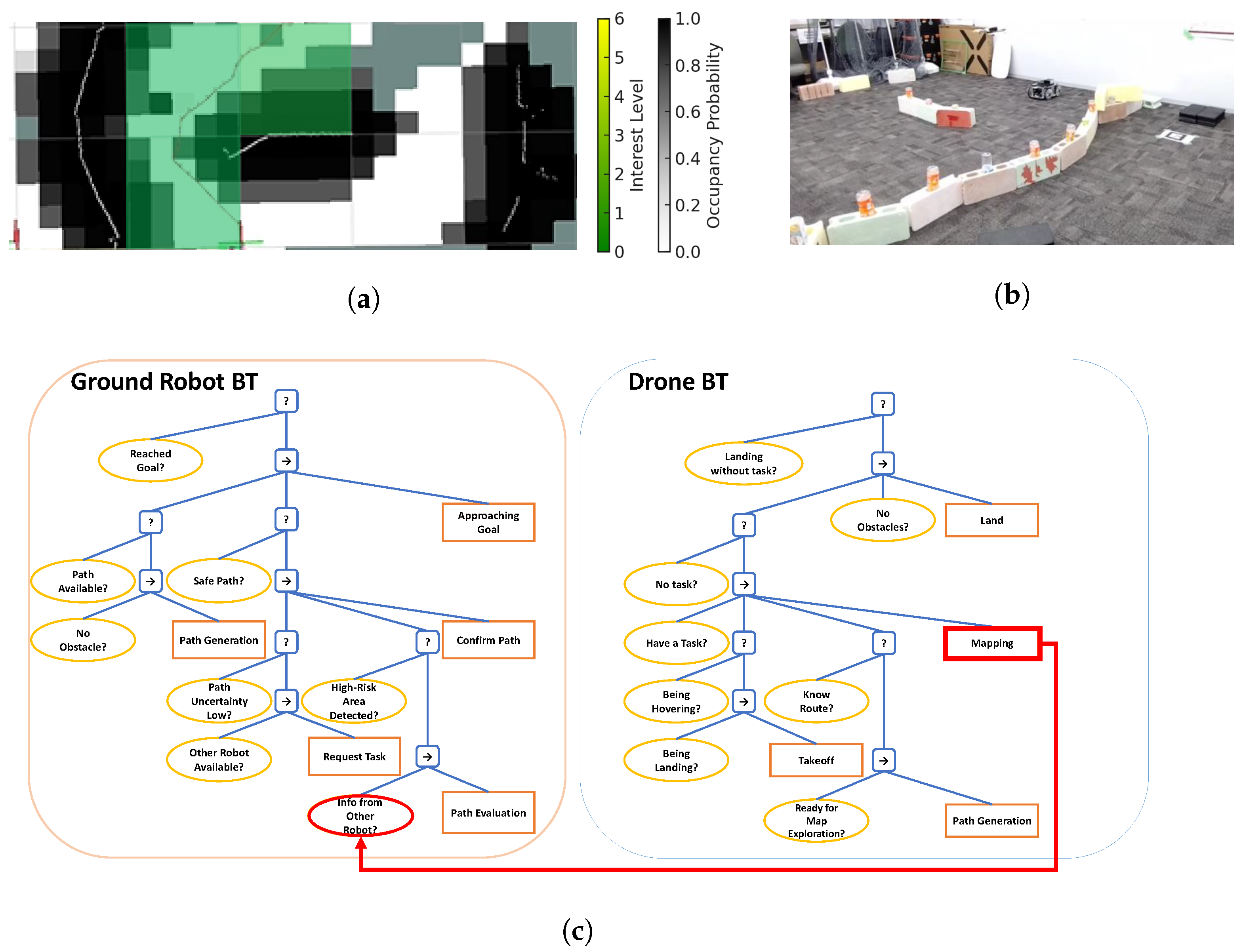
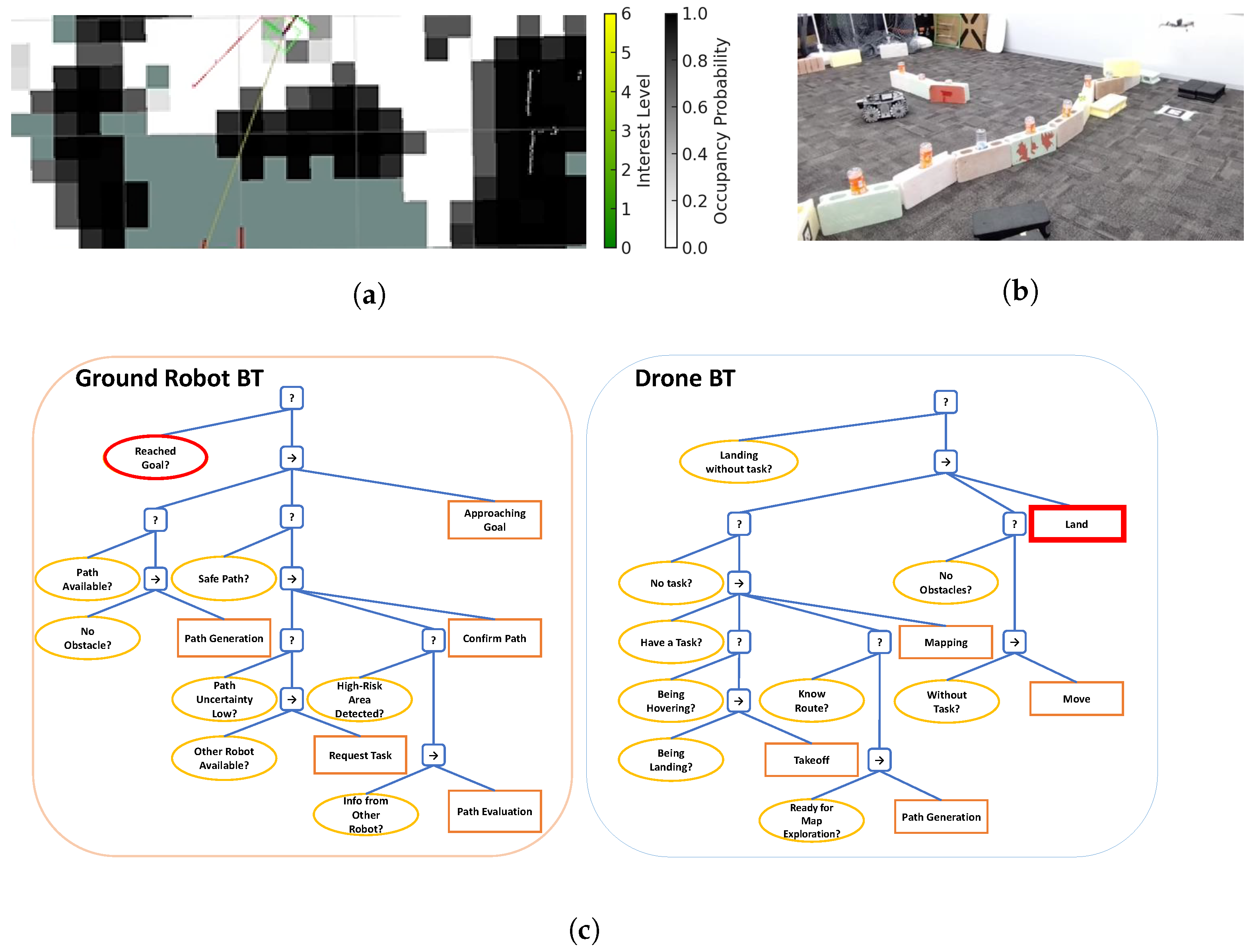
3.2.1. Ground Robot Operations
3.2.2. Drone Operations
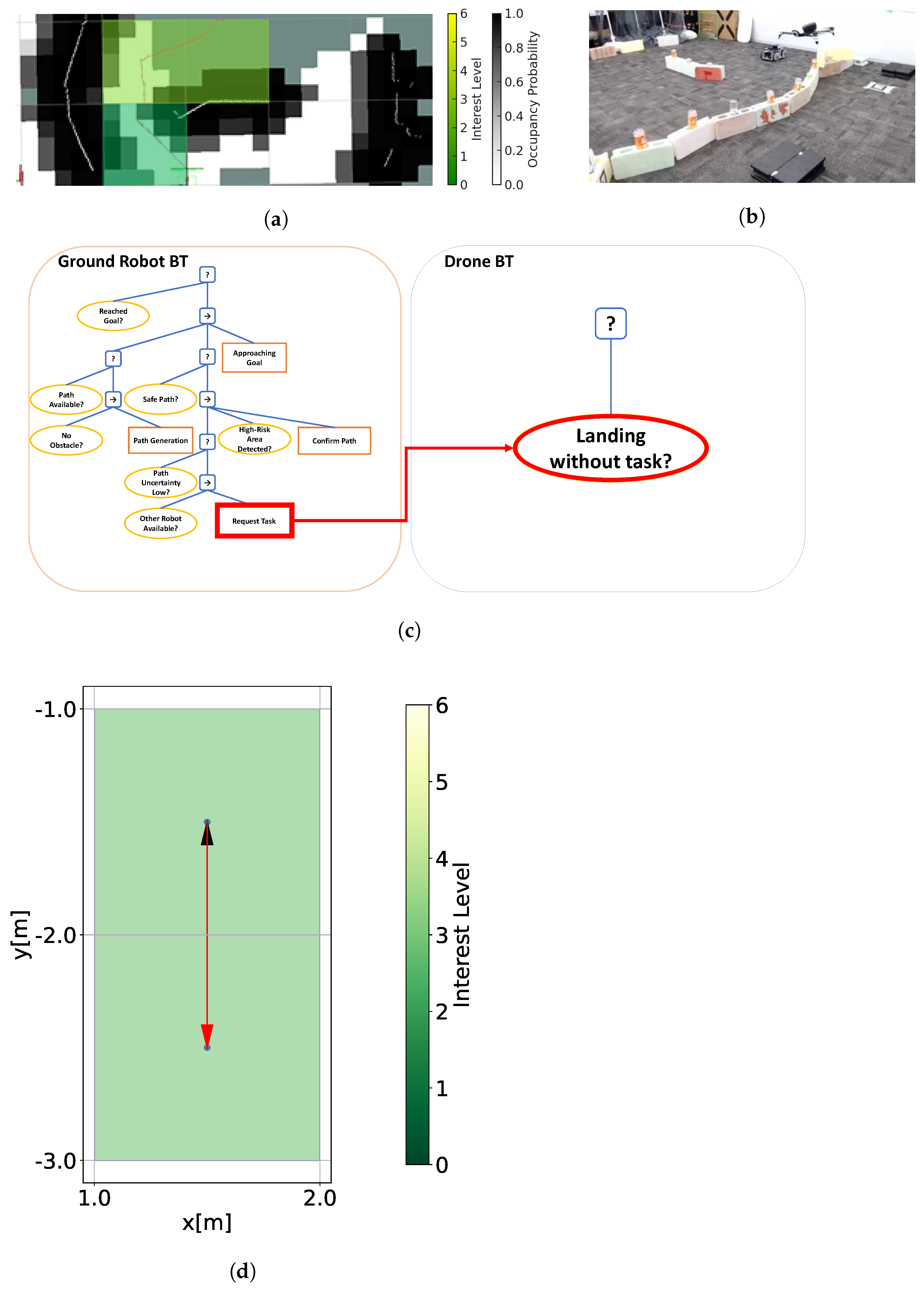
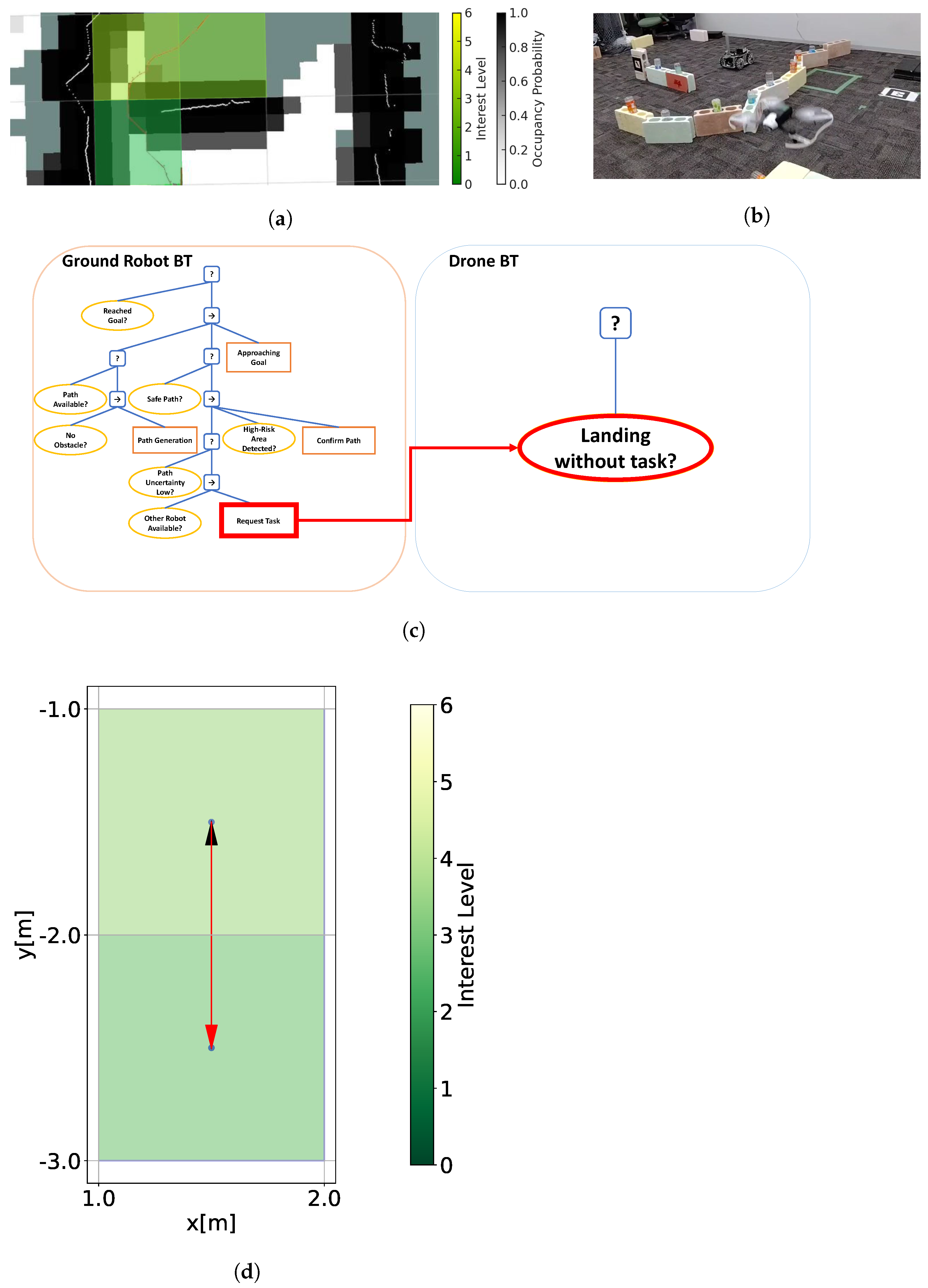
3.2.3. Interaction Between Drone and Ground Robot
3.2.4. Experimental Visualization and Flowchart
4. Action Planning and Mapping Framework for Multi-Robot Coordination System
4.1. Action Planning System
4.1.1. Overview of BTs
- Sequence Node: These nodes require all child nodes to succeed; if one fails, the entire sequence is considered a failure. This structure strictly manages the order of task execution.
- Fallback Node: These nodes attempt to execute their child nodes one at a time until one succeeds. If all child nodes fail, the Fallback Node itself fails.
- Action Node: These nodes execute specific commands directing the robot’s actions, such as “move forward” or “grasp an object”.
- Condition Node: These nodes evaluate the system’s state to determine whether specific conditions are met. If the conditions are fulfilled, the node succeeds; otherwise, it fails.
4.1.2. Planning and Acting Using Behavior Tree (PA-BT)
4.1.3. Generation and Elaboration of the BT
| Algorithm 1: Reactive Execution with BT and Task Requests to Other Robots |
 |
| Algorithm 2: BTs, Expand Tree |
 |
4.2. Drone Self-Location Estimation and Occupancy Grid Map Creation
4.2.1. ORB-SLAM
4.2.2. Coordinate Transformation
4.2.3. Occupancy Grid Map
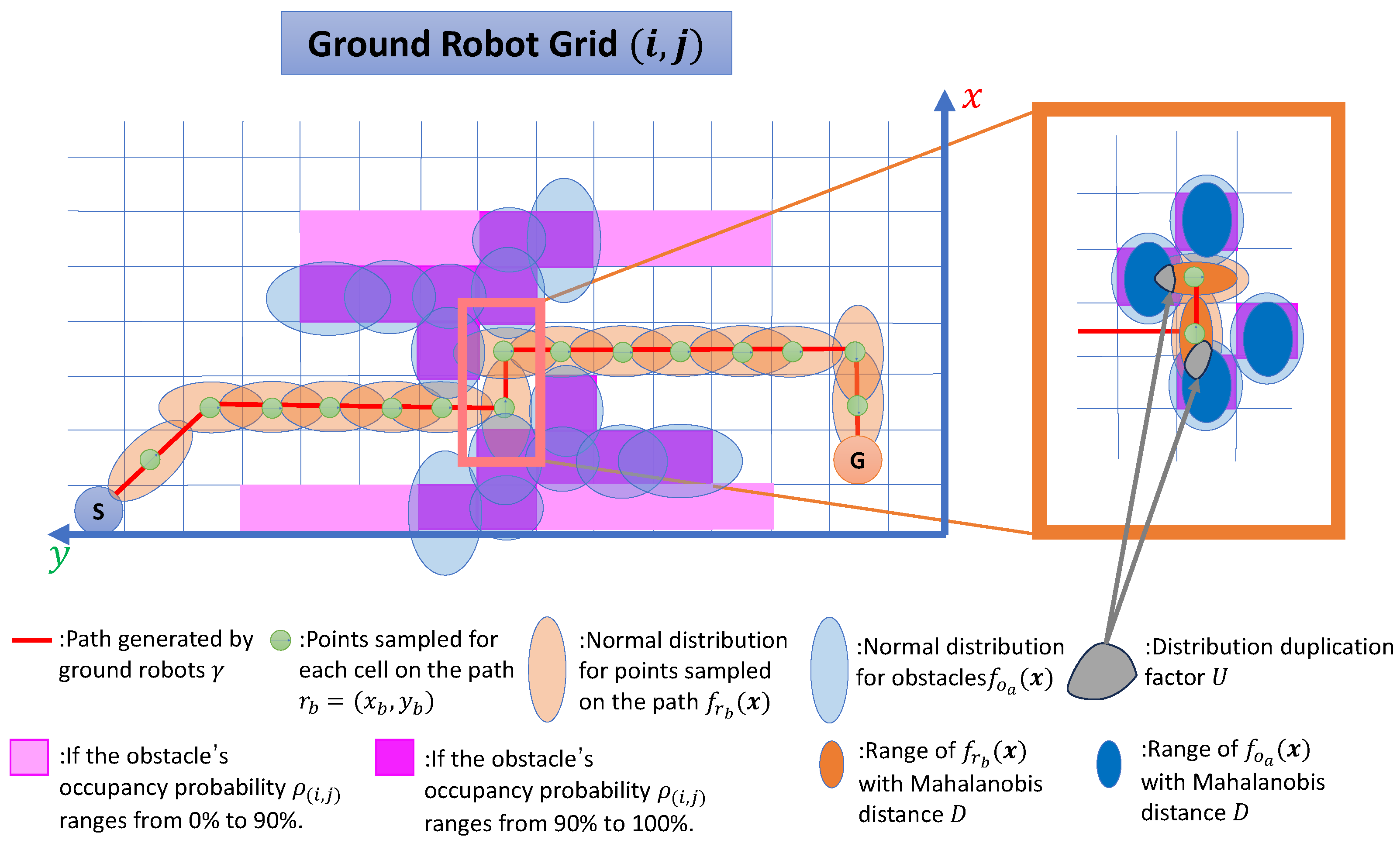
4.3. Path Planning for Drones
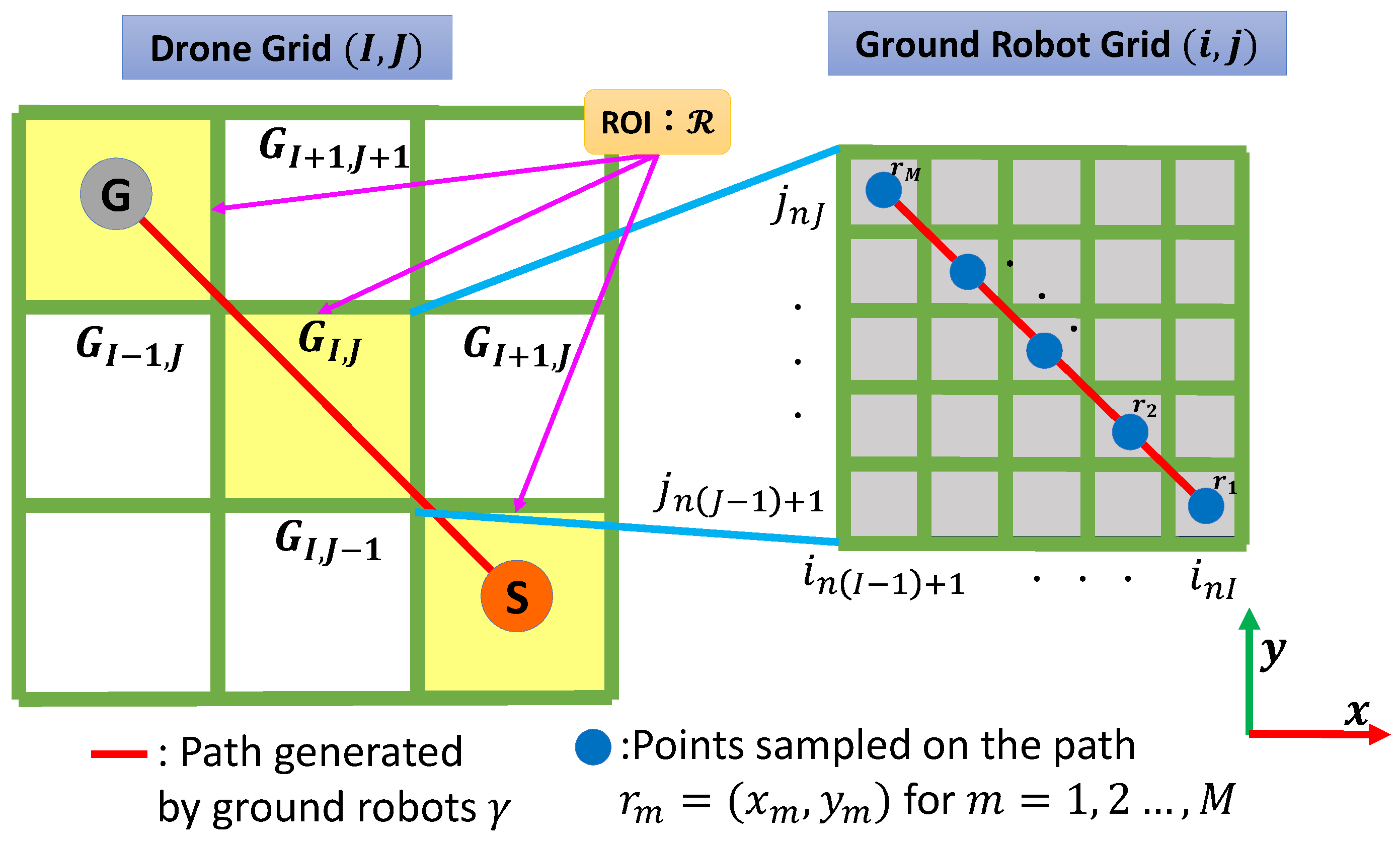
4.3.1. Drone-Assisted Path Planning for High-Uncertainty Areas Using Hierarchical Grids
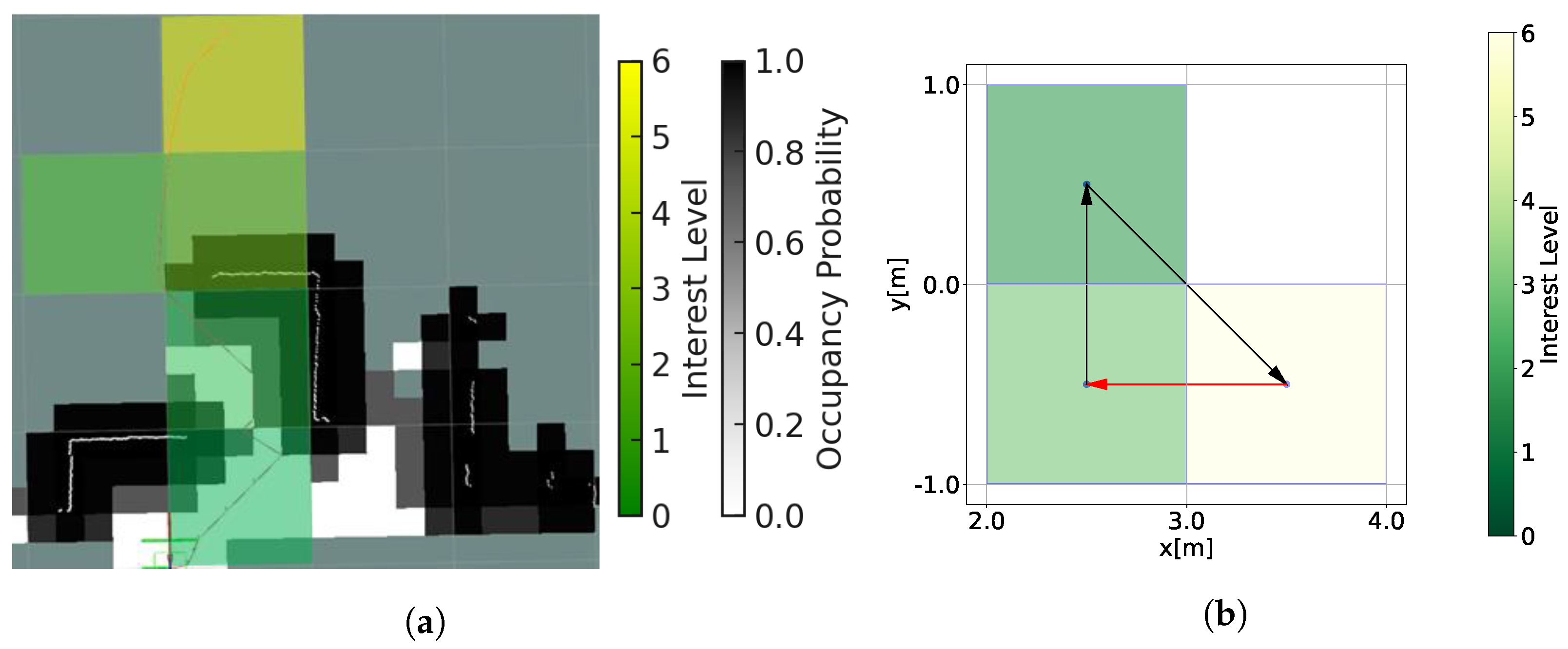
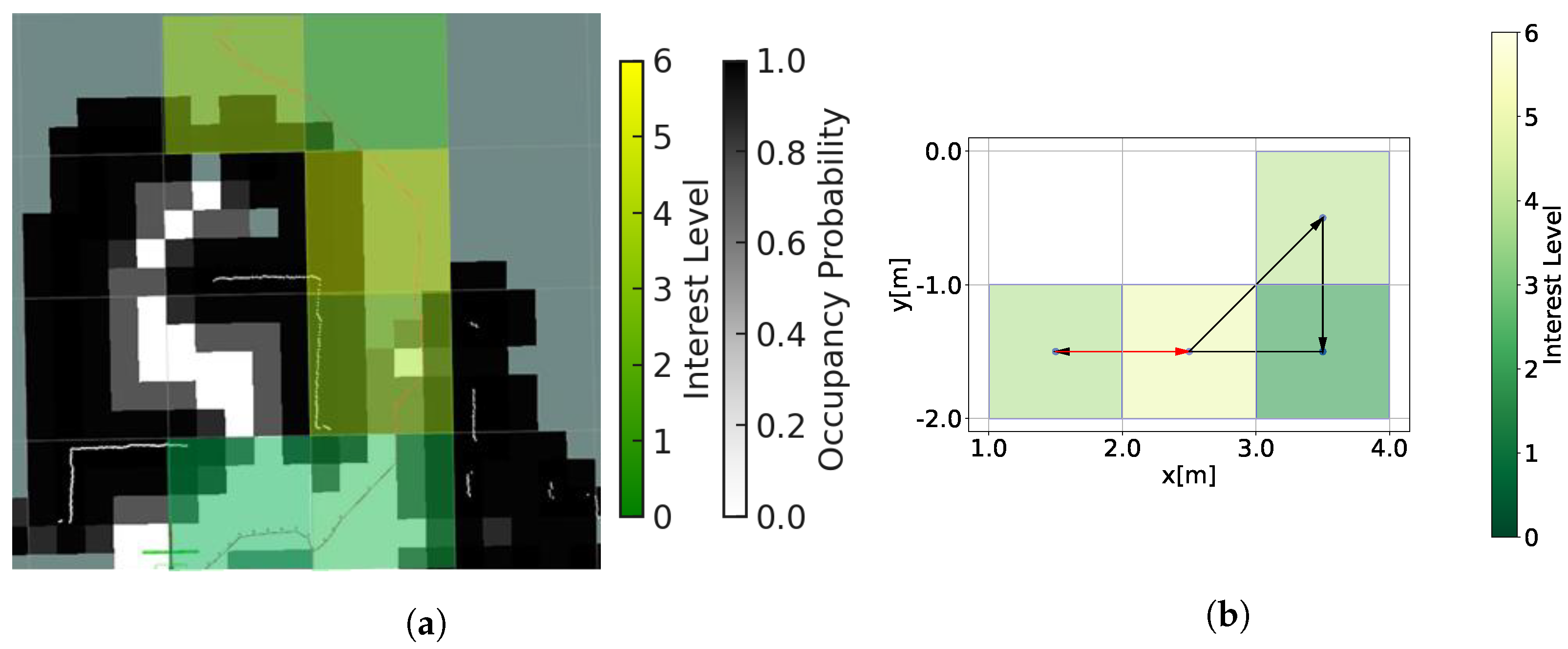
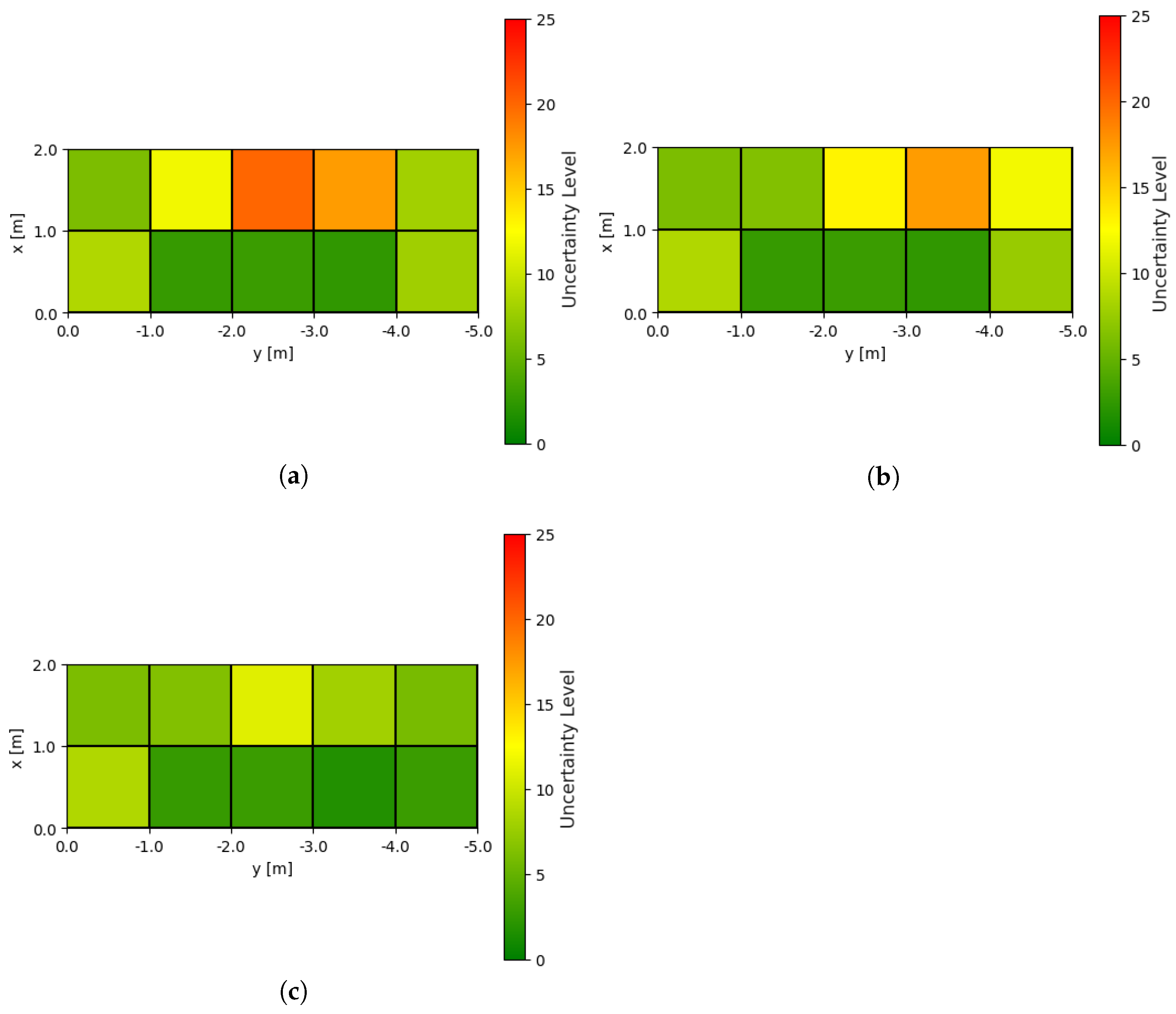
4.3.2. Extraction of the ROI and Calculation of Interest Levels
4.3.3. Path Planning with Genetic Algorithm
4.4. Risk Assessment and Passability Through Mutual Information Sharing Between Drones and Ground Robots
4.4.1. Risk Assessment of Ground Robot Paths Conducted by Drones
4.4.2. Passability Evaluation of Ground Robot Based on Drone Risk Assessment
5. Experimental Equipment
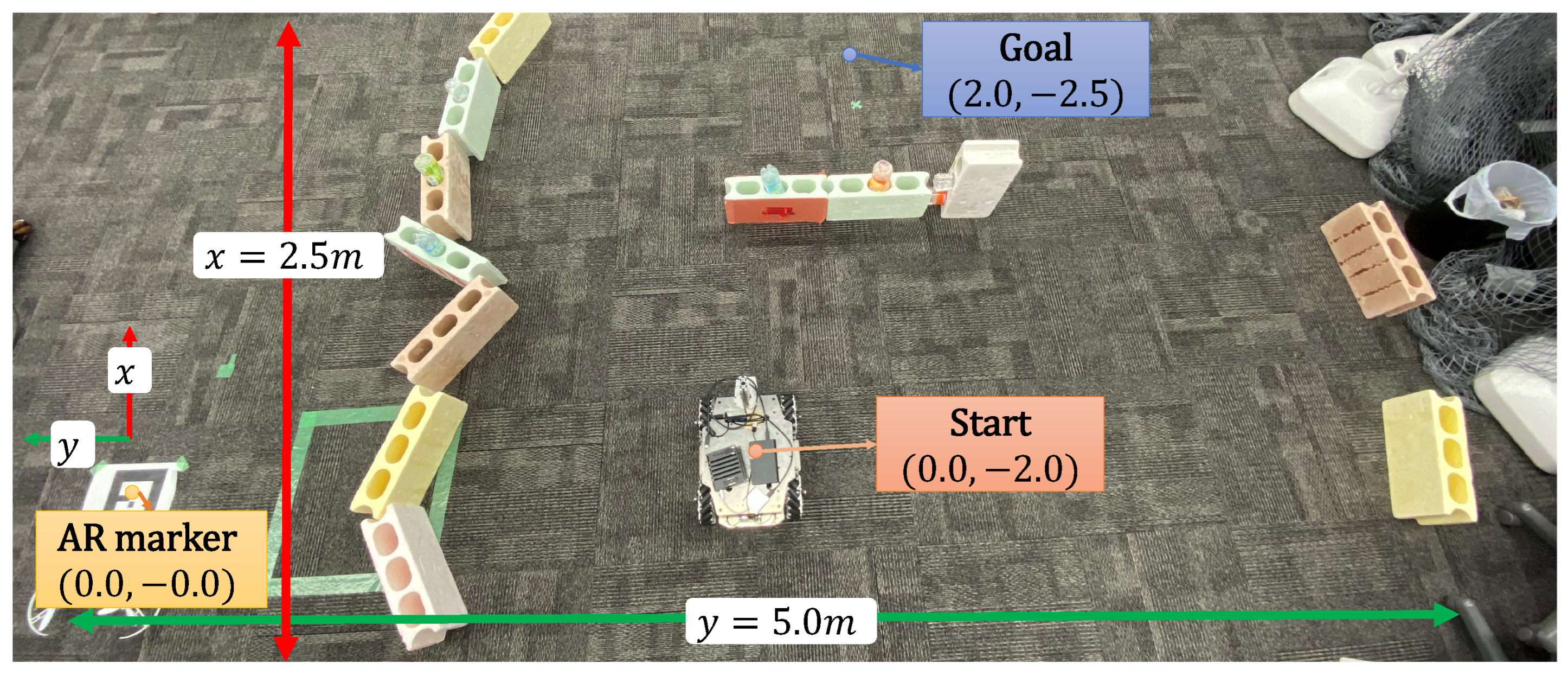
5.1. Experimental Setup
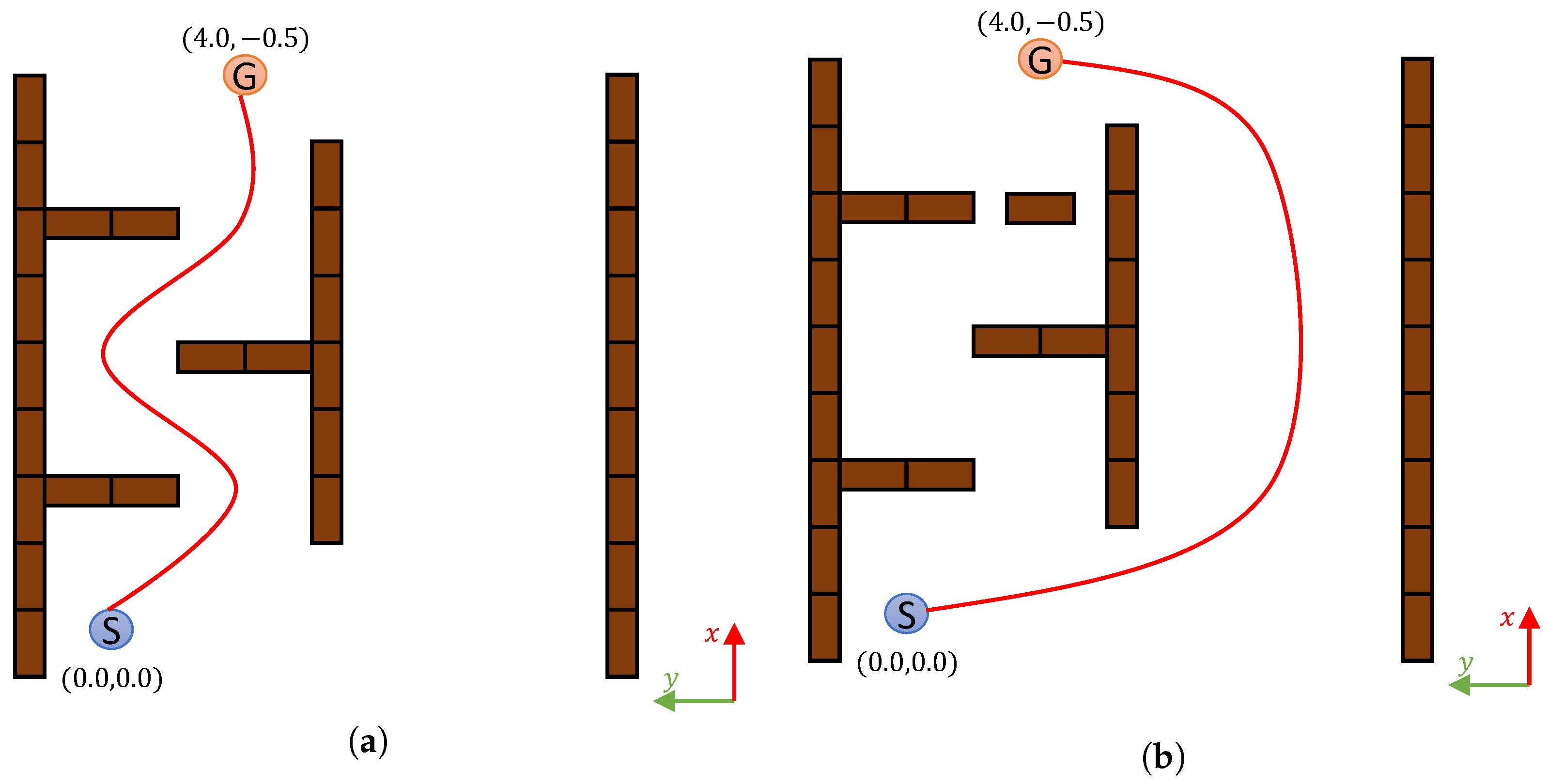
5.2. Experimental Results
5.3. Analysis of Experimental Data
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.; Xin, B.; Chen, J. A Review of Recent Advances in Coordination Between Unmanned Aerial and Ground Vehicles. Unmanned Syst. 2021, 9, 97–117. [Google Scholar] [CrossRef]
- Cheng, C.; Li, X.; Xie, L.; Li, L. A Unmanned Aerial Vehicle (UAV)/Unmanned Ground Vehicle (UGV) Dynamic Autonomous Docking Scheme in GPS-Denied Environments. Drones 2023, 7, 613. [Google Scholar] [CrossRef]
- Ivancevic, V.; Yue, Y. Hamiltonian dynamics and control of a joint autonomous land–air operation. Nonlinear Dyn. 2016, 84, 1853–1865. [Google Scholar] [CrossRef]
- Moon, J.; Lee, B.-H. PDDL Planning with Natural Language-Based Scene Understanding for UAV-UGV Cooperation. Appl. Sci. 2019, 9, 3789. [Google Scholar] [CrossRef]
- Gao, W.; Luo, J.; Zhang, W.; Yuan, W.; Liao, Z. Commanding Cooperative UGV-UAV with Nested Vehicle Routing for Emergency Resource Delivery. IEEE Access 2020, 8, 215691–215704. [Google Scholar] [CrossRef]
- He, J.; Zhou, Y.; Huang, L.; Kong, Y.; Cheng, H. Ground and Aerial Collaborative Mapping in Urban Environments. IEEE Robot. Autom. Lett. 2021, 6, 95–102. [Google Scholar] [CrossRef]
- Ramezani, M.; Amiri Atashgah, M.A.; Rezaee, A. A Fault-Tolerant Multi-Agent Reinforcement Learning Framework for Unmanned Aerial Vehicles–Unmanned Ground Vehicle Coverage Path Planning. Drones 2024, 8, 537. [Google Scholar] [CrossRef]
- Stolfi, D.H.; Brust, M.R.; Danoy, G.; Bouvry, P. UAV-UGV-UMV Multi-Swarms for Cooperative Surveillance. Front. Robot. AI 2021, 8, 616950. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kobori, H.; Sekiyama, K. Cooperative System of Ground Robots based on dynamic exploration of Drone Occupancy Grid Maps. In Proceedings of the 2023 62nd Annual Conference of the Society of Instrument and Control Engineers (SICE), Tsu, Japan, 6–9 September 2023; pp. 1074–1079. [Google Scholar] [CrossRef]
- Queralta, J.P.; Taipalmaa, J.; Pullinen, B.C.; Sarker, V.K.; Gia, T.N.; Tenhunen, H.; Gabbouj, M.; Raitoharju, J.; Westerlund, T. Collaborative Multi-Robot Search and Rescue: Planning, Coordination, Perception, and Active Vision. IEEE Access 2020, 8, 191617–191643. [Google Scholar] [CrossRef]
- Chen, S.; O’Brien, M.J.; Talbot, F.; Williams, J.; Tidd, B.; Pitt, A.; Arkin, R.C. Multi-modal User Interface for Multi-robot Control in Underground Environments. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 9995–10002. [Google Scholar] [CrossRef]
- Dufek, J.; Xiao, X.; Murphy, R.R. Best Viewpoints for External Robots or Sensors Assisting Other Robots. IEEE Trans. Hum. Mach. Syst. 2021, 51, 324–334. [Google Scholar] [CrossRef]
- Minaeian, S.; Liu, J.; Son, Y.-J. Vision-Based Target Detection and Localization via a Team of Cooperative UAV and UGVs. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 100-5-1016. [Google Scholar] [CrossRef]
- Elmakis, O.; Shaked, T.; Degani, A. Vision-Based UAV-UGV Collaboration for Autonomous Construction Site Preparation. IEEE Access 2022, 10, 51209–51220. [Google Scholar] [CrossRef]
- Miller, I.D.; Cladera, F.; Smith, T.; Taylor, C.J.; Kumar, V. Stronger Together: Air-Ground Robotic Collaboration Using Semantics. IEEE Robot. Autom. Lett. 2022, 7, 9643–9650. [Google Scholar] [CrossRef]
- Yang, Q.; Parasuraman, R. Needs-driven Heterogeneous Multi-Robot Cooperation in Rescue Missions. In Proceedings of the 2020 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Abu Dhabi, United Arab Emirates, 4–6 November 2020; pp. 252–259. [Google Scholar] [CrossRef]
- Moreira, M.S.M.; Villa, D.K.D.; Sarcinelli-Filho, M. Controlling a Virtual Structure Involving a UAV and a UGV for Warehouse Inventory. J. Intell. Robot. Syst. 2024, 110, 121. [Google Scholar] [CrossRef]
- Blum, A.L.; Furst, M.L. Fast planning through planning graph analysis. Artif. Intell. 1997, 90, 281–300. [Google Scholar] [CrossRef]
- Chu, F.-J.; Xu, R.; Seguin, L.; Vela, P.A. Toward Affordance Detection and Ranking on Novel Objects for Real-World Robotic Manipulation. IEEE Robot. Autom. Lett. 2019, 4, 4070–4077. [Google Scholar] [CrossRef]
- Colledanchise, M.; Ögren, P. Behavior Trees in Robotics and AI: An Introduction; CRC Press: Boca Raton, FL, USA, 2018; pp. 93–126. [Google Scholar]
- Brooks, R. A robust layered control system for a mobile robot. IEEE J. Robot. Autom. 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Nils, J.N. Teleo-reactive programs for agent control. JAIR 1994, 1, 139–158. [Google Scholar]
- Iovino, M.; Scukins, E.; Styrud, J.; Ögren, P.; Smith, C. A survey of Behavior Trees in robotics and AI. Robot. Auton. Syst. 2022, 154, 104096. [Google Scholar] [CrossRef]
- Bernardo, R.; Sousa, J.M.C.; Botto, M.A.; Gonçalves, P.J.S. A Novel Control Architecture Based on Behavior Trees for an Omni-Directional Mobile Robot. Robotics 2023, 12, 170. [Google Scholar] [CrossRef]
- Colledanchise, M.; Almeida, D.; Ögren, P. Towards Blended Reactive Planning and Acting using Behavior Trees. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8839–8845. [Google Scholar] [CrossRef]
- Macenski, S.; Martín, F.; White, R.; Clavero, J.G. The Marathon 2: A Navigation System. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 2718–2725. [Google Scholar] [CrossRef]
- Venkata, S.S.O.; Parasuraman, R.; Pidaparti, R. KT-BT: A Framework for Knowledge Transfer Through Behavior Trees in Multirobot Systems. IEEE Trans. Robot. 2023, 39, 4114–4130. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Emambocus, B.A.S.; Jasser, M.B.; Hamzah, M.; Mustapha, A.; Amphawan, A. An Enhanced Swap Sequence-Based Particle Swarm Optimization Algorithm to Solve TSP. IEEE Access 2021, 9, 164820–164836. [Google Scholar] [CrossRef]
- Zhou, A.-H.; Zhu, L.-P.; Hu, B.; Deng, S.; Song, Y.; Qiu, H.; Pan, S. Traveling-Salesman-Problem Algorithm Based on Simulated Annealing and Gene-Expression Programming. Information 2019, 10, 7. [Google Scholar] [CrossRef]









| Reference | Cooperation Type | Task Request Directionality |
|---|---|---|
| Queralta et al. [10] | Planned | Unidirectional |
| Elmakis et al. [14] | Planned | Unidirectional |
| Yang et al. [16] | Needs-driven flexible | Unidirectional |
| Own Previous Research [9] | Needs-driven flexible | Unidirectional |
| Proposed Method | Needs-driven flexible | Bidirectional |
| Parameter | Value |
|---|---|
| Population Size | 100 |
| Crossover Rate | 0.8 |
| Mutation Rate | 0.05 |
| Number of Generations | 50 |
| Selection Method | Tournament Selection |
| Crossover Method | Partially Mapped Crossover |
| Mutation Method | Swap Mutation |
| Path Type | Drone Exploration Stage | Change in ROI | |
|---|---|---|---|
| Straight Path | 1st | ||
| Alternative Path | 1st | ||
| 2nd | |||
| Path Type | Drone Exploration Stage | High-Risk Position | E | T | Remark |
|---|---|---|---|---|---|
| Straight Path | 1st | (1.4, −1.5) | 0.137 | None | No Issues |
| (1.2, −1.5) | 0.157 | 45 | Passable | ||
| (1.0, −1.5) | 0.155 | 52 | Passable | ||
| (0.8, −1.4) | 0.152 | 48 | Passable | ||
| (0.6, −1.6) | 0.154 | 48 | Passable | ||
| (0.4, −1.6) | 0.142 | None | No Issues | ||
| Alternative Path | 1st | (1.4, −1.6) | 0.147 | None | No Issues |
| (1.2, −1.6) | 0.155 | 45 | Passable | ||
| (1.0, −1.4) | 0.161 | 85 | Impassable | ||
| (0.8, −1.4) | 0.157 | 80 | Impassable | ||
| (0.6, −1.6) | 0.156 | 65 | Passable | ||
| (0.4, −1.6) | 0.142 | None | No Issues | ||
| 2nd | (1.4, −3.8) | 0.129 | None | No Issues | |
| (1.2, −3.8) | 0.132 | None | No Issues | ||
| (1.0, −3.8) | 0.136 | None | No Issues | ||
| (0.8, −3.8) | 0.134 | None | No Issues | ||
| (0.6, −3.6) | 0.131 | None | No Issues | ||
| (0.4, −3.4) | 0.124 | None | No Issues |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kobori, H.; Sekiyama, K. Mutual Cooperation System for Task Execution Between Ground Robots and Drones Using Behavior Tree-Based Action Planning and Dynamic Occupancy Grid Mapping. Drones 2025, 9, 95. https://doi.org/10.3390/drones9020095
Kobori H, Sekiyama K. Mutual Cooperation System for Task Execution Between Ground Robots and Drones Using Behavior Tree-Based Action Planning and Dynamic Occupancy Grid Mapping. Drones. 2025; 9(2):95. https://doi.org/10.3390/drones9020095
Chicago/Turabian StyleKobori, Hiroaki, and Kosuke Sekiyama. 2025. "Mutual Cooperation System for Task Execution Between Ground Robots and Drones Using Behavior Tree-Based Action Planning and Dynamic Occupancy Grid Mapping" Drones 9, no. 2: 95. https://doi.org/10.3390/drones9020095
APA StyleKobori, H., & Sekiyama, K. (2025). Mutual Cooperation System for Task Execution Between Ground Robots and Drones Using Behavior Tree-Based Action Planning and Dynamic Occupancy Grid Mapping. Drones, 9(2), 95. https://doi.org/10.3390/drones9020095







