Measurement and Analysis of the Rician K-Factor for Low-Altitude UAV Air-to-Ground Communications at 2.5 GHz
Abstract
1. Introduction
2. Radio Propagation Measurement Method
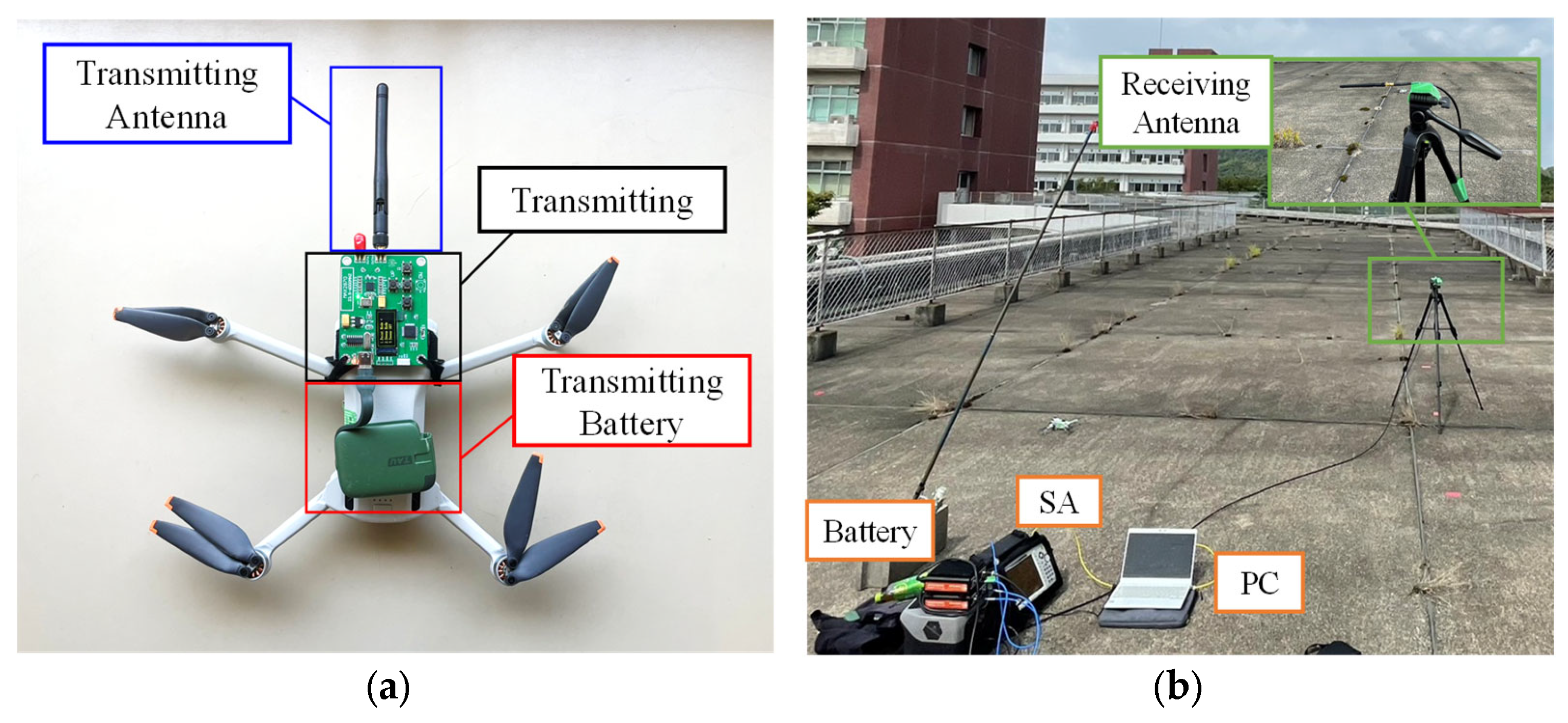
2.1. Radio Propagation Measurement Setup
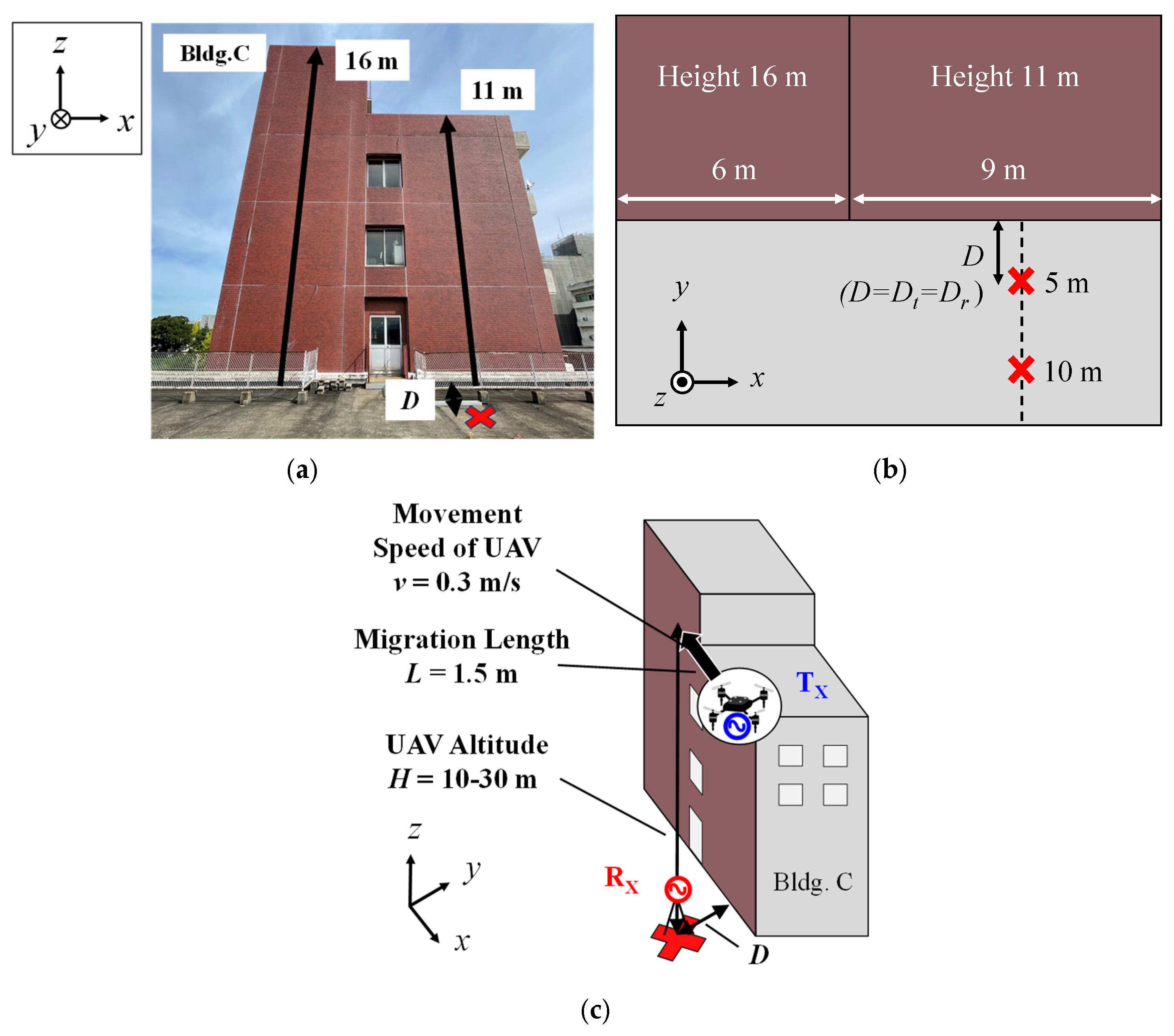
2.2. Radio Propagation Measurement Environment
2.2.1. Simple Measurement Environment
2.2.2. Complex Measurement Environment
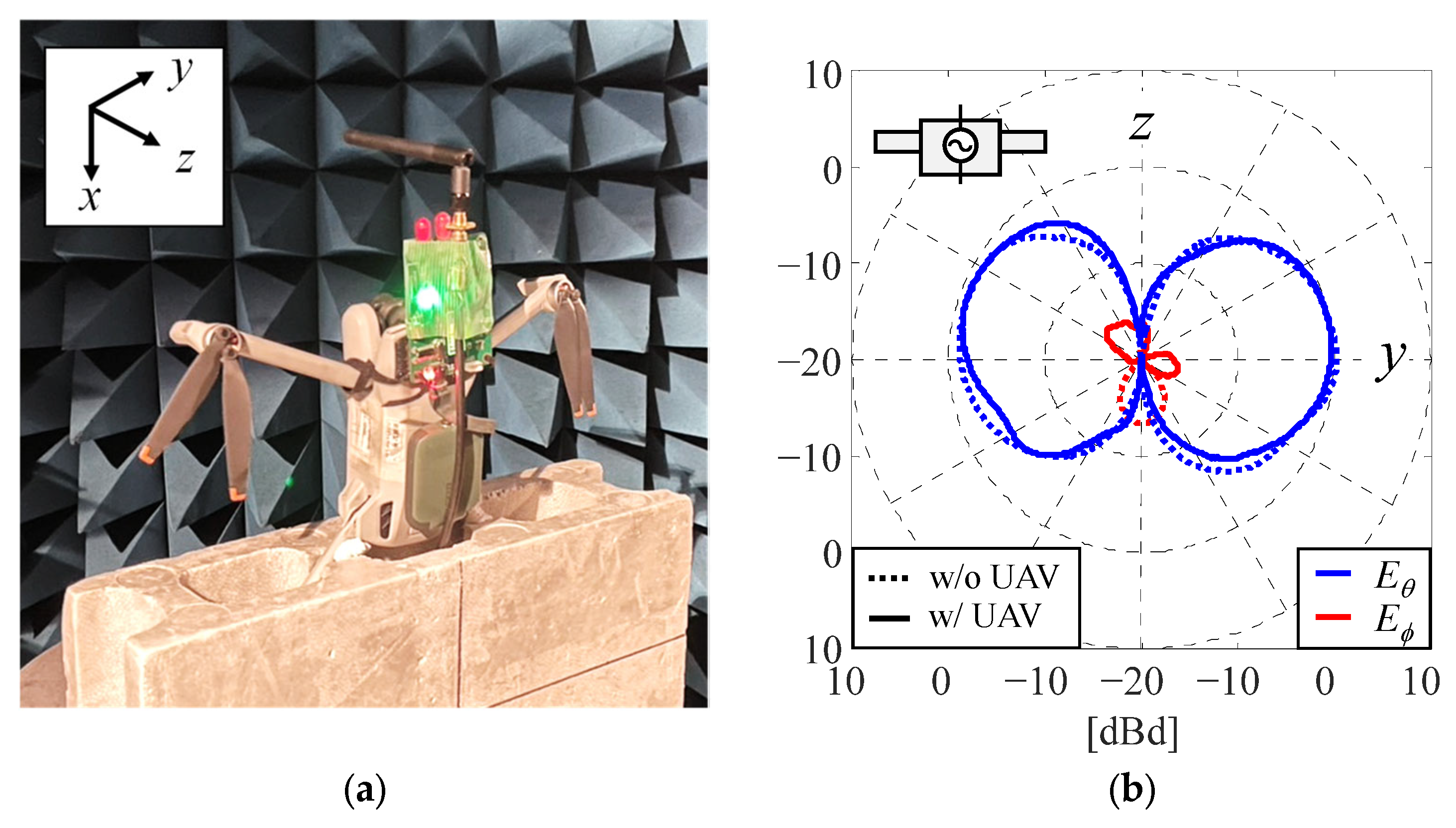
2.3. Directivity Evaluation Considering the UAV
3. Radio Wave Propagation Analysis
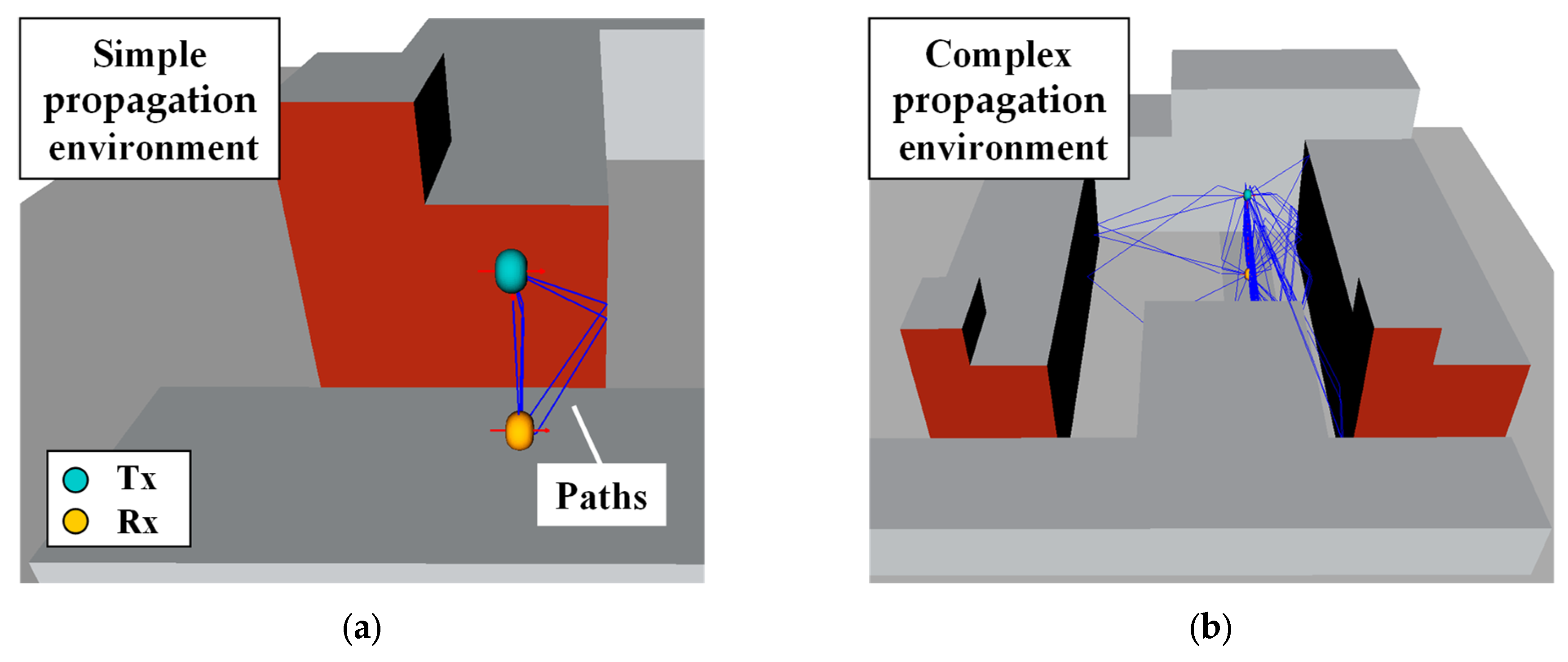
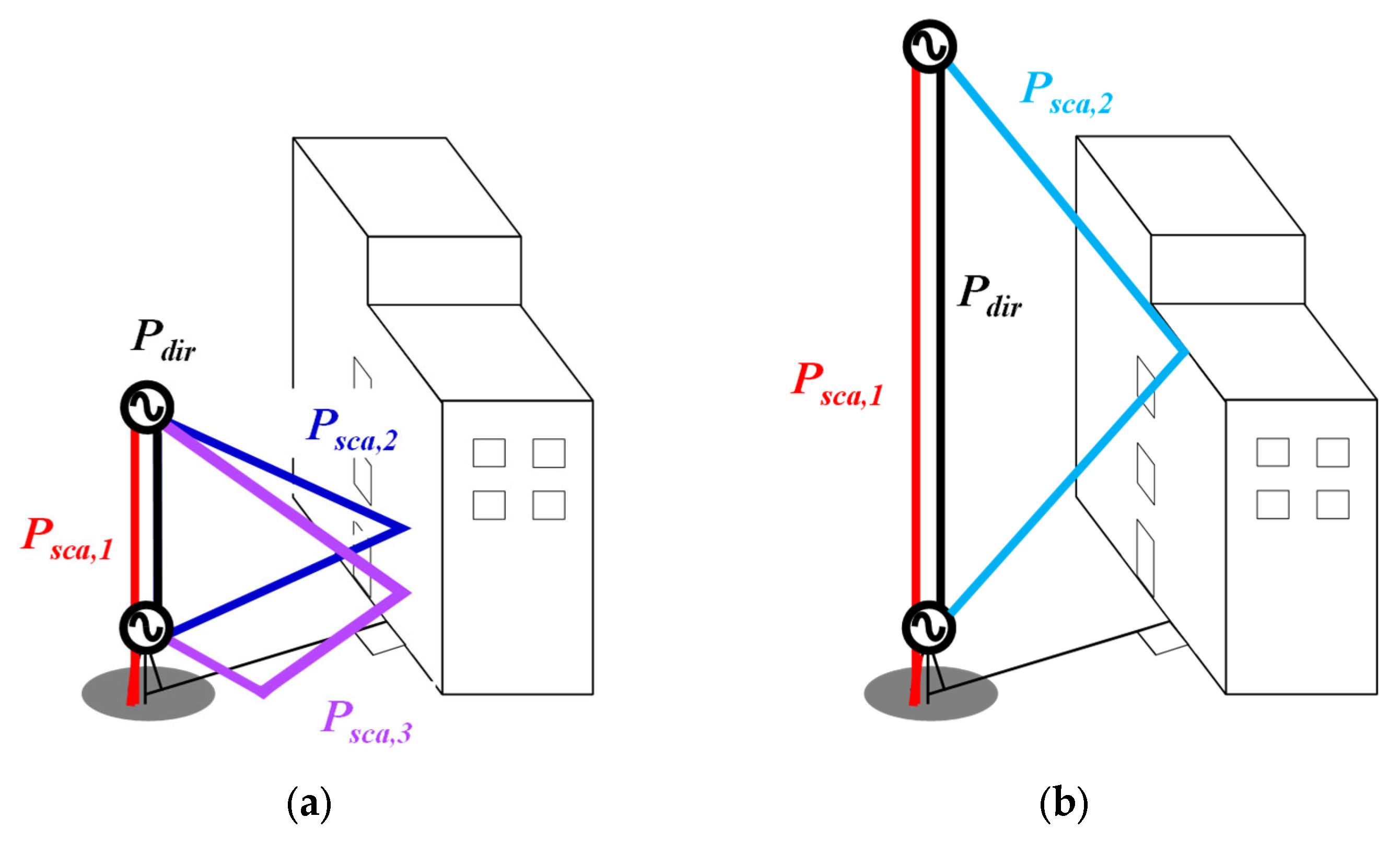
3.1. Channel Analysis Based on the Ray-Tracing Method
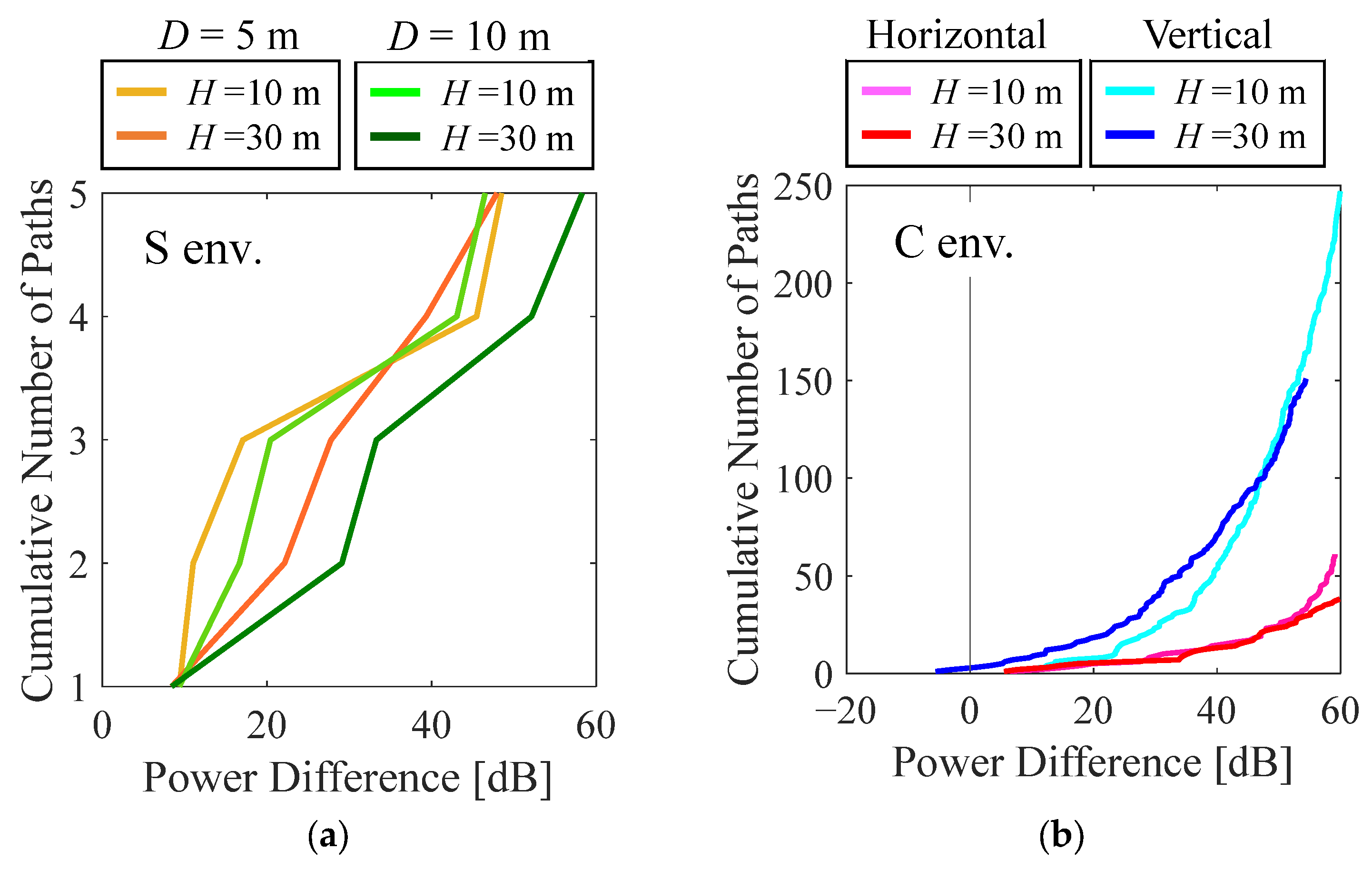
3.2. Results of the Channel Analysis
3.3. Dummy Fading Signal Generation Based on the Static Paths
3.4. Estimation of the Ricean K-Factor
4. Rician K-Factor Characteristics
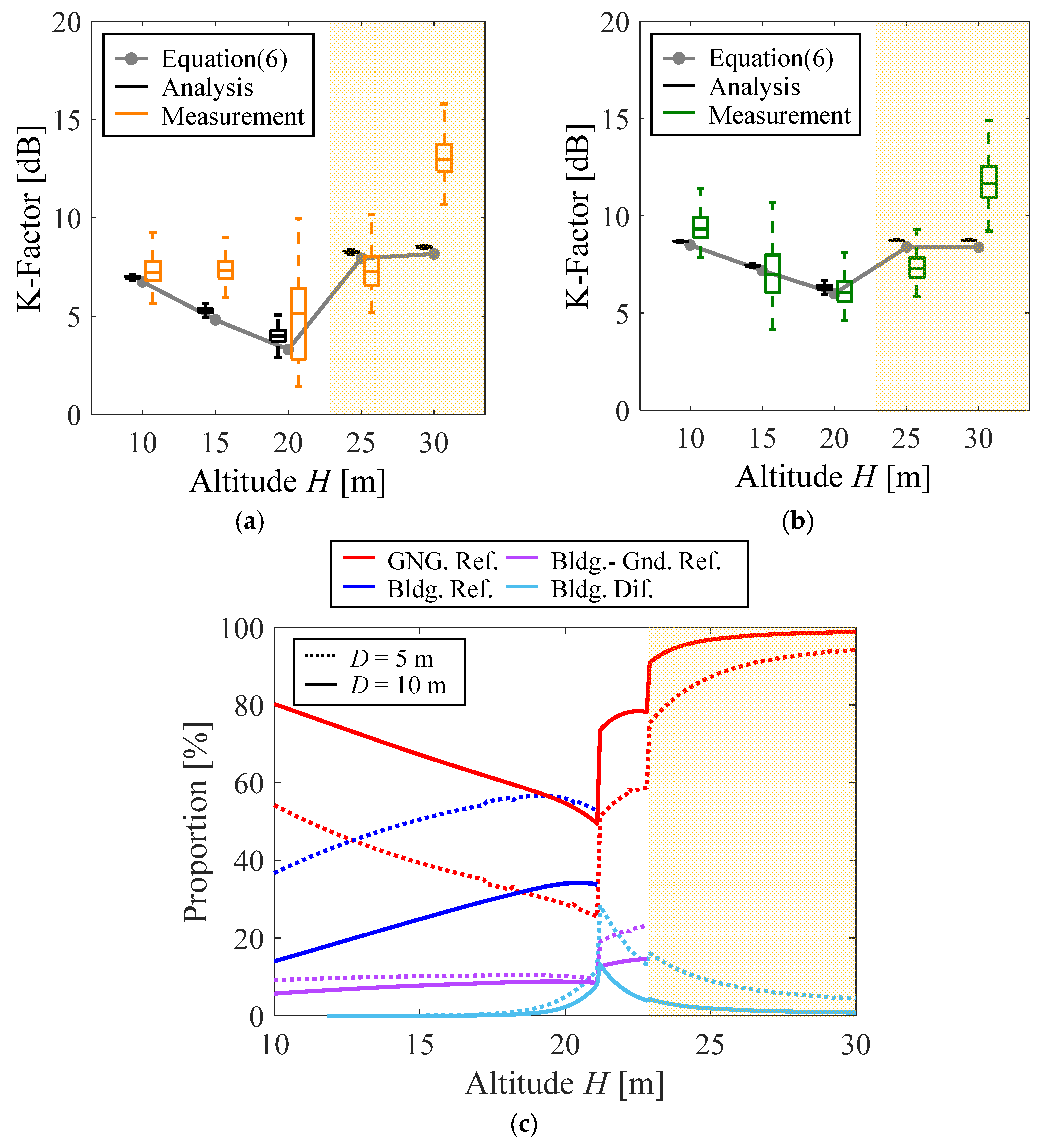
4.1. Rician K-Factor in Simple Propagation Environment
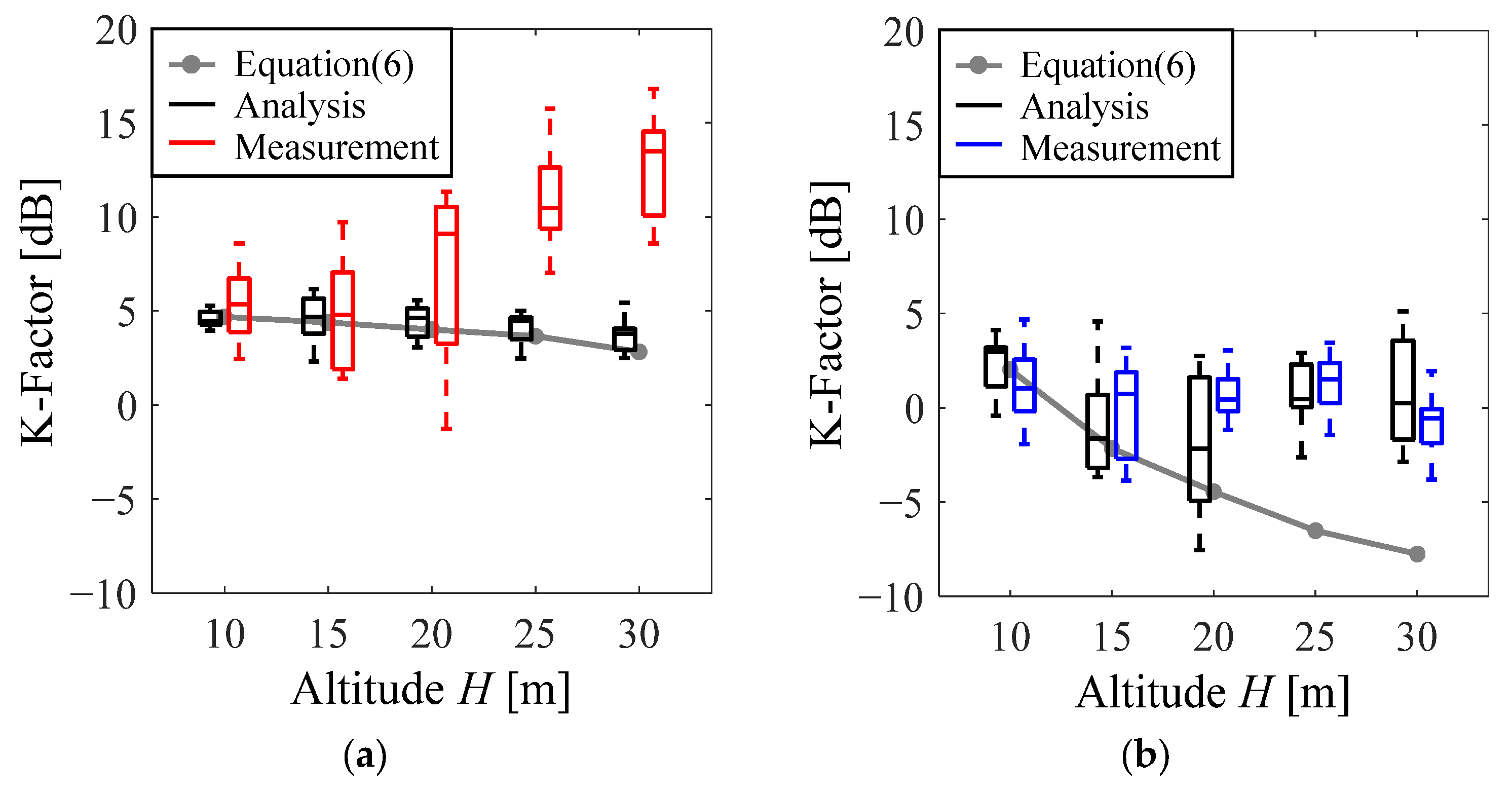
4.2. Rician K-Factor in Complex Propagation Environment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless Communications with Unmanned Aerial Vehicles: Opportunities and Challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Valavanis, K.P.; Vachtsevanos, G.J. (Eds.) Handbook of Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2015; ISBN 978-90-481-9706-4. [Google Scholar]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned Aerial Vehicles (UAVs): Practical Aspects, Applications, Open Challenges, Security Issues, and Future Trends. Intel. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef] [PubMed]
- Telli, K.; Kraa, O.; Himeur, Y.; Ouamane, A.; Boumehraz, M.; Atalla, S.; Mansoor, W. A Comprehensive Review of Recent Research Trends on Unmanned Aerial Vehicles (UAVs). Systems 2023, 11, 400. [Google Scholar] [CrossRef]
- Höhrová, P.; Soviar, J.; Sroka, W. Market Analysis of Drones for Civil Use. LOGI Sci. J. Transp. Logist. 2023, 14, 55–65. [Google Scholar] [CrossRef]
- Outay, F.; Mengash, H.A.; Adnan, M. Applications of Unmanned Aerial Vehicle (UAV) in Road Safety, Traffic and Highway Infrastructure Management: Recent Advances and Challenges. Transp. Res. Part A Policy Pract. 2020, 141, 116–129. [Google Scholar] [CrossRef]
- Butilă, E.V.; Boboc, R.G. Urban Traffic Monitoring and Analysis Using Unmanned Aerial Vehicles (UAVs): A Systematic Literature Review. Remote Sens. 2022, 14, 620. [Google Scholar] [CrossRef]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual Monitoring of Civil Infrastructure Systems via Camera-Equipped Unmanned Aerial Vehicles (UAVs): A Review of Related Works. Vis. Eng. 2016, 4, 1. [Google Scholar] [CrossRef]
- Bruni, M.E.; Khodaparasti, S.; Perboli, G. Energy Efficient UAV-Based Last-Mile Delivery: A Tactical-Operational Model with Shared Depots and Non-Linear Energy Consumption. IEEE Access 2023, 11, 18560–18570. [Google Scholar] [CrossRef]
- Sarvesh, E.; Jose, J.; Chitrakala, S. MedUAV: Drone-Based Emergency Medical Supply System Using Decentralized Autonomous Organization (DAO). Procedia Comput. Sci. 2023, 230, 737–748. [Google Scholar] [CrossRef]
- 802.11-2012; IEEE Standard for Information Technology–Telecommunications and Information Exchange Between Systems Local and Metropolitan Area Networks—Specific Requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; 802.11-2012 (Revision of IEEE Std 802.11-2007). IEEE: New York, NY, USA, 2012; pp. 1–2793. [CrossRef]
- 802.11-2020; IEEE Standard for Information Technology–Telecommunications and Information Exchange Between Systems—Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications—Redline; 802.11-2020 (Revision of IEEE Std 802.11-2016). IEEE: New York, NY, USA, 2021; pp. 1–7524.
- Abdalla, A.S.; Marojevic, V. Communications Standards for Unmanned Aircraft Systems: The 3GPP Perspective and Research Drivers. IEEE Commun. Stand. Mag. 2021, 5, 70–77. [Google Scholar] [CrossRef]
- Characteristics of Unmanned Aircraft Systems and Spectrum Requirements to Support Their Safe Operation in Non-Segregated Airspace. Available online: https://store.accuristech.com/standards/itu-r-report-m-2171?product_id=2824436&srsltid=AfmBOopUhuKXUvApb7cuZ-5l_olP0K_5Xo1QmBwM_WWJOUIIMR-Tqe1k (accessed on 23 December 2024).
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.-C.; Schneckenburger, N. A Survey of Air-to-Ground Propagation Channel Modeling for Unmanned Aerial Vehicles. IEEE Commun. Surv. Tutor. 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Wang, C.-X.; Ye, X.; Gomez-Ponce, J.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A Survey on Channel Sounding Technologies and Measurements for UAV-Assisted Communications. IEEE Trans. Instrum. Meas. 2024, 73, 1–24. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.-H.; Debbah, M. A Tutorial on UAVs for Wireless Networks: Applications, Challenges, and Open Problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- 3GPP. Study on Channel Model for Frequencies from 0.5 to 100 GHz; Technical Report (TR) 38.901, Version 14.0.0; 3rd Generation Partnership Project (3GPP). 2017. Available online: https://www.3gpp.org/ftp/specs/archive/38_series/38.901/ (accessed on 10 January 2025).
- 3GPP. Enhanced LTE Support for Aerial Vehicles; Technical Report (TR) 36.777, Version 15.0.0; 3rd Generation Partnership Project (3GPP). 2017. Available online: https://www.3gpp.org/ftp/specs/archive/36_series/36.777/ (accessed on 10 January 2025).
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef]
- Lin, X.; Yajnanarayana, V.; Muruganathan, S.D.; Gao, S.; Asplund, H.; Maattanen, H.-L.; Bergstrom, M.; Euler, S.; Wang, Y.-P.E. The Sky Is Not the Limit: LTE for Unmanned Aerial Vehicles. IEEE Commun. Mag. 2018, 56, 204–210. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Unmanned Aerial Vehicle with Underlaid Device-to-Device Communications: Performance and Tradeoffs. IEEE Trans. Wirel. Commun. 2016, 15, 3949–3963. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for UAV-Enabled Multiple Access. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Leite, D.L.; Alsina, P.J.; de Medeiros Campos, M.M.; de Sousa, V.A.; de Medeiros, A.A.M. Unmanned Aerial Vehicle Propagation Channel over Vegetation and Lake Areas: First- and Second-Order Statistical Analysis. Sensors 2022, 22, 65. [Google Scholar] [CrossRef]
- Alzenad, M.; Yanikomeroglu, H. Coverage and Rate Analysis for Unmanned Aerial Vehicle Base Stations with LoS/NLoS Propagation. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–7. [Google Scholar]
- Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling Air-to-Ground Path Loss for Low Altitude Platforms in Urban Environments. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2898–2904. [Google Scholar]
- Michailidis, E.T.; Nomikos, N.; Trakadas, P.; Kanatas, A.G. Three-Dimensional Modeling of mmWave Doubly Massive MIMO Aerial Fading Channels. IEEE Trans. Veh. Technol. 2020, 69, 1190–1202. [Google Scholar] [CrossRef]
- Matolak, D.W.; Sun, R. Air–Ground Channel Characterization for Unmanned Aircraft Systems—Part III: The Suburban and Near-Urban Environments. IEEE Trans. Veh. Technol. 2017, 66, 6607–6618. [Google Scholar] [CrossRef]
- Lyu, Y.; He, Y.; Liang, Z.; Wang, W.; Yu, J.; Shi, D. Measurement-Based Tapped Delay Line Channel Modeling for Fixed-Wing Unmanned Aerial Vehicle Air-to-Ground Communications at S-Band. Drones 2024, 8, 492. [Google Scholar] [CrossRef]
- Cui, Z.; Briso-Rodríguez, C.; Guan, K.; Calvo-Ramírez, C.; Ai, B.; Zhong, Z. Measurement-Based Modeling and Analysis of UAV Air-Ground Channels at 1 and 4 GHz. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1804–1808. [Google Scholar] [CrossRef]
- Bithas, P.S.; Nikolaidis, V.; Kanatas, A.G.; Karagiannidis, G.K. UAV-to-Ground Communications: Channel Modeling and UAV Selection. IEEE Trans. Commun. 2020, 68, 5135–5144. [Google Scholar] [CrossRef]
- Fuschini, F.; Barbiroli, M.; Vitucci, E.M.; Semkin, V.; Oestges, C.; Strano, B.; Degli-Esposti, V. An UAV-Based Experimental Setup for Propagation Characterization in Urban Environment. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Qiu, Z.; Chu, X.; Calvo-Ramirez, C.; Briso, C.; Yin, X. Low Altitude UAV Air-to-Ground Channel Measurement and Modeling in Semiurban Environments. Wirel. Commun. Mob. Comput. 2017, 2017, 1587412. [Google Scholar] [CrossRef]
- Khawaja, W.; Ozdemir, O.; Erden, F.; Guvenc, I.; Matolak, D.W. Ultra-Wideband Air-to-Ground Propagation Channel Characterization in an Open Area. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4533–4555. [Google Scholar] [CrossRef]
- Cai, X.; Rodríguez-Piñeiro, J.; Yin, X.; Wang, N.; Ai, B.; Pedersen, G.F.; Yuste, A.P. An Empirical Air-to-Ground Channel Model Based on Passive Measurements in LTE. IEEE Trans. Veh. Technol. 2019, 68, 1140–1154. [Google Scholar] [CrossRef]
- Ning, B.; Li, T.; Mao, K.; Chen, X.; Wang, M.; Zhong, W.; Zhu, Q. A UAV-Aided Channel Sounder for Air-to-Ground Channel Measurements. Phys. Commun. 2021, 47, 101366. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Qiu, Y.; Liu, X.; Song, M.; Fan, W.; Kokkeler, A.B.J.; Miao, Y. A UAV-Aided Real-Time Channel Sounder for Highly Dynamic Nonstationary A2G Scenarios. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar] [CrossRef]
- Cui, Z.; Briso, C.; Guan, K.; Matolak, D.W.; Calvo-Ramírez, C.; Ai, B.; Zhong, Z. Low-Altitude UAV Air-Ground Propagation Channel Measurement and Analysis in a Suburban Environment at 3.9 GHz. IET Microw. Antennas Propag. 2019, 13, 1503–1508. [Google Scholar] [CrossRef]
- Rodríguez-Piñeiro, J.; Domínguez-Bolaño, T.; Cai, X.; Huang, Z.; Yin, X. Air-to-Ground Channel Characterization for Low-Height UAVs in Realistic Network Deployments. IEEE Trans. Antennas Propag. 2021, 69, 992–1006. [Google Scholar] [CrossRef]
- Cui, Z.; Guan, K.; Oestges, C.; Briso-Rodríguez, C.; Ai, B.; Zhong, Z. Cluster-Based Characterization and Modeling for UAV Air-to-Ground Time-Varying Channels. IEEE Trans. Veh. Technol. 2022, 71, 6872–6883. [Google Scholar] [CrossRef]
- Aoki, K.; Honda, K. K-Factor Characteristics According to the Polarizations of Drone-to-Ground Communication. In Proceedings of the 2024 International Conference on Emerging Technology for Communications (ICETC), Kitakyushu, Japan, 25–27 November 2024. [Google Scholar] [CrossRef]
- DJI Mini 3. So Fly. Available online: https://www.dji.com/global/mini-3?site=brandsite&from=landing_page (accessed on 23 December 2024).
- Overview. Available online: https://www.google.com/earth/about/ (accessed on 23 December 2024).
- P.2040: Effects of Building Materials and Structures on Radiowave Propagation above about 100 MHz. Available online: https://www.itu.int/rec/R-REC-P.2040-2-202109-S/en (accessed on 23 December 2024).
- KKE―Innovating for a Wise Future. Available online: https://www.kke.co.jp/en/ (accessed on 23 December 2024).
- Jakes, W.C. Microwave Mobile Communications; IEEE: New York, NY, USA; Wiley-Interscience: Hoboken, NJ, USA, 1994; ISBN 978-0-7803-1069-8. [Google Scholar]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; ISBN 978-0-13-042232-3. [Google Scholar]
- Greenstein, L.J.; Michelson, D.G.; Erceg, V. Moment-Method Estimation of the Ricean K-Factor. IEEE Commun. Lett. 1999, 3, 175–176. [Google Scholar] [CrossRef]






| Reference | Frequency [GHz] | Sampling Interval of Each Snapshot | UAV Speed [m/s] | Altitude [m] | Channel Modeling | Channel Characteristics |
|---|---|---|---|---|---|---|
| [32] | 27/38 | 500 ms | — | 16, 19, 50 | — | Path loss, direction |
| [33] | 1.2/4.2 | 100 ms | 0.7, 1.2 | 0–100 | FE2R | Path loss, Rician K-factor |
| [34] | 3.95 | 100 ns | 6.1 | 10, 20, 30 | Ray tracing | Rician K-factor, direction |
| [35] | 2.5 | 40 ns | 5.6 | 15, 30, 50, 75, 100 | SAGE | Path loss, Rician K-factor |
| [36] | 1.2–6 | 12.5 μs | — | 80 | — | Path loss |
| [37] | 2.4/3.5 | 10.24 μs | 2 | 0–60 | SAGE | Path loss, Rician K-factor |
| [38] | 3.9 | 2 μs | — | 0–40 | Ray tracing | Path loss |
| [39] | 2.5 | — | 5 | 15–105 | — | Path loss, Rician K-factor |
| [40] | 6.5 | — | — | 0–30 | SAGE | Rician K-factor |
| Our work | 2.5 | 10 ms | 0.3 | 10, 15, 20, 25, 30 | Ray tracing | Rician K-factor |
| Parameter | Simple Propagation Environment | Complex Propagation Environment | ||
|---|---|---|---|---|
| Measurement time | 5 s | 10 s | ||
| Migration length L | 1.5 m | 3 m | ||
| Movement speed of UAV v | 0.3 m/s | |||
| UAV altitude H | 10–30 m | |||
| Distance between the nearest building and transmitting antenna (UAV) Dt | 5 m | 10 m | 5 m | |
| Distance between the nearest building and receiving antenna Dr | 5 m | 10 m | 15 m | |
| Frequency f | 2.5 GHz | |||
| Transmitting antenna | Half-wavelength dipole antenna | |||
| Receiving antenna | Half-wavelength dipole antenna | |||
| Antenna arrangement | Horizontal installation | Horizontal installation | Vertical installation | |
| Parameter | Simple Propagation Environment | Complex Propagation Environment |
|---|---|---|
| Frequency f | 2.5 GHz | |
| Transmitting antenna | Half-wavelength dipole antenna | |
| Receiving antenna | Half-wavelength dipole antenna | |
| Ground material | Concrete | |
| Relative permittivity εr | 5.31 | |
| Conductivity ρ [S/m] | 0.194 | |
| Wall material | Brick | Concrete |
| Relative permittivity εr | 3.91 | 5.31 |
| Conductivity ρ [S/m] | 0.024 | 0.194 |
| Maximum number of reflections | 3 | |
| Maximum number of diffractions | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aoki, K.; Honda, K. Measurement and Analysis of the Rician K-Factor for Low-Altitude UAV Air-to-Ground Communications at 2.5 GHz. Drones 2025, 9, 86. https://doi.org/10.3390/drones9020086
Aoki K, Honda K. Measurement and Analysis of the Rician K-Factor for Low-Altitude UAV Air-to-Ground Communications at 2.5 GHz. Drones. 2025; 9(2):86. https://doi.org/10.3390/drones9020086
Chicago/Turabian StyleAoki, Kaisei, and Kazuhiro Honda. 2025. "Measurement and Analysis of the Rician K-Factor for Low-Altitude UAV Air-to-Ground Communications at 2.5 GHz" Drones 9, no. 2: 86. https://doi.org/10.3390/drones9020086
APA StyleAoki, K., & Honda, K. (2025). Measurement and Analysis of the Rician K-Factor for Low-Altitude UAV Air-to-Ground Communications at 2.5 GHz. Drones, 9(2), 86. https://doi.org/10.3390/drones9020086






