Risk-Based Design of Urban UAS Corridors

Highlights

What are the main findings?

• An algorithm was developed to generate safe aerial corridors for drones by integrating a quantitative model that estimates both ground and air risk, allowing the selection of the trajectory with the lowest total exposure.
• A reproducible methodology was implemented to identify and classify high-risk or restricted zones, such as hospitals, airports, and densely populated areas, gen-erating risk maps that support the design of urban UAS corridors.

What are the implications of the main findings?

• The trajectories generated by the algorithm avoid critical and high-risk zones, ensuring safer operations and compliance with regulatory constraints in dense urban environments.
• The methodology enables the discretization of the urban space to determine, based on quantitative criteria, which sectors present higher operational risk, providing a practical tool for UAM corridor planning and regulatory deci-sion-making.

Abstract

The rapid expansion of Advanced Air Mobility (AAM) and Urban Air Mobility (UAM) poses significant challenges for the integration of Unmanned Aircraft Systems (UAS) into dense urban environments, where safety risks and population exposure are particularly high. This study proposes and applies a methodology based on probabilistic assessment of both ground and air risk, grounded in the principles of safety management and the use of geospatial data from OpenStreetMap (OSM), official aeronautical charts, and digital urban models. The urban area is discretized into a spatial grid on which independent risks are calculated per cell and later combined through a cumulative probabilistic fusion model. The resulting risk estimates enable the construction of cost matrices compatible with path-search algorithms. The methodology is applied to a case study in Medellín, Colombia, connecting the Oviedo and San Diego shopping centers through Beyond Visual Line of Sight (BVLOS) operations of a DJI FlyCart 30 drone. Results show that planning with the A* algorithm produces safe routes that minimize exposure to critical areas such as hospitals and restricted air corridors, while maintaining operational efficiency metrics. This approach demonstrates a practical bridge between regulatory theory and operational practice in UAM corridor design, offering a replicable solution for risk management in urban scenarios.

1. Introduction

Within the framework of AAM, an advanced air transportation system is envisioned through the use of electric or hybrid vehicles, including drones and electric Vertical Take-Off and Landing (eVTOL) aircraft, designed to operate in urban, suburban, and regional environments. According to the National Aeronautics and Space Administration (NASA) and the American Institute of Aeronautics and Astronautics (AIAA), these systems cover trajectories ranging from tens to hundreds of kilometers and reach altitudes of up to 1500 m, with an emphasis on efficiency, sustainability, and multimodal connectivity [1,2].

Within this broader paradigm, UAM focuses on short-distance flights within urban environments, intended for passenger transport, light cargo delivery, or emergency services. UAM holds the promise of mitigating road congestion, reducing travel times, lowering pollutant emissions, and enabling innovative logistical models in cities. However, this evolution also entails significant challenges, particularly due to the introduction of unmanned vehicles operating at low altitudes over densely populated areas [3].

Among the most pressing challenges is operational safety, stemming from the increasing likelihood of collisions with foreign objects (such as birds or other drones), urban structures, and potential technical failures. A recent study specifically examines the safety of eVTOL aircraft and UAS in urban environments, highlighting how low-altitude operations exacerbate these risks [4,5,6]. Added to this is the complexity of airspace design, which must incorporate corridors, geofences, and well-structured aerial networks; Yang et al. [3] review grid-based, stratification, and network models for organizing UAM airspace [6].

Operationally, low-altitude traffic management is addressed through the concept of Unmanned Traffic Management (UTM). This system provides digital services for the authorization, monitoring, and deconfliction of UAS and eVTOL flights within airspace not controlled by Air Traffic Management (ATM). Examples include the UTM programs developed by the Federal Aviation Administration (FAA) and the NASA in the United States, with tools such as Low Altitude Authorization and Notification Capability (LAANC), and their European counterpart known as U-space [7].

Several researchers and agencies have proposed frameworks to integrate operational safety into UAM and AAM through airspace management models, risk assessment methodologies, and separation schemes. The FAA Order 8040.6A UAS Safety Risk Management (SRM) Policy, effective since 1 September 2023, represents the official framework of the United States FAA for managing risk in UAS operations within the national airspace. It defines operational roles such as the Air Traffic Organization (ATO) and Aviation Safety (AVS), establishes triage criteria and SRM activation triggers, and incorporates a quantitative probability severity matrix along with a catalog of mitigable hazards (e.g., Communication, Navigation, and Surveillance (CNS) failures or collisions). This approach provides SRM with an institutionalized and repeatable character, aligning risk management with the FAA’s Safety Management System (SMS) policies [8].

For its part, the Specific Operations Risk Assessment (SORA) model, developed by the Joint Authorities for Rulemaking on Unmanned Systems (JARUS) and accepted by the European Union Aviation Safety Agency (EASA) as a means of compliance with Regulation (EU) 2019/947, establishes a rigorous and systematic 10-step methodology for evaluating the operational risk of specific UAS operations. This framework divides risk into two main components: the Ground Risk Class (GRC), which quantifies the probability and severity of ground damage based on variables such as population density, UAS mass, and velocity; and the Air Risk Class (ARC), which assesses the probability of midair collisions depending on the flight environment and the capabilities of CNS systems. The combination of GRC and ARC determines the Specific Assurance and Integrity Level (SAIL), which requires compliance with an increasingly demanding set of Operational Safety Objectives (OSO) tailored to the assessed level of risk [9].

From an academic perspective, Yang et al. [3] present a comprehensive review on the design of UAM airspace. Their study identifies three fundamental approaches: grid-based systems, vertical stratification, and node networks. They also analyze collision risk assessment models, emphasizing that each approach presents limitations in terms of scalability or adaptability to dynamic interferences [3]. To address real-time collision risk, Bijjahalli et al. [10] propose an air risk management framework that translates CNS system errors into spatial domains. By using virtual protection volumes and comprehensive collision probability models, this framework defines CNS performance requirements to meet a specific safety objective [10]. Another relevant study by Sláma et al. [11] highlights the impracticality of maintaining absolute no-fly zones in urban airspace due to high population density. Instead, they propose generating risk maps and applying algorithms such as Risk-A* to derive minimum-risk trajectories, thereby structuring safe corridor modules [12].

Sláma, Váňa, and Faigl [11] propose an effective solution for low-risk trajectory planning in UAM through the creation of safe corridors—secure zones derived from multiple optimized trajectories. Instead of executing complex methods for each individual flight, they construct a reusable graph that enables efficient and coordinated planning for multiple aircraft, significantly reducing computational load while generating less risky trajectories in realistic urban environments [11]. Verma et al. [13] investigate UAM corridor design in a realistic airport-adjacent setting, with the objective of reducing the workload of Air Traffic Control (ATC) and enabling safe operations of eVTOL aircraft. By applying Class B airspace separation criteria and wake turbulence advisory standards, they developed corridors in the Dallas–Fort Worth area that minimize ATC interactions and meet operational requirements under various airport traffic flow scenarios. Their results reveal that, although some segments do not satisfy standard separation criteria, corridors can be repositioned outside controlled airspace, thereby enhancing operational feasibility and limiting reliance on ATC [14].

Verma et al. [13] present a study focused on the design and analysis of UAM corridors in the Dallas–Fort Worth (DFW) area, with the objective of minimizing ATC intervention and facilitating integration with conventional aircraft. The study defines heuristics for delimiting three-dimensional air volumes within controlled airspace (Classes B, E, and G) and subjects the corridors to Class B separation and wake-avoidance criteria. The results indicate that certain segments do not meet standard separation or wake advisory requirements under north–south traffic conditions, suggesting the need to reposition portions of the corridor. This approach, evaluated through rapid simulations, demonstrates how to structure safe and efficient corridors for electric eVTOL operations in a complex airport environment [13].

In the context of large-scale traffic, Weng et al. [15] developed a framework that integrates route guidance and real-time collision avoidance. Using fast computational approaches and velocity obstacle models, this framework optimizes spatiotemporal distribution and prevents conflicts in multiple-corridor environments, demonstrating improvements of up to 70% in average speed compared to static corridors [15]. Regarding network infrastructure, Wei et al. [16] propose UAM network designs with redundancy—that is, alternative corridors and vertiports that mitigate operational disruptions. Through mathematical programming, they optimize traffic capacity under scenarios of failure or congestion [16]. Finally, in terms of separation and operational standards, Tang et al. [17] evaluated different minimum separation distances between UAM aircraft, as well as between UAM and conventional traffic, through rapid simulations in terminal approach areas. Their study provides operational metrics and proposes probabilistic parameters for the execution of evasive maneuvers [17].

Based on the gaps identified in the literature, such as the lack of integration between ground and air risk models, the high computational burden of multi-agent planning, and the need for tools tailored to dense urban environments, there arises a need for a methodological approach that combines operational efficiency with rigor in risk assessment. Accordingly, the objective of this research is to develop a model for the design of UAS corridors in urban environments, grounded in a risk analysis structured according to the SORA methodology. Ground risk was estimated through an adaptation of the Intrinsic Ground Risk Class (iGRC), considering environmental type, population density, and drone characteristics. Air risk was assessed as a function of proximity to Obstacle Limitation Surfaces (OLS) and controlled air traffic zones. Both factors were integrated into a continuous spatial matrix and used as input for an A* planning algorithm, aimed at generating routes that minimize cumulative risk exposure.

In summary, the proposed methodological framework is grounded in internationally recognized regulatory systems that define the principles of safety and risk management for UAS operations. At the global level, the FAA Safety Risk Management (SRM) Policy—Order 8040.6A (2023) institutionalizes a quantitative approach to hazard identification and mitigation within the Safety Management System (SMS), while the JARUS Specific Operations Risk Assessment (SORA v2.0), adopted by EASA under Regulation (EU) 2019/947, provides a harmonized methodology for assessing operational risk through Ground Risk Class (GRC), Air Risk Class (ARC), and Specific Assurance and Integrity Level (SAIL) criteria. At the national level, these frameworks are consistent with the Colombian Aeronautical Regulations (RAC 100), which establish operational, technical, and safety requirements for BVLOS missions within the specific category. By aligning with these regulatory standards, the present study bridges the conceptual structure of international UAS safety regulations with a quantitative, spatially explicit model suitable for practical implementation in urban environments.

2. Materials and Methods

This study proposes a structured methodology for designing safe urban air corridors for UAS by combining spatial risk analysis with optimal trajectory planning through search algorithms. First, the regulatory framework of the SORA is adapted to continuously estimate both Ground Risk Class (GRC) and ARC at the geospatial cell level, as previously applied in safety assessments of BVLOS flights in urban environments [18,19,20].

Next, integrated risk maps are generated to reflect population exposure, urban density, and proximity to controlled airspace or OLS, following recent methodologies such as Gao et al. [5] in the development of “3D virtual risk terrain”. Finally, the methodology incorporates trajectory planning through the A* algorithm applied to a cost grid derived from risk values, a technique consistent with prior approaches to safe drone navigation in urban areas [21,22]. This procedure enables the generation of reusable, low-risk corridors, facilitating the coordination of multiple UAS while reducing computational load compared to one-time query or random-sampling methods.

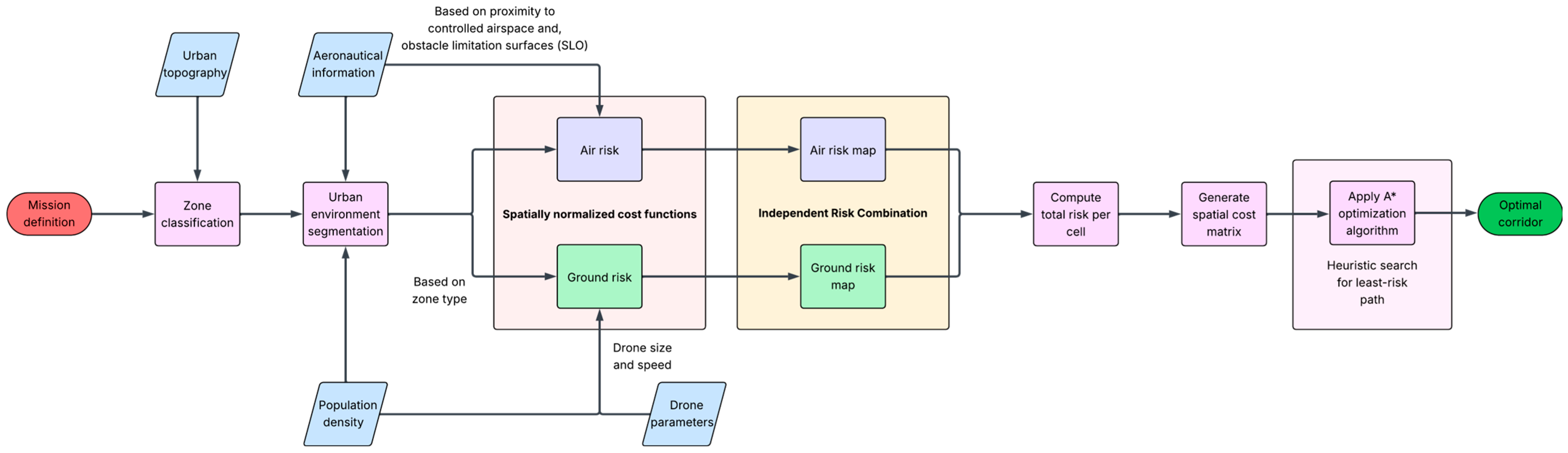
The methodology developed for the design of urban air corridors for UAS is illustrated in Figure 1. The process begins with the mission definition stage, where fundamental parameters such as the origin, destination, and operational conditions of the flight are established. Based on this information, an urban environment zoning classification is performed, integrating variables such as topography, population density, and available aeronautical data.

This enables the functional segmentation of urban space into areas of varying operational sensitivity. This segmentation feeds into two key blocks of risk evaluation. On the one hand, ground risk is estimated based on drone characteristics (mass and velocity) and zonal classification, generating a spatially normalized cost function associated with the potential severity of impact. On the other hand, air risk is determined by the proximity to OLS and controlled airspace, considering the aeronautical environment and potential conflicts with manned aviation. Both risk dimensions are represented as independent maps, which are then combined through an independent risk combination process to generate a spatial matrix of total risk per cell. This matrix quantifies, at each point in space, the cumulative exposure to risk derived from both ground and air conditions. A heuristic A* search algorithm is applied to this matrix to optimize the trajectory according to the criterion of minimum cumulative risk. The result is an optimal air corridor whose geometry ensures a viable route for UAS in dense urban environments, while simultaneously minimizing exposure to high operational risk conditions.

2.1. Mission Definition

The mission definition phase establishes the objectives and fundamental parameters that guide the entire air corridor planning process. In this stage, the origin and destination points are determined, along with the nature of the mission (e.g., cargo delivery, technical inspection, or urban surveillance), which will shape the operational profile of the flight and its safety requirements. In addition, the technical parameters of the UAS are recorded, including mass, dimensions, cruise speed, endurance, and maneuvering capability. These elements are essential for assessing ground risk, since they determine the potential damage in case of impact, and for evaluating air risk, as they influence the aircraft’s ability to avoid obstacles and potential victims.

Finally, operational environment constraints are incorporated, which include regulatory limitations (e.g., no-fly zones, altitude limits), urban geomorphology (presence of buildings and elevations), and aeronautical aspects (controlled airspace and OLS), all of which provide critical contextual information [23,24].

The outcome of this phase is a formal mission specification that consolidates:

• The destination and purpose of the flight;
• The characteristics of the drone;
• The technical, legal, and environmental constraints.

2.2. Urban Zone Classification

This step focuses on the georeferenced identification of urban Points of Interest (POI), using OSM as the primary data source. At this stage, no risk values are calculated, and no raster exposure layers are generated; instead, the purpose is to build a reliable inventory of critical infrastructures for subsequent spatial classification. To achieve this, geographic records corresponding to relevant infrastructures within the study area are extracted, including hospitals, airports, heliports, police stations, city halls, main roads, and residential zones.

These POI datasets are carefully reviewed and validated to ensure their accuracy and coverage, following practices that have been evaluated in prior research on the quality and usefulness of OSM as a source of urban geospatial data. The selection of urban elements is based on the standard semantic tagging provided by OSM (e.g., amenity = hospital, aeroway = airport, aeroway = helipad, etc.) [25].

The outcome is structured as a table or vector layer that stores, for each POI, its operational classification and coordinates. This inventory does not include risk analysis; rather, it serves as an essential and prevalidated input for the subsequent phase of urban environment segmentation, ensuring that only relevant and validated POIs are included in the stages of spatial labeling [26].

2.3. Urban Environment Segmentation

The urban environment segmentation phase integrates urban and aeronautical geospatial resources with the objective of mapping and classifying infrastructures and critical zones relevant to UAS operations. Data from OSM are combined with Digital Terrain Models (DTM) and Digital Surface Models (DSM), municipal cadastral records, and aeronautical charts from the Aeronautical Information Publication (AIP). These charts include information on heliports, airports, prohibited areas (“P”), restricted areas (“R”), military zones, and training areas, as well as OLS [27].

The conceptual process is based on an automated geospatial extraction and modeling module, inspired by OSMnx, which performs three fundamental tasks: (1) systematic querying of the region of interest to retrieve infrastructures and POI tagged in OSM, (2) processing of AIP charts to obtain regulated airspace zones, and (3) generation of a circular buffer with a 1 km diameter around heliports to delineate their operational influence area. At this stage, the POIs had already been preselected in the previous phase, ensuring that only validated elements are incorporated into the final segmentation.

The resulting data are integrated into a georeferenced vector structure, where each spatial entity (point or polygon) receives a corresponding label, for example, hospital_zone, military_zone, residential_zone, road_zone, or airport_zone, without the assignment of quantitative risk values. This labeling constitutes a functional spatial inventory that establishes the foundation for risk estimation in subsequent phases.

As output, a classified GeoJSON file is generated, containing geometries labeled by type of infrastructure or air zone, ready to feed into the ground risk assignment phase $\left(R_{base}\right)$ and the air risk proximity assessment (Air Risk Class, ARC). This automated, reproducible, and scalable approach is consistent with studies that employ OSMnx for the extraction and analysis of complex urban networks, ensuring both geographic accuracy and topological consistency [28,29].

2.4. Ground and Air Risk Estimation

This section describes the method for estimating the operational risk of UAS missions across two complementary dimensions: Ground Risk and Air Risk, following the methodological framework of the SORA [9]. The estimation begins with the iGRC, which considers the physical characteristics of the vehicle and the population density in the operational area [30]. In parallel, air risk (Air Risk Class, ARC) is assessed based on proximity to controlled airways, type of airspace, and the density of manned traffic, using standardized decision trees [31].

Both risk components are then combined to obtain a total risk value per location, through probabilistic fusion under the assumption of statistical independence. This approach enables the quantification of overall risk exposure and provides critical input for subsequent stages of route planning and the design of urban corridors [32].

2.4.1. Ground Risk

Ground risk is understood as the probability of potential harm to people or property in the event of loss of control of the UAS. It is conceptualized as an index $\left(GR{I}_{zone}\right)$ that quantifies the intrinsic exposure of each category of urban infrastructure to the operational passage of an unmanned aircraft, adjusted by the characteristics of the vehicle (size and speed). Normatively, this concept is grounded in the SORA methodology developed by the JARUS and accepted by the EASA. This metric is derived from the calculation of the iGRC [33].

The methodological estimation of ground risk consists of three stages. First, the Critical Area of the UAS is calculated, defined as the ground area where a fatal impact is likely to occur in the event of a failure. This calculation follows the physical model specified in Annex F of the SORA, considering characteristics such as the maximum size of the UAS, its cruise speed, and its kinetic energy upon impact. In particular, the JARUS low-speed model is used as the default, with an alternative based on steep-angle descent (≥60°) for multi-rotor aircraft or vehicles without gliding capability [34]. In parallel, the population density of the operational environment is analyzed.

According to SORA, it is necessary to identify the maximum population density within the route volume and contingency corridor, using official data with adequate resolution (e.g., 200 × 200 m or 400 × 400 m depending on altitude) [34]. For this study, population density data for the city of Medellín were obtained from the WorldPop 2023 dataset with a 100 m grid resolution, calibrated with demographic data from the DANE. The weighting factor w(ρ_p) represents the relative density of each grid cell, normalized to [0, 1] according to thresholds derived from the urban structure of Medellín:

• ρ_p > 20,000 hab/km² → w(ρ_p) = 1.0 (high density);
• 10,000 ≤ ρ_p ≤ 20,000 → w(ρ_p) = 0.5 (medium density);
• ρ_p < 10,000 → w(ρ_p) = 0.2 (low density).

Second, a base risk value $\left(R_{base}\right)$ is calculated by combining the Critical Area with the population density of the operational environment. This value is normalized within the interval [0, 1], so that critical zones such as airports or military areas are assigned high $R_{base}$ values (≥0.85), while low-criticality zones receive lower values (≈0.15–0.30) [34]. The equation for deriving $R_{base}$ is as follows:

$$R_{base,i}={\displaystyle \frac{A_{crit,i}}{{max}_j A_{crit,j} }} w({\rho }_p),$$

(1)

where $A_{crit,i}$ is the Critical Area associated with zone category i; ${max}_j A_{crit,j}$ is the maximum Critical Area observed among all categories considered; and $w({\rho }_p)$ is a weighting factor that reflects population density (e.g., 1.0 for high-density zones and 0.5 for medium-density zones) [35].

To capture the effect of the operational components of the UAS, specifically its size $\left(L\right)$ and velocity $\left(V\right)$, a linear sensitivity model is introduced:

$$GRI=\mathrm{m}\mathrm{i}\mathrm{n} (R_{base} ·\left(1+\alpha ·L+\beta ·V\right), 1.0),$$

(2)

where $R_{base}$ is the intrinsic risk value associated with the zone category, normalized within the interval [0, 1]; $L$ corresponds to the characteristic dimension of the UAS, defined as the maximum diagonal of the aircraft including propeller span (in meters); $V$ is the UAS velocity (m/s), typically the maximum cruise or terminal speed; and $\alpha and \beta$ are sensitivity coefficients that adjust the influence of size and velocity on operational risk. $\alpha and \beta$ quantify how risk varies with changes in the physical characteristics of the vehicle. Calibration is carried out based on probabilistic models and empirical statistical analyses, supported by the literature on operational risk assessment for UAS [36].

The coefficients $\alpha and \beta$ were obtained through empirical calibration, combining data from the literature on urban UAS safety and a Monte Carlo simulation dataset of 1000 synthetic flight events [37]. This dataset sampled UAS dimensions, speeds, and population densities representative of typical logistics operations in urban areas. The calibration process followed a least-squares optimization minimizing the residuals between observed or simulated risk values $R_{obs,k}$ and the estimated $R_{base,i}·\left(1+\alpha L_K+{\beta V}_k\right)$:

$${\displaystyle \frac{min}{\alpha ,\beta }}\sum _{k=1}^N{(R_{obs,k}-R_{base,i}·\left(1+\alpha L_K+{\beta V}_k\right))}^2,$$

(3)

This statistical procedure identifies the values of $\alpha and \beta$ that best explain how variations in size and velocity influence the final estimated risk. The approach is consistent with methods applied in the literature that model the probability of damage as a function of kinetic energy, population density, and the mass of the UAS [38].

The coefficients have the following interpretation: α represents the incremental increase in risk per additional meter of UAS size, reflecting the proportional growth of the impact footprint, while β represents the incremental increase in risk per additional meter per second of velocity, capturing the sensitivity of ground impact energy.

For instance, in the aero_zone category (areas adjacent to airport facilities), α = 0.020 and β = 0.010, meaning that each additional meter of diagonal or each 1 m/s increase in velocity raises the adjusted ground risk by approximately 2% and 1%, respectively, relative to R_base. Conversely, for roadway areas, the coefficients are notably smaller (α ≈ 0.004, β ≈ 0.002), indicating lower sensitivity to size and speed due to reduced intrinsic exposure.

To illustrate, the model was applied using the DJI FlyCart 30 specifications (L = 3.0 m, V = 20 m/s) and representative R_base values for several urban categories.

Table 1. Example of Ground Risk Index (GRI) computation for representative urban zone categories using the DJI FlyCart 30 (L = 3.0 m, V = 20 m/s).

Zone Category	R_base	α	β	Computed GRI	SORA Risk Level	Interpretation
Aero_zone (airport vicinity)	0.80	0.020	0.010	0.97	High (≥0.81)	Critical zone near airport operations; exposure increases sharply with velocity.
Urban_high_density (CBD/commercial)	0.70	0.015	0.008	0.88	High	High probability of third-party exposure; moderate risk growth with size.
Residential_moderate	0.55	0.010	0.005	0.74	Moderate	Densely built but not critical; risk remains below SORA high threshold.
Roadway (arterial corridors)	0.40	0.004	0.002	0.55	Moderate–Low	Transient pedestrian exposure; minimal sensitivity to velocity.
Park_or_open_space	0.25	0.002	0.001	0.32	Low	Open areas with low population density; negligible incremental risk.

shows the resulting Ground Risk Index (GRI) values obtained for each case.

These results are consistent with the spatial pattern observed in the Medellín case study, where aero_zone and urban_high_density sectors reach High Ground Risk Index (GRI ≥ 0.81) values due to the concentration of population and critical infrastructure. In contrast, urban_moderate and roadway_corridor areas maintain Moderate exposure levels, reflecting intermediate population densities and lower operational criticality, while suburban_green zones remain within the Low-Risk range.

This behavior confirms the model’s ability to accurately distinguish exposure gradients according to the urban typology, demonstrating spatial coherence in the relationship between density, infrastructure type, and operational risk. By calibrating the sensitivity coefficients α and β through empirical and simulated data, the model achieves three key objectives: (i) it provides a quantitative estimation of how ground risk scales with vehicle size and velocity; (ii) it adapts the formulation to different UAS classes and urban morphologies; and (iii) it ensures consistency with the SORA methodological framework, which integrates exposure time, mass, and kinetic energy into ground-risk estimation.

2.4.2. Air Risk

The estimation of air risk for UAS operations in urban environments is based on a quantitative evaluation model of critical variables related to the probability of interaction with conventional air traffic. This risk is calculated through a weighted formulation that integrates three fundamental components: general air traffic density ($D$), helicopter traffic intensity (H) and proximity to obstacle limitation surfaces (A), all defined within the interval [0, 1]. The adopted air risk function is:

$$R_{air}=\left({\gamma }_1·D+{\gamma }_2·H+{\gamma }_3·A\right)·\delta \left(h\right),$$

(4)

To avoid dependence on real aircraft positional data—often incomplete or restricted due to confidentiality and limited temporal coverage—this study adopted the Obstacle Limitation Surfaces (OLS) defined in ICAO Annex 14, Volume I, as a spatial proxy for the operational volumes used by manned aircraft. These surfaces were treated as reference envelopes for conventional traffic, representing potential zones of interaction between unmanned and manned operations.

This approach enables air-risk estimation based on well-defined aeronautical geometries such as take-off, approach, transitional, and inner horizontal surfaces, ensuring methodological reproducibility even in the absence of detailed radar datasets.

The variable D represents the relative density of air traffic as a function of whether a route intersects with critical zones known as OLS. Among these surfaces, the most critical is the Take-Off and Final Approach Surface (TOFPA), which encompasses runways and their approach strips. This zone concentrates the highest level of aeronautical activity, as aircraft are in the most sensitive flight phases—take-off and final approach—where any interaction represents elevated risk.

Surrounding the TOFPA is the transitional surface, which protects the lateral sides of the runway axis and provides space for entry and exit maneuvers. Beyond this lies the inner horizontal surface, covering areas farther from the operational center at relatively constant altitudes, where traffic density is lower but still under airport control. When there is no intersection with any OLS, the environment is considered to have low air activity, typically lacking nearby airport infrastructure and characterized by dispersed or sporadic traffic [39].

The values of $D$ are derived from a model weighted by proximity and density, expressed as:

$$D\left(s\right)={\omega }_s, { \omega }_sϵ[0,1],$$

(5)

where $s$ represents the type of OLS. The values of $D\left(s\right)$ reflect the expected average exposure, determined by the observed frequency of air traffic within each type of surface and by the operational proximity to approach and take-off maneuvers versus peripheral areas.

The variable H corresponds to the relative intensity of helicopter traffic within the analysis area. Its estimation is based on the spatial overlap between the planned UAS trajectory and the helicopter routes published in the AIP Colombia [40]. These routes represent the authorized and routinely used corridors by rotary-wing aircraft under VFR conditions in urban and suburban areas of the country.

Routes were treated as bidirectional corridors with operational altitude bands between 500 ft and 1500 ft AGL, consistent with typical rotary-wing profiles in metropolitan environments such as Medellín. Each route was modeled as a central polyline with a lateral buffer of ±250 m (total width 500 m), corresponding to the minimum horizontal separation between two aircraft operating under VFR conditions, as defined in ICAO Annex 2, Doc 4444 (PANS-ATM) [41]. The parameter H was assigned as H = 1 for cells intersecting the helicopter corridor, decaying linearly to H = 0 at lateral distances greater than 500 m.

This approach reflects the incremental risk of sharing airspace with aircraft that operate at altitude ranges similar to those of UAS, and that in many cases do not follow rigid routes like commercial aviation. The use of actual routes obtained from official aeronautical charts and visual navigation data enabled the construction of an intensity map that serves as an input for air risk estimation, consistent with criteria previously suggested in studies on urban airspace management [42,43,44].

The variable A represents a relative proximity index between the UAS and critical airport infrastructures such as runways, taxiways, aprons, and heliports. This parameter is essential in air-risk analysis since proximity to airport zones directly correlates with the likelihood of conflict with manned aircraft and the need for coordination or separation. The minimum geodesic distance d between each cell of the projected UAS trajectory and the perimeter boundaries of airport infrastructure was computed using the AIP Colombia geospatial datasets [42,43,44].

The proximity index was normalized within [0, 1], where $A$ = 1 corresponds to direct intersection with an airport or heliport safety perimeter (critical zone), and $A$ = 0 corresponds to distances beyond 3 km. Intermediate distances were modeled using an exponential decay function:

$$A\left(d\right)=e^{-\lambda d},$$

(6)

where d is the distance (m) to the nearest critical infrastructure, and λ is an attenuation coefficient. For the Medellín case study, λ = 0.004 m⁻¹ was used, calibrated empirically so that A(d) ≈ 0.01 at approximately 1150 m from the airport perimeter. This calibration aligns with sensitivity analyses of proximity-based conflict modeling in terminal airspace [42,43,44].

To account for the variability of air risk as a function of operational altitude, an altitude correction coefficient denoted as $\delta \left(h\right)$, is incorporated, which adjusts the final estimated air risk value. This factor considers the differential exposure faced by unmanned aircraft when operating at different vertical levels within very-low-altitude airspace. The weighting function $\delta \left(h\right)$ is defined by altitude segments based on the analysis of relative air traffic density and probability of interaction, as follows:

$$\delta \left(h\right)=\left\{\begin{array}{c}1.0, si h\ge 300\mathrm{ft},\\ 0.7, si 150\le h<300\mathrm{ft}\\ 0.4, si h<150\mathrm{ft}.\end{array}\right.,$$

(7)

The breakpoints at 150 ft and 300 ft AGL were defined via analysis of vertical traffic density data in the case-study metropolitan area and align with conceptual very-low-altitude segmentation used in UAS operations. The ratios (1.0, 0.7, 0.4) reflect exposure gradations from near-ground to shared manned-aircraft corridors. These thresholds are considered generalizable to other urban contexts, although numerical calibration may be adapted based on local heliport density and air-traffic profile [45,46].

The selection of three altitude bands was intentionally designed to balance operational realism and computational efficiency.

The first band (<150 ft AGL) corresponds to typical UAS take-off and landing envelopes and low-level logistics operations, where the probability of encounter with manned aircraft is negligible. The second band (150–300 ft) captures transitional segments that occasionally overlap with helicopter routes and U-space tactical operations. The upper band (>300 ft) represents the threshold of increased exposure, where conventional traffic and VFR operations are most likely to occur.

This tripartite segmentation mirrors the very-low-level (VLL) structure adopted in international frameworks such as the EASA U-space Concept of Operations [47], and the JARUS WG-105 Specific Operations Risk Assessment [9], both of which employ discrete altitude intervals to characterize operational exposure.

Preliminary tests with finer segmentation (e.g., 100 ft intervals) did not yield significant improvements in predictive accuracy (<2% variation in cumulative risk), confirming that the three-level model is sufficient to capture vertical risk gradients while maintaining methodological simplicity and interpretability.

2.5. Independent Risk Combination

A comprehensive evaluation of the risk associated with an aerial trajectory cannot be limited to a single domain. Since UAS operations pose potential impacts both on the ground environment and within the airspace, it is necessary to integrate both components into a single composite risk metric [33]. To achieve this, a probabilistic aggregation model is adopted, which accounts for the joint occurrence of adverse events on the ground and in the air, expressed as follows:

$$R_{Total}=1-\left(1-R_{ground}\right)\left(1-R_{air}\right),$$

(8)

The equation is based on the complementary probability rule for non-mutually exclusive events. Assuming that $R_{ground}$ and $R_{air}$ represent the independent probabilities of an adverse event occurring in each domain, the probability that no event occurs is the product of their complements; therefore, the total risk probability (at least one of the two events occurring) is defined as the complement of that product. This approach enables modularity in modeling, since the components can be estimated separately; it is conservative, as a high value in either risk component is immediately reflected in the total risk; and it maintains the metric normalized within [0, 1], thus facilitating comparisons across routes and scenarios [9,38].

2.6. Cost Matrix per Geographic Cell

Terrain segmentation constitutes the structural foundation of the risk calculation model, enabling the representation of the urban study area as a finite set of discrete spatial units through a regular grid $\mathcal{G}$. This procedure is implemented by generating a regular mesh of square cells, which serves as the framework for geospatial analysis [9]. Formally, let $\mathrm{A}\subset {\mathbb{R}}^2$ denote the spatial domain corresponding to the study area. A partition of this domain is defined as a set of cells ${\left\{c_i\right\}}_{i=1}^n$, such that:

$$\mathcal{G}=\bigcup _{i=1}^n{c}_i where c_i\in {\mathbb{R}}^2 and area \left(c_i\right)=r^2,$$

(9)

where $r$ is the spatial resolution (e.g., 1 m or 5 m). This grid models the terrain as a finite spatial structure, facilitating both vector and raster processing of georeferenced data. Each cell $c_i$ is treated as an independent unit for risk evaluation, with attributes derived from layers of ground infrastructure (POIs) and airspace elements (OLS, corridors, etc.) [9,26,33]. Each cell $c_i$ contains two main risk components: ground risk $R_{ground}$ and air risk $R_{air}$, previously defined through structured models based on sensitivity functions relative to operational and geographic variables. The total risk $R_{Total}$ is then calculated using the principle of cumulative probabilistic fusion of independent events.

From this total risk matrix, a cost matrix $C\in {\mathbb{R}}^{mXn}$, is constructed, which is fundamental for the implementation of trajectory planning algorithms. In this context, each cell $c_i$ with discrete coordinates $\left(x_i,y_i\right)$ is assigned a cost value $C\left(x_i,y_i\right)$, which is modeled as an increasing function of the total risk previously determined for that cell [9].

Formally, the cost function is expressed as:

$$C\left(x_i,y_i\right)=f\left(R_{total,i}\right) with f:\left[0,1\right] \to {\mathbb{R}}^{+},$$

(10)

With $f$ defined as a penalized linear function of the form:

$$f\left(R\right)=1+k·R,$$

(11)

The cost function transforms the normalized total risk ($R_{total,i}$) into a positive traversal cost used by the trajectory optimization algorithm. It follows the penalized linear form defined in Equation (11), where $k\ge 0$ is a penalty parameter that amplifies the influence of local risk on route selection. Larger kkk values strongly discourage trajectories crossing high-risk areas by increasing their associated cost, whereas smaller values allow a more balanced trade-off between safety and efficiency. This formulation ensures that cells with higher perceived risk are assigned proportionally greater costs, effectively steering the algorithm toward safer and more operationally robust paths [33,48].

Once the cumulative total risk has been calculated, the results are consolidated and represented on a geospatial basis in GeoJSON format, using segmented polygons that reflect functional territorial units such as residential, hospital, commercial, or industrial areas, as well as air-exclusion zones. Instead of displaying a grid of unit cells, the visualization groups cells according to their membership within the same geographic polygon, producing a more structured and readable thematic map suitable for operational and regulatory decision-making [49].

Each geographic entity in the GeoJSON file contains the following elements: the polygon geometry defined by the spatial boundaries of the urban or aerial segment (e.g., a hospital area or the contour of an OLS), the cumulative total risk value calculated from the aggregation of the risks of the cells included within that polygon (either through weighted averages or maximum values, depending on the adopted safety criterion), the polygon identifier, and the zone type (e.g., hospital, military zone, transitional airspace). This representation allows for a more synthetic interpretation of risk levels, facilitating strategic analysis for UAS route planning, the delineation of prohibited or restricted flight zones, and the evaluation of population exposure [50].

2.7. Application of the A* Algorithm for Risk-Penalized Route Planning

Optimal trajectory planning for UAS in dense urban environments requires the use of search algorithms that account for both route efficiency and exposure to operational risk factors. In this context, the A* algorithm has been consolidated as a suitable solution due to its ability to identify minimum-cost routes over weighted graphs, while employing admissible heuristics that enable efficient path optimization. This algorithm has been extensively validated in applications such as robotic navigation, geospatial analysis, and automated planning [51,52].

For its application, the environment previously segmented through a regular grid is modeled as a directed and weighted graph.

$$G=\left(V,E\right),$$

(12)

where $V$ represents the set of nodes. Each node $v_i\in V$ corresponds to a cell $c_i$ of the spatial grid, and $E$ is the set of edges. An 8-neighbor connectivity is established, allowing each node to be connected with the eight adjacent cells (horizontal, vertical, and diagonal), thereby increasing realism in navigation. Each edge $e_{ij}\in E$, which connects node $v_i$ with node $v_j$, is weighted with a transit cost associated with the destination cell $C_J$, defined as an increasing function of the previously calculated total risk:

$$Costo\left(e_{ij}\right)=(1+k_d·d_{ij})·\left(1+k·R_{total,j}\right),$$

(13)

where $d_{ij}$ is the Euclidean distance between the two nodes $R_{total,j}$∈ [0, 1] is the normalized total risk at the destination cell, $k$ is a risk weighting coefficient, and $k_d$ is a distance penalty factor.

This formulation ensures that both safety and efficiency contribute to the cost function: larger $k$ values prioritize safer routes by penalizing high-risk zones, whereas higher $k_d$ values favor shorter trajectories and reduced flight time. In this study, $k=1.0$ and $k_d=0.25$ were empirically calibrated to provide an optimal compromise between minimal exposure and realistic operational feasibility for the DJI FlyCart 30. Consequently, the A* algorithm does not exclusively minimize risk, but rather seeks a balanced trade-off between safety and flight efficiency, consistent with practical mission-planning requirements [53].

The A* algorithm searches for the minimum-cost path from a source node $s\in V$ to a destination node $d\in V$, by minimizing a composite evaluation function:

$$f\left(n\right)=g\left(n\right)+h\left(n\right),$$

(14)

where $g\left(n\right)$ is the accumulated cost from the initial node to the current node $n$, calculated as the sum of risk-weighted costs in each transition, and $h\left(n\right)$ is the heuristic function that estimates the remaining cost from the current node $n$ to the destination node $d$ [51,52].

In this study, the heuristic used is the Euclidean distance between the current node and the destination:

$$h\left(n\right)=\sqrt{{\left(x_n-x_d\right)}^2+{(y_n-y_d)}^2},$$

(15)

This heuristic satisfies the admissibility and consistency conditions for A* and integrates coherently with the implemented octagonal connectivity graph. Once the planning process is completed using the A* algorithm, the optimal route is represented as an ordered sequence of connected nodes that describe the trajectory from the origin point to the destination. This trajectory is structured as a LineString geometry and exported in GeoJSON format.

The GeoJSON file contains the geographic coordinates of each point along the trajectory in WGS 84 (latitude and longitude in decimal degrees), allowing its interpretation as a series of waypoints that can be directly used in autonomous or semi-autonomous UAV missions. These waypoints can be processed by flight control systems or exported into other compatible formats such as KML, GPX, or CSV, depending on the mission-planning software used. In addition to the main route geometry, the file can be enriched with supplementary attributes such as total distance traveled, accumulated risk along the trajectory, average or segment-specific altitude, and the intended mode of operation (e.g., cruise, descent, or surveillance). This complementary information enables a more comprehensive mission assessment in terms of operational safety, energy efficiency, and regulatory compliance, particularly in urban areas where restrictions are stricter.

3. Results

In order to validate the applicability of the proposed model for UAS trajectory planning in urban environments, a test scenario was designed to simulate a logistics operation under real-world conditions. This scenario integrates all the methodological stages previously developed, from terrain segmentation and geospatial risk calculation to the generation of the cost matrix and the execution of the A* search algorithm, with the objective of evaluating its performance in a complex and densely populated environment. The implementation was carried out using real data, discrete spatial structures, and operational criteria compatible with current unmanned traffic management (UTM) systems.

3.1. Mission Definition (Case Study)

The selection of Medellín as the application scenario for this methodology is justified by its complex geographical configuration, characterized by mountainous terrain that limits urban expansion and constrains the design of air corridors for UAS. This particular feature, combined with high population density and the presence of critical infrastructure such as airports and major road axes, makes the city an ideal environment for evaluating route planning methodologies that integrate both risk and operational efficiency criteria.

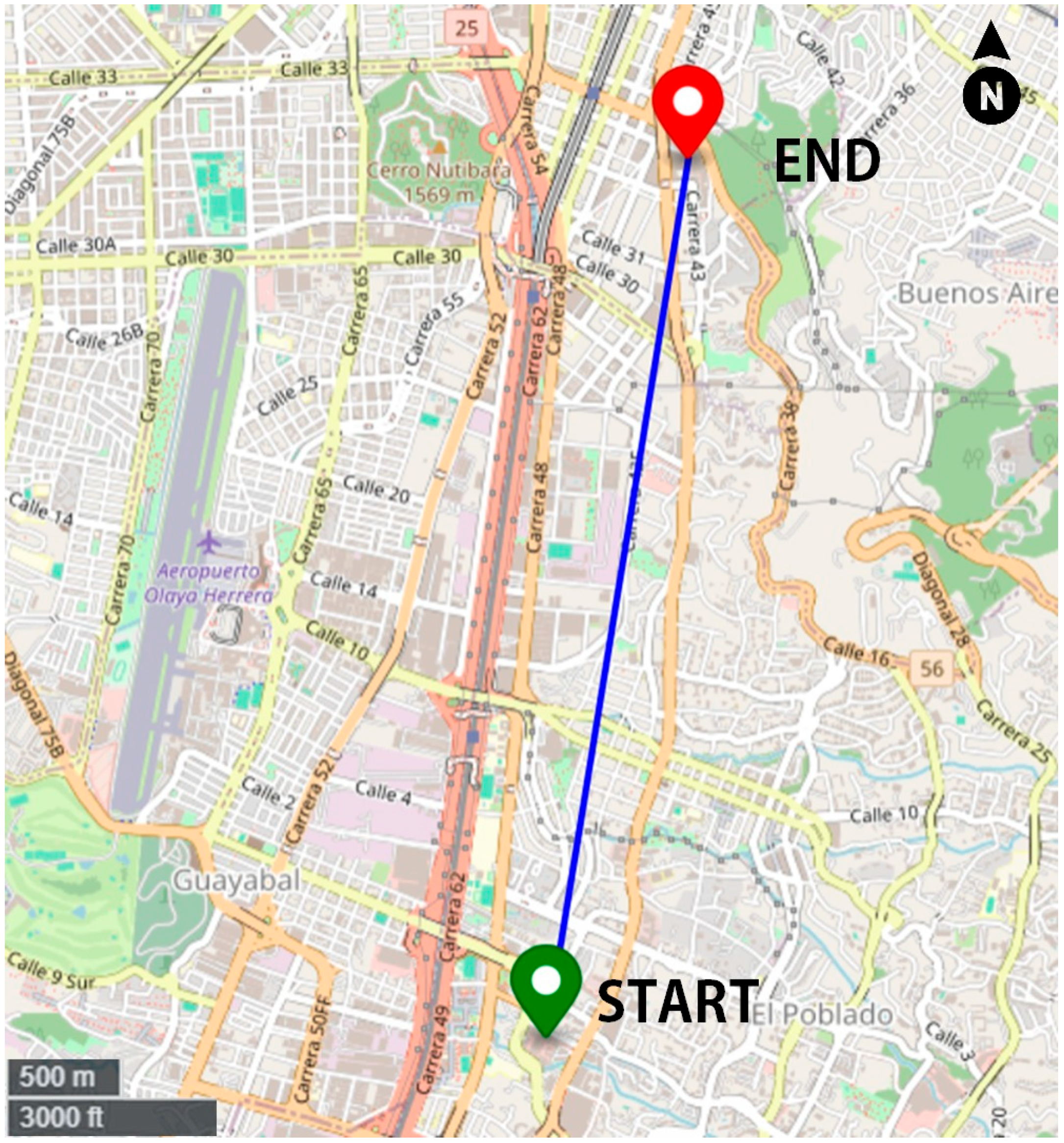
In this study, the mission objective was defined as the design of a route connecting the Oviedo Shopping Center with the San Diego Shopping Center, both located in strategic, high-traffic areas of Medellín. This choice enables the analysis of the feasibility of integrating UAS operations into a real urban context, connecting two relevant commercial hubs and simulating a logistics or rapid delivery scenario. The geographic coordinates used to define the mission correspond to the Oviedo Shopping Center (latitude 6.2358°, longitude −75.5692°) and the San Diego Shopping Center (latitude 6.1997°, longitude −75.5751°).

In Figure 2, the base map of the city is presented with the geographic location of the route’s start and end points. The green marker (START) corresponds to the Oviedo Shopping Center, located in the southern part of the city, while the red marker (END) indicates the San Diego Shopping Center, situated further northeast in proximity to major road corridors. The cartography used is derived from OpenStreetMap data, showing the main roads, neighborhoods, and the Olaya Herrera Airport, whose presence introduces additional considerations of operational safety and airspace restrictions.

The geodesic distance between the two points is approximately 4.3 km, which categorizes the operation under the concept of BVLOS, given the limitations of direct visibility in a dense urban environment with tall buildings. This type of operation requires more rigorous planning, as well as the use of reliable navigation and communication systems to ensure operational safety throughout the entire route.

For the development of the mission, the technical capabilities of the DJI FlyCart 30 were considered. This cargo drone is specifically designed for medium- and long-range logistics operations. The model features redundant twin-motor propulsion and advanced flight control systems that enhance safety in BVLOS operations. Its payload capacity reaches 30 kg, while its flight endurance with maximum load is approximately 16 km, extending to more than 28 km with reduced payloads. The drone operates at a cruise speed of around 20 m/s (72 km/h), which allows it to cover the distance between Oviedo and San Diego in about 3.5 to 4 min under nominal conditions, not accounting for margins required for maneuvers or adverse environmental factors.

In terms of performance, the DJI FlyCart 30 is equipped with high-capacity TB65 intelligent batteries featuring thermal management and real-time monitoring, optimizing energy efficiency while reducing risks associated with power failures. In addition, it incorporates an omnidirectional detect-and-avoid system with an effective range of over 50 m, making it well-suited for navigating obstacles in complex urban environments. The flight control system supports both automatic and semi-automatic modes, enabling the drone to execute preprogrammed waypoint trajectories and perform dynamic adjustments in response to environmental changes or flight conditions [54].

3.2. Zone Classification (Case Study)

The second stage of the case study corresponds to the classification of critical urban zones, based on the georeferenced identification of POI within the Medellín area. For this purpose, OSM data were primarily employed, complemented with manual verification to ensure consistency in the location of key infrastructures. This phase does not aim to calculate risk values but rather to build an inventory of relevant infrastructures that will support subsequent risk estimation and spatial segmentation. The POIs identified include categories such as airports, heliports, hospitals, police stations, city halls, shopping centers, fuel stations, military bases, main roads, residential areas, parks, and other urban areas of strategic interest. The classification follows OSM geospatial tagging standards, which are widely documented in studies on the quality and applicability of these data in dense urban environments.

Figure 3 is the geographic representation of the identified POI in Medellín. Each marker corresponds to the centroid of a detected infrastructure and is displayed with a distinctive color according to its classification. Red markers represent airports and heliports (aero_zone); orange markers correspond to fuel stations (flammable_zone); green markers indicate city halls and government buildings (cityhall_zone); blue markers denote hospitals and healthcare centers (hospital_zone); and finally, purple markers represent shopping centers, residential areas, parks, and other urban services (commercial_zone, residential_zone, park_zone, and point_interest).

To complement the visualization,

Table 2. Zone categories identified and colors assigned in the thematic map.

Category	Description	Map Color
zona_aero	Airports and heliports	Red
zona_inflamable	Fuel stations	Orange
zona_alcaldia	City halls and government buildings	Green
zona_hospital	Hospitals and healthcare centers	Blue
zona_comercial	Shopping centers	Purple
zona_residencial	Residential areas	Purple
zona_parque	Parks and recreational areas	Purple
punto_interes	Cultural/social infrastructure	Purple
zona_militar	Military bases and police stations	Red
zona_otras	Other complementary infrastructures	Purple

presents a summary of the detected zone categories, and the color assigned to each zone. This information constitutes the essential input for the urban environment segmentation stage and the subsequent assignment of risk levels.

3.3. Urban Environment Segmentation (Case Study)

Urban environment segmentation was carried out using the OSMnx library, widely applied in urban spatial analysis and infrastructure planning. This tool transforms OSM data into structured mathematical representations, generating a computational model of the urban environment in the form of graphs and polygonal geometries. The approach employed integrates both the previously identified critical infrastructures and the spatial elements that define the urban and aeronautical dynamics of Medellín.

From a technical perspective, OSMnx organizes OSM data within a vector framework that combines two main components: nodes and edges. Nodes correspond to georeferenced coordinates representing intersections, infrastructure points, or polygon vertices, while edges are segments that connect adjacent nodes, representing roads, urban perimeters, or functional boundaries. Based on these structures, topological geometries are constructed to accurately represent elements such as residential blocks, parks, main roads, commercial zones, and airport areas.

The applied process consisted of extracting and delineating areas of urban interest based on standardized semantic tags in OSM (e.g., amenity = hospital, aeroway = airport, landuse = residential) and transforming them into coherent geographic polygons. In the case of airport zones, the data were complemented with official aeronautical charts from the Colombian AIP, which allowed the incorporation of OLS, prohibited and restricted zones, and air training areas. For heliports, where the information available in OSM is often limited to point data, an operational radius equivalent to 500 m around their location was defined, generating a circular zone of 1 km in diameter that represents their area of influence.

Finally, the segmented urban environment was consolidated into a GeoJSON file, in which each polygon is associated with a functional category such as hospital, residential area, park, commercial zone, or airport infrastructure. This polygonal representation not only facilitates visualization in geographic information systems (GIS) such as QGIS or Leaflet but also serves as a fundamental input for the calculation of both ground and air risk.

Figure 4 presents the result of this process, where the different infrastructure categories are visually distinguished, providing an integrated view of the classified urban environment.

Table 3. Ground risk parameters by zone category.

Category	Color	Number of Polygons	Total Area (m2)
aero_zone	Red	2	1,523,487
military_zone	Blue	1	842,935
hospital_zone	Green	5	356,412
flammable_zone	Orange	3	127,544
cityhall_zone	Purple	1	48,956
commercial_zone	Yellow	8	679,234
road_zone	Brown	12	1,945,327
park_zone	Pink	6	1,134,223
residential_zone	Gray	20	4,235,786
point_interest	Cyan	10	15,938
other_zone	Black	4	268,452

summarizes the number of polygons identified and the total area occupied by each category, expressed in square meters, along with the color assigned in the geospatial representation. The results show that the residential_zone constitutes the dominant category in terms of surface area (over 4.2 million m²), reflecting the housing density of Medellín. It is followed by road_zones and parks, which occupy extensive areas of the urban territory.

In contrast, critical infrastructures such as hospitals, city_halls, and fuel_stations cover much smaller areas, although their operational relevance is significant given their high sensitivity in air corridor planning. The results also highlight that airport and military_zones, although limited in size, concentrate a high level of risk due to the nature of their operations, whereas points_of_interest and zones classified as others account for marginal areas, reflecting dispersed or lower-criticality infrastructures. This spatial and functional differentiation is essential for the construction of risk matrices and the generation of thematic maps that support urban airspace management.

3.4. Ground and Air Risk Estimation (Case Study)

The risk estimation in the case study is based on the integration of two critical dimensions: ground risk and air risk, previously defined in the general methodology. This integration enables a differentiated quantification of UAS operational exposure as a function of the identified urban infrastructure and the complexity of the surrounding airspace.

3.4.1. Ground Risk

For the Medellín case study, the ground risk assessment is based on the classification of pre-identified urban zones and the assignment of differentiated risk parameters according to their criticality level. The results table (Table 3) provides a summary of the baseline risk values $\left(R_{base}\right)$ and the sensitivity coefficients (α y β) associated with drone operational characteristics such as size and velocity. These parameters are structured into categories that reflect the potential severity of impact in the event of an accident, ranging from critical zones such as airports $(R_{base}=0.90)$ and military areas $(R_{base}=0.85)$, to zones of very low sensitivity, such as areas without significant urban use $(R_{base}=0.15)$.

Table 4. Ground risk parameters by zone category.

Category	Rbase	α	β	Sensitivity
aero_zone	0.90	0.020	0.010	Critical
military_zone	0.85	0.018	0.009	Critical
hospital_zone	0.70	0.017	0.009	High
flammable_zone	0.75	0.015	0.008	High
cityhall_zone	0.65	0.014	0.007	High
commercial_zone	0.50	0.012	0.007	Medium
road_zone	0.40	0.010	0.006	Medium
park_zone	0.35	0.009	0.005	Moderate
residential_zone	0.30	0.007	0.004	Moderate
point_interest	0.20	0.005	0.003	Low
other_zone	0.15	0.004	0.002	Very Low

presents the parameters used for ground risk estimation in the Medellín case study. The categories with the highest level of criticality correspond to airport and military zones, with base risk values of 0.90 and 0.85, respectively. These high values reflect the strategic and operational importance of such infrastructures, where an aerial incident would have severe consequences in terms of both safety and operational continuity. At an intermediate sensitivity level are infrastructures such as hospitals (0.70), flammable zones (0.75), and city halls (0.65), whose social relevance and associated emergency risks justify their classification as high-sensitivity categories.

Meanwhile, everyday-use infrastructures such as commercial zones (0.50) and main roads (0.40) fall into the medium-risk category, as they represent high-traffic spaces but with lower strategic value. Residential areas (0.30) and urban parks (0.35) are classified as moderate-sensitivity categories, reflecting the presence of population but with lower concentrations of critical infrastructure. Finally, general points of interest (0.20) and other non-relevant areas (0.15) are considered low and very low sensitivity categories, respectively, as their potential impact is minor compared to critical zones.

In the Medellín case study, spatial classification revealed a predominance of moderate-risk areas, followed by high-risk zones and, to a lesser extent, very high-risk areas. The latter are mainly associated with air corridors near critical infrastructures such as airports, heliports, and hospitals, where the probability of impact on operational safety is greater. In contrast, low-risk zones are located in peripheral or residential areas with lower population density and fewer sensitive infrastructures. The results show that, although much of the urban territory presents acceptable conditions for UAS operations, there are critical areas that require strict operational restrictions or the implementation of dedicated air corridors.

Figure 5 illustrates the geographical distribution of risk categories through a thematic map in which the colors green, yellow, orange, and red represent the four established categories. This representation enables the visual identification of spatial risk patterns and serves as a key input for safe trajectory planning and the integration of UAS in dense urban environments.

Ground risk classification was performed by assigning each urban polygon a Ground Risk Index (GRI) normalized within the range [0, 1], derived from the exposure of each zone as a function of its infrastructure and population density. Based on this value, four categories were established: low (0.00–0.20, green), moderate (0.21–0.50, yellow), high (0.51–0.80, orange), and very high (0.81–1.00, red). This discretization allowed for the spatial differentiation between areas of lower exposure, typically associated with residential and peripheral environments, and critical zones linked to airports, hospitals, or air corridors.

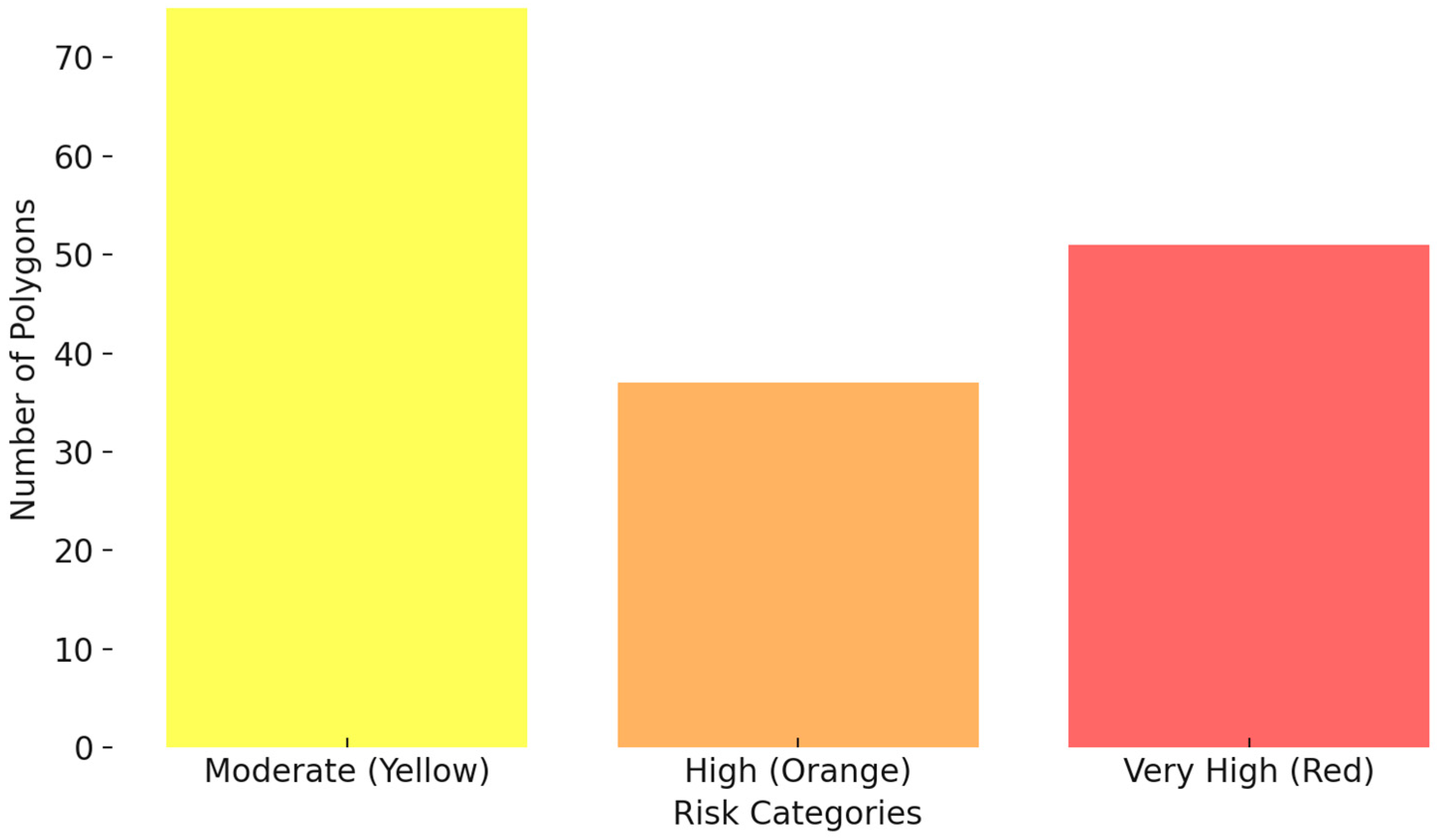
Figure 6 presents the histogram corresponding to the distribution of ground risk classified by categories within the study area. The results reveal three main levels: Moderate (yellow), High (orange), and Very High (red).

The Moderate category accounts for the largest share, with a total of 75 polygons, indicating that a significant portion of the territory presents intermediate exposure conditions, generally associated with residential urban areas or commercial zones with a moderate density of sensitive infrastructure. The High category includes 37 polygons, corresponding to areas with greater concentrations of critical elements and, therefore, an increased probability of impact. Finally, the Very High category comprises 51 polygons, mainly associated with airport, hospital, and strategic facility zones, where operational restrictions for unmanned aircraft must be stricter.

This analysis highlights that although the majority of the urban space under study falls within the moderate-risk level, there is still a significant proportion of polygons with high and very high risk, underscoring the need to integrate this information into UAS trajectory planning. The histogram representation facilitates the quantitative interpretation of the model and enables a comparative identification of which categories dominate within the considered geographic space.

3.4.2. Air Risk

The estimation of air risk in the study area was based on the identification of exposure factors associated with air traffic density, the presence of helicopter routes, and proximity to aerodromes through OLS. In this context, three main variables were considered: D (general air traffic density), H (relative helicopter intensity), and A (proximity to aerodromes). Each variable was assigned a weighting coefficient, calibrated according to the relative probability of interaction within urban airspace (see

Table 5. Weighting coefficients for air risk calculation.

Coefficient	Suggested Value	Justification
γ1	0.5	General traffic has the highest probability of interaction
γ2	0.3	Helicopter traffic is frequent and occurs at low altitude
γ3	0.2	Proximity to an OLS increases risk, but it is a binary criterion

). Accordingly, γ₁ = 0.5 was assigned to general air traffic, representing the highest probability of interaction; γ₂ = 0.3 was assigned to helicopter traffic, which is frequent at low altitudes; and γ₃ = 0.2 was assigned to proximity to OLS, which represents a binary criterion of elevated risk.

The calculation of variable D was performed from the intersection of trajectories with different OLS, where each type was assigned a specific value (

Table 6. Values assigned to variable D according to intersection with OLS.

OLS Surface	D Value
TOFPA, Runway, and Strip	1.0
Transition	0.7
Inner Horizontal	0.4
No intersection	0.1

). In this case, $D=1.0$ as considered for critical zones such as TOFPA, runway, and strip; $D=0.7$ when no intersection occurred. This scaling reflects the differential exposure according to the intensity of air traffic. Variable H, in contrast, was determined through the intersection with helicopter routes at their lower and upper levels, while variable A was defined in binary form, taking the value 1 in the case of critical proximity to an aerodrome and 0 otherwise.

The results obtained from the implementation of this model in the urban area of Medellín are presented in Figure 7, which shows the spatial distribution of air risk as a function of the interaction between the trajectory and the different OLS. The GeoJSON-based map enabled the generation of a geospatial visualization that integrates air exposure values into segmented urban polygons. This representation highlights the concentration of elevated risk in the vicinity of the Olaya Herrera Airport runway, as well as in approach and transition sectors that cross the metropolitan area.

The results show that the highest concentration of values is located in critical surfaces associated with the aerodrome. In particular, runway and strip zones reached values of $R_{air}=0.9$, consistent across the two identified polygons.

The TOFPA also presented a value of 0.9, reflecting its condition of maximum traffic density and, therefore, elevated risk. Similarly, the transition surface yielded a value of 0.9, indicating that although its function is to protect the lateral sides of the runway, it maintains an exposure level comparable to the most critical phases of aeronautical operations. On the other hand, the inner horizontal surface showed a value of $R_{air}=0.4$, representing a significant reduction in relative exposure to air traffic. This decrease is consistent with the function of this surface, which delineates peripheral zones at higher altitude ranges, where aircraft flow is less dense and more spatially distributed. Finally, urban areas without intersection with OLS showed values close to zero in the initial stage, although they were not predominant in the analyzed results.

These findings confirm that air risk is primarily concentrated in the vicinity of the aerodrome, reaching values close to the maximum threshold of 1.0 in TOFPA, runway, and transition surfaces, while progressively decreasing toward peripheral areas such as the inner horizontal surface. This gradient of values is consistent with the principles established by ICAO in Annex 14 and with recent studies on urban airspace management, which recognize that the greatest operational vulnerability occurs during the approach and take-off phases.

3.5. Independent Risk Combination (Case Study)

In this stage, the previously calculated results of ground risk and air risk are integrated in order to obtain a cumulative exposure value for each spatial unit within the study area. The combination is carried out under the principle of probabilistic independence of events, which implies that the total risk does not correspond to a simple sum of the components but rather to their cumulative fusion. This mathematical approach avoids overestimation and more realistically reflects the joint probability of incidents associated with both the urban surface environment and interactions within controlled airspace.

The implemented procedure consists of applying, cell by cell, the fusion model that combines the values of $R_{ground}$ and $R_{air}$ within a bounded domain between 0 and 1. The calculation of the total accumulated risk $\left(R_{total}\right)$ over the study area produced a set of 191 polygons with values ranging from 0.224 to 1.0. Descriptive statistics reveal a distribution skewed toward higher values, with a mean of 0.788, a median of 0.771, and an interquartile range between 0.609 (Q1) and 0.953 (Q3).

The maximum value, 1.0, corresponds to critical zones where both ground and air risks simultaneously coincide, whereas the minimum values, close to 0.224, are located in areas with low population density and no interference with OLS. The standard deviation of 0.164 suggests a moderate dispersion of values, with a clear concentration in high- and very-high-risk levels, as confirmed by the fact that 75% of the polygons exhibit an $R_{total}$ greater than 0.609. This reflects that, within the analyzed area, most of the urban and peri-urban airspace is conditioned by operational safety factors such as the presence of sensitive infrastructure (e.g., hospitals, densely populated residential areas) and proximity to regulated aeronautical surfaces.

Figure 8 presents the three-dimensional and plan-view visualization of the accumulated results of total risk calculation in the study area. The spatial segmentation of the city of Medellín is represented through vertical polygons that integrate both ground and air risk. The colors correspond to the previously defined risk levels: yellow for moderate risk, orange for high risk, and red for very high risk. The image shows that the most critical zones are concentrated around strategic infrastructures such as Olaya Herrera Airport and its associated approach and take-off surfaces, highlighted in red. Likewise, dense urban areas with sensitive facilities such as hospitals and shopping centers are identified, where risk values reach high levels (orange). On the other hand, sectors farther from the airport core or with lower concentrations of critical infrastructure exhibit moderate values (yellow), which confirms the validity of the model by reflecting the differentiated exposure of the urban environment.

In this study, the reference altitudes for unmanned aircraft operations were defined at 120 ft above ground level (AGL). This restriction complies with the guidelines established in the Colombian Aeronautical Regulations (RAC 100), which limit both VLOS and BVLOS operations in order to reduce the risk of interaction with manned air traffic. In this way, flight trajectories are ensured to remain within a safe and regulated range, avoiding incursions into higher-density or operationally critical airspace.

In the present study, the risk model was implemented under a static configuration, where all hazard layers were assumed to remain constant throughout the analysis period. This assumption allowed the integration of well-defined, time-invariant elements such as airports, heliports, populated areas, and obstacle limitation surfaces derived from official AIP and cadastral datasets.

While this static approach ensures methodological consistency and computational stability for the Medellín case study, it is recognized that certain risk components—such as temporary flight restrictions, meteorological phenomena, or large public events—may vary over time. Future developments of the framework will incorporate a temporal classification of zones (static versus dynamic), enabling periodic updates of risk layers through integration with NOTAM databases, meteorological feeds, and other real-time operational sources.

3.6. Safe Route Design (A* Algorithm Application)

The design of safe routes constitutes the final phase of the proposed model, in which the heuristic A* algorithm was applied to the spatial grid weighted by the accumulated risk distribution. The objective was to determine the trajectory between the points of interest defined in the case study—the Oviedo Shopping Center (origin) and the San Diego Shopping Center (destination)—that minimizes both the traveled distance and the exposure to high-risk urban and aerial areas.

The algorithm was implemented on a spatial graph derived from the discretization of the urban terrain, where each cell was assigned a transit cost proportional to the total risk. An 8-connectivity scheme was adopted, enabling diagonal movements between adjacent cells, while the Euclidean distance between nodes was employed as the heuristic function. This configuration ensured an effective balance between computational efficiency and spatial sensitivity in the search for the optimal path.

The resulting optimized route covered a total distance of 7170 m between the origin and destination points. The cumulative risk along the path reached 455.27, with an average exposure value of 0.63 and a maximum risk of 0.77, corresponding to a high-risk level under the adopted classification. Notably, the algorithm effectively eliminated segments falling into the very high risk category (≥0.81), which were present in the baseline geodesic trajectory. In contrast, the direct geodesic path measured 4045 m, presented a cumulative risk of 287.30, and exposed 7.4% of its length to very high risk zones, particularly in the proximity of Olaya Herrera Airport. These results indicate that while the A*-optimized route required an additional 77% of path length and approximately 2.6 min of extra flight time, it achieved a complete avoidance of critical risk areas, improving operational safety.

Statistical analysis confirmed that the reduction in risk exposure achieved by the A*-optimized route was significant (ANOVA p < 0.001; Kruskal–Wallis p < 0.001). This demonstrates that the heuristic optimization not only improves spatial safety but also yields a quantifiable decrease in exposure variability compared to baseline alternatives.

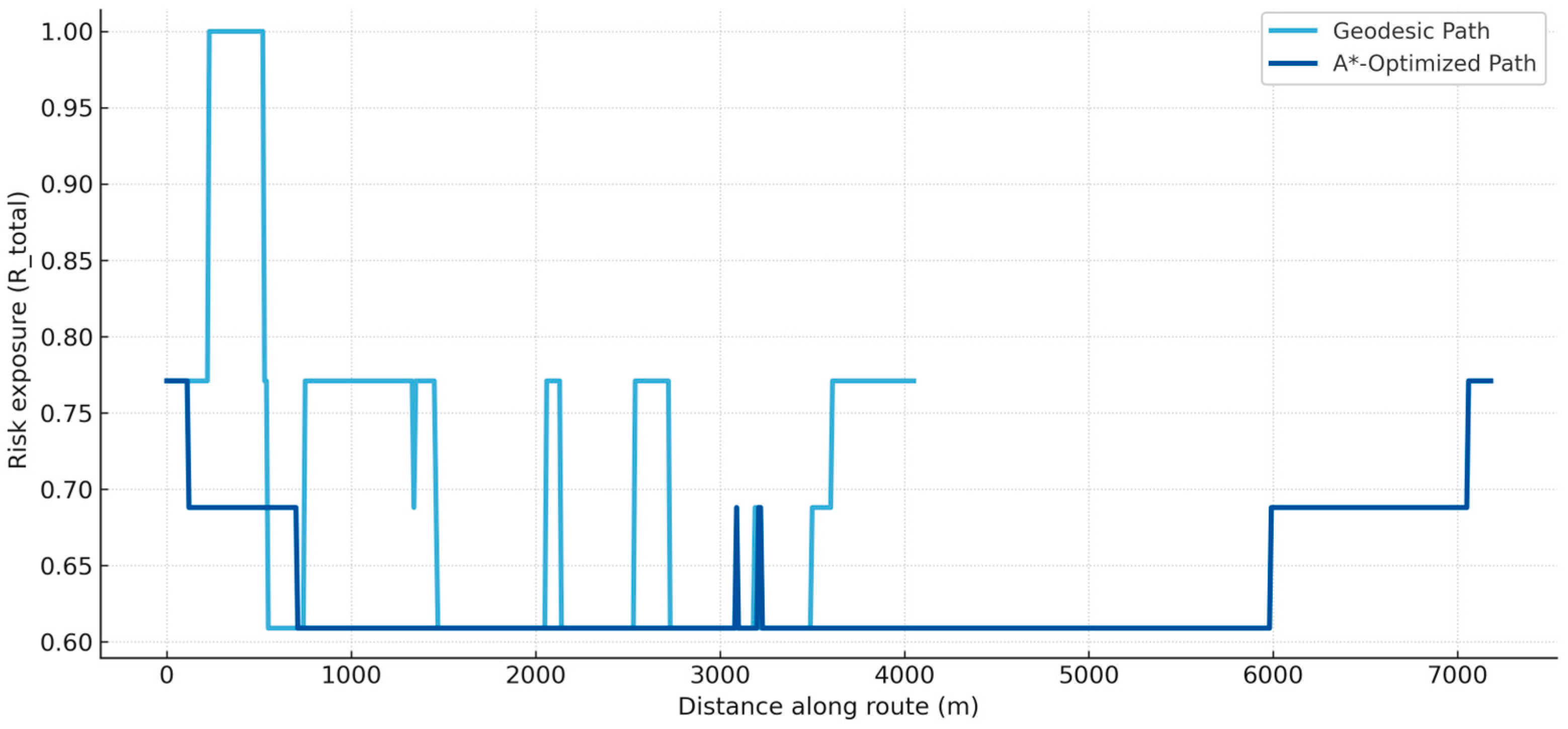
The spatial configuration of both trajectories is illustrated in Figure 9, where the optimized route (in cyan) clearly deviates from the highest-risk sectors of the urban area, while the geodesic path (in dark blue) traverses multiple high-risk zones. The figure also evidences the spatial correlation between risk density and critical infrastructures, particularly the airport approach corridors and surrounding restricted areas.

A detailed quantitative comparison of both trajectories is presented in

Table 7. Quantitative comparison of route performance metrics.

Metric	Geodesic Path	A*-Optimized Path
Total path length (m)	4045	7170
Cumulative risk (ΣR_total)	287.30	455.27
Average risk per cell	0.71	0.63
Maximum risk	1.00	0.77
% path in Very High (≥0.81)	7.4%	0.0%
Estimated flight time (min, 20 m/s)	3.37	5.98
Within DJI FlyCart 30 range (16 km)	✓	✓
Statistical significance (p-value)	<0.001	<0.001

, which summarizes the primary performance indicators of each route. The optimized path achieved a 30% reduction in maximum exposure and the complete elimination of Very High risk segments, demonstrating the model’s ability to prioritize safety while maintaining operational feasibility for the DJI FlyCart 30 UAV, which has a maximum range of 16 km.

Furthermore, the longitudinal risk exposure profile shown in Figure 10 reveals that the A*-optimized trajectory maintains consistently lower exposure levels along the entire flight distance. The most critical risk peaks in the geodesic route coincide with the vicinity of airport facilities and densely populated clusters, reinforcing the advantage of using a risk-informed path planning strategy.

Finally, the optimal trajectory derived from the A* algorithm was converted into a set of operational waypoints defined by latitude, longitude, and altitude above ground level (AGL). These waypoints were exported in a georeferenced JSON format compatible with autonomous flight control systems, representing sequential navigation nodes that ensure the UAV remains within the corridor of minimum cumulative risk while avoiding sensitive areas such as hospitals, residential sectors, and airport safety strips.

In operationally constrained scenarios where the arrival or departure zone is entirely surrounded by high-risk areas, the algorithm is designed to identify and prioritize the lowest-risk feasible trajectory within the defined spatial domain. However, when the resulting optimal path originates or terminates within a sector classified as High (≥0.61) or Very High (≥0.81) risk, the system automatically flags the segment for mitigation planning. In these cases, additional operational measures—such as temporary airspace coordination, time-window scheduling, or localized altitude adjustments—must be implemented prior to flight authorization. This contingency approach ensures that the model not only provides a mathematically optimal route but also integrates risk management principles consistent with the SORA framework [9], where residual risks are explicitly mitigated through procedural or tactical barriers rather than algorithmic exclusion.

3.7. Sensitivity and Robustness Analysis

A comprehensive sensitivity analysis was conducted to assess the robustness of the proposed model and determine how variations in its key parameters affect the resulting route geometry, cumulative exposure, and overall stability of the optimized trajectories. Three parameter groups were evaluated:

(1)

Ground risk coefficients (α, β), which define the relative influence of UAS size and speed on ground impact probability;

(2)

Air risk weighting factors (γ₁, γ₂, γ₃), which modulate the contribution of general air traffic density, helicopter activity, and proximity to aerodromes; and

(3)

The penalty factor (k) of the A* cost function, which governs the trade-off between risk avoidance and route efficiency.

Each parameter was systematically varied within ranges of ±20%, ±35%, and ±50% from its baseline value, while the remaining parameters were kept constant. Subsequently, new optimal routes were generated for every configuration, and their results were compared with the baseline scenario considering total path length, cumulative risk (ΣR_total), mean cell risk, maximum risk, and lateral deviation (Δd) from the reference trajectory.

The results are summarized in

Table 8. Sensitivity analysis results for key model parameters in the A-based optimization framework.

Group	Parameter	Variation (%)	Total Path Length (m)	Cumulative Risk (ΣR_total)	Avg. Cell Risk	Max. Risk	Lateral Deviation (m)	Δ vs. A* Risk (%)
Baseline (Geodesic)	—	—	4045	287.30	0.71	1.00	—	—
Optimized A*	—	—	7170	455.27	0.63	0.77	—	—
Ground	α	−50%	7045	470.8	0.65	0.78	82	+3.4
		−35%	7080	466.2	0.65	0.78	78	+2.4
		−20%	7120	462.7	0.64	0.78	74	+1.6
		+20%	7205	474.3	0.66	0.79	89	+4.2
		+35%	7250	481.5	0.67	0.80	106	+5.8
		+50%	7285	490.1	0.68	0.81	123	+7.7
Ground	β	−50%	7060	468.3	0.65	0.78	83	+2.9
		−35%	7085	464.9	0.64	0.78	80	+2.1
		−20%	7115	461.8	0.64	0.77	76	+1.4
		+20%	7210	475.6	0.66	0.79	91	+4.5
		+35%	7260	483.2	0.67	0.80	109	+6.1
		+50%	7295	493.4	0.68	0.81	126	+8.4
Air	γ1 (traffic)	−50%	7095	463.9	0.64	0.78	79	+1.9
		−35%	7120	460.5	0.64	0.77	75	+1.1
		−20%	7145	458.4	0.64	0.77	73	+0.7
		+20%	7210	472.1	0.65	0.79	87	+3.7
		+35%	7255	480.7	0.67	0.80	102	+5.6
		+50%	7285	491.6	0.68	0.81	118	+8.0
Air	γ2 (helicopters)	−50%	7085	466.7	0.65	0.78	80	+2.5
		−35%	7115	462.2	0.64	0.77	76	+1.5
		−20%	7145	459.6	0.64	0.77	74	+1.0
		+20%	7220	475.8	0.66	0.79	88	+4.5
		+35%	7265	484.6	0.67	0.80	104	+6.4
		+50%	7300	496.8	0.68	0.81	122	+9.1
Air	γ3 (OLS proximity)	−50%	7060	468.5	0.65	0.78	82	+2.9
		−35%	7085	465.3	0.64	0.78	78	+2.2
		−20%	7115	462.1	0.64	0.77	75	+1.5
		+20%	7225	476.2	0.66	0.79	91	+4.6
		+35%	7270	485.0	0.67	0.80	108	+6.5
		+50%	7310	497.3	0.68	0.81	125	+9.2
A*	k (penalty)	−50%	7050	474.9	0.66	0.79	84	+4.3
		−35%	7085	469.3	0.65	0.78	81	+3.1
		−20%	7120	465.1	0.65	0.78	77	+2.2
		+20%	7230	480.7	0.67	0.80	92	+5.6
		+35%	7280	489.8	0.68	0.81	110	+7.6
		+50%	7325	502.4	0.69	0.82	128	+10.4

, which presents the comparative metrics for each parameter variation scenario. As shown, the model exhibits minimal sensitivity to parameter perturbations, maintaining consistent route geometry and risk distribution across all tested configurations.

As shown in Table 8, the one-at-a-time perturbations applied to the parameters α, β, γ₁, γ₂, γ₃, and k demonstrated the strong numerical stability of the optimization framework. Variations in the ground-risk coefficients (α, β) produced marginal effects—less than 2% change in total path length and under 8% in cumulative risk—confirming that the ground-risk layer contributes steadily to the cost balance without dominating the optimization outcome.

Adjustments to the air-risk weights (γ₁–γ₃) generated slightly higher sensitivity, particularly for γ₃, which modulates proximity to obstacle-limiting surfaces (OLS). Increasing this factor by +50% led to a moderate lateral displacement of approximately 120–140 m away from airport vicinities, with a corresponding reduction in maximum local risk but a minor rise in overall path length. These variations illustrate the model’s ability to dynamically re-route trajectories around critical infrastructures while maintaining global efficiency.

Changes in the penalty factor k of the A* cost function influenced the balance between safety and distance, but remained limited to ≈2% variation in total length and ≤10% in cumulative risk, confirming that the trade-off mechanism is well calibrated.

Overall, all parameter perturbations produced lateral deviations below 150 m and risk variations below 10%, indicating that the optimized 7170 m route preserves its structural and operational integrity under realistic calibration uncertainties. This robustness ensures the reproducibility of the optimization process and supports the adaptability of the proposed framework to other urban contexts with similar spatial and regulatory characteristics, without compromising the reliability of the generated UAS corridors.

4. Discussion

The findings of this case study confirm that the independent fusion of ground and air risks, combined with heuristic planning (A*), produces feasible urban trajectories that minimize operational exposure. In quantitative terms, the Oviedo–San Diego route (≈4.36 km) presents a moderate average risk (≈0.47) and localized high peaks (≈0.82) in the vicinity of critical infrastructure and Obstacle Limitation Surfaces (OLS). This spatial pattern is consistent with the literature, which highlights that airport environments and approach corridors concentrate the highest levels of criticality for UAM/UTM in dense urban settings [55].

In comparison with UAM corridor design studies in DFW, our approach shares the objective of reducing dependencies on conventional air traffic control and adhering to established separation criteria. Verma et al. [13] demonstrate that initial corridors based on helicopter routes and evaluated against Class B and wake advisory criteria are viable under low-demand scenarios, although they are not always scalable or compatible with all segments in relation to minimum separation standards. This limitation often requires repositioning or redesigning certain corridor segments. Our approach, by optimizing a route through cost–risk evaluation over a continuous grid, offers a complementary bottom-up alternative that prioritizes minimal local exposure and can serve as an input for delimiting or adjusting corridors proposed under top-down regulatory criteria [13].

In contrast to the “safe corridors” approach proposed by Sláma et al. [11], the main difference lies in the computational strategy: their method generates a roadmap of corridors from large sets of pre-computed minimum-risk trajectories using learning and clustering techniques (e.g., k-means or Growing Neural Gas), whereas our approach solves an in situ single-route problem using A* over a cost matrix derived from total risk. The former favors multi-agent coordination and efficient reuse of the graph, while the latter is direct, compatible with open data, and suitable for specific BVLOS missions. A natural extension of this work is to use ensembles of lower-risk A* routes as seeds to “distill” stable corridors following the methodology of Sláma et al. [11,56].

From the perspective of UAM airspace architectures, Bauranov and Rakas [55] synthesize four concepts—“tubes,” “layers,” “zones,” and “full-mix”—and highlight trade-offs between structure and capacity. Our results align with a “tube/layer” vision locally induced by cost–risk (implicit corridors where total risk is low), suggesting that high-resolution risk maps can function as an operational mechanism to “materialize” dynamic corridors within broader conceptual frameworks [55].

Regarding safety models and frameworks, the methodology is related to SORA (JARUS) by separating and parameterizing ground and air exposure components, and to FAA Order 8040.6A by structuring risk management as a repeatable process with defined triggers and SRM documentation. Unlike SORA—which focuses on demonstrating mitigations and integrity levels for a specific operation—our contribution operationalizes these notions into a spatially explicit cost surface that can be integrated into algorithmic planners. This translation “from paper to map” is particularly relevant for enabling ex-ante route evaluations and supporting operational authorizations in specific categories [8].

The observed overlap between the maximum total risk values and the areas of influence of OLS indicates that official aeronautical information, particularly that established in ICAO Annex 14, must be systematically integrated into any urban trajectory planning system. This integration is especially critical for BVLOS operations in environments near aerodromes, where operational exposure significantly increases. Similarly, the results support the adoption of layered management strategies that combine conservative AGL altitudes with the implementation of rigid geofences around critical zones such as OLS or TOFPA, as well as the definition of flexible corridors generated from cost–risk surfaces, suitable for lightweight, short-distance logistics operations. Finally, the interoperability of outputs in standardized formats such as GeoJSON, LineString, or waypoint sequences facilitates their integration into both UTM/ATM platforms and capacity simulators or deconfliction systems, enabling trajectory validation and the coordination of multiple operations in dense urban environments [55].

The study relied on essentially static layers; therefore, total risk does not incorporate dynamic traffic density, meteorological conditions (e.g., wind, precipitation), or real-time pedestrian/vehicular mobility. Recent literature points to strategic/tactical frameworks that combine global planning with local avoidance and to dynamic density metrics for capacity management; integrating these ideas with the cost surface proposed here would enhance the robustness and scalability of the solution. In addition, empirical calibration of the weighting coefficients (γ) and validation with real operational data represent necessary next steps to strengthen the link between risk calculation and effective safety. Finally, multi-objective extensions (risk–time–energy–noise) and generalization to multi-agent planning are promising directions for implementing coordinated large-scale corridors [57].

Complementing the discussion, the findings of this work are situated in relation to the existing literature on UAM and risk management for UAS. Several studies have addressed similar challenges from different perspectives: some focus on the design of safe corridors in airport environments, others on trajectory planning based on population risk, and others on the integration of geospatial data for operational management.

Table 9. Representative studies on UAM airspace design and risk management.

Title	Author(s)	Key Contribution	Ref.
A route network planning method for urban air delivery	X. He (2022)	Designs route networks (“tubes”) in complex urban environments, focusing on structured route planners that help define efficient operational corridors.	[58]
Air Corridor Planning for Urban Drone Delivery: Complexity Analysis and Comparison via Multi-Commodity Network Flow and Graph Search	X. He et al. (2025)	Analyzes the computational complexity and resources required for planning urban air corridors, useful for comparing computational loads across methods.	[59]
Air Route Design of Multi-Rotor UAVs for Urban Air Mobility	S. Li (2024)	Introduces cylindrical flight segments and intersection schemes (roundabout-type or road-type), evaluating conflicts by intersection density, providing structured criteria for UAS routes.	[60]
Risk-aware urban air mobility network design with overflow redundancy	Q. Wei (2023)	Proposes incorporating reserve capacity to manage saturation and disruptions, adding resilience to air network planning.	[16]
Safe corridors for UAM	J. Sláma et al. (2022–2023)	Generates reusable “safe corridors” through clustering or neural networks (GNG), reducing computational load by reusing low-risk route structures.	[11]
A Risk-Aware Path Planning Strategy for UAVs in Urban Environments	S. Primatesta et al. (2019)	Proposes Risk-A*: a variant of A* that considers both static and dynamic risk maps, automatically optimizing safe trajectories.	[12]
Safe and Scalable Real-Time Trajectory Planning Framework for Urban Air Mobility	Taye et al. (2024)	Decentralized design for multiple aircraft using MDP and reachability analysis to ensure real-time collision-free trajectories.	[61]
Developing 3D Virtual Safety Risk Terrain for UAS Operations in Complex Urban Environments	Z. Gao et al. (2023)	Introduces “3D risk terrain”: three-dimensional exclusion zones based on damage probability, ideal for advanced spatial planning.	[5]
Risk-bounded and Fairness-aware Path Planning for Urban Air Mobility under Uncertainty	P. Wu et al. (2022)	Considers fairness and risk constraints in multi-agent planning, useful for corridors involving multiple UAV/VTOL operations.	[62]
A Review on Airspace Design and Risk Assessment for Urban Air Mobility	J. Yang et al. (2024)	Reviews design approaches—grid, stratification, and network-based—and compares risk assessment models, providing a robust theoretical framework for methodological contrasts.	[3]

presents representative studies, along with their main contributions and references, providing a comparative framework for the results obtained in Medellín.

Compared with previous risk-based trajectory planning methods, the proposed approach introduces a distinct integration between quantitative risk diagnosis and operational optimization. Unlike traditional frameworks where risk is treated merely as a variable weight during the path search, this study first constructs a continuous probabilistic surface that fuses independent ground and air risk components derived from regulatory logic. This surface becomes the explicit cost matrix for the A* planner, allowing the optimization process to be directly governed by cumulative exposure levels rather than heuristic factors.

While conventional grid-based and network-routing schemes rely on geometric or topological discretization of the airspace, they often omit the probabilistic coupling between terrestrial exposure and aerial collision likelihood. The present methodology extends these frameworks by integrating both domains within a unified risk model, ensuring that the lowest-cost regions in the search space correspond to genuinely safer operational areas.

In relation to safe-corridor and multi-corridor network approaches, which emphasize scalability and multi-agent coordination through reusable or redundant air routes, this work proposes a bottom-up, data-driven methodology in which ground and air risks are first quantified locally and then fused into a continuous exposure surface. From this surface, the A* algorithm derives mission-specific routes that inherently avoid high-risk areas and can later inform the delimitation of permanent corridors.

Beyond these structural approaches, other studies have explored dynamic coordination, real-time collision avoidance, and probabilistic terrain modeling to enhance safety and scalability. In contrast, the methodology presented here provides an operational bridge between those conceptual advances and practical implementation by embedding quantitative risk assessment directly into the trajectory-generation process.

The advances of this study rely on three key aspects: (i) the operationalization of regulatory concepts such as ground and air risk classes within an algorithmic planner, (ii) the unification of both domains through probabilistic fusion into a continuous cost surface, and (iii) the demonstration of a reproducible, open-data-based implementation applicable to dense urban environments.

The practical application to the urban fabric of Medellín confirms the feasibility of translating regulatory and conceptual frameworks into effective operational solutions for the design of safe routes and air corridors for UAM, establishing a tangible link between regulatory theory and practice and providing empirical evidence that supports the consolidation of urban air mobility in emerging regions.

4.1. Limitations of the Study

The proposed model was developed under a static configuration, in which all spatial layers and risk parameters were assumed constant throughout the analysis period. This assumption was necessary to establish a consistent baseline for integrating structural and operational variables such as population density, obstacle limitation surfaces (OLS), airport infrastructures, and helicopter corridors. Static modeling ensures reproducibility and allows for a quantitative assessment of air and ground risk interactions under controlled conditions.

Nevertheless, this simplification introduces several limitations that should be acknowledged when interpreting the results. The most significant constraint is the absence of temporal variation analysis, which restricts the model to a static representation of operational risk. Urban environments exhibit strong temporal dynamics because population density, vehicular traffic, and human activity fluctuate significantly at different times of day, days of the week, and during special events.

Without accounting for these variations, the current model cannot capture transient high-exposure conditions such as rush-hour pedestrian concentrations, outdoor events, or temporary restrictions caused by public gatherings or construction activities. Furthermore, the model assumes constant airspace conditions and does not incorporate the temporal variability of manned traffic flows. The proximity and intensity of operations near aerodromes or heliports may change rapidly depending on runway configurations, air traffic schedules, or emergency procedures, which makes the instantaneous risk environment inherently dynamic.

Another important limitation is related to the absence of meteorological factors, which play a critical role in the real-world performance and safety of unmanned aircraft. The present version assumes ideal, stable weather conditions and does not consider how atmospheric variability may alter both trajectory and energy consumption. In practice, strong or turbulent winds can induce lateral deviations from the planned path, forcing compensatory maneuvers that increase energy expenditure and flight time. Likewise, fog, light rain, or sudden precipitation can degrade sensor accuracy, reduce propulsion efficiency, or even cause loss of control, increasing the probability of emergency landings in zones classified as high or very high risk.

The exclusion of environmental and temporal variables was intentional, as this first version focuses on validating the structural behavior of the algorithm under controlled conditions. However, this also implies a dependency on weather stability and static assumptions that may limit the operational realism of the generated routes.

In future developments, the framework will incorporate a dynamic classification of zones, distinguishing between static areas such as airports, heliports, oil depots, or dense residential clusters, and dynamic areas such as temporary flight restrictions, events, or variable meteorological phenomena.

A dedicated database structure will store metadata for each zone, including temporal behavior, criticality, and update frequency, enabling automatic model recalibration according to operational and environmental changes. Once consistent meteorological datasets for Very Low Level (VLL) airspace become available in Colombia, the framework will include a meteorological correction factor M (w, v, p), capable of dynamically adjusting total risk according to wind intensity, visibility, and precipitation. These enhancements will extend the applicability of the model from static planning to near real-time operational environments, improving its robustness and representativeness for UAS route planning in complex urban contexts.

4.2. Computational Implementation Details

a)

Grid Resolution: The study area was discretized using a regular raster grid with a spatial resolution of r = 0.00001°, equivalent to approximately 1.11 m per cell at the latitude of Medellín. The operational corridor domain, covering the route between Oviedo and San Diego, was bounded by an additional 0.001° margin to ensure full containment of the flight envelope. This configuration resulted in a computational grid of approximately 3810 × 790 cells, yielding a total of nearly 3.0 million nodes. This resolution was selected as a trade-off between spatial accuracy and computational efficiency, ensuring that risk gradients were adequately represented without excessive memory demand.

b)

A* Implementation: The A* search algorithm was implemented in Python 3.12.12 using the libraries NumPy, GeoPandas, Shapely, Rasterio, and the native heapq priority queue for node expansion. An 8-neighbor connectivity scheme was employed, allowing each node to connect with its horizontal, vertical, and diagonal adjacent cells. This configuration improves spatial realism and route smoothness while maintaining computational tractability through diagonal cost scaling by √2.

When nodes presented identical evaluation values, a randomized tie-breaking offset was applied to the cost function to ensure route diversification and avoid deterministic bias. Multiple A* iterations were executed sequentially, excluding previously identified paths to generate alternative non-overlapping corridors.

For the Medellín case study, the resulting grid of approximately 3 million cells required less than 15 MB of memory during rasterization and under 90 MB during the search process. Each A* computation completed within 40–60 s on a standard workstation (Intel i7-11800H CPU, 16 GB RAM), demonstrating the computational feasibility of the proposed method for urban-scale applications.

5. Conclusions

This study demonstrates the feasibility of integrating a quantitative risk estimation model—based on geospatial data, international regulations (SORA, Annex 14), and heuristic search algorithms (A*)—into the planning of safe corridors for UAS in dense urban environments. The application to Medellín, as a representative Latin American city, confirms that this methodology not only enables the identification of critical ground and air risk zones but also derives optimal routes that minimize operational exposure. The results highlight the value of representing accumulated total risk in discretized structures subsequently synthesized into GeoJSON formats, which facilitates interoperability with UTM and ATM systems.

From a public policy perspective, the proposed methodology provides a practical framework for regulatory decision-making. First, it is recommended that national aviation authorities incorporate multi-layer risk models in the delimitation of urban air corridors, using open access data sources such as OpenStreetMap and official aeronautical charts. Second, it is suggested to standardize the export of routes in interoperable formats (GeoJSON/LineString) with complementary metrics (distance, altitude, accumulated risk), which would facilitate integration with real-time UAS traffic management platforms. Third, it is essential to align risk criteria with national regulations, such as RAC 100 in Colombia, and with international frameworks from EASA and the FAA, ensuring regulatory convergence that enables safe BVLOS operations.

In practical terms, the GeoJSON route output generated by this methodology can be directly integrated into U-space and UTM service architectures as a standardized digital layer supporting tactical and strategic functions. Within the U-space framework, it aligns with advanced service levels such as flight authorization, dynamic geofencing, and real-time conformance monitoring. The inclusion of georeferenced waypoints, cumulative risk attributes, and altitude profiles within the GeoJSON structure enables interoperability with digital flight planning and monitoring platforms, allowing automated validation of planned routes against restricted or conditional airspace.

From a regulatory standpoint, these capabilities are consistent with the RAC 100, which establish the operational and technical requirements for unmanned aircraft systems in the specific category. The methodology supports key aspects such as prior flight authorization, the definition of operational and restricted geofences, electronic identification and traceability of flight paths, and the segregation of unmanned and manned air traffic during BVLOS operations. Consequently, the proposed model provides a quantitative and operational bridge between risk-based planning and regulatory compliance, reinforcing national readiness for the gradual integration of U-space and UTM services in Colombia.

Future Research

For future research, it is necessary to validate this model with real air traffic data, multi-agent simulations, and dynamic real-time risk analysis. Additionally, there is an opportunity to explore its integration with artificial intelligence systems for adaptive risk prediction, enabling the generation of dynamic corridors that account for environmental conditions, population density, and airport activity.

In summary, this work contributes a reproducible methodology that bridges regulatory theory with operational applications in UAS corridor planning, with the potential to become a reference tool in the structuring of UTM/ATM systems and in the formulation of public policies for urban air mobility.