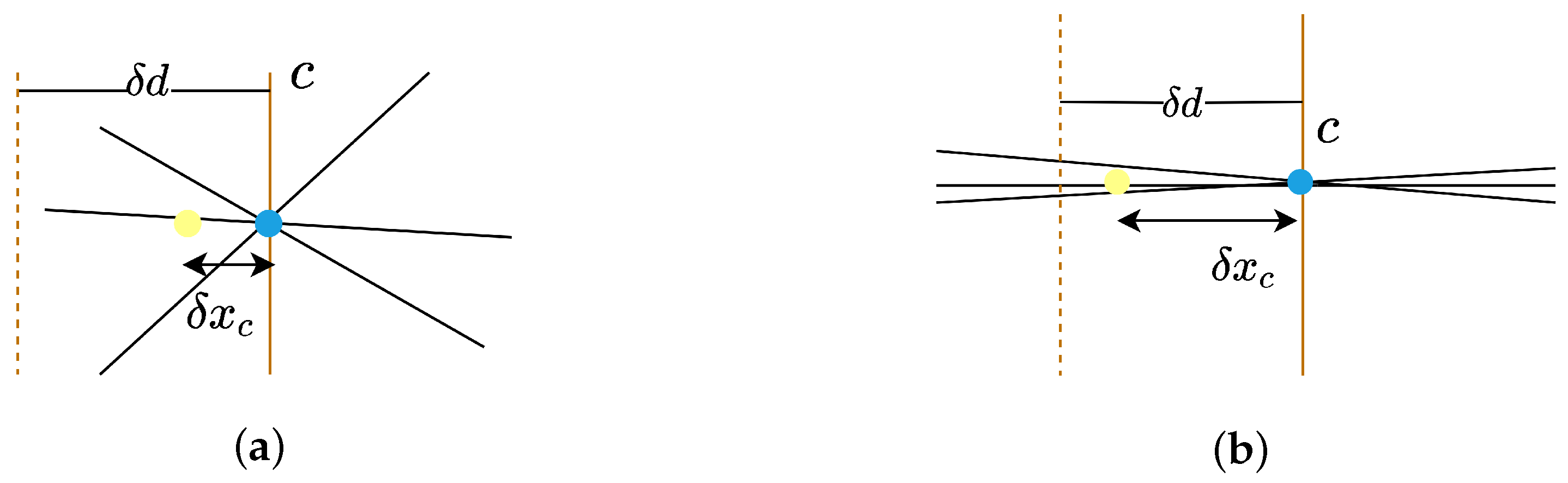Self-Correcting Cascaded Localization to Mitigate Drift in Mining Vehicles’ Kilometer-Scale Travel

Highlights

What are the main findings?

• A three-stage cascaded filtering system was developed to provide scenario-adapted, self-correcting localization by fusing multi-source onboard sensor data (LiDAR, IMU, wheel speed, steering angle) to overcome the unique challenges of underground mining environments.
• The system successfully addresses non-Gaussian noise from wheel slippage via an anti-slip prior estimation algorithm, and resolves geometric-degraded localization failures through an anti-degradation algorithm utilizing point cloud degradation-derived regularization constraints.

What are the implications of the main findings?

• The achieved sub-meter accuracy and full-area coverage localization establish a high-reliability, self-contained positioning solution for kilometer-scale underground autonomous vehicles, which is essential for mitigating collision risks and enabling wider deployment.
• The work introduces a safety-oriented paradigm for autonomous vehicle scaling, offering a robust and stable localization framework applicable to other critical, signal-free, and feature-deprived environments beyond mining.

Abstract

High-reliability localization is essential for underground mining autonomous vehicle, as inaccurate positioning triggers collision risks and limits deployment in safety-critical environments. Underground mining localization faces unique challenges: kilometer-scale signal-free tunnels restrict traditional technologies, while wheel slippage-induced non-Gaussian noise and geometric-degraded tunnel localization failures further reduce accuracy—issues existing methods cannot address simultaneously. To resolve these bottlenecks, this study develops a scenario-adapted, self-correcting positioning system for underground autonomous vehicles, fusing multi-source onboard sensor data to suppress slip noise and ensure feature-deficient environment robustness. We propose a three-stage cascaded filtering system: it first fuses LiDAR, IMU, wheel speed, and steering angle data for a self-contained framework, then adds two dedicated modules for core challenges. For wheel slippage noise, an anti-slip prior estimation algorithm integrates kinematic models with IMU data, plus a low-adhesion mine surface-tailored slip compensation mechanism to ensure reliable state estimation and eliminate slip deviations. For geometrically degraded tunnel failures, an anti-degradation algorithm uses point cloud degradation-derived regularization constraints and regularized Kalman filtering to enable stable positioning updates. Experiments show that the system achieves sub-meter accuracy and full-area coverage underground, with improved performance under severe wheel slip and in feature-deprived zones. This work fills the gap in high-reliability, self-contained localization for kilometer-scale underground mining vehicles and provides a safety-oriented paradigm for autonomous vehicle scaling, aligning with critical scenario driving safety demands.

1. Introduction

Underground coal mine autonomous driving represents a key frontier in industrial safety and efficiency, where real-time trajectory planning and control—core elements for collision avoidance and operational safety—depend critically on continuous, reliable positioning [1,2]. Current positioning approaches are shifting from single-sensor to multi-sensor fusion paradigms: GNSS/5G/INS combinations dominate outdoor autonomous driving scenarios, while UWB/5G solutions and kinematic dead reckoning (integrating INS with wheel odometry) are widely applied in GNSS-denied areas [3]. However, these methods often fail to meet safety-critical requirements in underground coal mines, where harsh conditions amplify the consequences of positioning instability. Advances in LiDAR and camera technologies have established simultaneous localization and mapping (SLAM) as a key enabling technology for high-precision 3D mapping and navigation in complex environments. Yet visual approaches suffer from inherent depth perception limitations and sensitivity to prevalent underground conditions like dust, low light, and high humidity, compromising operational safety continuity. While LiDAR solutions offer better robustness and data accuracy for underground environments, their application requires further optimization for mine-specific challenges [4].

Underground coal mine environments present unique, safety-centric challenges distinct from conventional autonomous driving scenarios. Kilometer-scale unstructured tunnels—with highly repetitive geometric features, persistently high dust/humidity levels, reduced road adhesion from watering operations, and axial feature deficiencies in long sections—create critical obstacles for safe autonomous driving. Existing research primarily addresses short-term positioning needs, leaving significant technical gaps for long-duration, kilometer-scale navigation [5]. Key challenges include severe occlusion and multipath effects causing signal-based positioning failures in long tunnels, with incomplete base station coverage leading to intermittent positioning interruptions that increase collision and path deviation risks [6]; wheel slippage phenomena exacerbated by watering operations that reduce road adhesion, introducing non-Gaussian noise in wheel speed measurements and compromising trajectory tracking accuracy; and the compounding effects of axial feature deficiency and uncompensated cumulative drift, where reduced LiDAR spatial matching constraints combined with long-term navigation drift produce significant positioning deviations that compromise operational safety and continuity [4].

To overcome these challenges above—including signal obstruction in confined tunnels, non-Gaussian disturbances during wheel slippage, and geometric degradation undermining LiDAR constraints—this work makes four key contributions:

1

Onboard-sensor-only self-contained localization for full-scenario coverage: A multi-sensor integration strategy (fusing LiDAR, IMU, wheel speed, and steering angle) is proposed to eliminate reliance on external localization signals. This design enables continuous self-contained localization, achieving seamless coverage even in confined or signal-denied tunnel environments.

2

Cascaded filtering architecture for cross-condition localization robustness: A dedicated cascaded filtering mechanism is embedded into the localization system, with integrated anti-slip and anti-degradation functional modules. This architecture establishes a stable technical foundation for maintaining high-precision localization performance across diverse working conditions.

3

Low-adhesion-adapted state estimation with slip compensation: An anti-slip prior estimation approach tailored to mine road characteristics is developed. It fuses kinematic models (derived from wheel speed and steering angle) with IMU data and embeds a targeted wheel slip compensation mechanism to ensure reliable state estimation on low-adhesion surfaces.

4

Regularized state update for LiDAR degradation resilience: An anti-degradation estimation strategy for LiDAR constraints is presented. It extracts regularization constraints from point cloud degradation states and embeds them into a recursive Bayesian state estimation framework, effectively stabilizing localization updates in geometrically degraded environments.

The remainder of this paper is structured as follows: Section 2 briefly covers the related work of this study. Section 3 details the system architecture and technical implementation of core modules. Section 4 presents experiments based on simulation and field vehicle data. Finally, Section 5 summarizes contributions and outlines future research directions.

2. Related Work

In the field of vehicular localization, autonomous localization techniques relying solely on onboard sensors (without external infrastructure support) have become a pivotal research direction, driven by the demand for reliable positioning in complex and unstructured environments. With the limitations of single-sensor systems in robustness and accuracy, the paradigm has gradually shifted toward multi-sensor fusion, in which simultaneous localization and mapping (SLAM) technology stands out as a core enabling approach—its ability to acquire real-time 3D spatial information through sensor data matching makes it widely applicable in scenarios where traditional positioning methods fail. For environments with variable lighting or visual obstruction, LiDAR’s illumination invariance and high-precision distance measurement capabilities have established LiDAR-centric SLAM as a preferred technical route, with research initially focusing on optimizing feature extraction, motion estimation, and loop closure detection to enhance performance in general indoor and outdoor scenes.

However, underground coal mine environments present unique challenges that distinguish them from conventional autonomous driving scenarios, placing higher demands on SLAM-based localization systems and exposing critical gaps in existing research. Kilometer-scale unstructured tunnels are characterized by highly repetitive geometric features, persistently high dust and humidity levels, reduced road adhesion due to regular watering operations, and axial feature deficiencies in long sections—these factors collectively degrade sensor performance and disrupt positioning continuity. Visual SLAM systems, for instance, suffer from depth perception failures under low light and dust interference; while LiDAR-based solutions offer better robustness, they still face issues such as reduced spatial matching constraints under feature degradation, and wheel odometry is prone to non-Gaussian noise from wheel slippage. Existing SLAM studies either focus on general scenes (e.g., urban roads, indoor spaces) without adapting to mine-specific harsh conditions, or only address partial challenges while neglecting long-duration, kilometer-scale navigation stability and anti-slip requirements, leaving significant technical gaps for safety-critical underground mining operations [4,5].

Against this background, research on LiDAR-centric SLAM has evolved toward multi-sensor fusion to enhance adaptability, with three main technical branches emerging based on sensor combinations. The first branch focuses on laser-only SLAM, where classic algorithms like LOAM lay the foundation by extracting line and plane features for frame-to-frame motion estimation [7]; subsequent optimizations such as A-LOAM and Lego-LOAM improve real-time performance and accuracy [8,9], while LiTAMIN series algorithms reduce registration points through geometric approximation and optimize loop closure to suppress mismatches [10,11]. IMLS-SLAM introduces implicit moving least-squares surfaces for submap matching [12], and methods like Neighborhood Information Constraint enhance adaptability to rugged terrain [13], though these laser-only systems still struggle in feature-degraded mine tunnels where LiDAR data reliability drops sharply. The second branch integrates LiDAR with IMU to compensate for LiDAR limitations—algorithms like LIO-SAM (graph optimization-based optimization) and FAST-LIO (error-state Kalman framework-based optimization) leverage IMU’s short-term motion estimation accuracy to enhance robustness [14,15], with FAST-LIO2 further improving computational efficiency via ikd-tree real-time balancing [16]. Adaptations for underground robots have also been explored, such as modified LIO-SAM validated in simulated mines [17], FAST-LIO2 implemented in coal mine tunnels with artificial landmarks to mitigate feature degradation [18], and FAST-LIO2 adapted for drone navigation in mining tunnels with cumulative error correction via prior map alignment [19]. However, these LiDAR-IMU fusion systems face two key limitations in mines: some lack analysis of extreme feature degradation [17,19], while others rely on artificial landmarks, reducing generalizability [18]; additionally, during severe degradation (when LiDAR becomes unreliable), IMU drift accumulates rapidly without effective constraints—though methods like quantifiable degradation metrics to suppress IMU updates have been proposed, they still suffer from substantial estimation errors at high speeds due to the absence of absolute references [20].

The third branch further incorporates wheel odometry into LiDAR-IMU fusion to add motion constraints, as seen in LIWO-SLAM (factor graph optimization) validated in tunnel environments [21] and LIW-OAM (bundle adjustment-based fusion) [22]; related architectures have also been tested on indoor vehicles (via EKF-based fusion of wheel speed, IMU, and LiDAR) [23] and urban roads (via factor graph optimization) [24]. Nevertheless, existing LiDAR–IMU–wheel fusion methods are designed for ideal road conditions and lack targeted anti-slip mechanisms—frequent wheel slippage/lockup in mines (caused by explosion-proof water spraying) introduces non-Gaussian noise to wheel measurements, severely compromising localization stability in practical mining operations. Beyond LiDAR–IMU and LiDAR–IMU–wheel fusion, LiDAR–ultrasonic combinations have shown promise for robust localization. Wiseman [25] proposed an ultrasonic rangefinder for autonomous vehicles, which complements LiDAR’s short-range and low-reflectivity measurement limitations—critical for dusty, irregular underground mine tunnels. Premnath et al. [26] further validated LiDAR–ultrasonic–wheel encoder fusion, showing enhanced localization in narrow spaces by supplementing LiDAR’s missing environmental constraints, though both studies lack adaptation to mining’s high humidity and kilometer-scale needs.

In summary, while existing multi-sensor fusion-based SLAM research has advanced vehicular autonomous localization, critical limitations persist for safety-critical underground coal mine scenarios. Laser-only SLAM exhibits inherent limitations in feature-degraded long tunnels; LiDAR-IMU fusion methods either lack adaptability to extreme mine conditions, depend on non-generalizable artificial landmarks, or fail to constrain IMU drift effectively under severe LiDAR unreliability. Though LiDAR–IMU–wheel fusion adds motion constraints, its design for ideal road surfaces omits targeted anti-slip mechanisms to mitigate non-Gaussian noise from mine-specific wheel slippage (induced by watering operations). These collective gaps result in inadequate localization stability and continuity for kilometer-scale underground mining navigation—motivating the development of a dedicated localization framework to address these mine-specific challenges comprehensively.

3. Methodology

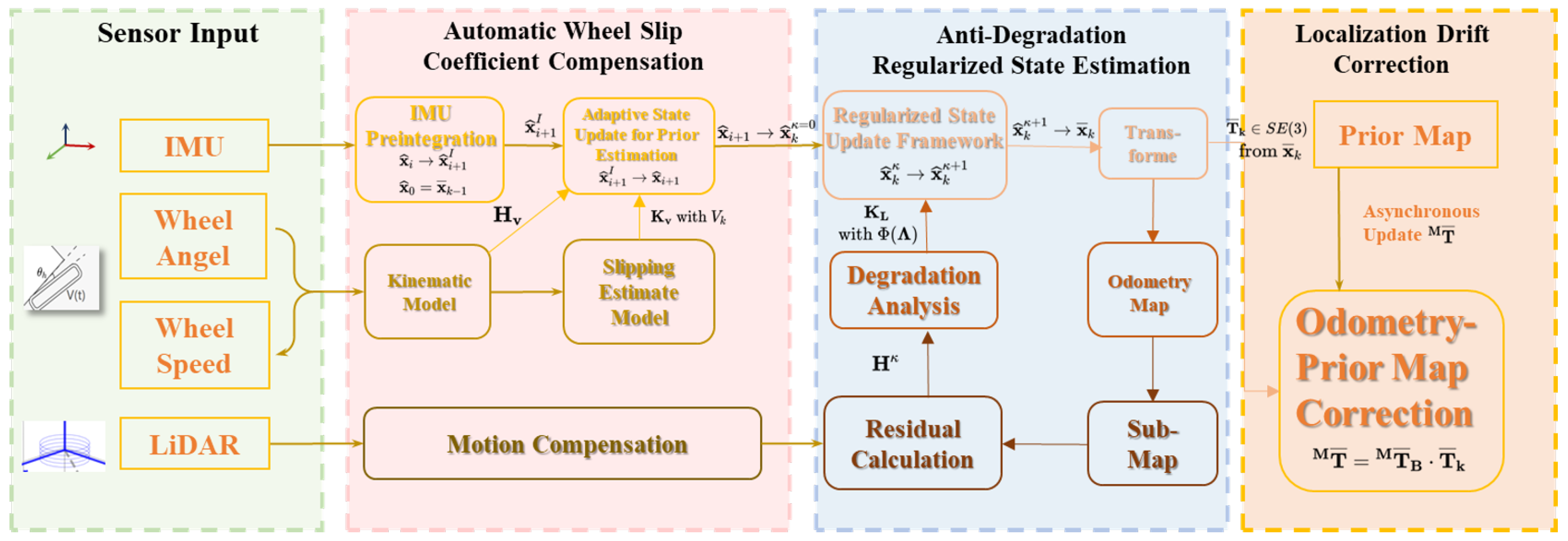
To address large-scale signal-free navigation challenges in underground mines, we pioneer a multi-sensor fusion cascaded filtering SLAM localization system. This innovative architecture aligns with the proposed research contributions and comprises three core components, the system overview as illustrated in Figure 1:

Multi-sensor fusion cascaded filtering framework: Integrates LiDAR, IMU, wheel speed, and steering angle data to achieve continuous positioning in kilometer-scale lightless tunnels. This framework serves as the core architecture for realizing full-scenario coverage, eliminating reliance on external localization signals and ensuring baseline stability for high-precision localization. Scenario-adapted specialized filtering modules were also used.

An Automatic Wheel Slip Coefficient Compensation Method (Section 3.1): Tailored for low-adhesion mine road surfaces, this method fuses IMU measurements with vehicle kinematic models derived from wheel speed and steering angle. By extracting non-Gaussian noise features induced by wheel slippage, it constructs an adaptive recursive Bayesian state estimation framework, dynamically adjusting the noise covariance matrix in real time. This mechanism effectively suppresses anomalies caused by slippage, resolving non-Gaussian interference and enhancing system stability in mine environments.

Anti-degradation regularized state estimation module (Section 3.2): This module addresses geometric degradation in tunnels by constructing observation models based on point-to-plane geometric features between LiDAR point clouds and local maps. It computes Jacobian matrices for the observation model and implements state updates via a nonlinear state estimation framework. To mitigate feature degradation impacts, constraint strength is quantified through residual Jacobian analysis, and a regularization model reflecting system constraint intensity is developed. By embedding feature constraint regularization terms into the state estimation process, updates along weakly constrained directions are explicitly restricted, significantly enhancing robustness in feature-degraded sections.

The state variables involved in the estimation process and their evolution are systematically defined in

Table 1. State variable definitions and evolution process.

State Symbol	Definition Description
${\overline{\mathbf{x}}}_{k-1}$	Optimal state estimate from LiDAR frame $k-1$, used as initial state for IMU integration.
${\widehat{\mathbf{x}}}_i$	Filtered state after kinematic correction, fusing IMU and odometry data, written as ${\widehat{\mathbf{x}}}_0={\overline{\mathbf{x}}}_{k-1}$
${\widehat{\mathbf{x}}}_i^I$	IMU-integrated state prediction, prone to error accumulation. Derived recursively from Equation (3).
${\tilde{\mathbf{x}}}_i$	Error state representing deviation between estimated and true state.
${\widehat{\mathbf{x}}}_k$	Upon arrival of the k-th LiDAR frame, the current state ${\widehat{\mathbf{x}}}_i$ is denoted as ${\widehat{\mathbf{x}}}_k$
${\widehat{\mathbf{x}}}_k^{\kappa }$	State for iterative Kalman filter, written as ${\widehat{\mathbf{x}}}_k^{\kappa =0}={\widehat{\mathbf{x}}}_k$.
${\overline{\mathbf{x}}}_k$	Final optimal state after $\kappa$ Kalman filter iterations, used for next frame’s initialization.

. The overall workflow proceeds as follows: The IMU prior propagation, which yields the predicted state ${\widehat{\mathbf{x}}}^I$ based on raw inertial data integration, is comprehensively derived and explained in Section 3.1.1. This prior estimate is subsequently refined using kinematic constraints in Section 3.1.4, producing the primary filtered state estimate $\widehat{\mathbf{x}}$ and its associated error state $\tilde{\mathbf{x}}$. This IMU-Kinematic filtering loop operates iteratively between LiDAR frames.

Upon arrival of the k-th LiDAR point cloud, the framework enters the scan-matching phase. The state from the final IMU–kinematic iteration, $\widehat{\mathbf{x}}$, is designated as the initial value ${\widehat{\mathbf{x}}}_k$ for LiDAR alignment. The core iterative Kalman filter update, initialized with ${\widehat{\mathbf{x}}}_k^{\kappa =0}={\widehat{\mathbf{x}}}_k$, is then executed to optimally fuse the LiDAR observations. The complete derivation and implementation of this process, which culminates in the final optimal state estimate ${\overline{\mathbf{x}}}_k$, are presented in Section 3.2.3. This cascaded structure ensures computational efficiency and estimation accuracy by decoupling high-frequency propagation from high-precision, low-frequency correction.

Localization drift correction module (Section 3.3): This module eliminates cumulative errors through prior map constraints, achieving drift-free localization. By matching real-time LiDAR scans with high-precision prior maps, this module performs closed-loop compensation for accumulated localization errors, ensuring sustained high-precision performance during long-range navigation in mining environments.

3.1. Automatic Wheel Slip Coefficient Compensation Method

This section details the construction of a tightly coupled filter for prior pose estimation, which integrates IMU measurements with vehicle kinematic models (derived from wheel speed and steering angle) to implement the Automatic Wheel Slip Coefficient Compensation Method. By analyzing the non-Gaussian disturbance characteristics of wheel speed measurements induced by mine road slippage, we design an adaptive recursive Bayesian state estimation framework for dynamic update. This prior state estimation approach effectively compensates for slip-induced errors, achieving enhanced robustness and improved localization accuracy in low-adhesion underground mine environments.

3.1.1. IMU Integration Model

The IMU evaluates object motion states by measuring three-dimensional acceleration and triaxial angular velocity, providing high accuracy over short durations. We assume rigid connections between the IMU, LiDAR, and vehicle kinematic center, with the IMU (denoted as I) state representing the body localization state. Referencing the definitions of generalized addition ⊞ and subtraction ⊟ from [27], the discrete pre-integration model is defined as follows, where i denotes the IMU measurement index:

$${\mathbf{x}}_{i+1}={\mathbf{x}}_i⊞\left(\mathrm{\Delta }t·\mathbf{f}\left({\mathbf{x}}_i,{\mathbf{u}}_i,{\mathbf{w}}_i\right)\right)$$

(1)

According to the model definition in [15], the function $\mathbf{f}$, state $\mathbf{x}$, input $\mathbf{u}$, and noise $\mathbf{w}$ are defined as

$$\begin{array}{c}\mathcal{M}=\mathrm{SO}\left(3\right)\times {\mathbb{R}}^{15},dim\left(\mathcal{M}\right)=18\\ \mathbf{x}\doteq {\left[\begin{array}{cccccc}{}^G\mathbf{R}_I^T& {}^G\mathbf{P}_I^T& {}^G\mathbf{v}_I^T& {\mathbf{b}}_{\omega }^T& {\mathbf{b}}_a^T& {}^G\mathbf{g}^T\end{array}\right]}^T\in \mathcal{M}\\ \mathbf{u}\doteq {\left[\begin{array}{cc}{\omega }_m^T& {\mathbf{a}}_m^T\end{array}\right]}^T,\mathbf{w}\doteq {\left[\begin{array}{cccc}{\mathbf{n}}_{\omega }^T& {\mathbf{n}}_a^T& {\mathbf{n}}_{b\omega }^T& {\mathbf{n}}_{ba}^T\end{array}\right]}^T\\ \mathbf{f}\left({\mathbf{x}}_i,{\mathbf{u}}_i,{\mathbf{w}}_i\right)=\left[\begin{array}{c}{\omega }_{m_i}-{\mathbf{b}}_{{\omega }_i}-{\mathbf{n}}_{{\omega }_i}\\ {}^G\mathbf{v}_{I_i}\\ {}^G\mathbf{R}_{I_i}\left({\mathbf{a}}_{m_i}-{\mathbf{b}}_{a_i}-{\mathbf{n}}_{a_i}\right)+{\phantom{­}}^G{\mathbf{g}}_i\\ {\mathbf{n}}_{b{\omega }_i}\\ {\mathbf{n}}_{b{a}_i}\\ {\mathbf{0}}_{3\times 1}\end{array}\right]\end{array}$$

(2)

Variable Definitions:

• ${\phantom{­}}^G{\mathbf{R}}_I$: Rotation matrix from IMU frame to global frame (SO(3));
• ${\phantom{­}}^G{\mathbf{p}}_I$: IMU position in global coordinates;
• ${\phantom{­}}^G{\mathbf{v}}_I$: IMU velocity in global coordinates;
• ${\mathbf{b}}_{\omega },{\mathbf{b}}_{\mathbf{a}}$: Gyroscope and accelerometer biases;
• ${\phantom{­}}^G\mathbf{g}$: Gravity vector in global coordinates;
• ${\omega }_m,{\mathbf{a}}_m$: Raw IMU angular velocity and acceleration measurements;
• ${\mathbf{n}}_{(·)}$: White noise components.

Since the optimal state estimate after fusing the last (i.e., $\mathrm{k}-1-\mathrm{th}$) LiDAR scan is ${\overline{\mathbf{x}}}_{k-1}$, when IMU measurement data is received, the system performs forward propagation. Specifically, the state is propagated following Equation (3) by setting the process noise ${\mathbf{w}}_i$ to zero.

$${\widehat{\mathbf{x}}}_{i+1}^I={\widehat{\mathbf{x}}}_i⊞\left(\mathrm{\Delta }t\mathbf{f}\left({\widehat{\mathbf{x}}}_i,{\mathbf{u}}_i,\mathbf{0}\right)\right);{\widehat{\mathbf{x}}}_0={\overline{\mathbf{x}}}_{k-1}$$

(3)

Using the error state as the update state effectively enhances system linearity and avoids singularities when representing rotational states. The IMU error state forward propagation method is as follows:

$$\begin{array}{cc}\hfill {\tilde{\mathbf{x}}}_{i+1}^I& ={\mathbf{x}}_{i+1}\boxminus {\widehat{\mathbf{x}}}_{i+1}^I\hfill \\ \hfill & =\left({\mathbf{x}}_i⊞\mathrm{\Delta }t·\mathbf{f}\left({\mathbf{x}}_i,{\mathbf{u}}_i,{\mathbf{w}}_i\right)\right)\boxminus \left({\widehat{\mathbf{x}}}_i⊞\mathrm{\Delta }t·\mathbf{f}\left({\widehat{\mathbf{x}}}_i,{\mathbf{u}}_i,\mathbf{0}\right)\right)\hfill \\ \hfill & \simeq {\mathbf{F}}_{\tilde{\mathbf{x}}}{\tilde{\mathbf{x}}}_i+{\mathbf{F}}_{\mathbf{w}}{\mathbf{w}}_i\hfill \end{array}$$

(4)

During updates, the covariance between true and estimated states is continuously updated:

$$\begin{array}{c}\hfill {\widehat{\mathbf{P}}}_{i+1}^I={\mathbf{F}}_{\tilde{\mathbf{x}}}{\widehat{\mathbf{P}}}_i{\mathbf{F}}_{\tilde{\mathbf{x}}}^T+{\mathbf{F}}_{\mathrm{w}}\mathbf{Q}{\mathbf{F}}_{\mathrm{w}}^T;{\widehat{\mathbf{P}}}_0={\overline{\mathbf{P}}}_{k-1}\end{array}$$

(5)

where $\mathbf{Q}$ is the noise covariance and ${\overline{\mathbf{P}}}_0$ is initialized as follows:

${\phantom{­}}^G{\mathbf{R}}_I$ is initialized via gravity vector alignment with high confidence (${\sigma }^2=1\times {10}^{-5}$) under static conditions.

${\phantom{­}}^G{\mathbf{p}}_I$ assumes origin initialization with high confidence (${\sigma }^2=1\times {10}^{-5}$).

${\phantom{­}}^G{\mathbf{v}}_I$ retains moderate uncertainty (${\sigma }^2=1.0$) for robustness, despite typical stationary assumptions.

${\mathbf{b}}_{\omega }$ is initialized with ${\sigma }^2=1\times {10}^{-4}$, reflecting moderate uncertainty in initial bias estimation.

${\mathbf{b}}_a$ is initialized with ${\sigma }^2=1\times {10}^{-3}$, accounting for higher time-varying uncertainty characteristics.

${\phantom{­}}^G\mathbf{g}$ is initialized from normalized accelerometer data with high confidence (${\sigma }^2=1\times {10}^{-5}$).

This initialization strategy balances convergence speed and estimation stability through appropriate parameter weighting in the state estimation process.

Now we define

$$\begin{array}{c}\hfill \mathbf{g}\left({\tilde{\mathbf{x}}}_i,{\mathbf{w}}_i\right)=\mathbf{f}\left({\mathbf{x}}_i,{\mathbf{u}}_i,{\mathbf{w}}_i\right)\mathrm{\Delta }t=\mathbf{f}\left({\widehat{\mathbf{x}}}_i⊞{\tilde{\mathbf{x}}}_i,{\mathbf{u}}_i,{\mathbf{w}}_i\right)\mathrm{\Delta }t\end{array}$$

(6)

The IMU integration-based error state estimate ${\tilde{\mathbf{x}}}_{i+1}^I$ is computed as

$$\begin{array}{cc}\hfill {\tilde{\mathbf{x}}}_{i+1}^I& =\left(\left({\widehat{\mathbf{x}}}_i⊞{\tilde{\mathbf{x}}}_i\right)⊞\mathbf{g}\left({\tilde{\mathbf{x}}}_i,{\mathbf{w}}_i\right)\right)\boxminus \left({\widehat{\mathbf{x}}}_i⊞\mathbf{g}(\mathbf{0},\mathbf{0})\right)\hfill \\ & \stackrel{\mathrm{def}}{=}\mathbf{G}\left({\tilde{\mathbf{x}}}_i,\mathbf{g}\left({\tilde{\mathbf{x}}}_i,{\mathbf{w}}_i\right)\right)\hfill \end{array}$$

(7)

The Jacobians $F_{\tilde{x}}$ and $F_w$ are then calculated as

$$\begin{array}{cc}\hfill F_{\tilde{x}}& ={\left.{\displaystyle \frac{\partial G(\tilde{x},g(0,0))}{\partial \tilde{x}}}+{\displaystyle \frac{\partial G(0,g(\tilde{x},0))}{\partial g(\tilde{x},0)}}{\displaystyle \frac{\partial g(\tilde{x},0)}{\partial \tilde{x}}}\right|}_{\tilde{x}=0}\hfill \\ \hfill F_w& ={\left.{\displaystyle \frac{\partial G(0,g(0,w\left)\right)}{\partial g(0,w)}}{\displaystyle \frac{\partial g(0,w)}{\partial w}}\right|}_{w=0}\hfill \end{array}$$

(8)

This completes the discrete-state IMU integration for localization estimation. However, obtaining accurate localization results requires not only high-precision IMU measurements but also reliable estimation of inertial biases and gravity components. Both pose significant challenges in underground mining environments. Specifically, road roughness in mines severely degrades IMU measurement accuracy, while frequent tunnel slopes introduce large errors into gravity direction estimation; these factors collectively amplify sensor measurement deviations.

Owing to error propagation arising from the aforementioned unreliable measurements, IMU integration inevitably leads to the accelerated accumulation of significant localization errors. Consequently, constraints derived from vehicle kinematics (based on wheel speed and steering angle) and LiDAR observations are indispensable for correcting the output of IMU integration—this correction step serves as a critical prerequisite for the subsequent implementation of the Automatic Wheel Slip Coefficient Compensation Method.

3.1.2. Vehicle Kinematic Model

To correct the cumulative errors arising from IMU integration, a vehicle kinematic model is introduced to refine state variables including velocity. The longitudinal velocity of the vehicle (${\mathbf{v}}_W$) is measured via wheel speed sensors, while the yaw rate at the kinematic center is determined by the steering angle (${\delta }_f$). The velocity at the kinematic center is decomposed as follows:

$$\begin{array}{c}\hfill {\mathbf{v}}_h=\left[\begin{array}{c}{\mathbf{v}}_{W}cos{\delta }_f\\ {\mathbf{v}}_{W}sin{\delta }_f\\ 0\end{array}\right]\end{array}$$

(9)

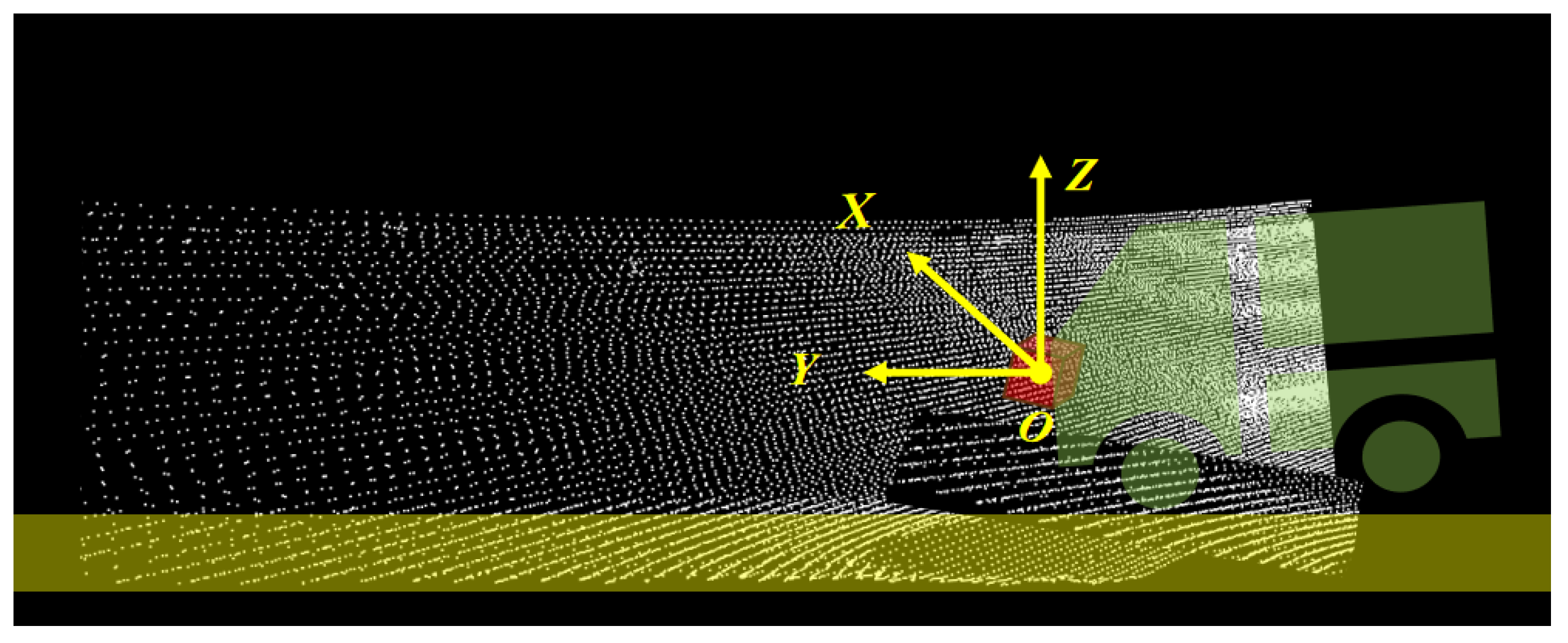
As illustrated in Figure 2, the IMU is mounted at the front of the vehicle, resulting in a discrepancy between the motion states of the vehicle’s kinematic center (i.e., the rear axle) and the IMU measurement frame. Given the extrinsic parameter ${\phantom{­}}^W{\mathbf{T}}_I={(}^W{\mathbf{R}}_I,{\phantom{­}}^W{\mathbf{p}}_I)$ that describes the transformation between the IMU and the rear axle, the relationship between the IMU-integrated states and the kinematically estimated states is formulated as follows:

$$\begin{array}{cc}\hfill {\mathbf{h}}_v\left(\mathbf{x}\right)& ={\mathbf{v}}_h\hfill \\ & ={\phantom{­}}^W{\mathbf{R}}_I{\left({\phantom{­}}^G{\mathbf{R}}_I\right)}^{\top }·{\phantom{­}}^G{\mathbf{v}}_I+{\phantom{­}}^W{\mathbf{R}}_I\left({\left({\omega }^b\right)}^{\wedge }·{\phantom{­}}^W{\mathbf{p}}_I\right)\hfill \end{array}$$

(10)

where ${\omega }^b={\omega }_m-{\mathbf{b}}_{\omega }$. The observation Jacobian matrix ${\mathbf{H}}_{\mathbf{v}}$ is computed as

$$\begin{array}{cc}\hfill {\mathbf{H}}_{\mathbf{v}}& \triangleq {\displaystyle \frac{\partial h_v}{\partial \delta \mathbf{x}}}\hfill \\ \hfill & =\left[\begin{array}{cccccc}{\mathbf{H}}_{\theta }\hfill & {\mathbf{0}}_{3\times 3}\hfill & {\mathbf{H}}_v\hfill & {\mathbf{H}}_{b\omega }\hfill & {\mathbf{0}}_{3\times 3}\hfill & {\mathbf{0}}_{3\times 3}\hfill \end{array}\right]\hfill \end{array}$$

(11)

with its components defined as

$$\begin{array}{cc}\hfill {\mathbf{H}}_{\theta }& ={\phantom{­}}^W{\mathbf{R}}_I{\left({\phantom{­}}^G{\mathbf{R}}_I^{\top }{\phantom{­}}^G{\mathbf{v}}_I\right)}^{\wedge }\hfill \\ \hfill {\mathbf{H}}_v& ={\phantom{­}}^W{\mathbf{R}}_I{\left({\phantom{­}}^G{\mathbf{R}}_I\right)}^T\hfill \\ \hfill {\mathbf{H}}_{b\omega }& =-{\phantom{­}}^W{\mathbf{R}}_I{\left({\phantom{­}}^W{\mathbf{p}}_I\right)}^{\wedge }\hfill \end{array}$$

(12)

The observation noise covariance matrix incorporates errors from both wheel speed and steering angle measurements, expressed as

$$\begin{array}{c}\hfill V_0=\left[\begin{array}{ccc}{\sigma }_{{\mathbf{v}}_W}^2{cos}^2{\delta }_f& 0& 0\\ 0& {\sigma }_{{\delta }_f}^2{{\mathbf{v}}_W}^2& 0\\ 0& 0& {\sigma }_{\mathbf{z}}^2\end{array}\right]\end{array}$$

(13)

Here, ${\sigma }_{{\mathbf{v}}_W}^2$ and ${\sigma }_{{\delta }_f}^2$ represent the variances of wheel speed and steering angle, respectively, while ${\sigma }_{\mathbf{z}}$ accounts for longitudinal vibration during vehicle operation.

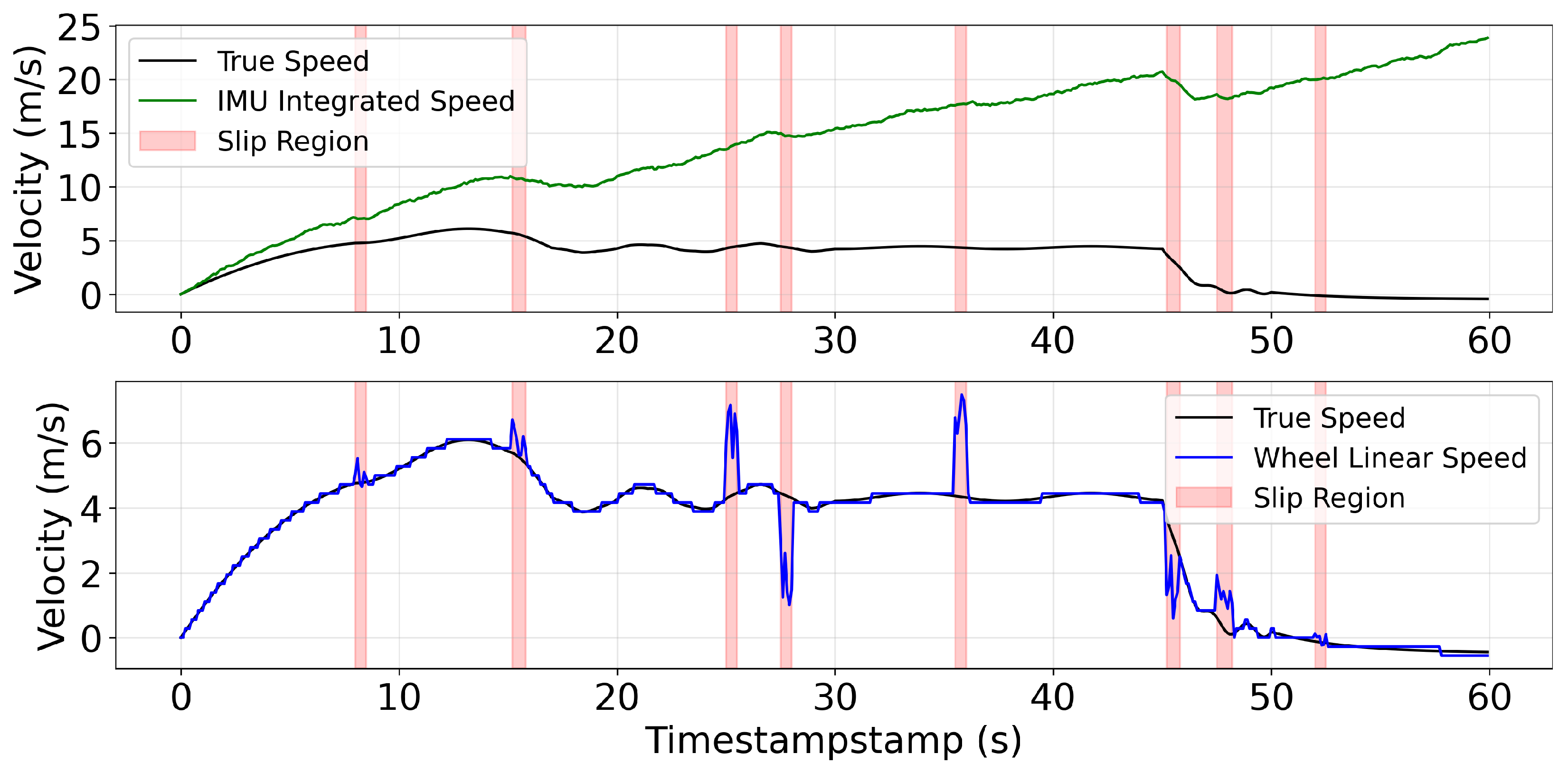
This kinematic model enables accurate estimation of horizontal motion and establishes an observation model for velocity states in IMU integration. However, conventional kinematic modeling frameworks only account for inherent measurement noise and lack the capability to filter non-Gaussian slip-induced noise as a critical limitation that compromises localization robustness in underground mine environments where wheel slippage is prevalent. Consequently, an adaptive covariance estimation strategy that accounts for the characteristics of non-Gaussian slip noise is essential to maintain reliable prior state estimation under slippage disturbances, forming a key component of the Automatic Wheel Slip Coefficient Compensation Method.

3.1.3. Adaptive Covariance Estimation

Traditional Kalman filtering assumes Gaussian-distributed sensor measurement errors. For wheel speed measurements, beyond sensor noise, we must account for non-Gaussian errors induced by wheel slippage on wet underground mine surfaces. This paper designs a slip ratio-based adaptive covariance estimation method that dynamically adjusts wheel speed noise covariance according to slippage conditions, mitigating slip impacts. The slip ratio feature is defined as:

$$\begin{array}{c}\hfill {\gamma }_{\mathrm{slip}}=\left\{\begin{array}{cc}0\hfill & \left|{\mu }_k\right|<0.1\hfill \\ k·\left|{\mathbf{v}}_{\mathbf{W}}-{\mu }_k\right|\hfill & \mathrm{other}\hfill \end{array}\right.\end{array}$$

(14)

Additionally, we consider slip ratio gradient features as follows:

$$\begin{array}{c}\hfill {\gamma }_{\mathrm{grad}}=\left|\nabla {\gamma }_{\mathrm{slip}}^{\left(\mathrm{recent}\right)}\right|\end{array}$$

(15)

$$\begin{array}{c}\hfill {\gamma }_{\mathrm{jerk}}=\left|{\nabla }^2{\gamma }_{\mathrm{slip}}^{\left(\mathrm{recent}\right)}\right|\end{array}$$

(16)

Since longitudinal slippage dominates in most scenarios, we define the comprehensive feature vector for longitudinal slip as follows:

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_k={\left[{\gamma }_{\mathrm{slip}},{\gamma }_{\mathrm{grad}},{\gamma }_{\mathrm{jerk}}\right]}^{\top }\end{array}$$

(17)

where

$$\begin{array}{c}\hfill {\mu }_k={\displaystyle \frac{1}{\left|{\mathcal{W}}_k\right|}}\sum _{{\mathbf{v}}_{\mathbf{W}}i\in {\mathcal{W}}_k}{\mathbf{v}}_{\mathbf{W}}i\end{array}$$

(18)

${\mathcal{W}}_k$ represents the sliding window for speed measurements. The weight matrix $\mathbf{W}$ updates via

$$\begin{array}{c}\hfill {\mathbf{W}}_k={\mathbf{W}}_{k-1}+\eta \left({\mathrm{\Gamma }}_k{\mathrm{\Gamma }}_k^{\top }-{\mathbf{W}}_{k-1}\right)\end{array}$$

(19)

The learning rate $\eta$, which controls the update step size, can be tuned based on practical scenarios and has been empirically set to 0.6 in our implementation as this value demonstrates optimal adaptation performance for the current application context. This recursive form implements an exponential moving average, allowing the system to continuously adapt to changing road conditions by emphasizing recent anomaly observations while gradually forgetting distant data. The term ${\mathrm{\Gamma }}_k{\mathrm{\Gamma }}_k^{\top }$ represents the instantaneous outer product of the anomaly vector, serving as a local estimate of the covariance structure at time step k. To ensure numerical stability and maintain the mathematical integrity of the covariance structure, positive definiteness is enforced through spectral decomposition and reconstruction:

$$\begin{array}{c}\hfill {\mathbf{W}}_k=\mathrm{\Phi }·{\mathrm{\Lambda }}^{+}·{\mathrm{\Phi }}^{\top }\end{array}$$

(20)

The detailed procedure involves performing eigenvalue decomposition $\mathbf{W}=\mathrm{\Phi }\mathrm{\Lambda }{\mathrm{\Phi }}^{\top }$, where $\mathrm{\Phi }$ contains the eigenvectors and $\mathrm{\Lambda }=diag\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$ contains the eigenvalues. We compute the modified eigenvalue matrix ${\mathrm{\Lambda }}^{+}=diag\left(max\left({\lambda }_1,ϵ\right),max\left({\lambda }_2,ϵ\right),max\left({\lambda }_3,ϵ\right)\right)$ with $ϵ>0$, where we choose $ϵ=1\times {10}^{-6}$ to be a small positive threshold to eliminate non-positive eigenvalues and reconstruct the positive semi-definite matrix via (20).

This is followed by a unit trace constraint:

$$\begin{array}{c}\hfill {\widehat{\mathbf{W}}}_k={\displaystyle \frac{{\mathbf{W}}_k}{tr\left({\mathbf{W}}_k\right)}}\end{array}$$

(21)

We thus obtain a learning factor and positive-definite weight matrix, enabling adaptive observation noise estimation:

$$\begin{array}{c}\hfill V_k=V_0\left[\begin{array}{ccc}1+\alpha ·{\mathrm{\Gamma }}_k^{\top }{\widehat{\mathbf{W}}}_k{\mathrm{\Gamma }}_k& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\end{array}$$

(22)

This method achieves wheel speed noise adaptation based on slippage characteristics, which is crucial for subsequent gain calculations.

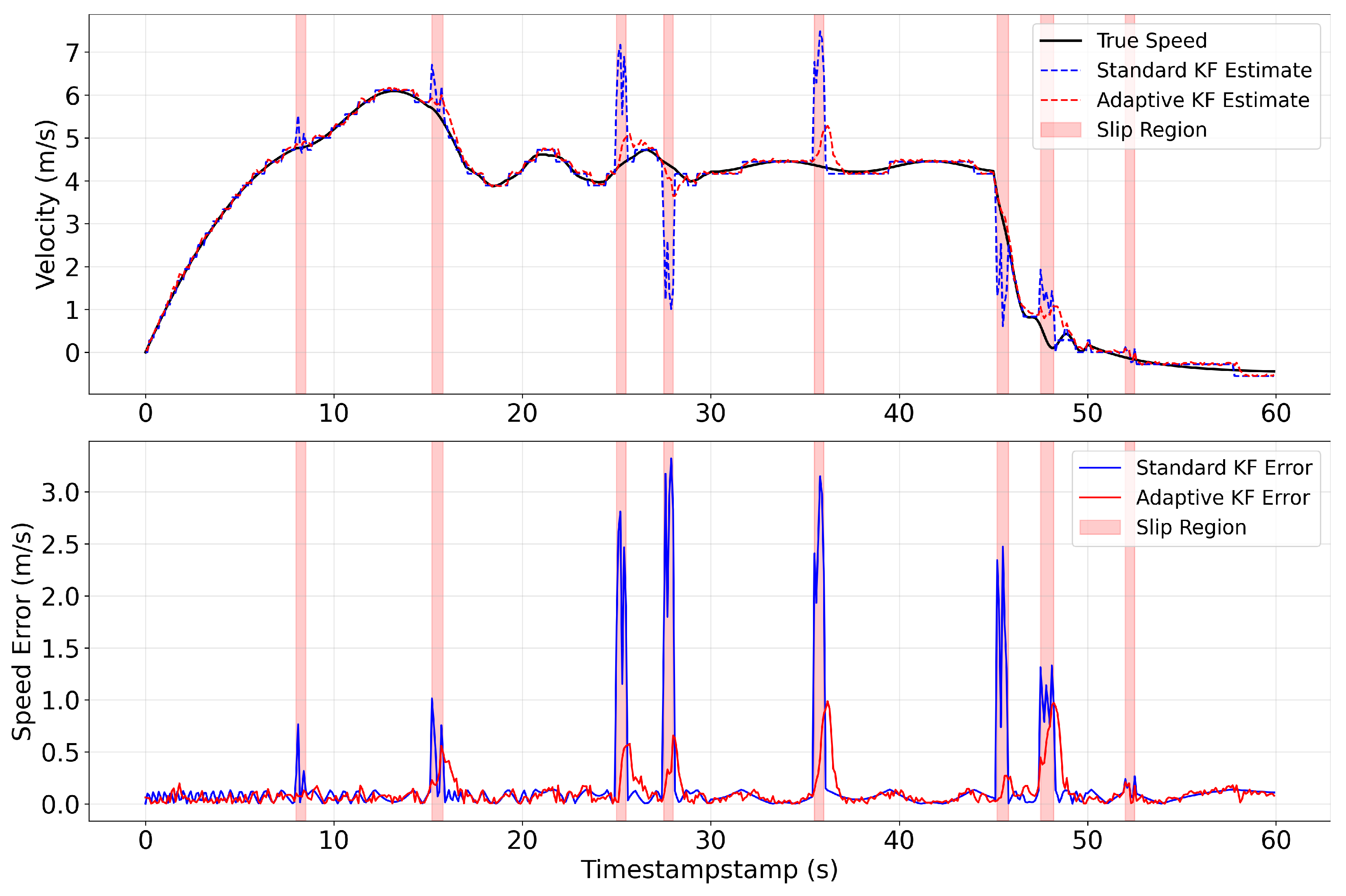
3.1.4. Adaptive State Update for Prior Estimation

The adaptive state update process follows the error-state recursive Bayesian estimation workflow, with a key modification: fixed noise covariance is replaced by the adaptive noise covariance $V_k$ (derived in the previous subsection) during velocity fusion gain computation. This modification ensures that the estimation process dynamically responds to slippage-induced non-Gaussian noise. The core update equations are formulated as follows:

$$\begin{array}{cc}\hfill {\mathbf{K}}_{\mathbf{v}}& ={\widehat{\mathbf{P}}}_{i+1}^I{\mathbf{H}}_{\mathbf{v}}^{\top }{\left({\mathbf{H}}_{\mathbf{v}}{\widehat{\mathbf{P}}}_{i+1}^I{\mathbf{H}}_{\mathbf{v}}^{\top }+V_k\right)}^{-1}\hfill \\ \hfill {\widehat{\mathbf{P}}}_{i+1}& =(\mathbf{I}-{\mathbf{K}}_{\mathbf{v}}{\mathbf{H}}_{\mathbf{v}}){\widehat{\mathbf{P}}}_{i+1}^I\hfill \\ \hfill \delta \widehat{\mathbf{x}}& ={\mathbf{K}}_{\mathbf{v}}\left({\mathbf{v}}_h-h\left({\widehat{\mathbf{x}}}_{i+1}^I\right)\right)\hfill \end{array}$$

(23)

where $\widehat{\delta \mathbf{x}}$ represents the estimated error state between the kinematically derived states and the IMU-integrated states. The updated states are then obtained via generalized addition and subtraction operations:

$$\begin{array}{c}\hfill {\widehat{\mathbf{x}}}_{i+1}={\widehat{\mathbf{x}}}_{i+1}^I⊞\delta \widehat{\mathbf{x}}\end{array}$$

(24)

$$\begin{array}{c}\hfill {\tilde{\mathbf{x}}}_{i+1}={\tilde{\mathbf{x}}}_{i+1}^I\boxminus \delta \widehat{\mathbf{x}}\end{array}$$

(25)

This completes the adaptive state update workflow under dynamically varying noise conditions, thereby facilitating tight coupling between IMU integration and vehicle kinematics. Specifically, dynamic evaluation and adjustment of the wheel speed noise covariance—guided by slippage characteristics—enable the system to maintain robust anti-interference capability in non-Gaussian noise scenarios. Crucially, this capability is foundational to ensuring reliable prior state estimation, a requirement for safe and continuous navigation in underground mine environments. The efficacy of the proposed algorithm is validated through simulation experiments, with detailed results and analysis provided in Section 4.3.1.

3.2. Anti-Degradation Regularized State Estimation Module

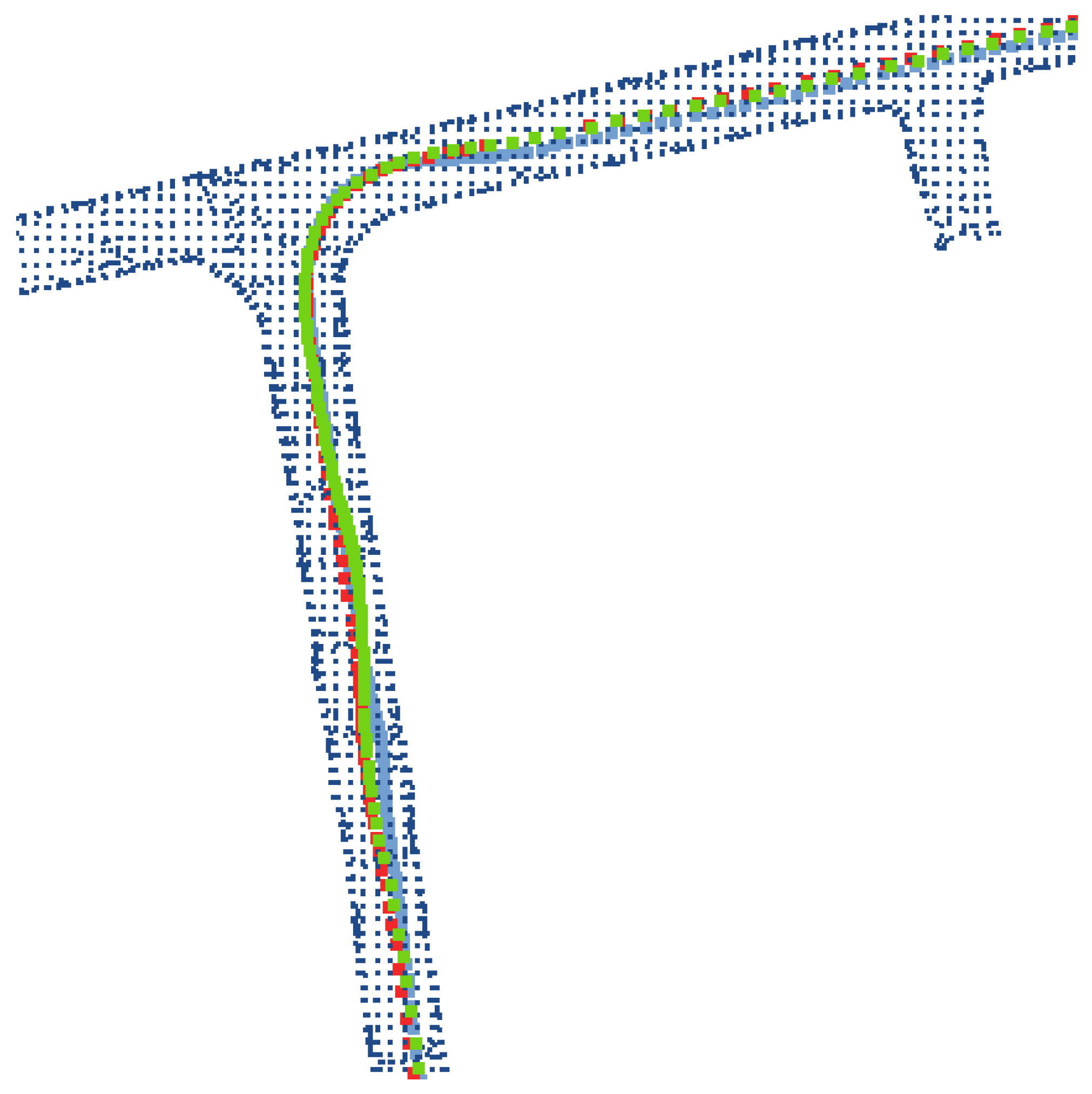
To achieve high-precision pose estimation, posterior refinement of the prior localization state is required, leveraging LiDAR observations as constraints. In feature-degraded underground mining environments (as illustrated in Figure 3), the majority of LiDAR point clouds are distributed along tunnel roofs, floors, and sidewalls. While these points provide effective constraints in the x and z directions, they exhibit weak constraint capability in the vehicle’s forward direction (y-axis)—a phenomenon that can compromise localization stability. To address this, a degradation-characterizing regularization term is incorporated into the LiDAR observation-based state estimation framework, which restricts posterior state updates along geometrically degenerate directions. This design enhances system robustness under extreme feature degradation scenarios.

3.2.1. LiDAR Observation Model

Following prior state estimation, the prior state ${\widehat{\mathbf{x}}}_{i+1}$ is denoted as ${\widehat{\mathbf{x}}}_k$ (serving as the input for posterior refinement), and the prior covariance ${\widehat{\mathbf{P}}}_{i+1}$ is denoted as ${\widehat{\mathbf{P}}}_k$. To mitigate nonlinear errors in posterior estimation, an iterative update strategy is adopted. Let ${\widehat{\mathbf{x}}}_k^{\kappa }$ represent the state at the $\kappa$-th iteration, with the initial iteration state set as ${\widehat{\mathbf{x}}}_k^{\kappa =0}={\widehat{\mathbf{x}}}_k$. Motion-compensated LiDAR points ${\{}^L{\mathbf{p}}_{poin{t}_j}\}$ are transformed into the global coordinate frame using the following formulation:

$$\begin{array}{c}\hfill {\phantom{­}}^G{\widehat{\mathbf{p}}}_{poin{t}_j}^{\kappa }={\phantom{­}}^G{\widehat{\mathbf{T}}}_{I_k}^{\kappa }{\phantom{­}}^I{\mathbf{T}}_L{\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}\end{array}$$

(26)

where ${\phantom{­}}^G{\widehat{\mathbf{T}}}_{I_k}^{\kappa }=\left({\phantom{­}}^G{\widehat{\mathbf{R}}}_{I_k}^{\kappa },{\phantom{­}}^G{\widehat{\mathbf{p}}}_{I_k}^{\kappa }\right)$ denotes the estimated transformation from the IMU frame to the global frame at the $\kappa$-th iteration, and ${\phantom{­}}^I{\mathbf{T}}_L$ is the pre-calibrated extrinsic transformation between the LiDAR and IMU frames. Residuals between the transformed LiDAR points ${\phantom{­}}^G{\widehat{\mathbf{p}}}_{poin{t}_j}^{\kappa }$ and their nearest corresponding points ${\phantom{­}}^G{\mathbf{q}}_j$ on the local map plane are computed as

$$\begin{array}{c}\hfill {\mathbf{z}}_j^{\kappa }={\mathbf{G}}_j\left({\phantom{­}}^G{\widehat{\mathbf{p}}}_{poin{t}_j}^{\kappa }-{\phantom{­}}^G{\mathbf{q}}_j\right)\end{array}$$

(27)

Here, ${\mathbf{G}}_j={\mathbf{u}}_j^T$, with ${\mathbf{u}}_j$ representing the unit normal vector of the local map plane at the point ${\phantom{­}}^G{\mathbf{q}}_j$. For the true state ${\mathbf{x}}_k$, the LiDAR observation model is defined as

$$\begin{array}{cc}\hfill {\mathbf{h}}_j\left({\mathbf{x}}_k,{\phantom{­}}^L{\mathbf{n}}_{poin{t}_j}\right)={\mathbf{G}}_j& \left({\phantom{­}}^G{\mathbf{T}}_{I_k}{\phantom{­}}^I{\mathbf{T}}_L\left({\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}-{\phantom{­}}^L{\mathbf{n}}_{poin{t}_j}\right)-{\phantom{­}}^G{\mathbf{q}}_j\right)\hfill \end{array}$$

(28)

Using the error state definition (where ${\tilde{\mathbf{x}}}_k^{\kappa }$ represents the error between the true state and the estimated state at the $\kappa$-th iteration), we obtain

$$\begin{array}{c}\hfill {\tilde{\mathbf{x}}}_k^{\kappa }={\mathbf{x}}_k\boxminus {\widehat{\mathbf{x}}}_k^{\kappa }\end{array}$$

(29)

A first-order Taylor expansion of the observation model around ${\tilde{\mathbf{x}}}_k^{\kappa }=0$ yields

$$\begin{array}{cc}\hfill {\mathbf{h}}_j\left({\mathbf{x}}_k,{\phantom{­}}^L{\mathbf{n}}_{poin{t}_j}\right)& ={\mathbf{h}}_j\left({\widehat{\mathbf{x}}}_k^{\kappa }⊞{\tilde{\mathbf{x}}}_k^{\kappa },{\phantom{­}}^L{\mathbf{n}}_{poin{t}_j}\right)\hfill \\ \hfill & \simeq {\mathbf{h}}_j\left({\widehat{\mathbf{x}}}_k^{\kappa },\mathbf{0}\right)+{\mathbf{H}}_j^{\kappa }{\tilde{\mathbf{x}}}_k^{\kappa }+{\mathbf{v}}_j\hfill \\ \hfill & ={\mathbf{z}}_j^{\kappa }+{\mathbf{H}}_j^{\kappa }{\tilde{\mathbf{x}}}_k^{\kappa }+{\mathbf{v}}_j\hfill \end{array}$$

(30)

In this expression, ${\mathbf{H}}_j^{\kappa }$ denotes the Jacobian matrix of the observation function $\mathbf{h}\left(\mathbf{x},\mathbf{n}\right)$ evaluated at ${\tilde{\mathbf{x}}}_k^{\kappa }=0$, and ${\mathbf{v}}_j\in \mathcal{N}\left(\mathbf{0},{\mathbf{R}}_j\right)$ represents the observation noise induced by LiDAR measurement errors ${\phantom{­}}^L{\mathbf{n}}_{poin{t}_j}$, with ${\mathbf{z}}_j^{\kappa }$ being the observed residual at the $\kappa$-th iteration. The Jacobian matrix ${\mathbf{H}}_j$ is computed via the chain rule of partial derivatives:

$$\begin{array}{c}\hfill {\mathbf{H}}_j={\displaystyle \frac{\partial {\mathbf{h}}_{\mathbf{j}}}{\partial \left({\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}\right)}}{\displaystyle \frac{\partial \left({\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}\right)}{\partial {\tilde{\mathbf{x}}}_j}}\end{array}$$

(31)

This simplifies to the following form:

$$\begin{array}{c}\hfill {\mathbf{H}}_j=\left[-{\overrightarrow{\mathit{n}}}^G{\widehat{\mathbf{R}}}_I{\left({\phantom{­}}^I{\mathbf{R}}_L{\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}+{\phantom{­}}^I{\mathbf{T}}_L\right)}^{\wedge },\overrightarrow{\mathit{n}},0,0,0,0\right]\end{array}$$

(32)

where $\overrightarrow{\mathit{n}}$ is the unit normal vector of the plane formed by the nearest neighbors of the LiDAR point ${\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}$.

3.2.2. Feature Degradation Scenario Analysis

Leveraging the residuals and Jacobian matrices ${\mathbf{H}}_j$ derived from the LiDAR observation model, maximum a posteriori (MAP) state estimation is achieved by minimizing the residual norm between observed and estimated values. This optimization problem is formulated as

$$\begin{array}{c}\hfill \underset{{\tilde{\mathbf{x}}}_k^{\kappa }}{min}\left({∥\mathbf{r}+{\mathbf{H}}^{\kappa }{\tilde{\mathbf{x}}}_k^{\kappa }∥}_{{\mathbf{R}}_j^{-1}}^2\right)\end{array}$$

(33)

where $\mathbf{r}={\left[{\mathbf{z}}_1^{\kappa },\dots ,{\mathbf{z}}_m^{\kappa }\right]}^{\top }$ and ${\mathbf{H}}^{\kappa }={\left[{\mathbf{H}}_1^{{\kappa }^{\top }},\dots ,{\mathbf{H}}_m^{{\kappa }^{\top }}\right]}^{\top }$ denote the aggregated residuals of all LiDAR point clouds and their corresponding Jacobian matrices, respectively.

This posterior state estimation problem is solved as a least-squares optimization, whose solution accuracy is critically dependent on the structural characteristics of ${\mathbf{H}}^{\kappa }$. To intuitively illustrate this dependency, the problem can be analogized to finding the closest point to a set of hyperplanes—with a 2D case (locating the point nearest to three lines) used as a representative example, as shown in Figure 4.

In Figure 4, black lines represent constraint boundaries and the blue point denotes the optimal estimation solution. Introducing an additional constraint plane $\mathbf{c}$ passing through this optimal point does not alter the solution. However, when the constraint plane $\mathbf{c}$ is perturbed by $\delta d$, the solution shifts to the yellow point with a displacement of $\delta x_c$. Under strong constraint conditions, as shown in Figure 4a, such perturbations induce minimal changes in the solution; in contrast, constraint conditions like in Figure 4b result in significant sensitivity to perturbations, leading to large solution deviations. The optimal solution to the least-squares problem is computed using the left pseudoinverse of ${\mathbf{H}}^{\kappa }$:

$$\begin{array}{c}\hfill x_0={\left({\mathbf{H}}^{\kappa }\right)}_{left}^{-1}(-{\mathbf{z}}^{\kappa })\end{array}$$

(34)

where ${\left({\mathbf{H}}^{\kappa }\right)}_{left}^{-1}$ denotes the left pseudoinverse, defined as follows:

$$\begin{array}{c}\hfill A_{left}^{-1}={\left(A^{\top }A\right)}^{-1}{A}^{\top }\end{array}$$

(35)

When an additional constraint $\mathit{c}$ (passing through the optimal solution $x_0$) is incorporated, the solution remains unchanged, as expressed by

$$\begin{array}{c}\hfill x_0={\left[\begin{array}{c}{\mathbf{H}}^{\kappa }\\ {\mathit{c}}^{\top }\end{array}\right]}_{left}^{-1}\left[\begin{array}{c}-{\mathbf{z}}^{\kappa }\\ {\mathit{c}}^{\top }{\mathbf{x}}_0\end{array}\right]\end{array}$$

(36)

In the presence of a perturbation $\delta d$ applied to the constraint $\mathbf{c}$, the perturbed solution becomes

$$\begin{array}{c}\hfill x_0+\delta x={\left[\begin{array}{c}{\mathbf{H}}^{\kappa }\\ {\mathit{c}}^{\top }\end{array}\right]}_{left}^{-1}\left[\begin{array}{c}-{\mathbf{z}}^{\kappa }\\ {\mathit{c}}^{\top }{\mathbf{x}}_0+\delta d\end{array}\right]\end{array}$$

(37)

The displacement $\delta x$ induced by the perturbation $\delta d$ is derived as

$$\begin{array}{c}\hfill \delta x={\left({{\mathbf{H}}^{\kappa }}^{\top }{\mathbf{H}}^{\kappa }+\mathit{c}{\mathit{c}}^{\top }\right)}^{-1}\mathit{c}\delta d\end{array}$$

(38)

The component of this displacement along the direction of the unit vector $\mathit{c}$ (denoted as $\delta x_c$) is calculated as $\delta x_c={\mathit{c}}^{\top }\delta x$, which simplifies to

$$\begin{array}{c}\hfill \delta x_c={\left({\mathit{c}}^T{{\mathbf{H}}^{\kappa }}^{\top }{\mathbf{H}}^{\kappa }\mathit{c}+1\right)}^{-1}\delta d\end{array}$$

(39)

The maximum value of $\delta x_c$ (i.e., the direction of greatest sensitivity to perturbations) is determined by solving the following optimization problem:

$$\begin{array}{c}\hfill arg\underset{\mathit{c}}{min}{\mathit{c}}^{\top }{{\mathbf{H}}^{\kappa }}^{\top }{\mathbf{H}}^{\kappa }\mathit{c},\mathrm{s}.\mathrm{t}.\left|\mathit{c}\right|=1\end{array}$$

(40)

Solving this Rayleigh quotient problem reveals that $\delta x_c$ is maximized when $\mathit{c}$ is aligned with the eigenvector corresponding to the minimum eigenvalue of ${{\mathbf{H}}^{\kappa }}^{\top }{\mathbf{H}}^{\kappa }$. The eigenvalue decomposition of ${{\mathbf{H}}^{\kappa }}^{\top }{\mathbf{H}}^{\kappa }$ thus enables quantitative evaluation of the system’s disturbance resistance across different directions, providing critical insights for directional suppression of state updates in feature-degraded underground mine environments.

3.2.3. Regularized State Update Framework

Building on the prior state estimation and observation models, posterior state refinement is achieved through an error-state recursive Bayesian estimation framework. The error state (defined as the discrepancy between the true state and the estimated state) satisfies the following relationship:

$$\begin{array}{c}\hfill {\tilde{\mathbf{x}}}_k={\mathbf{x}}_k\boxminus {\widehat{\mathbf{x}}}_k={\widehat{\mathbf{x}}}_k^{\kappa }\boxminus {\widehat{\mathbf{x}}}_k+{\mathbf{J}}^{\kappa }{\tilde{\mathbf{x}}}_k^{\kappa }\end{array}$$

(41)

where the Jacobian matrix ${\mathbf{J}}^{\kappa }$ (accounting for state transformation linearization) is formulated as follows:

$$\begin{array}{c}\hfill {\mathbf{J}}^{\kappa }=\left[\begin{array}{cc}\mathbf{A}{\left({\phantom{­}}^G{\widehat{\mathbf{R}}}_{I_k}^{\kappa }{\boxminus }^G{\widehat{\mathbf{R}}}_{I_k}\right)}^{-\top }& {\mathbf{0}}_{3\times 15}\\ {\mathbf{0}}_{15\times 3}& {\mathbf{I}}_{15\times 15}\end{array}\right]\end{array}$$

(42)

The operator $\mathbf{A}\left(\mathbf{u}\right)$ follows the definition provided in [28]. After the $\kappa$-th iteration, the state covariance matrix is updated via the inverse transformation of ${\mathbf{J}}^{\kappa }$:

$$\begin{array}{c}\hfill {\widehat{\mathbf{P}}}_k^{\kappa +1}={\left({\mathbf{J}}^{\kappa }\right)}^{-1}{\widehat{\mathbf{P}}}_k^{\kappa }{\left({\mathbf{J}}^{\kappa }\right)}^{-\top }\end{array}$$

(43)

Maximum a posteriori (MAP) estimation is employed to fuse prior state information with LiDAR observations, formulated as the following optimization problem that minimizes the weighted residual norm:

$$\begin{array}{c}\hfill \underset{{\tilde{\mathbf{x}}}_k^{\kappa }}{min}\left({∥{\mathbf{x}}_k\boxminus {\widehat{\mathbf{x}}}_k∥}_{{\left({\widehat{\mathbf{P}}}_k^{\kappa }\right)}^{-1}}^2+\sum _{j=1}^m{∥{\mathbf{z}}_j^{\kappa }+{\mathbf{H}}_j^{\kappa }{\tilde{\mathbf{x}}}_k^{\kappa }∥}_{{\mathbf{R}}_j^{-1}}^2\right)\end{array}$$

(44)

Using aggregated terms (where ${\mathbf{H}}^{\kappa }={\left[{\mathbf{H}}_1^{{\kappa }^{\top }},\dots ,{\mathbf{H}}_m^{{\kappa }^{\top }}\right]}^{\top }$ denotes the stacked Jacobian matrix, $\mathbf{R}=diag\left({\mathbf{R}}_1,\dots {\mathbf{R}}_m\right)$ is the block-diagonal observation noise covariance, and $\mathbf{r}={\left[{\mathbf{z}}_1^{\kappa },\dots ,{\mathbf{z}}_m^{\kappa }\right]}^{\top }$ represents the aggregated residuals), the cost function simplifies to

$$\begin{array}{c}\hfill J\left(\tilde{\mathbf{x}}\right)={\parallel \tilde{\mathbf{x}}\parallel }_{{\mathbf{P}}^{-1}}^2+{∥\mathbf{r}+{\mathbf{H}}^{\kappa }\tilde{\mathbf{x}}∥}_{{\mathbf{R}}^{-1}}^2\end{array}$$

(45)

As analyzed in Section 3.2.2, geometric feature degradation leads to weak observation constraints in specific directions. To address this, a regularization term is introduced to ${\mathbf{H}}^{\kappa }$ for directional constraint enhancement. First, eigenvalue decomposition is performed on the Gram matrix of ${\mathbf{H}}^{\kappa }$:

$$\begin{array}{c}\hfill {\mathbf{H}}^{\kappa \top }{\mathbf{H}}^{\kappa }=\mathbf{V}\mathrm{\Lambda }{\mathbf{V}}^{\top }\end{array}$$

(46)

where $\mathrm{\Lambda }=diag\left({\lambda }_1,\dots ,{\lambda }_6,0\dots ,0\right)$ (with ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_6$ representing non-zero eigenvalues) and $\mathbf{V}$ denotes the matrix of corresponding eigenvectors. The regularized cost function is then defined as

$$\begin{array}{c}\hfill J_{\mathrm{reg}}\left(\tilde{\mathbf{x}}\right)=J\left(\tilde{\mathbf{x}}\right)+\alpha ·\mathrm{\Phi }\left(\mathrm{\Lambda }\right)\end{array}$$

(47)

Here, $\alpha$ is the regularization weight and $\mathrm{\Phi }\left(\mathrm{\Lambda }\right)$ is the regularization function, expressed as

$$\begin{array}{c}\hfill \mathrm{\Phi }\left(\mathrm{\Lambda }\right)={\tilde{\mathbf{x}}}^{\top }\mathbf{V}\mathbf{D}{\mathbf{V}}^{\top }\tilde{\mathbf{x}}\end{array}$$

(48)

In this formulation, $\mathbf{D}=diag\left(d_1,\dots ,d_n\right)$ is a diagonal matrix applying eigenvalue-dependent penalties to suppress updates along weakly constrained directions:

$$\begin{array}{c}\hfill d_i=\left\{\begin{array}{cc}{({\lambda }_i+ϵ)}^{-1}\hfill & {\lambda }_i>\tau ,i<7\hfill \\ {ϵ}^{-1}\hfill & {\lambda }_i\le \tau ,i<7\hfill \\ 0\hfill & i\ge 7\hfill \end{array}\right.\end{array}$$

(49)

where $ϵ>0$ is a small constant to avoid matrix singularity and $\tau$ is the eigenvalue threshold distinguishing between strong and weak constraints. For practical implementation, $ϵ$ is typically set to ${10}^{-2}$ to ensure numerical stability, while $\tau$ is empirically chosen as $0.1$ based on the environmental characteristics. The regularization weight $\alpha$ should typically be set within the range of 0.1 to 10.0 and can be adaptively adjusted based on point cloud density.

The index threshold $i<7$ corresponds to the positional and orientational degrees of freedom in the state vector. This penalty mechanism inversely weighs the projection of the error state ${\mathbf{V}}^{\top }\tilde{\mathbf{x}}$ against eigenvalue magnitude, thereby strongly suppressing state updates along geometrically degenerate directions. Expanding the regularized cost function into a quadratic form yields

$$\begin{array}{cc}\hfill J_{\mathrm{reg}}\left(\tilde{\mathbf{x}}\right)& ={\tilde{\mathbf{x}}}^{\top }{\mathbf{P}}^{-1}\tilde{\mathbf{x}}+{\mathbf{r}}^{\top }{\mathbf{R}}^{-1}\mathbf{r}+2{\tilde{\mathbf{x}}}^{\top }{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}\mathbf{r}\hfill \\ \hfill & +{\tilde{\mathbf{x}}}^{\top }{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}{\mathbf{H}}^{\kappa }\tilde{\mathbf{x}}\hfill \\ \hfill & +\alpha {\tilde{\mathbf{x}}}^{\top }\mathbf{V}\mathbf{D}{\mathbf{V}}^{\top }\tilde{\mathbf{x}}\hfill \end{array}$$

(50)

To solve the optimization problem, the partial derivative of $J_{\mathrm{reg}}\left(\tilde{\mathbf{x}}\right)$ with respect to $\tilde{\mathbf{x}}$ is computed and set to zero (a necessary condition for the minimum):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial J_{\mathrm{reg}}}{\partial \tilde{\mathbf{x}}}}& =2{\mathbf{P}}^{-1}\tilde{\mathbf{x}}+2{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}{\mathbf{H}}^{\kappa }\tilde{\mathbf{x}}\hfill \\ \hfill & +2{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}\mathbf{r}+2\alpha \mathbf{V}\mathbf{D}{\mathbf{V}}^{\top }\tilde{\mathbf{x}}=0\hfill \end{array}$$

(51)

Rearranging this equation to solve for $\tilde{\mathbf{x}}$ gives

$$\begin{array}{c}\hfill \tilde{\mathbf{x}}=-{\left[{\mathbf{P}}^{-1}+{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}{\mathbf{H}}^{\kappa }+\alpha \mathbf{V}\mathbf{D}{\mathbf{V}}^{\top }\right]}^{-1}{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}\mathbf{r}\end{array}$$

(52)

The regularized update gain (analogous to the optimal weight in recursive estimation) ${\mathbf{K}}_{\mathbf{L}}$ is thus defined as

$$\begin{array}{c}\hfill {\mathbf{K}}_{\mathbf{L}}={\left[{\mathbf{P}}^{-1}+{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}{\mathbf{H}}^{\kappa }+\alpha \mathbf{V}\mathbf{D}{\mathbf{V}}^{\top }\right]}^{-1}{\mathbf{H}}^{\kappa \top }{\mathbf{R}}^{-1}\end{array}$$

(53)

The state is updated iteratively using the following formulation, which incorporates both the regularized gain and prior state correction:

$$\begin{array}{c}\hfill {\widehat{\mathbf{x}}}_k^{\kappa +1}={\widehat{\mathbf{x}}}_k^{\kappa }⊞\left(-{\mathbf{K}}_{\mathbf{L}}\mathbf{r}-(\mathbf{I}-{\mathbf{K}}_{\mathbf{L}}{\mathbf{H}}^{\kappa }){\left({\mathbf{J}}^{\kappa }\right)}^{-1}\left({\widehat{\mathbf{x}}}_k^{\kappa }\boxminus {\widehat{\mathbf{x}}}_k\right)\right)\end{array}$$

(54)

The iteration terminates when the state change between consecutive iterations falls below a predefined threshold: $∥{\widehat{\mathbf{x}}}_k^{\kappa +1}\boxminus {\widehat{\mathbf{x}}}_k^{\kappa }∥<ϵ$. The optimal posterior state and corresponding covariance matrix are then

$$\begin{array}{c}\hfill {\overline{\mathbf{x}}}_k={\widehat{\mathbf{x}}}_k^{\kappa +1},{\overline{\mathbf{P}}}_k=(\mathbf{I}-{\mathbf{K}}_{\mathbf{L}}{\mathbf{H}}^{\kappa }){\widehat{\mathbf{P}}}_k^{\kappa +1}\end{array}$$

(55)

Finally, LiDAR feature points are projected into the global map coordinate frame using the optimal transformation matrix ${\phantom{­}}^G{\overline{\mathbf{T}}}_{I_k}=\left({\phantom{­}}^G{\overline{\mathbf{R}}}_{I_k},{\phantom{­}}^G{\overline{\mathbf{p}}}_{I_k}\right)$:

$$\begin{array}{c}\hfill {\phantom{­}}^G{\overline{\mathbf{p}}}_{f_j}={\phantom{­}}^G{\overline{\mathbf{T}}}_{I_k}{\phantom{­}}^I{\mathbf{T}}_L{\phantom{­}}^L{\mathbf{p}}_{poin{t}_j}\end{array}$$

(56)

For navigation in new underground mine areas, this integrated framework maximizes pose correction and real-time error suppression to achieve high-precision real-time localization, thereby enabling robust adaptation to the dual challenges of slippery road surfaces and feature-deprived environments inherent to underground mining scenarios. While the framework itself delivers effective pose refinement, mine sections subjected to long-term repeated travel allow for further optimization: backend correction leveraging high-quality prior maps emerges as an effective approach to refine pose estimation—these prior maps provide additional spatial references that extend the performance limits of real-time-only localization systems.

3.3. Backend Cumulative Error Correction Module

In the absence of satellite positioning signals or loop closure constraints, conventional SLAM algorithms inevitably accumulate localization drift. Even minor initial errors propagate and amplify over time, gradually compromising the long-term reliability of localization results. In underground mines lacking satellite coverage and loop closure opportunities, significant drift accumulates before potential loop detection. Mining vehicles typically operate along fixed routes in confined areas, enabling high-precision scan-to-map matching with prior maps for drift correction.

We define the odometry-to-map error transform as ${\phantom{­}}^{\mathbf{M}}{\mathbf{T}}_{\mathbf{B}}$, with current estimate ${\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B} n}$. The residual between-prior map point ${\phantom{­}}^M{\mathbf{p}}_{ma{p}_j}$ and registered scan point ${\phantom{­}}^G{\overline{\mathbf{p}}}_{f_j}$ are defined as

$$\begin{array}{c}\hfill d_j^{\left({\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B} n}\right)}={\phantom{­}}^M{\mathbf{p}}_{ma{p}_j}-{\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B}}n{\phantom{­}}^G{\overline{\mathbf{p}}}_{f_j}\end{array}$$

(57)

The residual distribution follows:

$$\begin{array}{c}\hfill d_j^{\left(\overline{\mathbf{T}}\right)}\sim \mathcal{N}\left(0,C_j^B+\overline{\mathbf{T}}{C}_j^A{\overline{\mathbf{T}}}^T\right)\end{array}$$

(58)

where $\overline{T}$ denotes the optimal transform. Covariance matrices $C_j^A$ and $C_j^B$ are defined as

$$\begin{array}{c}\hfill C_j^A={\mathbf{R}}_{{\nu }_j}·\left(\begin{array}{ccc}ϵ& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)·{\mathbf{R}}_{{\nu }_j}^{\top }\end{array}$$

(59)

$$\begin{array}{c}\hfill C_j^B={\mathbf{R}}_{{\mu }_j}·\left(\begin{array}{ccc}ϵ& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)·{\mathbf{R}}_{{\mu }_j}^{\top }\end{array}$$

(60)

Here ${\mu }_j$ and ${\nu }_j$ are normal vectors of local surfaces around ${\phantom{­}}^M{\mathbf{p}}_{ma{p}_j}$ and ${\phantom{­}}^G{\overline{\mathbf{p}}}_{f_j}$, respectively.

Per the Generalized-ICP (GICP) theory, the error state updates via

$$\begin{array}{c}\hfill {\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B} n+1}=\underset{\mathbf{T}}{argmin}\sum _j{d}_j^{{\mathbf{T}}^{\top }}{\left(C_j^B+\mathbf{T}{C}_j^A{\mathbf{T}}^{\top }\right)}^{-1}{d}_j^{\mathbf{T}}\end{array}$$

(61)

where $\mathbf{T}={\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B} n}$. The optimal transform ${\phantom{­}}^{\mathbf{M}}{\overline{\mathbf{T}}}_{\mathbf{B}}$ is solved via the conjugate gradient method:

$$\begin{array}{c}\hfill {\phantom{­}}^{\mathbf{M}}{\overline{\mathbf{T}}}_{\mathbf{B}}={\phantom{­}}^{\mathbf{M}}{\widehat{\mathbf{T}}}_{\mathbf{B} n+1}\end{array}$$

(62)

The corrected position is derived as

$$\begin{array}{c}\hfill {\phantom{­}}^{\mathbf{M}}\overline{\mathbf{T}}={\phantom{­}}^{\mathbf{M}}{\overline{\mathbf{T}}}_{\mathbf{B}}·{\overline{\mathbf{T}}}_{\mathbf{k}}\end{array}$$

(63)

where ${\overline{\mathbf{T}}}_{\mathbf{k}}\in SE\left(3\right)$ is the homogeneous transformation matrix constructed from the pose components of the state vector ${\overline{\mathbf{x}}}_k$. Since the posterior state error evolves slowly, low-frequency estimation suffices for accuracy and stability, significantly reducing computational load.

4. Experiment

4.1. Experimental Platform Setup

The hardware configuration for the field testing platform is detailed in Table 2, along with the definition of D(maxAE, MAE, medAE). After obtaining the full error sequence ($\left\{e_p\left(t^{\prime }\right)\right\}$ for position and $\left\{e_v\left(t^{\prime }\right)\right\}$ for velocity), we calculate three statistical metrics to characterize overall performance. maxAE (maximum absolute error) is the largest value in the error sequence, reflecting the worst-case error:

$$\mathrm{maxAE}=max\left(\left\{e\left(t^{\prime }\right)\right\}\right)$$

MAE (mean absolute error) is the average of the error sequence, reflecting the overall error level:

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}e\left(t_i^{\prime }\right)$$

(where N is the total number of state pairs). medAE (median absolute error) is the median of the sorted error sequence, avoiding bias from extreme values:

$$\mathrm{medAE}=\mathrm{median}\left(\mathrm{sorted}\left\{e\left(t^{\prime }\right)\right\}\right).$$

Table 2. Experimental hardware configuration.

Category	Device Model	Technical Specifications
Main Controller	MiiVii AD10	Platform: Jetson AGX Orin 32 GB CPU: 8-core Arm Cortex-A78AE v8.2 Architecture: 64-bit
LiDAR	Ouster OS1-64	Channels: 64 Vertical FOV: ${45}^{\circ }$ Horizontal FOV: ${360}^{\circ }$
Motion Sensors	Wire-Controlled Chassis ECU	Output: Real-time velocity Output: Wheel steering angle Interface: CAN bus
Data Sources		LiDAR point cloud: Ouster OS1 (10 Hz) IMU: Ouster built-in IMU (100 Hz) Kinematic estimation: ECU speed/angle (100 Hz)
Carrier Platform	Modified Test Vehicle (Figure 5)	Type: Underground mining vehicle Integrated devices: LiDAR/ECU

Table 2. Experimental hardware configuration.

Category	Device Model	Technical Specifications
Main Controller	MiiVii AD10	Platform: Jetson AGX Orin 32 GB CPU: 8-core Arm Cortex-A78AE v8.2 Architecture: 64-bit
LiDAR	Ouster OS1-64	Channels: 64 Vertical FOV: ${45}^{\circ }$ Horizontal FOV: ${360}^{\circ }$
Motion Sensors	Wire-Controlled Chassis ECU	Output: Real-time velocity Output: Wheel steering angle Interface: CAN bus
Data Sources		LiDAR point cloud: Ouster OS1 (10 Hz) IMU: Ouster built-in IMU (100 Hz) Kinematic estimation: ECU speed/angle (100 Hz)
Carrier Platform	Modified Test Vehicle (Figure 5)	Type: Underground mining vehicle Integrated devices: LiDAR/ECU

Figure 5. Test vehicle.

Figure 5. Test vehicle.

4.2. Comparative Experiment

This subsection validates the effectiveness of the proposed localization method in feature-degraded mining environments. By employing precise kinematic models to constrain IMU integration results, reliable motion estimation is maintained even under feature degradation. To demonstrate the superiority of our approach, we conduct comparative experiments against other high-performance LiDAR-IMU fusion SLAM algorithms, evaluating localization accuracy and stability in feature-deprived scenarios as Figure 6.

We first establish the ground truth by replacing the odometry’s internal map with a high-precision surveyed map, obtaining unbiased state estimates. Specifically, we employ a purely positioning framework with map constraints. By scanning–matching each laser radar data with the pre-built high-precision map, we output a continuous and drift-free sequence of positions/velocities. This sequence, which is not affected by map updates, serves as the benchmark for calculating the errors of all algorithms. The map is built via a segmented method combining all stations and handheld 3D laser scanners. Millimeter-level control points correct segmental drift, and final fusion achieves ±1 cm global accuracy.

With the backend cumulative error correction module disabled, comparative tests are performed under identical conditions against other SLAM algorithms, recording position and velocity data. Localization trajectories and velocity error curves are shown in Figure 7 and Figure 8:

The experimental trajectory commences at the origin (0, 0, 0) and concludes at coordinates (330.993, −496.209, 113.567), with the vehicle negotiating a curved section at approximately the 280-meter mark. As illustrated in Figure 7, the proposed algorithm maintains precise alignment with ground truth trajectories, confining total deviation within controllable bounds without accumulated error correction. Conversely, comparative algorithms exhibit significant positioning errors resulting from motion state estimation failures induced by feature degradation, as quantitatively demonstrated in

Table 3. Distance error distribution of different algorithms.

Algorithm	Min Error/m	Mean Error/m	Median Error/m	Max Error/m	RMSE/m
PLACE-LIO [29]	0.024	11.264	4.312	41.541	16.099
FAST-LIO2 [16]	0.092	20.665	17.445	39.471	24.574
Point-LIO [30]	0.036	83.086	109.857	162.054	108.892
ours	0.010	0.428	0.253	2.280	0.666

.

Figure 8 depicts velocity error curves along the X and Y axes, representing discrepancies between estimated and true velocities. Analysis indicates that while FAST-LIO2 achieves reasonable X-axis velocity estimation, it develops substantial Y-axis drift during the latter trajectory phase, culminating in significant terminal positioning error along the Y-axis. Point-LIO demonstrates motion state estimation failures during both initialization and post-curve navigation, yielding considerable positioning errors along both axes. PLACE-LIO suffers complete localization failure in the latter segment, generating trajectories inconsistent with the actual path. The quantitative comparison of velocity estimation accuracy presented in

Table 4. Velocity cumulative error correction.

Dataset	maxAE/(m/s)	MAE/(m/s)	medAE/(m/s)
PLACE-LIO [29]	6.031	2.478	2.979
FAST-LIO2 [16]	7.217	0.191	0.970
Point-LIO [30]	13.149	1.831	0.872
ours	0.701	0.139	0.120

further validates the superior performance of our method, with consistently lower error metrics across all evaluation criteria.

In summary, the comparative experiments demonstrate that the proposed algorithm maintains reliable positioning results even in segments where competing methods exhibit significant deviations. It confines localization errors within acceptable thresholds, empirically validating its superior robustness in degraded scenarios. This substantiates the algorithm’s enhanced accuracy and stability under feature-deprived conditions.

4.3. Ablation Experiment

4.3.1. Adaptive Filtering Simulation Test

Based on actual underground mining conditions, we designed scenarios including vehicle acceleration startup, high-speed stable operation, emergency braking, and low-speed driving. In the simulation, additional noise was added to wheel speed measurements in red-marked areas to simulate non-Gaussian errors caused by wheel slippage. Considering the wheel-speed measurement accuracy of 1 km/h, measurements were discretized to ensure authenticity. The ground-truth velocity, IMU-integrated velocity, and disturbed wheel speed measurements are shown in Figure 9.

For the reliability of velocity error evaluation, the ground-truth velocity was derived from a high-precision position sequence. Using the central difference method to reduce discrete sampling errors, velocity components at each timestamp were calculated by dividing the position difference of adjacent timestamps by the corresponding time interval to reflect real motion states.

We achieved high-precision IMU–wheel speed fusion through error-state management and enabled adaptive adjustment of data fusion processes using the proposed slip feature extraction module. The slip ratio was estimated from wheel speed data, with calculation results shown in Figure 10.

The proposed feature extraction algorithm effectively characterizes slippage in most scenarios, though estimation deviations occur during complex speed changes, with occasional missed detections under mild slippage. Despite this, the algorithm significantly enhances anti-slip performance, as shown in Figure 11:

The proposed method shows substantially lower sensitivity to wheel slippage than conventional approaches, maintaining velocity estimation stability under severe measurement disturbances. Velocity estimation remains reliable even during false-positive or false-negative slip detection events, meeting mining localization robustness requirements.

During slippage events, velocity error decreases by 74.9%, confirming effective suppression of slippage-induced disturbances. Overall velocity estimation accuracy improves by 61.6% (baseline RMSE: 0.4913 m/s → optimized: 0.1888 m/s), demonstrating the method’s dual capability: stabilizing navigation during slippage while maintaining precision in normal conditions.

4.3.2. Localization Repeatability Experiment

Although the proposed cascaded filtering framework ensures localization stability, it exhibits error accumulation during extended operation, which impairs repeatability and renders the results inadequate for autonomous driving scenarios. To verify whether the backend cumulative error correction module can effectively mitigate error accumulation and meet high-precision localization requirements, we conducted experiments in a 1.5 km typical mining tunnel. Three independent sensor datasets ($Segmen{t}_{01}$–$Segmen{t}_{03}$) were collected, and the system performance with and without map correction was compared against high-precision surveying ground truth.

The quantitative localization errors are summarized in

Table 5. Without cumulative error correction.

Segment	maxAE/m	MAE/m	medAE/m
$Segmen{t}_{01}$	61.81	15.65	3.87
$Segmen{t}_{02}$	130.58	39.18	29.87
$Segmen{t}_{03}$	167.50	45.98	31.62

and

Table 6. With cumulative error correction.

Segment	maxAE/m	MAE/m	medAE/m
$Segmen{t}_{01}$	1.28	0.33	0.22
$Segmen{t}_{02}$	1.47	0.58	0.50
$Segmen{t}_{03}$	1.59	0.48	0.38

. Table 5 presents the error metrics without cumulative error correction, showing substantial positioning deviations with maximum absolute errors (maxAE) reaching up to 167.50 m. In contrast, Table 6 demonstrates the significant improvement achieved with map correction, where all error metrics are reduced to below 1.6 m.

Figure 12 displays repeated localization results across three trials. Subfigure (a) shows results without prior map correction, where unconstrained localization produces divergent trajectories from the same route at different times, with errors amplifying over distances unsuitable for long-range autonomous localization. Subfigure (b) demonstrates consistent trajectories with map correction, where minor variations originate from actual path differences during data collection.

Projecting the trajectories from (b) onto the point cloud map (Figure 13) confirms that all points remain within map boundaries, verifying that prior map correction maintains alignment with ground truth and satisfies autonomous driving localization requirements.

5. Conclusions

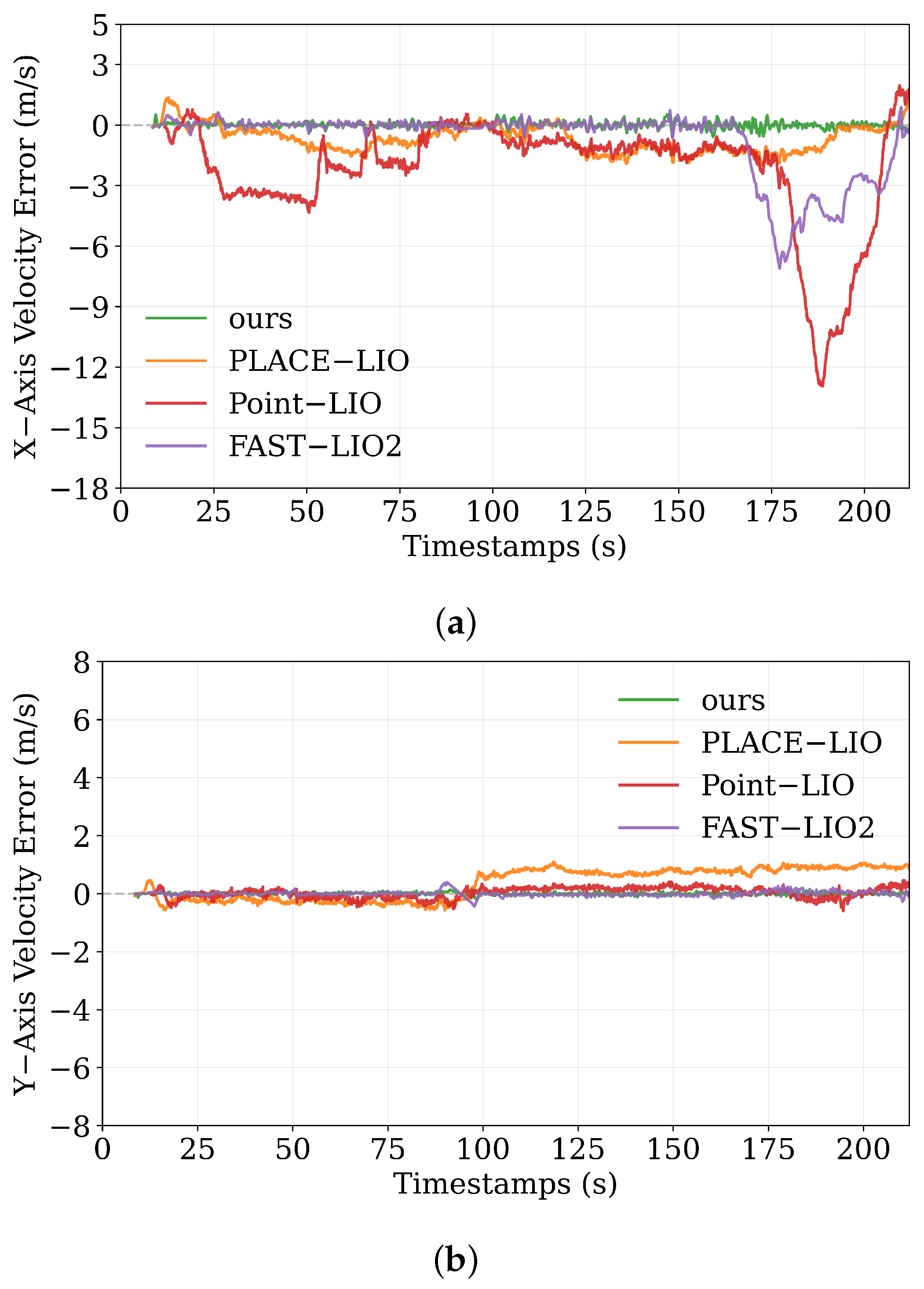
This study develops a scenario-adapted, self-correcting positioning system for underground mining autonomous vehicles, addressing three unmet challenges in mining localization: kilometer-scale signal-free tunnel restrictions, wheel slippage-induced non-Gaussian noise, and geometric-degraded tunnel localization failures. The system adopts a three-stage cascaded filtering framework, fusing LiDAR, IMU, wheel speed, and steering angle data to build a self-contained localization architecture, with two dedicated modules: an anti-slip prior estimation algorithm for slippage noise and an anti-degradation algorithm for geometric degradation.

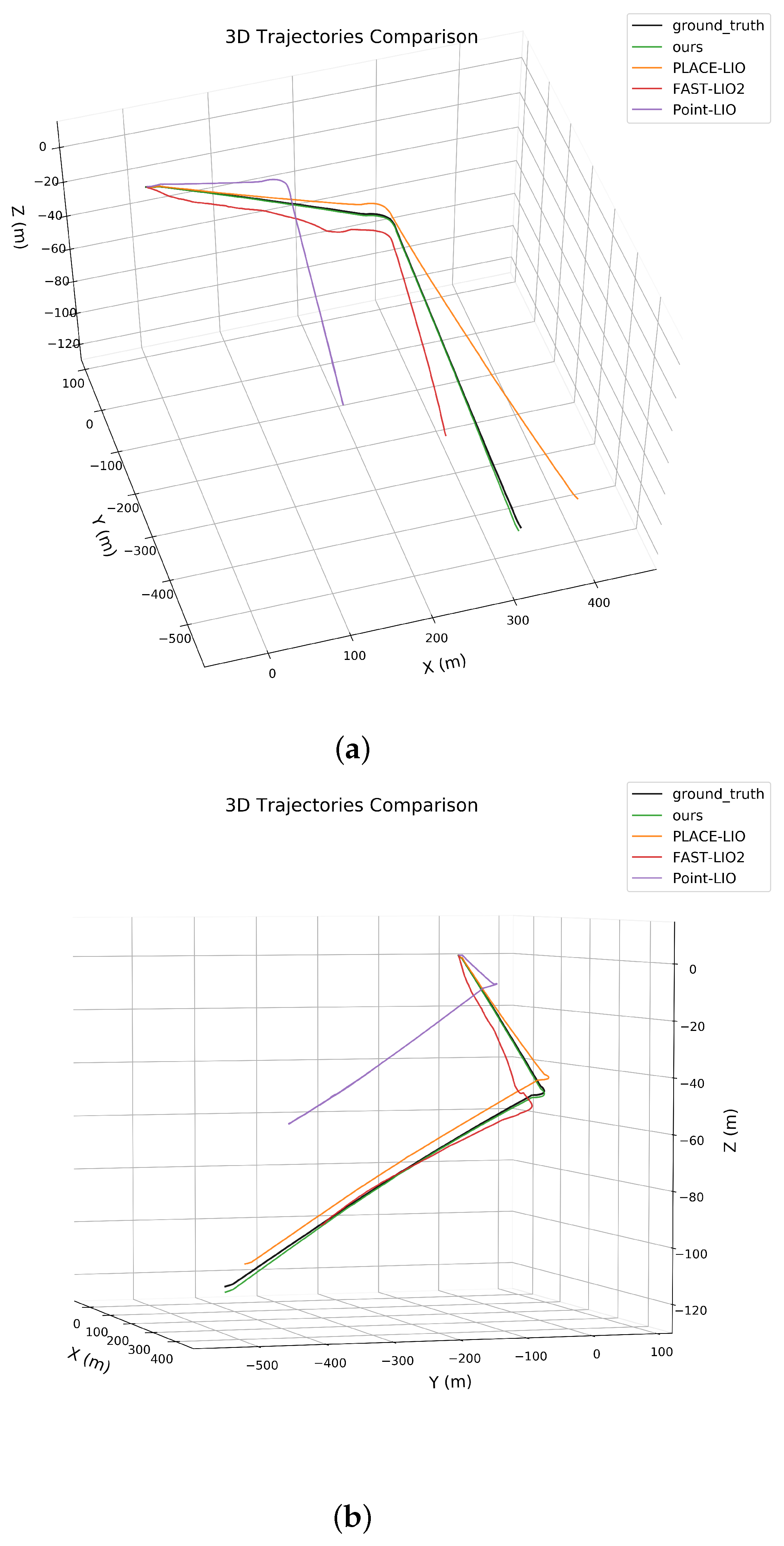
Field tests in a 1.5 km mining tunnel validate the system’s superior performance: compared with existing algorithms, it maintains sub-meter localization accuracy and full-area coverage, with significant improvements in positioning stability. Under severe wheel slip, the anti-slip module reduces velocity error by 74.9%, effectively suppressing slippage-induced disturbances; with prior map correction, the system achieves much lower maximum localization error compared to uncorrected conditions, further enhancing long-range navigation reliability. This system fills the gap in high-reliability, self-contained localization for kilometer-scale underground mining vehicles, meeting the precision and safety demands of autonomous mining operations.