A Flight Route Design Method Considering Multi-Hop Communication Using Delivery UAVs
Highlights
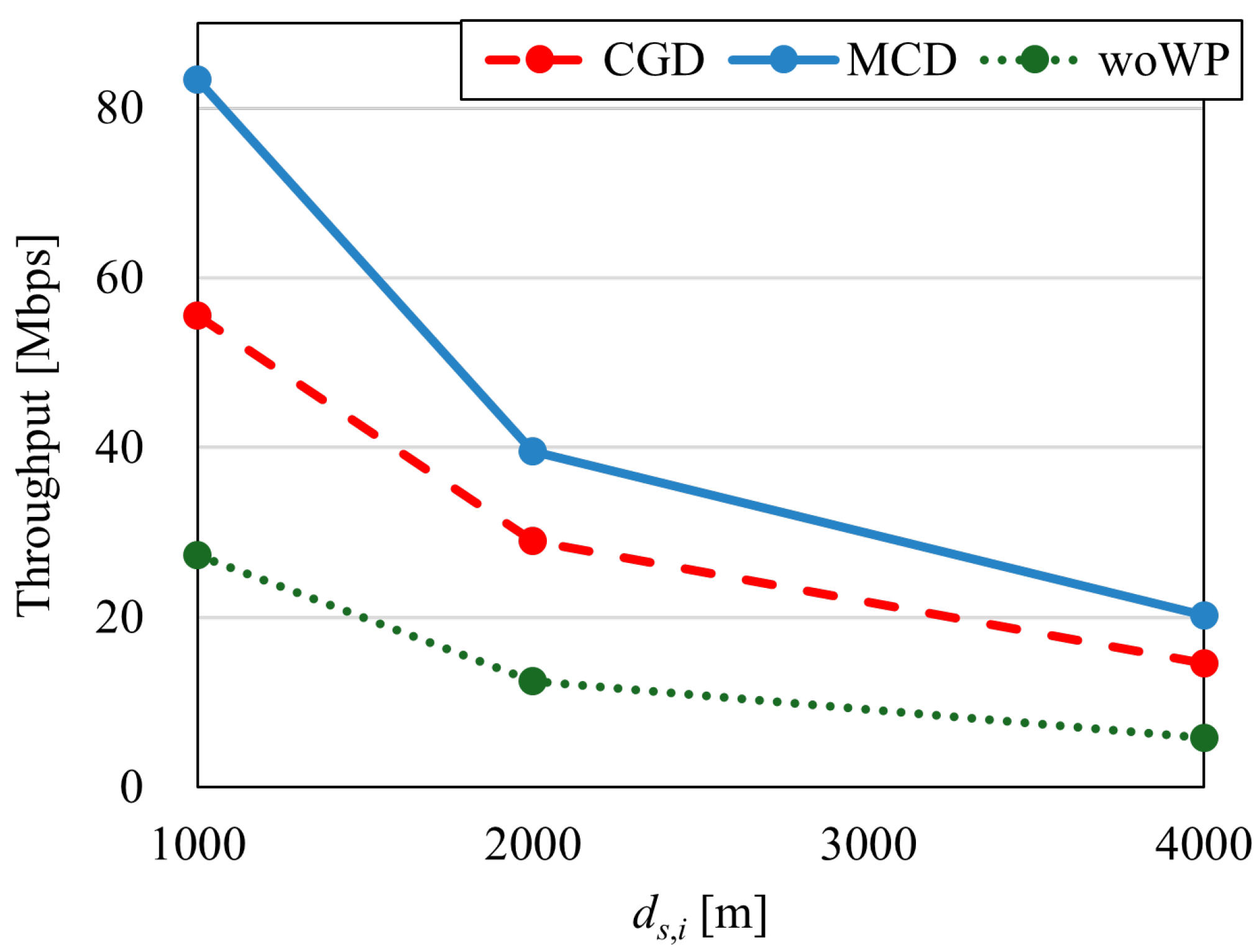
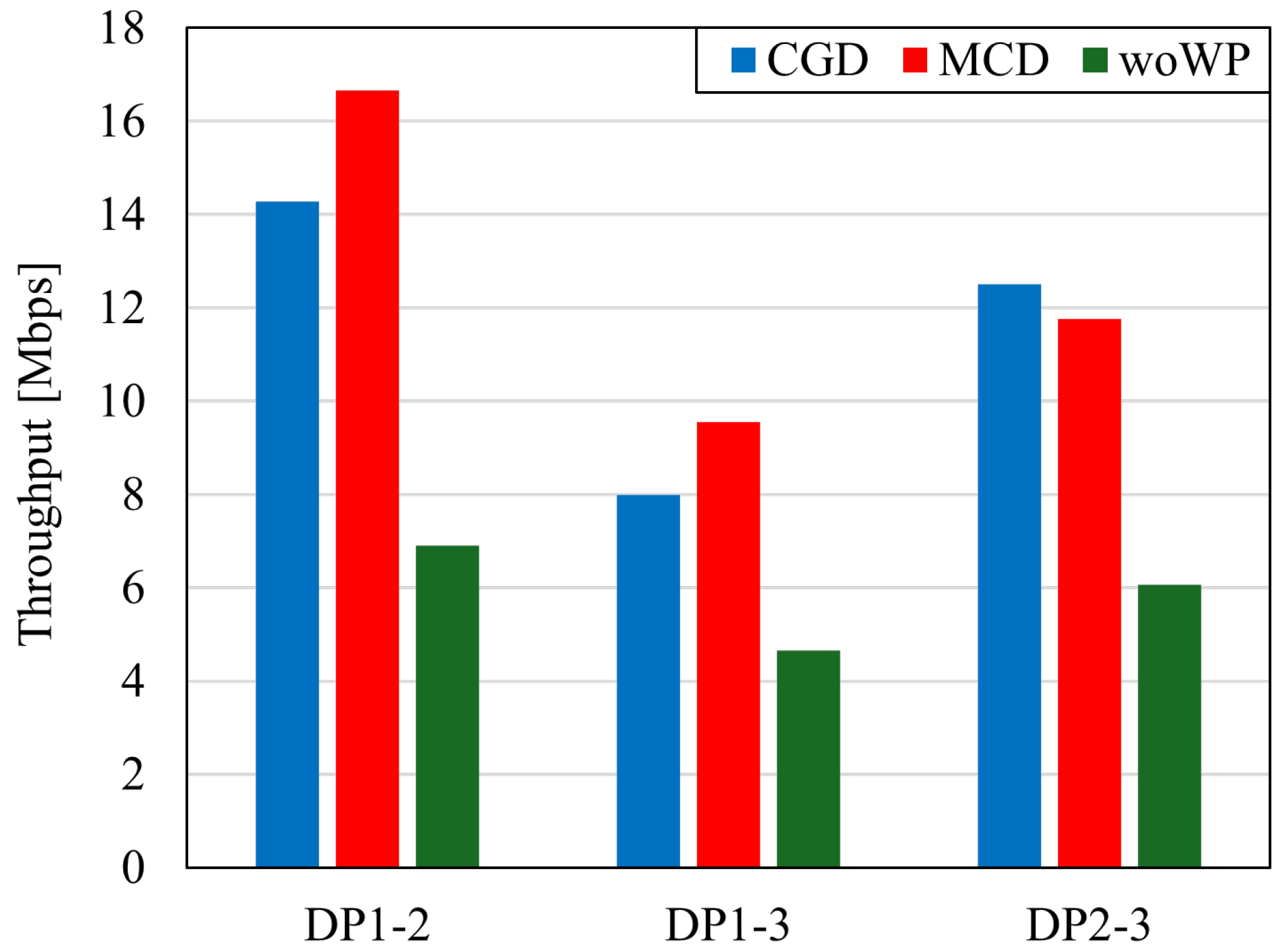
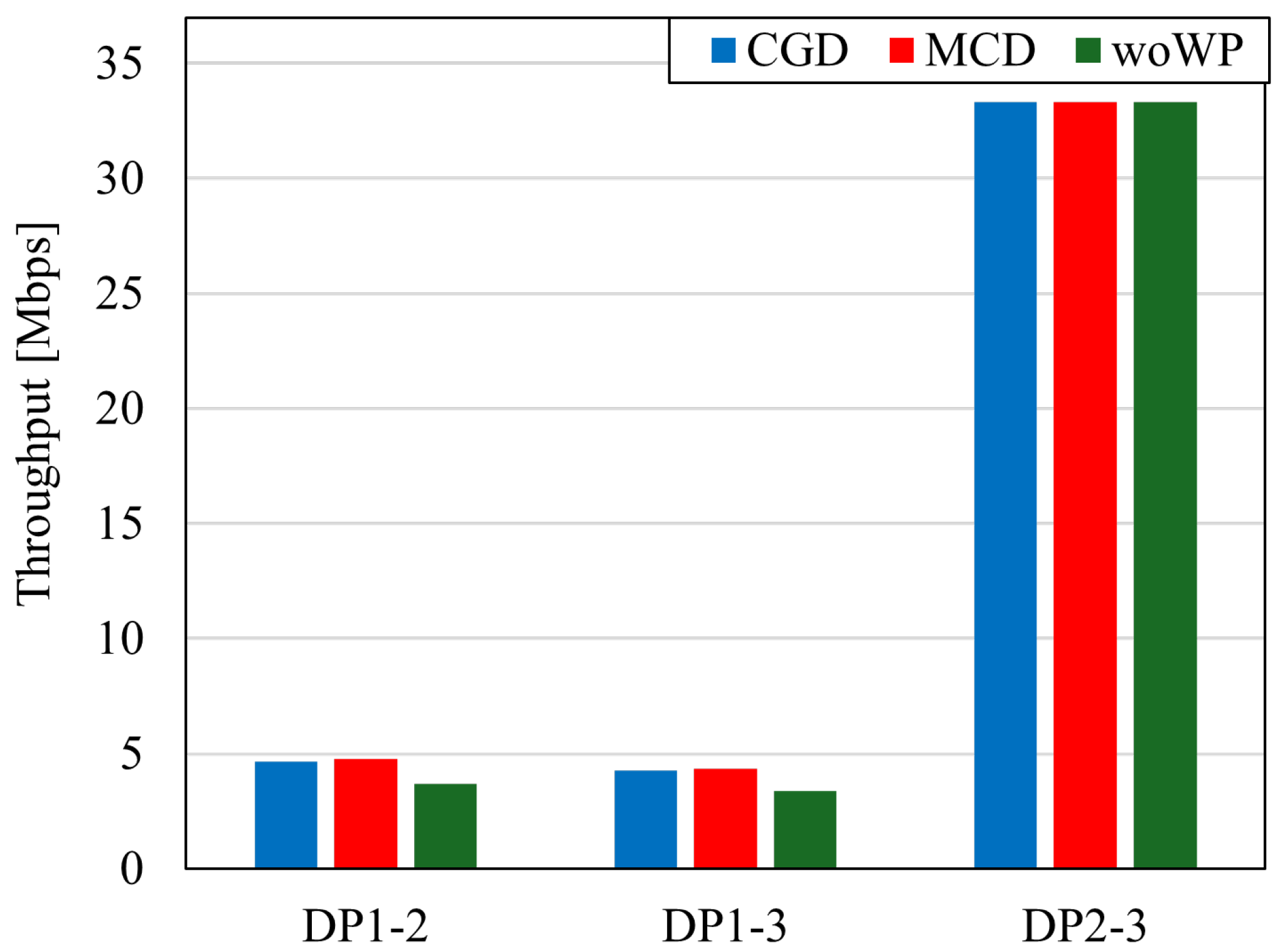
- The flight path using Waypoints (WPs) improves the throughput compared to that without WPs.
- We confirmed that the proposed route selection algorithm that places WPs to minimize the communication distance between DPs can improve the average throughput characteristics.
- The proposed method offers a practical solution for establishing a UAV-based communications platform in areas where it is challenging to install ground-based stations in emergencies.
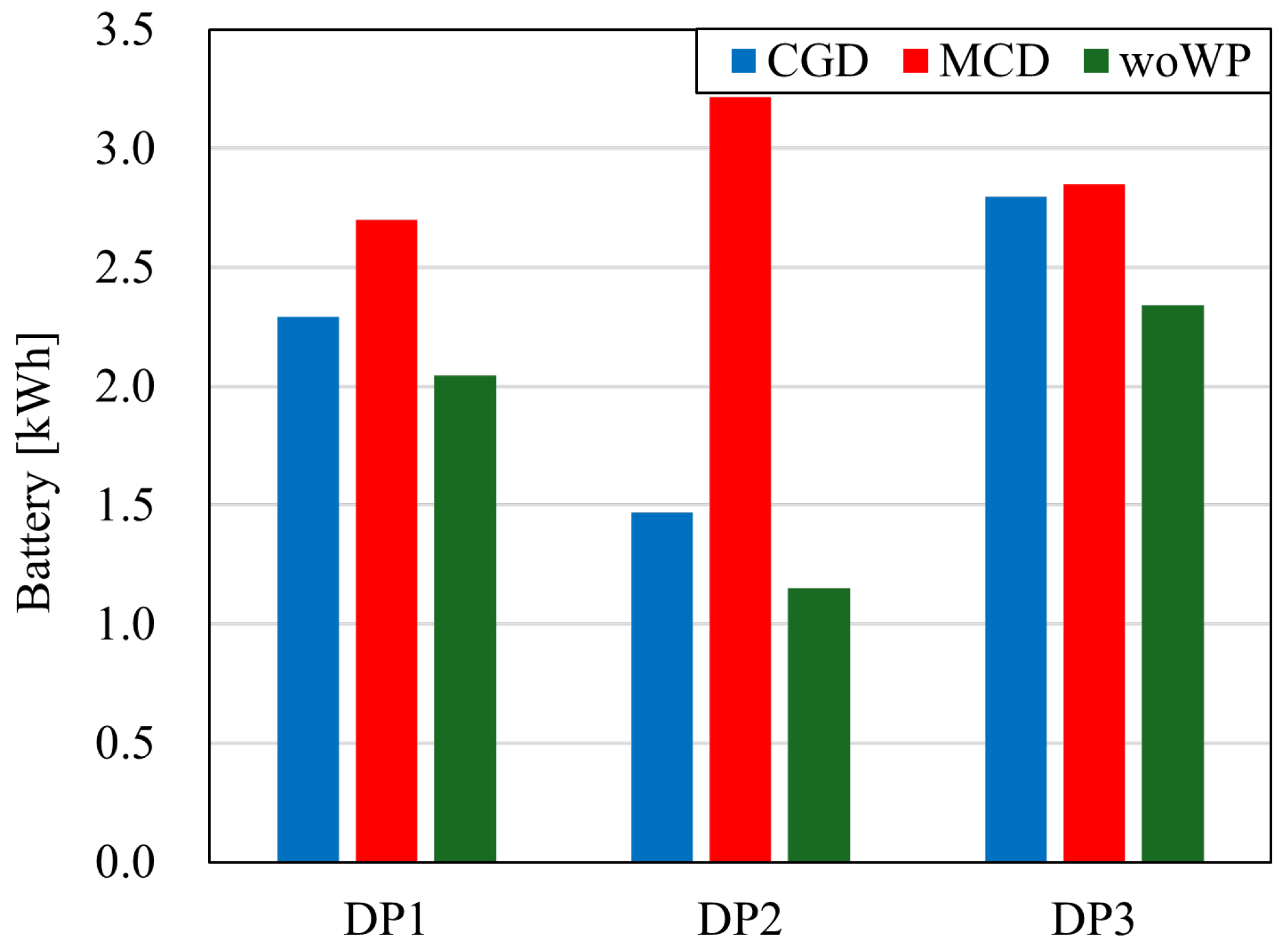
- Realizing a multi-hop communications system using delivery UAVs will enable the creation of a low-cost communications system.
Abstract
1. Introduction
2. Related Research
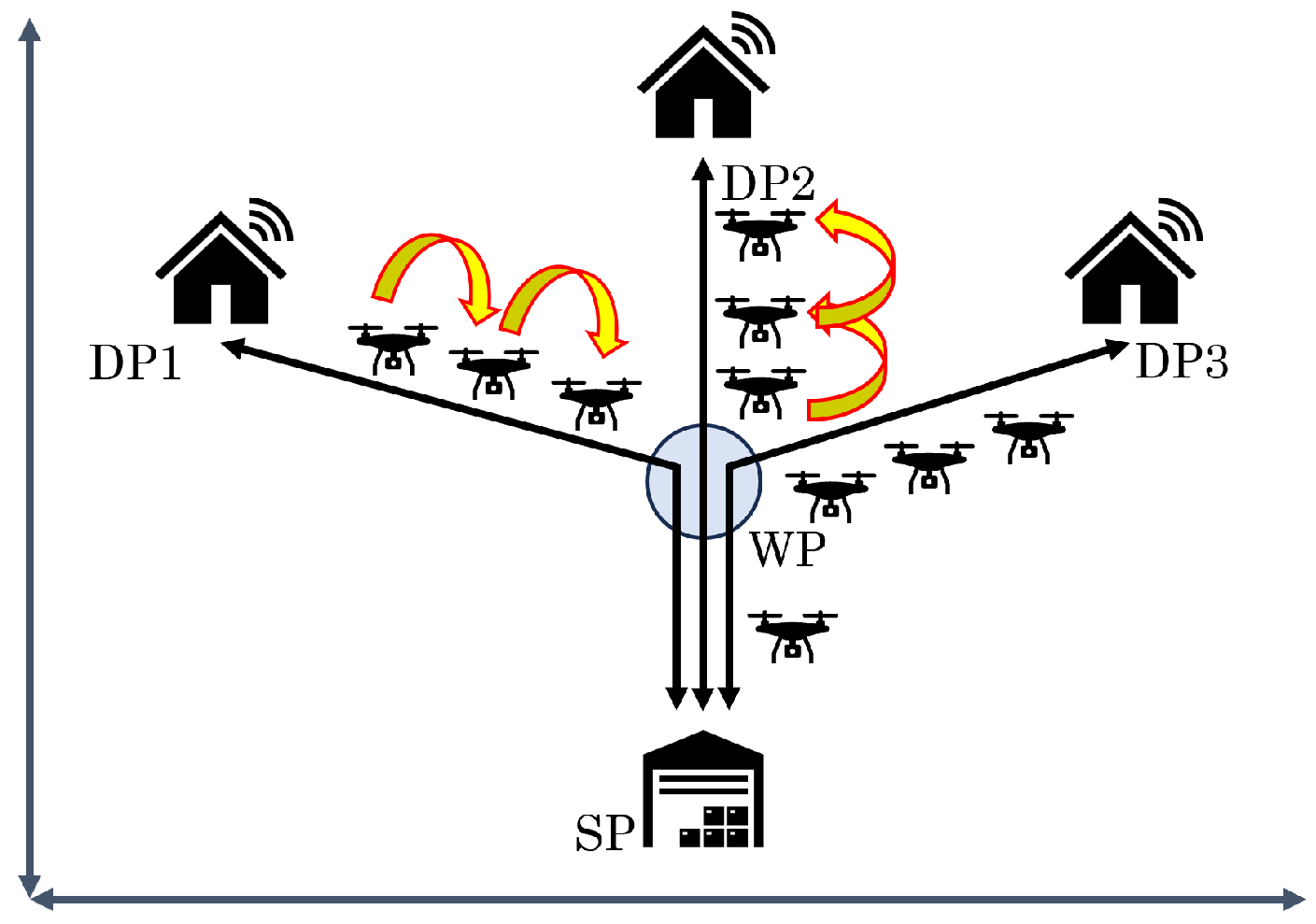
3. System Model
4. Flight Path Planning Method Using Multiple UAVs
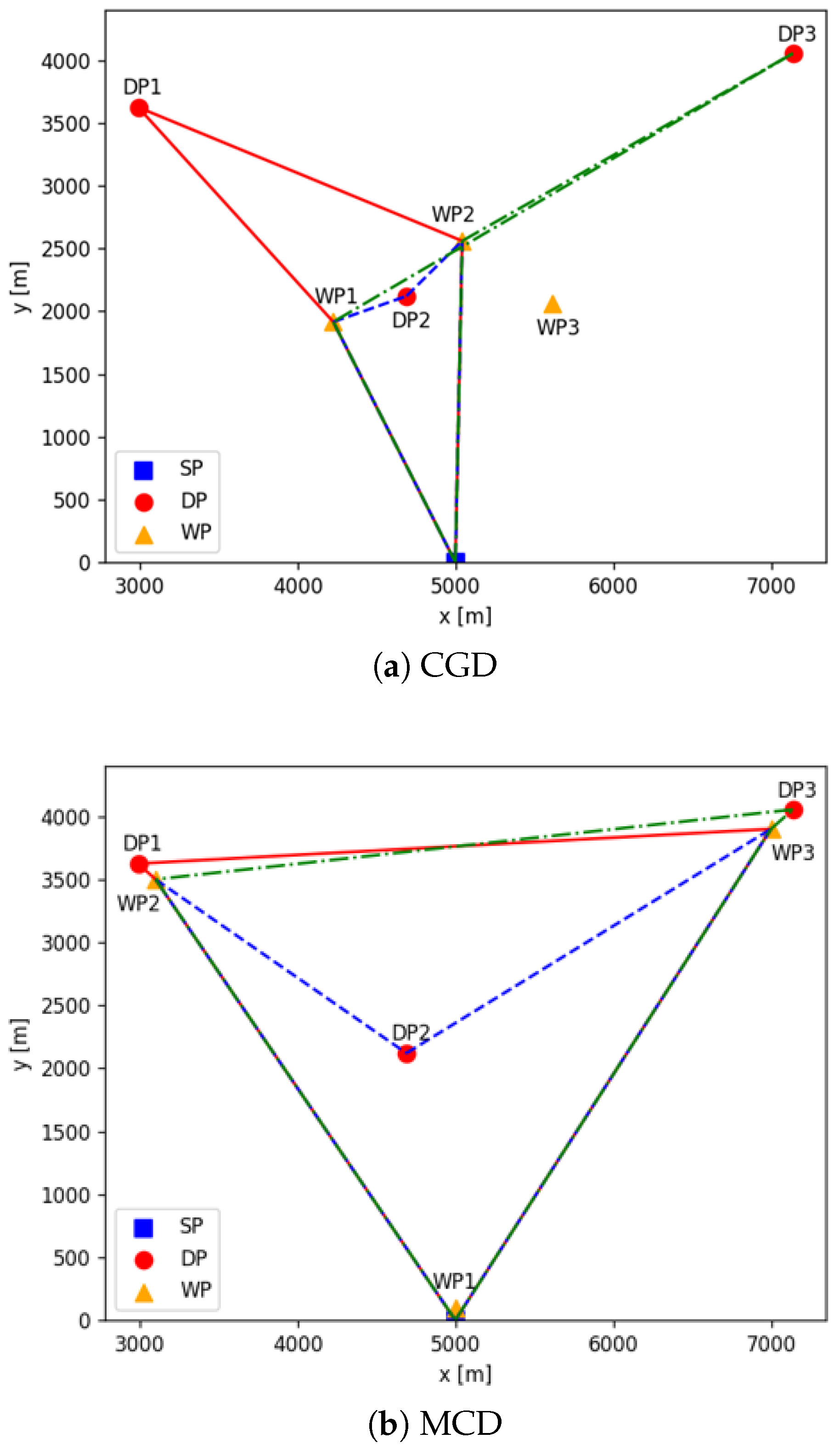
4.1. WP Placement Algorithms
4.1.1. Center of Gravity Determination Method (CGD)
4.1.2. Minimum Communication Distance Determination Method (MCD)
| Algorithm 1 Search algorithm for WP combination with minimum total communication distance. |
| Input: Output:
|
4.2. Flight Path Planning for UAVs
5. Simulation Results
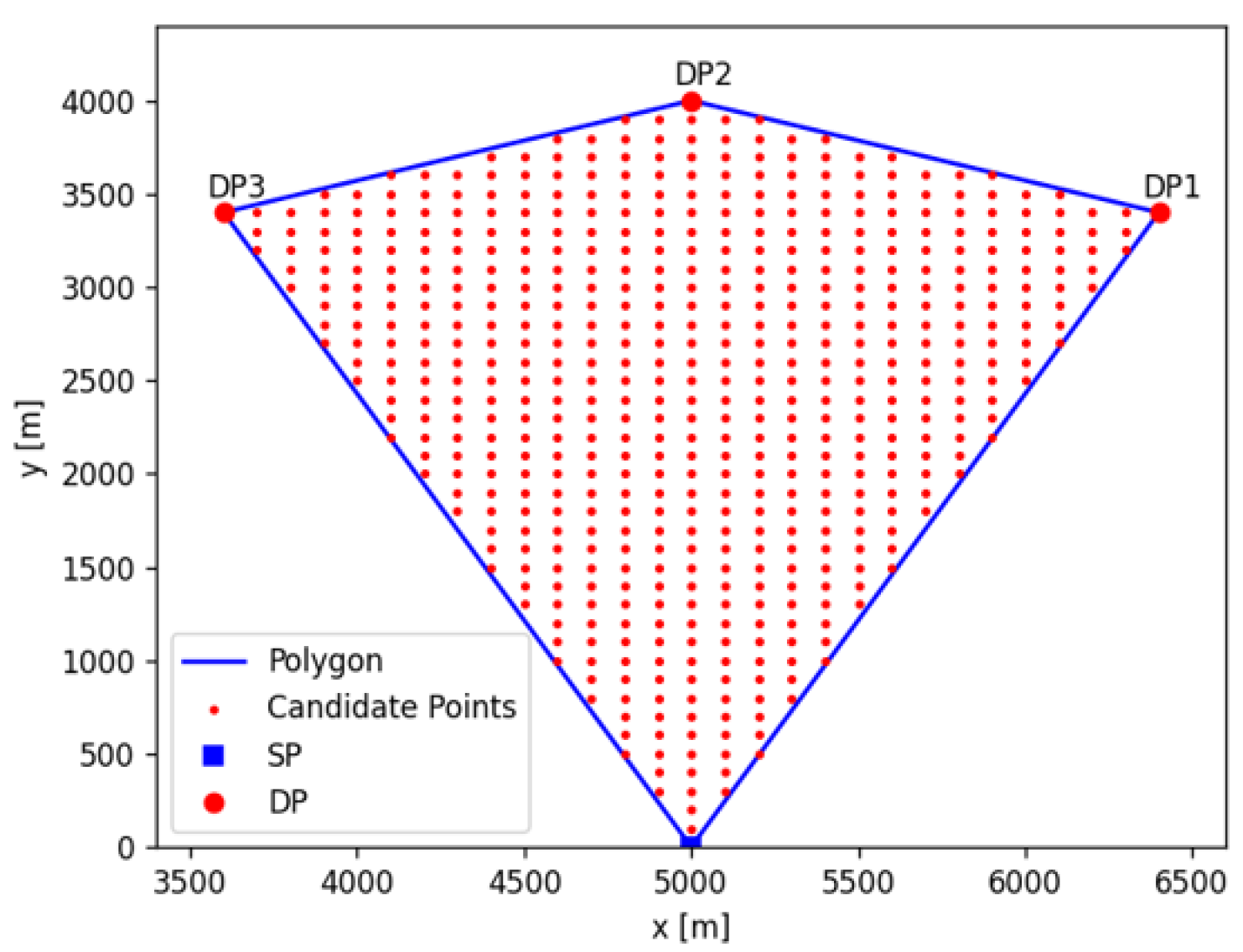
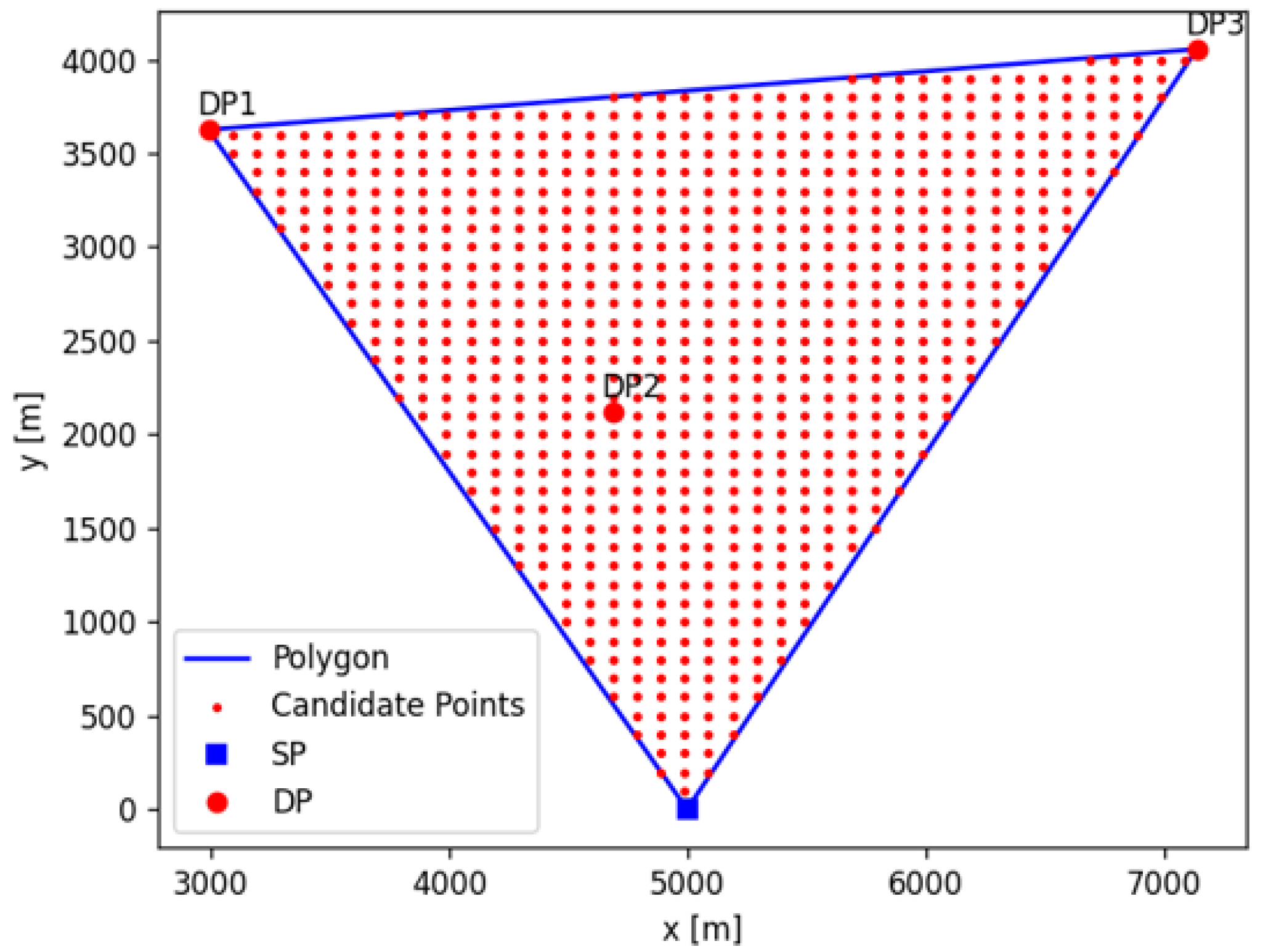
5.1. Simulation Parameters
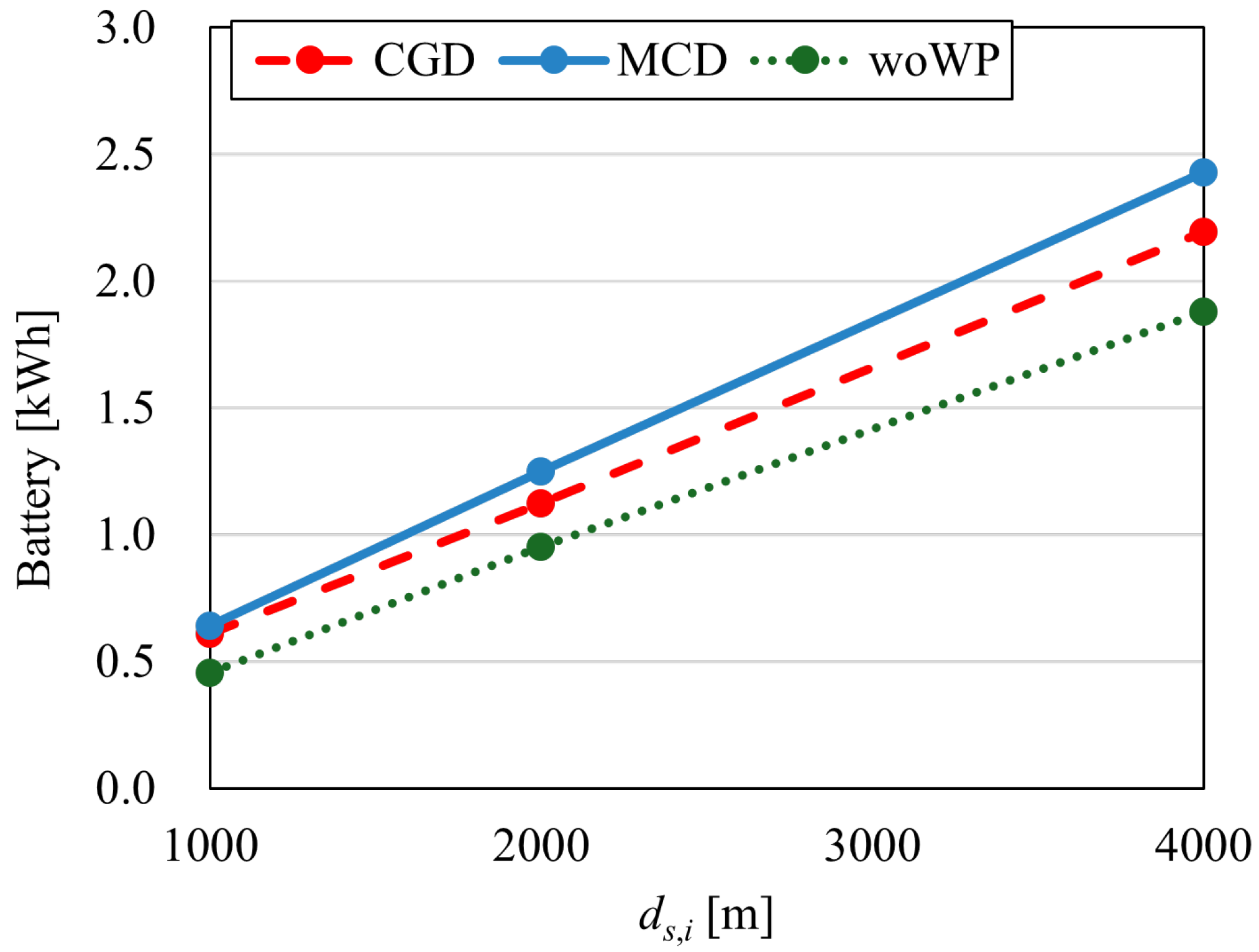
5.2. Evaluation for Flight Distance
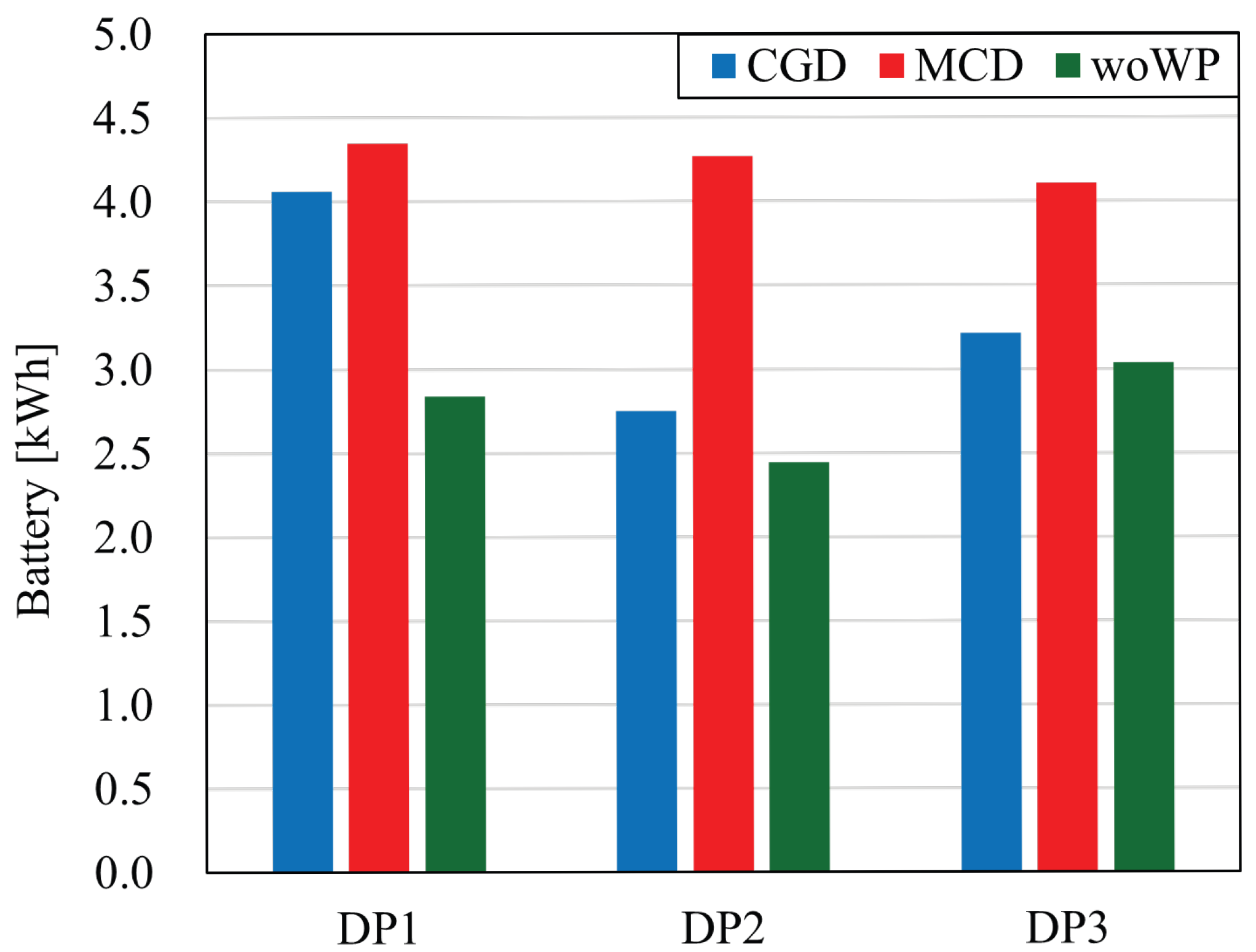
5.3. Evaluation of Positional Relationship of DPs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2019, 6, 2241–2263. [Google Scholar] [CrossRef]
- Mishra, D.; Natalizio, E. A survey on cellular-connected UAVs: Design challenges, enabling 5G/B5G innovations, and experimental advancements. Comput. Netw. 2020, 182, 107451. [Google Scholar] [CrossRef]
- Cheng, N.; Xu, W.; Shi, W.; Zhou, Y.; Lu, N.; Zhou, H.; Shen, X. Air-ground integrated mobile edge networks: Architecture, challenges, and opportunities. IEEE Commun. Mag. 2018, 56, 26–32. [Google Scholar] [CrossRef]
- Sekander, S. Tabassum and E. Hossain. Multi-Tier Drone Architecture for 5G/B5G Cellular Networks: Challenges, Trends, and Prospects. IEEE Commun. Mag. 2018, 56, 96–103. [Google Scholar] [CrossRef]
- Athanasiadou, G.E.; Batistatos, M.C.; Zarbouti, D.A.; Tsoulos, G.V. LTE Ground-to-Air Field Measurements in the Context of Flying Relays. IEEE Wirel. Commun. 2019, 26, 12–17. [Google Scholar] [CrossRef]
- Mozaffari, M.; Kasgari, A.T.Z.; Saad, W.; Bennis, M.; Debbah, M. Beyond 5G with UAVs: Foundations of a 3D Wireless Cellular Network. IEEE Trans. Wirel. Commun. 2019, 18, 357–372. [Google Scholar] [CrossRef]
- Cai, Y.; Wei, Z.; Hu, S.; Ng, D.W.K.; Yuan, J. Resource allocation for power-efficient IRS-Assisted UAV communications. In Proceedings of the 2020 IEEE International Conference on Communications Work, ICC Work, Dublin, Ireland, 7–11 June 2020. [Google Scholar]
- Chaalal, E.; Senouci, S.-M.; Reynaud, L. A New Framework for Multi-Hop ABS-Assisted 5G-Networks with Users’ Mobility Prediction. IEEE Trans. Veh. Technol. 2022, 71, 4412–4427. [Google Scholar] [CrossRef]
- Bae, J.; Sohn, K.Y.; Lee, H.; Lee, H.; Lee, H. Structure of UAV-Based Emergency Mobile Communication Infrastructure. In Proceedings of the 2021 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 20–22 October 2021; pp. 634–636. [Google Scholar]
- Abubakar, A.I.; Mollel, M.S.; Onireti, O.; Ozturk, M.; Ahmad, I.; Asad, S.M.; Sambo, Y.; Zoha, A.; Hussain, S.; Imran, M.A. Coverage and throughput analysis of an energy efficient UAV base station positioning scheme. Comput. Netw. 2023, 232, 109854. [Google Scholar] [CrossRef]
- Saif, A.; Dimyati, K.; Noordin, K.A.; Alsamhi, S.; Haubani, A. Multi-UAV and SAR collaboration model for disaster management in B5G networks. Internet Technol. Lett. 2021, 7, e310. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, H.; Zeng, Y.; Cui, M.; Liu, Y. Trajectory Optimization and Power Allocation for Multi-Hop UAV Relaying Communications. IEEE Access 2018, 6, 48566–48576. [Google Scholar] [CrossRef]
- Hamza, A.S.; Khalifa, S.S.; Hamza, H.S.; Elsayed, K. A survey on inter-cell interference coordination techniques in OFDMA-based cellular networks. IEEE Commun. Surveys Tuts. 2013, 15, 1642–1670. [Google Scholar] [CrossRef]
- So, H. Evaluation of radio interference areas by flight path and antenna directivity of UAV in urban area. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 1–5 October 2024. [Google Scholar]
- Wei, X.; Mei, W.; Chen, Z. Hybrid Linear and Nonlinear Uplink Cooperative Interference Cancellation for Cellular-Connected UAV. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–5. [Google Scholar]
- So, H.; Maruta, K. Directional antenna with lightweight metamaterial reflector for UAV-based networks. IEEE Access 2021, 9, 78735–78741. [Google Scholar] [CrossRef]
- So, H.; Maruta, K. Sector design using multiband antenna with metamaterial reflector for cellular UAV system. IEEE Access 2022, 10, 4924–4933. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, W.; Zheng, G. Optimum placement of UAV as relays. IEEE Commun. Lett. 2018, 22, 248–251. [Google Scholar] [CrossRef]
- Li, L.; Chang, T.-H.; Cai, S. UAV positioning and power control for two-way wireless relaying. arXiv 2019, arXiv:1904.08280. [Google Scholar] [CrossRef]
- So, H. Optimal relay positions in cooperative UAV relay networks. IEICE Commun. Express (ComEX) 2025, 14, 287–291. [Google Scholar] [CrossRef]
- Burhanuddin, L.A.B.; Liu, X.; Deng, Y.; Elkashlan, M.; Nallanathan, A. Inter-Cell Interference Mitigation for Cellular-Connected UAVs Using MOSDS-DQN. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1596–1609. [Google Scholar] [CrossRef]
- Mei, W.; Zhang, R. Cooperative Downlink Interference Transmission and Cancellation for Cellular-Connected UAV: A Divide-and-Conquer Approach. IEEE Trans. Commun. 2020, 68, 1297–1311. [Google Scholar] [CrossRef]
- Lv, C.; Ren, Y.; Li, X.; Wang, P.; Du, Z.; Ma, G.; Chi, H. Unmanned Aerial Vehicle-Assisted Sparse Sensing in Wireless Sensor Networks. IEEE Wirel. Commun. Lett. 2023, 12, 977–981. [Google Scholar] [CrossRef]
- Horiuchi, M.; Nishiyama, H.; Kato, N.; Ono, F.; Miura, R. Throughput maximization for long-distance real-time data transmission over multiple UAVs. In Proceedings of the IEEE ICC, Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Pan, W.; Lv, N.; Hou, B.; Ren, Z. Resource Allocation and Outage Probability Optimization Method for Multi-Hop UAV Relay Network for Servicing Heterogeneous Users. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2769–2781. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, N.; Ding, Z.; Alouini, M.-S. Multiple UAVs as relays: Multi-hop single link versus multiple dual-hop links. IEEE Trans. Wirel. Commun. 2018, 17, 6348–6359. [Google Scholar] [CrossRef]
- Hosseinalipour, S.; Rahmati, A.; Dai, H. Interference Avoidance Position Planning in Dual-Hop and Multi-Hop UAV Relay Networks. IEEE Trans. Wirel. Commun. 2020, 19, 7033–7048. [Google Scholar] [CrossRef]
- Kim, T.; Qiao, D. Energy-Efficient Data Collection for IoT Networks via Cooperative Multi-Hop UAV Networks. IEEE Trans. Veh. Technol. 2020, 69, 13796–13811. [Google Scholar] [CrossRef]
- Ding, R.; Chen, J.; Wu, W.; Liu, J.; Gao, F.; Shen, X. Packet Routing in Dynamic Multi-Hop UAV Relay Network: A Multi-Agent Learning Approach. IEEE Trans. Veh. Technol. 2022, 71, 10059–10072. [Google Scholar] [CrossRef]
- Fan, J.; Cui, M.; Zhang, G.; Chen, Y. Throughput Improvement for Multi-Hop UAV Relaying. IEEE Access 2019, 7, 147732–147742. [Google Scholar] [CrossRef]
- Lai, C.-C.; Bhola; Tsai, A.-H.; Wang, L.-C. Adaptive and Fair Deployment Approach to Balance Offload Traffic in Multi-UAV Cellular Networks. IEEE Trans. Veh. Technol. 2023, 72, 3724–3738. [Google Scholar] [CrossRef]
- Matar, A.S.; Shen, X. Joint Subchannel Allocation and Power Control in Licensed and Unlicensed Spectrum for Multi-Cell UAV-Cellular Network. IEEE J. Sel. Areas Commun. 2021, 39, 3542–3554. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Tang, B.; Tan, G. Handover and Coverage Analysis in 3-D Mobile UAV Cellular Networks. IEEE Internet Things J. 2024, 11, 29911–29925. [Google Scholar] [CrossRef]
- DJI. DJI Flycart 30 Spec. Available online: https://www.dji.com/jp/flycart-30/specs (accessed on 26 October 2025).
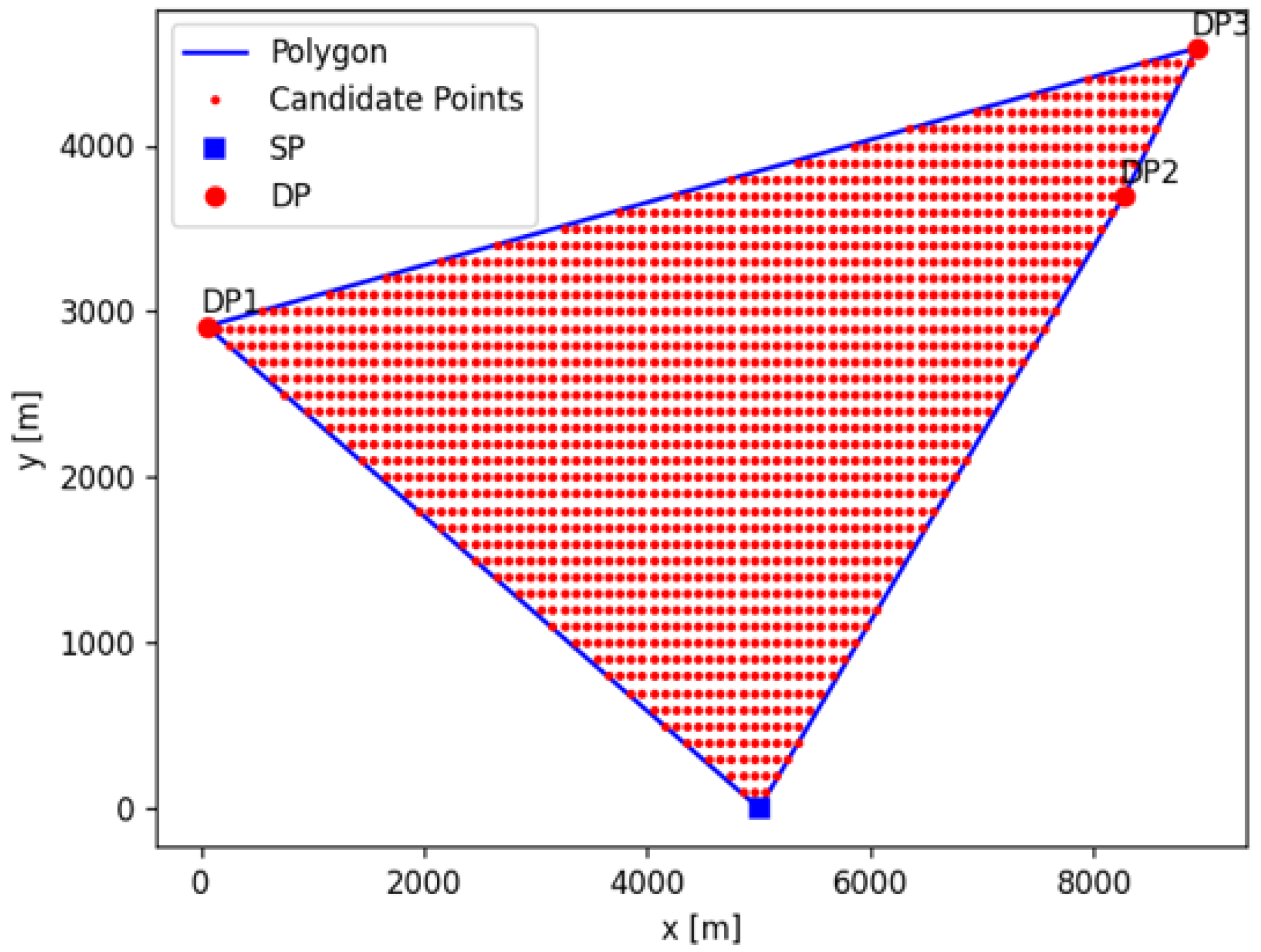
| Parameter | Value | |
|---|---|---|
| Area | ||
| Number of SPs | 1 | |
| Position of SP | (5000 m, 0 m) | |
| Number of DPs | 3 | |
| Number of WPs | 3 | |
| The flight altitude of the UAV | 150 m | |
| Velocity of UAV | v | 15 km/h |
| Operating time of UAV/day | 8 h | |
| Battery consumption per minute | loaded | 4.63 W |
| not loaded | 1.99 W | |
| Maximum throughput of one link | 200 Mbps | |
| Maximum communication distance | 200 m | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soya, H.; Inagaki, K.; So, H. A Flight Route Design Method Considering Multi-Hop Communication Using Delivery UAVs. Drones 2025, 9, 751. https://doi.org/10.3390/drones9110751
Soya H, Inagaki K, So H. A Flight Route Design Method Considering Multi-Hop Communication Using Delivery UAVs. Drones. 2025; 9(11):751. https://doi.org/10.3390/drones9110751
Chicago/Turabian StyleSoya, Hayato, Kazuki Inagaki, and Hideya So. 2025. "A Flight Route Design Method Considering Multi-Hop Communication Using Delivery UAVs" Drones 9, no. 11: 751. https://doi.org/10.3390/drones9110751
APA StyleSoya, H., Inagaki, K., & So, H. (2025). A Flight Route Design Method Considering Multi-Hop Communication Using Delivery UAVs. Drones, 9(11), 751. https://doi.org/10.3390/drones9110751






