Self-Adaptable Computation Offloading Strategy for UAV-Assisted Edge Computing

Highlights

What are the main findings?

• A deep neural network (DNN) is employed as an efficient approximate solver to produce real-time binary offloading decisions in UAV-assisted edge computing, effectively addressing the 0–1 mixed-integer programming problem.
• An online learning mechanism enables automatic adaptation to variations in key parameters (e.g., computing resources and task sizes), eliminating the need for time-consuming policy recomputation.

What are the implications of the main findings?

• The proposed QO2 method resolves the fundamental trade-off between computational complexity and decision timeliness in traditional optimization, supporting decision-making with high timeliness.
• It overcomes the limitations of conventional static optimization strategies, which fail under environmental changes, thereby reducing operational overhead and providing a theoretical foundation for deploy-and-adapt edge-computing systems.

Abstract

Unmanned Aerial Vehicle-assisted Edge Computing (UAV-EC) leverages UAVs as aerial edge servers to provide computation resources to user equipment (UE) in dynamically changing environments. A critical challenge in UAV-EC lies in making real-time adaptive offloading decisions that determine whether and how UE should offload tasks to UAVs. This problem is typically formulated as Mixed-Integer Nonlinear Programming (MINLP). However, most existing offloading methods sacrifice strategy timeliness, leading to significant performance degradation in UAV-EC systems, especially under varying wireless channel quality and unpredictable UAV mobility. In this paper, we propose a novel framework that enhances offloading strategy timeliness in such dynamic settings. Specifically, we jointly optimize offloading decisions, transmit power of UEs, and computation resource allocation, to maximize system utility encompassing both latency reduction and energy conservation. To tackle this combinational optimization problem and obtain real-time strategy, we design a Quality of Experience (QoE)-aware Online Offloading (QO2) algorithm which could optimally adapt offloading decisions and resources allocations to time-varying wireless channel conditions. Instead of directly solving MIP via traditional methods, QO2 algorithm utilizes a deep neural network to learn binary offloading decisions from experience, greatly improving strategy timeliness. This learning-based operation inherently enhances the robustness of QO2 algorithm. To further strengthen robustness, we design a Priority-Based Proportional Sampling (PPS) strategy that leverages historical optimization patterns. Extensive simulation results demonstrate that QO2 outperforms state-of-the-art baselines in solution quality, consistently achieving near-optimal solutions. More importantly, it exhibits strong adaptability to dynamic network conditions. These characteristics make QO2 a promising solution for dynamic UAV-EC systems.

1. Introduction

Unmanned aerial vehicles (UAVs) are utilized for a wide range of applications, such as military reconnaissance and disaster relief, due to the high maneuverability and adaptive capabilities [1]. The role of UAVs is evolving beyond traditional sensing, being leveraged as mobile computing units for edge computing [2]. This emerging role is particularly valuable given the limitations of traditional cloud computing, where reliance on remote servers often leads to high latency and limited responsiveness [3]. Compared with fixed terrestrial edge-computing infrastructures, UAV-assisted edge computing (UAV-EC) further offers unique advantages: rapid deployment in dynamic or infrastructure-scarce areas, extended coverage for remote or disaster-affected regions, and adaptive positioning to enhance communication and computation efficiency. Thus, UAV-EC has established itself as an attractive model, in which UAVs function as edge servers in the air to offer immediate and adaptable computing services for user equipment (UE).

The core challenge in UAV-EC systems lies in determining whether and how UE should offload their computation tasks to UAV-based edge servers. This offloading optimization problem inherently requires joint consideration of multiple time-varying factors, including wireless channel conditions, UAV rajectory and mobility patterns, heterogeneous task characteristics, and resource constraints. Designing efficient and adaptive offloading strategies that can promptly accommodate these dynamic variations remains a significant research challenge.

This challenge has led to extensive research in recent years, with a particular focus on the offloading problem under different deployment scenarios such as signal UAV [4], multiple UAVs [5] and cloud–edge–terminal collaborative architecture [6], with diverse objectives, including improving user experience [7] and increasing the revenue of Internet Service Providers (ISPs) [8]. These studies have examined a variety of task models, including continuous arrival tasks [9], indivisible tasks [10], Directed Acyclic Graph (DAG) tasks [11], and independent tasks [12], under various multi-access control manners such as Time-Division Multiple Access (TDMA) [13], Frequency-Division Multiple Access (FDMA) [14], and Non-Orthogonal Multiple Access (NOMA) [15]. The significant benefits of edge computing further stimulate research into hybrid architectures, leading to innovations in device-to-device (D2D)-assisted MEC networks [16], Reconfigurable Intelligent Surface (RIS)-assisted MEC networks [17], and other emerging technological convergences.

While these works provide valuable insights, a critical aspect, i.e., offloading strategy timeliness, remains inadequately addressed, despite its critical importance for practical deployment in dynamic environments. Specifically, when dealing with indivisible tasks, offloading decisions are commonly modeled as a Mixed-Integer Programming (MIP) problem due to the binary (0–1) nature of the offloading decision. Conventional approaches to MIP problems rely heavily on dynamic programming and branch-and-bound methodologies. However, these numerical optimization-based methods exhibit two fundamental limitations that compromise their practical applicability: (i) the speed of problem solving limits timeliness of the proposed strategy; and (ii) lack of correlation between strategies under different settings leads to excessive and invalid calculations. More specifically,

• Computational Timeliness Deficiency: The solving time of these methods significantly impairs strategy timeliness, and thus even fails to harvest MEC. Specifically, time-varying wireless channel conditions largely impact offloading performance, which requires optimal adaptation of offloading decisions and resource allocations. This demands solving the combinatorial optimization problem within channel coherence time. However, the computation complexity is prohibitively high, particularly in large-scale networks. Methods like heuristic local search and convex relaxation often require numerous iterations to reach a satisfying local solution, making them unsuitable for real-time offloading decisions in fast-changing channels.
• Environment Adaptability Limitations: Existing algorithms are predominantly designed for fixed network parameter sets, while failing to exploit correlations between strategies under different environmental conditions. This limitation prevents effective utilization of historical computational data to rapidly adjust offloading and resource-allocation decisions. Consequently, when network environments change, strategy recalculation is necessary. For UAV-EC systems with rapidly changing environments, this constant recalculation would lead to substantial computational overhead.

To this end, this paper introduces a novel approach to enhance the timeliness and robustness of offloading strategies in UAV-EC systems. We model a joint optimization problem that integrates task offloading decisions, transmission power control, and resource allocation to achieve holistic utility maximization. The primary challenge lies in achieving efficient real-time optimization under rapidly varying wireless channel conditions and dynamic resource availability. To tackle this challenge, we introduce the QoE-aware Online Offloading (QO2) algorithm. By incorporating deep neural network (DNN) inference, the QO2 algorithm significantly improves the timeliness of offloading decisions while maintaining high robustness. To further enhance its robustness, we also design a Priority-Based Proportional Sampling (PPS) strategy. Empirical results confirm the superior performance of QO2 over state-of-the-art baselines, as it consistently produces near-optimal solutions. Moreover, QO2 algorithm exhibits strong adaptability to dynamic network conditions such as available computation resources, task characteristics, and user priority distributions. The algorithm demonstrates rapid re-convergence capability to near-optimal solutions, with re-convergence time scaling proportionally to the magnitude of environmental changes. The main contributions are threefold:

• Joint Optimization Framework: We introduce a joint optimization framework for UAV-EC systems that simultaneously co-designs computation offloading decisions and resource allocation. This integrated approach is tailored for dynamic settings, explicitly accounting for time-varying wireless channels to deliver real-time solutions.
• Novel QO2 Algorithm with PPS Strategy: We design the QO2 algorithm, which leverages DNN-based learning to generate binary offloading decisions in real-time, eliminating the computational burden of traditional MINLP solvers. In addition, we design the PPS strategy, which leverages historical optimization patterns to enhance algorithmic robustness across varying environmental conditions.
• Comprehensive Performance Validation: Extensive simulations demonstrate that QO2 achieves superior solution quality compared to state-of-the-art baselines, consistently finding solutions closer to the global optimum. Our approach exhibits strong adaptability to dynamic network conditions and demonstrates rapid re-convergence capability under varying operational scenarios, with convergence time appropriately scaling with the magnitude of environmental changes.

The rest is organized as below. Section 2 presents related work. Section 3 gives system model and the problem formulation, which is followed by QO2 algorithm design in Section 4. Finally, simulations and conclusions are presented in Section 5 and Section 6, respectively.

2. Related Work

In this section, we review literature on traditional methods for offloading problem and discuss recent studies on intelligent approaches. Finally, we highlight the unique aspects of our research.

2.1. Computation Offloading

Computation offloading has emerged as a fundamental paradigm to enhance system performance in mobile edge computing (MEC) systems. The existing studies span various scenarios, including single edge servers [18], multiple edge servers [19], and cloud–edge–terminal collaborative architectures [20]. These studies pursue varying optimization objectives tailored to specific application contexts. Some studies prioritize reducing total system latency [21,22,23] or energy consumption [24,25,26,27], while others focus on maximizing user experience quality [28,29] or enhancing system security and computing capabilities [30,31]. Moreover, the significant advantages of edge-computing technology also motivate its integration with emerging technologies, leading to innovative paradigms such as UAV-assisted MEC networks [15,32], RIS-assisted MEC networks [30,33,34,35,36], and blockchain-assisted MEC networks [22,37,38]. Representative works in this domain include Zhang et al. [22], which pioneered a blockchain-secured UAV-EC architecture. Their approach formulates an optimization problem to minimize delay through the combined management of UAV trajectory, computation offloading, and resource allocation, leveraging a block coordinate descent method to find solutions.Similarly, Mao et al. [25] tackle channel uncertainty through the co-optimization of multi-antenna UAV trajectory, computational resources, and communication strategies. They develop an algorithm based on successive convex approximation (SCA) to resolve the associated non-convex energy minimization problem. Basharat et al. [39] propose a digital twin-assisted task offloading scheme for energy-harvesting UAV-MEC networks using branch-and-bound methods, aiming to minimize latency while maximizing associated IoT devices under various constraints.

Despite these significant contributions, traditional offloading strategies often rely on static models that struggle to adapt to dynamic environments and complex task characteristics.This fundamental limitation constrains the full potential of edge-computing systems, particularly in scenarios involving time-varying channel conditions and mobile UAV deployments. Consequently, many researchers have increasingly focused on developing adaptive approaches that could respond effectively to environmental dynamics.

2.2. Learning-Based Offloading Decision Making

As the demand for sophisticated and dynamic business scenarios increases, the intersection of edge computing and machine learning has emerged as a significant research area. Machine learning enables systems to learn from historical data and real-time environments to intelligently predict task loads and resource demands.This capability enables adaptive task scheduling and resource allocation, ultimately improving system performance, energy efficiency, and quality of service.

Compared to traditional algorithms, machine learning approaches performs better in handling nonlinear relationships, complex task offloading decisions, resource allocation, and traffic prediction in edge-computing domains. Deep Q-Networks (DQNs) have demonstrated considerable efficacy in edge computing, owing to their capacity to navigate high-dimensional states and facilitate optimal decision-making for task scheduling and resource distribution. This capability is crucial in dynamic settings with uncertain channels, fluctuating node loads, and evolving network topologies, making DQNs especially suitable for discrete-action-space problems. Ding et al. [40] employ a Double Deep Q-Networks (DDQN) approach to tackle trajectory optimization and resource allocation in UAV-aided MEC systems. Their model jointly optimizes UAV flight path, time allocation, and offloading decisions to maximize the average secure computing capacity. To improve efficiency, they accelerate DDQN convergence through a reduction of the action space. Similarly, Liu et al. [41] propose a collaborative optimization method combining Double Deep Q-Networks (DDQN) and convex optimization for joint 3D trajectory planning and task offloading in UAV-EC systems. However, DQN exhibits limitations in sample efficiency and training stability, which may result in performance degradation, particularly in non-stationary environments.

However, DQN-based approaches exhibit limitations in sample efficiency and training stability, potentially leading to performance degradation in non-stationary environments. To address continuous-action spaces, Deep Deterministic Policy Gradient (DDPG) algorithms have been employed for fine-grained resource allocation and task offloading control. Lin et al. [42] propose a PDDQNLP algorithm that integrates DDPG to handle mixed continuous-action spaces, addressing the mixed-integer nonlinear problem of jointly optimizing offloading decisions, UAV 3D trajectory, and flight time. In [43], Du et al. use DDPG to construct a dynamic programming model with a large continuous-action space, addressing the data relaying and bandwidth allocation problems in UAV-assisted Internet of Things (IoT) systems. While DDPG demonstrates effectiveness in continuous control, it suffers from sensitivity to hyperparameter settings and overfitting tendencies. Ale et al. [44] investigate multi-device MEC systems and propose an enhanced DDPG algorithm to address constrained hybrid action-space challenges in task partitioning and computation offloading, demonstrating efforts to improve DDPG’s robustness in complex scenarios.

Soft Actor–Critic (SAC) algorithms have emerged as an alternative, combining stochastic policy exploration with continuous-action-handling capabilities. SAC demonstrates superior stability and accelerated convergence when dealing with high-dimensional continuous-action spaces. It also maintains a more effective balance between exploration and exploitation, which facilitates more efficient and resilient resource management and task offloading in dynamic settings. Wang et al. [45] combine SAC with a two-stage matching association strategy to jointly optimize trajectories and user associations of multiple UAVs. Goudarzi et al. [46] leverage SAC’s stochastic exploration and continuous-action-handling capabilities to implement the optimal offloading mechanism, addressing the challenge of edge resource scarcity in both high-density urban areas and remote regions. Li et al. [47] proposed the Soft Actor–Critic for Covert Communication and Charging (SAC-CC) algorithm to enhance UAV endurance and adaptability by jointly optimizing trajectory and bandwidth allocation. Bai et al. [48] introduced a multimodal SAC method that combines convolutional neural networks (CNN) and multilayer perceptrons (MLP) for the real-time joint optimization of UAV status, position, and power in dynamic environments. Wang et al. [49] combined a continuous SAC algorithm to optimize the UAV trajectory with a discrete SAC algorithm enhanced by invalid action masking (IAM) to optimize task offloading decisions, achieving collaborative optimization in multi-channel parallel processing scenarios. However, it is important to note that SAC involves high implementation complexity and demands more computational resources.

Despite their effectiveness, these DQN, DDPG, and SAC approaches face common challenges including extensive training data requirements, meticulous hyperparameter tuning, potential convergence instability, and high implementation complexity. To address these limitations, recent research has explored simplified neural network architectures that prioritize system robustness and strategy timeliness which could maintain performance while reducing implementation complexity and adaptation requirements. Huang et al. [50] introduced a Deep Reinforcement learning-based Online Offloading (DROO) framework for wireless powered MEC. Their approach achieves real-time decision-making, demonstrating computational latency under 0.1 s in a network of 30 users. Similarly, our previous work [51] proposes the Intelligent Online Computation Offloading (IOCO) algorithm, which learns historical optimal strategies via a deep neural network to make intelligent offloading decisions in dynamic wireless environments. IOCO incorporates quantization and sampling techniques to improve execution speed and resilience to environment fluctuations. However, IOCO algorithm overlooks the impact of power control on offloading.

The limitations observed in the existing literature serve as the primary motivation for our work. First, while numerous studies focus on optimization accuracy, the timeliness of offloading strategies receives insufficient attention, particularly in UAV-EC systems where environmental conditions change rapidly. Second, most existing approaches fail to jointly consider offloading decisions, power control, and computation resource allocation in a unified optimization framework. Third, the robustness of learning-based algorithms under highly dynamic conditions requires further enhancement to ensure consistent performance across diverse operational scenarios.

To address these limitations, this paper proposes a novel framework that enhances offloading strategy timeliness in UAV-EC systems. Unlike existing approaches that sacrifice strategy timeliness for optimization accuracy, our framework prioritizes real-time adaptation while maintaining near-optimal solution quality. Specifically, we design an adaptive online algorithm that jointly optimizes offloading decisions, the transmitting power of UE, and computation resource allocation. By incorporating power control into our unified decision-making framework, our approach achieves a more comprehensive optimization, resulting in improved overall system performance. Furthermore, through the design of advanced network architectures, quantization methods, and sampling strategies, we enhance the algorithm’s adaptability to dynamic environmental conditions.

3. System Model and Problem Formulation

This section presents network model, following by problem formulation and its analysis. Key notations are summarized in

Table 1. Main notations.

Symbol	Description
K	Number of UE
$h_k$	Channel gain from UE k to ES
N	Number of subchannels
$F_k$	Computational speed of UE k
$I_k$	Input data bits of application k
$f_k$	Allocated computational speed for UE k
${\alpha }_k$	Computation intensive degree
$F_{max}$	Total computational speed of MEC server
$x_k$	Offloading indicator
$R_k$	Uplink rate of UE k
$\epsilon$	Coefficient of CPU energy consumption
$T_k^l/E_k^l$	Time/energy consumption of local execution
W	Subchannel bandwidth
$T_k^c/E_k^c$	Time/energy consumption of offloading
$N_0$	Noise power
$T_k/E_k$	Total time/energy consumption of UE k
$p_0$	Static power consumption
${\gamma }_k^T/{\gamma }_k^E$	User preference time/energy consumption
$p_k$	Transmit power of UE k
$w_k$	Weighting factor of UE k
$\rho$	Inverse of the power amplifier efficiency
$\upsilon$	Sampling related coefficient
$P_{k,max}$	Maximum transmit power of UE k
$\Delta$	Training interval

.

3.1. Network Model

Here, we consider a quasi-static MEC system with an UAV functioning as the edge server (ES) and K fixed UE denoted as a set $\mathcal{K}=\{1,2,\dots K\}$ in its range. Without loss of generality, we assume a block-fading channel model where the channel coefficients remain constant during the uplink transmission period of each offloaded task, but may vary independently across different transmission slots. Since our problem formulation is considered in one block, for the sake of brevity, subscripts t of blocks would be omitted, without causing confusion.

Each UE has a computing task characterized by $\left(I_k,{\alpha }_k\right)$ to be processed, where $I_k$ and ${\alpha }_k$ present data size and application-specific computational complexity, respectively. Hence, number of CPU cycles needed for task k is ${\alpha }_k{I}_k$ [7]. Here, we consider atomic tasks which could not be divided into subtasks. Since UAV has larger computational capability than UE, UE can offload their tasks to UAV. Here, we adopt a binary offloading mode, i.e., task could be either computed locally at the UE or offloaded to the UAV. Let $x_k\in \{0,1\}$ be an indicator variable. Specifically, $x_k=1$ means that UE k offloads its task to the ES, and $x_k=0$ elsewise.

3.1.1. Local Computation Model

Computational power consumption is modeled as $P=\epsilon f^3$ [52], where $\epsilon$ is a coefficient dependent on the chip architecture, and f denotes the computational speed in CPU cycles per second. When computation task of UE k is process locally, the execution time $T_k^l$ and corresponding energy consumption $E_k^l$ could be expressed as

$$T_k^l={\displaystyle \frac{{\alpha }_k{I}_k}{F_k}},$$

(1)

$$E_k^l={\alpha }_k{I}_k\epsilon F_k^2,$$

(2)

respectively, where $F_k$ denotes computational speed of UE k.

3.1.2. Edge Computation Model

A typical edge computation process consists of three steps. First, UE offload its task to the ES through the allocated uplink channel. Then, the ES allocates computation resources and then executes the offloaded tasks on behalf of UE. Finally, the ES transmits results back to UE. Since the number of results is much smaller than that of the data offloaded to the ES, and the downlink capacity is much larger than that of the uplink, we safely ignore the overhead of the results transmission [53]. Next, we give more details for the former two steps.

• Uplink Transmission: Each uplink channel is a block-fading Rayleigh channel with block length no less than the maximum execution time of offloaded tasks. The channel gain of UE k, denoted $h_k$, accounts for the overall effects of path loss and small-scale fading. To emphasize again, we ignore subscripts t of $h_k$ to simplify labeling. Considering the white Guassian noise power is $N_0$ and user bandwidth is W, the data rate of UE k could be given by $R_k=W{log}_2\left(1+{\displaystyle \frac{p_k{h}_k}{N_0}}\right),$ where $p_k$ is the transmitting power of UE k and could be configured flexibly.
• Edge Execution: We assume that ES could serve K UE concurrently by allocating computational resource $f_k$ to UE k.

As aforementioned, we could obtain the total time for offloading task $T_k^c$ as

$$T_k^c(p_k,f_k)={\displaystyle \frac{{\beta }_k{I}_k}{R_k}}+{\displaystyle \frac{{\alpha }_k{I}_k}{f_k}},$$

(3)

where ${\beta }_k$ refers touplink channel cost, e.g., channel encoding. Correspondingly, the energy consumption $E_k^c$ as

$$E_k^c\left(p_k\right)=(p_0+\rho p_k){\displaystyle \frac{{\beta }_k{I}_k}{R_k}}$$

(4)

with $p_0$ and $\rho$ denoting static power consumption and inverse of power amplifier efficiency, respectively.

3.2. Problem Formulation

3.2.1. QoE-Aware System Utitily

In such a UAV-EC system, Quality of Experience (QoE) of UE k mainly concerns task completion time $T_k$ and energy consumption $E_k$, which could be given by

$$T_k(x_k,p_k,f_k)=(1-x_k)T_k^l+x_k{T}_k^c,$$

(5)

$$E_k(x_k,p_k,f_k)=(1-x_k)E_k^l+x_k{E}_k^c,$$

(6)

respectively. To normalize these two metrics with different units, we define a utility function of UE k as

$$\begin{array}{cc}\hfill u_k(x_k,p_k,f_k)& ={\gamma }_k^T{\displaystyle \frac{T_k^l-T_k}{T_k^l}}+{\gamma }_k^E{\displaystyle \frac{E_k^l-E_k}{E_k^l}}\hfill \end{array}$$

(7)

with ${\gamma }_k^T,{\gamma }_k^E\in [0,1]$ denoting user preferences on task completion time and energy consumption. Since Equation (7) could be rewritten as $u_k(x_k,p_k,f_k)=x_k\left({\gamma }_k^T{\displaystyle \frac{T_k^l-T_k^c}{T_k^l}}+{\gamma }_k^E{\displaystyle \frac{E_k^l-E_k^c}{E_k^l}}\right)$, it could measure QoE improvements via computation offloading compared with local execution. Further, we define the system utility as

$$U({\mathit{x}}_{\mathit{t}},{\mathit{p}}_{\mathit{t}},{\mathit{f}}_{\mathit{t}}|{\mathit{h}}_{\mathit{t}})=\sum _{k=1}^K{w}_k{u}_k(x_k,p_k,f_k)$$

(8)

with $w_k\in [0,1]$ reflecting the preferences of ES on UE, ${\mathit{x}}_{\mathit{t}}=\left\{x_k\mathrm{in}\mathrm{block}t\mid k\in \mathcal{K}\right\}$, ${\mathit{p}}_{\mathit{t}}=\left\{p_k\mathrm{in}\mathrm{block}t\mid k\in \mathcal{K}\right\}$, and ${\mathit{f}}_{\mathit{t}}=\left\{f_k\mathrm{in}\mathrm{block}t\mid k\in \mathcal{K}\right\}$. Equation (8) not only measures the overall utility of UE but also considers the interest of ES. Without confusion, we use $x_k$ to denote $x_k\mathrm{in}\mathrm{block}$, and the same for the other two notations.

3.2.2. Utility Maximization Problem

The system utility maxmization problem can be formulated as

$$\begin{array}{cc}\hfill \mathrm{P}1:\underset{{\mathit{x}}_{\mathit{t}},{\mathit{p}}_{\mathit{t}},{\mathit{f}}_{\mathit{t}}}{max}& U({\mathit{x}}_{\mathit{t}},{\mathit{p}}_{\mathit{t}},{\mathit{f}}_{\mathit{t}}|{\mathit{h}}_{\mathit{t}})\hfill \\ \hfill s.t.& \mathrm{C}1:x_k\in \{0,1\},\forall k\hfill \\ \hfill & \mathrm{C}2:\sum _{k=1}^K{x}_k\le N,\hfill \\ \hfill & \mathrm{C}3:0\le p_k\le P_{k,max},\forall k\hfill \\ \hfill & \mathrm{C}4:f_k\ge 0,\forall k\hfill \\ \hfill & \mathrm{C}5:\sum _{k=1}^K{f}_k\le F_{max}.\hfill \end{array}$$

In P1, C1 indicates that binary offloading model is adopted; C2 states that at most N UE are allowed to transmit simultaneously to guarantee orthogonality; C3 means that the transmission power should be non-negative and must not exceed the power budget; C4 reveals the non-negative feature of allocated computation resource; C5 means that the sum of obtained computation resources could not exceed the computation capability of ES.

3.2.3. Problem Analysis

We observed that P1 is a mixed-integer nonlinear programming. In more detail, it consists of two subproblems; one is the offloading decision, the other is resource allocation. Several tricky points in solving P1 could be summarized as follows:

• A tight coupled relationship among subproblems: More specifically, offloading decision would affect resource allocation and vice versa.
• Integer feature of offloading decision subproblem: Due to rgw integer feature of $\mathit{x}$, it always needs to search among $2^K$ possible actions to find the optimal solution. Obviously, a violent search is not suitable for exponentially large search spaces.
• Non-convexity of resoure allocation subproblem: Even for a given offloading decision, it is still difficult to solve the resource-allocation problem due to its non-convexity.

Besides these three points, another challenge lies in guaranteeing timely decisions before channel changes, since P1 needs to be re-solved once the channel varies. Next, we would overcome these tricky problems, and propose a QoE-aware Online Offloading (QO2) algorithm which could work in an online manner.

4. Proposed Algorithm

In this section, we first show an overview of the QO2 algorithm. Then, three main steps of the QO2 algorithm are introduced. Finally, several implementation issues are discussed.

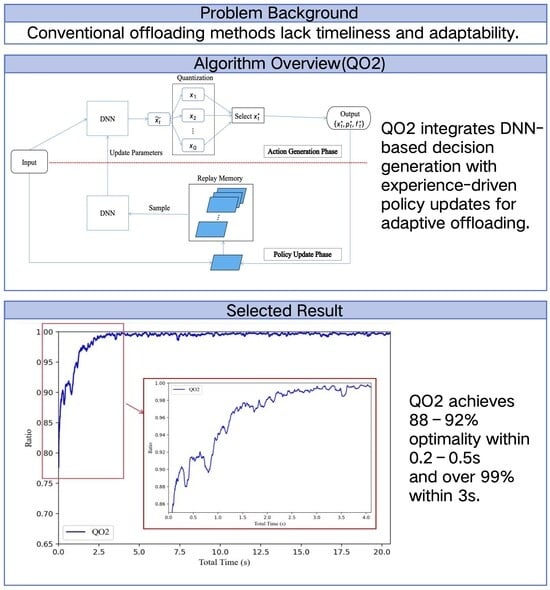
4.1. Algorithm Overview

The struture of the QO2 algorithm is illustrated in Figure 1, which consists of action generation and policy update. Specifically,

• Action Generation: First, a relaxed offloading decision $\widetilde{{\mathit{x}}_{\mathit{t}}}$ is obtained firstly via utilizing a DNN with parameters $\theta$. Then, a quantization operation is performed to guarantee its integer feature and uplink capacity constraint. Finally, the ES selects the optimal offloading action through solving RA and comparing utility for each quantized offloading decision; meanwhile, it determines the optimal resource-allocation strategy.
• Policy Update: To obtain more intelligent action, the ES would first add experience data to replay memory based on a given caching rule. Then, it would sample a batch of cached data to retrain DNN and accordingly update network parameters, which would be used to generate a new action in the next several blocks.

To sum up, in the action-generation phase, in addition to using a DNN-based method to obtain the offloading decision, a decouplation-based method is designed to solve the resource-allocation problem. In policy update phase, experience replay technique is utilized to update DNN-based offloading policy. The descriptions of three methods are detailed in the following subsections.

Figure 1. Illustration of QO2 algorithm flow.

Figure 1. Illustration of QO2 algorithm flow.

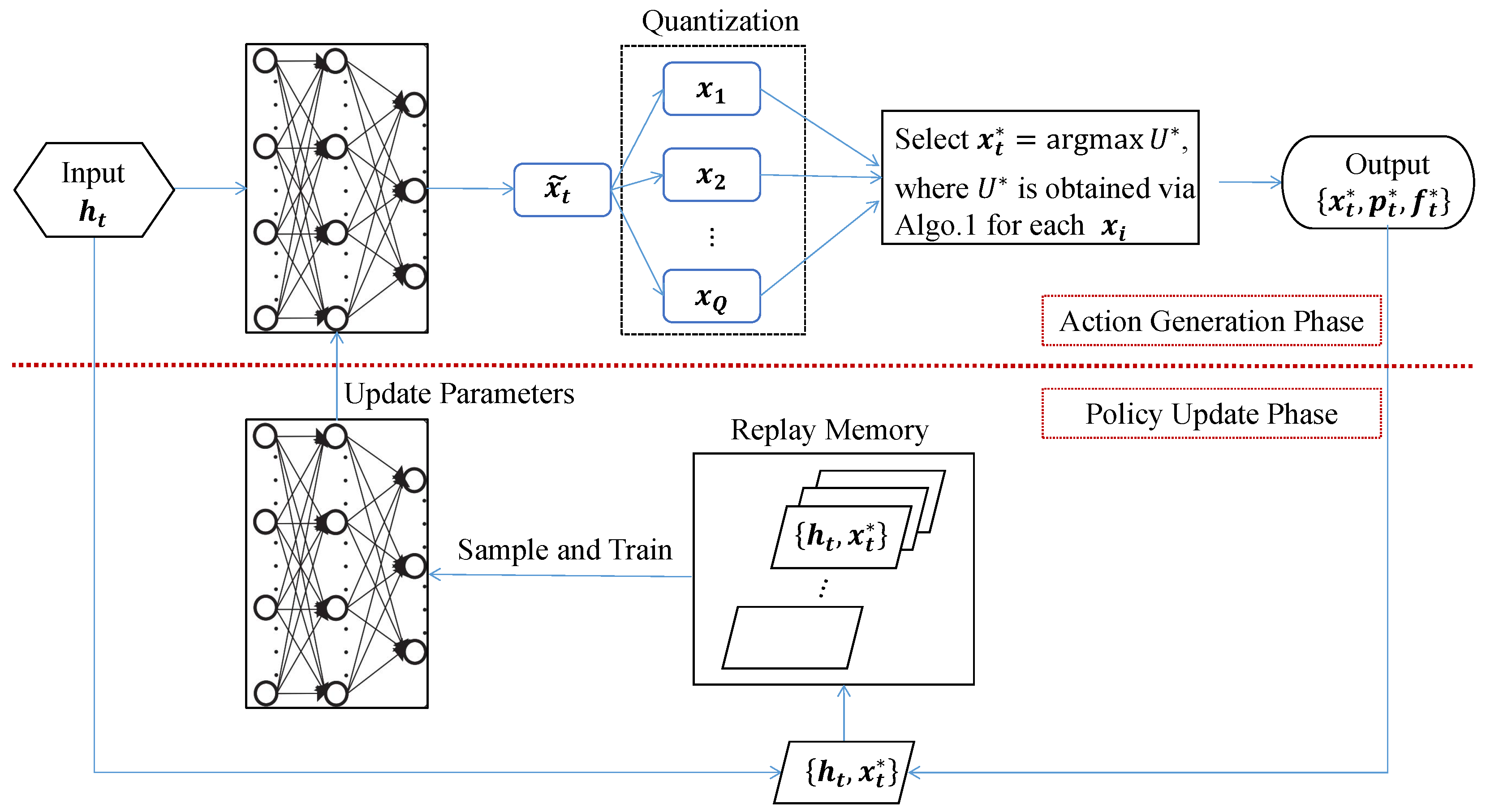
4.2. Action Generation: Offloading Decision

Essentially, we aim to obtain an offloading policy function $f_{\theta }$ which could quickly generate offloading decision ${\mathit{x}}_{\mathit{t}}^{*}$ for any channel realization ${\mathit{h}}_{\mathit{t}}\in {\mathbb{R}}^K$, i.e.,

$$f_{\theta }:{\mathit{h}}_{\mathit{t}}\mapsto {\mathit{x}}_{\mathit{t}}^{*}.$$

(9)

This is inspired by (i) the universal approximation theorem, which guarantees that a DNN with sufficiently hidden neurons and a linear output layer is capable of representing any continuous mapping function if proper activation functions are applied at neurons, and (ii) inference via forward network could work in the online mode because it is less time consuming; we decide to utilize a DNN with parameters $\theta$ to fit Equation (9). Note that the normalization of input features is generally a critical preprocessing step for stable DNN training, particularly for scenarios with wide numerical ranges. Common techniques include min–max scaling and z-score standardization. Since it is not practical to construct such a DNN with infinite hidden layers, we approximate Equation (9) through the following two steps.

4.2.1. Relaxation Operation

We utilize a DNN with parameters $\theta$ to obtain a relaxed offloading decision. Specifically, we use the ELU and Sigmoid function as the activation function of hidden neurons and output layer, respectively. As such, the output of DNN, denoted $\widetilde{{\mathit{x}}_{\mathit{t}}}$, could satisfy $0\prec \widetilde{{\mathit{x}}_{\mathit{t}}}\prec 1$.

4.2.2. Quantization and Select Operations

Overall, we first quantize $\widetilde{{\mathit{x}}_{\mathit{t}}}$ to obtain Q binary offloading decisions $\left\{{\mathit{x}}_t^1,\dots {\mathit{x}}_t^j,\dots {\mathit{x}}_t^Q\right\}$, and then select the optimal ${\mathit{x}}_{\mathit{t}}^{*}$ based on the following rule:

$${\mathit{x}}_{\mathit{t}}^{*}=arg\underset{j\in \left\{1,\dots ,Q\right\}}{max}{U}^{*}({\mathit{x}}_t^j,{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}}).$$

(10)

Here, $U^{*}({\mathit{x}}_t^j,{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})$ could be obtained via Equations (14) and (18), given later in Section 4.3.

We observed from Equation (10) that the larger Q, the better the algorithm performance, though the higher the complexity. To balance the performance and complexity, we design an order-preserving and $L_0$-norm-limiting quantization method. Here, taking quantized action ${\mathit{x}}_t^j$ as an example, order-preserving means that for ${\mathit{x}}_t^j$, $x_{t,m}^j\ge x_{t,n}^j$ should hold if $\widetilde{x_{t,m}^j}\ge \widetilde{x_{t,n}^j}$ for all $m,n\in \mathcal{K}$. In addition, $L_0$-norm-limiting rule guarantees an uplink capacity constraint, i.e., C2 should be satisfied during quantization. Under these two criteria, the value of Q could be altered from 1 to $K+1$. Next, we present the details of this quantization method.

• First, we sort entries of $\widetilde{{\mathit{x}}_{\mathit{t}}}$ in a descending order, e.g., ${\tilde{x}}_{t,\left(1\right)}\ge {\tilde{x}}_{t,\left(2\right)}\ge \dots \ge {\tilde{x}}_{t,\left(k\right)}\ge \dots \ge {\tilde{x}}_{t,\left(K\right)}$ where ${\tilde{x}}_{t,\left(k\right)}$ is the k-th order statistic of $\widetilde{{\mathit{x}}_{\mathit{t}}}$. Define

  $${\mathcal{T}}_{topN}=\left\{\left(k\right)|k=1,\dots ,N\right\}.$$

  (11)
  Then, the first binary offloading decision ${\mathit{x}}_t^1$ could be achieved by

  $$x_{t,k}^1=\left\{\begin{array}{cc}1\hfill & {\tilde{x}}_{t,k}>0.5\&\&k\in {\mathcal{T}}_{topN}\hfill \\ 0\hfill & else\hfill \end{array}\right.$$

  (12)

  for $k=1,\dots ,K$.
• To generate the remaining offloading actions, we first order entries of $\widetilde{{\mathit{x}}_{\mathit{t}}}$ respective to their distances to 0.5, $\left|{\tilde{x}}_{t,\left[1\right]}-0.5\right|\le \left|{\tilde{x}}_{t,\left[2\right]}-0.5\right|\le \dots \le \left|{\tilde{x}}_{t,\left[q\right]}-0.5\right|\le \dots \le \left|{\tilde{x}}_{t,\left[K\right]}-0.5\right|$, where ${\tilde{x}}_{t,\left[q\right]}$ is the q-th order statistic of $\widetilde{{\mathit{x}}_{\mathit{t}}}$. Then, the binary offloading decision ${\mathit{x}}_t^q,q=2,\dots ,Q$ could be achieved by

  $$x_{t,k}^q=\left\{\begin{array}{cc}1\hfill & {\tilde{x}}_{t,k}>{\tilde{x}}_{t,\left[q-1\right]}\&\&k\in {\mathcal{T}}_{topN}\hfill \\ 1\hfill & {\tilde{x}}_{t,k}={\tilde{x}}_{t,\left[q-1\right]}\&\&{\tilde{x}}_{t,\left[q-1\right]}\le 0.5\&\&k\in {\mathcal{T}}_{topN}\hfill \\ 0\hfill & else\hfill \end{array}\right.$$

  (13)

  for $k=1,\dots ,K$.

Remark 1. 

Although the proposed quantization method given in (12) and (13) could only generate at most $K+1$ quantized actions, it suffices to achieve good system performance, as shown later in Section 5.

4.3. Action Generation: Resource Allocation

For a given quantized offloading action ${\mathit{x}}_t^j$, P1 could be transformed to the following equivalent problem:

$$\begin{array}{cc}\hfill \mathbf{P}2:\underset{\mathit{p},\mathit{f}}{\min }& \sum _{k=1}^K\left({\displaystyle \frac{{\eta }_k+{\tau }_k{p}_k}{{log}_2\left(1+\frac{p_k{h}_k}{N_0}\right)}}+{\displaystyle \frac{{\lambda }_k}{f_k}}\right)\hfill \\ \hfill s.t.& \mathrm{C}3,\mathrm{C}4,\mathrm{C}5,\hfill \end{array}$$

where ${\eta }_k=x_{t,k}^j{w}_k{\beta }_k{I}_k\left({\gamma }_k^T/T_k^{l}W+{\gamma }_k^E{p}_0/E_k^{l}W\right)$, ${\tau }_k=x_{t,k}^j{w}_k{\beta }_k{I}_k{\gamma }_k^E\rho /E_k^{l}W$, and ${\lambda }_k=x_{t,k}^j{w}_k{\gamma }_k^T{\alpha }_k{I}_k/T_k^l$ for simplicity. Observe that uplink power $\mathit{p}$ and computation resource allocation $\mathit{f}$ are decoupled from each other in both objective and constraints of P2. Hence, we could handle P2 by performing uplink power control and computation resource allocation independently. Details are as below.

4.3.1. Uplink Power Control

Once the offloading decision is fixed, UE are independent of each other in terms of uplink power control. Hence, each UE could assign its transmission power via solving the following problem (Obviously, it is also advisable to optimize uplink transmission power using the ES in a centralized manner.)

$$\begin{array}{cc}\hfill \mathbf{P}3:\underset{p_k}{\min }& {\displaystyle \frac{{\eta }_k+{\tau }_k{p}_k}{{log}_2\left(1+\frac{p_k{h}_k}{N_0}\right)}}\triangleq f\left(p_k\right)\hfill \\ \hfill s.t.& \mathrm{C}3.\hfill \end{array}$$

By analyzing the special structure of P3 [54], we achieve the optimal solution in closed forms in Theorem 1, based on which we propose a bisection-based uplink transmission power control policy.

Theorem 1. 

The optimal solution of P3 could be given by

$$p_k^{*}=\left\{\begin{array}{cc}{P}_{k,max}\hfill & \varphi \left(P_{k,max}\right)\le 0\hfill \\ \widehat{p}\hfill & else\hfill \end{array}\right.,$$

(14)

where $\widehat{p}$ is the unique solution of $\varphi \left(p_k\right)=0$ in $(0,P_{k,max})$, with

$$\varphi \left(p_k\right)={\tau }_k{log}_2\left(1+{\displaystyle \frac{p_k{h}_k}{N_0}}\right)-{\displaystyle \frac{h_k}{N_{0}ln2}}{\displaystyle \frac{{\eta }_k+{\tau }_k{p}_k}{1+\frac{p_k{h}_k}{N_0}}}$$

(15)

Proof. 

See in Appendix A.    □

Based on Theorem 1, we propose a bisection-based power control algorithm (BPC) with low-complexity to solve P3, the specific steps of which are presented in Algorithm 1.

Algorithm 1 Bisection-based power control algorithm (BPC).

1: Calculate $\varphi \left(P_{k,max}\right)$  2: if  $\varphi \left(P_{k,max}\right)\le 0$  then  3:    $p_k^{*}=P_{k,max}$  4: else  5:    Initialize $p_l=0$ and $p_u=P_{k,max}$  6:    repeat  7:      $p_m=\left(p_u+p_l\right)/2$  8:      if $\varphi \left(p_m\right)\le 0$ then  9:         $p_l=p_m$ 10:      else 11:         $p_u=p_m$ 12:      end if 13:    until $p_u-p_l\le ϵ$ 14:    $p_k^{*}=\left(p_u+p_l\right)/2$ 15: end if

4.3.2. Computation-Resources Allocation

From P2, we formulate the computation-resources allocation problem as

$$\begin{array}{cc}\hfill \mathbf{P}4:\underset{\mathit{f}}{\min }& \sum _{k=1}^K{\displaystyle \frac{{\lambda }_k}{f_k}}\hfill \\ \hfill s.t.& \mathrm{C}4,\mathrm{C}5.\hfill \end{array}$$

Since both the objective function and feasible region are convex, P4 is a convex optimization problem. Detailed proof is provided in Appendix B. Here, we adopt the Lagrangian dual method to solve P4. Specifically, by denoting $\mu$ as the Lagrange multiplier for C5, we obtain Lagrangian dual problem of P4 as

$$\begin{array}{cc}\hfill \mathbf{P}5:\underset{\mu \ge 0}{\max }& D\left(\mu \right)\hfill \end{array}$$

where Lagrangian dual function $D\left(\mu \right)$ is given by

$$D\left(\mu \right)=\underset{\left\{f_k\in \mathrm{C}4\right\}}{inf}L\left(f_k,\mu \right)$$

(16)

with Lagrangian function expressed as

$$L\left(f_k,\mu \right)=\sum _{k=1}^K{\displaystyle \frac{{\lambda }_k}{f_k}}+\mu \left(\sum _{k=1}^K{f}_k-F_{max}\right).$$

(17)

Using Karush–Kuhn–Tucker (KKT) conditions, i.e., ${\displaystyle \frac{\partial L\left(f_k,\mu \right)}{\partial f_k}}{\mid }_{f_k=f_k^{*}}=0$ and ${\displaystyle \frac{dD\left(\mu \right)}{d\mu }}{\mid }_{\mu =u^{*}}=0$, we could express the optimal solution of $f_k$ as

$$f_k^{*}={\displaystyle \frac{F_{max}\sqrt{{\lambda }_k}}{{\sum }_{k=1}^K\sqrt{{\lambda }_k}}}.$$

(18)

Finally, via substituting (14) and (18) into (8), we could obtain $U^{*}({\mathit{x}}_j,{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})$ for any given ${\mathit{x}}_j$. Further, we could select the optimal offloading decision ${\mathit{x}}_{\mathit{t}}^{*}$, as (10) stated.

At this point, we have completed action-generation phase, within which QO2 could output the offloading action ${\mathit{x}}_{\mathit{t}}^{*}$ along with its corresponding optimal resource allocation $\left({\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}\right)$ for channel realization ${\mathit{h}}_{\mathit{t}}$. In the next subsection, we express how QO2 realizes self-evolution for better performance.

4.4. Policy Update

The main idea of policy update is to utilize the offloading decision generated in the first phase to help DNN evolve into a better one. Put simply, the newly generated $\left\{{\mathit{h}}_{\mathit{t}},{\mathit{x}}_{\mathit{t}}^{*}\right\}$ would be added to our maintained memory space at each iteration. When the memory is full, the oldest data will be deleted. Additionally, we utilize an experience replay technique and periodically sample a batch of data from memory to update DNN. Here, we take one iteration as an example to illustrate some highlights in the update process.

• Sample Strategy: We sample a batch of data $\left\{\left({\mathit{h}}_{\varphi },{\mathit{x}}_{\varphi }^{*}\right)\mid \varphi \in {\mathsf{\Phi }}_t\right\}$, marked by a set of time indices ${\mathsf{\Phi }}_t$ to train DNN (the reward signal is implicitly encoded in ${\mathit{x}}_{\mathit{t}}^{*}$ through the utility-maximization process. Specifically, ${\mathit{x}}_{\mathit{t}}^{*}$ is selected as the candidate achieving the maximum utility value among quantized alternatives, thus representing the optimal reward-maximizing action under the given channel state ${\mathit{h}}_{\mathit{t}}$.). Intuitively, the latest data comes from a smarter DNN, and thus contributes more to policy update. However, relying solely on latest data to train DNN would lead to poor stability. To achieve a better balance, we propose a PPS strategy. Specifically, we record sample frequency of data i as $c_i$, based on which we set its sample priority as $c_i^{-\upsilon }$. Here, $\upsilon$ is a coefficient to balance update efficiency and stability. Then, data i would be sampled with probability of ${\displaystyle \frac{c_i^{-\upsilon }}{\sum c_i^{-\upsilon }}}$. As shown in Section 5, PPS method outmatches Random Sampling (RS) method [50] and Priority-based Sampling (PS) method in terms of convergence rate and stability, respectively.
• Loss Function and Optimizer: Mathematically, training DNN with weights ${\theta }_i$ could be considered a logistic regression problem. Hence, we could choose cross-entropy as the loss function, defined as

  $$L\left({\theta }_i\right)=\sum _{\varphi \in {\mathsf{\Phi }}_t}\left({\mathit{x}}_{\varphi }^{*}·ln{f}_{{\theta }_i}\left({\mathit{h}}_{\varphi }\right)+\left(1-{\mathit{x}}_{\varphi }^{*}\right)·ln\left(1-f_{{\theta }_i}\left({\mathit{h}}_{\varphi }\right)\right)\right)$$

  (19)

  with “·” denoting the dot product of two vectors. Additionally, Adam algorithm is utilized as our optimizer to reduce loss defined in (19). The details of the Adam algorithm are omitted for brevity.

The sketch of this algorithm is presented in Algorithm 2.

Algorithm 2 QoE-aware Online Offloading (QO2) Algorithm

1: Initialize the DNN with random parameters ${\theta }_1$  2: Let $i=1$  3: for  $t=1,2,\dots T$  do  4:    Generate a relaxed offloading decision $\widetilde{{\mathit{x}}_{\mathit{t}}}=f_{{\theta }_i}\left({\mathit{h}}_{\mathit{t}}\right)$  5:    Quantize $\widetilde{{\mathit{x}}_{\mathit{t}}}$ into Q binary actions ${\mathit{x}}_t^j,j\in \left\{1,2,\dots Q\right\}$  6:    Calculate $U^{*}({\mathit{x}}_t^j,{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})$ for these Q binary offloading actions via Algorithm 1 and Equation (18)  7:    Select the best actions as Equation (10)  8:    Output $\left\{{\mathit{x}}_{\mathit{t}}^{*},{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}\right\}$  9:    Add $\left\{{\mathit{h}}_{\mathit{t}},{\mathit{x}}_{\mathit{t}}^{*}\right\}$ into the memory 10:    if t mod $\Delta$ = 0 then 11:      Sample a batch of dataset $\left\{{\mathit{h}}_{\mathit{t}},{\mathit{x}}_{\mathit{t}}^{*}\right\}$ with the PPS method 12:      Train DNN to update ${\theta }_i$ to ${\theta }_{i+1}$ with the Adam algorithm 13:    end if 14: end for

4.5. Computational Complexity Analysis and Deployment Issues

At each time slot t, the relaxation operation (Line 4 in Algorithm 2) passes ${\mathit{h}}_t$ through the DNN $f_{{\theta }_i}(·)$, where both the input and output layers have dimension K. This operation incurs a time complexity of $O\left(K\right)$. The quantization and selection operations (Line 5) involve sorting the vector $\widetilde{{\mathit{x}}_{\mathit{t}}}$ and generating Q binary offloading decisions, where $Q\le K+1$, resulting in a time complexity of $O(KlogK)+O\left(QK\right)=O\left(K^2\right)$. Consequently, the overall time complexity for the offloading decision is $O\left(K\right)+O\left(K^2\right)=O\left(K^2\right)$. In the resource-allocation phase (Line 6), a computation resource allocation scheme, along with utility calculation and selection, exhibit time complexities of $O(Klog(1/ϵ\left)\right)$, $O\left(K\right)$, and $O\left(K\right)$ per binary offloading decision, respectively. Here, $ϵ$ denotes the stopping tolerance of bisection method. For all Q decisions, the total time complexity for resource allocation is $O(K^{2}log(1/ϵ))$. Thus, the aggregate time complexity per decision window is $O\left(K^2\right)+O(K^{2}log(1/ϵ))=O(K^{2}log(1/ϵ))$.

Additionally, every $\Delta$ iterations (Line 10), the framework performs DNN training to update parameters from ${\theta }_i$ to ${\theta }_{i+1}$. The PPS method (Line 11) samples a mini-batch of size B from the replay memory of size M, which incurs a time complexity of $O(M+B)$. Subsequently, the DNN training step (Line 12) incurs a time complexity of $O\left(BK\right)$. Since training occurs once every $\Delta$ iterations, the amortized training complexity per iteration is $O\left({\displaystyle \frac{M+B}{\Delta }}\right)+O\left({\displaystyle \frac{BK}{\Delta }}\right)$. In summary, the total time complexity per iteration of QO2 is $O\left(K^{2}log(1/ϵ)+{\displaystyle \frac{M+B}{\Delta }}+{\displaystyle \frac{BK}{\Delta }}\right)$.

Remark 2. 

Although QO2 is designed for UAV-EC system with time-varying channels, it could handle other time-varying parameters, e.g., the available computation resources of ES. All we should modify is the neuron number of the input layer, to be consistent with that of varying parameters. Further, QO2 could even handle other complex problems with less modification, e.g., intelligence access control problems.

5. Numerical Results

In this section, we first demonstrate the effectiveness and convergence of our proposed QO2 algorithm. Further, the effect of different algorithm parameters on effectiveness and convergence is given. Then, we present performance comparison with several benchmarks from the perspective of sampling strategy. Finally, the QO2 algorithm is applied to an extended scenario with time-varying computation resource and task workloads to show its adaptability and robustness.

5.1. Simulation Setup

We conduct simulations in a Python 3.10.16 environment on a MacBook Air with an Apple M1 chip. If not specified, the below default simulation parameters are adopted:

• Communication parameters: We consider that $K=10$ UEs are randomly distributed within a $100\mathrm{m}\times 100\mathrm{m}$ area and a UAV is positioned at the center of the area at an altitude of $10\mathrm{m}$. Here, the free-space path loss model, i.e., $G_t{\left({\displaystyle \frac{3\times {10}^8}{4\pi f_c{d}_k}}\right)}^{\iota }$, is adopted to characterize path loss between UE k and ES, where $G_t=3$, $f_c=915$ MHz, and $\iota =3$ denote antenna gain, carrier frequency, and path loss exponent, respectively. In addition, the small-scale channel fading follows Rayleigh fading, i.e., $\mathcal{CN}(0,1)$, and the power density of noise is —174 dBm [55]. Moreover, we consider that there are $N=12$ uplink subchannels with equal bandwidth $W=2$ MHz. Finally, we set the maximum transmit power $P_{k,max}=2$ W, static transmit power $p_0=0.5$ W, inverse of power amplifier efficiency $\rho =2$, and uplink channel cost ${\beta }_k=1$.
• Computation parameters: Computational speed of UE $F_k$ and power coefficient are set as $1.0\times {10}^9$ cycles/s and $2.0\times {10}^{-26}$. Moreover, we set computation capacity of ES as $F_{max}=1.3\times {10}^{10}$ cycles/s [55].
• Application parameters: We set the input data size $I_k$ and its computation intensive degree ${\alpha }_k$ as 10 Mb and 100 cycles/bit, respectively.
• Preference parameters: We set ${\gamma }_k^T={\gamma }_k^E=1$. Additionally, we set $w_k=0.3$ if k is an odd number and $w_k=0.7$ otherwise.
• Algorithm parameters: We choose a fully connected DNN consisting of one input layer and two hidden layers with 120 and 80 hidden neurons, respectively, and one output layer in our proposed QO2 algorithm (the 2-layer architecture with 120 and 80 neurons was selected through a systematic hyperparameter search, which explored configurations with 1–3 layers and various neuron combinations. This configuration demonstrated optimal convergence and robustness across different parameter settings.). Via experiments, we finally set the memory size, batch size, training interval $\Delta$, and learning rate of Adam optimizer as 1024, 128, 5, and 0.01, respectively. Additionally, we set sample parameter $\upsilon$ as 1 to balance policy efficiency and stability.

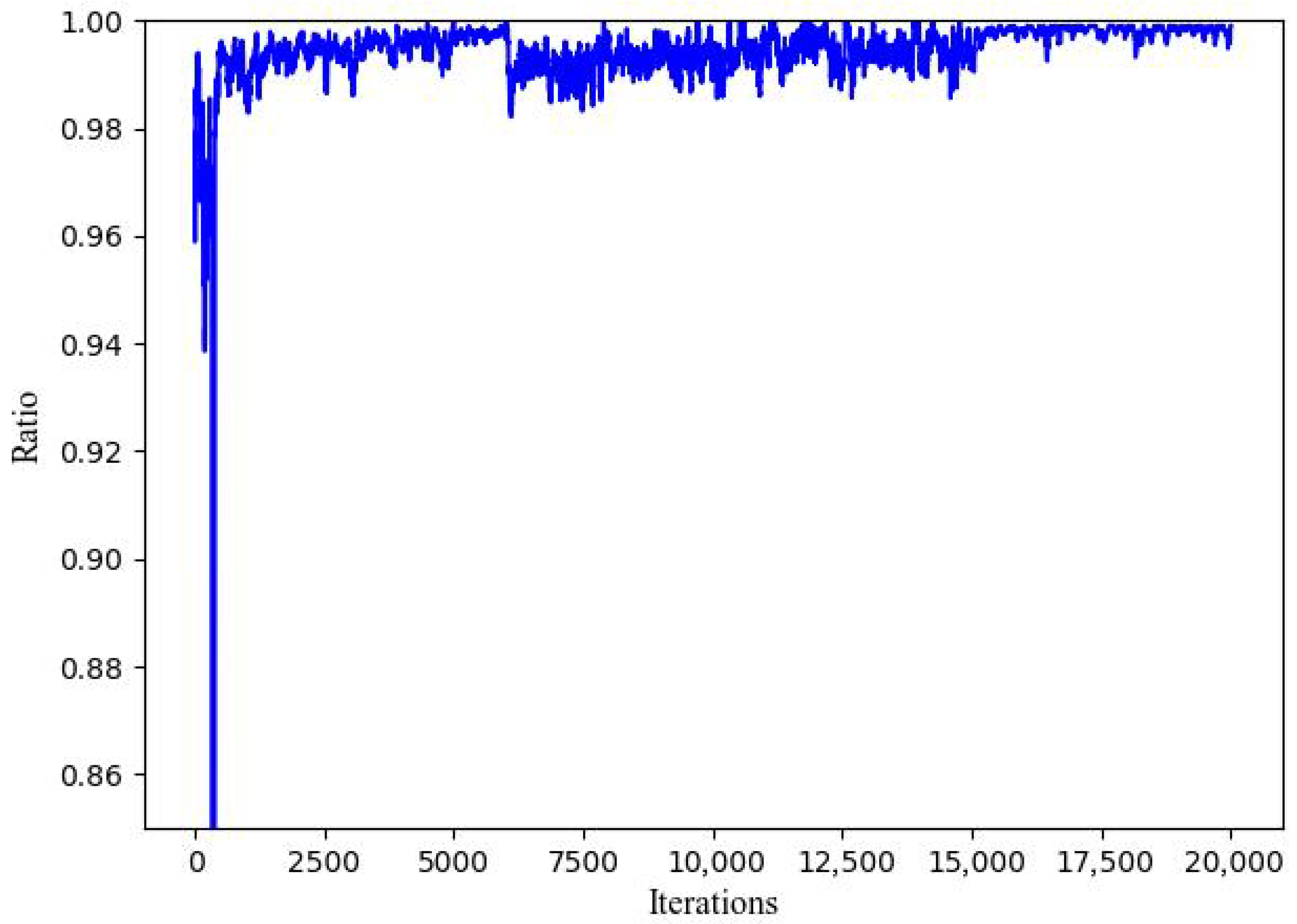
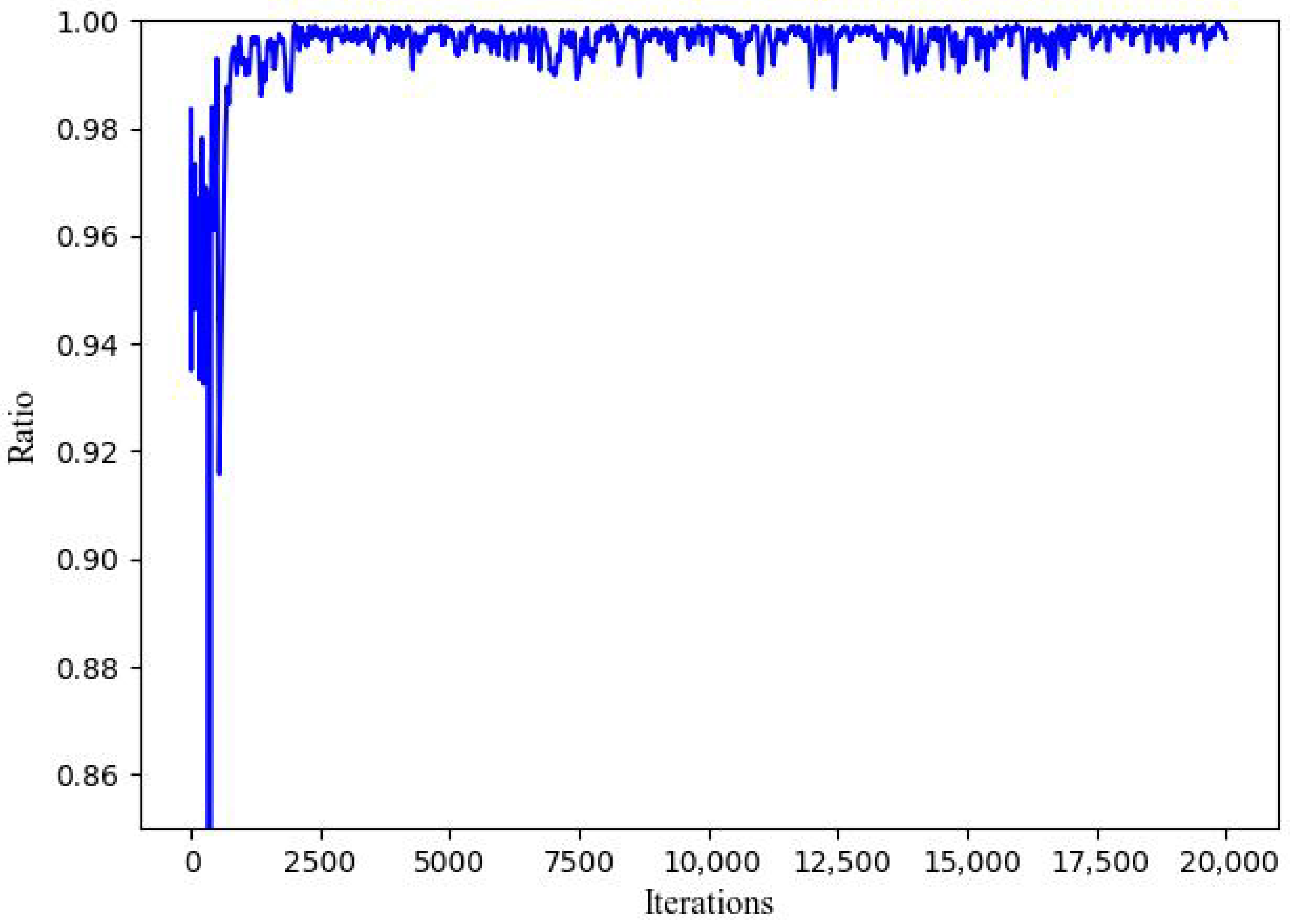
5.2. Convergence and Effectiveness Performance of QO2

We define a utility ratio to reveal the effectiveness of QO2 algorithm. Specifically,

$$Ratio={\displaystyle \frac{U^{*}({{\mathit{x}}_{\mathit{t}}}^{*},{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})}{{\displaystyle \underset{\overline{{\mathit{x}}_{\mathit{t}}}\in {\left\{0,1\right\}}^K}{max}}{U}^{*}(\overline{{\mathit{x}}_{\mathit{t}}},{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})}},$$

where $U^{*}({{\mathit{x}}_{\mathit{t}}}^{*},{\mathit{p}}_{\mathit{t}}^{*},{\mathit{f}}_{\mathit{t}}^{*}|{\mathit{h}}_{\mathit{t}})$ is obtained via QO2, while the optimal solution in the denominator is achieved by enumerating all the $2^K$ offloading actions. It is easy to see that $Ratio\in [0,1]$. The closer $Ratio$ is to 1, the better QO2 performs.

As Figure 2 shows, QO2 could converge to the state with ratio close to 1 within 5000 iterations, demonstrating its good performance in both convergence speed and effectiveness. Initially, since QO2 needs to interact with the environment to accumulate experience, the ratio starts at a relatively low level. However, with the number of iterations increasing, the ratio steadily improves and rapidly approaches 1. Notably, after about 2000 iterations, the ratio stabilizes around 1 with little fluctuation, which indicates that the offloading and resource-allocation decisions generated by QO2 are near-optimal.

Figure 3 and Figure 4 illustrate the impact of UE number K and subchannel number N on the convergence rate of QO2, respectively. We observed from Figure 3 that the larger K is, the slower QO2 converges. The reasons are for this related to the order-preserving and $L_0$-norm-limiting quantization method proposed in Section 4.2.2. Specifically, in each iteration, $K+1$ alternative offloading decisions are selected from all $2^K$ possible offloading decisions, and then the optimal offloading decision is determined based on Equation (10). Hence, as K increases, the probability that the optimal decision lies within this candidate set decreases, thereby requiring more iterations to approach the optimum. Figure 4 indicates that the smaller N is, the faster QO2 converges. This is because that a smaller N means that less UE could choose to offload simultaneously, effectively reducing the decision space. With fewer available options, the algorithm requires fewer iterations to reach the optimal state.

In Figure 5, we investigate how key hyperparameters influence on QO2’s performance. Observed from Figure 5a that convergence and effectiveness performance of QO2 are relatively insensitive to memory size. This is mainly attributed to our proposed PPS, which could consistently pick the most useful data to update the policy. Considering both convergence speed and effectiveness, we adopt a memory size of 1024 in the following simulations. Figure 5b shows the effect of batch size. Overly large batches (=1024) tend to include redundant data, while very small ones (=32) fail to fully utilize stored samples, both leading to slower convergence. Additionally, large batches increase computational cost. To strike a balance between training efficiency and speed, the batch size is set to 128. In Figure 5c, the effect of training interval is examined. In theory, the smaller the value, the more updates of QO2. However, our findings suggest that overly frequent DNN training provides limited benefit. Thus, we set $\Delta$ as 5. Finally, Figure 5d presents the influence of the learning rate in the Adam optimizer. An excessively small learning rate (=0.00001) would converge QO2 to suboptimal solution, and thus suffer lower ratio. In the following simulations, we set the learning rate as 0.01. Sensitivity analysis reveals that performance of QO2 remains relatively stable with moderate variations in most hyperparameters (e.g., memory size 256–1024, learning rate 0.001–0.01, batch size 64–256), while training interval and extremely small learning rates (<0.001) show higher sensitivity. To sum up, the final settings for memory size, batch size, $\Delta$, and learning rate are 1024, 128, 5, and 0.01, respectively.

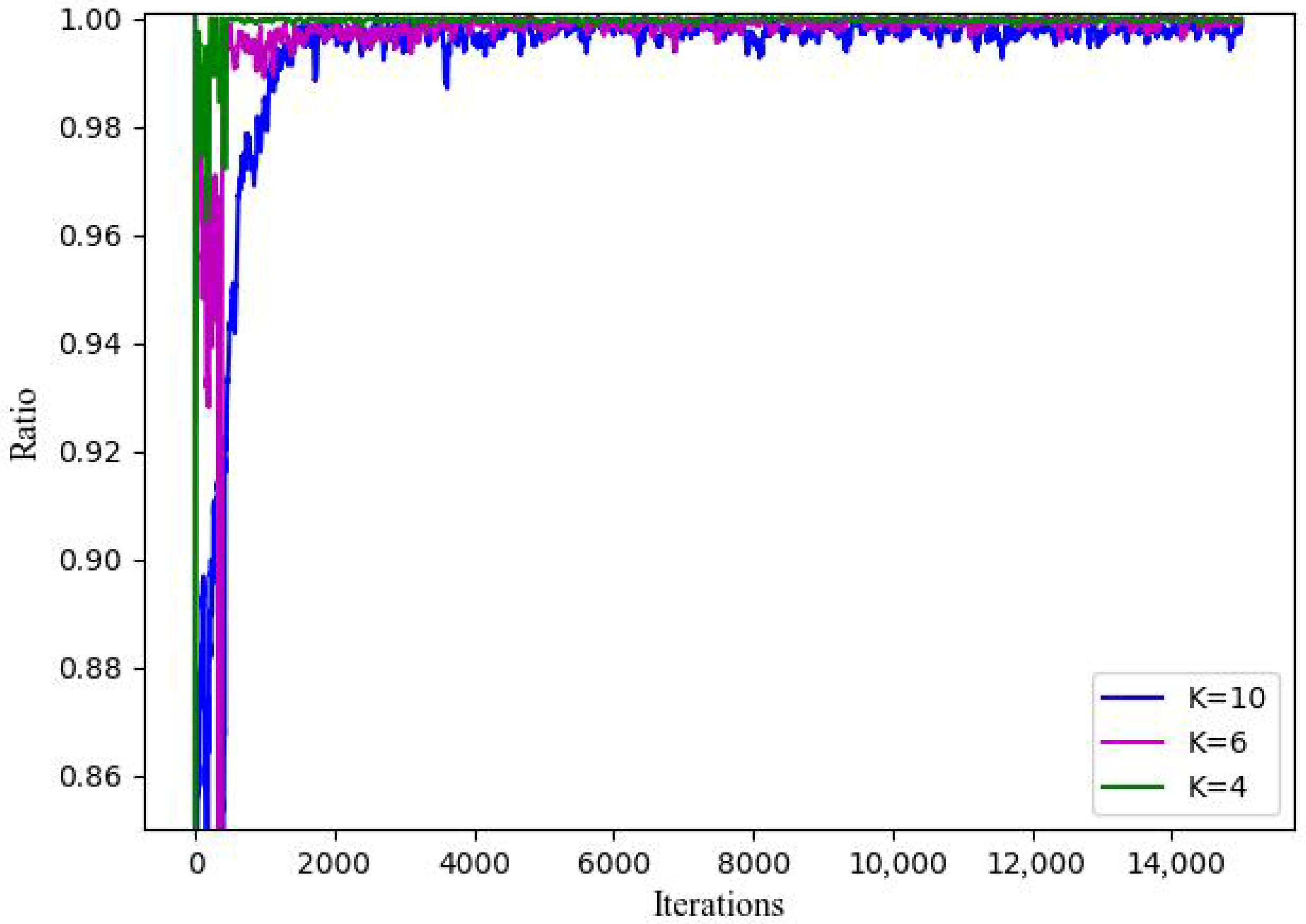
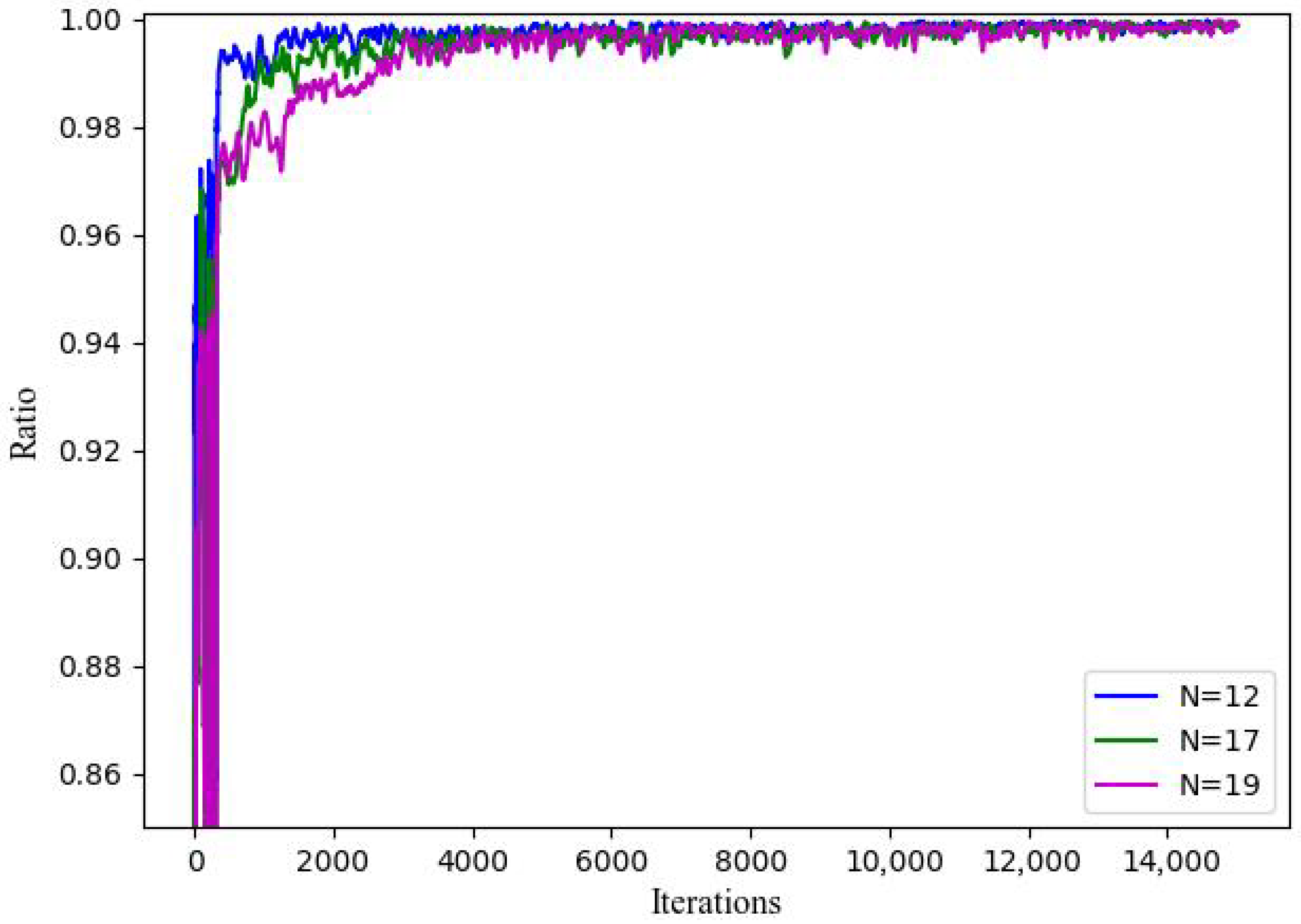
5.3. Adaptability Performance of QO2

Figure 6 and Figure 7 present the performance of the QO2 algorithm as the total computational speed of the edge server changes. Two scenarios are simulated: an abrupt change in the computing rate and periodic fluctuations. In the first scenario, the initial total computing rate is set to $F=1.3\times {10}^{10}$. At iteration 6000, the computing rate is reduced to $F=1.0\times {10}^{10}$, and at iteration 15,000, it is restored to its original value. As shown in Figure 6, the benefit ratio drops significantly following the reduction at iteration 6000 but quickly recovers and converges. A similar pattern is observed at iteration 15,000. In the second scenario, the initial computing rate remains $F=1.3\times {10}^{10}$, but it fluctuates within a 10% range, cycling through values of $1.3\times {10}^{10}$, $1.15\times {10}^{10}$, and $1.45\times {10}^{10}$. As depicted in Figure 7, despite these periodic changes, the impact on QO2’s convergence is minimal, with the benefit ratio exhibiting only slight fluctuations.

Figure 8 further shows the performance of the QO2 algorithm when the task data size varies periodically. The initial task data size is set to $1.0\times {10}^7$, and it fluctuates within a 10% range, cycling between $1.0\times {10}^7$, $0.9\times {10}^7$, and $1.1\times {10}^7$. As illustrated in Figure 8, QO2 consistently converges to a benefit ratio near 1 with only minor fluctuations, even under varying task sizes.

Overall, these results indicate that the QO2 algorithm is robust to environmental variations: the more drastic the change, the longer it takes to re-converge, whereas mild changes require only a few iterations. This aligns with practical intuition and demonstrates QO2’s capability to sustain near-optimal offloading decisions under dynamic conditions. Note that the adaptability to dynamic environments constitutes a core contribution of QO2. Unlike static heuristics that prioritize computational simplicity at the cost of environmental responsiveness, QO2 is designed to provide adaptive decision-making capability while maintaining reasonable computational overhead. This design trade-off is crucial for time-varying edge-computing scenarios.

5.4. Performance of Sampling Method

Figure 9 analyze the impact of different sampling methods used during the training of DNNs on the convergence and performance of QO2. Here, we compare PPS strategy with three alternative methods:

• Priority Sampling (PS): Selects the most recent experiences equal to the batch size from memory.
• Random Sampling (RS): Randomly selects experiences equal to the batch size from all stored experiences.
• Probability-first Random Sampling (PRS): Sets the sampling probability for each experience based on its sampling frequency, then chooses a batch of experiences according to these probabilities.

As shown in Figure 9, the benefit ratio curves for all four sampling methods eventually converge to 1. However, the convergence performance of the PS and RS methods are relatively poor. The PS method suffers from low diversity of experiences, while the RS method, despite its high diversity, often includes outdated or less relevant experiences, thus requiring more training data to reach optimal convergence. In contrast, the PRS and PPS methods demonstrate better convergence performance.

Figure 9. Convergence performance of different sampling methods.

Figure 9. Convergence performance of different sampling methods.

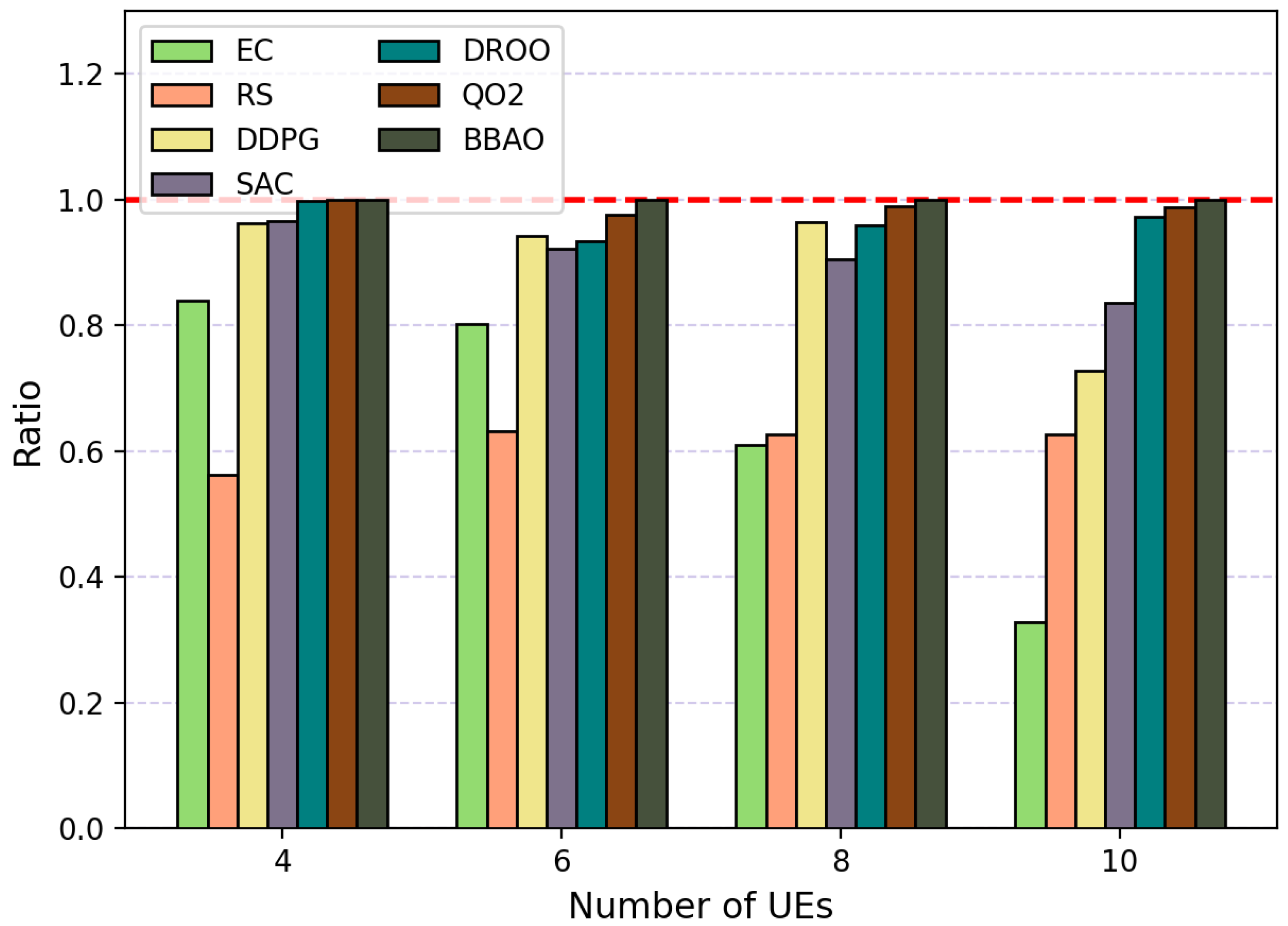
5.5. Performance Comparison

Here, we compare our QO2 algorithm with representative benchmarks as follows:

• Edge computing (EC): All tasks are offloaded.
• Random scheduling (RS): All UE are randomly offloaded to the UAV.
• Branch-and-bound-aided offloading (BBAO) [39]: The branch-and-bound approach is utilized to obtain offloading decisions.Specifically, BBAO uses identical system parameters as other algorithms. For each time slot, it exhaustively enumerates all feasible resource allocations via depth-first search (DFS), computes the system rate for each allocation using the bisection method, and selects the allocation with maximum utility as the optimal solution. This process provides a near-optimal benchmark for performance comparison.
• Deep Reinforcement learning-based Online Offloading (DROO) [50]: DROO algorithm utilizes DRL technique to obtain offloading decision, where random sampling strategy is adopted in the policy update phase.
• Soft-actor–critic method (SAC) [46] scheme: Taking the wireless channel gain between the UE and the edge server as input, use SAC to output binary offloading decisions, and obtain the optimal system utility as a reward to train the SAC policy.
• Deep deterministic policy gradient (DDPG) [44] scheme: Similar to SAC scheme, use DDPG to take the wireless channel gain as input to output binary offloading decisions, and obtain the optimal system utility to train the DDPG policy (to ensure a relatively fair comparison, SAC and DDPG are integrated into QO2 framework via replacing the DNN component, rather than being standalone implementations of the original algorithm).

As shown in Figure 10, we compare convergence performance of various algorithms versus different numbers of UE. Notably, the QO2 algorithm exhibits performance comparable to BBAO, while outperforming the other five algorithms. This is primarily due to QO2’s consideration of additional dimensions, which significantly enhances its performance over EC and RS. Furthermore, unlike actor–critic algorithms such as DDPG and SAC, the QO2 algorithm directly employs a reward function, rather than relying on a critic network, to evaluate the actor. This design enables the objective function to accurately assess the value of the current action based on the true outcomes observed in the environment, thereby delivering superior performance compared to SAC and DDPG. Compared with DROO, QO2 further benefits from its efficient sampling method during experience replay, which enables its ability to leverage historical interactions and produce more effective offloading decisions.

Figure 11 illustrates the time consumption of each algorithm under varying numbers of UEs, presented in two sub-graphs for clarity. Figure 11b is a locally enlarged version of Figure 11a. In Figure 11a, we find that as the scale of UE increases, the computational complexity of BBAO escalates dramatically, while SAC and DDPG exhibit a more moderate growth but still require substantially more time than the other algorithms. Figure 11b indicates that although QO2’s time consumption is slightly higher than that of EC and RS, it remains within a controllable range. Moreover, the time consumption of QO2 is lower than DROO, demonstrating its superior computational efficiency.

To further demonstrate the computational efficiency advantage of QO2, Figure 12 compares the convergence performance of four algorithms (QO2, DROO, DDPG, and SAC) versus total computation time. For fair comparison, the 10,000 iteration cycles are converted into their corresponding wall-clock time consumption. The results in Figure 12 reveal that QO2 exhibits remarkably rapid convergence, achieving a ratio of approximately 0.99 within merely 10 s. In contrast, DDPG and SAC require approximately 100 and 200 s, respectively, representing 10× and 20× longer computation times to attain comparable performance. Although DROO demonstrates faster initial convergence, its overall time consumption remains similar to that of QO2. These results confirm that QO2 not only achieves near-optimal performance but also demonstrates superior timeliness, making it particularly well-suited for time-sensitive edge-computing scenarios where rapid decision-making is critical.

As shown in Figure 10, Figure 11 and Figure 12, the proposed QO2 algorithm demonstrates computational efficiency suitable for quasi-static to moderately dynamic channel conditions, achieving high-quality approximate solutions through adaptive early stopping. Deployment feasibility in highly dynamic scenarios depends on hardware capabilities and application-specific latency requirements.

6. Conclusions and Future Work

This paper addressed the offloading timeliness in UAV-EC systems. By leveraging deep neural networks, we proposed a novel QO2 algorithm, optimizing offloading decisions, transmit power, and resource allocation to improve system performance. Furthermore, we designed a PPS strategy to enhance the robustness of QO2. Finally, simulation results validated that QO2 could achieve fast convergence and reduce re-convergence time.

While QO2 demonstrates outstanding performance, several limitations still exist. (1) DNN architecture is designed for a fixed number of UE K. When K changes, the network requires retraining, which limits its deployment flexibility. Promising solutions include permutation-invariant architectures, meta-learning techniques, and transfer learning. (2) Performance validation relies solely on simulation-based analysis rather than empirical measurements under real channel dynamics. Future work should incorporate hardware acceleration and real-world testbeds to validate real-time performance under practical channel coherence time constraints and diverse mobility scenarios. (3) This work focuses on single-UAV deployments to establish algorithmic fundamentals. While the core QO2 framework could potentially extend to multi-UAV scenarios, such extensions introduce additional algorithmic challenges, including user association, inter-UAV coordination, and distributed decision-making architectures.