Cooperative Encirclement and Obstacle Avoidance of Fixed-Wing UAVs via MADDPG with Curriculum Learning

Highlights

What are the main findings?

• The proposed curriculum-learning-based MADDPG framework effectively im-proves the training stability and convergence efficiency in cooperative fixed-wing UAV encirclement tasks.
• Experimental results show that fixed-wing UAVs achieve over 95% encirclement success rates in simple environments and maintain above 70% success rates in complex environments with obstacles and moving targets.

What is the implication of the main finding?

• The study demonstrates that curriculum learning is a practical solution for over-coming sparse rewards, local optima, and high task complexity in UAV swarm training.
• The proposed approach provides a promising pathway for applying cooperative reinforcement learning to real-world UAV systems operating in dynamic and high-risk environments.

Abstract

Multi-UAV cooperative encirclement tasks have attracted considerable attention in areas such as military defense and target interception. Fixed-wing UAVs face substantial challenges due to intrinsic dynamic limits, including their minimum velocity and turning radius, particularly when engaging evasive target and navigating in obstacle environments. This paper presents a hybrid deep reinforcement learning approach, in which a cooperative task environment is developed for fixed-wing UAVs that jointly integrates encirclement and obstacle avoidance. A composite MADDPG framework enhanced with curriculum learning is designed, employing progressive task staging and reward optimization to accelerate convergence and improve policy stability. Simulation results demonstrate that the proposed method achieves single-step encirclement success rates exceeding 80% in complex environments, while maintaining 10-step success rates around 70%, thereby strengthening both encirclement capability and obstacle avoidance safety in fixed-wing UAV swarm. This study provides new insights into the intelligent cooperative control of fixed-wing UAVs in high-risk missions.

1. Introduction

In recent years, unmanned aerial vehicles (UAVs) have played a significant role in various military operations, including the Russia–Ukraine conflict, and have become a pivotal force in modern warfare [1]. Owing to their affordability, rapid deployment, and high maneuverability, UAVs have been widely applied in surveillance [2], search [3], communication [4], and transportation [5]. Nevertheless, an individual UAV is inherently limited by restricted payload capacity, short endurance, and constrained onboard functionality [6], making it challenging to accomplish diverse missions in complex environments. In contrast, multiple UAVs can achieve enhanced flexibility, robustness, and broader task coverage through cooperative sensing, distributed decision-making, and task allocation [7], thus becoming a research frontier in intelligent control and swarm intelligence.

With the rapid development of deep reinforcement learning (DRL) [8], multi-agent deep reinforcement learning (MADRL) has been increasingly applied to UAV encirclement tasks, aiming to overcome the limitations of traditional rule-based and model predictive control approaches in high-dimensional, nonlinear, and adversarial environments [9]. Early studies such as Value-Decomposition Networks (VDN) [10] and QMIX [11] enabled multi-agent cooperation through value function decomposition, which proved effective in discrete action spaces. However, these approaches cannot be directly applied to physical systems with continuous control inputs, such as UAVs. To address this issue, Lowe et al. proposed Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [12], which incorporates the centralized training and decentralized execution (CTDE) paradigm. This framework allows multiple agents to efficiently perform cooperative learning and dynamic coordination in continuous action spaces. Owing to these advantages, MADDPG has shown strong potential in UAV swarm control, formation, and encirclement. Subsequently, variants such as COMA [13] and MAPPO [14] were developed to improve credit assignment and stability; nevertheless, MADDPG remains one of the most representative and practical policy gradient methods in continuous UAV control.

Encirclement (pursuit–evasion) is a representative multi-agent cooperative control problem with critical applications in battlefield target interception, counter-UAV operations, and sensitive area defense [15]. The encirclement task requires UAV swarm to jointly capture a maneuverable target in complex scenarios, which poses high demands on maneuverability, task allocation, and global coordination. For example, Du et al. [16] applied curriculum learning with multirotor UAVs to achieve cooperative encirclement of intruders in urban airspace. Fang et al. [17] investigated the interception of a high-speed evader by distributed encircling UAVs, confirming the advantages of decentralized control in high-speed environments. Zhang et al. [18] proposed the GM-TD3 algorithm for intercepting high-speed targets with multiple fixed-wing UAVs in obstacle-rich environments, further enhancing stability and coordination.

In complex environments, UAV swarm must achieve mission objectives while avoiding collisions with both environmental obstacles and teammates. Traditional obstacle avoidance methods, such as geometric approaches, artificial potential fields, and optimization-based control, are often limited in handling high-dimensional continuous state–action spaces and are prone to local optima in unstructured environments [19]. In contrast, MADRL-based methods have demonstrated stronger adaptability and flexibility. Xiang and Xie [20] introduced coupled rules in adversarial tasks, significantly improving the success rate of UAV swarm. Li et al. [21] proposed a dual-layer experience replay mechanism to enhance policy generalization. Zhao et al. [22] combined meta-learning with MADDPG and proposed the MW-MADDPG framework to strengthen group decision-making. Cao and Chen [23] incorporated attention mechanisms into MADDPG, accelerating convergence and improving decision accuracy. Xie et al. [24] addressed obstacle avoidance for multirotor UAV formations in environments with static and dynamic obstacles, demonstrating the adaptability of DRL in diverse scenarios.

In addition to task complexity, UAV platform characteristics are also critical to cooperative control. Multirotor UAVs, while offering hovering and high maneuverability, are limited in range and speed, making them unsuitable for high-speed encirclement. By contrast, fixed-wing UAVs have distinct advantages in endurance and velocity, making them more suitable for long-range cruising and fast target interception [25]. However, fixed-wing UAVs also introduce nonlinear and coupled challenges due to constraints such as minimum speeds, minimum turning radii, and inability to hover [26]. To address these challenges, DRL methods have been increasingly applied to fixed-wing UAV decision-making and control. For example, Yan et al. [27] proposed the PASCAL algorithm, which integrates curriculum learning with MADRL to achieve collision-free formation flight of large-scale fixed-wing UAV swarms. Yan et al. [28] further enhanced efficiency and scalability by employing attention-based DRL with parameter sharing. Zhuang et al. [29] studied penetration strategies for high-speed fixed-wing UAVs, validating the effectiveness of DRL in maneuvering tasks. Li et al. [30] combined DQN with PID control for autonomous longitudinal landing, demonstrating the potential of DRL in low-level flight dynamics control.

Despite these advances, several limitations remain. First, many studies focus on single-task scenarios, such as those that involve only encirclement or only obstacle avoidance, whereas real-world missions typically require UAVs to simultaneously execute multiple tasks, including encirclement, obstacle avoidance, and formation maintenance. Second, although curriculum learning has shown promise in improving training efficiency and convergence in MADRL [31], its application to fixed-wing UAV cooperative missions remains underexplored, particularly in terms of systematically integrating composite tasks with dynamic constraints.

Based on the above background, this paper proposes a composite deep reinforcement learning method with curriculum learning to address the challenges faced by fixed-wing UAV swarm in simultaneously executing encirclement and obstacle avoidance tasks in complex environments. The main contributions are summarized as follows:

• Task modeling: A cooperative multi-agent fixed-wing UAV environment is developed, integrating encirclement and obstacle avoidance with realistic fixed-wing dynamics, maneuverable multirotor evaders, and laser-based local perception;
• Method design: A composite MADDPG framework enhanced with curriculum learning is introduced, employing progressively staged tasks and reward optimization to accelerate convergence and enhance policy generalization;
• Performance validation: Comparative experiments are conducted in a simulation environment, evaluating metrics such as encirclement duration, capture success rate, and obstacle avoidance safety rate, thereby verifying the effectiveness and superiority of the proposed method in complex scenarios.

2. Problem Formulation

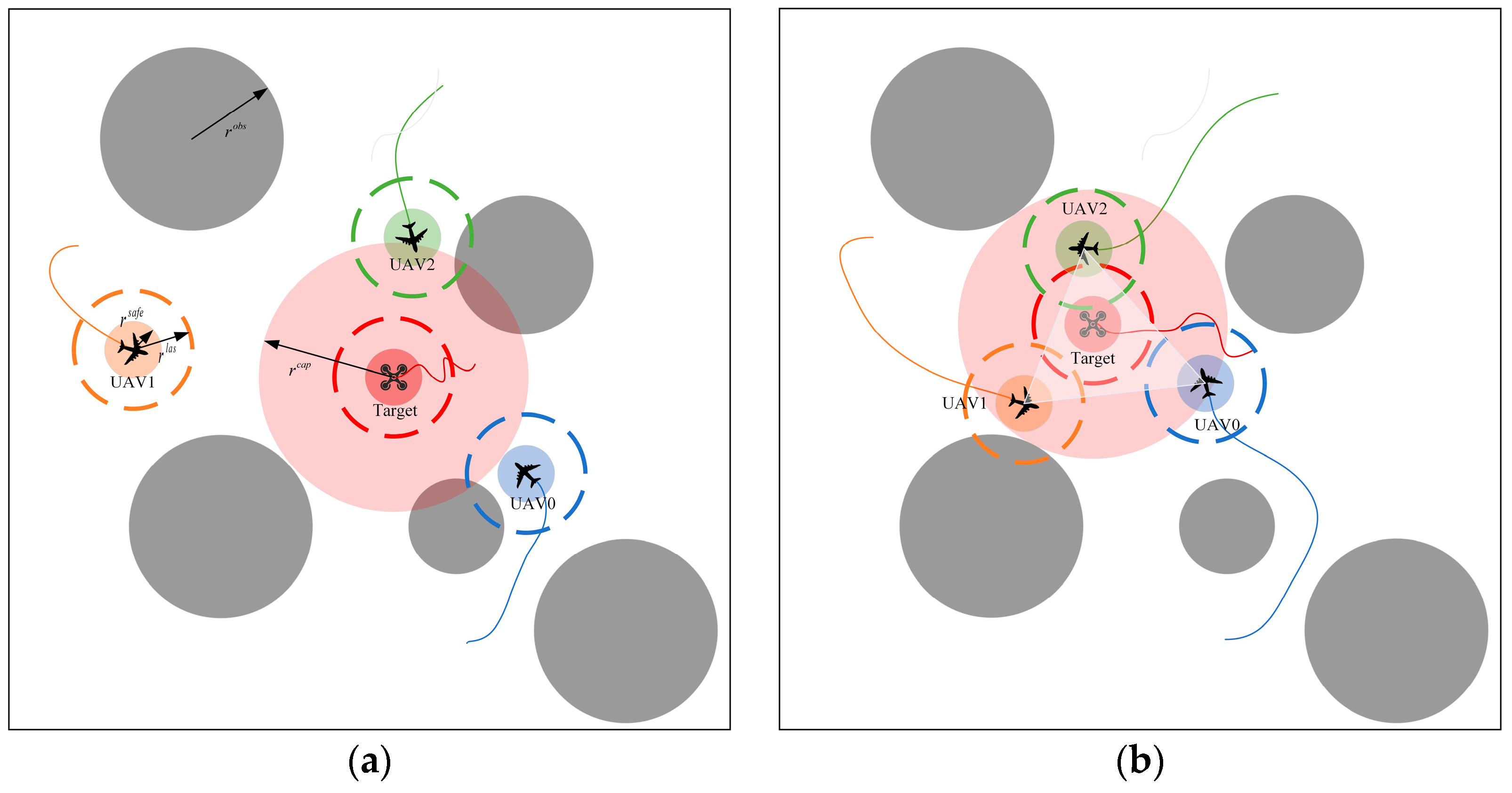
This paper investigates multi-agent deep reinforcement learning (MADRL) for encirclement tasks in obstacle-rich environments, focusing on a scenario where multiple fixed-wing UAVs encircle a multirotor UAV. At the beginning of each episode, the positions and orientations of the UAVs, as well as the positions and radius of the obstacles, are randomly initialized. The scenario setup is illustrated in Figure 1a. The pursuit is considered successful only if all fixed-wing encircling UAVs (UAVs_e), without collision or leaving the bounded area, are able to keep the multirotor target UAV (UAV_t) within the capture range for a specified number of steps, as illustrated in Figure 1b.

The environment is modeled as a rectangular area with dimensions $\left[W,H\right]$. The UAVs_e swarm consists of $N^{enc}$ agents, where the position of the $i$-th fixed-wing UAV is $p_i^{enc}=\left(x_i^{enc},y_i^{enc}\right),$ and its safety radius is denoted as $r^{safe}$. The UAV_t is defined as the target, whose position is represented as $p^{tar},$ with a capture radius $r^{cap}$.

The environment also contains multiple clusters of trees and restricted zones, abstracted as static circular obstacles. The total number of obstacles is $N^{obs}$, where the center of the $j$-th obstacle is denoted as $p_j^{obs},$ and its radius as $r_j^{obs}.$

The perception of each UAV is modeled using laser beams. A total of $N^{las}$ beams are employed, with a detection range of $L$. The direction of the $k$-th beam is denoted as ${\theta }_k^{las}$, and its detected distance is given by $r_k^{las}$.

2.1. UAV Modeling

Establishing the UAV motion equations involves coordinate transformations. The ground coordinate system $Oxy{z}^{(g)}$ is fixed on the Earth, defined according to the North-East-Down convention, with its origin located at the takeoff point. The $O{x}^{(g)}$ axis points north, the $O{z}^{(g)}$ axis points vertically downward, and the $O{y}^{(g)}$ axis is perpendicular to the $Ox{z}^{(g)}$ plane, pointing east.

The trajectory coordinate system $Oxy{z}^{(k)}$ has its origin at the UAV’s center of mass. The $O{x}^{(k)}$ axis is aligned with the velocity direction, $O{z}^{(k)}$ lies in the vertical plane containing $O{x}^{(k)}$, perpendicular to $O{x}^{(k)}$, and points downward, while $O{y}^{(k)}$ is perpendicular to the $Ox{y}^{(k)}$ plane and points to the right.

The primary forces acting on a fixed-wing UAV originate from engine thrust and aerodynamic forces. Aerodynamic forces depend on the deflection angles of ailerons, rudder, and elevator, as well as the UAV’s airspeed and body shape. Neglecting the three-dimensional attitude of the fixed-wing UAV, the acceleration in the trajectory coordinate system is simplified as:

$$\left\{\begin{array}{l}{a}_x^{(k)}={\displaystyle \frac{F_T-F_D-F_g\sin \gamma }{m}}\hfill \\ a_y^{(k)}={\displaystyle \frac{F_Y}{m}}\hfill \\ a_z^{(k)}={\displaystyle \frac{F_L-F_g\cos \gamma }{m}}\hfill \end{array}\right.$$

(1)

where the flight path angle $\gamma$ is defined as the angle between the $O{x}^{(k)}$ axis and the $Ox{y}^{(g)}$ plane, positive upward; thrust $F_T$ is generated by the engine along the body $x$ axis; drag $F_D$ opposes the velocity direction; gravity $F_g$ has magnitude $mg$ and points vertically downward; lift $F_L$ is generated by the wings and is perpendicular to the incoming airflow; lateral force $F_Y$ is generated by banking and yaw control surfaces. The coordinate system together with the force and attitude angles is illustrated in Figure 2.

In the simplified model, the velocity coordinate system coincides with the body coordinate system, and the flight altitude is assumed low, with the ground approximated as a plane. The transformation matrix from the trajectory coordinate system to the ground coordinate system is given by:

$$\begin{gathered} L_{gk}=L_z(\chi )L_y(\gamma )=\left[\begin{array}{ccc}\cos \gamma \cos \chi & -\sin \chi & \sin \gamma \cos \chi \\ \cos \gamma \sin \chi & \cos \chi & \sin \gamma \sin \chi \\ -\sin \gamma & 0& \cos \gamma \end{array}\right] \\ {L}_x=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & \sin \theta \\ 0& -\sin \theta & \cos \theta \end{array}\right] L_y=\left[\begin{array}{ccc}\cos \theta & 0& -\sin \theta \\ 0& 1& 0\\ \sin \theta & 0& \cos \theta \end{array}\right] L_z=\left[\begin{array}{ccc}\cos \theta & \sin \theta & 0\\ -\sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right] \end{gathered}$$

(2)

where the heading angle $\chi$ is defined as the angle between the projection of the $O{x}^{(v)}$ axis onto the $Ox{y}^{(g)}$ plane and the $O{x}^{(g)}$ axis, positive to the right, and $L_x$, $L_y$, $L_z$ are the rotation matrices about the $x$, $y$, and $z$ axes, respectively.

The UAV velocity can be expressed as:

$${\displaystyle \frac{d{v}^{(g)}}{dt}}=L_{gk}\left[\begin{array}{c}{a}_x^{(k)}\\ a_y^{(k)}\\ a_z^{(k)}\end{array}\right]$$

(3)

Since the $O{z}^{(g)}$ axis in the ground coordinate system points downward, which is opposite to the figure coordinate system $Oxy{z}^{(f)}$ used for visualization in which the $O{z}^{(f)}$ axis points upward, the final plotting requires the following transformation:

$$L_{fg}=L_x(\pi )$$

(4)

For multirotor UAVs, the kinematic equations in the image coordinate system are directly employed for modeling.

To reduce computational complexity and highlight the core design of the control algorithm, all UAV dynamic models in this study are based on simplified assumptions, without considering actuator dynamics, wind field effects, or six-degree-of-freedom (6 DoF) coupling.

2.2. Constraint Settings and State Calculation

In reality, the magnitude of forces and the payload capacity of UAVs are limited, so velocity cannot change abruptly. In this study, the motion space is defined in terms of acceleration, and the acceleration vector is constrained as:

$$\begin{gathered} a=\mathrm{clip}(a,a_{\min },a_{\max }) \\ \mathrm{clip}(x,a,b)=\max \left\{\min \right\{x,b\},a\},a\le b \end{gathered}$$

(5)

where $\mathrm{clip}(\cdot )$ denotes the interval clipping function, which saturates the value to the boundary if it exceeds the upper or lower limits. The maximum and minimum accelerations along the three axes differ for fixed-wing UAVs, while they are identical for multirotor UAVs. The simplified computation of acceleration limits is given by:

$$\left\{\begin{array}{l}{\left|a_x^{fix}\right|}_{\max }^{(k)}={\displaystyle \frac{V_{\max }-V_{\min }}{\kappa \cdot \Delta t}}\hfill \\ {\left|a_y^{fix}\right|}_{\max }^{(k)}={\displaystyle \frac{V_{\max }^2}{r_{\min }}}\hfill \end{array}\right.,{\left|a^{tar}\right|}_{\max }^{(f)}={\displaystyle \frac{V_{\max }^{tar}-V_{\min }^{tar}}{{\kappa }^{tar}\cdot \Delta t}}$$

(6)

where $\Delta t$ denotes the time step, $\kappa$ the time scaling coefficient, $V_{\max }$ and $V_{\min }$ the maximum and minimum UAV speeds, respectively, and $r_{\min }$ the minimum turning radius.

For multirotor UAVs, the minimum speed is 0. For fixed-wing UAVs, a certain forward flight speed is required, so the velocity range is limited. The speed magnitude is constrained as:

$$\begin{gathered} v(t+1)={\mathrm{sat}}_{[V_{\min },V_{\max }]}(v(t)+a(t)\Delta t) \\ {\mathrm{sat}}_{[a,b]}(z)={\displaystyle \frac{\mathrm{clip}(\Vert z\Vert ,a,b)}{\Vert z\Vert }}z \end{gathered}$$

(7)

where ${\mathrm{sat}}_{[\cdot ,\cdot ]}(\cdot )$ is the velocity saturation operator that limits the speed magnitude within $[V_{\min },V_{\max }]$. The discrete-time position update is given by:

$$p(t+1)=p(t)+v(t+1)\Delta t$$

(8)

2.3. Laser-Based Environment Perception

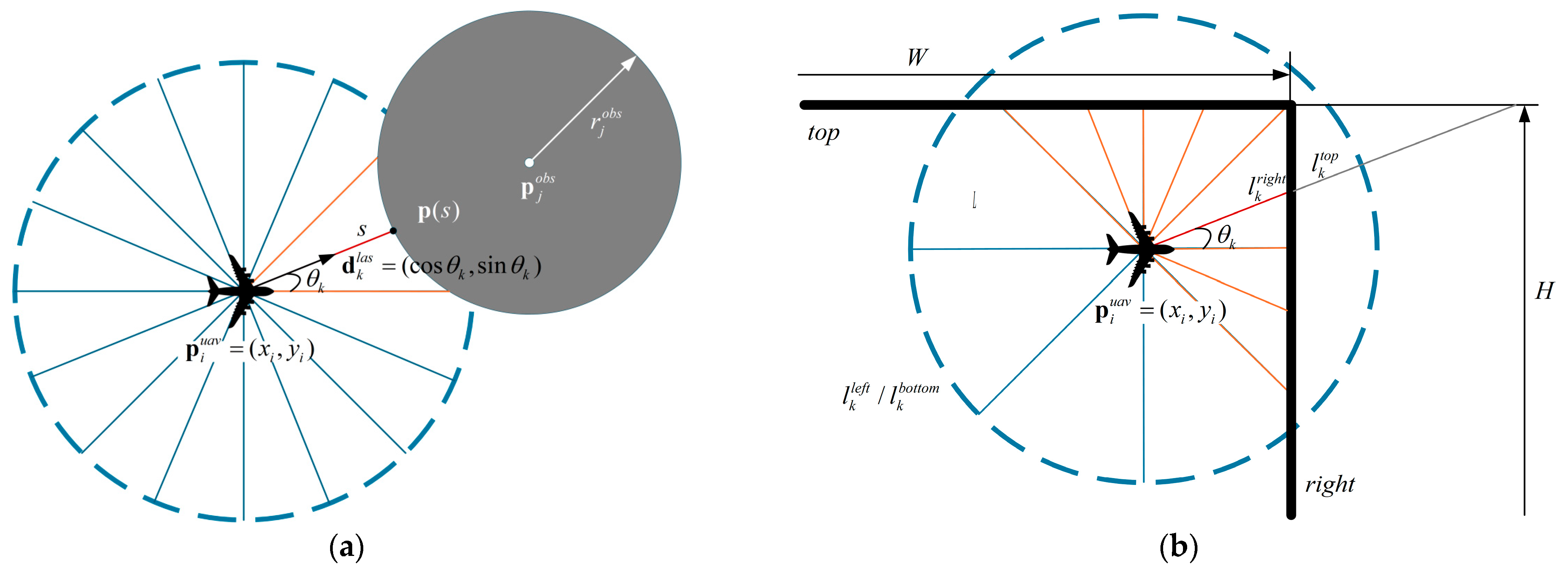
The core of radar-based detection is to acquire spatial information by analyzing the interaction between electromagnetic waves and targets or the environment. In this work, to ensure computational efficiency while maintaining reasonable positioning accuracy, the radar beam propagation and environmental obstacles are geometrically simplified, allowing real-time computation of beam lengths at different angles.

The simplified model abstracts the radar-emitted electromagnetic waves as straight rays of length $L$, divided into $N^{las}$ beams.

Figure 3a shows the intersections of laser rays with circular obstacle. Using analytic geometry, the intersection points between the $k$-th ray and the surface of the $j$-th obstacle are obtained by solving the corresponding system of Equation (9):

$$\Vert p(s)-p_j^{obs}{\Vert }^2={\left(r_j^{obs}\right)}^2,p(s)=p_i^{uav}+s{d}_k^{las},t\ge 0$$

(9)

where $p(s)$ denotes the intersection point coordinates between the UAV laser ray and the circular obstacle, $d_k^{las}$ is the direction vector of the laser, and $s$ is the parameterized distance along the ray.

For a rectangular environment with radar-detectable boundaries, the intersections of the ray with the top, bottom, left, and right boundaries are evaluated individually:

$$\left\{\begin{array}{c}{l}_k^{top}={\displaystyle \frac{H-y_i^{uav}}{\sin {\theta }_k^{las}}},\sin {\theta }_k^{las}>0\\ l_k^{bottom}={\displaystyle \frac{-y_i^{uav}}{\sin {\theta }_k^{las}}},\sin {\theta }_k^{las}<0\\ l_k^{right}={\displaystyle \frac{W-x_i^{uav}}{\cos {\theta }_k^{las}}},\cos {\theta }_k^{las}>0\\ l_k^{left}={\displaystyle \frac{-x_i^{uav}}{\cos {\theta }_k^{las}}},\cos {\theta }_k^{las}<0\end{array}\right.$$

(10)

As an example, Figure 3b illustrates the intersection points with the top and right boundaries.

Since a ray may be intercepted by nearby obstacles first, the minimum distance is taken as the real-time ray length:

$$l_k=\min {\{L,l^{top},l^{bottom},l^{right},l^{left},s\}}_k$$

(11)

3. Proposed Method

This section first introduces the basic modeling approach for multi-UAV collision avoidance, i.e., the Partially Observable Markov Game (POMG), and defines the state space, action space, and reward function within this framework. Subsequently, the application mechanism of Multi-Agent Deep Deterministic Policy Gradient (MADDPG), a representative framework in MADRL, is presented for collaborative pursuit and obstacle avoidance tasks.

Furthermore, the concept of Curriculum Learning (CL) is incorporated, employing a graded environment difficulty design and dynamic task scheduling to significantly enhance training stability and the generalization capability of learned policies. Based on this idea, a curriculum-learning-enhanced composite multi-agent deep reinforcement learning algorithm (MADRL_CL), is proposed.

This method not only effectively addresses collision avoidance and pursuit challenges of fixed-wing UAVs in highly dynamic target and complex obstacle environments, but also demonstrates advantages in collaboration efficiency and learning convergence.

3.1. MADRL

3.1.1. POMG

The multi-UAV collaborative obstacle avoidance and pursuit problem is a typical cooperative MADRL task. It is commonly modeled as a POMG [32], formally defined as an 8-tuple:

$$\mathcal{M}=(\mathcal{N},\mathcal{S},\mathcal{A},\mathcal{O},P,R,O,\gamma )$$

(12)

where $\mathcal{N}=\{1,\dots ,n\}$ denotes the set of agents; $\mathcal{S}={\displaystyle \prod _{i=1}^n{\mathcal{S}}^i}$ is the joint state space; $\mathcal{A}={\displaystyle \prod _{i=1}^n{\mathcal{A}}^i}$ is the joint action space; $\mathcal{O}={\displaystyle \prod _{i=1}^n{\mathcal{O}}^i}$ is the joint observation space; $R$ is the joint reward function; $P$ is the state transition probability function; $O$ is the observation function; and $\gamma \in [0,1)$ is the discount factor.

At each time step $t\in \mathbb{N}$, each agent $i\in \mathcal{N}$ receives a local observation $o_t^i~O^i(\cdot \mid s_t)$ from the environment and selects an action $a_t^i~{\mu }^i(\cdot \mid o_t^i)$ according to its policy. All agents act simultaneously without sequential dependencies. The joint action $a_t=(a_t^1,\dots ,a_t^n)$ drives the state transition $s_{t+1}~P(\cdot \mid s_t,a_t)$, and the team receives a shared reward $r_t=R(o_t,a_t)$. The objective is to find an optimal policy ${\mu }^{*}(a\mid o)$ that maximizes the expected cumulative return $G_t={\displaystyle \sum _{k=0}^{\infty }{\gamma }^k}{r}_{t+k+1}$ given the environment dynamics:

$${\mu }^{*}=\arg {\max }_{\mu }{\mathbb{E}}_{\mu }\left[G_t\right]$$

(13)

3.1.2. State Space and Action Space

The state space of the $i$-th UAV is defined as $s_i=\{s_i^{env},s_i^{uav}\}$, where the environment state $s^{env}$ includes the boundaries and obstacle positions, and the UAV state $s^{uav}$ contains the UAV's position and velocity.

Since the environment is partially observable, the environment state is perceived by the UAV through laser-based detection, the states of other UAVs_e are obtained via inter-UAV communication, and the UAV_t’s state is provided by the ground station.

The observation of the $i$-th UAV_e is given by:

$$o_i={\{o^{uav},o^{team},o^{goal},o^{las}\}}_i$$

(14)

where self-observation $o_i^{uav}={\{x,y,u,v\}}_i^{(f)}$ represents the UAV’s position and velocity; team observation $o_i^{team}={\{p_m\mid m=1,2,\dots ,N^{uav},m\ne i\}}_i^{(f)}$ represents the positions of other UAVs; goal observation $o_i^{goal}={\{d,\theta \}}_i^{(f)}$ represents the distance and relative angle to the UAV_t; laser observation $o_i^{las}={\{l_1,l_2,\dots ,l_{N^{las}}\}}_i$ represents the lengths of rays emitted in multiple directions.

The observation of the UAV_t is:

$$o_{tar}={\{o^{uav},o^{enemy},o^{las}\}}_{tar},$$

(15)

where enemy observation $o_{tar}^{enemy}={\{d_1,d_2,\dots ,d_{N^u}\}}_{tar}$ denotes the distances from each UAV to the target.

The action space of fixed-wing UAVs is defined in the trajectory coordinate system as:

$$a_i={\{a_x,a_y\}}_i^{(k)},$$

(16)

While the action space of multirotor UAV is defined in the image coordinate system as:

$$a_{tar}={\{a_x,a_y\}}_{tar}^{(f)}.$$

(17)

Furthermore, since different state variables may have different dimensions and ranges, directly using them can lead to unstable or inefficient learning. In deep reinforcement learning, state and observation spaces are normalized as a preprocessing step, calculated as:

$$f(\cdot )=\left\{\begin{array}{lllllll}x/L\hfill & y/L\hfill & u/V_{\max }\hfill & v/V_{\max }\hfill & d/(\sqrt{W^2+H^2})\hfill & \theta /\pi \hfill & l/L\hfill \end{array}\right\}$$

(18)

3.1.3. MADDPG

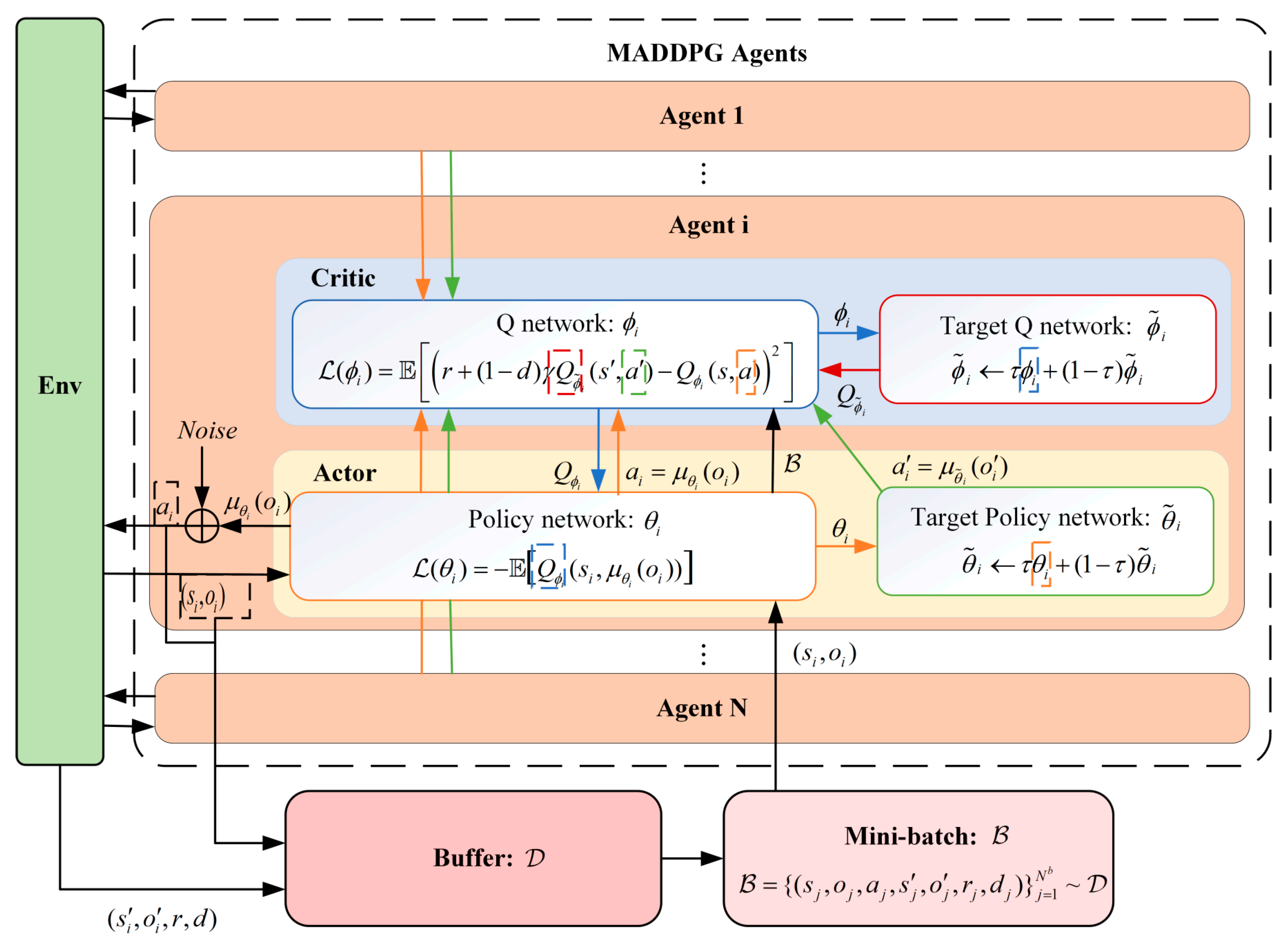
MADDPG is a typical actor–critic based multi-agent reinforcement learning method, extending single-agent DDPG to multi-agent scenarios. The core idea is that each agent’s Critic can access information from all other agents, enabling centralized training with decentralized execution (CTDE). Specifically, during training, a centralized Critic with global observation guides the Actor’s learning to improve stability, while during execution, only the Actor with local observation is used, aligning with real-world conditions.

The Actor network, i.e., the policy network, is defined as $a_i={\mu }_{{\theta }_i}(o_i)$, indicating that the Actor selects action $a_i$ based solely on its own observation $o_i$. The Critic network $Q_{{\varphi }_i}(o,a)$ evaluates the value using the joint observation $o$ and joint action $a$ of all agents.

Since the update relies on bootstrapping, directly using the online network parameters to compute target values would couple the target function with the network parameters being updated. This can lead to instability or divergence during training. To mitigate this, a target network mechanism is introduced. The target Actor and target Critic networks are updated via a soft update:

$${\tilde{\theta }}_i\leftarrow \tau {\theta }_i+(1-\tau ){\tilde{\theta }}_i,{\tilde{\varphi }}_i\leftarrow \tau {\varphi }_i+(1-\tau ){\tilde{\varphi }}_i$$

(19)

where $\tau \in (0,1)$ is the update rate, and $\tilde{\varphi },\tilde{\theta }$ denote the parameters of the target Q-network and target policy network, respectively.

The Critic network of agent $i$ is updated by minimizing the temporal-difference (TD) loss:

$$\mathcal{L}({\varphi }_i)={\mathbb{E}}_{(s,o,a,s^{\prime },r,d)~\mathcal{D}}\left[{\left(r+(1-d)\gamma Q_{\widetilde{{\varphi }_i}}(s^{\prime },{\mu }_{\widetilde{{\theta }_i}}({o^{\prime }}_i))-Q_{{\varphi }_i}(s,{\mu }_{{\theta }_i}(o_i))\right)}^2\right]$$

(20)

where $\mathcal{D}$ is the experience replay buffer, and $d\in \{0,1\}$ indicates episode termination. This minimizes the mean squared error between the predicted value and TD-target, enabling the Critic to learn accurate value estimates.

Simultaneously, the Actor network is optimized using the deterministic policy gradient:

$${\nabla }_{{\theta }_i}J({\theta }_i)={\mathbb{E}}_{s_i~\mathcal{D}}{[{\nabla }_{{\theta }_i}{\mu }_{{\theta }_i}(o_i){\nabla }_{a_i}{Q}_{{\varphi }_i}(s_i,a_i)]}_{a_i={\mu }_{{\theta }_i}(o_i)}$$

(21)

During action selection, exploration noise is added in a decaying manner during training, while deterministic outputs are used during evaluation. The final action executed in the training phase is:

$$a_t=\mathrm{clip}\left(a_t+{\sigma }_t{ϵ}_t,-1,1\right)$$

(22)

where ${ϵ}_t$ is a random noise within a certain range and ${\sigma }_t$ is the decay scaling factor.

The overall process is illustrated in Figure 4.

3.2. Curriculum Learning Strategy Design

During the pursuit process, the core challenge for fixed-wing UAVs compared to multirotor UAVs lies in their flight characteristics: they cannot hover or fly backward when encountering obstacles. Determining how to perform deceleration and turning control in advance based on radar detection distances becomes a critical challenge for deep reinforcement learning algorithms.

Due to the size of the pursuit area, obstacle distribution, and dynamic interference from other UAVs, collisions may occur, potentially terminating training episodes prematurely. If highly complex environments are used at the initial stage, UAVs may adopt local suboptimal strategies such as hovering in place to avoid severe collision penalties. Frequent collisions during exploration also hinder the search for global optimal solutions, significantly increasing training difficulty. Therefore, a progressively increasing task and environment complexity strategy is more reasonable, allowing UAV agents to gradually optimize their parameters and eventually master effective pursuit control policies.

To incrementally enhance task difficulty and generalization, we employ a CL mechanism to design the pursuit task in a staged manner. By gradually introducing obstacles, target mobility, and spatial constraints, the stability and convergence efficiency of training are effectively improved.

The task is divided into four curriculum levels: Level 0 to Level 3:

Level 0: basic environment, no obstacles, stationary target, small initial positions, long capture radius;

Level 1: introduces obstacles, enlarges the initial range, reduces the capture radius;

Level 2: enables the UAV_t to move, further enlarges the initial range, reduces the capture radius again;

Level 3: the initial range almost covers the entire scene, with the smallest capture radius.

To reduce training steps, a performance-driven curriculum scheduler is introduced. This mechanism dynamically adjusts task difficulty based on task performance and training progress. The system adaptively increases the curriculum level according to the pursuit success rate over a recent window of episodes, calculated as:

$$\begin{array}{cc}{\overline{C}}^{(M)}={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=e-M+1}^e{c}_m},& c_m=\left\{\begin{array}{ll}1,\hfill & \mathrm{Encicle}=\mathrm{True}\hfill \\ 0,\hfill & \mathrm{Encicle}=\mathrm{False}\hfill \end{array}\right.\end{array}$$

(23)

where $M$ is the number of recent episodes in the sliding window, and an episode is considered successful if all UAVs enter the UAV_t’s capture range and remain within it for a specified number of steps. If any UAV leaves the capture range, the step count is reset to zero.

To prevent premature level promotion, a dual-condition mechanism is adopted. Level switching occurs only if both the performance threshold and training quantity conditions are satisfied. The threshold condition requires a minimum experience: the number of episodes in the current stage must be at least twice the check window, and the cumulative steps must exceed twice the replay buffer capacity. The pseudocode is shown in Algorithm 1.

Algorithm 1: MADDPG_CL (Multi-Agent Deep Deterministic Policy Gradient with Curriculum Learning)
Input: Level = 0, number of agents $\mathcal{N}$, hyperparameters.
Output: Environmental rewards, task success rate.
1.	Initialize replay buffer $\mathcal{D}$
2.	$\mathbf{for}\mathrm{agent}i=1$ $\mathcal{N}$ do
3.	Initialize actor, critic, target actor, target critic networks with parameters $\theta i,\varphi i,\tilde{\theta }i,\tilde{\varphi }i$
4.	end for
5.	$\mathbf{for}\mathrm{episode}e=1$ $\mathcal{M}$ do
6.	Initialize environment and agent states
7.	$\mathbf{for}\mathrm{step}t=1$ $\mathrm{to}{T}^{\max }$ do
8.	$\mathrm{Each}\mathrm{agent}\mathrm{observes}{o}_i$ $\mathrm{and}\mathrm{selects}\mathrm{action}{a}_i$ via actor network
9.	Environment updates, returning reward $r$ and next state $s'$
10.	$\mathrm{Store}\mathrm{transition}(s,o,a,s^{\prime },o^{\prime },r,d)$ into $\mathcal{D}$
11.	$\mathbf{if}d==\mathrm{True}$ then
12.	$\mathbf{if}{t}^{cap}\ge T^{cap}$ $\mathbf{then}{c}_m=1$ end if
13.	break
14.	end if
15.	$s\leftarrow s^{\prime }$
16.	$\mathbf{for}\mathrm{agent}i=1$ $\mathcal{N}$ do
17.	$\mathrm{Sample}\mathrm{minibatch}\mathcal{B}={\{(s_j,o_j,a_j,{s^{\prime }}_j,{o^{\prime }}_j,r_j,d_j)\}}_{j=1}^{N^b}~\mathcal{D}$
18.	$\mathrm{Update}\mathrm{critic}:\mathcal{L}({\varphi }_i)=\mathbb{E}\left[{\left(r+(1-d)\gamma Q_{\widetilde{{\varphi }_i}}(s^{\prime },a^{\prime })-Q_{{\varphi }_i}(s,a)\right)}^2\right]$
19.	$\mathrm{Update}\mathrm{actor}:{\nabla }_{{\theta }_i}J({\theta }_i)=\mathbb{E}{[{\nabla }_{{\theta }_i}{\mu }_{{\theta }_i}(o_i){\nabla }_{a_i}{Q}_{{\varphi }_i}(s_i,a_i)]}_{a_i={\mu }_{{\theta }_i}(o_i)}$
20.	$\mathrm{Update}\mathrm{target}\mathrm{networks}:{\tilde{\theta }}_i\leftarrow \tau {\theta }_i+(1-\tau ){\tilde{\theta }}_i,{\tilde{\varphi }}_i\leftarrow \tau {\varphi }_i+(1-\tau ){\tilde{\varphi }}_i$
21.	end for
22.	end for
23.	$\mathrm{Compute}\mathrm{sliding}\mathrm{window}\mathrm{success}\mathrm{rate}:{\overline{C}}^{(M)}={\displaystyle \frac{1}{M}}{\displaystyle \sum _{m=e-M+1}^e{c}_m}$
24.	$\mathbf{if}{\overline{C}}^{(M)}\ge C^{leve{l}_{u}p}$ $\mathrm{and}{e}^{level}\ge E^{leve{l}_{u}p}$ $\mathrm{and}{t}^{level}\ge T^{leve{l}_{u}p}$ then
25.	Level $\leftarrow$ Level + 1
26.	end if
27.	end for

3.3. Reward Function Design

The reward function is the core mechanism guiding agents to learn effective pursuit strategies. It needs to account for multiple aspects of UAV behavior, including approaching the target, collision avoidance, and cooperative encirclement. In pursuit tasks, the primary capture reward is typically sparse, so shaping dense intermediate rewards is introduced to provide continuous feedback and prevent learning stagnation.

To keep the sparse and dense rewards within a reasonable scale, the terminal discounted reward is computed as:

$$R_{\mathrm{final}}={\gamma }^T\cdot R_{\mathrm{sparse}}+{\displaystyle \frac{1-{\gamma }^T}{1-\gamma }}{R}_{\mathrm{dense}},$$

(24)

where $\gamma$ is the discount factor, $T$ is the episode length, $R^{\mathrm{sparse}}$ represents the sparse terminal reward, and $R^{\mathrm{dense}}$ represents the continuous reward.

The terminal discounted reward also adjusts the relative weighting of different behavioral rewards and differentiates the reward logic between UAVs_e and UAV_t, forming an adversarial learning framework. The per-step reward $R$ is defined as:

$$R={\displaystyle \sum _{i=1}^n{R}_i},R_i={\mu }_i\cdot r_i,$$

(25)

where ${\mu }_i$ is a reward coefficient that can be positive or negative, and $r_i$ is the normalized reward for each behavior.

3.3.1. Reward Function for Encircling UAVs

In collision avoidance and pursuit tasks, multiple UAVs_e need to autonomously plan optimal trajectories to efficiently encircle the UAV_t. This requires simultaneously satisfying safety constraints, time-optimality, and cooperative encirclement objectives. The total reward for UAVs_e consists of collision penalty, distance reward, distance rate reward, encirclement reward, completion reward, and time penalty, formulated as:

$$R_{\mathrm{enc}}=R_c+R_d+R_{dd}+R_{\mathrm{enc}}+R_t+R_{\mathrm{suc}}+R_{\mathrm{comp}}$$

(26)

The components are defined as follows:

• Collision penalty: Penalizes collisions with obstacles, boundaries, or other UAVs.

$$R_c={\mu }_c\cdot r_c,r_c=\left\{\begin{array}{ll}1,\hfill & \mathrm{if}\mathrm{collision}\mathrm{occurs}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(27)

where ${\mu }_c=-60$ is the collision penalty coefficient, and $r_c$ is the collision indicator.

• Distance reward: Encourages UAVs_e to approach the UAV_t.

$$R_d={\mu }_d\cdot r_d,r_d=1-\mathrm{clip}\left({\displaystyle \frac{2d}{\sqrt{W^2+H^2}}},0,1\right)$$

(28)

where ${\mu }_d=0.1$ is the distance reward coefficient, and $d$ is the current distance between the UAV_e and the UAV_t.

• Distance rate reward: Provides directional guidance towards the UAV_t.

$$R_{dd}={\mu }_{dd}\cdot r_{dd},r_{dd}={\displaystyle \frac{\Delta d}{V_{\max }\cdot \Delta t}}$$

(29)

where ${\mu }_{dd}=0.1$ is the rate coefficient, and $\Delta d$ is the distance change from the previous step.

• Encirclement reward: Promotes cooperative encirclement formation, quantified by the area ratio of triangles formed by UAVs.

$$R_{\mathrm{enc}}={\mu }_{\mathrm{enc}}\cdot r_{\mathrm{enc}},r_{\mathrm{enc}}={\displaystyle \frac{S_0}{S_1+S_2+S_3}}$$

(30)

where ${\mu }_{\mathrm{enc}}=0.1$, $S_1,S_2,S_3$ are areas of triangles formed by the UAV_t and any two UAVs_e, and $S_0$ is the area formed by the three UAVs_e.

• Time penalty: Penalizes unnecessary hovering or oscillatory movement to reduce local optima.

$$R_t={\mu }_t\cdot r_t,r_t=1,{\mu }_t=-({\mu }_d+{\mu }_{dd}+{\mu }_{\mathrm{cap}})$$

(31)

where ${\mu }_t=-0.3$ is the negative sum of other positive reward coefficients, and $r_t$ is the time step indicator.

• Single-UAV success reward: Rewards when a UAV_e enters the encirclement range.

$$R_{\mathrm{suc}}={\mu }_{\mathrm{suc}}\cdot r_{\mathrm{suc}},r_{\mathrm{suc}}=\left\{\begin{array}{ll}1,\hfill & d\le r^{cap}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(32)

where ${\mu }_{\mathrm{done}}=0.5$ is the reward coefficient for entering the capture radius.

• Multi-UAV Completion Reward: Rewards maintaining encirclement for a specified number of steps.

$$R_{\mathrm{comp}}={\mu }_{\mathrm{comp}}\cdot r_{\mathrm{comp}},r_{\mathrm{comp}}=\left\{\begin{array}{ll}1,\hfill & t_{\mathrm{round}}\ge T_{\mathrm{round}}\hfill \\ 0,\hfill & t_{\mathrm{round}}<T_{\mathrm{round}}\hfill \end{array}\right.$$

(33)

where ${\mu }_{\mathrm{comp}}=80$ is the sparse reward coefficient for completing the encirclement objective when all UAVs_e remain within the capture radius for the required steps.

3.3.2. Reward Function for Target UAV

The reward mechanism for the UAV_t is adversarial to the UAVs_e, aiming to avoid encirclement and perform autonomous collision avoidance. The total reward is formulated as:

$$R_{\mathrm{tar}}=R_{\mathrm{cap}}+R_{\mathrm{cen}}+R_c$$

(34)

The components are defined as follows:

• Encirclement Penalty: Penalizes the encirclement tendency of the UAVs_e.

$$R_{\mathrm{cap}}={\mu }_{\mathrm{cap}}\cdot r_{\mathrm{cap}},r_{\mathrm{cap}}={\displaystyle \frac{1}{N^{\mathrm{fix}}}}{\displaystyle \sum _{i=1}^{N^{\mathrm{fix}}}{r}_{dd,i}}$$

(35)

• Center Guidance Reward: Encourages the UAV_t to move towards the center.

$$R_{\mathrm{cen}}={\mu }_{\mathrm{cen}}\cdot r_{\mathrm{cen}},r_{\mathrm{cen}}=1-\mathrm{clip}\left({\displaystyle \frac{2d_{\mathrm{cen}}}{\sqrt{W^2+H^2}}},0,1\right)$$

(36)

• Collision and Obstacle Avoidance Reward: Encourages the UAV to avoid collisions.

$$R_c={\mu }_c\cdot r_c,r_c=\left\{\begin{array}{ll}1,\hfill & \mathrm{if}\mathrm{collision}\mathrm{occurs}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(37)

where ${\mu }_{\mathrm{cap}}=-1$ is the encirclement penalty coefficient, ${\mu }_{\mathrm{cen}}=1$ is the center guidance reward coefficient, and ${\mu }_c=-5$ is the collision penalty coefficient.

4. Experiments and Results

The experiments were conducted in a custom UAV simulation environment built on Python 3.10.17 and Gymnasium 1.1.1, incorporating dynamics models for both fixed-wing and multirotor UAVs.

In terms of computational performance, all experiments were carried out on a laptop equipped with an Intel Core Ultra 9 275HX (2.70 GHz) processor (Intel, Santa Clara, CA, USA), an NVIDIA RTX 5060 GPU with CUDA acceleration (NVIDIA, Santa Clara, CA, USA), and 32 GB of RAM. During training, the GPU utilization was approximately 80%, with CPU usage around 10% and memory consumption of about 3 GB. Under these hardware conditions, the average training efficiency was approximately 10,000 episodes per 6 h, and the complete curriculum training of 40,000 episodes took about 24 h in total.

4.1. Parameter Settings

Table 1. Simulation Parameter Settings.

Title 1	Parameter	Symbol	Value	Unit
Environment	Side Length	$\left[W,H\right]$	[1000, 1000]	$\mathrm{m}$
	Time Step	$\Delta t$	0.5	$\mathrm{s}$
	Safety Radius	$r_{safe}$	10	$\mathrm{m}$
	Curriculum Level	$\mathcal{C}$	[0, 3]
	Noise Amplitude	$ϵ$	[0.01, 0.75]
	Noise Decay Rate	$\sigma$	0.999995
	Obstacle Number	$N^{obs}$	4
	Obstacle Radius	$r^{obs}$	[50, 100]	$\mathrm{m}$
Fixed-wing UAV	Number	$N^{fix}$	3
	Maximum Speed	$V_{\max }$	32	$\mathrm{m}/\mathrm{s}$
	Minimum Speed	$V_{\min }$	20	$\mathrm{m}/\mathrm{s}$
	Maximum Longitudinal Acceleration	${\left|a_x^{fix}\right|}_{\max }^{(k)}$	2.4	$\mathrm{m}/{\mathrm{s}}^2$
	Maximum Lateral Acceleration	${\left|a_y^{fix}\right|}_{\max }^{(k)}$	2.5	$\mathrm{m}/{\mathrm{s}}^2$
	Minimum Turning Radius	$r_{\min }$	40	$\mathrm{m}$
Multirotor UAV	Maximum Speed	$V_{\max }^{tar}$	[0, 10, 15]	$\mathrm{m}/\mathrm{s}$
	Minimum Speed	$V_{\min }^{tar}$	0	$\mathrm{m}/\mathrm{s}$
	Maximum Acceleration	${\left|a^{tar}\right|}_{\max }^{(f)}$	[0, 3]	$\mathrm{m}/{\mathrm{s}}^2$
Sensor	Maximum Sensing Distance	$L$	160	$\mathrm{m}$
	Number of Beams	$N^{las}$	16

summarizes the parameters of the environment, UAVs, and onboard radar sensors, balancing scenario realism with computational feasibility.

To validate the rationality of the adopted simplified model parameters, a comparative analysis was conducted based on the standard Coordinated Turn Model. The governing equations are given as:

$$a_y={\displaystyle \frac{V^2}{R}}=g\tan \varphi ,n={\displaystyle \frac{1}{\cos \varphi }}$$

(38)

where $V$ is the flight speed, $R$ is the turning radius, $g$ is the gravitational acceleration, $\varphi$ is the roll angle, and $n$ is the load factor.

Considering the maneuvering characteristics of small fixed-wing UAVs, when the flight speed is within 20–32 m/s and the maximum lateral acceleration is 2.5 m/s², the corresponding roll angle is approximately 14.3°, and the load factor is $n$ = 1.03, which represents a light-load coordinated turn. This parameter range is consistent with typical small fixed-wing UAVs, whose load factors during level coordinated turns usually range between 1.0 and 1.4. These results demonstrate that the simplified point-mass model adopted in this study provides reasonable dynamic consistency and physical interpretability for planar flight tasks.

The hyperparameters of MADDPG are given in

Table 2. MADDPG Parameter Settings.

Parameter	Symbol	Value
Action Dimension	$N^a$	2
Observation Dimension of UAV_e	$N_{fix}^o$	26
Observation Dimension of UAV_t	$N_{tar}^o$	23
Batch Size	$n$	256
Replay Buffer Size	$N^b$	106
Optimizer		Adam
Discount Factor	$\gamma$	0.99
Soft Update Coefficient	$\tau$	0.01
Hidden Layer Dimension	$d_h$	128, 128
Actor Learning Rate	$\alpha$	10−4
Critic Learning Rate	$\beta$	4 × 10−4

, with most values adopted from common practices in multi-agent reinforcement learning. The learning rate and discount factor were tuned through preliminary experiments to ensure stable convergence. The parameter settings of the four curriculum levels are listed in

Table 3. Curriculum Level Parameter Settings.

Level	Max Steps	UAV_t Max Speed (m/s)	Number of Obstacles	UAV_t Initial Range (m)	UAV_e Initial Range (m)	Capture Radius (m)
0	100	0	0	40	640	120
1	120	0	0	320	800	112
2	140	10	4	640	800	104
3	160	15	4	920	920	100

, where task complexity is progressively increased by adjusting UAV initial positions, obstacle density, and target maneuverability. The coefficients of the reward function are detailed in Section 3.3. All experiments were conducted with fixed random seeds to ensure both randomness and reproducibility.

4.2. Experimental Results

A collision failure is determined if any UAV approaches an obstacle, another UAV, or the environment boundary closer than the predefined safety radius. An encirclement step is considered complete when all UAVs_e enter the UAV_t’s capture range without collision and form a surrounding trend, as illustrated in Figure 1b. Within the maximum number of steps allowed per episode, if the UAVs_e swarm successfully completes the required number of encirclement steps, the pursuit is regarded as successful. During training, several issues may arise, including constraints imposed by the environment boundaries, collisions with obstacles, collisions among UAVs, and stuck in local optimum. These issues are partially illustrated in Figure 5.

To more intuitively demonstrate the learning effect of the pursuit task, we plotted the successful pursuit scenarios at different training stages. The results are autonomously generated by the trained neural network policies, and GIF animations are provided in the Supplementary Materials. To ensure clarity, the illustrations for Level 0 and Level 1 are displayed until the final step of task completion, as shown in Figure 6. In Level 0, UAVs_e enter the capture range and circle around the UAV_t. Level 1 UAVs can avoid obstacles while approaching the UAV_t.

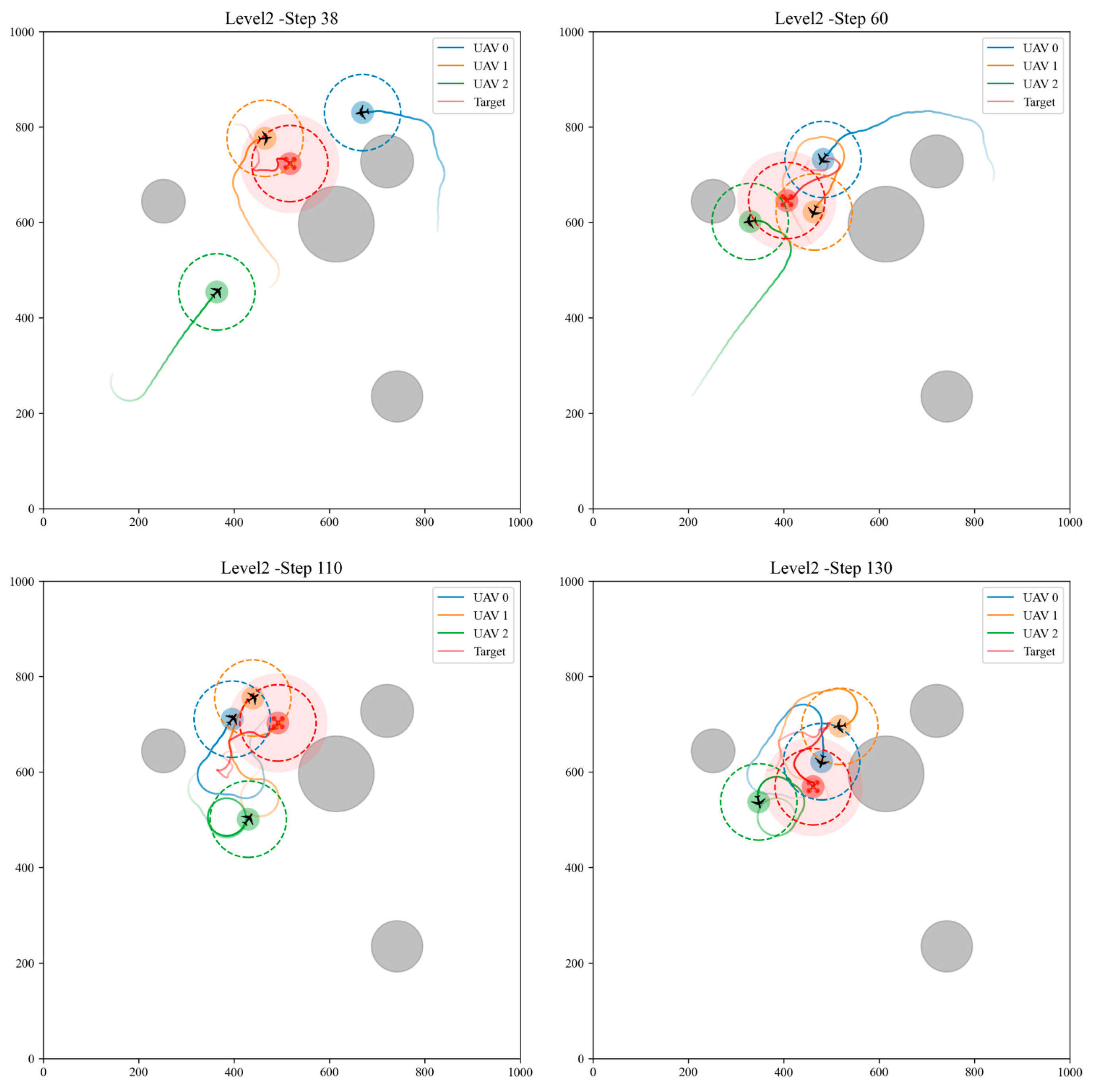
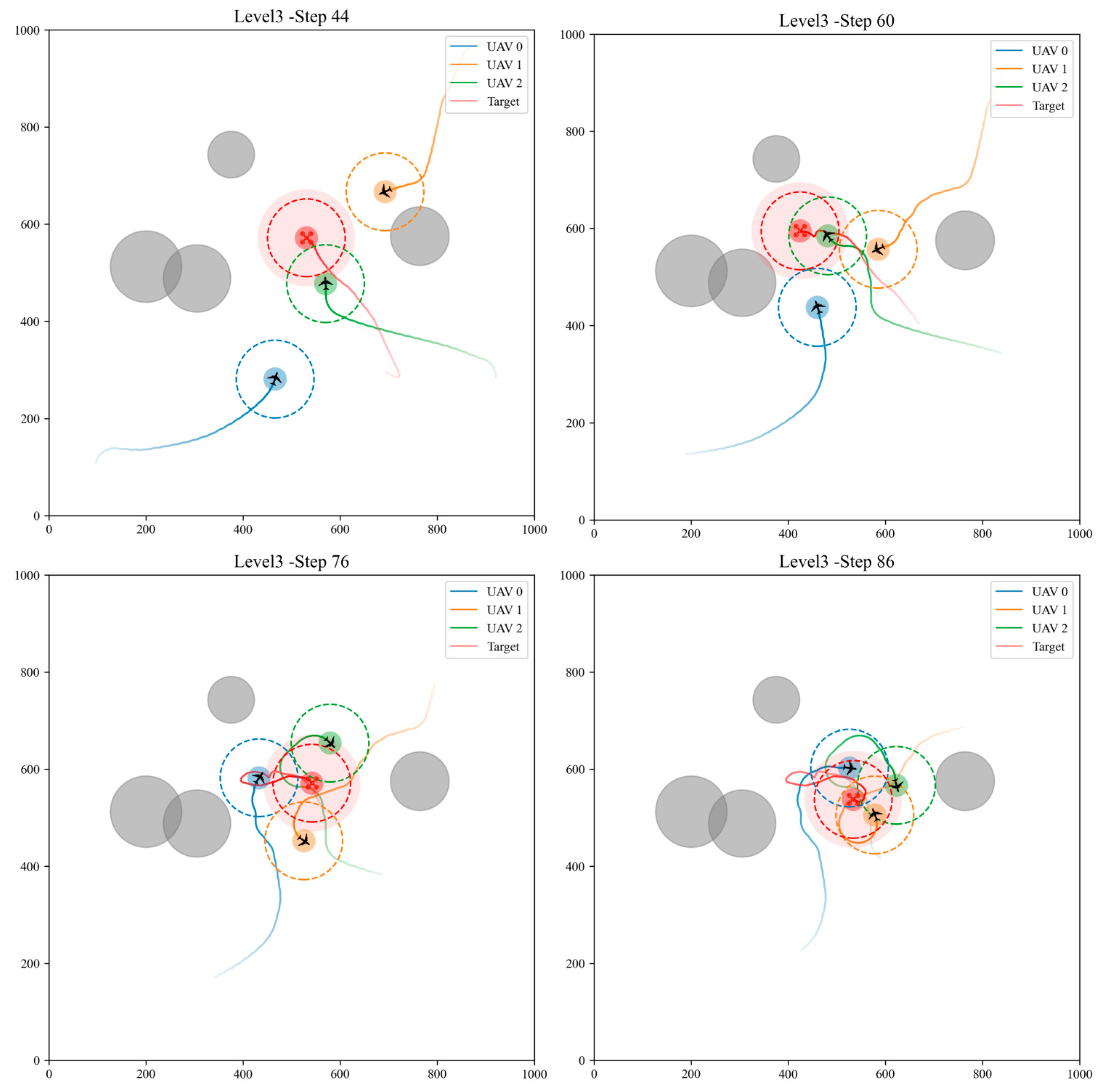
The illustrations for Level 2 and Level 3 show successful pursuit after exceeding 10 capture steps, with early termination. The Level 2 results are shown in Figure 7, and Level 3 results in Figure 8. In Level 2, the fixed-wing UAVs can turn in time to pursue when the multirotor moves backward. In Level 3, even when initial positions cover the entire scene, UAVs can still successfully complete the pursuit task.

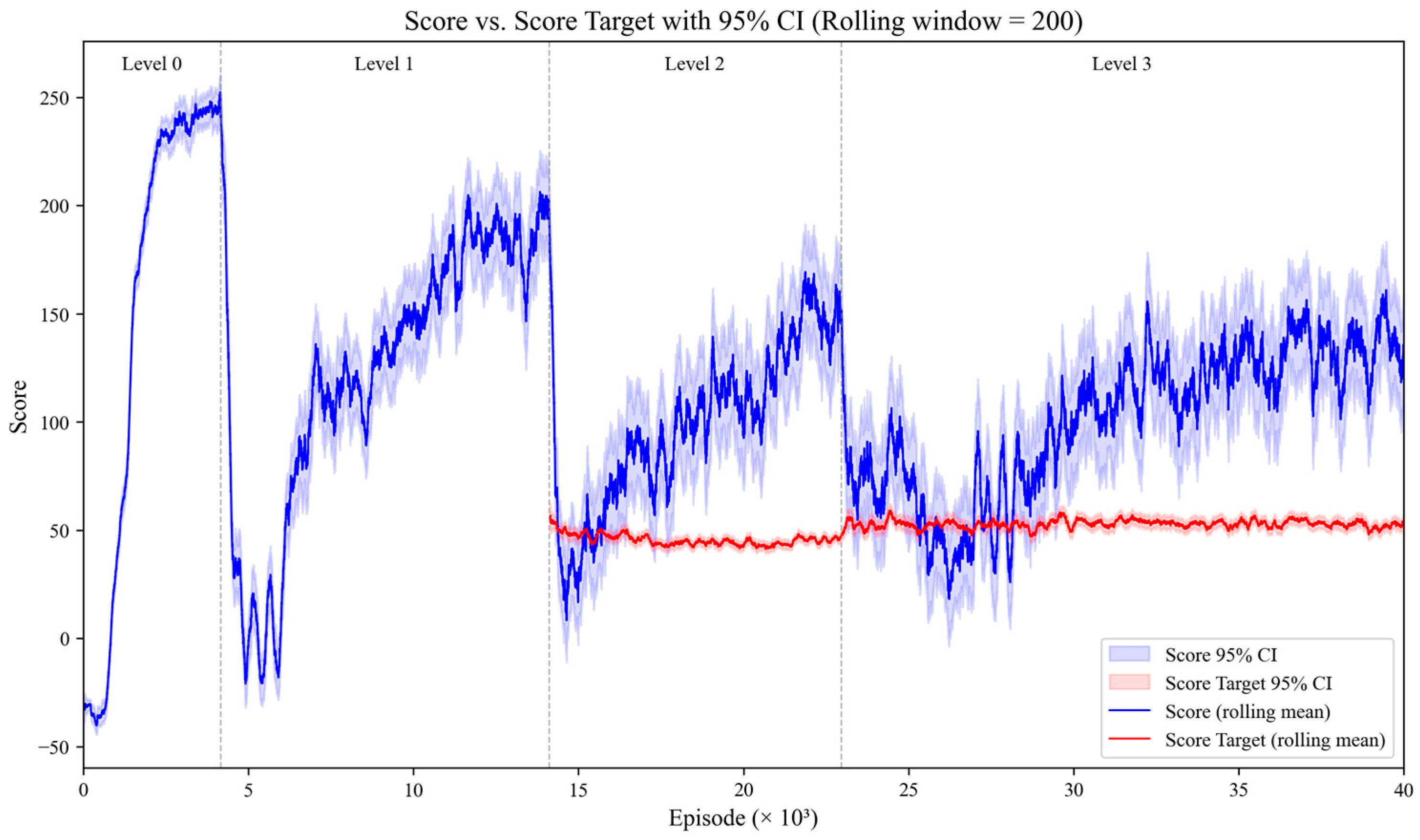
The reward function evolution during training is shown in Figure 9. In Level 0, the UAVs_e first learn to fly within the environment boundaries and successfully encircle a stationary UAV_t. After entering Level 1, obstacles are introduced in the environment, resulting in negative rewards for collisions. UAVs gradually learn obstacle avoidance behavior. In Level 2, the UAV_t is capable of motion, making early-stage pursuit difficult and rewards relatively low; through learning, UAVs_e gradually master target identification and tracking strategies. Level 3 further enlarges the initial generation range and reduces the capture area, significantly increasing task difficulty. The final reward stabilizes around 125 points. As the task level increases, the required time for pursuit increases, and cumulative rewards decrease due to time penalties.

In experimental evaluation, 1000 episodes were conducted for each level, calculating capture success rates for every 100 episodes. To ensure robustness, error bars are included. The results are shown in Figure 10, illustrating differences in performance under different levels and capture step requirements. Overall, the success rate remains above 70%, with failures mainly due to collisions with obstacles, teammates, or the UAV_t. Other failures are mostly due to not completing the pursuit within the limited steps. In obstacle-free, stationary target scenarios, the success rate exceeds 95%. With increasing capture step requirements, success rates slightly decline. In the most complex Level 3 scenario (global random initial positions, random initial headings, maximum steps 200, capture range within 100 m), the single-step encirclement success rates exceed 80%, and the 10-step success rates remain around 70%, demonstrating the method's effectiveness and robustness in complex environments.

5. Conclusions

This paper addresses the challenges of fixed-wing UAVs performing encirclement and obstacle avoidance tasks in complex environments, and proposes a curriculum-based composite deep reinforcement learning method. A multi-agent fixed-wing UAV collaborative task environment is constructed, integrating pursuit and obstacle avoidance, while fully accounting for UAV dynamic constraints, multirotor target UAV maneuverability, and local perception in obstacle-rich scenarios, thereby validating the effectiveness of the proposed approach.

Experimental results demonstrate that the composite MADDPG_CL framework effectively mitigates issues such as local optima and slow convergence during training, substantially enhancing policy stability and generalization. The multirotor target UAVs are also controlled via deep reinforcement learning, exhibiting strong maneuvering and adversarial capabilities that often induce collisions for the encircling UAVs, further increasing task complexity. In obstacle-free environments, fixed-wing encircling UAVs complete encirclement tasks efficiently, achieving success rates exceeding 95%. Even in complex environments with moving targets and random initial conditions, success rates remain around 70%. The proposed method also demonstrates robust performance in collision avoidance and extended capture duration.

Overall, this study provides a novel solution for intelligent collaborative control of fixed-wing UAV swarm in high-risk, complex environments. Although the UAVs_e used in the current training are homogeneous, the training framework itself supports heterogeneity in both parameters and dynamics models. Moreover, training results with UAV_t demonstrate that the same neural network can adapt to cooperative tasks involving different types of UAVs. Future work will focus on more realistic scenarios, incorporating communication constraints, sensor noise, and dynamic obstacles, and will explore transfer learning and imitation learning to further enhance the adaptability and robustness of the framework in real-world systems. Validation experiments will be conducted on the PX4-SITL platform and the Gazebo 6-DOF simulation environment to achieve seamless integration and testing of the algorithms within a high-fidelity flight control system.