Autonomous Navigation of Unmanned Ground Vehicles Based on Micro-Shell Resonator Gyroscope Rotary INS Aided by LDV
Abstract
1. Introduction
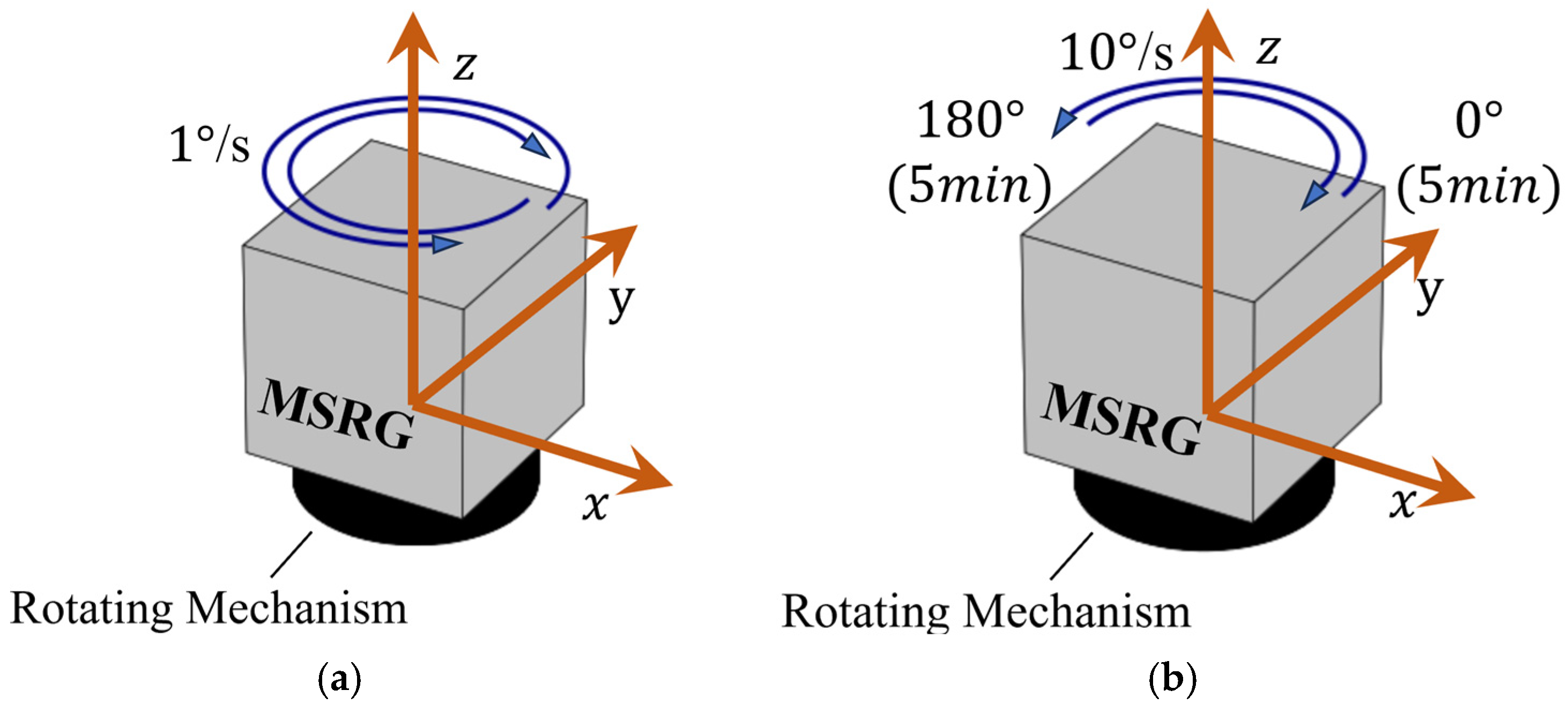
- A dynamic switching mechanism between force-rebalanced mode and whole-angle mode was established. An 18 position self-calibration method was designed;
- A magnetometer-assisted rotary modulation self-alignment algorithm was proposed. Incorporating state-transformation extended Kalman filter (STEKF), the algorithm enables fast azimuth error estimation convergence, even with significant misalignment-angle-induced magnetometer interference;
- An error analysis was conducted on the MSRG-specific bias. A reciprocating rotation path with a period of 4π was designed. Additionally, LDV was integrated to provide velocity observations for the MSRG–RINS, thereby enhancing the accuracy and robustness of the system state estimation.

2. Initial Self-Alignment Method Based on STEKF and Rotary Modulation
2.1. Virtual Rotation Self-Calibration Method Based on MSRG Pattern Angle Control
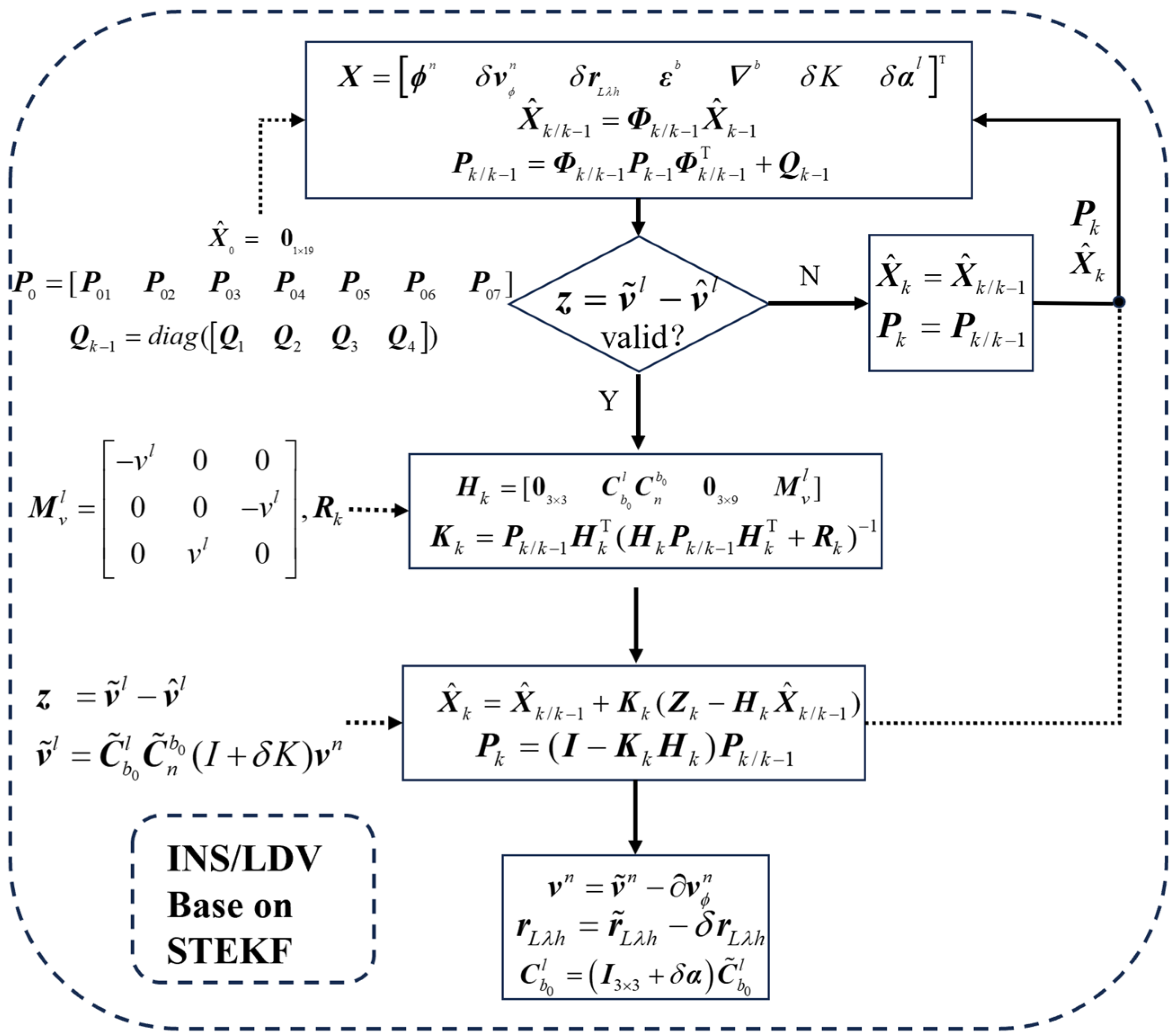
2.2. Initial Alignment Algorithm Based on State-Transformation Kalman Filtering
3. LDV-Assisted RINS Based on MSRG
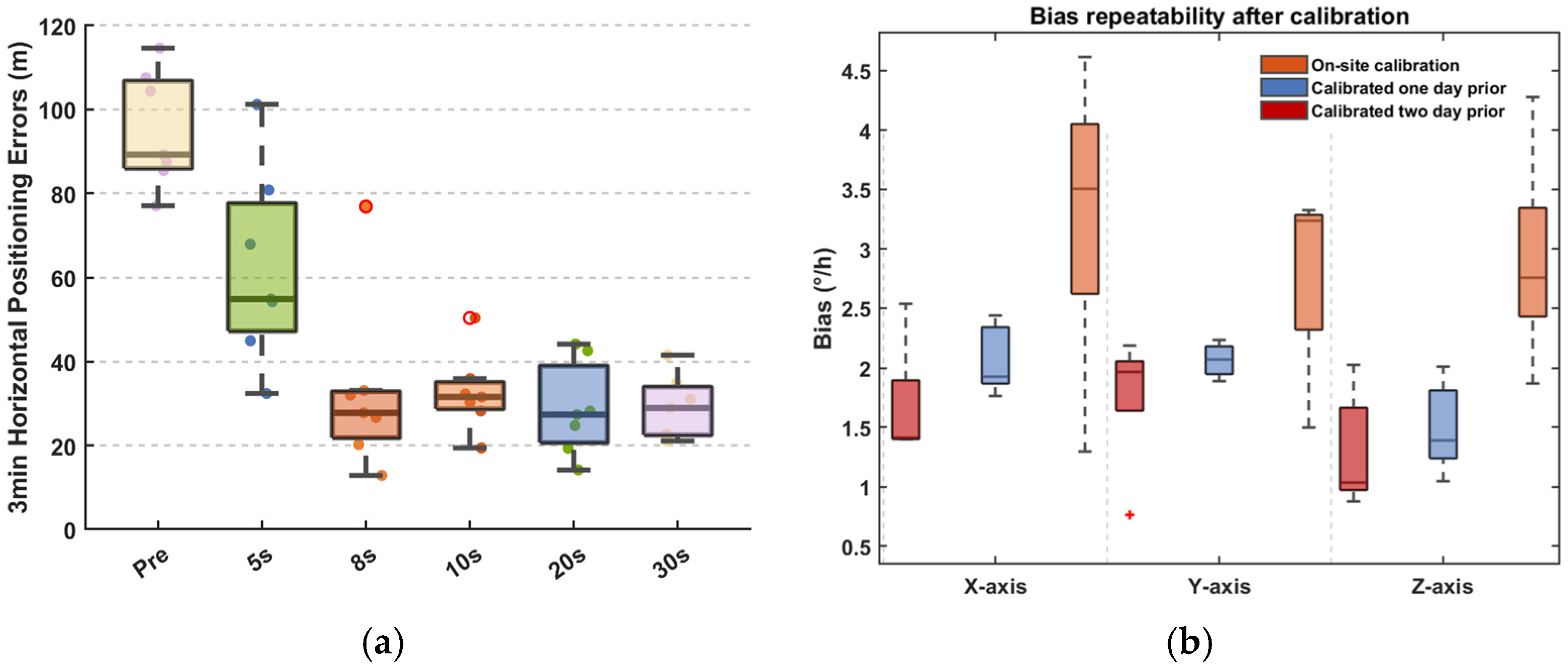
3.1. Calibration of Rotary Modulation MSRG–RINS
3.2. Bias Error Analysis of Rotary Modulation Methods
3.3. Combined RINS/LDV Navigation Method Based on STEKF
4. Experiment
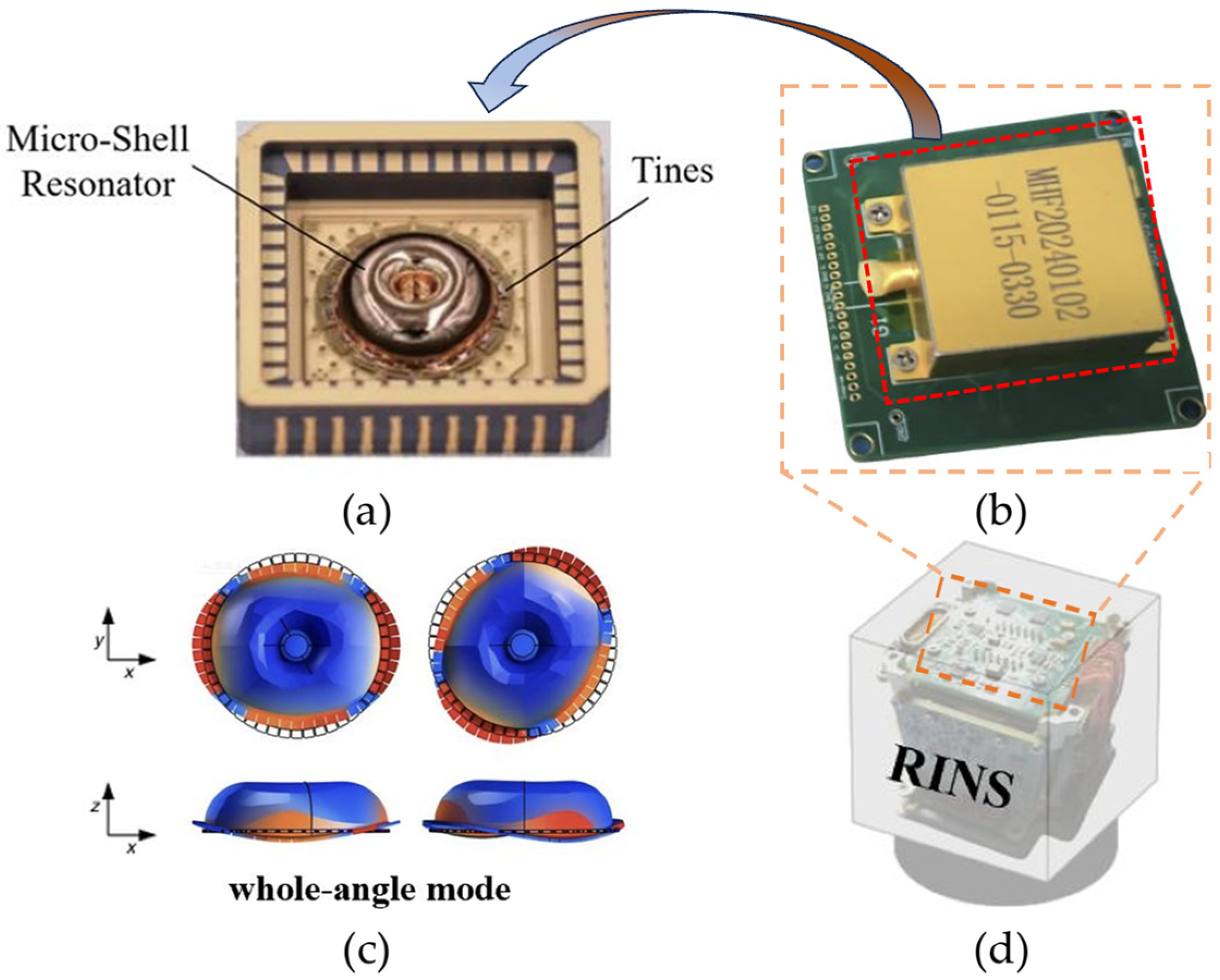
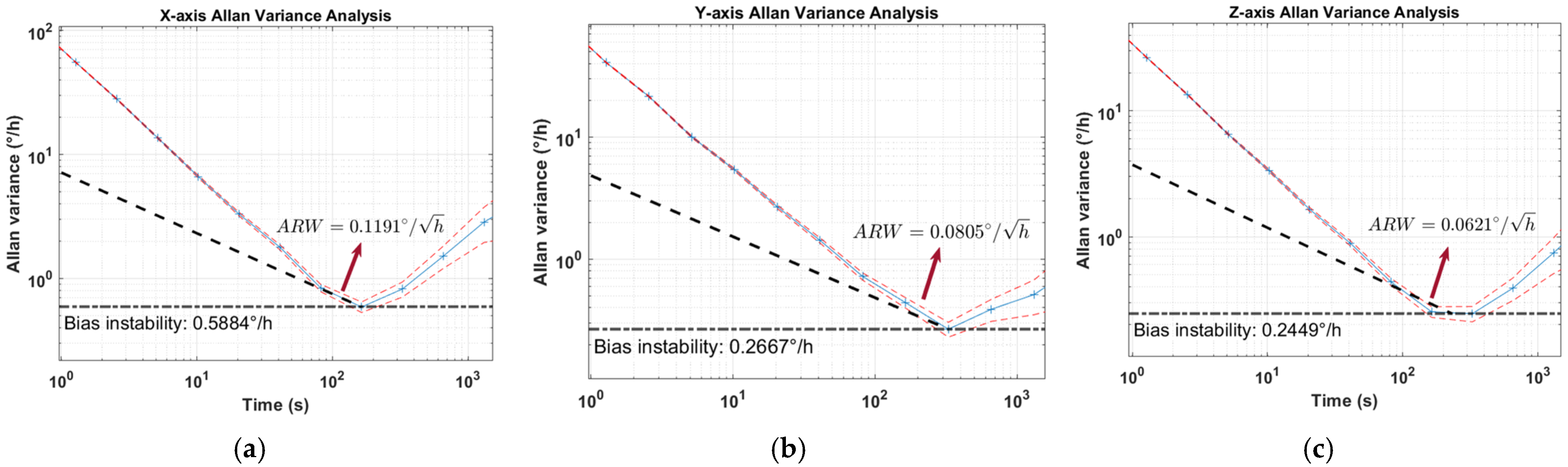
4.1. Technical Indicators of the MSRG and LDV
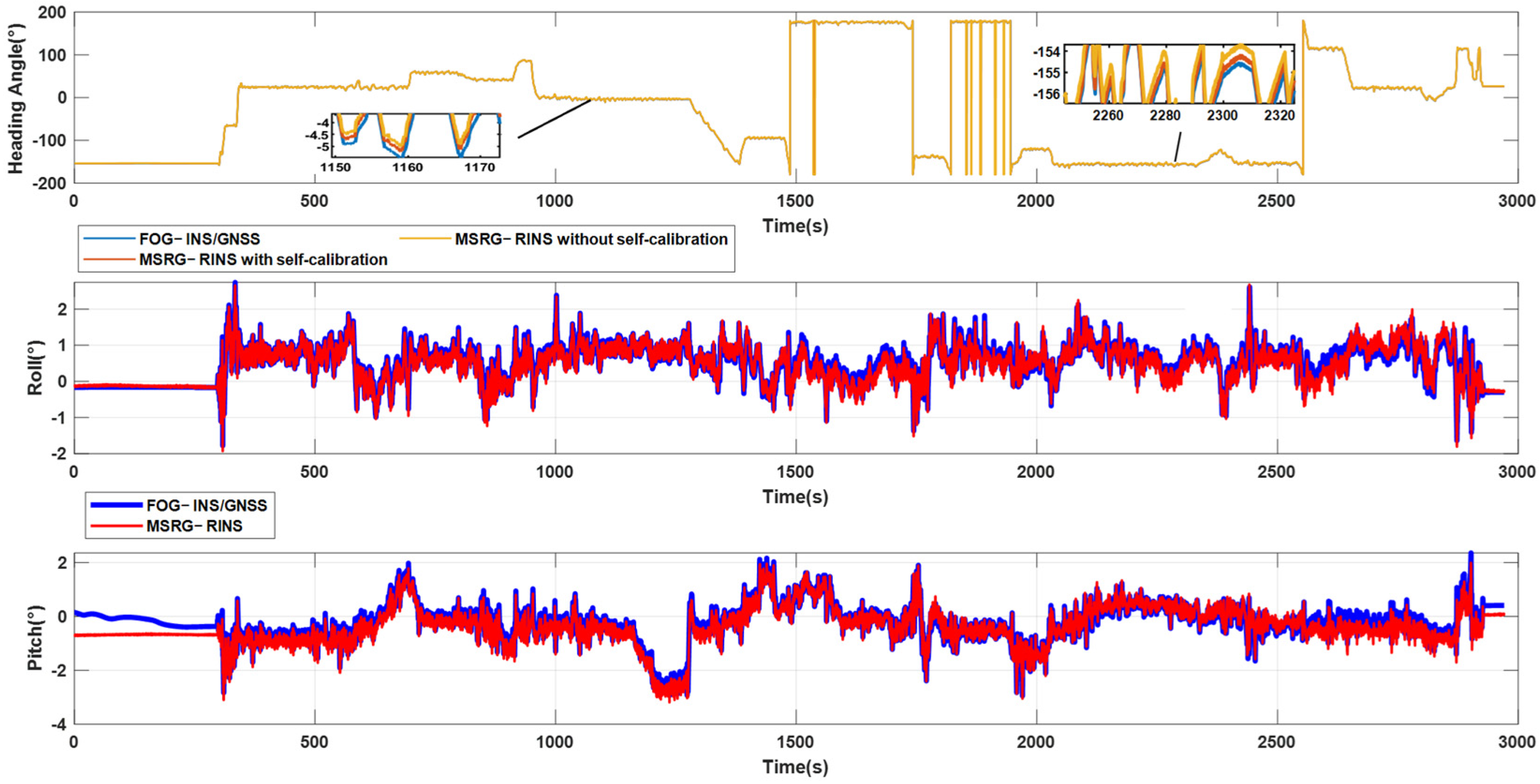
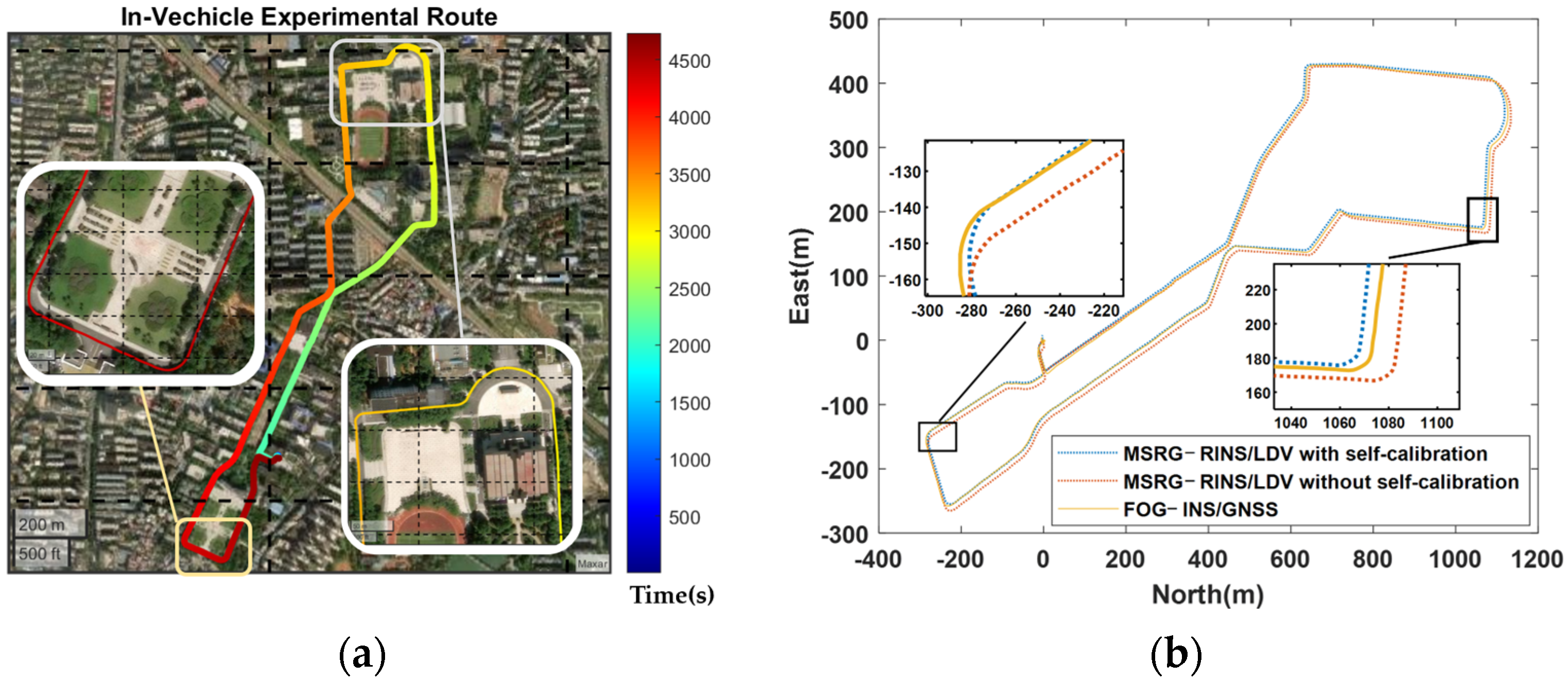
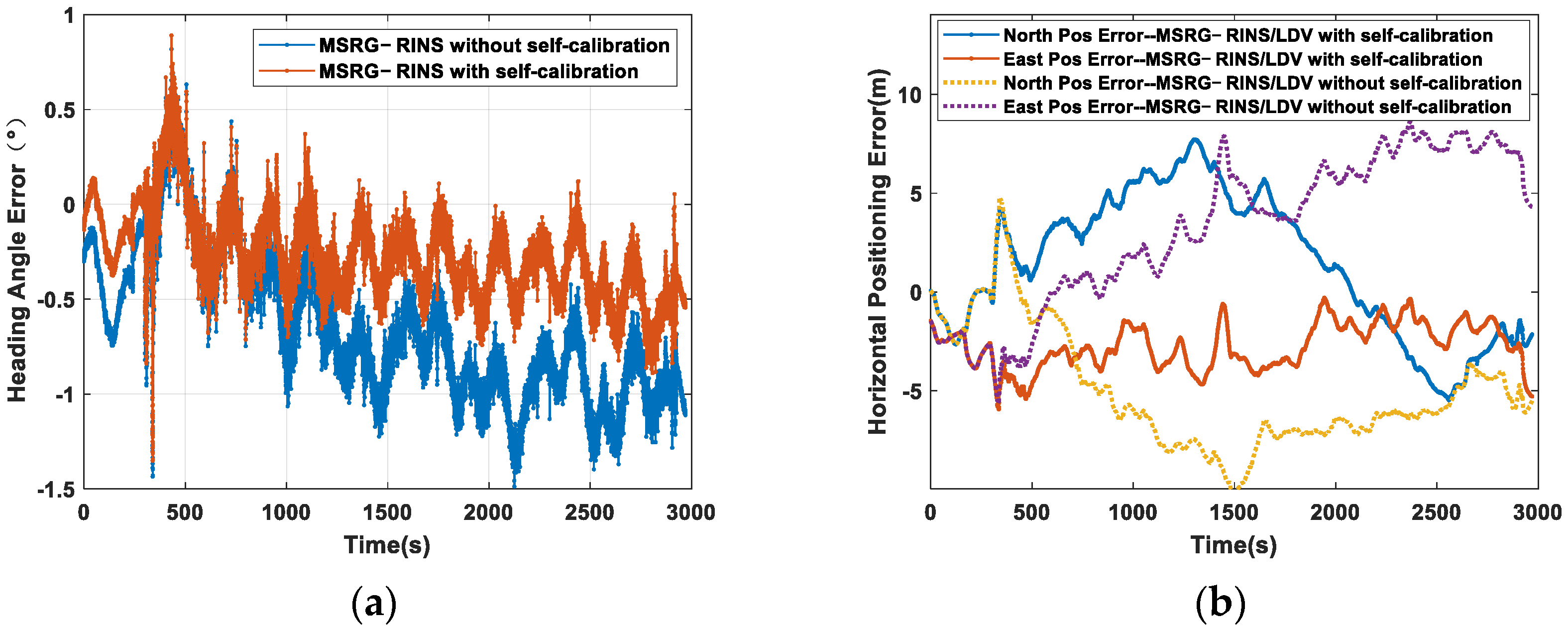
4.2. UGV Autonomous Navigation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARW | Angle Random Walk |
| FOG | Fiber Optic Gyroscope |
| IMU | Inertial Measurement Unit |
| LDV | Laser Doppler Velocimetry |
| MEMS | Micro-Electro-Mechanical System |
| MSRG | Micro-Shell Resonator Gyroscope |
| RINS | Rotary Inertial Navigation System |
| MSRG–IMU | Micro-Shell Resonator Gyroscope Inertial Measurement Unit |
| STEKF | State-Transformation Extended Kalman Filter |
| SWaP | Size, Weight and Power |
| SINS | Strapdown Inertial Navigation System |
| UGVs | Unmanned Ground Vehicles |
References
- Sapkota, R.; Roumeliotis, K.I.; Karkee, M. UAVs Meet Agentic AI: A Multidomain Survey of Autonomous Aerial Intelligence and Agentic UAVs. arXiv 2025, arXiv:2506.08045. [Google Scholar] [CrossRef]
- Shahar, F.S.; Sultan, M.T.H.; Nowakowski, M.; Bukaszewicz, A. UGV-UAV Integration Advancements for Coordinated Missions: A Review. J. Intell. Robot. Syst. 2025, 111, 69. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Yang, C.; Fan, Z.; Zhu, Q.; Yang, P.; Mei, C.; Lu, B. Robust navigation system for UGV based on the IMU/vision/geomagnetic fusion. Int. J. Intell. Robot. 2023, 7, 321–334. [Google Scholar] [CrossRef]
- Ioannides, R.T.; Pany, T.; Gibbons, G. Known Vulnerabilities of Global Navigation Satellite Systems, Status, and Potential Mitigation Techniques. Proc. IEEE 2016, 104, 1174–1194. [Google Scholar] [CrossRef]
- Zangenehnejad, F.; Gao, Y. GNSS smartphones positioning: Advances, challenges, opportunities, and future perspectives. Satell. Navig. 2021, 2, 24. [Google Scholar] [CrossRef]
- Lušić, Z.; Pinčetić, T.; Esko Krančević, P. The role of celestial navigation in modern day and future navigation. In Proceedings of the 10th International Conference on Maritime Transport, Barcelona, Spain, 5–7 June 2024. [Google Scholar]
- Chen, K.; Liang, W.; Zeng, C.; Guan, R. Multi-geomagnetic-component assisted localization algorithm for hypersonic vehicles. J. Zhejiang Univ. A Sci. 2021, 22, 357–368. [Google Scholar] [CrossRef]
- Zidan, J.; Adegoke, E.I.; Kampert, E.; Birrell, S.A.; Ford, C.R.; Higgins, M.D. GNSS Vulnerabilities and Existing Solutions: A Review of the Literature. IEEE Access 2021, 9, 153960–153976. [Google Scholar] [CrossRef]
- Yan, Z.; Yu, H.; Leng, Z.; Yao, Y.; Zhao, X.; Wang, Z. Comprehensive interference estimation and correction methods based on Unscented Kalman Filter for magnetic anomaly detection. Meas. J. Int. Meas. Confed. 2025, 248, 116858. [Google Scholar] [CrossRef]
- Huang, L.; Wang, Z.; Xiong, Q.; Qu, R.; Yao, C.; Li, C. Mamba-VNPS: A Visual Navigation and Positioning System with State-Selection Space. Drones 2024, 8, 663. [Google Scholar] [CrossRef]
- Cai, W.; Huang, S.; Cheng, G.; Long, Y.; Gao, P.; Sun, C.; Dong, H. Bridging Zero-shot Object Navigation and Foundation Models through Pixel-Guided Navigation Skill. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Zheng, C.; Xu, W.; Zou, Z.; Hua, T.; Yuan, C.; He, D.; Zhou, B.; Liu, Z.; Lin, J.; Zhu, F.; et al. FAST-LIVO2: Fast, Direct LiDAR–Inertial–Visual Odometry. IEEE Trans. Robot. 2025, 41, 326–346. [Google Scholar] [CrossRef]
- Gao, J.; Li, K.; Chen, Y. Study on Integration of FOG Single-Axis Rotational INS and Odometer for Land Vehicle. IEEE Sens. J. 2018, 18, 752–763. [Google Scholar] [CrossRef]
- Poletti, L.; Sanchis, D.S.; Siryani, R. A direct approach for high-quality MEMS based IMU/INS production. In Proceedings of the Conference on DGON Inertial Sensors and Systems, Braunschweig, Germany, 15–16 September 2020; pp. 1–19. [Google Scholar]
- Sun, W.; Huang, H.; Sun, P.; Ding, W. MEMS strapdown inertial attitude measurement system using rotational modulation technology. PLoS ONE 2024, 19, e298168. [Google Scholar] [CrossRef] [PubMed]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Zhang, L.; Ye, W.; Yan, J.; Zhang, H.; Betz, J.; Yin, H. Loosely Coupled Stereo VINS Based on Point-Line Features Tracking With Feedback Loops. IEEE Trans. Veh. Technol. 2024, 73, 10916–10931. [Google Scholar] [CrossRef]
- Long, Z.; Xiang, Y.; Lei, X.; Li, Y.; Hu, Z.; Dai, X. Integrated Indoor Positioning System of Greenhouse Robot Based on UWB/IMU/ODOM/LIDAR. Sensors 2022, 22, 4819. [Google Scholar] [CrossRef]
- Han, X.; Li, H.; Hui, N.; Zhang, J.; Yue, G. A Multi-Sensor Fusion-Based Localization Method for a Magnetic Adhesion Wall-Climbing Robot. Sensors 2025, 25, 5051. [Google Scholar] [CrossRef]
- He, L.; Li, B.; Chen, G. PLACE-LIO: Plane-Centric LiDAR-Inertial Odometry. IEEE Robot. Autom. Lett. 2025, 10, 6231–6238. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, W.; Li, W.; Zhou, S.; Zhao, X.; Chen, W. OWP-LIO: A method and experimental study for pose measurement of offshore wind power O&M vessels using Lidar-Inertial odometry. Ocean Eng. 2025, 317, 120107. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, D.; Huo, J. Mounting Misalignment and Time Offset Self-Calibration Online Optimization Method for Vehicular Visual-Inertial-Wheel Odometer System. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Zhou, J.; Nie, X.; Lin, J. A novel laser Doppler velocimeter and its integrated navigation system with strapdown inertial navigation. Opt. Laser Technol. 2014, 64, 319–323. [Google Scholar] [CrossRef]
- Xiang, Z.; Wang, Q.; Huang, R.; Xi, C.; Nie, X.; Zhou, J. A Fast Robust In-Motion Alignment Method for Laser Doppler Velocimeter-Aided Strapdown Inertial Navigation System. IEEE Sens. J. 2022, 22, 17254–17265. [Google Scholar] [CrossRef]
- Xiang, Z.; Wang, Q.; Huang, R.; Jin, S.; Nie, X.; Zhou, J. A Robust Online Calibration Method for SINS/LDV Integrated Navigation System Based on Position Observation. IEEE Sens. J. 2024, 24, 895–908. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, X.; Zheng, J.; Xiong, H.; Zhao, Y. Using GPS Time-Differenced Carrier Phase Observations to Calibrate LDV/INS Integrated Navigation Systems. IEEE Sens. J. 2020, 20, 405–414. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Wang, X.; Huang, C.; Yang, B. 4.11-million Q-factor whole-angle MEMS hemispherical resonator gyroscope with 0.013°/h bias instability. Meas. Sci. Technol. 2024, 35, 115116. [Google Scholar] [CrossRef]
- Ding, X.; Ruan, Z.; Pu, Y.; Zhang, H.; Li, H.; Zhao, L. Bias Modulation of Force-to-Rebalanced Micro Hemispherical Resonator Gyroscope Based on Mode-Rotation. IEEE Sens. J. 2022, 22, 15802–15816. [Google Scholar] [CrossRef]
- Chen, W.; Ding, X.; Qin, Z.; Li, H. Modeling, Characterization, and Compensation of Detection and Actuation Coupling Errors for Whole-Angle Micro Hemispherical Resonant Gyroscope. IEEE Trans. Instrum. Meas. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Nan, F.; Gao, Z.; Han, Y.; Cui, H.; Shang, L.; Zhang, Y. Self-calibration for phase shift in Coriolis vibratory gyroscope with whole-angle mode operation. Measurement 2025, 242, 116043. [Google Scholar] [CrossRef]
- Chen, W.; Ding, A.; Ding, X.; Li, H. A Novel Phase Error Quantitative Characterization Method for Whole-Angle Micro Hemispherical Resonant Gyroscope. In Proceedings of the 2024 IEEE SENSORS, Kobe, Japan, 20–23 October 2024; pp. 1–4. [Google Scholar]
- Sun, J.; Yu, S.; Zhang, Y.; Li, Q.; Xi, X.; Lu, K.; Wu, X.; Xiao, D. 0.79 ppm scale-factor nonlinearity whole-angle microshell gyroscope realized by real-time calibration of capacitive displacement detection. Microsyst. Nanoeng. 2021, 7, 79. [Google Scholar] [CrossRef]
- Han, H.; Wang, L.; Wang, M. A Dynamic Gyro Scale Factor Error Calibration Method for RINSs. IEEE Sens. J. 2021, 21, 20817–20823. [Google Scholar] [CrossRef]
- Gargiulo, A.M.; di Stefano, I.; Genova, A. Model-Based Slippage Estimation to Enhance Planetary Rover Localization with Wheel Odometry. Appl. Sci. 2021, 11, 5490. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, C.; Teng, L.; He, X.; Zhou, W.; Zhang, L. POL-VIO: A Visual Inertial Odometry with Polarization Skylight Compass in Challenge Environment. IEEE Robot. Autom. Lett. 2025, 10, 1–8. [Google Scholar] [CrossRef]
- Li, W.; Wang, G.; Zhang, Q.; Liu, J. LG-VIWO: Visual-Inertial-Wheel Odometry Leveraging the Depth-Aided Local Ground Constraints for Mobile Robots. IEEE Trans. Instrum. Meas. 2025, 74, 8507911. [Google Scholar] [CrossRef]
- Wu, Y.; Kuang, J.; Niu, X. Wheel-INS2: Multiple MEMS IMU-Based Dead Reckoning System With Different Configurations for Wheeled Robots. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3064–3077. [Google Scholar] [CrossRef]
- Tan, C. Dead Reckoning Localization Using a Single Wheel-Mounted IMU With the Simultaneous Estimation of Mounting Parameters. IEEE Sens. J. 2024, 24, 3797–3810. [Google Scholar] [CrossRef]
- Deng, K.; Pan, Y.; Xiao, P.; Tang, X.; Li, J.; Xia, T.; Yuan, J. Separation, Identification, and Compensation of Damping, Detection, and Actuation Errors for Rate-Integrating Hemispherical Resonator Gyroscopes. IEEE Trans. Instrum. Meas. 2025, 74, 1–13. [Google Scholar] [CrossRef]
- Wang, M.; Wu, W.; Zhou, P.; He, X. State transformation extended Kalman filter for GPS/SINS tightly coupled integration. GPS Solut. 2018, 22, 112. [Google Scholar] [CrossRef]





| Method | Heading Error | PRMSE | Odometric Error | Publication Date | Explanation |
|---|---|---|---|---|---|
| Anna Maria Gargiulo et al. [37] | 2° | — | 4% (500 m) | 2021 | Inertial-Wheel Odometry |
| POL-VIO [38] | 1.82° | 8.77 m | —(4.9 km) | 2025 | Visual Inertial Odometry |
| LG-VIWO [39] | — | 10.6 m | —(4 km) | 2025 | Visual-Inertial-Wheel Odometry |
| Wheel-INS2 [40] | 0.55° | — | 0.69% | 2023 | Wheel-INS |
| Caiming Tan [41] | 0.85° | 5.1 m | 0.25% | 2024 | Wheel-INS |
| Ours | 0.35° | 4.9 m | 0.24% (3.7 km) | - | MSRG–RINS/LDV |
| Method | Roll Angle Error | Pitch Angle Error |
|---|---|---|
| Uncalibrated | 0.54 | 0.14 |
| Calibrated | 0.03 | 0.02 |
| Experimental Group | Dual-Position (Calibrated) Horizontal Positioning Error | Reciprocation (Calibrated) Horizontal Positioning Error |
|---|---|---|
| 1 | 40.38 m | 30.19 m |
| 2 | 28.28 m | 35.95 m |
| 3 | 60.87 m | 31.53 m |
| 4 | 32.57 m | 28.18 m |
| 5 | 39.36 m | 19.43 m |
| RMS | 41.82 m | 29.56 m |
| Sensor Categories | Parameter | Technical Indicators |
|---|---|---|
| Gyroscope | Gyroscope Range | ±1000°/s |
| Gyroscope Bandwidth | 100 Hz | |
| Gyroscope Scale Factor Stability | <10 ppm | |
| Accelerometers | Accelerometers Range | ±50 g |
| Bias Instability (warm-up at ambient temperature) | 20 ug | |
| Accelerometers Power Spectral Density | 30 ug/√Hz | |
| LDV | Velocity measurement precision of LDV | <0.1% |
| Velocity limit of LDV | 0.1~40 m/s |
| Experimental Platform | Parameter | Technical Indicators |
|---|---|---|
| UGV | Maximum unloaded speed | 1.6 m/s |
| Overall dimensions | 980 × 745 × 380 mm | |
| Weight | 65 kg | |
| Maximum payload | 150 kg |
| Parameter | Calibrated | Uncalibrated |
|---|---|---|
| Pure-INS Heading Error (RMS) | 0.35° | 0.75° |
| Pure-INS Horizontal Attitude Error (RMS) | 0.17° | 0.25° |
| Horizontal Positioning Error (RMSE) | 4.9 m | 7.7 m |
| Odometric Error (3.7 km) | 0.24% | 0.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Wu, Y.; Chang, L.; Kong, Y.; Sun, H.; Wu, W.; Sun, J.; Zhang, Y.; Xi, X.; Miao, T. Autonomous Navigation of Unmanned Ground Vehicles Based on Micro-Shell Resonator Gyroscope Rotary INS Aided by LDV. Drones 2025, 9, 706. https://doi.org/10.3390/drones9100706
Cao H, Wu Y, Chang L, Kong Y, Sun H, Wu W, Sun J, Zhang Y, Xi X, Miao T. Autonomous Navigation of Unmanned Ground Vehicles Based on Micro-Shell Resonator Gyroscope Rotary INS Aided by LDV. Drones. 2025; 9(10):706. https://doi.org/10.3390/drones9100706
Chicago/Turabian StyleCao, Hangbin, Yuxuan Wu, Longkang Chang, Yunlong Kong, Hongfu Sun, Wenqi Wu, Jiangkun Sun, Yongmeng Zhang, Xiang Xi, and Tongqiao Miao. 2025. "Autonomous Navigation of Unmanned Ground Vehicles Based on Micro-Shell Resonator Gyroscope Rotary INS Aided by LDV" Drones 9, no. 10: 706. https://doi.org/10.3390/drones9100706
APA StyleCao, H., Wu, Y., Chang, L., Kong, Y., Sun, H., Wu, W., Sun, J., Zhang, Y., Xi, X., & Miao, T. (2025). Autonomous Navigation of Unmanned Ground Vehicles Based on Micro-Shell Resonator Gyroscope Rotary INS Aided by LDV. Drones, 9(10), 706. https://doi.org/10.3390/drones9100706





