UAV-Centric Privacy-Preserving Computation Offloading in Multi-UAV Mobile Edge Computing

Abstract

Unmanned aerial vehicles (UAVs) offer high mobility, cost-effectiveness and flexible deployment, but their limited computing and battery resources constrain their development. Mobile edge computing (MEC) can alleviate these constraints by computation offloading. Although reinforcement learning (RL) has recently been applied to optimize offloading strategies, using raw UAV data poses a risk of privacy leakage. To address this issue, we design a privacy-preserving RL-based offloading approach that applies local differential privacy (LDP) to perturb decision trajectories. We theoretically derive the $\mathcal{O}(\sqrt{M}/ϵ)$ regret bound and achieve $(ϵ,\delta )$-LDP for the perturbation mechanism. Finally, we evaluate the efficiency of the proposed approach through experiments.

1. Introduction

With the rapid development of UAV technology, UAVs can quickly reach locations inaccessible by other means of transportation due to their high mobility and flexibility. In areas with insufficient network coverage, UAVs can quickly serve as mobile communication relay stations. Consequently, UAV systems have been widely used for traffic monitoring, forest rescue, precision agriculture, disaster emergency response, and aerial remote sensing. However, their performance in complex scenarios is severely restricted by their limited onboard computing resources, insufficient processing power, and battery capacity, as well as communication latency and stability issues faced in high-demand real-time tasks.

In recent years, Internet of Things (IoT) technology has developed rapidly. The IoT connects a large number of devices together to collect and process device data [1]. The numerous IoT devices require a large amount of storage and computing resources [2]. Traditional cloud computing technology uses remote cloud servers as storage and computing servers for IoT devices. In recent years, computing-intensive tasks have emerged due to the rapid development of mobile terminals and IoT devices. However, traditional cloud computing technology involves transmitting these tasks, which can cause traffic congestion and time delays. In response to the above problems, mobile edge computing (MEC) has emerged [3].

By offloading computation-intensive tasks from IoT devices to nearby MEC servers, MEC technology leverages proximate storage and computational resources. This approach effectively mitigates the network congestion and latency issues inherent in traditional cloud computing paradigms [4]. Among the various MEC technologies, computation offloading can effectively reduce processing delays for mobile UAVs and conserve device energy consumption [5]. In dynamic MEC networks, RL algorithms have been extensively explored for addressing computation offloading problems [6]. Applying mobile edge computing technology to unmanned systems and offloading computing tasks to edge nodes can effectively expand the computing power of UAVs, reduce energy consumption, and improve response efficiency. This technology is the key to overcoming the bottleneck of UAV resources [7].

Due to inherent flaws in RL, training RL algorithms requires powerful cloud servers, which drones must disclose sensitive data to. Attackers can easily obtain this sensitive information and use it to infer the value function in the RL algorithm. The value function represents the private information about the drone’s action preferences in a given state, leading to privacy leaks [8,9,10].

However, the Differential Privacy (DP) technology introduced in existing research will reduce the performance of offloading strategies. Furthermore, the extent of performance loss caused by the addition of DP is unknown until after the offloading strategy has been trained. This leads to significant performance loss in the offloading strategy due to the introduction of DP, wasting computational power and resources. Therefore, establishing the relationship between privacy budget and performance loss before offloading strategy training is an important and necessary research issue, but existing research has failed to establish this quantitative relationship. These limitations pose challenges to the application of RL-based computation offloading methods in practical tasks.

For this purpose, we propose a UAV-centric privacy-preserving RL-based computation offloading approach. This approach adopts the LDP technique to perturb the decision trajectories of UAVs. In order to ensure that the RL-based computation offloading approach converges, we do not simply add LDP noise into decision trajectories. Instead, we model the computation offloading problem as a finite-horizon Markov decision process (FH-MDP), and then add LDP noise to randomize the frequency of each state–action pair in decision trajectories. Finally, we provide a regret bound for the proposed approach. The contributions of this paper are summarized as follows:

1.

We propose a privacy-preserving computation offloading approach for multi-UAV MEC from a UAV-centric perspective. To achieve desirable UAV performance, we establish the relationship between privacy budget and the performance of the offloading policy.

2.

To protect the privacy of decision trajectories of UAVs, we firstly model the computation offloading problem as a finite-horizon Markov decision process. Then, the LDP mechanism is employed to produce Gaussian noise or Randomized Response noise and perturb the count of state–action pairs in the decision trajectory with Gaussian noise or Randomized Response noise.

3.

We theoretically derive the $\mathcal{O}(\sqrt{M}/ϵ)$ regret bound and achieve $(ϵ,{\delta }^{\prime })$-LDP for the Gaussian perturbation mechanism and $(ϵ,0)$-LDP for the Randomized Response mechanism. Then, we conduct experiments to evaluate the effectiveness of the proposed approach.

The remainder of this paper is structured as follows. Section 2 reviews related works. Section 3 introduces the system model and problem formulation. The proposed approach is detailed in Section 4. Theoretical analysis and experimental evaluation are presented in Section 5 and Section 6, respectively. Supplementary discussions are provided in Section 7, and Section 8 concludes the paper.

2. Related Works

Currently, many papers have proposed new methods for optimizing computational offloading strategies, which can be roughly divided into two categories. The first category involves algorithms based on optimization problems. For example, Yan et al. [11] studied the optimization problem of computational offloading strategies, constructed a potential game in an End-Edge Cloud Computing (EECC) environment, in which each user device selfishly minimizes its payoff, and developed two potential game-based algorithms. He et al. [12] used a queuing model to characterize all computing nodes in an environment and established a mathematical model to describe the scenario. They transformed the offloading decision of the target mobile device into three multi-variable optimization problems to study the trade-off between cost and performance. Zhao et al. [13] approached the partial task offloading problem as a dynamic long-term optimization problem to minimize task delays. Lyapunov stochastic optimization tools were used to separate long-term delay minimization from stability constraints, transforming the problem into a per-slot scheduling problem that meets the system’s time-dependent stability requirements. Zhang et al. [14] established a joint optimization problem for offloading decisions, resource allocation, and trajectory planning. Dynamic Terminal Users (TUs) moved using a Gaussian–Markov stochastic model. The goal of the optimization problem was to maximize the minimum secure computing capacity of the TUs. A Joint Dynamic Programming and Bidding (JDPB) algorithm was proposed to solve the optimization problem. Liu et al. [15] introduced cooperative transmission and a reconfigurable intelligent surface (RIS) to jointly optimize user association, beamforming, power allocation, and the task partitioning strategy for local computation and offloading. They exploited the implicit relationships between these and transformed them into explicit forms for optimization. Yang et al. [16] minimized the total energy consumption of all devices by jointly optimizing the binary offloading patterns, CPU frequency, offloading power, offloading time, and intelligent reflecting surface (IRS) phase shift across all devices. Two greedy and penalty-based algorithms were proposed to solve the challenging nonconvex and discontinuous problem.

However, traditional optimization-based algorithms typically assume that the environment is known or static, requiring accurate system models such as channel models. Dynamic changes in the environment require remodeling and solving. And high-dimensional, continuous action spaces, or non-linear problems, are difficult to solve and require a large amount of computation. RL, on the other hand, excels at processing high-dimensional action state spaces through autonomous learning through interaction with the environment. RL can better adapt to dynamic and uncertain environments, discover strategies that are difficult to obtain through analytical methods, and does not require a precise model of the environment, relying on data-driven learning [17]. Therefore, applying RL technology to the training of computational offloading strategy decisions is a relatively common approach in current research.

There are many papers that have proposed RL methods for optimizing strategies in computation offloading. Huang et al. [18] introduced a deep reinforcement learning (DRL) framework that dynamically adjusts task offloading and wireless resources based on changing channel conditions, simplifying the optimization process. Lei et al. [19] developed a Q-learning and DRL framework that balances immediate rewards with long-term goals to minimize time delay and energy cost in mobile edge computing. Wang et al. [20] proposed a task offloading method based on meta-reinforcement learning, which can quickly adapt to new environments with a small number of gradient updates and samples. They proposed a method of coordinating first-order approximation and clipping proxy objectives, and customized sequence-to-sequence (seq2seq) neural networks to model the offloading strategy. Feng et al. [21] developed a distributed offloading algorithm using deep Q-learning to reduce latency and manage energy cost in edge components of the Internet of Vehicles. Liu et al. [22] applied reinforcement learning based on a Markov chain to reduce task completion times within energy limits and created a cooperative task migration algorithm. The above works use RL and other approaches to optimize system latency and energy cost in computation offloading, but do not consider privacy protection.

Recently, the existing works aim to preserve users’ offloading preferences [23], localization [24], and usage patterns [25] for RL-based computation offloading approaches. To provide strict and provable privacy guarantees, DP is adopted to mitigate privacy leakage [9]. Privacy protection in computation offloading can be divided into two main areas: (1) User data privacy protection: Cui et al. [26] proposed a novel lightweight certificate-less edge-assisted encryption scheme (CL-EAED) to offload computationally intensive tasks to edge servers, ensuring that edge-assisted processing does not expose sensitive information, effectively preventing data leakage and improving the efficiency and security of task offloading. A security-aware resource allocation algorithm is proposed for multimedia in MEC [27], focusing on data confidentiality and integrity to minimize latency and energy cost while ensuring security. (2) Privacy protection of offloading strategies: Xu et al. [28] developed a two-stage optimization strategy for offloading in IoT, with the aim of maximizing resource use while minimizing time delay and balancing privacy and performance. Wang et al. [24] proposes a disturbance region determination mechanism and an offloading strategy generation mechanism, which adaptively selects a suitable disturbance region according to a customized privacy factor and then generates an optimal offloading strategy based on the disturbance location within the determined region. However, when privacy protection is introduced, the policy performance will be lost, and the policy performance loss caused by privacy protection in the above studies is inestimable. In order to address this limitation, we propose our approach and make an intuitive comparison with the existing solutions in

Table 1. An intuitive comparison with existing solutions.

Properties	Lei et al.’s [19]	Wang et al.’s [24]	Li et al.’s [27]	Cui et al.’s [26]	Xu et al.’s [28]	Ours
User value privacy	×	×	✓	✓	×	✓
Policy privacy	×	✓	×	×	✓	✓
Time delay	✓	✓	✓	✓	✓	✓
Energy cost	✓	✓	✓	✓	✓	✓
Performance regret	×	×	×	×	×	✓

× and ✓ denote support and nonsupport, respectively.

.

3. System Model and Problem Formulation

3.1. Network Model

In this paper, the network model of multi-UAV MEC is shown in Figure 1, which contains M UAVs, J edge computing servers (ECSs), and a cloud server (CS). In this system, each UAV uploads its own decision trajectory to the cloud server. The decision trajectory of the m-th UAV consists of a sequence of states s, actions a, and rewards r in chronological order. Formally, the decision trajectory of the m-th UAV is $T{r}_m=\left\{(s_{t,m},a_{t,m},r_{t,m})\right|t\in [0,T-1],m\in [1,M]\}\}$. Note that the decision trajectory may encompass sensitive UAV information from which its preferences and location can be deduced. The cloud server will adopt the RL algorithm to train the efficiency of the offloading policy, and then the cloud server will deploy the trained policy to the UAVs. In time slot t, the task of the m-th UAV is denoted by five variables $(I_m,v_l,v_s,B_m,{\tau }_m)$, where $I_m$ is the size of the task in bits, $v_l$ is the CPU frequency of the m-th UAV, $v_s$ is the CPU frequency of the ECS j, $B_m$ represents the remaining battery capacity of the drone, and ${\tau }_m$ represents the deadline for this task. We assume that all UAVs have the same CPU frequency, while each ECS also has the same CPU frequency [23]. Then, the UAV makes the decision based on its own offloading policy. In this paper, we consider a full offloading model in which the UAV makes the offloading decision.

3.2. Cost Model

There are two kinds of costs, time delay and energy cost. Note that due to the abundant energy in cloud servers, the energy consumption and latency of their training offloading policy are not taken into account. If the m-th UAV processes the task locally, the local time delay $D_{l,m}$ is taken by its onboard CPU to complete the computation. This local execution delay is calculated as follows:

$$D_{l,m}\left(t\right)={\displaystyle \frac{I_m\left(t\right)d}{v_l}}.$$

(1)

Here, the local time delay $D_{l,m}$ is proportional to the total computational workload, which is the product of the task size $I_m\left(t\right)$ and the the number of CPU cycles d required per bit. It is inversely proportional to the UAV’s processing speed $v_l$. A larger task or a more complex task will take longer, while a faster CPU will reduce the delay. According to [29], the local energy consumption $E_{l,m}\left(t\right)$ is given by

$$E_{l,m}\left(t\right)=\gamma v_l^2{I}_m\left(t\right)d,$$

(2)

where $\gamma$ is the effective capacitance coefficient based on the CPU architecture [30]. The local energy consumption is proportional to the square of the CPU frequency ($v_l^2$) and the total number of CPU cycles ($I_m\left(t\right)\times d$). If the m-th UAV decides to offload a task to an ECS j, the offloading time delay $D_{s,m}$ is the sum of two components: (1) the time taken to transmit the task data to the ECS over the wireless channel; (2) the time for the ECS to execute the task:

$$D_{s,m}\left(t\right)={\displaystyle \frac{I_m\left(t\right)}{L\left(t\right)}}+{\displaystyle \frac{I_m\left(t\right)d}{v_s}},$$

(3)

Here, the first term ${\displaystyle \frac{I_m\left(t\right)}{L\left(t\right)}}$ is the transmission delay. It depends on the task size $I_m\left(t\right)$ and the achievable transmission rate $L\left(t\right)$. The second term ${\displaystyle \frac{I_m\left(t\right)d}{v_s}}$ is the remote computation delay at the ECS, analogous to the local time delay but using the ECS’s CPU frequency $v_s$. Based on [29], the energy cost of offloading $E_{s,m}$ from UAV m to the ECS j is given by

$$E_{s,m}\left(t\right)={\displaystyle \frac{p{I}_m\left(t\right)}{L\left(t\right)}},$$

(4)

where p is the transmission power of the m-th UAV. The energy cost of loading is the product of the transmission power p and the transmission time (${\displaystyle \frac{I_m\left(t\right)}{L\left(t\right)}}$).

3.3. Privacy Threat

We consider an honest-but-curious cloud server with the capability to accurately execute the RL algorithm process for training offloading policy, though it is susceptible to leaking decision trajectories of UAVs to potential adversaries. Once the adversary acquires the UAV’s decision trajectories, they can utilize techniques such as inverse reinforcement learning (IRL) to extract the UAV’s offloading preferences and usage patterns from the trajectory [9,23]. Then, this privacy information can be used to determine whether a specific UAV is present in the current area, potentially compromising UAV location privacy. Privacy concerns related to this issue have been extensively discussed in [24] with a heuristic privacy metric, and a similar privacy metric was considered in the healthcare IoT [31] and mobile blockchain network [32]. However, the existing approaches primarily focus on ensuring privacy from the perspective of offloading behavior in the case of a trusted cloud server, neglecting to address the potential privacy risks posed by an honest-but-curious cloud server. Hence, a previous work [33] introduced a privacy-aware offloading approach based on DP. However, the proposed approach fails to preserve UAV privacy during the training process of the offloading policy. Similarly to this paper, existing works [34] have proposed privacy-aware offloading approaches based on LDP. However, they fail to anticipate the impact of the privacy budget on the performance of the offloading policy before training.

3.4. Problem Formulation

In this section, we formulate an FH-MDP $\mathcal{M}=(\mathcal{S},\mathcal{A},q,r,T)$, where $\mathcal{S}$ is the state space, $\mathcal{A}$ is the action space, $q(·|s,a)$ is a transition distribution for the new state under the current state, r is a distribution of reward with mean $r(s,a)\in [0,1]$, and $T\in {\mathbb{N}}^{+}$ is the horizon. In this context, the offloading policy $\pi$ is defined as a series of mappings from states to actions. Formally, $\pi =\left\{{\pi }_t\right|1\le t\le T,{\pi }_t:\mathcal{S}\to \mathcal{A}\}$. Under the LDP privacy guarantee, we aim to find the optimal offloading policy ${\pi }^{*}=\left\{{\pi }_t^{*}\right|1\le t\le T,{\pi }_t:\mathcal{S}\to \mathcal{A}\}$ to minimize the total cost $G\left(t\right)$ of time delay and energy consumption for all UAVs, where ${\pi }_t^{*}=arg{max}_a{Q}_t^{*}(s,a)$ and $Q_t^{*}(s,a)$ is the optimal expected cumulative rewards under a state–action pair, which can be derived by the Bellman equations [35]. The objective is to minimize a weighted total cost $G\left(t\right)$ that balances the time delay and energy consumption of the system. The cost function is defined as

$$G\left(t\right)=\eta \mathcal{K}(\sum _{m=1}^M\left(D_m\left(t\right)\right))+(1-\eta )\mathcal{K}(\sum _{m=1}^M\left(E_m\left(t\right)\right)).$$

(5)

$D_m\left(t\right)$ and $E_m\left(t\right)$ represent the composite delay and energy cost for m-th UAV, respectively, which are the sum of local and offloading components depending on the chosen action. $\mathcal{K}$ is the normalization function to scale the delay and energy values to a comparable range, and the weighted average $\eta$ allows the system to prioritize either low latency (when $\eta$ is close to 1) or energy efficiency (when $\eta$ is close to 0).

Based on the formulated FH-MDP, the state, action, and reward of this paper are defined as follows:

1.

State: The state $s_m\left(t\right)=(L\left(t\right),z)$, where $L\left(t\right)$ is the transmission rate and $z\in \{-1,0,1\}$. If $z=-1$, it means that the task of the m-th UAV has been terminated. The reason for this may be that the remaining battery capacity of the drone has been consumed, or the task has reached the deadline. If $z=0$, it indicates that the task pf the m-th UAV has been completed; otherwise, it denotes that the processing is still ongoing.

2.

Action: The action $a_m\left(t\right)\in 0,1$, If $a_m\left(t\right)=0$, it indicates that the m-th UAV processes its task locally; otherwise, the m-th UAV offloads its task to the ECS.

3.

Reward: The reward is the total cost of all UAVs. Formally, $r_m\left(t\right)=G\left(t\right)$.

The above defines a standard FH-MDP for the computation offloading problem. However, as discussed in the privacy threat model (Section 3.3), directly using the original decision trajectory $T{r}_m=\left\{(s_{t,m},a_{t,m},r_{t,m})\right|t\in [0,T-1],m\in [1,M]\}$ for policy training on the edge server introduces privacy risks. To address this issue, we introduce an LDP constraint. The core idea is that each drone perturbs its local trajectory $T{r}_m=\left\{(s_{t,m},a_{t,m},r_{t,m})\right|t\in [0,T-1],m\in [1,M]\}\}$ before offloading. The edge server then learns the offloading policy based solely on these perturbed trajectories. The next section (Section 4) will elaborate on the LDP perturbation mechanism and the corresponding offloading policy learning mechanism under this privacy guarantee.

4. Proposed Approach

4.1. Overview

In the proposed approach, the core idea is to add LDP noise to the decision trajectory of each UAV during policy training. However, simply introducing LDP noise into the decision trajectory will disrupt the temporal coherence of the decision trajectory, which will prevent algorithmic convergence. Hence, we adopt the Gaussian perturbation mechanism and the Randomized Response mechanism based on [36] to randomize the frequency of each state–action pair in the decision trajectory. Then, the honest-but-curious cloud server adopts the perturbed decision trajectories to train the offloading policy. In general, the proposed approach is divided into two parts, namely the LDP perturbation mechanism and offloading policy learning mechanism, with their detailed contents provided in the following.

4.2. LDP Perturbation Mechanism

During the training process, each UAV adopts the LDP mechanism to perturb its decision trajectory $T{r}_m$ locally for privacy preservation. Then, the perturbed decision trajectory ${\widehat{Tr}}_m$ is offloaded to the cloud served by each UAV. In this paper, we provide two LDP perturbation mechanisms, the Gaussian perturbation mechanism and the Randomized Response mechanism. The details are shown in Algorithm 1 and Algorithm 2, respectively.

4.2.1. Gaussian Perturbation Mechanism

At the beginning of Algorithm 1, the input is the decision trajectory of the m-th UAV $T{r}_m$, and the LDP parameters $ϵ$ and c. For each state–action pair $(s,a)$ in $T{r}_m$ (Line 1), the cumulative reward $R_m(s,a)$ and visiting frequency to the state–action pair $C_m(s,a)$ are calculated by Equations (6) and (7), respectively (Line 2):

$$R_m(s,a)=\sum _{t=1}^T{r}_{t,m}{\mathbb{I}}_{\{s_{t,m}=s,a_{t,m}=a\}},$$

(6)

and

$$C_m(s,a)=\sum _{t=1}^T{\mathbb{I}}_{\{s_{t,m}=s,a_{t,m}=a\}},$$

(7)

where $\mathbb{I}$ is the indicator function. Then, the noises $X_m(s,a)$ and $Y_m(s,a)$ are generated independently by Gaussian noise with a standard deviation of $\sigma$ (Line 3), where $\sigma ={\displaystyle \frac{T}{ϵ}}$ [36]. The perturbed cumulative reward $\widehat{R}(s,a)$ and perturbed visiting frequency to the state–action pair $\widehat{C}(s,a)$ are calculated (Lines 4–5). Moreover, the visiting frequency to the trajectory $C_m^{\prime }(s,a,s^{\prime })$ is calculated as follows (Line 7):

$$C_m^{\prime }=\sum _{t=1}^{T-1}{\mathbb{I}}_{\{s_{t,m}=s,a_{t,m}=a,s_{t+1,m}=s^{\prime }\}},$$

(8)

Then the perturbed ${\widehat{C^{\prime }}}_m(s,a,s^{\prime })$ is calculated based on the noise $Z_m(s,a,s^{\prime })$ (Lines 8–9). Finally, the perturbed cumulative reward ${\widehat{R}}_m(s,a)$, perturbed visiting frequency to the state–action pair ${\widehat{C}}_m(s,a)$, and perturbed visiting frequency to the trajectory $C_m^{\prime }(s,a,s^{\prime })$ are returned (Line 12).

Algorithm 1: Gaussian perturbation mechanism.

Input:  $T{r}_m=\left\{(s_{t,m},a_{t,m},r_{t,m})\right|t<T\}$, Parameters: $ϵ$, c;   1: for  $(s,a)\in \mathcal{S}\times \mathcal{A}$  do   2:    Calculate $R_m(s,a)$, and $C_m(s,a)$;   3:    $X_m(s,a),Y_m(s,a)\sim \mathcal{N}(0,{\sigma }^2)$;   4:    ${\widehat{R}}_m(s,a)=X_m(s,a)+R_m(s,a)$;   5:    ${\widehat{C}}_m(s,a)=Y_m(s,a)+C_m(s,a)$;   6:    for $s^{\prime }\in \mathcal{S}$ do   7:      Calculate $C^{\prime }(s,a,s^{\prime })$;   8:      $Z_m(s,a,s^{\prime })\sim \mathcal{N}(0,{\sigma }^2)$;   9:      ${\widehat{C^{\prime }}}_m(s,a,s^{\prime })=Z_m(s,a,s^{\prime })+C_m^{\prime }(s,a,s^{\prime })$; 10:    end for 11: end for 12: return ${\widehat{R}}_m(s,a)$, ${\widehat{C}}_m(s,a)$, $C_m^{\prime }(s,a,s^{\prime })$

4.2.2. Randomized Response Mechanism

The core of the Random Response mechanism algorithm is to perturb the binary indicators in the decision trajectory through biased Bernoulli sampling. These Bernoulli distributions are parameterized by the privacy budget ${ϵ}_0$. The detailed algorithm is shown in Algorithm 2.    

Algorithm 2: Randomized Response mechanism.

Input:  $T{r}_m=\left\{(s_{t,m},a_{t,m},r_{t,m})\right|t<T\}$, Parameters: ${ϵ}_0$   1: for  $(s,a)\in \mathcal{S}\times \mathcal{A}$  do   2:    for $t=1,...,T$ do   3:      Let $I_t={\mathbb{I}}_{\{s_{t,m}=s,a_{t,m}=a\}}$   4:      Sample $X_t\sim \mathrm{Ber}\left({\displaystyle \frac{e^{{ϵ}_0}-1}{e^{{ϵ}_0}+1}}·r_{t,m}·I_t+{\displaystyle \frac{1}{e^{{ϵ}_0}+1}}\right)$   5:      Update ${\widehat{R}}_m(s,a)\leftarrow {\widehat{R}}_m(s,a)+k·(X_t-c)$, where $k={\displaystyle \frac{e^{{ϵ}_0}+1}{e^{{ϵ}_0}-1}}$, $c={\displaystyle \frac{1}{e^{{ϵ}_0}+1}}$   6:      Sample $Y_t\sim \mathrm{Ber}\left({\displaystyle \frac{e^{{ϵ}_0}-1}{e^{{ϵ}_0}+1}}·I_t+{\displaystyle \frac{1}{e^{{ϵ}_0}+1}}\right)$   7:      Update ${\widehat{C}}_m(s,a)\leftarrow {\widehat{C}}_m(s,a)+k·(Y_t-c)$   8:      if $t\le T$ then   9:         for $s^{\prime }\in \mathcal{S}$ do 10:           Let $I_t^{\prime }={\mathbb{I}}_{\{s_{t,m}=s,a_{t,m}=a,s_{t+1,m}=s^{\prime }\}}$ 11:           Sample $Z_t\sim \mathrm{Ber}\left({\displaystyle \frac{e^{{ϵ}_0}-1}{e^{{ϵ}_0}+1}}·I_t^{\prime }+{\displaystyle \frac{1}{e^{{ϵ}_0}+1}}\right)$ 12:           Update ${\widehat{C}}_m^{\prime }(s,a,s^{\prime })\leftarrow {\widehat{C}}_m^{\prime }(s,a,s^{\prime })+k·(Z_t-c)$ 13:         end for 14:      end if 15:    end for 16: end for 17: return ${\widehat{R}}_m(s,a)$, ${\widehat{C}}_m(s,a)$, $C_m^{\prime }(s,a,s^{\prime })$

At the beginning of Algorithm 2, the input is the decision trajectory of the m-th UAV $T{r}_m$. The algorithm then iterates through each time step t in the trajectory (line 2). For each time step, the algorithm first checks whether the current state–action pair matches the target pair $(s,a)$ using the indicator function $I_t$ (line 3).

The perturbation process consists of three main parts: (1) Reward Perturbation (lines 4–5): For the reward component, the algorithm samples a Bernoulli variable $X_t$ with a probability proportional to the actual reward value $r_{t,m}$ when the state–action pair matches. The sampling probability is carefully designed to strike a balance between authenticity and random noise. The perturbed reward is then updated using a linear transformation to ensure an unbiased estimate. (2) Access Count Perturbation (Lines 6–7): Similarly, for access counts, the algorithm samples $Y_t$ from a Bernoulli distribution, where the probability reflects whether a state–action pair was actually accessed. This creates a noisy access record while preserving statistical properties. (3) Transition Count Perturbation (Lines 8–14): For state transitions, the algorithm also considers the next state $s^{\prime }$ and perturbs the transition indicator. This is crucial for preserving the Markov property in the learning model.

The key parameters k and c are derived from the privacy budget ${ϵ}_0$ and ensure that the expected value of each perturbation is equal to its true value, thus providing unbiased estimates under local differential privacy. The Bernoulli parameter is derived from the privacy budget ${ϵ}_0$ using the transformation ${\displaystyle \frac{e^{{ϵ}_0}-1}{e^{{ϵ}_0}+1}}·\mathrm{true}\mathrm{value}+{\displaystyle \frac{1}{e^{{ϵ}_0}+1}}$, thus ensuring the $(ϵ,0)$-LDP guarantee.

It should be noted that, according to [36], the noises $X_m(s,a)$, $Y_m(s,a)$, and $Z_m(s,a,s^{\prime })$ satisfy

$$\left|{\widehat{R}}_m(s,a)-R_m(s,a)\right|\le f_{m,1}\left(ϵ,{\delta }^{\prime },\delta \right),$$

(9)

$$\left|{\widehat{C}}_m(s,a)-C_m(s,a)\right|\le f_{m,2}\left(ϵ,{\delta }^{\prime },\delta \right),$$

(10)

$$\left|\sum _{s^{\prime }}{C}_m^{\prime }-{\widehat{C^{\prime }}}_m\right|\le f_{m,3}\left(ϵ,{\delta }^{\prime },\delta \right),$$

(11)

and

$$\left|C_m^{\prime }-{\widehat{C^{\prime }}}_m\right|\le f_{m,4}\left(ϵ,{\delta }^{\prime },\delta \right).$$

(12)

The above requirements can be satisfied by several perturbation mechanisms, such as Gaussian, Laplace, Randomized Response, and bounded noise mechanisms. But the regret and privacy guarantees of these perturbation mechanisms are of great importance. It can be seen from the above definition that these four functions are increasing functions with respect to m and are decreasing functions with respect to $\delta$. Moreover, according to the characteristics of the local differential privacy mechanism, these four limited strict positive functions can be calculated. We will show the calculation in Section 5.

4.3. Offloading Policy Learning Mechanism

In the offloading policy learning mechanism, the policy is updated by a modified Bellman equation, with details shown in Algorithm 3. In the algorithm, the inputs are the privacy parameters $ϵ$, ${\delta }^{\prime }$, $\delta$, and the outputs of Algorithm 1. Then, for each UAV, the privatization reward ${\widehat{r}}_m(s,a)$ and privatization transition function $\widehat{w}\left(s^{\prime }\mid s,a\right)$ are calculated based on Equation (13) and Equation (14), respectively, which are shown as follows (Line 2).

$${\widehat{r}}_m(s,a)={\displaystyle \frac{{\widehat{R}}_m(s,a)}{{\widehat{C}}_m(s,a)+\alpha f_{m,2}\left(ϵ,{\delta }^{\prime },\delta \right)}},$$

(13)

and

$${\widehat{w}}_m\left(s^{\prime }\mid s,a\right)={\displaystyle \frac{{\widehat{C^{\prime }}}_m\left(s,a,s^{\prime }\right)}{{\widehat{C}}_m(s,a)+\alpha f_{m,3}\left(ϵ,{\delta }^{\prime },\delta \right)}},$$

(14)

where $\alpha$ is a parameter for precision selection and $\alpha \ge 1$. Based on Prop.4 of [36], to achieve the $(ϵ,1-2\delta )-$LDP, the ${\widehat{r}}_m(s,a)$ and $r(s,a)$, as well as $w_m\left(s^{\prime }\mid s,a\right)$ and ${\widehat{w}}_m(s^{\prime }\mid s,a)$, should meet the following constraints, respectively:

$$\begin{array}{c}\hfill \left|r_m(s,a)-{\widehat{r}}_m(s,a)\right|\le p_m(s,a),\end{array}$$

(15)

and

$$\begin{array}{cc}\hfill |w_m-{\widehat{w}}_m|& \le p_m^{\prime }(s,a),\hfill \end{array}$$

(16)

where $ϵ>0,{\delta }^{\prime }\ge 0,\delta >0,\alpha >1$. Then, the modified Bellman equation is shown as follows to update the Q function (Line 3).

$$\begin{array}{cc}\hfill Q_{t,m}(s,a)& ={\widehat{r}}_m(s,a)+b_{t,m}(s,a)+{\widehat{w}}_m{\left(·\mid s,a\right)}^{\top }{V}_{t+1,m},\hfill \end{array}$$

(17)

where $b_{t,m}(s,a)=(T-t+1)·p_m^{\prime }(s,a)+p_m(s,a)$ is a bias compensation term to ensure convergence under LDP noise. Therefore, the offloading policy is calculated by (Line 3)

$${\pi }_{t,m}\left(s\right)=argmax{Q}_{t,m}(s,a).$$

(18)

Algorithm 3: Offloading policy learning mechanism.

Input:  ${\widehat{R}}_m(s,a)$, ${\widehat{C}}_m(s,a)$, $C_m^{\prime }(s,a,s^{\prime })$, Parameters ${ϵ}_0$, ${\delta }_0$, $\delta$   1: for  $m\in [1,M]$  do   2:    Compute ${\widehat{r}}_m(s,a)$, ${\widehat{w}}_m\left(s^{\prime }\mid s,a\right)$ via Equation (13) and Equation (14), respectively;   3:    According to Equations (17) and (18), update the offloading policy ${\pi }_m$;   4:    Send ${\pi }_m$ to m-th UAV. After executing the offloading policy, m-th UAV collects     the decision trajectory $T{r}_m$;   5:    m-th UAV sends back privatized version $\mathcal{L}\left(T{r}_m\right)$ via Algorithm 1;   6: end for

Finally, the cloud server sends ${\pi }_m$ to the m-th UAV, which will collect the decision trajectory $T{r}_m$ and send back a privatized version ${\widehat{Tr}}_m$ via Algorithm 1.

Our perturbation mechanism adds LDP noise to the frequency of state–action pairs, maintaining the convergence of reinforcement learning while preserving privacy. The Markov property relies on the independence of state transitions, and the frequency perturbation is performed on aggregate statistics, which does not destroy the Markov property of individual state transitions. According to the theory of Garcelon et al. [36], as long as the perturbed reward and transition probability estimates are asymptotically consistent and updated via the modified Bellman equation, the RL algorithm will converge under the LDP condition. In Section 5, we prove that the regret bound is $\mathcal{O}(\sqrt{M}/ϵ)$, which theoretically guarantees the convergence of the algorithm in the long run.

5. Theoretical Analysis

In this section, we give the formal proof of $(ϵ,{\delta }^{\prime })-$LDP and regret bound of the proposed approach. The derivation of the regret bound implies the convergence of the algorithm under LDP perturbations. That is, when the number of training rounds is large enough, the policy performance will be close to the optimal policy. Firstly, we prove that the Gaussian perturbation mechanism has the $(ϵ,{\delta }^{\prime })-$LDP guarantee through Theorem 1.

Theorem 1.

Given $0\le ϵ<1$ and ${\delta }^{\prime }>0$, and $c>4ln\left({\displaystyle \frac{24}{{\delta }^{\prime }}}\right)$, the Gaussian perturbation mechanism can achieve $\left(ϵ,{\delta }^{\prime }\right)$-LDP.

Proof. 

Based on Prop.10 in [36], we assume that for the two trajectories $Tr=\left\{(s_t,a_t,r_t)\right|t<T\}$, $T{r}^{\prime }=\left\{(s_t^{\prime },a_t^{\prime },r_t^{\prime })\right|t<T\}$, and the perturbed trajectories $\mathcal{L}\left(Tr\right)=({\widehat{R}}_{Tr},{\widehat{C}}_{Tr},{\widehat{C^{\prime }}}_{Tr})$ and $\mathcal{L}\left({Tr}^{\prime }\right)=({\widehat{R}}_{{Tr}^{\prime }},{\widehat{C}}_{T{r}^{\prime }},{\widehat{C^{\prime }}}_{T{r}^{\prime }})$.

For a given vector $r\in {\mathbb{R}}^{S\times A}$, and since the Gaussian distribution is symmetric, $\forall (s,a)$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathbb{P}\left({\widehat{R}}_{Tr}(s,a)=r(s,a)\right)}{\mathbb{P}\left({\widehat{R}}_{{Tr}^{\prime }}(s,a)=r(s,a)\right)}}=\prod _{s,a}{\displaystyle \frac{\mathbb{P}\left(X_{Tr}={\sum }_{t=1}^T{r}_t{\mathbb{I}}_{\left\{s_t=s,a_t=a\right\}}-r\right)}{\mathbb{P}\left(X_{{Tr}^{\prime }}={\sum }_{t=1}^T{r}_t^{\prime }{\mathbb{I}}_{\left\{s_t^{\prime }=s,a_t^{\prime }=a\right\}}-r\right)}}.\hfill \end{array}$$

(19)

However, considering the squared term and following from Cauchy–Schwartz, we have the inequality

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathbb{P}\left({\widehat{R}}_{Tr}(s,a)=r(s,a)\right)}{\mathbb{P}\left({\widehat{R}}_{{Tr}^{\prime }}(s,a)=r(s,a)\right)}}\le exp\left({\displaystyle \frac{1}{2{\sigma }^2}}\left(2\sqrt{2}T\sqrt{\sum _{s,a}{r}^2}+3T^2\right)\right),\hfill \end{array}$$

(20)

where $\sigma =cT/ϵ$, where c is a constant value. Then, for $c^2\ge 4ln\left({\displaystyle \frac{3}{{\delta }_1}}\right)$, ${\delta }_1$ should satisfy $\mathbb{P}\left(X_{Tr}\in R_2\right)\le {\delta }_1$ and $\mathbb{P}\left(Y_{{Tr}^{\prime }}\in R_2\right)\le {\delta }_1$. Therefore, $\forall (s,a)$, we have

$$\begin{array}{cc}\hfill & \mathbb{P}\left({\widehat{R}}_{Tr}(s,a)=r(s,a)\right)\le \left(ϵ/3\right)\mathbb{P}\left({\widehat{R}}_{{Tr}^{\prime }}(s,a)=r(s,a)\right)+{\delta }_1.\hfill \end{array}$$

(21)

The same goes for $\widehat{C}$ and ${\widehat{C}}^{\prime }$. Then, because $X_{Tr}(s,a)$, $Y_{Tr}(s,a)$, and $Z_{Tr}\left(s,a,s^{\prime }\right)$ are independent, for any two trajectories $Tr$ and ${Tr}^{\prime }$, we have

$$\begin{array}{cc}\hfill & \mathbb{P}\left({\widehat{R}}_{Tr}=r,{\widehat{C}}_{Tr}=n,{\widehat{C}}_{Tr}^{\prime }=n^{\prime }\right)=\mathbb{P}\left({\widehat{R}}_{Tr}=r\right)\mathbb{P}\left({\widehat{C}}_{Tr}=n\right)\mathbb{P}\left({\widehat{C}}_{Tr}^{\prime }=n^{\prime }\right)\hfill \\ \hfill & \le e^{ϵ}\mathbb{P}\left({\widehat{R}}_{Tr}=r^{\prime }\right)\mathbb{P}\left({\widehat{C}}_{{Tr}^{\prime }}=n\right)·\mathbb{P}\left({\widehat{C}}_{{Tr}^{\prime }}^{\prime }=n^{\prime }\right)+2{\delta }_{1}exp\left(2ϵ/3\right)+2{\delta }_1^{2}exp\left(ϵ/3\right)+{\delta }_1^3.\hfill \end{array}$$

(22)

Thus, by choosing ${\delta }_1={\delta }^{\prime }/8$, it holds that $2{\delta }_{1}exp\left(2ϵ/3\right)+2{\delta }_1^{2}exp\left(ϵ/3\right)+{\delta }_1^3\le {\delta }^{\prime }$ for $ϵ\le 1$, and so we can conclude that the Gaussian mechanism is $\left(ϵ,{\delta }^{\prime }\right)$-LDP. □

Then, we prove that the Randomized Response mechanism has the $(ϵ,0)-$LDP guarantee through Theorem 2.

Theorem 2.

For $ϵ>0$ and the parameter ${ϵ}_0=ϵ/6T$, Algorithm 2 is $(ϵ,0)-LDP$.

Proof. 

Like the proof of Theorem 1, consider two trajectories $Tr=\left\{(s_g,a_g,r_g)\right|g<G\}$, $T{r}^{\prime }=\left\{(s_g^{\prime },a_g^{\prime },r_g^{\prime })\right|g<G\}$, the perturbed trajectory $\mathcal{G}\left(Tr\right)=({\widehat{R}}_{Tr},{\widehat{C}}_{Tr},{\widehat{C^{\prime }}}_{Tr})$ and $\mathcal{G}\left({Tr}^{\prime }\right)=({\widehat{R}}_{{Tr}^{\prime }},{\widehat{C}}_{T{r}^{\prime }},{\widehat{C^{\prime }}}_{T{r}^{\prime }})$.

For a given $r\in {\left\{{\displaystyle \frac{-1}{e^{{ϵ}_0}-1}},{\displaystyle \frac{e^{{ϵ}_0}}{e^{{ϵ}_0}-1}}\right\}}^{G\left|\mathcal{S}\right|\left|\mathcal{A}\right|}$, and for each $(g,s,a)\in G\times \mathcal{S}\times \mathcal{A}$, define $y_{g,s,a}^r={\displaystyle \frac{e^{{ϵ}_0}-1}{e^{{ϵ}_0+1}r}}+{\displaystyle \frac{1}{e^{{ϵ}_0+1}}}$ belongs to $\{0,1\}$ because $r\in {\left\{{\displaystyle \frac{-1}{e^{{ϵ}_0-1}}},{\displaystyle \frac{e^{{ϵ}_0}}{e^{{ϵ}_0}-1}}\right\}}^{G\left|\mathcal{S}\right|\left|\mathcal{A}\right|}$, and we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathbb{P}\left(\forall (g,s,a),{\widehat{R}}_{Tr}(g,s,a)=r_{g,s,a}\mid Tr\right)}{\mathbb{P}\left(\forall (g,s,a),{\widehat{R}}_{{Tr}^{\prime }}(g,s,a)=r_{g,s,a}\mid {Tr}^{\prime }\right)}}\hfill \\ \hfill & =\prod _{g,s,a}{\left({\displaystyle \frac{\left(e^{{ϵ}_0}-1\right)r_g\mathbb{G}+1}{\left(e^{{ϵ}_0}-1\right)r_g^{\prime }{\mathbb{G}}^{\prime }+1}}\right)}^{y_{g,s,a}^r}\times {\left({\displaystyle \frac{e^{{ϵ}_0}-\left(e^{{ϵ}_0}-1\right)r_g\mathbb{G}}{e^{{ϵ}_0}-\left(e^{{ϵ}_0}-1\right)r_g^{\prime }{\mathbb{G}}^{\prime }}}\right)}^{1-y_{g,s,a}^r},\hfill \end{array}$$

(23)

where $\mathbb{G}={\mathbb{1}}_{\left\{s_g=s,a_g=a\right\}},{\mathbb{G}}^{\prime }={\mathbb{1}}_{\left\{s_g^{\prime }=s,a_g^{\prime }=a\right\}}$.

Then, for a given $(g,s,a)$, since $r_g\in [0,1]$, the above formula can be simplified as

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\left(e^{{ϵ}_0}-1\right)r_g{\mathbb{1}}_{\left\{s_g=s,a_g=a\right\}}+1}{\left(e^{{ϵ}_0}-1\right)r_g^{\prime }{\mathbb{1}}_{\left\{s_g^{\prime }=s,a_g^{\prime }=a\right\}}+1}}\le exp\left({ϵ}_0\mathbb{S}\right){\displaystyle \frac{e^{{ϵ}_0}-\left(e^{{ϵ}_0}-1\right)r_g{\mathbb{1}}_{\left\{s_g=s,a_g=a\right\}}}{e^{{ϵ}_0}-\left(e^{{ϵ}_0}-1\right)r_g^{\prime }{\mathbb{1}}_{\left\{s_g^{\prime }=s,a_g^{\prime }=a\right\}}}}\le exp\left({ϵ}_0\mathbb{S}\right),\hfill \end{array}$$

(24)

where $\mathbb{S}={\mathbb{1}}_{\left\{s_g=s,a_g=a\right\}}+{\mathbb{1}}_{\left\{s_g^{\prime }=s,a_g^{\prime }=a\right\}}$. Therefore, through the inequality (24), we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathbb{P}\left(\forall (g,s,a),{\widehat{R}}_{Tr}(g,s,a)=r_{g,s,a}\mid Tr\right)}{\mathbb{P}\left(\forall (g,s,a),{\widehat{R}}_{{Tr}^{\prime }}(g,s,a)=r_{g,s,a}\mid {Tr}^{\prime }\right)}}\hfill \\ \hfill & \le \prod _{g,s,a}exp\left(y_{g,s,a}^r{ϵ}_0\mathbb{S}+\left(1-y_{g,s,a}^r\right){ϵ}_0\mathbb{S}\right)=\prod _{g,s,a}exp\left({ϵ}_0\mathbb{S}\right)=exp\left(2{ϵ}_{0}G\right).\hfill \end{array}$$

(25)

The same is true for $\widehat{C}$ and ${\widehat{C}}^{\prime }$. From this, it can be concluded that when ${ϵ}_0=ϵ/6G$, the formula based on the Randomized Response mechanism is $(ϵ,0)-$LDP. □

Then, we prove the regret bound of the proposed approach. Before proving, we provide the definition of regret.

Definition 1.

Given the finite-horizon Markov decision process (FH-MDP) $\mathcal{M}=(\mathcal{S},\mathcal{A},q,r,T)$ in Section 3.4, the regret $\mathsf{\Gamma }\left(M\right)$ in this paper is defined as the performance of the offloading policy, which is defined as the cumulative difference between $V_1^{*}\left(s_{1,m}\right)$ and $V_1^{{\pi }_m}\left(s_{1,m}\right)$ for all UAVs:

$$\mathsf{\Gamma }\left(\mathcal{M}\right)=\sum _{m=1}^M(V_1^{*}\left(s_{1,m}\right)-V_1^{{\pi }_m}\left(s_{1,m}\right)).$$

(26)

Theorem 3.

For any number of states $\left|\mathcal{S}\right|\ge 3$, actions $\left|\mathcal{A}\right|\ge 2$, and $T\ge 2{log}_{\left|\mathcal{A}\right|}\left(\right|\mathcal{S}|-2)+2$, the lower regret bound of the proposed approach satisfies ${\mathbb{E}}_{\mathcal{M}}\left(\mathsf{\Gamma }\left(\mathcal{M}\right)\right)\ge \Omega \left({\displaystyle \frac{T\sqrt{\left|\mathcal{S}\right|\left|\mathcal{A}\right|M}}{min\{exp(ϵ)-1,1\}}}\right)$, where $\mathcal{M}$ is the FH-MDP in this paper.

Proof. 

We set the FH-MDP with $\left|\mathcal{S}\right|$ states and $\left|\mathcal{A}\right|$ actions. Our FH-MDP is a $\left|\mathcal{A}\right|$-ary tree with $\left|\mathcal{S}\right|-2$ states, and each node has $\left|\mathcal{A}\right|$ child nodes. We use $x_t,\dots ,x_T$ to represent the leaf nodes of this tree. Each leaf node can be converted to receive a reward of 1 or 0. And each leaf node converts to reward 0 and reward 1 with the same probability. And we set that there exists a unique action $a^{★}$ and leaf $x_{t^{★}}$ such that $\mathbb{P}\left(1\mid x_{t^{★}},a^{★}\right)={\displaystyle \frac{1}{2}}+\Delta$, $\mathbb{P}\left(0\mid x_{t^{★}},a^{★}\right)={\displaystyle \frac{1}{2}}-\Delta$ for a chosen $\Delta$, and when $\Delta =0$, ${\mathbb{P}}_0\left(1\mid x_{t^{★}},a^{★}\right)={\displaystyle \frac{1}{2}}$, ${\mathbb{P}}_0\left(0\mid x_{t^{★}},a^{★}\right)={\displaystyle \frac{1}{2}}$.

We assume that $T\ge 2ln\left(\right|\mathcal{S}|-2)/ln\left(\right|\mathcal{A}\left|\right)+2$, $b-1$ is the depth of the tree, and the depth of the leaf node is b-1 or b-2. Here, we assume that all leaf nodes $x_t,\dots ,x_T$ are at $b-1$. So the number of leaf nodes is $T={\left|\mathcal{A}\right|}^{b-1}\ge \left(\right|\mathcal{S}|-2)/2$. Thus, our value function is as follows for a policy $\pi$:

$$\begin{array}{cc}\hfill & V^{\pi }\left(0\right)=(T-b)\left(1/2+\Delta \mathbb{P}\left(s_{b-1}=x_{i^{★}},a_{b-1}=a^{★}\right)\right).\hfill \end{array}$$

(27)

Therefore, according to Definition 1, the regret is given as follows:

$$\begin{array}{cc}\hfill & U(M,O)=(T-b)\Delta (M-\sum _{m=1}^M\mathbb{P}\left(s_{m,b-1}=x_{t^{★}},a_{m,b-1}=a^{★}\right))\hfill \end{array}$$

(28)

where we define that

$$F(M,O)=\sum _{m=1}^M{\mathbb{E}}_{\left\{s_{m,b-1}=x_{t^{★},},a_{m,b-1}=a^{★}\right\}}.$$

Thus, $F(M,O)$ is a function of the history observed by the algorithm, and $O=\left(x_{t^{★}},a^{★}\right)$ is the optimal state–action pair.

Considering the LDP setting, the history can be written as

$$\mathcal{L}\left({\mathcal{T}}_M\right)=\left\{\mathcal{L}\left(T{r}_m\right)\mid m\le M\right\},$$

(29)

where $\mathcal{L}$ is a local privacy protection mechanism satisfying $ϵ$-LDP and $T{r}_m=\left\{\left(s_{t,m},a_{t,m},r_{t,m}\right)\mid t\le T\right\}$ is the history trajectory. Thus $F(M,O)$ is a function of $\mathcal{L}\left({\mathcal{T}}_M\right)$. And according to [37], we have

$$\begin{array}{cc}\hfill & \mathbb{E}\left(F(M,O)\right)\le {\mathbb{E}}_0\left(F(M,O)\right)+M\sqrt{KL\left({\mathbb{P}}_0\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\parallel \mathbb{P}\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\right)},\hfill \end{array}$$

(30)

and because of the privacy mechanism $\mathcal{L}$, we also have

$$\begin{array}{cc}\hfill & \mathbb{E}\left(F(M,O)\right)\le {\mathbb{E}}_0\left(F(M,O)\right)+M\sqrt{KL\left({\mathbb{P}}_0\left({\mathcal{T}}_M\right)\parallel \mathbb{P}\left({\mathcal{T}}_M\right)\right)}.\hfill \end{array}$$

(31)

We set $Bound1=KL\left({\mathbb{P}}_0\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\parallel \mathbb{P}\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\right)$ and $Bound2=KL\left({\mathbb{P}}_0\left({\mathcal{T}}_M\right)\parallel \mathbb{P}\left({\mathcal{T}}_M\right)\right)$, and $\mathbb{E}\left(F\right(M,O\left)\right)$ is a special case when $\Delta =0$.

According to Equations (30) and (31), we have

$$\begin{array}{cc}\hfill & \mathbb{E}\left(F(M,K)\right)\le {\mathbb{E}}_0\left(F(M,K)\right)+Mmin\{\sqrt{\mathrm{KL}\left({\mathbb{P}}_0\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\parallel \mathbb{P}\left(\mathcal{L}\left({\mathcal{T}}_M\right)\right)\right.},\sqrt{\mathrm{KL}\left({\mathbb{P}}_0\left({\mathcal{T}}_M\right)\parallel \mathbb{P}\left({\mathcal{T}}_M\right)\right)}\}.\hfill \end{array}$$

(32)

Therefore, according to [36], we get

$$\begin{array}{cc}\hfill Bound1\le & 2{\left(e^{ϵ}-1\right)}^2\ast ln\left({\displaystyle \frac{1}{1-4{\Delta }^2}}\right){\mathbb{E}}_0\left(F(M,O)\right),\hfill \end{array}$$

(33)

and

$$\begin{array}{cc}\hfill Bound2=& {\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{1}{1-4{\Delta }^2}}\right){\mathbb{E}}_0\left(F(M,O)\right).\hfill \end{array}$$

(34)

Therefore, combining Equations (33) and (34),

$$\begin{array}{cc}\hfill & \mathbb{E}\left(F(M,O)\right)\le {\mathbb{E}}_0\left(F(M,O)\right)+Mmin\left\{\sqrt{2}\left(e^{ϵ}-1\right),{\displaystyle \frac{1}{\sqrt{2}}}\right\}\sqrt{{\mathbb{E}}_0\left(F(M,O)\right)ln\left({\displaystyle \frac{1}{1-4{\Delta }^2}}\right)}.\hfill \end{array}$$

(35)

Here, we set that ${\mathbb{E}}_O$ is the expectation of the random variable $\left(x_{t^{★}},a^{★}\right)$, and then there is

$${\mathbb{E}}_O{\mathbb{E}}_0\left(F(M,O)\right)={\displaystyle \frac{M}{T\left|\mathcal{A}\right|}}.$$

(36)

Thus, according to Jensen’s inequality, we have

$$\begin{array}{cc}\hfill & {\mathbb{E}}_{O}U(M,O)\ge (H-d)\Delta K\left(1-{\displaystyle \frac{1}{LA}}-min\left\{\sqrt{2}\left(e^{ϵ}-1\right),\right.\right.\left.\left.{\displaystyle \frac{1}{\sqrt{2}}}\right\}\sqrt{{\displaystyle \frac{K}{LA}}ln\left(1+{\displaystyle \frac{4{\Delta }^2}{1-4{\Delta }^2}}\right)}\right).\hfill \end{array}$$

(37)

So when $T\left|\mathcal{A}\right|\ge 2,M\ge {\displaystyle \frac{T\left|\mathcal{A}\right|}{min{\left\{8\left(e^{ϵ}-1\right),4\right\}}^2}},\Delta =\sqrt{{\displaystyle \frac{T\left|\mathcal{A}\right|}{K}}}\times {\displaystyle \frac{1}{16\sqrt{2}min\left\{\left(e^{ϵ}-1\right),\frac{1}{2}\right\}}}$, we have

$$\begin{array}{cc}\hfill & min\left\{\sqrt{2}(exp\left(ϵ\right)-1),{\displaystyle \frac{1}{\sqrt{2}}}\right\}\sqrt{{\displaystyle \frac{M}{T\mathcal{A}}}ln\left(1+{\displaystyle \frac{4{\Delta }^2}{1-4{\Delta }^2}}\right)}\le {\displaystyle \frac{1}{4}}.\hfill \end{array}$$

(38)

Therefore, we have

$$\begin{array}{cc}\hfill maxU(M,O)& \ge {\mathbb{E}}_{O}U(M,O)\ge {\displaystyle \frac{(T-b)\sqrt{MT\mathcal{A}}}{64min\left\{(exp\left(ϵ\right)-1),\frac{1}{2}\right\}}},\hfill \end{array}$$

(39)

and

$$U\left(M,O^{★}\right)\ge {\displaystyle \frac{(T-b)\sqrt{MT\left|\mathcal{A}\right|}}{64min\left\{(exp\left(ϵ\right)-1),\frac{1}{2}\right\}}},$$

(40)

where there is $O^{★}$ that $maxU(M,O)=$$U\left(M,O^{★}\right)$, because O is a finite random variable. Finally, we can prove that there exists an FH-MDP such that its regret is $\Omega \left({\displaystyle \frac{T\sqrt{\left|\mathcal{S}\right|\left|\mathcal{A}\right|M}}{min\{1,exp(ϵ)-1\}}}\right)$. □

6. Experiment Evaluation

6.1. Experimental Settings

In this section, we conduct the experiments to evaluate the convergence and the regret of the proposed approach. The experiments are simulated using Python and tested on drones. In the experiment, according to [38], we set the number of UAVs to $M=25$ and the number of ECSs to $J=6$. For each UAV, the discount factor $\delta$ is selected from $\{0.1,0.2,0.3,0.5,0.7,0.8,0.9\}$, the task size $I_m$ is selected from {100 KB, 300 KB}, and the transmission rate p is selected from {2 KB/s, 5 KB/s}. The CPU frequency of the m-th UAV $v_l$ and j-th ECS $v_s$ are set to 1 GHz and 3 GHz, respectively, while the number of CPU cycles required to complete each bit of the task is $d=1000$. The effective capacitance coefficient $\gamma$ is set to ${10}^{-26}$. These parameters were chosen based on the performance of commercial drones and edge servers. For example, the task size {100 KB, 300 KB} represents a single image frame or sensor data packet, while the CPU frequency (1 GHz for UAVs and 3 GHz for edge servers) is consistent with typical embedded processors such as the ARM Cortex-A78 and lightweight edge servers. The transmission rate simulates realistic wireless channel conditions over 4G/5G links. Then, to train the offloading policy, the episode is set to 7500, and there are $T=2$ learning steps in each episode.

Finally, we designed five experiments:

(1) We adopt the average loss to evaluate the convergence of the proposed approach by varying task sizes and privacy budgets using the Gaussian perturbation mechanism and the Randomized Response mechanism, respectively.

(2) We show the regret value of the proposed approach under different transmission rates and privacy budgets using the Gaussian perturbation mechanism and the Randomized Response mechanism, respectively.

(3) We compare our approach with a scheme without privacy protection to analyze the performance of the scheme after adding LDP perturbation.

(4) We select different discount factors, a fixed task size, and a transmission rate under the Gaussian perturbation mechanism to evaluate the impact of discount factors on the approach.

(5) We compare our approach with other privacy protection schemes based on reinforcement learning to see the advantages of our scheme.

6.2. Experiment Results

In this section, we use average loss to comprehensively evaluate user-related performance metrics, including time delay and energy consumption. The metric defined by Equation (5) is a weighted sum of time delay and energy consumption that directly reflects the performance at the user level. Furthermore, we use regret to measure the cumulative performance gap between the private mechanism and the offloading policy.

6.2.1. Convergence Evaluation of the Approach

The convergence of the proposed approach based on the Gaussian perturbation mechanism and the Randomized Response mechanism is shown in Figure 2. The privacy parameters $ϵ$ are set to $\{0.1,0.2,0.3,0.9\}$, respectively, and we set the task sizes to $I_m=100$ KB and 300 KB. From the experimental results, we can see the following: (1) The average loss of the offloading strategy gradually decreases with an increase in iterations, and finally, the algorithm reaches convergence. (2) For different task sizes, when the iterations reach 500, the algorithm based on the Gaussian perturbation mechanism reaches convergence, and when the iterations reach 300, the the algorithm based on the Randomized Response mechanism reaches convergence. The convergence speed of the Randomized Response mechanism is faster than the convergence speed of the algorithm based on the Gaussian perturbation mechanism. (3) As the task size increases, the convergence speed of the algorithm gradually slows down, and the task size has a certain influence on the convergence speed of the algorithm. (4) The offloading policy based on the Random Response perturbation mechanism has less performance loss compared to the Gaussian perturbation mechanism.

Although an increase in task size will lead to a slower convergence speed, the algorithm can still converge quickly within a reasonable range. Therefore, the proposed approach has good robustness and adaptability under different task sizes and privacy parameters.

6.2.2. Regret Value Evaluation of the Approach

The regret value of the proposed approach based on the Gaussian perturbation mechanism and the Randomized Response mechanism is shown in Figure 3. The privacy parameters $ϵ$ are set to $\{0.1,0.2,0.3,0.9\}$, respectively, and we set the transmission rate p to 2 KB/s and 5 KB/s. We can see the following: (1) As the number of iterations increases, the regret value of the approach gradually increases. The deviation between the trained strategy performance and the optimal strategy performance gradually accumulates, and the regret value can be quantitatively estimated. (2) As the transmission rate of the wireless communication increases, the regret value generally shows a slight decreasing trend. For the same transmission rate of the wireless communication, the regret values under different privacy parameters are different. (3) For the same transmission rate of the wireless communication, the regret value of the approach is greatly affected by the privacy parameter. (4) Compared with the approach based on the Gaussian perturbation mechanism, the approach based on the Random Response perturbation mechanism has a smaller regret value.

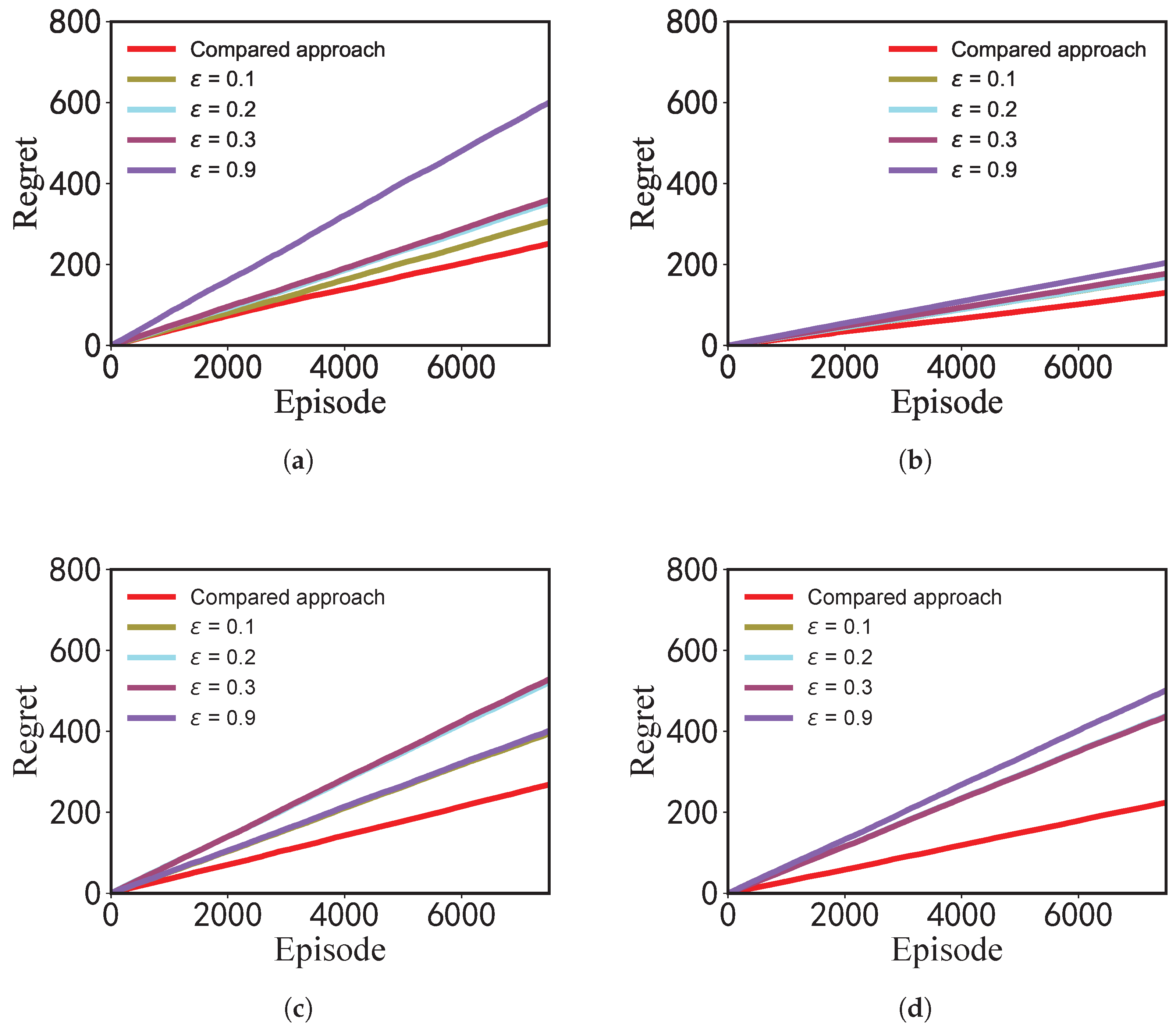
6.2.3. Comparison with Non-Private RL Baseline

To explicitly evaluate the performance loss imposed by the LDP perturbation mechanism in offloading policy learning, we compared our approach with a non-private reinforcement learning baseline [39] (the red “Compared approach” curve in Figure 2 and Figure 3). We adapted the states, actions in the literature [39].

Figure 2 show that the non-private baseline achieves the lowest average loss and the fastest convergence, as expected. Our LDP perturbation approach experiences a slight increase in loss and a slight slowdown in convergence, especially under strict privacy budgets. Figure 3 shows that the non-private baseline maintains the lowest regret throughout training. The regret of our LDP perturbation approach increases with increasing privacy requirements, but remains within an acceptable range.

Adding LDP perturbation results in a controllable but quantifiable performance loss, which is the inherent cost of achieving strict privacy guarantees. This loss can be calculated based on our theoretical analysis and adjusted using the privacy budget $ϵ$, making our approach practical even in environments with varying privacy requirements.

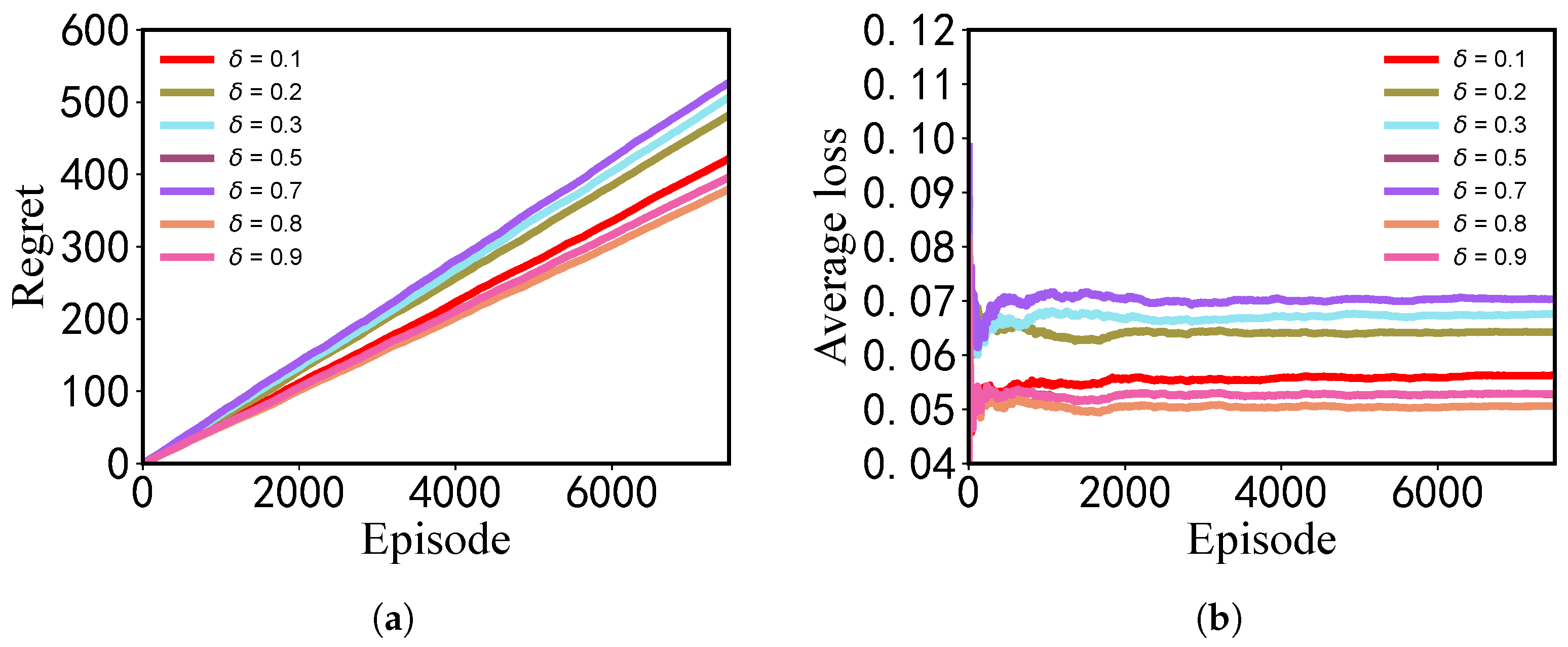
6.2.4. The Impact of Different Discount Factors on the Approach

The impact of different discount factors based on the Gaussian perturbation mechanism on the approach is shown in Figure 4. The discount factor $\delta$ is set to $\{0.1,0.2,0.3,0.5,0.7,0.8,0.9\}$, the task size $I_m$ is set to 100 KB, and the transmission rate p is set to 2 KB/s. The following can be seen from the figure: (1) With the increase of the number of iterations, the regret value of the approach gradually increases under different discount factors, but different discount factors bring different regret values. Among them, when $\delta =0.3$ the regret value is the smallest, while the regret value is the largest when $\delta =0.9$. (2) For different discount factors, when the number of iterations is less than 2000, the average performance loss fluctuates greatly. When the number of iterations reaches 2000, the average performance loss of the approach reaches stability. Corresponding to the regret value, the average performance loss is the smallest when $\delta =0.3$, and the average performance loss is the largest when $\delta =0.9$.

6.2.5. Impact of Privacy Mechanisms on Network Performance

While the LDP perturbation mechanism proposed in this paper effectively protects the privacy of drone offloading preferences, it also affects network performance in three aspects:

1.

Communication overhead: Since each drone must locally perturb its trajectory before uploading, this adds a small amount of computational and communication overhead. However, experiments show that this overhead is acceptable.

2.

Convergence speed: Privacy noise slows down the convergence of policy learning, especially when $ϵ$ is small, as shown in Figure 2.

3.

Policy performance loss: The addition of LDP noise perturbs the estimated state–action frequency, thus affecting the learned offloading policy.

However, through theoretical analysis in Section 5, we establish a theoretical regret bound $\mathcal{O}(\sqrt{M}/ϵ)$, which not only provides strict privacy guarantees but also allows for a tunable performance trade-off, making it suitable for practical drone applications.

6.2.6. The Comparison with Other RL Baseline

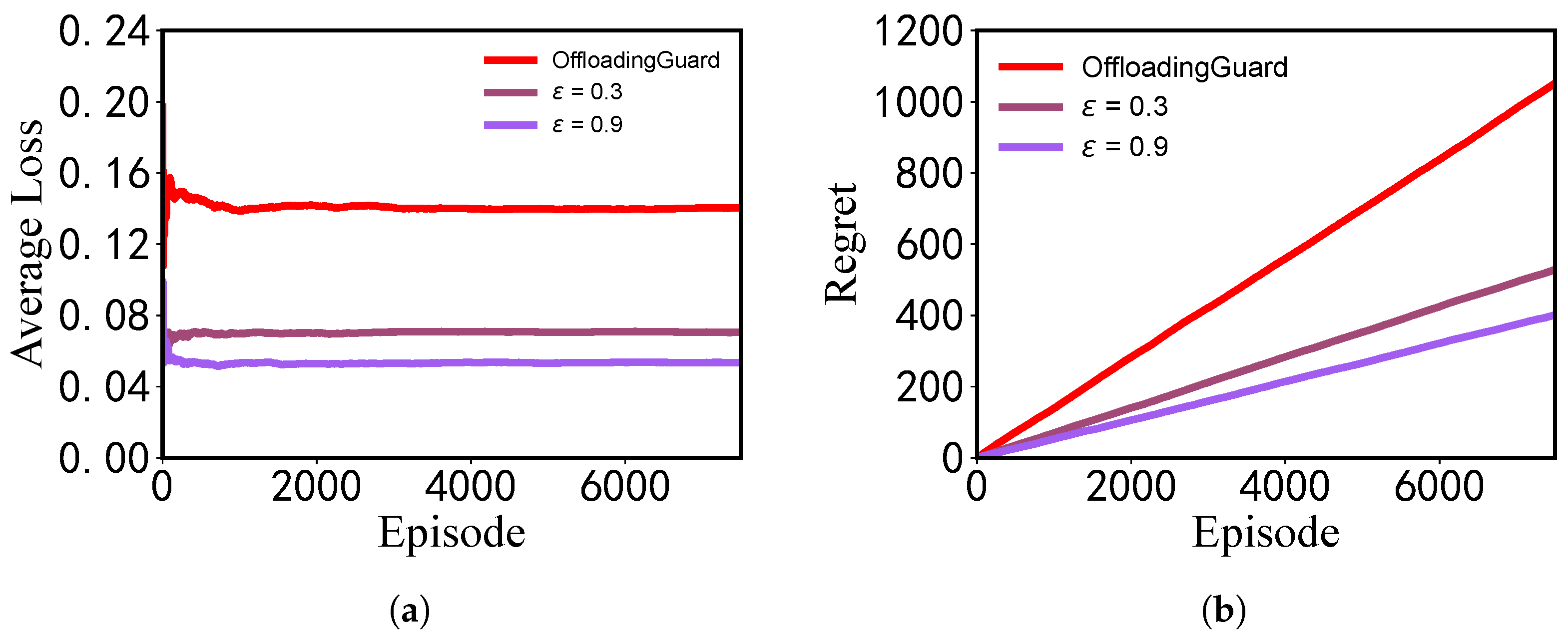
We compared our approach with OffloadingGuard [33]. In the experiment, we selected the Random Response perturbation mechanism in our approach, and set the privacy parameter $ϵ$ to $\{0.3,0.9\}$ and the task size to $I_m=100$ KB. A comparison of the convergence performance of the two methods is shown in Figure 5.

The experiment shows the following: (1) Our approach has a lower average loss than OffloadingGuard and converges faster than OffloadingGuard as the number of iterations increases. (2) The regret values of both methods increase with increasing iterations, but our approach has a smaller regret value than OffloadingGuard, indicating that the introduction of the privacy mechanism in our approach reduces the performance loss of the offloading strategy. Our approach is superior to OffloadingGuard.

Another major innovation of our approach is that it theoretically establishes a quantitative relationship between the introduced privacy perturbation mechanism and the performance loss of the offloading strategy, reducing unnecessary resource waste.

In practical applications, it is necessary to balance privacy protection and algorithm performance. Our experimental results verify the effectiveness and robustness of the approach in different wireless communication link conditions and with different privacy parameters.

7. Discussion

7.1. Partially Offloading

Our research focuses on a full offloading model, where computing tasks are performed entirely locally on the drone or entirely by edge computing servers. However, partially offloading computing tasks to edge servers, where both local and edge servers perform the computation, is a more efficient and versatile approach in MEC [40]. In this section, we discuss the feasibility of extending our approach to support partial offloading.

Extending our approach to partial offloading involves the following changes: (1) Action space: The action space is generalized from a binary action space $a_m\left(t\right)\in 0,1$ to a continuous fraction. For example, the action can be redefined as $a_m\left(t\right)=\rho \in [0,1]$, where $\rho$ represents the proportion of the task offloaded to the edge server, and the remainder is executed locally. (2) Cost model: The time delay and energy cost functions need to be restructured. The total time delay of a task is the maximum of the local computation time delay and the offload delay. The energy consumption is the sum of the local computation energy and the offload transmission energy. (3) State space: The state space contains more detailed information about the current computational task load of the drone and edge server.

The core privacy protection mechanisms of our approach remain highly applicable: (1) LDP perturbation mechanism: The LDP perturbation mechanism (Algorithms 1 and 2) operates on the frequencies of state–action pairs in the decision trajectory. When expanding the continuous action space, the perturbation mechanism remains essentially unchanged. In theory, the $(ϵ,\delta )$-LDP privacy guarantees would still hold. (2) Offloading policy learning mechanism: The offloading policy learning mechanism (Algorithm 3) needs to be adapted to the expanded action space, possibly using deep RL techniques.

7.2. Malicious Servers

Our approach protects the privacy of the offloading policy training in an RL algorithm based on honest-but-curious servers. However, malicious servers may still interfere with the algorithm’s execution process or steal sensitive data. To address these malicious servers, we can deploy the RL algorithm training process in a trusted execution environment (TEE). TEEs implement secure computing through memory isolation within an independent processing environment, offering hardware-based security and integrity protection. Currently, there are many mature TEE solutions, such as ARM Trustzone and Intel SGX. The existing TEE ecosystem is relatively mature and supports deployment on multiple CPU architectures. Although our solution does not directly design protection mechanisms against malicious servers, by leveraging TEEs and existing mature technologies we can deploy our solution on potentially malicious servers, maintaining the same functionality and performance without changing the core structure of our algorithm, effectively extending our approach to malicious-server scenarios [41].

7.3. Partical Use

The proposed UAV-centric privacy-preserving computation offloading scheme offers significant practical advantages in scenarios where UAVs handle privacy-sensitive tasks. It effectively addresses a critical vulnerability: if an honest-but-curious server discloses offloading strategies, attackers controlling edge computing servers (ECSs) could exploit this information to lure UAVs into offloading sensitive tasks to compromised ECSs. In public safety surveillance, this approach prevents the exposure of UAV patrol routes and deters the induced offloading of high-residency video footage. In precision agriculture, it safeguards crop data offloading policies and prevents leaks of yield-related information. For infrastructure inspection, it thwarts the disclosure of defect-data offloading preferences and blocks unauthorized transfers of vulnerability logs. In emergency relay scenarios, it avoids leakage of rescue-zone offloading strategies and thereby prevents voice data breaches. By incorporating local differential privacy (LDP) mechanisms, the proposed method perturbs the frequencies of state–action pairs, thereby securing offloading strategies and fundamentally eliminating the risk of such malicious induction. This provides essential protection for the future large-scale deployment of UAV-assisted edge computing networks.

8. Conclusions

In conclusion, we propose a UAV-centric privacy-preserving offloading approach via RL. Differing from existing works, the proposed approach adds LDP noise to randomize the frequency of each state–action pair in the decision trajectories. We provide two perturbation mechanisms, the Gaussian perturbation mechanism and the Random Response mechanism, and prove that they each achieve the $(ϵ,{\delta }^{\prime })$-LDP and $(ϵ,0)$-LDP guarantee, respectively. Furthermore, we theoretically derive the regret bound of this approach as $\mathcal{O}(\sqrt{M}/ϵ)$, and establish a quantitative relationship between the privacy budget and the performance loss of the offloading strategy before training the offloading strategy. Experiments verify the convergence and efficiency of our approach under different task sizes, transmission rates, and privacy parameters. Theoretical analysis and experimental results demonstrate that our approach provides a feasible and practical solution for protecting drone privacy in real-world MEC applications, enabling system designers to effectively balance privacy and performance based on specific mission requirements.

However, our work has some limitations. Our current system model assumes complete task offloading, but partial offloading is often more efficient and applicable. Furthermore, exploring the combination of other privacy-preserving techniques with our offloading approach and discussing better privacy–utility trade-offs is another promising direction.