Conflict-Free 3D Path Planning for Multi-UAV Based on Jump Point Search and Incremental Update

Abstract

To address the challenges of frequent path conflicts and prolonged computation times in path planning for large-scale multi-UAV operations within urban low-altitude airspace, this study proposes a conflict-free path planning method integrating 3D Jump Point Search (JPS) and an incremental update mechanism. A hierarchical algorithmic architecture is employed: the lower level utilizes the 3D-JPS algorithm for efficient single-UAV path planning, while the upper level implements a conflict detection and resolution mechanism based on a dual-objective cost function and incremental updates for multi-UAV coordination. Large-scale UAV path planning simulations were conducted using a 3D grid model representing urban low-altitude airspace, with performance comparisons made against traditional methods. The results demonstrate that the proposed algorithm significantly reduces the number of path search nodes and exhibits superior computational efficiency for large-scale UAV path planning. Specifically, under high-density scenarios of 120 UAVs per square kilometer, the proposed DOCBS + IJPS method can reduce the conflict-free path planning time by 35.56% compared to the traditional CBS + A* conflict search and resolution algorithm.

1. Introduction

With the vigorous development of the urban low-altitude economy, multiple Unmanned Aerial Vehicles (UAVs) demonstrate immense application potential across numerous domains, including logistics delivery [1], emergency response [2], and urban inspection [3]. Particularly in complex task scenarios such as autonomous urban logistics delivery and emergent disaster rescue operations, multi-UAV systems are highly favored due to their unique efficiency and flexibility. However, within the constrained airspace of urban low-altitude environments characterized by dense building structures, the probability of path conflicts among UAVs increases exponentially as their number grows. Furthermore, constraints such as dynamic changes in task destinations and the necessity of obstacle avoidance significantly exacerbate the probability of conflicts in multi-UAV planned paths, leading to a substantial increase in planning time [4]. Therefore, reducing the probability of path conflicts and enhancing the computational efficiency of planning and conflict resolution for large-scale multi-UAV systems within limited urban airspace constitutes a critical challenge for achieving safe and efficient UAV path planning.

1.1. Related Prior Work

This section will conduct a review of relevant research on multi-drone path planning and multi-drone path conflict detection and resolution.

The problem of drone path planning essentially falls within the domain of Multi-Agent Path Finding (MAPF). Existing path planning algorithms can be primarily categorized into four classes: graph search-based algorithms, sampling-based algorithms, swarm intelligence algorithms, and machine learning-based methods [5].

Among these, graph search-based algorithms such as A* [6] and Dijkstra [7] are the most widely applied. For instance, Biao Zhang et al. [8] proposed a weighted improved A* algorithm for path planning in radioactive environments, enhancing search efficiency. Zhe Xia et al. [9], based on Building Information Modeling (BIM), refined the boustrophedon-A* algorithm through multi-heuristic optimization, achieving complete coverage path planning for climbing robots in facility inspection. While these methods are relatively straightforward to implement, they exhibit suboptimal performance in adapting to dynamic environments and struggle in complex, high-dimensional scenarios. Furthermore, resolving path conflicts often relies on computationally expensive repeated replanning.

Sampling-based algorithms, such as Rapidly-exploring Random Trees (RRT) [10] and Artificial Potential Fields (APF) [11], offer advantages like low algorithmic complexity and high search efficiency. However, they cannot guarantee the optimality of the planned paths. Crucially, for path conflicts, random sampling significantly increases the probability of conflicts occurring.

Swarm intelligence algorithms, including Ant Colony Optimization (ACO) [12] and Particle Swarm Optimization (PSO) [13], can find near-optimal solutions for complex path planning problems. Nevertheless, these algorithms suffer from high complexity and depend on frequent interactions between agents. An increase in the number of drones leads to exponentially increasing computational complexity. Additionally, their reliance on iterative optimization means they may fail to converge in large-scale drone scenarios, potentially leaving path conflicts unresolved.

Within machine learning-based approaches, Reinforcement Learning (RL) [14] and Deep Reinforcement Learning (DRL) [15] are currently widely applied. These methods are suitable for path planning in unknown environments. For example, Hu Y. et al. [16]. utilized a graph neural network designed with role-based interaction to plan paths for each agent. While these methods demonstrate good adaptability to dynamic environments, they require substantial training data and consume significant computational resources.

Each of the aforementioned algorithm categories possesses distinct advantages for path planning. However, they all face significant challenges in effectively resolving path conflicts among drones in large-scale scenarios.

The detection and resolution of path conflicts among multiple drones, a critical technology for ensuring flight safety, has garnered widespread attention from researchers both domestically and internationally. Existing methods can be categorized into two types: coupled approaches [17] and decoupled approaches [18]. While coupled methods can guarantee solution optimality, their computational complexity increases exponentially in large-scale drone scenarios. In contrast, decoupled methods are generally employed for multi-drone task assignment/scheduling and path conflict resolution. For instance, Ming Wei et al. [19] and Gang Sun et al. [20] decoupled the task scheduling process into resource allocation and task offloading decisions. Similarly, in the context of path conflicts, the conflict resolution problem is typically decomposed into interrelated subproblems. This approach offers higher computational efficiency and greater potential for optimization, making it more suitable for large-scale drone scenarios.

The Conflict-Based Search (CBS) algorithm [21] is a classical decoupled method for solving multi-drone path planning and conflict resolution problems. CBS employs a hierarchical planning framework. At the low level, optimal paths are planned for each individual drone without considering inter-drone conflict constraints, and a conflict constraint tree is constructed based on path conflict detection. Building on this, the high-level planner resolves conflicts between different drone paths by adding constraints. This framework enables efficient planning for multiple drones while guaranteeing the optimality of the solution. Due to its flexibility and compatibility, CBS has been applied in areas such as multi-robot goods transportation in smart warehouses [22] and multi-drone path planning [23]. Researchers have also conducted extensive studies on improving CBS, achieving significant results. Ren et al. [24] proposed a Multi-Objective Conflict-Based Search (MO-CBS) algorithm, theoretically proving its ability to find all uniquely cost-optimal solutions. However, this method primarily enhances the optimality of the objective function and is suitable for scenarios with fewer agents in two-dimensional (2D) environments. As the number of objectives and agents increases, the size of the Pareto-optimal solution set can explode, leading to a sharp rise in computational overhead and hindering its ability to meet the requirements for efficient conflict resolution in large-scale drone path planning. Boyarski et al. [25] introduced priority strategies to classify and optimize path conflicts, proposing the Improved Conflict-Based Search (ICBS) algorithm. ICBS enhances the expansion efficiency of the conflict constraint tree, but its mechanism for judging conflict types is complex and computationally intensive. Sharon et al. [26] proposed the Meta-Agent Conflict-Based Search (MA-CBS) algorithm. This method, when conflicts exceed a certain threshold, selects a pair of conflicts to resolve by establishing a conflict resolution priority and reduces the search dimension of the constraint tree through the concept of meta-merging. While MA-CBS improves efficiency for 2D path planning to some extent, suboptimal meta-merging strategies can degrade solution efficiency or even prevent finding a feasible solution. Moreover, the computational cost for joint path search and conflict detection of meta-agents increases significantly with the number of agents. Felner et al. [27] designed a heuristic cost function based on the conflict constraint tree to reduce the number of node expansions, thereby improving the algorithm’s computational speed. Furthermore, Li et al. [28] incorporated two effective heuristic values into the ICBS cost function using dependency graphs and weighted dependency graphs to reduce computational load. However, poorly designed heuristic functions may prevent the algorithm from finding a feasible solution. Cohen et al. [29] improved algorithm efficiency by dividing the total search time into multiple segments and randomly reshuffling the planning order of agents within each segment before replanning. The methods mentioned above are all oriented towards path planning for agents in 2D space and cannot ensure their applicability and computational efficiency in three-dimensional (3D) space.

1.2. Our Contributions

Although significant progress has been made in the improvement and application of Conflict-Based Search (CBS) algorithms both domestically and internationally, existing research methods still face several challenges. To address these issues, this paper proposes a conflict-free path planning method based on an incremental update mechanism and 3D Jump Point Search (3D-JPS), specifically designed for large-scale unmanned aerial vehicle (UAV) operations in constrained urban airspace. The main contributions of this study are as follows:

(1) Enhanced Computational Efficiency: Considering the computational limitations of the A* algorithm in three-dimensional environments, we adopt the 3D-JPS algorithm as the underlying search algorithm to replace traditional A*. This addresses the challenges of large search spaces and extensive data processing in 3D environments, thereby improving the computational efficiency of UAV path planning.

(2) Incremental Update Mechanism: We establish an incremental update mechanism. This mechanism requires only local replanning when conflicts are detected in a drone’s path, thereby avoiding computationally expensive global replanning and significantly reducing planning time.

(3) Dual-Objective Cost Function: Using a traditional single-cost objective as the sole criterion can adversely affect conflict resolution efficiency. Instead, we adopt a dual-objective cost function. This approach reduces the expansion of nodes in the conflict tree, enabling faster identification of conflict-free paths and improving overall conflict resolution efficiency.

The remainder of this paper is structured as follows: Section 2 establishes a grid-based airspace model, along with constraint models for single and multiple drones, and analyzes flight constraints and conflict-free requirements. Section 3 details the improved CBS algorithm incorporating 3D-JPS [30] and the incremental update mechanism. Section 4 evaluates the algorithm’s performance through simulation experiments. Finally, the conclusion is presented in Section 5.

2. Problem and Description

The multi-UAV path planning problem is a specialized form of the multi-agent pathfinding problem, which can be approximately transformed into planning a set of conflict-free paths (P = {p₁,p₂,…,p_n}) for N UAVs in an undirected, unweighted 3D airspace map. The objective is to achieve optimal total path cost while ensuring safe and efficient completion of the designated mission [31]. In an undirected, unweighted graph G = (V,E), V represents the set of node center coordinates in the airspace map, and E denotes the collection of connecting edges between map nodes.

2.1. Grid-Based Airspace Environment Modeling

To provide a clearer and more intuitive description of UAV path planning and conflict issues in three-dimensional space, this study employs the GeoSOT spatial gridding method [32] to partition the actual urban low-altitude airspace into a grid map G composed of m × m × m unit grids. In this context, the undirected and unweighted graph G = (V,E) consists of a set V representing the central coordinates of grid nodes and a set E representing the connecting edges between these grid node centers, which can be specifically expressed as:

$$\left\{\begin{array}{l}V=V_O+V_N+V_S+V_E\\ V_N=\left\{g_{xyh}^{p}p=0\right\}\\ V_O=\left\{g_{xyh}^{p}p=1\right\}\\ V_S=\left\{g_{xyh}^{p}p=2\right\}\\ V_E=\left\{g_{xyh}^{p}p=3\right\}\end{array}\right.$$

(1)

where $g_{xyh}^p$ represents the unit grid, xyh denotes the coordinates of the grid center, and p represents the attribute information of the unit grid, which is used to distinguish between safe free grids $V_N$, obstacle grids $V_O$, task start grids $V_S$, and task end grids $V_E$.

The spatial grid partitioning method divides space into different scales, and the grid scale significantly impacts path planning. An excessively large grid scale causes the planned path to deviate from the theoretically optimal solution, while an overly small scale increases computational load. Since the grid center points serve as waypoints for UAV flight paths, and these paths must comply with UAV performance constraints, it is essential to rationally select the grid cell size based on UAV performance and mission requirements to achieve mutual alignment between grid scale and performance limitations.

2.2. Single UAV Path Planning Model

To address the global path planning problem for unmanned aerial vehicles (UAVs), this paper comprehensively considers UAV performance constraints and mission requirements to construct a multi-constrained single-UAV path planning model.

In path planning problems, by discretizing the planning time into a time series $T=\left\{T_0,T_1,T_2,\dots \right\}$, the UAV ($u_i$)’s flight path ($p_i$) is transformed into a mapping sequence from the time series to the coordinates of path nodes, which can be expressed as:

$$p_i=\left\{l_i\left(0\right),l_i\left(1\right),\dots ,l_i\left(t\right),\dots ,l_i\left(c_i\right)\right\}$$

(2)

$$l_i\left(t\right)=〈x_i,y_i,h_i,T_i〉$$

(3)

where $l_i(t_i)$ represents the grid cell occupied by the UAV $u_i$ at time $t_i$, x_i, y_i, h_i denotes the coordinate position of the grid cell, and c_i is the length of the flight path $p_i$. The flight paths planned by each UAV and the path segments between waypoints must satisfy the UAV performance constraints described below.

For the multi-UAV path planning problem studied in this paper, we select and derive a set of flight constraints suitable for this paper to consider the key performance constraints in UAV path planning. Given that this study focuses on preplanned path planning for UAVs under the assumption of uninterrupted communication bandwidth, the following three types of flight constraints are considered:

(1)

Maximum and minimum flight altitude constraints

During urban airspace operations, UAVs consume less energy when flying closer to the ground, but this also increases the risk of collisions with buildings and other structures, potentially causing casualties. Therefore, a minimum flight altitude must be established. Additionally, according to UAV flight management regulations, different types of UAVs have corresponding maximum altitude restrictions in urban airspace. Consequently, UAV flight paths must satisfy the following constraints:

$$H_{\min }\le h_i\le H_{\max }$$

(4)

where H_min and H_max represent the minimum and maximum flight altitudes, respectively, and h_i denotes the altitude of the UAV waypoint.

(2)

Maximum range constraints

The energy carried by the UAV is limited, and its maximum range is assumed to be L_max. If the planned range exceeds the maximum range, the mission cannot be completed. The single-flight range of the UAV should not exceed the maximum flight range, with the specific constraints as follows:

$${\displaystyle \sum _{i=1}^{c_i-1}d(l_i,l_{i+1})\le L_{\max }}$$

(5)

where L_max represents the maximum range, $d(l_i,l_{i+1})$ denotes the distance between each pair of waypoints, and c_i indicates the number of path segments.

(3)

Maximum horizontal turning angle, maximum climb angle constraints

Due to the limitations of the UAV’s own performance, the turning angle between adjacent waypoints during flight cannot exceed its maximum horizontal turning angle, which essentially constrains its turning radius. Similarly, the climb angle must not exceed its maximum climb angle. Exceeding these constrained angles during UAV flight may lead to unstable attitude, thereby affecting overall performance. Assuming the waypoint of the UAV flight is $l_i\left(t\right)=〈x_i,y_i,h_i,T_i〉$, the following constraints must be satisfied:

$$\left\{\begin{array}{l}{\phi }_i=\arccos ({\displaystyle \frac{\overrightarrow{l_{i-1}^{\prime }{l}_i^{\prime }}\cdot \overrightarrow{l_i^{\prime }{l}_{i+1}^{\prime }}}{\left|\overrightarrow{l_{i-1}^{\prime }{l}_i^{\prime }}\right|\cdot \left|\overrightarrow{l_i^{\prime }{l}_{i+1}^{\prime }}\right|}})\\ {\theta }_i=\arccos \left({\displaystyle \frac{\left|\overrightarrow{l_i^{\prime }{l}_{i+1}^{\prime }}\right|}{\left|\overrightarrow{l_i{l}_{i+1}}\right|}}\right)\\ \left|{\phi }_i\right|\le {\phi }_{\max }\left|{\theta }_i\right|\le {\theta }_{\max }\end{array}\right.$$

(6)

where $l_i^{\prime }$ represents the horizontal projection of the path node, while ${\phi }_{\max },{\theta }_{\max }$ denote the maximum horizontal turning angle and maximum climb angle, respectively.

2.3. Multi-UAV Path Conflict Model

When planning flight paths for multiple UAVs, ensuring the safety and conflict-free nature of the paths are critical constraints. Priority must be given to avoiding no-fly zones and airspace occupied by environmental obstacles to establish effective flight paths for UAV operations, subject to the following constraints:

$$l_i(t)\in \left\{\left.g_{xyh}^p\right|p=0\right\},\forall u_i\in U,t\in T$$

(7)

where $l_i(t)$ is the same as Equations (2) and (3) mentioned above, represents the grid node unit in the UAV flight path, indicating that only safe and obstacle-free grid units can be included in the UAV flight path.

More critically, it is essential to consider the conflict constraints between UAVs. The path conflicts of UAVs can be primarily categorized into node conflicts and edge conflicts. Node conflicts refer to the scenario where any two UAVs arrive at the same grid node simultaneously at any given moment, which can be expressed as the constraint information:

$$l_i(t)\ne l_j(t),\forall u_i,u_j\in U,t\in T,i\ne j$$

(8)

where $u_i,u_j$ represents any two UAVs belonging to the UAV set, and $l_i(t)$ denotes the grid node unit in the flight path of UAV.

Edge conflicts refer to the situation where any two drones exchange positions or traverse the same edge simultaneously, which can be expressed as the constraint:

$$\begin{array}{l}\forall u_i,u_j\in U,t\in T,i\ne j\\ l_i(t)\ne l_j(t+1),l_i(t+1)\ne l_j(t)\end{array}$$

(9)

The two aforementioned conflicts, as illustrated in Figure 1, indicate that a path conflict occurs between UAVs once they violate the conflict constraints specified in Equations (8) and (9), it means that a path conflict occurs between the UAVs, which is:

$$C_{ij}=〈u_i,u_j,l(t),t_i〉$$

(10)

where $u_i,u_j$ represents the two UAVs involved in the conflict, $l(t)$ denotes the grid node unit where the conflict occurs, and $t_i$ indicates the time of the conflict.

3. Incremental Update-Based Conflict Jump Point Search Algorithm

3.1. Conflict-Based Search Algorithm

The conflict-based search algorithm decouples the multi-UAV path planning process into a two-layer search structure. The lower-layer search decomposes the multi-UAV path planning problem into multiple single-UAV path planning tasks, thereby obtaining feasible solutions that satisfy constraints within a short time. The upper-layer search continuously detects and resolves path conflicts among UAVs.

In the upper layer of the conflict-based algorithm, a binary tree-structured constraint tree is constructed and maintained for search. Each node N in the constraint tree contains the conflict constraint information N.constraints for all UAV paths, the path set N.solution for all UAVs, and the total cost N.cost of all UAV paths. Any UAV in the multi-UAV system can access the path information of other UAVs. The upper layer of the algorithm detects and determines whether path conflicts exist among UAVs based on their global path information. During the upper-layer search, a priority queue OPEN is first established to store nodes to be searched, sorted in ascending order according to the node cost N.cost.

During the initial run of the algorithm, a root node without constraints is created, and the initial path planning is performed to obtain the N.solution of the root node. The node with the minimum cost is then extracted from the priority queue to check whether path conflicts exist in the path set. If conflicts are detected, constraints are added accordingly, and the lower-layer A* algorithm is employed to replan the paths after conflict resolution, thereby eliminating path conflicts between the two drones. Two child nodes are then generated and added to the priority queue OPEN. Following the minimum-cost strategy, a node is selected from OPEN to continue adding constraints and expanding nodes. This process iterates until no path conflicts remain in the path set. Among all conflict-free nodes, the one with the minimum cost is selected as the target node, whose solution represents the optimal conflict-free paths for multiple drones. The lower-layer algorithm typically employs the A* algorithm for both initial path planning and replanning after conflict detection. The primary advantage of conflict-based search algorithms lies in their ability to ensure optimality while planning conflict-free paths for multiple drones.

3.2. Incremental Update-Based 3D Jump Point Search Algorithm

The CBS algorithm typically employs the A* algorithm for initial low-level path planning and path replanning after conflict detection. However, the traditional A* algorithm exhibits exponential growth in computational complexity in three-dimensional environments. To accelerate the search process, this paper adopts the JPS algorithm as an alternative to the A* algorithm for low-level path searching. The JPS algorithm is a variant of the A* algorithm designed for grid-based maps. It leverages natural neighbor pruning and forced neighbor pruning rules to reduce the search space, thereby improving computational efficiency. The natural neighbor pruning rule states that when a node n in the neighborhood of the current node x contains no obstacles, and the path cost len from the parent node p(x) through the current node x to the target node n is less than that via other intermediate nodes, then node n is considered a natural neighbor node.

The forced neighbor pruning rule states that when there is an obstacle among the neighbors of the current node x, and the cost of the path from the parent node p(x) through the current node x to the target node n is less than the cost of any other path to node n that does not pass through x, then node n is identified as a forced neighbor node.

The jump point rule adds nodes that satisfy the natural neighbor and forced neighbor conditions to the search list, thereby reducing the search space. It then compares their heuristic cost function values to select the optimal node, ultimately obtaining the planned path through recursive iteration.

The JPS algorithm demonstrates significant efficiency advantages in planning single-agent flight paths and can handle complex scenarios in high-dimensional environments. However, its search rules need to be extended for three-dimensional space, and its heuristic function requires refinement to accommodate UAV constraints and safety requirements.

3.2.1. Expansion and Improvement of 3D Jump Point Search

The traditional Jump Point Search (JPS) algorithm is inherently designed for two-dimensional environments. When applied to three-dimensional space for initial path planning, it is necessary to extend its neighbor pruning rules. Specifically, the extension follows the method described in reference [30]. In the three-dimensional environment, both the forced neighbors and natural neighbors increase significantly, and the number of search directions expands to 26 possible movement directions, as illustrated in Figure 2. The rotorcraft UAV studied in this paper is capable of vertical take-off and landing. During the expanded search process, the algorithm evaluates each direction to verify whether it satisfies the motion constraints of the UAV outlined in Section 2.1, and excludes any directions that violate these constraints.

During the search for flight paths, each free grid is selected with equal probability, resulting in poor path safety. However, in practical scenarios, although certain grids may not collide with the UAV, the safety risks faced by the UAV vary due to differences in obstacle density around the grid. To enhance path safety by considering the disparity in obstacle density around grids, this paper defines a grid risk coefficient to quantify the safety risk level of each grid node, as follows:

$$r={\displaystyle \frac{n_{obstacle}}{n_{surround}}}$$

(11)

where r represents the grid risk coefficient, while $n_{obstacle},n_{surround}$ denotes the number of obstacle grids and the total number of surrounding grids in the neighborhood of the grid, respectively. The calculated risk coefficient ranges between 0 and 1.

As an improved variant of the A* algorithm, the JPS algorithm also employs a heuristic function for optimal path node search. Its cost function can be expressed as [30]:

$$f(n)=g(n)+h(n)$$

(12)

where f(n) represents the total estimated cost, g(n) denotes the actual flight distance from the starting point to the current node n, serving as the actual cost function; h(n) indicates the estimated cost from node n to the target endpoint, acting as the heuristic function.

In complex urban airspace, path planning based solely on path length as the cost may result in higher risks and excessive turns. By incorporating UAV constraints and risk factors, the cost function and heuristic function are improved. The enhanced cost function is as follows:

$$\begin{array}{l}{g}_s(n)=\sqrt{{(x_n-x_s)}^2+{(y_n-y_s)}^2+{(z_n-z_s)}^2}\\ g_r(n)=r(n)·g_s(n)\\ g(n)={\alpha }_1{g}_s(n)+{\alpha }_2{g}_r(n)\end{array}$$

(13)

where g_s(n) represents the Euclidean distance in three-dimensional space, which is the actual movement cost from the starting point to the current node; g_r(n) denotes the cumulative risk cost; ${\alpha }_1,{\alpha }_2$ are the weighting coefficients, satisfying ${\alpha }_1+{\alpha }_2=1$.

The improvement of the heuristic function, similar to the cost function, should also consider risk cost and three-dimensional distance as estimates. The improved heuristic function is as follows:

$$\begin{array}{l}{h}_s(n)=\sqrt{{(x_n-x_g)}^2+{(y_n-y_g)}^2+{(z_n-z_g)}^2}\\ h_r(n)=r(n)·h_s(n)\\ h(n)={\alpha }_1{h}_s(n)+{\alpha }_2{h}_r(n)\end{array}$$

(14)

Meanwhile, in order to improve the search speed, the heuristic function weight coefficients are designed, and the obtained cost function as follows:

$$\begin{array}{l}f(n)=g(n)+w(n)\times h(n)\\ w(n)=1+{\displaystyle \frac{d(n)}{d(s)}}\end{array}$$

(15)

where d(n) represents the Euclidean distance from the current node to the destination, d(s) denotes the Euclidean distance from the starting point to the destination, and the weighting coefficient w(n) dynamically varies with the node, accelerating approach toward the target when moving away from it.

3.2.2. Incremental Update Mechanism

After obtaining the initial flight path of the UAV and detecting path conflicts, the UAV involved in the conflict requires global path replanning, leading to low conflict resolution efficiency. Moreover, for multi-UAV planning, the occupancy of airspace grids is highly time-sensitive. Ignoring temporal constraints reduces the feasible solution space for planning, often resulting in unsolvable path planning scenarios, which contradicts real-world conditions. To address this, this paper introduces temporal dimension information into the paths planned by the 3D JPS algorithm by incorporating the concept of time steps. Conflict node constraints are treated as temporary obstacles with temporal information, thereby expanding the feasible solution space for planning. Additionally, an incremental path update mechanism is integrated into the 3D JPS algorithm, constructing the Incremental-update Jump Point Search (IJPS) algorithm. During path replanning, only the local path affected by conflicts is updated, serving as the path replanning algorithm. The specific principles are as follows.

Taking the path conflict occurring in a two-dimensional environment in Figure 3a as an example, UAV $u_1,u_2$ represents the two UAVs involved in the conflict, $l(3)=(6,4)$ denotes the grid node unit where the conflict occurs along with its coordinates, and $t=3$ indicates the time of the conflict. Traditional conflict resolution and replanning, as shown in Figure 3b, require completely avoiding the conflict node and performing global replanning from the start to the end point, resulting in low computational efficiency in planning.

The incremental update mechanism primarily involves incorporating the minimum predicted cost rhs value based on neighboring nodes, assessing the discrepancy between rhs and the actual cost g to perform local updates of the path. The calculation of rhs is as follows:

$$rhs(x)=\left\{\begin{array}{c}0,if x=x_{start}\\ {\min }_{x^{\prime }\in pred(x)}(d(x^{\prime },x)+g(x^{\prime })),otherwise\end{array}\right.$$

(16)

where x′ is the parent node of the current node x, d(x′,x) represents the cost between the current node and its parent node. During computation, the node that minimizes the rhs value among all predecessor nodes of x is selected as the parent node.

The conflict resolution under the incremental update mechanism is illustrated in Figure 3c. Based on the calculated path information from the initial planning records, all path nodes satisfy the condition, indicating node consistency. When a path conflict occurs, the conflicting node is designated as a temporary obstacle and marked in red. The attribute information p of its grid cell changes from 0 to 1. The conflicting node affects the rhs value of the path node, causing it to become inconsistent (i.e., rhs > g). This inconsistency propagates through the parent nodes, altering the rhs values of subsequent path nodes (shown as the red path in Figure 3c), indicating that this segment of the path is affected by the conflict. At this point, a new starting node (green node in Figure 3c) must be established to replan the path from the new starting point to the destination. Combining this newly planned path with the unaffected segments of the original path results in a conflict-free path.

The introduction of the incremental update mechanism reduces the complexity of the algorithm, making it possible to replan only one segment of the path when UAVs are in conflict for path replanning, avoiding global research. In terms of algorithm wholeness, the computational speed advantage of the 3D JPS algorithm is retained, and the computational efficiency of conflict elimination is improved so that it can be adapted to large-scale UAV path planning problems.

3.3. Binary Constraint Tree for Dual-Objective Cost Function

Conflict-based search algorithms often employ the total path cost N.cost as a single-objective cost function and the sole criterion for node expansion, leading to significant wasted search time among numerous nodes with identical cost values. When a conflict occurs between two drones, constraints are imposed on both, generating left and right child nodes. If the total path costs of the left and right child nodes are equal, the optimality of either node cannot be determined. In such cases, both child nodes must be expanded further, substantially increasing the number of node expansions and the frequency of path replanning algorithm invocations, thereby escalating the overall computational burden of the algorithm.

A dual-objective cost function is established by comprehensively considering the total path cost and the maximum individual path cost, and a dual-objective conflict-based search algorithm (DOCBS) is constructed. The algorithm prioritizes the total path cost between the two objectives. When multiple nodes have equal total path costs, node expansion is performed based on the maximum path cost. To reflect the difference in importance between the two objectives, the ratio of the maximum path cost to the total path cost is used to replace the maximum path cost, which is then added to the total path cost to form a new cost function, expressed as:

$$\left\{\begin{array}{l}S(P)=C(P)+M^{\ast }(P)\\ P=\left\{p_1,p_2,\dots ,p_n\right\}\\ C(P)={\displaystyle \sum _{i=1}^n{c}_i(p_i)}\\ M(P)=\underset{1\le i\le n}{\max }{c}_i(p_i)\\ M^{\ast }(P)=M(P)/C(P)\end{array}\right.$$

(17)

where, assuming that the UAV moves one unit grid per time step, ci(pi) represents the cost of path pi, C(P) denotes the total path cost, M(P) is the maximum path cost for a single UAV, and M* is the ratio of the maximum path cost to the total path cost, with a value range of (0,1). When comparing the magnitude of S(P), M* comes into play only when the total path costs are equal.

The dual-objective function node expansion is illustrated in Figure 4. When the total path costs of nodes N1 and N2 are equal, their maximum path costs are compared, leading to the expansion of only node N1 and thereby reducing the number of iterations. Compared to the traditional single-objective cost function, the dual-objective cost function effectively decreases both the number of expanded nodes and the frequency of invoking path replanning algorithms in terms of computational load. In terms of algorithmic performance, both types of objective cost functions can identify the target node with the optimal total path cost, preserving the optimality of the conventional CBS algorithm.

3.4. Framework for Multi-UAV Path Planning Methodology

The proposed framework for multi-UAV conflict-free path planning consists of two main components: single-UAV path planning and multi-UAV conflict detection and resolution.

At the lower level, which handles individual UAV path planning, the process begins by constructing a gridded airspace model based on real-world mission map data. Incorporating UAV performance constraints, an initial path for each UAV is generated using the three-dimensional Jump Point Search (3D JPS) algorithm.

At the upper level, dedicated to multi-UAV conflict resolution, the initial paths of all UAVs are first evaluated against a conflict model to detect potential conflicts. If no conflicts are detected, the global set of conflict-free paths is accepted. If conflicts are identified, a binary conflict constraint tree is constructed. This tree is expanded under the guidance of a dual-objective cost function (DOCBS), triggering an incremental update mechanism. This mechanism generates spatio-temporal temporary obstacles and updates the underlying mission map with additional constraints. Subsequently, the Incremental Jump Point Search (IJPS) algorithm at the lower level performs local path replanning for the conflicting UAVs. The newly generated paths are then fed back into the upper layer for further conflict detection. This iterative cycle—comprising conflict detection, constraint tree expansion, map updating, and IJPS-based local replanning—continues until all conflicts are resolved, ultimately yielding a globally conflict-free set of paths that satisfies the dual-objective cost function.

In summary, integrated with the problem model presented in Section 1, the overall framework of the DOCBS + IJPS method for multi-UAV conflict-free path planning is illustrated in Figure 5.

4. Simulation Experiments and Analysis

4.1. Simulation Environment and Parameter Settings

To validate the effectiveness and efficiency of the proposed Dual-Objective Conflict-Based Search with Incremental Jump Point Search (DOCBS + IJPS) method for large-scale UAV path planning, we acquired topographic data for a 1000 m × 1000 m × 200 m area in Hangzhou using oblique photogrammetry technology. The designated airspace range is set as follows: Longitude is 119.97° E–119.98° E, latitude is 30.35° N–32.36° N, altitude is 0–200 m. The oblique photography data was employed in our study because it enables the generation of highly detailed and accurate 3D models of urban environments, which is critical for realistic low-altitude UAV path planning. The data obtained through this method allowed us to construct a refined 3D grid model of the airspace that accurately replicates the real-world geometry, thereby enhancing the practical relevance and geometric fidelity of our simulation environment. This model was utilized as the experimental map for simulating UAV path planning. A gridded airspace map with dimensions of 63 × 63 × 13 was generated using a 16 m airspace grid unit scale, where obstacles were annotated based on actual terrain data. The environment was visualized using Python 3.12 (64–bit), as shown in Figure 6, with obstacles marked in gray and the start and end points of the UAV are marked in red and purple.

Simulation tests were conducted from both single-UAV and multi-UAV perspectives:

(1)

The single-UAV path planning experiments consist of parameter analysis tests and algorithm comparison tests. The parameter analysis experiments examine the effects of the cost weight coefficients α₁ and α₂, as well as the grid size, on the experimental results. The algorithm comparison experiments verified the computational efficiency advantage of the proposed lower-layer initial path planning algorithm compared to the original method.

(2)

Multi-UAV path planning experiments validated the capability of the proposed method in resolving large-scale UAV conflicts and compared it with traditional methods to demonstrate its superiority and robustness.

All the simulation experiments in this paper were conducted on a workstation equipped with a 12th Gen Intel(R) Core (TM) i7-12700 2.10 GHz CPU, 32 GB RAM and the equipment information is: Dell Inc, Vostro 3910, Hangzhou, China. The initial experimental simulation parameters are listed in

Table 1. Parameter setting.

Parameter Name and Unit	Value
Maximum flight altitude/m	200
Minimum flight altitude/m	60
Maximum range/m	2000
Maximum turning angle/degree	90
Maximum climb angle/degree	90
Actual cost weight coefficient α1	0.8
Risk cost weight coefficient α2	0.2
Grid scale size/m	16

.

4.2. Simulation Experiment of Single UAV Path Planning

4.2.1. Parameter Analysis Experiments

The cost function of the proposed JPS algorithm in this paper consists of two components: actual path cost and path risk cost. Different weightings of these costs influence the planned path outcomes. To analyze the impact of weighting coefficients α₁ and α₂ in the cost function on the experimental results, a series of tests were conducted based on an initial setting of α₁ = 0.8 and α₂ = 0.2, using the same start and end points for all tasks. Specifically, nine parameter trials were performed with α₁ ranging from 0.1 to 0.9. Evaluations were carried out from three perspectives: actual path cost, computational time, and path risk cost. Other parameters were configured as specified in Table 1. To mitigate randomness, each experiment was repeated five times, and the average values were used to generate the bar charts of various path metrics shown in Figure 7, with numerical labels included on each bar.

Analysis of the experimental results in Figure 7 indicates that when α₁ is relatively small, the optimal path obtained by the algorithm remains unchanged despite variations in α₁. As α₁ gradually increases, no consistent correlation is observed between the three evaluation metrics and the weighting coefficients, and no universal pattern emerges. After comprehensively considering the actual flight cost, computational time, and path risk cost, the values α₁ = 0.8 and α₂ = 0.2 are identified as the most reasonable. Although the metrics fluctuate across different settings, under this specific combination, the algorithm achieves the shortest planning time without increasing either the actual flight cost or the path risk cost, resulting in an overall favorable performance. For consistency, all subsequent experiments in this study uniformly adopt α₁ = 0.8 and α₂ = 0.2 as the cost weighting coefficients.

In addition to the weighting coefficients α₁ and α₂, the grid size of the airspace model, which serves as the simulation environment for UAV path planning, also significantly influences the planning outcomes. To analyze the impact of grid size on path cost and computational time, a parameter analysis was conducted based on an initial grid size of 16 m. Excluding excessively large or small grid sizes unsuitable for urban low-altitude UAV operations, the grid sizes were set to 8 m, 16 m, and 32 m for comparative evaluation. The results are presented in

Table 2. The influence of different grid scale sizes on algorithm performance.

Grid Scale Size/m	Algorithm Planning Time/s	Actual Path Cost/m	Path Risk Cost	Path Total Cost
32	0.25	796.69	24.16	820.86
16	1.34	748.29	11.25	759.54
8	14.48	755.78	10.73	766.51

.

Analysis of the experimental results in Table 2 indicates that as the grid size increases, the algorithm planning time decreases significantly. This is primarily attributed to the fact that, within the same airspace volume, a larger grid size results in a reduced number of grid cells, thereby diminishing the nodes to be searched by the algorithm. No clear correlation is observed between the actual path cost and the grid size. At a larger grid size of 32 m, the algorithm may overlook shorter paths, leading to a noticeable increase in actual path cost. Conversely, at a smaller grid size of 8 m, the increased number of grid cells may introduce more path turns, which could also elevate the actual path cost. The path risk cost decreases with smaller grid sizes, which is closely related to the grid risk coefficient. Finer grid sizes yield a more detailed airspace model with a greater number of risk-free grid cells, thereby reducing the overall grid risk coefficient.

Considering both path cost and computational efficiency, a grid size of 16 m is found to be more suitable for urban low-altitude UAV path planning. Furthermore, according to Reference [33], grid size should be correlated with the dimensions and performance parameters of the UAV. Given that most urban low-altitude UAVs are light-duty, a grid size of 16 m is consistently selected for the experiments in this study.

4.2.2. Algorithm Comparison Experiments

To evaluate the computational efficiency advantage of the incremental-update-based 3D JPS algorithm adopted for the initial path planning in this study compared to the traditional A* algorithm, a comparative experiment was conducted. The incremental-update-based JPS algorithm functions as the standard 3D JPS algorithm during initial planning (since single-UAV path planning does not involve incremental updates). Therefore, under the condition that all aforementioned parameter settings and path planning environments remain unchanged, the UAV paths were initially planned using both the 3D A* algorithm and the 3D JPS algorithm.

In a gridded airspace map of 63 × 63 × 13, 10 random start-end point pairs were selected for path planning, ensuring sufficient separation between start and end points to avoid non-generalizable results. Each algorithm was independently executed 20 times. The results are shown by the blue and yellow curves in Figure 8. Both algorithms enabled the UAV to safely navigate from the start to the end point while effectively avoiding obstacles in the low-altitude environment, and ensuring that the flight altitude and turning angle of the path meet performance constraints.

Figure 9 presents path comparisons for three different start-end point pairs. It can be observed that, compared to the 3D JPS algorithm, the paths planned by the 3D A* algorithm exhibit more turns and poorer smoothness.

Further analysis was conducted in terms of the average search time, average planned path length, and average number of explored nodes for algorithm-generated paths, with the data presented in

Table 3. Comparison of path planning results between A* algorithm and proposed JPS algorithm.

Map Size	Algorithm Type	Average Search Time/s	Average Planned Voyage/m	Average Number of Search Nodes
63 × 63 × 13	JPS algorithm in this paper	1.25	671.33	2154
	3D A* algorithm	1.67	659.56	3238

. The comparison reveals that the 3D JPS algorithm outperforms the 3D A* algorithm in both average path planning time and average number of explored nodes, achieving a 25.1% reduction in average time and at least a 33.48% decrease in the average number of explored nodes. However, the planned path length slightly increased by 1.75%, remaining within one grid unit difference. This minor increase in path length primarily stems from the forced neighbor pruning rule of the JPS algorithm, which may skip more optimal grid nodes in obstacle-dense regions. When evaluating algorithm optimality based on path length, the 3D A* and 3D JPS algorithms exhibit comparable performance, though the 3D A* algorithm demonstrates superior optimality in large-scale environments. The experimental results indicate that employing the 3D JPS algorithm as the lower-layer initial planning algorithm significantly enhances computational speed compared to the 3D A* algorithm. Particularly in urban environments with numerous obstacles and complex terrain, it reduces unnecessary node expansions and search overhead, exhibiting better adaptability and computational efficiency.

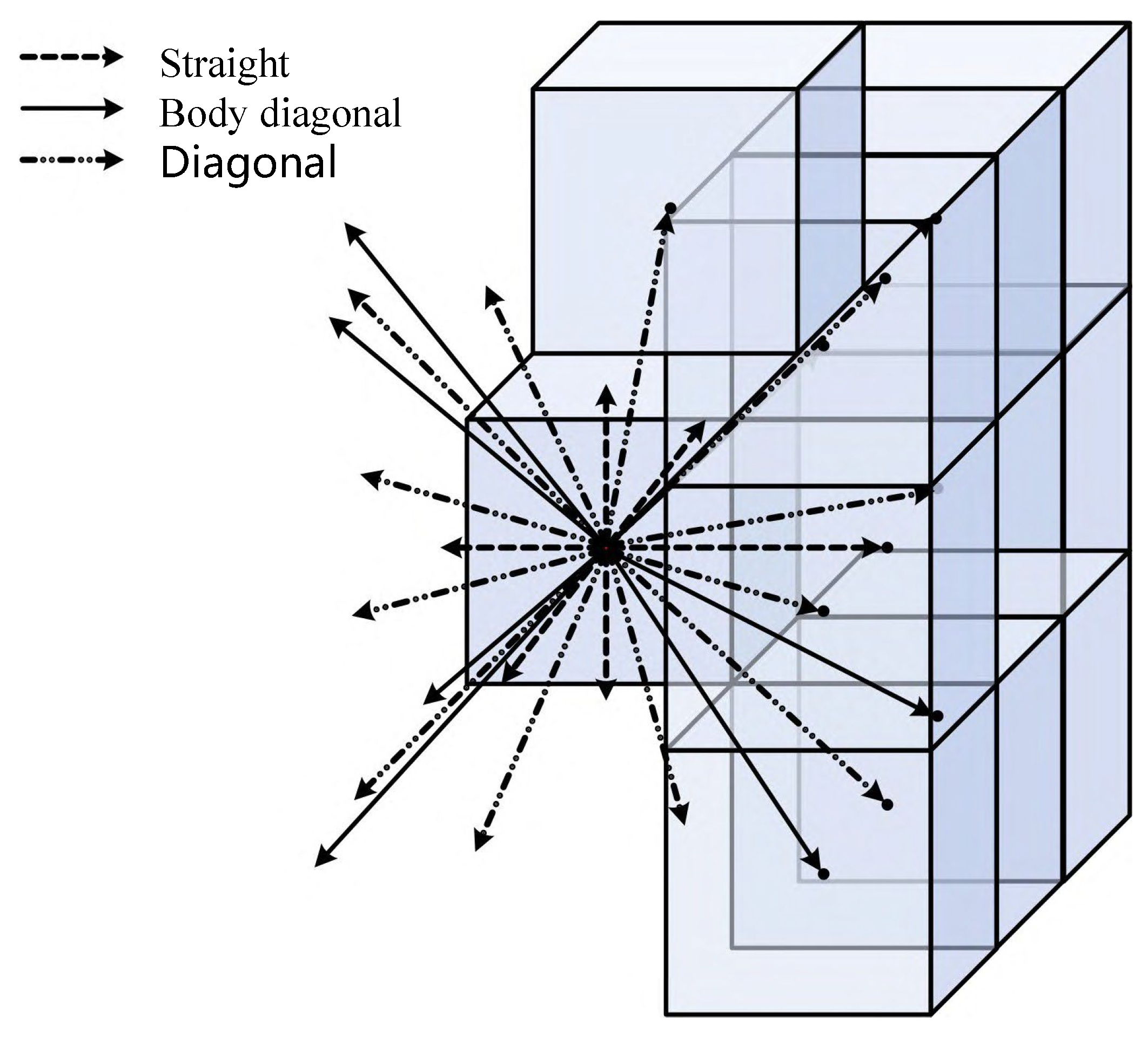
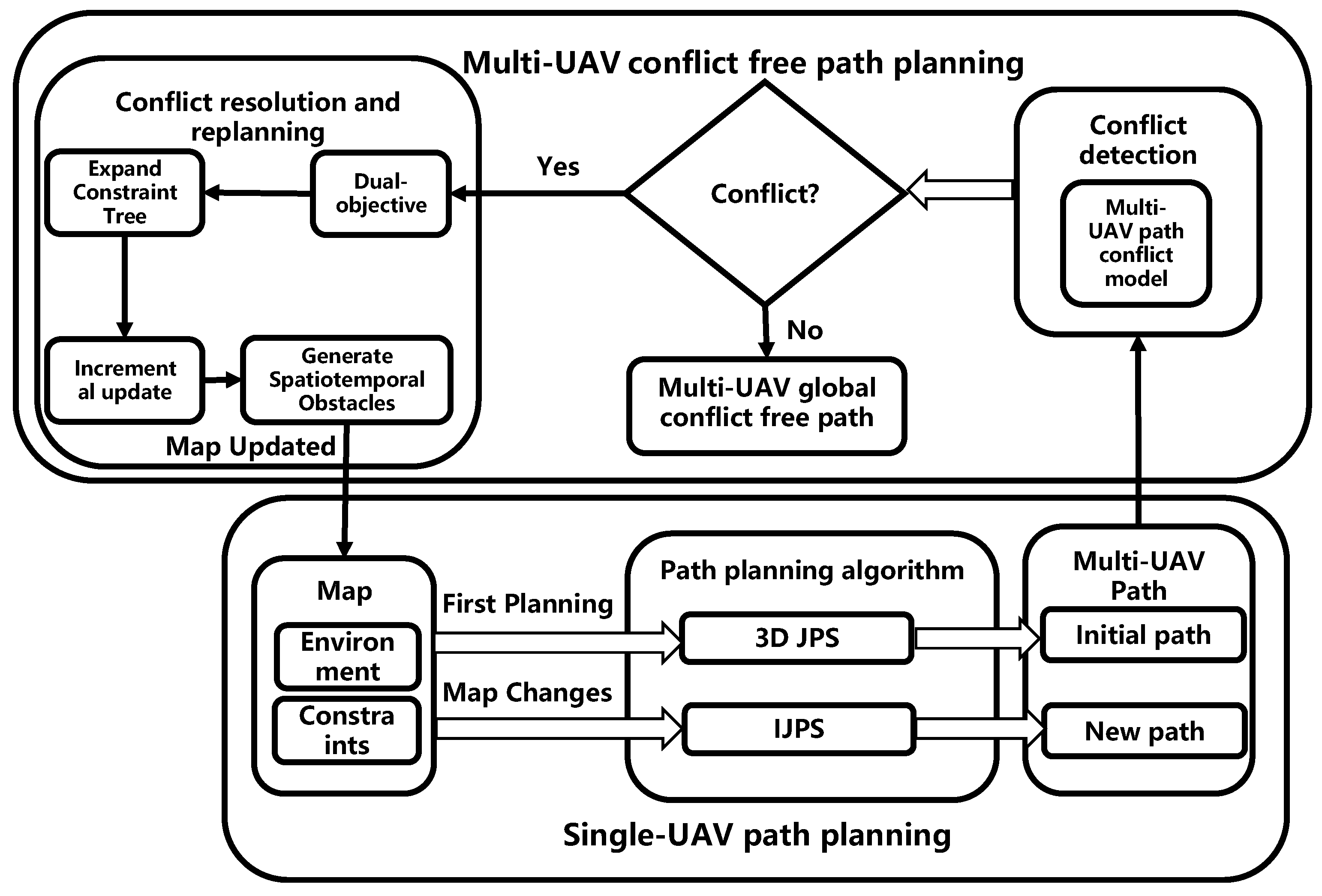
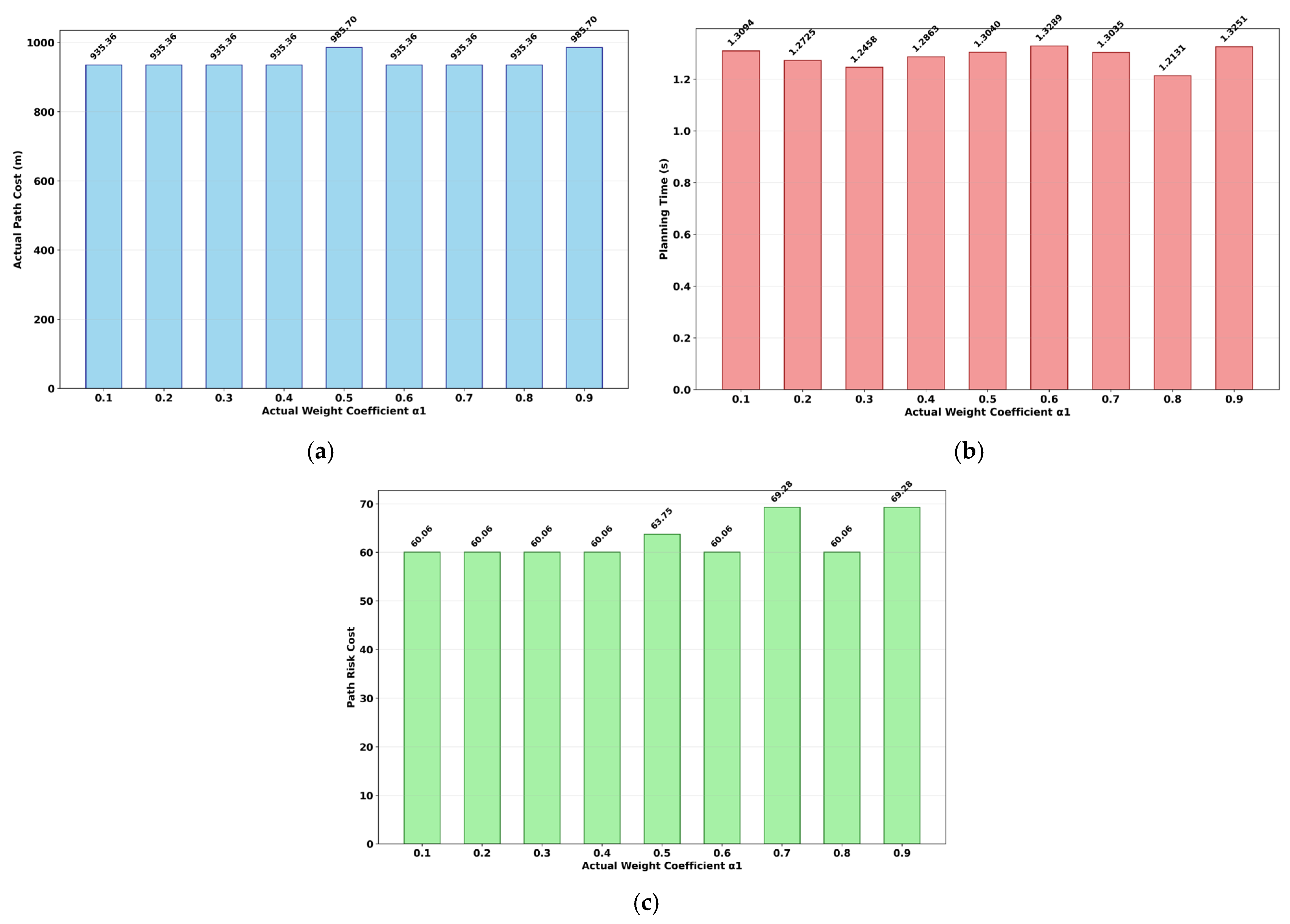
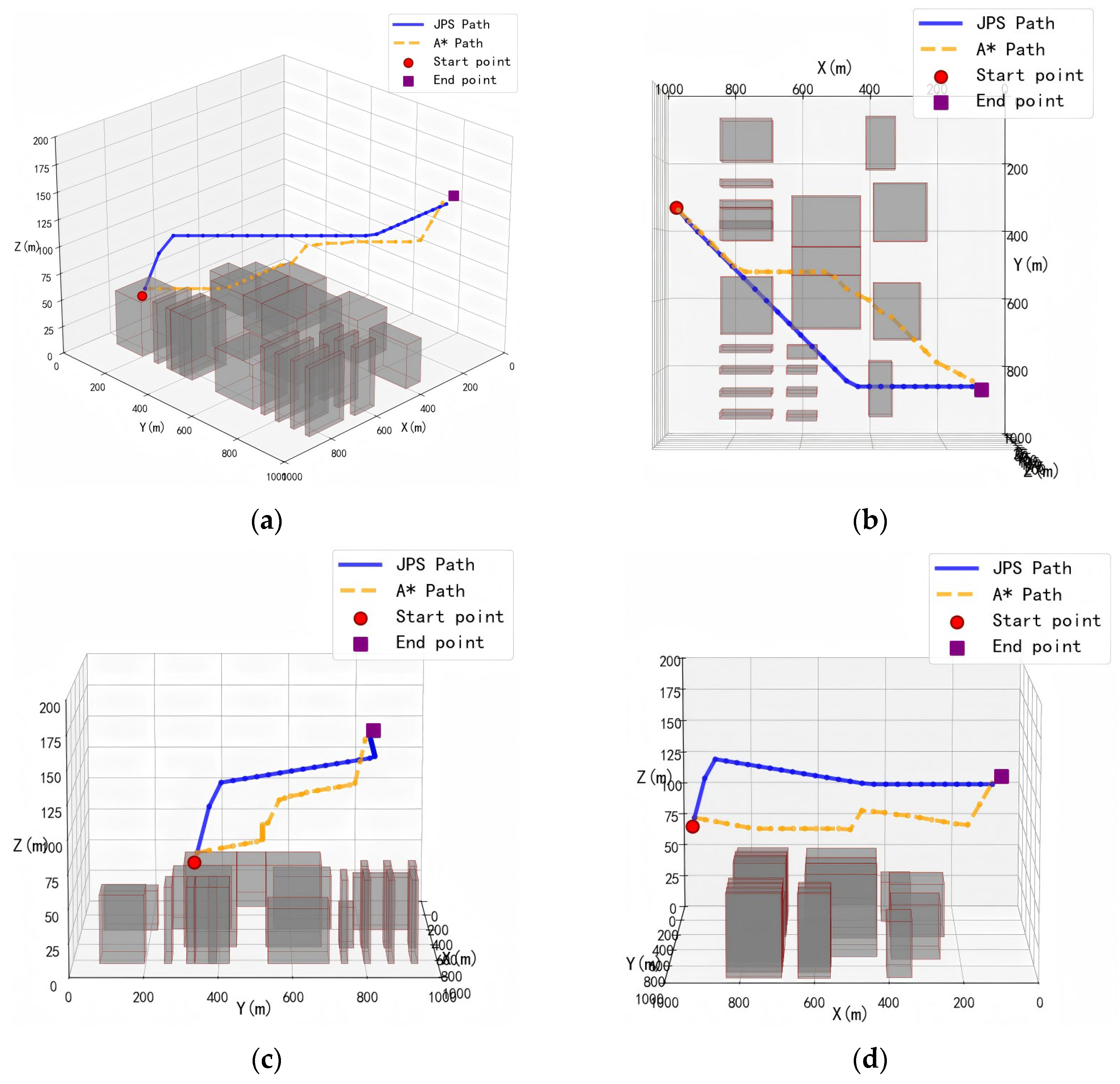
4.3. Simulation Experiment of Multi-UAV Path Planning

As the density of unmanned aerial vehicles (UAVs) within a unit airspace increases, the resolution of local path conflicts may induce new conflicts. Therefore, the scale of UAVs and the size of the airspace will directly affect the number of conflicts among multiple UAVs. To validate the conflict resolution capability of the proposed algorithm under different UAV scales, simulation experiments were conducted in the same gridded airspace map of 63 × 63 × 13, with obstacles set according to real-world map data. The start and end positions of each UAV were randomly generated within the map. To prevent the proximity of start and end points among UAVs from resulting in non-generalizable path conflict outcomes—which would fail to demonstrate the conflict resolution capability of the proposed method—a certain interval was maintained between randomly generated start points $(x_s,y_s,z_s)$ and end points $(x_e,y_e,z_e)$, satisfying the condition:

$$\sqrt{{(x_e-x_s)}^2+{(y_e-y_s)}^2+{(z_e-z_s)}^2}\ge 200$$

(18)

The conflict scenarios under different scales of UAVs are illustrated in Figure 10. Small-scale UAVs exhibit almost no path conflicts, making conflict resolution relatively easy to achieve. As the scale of UAVs increases, the number of initial path conflicts rises rapidly, leading to increased difficulty in conflict resolution. The binary constraint tree continuously expands, resulting in more iterations of replanning and ultimately prolonging the planning time for conflict resolution.

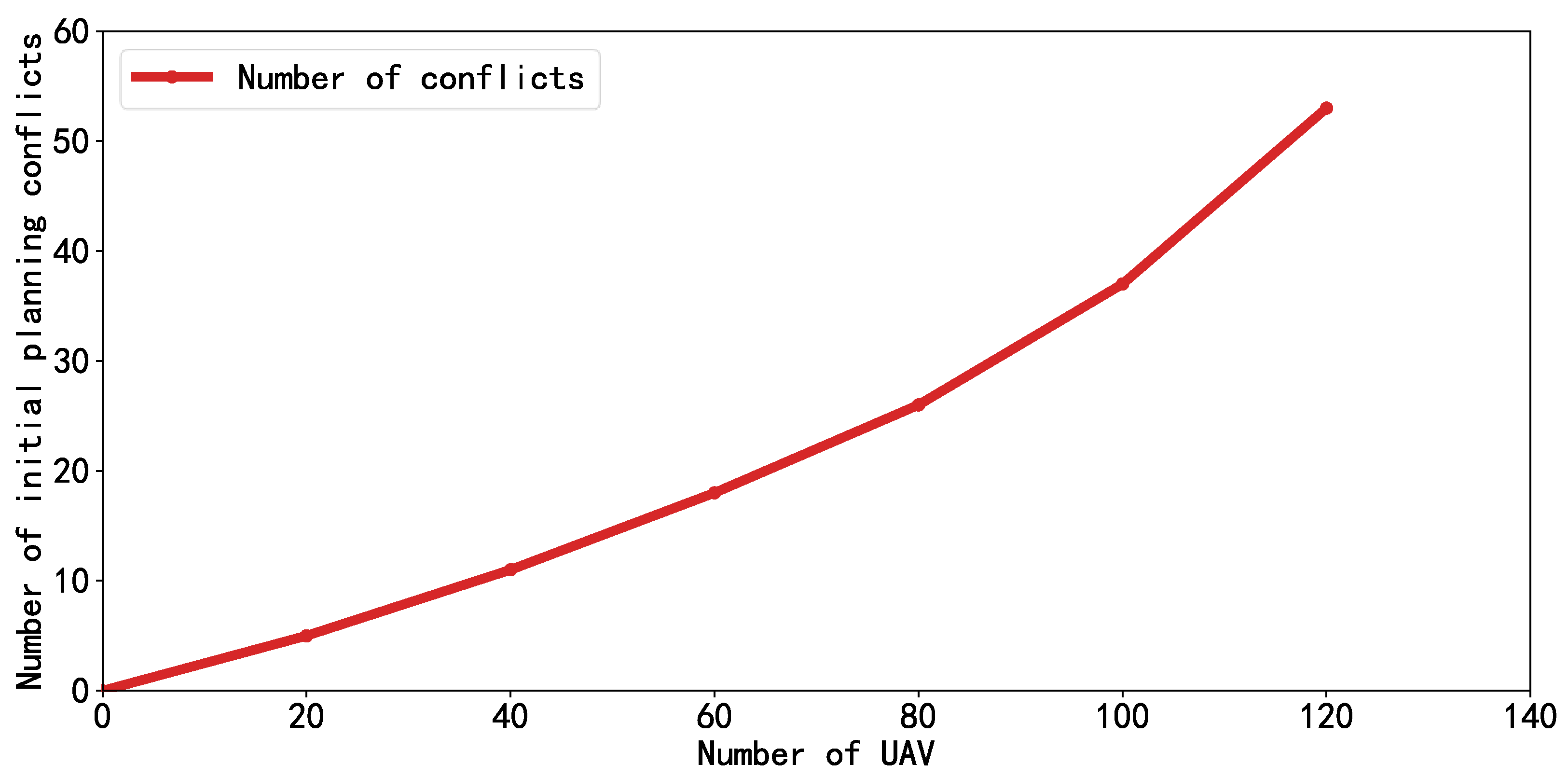
To further demonstrate the impact of the proposed algorithm on the number of conflict resolution iterations and the quantity of path conflicts in UAV path planning at different scales, Figure 11 presents the variation curves of conflict count with respect to resolution iterations under various UAV fleet sizes.

When the number of UAVs is relatively small, each iteration resolves one path conflict, as illustrated by the curves for 40 UAVs (blue curve) and 80 UAVs (red curve). The conflict resolution process exhibits a linear decline until all conflicts are resolved. As the scale of UAVs increases, exemplified by the 120-UAV scenario (green curve), the number of conflicts shows slight oscillations during the iterative process—such as at the 12th and 25th iterations—where the conflict count temporarily increases. This phenomenon occurs due to the high density of UAVs in constrained airspace, resulting in strong coupling among planned paths. During conflict resolution via binary tree replanning, the decoupling of one conflict may inadvertently introduce new coupled conflicts, leading to occasional fluctuations in the curve and imposing certain limitations on the algorithm’s conflict resolution capacity. Nevertheless, as the number of iterations increases, the proposed method (DOCBS + IJPS) remains capable of generating constraint-compliant conflict-free paths even for large-scale UAV fleets, thereby validating its overall conflict resolution performance.

The computation time of the algorithm under different UAV fleet sizes is summarized in

Table 4. Planning time of DOCBS + IJPS algorithm under different numbers of drones.

Number of UAV/Unit	Time Consumption of the Upper-Layer/s	Time Consumption of the Lower-Layer/s	Total Planning Time/s
40	14.07	52.32	66.4
80	43.41	87.14	130.5
120	116.18	119.07	235.3

and illustrated in the bar chart shown in Figure 12. As indicated by both the table and the figure, the total planning time increases with the number of UAVs. The higher number of conflicts also leads to increased computation time spent on conflict resolution at the upper planning level.

In the case of 120 UAVs, the total planning time reaches 235.3 s, with the conflict resolution and replanning time at the upper layer accounting for 116.18 s, approximately 49.4% (116.18 s/235.3 s) of the total time. On average, each UAV requires about 1.96 s to compute a conflict-free path.

These results demonstrate that the proposed Dual-Objective Conflict-Based Search with Incremental Jump Point Search (DOCBS + IJPS) method exhibits effective conflict resolution capability and efficient computational performance across different UAV fleet scales.

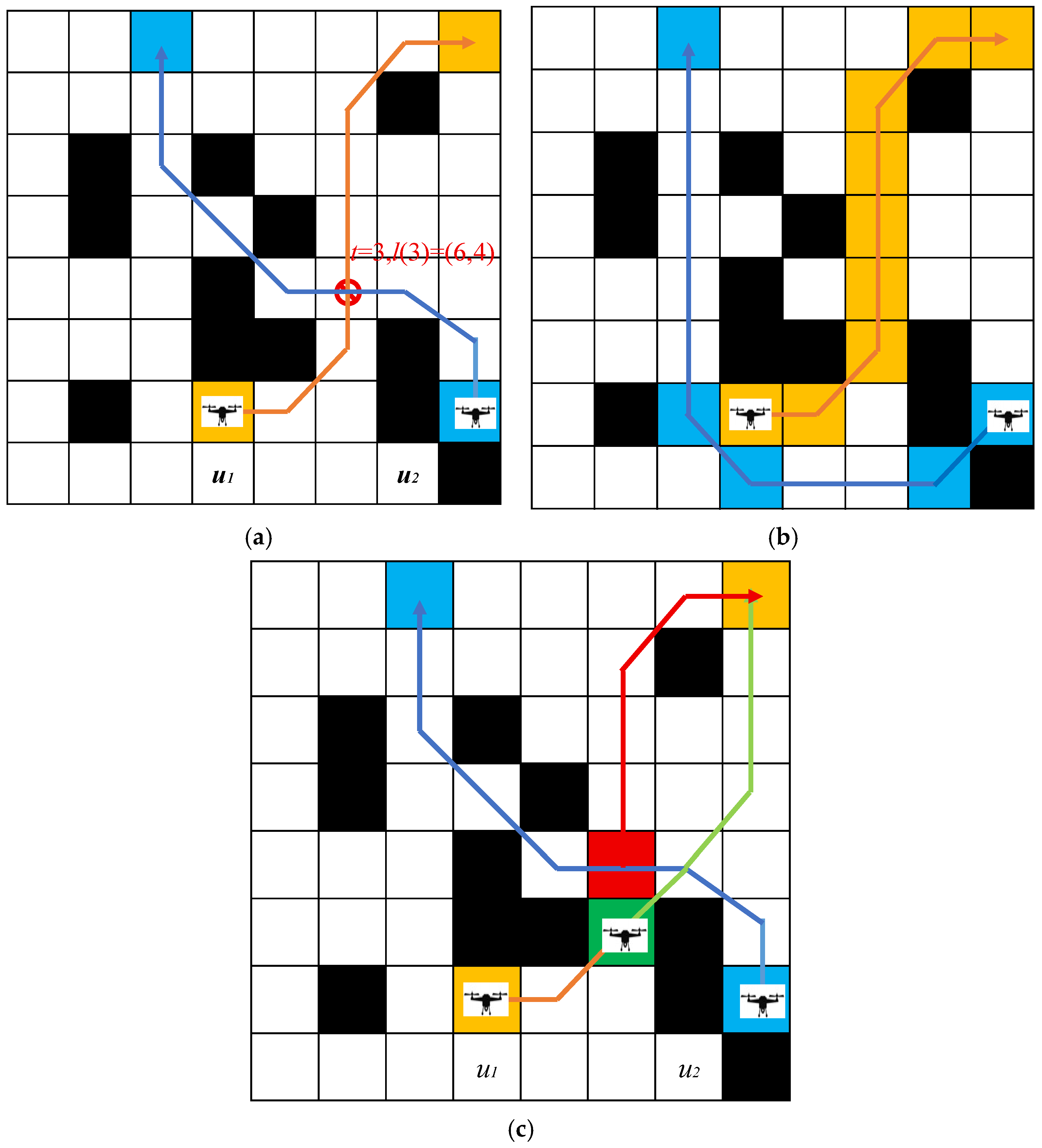
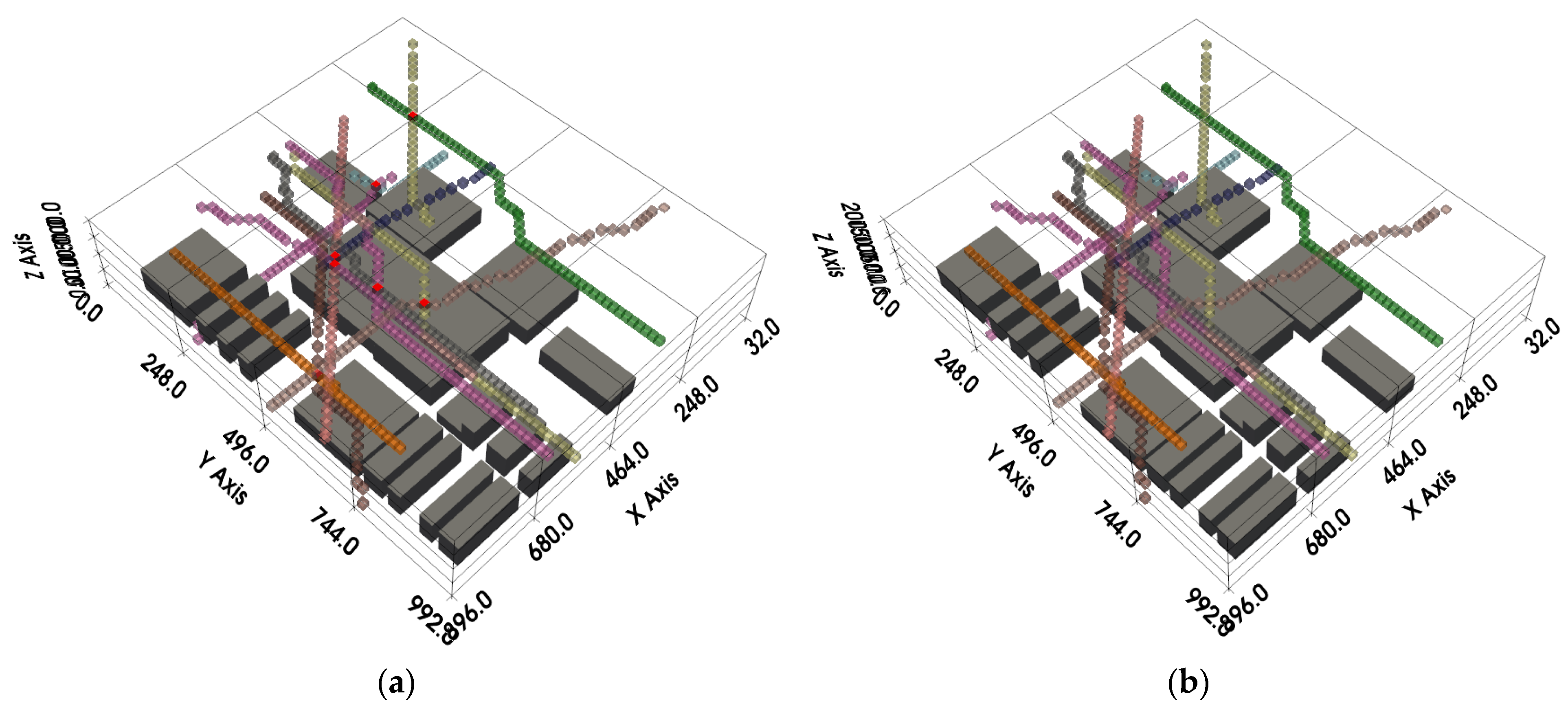
A comparison of flight paths before and after conflict resolution is shown in Figure 13. Figure 13a displays the conflicting flight paths in a scenario involving 120 drones, visualized using Python. The flight paths are represented by semi-transparent grid nodes in different colors, with red nodes indicating conflict points. After conflict detection, path conflict resolution was performed to replan the paths of the conflicting drones. The results, presented in Figure 13b, show that the newly planned paths contain no conflicts, thereby achieving a globally conflict-free set of flight paths.

To further validate the performance advantages of the proposed DOCBS + IJPS algorithm in large-scale UAV conflict-free path planning, each algorithm was independently executed 10 times under the same simulation map environment. The simulation settings remained consistent with the previous section, utilizing a gridded airspace map of 63 × 63 × 13. As shown in

Table 5. Different planning algorithms involved in simulation comparison.

Comparing Methods	Upper Level Methods	Lower Level Methods
method 1	CBS	A*
method 2	CBS	IJPS
method 3	DOCBS	IJPS

, since the proposed method adopts a hierarchical architecture based on the conflict-based search algorithm, the comparative algorithms also followed this framework. The upper-layer planning compared the total planning time to verify the computational efficiency of conflict resolution and replanning, while the lower-layer planning compared the total planned flight distance to evaluate the optimality of the algorithms.

Table 6. Total range of path planning using three comparative algorithms under different numbers of drones.

Number of UAV/Unit	CBS + A*	CBS + IJPS	DOCBS + IJPS
40	26,362.5 m	26,873.9 m	26,866.7 m
60	38,359.8 m	39,241.9 m	39,250.7 m
80	48,970.6 m	50,251.6 m	50,241.1 m
100	62,813.5 m	64,250.4 m	64,261.4 m
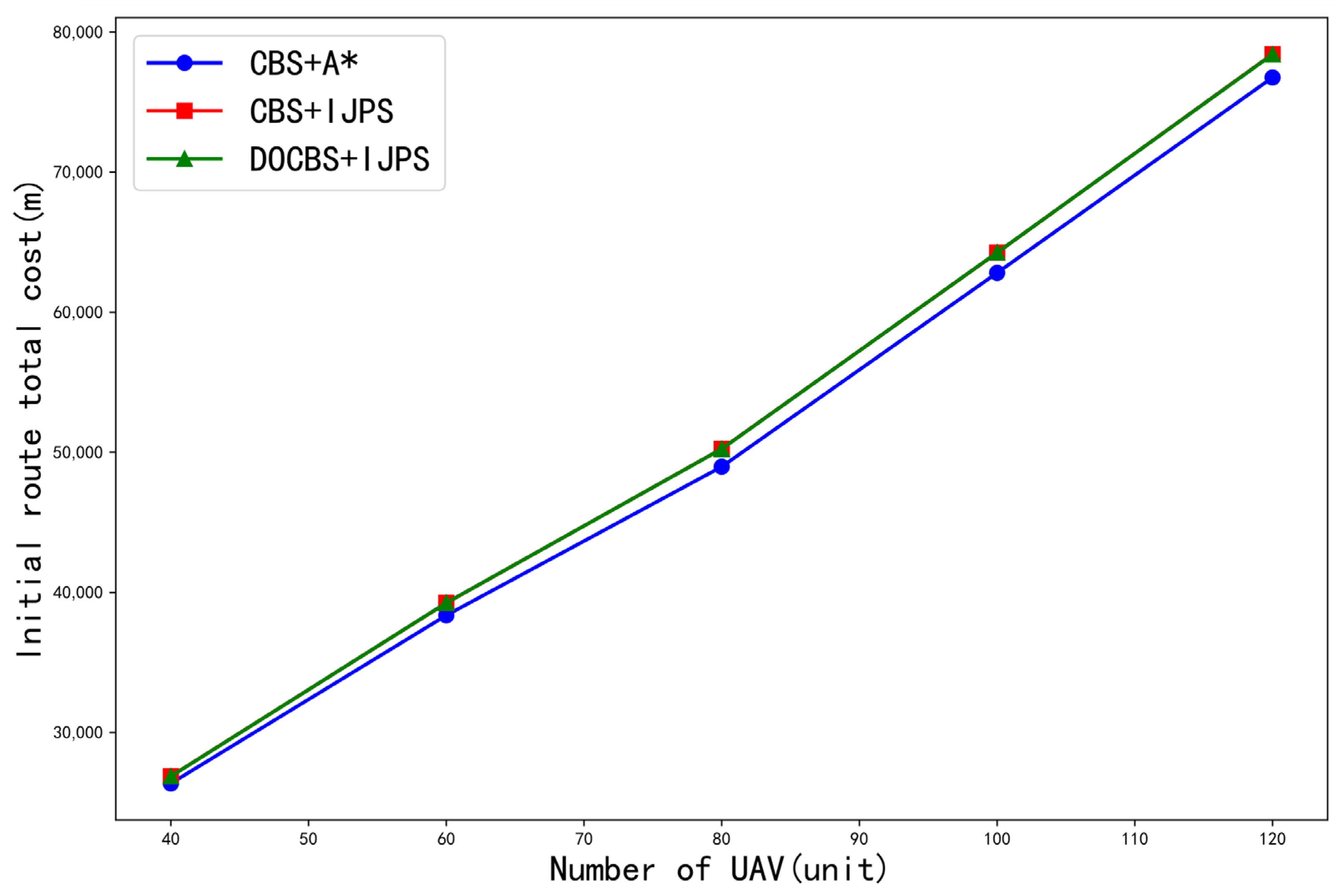
120	76,758.9 m	78,428.1 m	78,405.4 m

summarizes the total path lengths of the initial low-level path planning for three comparison algorithms under different numbers of UAVs, and the corresponding curves are plotted in Figure 14. Based on the results in Table 6 and Figure 14, using the total path length as the metric for evaluating the optimality of conflict-free path solutions, it can be concluded that the CBS + A* method achieves the best optimality, slightly outperforming both the CBS + IJPS and DOCBS + IJPS methods. This is primarily because the A* algorithm generally exhibits slightly better optimality than the JPS algorithm in large-scale maps. Using the total path length of the conventional CBS + A* algorithm as a baseline, the total path length planned by the DOCBS + IJPS algorithm is approximately 2.5% (calculated from the data in Table 6) longer. Overall, the CBS + IJPS and DOCBS + IJPS methods demonstrate comparable optimality to the CBS + A* method. Due to their shared underlying algorithm, the total path lengths of CBS + IJPS and DOCBS + IJPS are approximately equal, and their optimality performances are consistent.

The computation time results of the three algorithms under different numbers of UAVs are presented in

Table 7. Comparison of three algorithms for planning time under different numbers of drones.

Number of UAV/Unit	Algorithm Planning Time Consuming	CBS + A*	CBS + IJPS	DOCBS + IJPS
40	Lower-layer	69.87 s	52.4 s	52.3 s
	Upper-layer	24.05 s	19.72 s	14.07 s
	Total	93.92 s	72.12 s	66.37 s
60	Lower-layer	96.66 s	72.86 s	72.36 s
	Upper-layer	43.93 s	35.41 s	25.17 s
	Total	140.59 s	108.27 s	97.53 s
80	Lower-layer	117.64 s	88.14 s	87.14 s
	Upper-layer	76.07 s	60.76 s	43.4 s
	Total	193.71 s	148.9 s	130.54 s
100	Lower-layer	141.52 s	104.08 s	104.98 s
	Upper-layer	129.99 s	101.25 s	73.37 s
	Total	271.51 s	206.23 s	177.35 s
120	Lower-layer	161.92 s	120.6 s	119.06 s
	Upper-layer	203.12 s	162.8 s	116.17 s
	Total	365.04 s	283.4 s	235.23 s

and Figure 15. All algorithms were tested under the same simulation scenario and parameter settings. All algorithm performance data in this experiment were calculated from the data in Table 7 and the time consumption for low-level path planning is compared in Figure 15a. Under the condition that the high-level layer uses the CBS algorithm, the IJPS-based low-level planning method significantly reduces the computation time compared to the A*-based method. Based on the data in Table 7, the average time consumption is reduced by approximately 25.62% (${\displaystyle \frac{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{low}-\mathrm{level} \mathrm{time}}-({\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{low}-\mathrm{level} \mathrm{time}}+{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{low}-\mathrm{level} \mathrm{time}})/2}{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{low}-\mathrm{level} \mathrm{time}}}}\times 100\%$). Since both CBS + IJPS and DOCBS + IJPS employ the same underlying planning method, their low-level planning times are nearly identical.

A separate comparison of the high-level conflict resolution time is shown in Figure 15b. When the high-level layer employs the CBS algorithm, the IJPS algorithm—equipped with an incremental update mechanism—only requires local path replanning, leading to an average reduction in high-level computation time of 20.02% (${\displaystyle \frac{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{high}-\mathrm{level} \mathrm{time}}-{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{high}-\mathrm{level} \mathrm{time}}}{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{high}-\mathrm{level} \mathrm{time}}}}\times 100\%$) compared to the A* algorithm. Furthermore, when the low-level planner uses IJPS in both cases, the DOCBS method reduces the number of conflict resolution iterations and decreases the frequency of replanning calls compared to the conventional CBS method, resulting in an additional 27.94% (${\displaystyle \frac{{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{high}-\mathrm{level} \mathrm{time}}-{\mathrm{DOCBS}+\mathrm{IJPS}}_{\mathrm{high}-\mathrm{level} \mathrm{time}}}{{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{high}-\mathrm{level} \mathrm{time}}}}\times 100\%$) average reduction in high-level computation time. Moreover, as the number of UAVs and conflicts increases, the extent of time reduction becomes more pronounced.

From the perspective of the two-layer planning framework, the total planning time is shown in Figure 15c,d. The DOCBS + IJPS method achieved the shortest computation time for generating conflict-free paths in large-scale drone scenarios. Compared to the CBS + A* and CBS + IJPS methods, it reduced the average planning time by 35.56% (${\displaystyle \frac{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{total} \mathrm{time}}-{\mathrm{DOCBS}+\mathrm{IJPS}}_{\mathrm{total} \mathrm{time}}}{{\mathrm{CBS}+\mathrm{A}*}_{\mathrm{total} \mathrm{time}}}}\times 100\%$) and 17.02% (${\displaystyle \frac{{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{total} \mathrm{time}}-{\mathrm{DOCBS}+\mathrm{IJPS}}_{\mathrm{total} \mathrm{time}}}{{\mathrm{CBS}+\mathrm{IJPS}}_{\mathrm{total} \mathrm{time}}}}\times 100\%$), respectively. However, considering the total range, adopting an incremental update mechanism increases the total range by about 2.5% (calculated from the data in Table 6), sacrificing a small part of optimality to achieve a huge improvement in computational efficiency. The simulation results demonstrate the significant computational efficiency advantages of the proposed DOCBS + IJPS method.

5. Conclusions

This paper addresses the large-scale multi-UAV conflict-free path planning problem in urban low-altitude airspace and proposes a hierarchical improved conflict-based search algorithm framework based on an incremental update mechanism and three-dimensional jump point search. The lower layer employs the 3D Jump Point Search (3D JPS) algorithm, while the upper layer integrates the Dual-Objective Conflict-Based Search (DOCBS) algorithm with the Incremental Jump Point Search (IJPS) mechanism. Simulation experiments based on a gridded urban airspace model validate the effectiveness of the proposed method, with the main conclusions as follows:

(1)

The introduction of the 3D JPS algorithm into the lower-layer path planning effectively reduces the search space. Experimental results demonstrate that, under identical environments and constraints, the 3D JPS algorithm reduces the average search time by 25.1% and decreases the average number of search nodes by 33.48% compared to the traditional 3D A* algorithm. Although the average planned path length slightly increases (approximately 1.75%, within one grid scale), its computational speed advantage is significant, particularly in complex urban low-altitude environments with numerous obstacles. This lays the foundation for conflict resolution in large-scale UAV operations.

(2)

The proposed incremental jump point search (IJPS) mechanism effectively addresses the issue of excessive time consumption in global replanning during traditional conflict resolution. Upon detecting a conflict, IJPS only replans the affected local path segments. Experimental results demonstrate that this mechanism reduces the average replanning time by 20.02% compared to traditional A* global replanning during conflict resolution. Such a local update strategy significantly enhances the algorithm’s adaptability and overall efficiency in conflict-prone environments.

(3)

The proposed Dual-Objective Conflict-Based Search (DOCBS) algorithm optimizes the node expansion strategy of the constraint tree by constructing a cost function that prioritizes total path cost as the primary objective and maximum single-agent path cost as the secondary objective. This approach significantly reduces the expansion of invalid nodes and the number of iterations required for conflict resolution. Experimental results demonstrate that, compared to the traditional CBS algorithm, the DOCBS algorithm achieves a 27.94% reduction in average computation time for high-level conflict resolution.

(4)

The integrated application of the lower-layer 3D JPS, the upper-layer DOCBS, and the IJPS mechanism demonstrates significant advantages in overall planning efficiency. Trend analysis indicates that as the scale of UAVs and the number of initial conflicts increase, the total planning time of the proposed method grows at a notably slower rate compared to the traditional CBS + A* approach. In a high-density scenario with 120 UAVs per square kilometer, the total planning time is 235.3 s, of which the upper-layer conflict resolution and replanning account for approximately 116.2 s (49.4% of the total time). On average, each UAV takes about 1.96 s to generate a conflict-free path. Compared to the traditional CBS + A* method, the DOCBS + IJPS framework reduces the total planning time by an average of 35.56% while maintaining comparable optimality in total path cost. This fully validates the efficiency and practicality of the proposed method in addressing large-scale UAV conflict-free path planning problems.

It should be noted that research on conflict-free path planning technologies for large-scale UAVs in urban airspace is still in its early stages, and the findings of this study are derived primarily from simulation-based experiments. While the results demonstrate significant improvements in computational efficiency and conflict resolution capability, their performance in real-world physical environments may vary due to factors such as UAV payload variations, sudden weather changes (e.g., gusts or crosswinds), and unexpected dynamic obstacles. These factors can substantially influence UAV flight dynamics and path stability, which are not fully captured in the current static environment model.

Furthermore, the proposed method is currently designed for static or predictable environments. Its extensibility to highly dynamic scenarios—such as those involving sudden obstacles, UAV failures, or real-time airspace changes—requires further investigation. Future work will focus on extending the incremental update mechanism to handle dynamic obstacles by integrating predictive models and real-time sensor data. Additionally, we plan to incorporate robustness optimization strategies and disturbance rejection mechanisms to enhance the algorithm’s adaptability to environmental uncertainties. Hardware-in-the-loop (HIL) simulations and real-flight tests are also planned to validate the method’s performance under more realistic and challenging conditions.

Finally, the development of a distributed version of the proposed framework could further improve scalability and real-time responsiveness for large-scale UAV deployments in urban airspace.