Pillar-Bin: A 3D Object Detection Algorithm for Communication-Denied UGVs
Abstract
Highlights
- This study proposed a Pillar-Bin 3D object detection algorithm based on interval discretization strategy (Bin).
- Based on the Pillar-Bin algorithm, we developed a pose extraction scheme for preceding vehicles in leader-follower unmanned ground vehicle (UGV) formations, effectively addressing the challenge of pose acquisition in complex environments.
- Experiments on the KITTI dataset demonstrated that the Pillar-Bin algorithm maintained superior detection accuracy while ensuring high real-time performance. Furthermore, real-vehicle test data confirmed that the pose data output by the proposed extraction scheme exhibited high accuracy and reliability, showcasing the algorithm’s significant engineering application value.
- The Pillar-Bin algorithm and its matching pose extraction scheme effectively address the technical bottleneck of leader UGV pose perception in communication-denied scenarios. With strict control of X/Y-axis positioning errors (<5 cm) and heading angle errors (<5°), it provides stable perception support for the continuous operation of leader-follower UGV formations, and can serve as a reference for subsequent research on sensor-based communication-free multi-vehicle coordination.
Abstract
1. Introduction
2. Materials and Methods
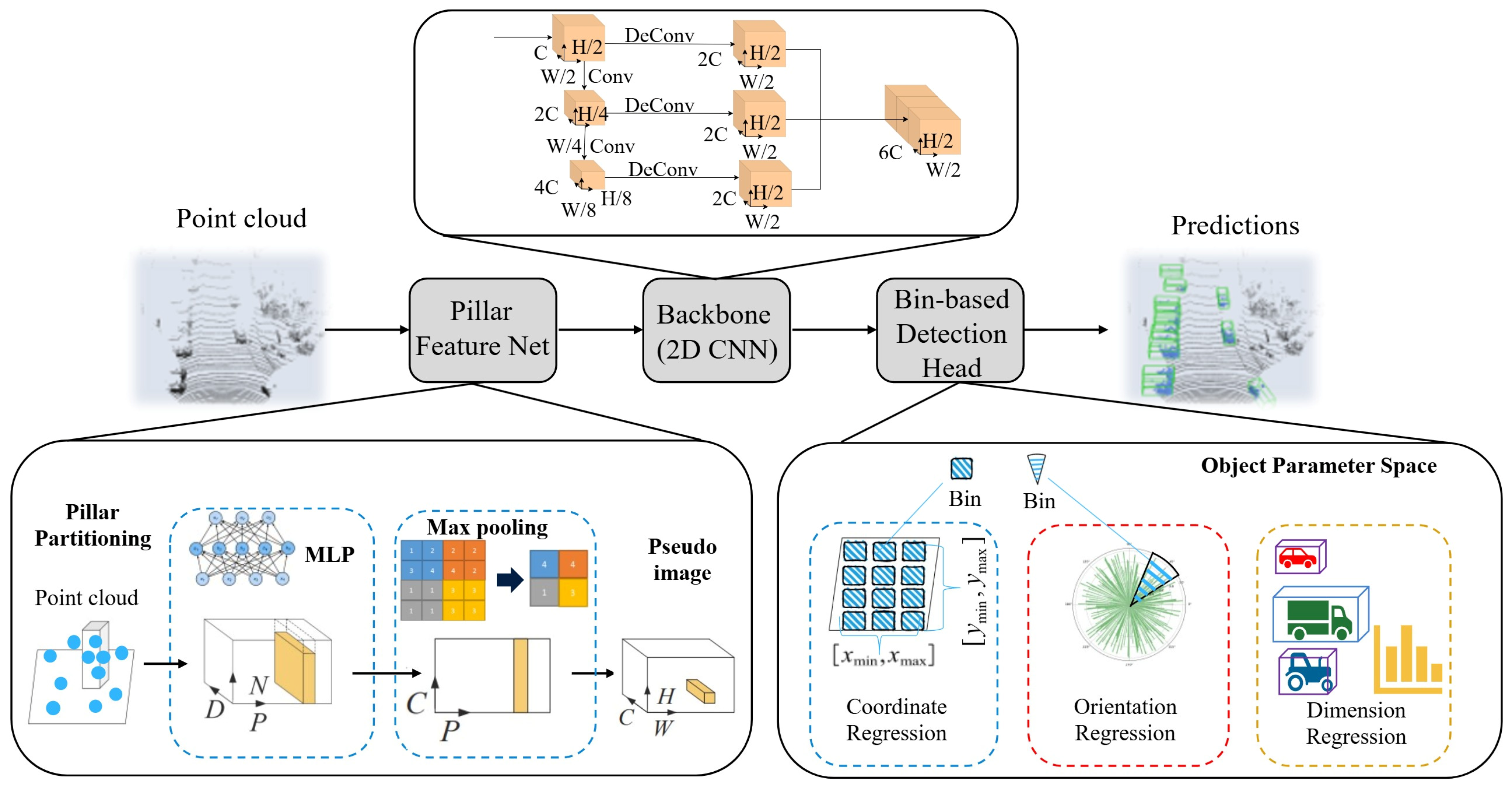
2.1. Pillar-Bin Algorithm Architecture
2.1.1. Pillar Feature Net
- (x, y, z, r): Spatial coordinates and reflectance intensity;
- (xc, yc, zc): Geometric centroid of pillar points;
- (xp, yp, zp): Point’s offset relative to pillar center.
- First item; Pillar count is limited to P = 12,000;
- Maximum points per pillar capped at n = 100.
- Zero-padding for pillars with <100 points;
- Random sampling for pillars with >100 points.
2.1.2. Backbone
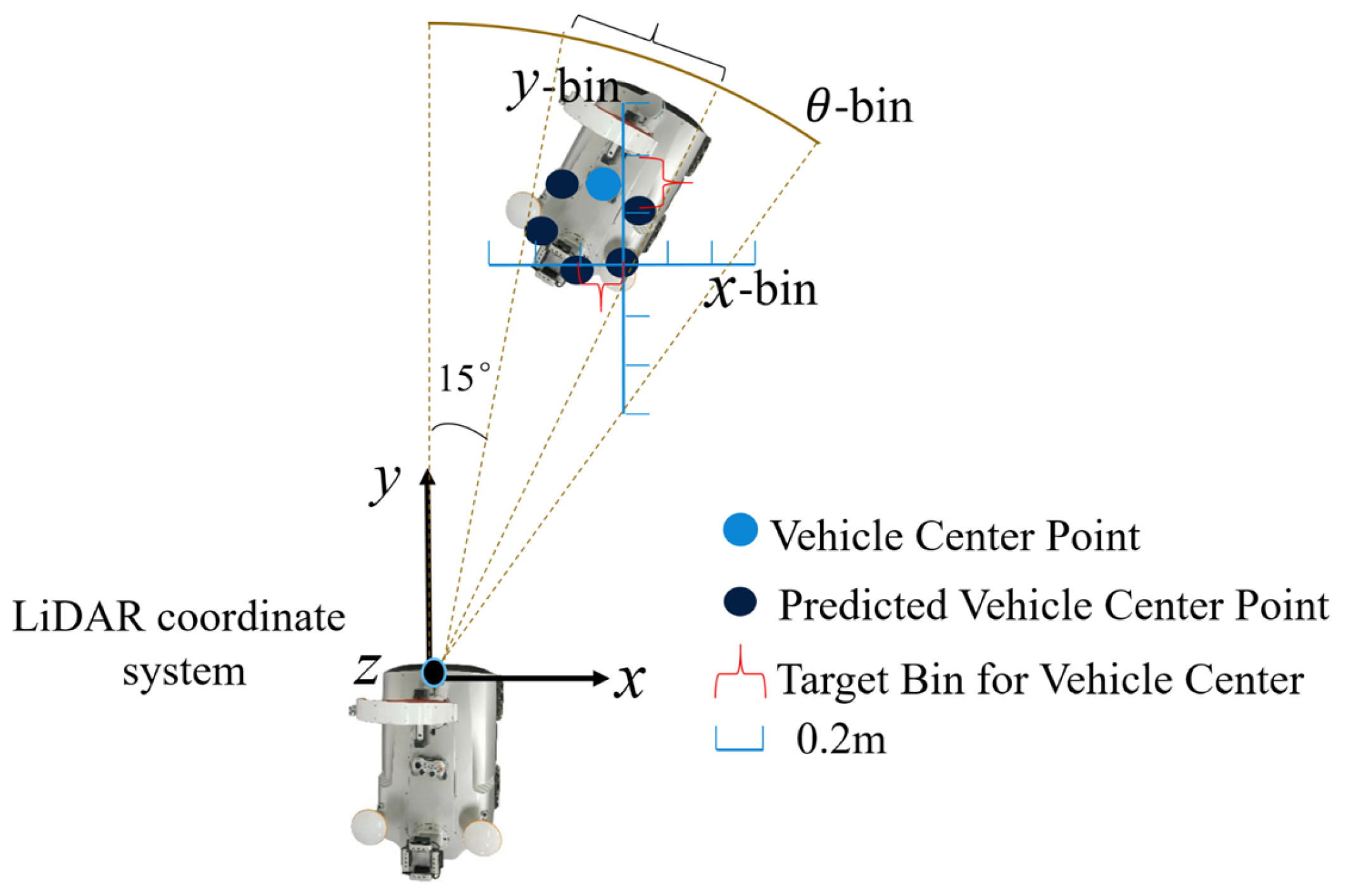
2.1.3. Bin-Based Detection Head
- Bin Classification: Assigning target parameters (position, dimensions, orientation) to predefined discrete intervals (bins), using bin centers as initial estimates;
- Residual Regression: Predicting fine-grained offsets (residuals) relative to bin centers.
| Algorithm 1: Pillar-Bin Detection Head |
| 1: Input: Feature maps F 2: Output: 3D Bounding Box 3: for each foreground point p_i in F do 4: // 1. Parameter Discretization (Bin Creation) 5: Define search bins for x, y, θ and size templates for w,l,h. 6: // 2. Coarse Localization (Bin Classification) 7: bin_x*, bin_y*= argmax(Heatmap_xy(p_i)) 8: bin_θ* = argmax(Heatmap_θ(p_i)) 9: template*te = argmax(SizeScore(p_i)) 10: // 3. Fine Regression (Residual Offset) 11: δ_x, δ_y, δ_θ, δ_w, δ_l, δ_h = Regressor(p_i) 12: // 4. Final Prediction 13: x, y = CenterOf(bin_x*, bin_y*) + δ_x, δ_y 14: θ = CenterOf(bin_θ*) + δ_θ 15: w, l, h = template* + δ_w, δ_l, δ_h 16: z = DirectRegression(p_i) // No binning for height 17: end for 18: return Refined boxes after NMS. |
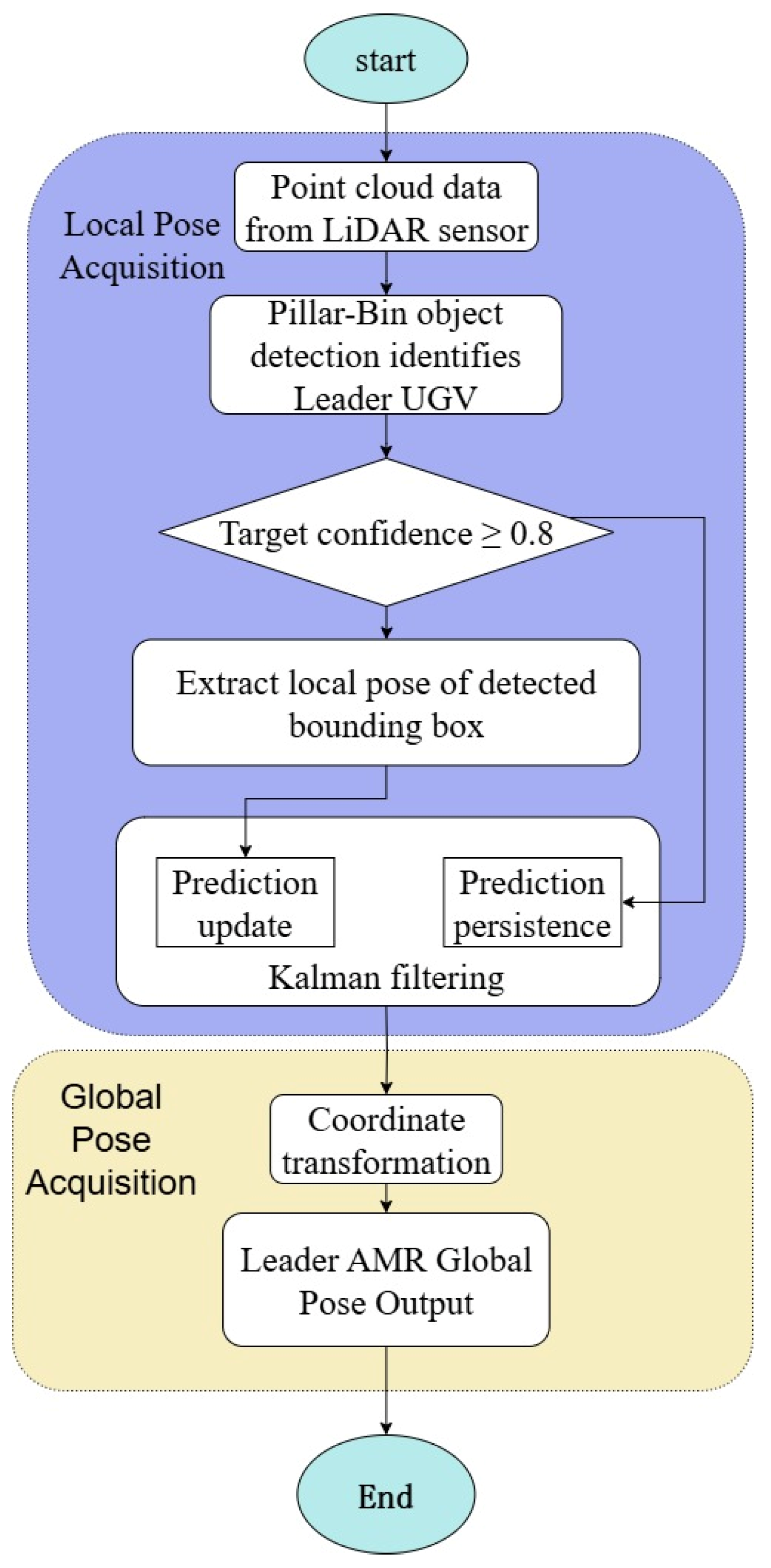
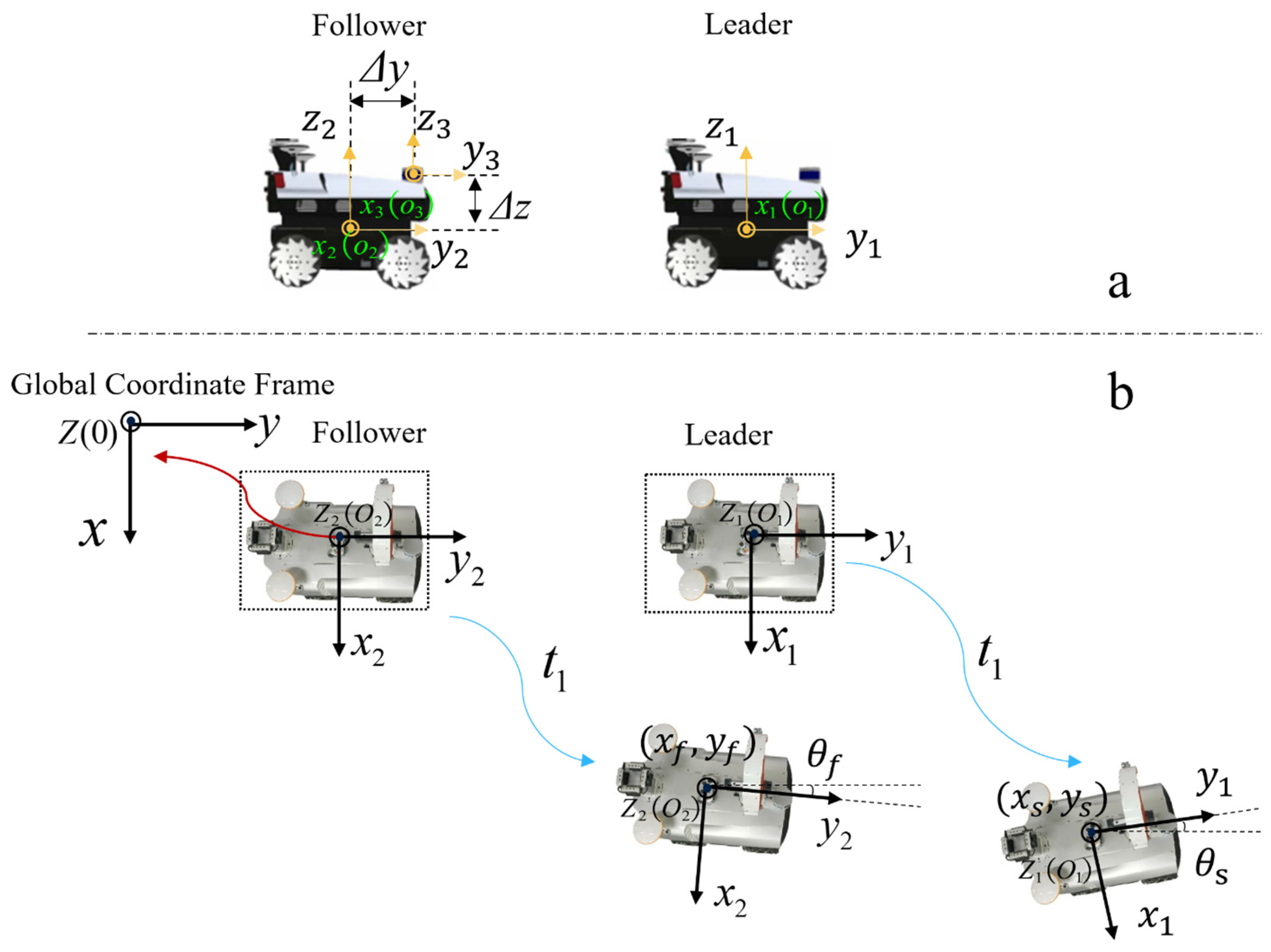
2.2. Design of Leader UGV Pose Estimation Scheme Using Pillar-Bin Algorithm
2.2.1. Local Pose Acquisition
2.2.2. Global Pose Acquisition
3. Experiments and Result Analysis
3.1. Validation of the Pillar-Bin Algorithm on the KITTI Dataset
3.1.1. Experimental Dataset
3.1.2. Experimental Environment and Parameter Settings
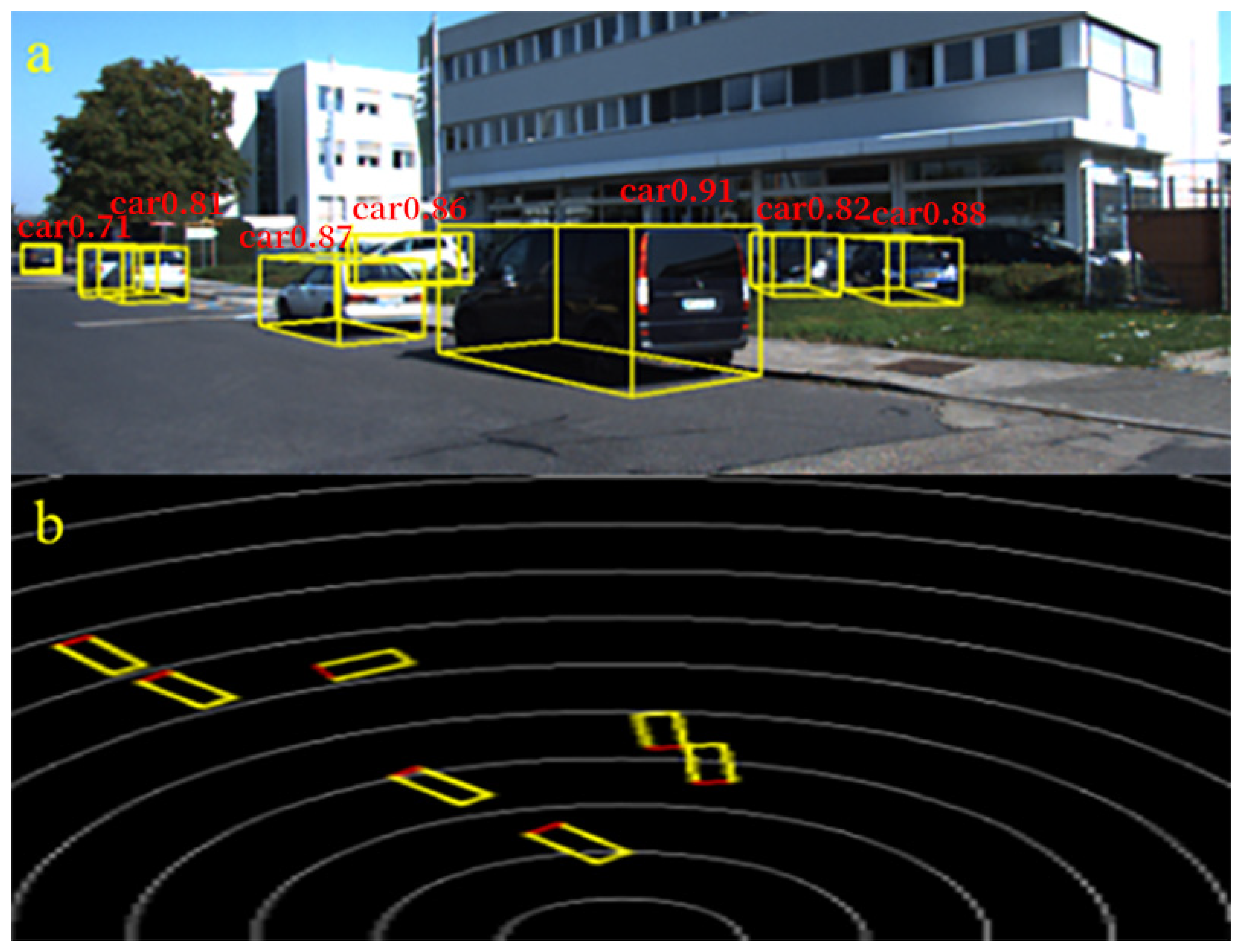
3.1.3. Experimental Results and Analysis of Object Detection Algorithms
3.1.4. Ablations and Trade-Offs
3.2. Real-World Vehicle Experiments with Pillar-Bin Algorithm
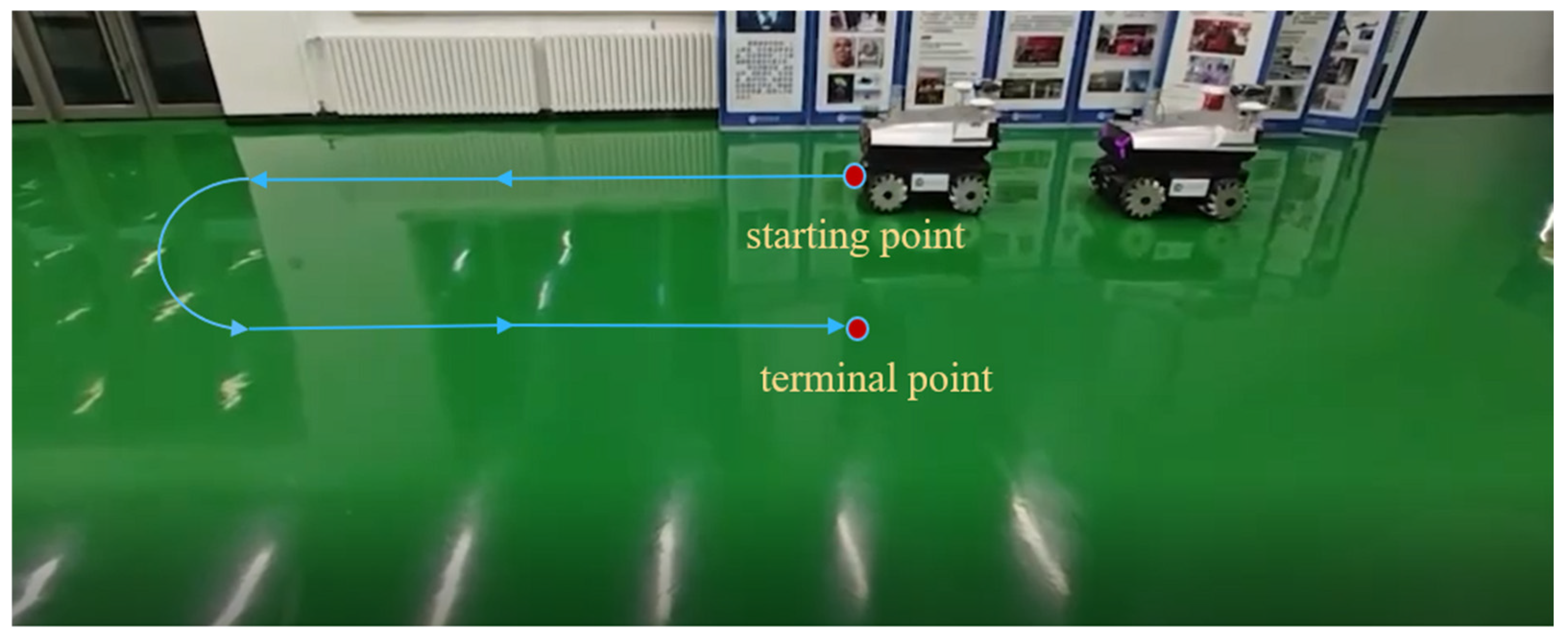
3.2.1. Real-World Vehicle Experiment Design
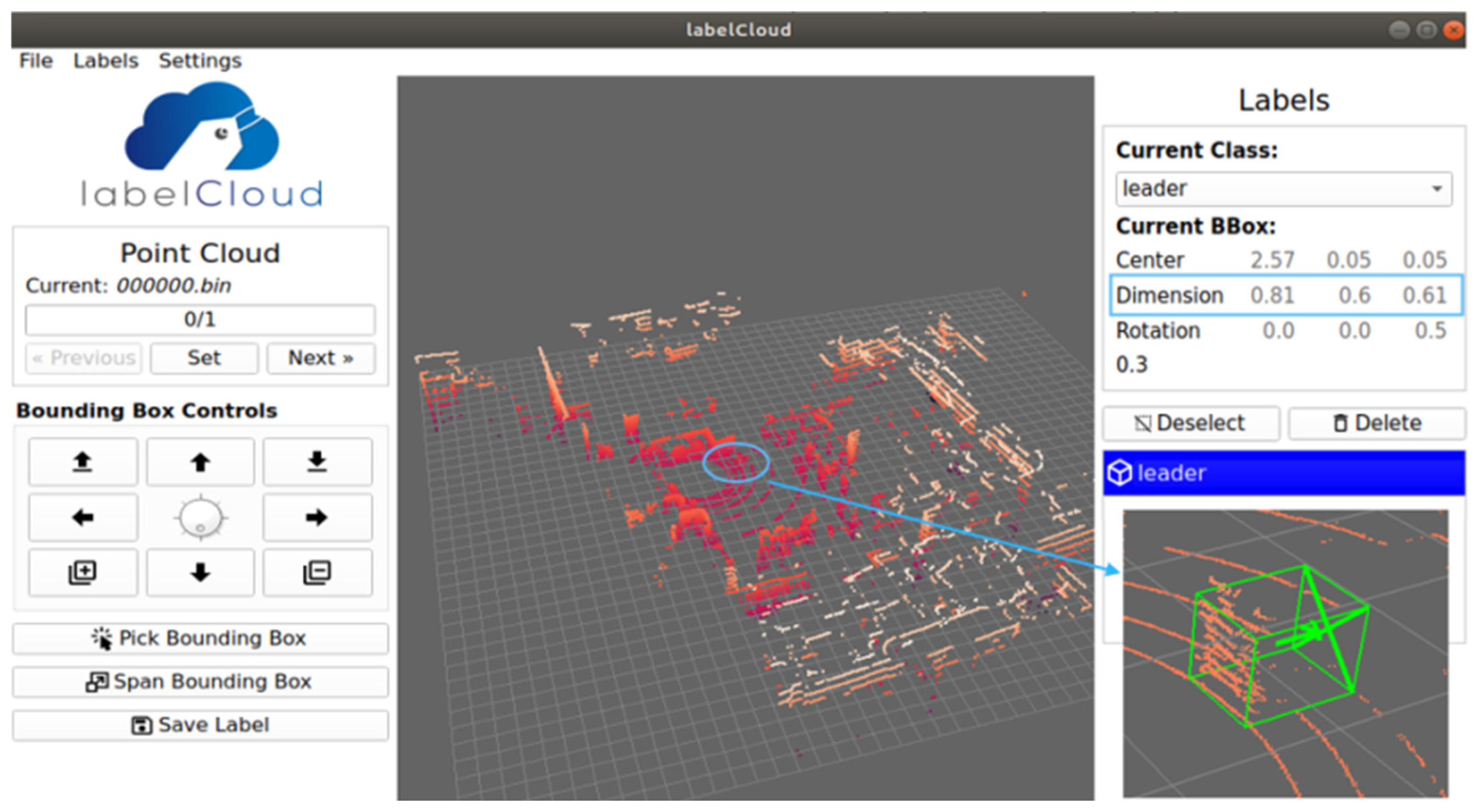
3.2.2. Development of Proprietary Dataset for Pillar-Bin Training
- It significantly improved the dataset annotation consistency by eliminating potential size variations from manual labeling, allowing the Pillar-Bin model to focus on learning critical features without interference from dimensional discrepancies;
- Combined with the experimental environment’s flat road surface characteristics, it effectively mitigated the localization drift issues;
- It substantially enhanced the target pose estimation accuracy, providing more reliable data support for subsequent pose estimation research.
3.2.3. Vehicle Stability Analysis Under Real-Vehicle Conditions
- Pose Jitter Characteristics: Ensuring Formation Control Smoothness;
- 2.
- Confidence Calibration and Gating: Ensuring Formation Decision Safety;
- 3.
- Re-Locking After Occlusion: Preventing Formation Tracking Interruption;
- 4.
- End-to-End Latency Breakdown: Meeting Real-Time Formation Control Requirements;
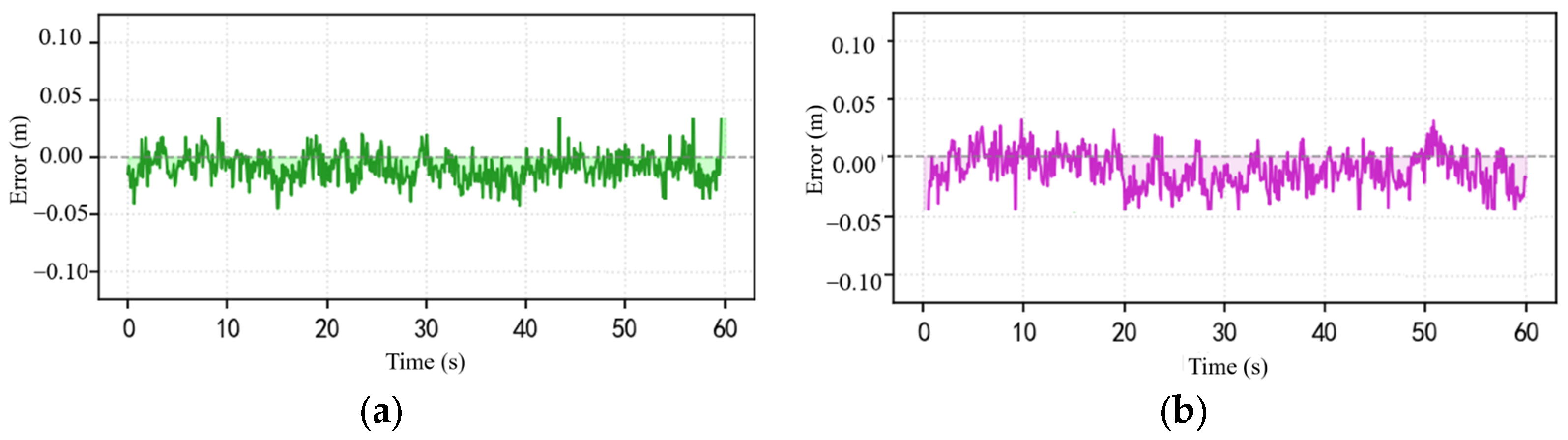
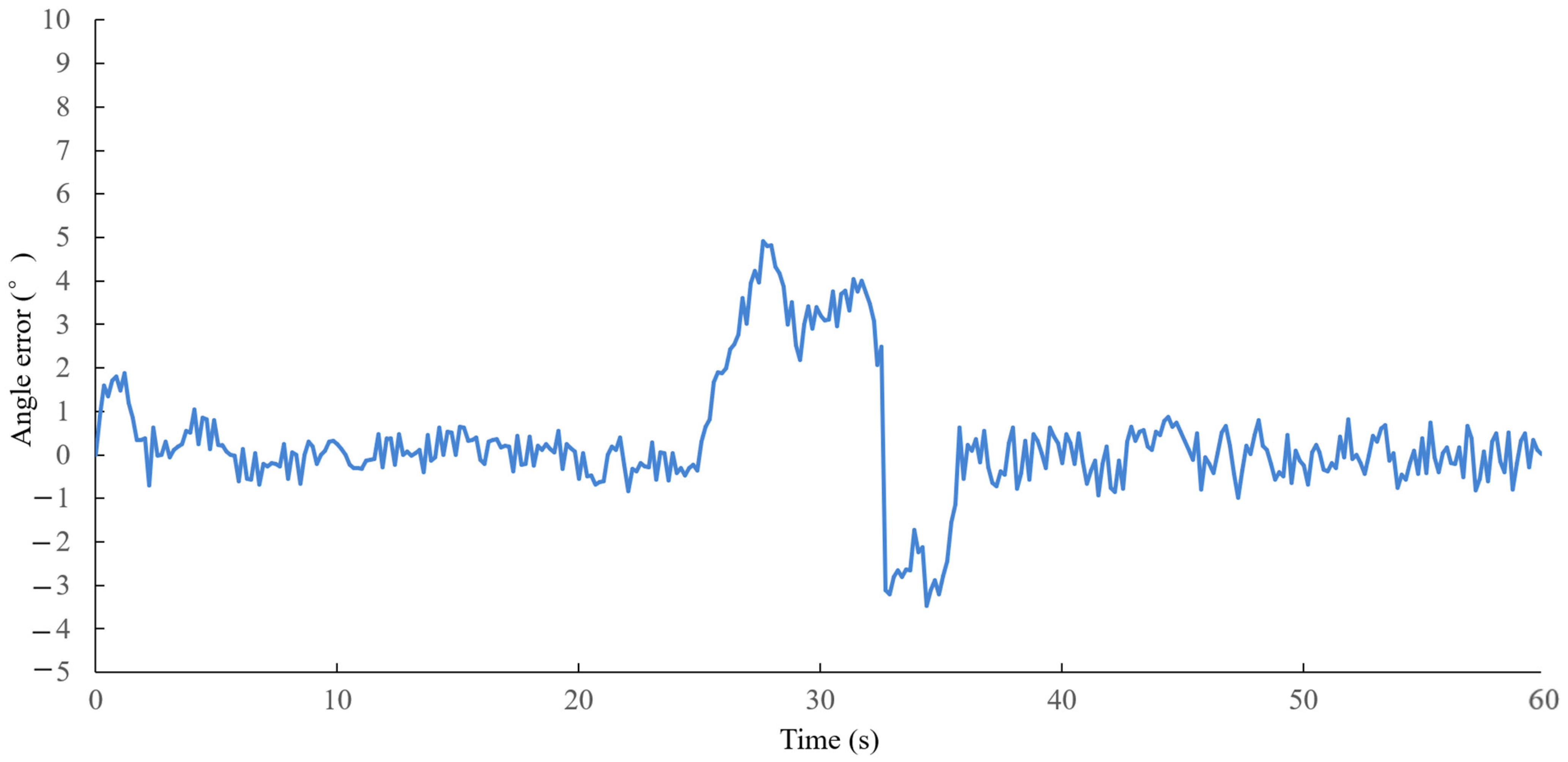
3.2.4. Real-Vehicle Experimental Results Analysis
4. Discussion
- Spatial Constraint Effect: Preset discrete intervals (e.g., ±0.6 m along coordinate axes, Figure 2) transform global spatial searches into finite-region matching, substantially reducing computational redundancy;
- Enhanced Noise Robustness: Using interval centroids as regression benchmarks (Equation (1)) effectively mitigates the impact of local point cloud perturbations on final parameter estimation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Zhao, W.; Meng, Q.; Chung, P.W.H. A Heuristic Distributed Task Allocation Method for Multivehicle Multitask Problems and Its Application to Search and Rescue Scenario. IEEE Trans. Cybern. 2015, 46, 902–915. [Google Scholar] [CrossRef] [PubMed]
- Nie, Z.; Chen, K.-C.; Jin Kim, K. Social-Learning Coordination of Collaborative Multi-Robot Systems Achieves Resilient Production in a Smart Factory. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6009–6023. [Google Scholar] [CrossRef]
- Wang, Y.; de Silva, C.W. Sequential Q-Learning With Kalman Filtering for Multirobot Cooperative Transportation. IEEE-ASME Trans. Mechatron. 2010, 15, 261–268. [Google Scholar] [CrossRef]
- Huang, H.J.E. Adaptive Distributed Control for Leader–Follower Formation Based on a Recurrent SAC Algorithm. Electronics 2024, 13, 3513. [Google Scholar] [CrossRef]
- Lin, J.; Miao, Z.; Zhong, H.; Peng, W.; Rafael, F. Adaptive Image-Based Leader-Follower Formation Control of Mobile Robots With Visibility Constraints. IEEE Trans. Ind. Electron. 2020, 68, 6010–6019. [Google Scholar] [CrossRef]
- Luo, W.; Sun, P.; Zhong, F.; Liu, W.; Zhang, T.; Wang, Y. End-to-End Active Object Tracking and Its Real-World Deployment via Reinforcement Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1317–1332. [Google Scholar] [CrossRef]
- Ramírez-Neria, M.; Luviano-Juárez, A.; Madonski, R.; Ramírez-Juárez, R.; Lozada-Castillo, N.; Gao, Z. Leader-Follower ADRC Strategy for Omnidirectional Mobile Robots without Time-Derivatives in the Tracking Controller. In Proceedings of the American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2023; IEEE: Hoboken, NJ, USA, 2023; pp. 405–410. [Google Scholar]
- Arrichiello, F.; Chiaverini, S.; Indiveri, G.; Pedone, P. The Null-Space-based Behavioral Control for Mobile Robots with Velocity Actuator Saturations. Int. J. Robot. Res. 2010, 29, 1317–1337. [Google Scholar] [CrossRef]
- Xiao, H.; Chen, C.L.P. Incremental Updating Multirobot Formation Using Nonlinear Model Predictive Control Method With General Projection Neural Network. IEEE Trans. Ind. Electron. 2019, 66, 4502–4512. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. A Decentralized Cooperative Control Scheme With Obstacle Avoidance for a Team of Mobile Robots. IEEE Trans. Ind. Electron. 2014, 61, 347–354. [Google Scholar] [CrossRef]
- Zhao, S.; Zelazo, D. Bearing Rigidity and Almost Global Bearing-Only Formation Stabilization. IEEE Trans. Autom. Control 2016, 61, 1255–1268. [Google Scholar] [CrossRef]
- Nie, J.; Zhang, G.; Lu, X.; Wang, H.; Sheng, C.; Sun, L. Obstacle avoidance method based on reinforcement learning dual-layer decision model for AGV with visual perception. Control Eng. Pract. 2024, 153, 106121. [Google Scholar] [CrossRef]
- Vora, S.; Lang, A.H.; Helou, B.; Beijbom, O. PointPainting: Sequential Fusion for 3D Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; IEEE: Hoboken, NJ, USA, 2020; pp. 4603–4611. [Google Scholar]
- Li, S.; Liu, Y.; Gall, J. Rethinking 3-D LiDAR Point Cloud Segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4079–4090. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, Y.; Zhang, S.; Ogai, H. Deep 3D Object Detection Networks Using LiDAR Data: A Review. IEEE Sens. J. 2021, 21, 1152–1171. [Google Scholar] [CrossRef]
- Zhou, J.; Tan, X.; Shao, Z.; Ma, L. FVNet: 3D Front-View Proposal Generation for Real-Time Object Detection from Point Clouds. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Suzhou, China, 19–21 October 2019. [Google Scholar]
- Zarzar, J.; Giancola, S.; Ghanem, B. PointRGCN: Graph Convolution Networks for 3D Vehicles Detection Refinement. arXiv 2019, arXiv:1911.12236. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J.J.I. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet plus plus: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhou, Q.; Yu, C. Point RCNN: An Angle-Free Framework for Rotated Object Detection. Remote Sens. 2022, 14, 2605. [Google Scholar] [CrossRef]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 31st IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Hoboken, NJ, USA, 2018; pp. 4490–4499. [Google Scholar]
- Yan, Y.; Mao, Y.; Li, B. SECOND: Sparsely Embedded Convolutional Detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O.; Soc, I.C. PointPillars: Fast Encoders for Object Detection from Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 12689–12697. [Google Scholar]
- Yin, T.; Zhou, X.; Krahenbuhl, P. Center-based 3D Object Detection and Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021; pp. 11779–11788. [Google Scholar]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Li, H.J.I. PV-RCNN: Point-Voxel Feature Set Abstraction for 3D Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) 2020, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Wu, P.; Gu, L.; Yan, X.; Xie, H.; Wang, F.L.; Cheng, G.; Wei, M. PV-RCNN plus plus: Semantical point-voxel feature interaction for 3D object detection. Vis. Comput. 2023, 39, 2425–2440. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, X.; Zhang, X.; Hao, X.; Wang, D.; He, Y. Multi Point-Voxel Convolution (MPVConv) for Deep Learning on Point Clouds. Comput. Graph. 2021, 112, 72–80. [Google Scholar] [CrossRef]
- Deng, P.; Zhou, L.; Chen, J. PVC-SSD: Point-Voxel Dual-Channel Fusion With Cascade Point Estimation for Anchor-Free Single-Stage 3-D Object Detection. IEEE Sens. J. 2024, 24, 14894–14904. [Google Scholar] [CrossRef]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection from Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, H.; Hu, J.; Li, X.; Peng, L. A Multi-Level Eigenvalue Fusion Algorithm for 3D Multi-Object Tracking. In Proceedings of the ASCE International Conference on Transportation and Development (ICTD)—Application of Emerging Technologies, Seattle, WA, USA, 31 May–3 June 2022; pp. 235–245. [Google Scholar]
- Liu, J.; Liu, D.; Ji, W.; Cai, C.; Liu, Z. Adaptive multi-object tracking based on sensors fusion with confidence updating. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103577. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Hayeon, O.; Yang, C.; Huh, K. SeSame: Simple, Easy 3D Object Detection with Point-Wise Semantics. In Proceedings of the Asian Conference on Computer Vision, Hanoi, Vietnam, 8–12 December 2024. [Google Scholar]




| Software Name | Software Version |
|---|---|
| Linux Operating System | Ubuntu 20.04LTS |
| ROS | Noetic |
| PyTorch | 1.7.0 |
| Python | 3.7 |
| cuda | 12.2 |
| OpenCV | 3.4.2 |
| Algorithms | Easy | Moderate | Hard | mAP |
|---|---|---|---|---|
| VoxelNet | 77.56 | 66.15 | 57.25 | 66.99 |
| SECOND | 82.15 | 73.64 | 68.43 | 74.74 |
| PointPillars | 82.65 | 76.28 | 69.10 | 76.01 |
| PV-RCNN++ | 86.35 | 80.62 | 69.67 | 78.88 |
| CenterPoint | 85.37 | 77.36 | 68.34 | 77.02 |
| SeSame | 84.75 | 77.36 | 69.51 | 77.21 |
| Pillar-Bin | 86.51 | 79.48 | 70.89 | 78.96 |
| Algorithms | Easy | Moderate | Hard | mAP |
|---|---|---|---|---|
| VoxelNet | 87.89 | 77.14 | 76.24 | 80.42 |
| SECOND | 88.21 | 79.58 | 77.37 | 81.72 |
| PointPillars | 88.45 | 85.36 | 83.15 | 85.65 |
| PV-RCNN++ | 90.35 | 85.31 | 82.67 | 86.11 |
| CenterPoint | 89.78 | 84.61 | 83.21 | 85.86 |
| SeSame | 88.35 | 82.32 | 81.68 | 84.12 |
| Pillar-Bin | 89.64 | 86.35 | 83.78 | 86.59 |
| Algorithms | GPU Memory/MB | Inference Speed/FPS |
|---|---|---|
| VoxelNet | 7945 | 18 |
| SECOND | 6861 | 22 |
| PointPillars | 3746 | 52 |
| PV-RCNN++ | 10,837 | 12.5 |
| CenterPoint | 8759 | 15 |
| SeSame | 7034 | 21 |
| Pillar-Bin | 4027 | 48 |
| RoIs | Recall (IOU = 0.5) | Recall (IOU = 0.7) |
|---|---|---|
| 10 | 86.35 | 29.14 |
| 20 | 90.21 | 32.58 |
| 50 | 92.45 | 40.36 |
| 100 | 95.75 | 40.31 |
| 200 | 96.38 | 74.61 |
| 300 | 98.03 | 78.32 |
| 500 | 98.11 | 83.35 |
| Bin_Width (m) | Search Space (m) | Bin_Yaw (°) | Size Templates | APM (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.4 | 0.4 | 0.6 | 0.8 | 1 | 10 | 15 | 30 | ||
| ✓ | ✓ | 77.38 | |||||||||
| ✓ | ✓ | 78.12 | |||||||||
| ✓ | ✓ | 77.56 | |||||||||
| ✓ | ✓ | 78.12 | |||||||||
| ✓ | ✓ | 78.87 | |||||||||
| ✓ | ✓ | 78.26 | |||||||||
| ✓ | ✓ | 78.02 | |||||||||
| ✓ | 78.38 | ||||||||||
| ✓ | 78.67 | ||||||||||
| ✓ | 76.11 | ||||||||||
| ✓ | 78.17 | ||||||||||
| ✓ | ✓ | ✓ | 79.14 | ||||||||
| ✓ | ✓ | 78.45 | |||||||||
| ✓ | ✓ | ✓ | 78.86 | ||||||||
| ✓ | ✓ | ✓ | ✓ | 79.48 | |||||||
| Parameter | Specification |
|---|---|
| Laser channels | 32-beam |
| Detection range | 100 m |
| Range accuracy | ±3 cm |
| Horizontal FOV | 360° (continuous rotating scan) |
| Vertical FOV | +10° to −30° |
| Angular resolution | Horizontal: 0.1°~0.4°; Vertical: 1.33° |
| Scanning frequency | 5 Hz~20 Hz |
| Point cloud output | ~700,000 points/second |
| Motion Scenario | Metric | PointPillars | Pillar-Bin | Relative Improvement |
|---|---|---|---|---|
| Straight Path | Position Jitter P95 (cm) | 6.2 | 2.9 | −53.2% |
| Position Jitter P99 (cm) | 7.5 | 3.3 | −56.0% | |
| Heading Angle Jitter P95 (°) | 1.6 | 0.7 | −56.2% | |
| Heading Angle Jitter P99 (°) | 2.3 | 1.1 | −52.2% | |
| Curved Path | Position Jitter P95 (cm) | 10.1 | 4.9 | −51.8% |
| Position Jitter P99 (cm) | 12.2 | 6.8 | −44.2% | |
| Heading Angle Jitter P95 (°) | 3.1 | 1.5 | −51.6% | |
| Heading Angle Jitter P99 (°) | 7.8 | 3.8 | −51.3% |
| Threshold τ | mAP (%) | Frames with Confidence < τ (%) | FP Rate (%) |
|---|---|---|---|
| 0.3 | 75.1 | 3.5 | 3.8 |
| 0.5 | 76.8 | 8.3 | 2.1 |
| 0.7 | 77.2 | 15.6 | 1.5 |
| 0.8 | 77.4 | 22.1 | 1.2 |
| Metric | PointPillars | Pillar-Bin |
|---|---|---|
| ECE (Vehicle Class) | 0.17 | 0.08 |
| mAP | 72.5 | 76.8 |
| Percentage of Time with Confidence < τ | 7.8 | 8.3 |
| FP Rate | 5.3 | 2.1 |
| Motion Scenario | Metric | PointPillars | Pillar-Bin | Relative Improvement |
|---|---|---|---|---|
| Straight Path | Average Re-Locking Time (s) | 0.24 | 0.09 | −62.5% |
| Maximum Re-Locking Time (s) | 0.35 | 0.15 | −57.1% | |
| Re-Locking Success Rate (%) | 86.7 | 98.3 | +13.4% | |
| Curved Path | Average Re-Locking Time (s) | 0.31 | 0.12 | −61.3% |
| Maximum Re-Locking Time (s) | 0.42 | 0.22 | −47.6% | |
| Re-Locking Success Rate (%) | 80.0 | 96.7 | +20.9% |
| Processing Stage | PointPillars (Baseline) | Pillar-Bin |
|---|---|---|
| LiDAR I/O | 476.19 | 476.19 |
| Detector | 54.05 | 49.26 |
| Pose Decode | 833.33 | 769.23 |
| Controller | 1000.00 | 1000.00 |
| End-to-End Frame Rate | 43.86 | 40.49 |
| Sensor | Parameter | Value |
|---|---|---|
| Gyroscope | Bias Repeatability | 0.1°/hour |
| Scale Factor Repeatability | <50 × 10−6 | |
| Scale Factor Nonlinearity | <100 × 10−6 | |
| Accelerometer | Bias Repeatability | <3.5 mg |
| Noise Density | 25 μg/sqrt(Hz) | |
| Scale Factor Nonlinearity | <1000 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Liu, Y.; Chen, J.; Tang, S. Pillar-Bin: A 3D Object Detection Algorithm for Communication-Denied UGVs. Drones 2025, 9, 686. https://doi.org/10.3390/drones9100686
Kang C, Liu Y, Chen J, Tang S. Pillar-Bin: A 3D Object Detection Algorithm for Communication-Denied UGVs. Drones. 2025; 9(10):686. https://doi.org/10.3390/drones9100686
Chicago/Turabian StyleKang, Cunfeng, Yukun Liu, Junfeng Chen, and Siqi Tang. 2025. "Pillar-Bin: A 3D Object Detection Algorithm for Communication-Denied UGVs" Drones 9, no. 10: 686. https://doi.org/10.3390/drones9100686
APA StyleKang, C., Liu, Y., Chen, J., & Tang, S. (2025). Pillar-Bin: A 3D Object Detection Algorithm for Communication-Denied UGVs. Drones, 9(10), 686. https://doi.org/10.3390/drones9100686






