Comparison of Regression, Classification, Percentile Method and Dual-Range Averaging Method for Crop Canopy Height Estimation from UAV-Based LiDAR Point Cloud Data
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
2. Materials and Methods
2.1. Study Area and Data Collection
2.1.1. Ground Truth Data Collection
2.1.2. UAV-Based LiDAR Data Collection
2.2. LiDAR Data Pre-Processing
2.3. Point Cloud Data Preparation
2.4. Machine Learning Regression Modeling
2.4.1. Random Forest Regression
2.4.2. Support Vector Regression
2.5. Ground Point Classification
2.5.1. CSF
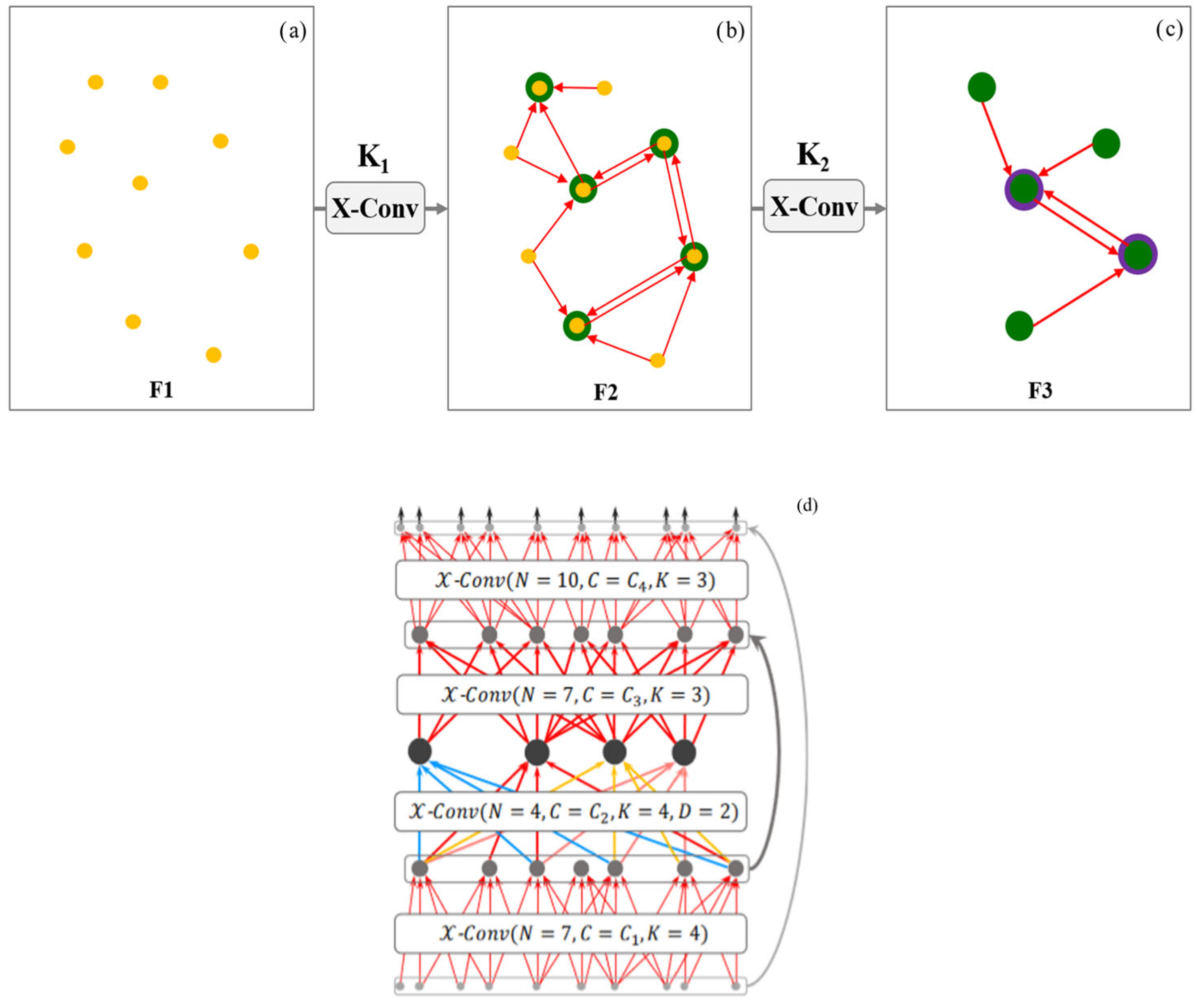
2.5.2. PointCNN
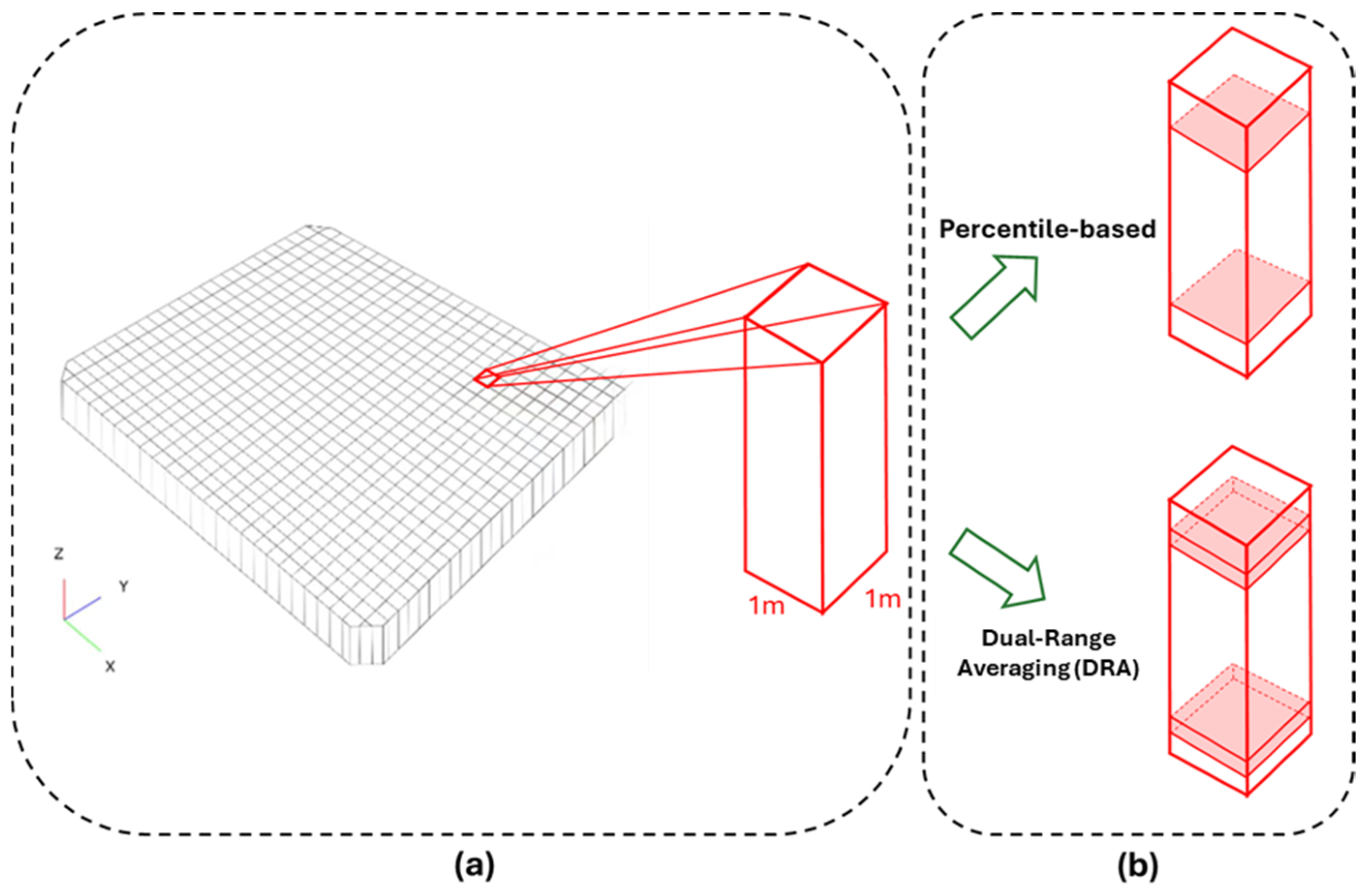
2.6. Percentile-Based Method and Dual-Range Averaging Method
2.6.1. Percentile-Based Method
2.6.2. Dual-Range Averaging Method
2.7. Accuracy Assessment
3. Results
3.1. Machine Learning Regression Modeling
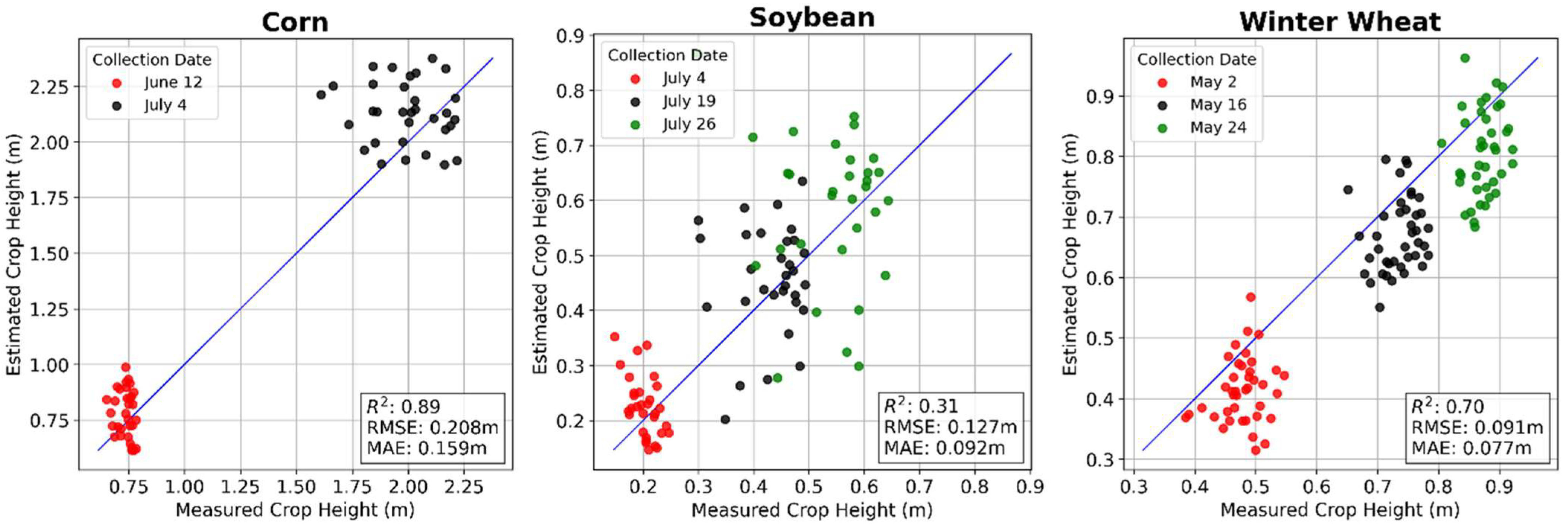
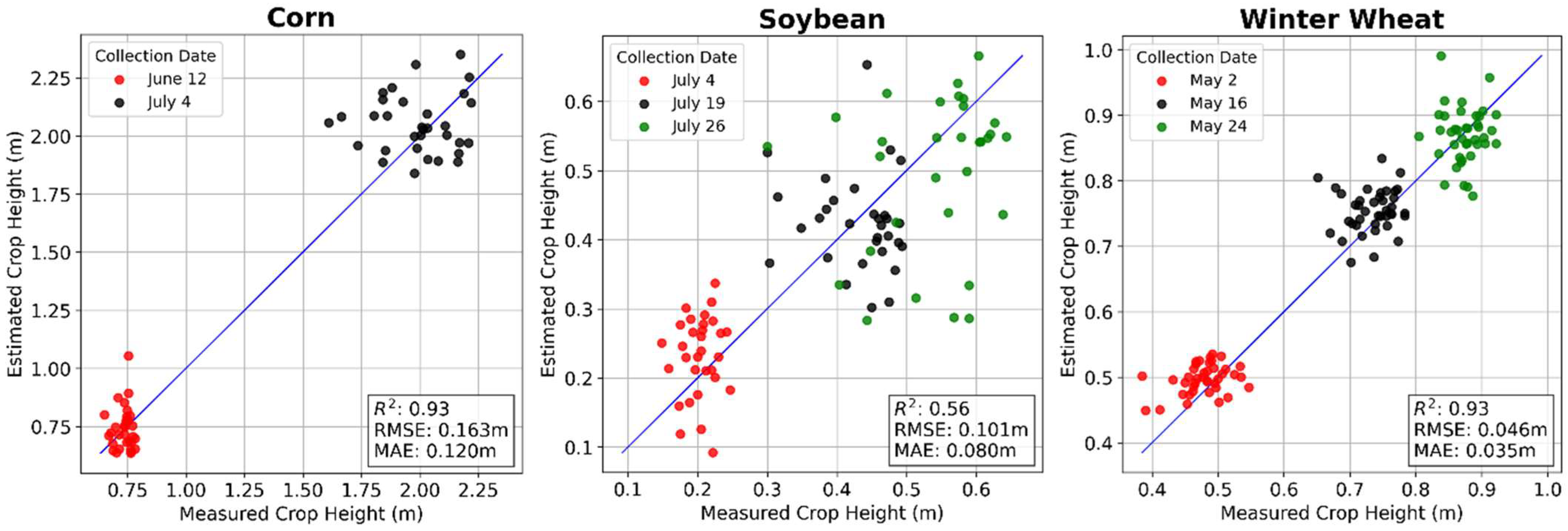
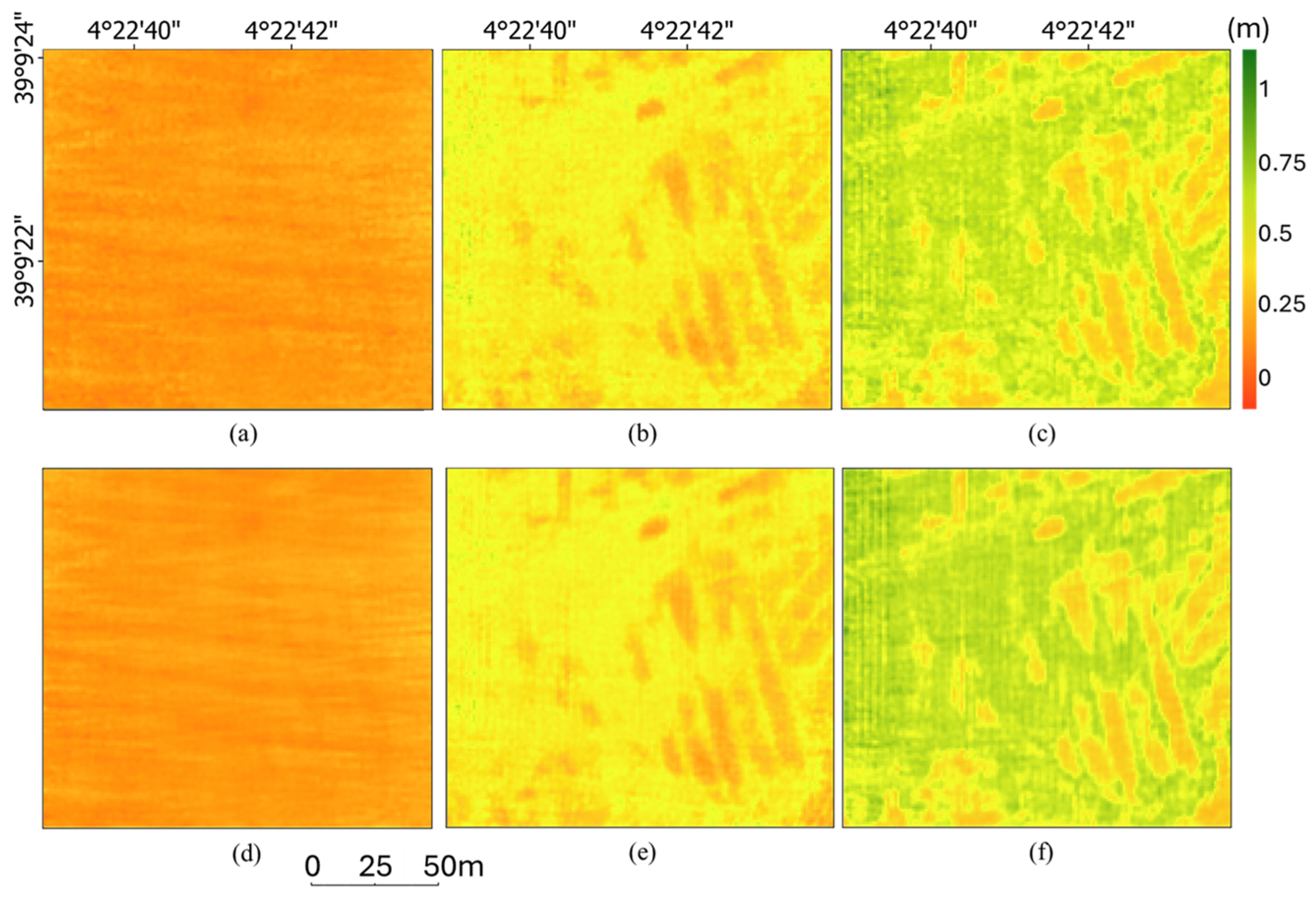
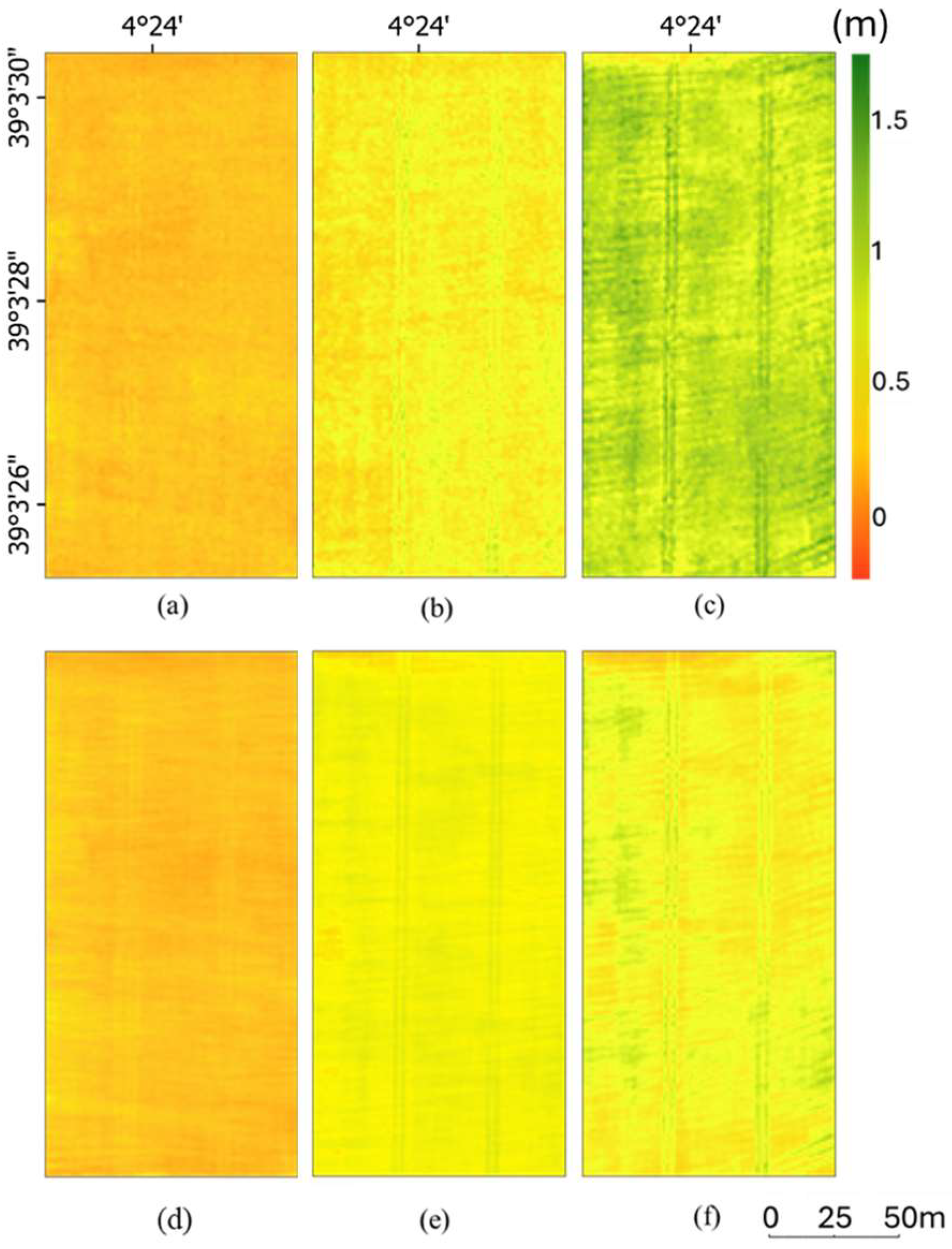
3.2. Ground Point Classification and Canopy Height Estimation
3.3. Percentile-Based Method and Dual-Range Averaging Method
4. Discussion
4.1. Performance Comparison of Crop Height Estimation Methods
4.2. Methodological Limitations and Practical Considerations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martos, V.; Ahmad, A.; Cartujo, P.; Ordoñez, J. Ensuring Agricultural Sustainability through Remote Sensing in the Era of Agriculture 5.0. Appl. Sci. 2021, 11, 5911. [Google Scholar] [CrossRef]
- Velten, S.; Leventon, J.; Jager, N.; Newig, J. What Is Sustainable Agriculture? A Systematic Review. Sustainability 2015, 7, 7833–7865. [Google Scholar] [CrossRef]
- Gebbers, R.; Adamchuk, V.I. Precision Agriculture and Food Security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An Overview of Current and Potential Applications of Thermal Remote Sensing in Precision Agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Rivera, G.; Porras, R.; Florencia, R.; Sánchez-Solís, J.P. LiDAR Applications in Precision Agriculture for Cultivating Crops: A Review of Recent Advances. Comput. Electron. Agric. 2023, 207, 107737. [Google Scholar] [CrossRef]
- Aarif K. O., M.; Alam, A.; Hotak, Y. Smart Sensor Technologies Shaping the Future of Precision Agriculture: Recent Advances and Future Outlooks. J. Sens. 2025, 2025, 2460098. [Google Scholar] [CrossRef]
- Chang, A.; Jung, J.; Maeda, M.M.; Landivar, J. Crop Height Monitoring with Digital Imagery from Unmanned Aerial System (UAS). Comput. Electron. Agric. 2017, 141, 232–237. [Google Scholar] [CrossRef]
- Guo, Y.; Xiao, Y.; Li, M.; Hao, F.; Zhang, X.; Sun, H.; De Beurs, K.; Fu, Y.H.; He, Y. Identifying Crop Phenology Using Maize Height Constructed from Multi-Sources Images. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103121. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Magney, T.S.; Vierling, L.A.; Greaves, H.E.; Zheng, G. An Automated Method to Quantify Crop Height and Calibrate Satellite-Derived Biomass Using Hypertemporal Lidar. Remote Sens. Environ. 2016, 187, 414–422. [Google Scholar] [CrossRef]
- Anthony, D.; Elbaum, S.; Lorenz, A.; Detweiler, C. On Crop Height Estimation with UAVs. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4805–4812. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies. BioScience 2002, 52, 19. [Google Scholar] [CrossRef]
- Cecchi, G.; Pantani, L. Fluorescence Lidar Remote Sensing of Vegetation: Research Advances in Europe. In Proceedings of the Proceedings of IGARSS ’94—1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 2, pp. 979–981. [Google Scholar]
- Husin, N.A.; Khairunniza-Bejo, S.; Abdullah, A.F.; Kassim, M.S.M.; Ahmad, D.; Azmi, A.N.N. Application of Ground-Based LiDAR for Analysing Oil Palm Canopy Properties on the Occurrence of Basal Stem Rot (BSR) Disease. Sci. Rep. 2020, 10, 6464. [Google Scholar] [CrossRef]
- Wu, D.; Johansen, K.; Phinn, S.; Robson, A. Suitability of Airborne and Terrestrial Laser Scanning for Mapping Tree Crop Structural Metrics for Improved Orchard Management. Remote Sens. 2020, 12, 1647. [Google Scholar] [CrossRef]
- Wendel, A.; Underwood, J.; Walsh, K. Maturity Estimation of Mangoes Using Hyperspectral Imaging from a Ground Based Mobile Platform. Comput. Electron. Agric. 2018, 155, 298–313. [Google Scholar] [CrossRef]
- Bai, G.; Ge, Y.; Hussain, W.; Baenziger, P.S.; Graef, G. A Multi-Sensor System for High Throughput Field Phenotyping in Soybean and Wheat Breeding. Comput. Electron. Agric. 2016, 128, 181–192. [Google Scholar] [CrossRef]
- Walter, J.D.C.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating Biomass and Canopy Height with LiDAR for Field Crop Breeding. Front. Plant Sci. 2019, 10, 1145. [Google Scholar] [CrossRef]
- Fareed, N.; Flores, J.P.; Das, A.K. Analysis of UAS-LiDAR Ground Points Classification in Agricultural Fields Using Traditional Algorithms and PointCNN. Remote Sens. 2023, 15, 483. [Google Scholar] [CrossRef]
- Thudi, M.; Palakurthi, R.; Schnable, J.C.; Chitikineni, A.; Dreisigacker, S.; Mace, E.; Srivastava, R.K.; Satyavathi, C.T.; Odeny, D.; Tiwari, V.K.; et al. Genomic Resources in Plant Breeding for Sustainable Agriculture. J. Plant Physiol. 2021, 257, 153351. [Google Scholar] [CrossRef]
- Gao, M.; Yang, F.; Wei, H.; Liu, X. Individual Maize Location and Height Estimation in Field from UAV-Borne LiDAR and RGB Images. Remote Sens. 2022, 14, 2292. [Google Scholar] [CrossRef]
- Dhami, H.; Yu, K.; Xu, T.; Zhu, Q.; Dhakal, K.; Friel, J.; Li, S.; Tokekar, P. Crop Height and Plot Estimation for Phenotyping from Unmanned Aerial Vehicles Using 3D LiDAR. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 2643–2649. [Google Scholar]
- Zhou, L.; Gu, X.; Cheng, S.; Yang, G.; Shu, M.; Sun, Q. Analysis of Plant Height Changes of Lodged Maize Using UAV-LiDAR Data. Agriculture 2020, 10, 146. [Google Scholar] [CrossRef]
- Luo, S.; Liu, W.; Zhang, Y.; Wang, C.; Xi, X.; Nie, S.; Ma, D.; Lin, Y.; Zhou, G. Maize and Soybean Heights Estimation from Unmanned Aerial Vehicle (UAV) LiDAR Data. Comput. Electron. Agric. 2021, 182, 106005. [Google Scholar] [CrossRef]
- Pun Magar, L.; Sandifer, J.; Khatri, D.; Poudel, S.; Kc, S.; Gyawali, B.; Gebremedhin, M.; Chiluwal, A. Plant Height Measurement Using UAV-Based Aerial RGB and LiDAR Images in Soybean. Front. Plant Sci. 2025, 16, 1488760. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, L.; Chen, Q.; Wang, G.; Luo, P.; Sharma, R.P.; He, P.; Li, M.; Wang, M.; Duan, G. Analysis of the Spatial Differences in Canopy Height Models from UAV LiDAR and Photogrammetry. Remote Sens. 2020, 12, 2884. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J. Winter Wheat Canopy Height Extraction from UAV-Based Point Cloud Data with a Moving Cuboid Filter. Remote Sens. 2019, 11, 1239. [Google Scholar] [CrossRef]
- Yang, W.; Wu, J.; Xu, W.; Li, H.; Li, X.; Lan, Y.; Li, Y.; Zhang, L. Comparative Evaluation of the Performance of the PTD and CSF Algorithms on UAV LiDAR Data for Dynamic Canopy Height Modeling in Densely Planted Cotton. Agronomy 2024, 14, 856. [Google Scholar] [CrossRef]
- Ten Harkel, J.; Bartholomeus, H.; Kooistra, L. Biomass and Crop Height Estimation of Different Crops Using UAV-Based Lidar. Remote Sens. 2019, 12, 17. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Peng, Y.; Yu, X.; Lu, L.; Liu, Y.; Song, Y.; Yin, D.; Zhao, S.; Wang, H.; et al. QTL Mapping of Maize Plant Height Based on a Population of Doubled Haploid Lines Using UAV LiDAR High-Throughput Phenotyping Data. J. Integr. Agric. 2024, in press. [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Erkbol, H.; Adrian, J.; Newcomb, M.; LeBauer, D.; Pauli, D.; Shakoor, N.; Mockler, T.C. UAV-Based Sorghum Growth Monitoring: A Comparative Analysis of Lidar and Photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 3, 489–496. [Google Scholar] [CrossRef]
- Šrollerů, A.; Potůčková, M. Evaluating the Applicability of High-Density UAV LiDAR Data for Monitoring Tundra Grassland Vegetation. Int. J. Remote Sens. 2024, 46, 42–76. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Cheng, Q.; Duan, F.; Zhai, W.; Li, Z.; Mao, B.; Ding, F.; Kuang, X.; Chen, Z. Estimating Maize Crop Height and Aboveground Biomass Using Multi-Source Unmanned Aerial Vehicle Remote Sensing and Optuna-Optimized Ensemble Learning Algorithms. Remote Sens. 2024, 16, 3176. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, S.; Yang, T.; Zhang, W.; Xu, Y.; Zhou, K.; Wu, W.; Zhao, Y.; Yao, Z.; Yang, G.; et al. Maize Height Estimation Using Combined Unmanned Aerial Vehicle Oblique Photography and LIDAR Canopy Dynamic Characteristics. Comput. Electron. Agric. 2024, 218, 108685. [Google Scholar] [CrossRef]
- Hütt, C.; Bolten, A.; Hüging, H.; Bareth, G. UAV LiDAR Metrics for Monitoring Crop Height, Biomass and Nitrogen Uptake: A Case Study on a Winter Wheat Field Trial. PFG 2023, 91, 65–76. [Google Scholar] [CrossRef]
- Madec, S.; Baret, F.; De Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-Throughput Phenotyping of Plant Height: Comparing Unmanned Aerial Vehicles and Ground LiDAR Estimates. Front. Plant Sci. 2017, 8, 2002. [Google Scholar] [CrossRef]
- Monnet, J.-M.; Chanussot, J.; Berger, F. Support Vector Regression for the Estimation of Forest Stand Parameters Using Airborne Laser Scanning. IEEE Geosci. Remote Sens. Lett. 2011, 8, 580–584. [Google Scholar] [CrossRef]
- Chen, G.; Hay, G.J.; Zhou, Y. Estimation of Forest Height, Biomass and Volume Using Support Vector Regression and Segmentation from Lidar Transects and Quickbird Imagery. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Zhang, F.; Hassanzadeh, A.; Kikkert, J.; Pethybridge, S.J.; Van Aardt, J. Comparison of UAS-Based Structure-from-Motion and LiDAR for Structural Characterization of Short Broadacre Crops. Remote Sens. 2021, 13, 3975. [Google Scholar] [CrossRef]
- Sangjan, W.; McGee, R.J.; Sankaran, S. Optimization of UAV-Based Imaging and Image Processing Orthomosaic and Point Cloud Approaches for Estimating Biomass in a Forage Crop. Remote Sens. 2022, 14, 2396. [Google Scholar] [CrossRef]
- Colaço, A.F.; Schaefer, M.; Bramley, R.G.V. Broadacre Mapping of Wheat Biomass Using Ground-Based LiDAR Technology. Remote Sens. 2021, 13, 3218. [Google Scholar] [CrossRef]
- Pearse, G.D.; Watt, M.S.; Dash, J.P.; Stone, C.; Caccamo, G. Comparison of Models Describing Forest Inventory Attributes Using Standard and Voxel-Based Lidar Predictors across a Range of Pulse Densities. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 341–351. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Modeling and Prediction of Turkey’s Electricity Consumption Using Support Vector Regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Jin, J.; Verbeurgt, J.; De Sloover, L.; Stal, C.; Deruyter, G.; Montreuil, A.-L.; Vos, S.; De Maeyer, P.; De Wulf, A. Support Vector Regression for High-Resolution Beach Surface Moisture Estimation from Terrestrial LiDAR Intensity Data. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102458. [Google Scholar] [CrossRef]
- Evans, J.S.; Hudak, A.T.; Faux, R.; Smith, A.M.S. Discrete Return Lidar in Natural Resources: Recommendations for Project Planning, Data Processing, and Deliverables. Remote Sens. 2009, 1, 776–794. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The Canopy Surface and Stand Development: Assessing Forest Canopy Structure and Complexity with near-Surface Altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Kwak, D.-A.; Lee, W.-K.; Cho, H.-K. Estimation of Lai Using Lidar Remote Sensing in Forest. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007. [Google Scholar]
- Zhang, J.; Zhao, X.; Chen, Z.; Lu, Z. A Review of Deep Learning-Based Semantic Segmentation for Point Cloud. IEEE Access 2019, 7, 179118–179133. [Google Scholar] [CrossRef]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. Review: Deep Learning on 3D Point Clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Hell, M.; Brandmeier, M.; Briechle, S.; Krzystek, P. Classification of Tree Species and Standing Dead Trees with Lidar Point Clouds Using Two Deep Neural Networks: PointCNN and 3DmFV-Net. PFG 2022, 90, 103–121. [Google Scholar] [CrossRef]
- Esri Train a Deep Learning Model for Point Cloud Classification—ArcGIS Pro|Documentation. Available online: https://pro.arcgis.com/en/pro-app/latest/help/data/las-dataset/train-a-point-cloud-model-with-deep-learning.htm (accessed on 10 April 2025).
- Babyak, M.A. What You See May Not Be What You Get: A Brief, Nontechnical Introduction to Overfitting in Regression-Type Models. Biopsychosoc. Sci. Med. 2004, 66, 411–421. [Google Scholar]
- Cui, Y.; Zhao, K.; Fan, W.; Xu, X. Retrieving Crop Fractional Cover and LAI Based on Airborne Lidar Data. Natl. Remote Sens. Bull. 2011, 15, 1276–1288. [Google Scholar] [CrossRef]
- Zhou, X.; Xing, M.; He, B.; Wang, J.; Song, Y.; Shang, J.; Liao, C.; Xu, M.; Ni, X. A Ground Point Fitting Method for Winter Wheat Height Estimation Using UAV-Based SfM Point Cloud Data. Drones 2023, 7, 406. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fareed, N.; Das, A.K.; Flores, J.P.; Mathew, J.J.; Mukaila, T.; Numata, I.; Janjua, U.U.R. UAS Quality Control and Crop Three-Dimensional Characterization Framework Using Multi-Temporal LiDAR Data. Remote Sens. 2024, 16, 699. [Google Scholar] [CrossRef]
- Hoffmeister, D.; Waldhoff, G.; Curdt, C.; Tilly, N.; Bendig, J.; Bareth, G. Spatial Variability Detection of Crop Height in a Single Field by Terrestrial Laser Scanning. In Precision agriculture ’13; Stafford, J.V., Ed.; Brill|Wageningen Academic: Wageningen, The Netherlands, 2013; pp. 267–274. ISBN 978-90-8686-224-5. [Google Scholar]
- Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.G.; Rebetzke, G.J.; James, R.A.; Bovill, W.D.; Furbank, R.T.; Sirault, X.R.R. High Throughput Determination of Plant Height, Ground Cover, and Above-Ground Biomass in Wheat with LiDAR. Front. Plant Sci. 2018, 9, 237. [Google Scholar] [CrossRef] [PubMed]
- Tirado, S.B.; Hirsch, C.N.; Springer, N.M. UAV-based Imaging Platform for Monitoring Maize Growth throughout Development. Plant Direct 2020, 4, e00230. [Google Scholar] [CrossRef]
- Cai, J.; Kumar, P.; Chopin, J.; Miklavcic, S.J. Land-Based Crop Phenotyping by Image Analysis: Accurate Estimation of Canopy Height Distributions Using Stereo Images. PLoS ONE 2018, 13, e0196671. [Google Scholar] [CrossRef] [PubMed]






| Corn | Soybean | Winter Wheat | ||||||
|---|---|---|---|---|---|---|---|---|
| 2024 | 2024 | 2024 | ||||||
| Date | Growth Stage | BBCH 1 | Date | Growth Stage | BBCH | Date | Growth Stage | BBCH |
| 12 June | Leaf Development | 19 | 4 July | Leaf Development | 11–13 | 2 May | Stem Elongation | 33–35 |
| 19 July | Inflorescence Emergence | 55–59 | 16 May | Booting | 43–47 | |||
| 4 July | Inflorescence Emergence, Heading | 40–51 | ||||||
| 26 July | Flowering | 61–65 | 24 May | Inflorescence Emergence, Heading | 55–59 | |||
| LiDAR-Derived Metrics | Description |
|---|---|
| Height_Max | Maximum height of the point cloud. |
| Height_Mean | Average height of the point. |
| Height_Std | Standard deviation of height values. |
| Height_Skewness | Measures the asymmetry of the height distribution. |
| Height_Kurtosis | Quantifies peakedness or flatness of the height distribution. |
| Height_Coefficient_of_Variation [47] | Normalized variability, calculated as ratio of standard deviation to mean height. |
| Canopy Relief Ratio (CRR) [48] | CRR = (Height_Mean − Height_Min)/ (Height_Max − Height_Min) |
| Laser Intercept Index (LII) [49] | LII = Nv/(Nv + Ng), where Nv and Ng are numbers of vegetation points and ground points separately. |
| P50–P99 | Percentile heights from 50th to 99th percentile (P50, P60, P70, P80, P85, P88, P90, P92, P95, P98, P99). |
| Date | Model | (n) | Training | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | p-Value | RMSE (m) | R2 | p-Value | RMSE (m) | |||
| June 12 | RFR | 32 | 0.83 | <0.05 | 0.014 | −0.6 | NS | 0.039 |
| SVR | 32 | 0.05 | NS | 0.033 | −0.43 | NS | 0.037 | |
| July 4 | RFR | 32 | 0.87 | <0.01 | 0.058 | −0.13 | NS | 0.155 |
| SVR | 32 | 0.23 | NS | 0.141 | −0.07 | NS | 0.151 | |
| June 12, July 4 | RFR | 64 | 0.99 | <0.001 | 0.066 | 0.93 | <0.001 | 0.164 |
| SVR | 64 | 0.97 | <0.001 | 0.106 | 0.95 | <0.001 | 0.137 | |
| Date | Model | (n) | Training | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | p-Value | RMSE (m) | R2 | p-Value | RMSE (m) | |||
| July 4 | RFR | 31 | 0.83 | <0.05 | 0.01 | −0.35 | NS | 0.026 |
| SVR | 31 | −0.05 | NS | 0.023 | −0.2 | NS | 0.025 | |
| July 19 | RFR | 31 | 0.93 | <0.001 | 0.014 | 0.45 | NS | 0.037 |
| SVR | 31 | 0.7 | NS | 0.03 | 0.34 | NS | 0.042 | |
| July 26 | RFR | 31 | 0.93 | <0.001 | 0.021 | 0.49 | NS | 0.055 |
| SVR | 31 | 0.82 | <0.05 | 0.032 | 0.4 | NS | 0.059 | |
| July 4, 19 | RFR | 62 | 0.96 | <0.001 | 0.023 | 0.74 | <0.001 | 0.059 |
| SVR | 62 | 0.81 | <0.001 | 0.053 | 0.7 | <0.001 | 0.066 | |
| July 4, 26 | RFR | 62 | 0.98 | <0.001 | 0.024 | 0.89 | <0.001 | 0.057 |
| SVR | 62 | 0.91 | <0.001 | 0.054 | 0.86 | <0.001 | 0.066 | |
| July 19, 26 | RFR | 62 | 0.96 | <0.001 | 0.018 | 0.68 | <0.001 | 0.049 |
| SVR | 62 | 0.82 | <0.001 | 0.037 | 0.65 | <0.001 | 0.052 | |
| July 4, 19, 26 | RFR | 93 | 0.98 | <0.001 | 0.024 | 0.83 | <0.001 | 0.061 |
| SVR | 93 | 0.87 | <0.001 | 0.055 | 0.81 | <0.001 | 0.065 | |
| Date | Model | (n) | Training | Validation | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | p-Value | RMSE (m) | R2 | p-Value | RMSE (m) | |||
| May 2 | RFR | 40 | 0.92 | <0.001 | 0.056 | 0.4 | NS | 0.12 |
| SVR | 40 | 0.7 | <0.05 | 0.11 | 0.35 | NS | 0.129 | |
| May 16 | RFR | 40 | 0.84 | <0.001 | 0.013 | −0.28 | NS | 0.029 |
| SVR | 40 | 0.09 | NS | 0.031 | −0.28 | NS | 0.029 | |
| May 24 | RFR | 40 | 0.86 | <0.001 | 0.01 | −0.1 | NS | 0.02 |
| SVR | 40 | 0.04 | NS | 0.026 | −0.16 | NS | 0.021 | |
| May 2, 16 | RFR | 80 | 0.91 | <0.001 | 0.049 | 0.37 | <0.05 | 0.109 |
| SVR | 80 | 0.65 | <0.001 | 0.099 | 0.36 | NS | 0.106 | |
| May 2, 24 | RFR | 80 | 0.92 | <0.001 | 0.055 | 0.66 | <0.001 | 0.08 |
| SVR | 80 | 0.85 | <0.001 | 0.075 | 0.63 | <0.001 | 0.091 | |
| May 16, 24 | RFR | 80 | 0.87 | <0.001 | 0.027 | 0.05 | NS | 0.063 |
| SVR | 80 | 0.24 | NS | 0.066 | 0.07 | NS | 0.063 | |
| May 2, 16, 24 | RFR | 120 | 0.92 | <0.001 | 0.049 | 0.58 | <0.001 | 0.082 |
| SVR | 120 | 0.76 | <0.001 | 0.082 | 0.52 | <0.001 | 0.093 | |
| Crop Type | Dataset Generation Strategy | Percentile Method | Range Method | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (m) | MAE (m) | R2 | RMSE (m) | MAE (m) | ||
| Corn | All Dates | 0.93 | 0.175 | 0.129 | 0.9 | 0.216 | 0.174 |
| Separate Date | 0.93 | 0.171 | 0.124 | 0.92 | 0.189 | 0.143 | |
| Soybean | All Dates | 0.66 | 0.08 | 0.071 | 0.66 | 0.08 | 0.072 |
| Separate Date | 0.91 | 0.037 | 0.027 | 0.93 | 0.032 | 0.024 | |
| Winter Wheat | All Dates | 0.29 | 0.146 | 0.121 | 0.33 | 0.145 | 0.122 |
| Separate Date | 0.86 | 0.066 | 0.05 | 0.91 | 0.055 | 0.038 | |
| Crop Type | Date | Percentile (%) | Range (%) | ||
|---|---|---|---|---|---|
| Top | Bottom | Top | Bottom | ||
| Corn | June 12 | 91.5 | 0.5 | 91–93 | 0–2 |
| July 4 | 91.5 | 0 | 98–100 | 0–2 | |
| Soybean | July 4 | 82 | 20 | 81–83 | 18–20 |
| July 19 | 87.5 | 5 | 80–82 | 0–6 | |
| July 26 | 83 | 3.5 | 81–85 | 2–4 | |
| Winter Wheat | May 2 | 80 | 2.5 | 85–97 | 10–14 |
| May 16 | 86.5 | 0 | 86–100 | 0–2 | |
| May 24 | 97 | 0.5 | 94–100 | 0–2 | |
| Crop Type | ML Regression | Ground Point Classification | Percentile | DRA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RFR | SVR | CSF | PointCNN | |||||||||
| R2 | RMSE (m) | R2 | RMSE (m) | R2 | RMSE (m) | R2 | RMSE (m) | R2 | RMSE (m) | R2 | RMSE (m) | |
| Corn | 0.93 | 0.164 | 0.95 | 0.137 | 0.89 | 0.208 | 0.93 | 0.163 | 0.93 | 0.171 | 0.92 | 0.189 |
| Soybean | 0.89 | 0.057 | 0.86 | 0.066 | 0.31 | 0.127 | 0.56 | 0.101 | 0.91 | 0.037 | 0.93 | 0.032 |
| Winter Wheat | 0.66 | 0.080 | 0.63 | 0.091 | 0.70 | 0.091 | 0.93 | 0.046 | 0.86 | 0.066 | 0.91 | 0.055 |
| Average Performance | 0.83 | 0.100 | 0.81 | 0.098 | 0.64 | 0.142 | 0.81 | 0.103 | 0.90 | 0.091 | 0.92 | 0.092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, P.; Wang, J.; Shan, B. Comparison of Regression, Classification, Percentile Method and Dual-Range Averaging Method for Crop Canopy Height Estimation from UAV-Based LiDAR Point Cloud Data. Drones 2025, 9, 683. https://doi.org/10.3390/drones9100683
Du P, Wang J, Shan B. Comparison of Regression, Classification, Percentile Method and Dual-Range Averaging Method for Crop Canopy Height Estimation from UAV-Based LiDAR Point Cloud Data. Drones. 2025; 9(10):683. https://doi.org/10.3390/drones9100683
Chicago/Turabian StyleDu, Pai, Jinfei Wang, and Bo Shan. 2025. "Comparison of Regression, Classification, Percentile Method and Dual-Range Averaging Method for Crop Canopy Height Estimation from UAV-Based LiDAR Point Cloud Data" Drones 9, no. 10: 683. https://doi.org/10.3390/drones9100683
APA StyleDu, P., Wang, J., & Shan, B. (2025). Comparison of Regression, Classification, Percentile Method and Dual-Range Averaging Method for Crop Canopy Height Estimation from UAV-Based LiDAR Point Cloud Data. Drones, 9(10), 683. https://doi.org/10.3390/drones9100683







