Angle Effects in UAV Quantitative Remote Sensing: Research Progress, Challenges and Trends

Highlights

What are the main findings?

• This paper summarizes the research progress on the angle effect in UAV quantitative remote sensing, covering theories, data acquisition techniques, data processing methods, and practical application.
• The article clearly outlines the current theoretical and technical challenges in studying the angle effect in UAV quantitative remote sensing and proposes future research directions.

What are the implications of the main findings?

• The article provides technical references and methodological support for practical engineering applications.
• The paper contributes to advancing theoretical innovation and technological breakthroughs in this field.

Abstract

In recent years, unmanned aerial vehicle (UAV) quantitative remote sensing technology has demonstrated significant advantages in fields such as agricultural monitoring and ecological environment assessment. However, achieving the goal of quantification still faces major challenges due to the angle effect. This effect, caused by the bidirectional reflectance distribution function (BRDF) of surface targets, leads to significant spectral response variations at different observation angles, thereby affecting the inversion accuracy of physicochemical parameters, internal components, and three-dimensional structures of ground objects. This study systematically reviewed 48 relevant publications from 2000 to the present, retrieved from the Web of Science Core Collection through keyword combinations and screening criteria. The analysis revealed a significant increase in both the number of publications and citation frequency after 2017, with research spanning multiple disciplines such as remote sensing, agriculture, and environmental science. The paper comprehensively summarizes research progress on the angle effect in UAV quantitative remote sensing. Firstly, its underlying causes based on BRDF mechanisms and radiative transfer theory are explained. Secondly, multi-angle data acquisition techniques, processing methods, and their applications across various research fields are analyzed, considering the characteristics of UAV platforms and sensors. Finally, in view of the current challenges, such as insufficient fusion of multi-source data and poor model adaptability, it is proposed that in the future, methods such as deep learning algorithms and multi-platform collaborative observation need to be combined to promote theoretical innovation and engineering application in the research of the angle effect in UAV quantitative remote sensing. This paper provides a theoretical reference for improving the inversion accuracy of surface parameters and the development of UAV remote sensing technology.

1. Introduction

In recent years, driven by the rapid advancement in the miniaturization of remote sensing sensors, platform automation, and intelligent processing algorithms, UAV quantitative remote sensing technology has emerged as a critical tool in areas such as agricultural monitoring [1,2], ecological environment assessment [3,4], and natural resource management [5,6]. Compared with traditional satellites and aerial remote sensing, UAVs, with their advantages of high spatiotemporal resolution, flexible observation perspectives, and low-cost deployment, not only significantly enhance the efficiency of multi-angle measurements in the field, but also effectively obtain multi-spectral and hyperspectral data with centimeter-level accuracy, providing an effective technical means for observing the bidirectional reflection features of ground objects, thereby providing a novel and effective means for the precise inversion of surface parameters. According to statistical reports, since 2020, the share of UAV platforms in the global agricultural remote sensing market has surpassed 35%, highlighting their indispensable role in applications such as crop phenotyping and early warning systems for pests and diseases [7,8,9].

However, UAV remote sensing still encounters substantial challenges in achieving the “quantification” objective. Due to the dynamic observation environment during low-altitude flights, the BRDF of surface targets significantly interferes with the radiometric signals captured by sensors [10,11]. This interference is evident as variations in the spectral responses of the same ground object at different observation angles (i.e., the angle effect). Such variations not only result in inversion errors for critical parameters such as vegetation index and leaf area index (LAI) [12,13], but may also obscure true physicochemical property information of ground objects. For example, in crop canopy monitoring, inclined observations can lead to estimation deviations in chlorophyll content exceeding 20%, thereby severely undermining the reliability of precision agricultural decisions [14,15].

The angle effect fundamentally elucidates the intricate interactions among the three-dimensional structure of the earth’s surface, the distribution of its components, and the radiative transport processes [16,17]. From a scientific standpoint, the angle effect is not merely an extraneous source of noise; rather, it encapsulates critical information regarding the spatial heterogeneity of ground objects, the geometric configuration of canopies, and microscopic scattering mechanisms. For instance, the hot spot effect observed in vegetation canopy can indicate leaf arrangement density and porosity, while polarization characteristics within multi-angle spectra are closely associated with variations in leaf waxy layer thickness [4,18]. Consequently, analyzing the angle effect not only enhances radiometric calibration accuracy but also imposes physical constraints on multi-dimensional inversions of surface parameters [19,20]. Nevertheless, current research encounters several challenges. High-resolution data (less than 10 cm) obtained from low-altitude UAV observations often struggle to align with macroscopic assumptions inherent in classical BRDF models—such as the PROSAIL and RT models—resulting in inadequate adaptability at canopy scales [9,21,22]. Additionally, fluctuations in UAV flight attitudes (e.g., pitch angle and roll angle), coupled with rapid changes in lighting conditions, exacerbate difficulties associated with correcting for angle effects. A universal framework for coordinating multi-angle data from UAVs with wide-coverage satellite observations and ground-measured data remains elusive [23,24,25]. Furthermore, most existing studies predominantly concentrate on analyzing angle effects related to single types of ground objects [26,27]; there is a notable deficiency in research addressing radiative transfer mechanisms within complex mixed pixels (e.g., transition zones between farmland and forest land) [28,29]. This gap significantly constrains the application potential of this technology for heterogeneous surface monitoring.

This paper aims to systematically review the research progress on the angle effect in UAV quantitative remote sensing, reveal its core role in the inversion of surface parameters, and explore the future technological breakthrough directions. The specific goals include: starting from the basic theory, analyzing the physical causes of the angle effect and the radiation transfer process; combining the current mainstream UAV platforms and remote sensing sensors to summarize the technological progress of multi-angle data acquisition by UAV; investigating the application scenarios and cases of UAV multi-angle remote sensing, and summarizing the role and application of the angle effect in quantitative remote sensing inversion; and reviewing the challenges and future development trends faced by UAV quantitative remote sensing. Finally, the research conclusions of this paper are presented.

2. Research Methods

The Web of Science Core Collection (https://webofscience.clarivate.cn/wos/woscc/basic-search, accessed on 23 July 2025) is one of the most authoritative academic literature databases globally. It includes sub-databases such as Science Citation Index-Expanded (Institute for Scientific Information INC., Eugene Garfield, PA, USA), Social Sciences Citation Index (Institute for Scientific Information INC., Eugene Garfield, PA, USA), and Conference Proceedings Citation Index (Institute for Scientific Information INC., Eugene Garfield, PA, USA), covering high-quality, high-impact academic journals, conference papers, books, and other scholarly resources. Additionally, it provides a unique citation indexing function, making it an essential tool for literature retrieval, academic evaluation, and knowledge discovery. Therefore, this study conducts a literature analysis based on the Web of Science Core Collection, with the following specific search criteria:

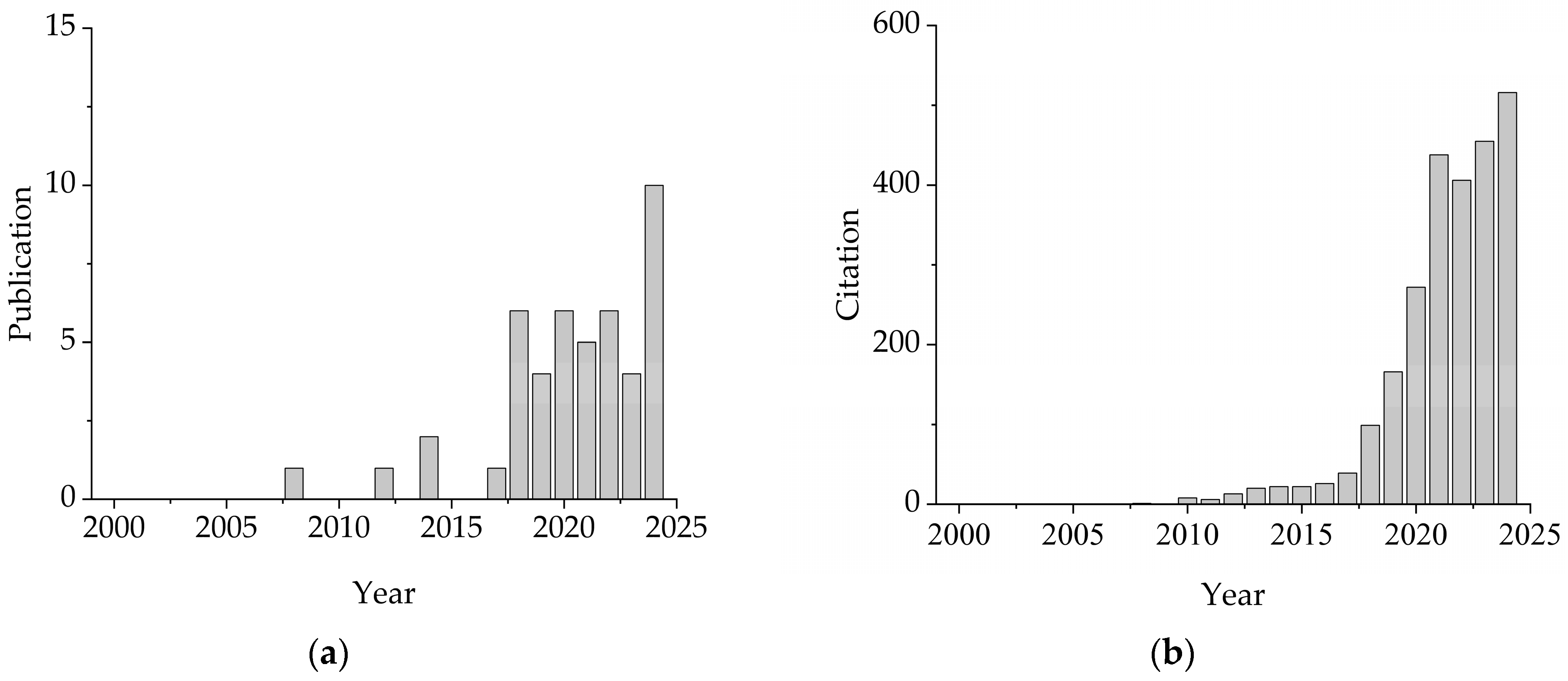
• Although UAV remote sensing has only recently gained popularity as a research field, the time span was set from 2000 to the present to ensure comprehensive literature coverage and to analyze the developmental trends of this field.
• Given that technical terms may include abbreviations or different word combinations, the keywords used for retrieval should be exhaustive and arranged in various combinations. The SQL query used in this study was:

• (Drone OR UAV OR “Unmanned Aerial Vehicle”)
• AND (BRDF OR “Bidirectional Reflectance” OR “Angle Effect” OR “Angular Effect”)
• AND (“Remote Sensing” OR “Quantitative Remote Sensing”)

• The topic of the paper should be in line with the angle effect in UAV quantitative remote sensing, so there should be a screening process.
• The paper should be published in a journal or conference, rather than in a simple investigation, review, or a certain chapter of a book.

Based on these criteria, 48 relevant publications were retrieved. The retrieved literature was visualized in terms of annual publication volume, annual citation frequency, and research domains. As shown in Figure 1, the number of publications on the angle effect in UAV quantitative remote sensing began to increase significantly after 2017, and citation frequency also exhibited rapid growth. This trend is closely linked to the technological advancements in UAV platforms and spectral sensors in recent years, indicating that this field has become a prominent research direction.

Table 1. Search for the research domains of the paper.

Research Areas	Article Count
Remote Sensing	35
Imaging Science/Photographic Technology	29
Environmental Sciences/Ecology	18
Geology	12
Agriculture	8
Engineering	6
Computer Science	4
Geochemistry Geophysics	3
Instruments Instrumentation	3
Chemistry	2
Physical Geography	2
Forestry	1
Spectroscopy	1
Meteorology Atmospheric Sciences	1
Plant Sciences	1

lists the research domains of the journals or conferences where these papers were published. The results demonstrate that studies on the angle effect in UAV quantitative remote sensing span multiple disciplines, highlighting their broad application potential. While most papers focus on remote sensing mechanisms and theoretical frameworks, a substantial number of applications are found in fields such as agriculture, forestry, and atmospheric Sciences, emphasizing their ecological and environmental significance.

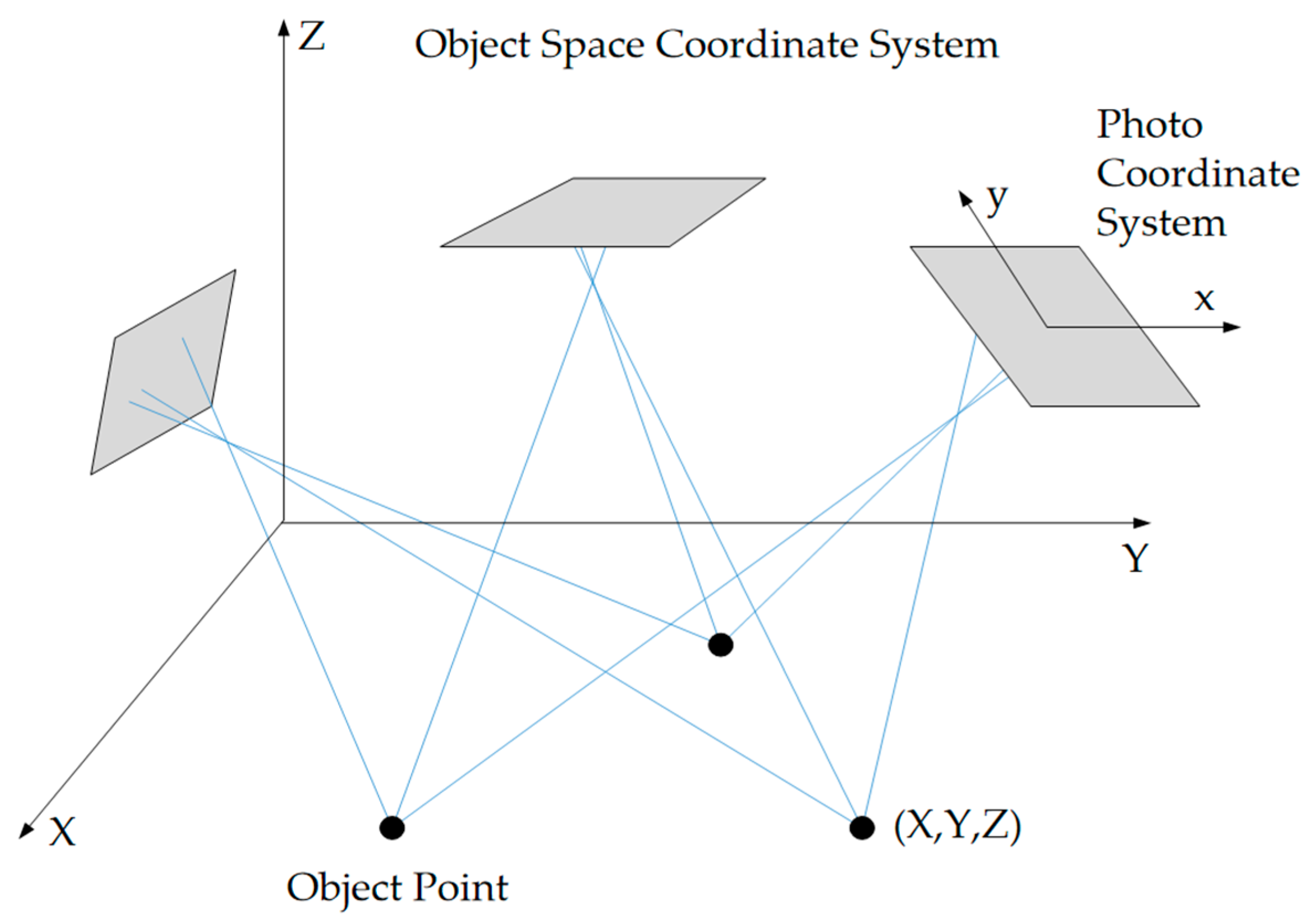
3. The Theoretical Basis of the Angle Effect

3.1. The Bidirectional Reflection Characteristics and Anisotropic Mechanism of Ground Objects

The BRDF of ground objects characterizes the relationship between the variation in surface-reflected radiative energy and the incident angle and observation angle, and it serves as the fundamental physical basis for the angle effect [21,22,30]. BRDF not only contains the directional spectral information of ground objects, but also the spatial structure information of ground objects, which is an important consideration factor for remote sensing to explore the quantitative information of targets. The mathematical formulation of BRDF is:

$$BRDF=f\left({\theta }_v,{\varphi }_v{,\theta }_s{,\varphi }_s\right)={\displaystyle \frac{d{L}_v\left({\theta }_v,{\varphi }_v{,\theta }_s{,\varphi }_s\right)}{d{E}_s\left({\theta }_v,{\varphi }_v\right)}}$$

(1)

where ${\theta }_s$ and ${\varphi }_s$ are the incident zenith angle and azimuth angle of the sun, respectively; ${\theta }_v$ and ${\varphi }_v$ are the observation zenith angle and azimuth angle of the sensor, respectively; $\mathrm{d}{L}_v$ is the reflected radiation brightness; and $\mathrm{d}{E}_s$ is the incident irradiance. The non-isotropic characteristics of BRDF (i.e., the anisotropy factor is greater than 1) indicate that there are significant differences in the intensity of reflected radiation from ground objects at different observation angles.

The three-dimensional structure of the earth’s surface can influence the reflection and scattering processes of light on the surface, thereby significantly impacting the directionality of reflection [28,31], as shown in Figure 2 specifically. Regarding vegetation canopies, the geometric arrangement of leaves (e.g., upright or spread types) and canopy porosity directly affect the hot spot effect. For instance, the anisotropic intensity of a corn canopy can be more than 1.5 times that of a wheat canopy [24,32]. For soil and rock surfaces, surface roughness and particle distribution alter the reflection direction through micro-topographic shadow effects; rough soil may exhibit a 10–15% decrease in reflectance due to shadow shielding when observed at an incline [33]. In the case of buildings and artificial structures, the specular reflection characteristics of urban building facades are markedly enhanced at specific observation angles, potentially causing spectral aliases. Additionally, at a finer spatial scale, the light incident on a rough surface is partially absorbed and partially reflected. The reflected portion may then illuminate other surfaces, where it is again absorbed or reflected. This process occurs countless times, resulting in a mutual reflection effect [34], as shown in Figure 3. Mutual reflection has a significant influence on the measurement of surface reflectance. Therefore, a bidirectional texture function (BTF) [35] is adopted at a more refined scale to characterize the surface of ground objects.

The classic BRDF models include empirical models, physical models, and semi-empirical models [36,37,38]. Empirical models fit observational data with linear combination of isotropic, bulk scattering, and geometric scattering components, which are computationally efficient but have unclear physical mechanisms, such as the Walthall model, which was proposed by Walthall et al. (1985) [39], based on a large amount of field experimental data for soil BRDF correction. At the same time, it can also simulate the directional reflectance of soybean crops well and is suitable for small-scale research areas. Furthermore, Liang and Strahler (1994) [40] added a hot spot kernel with two coefficients to the conventional Walthall model to fully consider the hot spot effect.

Physical models simulate radiative transport pathways based on canopy structure parameters such as leaf inclination angle and LAI, making them suitable for vegetation inversion [8,18,41]. However, their adaptability to high-resolution data from UAVs is limited, as seen in models like the PROSAIL and RT model [9,42]. Physical models can be classified by category into: radiative transport model, geometric optical model, hybrid model, and computer simulation model [43]. The specific descriptions are as follows:

• The radiative transport model is applicable to the reflection conditions of continuous vegetation canopies, such as vegetation in the growth period, large areas of grassland, etc., but not applicable to complex discontinuous vegetation canopies, such as forests, etc. The current research mainly combines PROSPECT-D with the SAI model or DART model to achieve the simulation of the optical characteristics of complex vegetation. The bidirectional gap ratio was introduced into the SAILH model to describe the hot spot effect [44,45]. The idea of random fields was introduced to extend the applicable objects of the radiative transport model to forests [46], etc.
• Geometric optical models are applicable to the inversion of discrete vegetation and rough surfaces, such as sparse forests, coniferous forests, orchards, etc. They can be used for macroscopic phenomena on a larger scale and provide a difference comparison for the scattering of ground objects and the atmosphere. At present, some mountain BRDF models applicable to coarse-resolution multi-slope remote sensing observations have been developed [47,48], but the multi-angle modeling and verification of complex mountains still need further research [49].
• Hybrid models, such as the GORT model, are applicable to sparse vegetation as well as discrete vegetation [50]. The combination of multiple models acting on a certain inversion task can effectively improve the inversion accuracy of the models. At present, a unified model of vegetation BRDF applicable to various vegetation types and different atmospheric conditions within the short-wave range of the sun has been developed [51]. This model creates more favorable conditions for the remote sensing inversion of vegetation parameters, and its modeling idea represents the long-term development direction of vegetation BRDF research [43].
• Computer simulation models can theoretically calculate the radiative transfer process expressed in any mathematical model, and can also be used as a tool to verify other models, such as the DIANA model based on the radiosity principle method [52], the RGM model [53], the Rapid model [54], the DART model based on the principle and method of ray tracing [55], the FLIGHT model [56], the Raytran model [57], etc. Computer models can accurately depict the radiation distribution of complex vegetation canopies and achieve realistic illumination and reflection effects. However, insufficient structural design, difficulty in understanding, and inversion have become the greatest shortcomings of computer simulation models. In recent years, in order to simulate large-scale surface and complex terrain, the LESS model, which can simultaneously perform forward ray tracing and backward ray tracing and make full use of the latest graphics technology to achieve more accurate and efficient simulation of large-scale scene remote sensing signals, has been developed [58,59].

The semi-empirical model combines the advantages of empirical and physical models. The parameters in this model are empirical but have some physical meaning and are simple and easy to calculate. Although it is widely used in multi-angle data correction of UAVs, it still needs to be optimized in complex ground object scenarios [60]. For example, the nuclear drive model [61] not only retains the advantage of the radiative transport model in describing the scattering characteristics of the body, but also inherits the advantage of the geometric optical model in characterizing the scattering characteristics of the surface. This model can parameterize the important factors, making it not only have certain physical significance, but also be simple and easy to calculate, and is suitable for large-scale vegetation inversion studies. At present, models that can improve the fitting accuracy of hot spot reflectance [62], models suitable for ice- and snow-covered surfaces [63], and multi-angle and multi-spectral core-driven models such as ASK [64] have been developed. In addition, a number of nuclear-driven models coupled with terrain have also been developed, such as the KDST model [65], the LKB_T model [66], etc. The RPV model [67] has a strong BRDF fitting ability, with a simple form and fewer parameters, and is easy to solve. This model is capable of describing the hot spot effect and has been tested in the forward and reverse modes of several datasets including field and laboratory data, providing satisfactory results [68,69,70,71,72]. To date, this model has mainly been used to simulate the reflectivity of non-flat canopy targets with backscattering behavior, rather than a single leaf feature [60]. In addition, to facilitate the linearization of the reflectance function during parametric inversion, the exponential function is used instead of the phase function [73].

3.2. The Radiation Transport Mechanism of UAV Multi-Angle Observation

The observation geometry of the UAV low-altitude remote sensing platform (flight altitude < 1000 m, flexible flight paths and perspectives) is fundamentally different from those of traditional satellites (outside the atmosphere, primarily for space-ground observation) and aerial remote sensing (flight altitude > 1000 m, fixed flight zones). Its dynamic multi-angle observation capability offers a unique advantage for studying angle effects. However, it also introduces new complexities in radiative transfer:

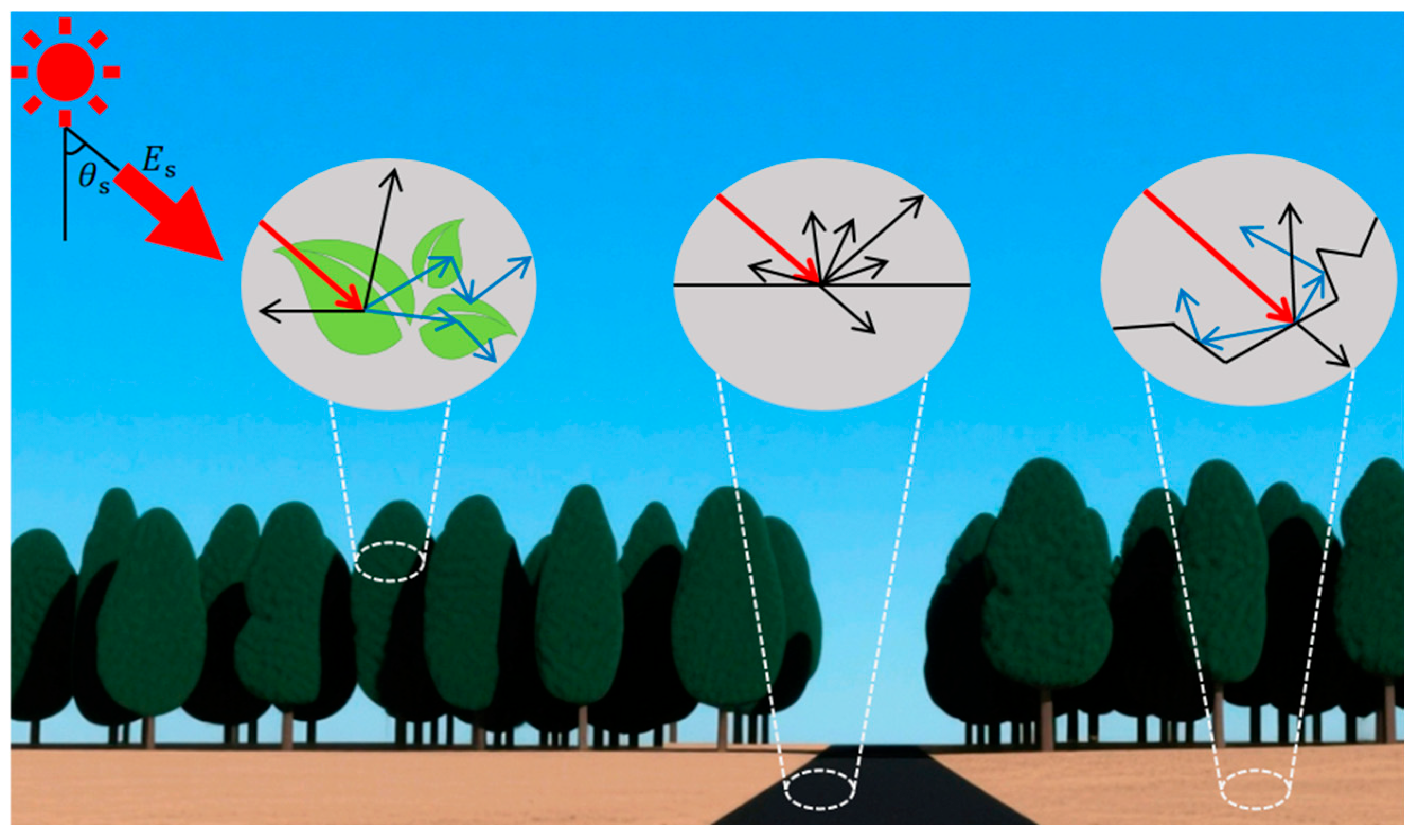
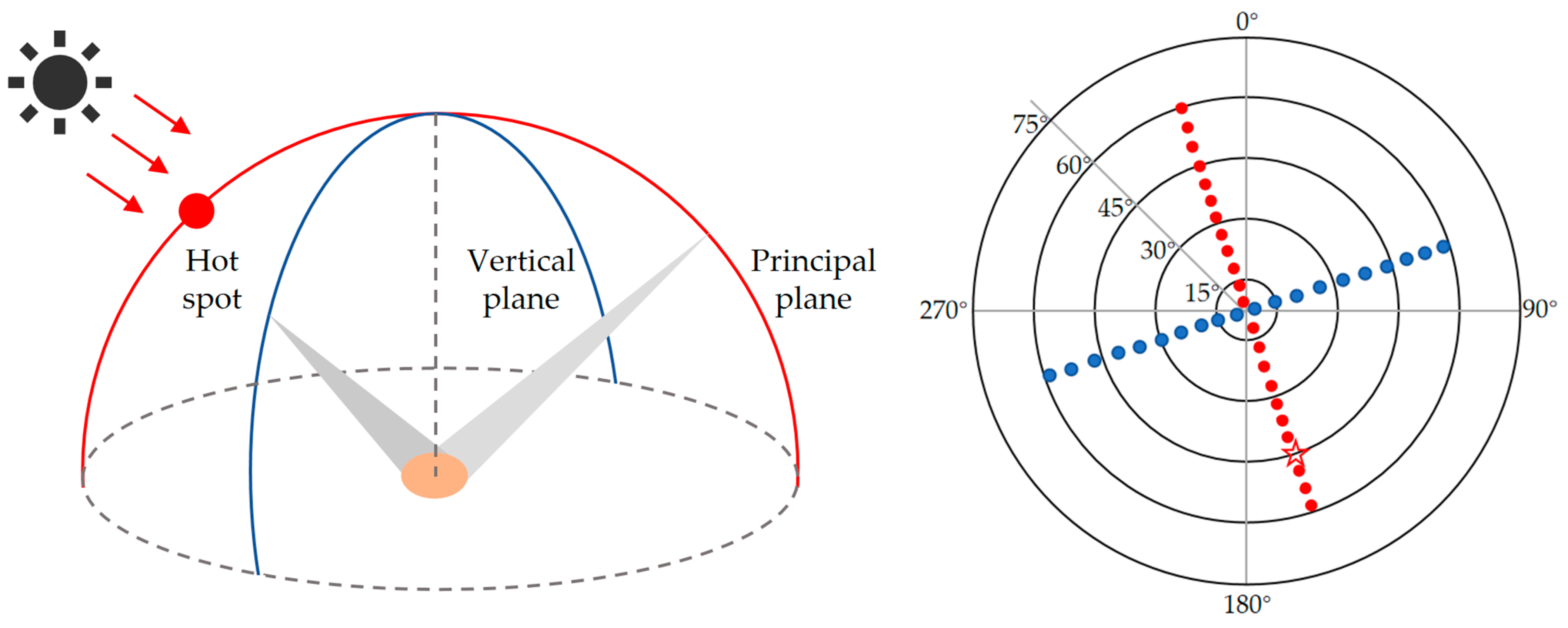
• Nadir observation (zenith angle < 10°) captures information on the vertical reflectance of the surface and is less affected by shadows but struggles to capture lateral structural features of the canopy.
• Tilted observation (zenith angle > 30°) enhances sensitivity to vertical canopy structure (e.g., stem density) and microscopic texture but is more susceptible to surface shadows and atmospheric scattering, as shown in Figure 3 below.
• Multi-angle observation combinations construct multi-angle datasets (e.g., hemispherical reflectance distribution) through multi-band flights or multi-lens synchronous acquisition, enabling joint retrieval of three-dimensional surface structures and physicochemical parameters.

From the perspective of remote sensing imaging, remote sensing vertical photography can only obtain the spectral characteristic projection of the target object in one direction, lacking sufficient information to infer reflective anisotropy and spatial structure [74]. Multi-angle observation of the target can provide information in multiple directions and extract more detailed and reliable spatial structure parameters [75] than single-direction observation, increasing the richness of the target observation information. However, the angle effect introduces spectral reflectance distortion into spectral radiation measurements. For instance, tilted observation results in an increased optical path length, enhances atmospheric aerosol scattering [76], and exhibits heightened sensitivity in the short-wave infrared band, potentially causing reflectance deviations exceeding 5% [77]. The dynamic spatial distribution of surface shadows and hotspot areas in low-altitude observations induces nonlinear responses of vegetation indices (e.g., NDVI) across different observation angles. For example, the NDVI value of soybean fields in the hotspot direction can be 0.15 higher than that observed under nadir conditions. Additionally, the polarization characteristics of reflected light on non-Lambertian surfaces (e.g., water surfaces and waxy leaves) vary significantly during inclined observations, which may compromise the inversion accuracy of chlorophyll fluorescence [78].

4. Progress in Multi-Angle Data Acquisition Technology for UAV Remote Sensing

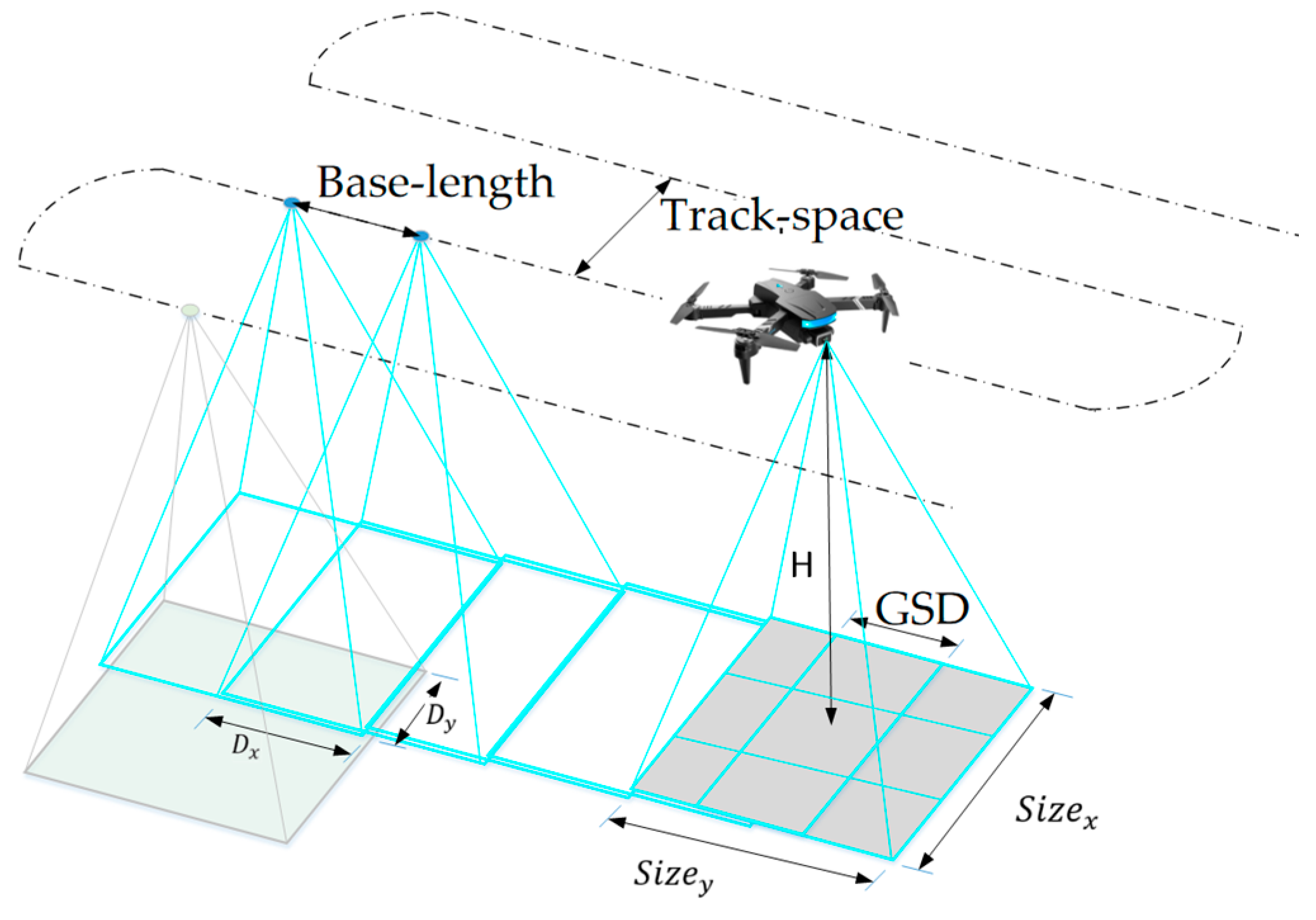
4.1. The Development of UAV Remote Sensing Platform Technology

The performance improvement of the UAV remote sensing observation platform depends on the collaborative innovation of the flight control system, sensor integration architecture, and attitude stability technology. The current mainstream platforms can be divided into two forms: multi-rotor UAVs are characterized by flexible hovering and low-altitude operation (<300 m), and can achieve single-lens multi-angle observation through tilt pitch adjustment (−90° to +90°), but are limited by short flight time (<30 min) and payload capacity (<5 kg); fixed-wing UAVs are suitable for multi-angle coverage over a large area (>10 km²). They obtain multi-view images through an oblique photography route design (with a lateral tilt angle of 15° to 40°), but the low altitude resolution (usually >10 cm) limits the resolution of microstructure, as shown in Figure 4 below. Multi-rotor UAVs benefit from their vertical take-off and landing as well as hovering capabilities, making them highly suitable for complex aerial photography tasks and thus dominating the market, such as DJI’s Mavic 3 series, Mini 4 Pro, Matrice 350 RTK, etc. In recent years, vertical take-off and landing (VTOL) hybrid UAVs have gradually emerged. These models, by integrating the technical features of fixed-wing and multi-rotor UAVs, maintain long endurance while also offering flight flexibility, making them particularly suitable for operational requirements in complex terrain environments. However, due to its relatively complex mechanical structure, the system failure rate of this type of UAV is significantly higher than that of traditional models. In addition, the high manufacturing cost severely restricts its market penetration rate. These factors jointly lead to the fact that VTOL UAVs have not yet achieved large-scale commercial application and are still mainly limited to professional fields such as military and emergency response.

The UAV platform integrates the Global Position System (GPS) and inertial measurement units (IMU). It dynamically adjusts the sensor observation direction through high-precision servo gimbal (angle measurement accuracy ±0.1°) and supports the collection of custom angle sequences, as shown in Figure 5.

4.2. Breakthroughs in Spectral Imaging Sensor Technology

UAV sensors come in various types and are developing rapidly, attracting significant attention from aerospace powers such as China, the United States, and Europe. Optical sensors and spectral detection technologies in European and American countries are leading. They have taken the lead in developing a number of light and small spectral remote sensors for UAVs, for example, the RedeDG-MX multispectral camera from the United States, the Parrot Sequoia multispectral camera from Switzerland, the HySpex Mjolnir hyperspectral camera from Norway, etc. [79]. China has also promptly launched UAV remote sensing systems such as the MS600 multispectral, DJI P4M, and GaiaSky mini3-VN hyperspectral [80]. The mainstream sensors at present are shown in

Table 2. Introduction to mainstream sensors.

Sensor	Country	Spectrum	FOV	Spatial Resolution	Product Photo	Source of Photo
DJI Mavic 3	China	Green, red, red-edge, NIR	HFOV: 61.2° VFOV: 48.1°	5.3 cm@h = 100 m		Web [81]
MS600 Pro	China	Blue, green, red, double red-edge, NIR	HFOV: 49.6° VFOV: 38°	8.65 cm@h = 120 m		Web [82]
MicaSense RedEdge-MX	America	Blue, green, red, Red-edge, NIR	HFOV: 47.2° VFOV: 35.4°	8 cm@h = 120 m		Web [83]
Parrot Sequoia	Switzerland	Green, red, red-edge, NIR	HFOV: 70.6° VFOV: 52.6°	8.5 cm@h = 120 m		Web [84]
GaiaSky mini3-VN	China	400–1000 nm 224 bands@2.7 nm 112 bands@5.5 nm 56 bands@10.8 nm	HFOV: 35.36°@16 mm 25°@23 mm VFOV: 0°	6.2 cm (@16 mm, h = 100 m) 4.3 cm (@23 mm, h = 100 m)		Web [85]
HySpex Mjolnir V-1240	Norway	400–1000 nm 200 bands@3 nm	HFOV: 20° VFOV: 0°	0.27/0.27 mrad		Web [86]
Headwall Co-aligned VNIR-SWIR	America	400–2500 nm VNIR: 270 bands@6 nm SWIR: 267 bands@8 nm	HFOV: 17°, 25°, 34° VFOV: 0°	VNIR: 3.1 cm@h = 100 m SWIR: 6.25 cm@h = 100 m		Web [87]

below. In the study of angle effects, the technical characteristics of various sensors have a significant impact on the observation results. Multispectral sensors, with their high spatial and temporal resolution, have become the preferred tool for vegetation BRDF research. Their narrow-band design can effectively capture the anisotropic features at the leaf scale, but the number of bands limits the analysis of complex reflection characteristics. Hyperspectral sensors provide a data basis for precise BRDF modeling through continuous sampling across the entire spectral band, but they face challenges in dynamic observation of large-scale scenes due to the limitations of the field of view and acquisition intervals.

4.3. Multi-Angle Data Collection Methods

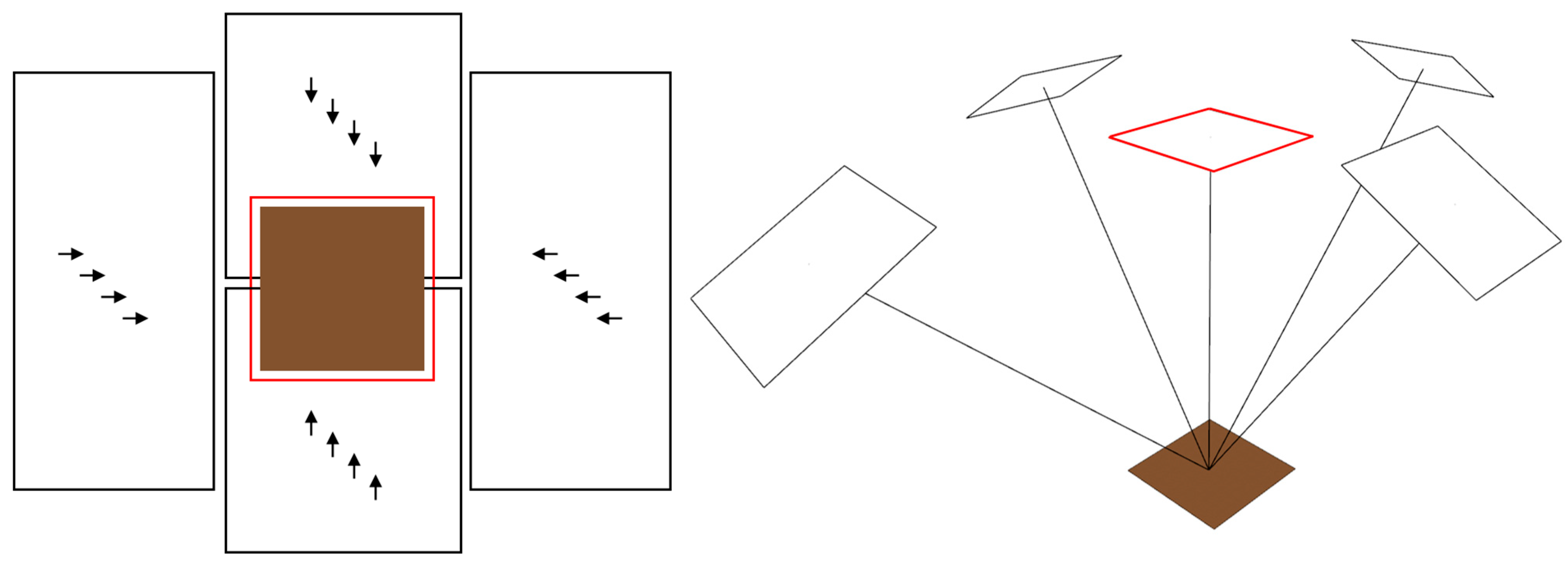
4.3.1. Nadir-Parallel Flight Path

This method conducts orthophoto shooting of the target area by carrying sensors on the UAV. The forward and lateral overlap rates of the collected images are relatively high. Then, the observation angle of each ground pixel is calculated by using the position of the UAV during image acquisition and the position of the geographic reference ground pixels, thereby forming a multi-angle data set for earth observation, as shown in Figure 6. The number of multiple angles obtained varies depending on the degree of overlap in UAV photography. This method is relatively simple to operate, and the number of multiple angles obtained is limited. However, it is also the basic method for the inversion of the surface properties of the observed target. For example, Roosjen et al. (2018) [14] effectively improved the accuracy in estimating the LAI and leaf chlorophyll content of potato crops based on this multi-angle observation method. The results show that the most accurate inversion results can be obtained when there are more observation angles, more uniform observation angles, and a larger zenith angle. In addition, this method can also be used for agricultural detection [88], three-dimensional modeling [89], and many other fields.

When this method is applied to areas with complex terrain and significant height differences, the fixed flight altitude pattern will lead to uneven resolution within the same image and may even cause the problem of low image overlap, resulting in the inability to conduct aerial triangulation in some areas with higher altitudes. Therefore, the method of flight altitude following the terrain can be adopted [90,91], conducting oblique photography to solve the above problems.

4.3.2. Oblique-Parallel Flight Path

This multi-angle measurement method consists of two parts: vertical and inclined. As shown in the following Figure 7, within the red box line, the sensor points directly downward. Within the four black frames, the imager is tilted 30° towards the study area for observation. Therefore, the theoretical observed zenith angle range obtained for the study area is 0 to 41°. This method utilizes a large amount of multi-angle image data with a high degree of overlap to extract multi-angle information and perform BRDF calculations. For instance, Deng et al. (2021) [92] obtained observation data from a wider viewing angle and more directions based on this approach, verifying the feasibility of UAVs in obtaining BRDF data with high spatial resolution, high precision, and spatial continuity.

4.3.3. Crisscrossing Flight Route

The flight path of the UAV is set along the near-principal plane with relative positions to the solar azimuth of 0° and 180°, and the vertical plane with relative positions to the solar azimuth of 90° and 270°, as shown in the following Figure 8. On the two heading directions, the sampling intervals are respectively set to achieve zenith angle sampling within the range from the backscattering region to the forward scattering region, and a separate observation is conducted in the hot spot direction. The camera carried by the UAV automatically adjusts, constantly pointing towards the center of the plot, and the distance between the UAV and the plot remains unchanged. Since the UAV flight routes involved in this multi-angle measurement method are relatively few, the movement of the sun in both the zenith angle and the azimuth angle within one observation period is less than 0.3. For simplicity, it is assumed that the zenith angle and the azimuth angle of the sun are constants during data processing [24].

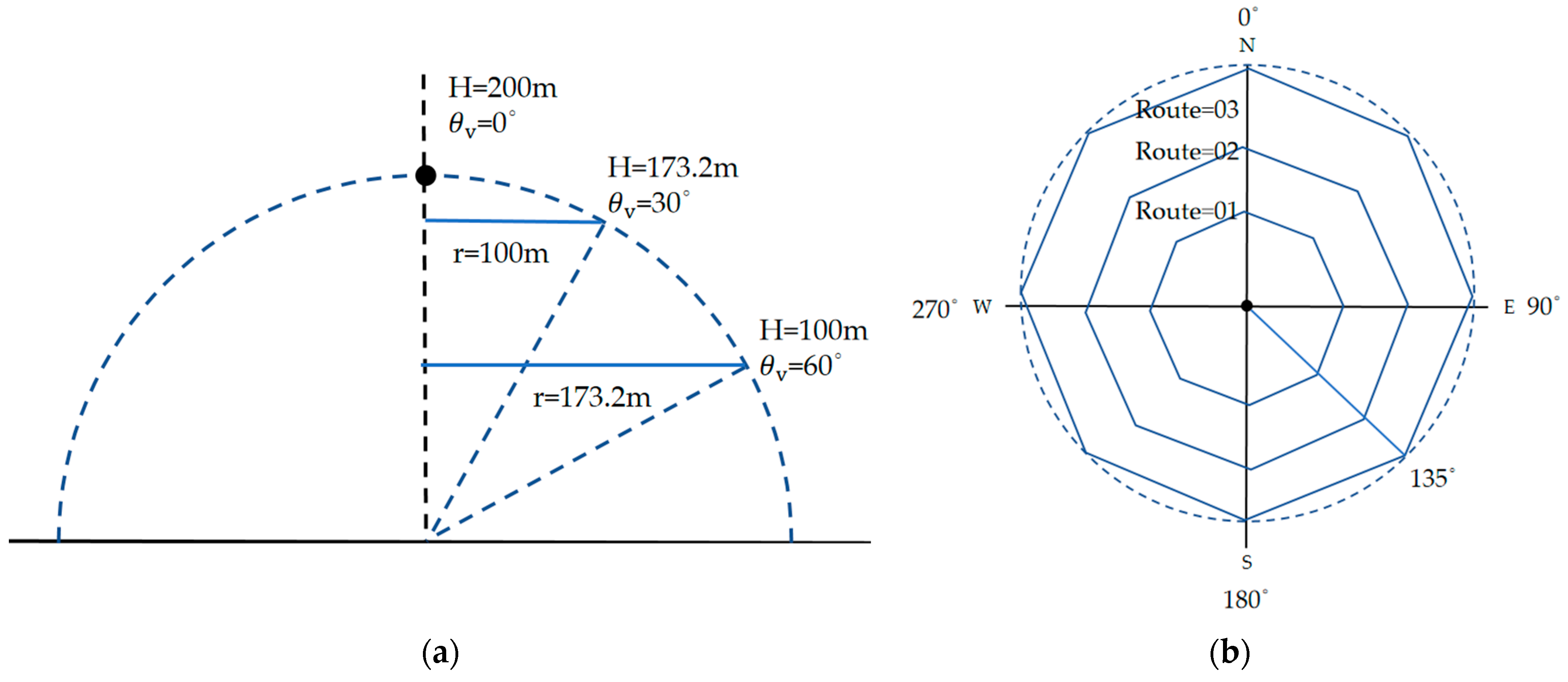
4.3.4. Spiral-Descending Flight Path

This method is an observation mode based on hemispherical flight, which can effectively obtain the reflection spectral characteristics of ground objects at multiple zenith angles and omnidirectional angles. As shown in the following Figure 9, by setting the flight course of the UAV, the observation azimuth can achieve all-round angle coverage from 0° to 360° at the set sampling interval. The observation zenith angle sampling is carried out within the range of 0° to 60° at the set sampling intervals. For vertical earth observation in the zenith direction, the observation zenith angle is 0°. When the observation zenith angle is within the range of 60° to 90°, it is greatly affected by shadow occlusion and generally does not conduct UAV observation. Throughout the entire observation process, the distance between the UAV and the target under test remains consistent, and the observation angle of the sensor probe is jointly determined by the UAV’s hovering position and the gimbal, ensuring that the lens always points towards the object under test. At present, the hovering descent route method is widely used in multi-angle measurements by UAV. For example, Cao et al. (2023) [10] used the DJI P4M UAV remote sensing system as the observation means and designed a polygonal flight path along the hemisphere, thereby achieving the measurement of the surface bidirectional reflection characteristics of the large zenith angle and all azimuth angles.

4.3.5. Radial-Descending Flight Path

This method is similar to the hovering descent route and can also achieve multi-zenith angle and all-azimuth angle earth observation. The difference is that at a certain observation zenith angle, instead of circling observation, a direct flight method is adopted. That is, for each observation zenith angle, the flight route is To—0—180—T0—45—225—To—90—270—To—135—315, as shown in the Figure 10. This method can be used to accurately determine the observation azimuth angles of each flight point. Especially for the calibration of large-field-of-view sensors, it is very important to consider the errors caused by inconsistent observation values. For instance, Pan et al. (2020) [19] adopted this multi-angle measurement method to obtain the direction data of the Dunhuang calibration field under different solar zenith angles and azimuth angles. The BRDF model significantly improved the calibration accuracy, especially in the case of large observation angles.

4.3.6. Comparison of Multi-Angle Data Collection Methods

The realization of multi-angle observation by UAVs involves multiple requirements such as flight path planning, camera control, data processing technology, and adaptation to different application scenarios, in order to effectively achieve high-quality multi-angle remote sensing observation. An analysis and summary of the advantages and disadvantages of the above five technical means and strategies are shown in

Table 3. Comparison of multi-angle data collection methods.

Methods	Technical Characteristics	Limitations
Nadir-Parallel Flight Path	Orthogonal photography with high overlap. Large area coverage per flight. Uniform resolution in flat terrain.	Limited angle diversity. Inconsistent resolution in complex terrain (requires terrain-following algorithms).
Oblique-Parallel Flight Path	Observation of low zenith angle. Rich facade information (side views of buildings/trees).	Shadow interference at low solar angles. High data volume.
Crisscrossing Flight Route	Principal plane and perpendicular plane intersections. Dedicated flight path for hot spot effect capture. Clear sun–object–sensor geometry.	Low flight efficiency. Data inconsistency under dynamic lighting.
Spiral-Descending Flight Path	Constant target distance. Hemispherical angle sampling. Full azimuth angle. Multi-zenith angle.	Low-precision azimuth angle. Stability issues in turbulent airflow. Hovering consumes high energy.
Radial-Descending Flight Path	Radial straight-line flights. Gimbal precision pointing. High-precision radiometric calibration. High-precision azimuth angle.	Redundant flight paths. Unsuitable for large-area surveys.

.

4.4. Data Processing and Correction Technologies

4.4.1. Spectral Data Radiation Correction

The original spectral data are formed by the combined influence of factors such as current surface conditions, atmospheric influence, topographic influence, and sensor characteristics [93], which enhances the importance of radiometric calibration in image processing [79]. Due to the complex relationship between the real reflected radiation of ground objects and the digital images measured by sensors, it is influenced by many factors, such as the vignetting effect of camera-related images and the geometric position of the sun related to the environment. The data processing of UAV remote sensing should focus on the relationship between the pixel values of the image and the true reflected radiation of the target. For example, to reduce the influence of dark current on the image, the commonly adopted method is the dark offset subtraction method [94,95], that is, subtracting the dark current signal from the pixel values of the original spectral image. To determine the vignetting effect in the image (as shown in Figure 11), the most direct method is to capture an image that is completely covered by a uniform scene area, so that the luminance variation can be attributed solely to vignetting [96,97,98]. There are many common methods for vignetting correction, such as the Lookup Table (LUT) correction method [98], and using parametric models to simplify estimates and minimize the influence of image noise [99]. For example, Valentine et al. (2008) [100] chose to use least squares mapping to two-dimensional polynomials to fit the radiation profile, thereby achieving a smooth approximation of the vignette effect. This polynomial function was used to create a filtering mask and would be applied to each image in a multiplicative manner to eliminate vignette. Furthermore, Gaussian filtering is a commonly used image processing technique. By applying the Gaussian filtering function, the high-frequency noise in the image will be smoothed out, while retaining the main features of the image without introducing obvious edge and detail blurring. To extract the true surface reflectivity, the simplest and most commonly used normalization method is dividing the luminance value in each image by the total luminance of the image [101]. However, the incident radiation is related to the solar zenith angle and atmospheric conditions. When calculating the vegetation spectral index using the results obtained by this method, it shows corresponding limitations [102]. Therefore, calculating the reflectance factor of the target surface using the reference target method has become the mainstream calculation method at present and is also used to correct large-scale aerial images [103]. For example, Hakala et al. (2010) [104] calculated the reflectance factor image using the calibrated white target as the reference, and the illumination changes during the image acquisition process were also corrected through the reference target.

4.4.2. Geometric Correction of Spectral Data

There are mainly two ways to obtain the azimuth angle, height angle and spatial position observed by remote sensing sensors:

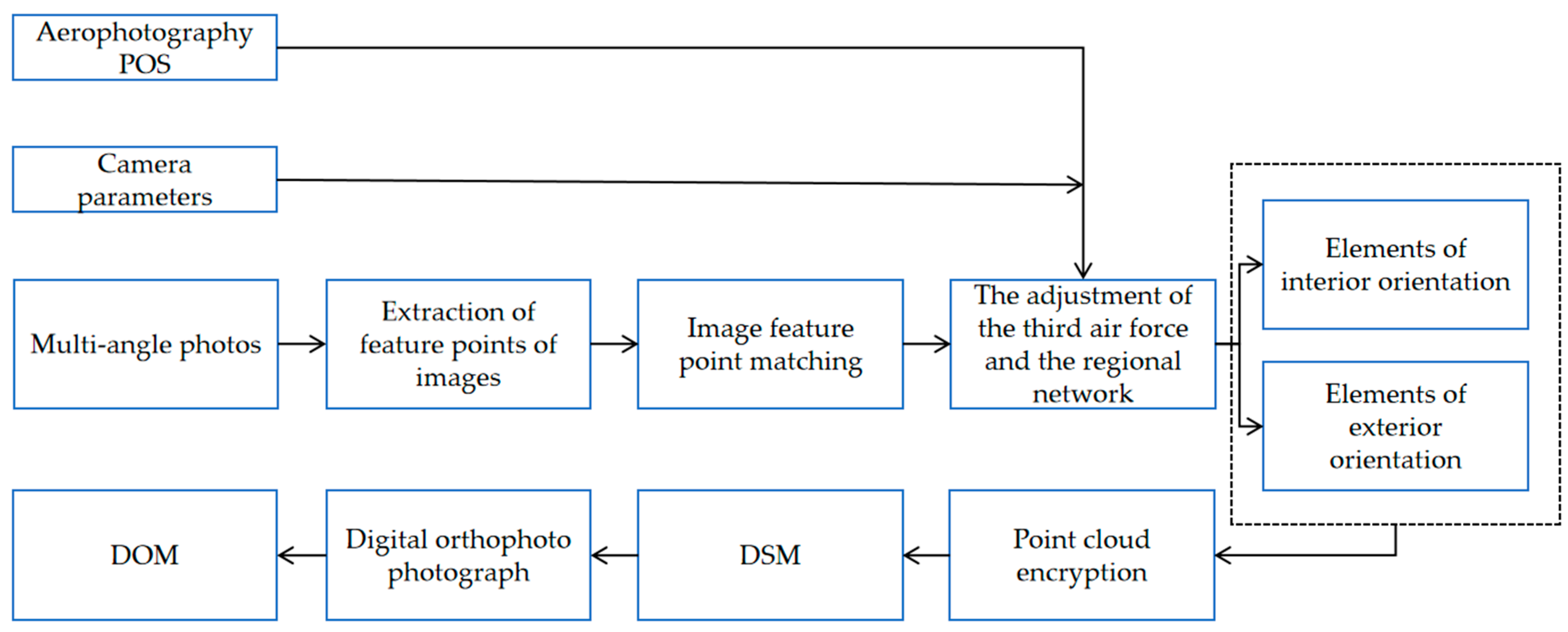
• Real-time measurement through precise inertial navigation and GPS. The angle measurement accuracy can reach 0.001°, and the position accuracy is better than the centimeter level. The measurement accuracy is high, but the equipment cost is expensive.
• Based on the principle of photogrammetry, the beam method regional network adjustment is carried out to correct the low-precision spatial position and attitude of the spectral image, obtaining centimeter-level accuracy of the center of photography coordinates and an attitude angle of the principal optical axis with an accuracy better than 0.01°.

The principle of image space triple correction is shown in Figure 12.

After correction, the digital orthophoto model (DOM) and the digital surface model (DSM) are generated. The specific process can be carried out within software such as Pix4D (v4.3) and Agisoft Metashape Professional (v2.1.0), as shown in Figure 13 below. The planar coordinate position of each pixel of the ground object is expressed in the DOM. The DSM expresses the elevation of each pixel. Therefore, based on DOM and DSM, the three-dimensional coordinates (x, y, z) of each pixel or ground object region can be extracted.

4.4.3. Obtaining the Position of the Sun

In remote sensing, the position of the sun refers to the altitude angle and azimuth angle of the sun in the horizontal coordinate system, representing the direction of illumination at a certain moment and location. This is related to the observation date, time and the spatial position of the target. The precise calculation of this parameter is a key step in surface reflectance correction and BRDF modeling. At present, there are methods for obtaining the position of the sun, such as instrument measurement methods and astronomical calculation methods. For example, the Spencer formula [105] has a maximum error of more than 0.25°. The algorithm proposed by Pitman and Vant-Hull (1978) [106] reduced the error to 0.02°. PSA algorithm [107] is 0.008°. Roberto (2008) [108] proposed a solar position calculation algorithm with high accuracy (maximum error of 0.0027°) and low complexity. In addition, the calculation of the solar altitude angle cannot be done without the solar declination angle and the solar time angle. Scholars at home and abroad have also conducted relevant research on this. For example, in terms of the solar declination angle, Li et al. (2019) [109] proposed an improved formula suitable for different years by using the numerical fitting method in response to the problem that the traditional solar declination angle algorithm does not fully consider the data differences of different years. The results show that the root mean square error of the improved solar declination angle algorithm by the fitting method can be controlled within the range of 10–3, and the improvement effect on the calculation accuracy is remarkable.

5. The Application of Angle Effect in Quantitative Remote Sensing Inversion

5.1. Research on Typical Surface Bidirectional Reflection Characteristics

With the continuous deepening of the theory of bidirectional reflection on the earth’s surface, more and more methods and techniques have been applied to study the reflection characteristics of object surfaces. In recent years, a series of surface bidirectional reflection studies based on UAV have been carried out. For example, Hakala et al. (2010) [104] used small consumer-grade cameras installed on UAV to obtain the reflection anisotropy of the snow-covered surface. Grenzdurffer et al. (2011) [110] used a consumer-grade camera installed on a drone to study the reflective anisotropy of winter wheat fields by capturing multi-angle images at different observation zenith angles and azimuth angles within a hemispherical range. Roosjen et al. (2016) [14] installed a hyperspectral sweep spectrometer on a multi-rotor UAV for multi-angle measurements to study the reflectance anisotropy of barley, potatoes and winter wheat at different growth stages. Tao et al. (2021) [111] used a six-rotor UAV and a stabilization platform equipped with a spectrometer to measure the BRDF characteristics of the Dunhuang radiation calibration field. In addition, the application of UAV multi-angle remote sensing can quantitatively assess the deviations of different BRDF models from the actual directional reflectance, especially in aspects such as hot spot direction, hot spot reflectance, ceiling angle reflectance, and BRDF shape.

5.2. Radiation Correction of UAV Multi-Angle Spectral Data

Traditional BRDF measurements are usually based on the assumption that the ambient light remains stable. However, in UAV imaging, environmental factors such as atmospheric conditions, cloud coverage, and changes in water vapor content constantly affect the transmission of electromagnetic radiation brightness. The random variation of illumination can directly affect the radiation consistency of the original multi-angle reflectance data, significantly affect the modeling accuracy of BRDF, and hinder the effective application of surface BRDF. Therefore, the quantitative acquisition and modeling of BRDF are not only affected by the reflection characteristics of ground objects, but also by the changes in the radiation characteristics of the imaging environment. Eliminating the influence of random changes in illumination on BRDF modeling is of crucial importance. Wierzbicki et al. (2018) [22] applied the BRDF model to the radiometric correction of UAV aerial images to eliminate the geometric influence of the atmosphere and lighting in the processing of low-altitude images. The Root Mean Square Error (RMSE) between orthographic image pairs can be maintained below 10%. Wang et al. (2024) [112] proposed a fast multi-angle information acquisition scheme for a high-precision BRDF modeling method considering illumination changes, mainly involving a lightweight BRDF acquisition system and three improved BRDF models considering illumination correction. The results show that the proposed method can obtain multi-angle information quickly and accurately by using push-sweep hyperspectral imaging, and the improved model eliminates the negative impact of illumination on BRDF modeling. Song et al. (2025) [113] collected UAV hyperspectral multi-angle data, corresponding illumination information and atmospheric parameter data, solving the problem that the existing BRDF modeling did not consider the limitation of modeling accuracy due to the variation of outdoor environmental illumination, and effectively optimized the radiation consistency of multi-angle data of BRDF. The error caused by the illumination variation in BRDF modeling has been reduced, and the accuracy of BRDF modeling has been improved.

5.3. Inversion and Structural Analysis of Ecological Element Parameters

The multi-angle measurement by UAV provides a new solution for the high-precision mapping of geological features. The mapping of geological features is of great significance for understanding the morphology of the earth’s surface, geological structure and the distribution of mineral resources. Traditional geological mapping methods, such as ground surveying and satellite remote sensing, although they can meet the basic mapping requirements to a certain extent, have many limitations when facing complex terrains and geological conditions. The emergence of multi-angle oblique photography technology by UAV has brought new research directions to the field of geological mapping. For instance, Li (2025) [114] utilized the multi-angle oblique photography method by UAV to conduct high-precision mapping of the geological features of typical landform feature areas (mainly mountains and hills), enabling precise mapping of the orientation, branches, and connections with the surrounding terrain of mountains. The location, width and relative layout of valleys, as well as the distribution range of different geological types, provide a solid data foundation for various researches and applications in the geological field. The oblique photogrammetry technology based on UAV is also widely used in the three-dimensional modeling of ground objects. By combining conventional sky-bottom images with multi-directional oblique images to establish three-dimensional models, it has become one of the most effective means for measuring the anisotropy of the earth’s surface. For example, in terms of agricultural landscapes (namely farmlands and pastures), Meinena and Robinson (2020) [115] conducted experiments on four different UAV image acquisition schemes, which simultaneously included multi-angle images of the sky, ground and tilt of agricultural land. Experiments have proved that the addition of inclined multi-angle images improves the relative accuracy of the three-dimensional surface model. On high and steep rock slopes, Zhao et al. (2023) [116] proposed a technical framework supporting the acquisition of high-quality three-dimensions models, called multi-angle object surface image acquisition. The texture distortion of the three-dimensional models established by this method is significantly reduced, and the recognisability is greatly improved.

Single-angle data from UAV can only represent the projection of ground objects in one direction and lack sufficient information to reflect their spatial structure. Multi-angle observations can obtain various information about ground objects, enhancing the richness of information and can be used for precise research on understory vegetation. For instance, Wang et al. (2021) [117] based on UAV multi-angle remote sensing data and using the local maximum value method, divide vegetation morphology into a discrete type and continuous type, and the undergrowth terrain corresponding to the vegetation morphology is inversely plotted by respectively using point cloud fabric filtering and the map forest density algorithm. The results show that for different vegetation forms, the terrain inversion results obtained by this technical route have high accuracy and can provide technical support for the UAV remote sensing investigation of forest undergrowth vegetation information in the southern red soil area.

Furthermore, the high-resolution data acquisition feature of the UAV system can effectively improve the accuracy in the classification of wetland land cover. For example, Liu et al. (2018) [118] utilized the multi-view information of multi-angle images of UAV. A multi-view object-based image analysis (MV-OBIA) method was studied, and its performance was compared with the traditional OBIA (Ortho-OBIA) method that only uses orthophoto images and the classification method based on BRDF simulation. The results show that, compared with Ortho-OBIA, MV-OBIA significantly improves the overall accuracy, regardless of the features used for classification and the wetland land cover type in the study area. Furthermore, compared with the BRDF-based method, MV-OBIA also shows higher efficiency in classifying using multi-view information because its overall accuracy is much higher. In the same year, Liu et al. (2018) [119] also studied a multi-view object-oriented classification method that uses the deep convolutional neural network method to process multi-angle images captured by UAV for land cover classification, effectively improving the accuracy of the traditional classification methods for orthologous images.

5.4. Precise Monitoring and Classification of Multiple Parameters of Crops

UAV remote sensing technology is less affected by cloud cover and weather, and can obtain high-throughput and high-resolution images. It can provide accurate data support for agricultural decision-making, meet the demands of various agricultural environments and scenarios in the process of smart agricultural management, and promote the efficiency and precision of agricultural production. UAV equipped with multispectral sensors have become part of precision agriculture [120,121,122,123]. In terms of vegetation parameter inversion, multi-angle observation data have significantly improved the inversion accuracy. For instance, Duan et al. (2014) [124], obtained hyperspectral image data of corn, potatoes and sunflowers through two consecutive UAV flight missions with different course directions, and constructed a multi-angle dataset by bidirectional observations in the overlapping areas of the flight routes, thereby conducting research on the inversion of crop LAI. The results show that the introduction of multi-angle observation data significantly improves the estimation accuracy of LAI. Pan et al. (2020) [19] conducted a study on remote sensing images obtained by UAV under small Field of View (FOV) conditions to explore the influence of observation angle differences on the inversion accuracy of Canopy Chlorophyll Content (CCC). The research has proved that the observed geometric changes can significantly affect the chlorophyll inversion results, thereby clarifying the role of BRDF in accurately estimating CCC. Lin et al. (2021) [125] explored the method of estimating the forest LAI from the point clouds generated from UAV multi-angle photos.

In addition, UAV multi-angle remote sensing also has significant application value in the growth and quality of crops. For instance, Wang (2023) [126] developed a method based on the fusion of multi-angle reflectance data and the inversion of reflectance using the BRDF model. In-depth research was carried out on analyzing the characteristic angles that affect the quality inspection of jujubes in southern Xinjiang, exploring the inversion method of jujube reflectance, and improving the detection accuracy through multi-angle data fusion, so as to achieve the goal of improving the accuracy of jujube quality inspection using UAV multispectroscopy.

In high-resolution remote sensing images, bidirectional reflection also provides important information such as land cover and the properties of object surfaces, becoming an effective technical means for the classification of ground features in remote sensing images. For example, Yan et al. (2019) [127] built a multi-angle hyperspectral remote sensing system using a hexarotor UAV and a Cubert S185 framework hyperspectral sensor. By combining the multi-angle remote sensing BRDF model with the object-oriented classification method, they studied the application of UAV multi-angle remote sensing in the fine classification of vegetation. This method can not only effectively reduce the phenomenon of “homographic foreign objects” where different objects have similar spectra, but also be conducive to the construction of BRDF in the vegetation canopy. Qiu et al. (2021) [128] based on UAV the multi-angle hyperspectral imaging system, conducted multi-angle observations of the coniferous forest canopy at constant angles and continuous intervals on the main plane, obtaining multi-angle (including hot and dark spots) hyperspectral images on the main plane. They compared and analyzed the observation results with the simulation results of the four-scale geometric optical model. The angle and hyperspectral information provided by the UAV multi-angle imaging observations in this study, especially the hot and dark spot information, has good application prospects in the research of ground object identification and classification, inversion of vegetation canopy structure, and acquisition of key parameters of the carbon cycle. It also has great potential in the study of other directional characteristics of ground objects such as reflection or thermal radiation.

5.5. High-Resolution Inversion of Surface Albedo in Typical Areas

Albedo is the proportion of solar radiation reflected by the earth’s surface and plays a significant role in climate models, energy balance, ice and snow melting monitoring, and agricultural production. Traditional satellite and ground observations are limited by problems such as low spatial resolution, single observation angle or insufficient temporal continuity, which restricts the development and application of surface albedo. Furthermore, ignoring the anisotropic reflection mode of the earth’s surface when calculating albedo can cause corresponding errors, especially when the zenith angle of the sun is large [129,130,131]. UAV multi-angle remote sensing provides a brand-new technical means for the study of surface albedo, which can effectively obtain the brightness of surface reflected radiation and estimate the surface albedo by inverting BRDF. For example, Dumont et al. (2011) [132] proposed a new method for extracting the albedo of frozen soil from the visible light and near-infrared bands, while considering the anisotropic reflectivity of the ice and snow surface. The radiative transfer model is used for the conversion from narrowband to broadband. However, this method cannot obtain reliable albedo measurement data under clouds and relies on assumptions about the atmospheric transmittance and reflection anisotropy of ice and snow, both of which are difficult to model and measure [133].

6. Challenges and Future Development Trends

6.1. The Challenges

• The theoretical model is poorly adapted to real-world scenarios. Most of the existing BRDF models are designed based on satellite or aerial platforms. However, in low-altitude dynamic observations by UAV, the rapid changes in the three-dimensional structure of the ground surface, lighting conditions and sensor attitudes limit the applicability of the models, and the uncertainty of the inversion results increases significantly. For instance, traditional BRDF models (such as the PROSAIL and RT models) assume that the canopy structure is uniform, while the ground objects observed by drones (such as forest shadows and soil backgrounds) have strong heterogeneity, which in turn leads to an increase in model inversion errors. Meanwhile, the heterogeneity of the canopy structure of complex crops (such as vegetation density and leaf inclination angle distribution) further intensifies the difficulty of modeling the angle effect. In addition, the current BRDF model still does not fully consider the mutual reflection effect of surfaces, especially at the micro-terrain scale, where multiple scatters between adjacent surface elements can significantly alter the distribution pattern of reflection characteristics.
• Difficult fusion and correction of multi-source data. The multispectral or hyperspectral payloads of UAV are prone to be affected by atmospheric disturbances, geometric distortions of sensors and non-uniformity of illumination during multi-angle observations such as inclined and sky-bottom conditions. The accuracy of radiation and geometric correction is difficult to guarantee. Meanwhile, the spatio-temporal matching and fusion processing of data from multiple sensors (such as thermal imagers and lidars) is highly complex and requires the support of more efficient algorithms. In addition, when fusing data from UAV and satellites, there are situations such as mismatch in temporal resolution and differences in angle sampling, which result in a large amount of data being unable to be used collaboratively.
• Stability of observations in a dynamic environment. Low-altitude flight of UAV is vulnerable to wind field disturbances, resulting in deviations in observation angles and insufficient overlap of images. Especially in complex terrains or areas with dense vegetation, it may cause data loss or distortion in radiation measurement. Furthermore, the instantaneous changes in lighting conditions (such as cloud occlusion) pose higher requirements for the comparability of multi-temporal angle effects.
• Lack of expansion and standardization of application scenarios. At present, most studies focus on single crops or typical ground feature types, while the research on angle effects for complex ecosystems such as forests and wetlands is still insufficient. Meanwhile, the lack of unified standards for the collection, processing and verification of UAV multi-angle remote sensing data has restricted its large-scale application and promotion.
• Issues of precise navigation and positioning. When UAV make sharp turns or fly at high speeds, GNSS signals may not be received in a timely manner, resulting in positioning drift. In addition, in areas with complex terrain such as cities and mountainous regions, satellite signals are prone to being blocked, resulting in increased positioning errors.

6.2. Future Development Trends

• Multi-angle sensors and intelligent observation network innovation. Develop lightweight and high-spectral resolution multi-angle imaging sensors, and combine them with the autonomous path planning technology of UAV to achieve multi-mode coordinated observations such as space-ground, inclined, and circumferential, and enhance the full-dimensional capture capability of the two-dimensional reflection characteristics of the earth’s surface. Meanwhile, a three-dimensional monitoring network of satellite-UAV-ground is constructed to reduce the uncertainty of inversion through data complementarity of multiple platforms. In addition, in master-slave UAV swarms, long-endurance fixed-wing UAV are responsible for covering large areas at a 15° angle, while multi-rotor UAV perform local 55° fine observations. This data collection method not only enhances efficiency but also enables high-precision relative positioning through cluster SLAM.
• Deep integration of mechanisms and data-driven models. Combining the physical radiation transfer model with deep learning algorithms and using high-resolution multi-angle data to train the end-to-end inversion model breaks through the limitations of traditional empirical models. For example, the spectral responses at different angles are simulated through the Generative Adversarial Network (GAN) to optimize the inversion accuracy of physicochemical parameters of vegetation; by using Transformer to process long-term and continuous multi-angle data, the deformation characteristics of BRDF caused by crop growth can be captured, thereby improving the prediction accuracy of BRDF, etc. In addition, the research on Quantum Convolutional Neural Networks (QCNN) can handle massive multi-angle datasets, and the theoretical computing speed can be increased by 10⁶ times.
• Dynamic environment adaptive correction technology breakthrough. Develop dynamic radiometric correction methods based on real-time meteorological data and sensor attitude information, combined with lidar point-cloud-assisted geometric correction, to improve data quality in complex scenarios. Furthermore, reinforcement learning algorithms are introduced to optimize flight control and reduce observation errors caused by external disturbances.
• Standardized application system and sharing platform construction. Formulate norms, processing procedures and verification standards for UAV multi-angle remote sensing data collection, and promote a cross-regional and cross-disciplinary data sharing mechanism. Meanwhile, a database of the angle effect characteristics of typical ground features is established to provide a reusable knowledge base for scenarios such as precise agricultural management and ecological disaster early warning.
• Multi-source fusion navigation and positioning. The tightly coupled system using RTK, visual odometer and IMU can achieve positioning accuracy of 1 cm in plane and 2 cm in elevation. Meanwhile, it is equipped with anti-interference GNSS modules (such as Septentrio Mosaic series), which effectively improves the positioning stability of UAV in complex urban environments by supporting multi-frequency and multi-constellation signal reception. This integrated navigation scheme not only ensures the high-precision positioning requirements but also enhances the system’s robustness in signal occlusion environments, providing a reliable position reference for multi-angle data acquisition under complex trajectories.

7. Conclusions

This paper systematically reviews the research progress on the angle effect in UAV quantitative remote sensing, providing a comprehensive summary of its theoretical foundations, data acquisition technologies, processing methods, and application scenarios. As an emerging interdisciplinary field integrating remote sensing science with precision agriculture and ecological monitoring, the study highlights the pivotal role of angle effects in vegetation parameter inversion, surface albedo estimation, and precision crop monitoring. It also identifies current challenges, including the inadequate adaptability of theoretical models, difficulties in multi-source data fusion, and observation stability issues in dynamic environments. Future advancements through the integration of deep learning algorithms, multi-platform collaborative observation, and innovative sensor technologies are expected to drive theoretical innovation and engineering applications in angle effect research. These developments will further enhance the accuracy of surface parameter inversion and the advancement of UAV remote sensing technology, thereby providing more reliable technical support for global change monitoring and sustainable development goals.