An Elite Wolf Pack Algorithm Based on the Probability Threshold for a Multi-UAV Cooperative Reconnaissance Mission

Abstract

In the task assignment problem of multi-UAV collaborative reconnaissance, existing algorithms have issues with inadequate solution accuracy, specifically manifested as large spatial spans and knots of routes in the task execution of UAVs. To address the above challenges, this paper presents a multi-UAV task assignment model under complex conditions (MTAMCC). To efficiently solve this model, this paper proposes an elite wolf pack algorithm based on probability threshold (EWPA-PT). The EWPA-PT algorithm combines the wandering behavior in the traditional wolf pack algorithm with the genetic algorithm. It introduces an ordered permutation problem to calculate the adaptive wandering times of the detective wolves in a specific direction. During the calling phase of the algorithm, the fierce wolves in the wolf pack randomly learn the task assignment results of the head wolf. The sieging behavior introduces the Metropolis criterion from the simulated annealing algorithm to replace the distance threshold in traditional wolf pack algorithms with a probability threshold, which dynamically changes during the iteration process. The wolf pack updating mechanism leverages the task assignment experience of the elite group to reconstruct individual wolves, thereby improving the individual reconstruction’s efficiency. Experiments demonstrate that the EWPA-PT algorithm significantly improves solution accuracy compared to typical methods in recent years.

1. Introduction

In recent years, UAVs have gained widespread application across various fields due to their advantages, including quick and easy deployment, high mobility, high economy, strong self-organizing ability, and scalability [1]. In practical applications, due to the large number and complexity of tasks, a single UAV will be limited by its individual performance, flight range, and payload, making it inefficient to complete all assigned tasks [2,3]. Based on the various defects of executing tasks with a single UAV and the promotion of practical needs, multi-UAV cooperation has become a focus of current research at home and abroad.

In multi-drone collaborative task scenarios, task assignment is the major component and prerequisite for improving mission execution efficiency and automatic control of the UAV swarm system. The multi-UAV task assignment problem mainly involves two aspects: the task assignment model and the task assignment algorithm [4].

The task assignment problem of multi-UAV cooperation is a type of NP-hard combinatorial optimization problem [5]. In recent years, scholars have established many models for the UAV task assignment problem to make the task assignment model more realistic. Zhang et al. [6] modeled the task assignment problem based on the background of UAV reconnaissance and evaluation. Zhu et al. [7] established a multi-UAV task planning model, which comprehensively considers the performance differences of heterogeneous UAVs and three performance indicators for task evaluation. Based on the background of UAV reconnaissance tasks, Wu et al. [8] presented a multi-UAV task assignment model by comprehensively considering factors such as the total range of the task, task threat degree, and task benefit. Gao et al. [9] focused on the performance of heterogeneous UAVs and proposed a task assignment model based on evaluation metrics such as task completion time and energy consumption.

Heuristic algorithms are commonly used to solve the multi-UAV task assignment models. In heuristic algorithms, the particle swarm algorithm has emerged as the mainstream approach due to its minimal parameters, simplicity of implementation, and fast solving speed [10]. Wang et al. [11] proposed an EPPSO algorithm that constructs an experienced pool with the top 20% particles based on fitness values. Individuals who do not satisfy the constraint conditions are reconstructed based on the experienced positions in the pool. This algorithm effectively maintains population diversity and expands the search scope of the solution space. Liu et al. [12] proposed the RPSO algorithm that uses adjustable Gaussian white noise to perturb the inertia weight and acceleration coefficients of particles randomly. This approach enhances the range of the algorithm’s search space to some extent and has a positive effect on helping the particle swarm to escape from local optima. Wang et al. [13] proposed the IPSO algorithm, where individuals selectively optimize in multiple directions during the iteration process. Additionally, the algorithm introduces a position abandonment mechanism to improve the overall optimization capability and perform better in escaping out of the local optimal solution. Tian et al. [14] proposed the MPSO algorithm to improve the population diversity during initialization by employing chaotic initialization, Sigmoid inertia weight, and a maximum focusing distance strategy. This approach effectively optimizes the algorithm’s iteration efficiency and demonstrates better stability when searching for global optimal solutions.

However, particle swarm optimization algorithms have significantly improved their search performance, accelerated their iteration speed, and enhanced their capability to escape local optima, making them competent for the task assignment of multi-UAV cooperation. But due to the inherent limitations in dealing with high-dimensional discrete problems and falling into local optima in the later stage, PSO’s ability to search for optimal solutions is still not satisfactory when dealing with the complex, high-dimensional, and discrete problem of multi-UAV task assignment.

The wolf pack algorithm is a relatively new type of swarm intelligence algorithm which primarily imitates the clear social division of labor and cooperative hunting behavior [15]. Compared to the particle swarm algorithm, the wolf pack algorithm has better global convergence, computational robustness, and effectiveness in handling high-dimensional and discrete problems. Therefore, the wolf pack algorithm demonstrates superior solving performance in multi-UAV task assignments.

In recent years, scholars have proposed numerous improvements to the wolf pack algorithm. Xu et al. [16] proposed the MDWPA algorithm, which combines the wandering, calling, and sieging behaviors with the genetic algorithm and elite strategy, significantly improving the convergence speed and solution accuracy. However, due to the excessively large scope of learning from the head wolf in calling and sieging behaviors, the diversity of the population is reduced, making it prone to local optima in the later iteration. Lu et al. [17] presented the MPPWPA algorithm, which divides the population into multiple subpopulations with approximately equal quality. Each subpopulation independently solves the problem and continuously evolves during the iteration process through information exchange between subpopulations. The algorithm accelerates the iteration and convergence speeds and performs well in handling low-dimensional problems. However, as the dimensionality increases, the accuracy of searching for the optimal solution gradually decreases. Zhu et al. [18] introduced the CDWPA algorithm, which enhances the quality of initial solutions through chaotic inverse initialization. Additionally, interference factors and adaptive step size are added to the iterative process to increase the ability to search the global optimal. However, the algorithm is prone to premature convergence during iterations, which leads to unstable optimization results.

The various improved wolf pack algorithms have achieved a certain degree of improvement in solution accuracy, but the final solutions still have issues such as large spatial spans and knots of routes in UAV task execution. In order to address the above challenges, this paper proposes a multi-UAV task assignment model under complex conditions (MTAMCC) to comprehensively take into account various factors such as the speed and range differences of heterogeneous UAVs, the time required for the UAV fleet to complete all reconnaissance tasks, target threat coefficients, and target area ranges. This model aims to align closely with practical applications by considering these multifaced aspects. To solve the MTAMCC model effectively, this paper proposes an elite wolf pack algorithm based on probability thresholds (EWPA-PT). The EWPA-PT algorithm significantly improves solution accuracy.

The remainder of this paper is arranged as follows: Section 2 introduces the task assignment model (MTAMCC). Section 3 presents the proposed algorithm (EWPA-PT) to solve the model. Section 4 introduces the experimental parameters and an analysis of the experimental results. Section 5 concludes this work and proposes directions for future improvements.

2. Task Assignment Model

2.1. Modeling Background

This chapter models the scenario of UAV swarm collaboratively performing reconnaissance tasks. A reconnaissance task involves UAVs taking off from the launch platform, flying to a designated target area, covering the entire region for reconnaissance, and returning to the launch platform upon completion. The following assumptions are made to mitigate the impact of uncertain factors and simplify the practical problem.

(1)

The UAV’s flight is constant and unaffected by exernal environmental factors.

(2)

The UAV is assumed to be secure during its flight; threats occur only during reconnaissance.

(3)

There are no obstacles during flight and distance is calculated using Euclidean distance.

(4)

Each reconnaissance task is performed only once.

2.2. Task Modeling

This paper represents the task model with a quadruple $<\mathrm{S},\mathrm{U},\mathrm{T},\mathrm{C}>$, where S is the set of the UAV launch platform. U is the set of UAVs. T is the set of target points, and C is the set of constraints.

Table 1. Object attributes and symbol interpretation.

Attributes
Platform:P	UAV launch platform: Np
	Initial position of the platform: $p_{\mathrm{loc}}$
	Launch platform drone type: $Typ{e}_{\mathrm{x}}$
UAV:U	Number of UAVs: Nu
	Initial position of UAVs: $u_{\mathrm{loc}}$
	Flight speed of UAVs: $ua{v}_{\mathrm{vc}}$
	Maximum range of UAVs: $ua{v}_{\mathrm{mr}}$
Target:T	Number of targets: Nt
	Initial position of targets: $t_{\mathrm{loc}}$
	Reconnaissance radius: $ta{r}_{\mathrm{range}}$
	Threat factor: $ta{r}_{\mathrm{risk}}$
Constraint:C	Maximum range of UAVs
	UAV threat factor

contains the attributes of each element in the quadruple.

2.3. Objective Function Construction

To enable the UAV swarm to accomplish the assigned tasks with minimal cost, maximal benefit, and the highest safety, this model will optimize based on the average flight time of the UAV swarm, the time required to complete the reconnaissance tasks, and the average threat level of the UAV swarm.

2.3.1. Reconnaissance Task Completion Time

The time required for UAVs to complete reconnaissance tasks includes the time for flying to the target point and conducting the reconnaissance. The completion time of the reconnaissance task is obtained as follows:

$$\begin{array}{cc}\hfill TCT& =\underset{i\in (1,Nu)}{max}tc{p}_i\hfill \end{array}$$

(1)

where $tc{p}_{\mathrm{i}}$ represents the time taken by the $UA{V}_i$ to depart from the launch platform to complete its corresponding assigned task. The calculation is obtained as follows:

$$\begin{array}{c}\hfill tc{p}_i={\displaystyle \frac{D_{u_i,t_1}+{\sum }_{k=1}^{n-1}{D}_{x_k,x_{k+1}}+{\sum }_{k=1}^{n}Dc{t}_{u_i,t_k}}{V_{u_i}}}\end{array}$$

(2)

where $D_{u_i,t_1}$ denotes the distance from $UA{V}_i$ to the first task point. $D_{x_k,x_{k+1}}$ represents the distance between task $poin{t}_k$ and task $poin{t}_{k+1}$. $Dc{t}_{u_i,t_k}$ represents the flying distance for $UA{V}_i$ to complete the reconnaissance task on $targe{t}_k$. $V_{u_i}$ represents the flying speed of the UAV.

2.3.2. Average Flight Time of UAV Swarm

The average flight time of the UAV is calculated as the average duration for the UAV swarm to take off from the launch platform, carry out the reconnaissance task, and return to the launch platform. The calculation is shown as follows:

$$\begin{array}{c}\hfill \mathrm{AFT}={\displaystyle \frac{{\sum }_{i=1}^{Nu}{T}_i}{Nu}}\end{array}$$

(3)

where $T_i$ represents the time when the $UA{V}_i$ finishes all assigned tasks and returns to the launch platform; $Nu$ represents the number of UAVs.

2.3.3. The Average Threat Coefficient of the UAV Swarm

The average threat coefficient of the UAVs refers to the average threat faced by the UAVs in completing all tasks. In this paper, the threat coefficient is related to the size of the area. For every additional kilometer of target reconnaissance range, the threat coefficient increases by 5. The calculation of the average threat coefficient is shown as follows:

$$\begin{array}{c}\hfill \mathrm{ATC}={\displaystyle \frac{{\sum }_{i=1}^{Nu}{\sum }_{k=1}^{Nt}ris{k}_{u_1,t_k}}{Nu}}\end{array}$$

(4)

2.3.4. Objective Function

Based on the preceding discussion, the optimization parameters for this model are the time the UAV swarm takes to complete reconnaissance tasks, the average flight time of the UAV swarm, and the average threat coefficient of the UAV swarm. Therefore, the objective function is calculated as follows:

$$\begin{array}{c}\hfill \mathrm{fitness}=\alpha \times TCT+\beta \times AFT+\gamma \times ATC\end{array}$$

(5)

Let $\alpha$, $\beta$, and $\gamma$ represent the weights for the UAV swarm tasks’ completion time, the UAV swarm’s average flight time, and the average threat coefficient of the UAV swarm, respectively. This paper sets the model parameters as $\alpha =\beta =0,3$, and $\gamma =0.4$. It is important to note that these model parameters can be dynamically adjusted based on the specific requirements of the scenario, provided that they adhere to the constraint $\alpha +\beta +\gamma =1$ [9,19]. Adjustments to the model parameters do not affect the algorithm’s performance. The rationale behind the chosen model parameters is to construct a general model. Ideally, we would prefer the parameters to be equal. However, due to the constraints, this is not feasible. Consequently, with a focus on safety considerations, the weight of the average threat coefficient of the UAVs is emphasized. This approach ensures that the UAV swarm can complete tasks with the maximum possible safety.

3. The Wolf Pack Algorithm

3.1. Traditional Wolf Pack Algorithm

As a relatively new swarm intelligence optimization method, the wolf pack algorithm employs a bottom-up design approach based on artificial wolf individuals and a cooperative search path structure based on division of labor [20]. It primarily mimics three hunting behaviors in wolf packs, wandering, calling, and sieging, with the head wolf at the core. Lastly, it implements a mechanism for leader wolf generation based on the “victor is king” rule in nature and an updating mechanism based on the “survival of the fittest” principle. The following will briefly describe the three behaviors and two mechanisms of the wolf pack algorithm in the order of algorithm implementation.

3.1.1. The Head Wolf Generation Mechanism

The head wolf generation mechanism is inspired by the ”victor is king” rule in nature, where the most capable individual wolf in the pack assumes the role of the head wolf. In the algorithm, the head wolf is determined by the individual wolf with the lowest fitness value in the pack, as the task assignment problem is a minimization problem.

3.1.2. Wandering Behavior

Detective wolves carry out the wandering behavior. In traditional wolf pack algorithms, the amount of wandering time and the detective wolf factor must be determined first. The detective wolf factor is an integer within the range $[{\displaystyle \frac{N}{a+1}},{\displaystyle \frac{N}{a}}]$ that is used to calculate the number of detective wolves in the current iteration. The position update of the ith detective wolf is calculated as follows:

$$\begin{array}{c}\hfill x_{i,d}^{k+1}=x_{i,d}^k+sin\left(2\pi \times {\displaystyle \frac{p}{h}}\right)\times {\mathrm{step}}_a\end{array}$$

(6)

3.1.3. Calling Behavior

The fierce wolves carry out the calling behavior. When a fierce wolf receives the call from the head wolf, it rapidly approaches the head wolf with a larger step, ${\mathrm{step}}_b$, and the position update is calculated as follows:

$$\begin{array}{c}\hfill x_i^{k+1}=x_i^k+{\mathrm{step}}_b\times {\displaystyle \frac{x_{\mathrm{head}}^k-x_i^k}{\left|x_{\mathrm{head}}^k-x_i^k\right|}}\end{array}$$

(7)

According to that, the fitness value is recorded after each wandering. If the fitness of the new position is superior to the head wolf’s fitness, the calling behavior stops, and the detection wolf becomes the new head wolf to initiate the calling behavior. If the fitness of the new position is superior to that of the original position, the new position is retained; otherwise, no change occurs.

In the calling behavior, to maintain population diversity and expand the search range, a distance threshold $d\_near$ is introduced, which is calculated as follows. If the distance between the head wolf and the fierce wolf exceeds the distance threshold, the fierce wolf will keep rushing towards the head wolf with a large step size. Otherwise, it switches to sieging behavior.

$$\begin{array}{c}\hfill d\_near={\displaystyle \frac{1}{D\times w}}\times \sum _{d=1}^D\left|ma{x}_d-mi{n}_d\right|\end{array}$$

(8)

3.1.4. Sieging Behavior

All individual wolves perform sieging behavior in the wolf pack except for the head wolf. Each wolf moves towards the position of the head wolf with a smaller step size. The position update is calculated as follows:

$$\begin{array}{c}\hfill x_i^{k+1}=x_i^k+\lambda \times {\mathrm{step}}_c\times \left|x_{\mathrm{head}}^k-x_i^k\right|\end{array}$$

(9)

The relationship of the step size for the three behaviors is as follows:

$$\begin{array}{c}\hfill {\mathrm{step}}_a={\displaystyle \frac{{\mathrm{step}}_b}{2}}=2\times {\mathrm{step}}_c={\displaystyle \frac{\left|ma{x}_d-mi{n}_d\right|}{s}}\end{array}$$

(10)

3.1.5. Wolf Pack Update Mechanism

The updating mechanism in the wolf pack algorithm mirrors the “survival of the fittest” rule in nature. Firstly, all individual wolves are sorted in ascending order based on their fitness value. Then, at the end of each iteration, based on the updating factor q, a random integer within the range $[{\displaystyle \frac{N}{2\times q}},{\displaystyle \frac{N}{q}}]$ is generated to determine the number of individual wolves that need to be updated.

3.2. The Proposed EWPA-PT Algorithm

The traditional wolf pack algorithm has demonstrated strong performance in handling multi-dimensional continuous problems. However, when it comes to the complex discrete problem of multi-UAV task assignment, this algorithm performs poorly and requires algorithmic improvements. Consequently, this paper proposes the EWPA-PT algorithm, which optimizes four aspects: wandering, calling, sieging, and the pack updating mechanism.

During the wandering behavior, the algorithm optimizes the task execution order for UAVs. Inspired by the problem of solving ordered permutation problems in mathematics, the traditional wolf pack algorithm’s maximum number of wandering times is replaced by the maximum potential for optimization in a specific direction, enabling each detective wolf to have its adaptive maximum number of wandering times in each direction.

The calling behavior is mainly inspired by genetic algorithms, where the fierce wolf randomly selects the task assignment solution of the head wolf for n tasks as its task assignment result.

Sieging behavior introduces the “acceptance probability” P based on the Metropolis criterion in the simulated annealing algorithm, where the value of P is calculated based on the difference in fitness between individual wolves and the head wolf. In the EWPA-PT algorithm, P is named the probability threshold, replacing the distance threshold in the traditional wolf pack algorithm.

The wolf pack updating mechanism refers to individuals in the wolf pack that rank lower in fitness, learning from elite wolves about task assignment schemes and adopting them for use, thereby ensuring the number of effective individuals during iterations.

Subsequent experiments have demonstrated that the algorithm’s elite-wolf-based updating mechanism shows significant performance advantages under complex constraints. The pseudocode of the algorithm is shown in Algorithm 1.

Algorithm 1: EWPA-PT

3.2.1. Individual Coding and Initialization

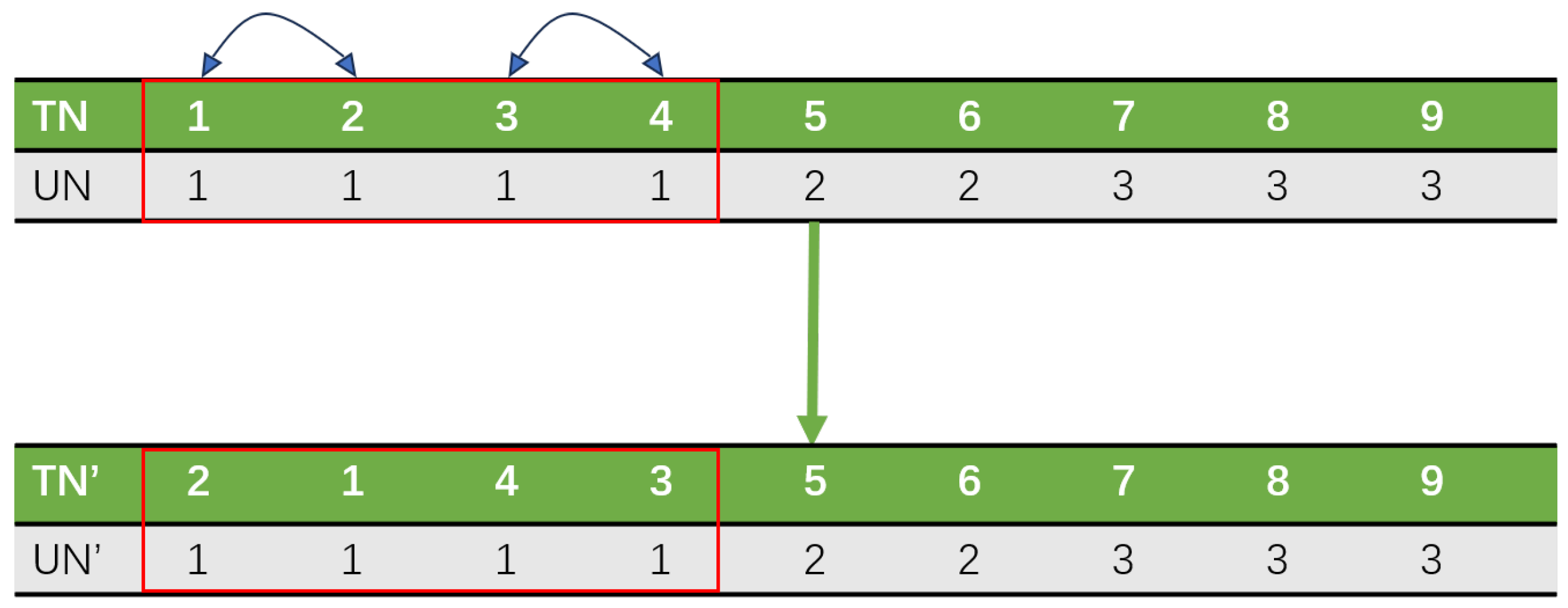
This algorithm uses integer encoding, where the task assignment is represented by the correspondence between two lists: the task list and the UAV list. The execution order of tasks is determined by the sequence of task numbers in the task list, as shown in Figure 1.

Figure 1 illustrates a scenario involving five UAVs and five tasks to be assigned, where the lists TN and UN represent the task list and the UAV list, respectively. For example, in the second column of the figure, the value 3 in the TN list and value 2 in the UN list indicate that the third task is assigned to the second UAV. Notably, the assignment allocation results in the third and fifth columns show that the fifth and fourth tasks are assigned to the fifth UAV, respectively. However, since the fifth task appears before the fourth task in the TN list, the fifth UAV prioritizes completing the fifth task before the fourth task; the task allocation results are as follows: $UA{V}_1:\left\{1\right\},UA{V}_2:\left\{3\right\},UA{V}_3:\left\{2\right\},UA{V}_4:\left\{\right\},UA{V}_5:\left\{5,4\right\}$.

Algorithm initialization primarily involves several aspects: population initialization, parameter initialization, UAV position initialization, and target position initialization. Among these, population initialization includes the following steps and the pseudocode is shown in Algorithm 2.

Algorithm 2: Population Initialization

1. Initialize the TN and UN lists, where both TN and UN consist of N sublists, each length Nt. Each element within the sublists of TN is a randomly generated integer within the range (1, Nt), with each integer appearing exactly once. In contrast, each element within the sublists of UN is a randomly generated integer within the range (1, Nu), with integers allowed to repeat.

2. The sublists in the TN and UN lists correspond one-to-one, collectively forming a task allocation solution. The decoded task allocation results are stored in the UdoT_list list. Subsequently, the feasibility of the task allocation solution is assessed against the constraint conditions. If the constraints are satisfied, the corresponding fitness value is computed using Formula (5). If the constraints are not satisfied, the fitness value is set to infinity.

3. Finally, the TN, UN, and UdoT_list lists are re-sorted according to the ascending order of fitness values. The completion of sorting marks the completion of population initialization.

3.2.2. Improvements in Wandering Behavior

Inspired by the problem of ordered permutations in mathematics, the algorithm introduces the concept of adaptive wandering times during the wandering behavior phase. The adaptive wandering times essentially reflect the number of possible adjustments in the task execution order for each UAV. Unlike the fixed wandering times used in traditional wolf pack algorithms, the adaptive wandering times enable a more rational allocation of computational resources and improve the optimization of UAV task execution sequences. The specific steps of the wandering behavior are as follows:

In the wandering behavior, firstly, a random integer is generated from the range $[{\displaystyle \frac{N}{a+1}},{\displaystyle \frac{N}{a}}]$ to determine the number of detective wolves, denoted as dnum. Then, the task assignment results for the detective wolves are traversed. For each detective wolf, the wandering direction can be understood as the tasks-assigned scheme for each UAV. The solution to an ordered permutation problem from mathematics inspires the calculation of the maximum number of wandering times in each direction. Based on the number of tasks assigned to a UAV, the maximum number of possible task orders is determined and denoted as poss_num. This poss_num is then used as the maximum number of wandering times for the corresponding direction of the detective wolf. It is worth noting that when a large number of tasks are assigned to the UAV, to expedite the execution efficiency of the wandering behavior, we can truncate poss_num to its maximum value. After determining the maximum number of wandering times, we need to find the tasks to be performed by the UAV. Next, the order of executing tasks is randomly shuffled, and the fitness value is calculated. The fitness value of the new assignment scheme is compared with the original assignment scheme. If the new scheme is better, it is retained; otherwise, no changes occur. Figure 2 illustrates the specific operational steps.

The main process of wandering behavior is illustrated in lines 5–13 of Algorithm 3. In fact, the essence of the improvement in the wandering behavior is optimizing the task execution order for UAVs. While ensuring that the UAV is assigned to appropriate tasks, the flight route of the UAV is improved by adjusting the order of the UAV executing tasks and reducing the fitness value at the same time so that the result of task assignment is more optimized.

Algorithm 3: Wandering behavior

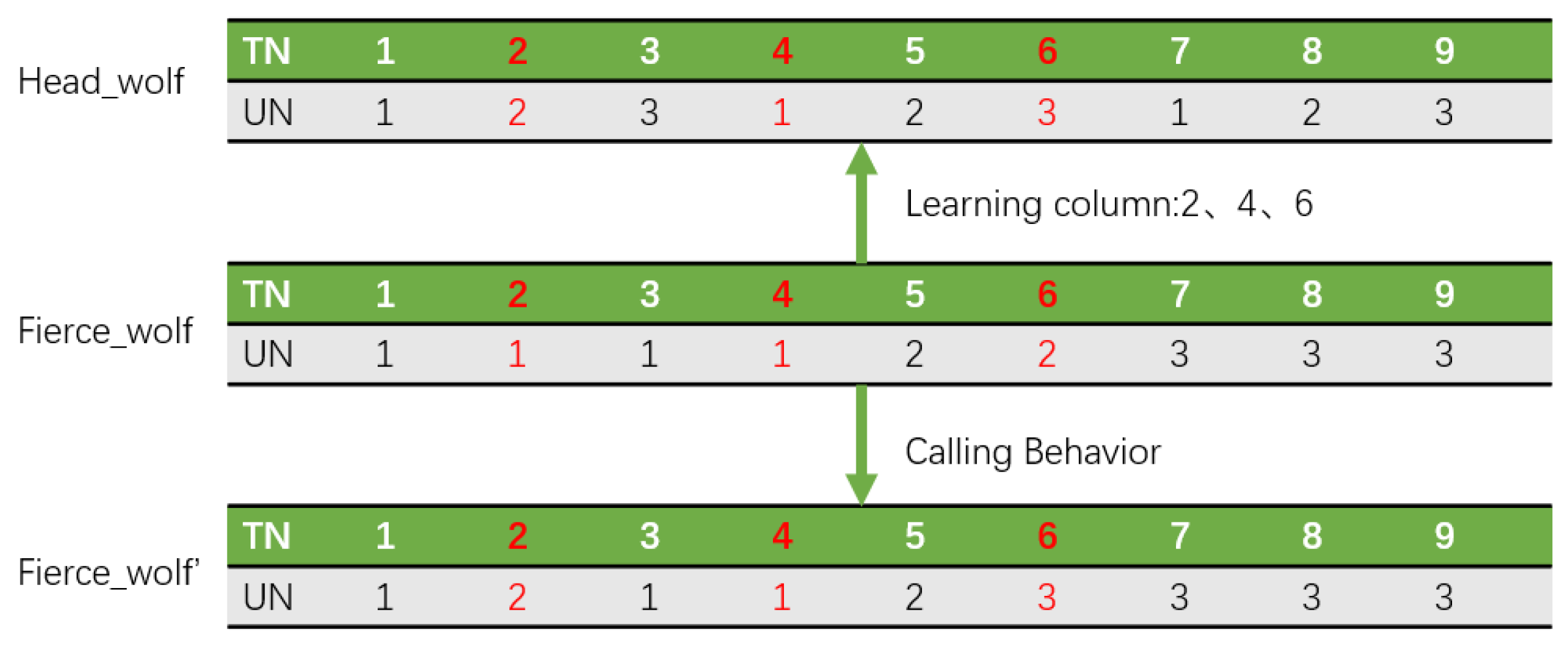
3.2.3. Improvement on Calling Behavior

The calling behavior is crucial for the entire wolf pack algorithm to converge to the optimal solution. The improved calling behavior is inspired by genetic and elite strategies. It requires several steps at the beginning of the algorithm. Firstly, we need to determine the number of fierce wolves, denoted as fnum (N - dnum - 1). Then, while ensuring that the task order in the TN list remains unchanged, a random positive integer is generated to determine the number of columns that the fierce wolf will alter in its calling behavior for this iteration. Subsequently, another random positive integer is generated to specify the exact column to be changed. After identifying the column, we need to find the corresponding task number. The fierce wolf learns from the head wolf’s assignment result for that task and updates its corresponding value in the UN list, achieving a rapid convergence towards the head wolf. If the fitness after updating is better than the original fitness, the assignment scheme is updated; Otherwise, it remains unchanged. If the fitness value after updating is better than that of the head wolf, the head wolf is immediately updated, and calling behavior continues based on the new head wolf’s position. The specific steps are shown in Figure 3.

The main process of calling behavior is illustrated in lines 3–8 of Algorithm 4. In the example illustrated in Figure 3, the random number R1 is 3. In subsequent iterations, the values of random number R2 are 2, 4, and 6, respectively. Then, the fierce wolf identifies the task numbers corresponding to these three columns as 2, 4, and 6, respectively. It learns from the head wolf’s assignment schemes for task 2, 4, 6 and updates its values in the UN list accordingly. If the updated position is better than the original position, the new position is retained; otherwise, no change occurs. If the updated position is better than the current head wolf’s position, the fierce wolf replaces the head wolf to initiate the calling behavior.

Algorithm 4: Calling behavior

3.2.4. Improvements in Sieging Behavior

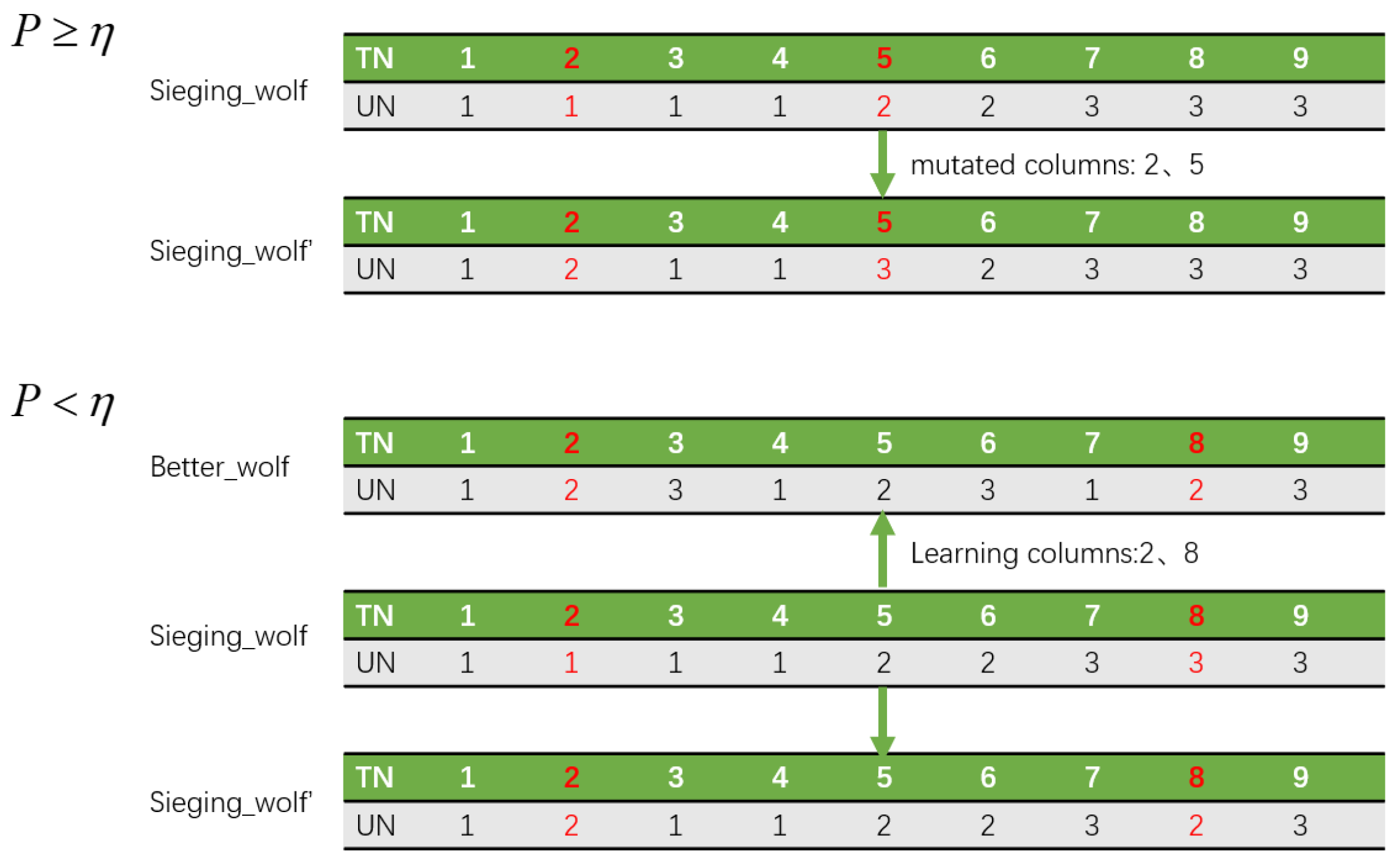
The process of sieging behavior involves all individual wolves, excluding the head wolf, converging towards the optimal solution by taking smaller steps. Since integer encoding cannot accurately represent the distance relationship between the head wolf and individual wolves, in the improved sieging behavior, the innovative aspect of the algorithm lies in replacing the traditional “distance threshold” with a “probability threshold”.

The “probability threshold” is computed based on the fitness difference between the head wolf and the individual wolf, effectively reflecting the similarity in task allocation effectiveness between them. If the fitness difference between the head wolf and the individual wolf is slight, it is assumed that their task allocation effects are similar. Consequently, in the current iteration, the “probability threshold” for that individual wolf is high, resulting in a greater probability of individual mutation.

Because the fitness value of individual wolves changes dynamically, going through a process of divergence followed by convergence throughout the algorithm’s iteration using a fixed fitness difference value leads to unsatisfactory results. Inspired by the simulated annealing algorithm, where the probability of accepting worse solutions decreases with increasing iterations, this aligns well with the need to set the threshold for sieging behavior. Therefore, the EWPA-PT algorithm incorporates the probability calculation formula from simulated annealing, denoted as the probability threshold in this algorithm, replacing the traditional distance threshold. With the fitness difference between the head wolf and individual wolves remaining constant, it is advisable to set a large probability threshold during the early stages of iteration. This is because, in the early stage, there is significant diversity in fitness value among individual wolves, and a large distance threshold allows individual wolves to explore the solution space more extensively around their current position. As the iteration progresses, the fitness values of all individual wolves gradually converge. Therefore, it is preferable to decrease the probability threshold during the later stages of iteration. This adjustment is necessary because maintaining the initial “similarity probability” throughout the later stage may lead the program to execute only one branch of the sieging behavior code. Additionally, a smaller distance threshold facilitates faster convergence towards the optimal solution.

This approach preserves the possibility of individual mutations, preventing excessive similarity between individual wolves and the head wolf during the iteration process, thus enhancing population diversity. Moreover, using a probability threshold enables the wolf pack to explore multiple points simultaneously when the task assignment results differ but yield similar effectiveness. This facilitates multi-point optimization while ensuring diversity and enhancing the ability to break out of local optimal solutions. The calculation of the probability threshold is calculated as follows:

$$\begin{array}{c}\hfill P=e^{-\left({\displaystyle \frac{F_{head}-F_i}{T\times \mu }}\right)}\end{array}$$

(11)

where T is the global temperature coefficient, which continuously decreases as the iteration progresses. $\mu$ is the adjustment coefficient. $F_{head}$ represents the fitness value of the head wolf. $F_i$ represents the value of the ith individual wolf. When the fitness values of the individual wolf and the head wolf are close, the probability threshold is larger; conversely, it is smaller.

In the improved sieging behavior, a random number $\eta$ is generated between 0 and 1 and compared with a probability threshold. If $\eta$ is less than the threshold, the task assignment effectiveness between the individual wolf and the head wolf is considered similar. In this case, two columns from the individual wolf’s UN list are randomly selected for mutation (lines 4–6). When $\eta$ is greater than the threshold, it suggests that there is still a gap in the task assignment effectiveness between the individual wolf and the head wolf. Following the elite strategy, a random wolf with a better fitness value than the current one is selected as the learning template. The corresponding TN and UN lists are then copied, and two columns in the copied UN list are randomly changed (lines 9–11). During the sieging behavior, the position is updated if the fitness value is lower after updating; otherwise, the original position is retained. The process is shown in Figure 4 and the pseudocode is shown in Algorithm 5.

Algorithm 5: Sieging behavior

3.2.5. The Improvement of the Wolf Pack Update Mechanism

The wolf pack updating mechanism eliminates some wolves with the poorest fitness values and regenerates them according to specific rules. The number of wolves to be updated is calculated according to Formula (12), with b as the updating factor. In the traditional wolf pack algorithm, the update rule is similar to individual initialization and is carried out through random generation. This approach maintains population diversity in the early stage. However, as the algorithm progresses, the randomly generated individuals lack competitiveness compared to those that have been adjusted through multiple iterations. This diminishes the effectiveness of the wolf pack updating mechanism within the overall algorithm.

$$\begin{array}{c}\hfill n=Random.ranint({\displaystyle \frac{N}{2\times b}},{\displaystyle \frac{N}{b}})\end{array}$$

(12)

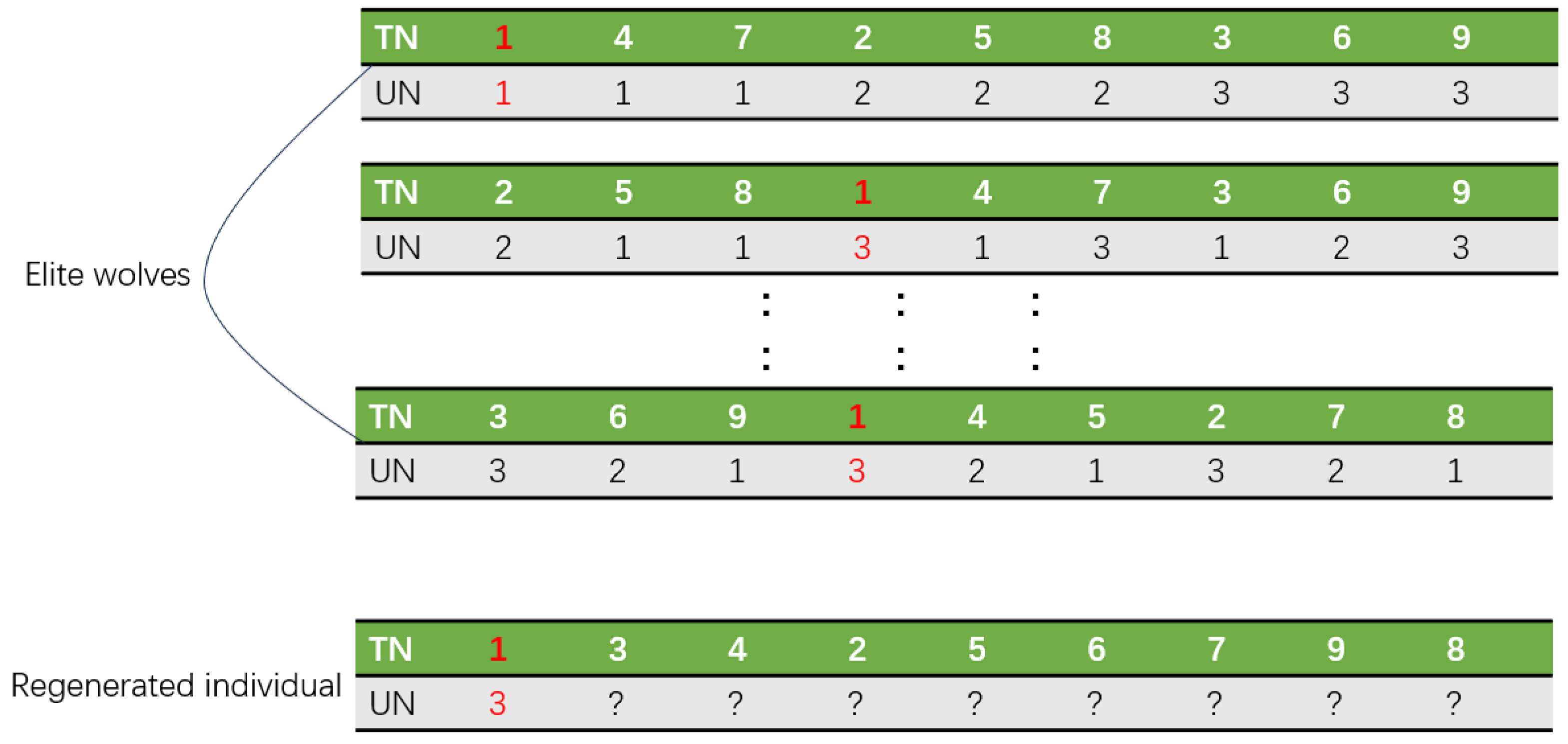
An individual reconstruction based on an elite strategy is proposed in the improved wolf pack updating mechanism. Specifically, the task allocation experiences of the elite wolves (the top 20% of wolves in terms of fitness ranking) will directly influence the results of individual reconstruction. For example, if most elite wolves agree that the first task should be assigned to the fifth UAV, then in the individual reconstruction process, the first task will be assigned to the fifth UAV. By statistically analyzing the task allocation experience of the elite wolves for all tasks, the new individual’s task allocation scheme is determined based on the majority opinion. The specific steps are as follows, and the pseudocode is shown in Algorithm 6.

1. Construct the experience pool. One should traverse the task allocation schemes of all elite wolves and statistically evaluate the allocation results for each task. The statistical result will reveal which UAV the elite wolves prefer for each task. The majority opinion on task allocation within the elite wolf group is considered the potential optimal allocation result for each task and is recorded in the experience pool.

2. Individual Reconstruction. The essence of individual reconstruction is to regenerate the task allocation scheme for the individual to be updated. First, the TN list of the individual to be updated is kept unchanged. Then, each task in the TN list is examined. For each task, allocation experience is retrieved from the experience pool and used to modify the corresponding values in the UN list, thereby completing the reconstruction of the individual.

For example, referring to Figure 5, it can be observed that the majority of elite wolves believe that the first task should be assigned to the third UAV. Therefore, in the individual to be updated, the first task will be assigned to the third UAV.

Algorithm 6: Wolf pack update mechanism

4. Simulation

To validate the performance of the EWPA-PT algorithm, this section selects the PSO algorithm [21], the well-performing EPPSO algorithm [11] among particle swarm optimization variants, and the MDWPA [16] and MPPWPA [17] algorithms, which are both noted for their performance in wolf pack optimization. These algorithms are all evaluated based on the MTAMCC model, with each being run 50 times to derive various experimental results.

In the experimental section, this paper standardizes the parameters across the above algorithms. The parameters for the PSO algorithm are set according to the original literature, as detailed in

Table 2. EPPSO algorithm parameter settings.

Parameter	Value
Number of individuals	N = 100
Inertia weight	${\omega }_{ini}$ = 0.9, ${\omega }_{end}$ = 0.4
Cognitive acceleration coefficient	$c_{1ini}$ = 2.5, $c_{1end}$ = 0.5
Social acceleration coefficient	$c_{2ini}$ = 0.5, $c_{2end}$ = 2.5
Size of experience pool	expsize = 20
Mutation probability of refactoring operations	$P_m$ = 0.01
Velocity limit	$V_{ini}:60\%$ of the searching space
	$V_{end}:60\%$ of the searching space
Maximum number of iterations	Iter = 800

. The parameters of the wolf pack algorithm are kept consistent, as detailed in

Table 3. Wolf pack algorithm parameter settings.

Parameter	Value
Number of individuals	N = 100
Maximum number of iterations	Iter = 800
Detective wolf factor	a = 4
Update factor	b = 7
Temperature	T = 100
Cooling coefficient	down = 0.125

.

To ensure the randomness of the experiment, the initialization process of individuals is performed randomly. Additionally, the positions of the launch platforms, the positions of the target points, and the sizes of the target points are all randomly generated within specified ranges. This approach ensures that the algorithm can handle various scenarios within the predefined environment.

The experiment was conducted using PyCharm IDE, with an Intel(R) Core(TM) i5-13500H processor running at a clock speed of 2.60 GHz.

4.1. Experiments Comparing Different Target Quantities

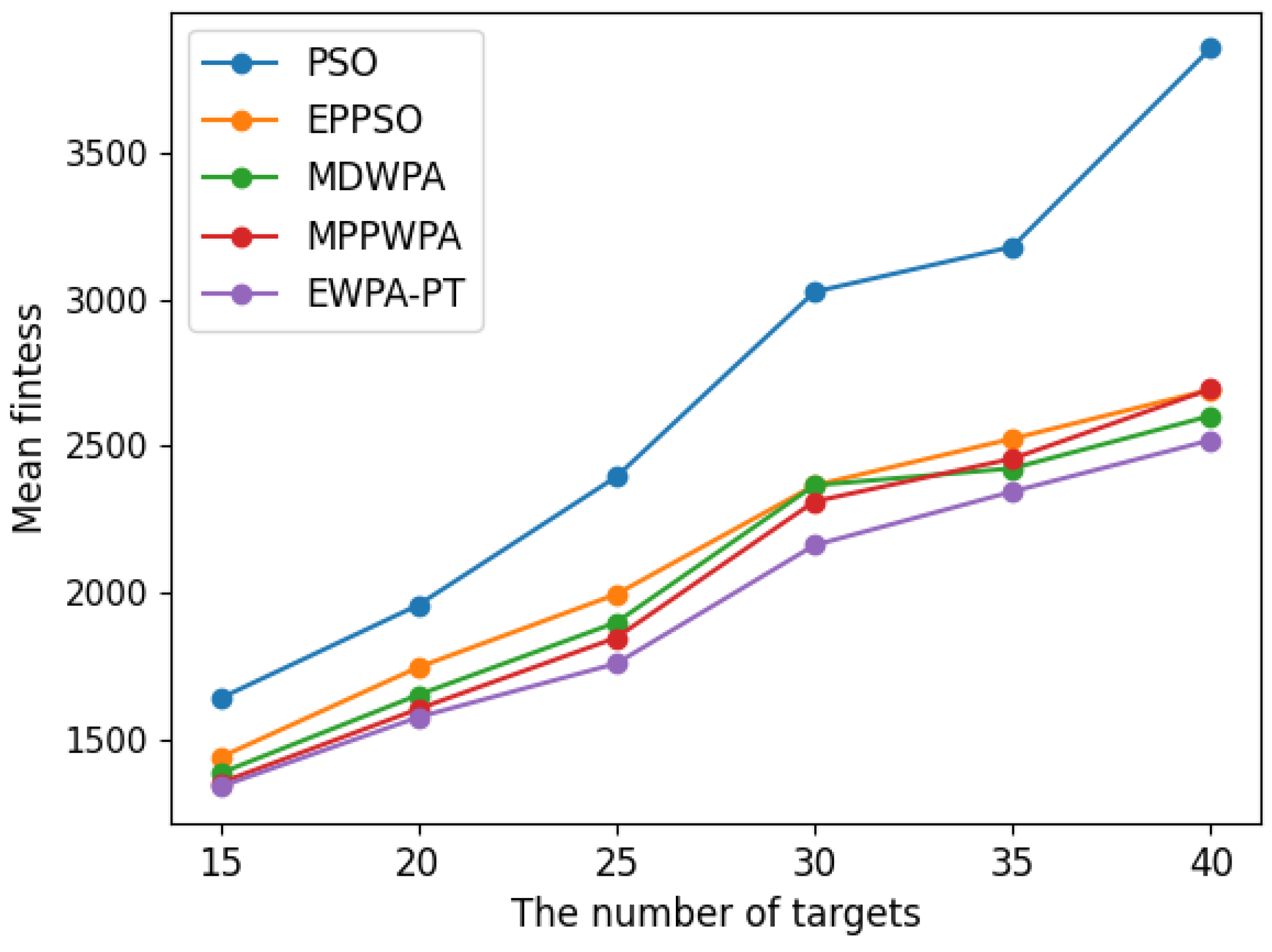
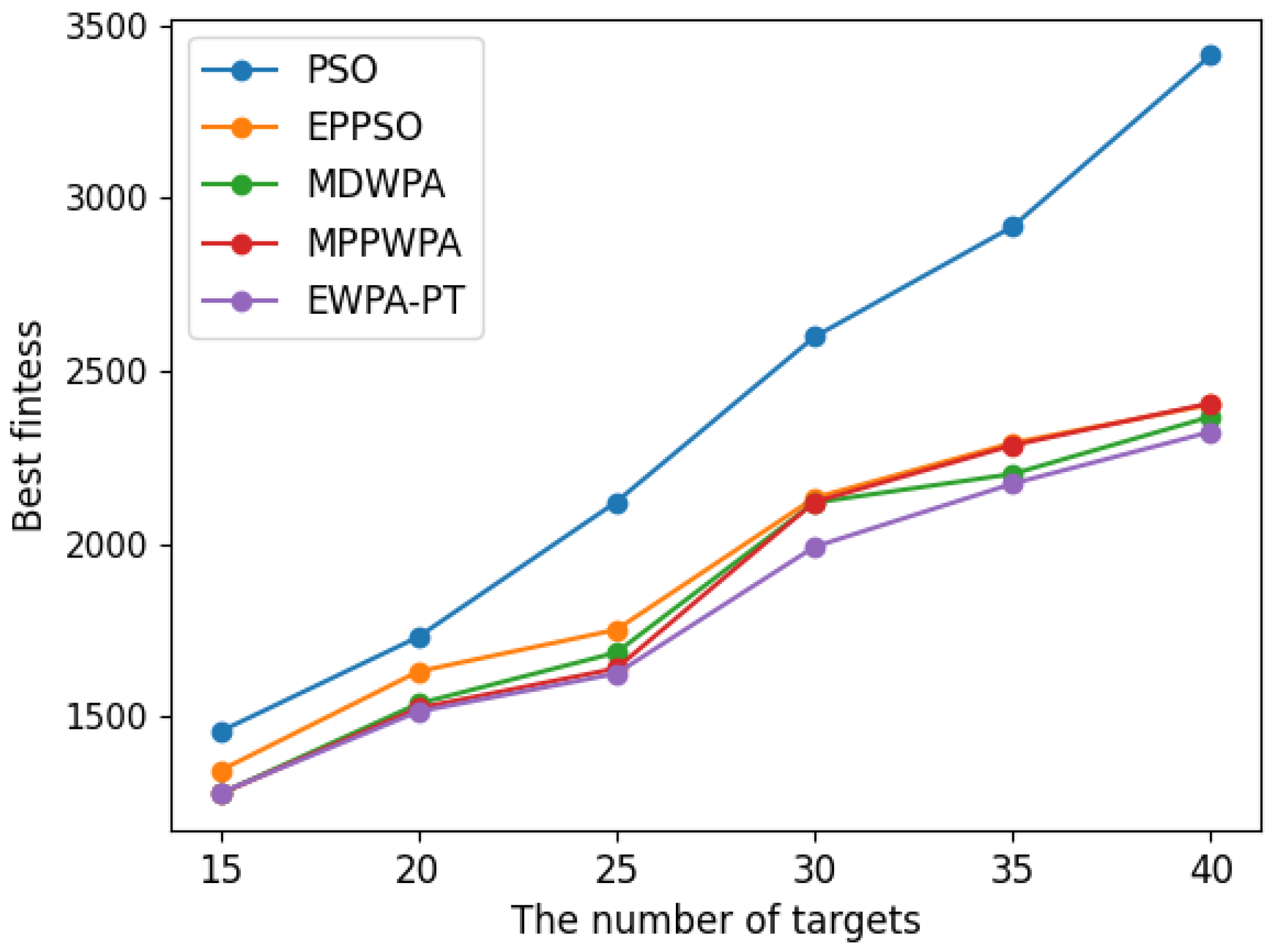
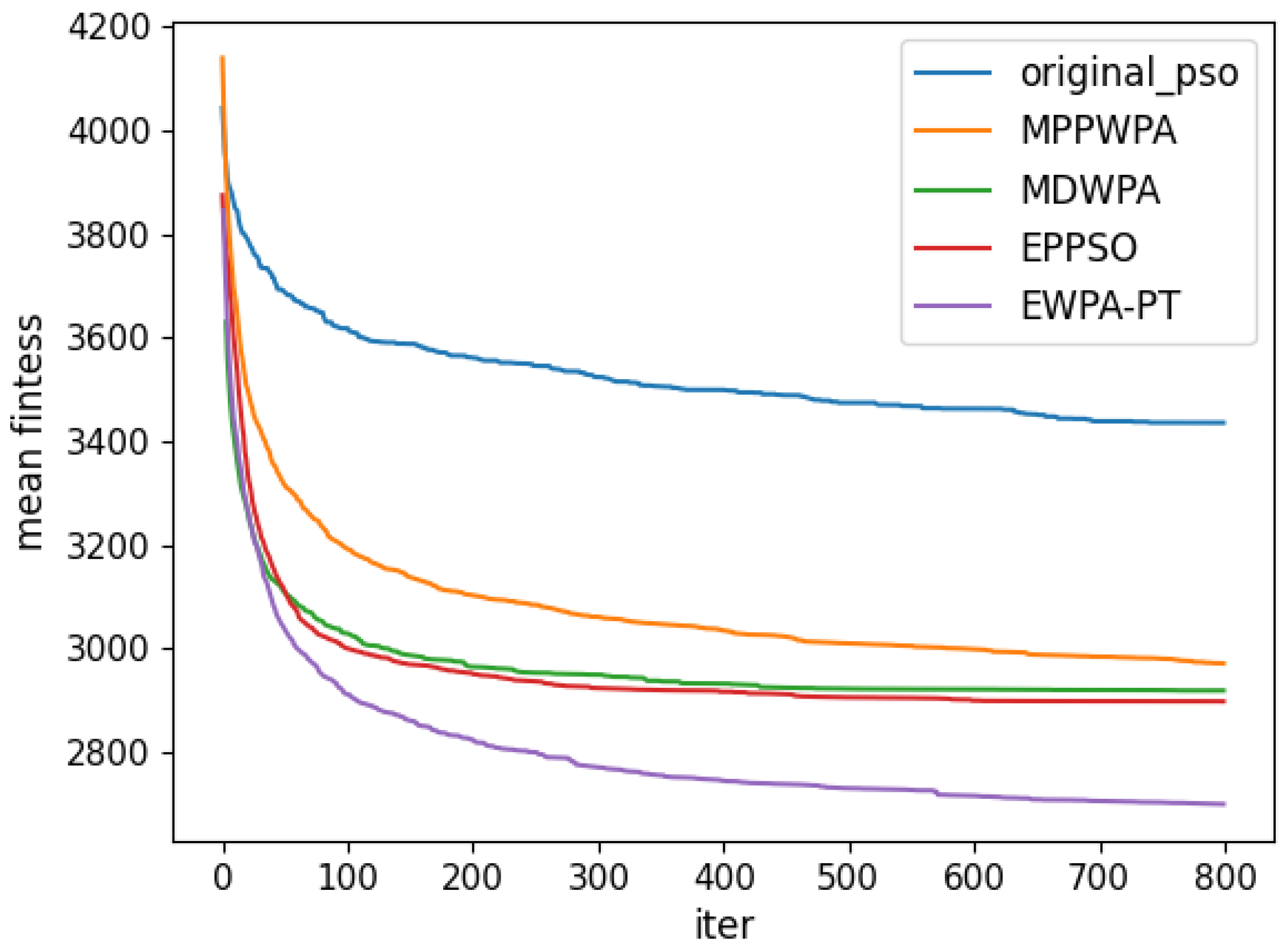
In multi-UAV task assignment models, the number of tasks directly determines the search dimension of the solution space. A higher dimension makes it more challenging to optimize the best solution. In the experiment, the number of UAVs is fixed at $Nu=10$, and the number of tasks $Nt$ varies as 15, 20, 25, 30, 35, and 40. 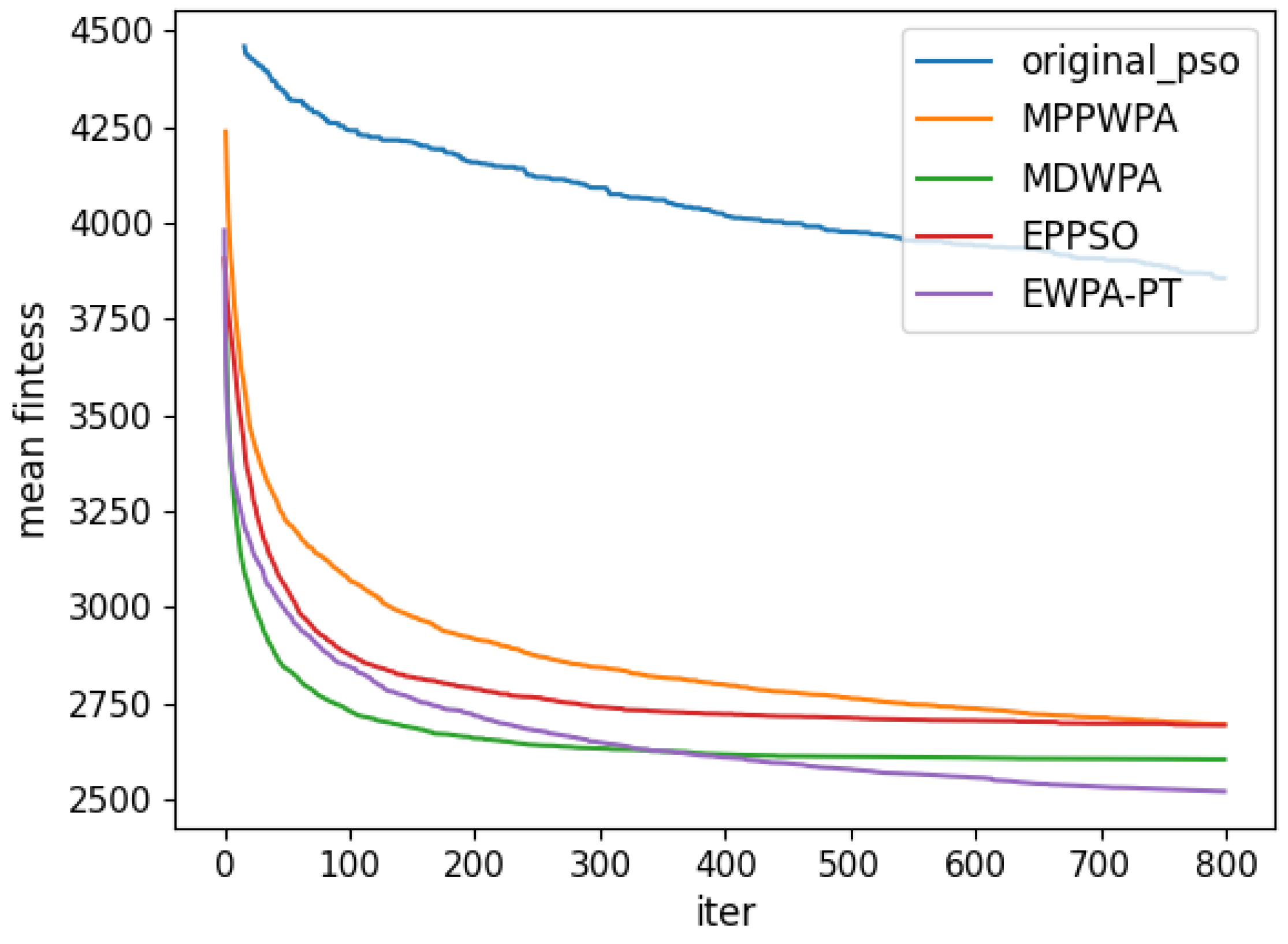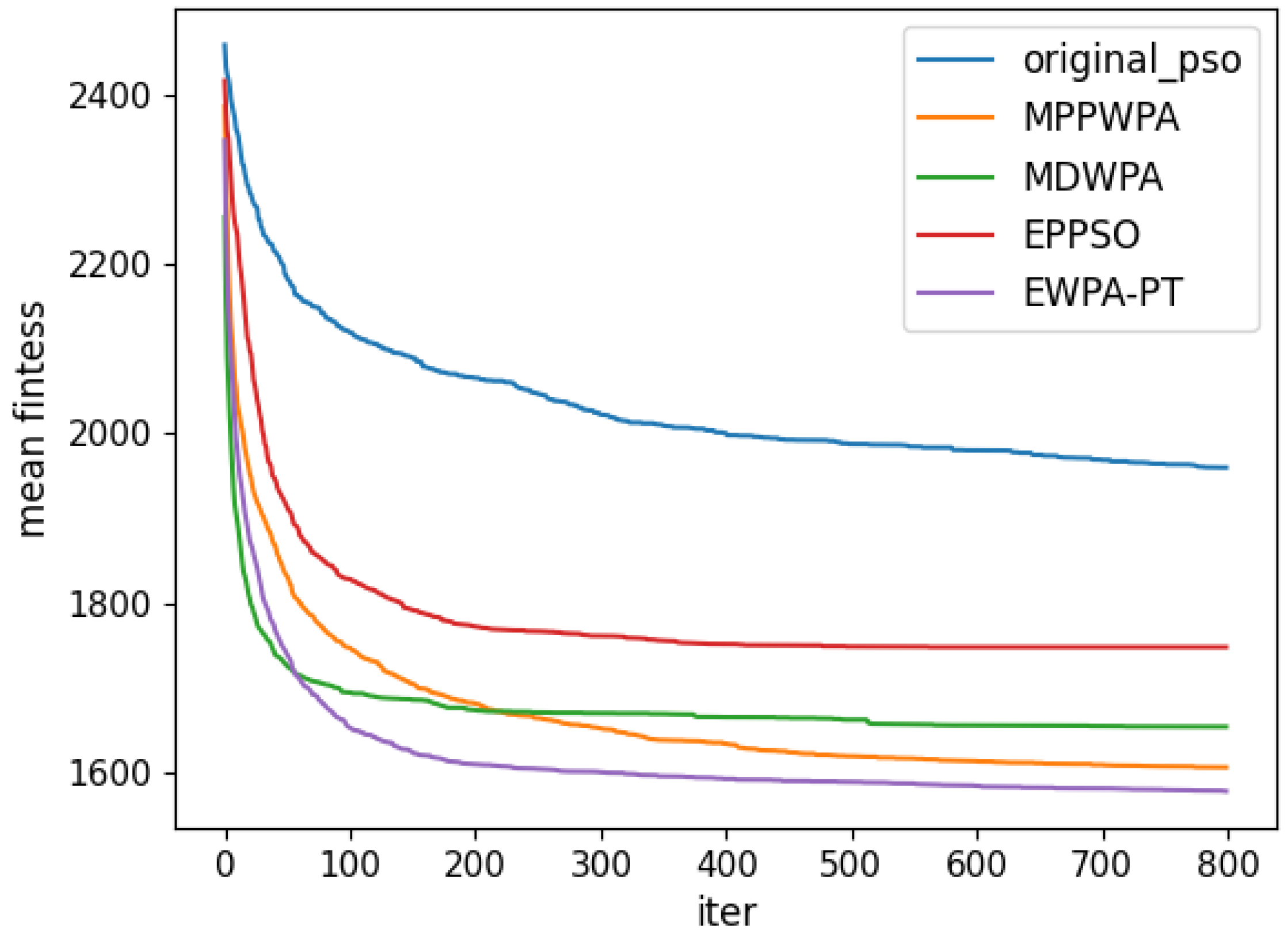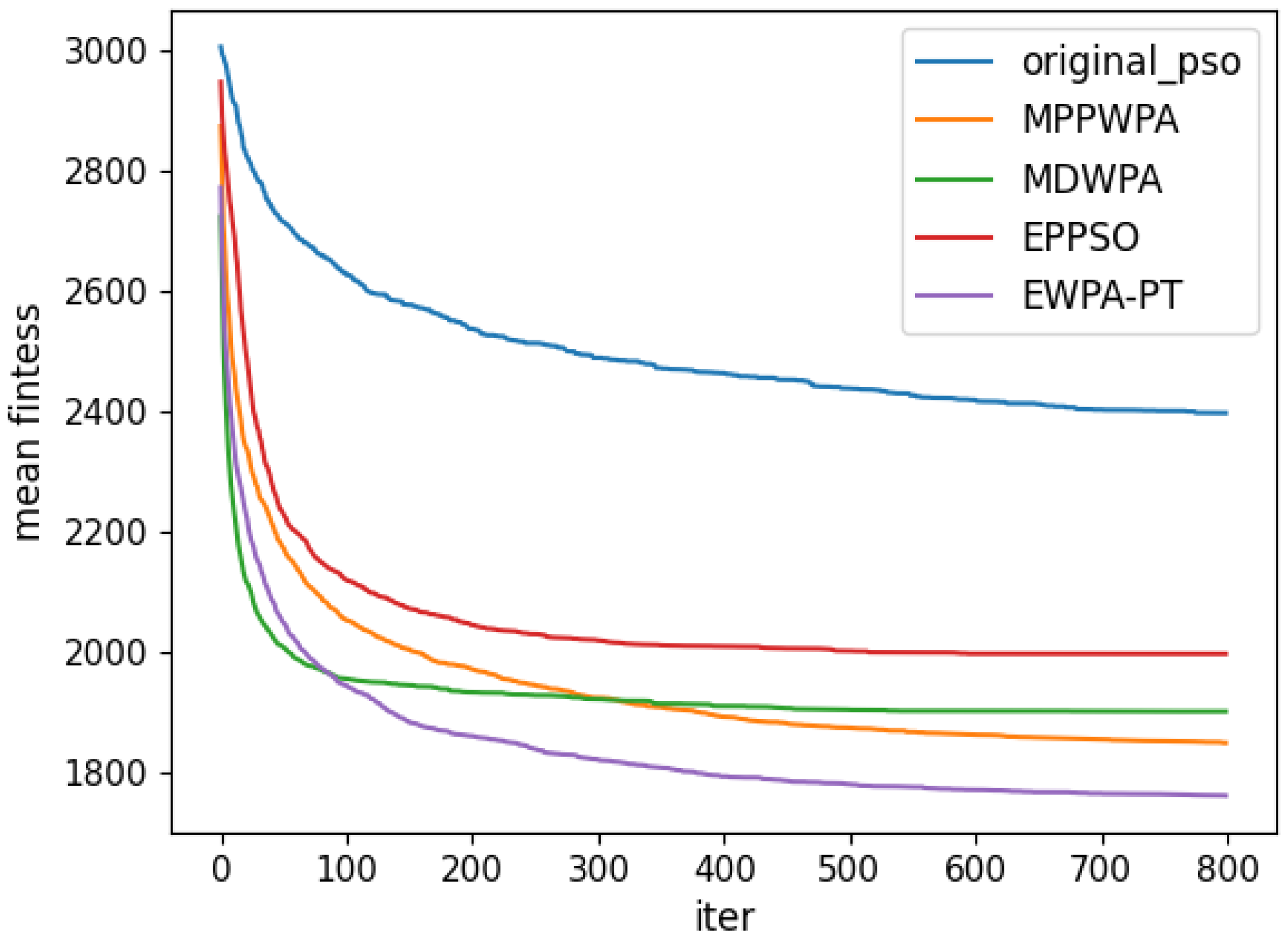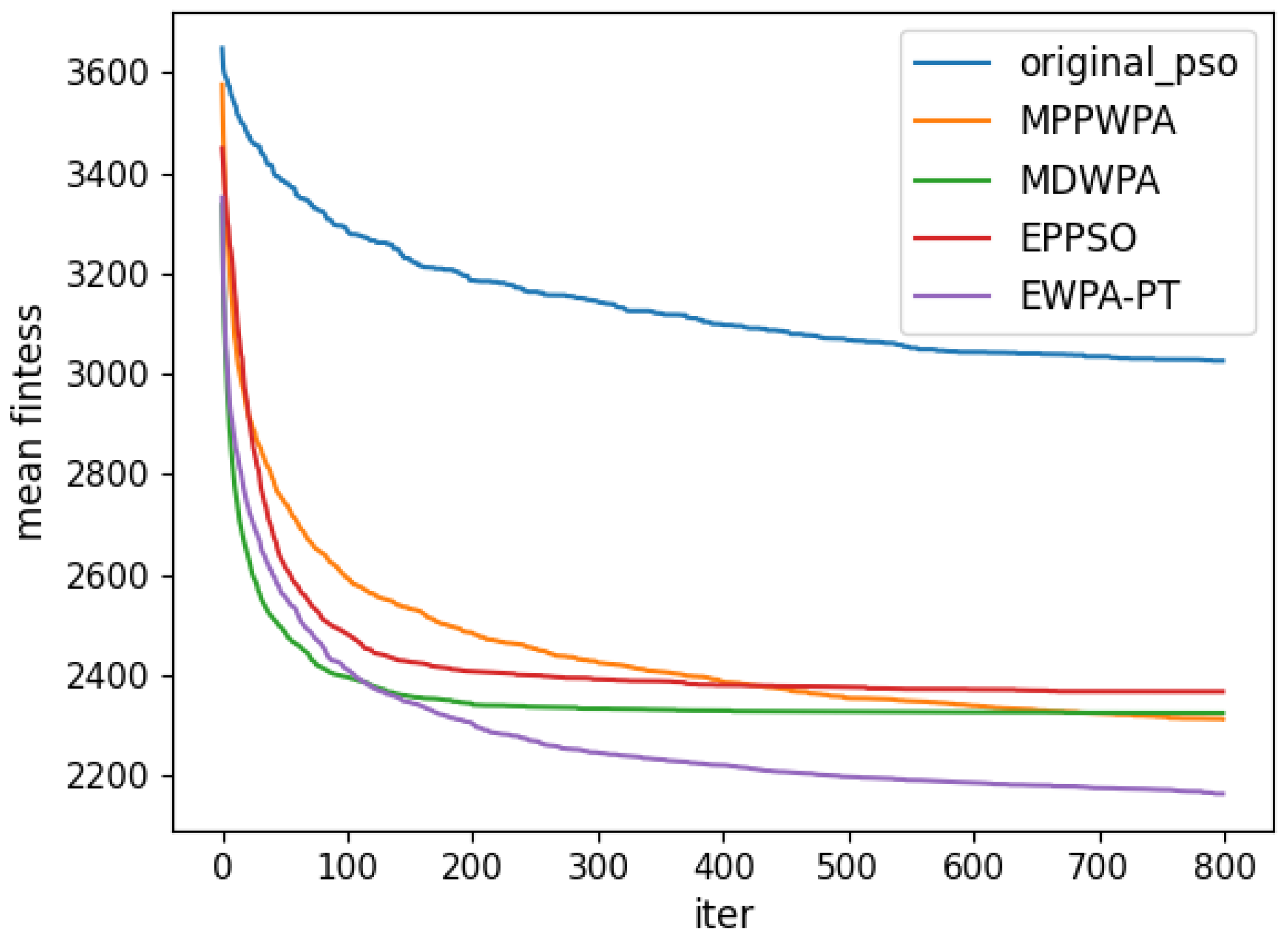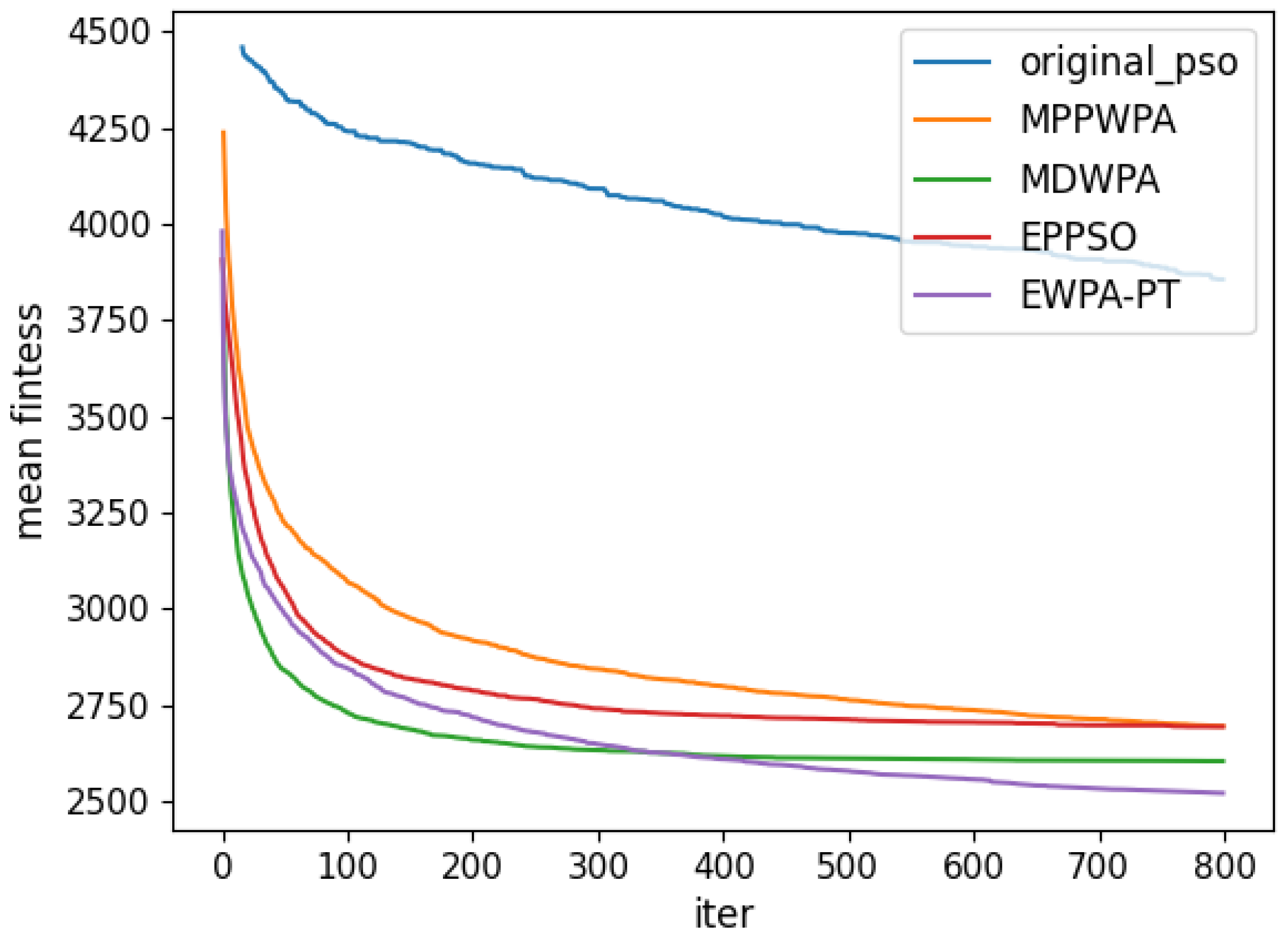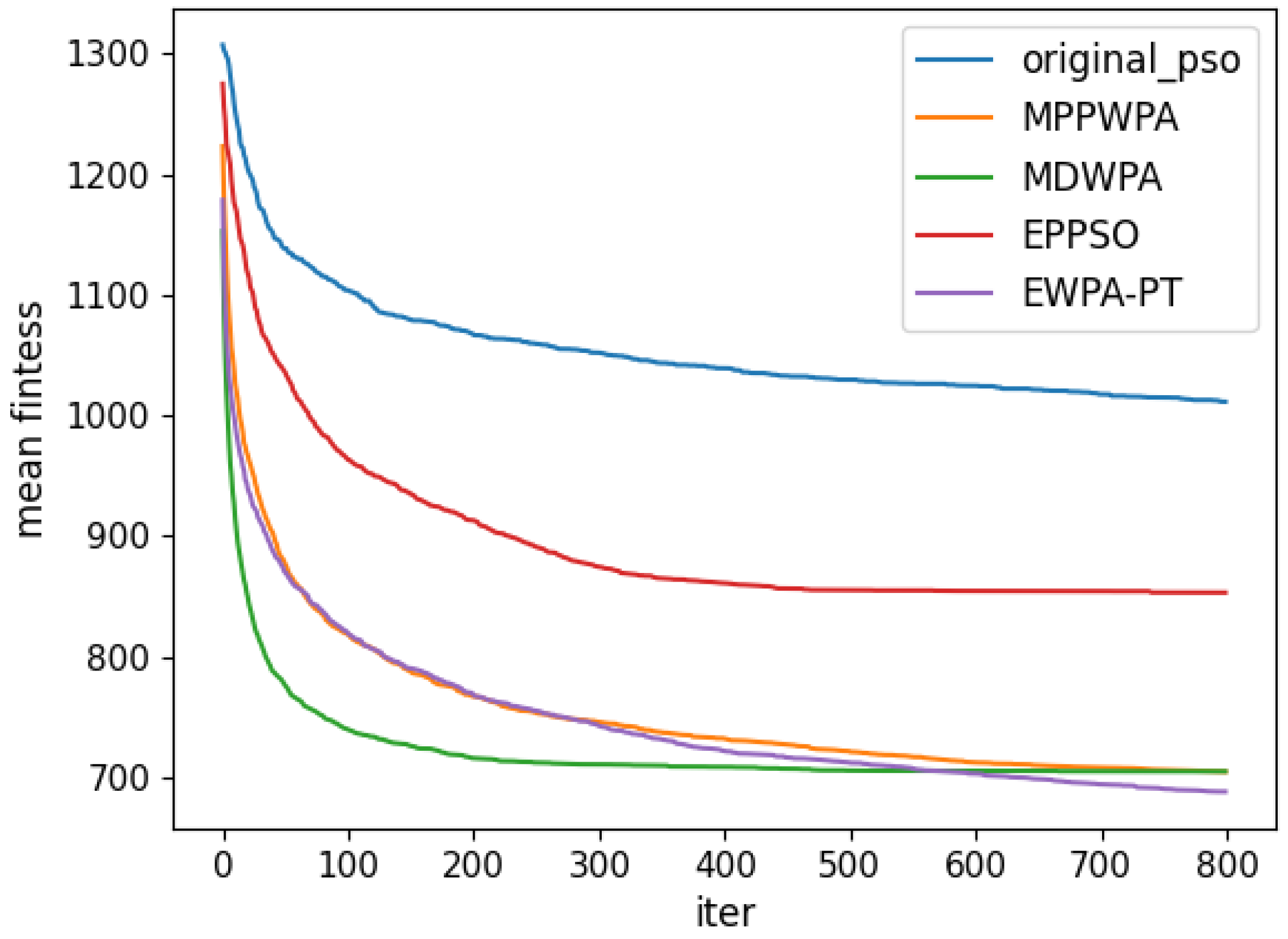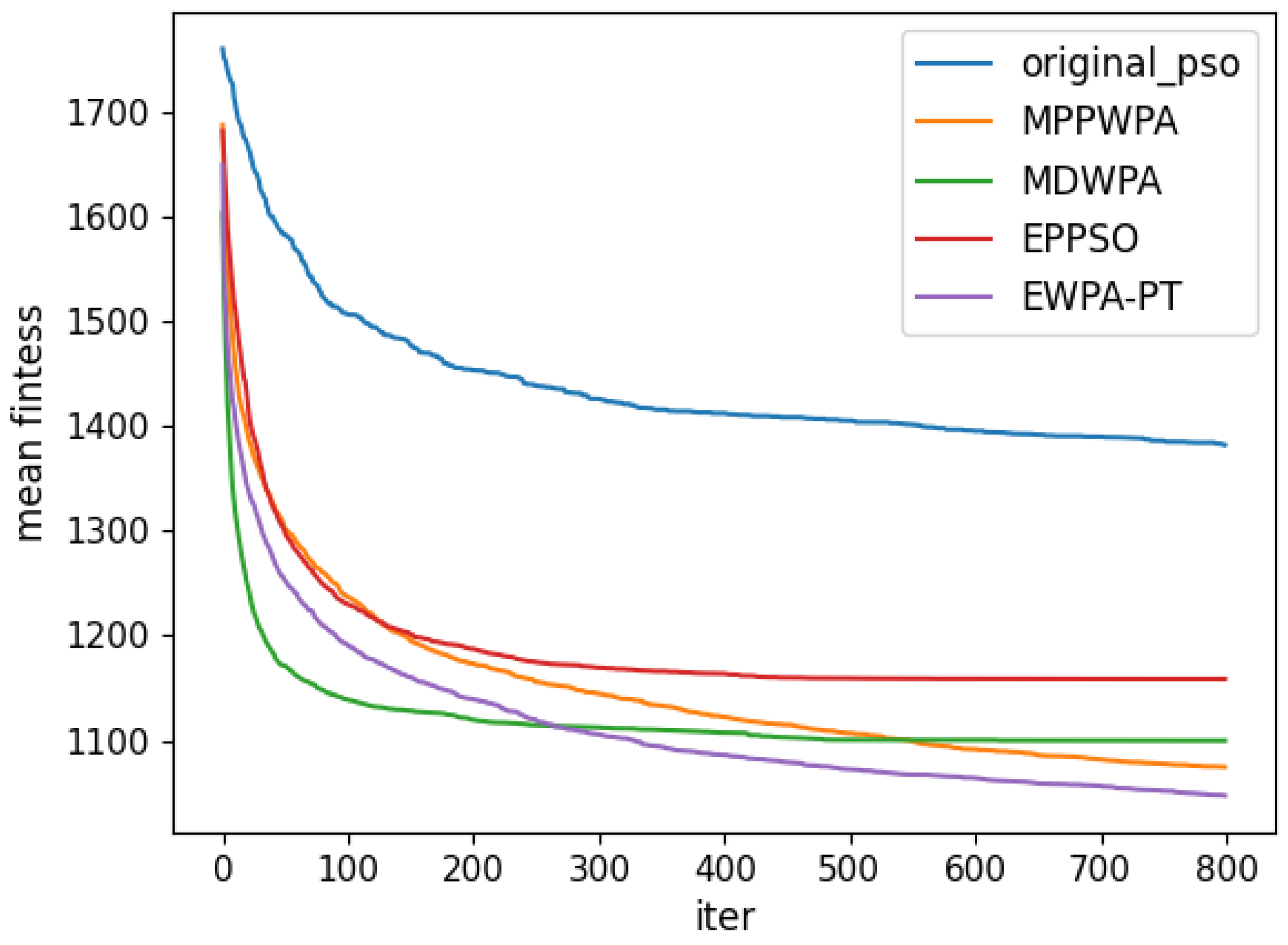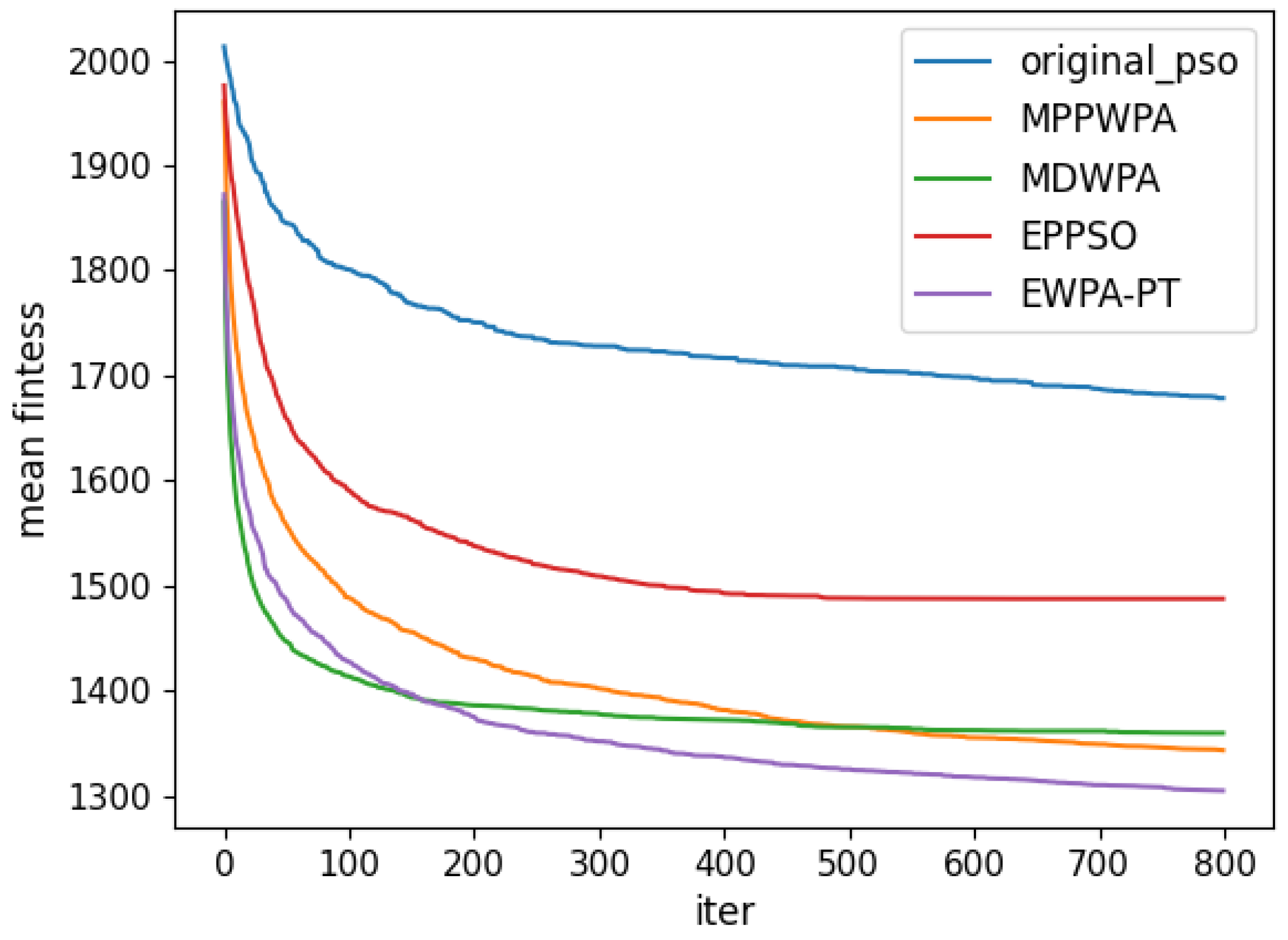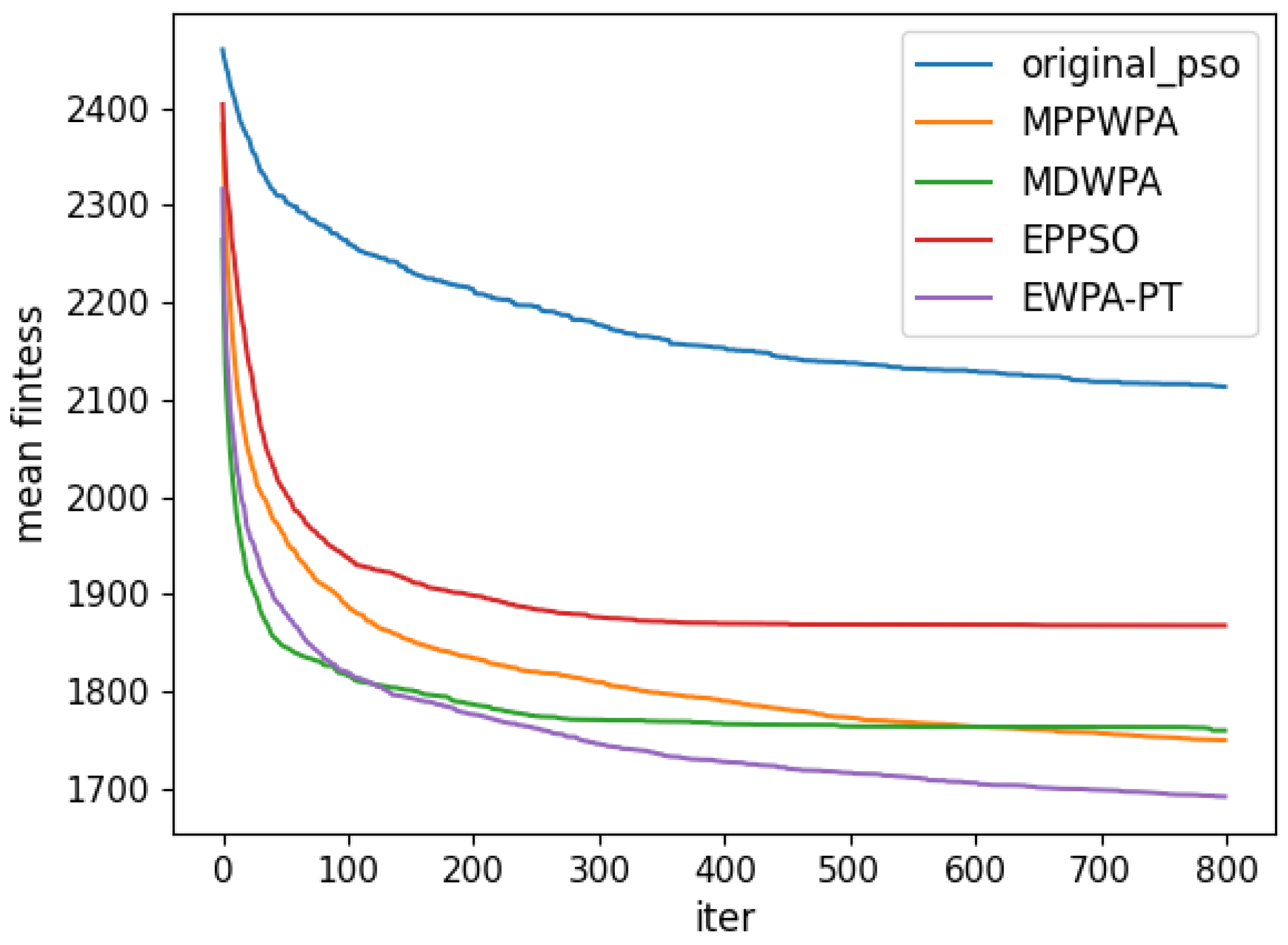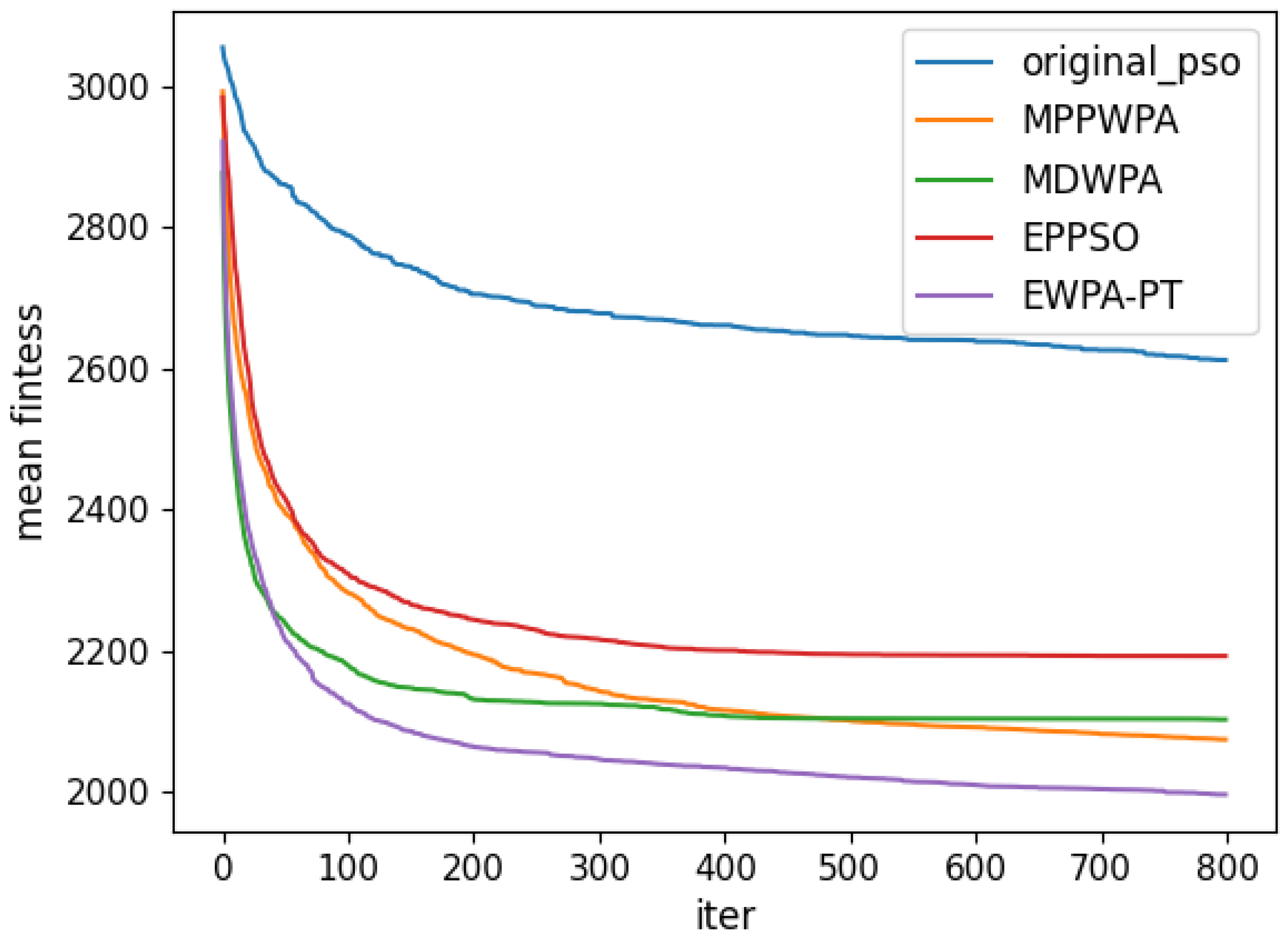To ensure the randomness of the experiments, the initial position of the UAVs is randomly generated within the range $[0,100]$ for both x and y coordinates, while the target points are randomly generated within the range $[100,300]$ for both x and y coordinates. The target distance is generated within the range of 1 to 5 km. Each algorithm is run 50 times. In the experiment, the X coordinate represents the number of iterations, and the Y coordinate represents the average fitness value obtained from 50 repeated runs at iteration X. 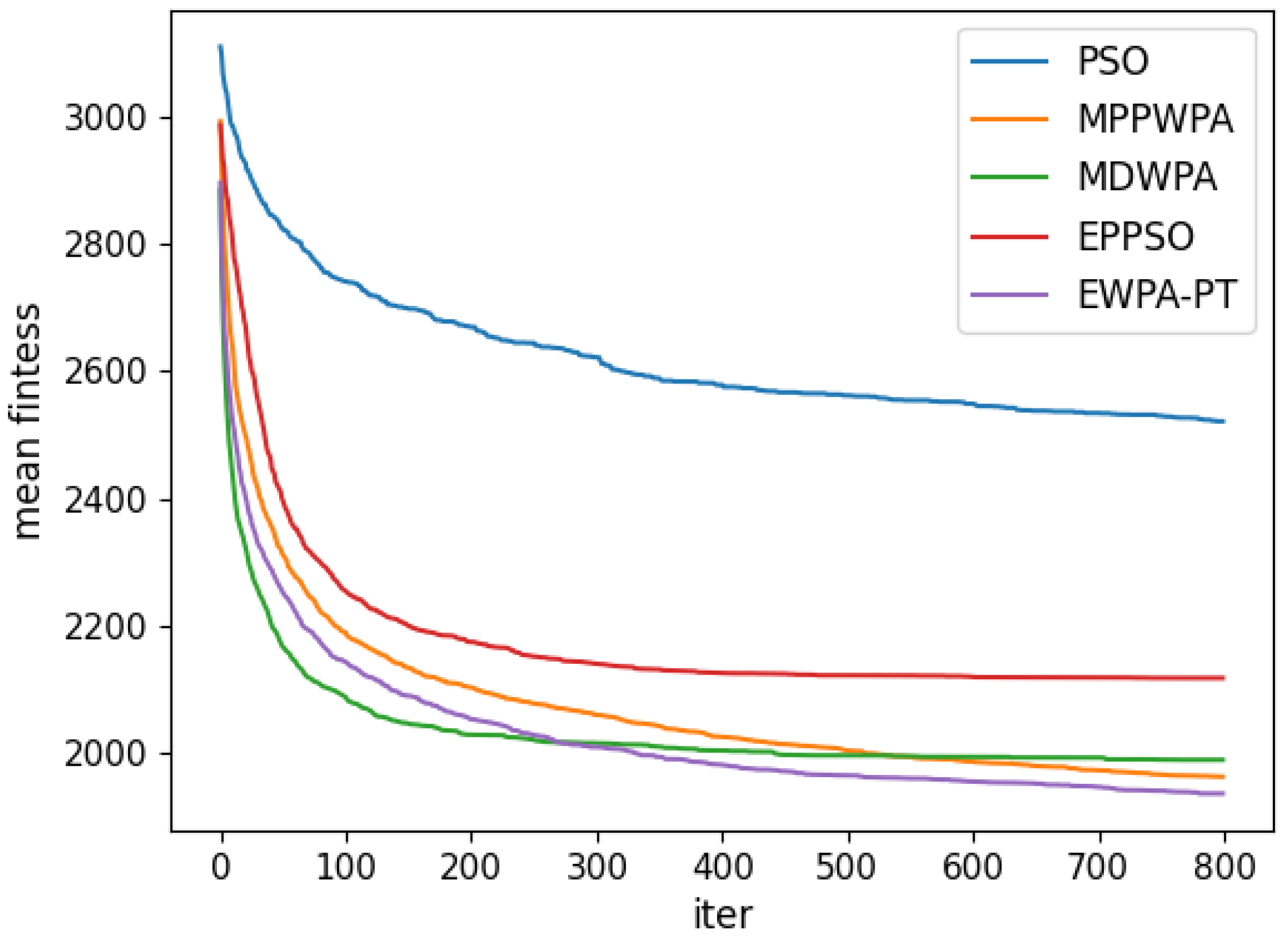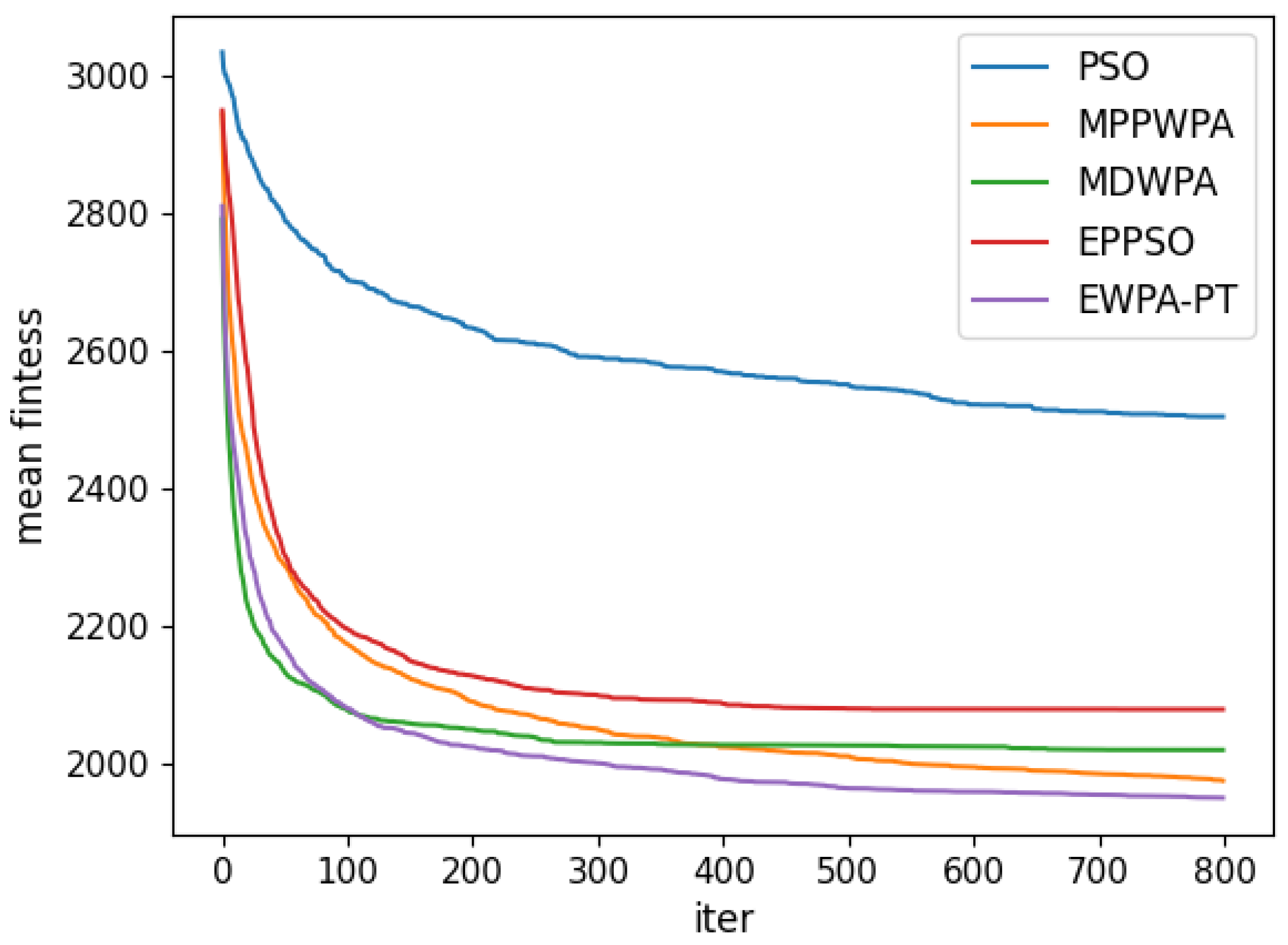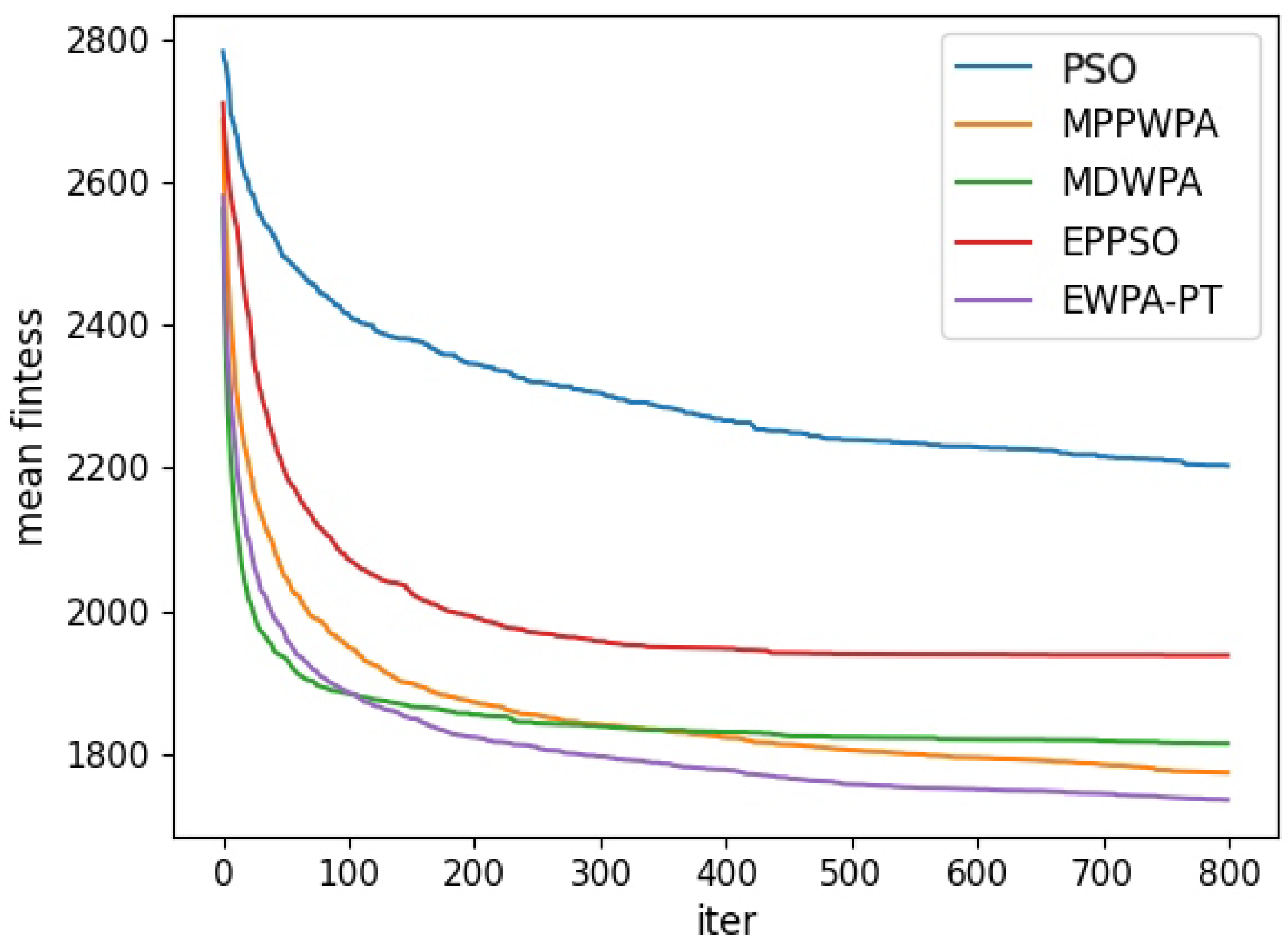The comparison results are illustrated in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 and

Table 4. Comparative experiments with different numbers of targets.

Algorithm	Criteria	15	20	25	30	35	40
PSO	Best fitness	1456	1730	2121	2599	2918	3414
	Average fitness	1641	1959	2396	3026	3180	3856
EPPSO	Best fitness	1343	1630	1751	2133	2292	2403
	Average fitness	1440	1747	1996	2367	2526	2693
MDWPA	Best fitness	1276	1537	1685	2119	2202	2368
	Average fitness	1386	1653	1900	2367	2425	2604
MPPWPA	Best fitness	1276	1524	1639	2121	2285	2407
	Average fitness	1353	1605	1848	2312	2458	2695
EWPA-PT	Best fitness	1278	1514	1624	1991	2174	2324
	Average fitness	1340	1577	1760	2163	2346	2521

.

When the number of UAVs is fixed, as the number of targets increases, the solution dimension will also increase, leading to a significant increase in the complexity of task assignments. From the comparison results, we can observe that the EWPA-PT algorithm demonstrates a precision advantage, and as the solution dimension increases, this algorithm’s precision advantage becomes more evident. This is because the improved sieging behavior enables multi-point optimization, greatly enhancing the algorithm’s ability to escape local optima. Additionally, as the number of tasks increases, the order in which UAVs perform tasks significantly impacts the assignment results. The enhanced wandering behavior enables better optimization of task execution order, thereby improving the accuracy of the final solution.

4.2. Experiments Comparing Different Target Locations

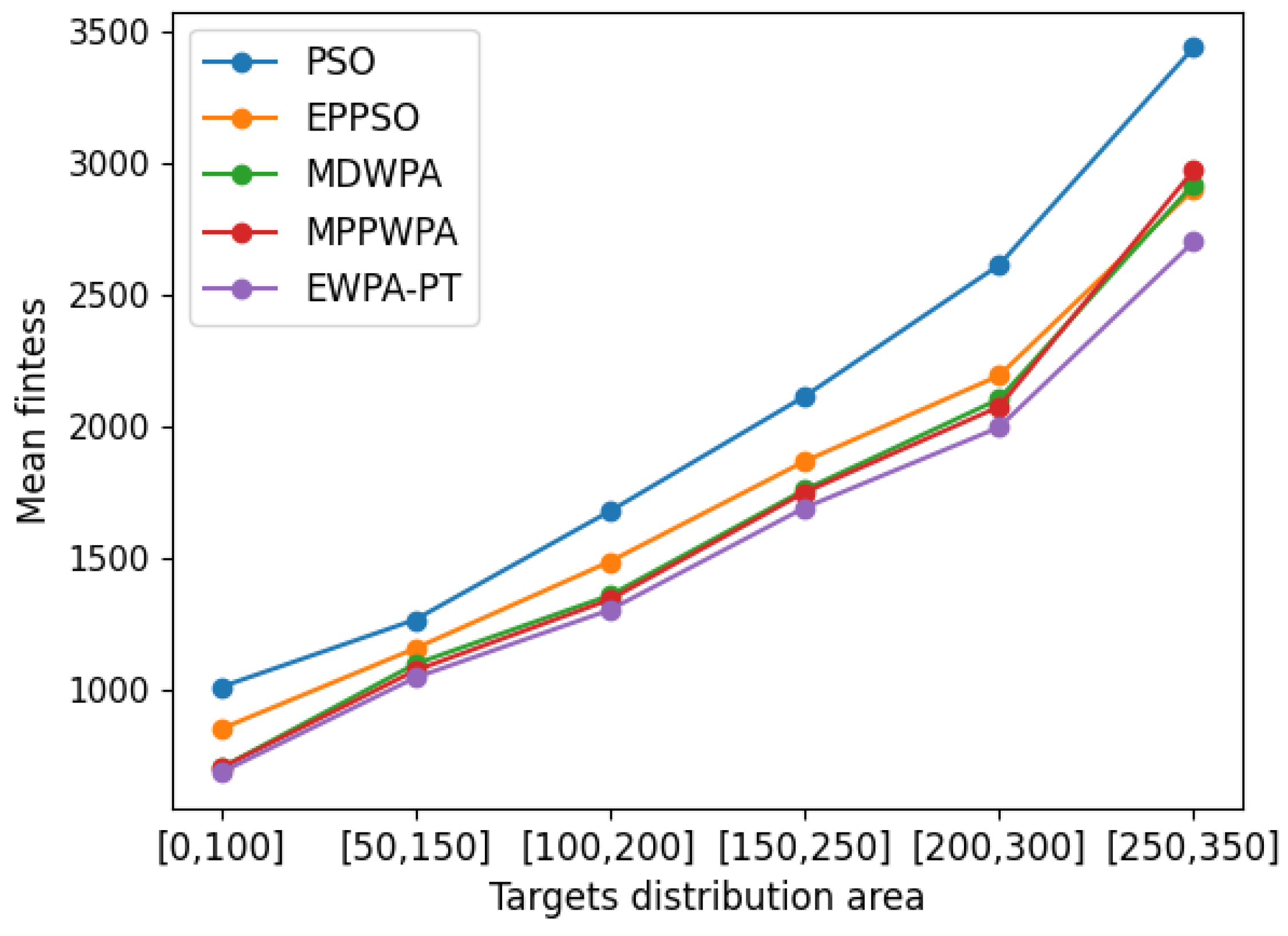
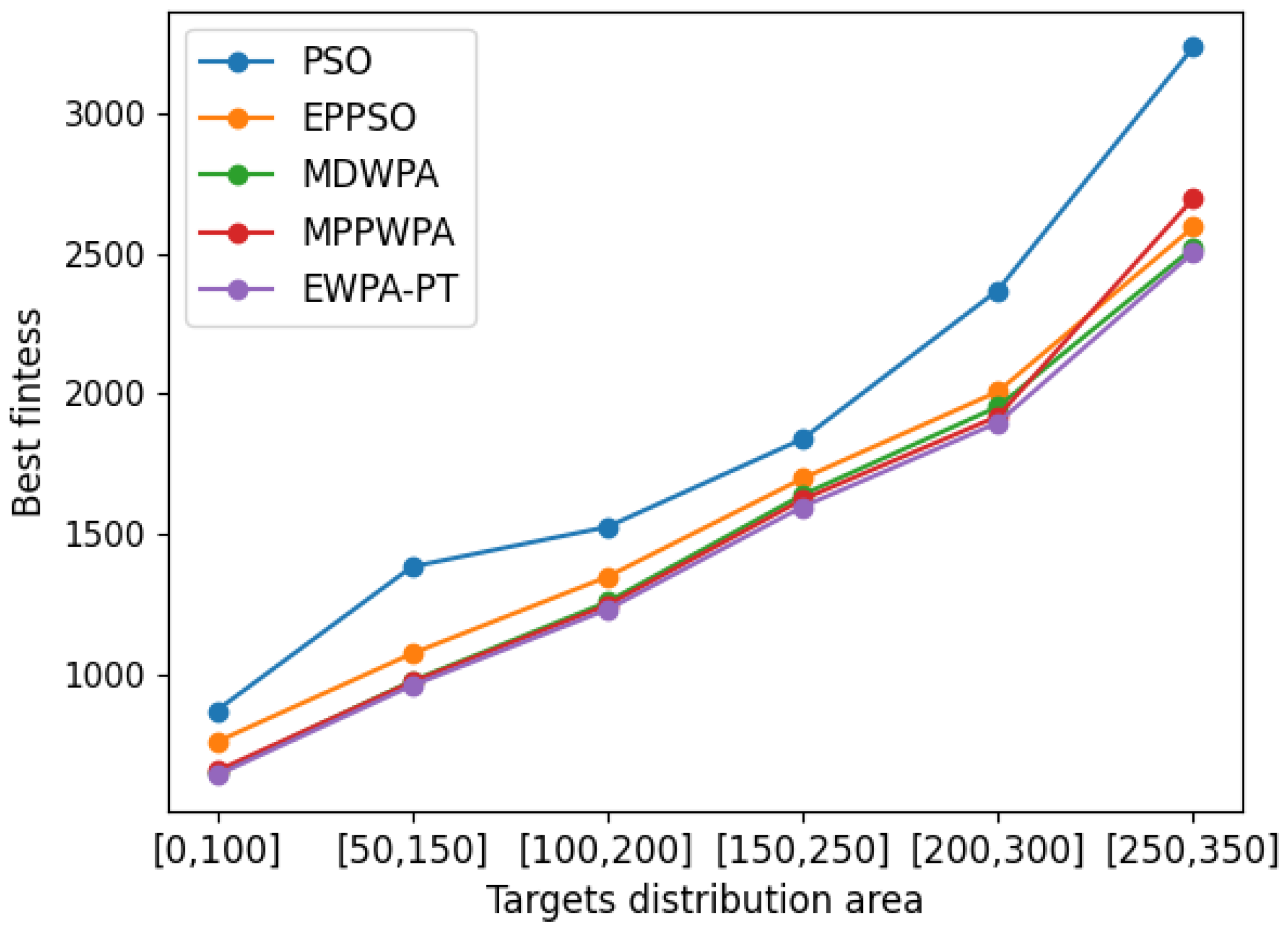
In the multi-UAV task assignment problem, the targets’ location directly impacts the UAVs’ fuel consumption and the time it takes to complete reconnaissance tasks. Furthermore, as the distance between targets and UAVs increases, the influence of constrained conditions during algorithm iterations also increases, making it more challenging to find optimal solutions with the algorithm. To verify the performance of the EWPA-PT algorithm, the number of targets is fixed at $NT=30$. The target distance is randomly generated within the range of 1 to 5 km. The target locations are divided into the following:

$$\begin{array}{cc}& [0,100]\times [0,100],[50,150]\times [50,150],\hfill \\ & [100,200]\times [100,200],[150,250]\times [150,250],\hfill \\ & [200,300]\times [200,300],[250,350]\times [250,350].\hfill \end{array}$$

Each algorithm is run 50 times. In the experiment, the X coordinate represents the number of iterations, and the Y coordinate represents the average fitness value obtained from 50 repeated runs at iteration X. The comparison results are illustrated in Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 and

Table 5. Comparative experiments with different target positions.

Algorithm	Criteria	15	20	25	30	35	40
PSO	Best fitness	869	1382	1524	1838	2369	3236
	Average fitness	1011	1267	1678	2113	2611	3436
EPPSO	Best fitness	757	1072	1346	1697	2007	2594
	Average fitness	852	1158	1487	1867	2192	2898
MDWPA	Best fitness	646	974	1256	1639	1953	2520
	Average fitness	704	1099	1359	1759	2103	2919
MPPWPA	Best fitness	653	971	1245	1622	1919	2696
	Average fitness	704	1074	1343	1749	2074	2971
EWPA-PT	Best fitness	638	958	1229	1596	1896	2503
	Average fitness	687	1047	1304	1691	1996	2700

.

When the number of task points remains fixed, the impact of constraints becomes increasingly important as the distance between task points and UAV launch platforms continues to increase. As shown in the comparison results, the EWPA-PT algorithm demonstrates certain advantages in solution accuracy under different task distribution scenarios. This is partly due to the novel individual reconstruction mechanism, which enhances the algorithm’s effective search space. Furthermore, as the distance between target points and departure points increases, there is a greater demand for optimizing the sequence of UAV task execution. The improved wandering behavior effectively addresses this issue, resulting in superior solution accuracy when task points are distributed across different regions.

4.3. Algorithm Stability Experiments

In the study of swarm intelligence algorithms, the stability and performance of the algorithms are influenced by various factors, with population size being a critical one. The size of the population can significantly affect the algorithm’s optimization ability and robustness. In the experiments, there were 10 UAVs and 25 tasks to be allocated, with fixed positions for the UAVs and target points, as detailed in

Table 6. Target attribution.

Targets	Location	Radius (km)
Targets1	(175.122, 293.220)	4.475
Targets2	(282.096, 214.658)	1.001
Targets3	(110.518, 209.367)	4.696
Targets4	(232.619, 289.573)	1.773
Targets5	(134.394, 212.129)	3.097
Targets6	(218.309, 158.736)	2.989
Targets7	(129.216, 178.339)	3.358
Targets8	(202.855, 291.466)	2.095
Targets9	(138.990, 151.092)	4.388
Targets10	(291.157, 251.372)	2.421
Targets11	(216.578, 118.050)	2.960
Targets12	(226.443, 245.922)	3.780
Targets13	(181.193, 296.027)	1.844
Targets14	(111.091, 213.164)	3.651
Targets15	(213.639, 228.066)	3.014
Targets16	(146.839, 195.993)	4.830
Targets17	(229.860, 264.698)	1.234
Targets18	(212.137, 202.245)	4.037
Targets19	(272.106, 160.008)	1.453
Targets20	(180.013, 116.216)	3.172
Targets21	(272.344, 204.400)	1.071
Targets22	(195.327, 121.874)	2.469
Targets23	(195.723, 223.340)	1.033
Targets24	(274.388, 293.648)	1.231
Targets25	(281.683, 263.907)	2.691

and

Table 7. UAV attribution.

UAVs	Location	Flight Speed (km/s)	Maximum Flight Range (km)
UAV1	(22.067, 30.579)	0.22	1000
UAV2	(22.067, 30.579)	0.18	1200
UAV3	(22.067, 30.579)	0.16	1500
UAV4	(80.365, 88.720)	0.22	1000
UAV5	(80.365, 88.720)	0.18	1200
UAV6	(80.365, 88.720)	0.16	1500
UAV7	(15.933, 24.293)	0.22	1000
UAV8	(15.933, 24.293)	0.30	800
UAV9	(75.097, 32.661)	0.18	1200
UAV10	(75.097, 32.661)	0.30	800

. The population sizes were set at 20, 40, 60, and 80. The experiments were repeated 50 times, and the results are presented in Figure 22, Figure 23, Figure 24 and Figure 25.

The experimental results indicate that regardless of variations in population size, the EWPA-PT algorithm consistently maintained superior solution accuracy, thereby demonstrating the algorithm’s stability and adaptability.

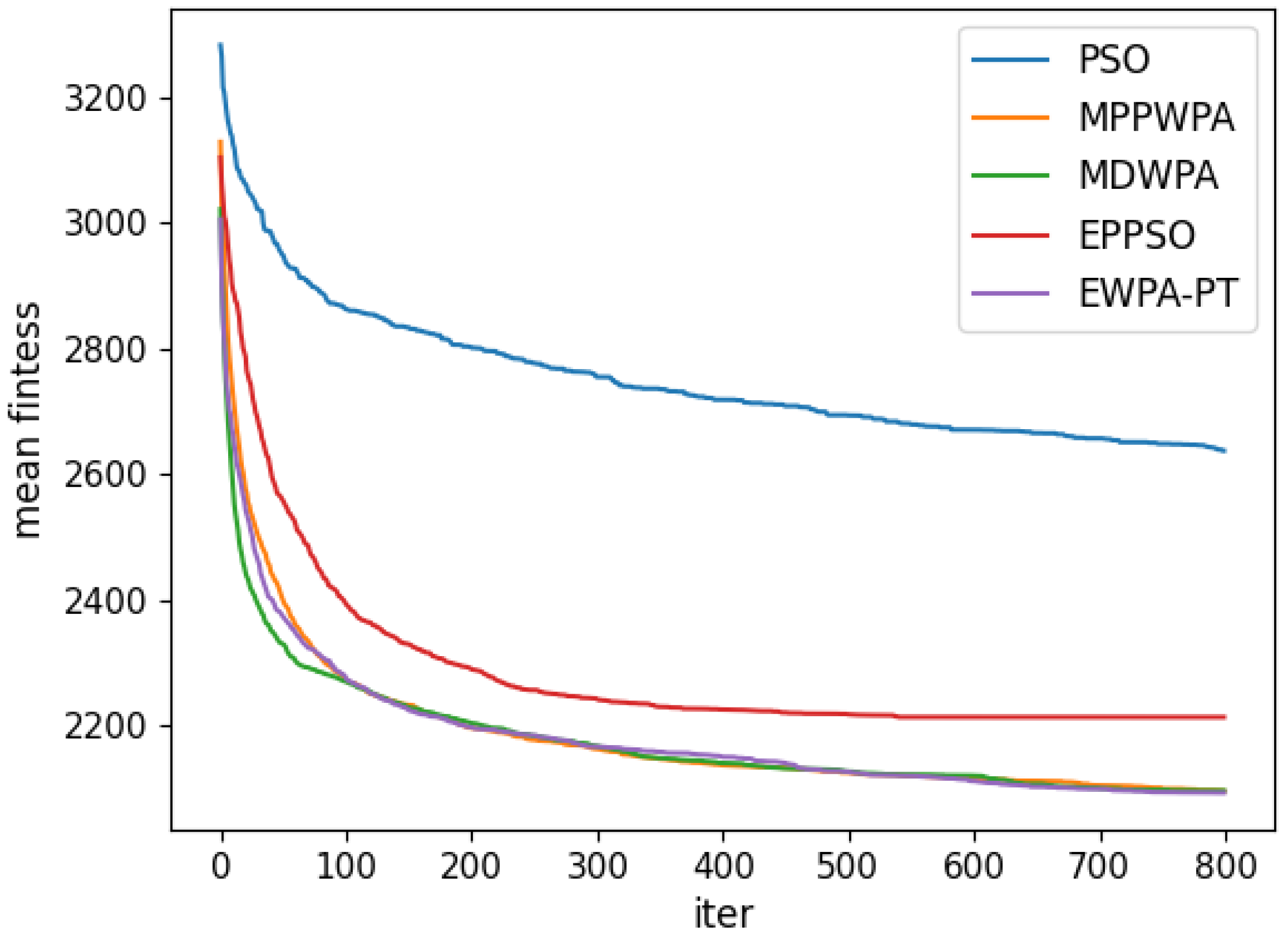
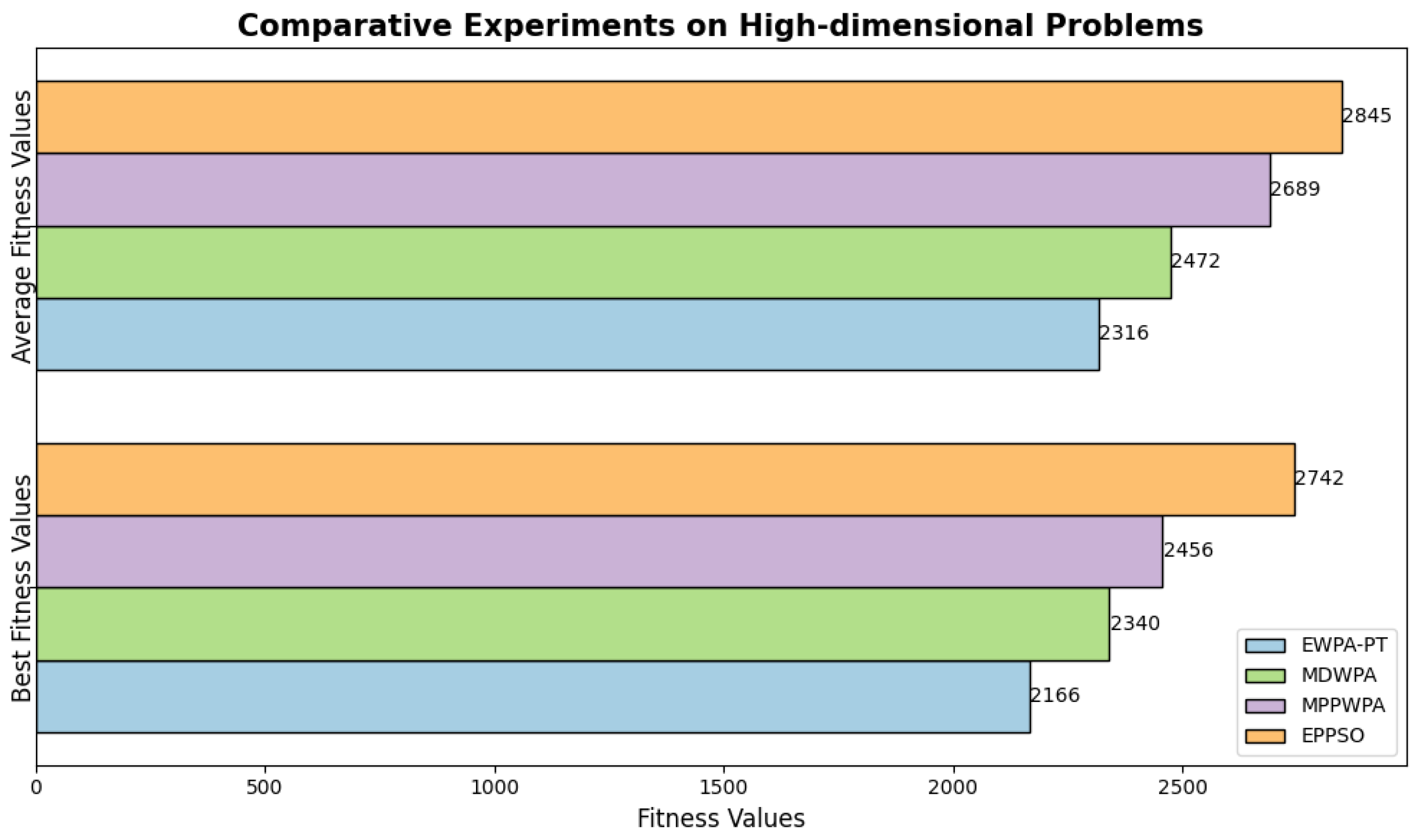
4.4. Comparative Experiments on High-Dimensional Problems

In this section, we present a comparative experiment to evaluate the EWPA-PT algorithm’s performance in solving high-dimensional optimization problems. In the experiment, the number of UAVs was set to 25, and the number of tasks was set to 100. Each algorithm was run 50 times to obtain the data. The results are shown in Figure 26.

The experimental results show that the EWPA-PT algorithm withstood the challenges of solving high-dimensional problems. It not only demonstrates an advantage in solution accuracy for low-dimensional problems but also maintains a good level of accuracy when handling high-dimensional problems. Therefore, it can be concluded that the EWPA-PT algorithm is suitable for application in high-dimensional complex environments.

4.5. Ablation Experiment of the Algorithm Parameters

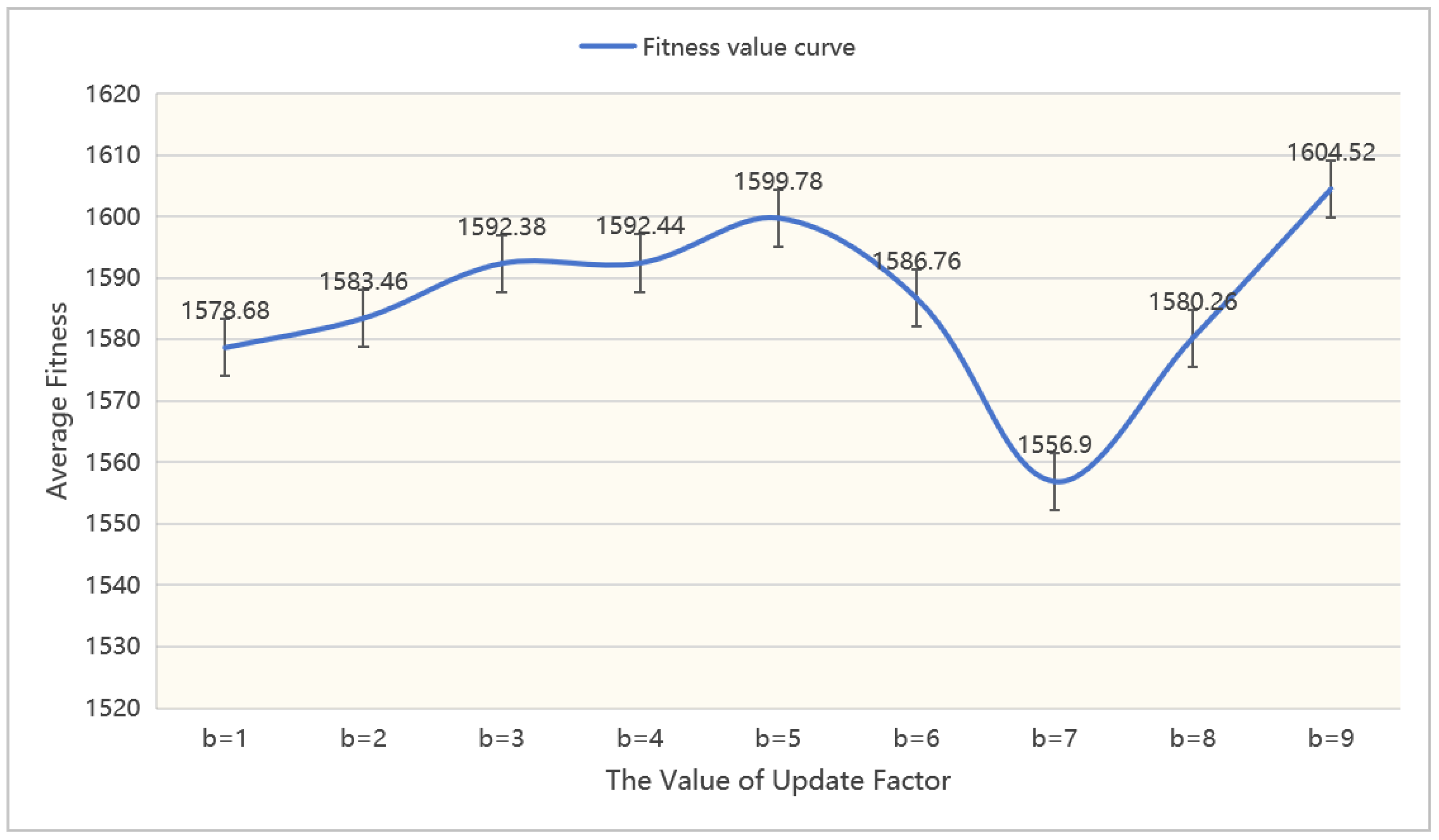
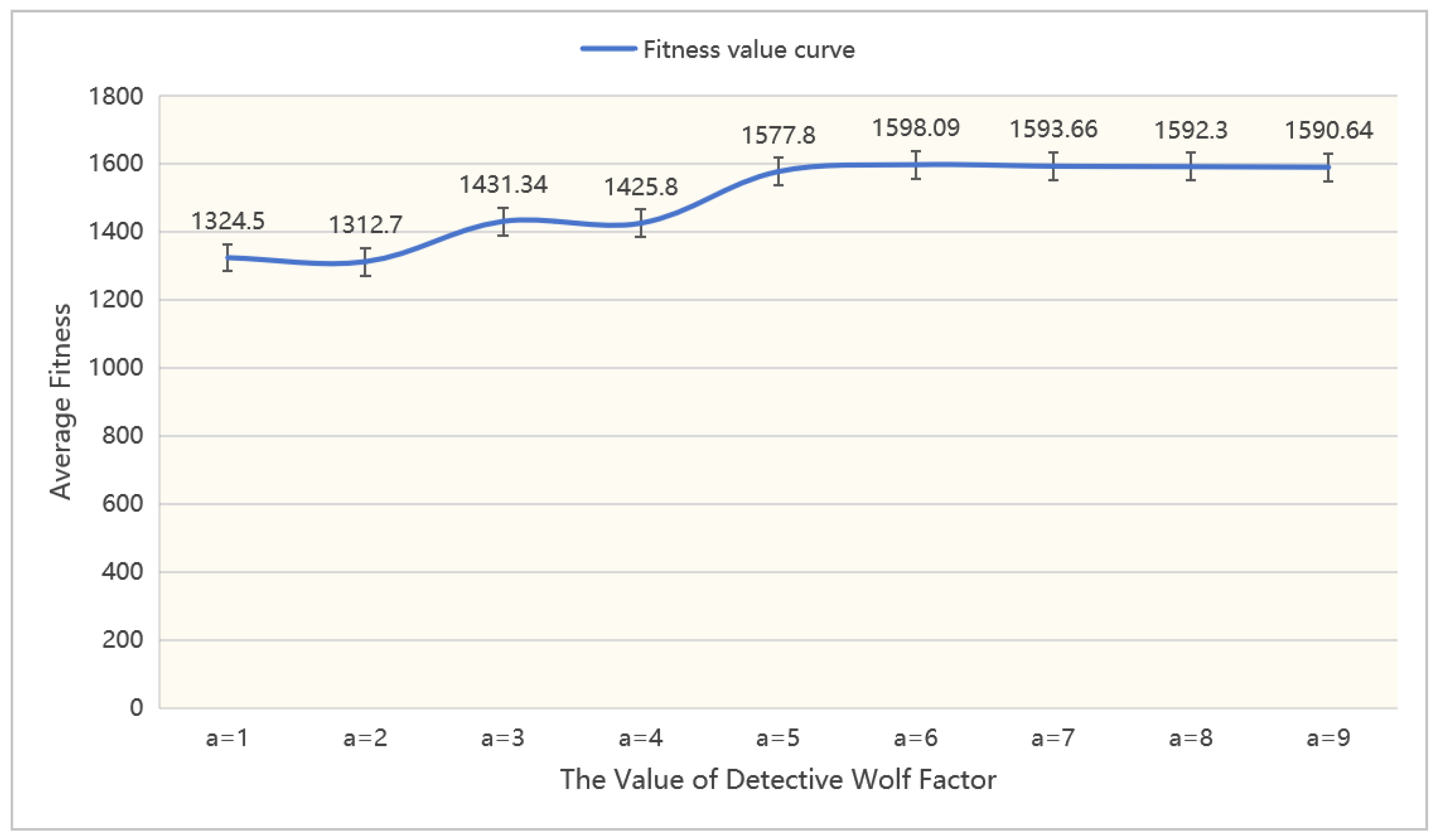
In this section, we perform an ablation experiment on the wolf pack algorithm’s detective wolf factor and updating factor to assess their effects on the performance of the EWPA-PT algorithm. The parameters are varied within the range of [1,9], and each experiment is repeated 50 times to calculate the effect of parameter changes on the fitness values. The data are illustrated in Figure 27 and Figure 28.

The ablation experiment on the algorithm parameters reveals their overall impact on the algorithm’s performance. In the wolf pack algorithm, the detective wolf factor and the update factor are inversely proportional to the final number of detective wolves and the number of individuals to be updated. In practice, a smaller detective wolf factor is desired as it increases the number of individuals benefiting from the wandering behavior optimization. Conversely, a larger update factor is preferred since it reduces the number of regenerated individuals, thereby enhancing population diversity. Experimental results indicate that the algorithm achieves optimal performance when the detective wolf factor is set to 2 and the update factor is set to 7, which aligns with our expectations.

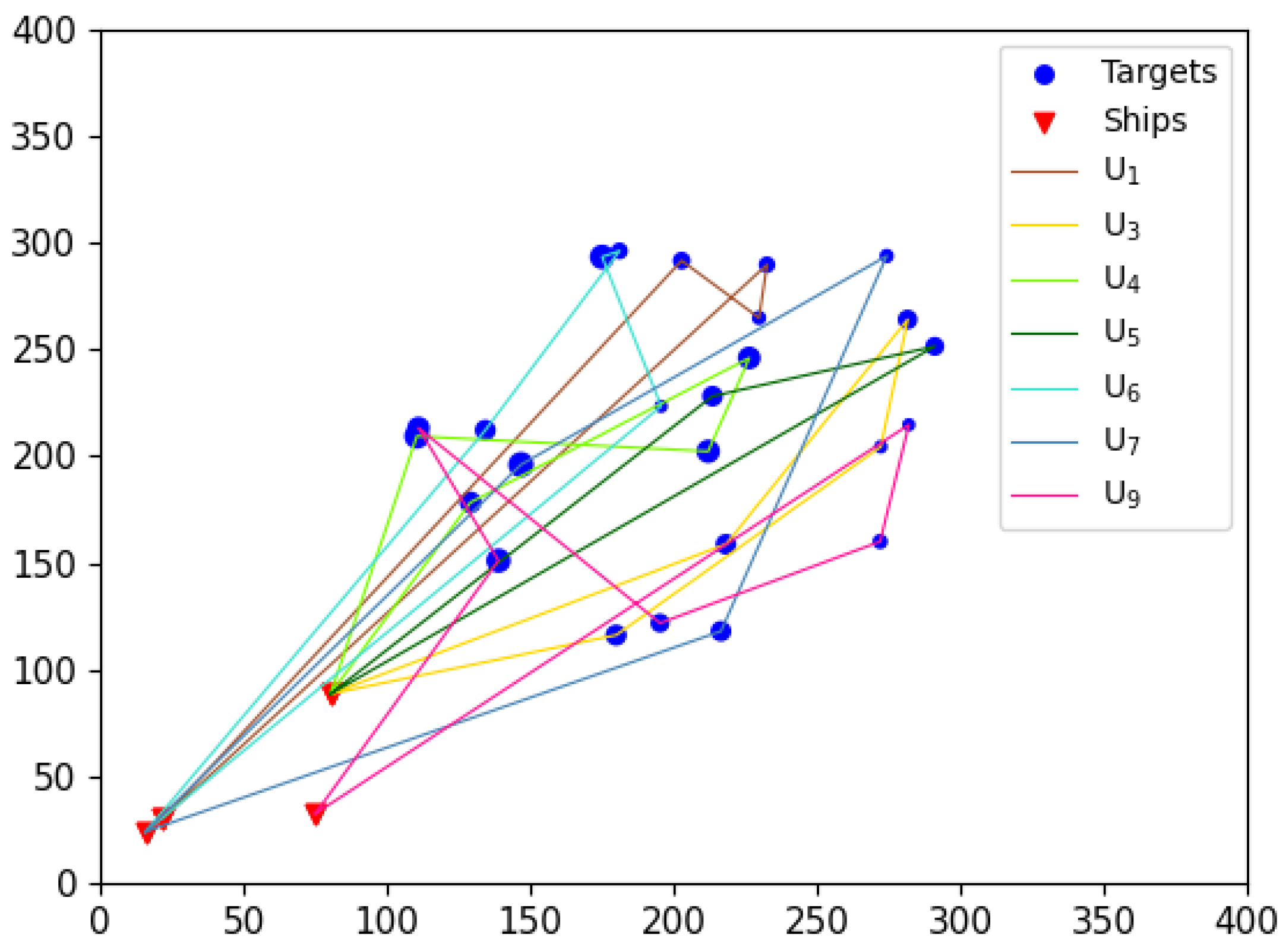
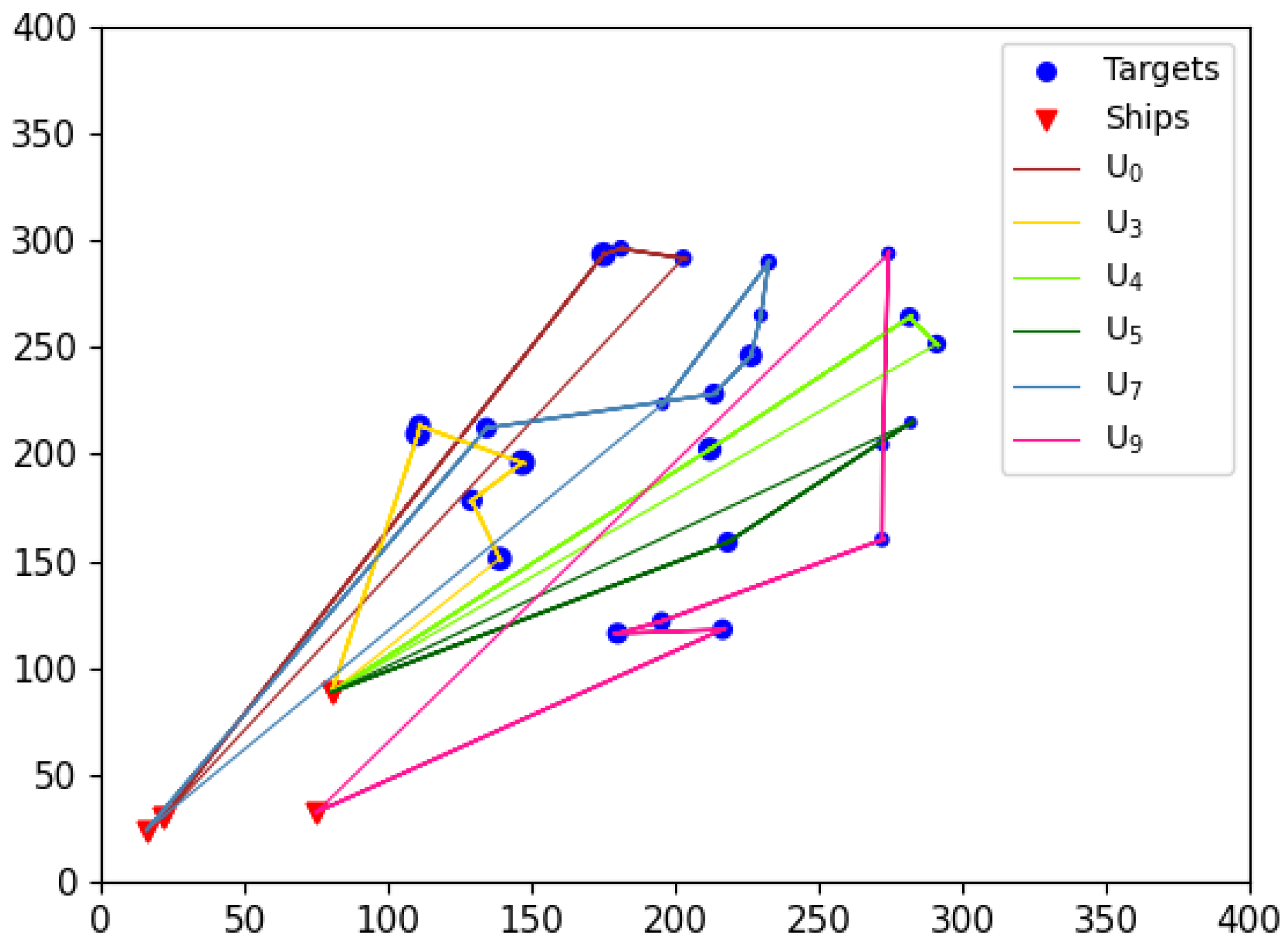
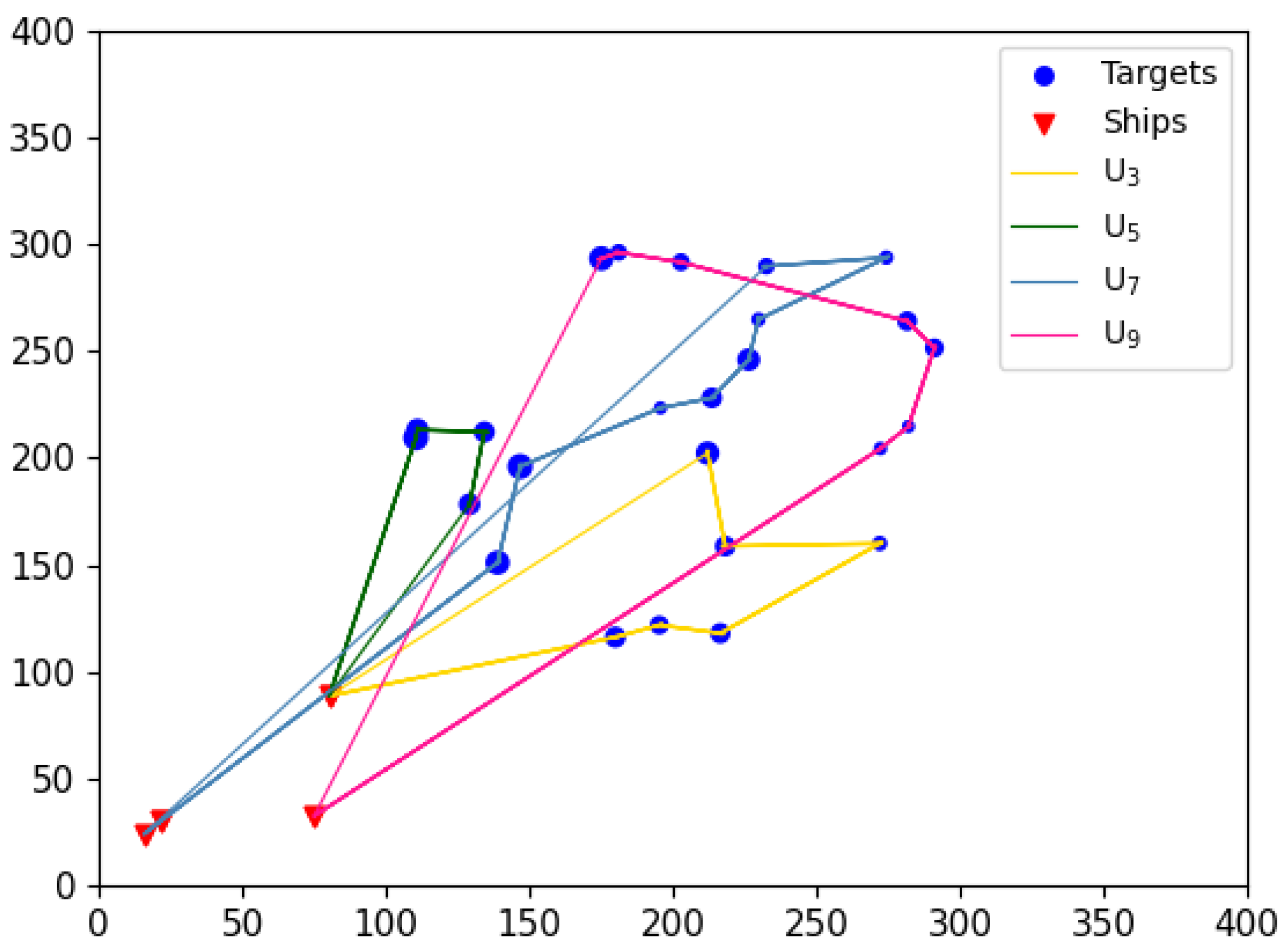
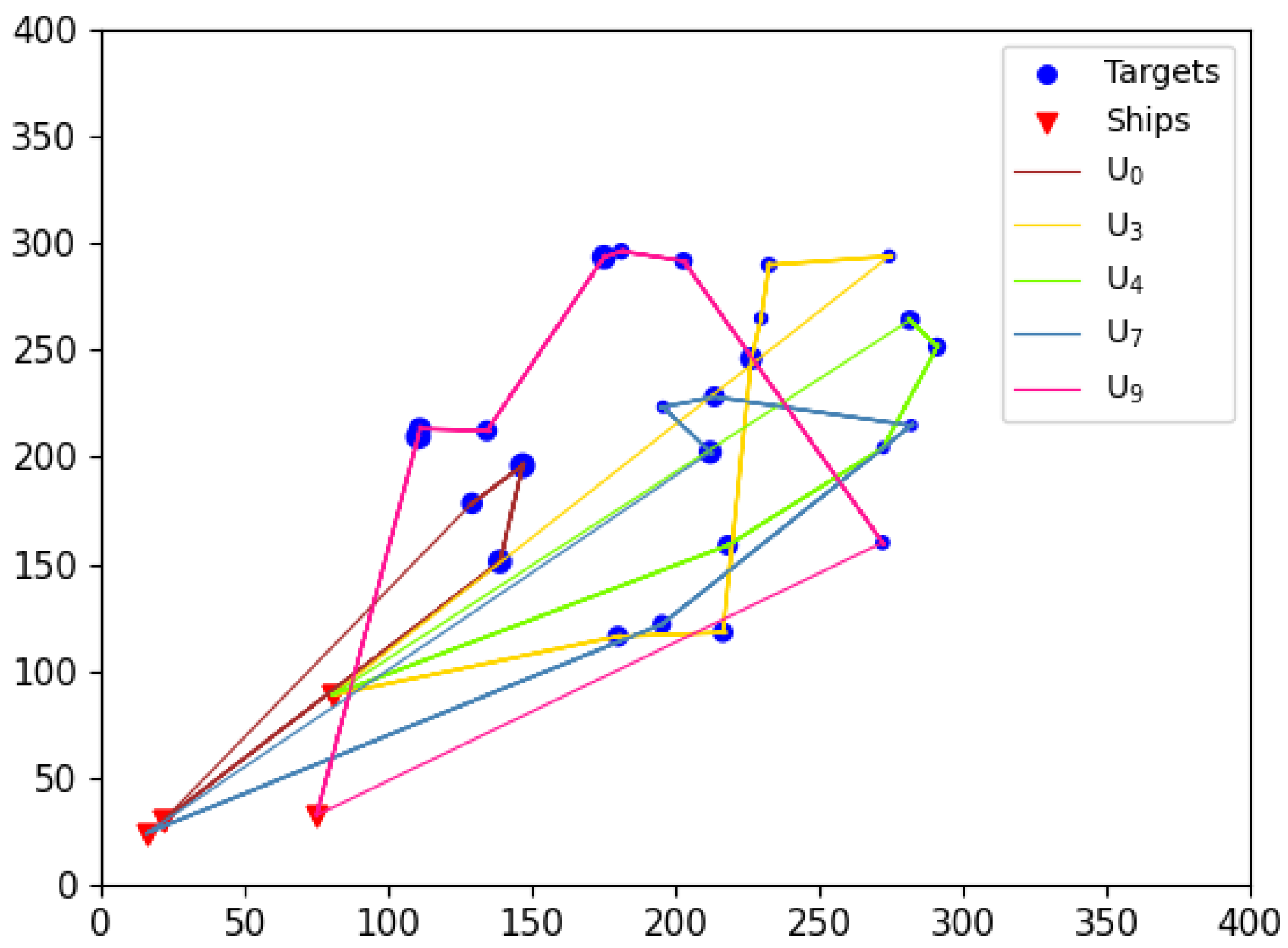
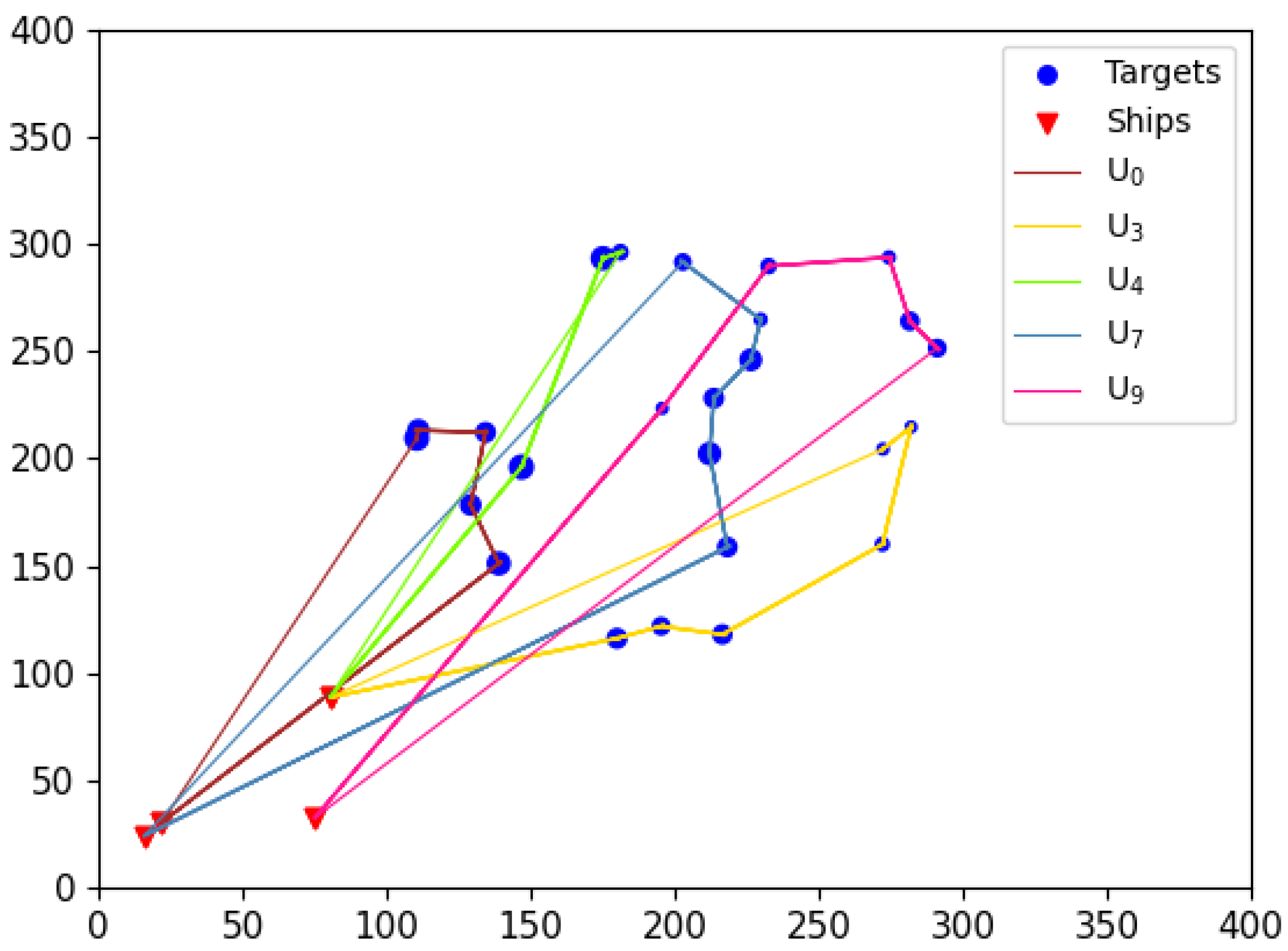
4.6. Visualization of Task Allocation Results

The experimental scenario in this subsection involves 10 UAVs and 25 tasks to be allocated. To ensure fairness in the experiment, the attributes of the UAVs and the targets are fixed. The position coordinates are listed in Table 6 and Table 7. The visualization results are shown in Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33.

In addition to quantitative metrics, the route taken by UAVs to execute tasks should also be considered an important criterion for evaluating task allocation results. This paper argues that an optimal UAV task execution route should include the following characteristics: minimal flight span for each UAV (to avoid overloading any single UAV), clear flight paths, and the absence of “knots” (to prevent unnecessary resource wastage during flight).

Although the comparison algorithms have achieved certain results in terms of computational accuracy, the visual results reveal that these algorithms inevitably exhibit issues such as “knotted” flight paths (e.g., $UA{V}_7$ in Figure 23, $UA{V}_7$ in Figure 24) and large flight spans (e.g., $UA{V}_9$ in Figure 24, $UA{V}_9$ in Figure 25) in the task allocation results. In contrast, the EWPA-PT algorithm generates route maps, where each UAV maintains a minimized flight span with a smooth route and no “knots”, resulting in an ideal outcome.

5. Conclusions

This paper introduces a multi-UAV task assignment model under complex conditions (MTAMCC), considering various factors such as UAV flight speed, maximum range, target point coverage, and threat coefficient in the context of multi-UAV cooperative reconnaissance tasks. To efficiently solve this model, a probability threshold-based elite wolf pack algorithm, called EWPA-PT, is proposed.

Through various comparative experiments, it has been observed that the EWPA-PT algorithm demonstrates higher solution accuracy when solving simple discretized problems with fewer tasks, and its convergence speed is also relatively ideal. As the number of tasks or the distance between UAVs and task points increases, the problem becomes significantly more complex. However, the EWPA-PT algorithm consistently maintains highly accurate solutions. Therefore, it can be concluded that the EWPA-PT algorithm has an advantage in solving multi-UAV task assignment problems.

Although the EWPA-PT algorithm maintains a commendable convergence speed and high solution accuracy, its overall running speed is slower than similar algorithms due to the adoption of dynamic step sizes during wandering behavior.

In the future, we will concentrate on optimizing both models and algorithms. When it comes to models, we will consider more detailed application scenarios and constraints that closely resemble real-world conditions. Regarding algorithms, our main objective will be to minimize runtime and improve scalability, ensuring that the algorithm can handle various dimensions without adjusting the parameters.