Enhanced Multi-UAV Formation Control and Obstacle Avoidance Using IAAPF-SMC

Abstract

In response to safety concerns pertaining to multi-UAV formation flights, a novel obstacle avoidance method based on an Improved Adaptive Artificial Potential field (IAAPF) is presented. This approach enhances UAV obstacle avoidance capabilities by utilizing segmented attraction potential fields refined with adaptive factors and augmented with virtual forces for inter-UAV collision avoidance. To further enhance the control and stability of multi-UAV formations, a Sliding Mode Control (SMC) method is integrated into the IAAPF-based obstacle avoidance framework. Renowned for its robustness and ability to handle system uncertainties and disturbances, the SMC method is combined with a feedback control system that utilizes inner and outer loops. The outer loop generates the desired path based on the leader’s state and control commands, while the inner loop tracks these trajectories and adjusts the follower UAVs’ motions. This design ensures that obstacle feedback is accounted for before the desired state information is received, enabling effective obstacle avoidance while maintaining formation integrity. Integrating leader-follower formation control techniques with SMC-based multi-UAV obstacle avoidance strategies ensures the effective convergence of the formation velocity and spacing to predetermined values, meeting the cooperative obstacle avoidance requirements of multi-UAV formations. Simulation results validate the efficacy of the proposed method in reaching otherwise unreachable destinations within obstacle-rich environments, while ensuring robust collision avoidance among UAVs.

1. Introduction

Compared with single UAVs, multi-UAV execute tasks more effectively and economically. With the development of lightweight electronics and sensors, the size and cost of UAVs have reduced, enabling swarms to consist of smaller UAVs [1]. Consequently, research on multi-UAV cooperative formation flight control has emerged as a cutting-edge topic in recent years. These systems not only possess the maneuverability of a single UAV, but also can collaborate with other UAVs to accomplish more complex tasks, making them typical multiagent systems [2]. The ability of UAVs to avoid obstacles in real time is a crucial performance indicator and a key factor in determining the success of UAV flights, thereby underscoring the importance of further studying cooperative obstacle avoidance control methods for multi-UAV formations.

Obstacle avoidance planning refers to finding an obstacle-free, optimal route from the initial position to the destination by integrating obstacle information data obtained by multi-UAV environmental perception sensors and considering factors such as UAV maneuverability [3]. Bashir et al. [4] proposed a mathematically proven obstacle avoidance path-planning technique. This method ensures UAVs follow their designated paths by defining collision-free edges around rectangular obstacles and their corner points. Aldao et al. [5] proposed a real-time collision-avoidance algorithm for built environments. The algorithm utilizes a simplified geometric model and 3D sensor information to detect and localize obstacles, estimate the trajectory of an obstacle when it is detected, and compute the obstacle avoidance path. Zhang et al. [6] proposed a novel formation control method in order to solve the problem of multiple UAVs colliding during obstacle avoidance. The method utilizes APF, combines UAV maneuvering constraints with a coherent formation control algorithm, optimizes the UAV velocity through a particle swarm optimization (PSO) algorithm, and employs the best coherent control algorithm to achieve the optimal convergence rate of the UAV formation. The aforementioned studies indicate that while various methods have their respective advantages and disadvantages, traditional planning methods based on the APF still have significant advantages in practical applications. This is due to their high computational efficiency and adaptability to real-time requirements and environmental changes. As a result, the choice of APF methods among conventional algorithms is primarily driven by their suitability for real-time applications and their ability to handle environmental variability effectively, especially in solving small-scale problems and environments with clear outcomes.

The artificial potential field method establishes an attractive potential field for the destination and a repulsive potential field for obstacles, and integrates these two forces by selecting appropriate potential field functions and their parameters and movement steps to generate a safe flight path [7]. When using the artificial potential field method for obstacle avoidance planning, only the current position of each step and the composite field generated by obstacles and the destination are considered: therefore, there is no need to generate a complete path in advance for the next step [8]. This algorithm has advantages such as simple mathematical and physical mechanisms, short computation times, real-time control requirements, and smooth and safe planned paths [9]. However, traditional artificial potential field methods have some drawbacks, such as the possibility of obstacles when obstacles are near the initial point of the UAV and the problem of being unable to reach the destination when obstacles are near the UAV.

In multi-UAV formation control, SMC is recognized for its robustness in addressing the system’s complex dynamic behaviors and inherent uncertainties [10]. Brahim et al. [11] introduced an adaptive SMC approach that guarantees finite-time convergence and ensures quadrotor stability despite unknown perturbations and actuator constraints, demonstrating enhanced robustness under conditions where conventional controllers may fail. Similarly, Xiong et al. [12] proposed a synthesis control method that effectively addressed the underactuated, highly coupled, and nonlinear characteristics of UAV dynamics by partitioning the system into fully actuated and underactuated subsystems, achieving greater control precision than traditional methods. In contrast to conventional strategies, such as PID, gain scheduling, and Backstepping, SMC enables rapid, precise trajectory tracking with strong resilience to parameter variations and external disturbances [13]. While gain-scheduling mechanisms like that of Melo et al. [14] enhance robustness against uncertainties, they often depend on predefined parameters, limiting adaptability in dynamic environments. Lyapunov-based designs, like the barrier-embedded method proposed by Tian et al. [15], offer robustness, but may face performance limitations in real time when dealing with significant disturbances. SMC, however, excels in handling discontinuous inputs and mitigating uncertainties more effectively. In formation control, SMC ensures that UAV formations are maintained by designing appropriate sliding surfaces to regulate relative positions, offering superior fault tolerance. For example, Li et al. [16] demonstrated a delay-dependent fault-tolerant consensus mechanism that ensures coordination in multiagent systems with non-identical initial states, which is crucial for UAV swarms. Wang et al. [17] further highlighted SMC’s scalability in nonlinear, highly coupled systems by addressing the numerical infeasibility posed by traditional methods reliant on a fixed Lyapunov matrix structure. While Backstepping, as implemented by Wang et al. [18], effectively handles modeling uncertainties, SMC offers a more flexible and adaptive framework, further enhancing control accuracy in dynamic scenarios. Its integration with adaptive command-filtered Backstepping demonstrates promise for eliminating differential signals, while efficiently managing external disturbances. Overall, while multiple control strategies, such as gain scheduling, Lyapunov-based designs, and Backstepping, have proven effective, SMC stands out for its robust performance in uncertain and dynamic environments, making it a superior choice for multi-UAV formation control.

The main contributions of this article are as follows:

(1)

Introduction of a Novel Obstacle Avoidance Method: In response to safety concerns pertaining to multi-UAV formation flights, a novel obstacle avoidance method based on the IAAPF is presented. The approach enhances UAV obstacle avoidance capabilities by utilizing segmented attraction potential fields, refined with adaptive factors, and augmented with virtual forces for inter-UAV collision avoidance.

(2)

Integration of SMC into IAAPF: To further enhance the control and stability of multi-UAV formations, a SMC method is integrated into the IAAPF-based obstacle avoidance framework. This design ensures that obstacle feedback is accounted for before the desired state information is received, enabling effective obstacle avoidance while maintaining formation integrity.

This work is organized as follows. In Section 2, we discuss the traditional two-dimensional artificial potential field method and its associated problems, such as the inability to reach a destination when obstacles are nearby and excessive attraction due to distant destinations. In Section 3, we address these issues by modifying the attractive potential field function to a segmented function, ensuring that the attraction does not increase beyond a certain distance from the destination, thereby reducing the risk of collision with obstacles that are far from the destination. In Section 4, we describe the design of the formation avoidance control system using the IAAPF-SMC method with a focus on achieving stable flight and obstacle avoidance in UAV formations. In Section 5, we present simulation experiments that validate the feasibility of the improved adaptive algorithm, demonstrating its ability to compute globally optimal, obstacle-free, and safe paths to reach a destination. Finally, conclusions are presented in Section 6.

2. Traditional Artificial Potential Field

In a given two-dimensional coordinate space $X_U\times Y_U$, quadcopters, obstacles, and destinations are all represented as point masses in a two-dimensional coordinate system to facilitate the analysis and simulation of multi-UAV motion and path planning [19,20]. Each point mass $q$ can be expressed as $q={\left[x,y\right]}^T$, where: $0\le x\le X_U$, and $0\le y\le Y_U$. The condition $0\le x\le X_U$ ensures that the x-coordinate of the point mass q remains within the horizontal bound of the coordinate space. Similarly, $0\le y\le Y_U$ ensures that the y-coordinate remains within the vertical bounds. These conditions ensure that the x and y coordinates of the point mass remain within the defined operational bounds of the coordinate space.

In the obstacle avoidance planning problem based on the traditional artificial potential field method, the UAV can be regarded as a point mass $q={\left[x,y\right]}^T$ in two-dimensional space. The general expressions for the attractive potential field function $U_{att}$ and the repulsive potential field function $U_{rep}$ can be represented as [21]:

$$U_{att}\left(q\right)={\displaystyle \frac{1}{2}}{k}_{att}{l}^2\left(q,q_g\right)$$

(1)

$$U_{rep}(q)=\left\{\begin{array}{ll}{\displaystyle \frac{1}{2}}{k}_{rep}{\left({\displaystyle \frac{1}{l\left(q,q_0\right)}}-{\displaystyle \frac{1}{l_0}}\right)}^2& ,0\le l\left(q,q_0\right)\le l_0\\ 0& , l\left(q,q_0\right)>l_0\end{array}\right.$$

(2)

where $k_{att}$ represents the gain factor of the attractive potential field, $k_{rep}$ is the gain factor of the repulsive potential field, $q\left(x,y\right)$ denotes the real-time position coordinates of the quadcopter, $q_g(x_g,y_g)$ is the position coordinates of the destination, $q_0\left(x_0,y_0\right)$ is the position coordinates of the obstacle, $l_0$ is a constant, representing the maximum impact distance of the repulsive force field around the obstacles on the UAV, $l(q,q_g)$ and $l\left(q,q_0\right)$ are vector distances and the Euclidean distance between two points.

The attractive potential field exerts an attractive force $F_{att}$ on the UAV, while the repulsive potential field exerts a repulsive force $F_{rep}$ on the UAV [22]. Both are negative gradient forces of the potential fields, as expressed below:

$$F_{att}\left(q\right)=-\nabla U_{att}\left(q\right)=-k_{att}l\left(q,q_g\right)$$

(3)

$$\begin{array}{l}{F}_{rep}(q)=-\nabla U_{rep}\left(q\right)\\ =\left\{\begin{array}{c}{k}_{rep}\left({\displaystyle \frac{1}{l\left(q,q_0\right)}}-{\displaystyle \frac{1}{l_0}}\right){\displaystyle \frac{1}{l^2\left(q,q_0\right)}}{\displaystyle \frac{\partial l(q,q_0)}{\partial (q)}},0\le l\left(q,q_0\right)\le l_0\\ 0 \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},l\left(q,q_0\right)<l_0\hfill \end{array}\right.\end{array}$$

(4)

According to the definition of potential fields, overlaying the attraction and repulsion fields yields an artificial potential field, establishing a combined potential field model [23]. The resulting potential field function and the resultant force are

$$U\left(q\right)=U_{att}(q)+U_{rep}(q)$$

(5)

$$F\left(q\right)=-\nabla U\left(q\right)=F_{att}(q)+F_{rep}(q)$$

(6)

Since the traditional artificial potential field algorithm only considers obstacles within the immediate vicinity when calculating obstacle avoidance, it lacks global information acquisition, leading to unsuccessful obstacle avoidance and pathfinding failure. When the destination is too close to an obstacle, the repulsion from the obstacle may exceed the attraction to the destination, causing the UAV to be unable to reach the destination position nearby, encountering local minima or failure in obstacle avoidance [24,25]. Additionally, when the destination is too far from the starting point, an overly strong attraction field may form around the starting point, leading to paths that pose high obstacle risks and restrict the multi-UAV range of movement.

3. Improved Adaptive Artificial Potential Field

Traditional artificial potential field algorithms often encounter limitations in obstacle avoidance due to their reliance on local information and the inability to consider global contexts. These limitations manifest when obstacles are either too close to the destination or when the destination is excessively distant from the starting point, resulting in suboptimal paths and potential obstacle risks. To overcome these challenges, an adaptive approach has been employed to redefine the potential field function. By incorporating adaptive thinking into the design process, the newly developed potential field function addresses the shortcomings of traditional algorithms by dynamically adjusting them to the surrounding environment. This adaptive function allows for a more comprehensive consideration of obstacles and destinations, enabling multi-UAVs to navigate efficiently in complex environments while minimizing obstacle risks.

3.1. Attraction Potential Field Improved by a Segmented Strategy

The UAV can be regarded as a point mass in two-dimensional space. In the APF algorithm that uses a segmented strategy, the attraction potential field function is expressed as follows:

$${U_{att}}^{*}\left(q\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{2}}{k}_{att}{l}^2\left(q,q_g\right),l\left(q,q_g\right)\le d_g\\ {\displaystyle \frac{1}{2}}{k}_{att}{d}_{g}l\left(q,q_g\right),l\left(q,q_g\right)\ge d_g\end{array}\right.$$

(7)

The improved attraction potential function is expressed as follows:

$${F_{att}}^{*}\left(q\right)=-\nabla {U_{att}}^{*}\left(q\right)=\left\{\begin{array}{c}-k_{att}l(q,q_g),l(q,q_g)\le d_g\\ -k_{att}{d}_g,l(q,q_g)\ge d_g\end{array}\right.$$

(8)

where $d_g$ represents the boundary value of the improved attraction potential field. When the distance between the UAV and the destination is greater than $d_g$, as indicated by Equations (7) and (8), the rate of increase in the attraction potential field slows down while the attractive force remains constant. This improvement addresses the issue of the attraction potential field being too strong when the UAV is too far from its destination. When there are obstacles at the starting position, the attraction potential field is reduced compared to before, and the attractive force remains unchanged, mitigating the problem of excessive attractive force when the UAV is too close to obstacles at startup.

3.2. Repulsion Potential Field with Adaptive Factors

To address the issue of UAVs being unable to reach destinations due to nearby obstacles, the repulsion potential field function has been improved by incorporating the relative distance between the UAV and the destination along with adaptive factors. The improved repulsive force is related not only to the distance between the UAV and obstacles but also to the distance between the UAV and the destination. The formula for the improved adaptive repulsion potential field is

$${U^{*}}_{rep}(q)=\left\{\begin{array}{c}{\displaystyle \frac{1}{2}}{k}_{rep}{({\displaystyle \frac{1}{l(q,q_0)}}-{\displaystyle \frac{1}{l_0}})}^2{l}^n(q,q_g),0\le l(q,q_0)\le l_0\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},l(q,q_0)>l_0\hfill \end{array}\right.$$

(9)

where n represents the adaptive factor. $n>0$. Thus, the improved repulsive force is

$${F^{*}}_{rep}(q)=-\nabla U_{rep}(q)=\left\{\begin{array}{c}{F^{*}}_{rep1}(q)+{F^{*}}_{rep2}(q),0\le l(q,q_0)\le l_0\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},l(q,q_0)>l_0\hfill \end{array}\right.$$

(10)

The adaptive factor n is a positive real number that adjusts the repulsive behavior of the potential field based on the UAV’s proximity to obstacles and its destination. This factor enables finer tuning of repulsive forces and smoothens the transition between obstacle avoidance and destination-seeking behavior. Specifically, the parameter n is dynamically computed based on the UAV’s velocity and its proximity to obstacles. Higher values of n are used in scenarios requiring rapid adjustments, such as when the UAV is in close proximity to obstacles, whereas lower values of n enable smoother control when the UAV is farther from potential hazards. By appropriately tuning n, the UAV can achieve an optimal balance between efficient trajectory tracking and effective obstacle avoidance, ensuring both safety and operational efficiency.

When the UAV is within the influence range of the repulsive force, the improved repulsive force consists of the following two vector components:

$${F^{*}}_{rep1}(q)=k_{rep}({\displaystyle \frac{1}{l(q,q_0)}}-{\displaystyle \frac{1}{l}}){\displaystyle \frac{l^n(q,q_g)}{l^2(q,q_0)}}{\displaystyle \frac{\partial l(q,q_0)}{\partial (q)}}$$

(11)

$${F^{*}}_{rep2}(q)=-{\displaystyle \frac{1}{2}}{k}_{rep}{({\displaystyle \frac{1}{l(q,q_0)}}-{\displaystyle \frac{1}{l_0}})}^{2}n{l}^{n-1}\left(q,q_g\right){\displaystyle \frac{\partial l(q,q_g)}{\partial (q)}}$$

(12)

The directions of the two vector components of the improved repulsive force are different. The direction of ${F^{*}}_{rep1}$ points away from the obstacles toward the UAV and the direction of ${F^{*}}_{rep2}$ points from the UAV toward the destination represent the combined force of ${F^{*}}_{tot}$ the improved potential field, as shown in Figure 1.

As illustrated in Figure 1, $F_{rep2}^{*}$ and $F_{att}^{*}$ have the same direction when the UAV navigates around the obstacles. This ensures that the UAV is directed toward the destination while avoiding obstacles.

In the improved repulsive potential field function, the adaptive factor n plays a crucial role in determining the strength and direction of the repulsive force based on the relative distance between the UAV and the destination. The improved repulsion function decreases as the relative distance $l(q,q_g)$ between the UAV and the destination increases, and the degree of decrease is related to the value of the adaptive factor n. When $0<n<1$ is such that the UAV is close to the destination, $l(q,q_g)\to 0$, with the first vector component ${F^{*}}_{rep1}(q)\to 0$ and the second vector component ${F^{*}}_{rep2}(q)\to \infty$, the resultant force on the UAV is greater than zero, and the UAV motion direction is from the UAV toward the destination, allowing the UAV to approach the destination more easily. When $n=1$ and $l(q,q_g)\to 0$, with the first vector component ${F^{*}}_{rep1}(q)\to 0$ and the second vector component ${F^{*}}_{rep2}(q)\to c$ (c is a constant), the resultant force on the UAV is greater than zero, and the UAV’s motion direction is from the UAV toward the destination, maintaining a safe distance between the UAV and the destination. When $n>1$ and $l(q,q_g)\to 0$, the improved repulsion function ${F^{*}}_{rep}(q)$ also gradually decreases, eventually ${F^{*}}_{rep}(q)\to 0$, allowing the UAV to move quickly in an environment without close-range obstacles. By combining the improved repulsion function with the adaptive factor, the UAV can navigate more flexibly and safely in various environments, effectively balancing the need for obstacle avoidance and destination orientation, and thus successfully reaching the destination point.

3.3. Improved Repulsive Force and Emergency Collision-Avoidance Strategy for UAVs

In the leader-follower method for multi-UAV formation control, the desired position calculated based on the leader’s destination exerts an attractive force on the follower UAVs. Therefore, the artificial potential field function between the UAVs need not consider attraction, only repulsion. This simplification reduces the complexity of the method and enhances the computational performance. In path planning for obstacle avoidance among multiple UAVs, an approach integrating the repulsive potential field with adaptive factors can be employed. This method dynamically adjusts the parameters of the repulsive potential field based on the inter-distance and velocity differences among the UAVs, aiming to prevent obstacles and abrupt changes in paths. The IAAPF function between $UA{V}_i$ and $UA{V}_j$ is

$$U_{rep}^{*}(q_{ij})={\displaystyle \frac{1}{2}}{({\displaystyle \frac{1}{l(q_i,q_j)}}-{\displaystyle \frac{1}{l_0}})}^2{l}^n(q_i,q_j)$$

(13)

where $q_{ij}$ is the potential value of the IAAPF generated by $UA{V}_j$ at the position of $UA{V}_i$; $l(q_i,q_j)$ is the displacement vector between $UA{V}_i$ and $UA{V}_j$.

The repulsive force is then defined as

$$F_{rep}^{*}(q_{ij})=-\nabla U_{rep}^{*}(q_{ij})=F_{rep1}^{*}(q_{ij})+F_{rep2}^{*}(q_{ij})$$

(14)

The corresponding improved repulsive force consists of the following two parts:

$$\left\{\begin{array}{c}{F^{*}}_{rep1}(q_{ij})=k_{rep}({\displaystyle \frac{1}{l(q_i,q_j)}}-{\displaystyle \frac{1}{l}}){\displaystyle \frac{l^n(q_i,q_j)}{l^2(q_i,q_j)}}{\displaystyle \frac{\partial l(q_i,q_j)}{\partial (q_i)}}\\ {F^{*}}_{rep2}(q_{ij})=-{\displaystyle \frac{1}{2}}{k}_{rep}{({\displaystyle \frac{1}{l(q_i,q_j)}}-{\displaystyle \frac{1}{l_0}})}^{2}n{l}^{n-1}\left(q_i,q_j\right){\displaystyle \frac{\partial l(q_i,q_j)}{\partial (q_i)}}\end{array}\right.$$

(15)

Considering that the introduction of the IAAPF will change the expected position of the current unmanned aerial vehicle, thereby reducing the control precision of the formation, in order to reduce its impact on control precision, the range of repulsive force is limited. The maximum range in which the repulsive force can act is $D_{\max }$:

$$F_{rep}^{*}(q_{ij})=\left\{\begin{array}{c}{F}_{rep1}^{*}(q_{ij})+F_{rep2}^{*}(q_{ij}),l(q_{ij})<D_{\max }\\ 0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},l(q_{ij})\ge D_{\max }\hfill \end{array}\right.$$

(16)

where $D_{\max }$ represents the maximum range within which the repulsive force $F_{rep}^{*}(q_{ij})$ between two UAVs acts to avoid collisions. $D_{\max }$ can be defined as follows:

$$D_{\max }=v_{\max }{t}_r+{\displaystyle \frac{v_{\max }^2}{2a_{\max }}}+s_s$$

(17)

where $v_{\max }$ is the maximum velocity of the UAV, $a_{\max }$ is the maximum deceleration or maneuverability of the UAV, $t_r$ is the UAV system’s reaction time, and $s_s$ is the minimum safe distance between the UAVs.

The introduction of $D_{\max }$ ensures that the repulsive field does not dominate the potential field, thereby preventing any misbehavior or instability in UAV control. This parameter facilitates a balanced interaction between repulsive and attractive forces, allowing for safe flight while maintaining the overall performance of the UAVs.

Additionally, considering the safety of the formation, when two UAVs are too close to each other, relying on the existing repulsive force of the artificial potential field may not be able to increase the distance between the two UAVs in a short time. Therefore, an emergency collision-avoidance strategy is considered, as shown in Figure 2.

When the distance between UAVs is too small, an emergency collision-avoidance repulsive force is added to create an altitude difference between the UAVs, thus achieving inter-UAV collision avoidance. Define the emergency collision-avoidance repulsive force as $F_{rep}^{*Emg}$. The emergency collision strategy applies an emergency collision-avoidance repulsive force $F_{rep}^{*Emg}$ to the two UAVs to create an altitude difference and avoid collisions between them. The emergency collision-avoidance repulsive force can be represented as follows:

$$F_{rep}^{*Emg}=\left\{\begin{array}{c}\left|F_{rep}^{*}(q_{ij})\right|\widehat{z} , \mathrm{i}>j\\ -\left|F_{rep}^{*}(q_{ij})\right|\widehat{z} , i<j\end{array}\right.=\left|F_{rep}^{*}(q_{ij})\right|sgn(i-j)\widehat{z}$$

(18)

where $\widehat{z}$ is the unit vector in the vertical direction, indicating the direction of the repulsive force; i and j represent the indices of the UAVs involved in the collision avoidance maneuver; and $q_{ij}$ denotes the relative position vector between $UA{V}_i$ and $UA{V}_j$.

An improved repulsion force $F_{rep}^{*Emg}$ is applied such that when $i>j$, $UA{V}_i$ is pushed upward, and when $i<j$, $UA{V}_i$ is pushed downward. This strategy creates a vertical separation between the UAVs, effectively preventing collisions.

As stated in Equation (18), the emergency collision-avoidance repulsive force for two UAVs about to collide has only a directional component, and the directions are opposite, facilitating the creation of an altitude difference between them. The magnitude of this repulsive force is directly proportional to that of the repulsive force $F_{rep}^{*}(q_{ij})$. When the distance between two UAVs is too close, $F_{rep}^{*}(q_{ij})$ is large; hence, $F_{rep}^{*Emg}(q_{ij})$ is also large, allowing one UAV to ascend and the other to descend in a short period. The emergency collision-avoidance distance is denoted as $D_{Emg}$, and the IAAPF repulsive force $F_{rep}(q_{ij})$ between the two UAVs is represented differently depending on the distance between them.

$$F_{rep}(q_{ij})=\left\{\begin{array}{c}\hspace{0.33em}\hspace{0.33em}0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}l(q_i,q_j)>D_{\max }\hfill \\ F_{rep}^{*}(q_{ij})\hspace{0.33em}\hspace{0.33em},D_{Emg}<l(q_i,q_j)\le D_{\max }\\ F_{rep}^{*}(q_{ij})+F_{rep}^{*Emg}\hspace{0.33em}\hspace{0.33em},(q_{ij}),l(q_{ij})\le D_{Emg}\end{array}\right.$$

(19)

To define $D_{Emg}$ in a way that aligns more closely with the UAV system’s emergency collision-avoidance strategy, the following equation can be proposed:

$$D_{Emg}={\displaystyle \frac{v_{re}^2}{2a_e}}+s_s$$

(20)

where $v_{re}$ is the relative velocity between two UAVs, which takes into account their combined velocity during an imminent collision, $a_e$ is the maximum deceleration of the UAVs, and $s_s$ is the minimum safe distance that ensures enough space for emergency maneuvers.

This formula represents the distance within which the emergency collision-avoidance repulsive force becomes active. $D_{Emg}$ ensures that UAVs have enough time to perform emergency evasive maneuvers, such as altitude adjustments or rapid deceleration, in order to avoid collisions when the standard repulsive force is no longer sufficient.

To address some inherent limitations of traditional APF methods, such as local minima and oscillations, the following improvements are proposed:

(a)

The segmented approach to the attractive potential field reduces the risk of UAVs becoming trapped in local minima by adjusting the strength of the attractive force based on their distance to the destination. When the UAV is far from the destination, a stronger attraction accelerates movement, while a reduced force near the destination ensures smoother flight and prevents overshooting or being stuck in confined spaces. This adaptive strategy enables the UAV to avoid local minima traps by modulating its path, depending on its proximity to obstacles or the destination.

(b)

Adaptive Factors in Repulsive Fields: The repulsive potential fields are combined with adaptive factors to dynamically adjust the repulsion based on the UAV environment and distance to obstacles. This adaptive mechanism ensures that the UAV can maneuver smoothly around obstacles without abrupt changes in the direction.

(c)

Virtual Forces for Inter-UAV Collision Avoidance: In a multi-UAV scenario, additional virtual forces are introduced to manage inter-UAV collisions. These forces ensure that UAVs maintain safe distances from each other while following the planned path.

The primary objective of these enhancements is to develop a more flexible and adaptive potential field capable of addressing real-world complexities, such as dynamic environments and interactions among multi-UAVs. To achieve this, we propose a novel segmentation strategy and a modified repulsion field aimed at improving the obstacle avoidance capabilities of UAVs. The segmentation strategy involves partitioning the environment into manageable segments, thereby simplifying the path-planning process. Concurrently, the improved repulsion field dynamically adjusts repulsive forces based on the UAV’s proximity to obstacles, facilitating smoother and more efficient flight. These innovations are designed to provide robustness against common challenges, such as local minima and oscillations, while ensuring safe operation within multi-UAV formations. Collectively, these contributions are essential for enhancing the overall performance of the IAAPF algorithm.

4. Formation Avoidance Control System Design

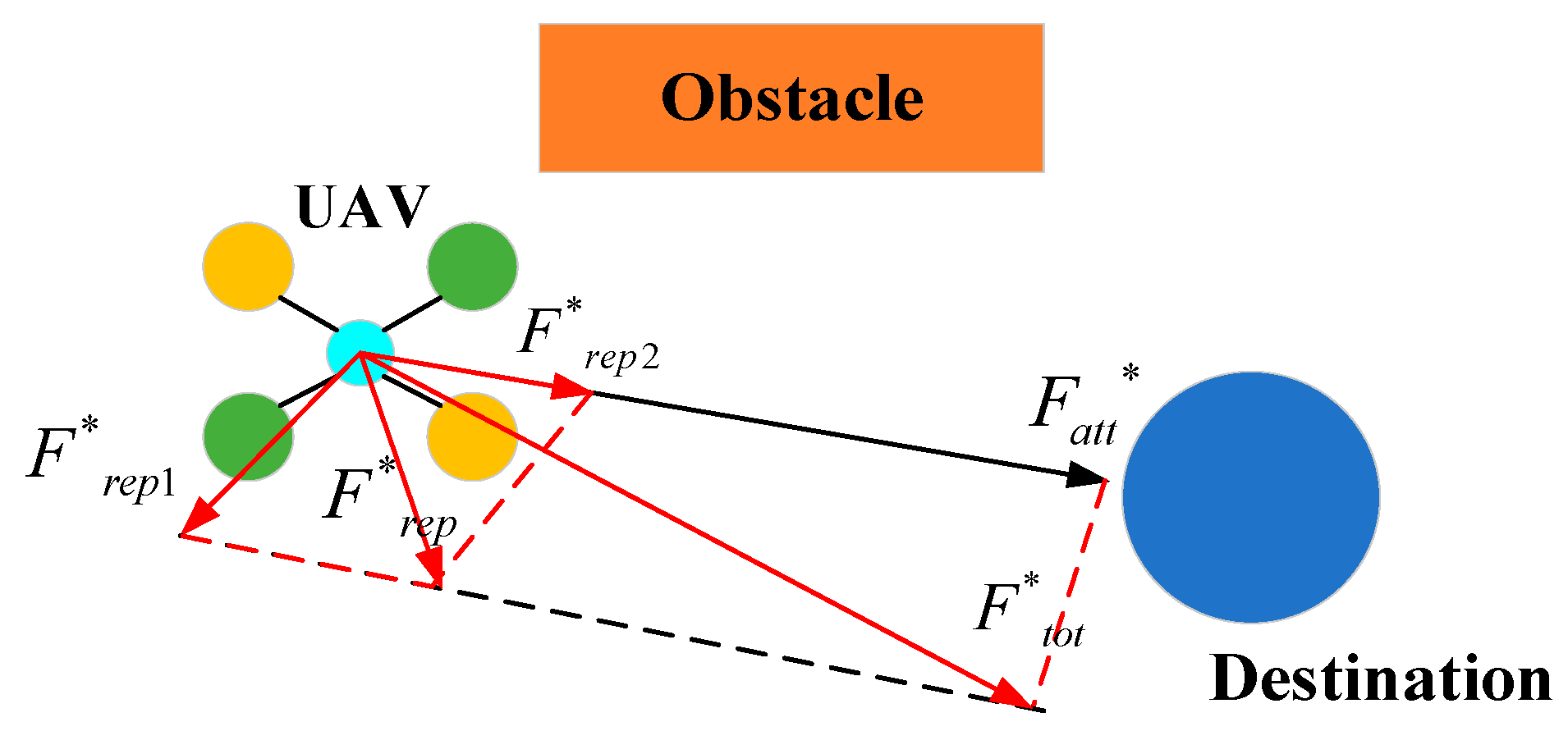
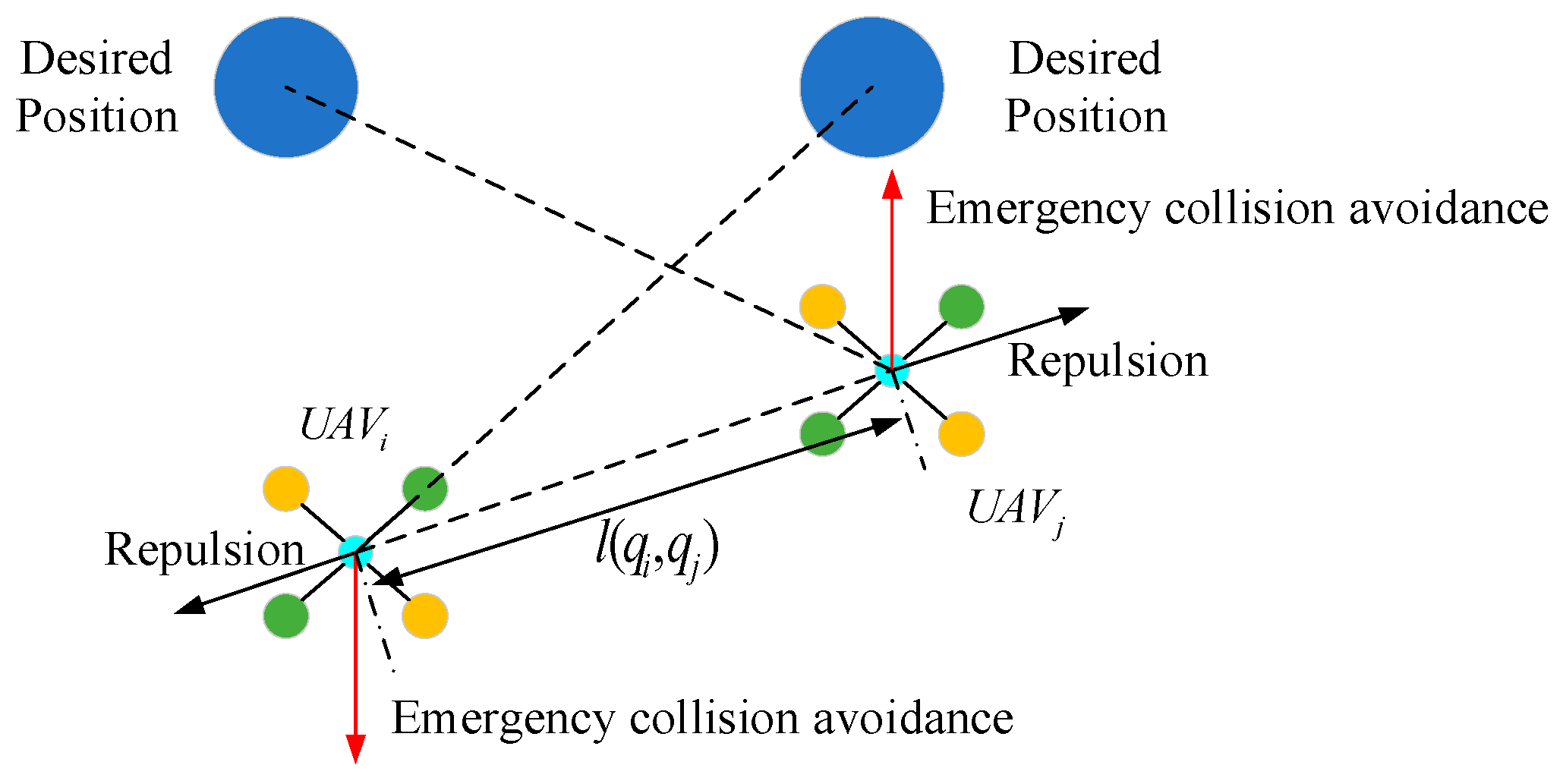
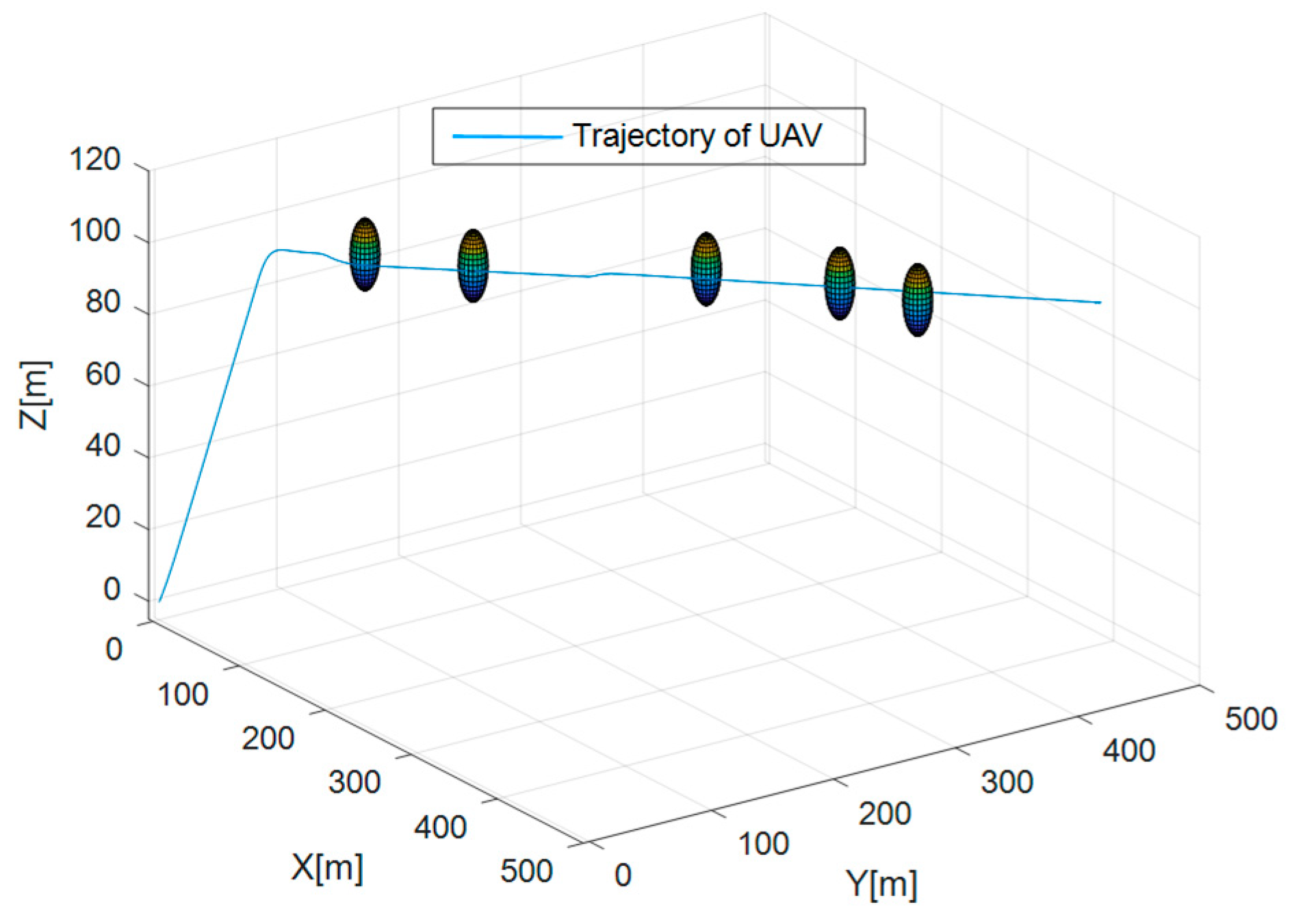
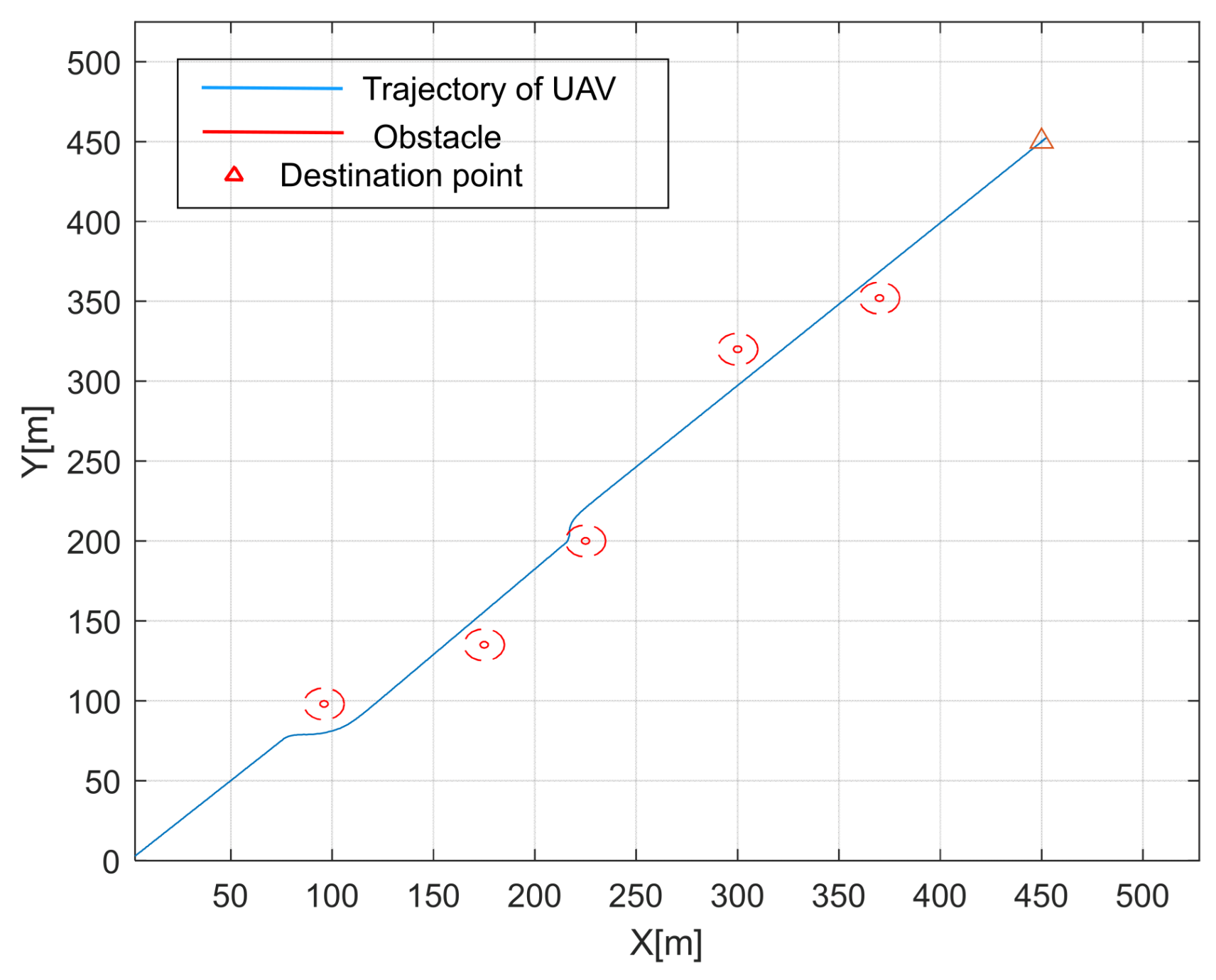
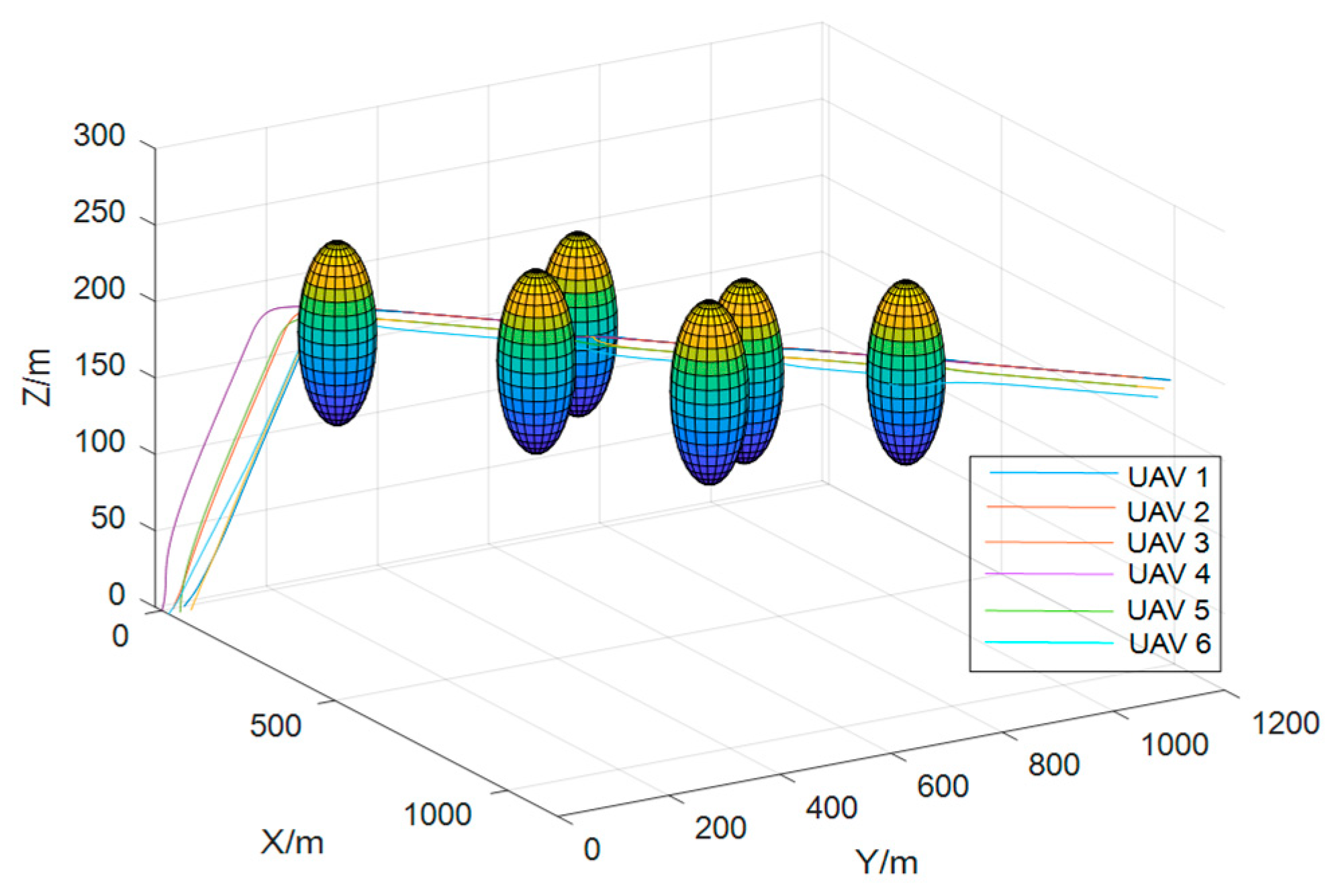
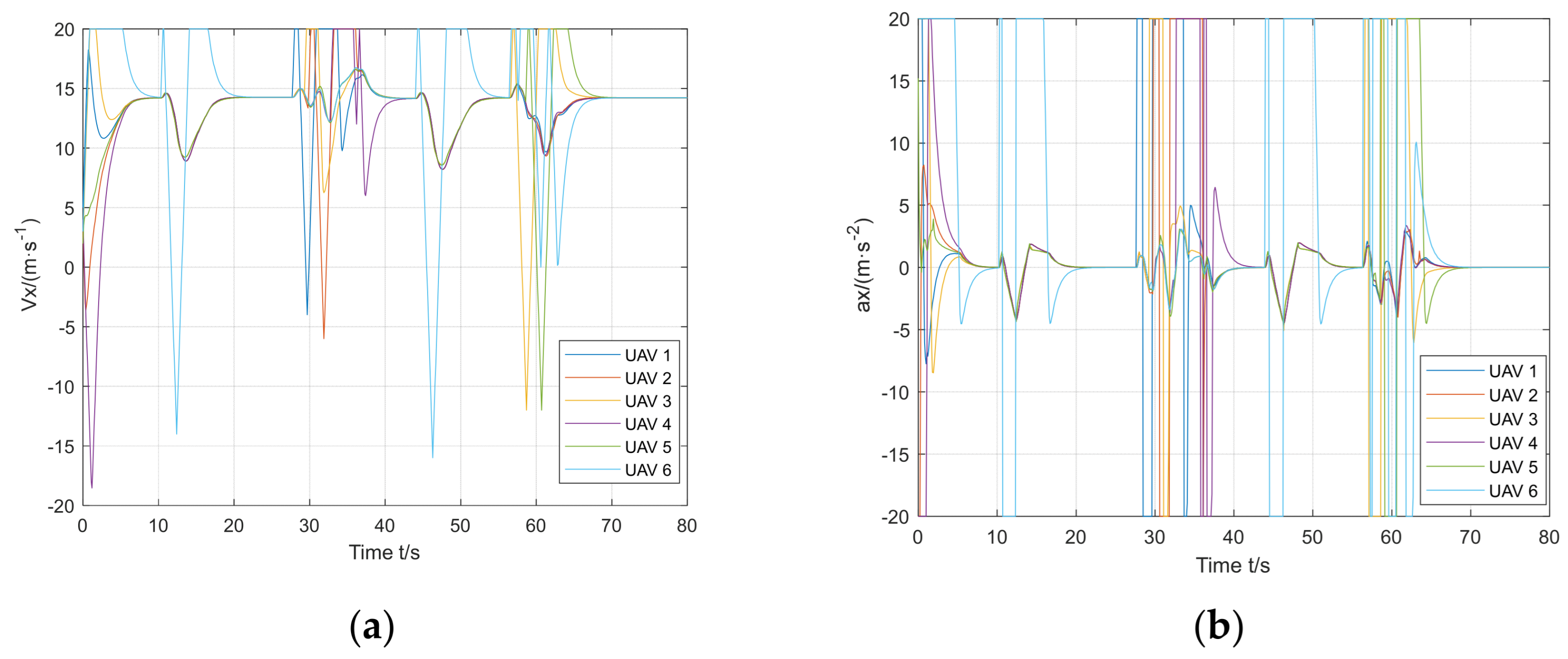
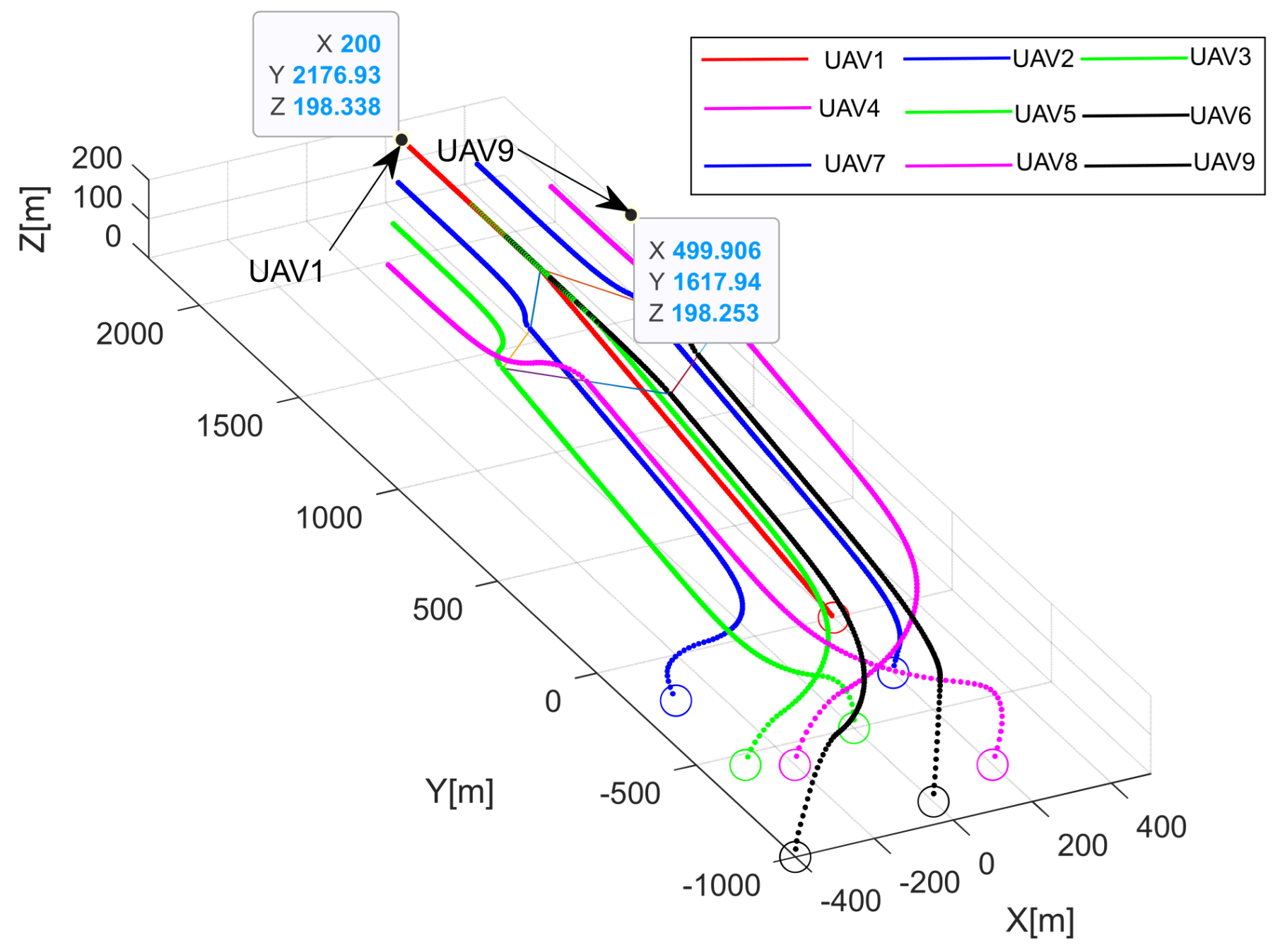
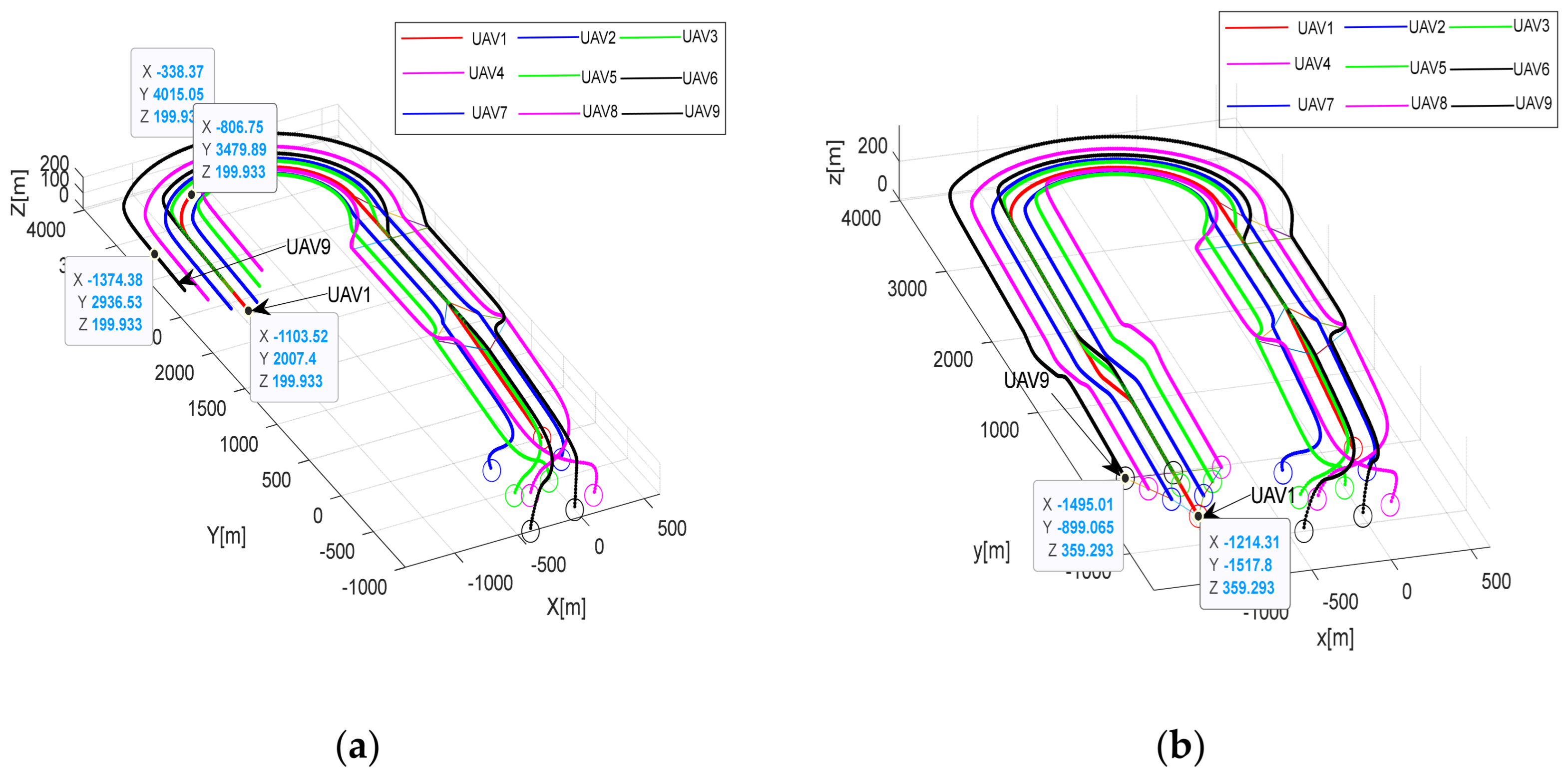
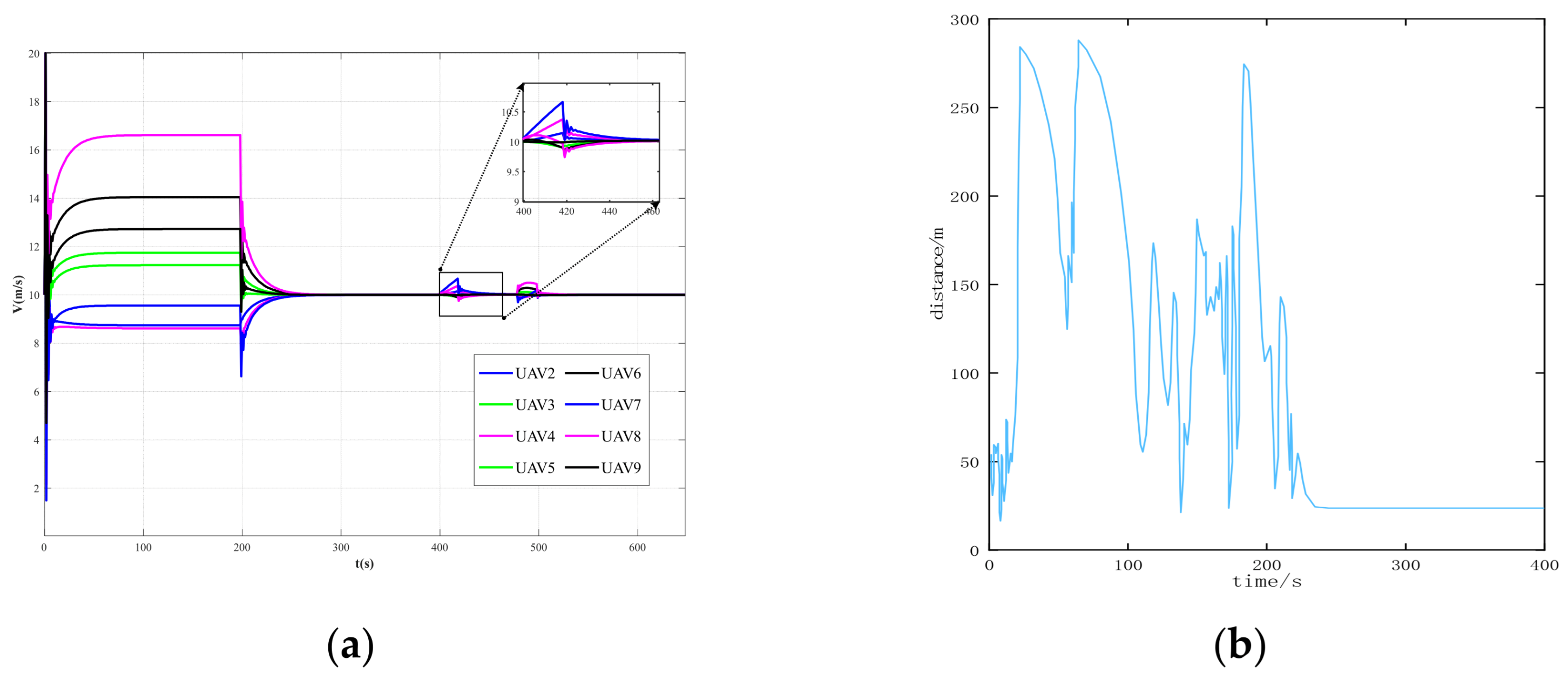
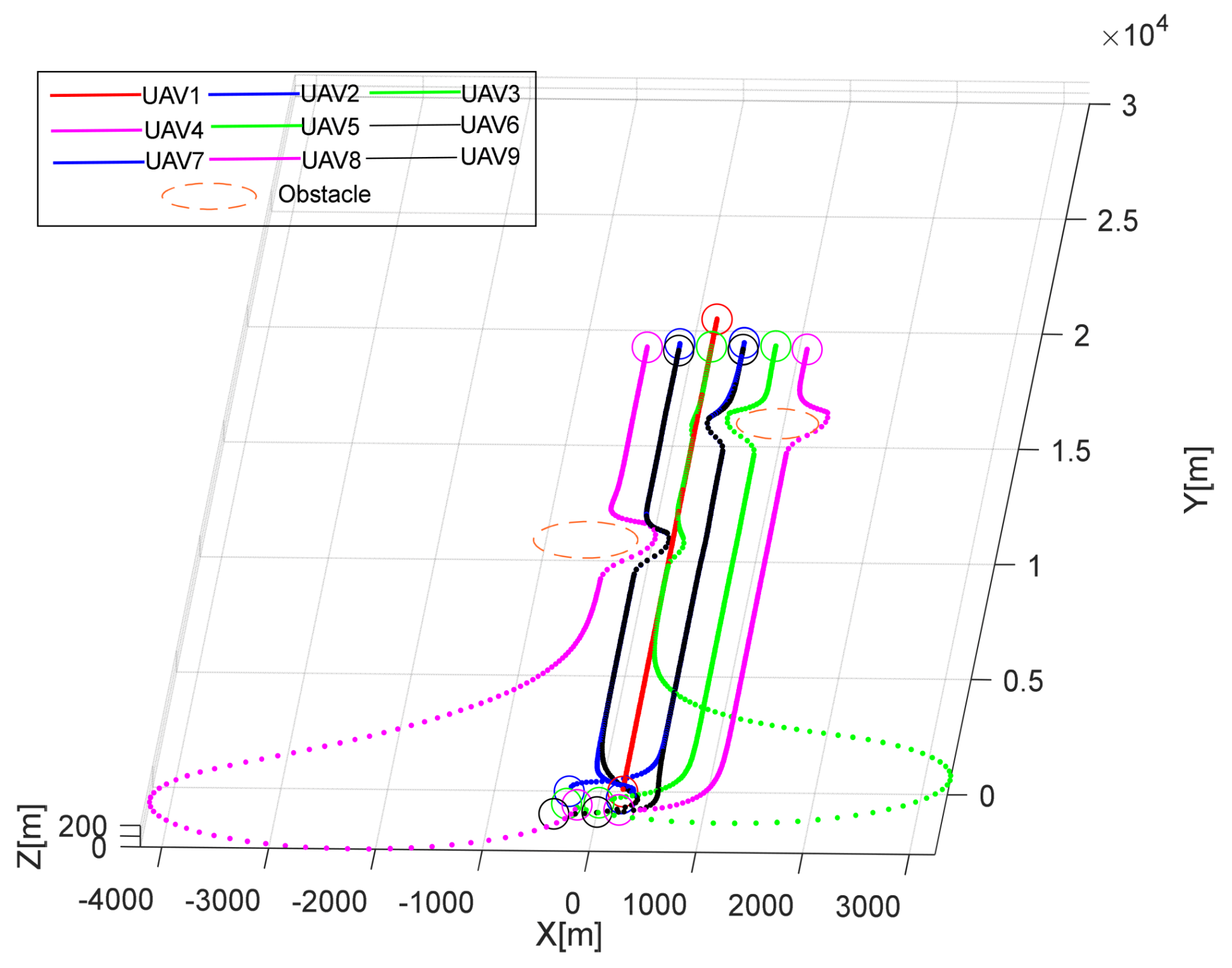
This section focuses on the design and development of the formation avoidance control system by integrating the IAAPF method with SMC. This system addresses the dynamic challenges associated with UAV formation flights in obstacle-rich environments. Specifically, the IAAPF method enhances traditional potential field approaches by introducing segmented attraction potential fields and adaptive factors, which allow for more refined control over obstacle avoidance. This is further strengthened by the integration of SMC, which is known for its robustness in dealing with system uncertainties and external disturbances. The combination of these two approaches ensures that UAV formations not only maintain stability during flight, but also effectively avoid collisions with both static and dynamic obstacles, even under challenging conditions. The design of the system plays a critical role in ensuring that UAVs can perform coordinated tasks while maintaining the integrity of their formation.

4.1. UAV Dynamics Modeling

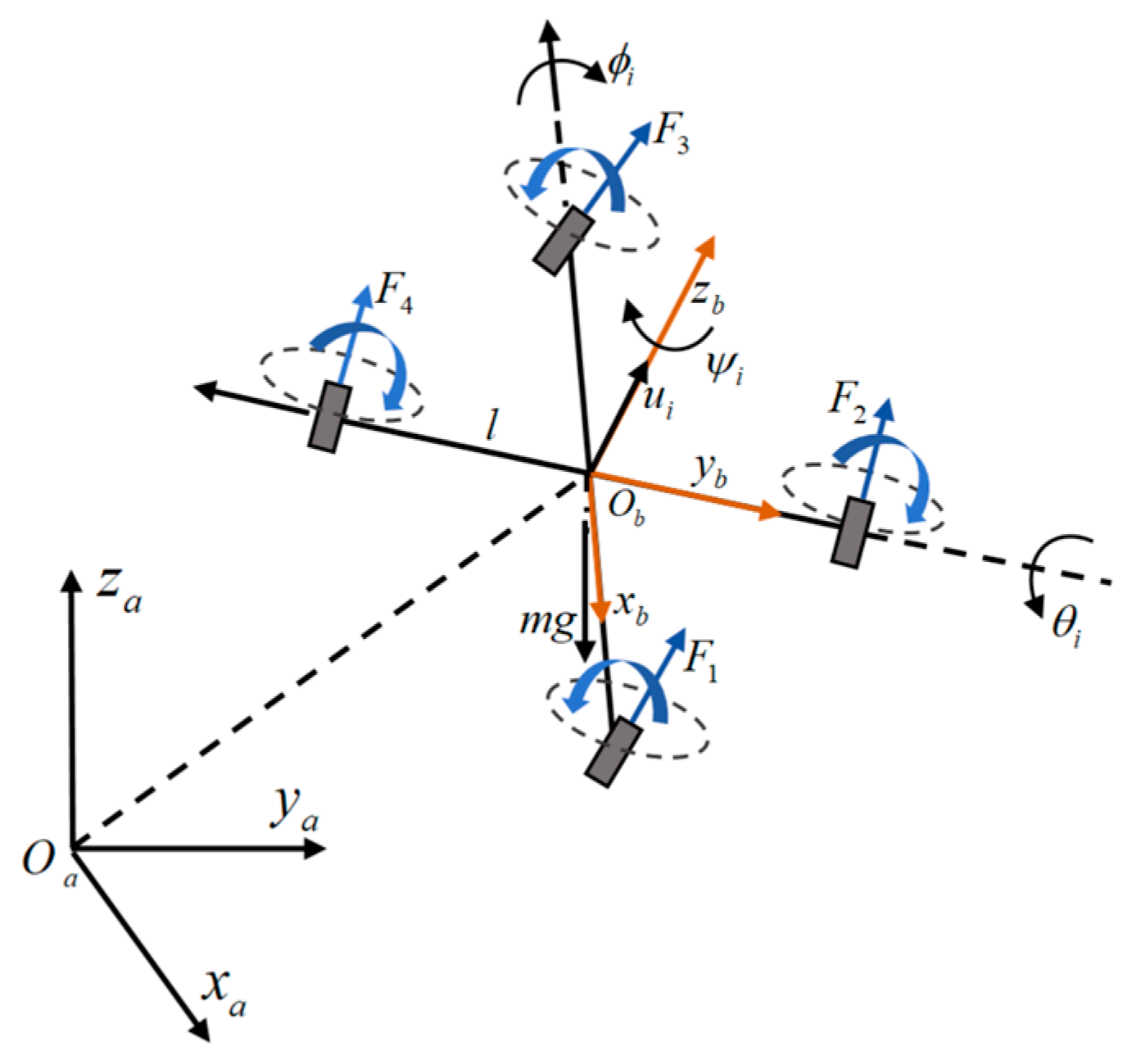
The dynamic model of a quadrotor UAV forms the basis of establishing a UAV controller system [26]. In this study, the quadrotor is modeled based on several standard assumptions to facilitate the design of the control system. Firstly, the UAV is assumed to be a rigid body, meaning that it does not undergo deformation during flight. This assumption allows for the omission of structural flexibility, which is typically negligible for small UAVs. Secondly, the quadrotor is considered to have a symmetrical structure that simplifies the inertia matrix and decouples rotational motions, making them easier to control. Finally, the center of gravity is assumed to coincide with the origin of the body-fixed frame, enabling a more straightforward application of the forces and torques in the dynamic equations. These assumptions are crucial for streamlining the development of control algorithms while ensuring reliable performance in most practical scenarios. The body coordinates are denoted as $Ob=[x_b,y_b,z_b]$ and the ground coordinates as $Oa=[x_a,y_a,z_a]$. Based on these, a rotational coordinate system is constructed, as shown in Figure 3. In this study, the quadrotor has six degrees of freedom, including three positional variables $(x,y,z)$ and three Euler angles $(\varphi ,\theta ,\psi )$.

The dynamics of the quadrotor UAV is modeled as expressed below:

$$\left\{\begin{array}{c}\ddot{x}={\displaystyle \frac{U_1}{m}}(\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi )\\ \ddot{y}={\displaystyle \frac{U_1}{m}}(\cos \phi \sin \theta \sin \psi -\sin \phi \sin \psi )\\ \ddot{z}={\displaystyle \frac{U_1}{m}}(\cos \phi \cos \theta )-g\\ \ddot{\phi }={\displaystyle \frac{\left(I_y-I_z\right)}{I_x}}\dot{\theta }\dot{\psi }+{\displaystyle \frac{l{U}_2}{I_x}}\\ \ddot{\theta }={\displaystyle \frac{\left(I_z-I_x\right)}{I_y}}\dot{\phi }\dot{\psi }+{\displaystyle \frac{l{U}_3}{I_y}}\\ \ddot{\psi }={\displaystyle \frac{\left(I_x-I_y\right)}{I_z}}\dot{\phi }\dot{\theta }+{\displaystyle \frac{l{U}_4}{I_z}}\end{array}\right.$$

(21)

In the equations: $U_1$, $U_2$, $U_3$, and $U_4$ are the control inputs of the virtual channels; $\phi$, $\theta$, and $\psi$ are the roll, pitch, and yaw angles, respectively; $I_x$, $I_y$, and $I_z$ are the moments of inertia around the x, y, and $Z$ axes, respectively; m is the mass of the quadrotor body; $l$ is the radius of the quadrotor frame; and g is the gravitational acceleration.

From the quadrotor UAV dynamics model, it can be observed that the quadrotor UAV is an underdriven model with four inputs and six outputs. In order to reduce the difficulty in designing the controller, it is converted to a fully driven model by introducing virtual control quantities $U_x$, $U_y$ and $U_z$. The virtual control quantities are as expressed below:

$$\left\{\begin{array}{c}{U}_x={\displaystyle \frac{U_1}{m}}(\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi )\\ U_y={\displaystyle \frac{U_1}{m}}(\cos \phi \sin \theta \sin \psi -\sin \phi \sin \psi )\\ U_z={\displaystyle \frac{U_1}{m}}(\cos \phi \cos \theta )\end{array}\right.$$

(22)

By inverting the attitude angles for $U_x$, $U_y$ and $U_z$, the desired inputs to the attitude control can be solved, which in turn enables full drive control [27]. The desired inputs for the roll angle ${\phi }_d$ and pitch angle ${\theta }_d$ are as expressed below:

$$U_1={\displaystyle \frac{U_{z}m}{\cos \phi \cos \theta }}$$

(23)

$${\phi }_d=\arctan ({\displaystyle \frac{U_x\cos \psi -U_y\sin \psi }{U_z}}\cos \theta )$$

(24)

$${\theta }_d=\arctan ({\displaystyle \frac{U_x\cos \psi +U_y\sin \psi }{U_z}})$$

(25)

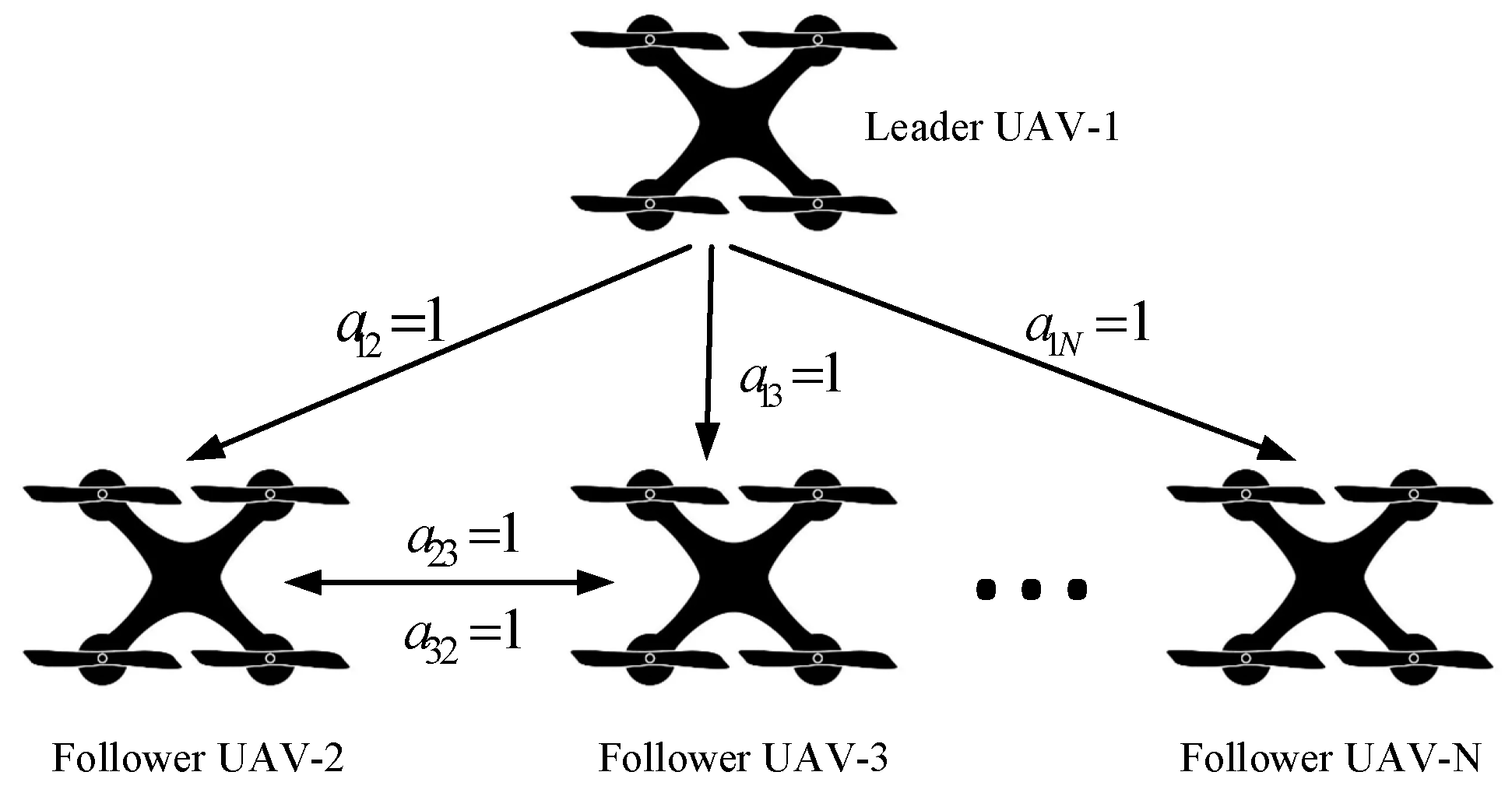
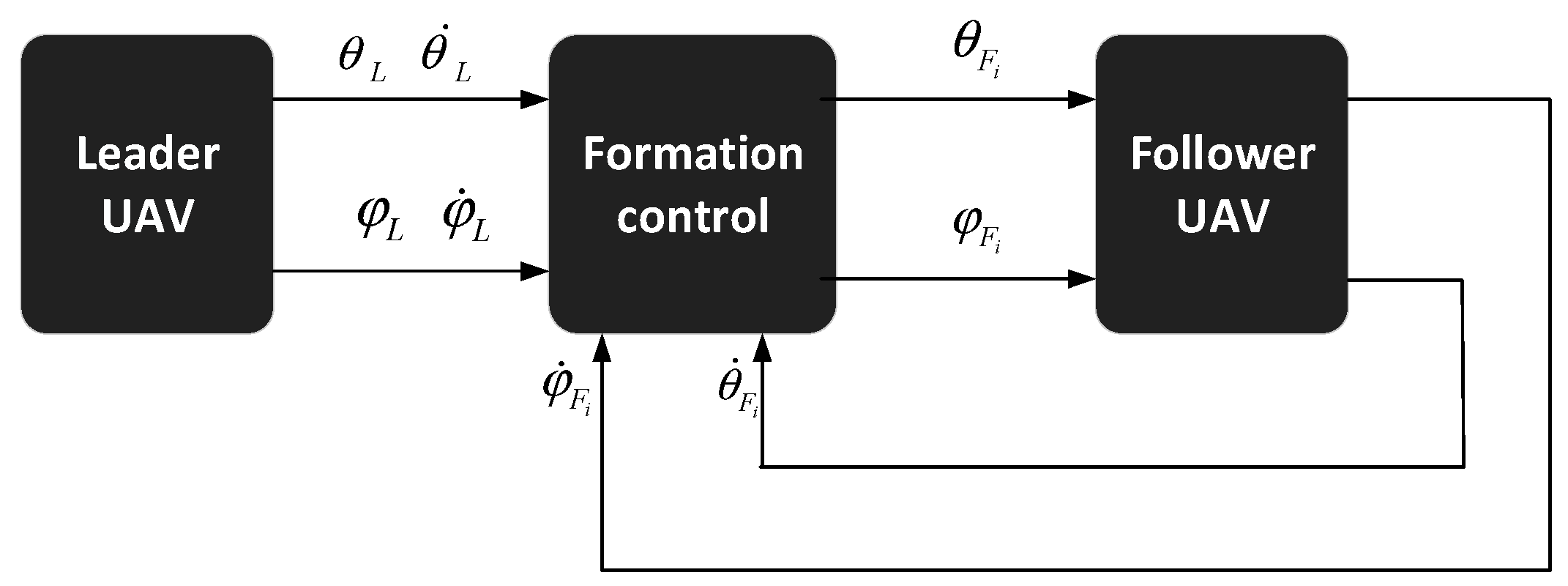
A multi-UAV formation control method is proposed to maintain a leader-follower formation, as illustrated in Figure 4. The method integrates the techniques of attraction potential field based on a segmented strategy and repulsion potential field combined with adaptive factors, as discussed earlier, aiming to achieve obstacle avoidance and formation flight among multiple UAVs. By dynamically adjusting the parameters of the repulsion potential field, the UAVs maintain the formation while avoiding obstacles and sudden changes in paths, ensuring the stability and safety of the formation flight.

Consider a formation consisting of I quadrotor UAVs using a leader-follower method, as denoted by $I\in \{L,2,3,\cdots ,N\}$ [28,29]. Where L represents the leader UAV, and N represents the number of follower UAVs. In Figure 4, the communication topology among N UAVs can be represented by a directed graph $G=(V,E)$, where each UAV is abstracted as a node, and the set of all nodes is denoted by $\nu =\left\{v_1,v_2,\cdots ,v_N\right\}$. The communication method, where a dot represents the sender and an arrow indicates the receiver, is represented by $e=(i,j)$ as the directed edges, indicating that UAV i can transmit information to UAV $j$, but not vice versa. $E\subset N\times N$ represents the set of all edges in the topology [30]. The adjacency matrix of the graph G is denoted by $A={\left[a_{ij}\right]}_{N\times N}$, where

$$a_{ij}=\left\{\begin{array}{c}{a}_{ij},(i,j)\in E\\ 0 ,other\end{array}\right.$$

(26)

As shown in Figure 4, UAV 1 can communicate with UAV 2, but UAV 2 cannot transmit information back to UAV 1. UAV 2 and UAV 3 can communicate with each other. UAV 3 can receive information from UAV 1 and UAV 2, but it cannot transmit its information to UAV 1. The adjacency matrix $A={\left[a_{ij}\right]}_{N\times N}$ represents the weight coefficients of the communication relations between the lead UAV and the follower UAVs.

As shown in Figure 5, the objective of the leader-follower formation controller is to achieve the desired configuration on the $X-Y$ plane, which can also be at the same desired altitude $Z$ at different altitudes. The formation topology is maintained by ensuring a constant distance d and the required angle $\alpha$ between each follower and the formation leader. (a) Relative Distance Components: The components $d_x$ and $d_y$ represent the distance in the X and Y directions, respectively, adjusted for the heading angle ${\psi }_L$. (b) Position Coordinates:$(X_L,Y_L)$ are the coordinates of the leader UAV, and $(X_F,Y_F)$ are the coordinates of the follower UAV. (c) Heading Angle Consideration: ${\psi }_L$ is the heading angle of the leader UAV, which defines its orientation relative to the X-axis. Thus, the equations are derived to maintain the formation structure by considering the relative positions and heading angles of the UAVs, ensuring that the follower UAV maintains the desired formation distance d and angle $\alpha$ relative to that of the leader UAV.

To account for the heading angle ${\psi }_L$ of the leader UAV, which defines its orientation relative to the X-axis, a rotation transformation is performed. This transformation is necessary to maintain the formation structure by considering the relative positions and heading angles of the UAVs. The transformed coordinates are derived as follows:

$$\left\{\begin{array}{c}{d}_x=-\Delta x\cos ({\psi }_L)-\Delta Y\sin ({\psi }_L)\\ d_y=\Delta x\sin ({\psi }_L)-\Delta Y\cos ({\psi }_L)\end{array}\right.$$

(27)

where $\Delta X=X_L-X_F$, $\Delta Y=Y_L-Y_F$ represent the position differences in global coordinates.

Substitution of position differences, the equations become

$$\left\{\begin{array}{c}{d}_x=-(X_L-X_F)\cos ({\psi }_L)-(Y_L-Y_F)\sin ({\psi }_L)\\ d_y=(X_L-X_F)\sin ({\psi }_L)-(Y_L-Y_F)\cos ({\psi }_L)\end{array}\right.$$

(28)

where $d_x$ and $d_y$ represent the $X$ and $Y$ coordinates of the actual distance $d$. This transformation ensures that the follower UAV maintains the desired formation distance $d$ and angle $\alpha$ relative to that of the leader UAV.

Equation (28) describes the relationship between the leader and follower UAVs’ positions in the $X-Y$ plane. Specifically, ${\psi }_L$ represents the heading angle of the leader UAV relative to the $X-axis$. The equations are derived as follows: (a) $d_x$ and $d_y$ are the components of the distance $d$ in the $X$ and $Y$ directions, respectively. (b) $(X_L,Y_L)$ and $(X_F,Y_F)$ are the coordinates of the leader and follower UAVs; (c) ${\psi }_L$ is the heading angle of the leader UAV, which defines its orientation.

Thus, these equations provide the necessary components for maintaining the formation structure by considering the relative positions and heading angles of the UAVs.

4.2. Position Control of the Multi-UAV

By applying an SMC, it is possible to maintain the formation of a UAV squadron even in disturbed or uncertain environments [31]. The formation control error must satisfy the following:

$$\left\{\begin{array}{c}\underset{t\to \infty }{\lim }\Vert e_x\Vert =\left|\right|d_x^d-d_x\Vert =0\\ \underset{t\to \infty }{\lim }\Vert e_y\Vert =\left|\right|d_y^d-d_y\Vert =0\end{array}\right.$$

(29)

where $d_x^d$ and $d_y^d$ are the expected distances between the pilot and the follower in coordinates $X$ and $Y$, respectively.

As shown in Figure 6, the SMC maintains the error between real-time information and expected information at zero, which is defined by the scalar equation $s(e,t)=0$ [32,33]. The SMC is utilized to minimize this error, thereby achieving formation control based on the SMC.

$$s(e,t)={({\displaystyle \frac{d}{dt}}+\lambda )}^{n-1}e$$

(30)

The second-order tracking problem can be transformed into a first-order stabilization problem; thus,

$$\left\{\begin{array}{c}\dot{s}=\ddot{e}+\lambda \dot{e}\\ {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}{s}^2\le -\eta |s|\end{array}\right.$$

(31)

where $s^2$ indicates the squared distance to the sliding surface, and $\eta$ is a positive constant.

The control law is designed to ensure that the system states follow the desired trajectories. In the context of SMC, the control input is typically applied to the system to drive the state s to zero. This approach ensures that the tracking error e and its derivative $\dot{e}$ are minimized.

The following equation can be used to control the formation of each follower in the formation:

$$\left\{\begin{array}{c}{\ddot{X}}_{F_i}={\ddot{X}}_L+{\lambda }_x({\dot{X}}_L-{\dot{X}}_{F_i})\\ {\ddot{Y}}_{F_i}={\ddot{Y}}_L+{\lambda }_y({\dot{Y}}_L-{\dot{Y}}_{F_i})\end{array}\right.$$

(32)

In this context, $\lambda$ represents a positive gain, and the control law is implicitly part of the dynamics, ensuring that $\dot{s}$ remains zero. To clarify, the Lyapunov candidate function used in SMC ensures that the error dynamics are driven to zero, stabilizing the system. Equation (31) aligns with this principle by setting up a condition where the sliding variable $s$ and its dynamics are bounded and driven toward stability.

The position control problem is transformed into an attitude control problem, and a direct estimation of the attitude can be used to control multi-UAV formation.

$$\left\{\begin{array}{c}{\theta }_{F_i}={\theta }_L+{\lambda }_{\theta }({\dot{\theta }}_L-{\dot{\theta }}_{F_i})\\ {\phi }_{F_i}={\phi }_L+{\lambda }_{\phi }({\dot{\phi }}_L-{\dot{\phi }}_{F_i})\end{array}\right.$$

(33)

where ${\lambda }_{\theta }$ and ${\lambda }_{\phi }$ are the formation control gains of ${\lambda }_{\theta }>0$, ${\lambda }_{\phi }>0$; $\theta$ and $\phi$ are the pitch and roll angles of the UAVs.

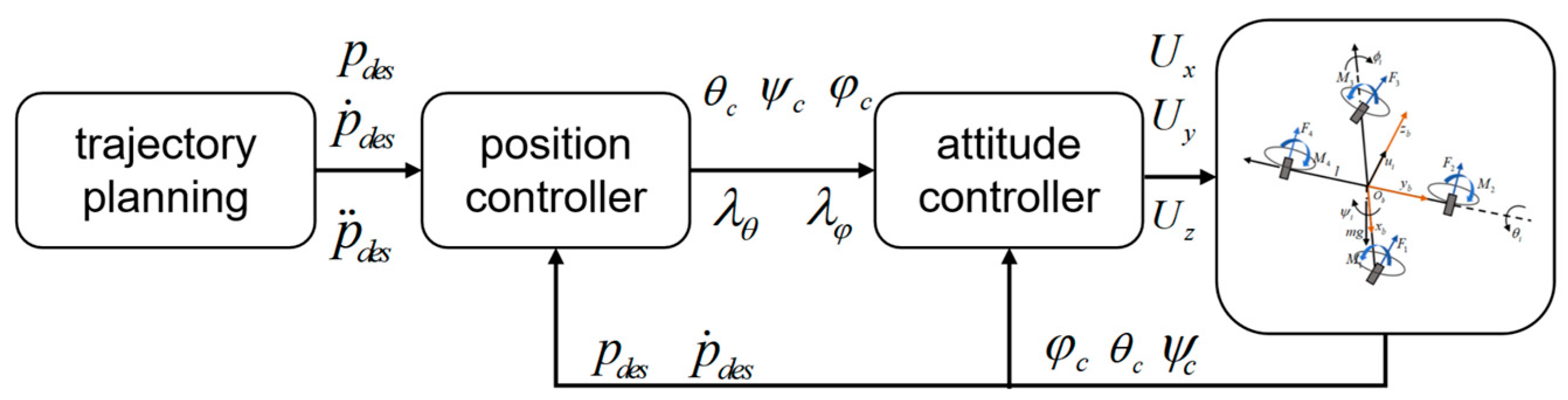
To better explain the working mechanism of this control method, as shown in Figure 7, the system is divided into four independent channels: altitude channel, $x-\theta$ cascade channel, $y-\phi$ cascade channel, and yaw channel. The altitude and yaw channels are controlled directly by the virtual control quantities $U_1$ and $U_4$, respectively. Finally, the position control problem is transformed into an attitude control problem, where the direct estimation of the attitude is used to control the formation [34,35].

(a)

Control of altitude position

The altitude channel is used as an independent channel with SMC. Define the position error of altitude as $e_{1z}$ as expressed below:

$$e_{1z}={\nu }_{1z}-x_{1z}$$

(34)

To derive the virtual control quantity for the altitude channel in this paper, the construction method of the roll channel controller presented in reference [36] is utilized.

$$U_1={\displaystyle \frac{1}{b_1}}\left(-c_{1z}^2{e}_{1z}+k_{2z}{\left|s_{1z}\right|}^{s_{1:}}\mathrm{sgn}\left(s_{1z}\right)\right.+k_{3z}{\left|s_{1z}\right|}^{{\xi }_{2z}}\mathrm{sgn}\left(s_{1z}\right)+c_{1z}{e}_{2z}+k_{1z}{s}_{1z}\left.-z_{3z}+{\ddot{v}}_{1z}\right)$$

(35)

where $c_{1z}$ acts as a gain or weighting factor, while $k_{1z}$, $k_{2z}$ and $k_{3z}$ define the system parameters and tune the controller; $0<{\xi }_{1z}<1$, $1<{\xi }_{2z}<2$; the sliding surface $s_{1z}$ of the altitude channel is $e_{2z}$; and $e_{2z}=c_{1z}{e}_{1z}+{\dot{\nu }}_{1z}-x_{2z}$.

Bringing the virtual control quantity $U_z$ into Equation (23) yields the control quantity $U_1$ for the altitude channel.

$$U_1={\displaystyle \frac{m}{b_1\cos \phi \cos \theta }}\left(-c_{1z}^2{e}_{1z}+k_{2z}{\left|s_{1z}\right|}^{y_{1z}}\mathrm{sgn}\left(s_{1z}\right)\right.+k_{3z}{\left|s_{1z}\right|}^{{\xi }_{2}z}\mathrm{sgn}\left(s_{1z}\right)+c_{1z}{e}_{2z}+k_{1z}{s}_{1z}\left.-z_{3z}+{\ddot{v}}_{1z}\right)$$

(36)

To avoid the singularities in Equation (36) when the $\phi$ or $\theta$ approach $\pm \pi /2$, a two-pronged strategy is adopted. Constraints are imposed on the pitch and roll angles to prevent them from reaching the critical values:

$$\left\{\begin{array}{c}\left|\theta \right|<{\displaystyle \frac{\pi }{2}}-ϵ\\ \left|\phi \right|<{\displaystyle \frac{\pi }{2}}-ϵ\end{array}\right.$$

(37)

where $ϵ$ is a small margin.

When the angles approach the critical limits, the control system switches to a quaternion-based representation. This representation avoids the singularities associated with the Euler angles. The quaternion-based control law for the altitude channel is given by

$$U_1={\displaystyle \frac{m}{b_1\cos \psi }}(-c_{1z}^2{e}_{1z}+k_{2z}{\left|s_{1z}\right|}^{{\xi }_{1z}}\mathrm{sgn}\left(s_{1z}\right)+k_{3z}{\left|s_{1z}\right|}^{{\xi }_{2z}}\mathrm{sgn}\left(s_{1z}\right)+c_{1z}{e}_{2z}+k_{1z}{s}_{1z}\left.-z_{3z}+{\ddot{x}}_{dz}\right)$$

(38)

where $\psi$ represents the yaw angle, and the use of the quaternion ensures smooth and continuous control without singularities.

• (b) Control of horizontal position

From Equation (21), the mathematical models for the x and y channels are similar; therefore, the x-channel is used as an example. From Equations (21) and (22), the equation of state of the x-channel is obtained as expressed below:

$$\left\{\begin{array}{c}{\dot{x}}_{1x}=x_{2x}\\ {\dot{x}}_{2x}=U_x\end{array}\right.$$

(39)

Since the mathematical model of the x-channel is a second-order system, an SMC for the x-channel needs to be designed.

First, define the tracking error $e_{1x}$ and velocity error $e_{2x}$ for the x-channel:

$$e_{1x}=x_{dx}-x_{1x}$$

(40)

The first-order derivative of the tracking error $e_{1x}$ is

$${\dot{e}}_{1x}={\dot{x}}_{dx}-{\dot{x}}_{1x}={\dot{x}}_{dx}-x_{2x}$$

(41)

To ensure stability, the first Lyapunov function is chosen as

$$V_3={\displaystyle \frac{1}{2}}{e}_{1x}^2$$

(42)

Derivation of Equation (42):

$${\dot{V}}_3=e_{1x}{\dot{e}}_{1x}=e_{1x}({\dot{x}}_{dx}-x_{2x})$$

(43)

Using $x_{2x}$ as the virtual control quantity, the desired virtual control quantity ${\alpha }_{1x}$ is when:

$${\alpha }_{1x}=c_{1x}{e}_{1x}+{\dot{x}}_{dx}$$

(44)

Define the error between the virtual control quantity $x_{2x}$ and the desired virtual control quantity ${\alpha }_{1x}$ as $e_{2x}$, as expressed below:

$$e_{2x}={\dot{x}}_{dx}+c_{1x}{e}_{1x}-x_{2x}$$

(45)

The derivation of Equation (45) is as follows:

$${\dot{e}}_{2x}={\ddot{x}}_{dx}+c_{1x}{\dot{e}}_{1x}-{\dot{x}}_{2x}$$

(46)

Based on the method used to define the sliding surface described above. Define the sliding surface as $s_{1x}=e_{2x}$ and derive it to obtain:

$${\dot{s}}_{1x}={\ddot{x}}_{dx}+c_{1x}{\dot{e}}_{1x}-U_x$$

(47)

A fast power-of-two convergence rate is used, the mathematical expression of which is shown below:

$${\dot{s}}_{1x}=-k_{1x}{s}_{1x}-k_{2x}{\left|s_{1x}\right|}^{E_{1x}}\mathrm{sgn}\left(s_{1x}\right)-k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}}\mathrm{sgn}\left(s_{1x}\right)$$

(48)

where $k_{ix}(i=1,2,3)$ defines the system parameters and tunes the controller, $0<{\xi }_{1x}<1$, $1<{\xi }_{2x}<2$.

The control rate is obtained by combining Equations (47) and (48) as expressed below:

$$U_x=-c_{1x}^2{e}_{1x}+c_{1x}{e}_{2x}+k_{1x}{s}_{1x}+k_{2x}{\left|s_{1x}\right|}^{{\xi }_{1x}}\mathrm{sgn}\left(s_{1x}\right)+k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}}\mathrm{sgn}\left(s_{1x}\right)+{\ddot{x}}_{dx}$$

(49)

Based on the above method, the virtual control rate $U_y$ for the y-channel can be obtained as expressed below:

$$U_y=-c_{1y}^2{e}_{1y}+c_{1y}{e}_{2y}+k_{1y}{s}_{1y}+k_{2y}{\left|s_{1y}\right|}^{{\xi }_{1y}}\mathrm{sgn}\left(s_{1y}\right)+k_{3y}{\left|s_{1y}\right|}^{{\xi }_{2y}}\mathrm{sgn}\left(s_{1y}\right)+{\ddot{y}}_{dy}$$

(50)

where $c_{1y}$, $k_{1y}(i=1,2,3)$ are constants with typical or standard values, $0<{\xi }_{1y}<1$, $1<{\xi }_{2y}<2$, and the sliding surface $s_{1y}$ is $e_{2y}$.

To ensure that the designs of $U_1$, $U_x$ and $U_y$ satisfy the relationship shown in Equation (22), a detailed verification process is provided. This process demonstrates that the individual designs of $U_1$, $U_x$ and $U_y$ align with the overall system dynamics and control objectives.

(a)

To clarify the relationships and equations used, the following restatements are made:

Firstly, the virtual control quantities are derived as previously shown in Equation (22).

Secondly, the designed control quantities are obtained from the previously presented Equations (36), (47) and (48).

This approach ensures that the individual designs of $U_1$, $U_x$ and $U_y$ align with the overall system dynamics and control objectives, as detailed in the aforementioned equations.

(b)

Expressing $U_1$ in Terms of $U_x$, $U_y$ and $U_z$

In addition, to verify consistency, $U_1$ is expressed with $U_x$ and $U_y$:

$$\left\{\begin{array}{c}{U}_1={\displaystyle \frac{m{U}_x}{\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi }}\\ U_1={\displaystyle \frac{m{U}_y}{\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi }}\end{array}\right.$$

(51)

(c)

Substituting Designed $U_1$ into $U_x$ and $U_y$

Next, the designed $U_1$ from Equation (36) is substituted into the expressions for $U_x$ and $U_y$ as follows:

$$\left\{\begin{array}{c}{U}_x={\displaystyle \frac{\left(\frac{m}{b_1\cos \phi \cos \theta }(-c_{1z}^2{e}_{1z}+k_{2z}|s_{1z}{|}^{{\xi }_{1z}}\mathrm{sgn}(s_{1z})+k_{3z}|s_{1z}{|}^{{\xi }_{2z}}\mathrm{sgn}(s_{1z})+c_{1z}{e}_{2z}+k_{1z}{s}_{1z}-z_{3z}+{\ddot{x}}_{dx})\right)}{m}}(\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi )\\ U_y={\displaystyle \frac{\left(\frac{m}{b_1\cos \phi \cos \theta }(-c_{1x}^2{e}_{1x}+k_{2z}|s_{1z}{|}^{{\xi }_{1z}}\mathrm{sgn}(s_{1z})+k_{3z}|s_{1z}{|}^{{\xi }_{2z}}\mathrm{sgn}(s_{1z})+c_{1z}{e}_{2z}+k_{1z}{s}_{1z}-z_{3z}+{\ddot{x}}_{dx})\right)}{m}}(\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi )\end{array}\right.$$

(52)

• (d) Verifying Consistency

Finally, the derived expressions for $U_x$ and $U_y$ are compared with their designed forms (Equations (49) and (50)) to ensure they match:

$$\left\{\begin{array}{c}{U}_x=-c_{1x}^2{e}_{1x}+c_{1x}{e}_{2x}+k_{1x}{s}_{1x}+k_{2x}{\left|s_{1x}\right|}^{{\xi }_{1x}}\mathrm{sgn}\left(s_{1x}\right)+k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}}\mathrm{sgn}\left(s_{1x}\right)+{\ddot{x}}_{dx}\\ U_y=-c_{1y}^2{e}_{1y}+c_{1y}{e}_{2y}+k_{1y}{s}_{1y}+k_{2y}{\left|s_{1y}\right|}^{{\xi }_{1y}}\mathrm{sgn}\left(s_{1y}\right)+k_{3y}{\left|s_{1y}\right|}^{{\xi }_{2y}}\mathrm{sgn}\left(s_{1y}\right)+{\ddot{y}}_{dx}\end{array}\right.$$

(53)

The steps taken demonstrate that the designed control quantities $U_1$, $U_x$ and $U_y$ are consistent with the quadrotor UAV dynamics described as described by Equation (22). This verification ensures the validity and reliability of the control design.

Formal proof of consistency for $U_1$ across axes.

Ensuring the consistency of the control input $U_1$ across the $x$, $y$, and $z$ axes is crucial for the reliable operation of the UAV under the proposed control framework. This section presents a rigorous proof that the value of $U_1$, derived from the control laws corresponding to each axis remains consistent under the specified control laws and system constraints.

(a)

Derivation of $U_1$ from each axis: The virtual control inputs $U_x$, $U_y$, and $U_z$ are defined in terms of the primary control input $U_1$ as follows.

$$\left\{\begin{array}{c}{U}_x=U_1\left({\displaystyle \frac{\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi }{m}}\right)\\ U_y=U_1\left({\displaystyle \frac{\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi }{m}}\right)\\ U_z=U_1\left({\displaystyle \frac{\cos \phi \cos \theta }{m}}\right)\end{array}\right.$$

(54)

From these relationships, the control input $U_1$ can be expressed for each axis as follows:

$$\left\{\begin{array}{c}{U}_1^x={\displaystyle \frac{m{U}_x}{\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi }}\\ U_1^y={\displaystyle \frac{m{U}_y}{\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi }}\\ U_1^z={\displaystyle \frac{m{U}_z}{\cos \phi \cos \theta }}\end{array}\right.$$

(55)

(b)

Establishing consistency conditions: To ensure the consistency of $U_1$ across all axes, it is necessary that:

$$U_1^x=U_1^y=U_1^z=U_1$$

(56)

This equality implies the following conditions:

$${\displaystyle \frac{m{U}_x}{\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi }}={\displaystyle \frac{m{U}_y}{\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi }}={\displaystyle \frac{m{U}_z}{\cos \phi \cos \theta }}$$

(57)

These conditions must hold true for the system to maintain consistent control across the $x$, $y$, and $z$ axes.

(c)

Addressing angular and acceleration dependencies: The consistency of $U_1$ across the axes requires careful consideration of the following factors:

The trigonometric terms involving $\phi$, $\theta$, and $\psi$ are functions of the UAV’s orientation. It is essential to ensure that these terms do not introduce any inconsistencies in the derived $U_1$ values. This is achieved by constraining the angular parameters to avoid singularities, particularly near critical angles, such as $\theta =\pm {\displaystyle \frac{\pi }{2}}$ or $\phi =\pm {\displaystyle \frac{\pi }{2}}$. These constraints prevent the denominators in the expressions for $U_1^x$, $U_1^y$, and $U_1^z$ from approaching zero, which could otherwise lead to significant variations in the calculated $U_1$.

The system’s dynamics, particularly the accelerations ${\ddot{x}}_d$, ${\ddot{y}}_d$, and ${\ddot{z}}_d$, play a significant role in the control inputs. The control gains $k_{2x}$, $k_{3x}$, $k_{2y}$, $k_{3y}$, $k_{2z}$, $k_{3z}$ are chosen to satisfy the following condition:

$$k_{2x},k_{3x}>{\displaystyle \frac{M}{\min ({\left|s_{1x}\right|}^{{\xi }_1+1},{\left|s_{1x}\right|}^{{\xi }_2+1})}}$$

(58)

This ensures that the acceleration terms do not introduce inconsistencies between the different $U_1$ values derived from the x, y, and z axes. Similar conditions are applied for the y and z axes.

(d)

Mathematical proof of negative definiteness: To further solidify the consistency of $U_1$ a Lyapunov function $V$ is defined, and its time derivative $\dot{V}$ is derived to demonstrate system stability.

$$\dot{V}=-k_{1x}{e}_{1x}^2-k_{2x}{\left|s_{1x}\right|}^{{\xi }_1+1}-k_{3x}{\left|s_{1x}\right|}^{{\xi }_2+1}+{\ddot{x}}_d$$

(59)

The terms in $\dot{V}$ are designed such that: $\dot{V}\le 0$ for all $s_{1x}$, $s_{1y}$, $s_{1z}$ and corresponding accelerations. The negative definiteness of $\dot{V}$ implies that the system’s error dynamics drive the system toward stability, thereby ensuring that the control input $U_1$ derived from any axis remains consistent.

Demonstrate the stability of the SMC using Lyapunov-Like Lemma to construct the Lyapunov function containing $s_{1x}$ and $s_{1x}$:

$$V_4={\displaystyle \frac{1}{2}}{e}_{1x}^2+{\displaystyle \frac{1}{2}}{s}_{1x}^2$$

(60)

The derivation of $V_4$ is obtained by combining Equations (44), (45) and (48):

$${\dot{V}}_4=e_{1x}{\dot{e}}_{1x}+s_{1x}{\dot{s}}_{1x}=e_{1x}{\dot{e}}_{1x}-k_{1x}{s}_{1x}^2-k_{2x}|s_{1x}{|}^{{\xi }_{1x}+1}-k_{3x}|s_{1x}{|}^{{\xi }_{2x}+1}$$

(61)

Construct the matrix ${\mathit{D}}_x$:

$${\mathit{D}}_x=\left[\begin{array}{cc}{k}_{1x}& k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}\\ k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}& k_{1x}{c}_{1x}^2\end{array}\right]$$

(62)

Available:

$$\begin{array}{ll}{\mathit{x}}^T{\mathit{D}}_x\mathit{x}& =\left[\begin{array}{ll}{\dot{e}}_{1x}\hfill & e_{1x}\hfill \end{array}\right]\left[\begin{array}{cc}{k}_{1x}& k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}\\ k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}& k_{1x}{c}_{1x}^2\end{array}\right]\left[\begin{array}{l}{\dot{e}}_{1x}\hfill \\ e_{1x}\hfill \end{array}\right]\\ & ={\dot{e}}_{1x}(k_{1x}{\dot{e}}_{1x}+(k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}})e_{1x})+e_{1x}((k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}){\dot{e}}_{1x}{e}_{1x}+k_{1x}{c}_{1x}^2{e}_{1x})\\ & =k_{1x}{\dot{e}}_{1x}^2+2(k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}}){\dot{e}}_{1x}{e}_{1x}+k_{1x}{c}_{1x}^2{e}_{1x}^2\end{array}$$

(63)

Substituting the error dynamics, given the sliding surface $s_{1x}$ and its relation to the error dynamics:

$$\left\{\begin{array}{c}{s}_{1x}={\dot{e}}_{1x}+c_{1x}{e}_{1x}\\ {\dot{e}}_{1x}=s_{1x}-c_{1x}{e}_{1x}\end{array}\right.$$

(64)

Rewriting in terms of the siding surface, substitute ${\dot{e}}_{1x}=s_{1x}-c_{1x}{e}_{1x}$ into the quadratic form:

$$\begin{array}{ll}{\mathit{x}}^T{\mathit{D}}_x\mathit{x}& =k_{1x}{(s_{1x}-c_{1x}{e}_{1x})}^2+2(k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}})(s_{1x}-c_{1x}{e}_{1x})e_{1x}+k_{1x}{c}_{1x}^2{e}_{1x}^2\\ & =k_{1x}{s}_{1x}^2-2k_{1x}{s}_{1x}{c}_{1x}{e}_{1x}+k_{1x}{c}_{1x}^2{e}_{1x}^2+2(k_{1x}{c}_{1x}{s}_{1x}{e}_{1x}-k_{1x}{c}_{1x}^2{e}_{1x}^2-{\displaystyle \frac{1}{2}}{s}_{1x}{e}_{1x}+{\displaystyle \frac{1}{2}}{c}_{1x}{e}_{1x}^2)+k_{1x}{c}_{1x}^2{e}_{1x}^2\\ & =k_{1x}{s}_{1x}^2+(k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}})s_{1x}{e}_{1x}\end{array}$$

(65)

This form shows that the quadratic term involving $k_{1x}{s}_{1x}^2$ dominates, ensuring the positive definiteness of the Lyapunov function derivative. Thus, Equation (65) holds when considering the sliding surface dynamics and error dynamics in the Lyapunov stability analysis.

If the matrix ${\mathit{D}}_x$ can be guaranteed to be positive definite then:

$${\dot{V}}_2={\mathit{x}}^T{\mathit{D}}_x\mathit{x}-k_{2x}{\left|s_{1x}\right|}^{{\xi }_{1x}+1}-k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}+1}\le 0$$

(66)

To ensure that matrix ${\mathit{D}}_x$ is positive definite, the determinant $\left|{\mathit{D}}_x\right|$ must satisfy the following condition:

$$\left|{\mathit{D}}_x\right|=k_{1x}^2{c}_{1x}^2-{(k_{1x}{c}_{1x}-{\displaystyle \frac{1}{2}})}^2=k_{1x}{c}_{1x}-{\displaystyle \frac{1}{4}}>0$$

(67)

The stability proof for the backstepped SMC in the y-channel is the same as that for the x-channel.

Consider a UAV system with the control laws $U_x$, $U_y$ and $U_z$ designed according to the relations provided in Equations (36), (49) and (50). Under these control laws, the UAV will avoid undesired equilibrium points in the presence of obstacles and disturbances.

To ensure the stability of the system, a Lyapunov function $V$ is constructed. The function is given by

$$V={\displaystyle \frac{1}{2}}(e_{1x}^2+e_{2x}^2+e_{1y}^2+e_{2y}^2+e_{1z}^2+e_{1z}^2)$$

(68)

where $e_{1x},e_{2x},e_{1y},e_{2y},e_{1z},e_{2z}$ are the tracking errors in the $x$, $y$ and $z$ directions, respectively.

The time derivative of $V$ along the trajectories of the system is

$$\dot{V}=e_{1x}{\dot{e}}_{1x}+e_{2x}{\dot{e}}_{2x}+e_{1y}{\dot{e}}_{1y}+e_{2y}{\dot{e}}_{2y}+e_{1z}{\dot{e}}_{1z}+e_{2z}{\dot{e}}_{2z}$$

(69)

Using the control laws and system dynamics, the expressions for ${\dot{e}}_{1x}$, ${\dot{e}}_{2x}$, ${\dot{e}}_{1y}$, ${\dot{e}}_{2y}$, ${\dot{e}}_{1z}$ and ${\dot{e}}_{2z}$ are substituted.

By incorporating the control laws $U_x$, $U_y$ and $U_z$ into the aforementioned derivative, the following result is obtained:

$$\begin{array}{ll}\dot{V}=& -k_{1x}^2{e}_{1x}^2-k_{2x}{s}_{1x}{\left|s_{1x}\right|}^{{\xi }_{1x}+1}-k_{3x}{s}_{1x}{\left|s_{1x}\right|}^{{\xi }_{2x}+1}+{\ddot{x}}_{dx}\\ & -k_{1y}^2{e}_{1y}^2-k_{2y}{s}_{1y}{\left|s_{1y}\right|}^{{\xi }_{1y}+1}-k_{3y}{s}_{1y}{\left|s_{1y}\right|}^{{\xi }_{2y}+1}+{\ddot{y}}_{dx}\\ & -k_{1z}^2{e}_{1z}^2-k_{2z}{s}_{1z}{\left|s_{1z}\right|}^{{\xi }_{1z}+1}-k_{3z}{s}_{1z}{\left|s_{1z}\right|}^{{\xi }_{2z}+1}+{\ddot{z}}_{dx}\end{array}$$

(70)

To ensure that $\dot{V}$ is negative definite, the control gains must satisfy the following inequalities:

$$\left\{\begin{array}{c}{k}_{2x}{\left|s_{1x}\right|}^{{\xi }_{1x}+1}+k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}+1}>{\ddot{x}}_d\\ k_{2y}{\left|s_{1y}\right|}^{{\xi }_{1y}+1}+k_{3y}{\left|s_{1y}\right|}^{{\xi }_{2y}+1}>{\ddot{y}}_d\\ k_{2z}{\left|s_{1z}\right|}^{{\xi }_{1z}+1}+k_{3z}{\left|s_{1z}\right|}^{{\xi }_{2z}+1}>{\ddot{z}}_d\end{array}\right.$$

(71)

These inequalities ensure that the negative contributions from the sliding surface terms outweigh the positive contributions from the desired accelerations.

The control gains $k_{2x}$, $k_{3x}$, $k_{2y}$, $k_{3y}$, $k_{2z}$ and $k_{3z}$ should be chosen such that they are sufficiently large to account for any changes in the signs of $s_{1x}$, $s_{1y}$ and $s_{1z}$. Specifically, the gain terms must ensure that

$$\left\{\begin{array}{c}{k}_{2x}>{\displaystyle \frac{{\ddot{x}}_d}{{\left|s_{1x}\right|}^{{\xi }_{1x}+1}}},k_{3x}>{\displaystyle \frac{{\ddot{x}}_d}{{\left|s_{1x}\right|}^{{\xi }_{2x}+1}}}\\ k_{2y}>{\displaystyle \frac{{\ddot{y}}_d}{{\left|s_{1y}\right|}^{{\xi }_{1y}+1}}},k_{3y}>{\displaystyle \frac{{\ddot{y}}_d}{{\left|s_{1y}\right|}^{{\xi }_{2y}+1}}}\\ k_{2z}>{\displaystyle \frac{{\ddot{z}}_d}{{\left|s_{1z}\right|}^{{\xi }_{1z}+1}}},k_{3z}>{\displaystyle \frac{{\ddot{z}}_d}{{\left|s_{1z}\right|}^{{\xi }_{2z}+1}}}\end{array}\right.$$

(72)

This condition ensures that even if $s_{1x}$, $s_{1y}$, or $s_{1z}$ change signs, the corresponding gains will still dominate, keeping $\dot{V}$ negative.

Formal proof of negative definiteness:

(a)

Assumption on acceleration terms: The desired accelerations ${\ddot{x}}_d$, ${\ddot{y}}_d$ and ${\ddot{z}}_d$ are bounded by a known positive constant $M>0$. This assumption is reasonable in practical scenarios, as UAVs typically operate within physical limits and their accelerations cannot grow unbounded.

$$\left\{\begin{array}{c}\left|{\ddot{x}}_d\right|\le M\\ \left|{\ddot{y}}_d\right|\le M\\ \left|{\ddot{z}}_d\right|\le M\end{array}\right.$$

(73)

This boundedness condition ensures that any potential positive contribution from the desired acceleration terms in the expression for $\dot{V}$ can be counteracted by appropriately chosen control gains.

(b)

Selection of control gains: The control gains $k_{2x}$, $k_{3x}$, $k_{2y}$, $k_{3y}$, $k_{2z}$ and $k_{3z}$ are selected to dominate any positive contributions from the desired accelerations. Specifically, the gains must satisfy the following conditions:

$$\left\{\begin{array}{c}{k}_{2x},k_{3x}>{\displaystyle \frac{M}{\min ({\left|s_{1x}\right|}^{{\xi }_{1x}+1},{\left|s_{1x}\right|}^{{\xi }_{2x}+1})}}\\ k_{2y},k_{3y}>{\displaystyle \frac{M}{\min ({\left|s_{1y}\right|}^{{\xi }_{1y}+1},{\left|s_{1y}\right|}^{{\xi }_{2y}+1})}}\\ k_{2z},k_{3z}>{\displaystyle \frac{M}{\min ({\left|s_{1z}\right|}^{{\xi }_{1z}+1},{\left|s_{1z}\right|}^{{\xi }_{2z}+1})}}\end{array}\right.$$

(74)

These inequalities ensure that the negative terms involving the sliding surfaces $s_{1x}$, $s_{1y}$ and $s_{1z}$ in the expression for $\dot{V}$ outweigh any positive contribution from the desired accelerations ${\ddot{x}}_d$, ${\ddot{y}}_d$ and ${\ddot{z}}_d$.

(c)

Substitution into the Lyapunov derivative: With the selected control gains, substitute these conditions back into the expression for $\dot{V}$ derived earlier. The control gains $k_{2x}$, $k_{3x}$, $k_{2y}$, $k_{3y}$, $k_{2z}$ and $k_{3z}$ have been chosen such that the negative terms $-k_{2x}{\left|s_{1x}\right|}^{{\xi }_{1x}+1}$, $-k_{3x}{\left|s_{1x}\right|}^{{\xi }_{2x}+1}$ and their counterparts for the $y$ and $z$ axes dominate any positive terms from the desired accelerations ${\ddot{x}}_d$, ${\ddot{y}}_d$ and ${\ddot{z}}_d$. This implies $\dot{V}>0$ for all $s_{1x}$, $s_{1y}$, $s_{1z}$ and corresponding accelerations.

Since all terms contributing to $\dot{V}$ are either negative or zero, $\dot{V}$ is conclusively proven to be negative definite. This result ensures that the Lyapunov function $V$ decreases over time, which is a critical indicator of system stability. The negative definiteness of $\dot{V}$ implies that the UAV’s control system will naturally drive the state errors $e_{1x}$, $e_{1y}$ and $e_{1z}$ to zero, along with the sliding surfaces $s_{1x}$, $s_{1y}$ and $s_{1z}$, thereby ensuring convergence to the desired trajectory and avoiding undesired equilibrium points.

The control gains $k_{1x},k_{2x},k_{3x},k_{1y},k_{2y},k_{3y},k_{1z},k_{2z},k_{3z}$ are chosen such that $\dot{V}$ is negative definite. This ensures that $V$ is always decreasing, leading to the stability of the system and convergence of the errors to zero. The terms ${\ddot{x}}_{dx}$, ${\ddot{y}}_{dx}$, and ${\ddot{z}}_{dx}$ represent the desired acceleration components. The design ensures that these terms drive the system away from undesired equilibrium points by continuously updating the desired trajectories based on the obstacle feedback and state errors.

By segmenting the control system into these distinct channels, the UAV’s altitude and yaw can be managed independently, allowing for precise control through the direct input of the virtual control quantities. This approach simplifies the overall control strategy by breaking it down into manageable parts and leveraging the direct estimation of the attitude to achieve cohesive formation control.

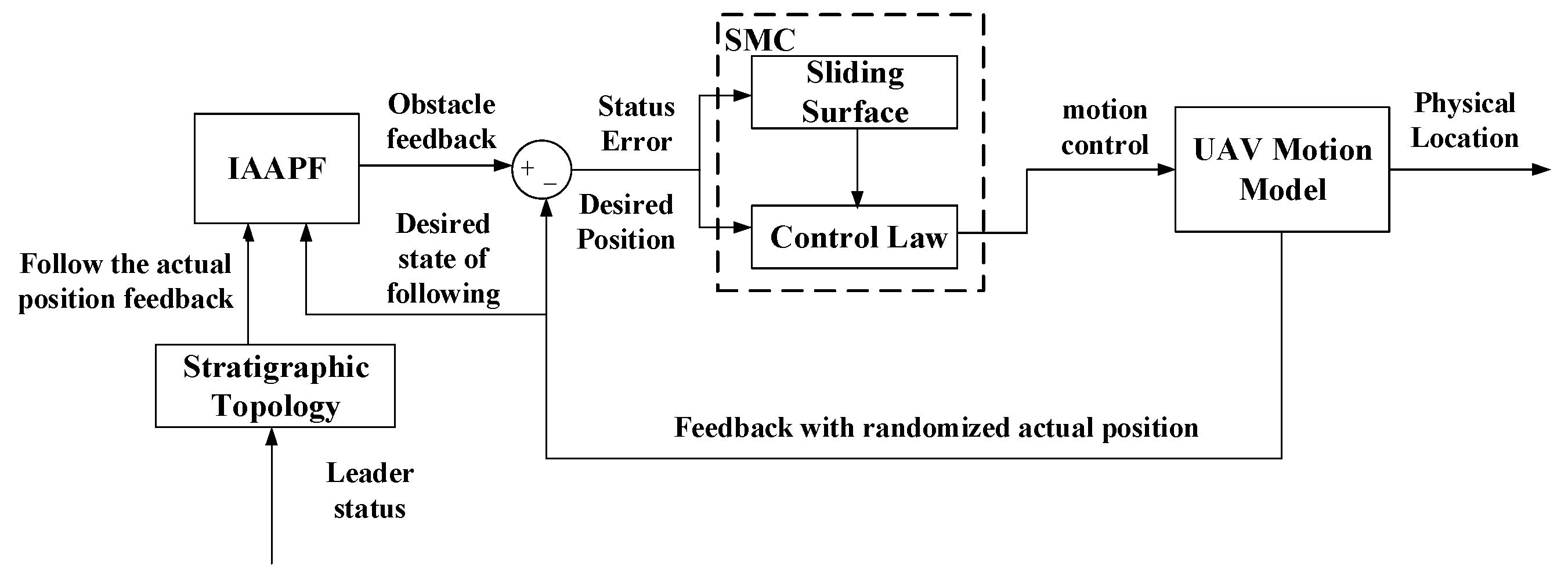
In the design of a dynamic trajectory planning method for multi-UAVs, the obstacle avoidance method, as an independent module, needs to be connected to the formation control module and primarily operates before the motion controller of the follower receives the desired state information [37]. This paper adopts a feedback control system with inner and outer loops to connect the obstacle avoidance module based on the IAAPF (inner loop) and the SMC module based on the leader-following method (outer loop). In this design, the outer loop is responsible for generating the desired path or trajectory, while the inner loop is responsible for tracking these trajectories. The state error passed to the motion controller of the follower is no longer directly calculated from the desired state based on the leader’s state and control commands, but rather derived from the obstacle feedback obtained by the IAAPF based on the desired state of the follower and the actual states of each UAV, which is then combined with the position error of the actual state of the follower and input into the follower’s motion controller. The follower motion controller considers obstacle feedback before receiving the desired state information. This approach ensures effective obstacle avoidance while maintaining the shape of the formation, as shown in Figure 8.

In this closed-loop control system, the key lies in the computation of the corrected desired state and corrected control commands. Here, the obstacle feedback is integrated into the desired state, and the state error is used to correct the control commands. The corrected desired state $X_{ref,corrected}$, state error $e$, and corrected control commands $u_{corrected}$ are as follows:

$$\left\{\begin{array}{c}{X}_{ref,corrected}=X_{ref}+F_{obs}\\ e=X_{ref,corrected}-X_{actual}\\ u_{corrected}=u+K_{p}e\end{array}\right.$$

(75)

where $X_{ref}$ is the desired position state vector, $X_{actual}$ is the actual position state vector, $u$ is the original attitude control vector, $F_{obs}$ is the obstacle feedback vector, $e$ is the state error vector, and $K_p$ is the proportional gain matrix.

The computation of the corrected desired state and corrected control commands is integral. The desired state ($X_{ref}$) is modified by incorporating the obstacle feedback ($F_{obs}$), resulting in a corrected desired state ($X_{ref,corrected}$). The state error ($e$) is derived from the difference between this corrected desired state and the actual state ($X_{actual}$). The original control commands ($u$) are then adjusted based on this state error to form the corrected control commands ($u_{corrected}$), ensuring that the UAV follows the desired trajectory while effectively avoiding obstacles.

5. Simulation Verification

This section provides comprehensive validation of the proposed IAAPF-SMC system through a series of simulation experiments. These simulations are conducted to evaluate the system’s performance in various obstacle environments and demonstrate its effectiveness in maintaining formation stability and achieving obstacle avoidance. By comparing the results of the traditional artificial potential field methods with those of the improved IAAPF approach, Section 5 highlights how the adaptive and segmented potential fields significantly reduce the occurrence of local minima and improve path smoothness, thereby enhancing the overall flight efficiency. The results of the simulations offer crucial insights into the practical application of the proposed control system, illustrating its capability to generate safe and optimal flight paths in real time, ensuring that UAV formations reach their destinations without collisions.

5.1. Simulation Validation of Obstacle Avoidance Algorithm with IAAPF

To verify the effectiveness of the IAAPF in solving the problem of multi-UAVs being unable to reach their target due to nearby obstacles, a simulation verification is conducted. This involves comparing the traditional APF algorithm with an improved version. Simulations were performed to validate the two-dimensional planar environment with multiple obstacles. In the simulation environment, each obstacle is defined by its radius and centroid position. The specific simulation conditions and settings are as follows:

The effectiveness of this path-planning algorithm in complex obstacle environments can be verified by the above setup, as shown in Figure 9.

As shown in Figure 9, compared to the traditional artificial potential field algorithm, the UAV using the artificial potential field algorithm with an adaptive factor not only can dynamically adjust the repulsive force based on the distance to obstacles, effectively solving the problem of multi-UAVs being unable to reach their target due to nearby obstacles, but it can also introduce a smoothing factor in the calculation of the repulsive force. This allows the UAV to choose a smoother path to circumvent obstacles rather than making sudden turns to avoid them, preventing the oscillation phenomena often seen in the traditional artificial potential field algorithms due to abrupt changes in heading.

The improved method, by smoothing the path planning and dynamically adjusting the repulsive force of obstacles, makes the UAV more stable during obstacle avoidance, reducing the time of oscillation, as shown in Figure 10.

As shown in Figure 10, the oscillation time for the traditional artificial potential field method is 45 s, while with our improved artificial potential field method, the oscillation time is reduced to 39 s, a decrease of 13.33%. The improved method is more stable compared to the traditional artificial potential field method, reducing the oscillations during obstacle avoidance and enhancing the efficiency and performance of path planning, which leads to smoother trajectories. The reduction in oscillation time is crucial as it directly impacts the stability and control of the UAVs, leading to more reliable and predictable flight paths.

In this simulation, the aim is to verify the efficiency of IAAPF, an algorithm that uses a potential field to navigate a robotic agent from a starting point to a destination point while avoiding obstacles. The environment is a 3D space filled with several spherical obstacles. The coordinates and radii of the obstacles are as follows: Obstacle 1, Center: (80, 85, 100), Radius: 3; Obstacle 2, Center: (175, 135, 100), Radius: 3; Obstacle 3, Center: (225, 200, 100), Radius: 3; Obstacle 4, Center: (300, 320, 100), Radius: 3; Obstacle 5, Center: (370, 350, 100), Radius: 3. The other potential field parameters are the same as those in

Table 1. Comparison of simulation parameters of the artificial potential field method.

Parameters	Value
Destination (m)	(95, 70)
Start (m)	(5, 5)
k	100
r	1011
Velocity (m/s)	15
Obstacle 1 (m)	(25, 75), R = 9
Obstacle 2 (m)	(81, 30), R = 8
Obstacle 3 (m)	(70, 70), R = 18
Obstacle 4 (m)	(32, 27), R = 14

.

The performance of the IAAPF algorithm was validated through Monte Carlo (MC) simulations, which involved multiple scenarios with varying numbers and configurations of obstacles. This process involved several key steps:

(a) In each simulation run, obstacles were randomly placed within the environment. This ensured that the UAV encountered a variety of obstacle configurations, testing the robustness of the IAAPF algorithm under different conditions. (b) Each simulation also included random initial conditions for the UAV, such as starting position and initial velocity, to further assess the algorithm’s adaptability.

Figure 11 shows the IAAPF path planning in a 3D space, depicting the trajectory of the UAV as it navigates through the environment. Figure 12 displays the obstacle avoidance trajectory based on IAAPF, with the blue curve representing the path from the start point to the endpoint. This path demonstrates how the UAV moves from one destination to another while avoiding obstacles. The significant curvature of the path when approaching obstacles indicates that the path-planning algorithm has optimized the route to avoid collisions, showcasing the algorithm’s ability to adapt to complex environments, particularly its spatial awareness and decision-making capabilities when dealing with multiple obstacles.

The results of the MC simulations confirmed the algorithm’s capability to handle various unpredictable scenarios, ensuring more reliable and predictable flight paths for the UAV. The significant reduction in oscillation time and optimized trajectories underscore the robustness and effectiveness of the IAAPF algorithm in diverse and complex environments.

5.2. IAAPF-SMC Simulation Validation for Multi-UAV Formations

The simulation study in this section aims to analyze the dynamic behavior of IAAPF-SMC in multi-UAV in obstacle avoidance and path planning. According to Equation (53) system model and control strategy, the simulation conditions are set as follows for this purpose: the simulation conditions and parameters are set to ensure the validity and reliability of the simulation results. By adopting a system containing six UAVs, its adjacency matrix $A$ defines the communication topology between the UAVs:

$$A=\left[\begin{array}{cccccc}0& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 1\\ 0& 1& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 0\end{array}\right]$$

By using the degree matrix $D$ and the Laplace matrix $L=D-A$, the connectivity and communication range between UAVs are determined. The $D$ matrix is a diagonal matrix that represents the degree of each node (the number of edges connected to each node) in the UAV network. Specifically, the diagonal element $D_{ii}$ of the $D$ matrix denotes the degree of node $i$, which is the sum of the elements of a row (or column) $i$ in the adjacency matrix $A$. Rows (or columns) of the adjacency matrix. Thus, the $D$ matrix is expressed as follows:

$$D=\left[\begin{array}{cccccc}2& 0& 0& 0& 0& 0\\ 0& 2& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 2& 0& 0\\ 0& 0& 0& 0& 2& 0\\ 0& 0& 0& 0& 0& 2\end{array}\right]$$

The matrix $D$ is used to calculate the Laplace matrix $L=D-A$, which helps in analyzing the connectivity and communication range in the UAV formation.

$$L=\left[\begin{array}{cccccc}2& -1& -1& 0& 0& 0\\ -1& 2& 0& -1& 0& 0\\ -1& 0& 2& 0& 0& -1\\ 0& -1& 0& 2& -1& 0\\ 0& 0& 0& -1& 2& -1\\ 0& 0& -1& 0& -1& 2\end{array}\right]$$

The initial position ($x,y,z$) and velocity ($v_x,v_y,v_z$) of the UAS are set as those in

Table 2. IAAPF-SMC simulation conditions and parameters.

Parameters	Parameter Value	Meaning
$x(\mathrm{m})$	$\left[0; 0; 20; 0; 20; 20\right]$	Initial Position
$y(\mathrm{m})$	$\left[40; 20; 40; 0; 20; 0\right]$	Initial Position
$z(\mathrm{m})$	$\left[0; 0; 0; 0; 0; 0\right]$	Initial Position
$v_x/(\mathrm{m}/\mathrm{s})$	$\left[5; 3; 2; 4; 2; 3\right]$	Initial Velocity
$v_y/(\mathrm{m}/\mathrm{s})$	$\left[6; 4; 7; 4; 5; 1\right]$	Initial Velocity
$v_z/(\mathrm{m}/\mathrm{s})$	$\left[5; 2; 5; 8; 3; 3\right]$	Initial Velocity
$v_{xy}\max /(\mathrm{m}/\mathrm{s})$	20	Maximum Velocity
$v_z\max /(\mathrm{m}/\mathrm{s})$	20	Maximum Velocity
$a_{xy}\max /({\mathrm{m}/\mathrm{s}}^2)$	20	Maximum Acceleration
$a_z\max /({\mathrm{m}/\mathrm{s}}^2)$	15	Maximum Acceleration
$l_0(\mathrm{m})$	5	Threshold distance for repulsive force activation
$n$	0.8	Adaptive factor in the repulsive force equation
$D_{\max }(\mathrm{m})$	10	Maximum range of the repulsive force
$D_{Emg}(\mathrm{m})$	3	Emergency distance for collision avoidance
$d_{xd}$	15	X-coordinate of distance
$d_{yd}$	15	Y-coordinate of distance
$m(\mathrm{kg})$	0.9	Mass
$g(\mathrm{m}/s^2)$	9.8	Gravitational acceleration
$l(\mathrm{m})$	0.175	Radius of the quadrotor fuselage
$I_x(\mathrm{kg}\cdot {\mathrm{m}}^2)$	$8.276\times {10}^{-3}$	Moment of inertia about the X-axis
$I_y(\mathrm{kg}\cdot {\mathrm{m}}^2)$	$8.276\times {10}^{-3}$	Moment of inertia about the Y-axis
$I_z(\mathrm{kg}\cdot {\mathrm{m}}^2)$	$1.612\times {10}^{-3}$	Moment of inertia about the Z-axis

:

5.2.1. Static Obstacle Avoidance Simulation Verification

The target position of each UAV was set in three-dimensional space, and the position and size of the 10 obstacles were specified, as shown in

Table 3. Obstacle and target position.

Parameters	Parameter Value	Meaning
Obstacle (m)	$\left[\begin{array}{l} 250, 160, 200;\\ 520, 350, 200;\\ 400, 500, 200; \\ 780, 500, 200; \\ 720, 600, 200; \\ 910, 810, 200; \end{array}\right]$	Obstacle Position
Target (m)	$\left[\begin{array}{l} 4500, 4500, 200; \\ 4470, 4470, 200; \\ 4530, 4470, 200; \\ 4440, 4540, 200; \\ 4500, 4440, 200; \\ 4560, 4440, 200 \end{array}\right]$	Target Position

. In addition, the obstacle avoidance range $R=20$ and the altitude stagger range between UAVs are set $R=20$ to ensure a safe distance for the UAV in 3D space.

The simulation results obtained by combining the IAAPF-SMC are shown in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18.

Figure 13 illustrates the flight trajectories of a multi-UAV while avoiding obstacles in a three-dimensional space. The simulation results confirm the effectiveness of the IAAPF-SMC obstacle avoidance algorithm. Each UAV successfully navigates around the obstacles, maintaining a safe distance and ultimately reaching its destination.

Figure 14 depicts the changes in velocity and acceleration of the UAVs in the X-direction over time. Initially, UAVs experience significant fluctuations due to obstacle avoidance maneuvers, but they eventually stabilize and converge to the desired velocities. This behavior confirms the robustness and efficiency of the control algorithm integrated with the IAAPF-SMC. Figure 15 shows the velocity and acceleration changes in the Y-direction. Similar to the X-direction, UAVs exhibit fluctuations during obstacle avoidance, but achieve steady-state values afterward. This indicates that the control algorithm effectively handles lateral maneuvers while maintaining formation stability. Figure 16 presents the changes in vertical velocity and acceleration. The UAVs adjust their altitudes to avoid obstacles, as reflected by the initial variations. Post-avoidance, they stabilize, showcasing the algorithm’s capability for vertical maneuvering and maintaining the desired altitude. Figure 17 illustrates the distances between UAVs during the flight. The results show that under the control of the collision-avoidance algorithm, all inter-UAV distances remain above the minimum threshold, preventing collisions. This highlights the effectiveness of the proposed method in ensuring safe and coordinated flight within a formation.

By analyzing these figures, it is evident that the proposed IAAPF-SMC method effectively enables multi-UAV systems to navigate through obstacle-filled environments while maintaining formation integrity and ensuring collision-free operation. To further validate the feasibility of this method in even more complex environments, additional simulations were conducted. These simulations tested the IAAPF-SMC method’s robustness and adaptability in scenarios with varying obstacle densities and dynamic obstacle movements. To better verify the robustness and adaptability of this method in complex environments with different obstacle densities, the obstacle parameters were increased, as shown in

Table 4. Added obstacle.

Parameters	Parameter Value	Meaning
Obstacle (m)	$\left[\begin{array}{l}300, 300, 160; \\ 600, 620, 240; \\ 700, 770, 200; \\ 520, 600, 200 \end{array}\right]$	Obstacle Position

.

By recording the 3D position, velocity, and relative angle of the UAV at one time, the dynamic behavior and obstacle avoidance effect of the UAV can be analyzed in detail, as shown in Figure 19.

The effectiveness of the IAAPF-SMC control algorithm in a multi-UAV system was validated through MC simulations. During these simulations, the UAV successfully navigated the obstacles labeled in the figures by adjusting its altitude and path planning throughout its flight. The obstacles, represented by spheres, indicate their positions in three-dimensional space. In each MC simulation run, obstacles were randomly placed within the environment to ensure a variety of configurations, thereby testing the robustness of the IAAPF algorithm under different conditions. Despite the multiple obstacle avoidance processes, the UAV’s trajectory remained relatively smooth, without significant oscillations or instability. This smoothness demonstrates the algorithm’s capability to maintain stable flight paths even when encountering numerous randomly placed obstacles. Additionally, the relative angle change of the UAV over time was monitored, further confirming the algorithm’s efficiency in maintaining control and stability.

At the beginning of the simulation, the relative angle of the UAV varied significantly, indicating that the UAV made more adjustments in finding the optimal path and avoiding obstacles. At this point, the UAV needs to make frequent reorientations to avoid obstacles and correct its flight path. In the later stage of the simulation, the relative angle gradually stabilizes, indicating that the UAV has entered a smooth flight state with less path adjustment. At this time, the UAV’s flight path has been optimized, the obstacle avoidance process has been completed, and the flight direction tends to be stable.

5.2.2. Dynamic Obstacle Avoidance Simulation Verification

In this part of the simulation, two groups of dynamic obstacles with different movement velocities were set up, and the number of obstacles in each group was three. Their related information is shown in

Table 5. Dynamic obstacle information.

Obstacle Number	Obstacle Coordinates (m)	Obstacle Velocity (m/s)
1	[290, 500, 200]	[2, −2]
2	[300, 500, 200]	[2, −2]
3	[310, 510, 200]	[2, −2]
4	[900, 850, 200]	[5, −5]
5	[910, 850, 200]	[5, −5]
6	[920, 870, 200]	[5, −5]

. The rest of the simulation parameters are consistent with those in Section 5.2, and the simulation results are shown in Figure 20 and Figure 21.

Figure 20 and Figure 21 illustrate the trajectory of the UAV as it maneuvers around the dynamic obstacles. These results were obtained through MC simulations, in which the UAV performance was evaluated under various randomly placed dynamic obstacle scenarios. Figure 20 shows that the UAV successfully achieved the desired formation after completing the obstacle avoidance process. Figure 21 highlights the UAV’s obstacle avoidance maneuvers at four different time points, showcasing the effectiveness of the IAAPF-SMC method in preventing collisions with dynamic obstacles. The smooth and stable trajectories observed during these simulations confirm that the formation control algorithm enables UAVs to achieve and maintain formation flight under dynamic conditions, demonstrating the robustness and reliability of the IAAPF-SMC control algorithm in diverse environments.

5.2.3. Multi-UAV Formation with Nine Units

In order to verify the effectiveness of the improved artificial potential field method for UAV formation flying, simulations are conducted to analyze the planning and obstacle avoidance effects.

Table 6. Experimental simulation parameters.

Parameters	Parameter Value	Meaning
$k$	100	Gravitational Gain
$l/(\mathrm{m})$	1011	Formation Distance
$V_l/(\mathrm{m}/\mathrm{s})$	20	Leading Velocity
$V_m/(\mathrm{m}/\mathrm{s})$	20	Following Velocity
$k_T/(\mathrm{kg}\cdot \mathrm{m})$	0.001	Control Parameters
$k_D/(\mathrm{kg}\cdot {\mathrm{m}}^2)$	0.00002	Control Parameters
$v/(\circ )$	45	Formation Angle
$k_{pot}$	130	Repulsion Coefficient

and

Table 7. Initialization simulation parameters.

Serial Number	Parameter Name	Parameter Value
1	UAV1 Initial Position	(200, 0, 0)
2	UAV2 Initial Position	(−300, −200, 0)
3	UAV3 Initial Position	(200, −300, 0)
4	UAV4 Initial Position	(0, −500, 0)
5	UAV5 Initial Position	(−300, −550, 0)
6	UAV6 Initial Position	(−200, −600, 0)
7	UAV7 Initial Position	(200, −800, 0)
8	UAV8 Initial Position	(0, −900, 0)
9	UAV9 Initial Position	(−400, −1000, 0)

list the parameters used in the simulation.

This simulation scenario involves nine multi-UAVs performing formation changes, obstacle avoidance, and flight, achieving dynamic trajectory planning in multi-UAV formation flight.

As shown in Figure 22, the multi-UAVs start from different initial positions and successfully achieve formation flight. They fly stably in a leader-follower formation at an altitude of 200 m, maintaining appropriate spacing. This demonstrates that the designed formation control algorithm effectively guides the multi-UAVs to form a stable formation under various initial conditions, validating the robustness and applicability of the algorithm.

The simulation results, as illustrated in Figure 23, validate the effectiveness of the designed control algorithm in maintaining a stable multi-UAV formation. In this scenario, the leader UAV dictates the flight path and the follower UAVs are programmed to maintain a specified formation relative to the leader UAV. When the leader UAV changes its trajectory, the follower UAVs detect these changes through control signals and adjust their paths to follow the leader accurately. This dynamic adjustment includes modifications in flight attitude (pitch, roll, and yaw) and velocity (both linear and angular) to maintain the formation geometry, thus confirming the control algorithm’s robustness and effectiveness in preserving a stable multi-UAV formation.

As depicted in Figure 24, the feedback control system utilizing the inner and outer loops enables the multi-UAV to coordinate effectively during flight and maintain a stable formation. When UAVs come too close to one another, an altitude difference is strategically created to avoid collisions, ensuring safe flight. Each UAV consistently maintains a velocity of 10 m/s, with inter-UAV distances precisely held at 20 m. The system’s real-time adjustments to flight velocity and inter-UAV distances allow the UAVs to dynamically maintain their formation shape, adapting seamlessly to varying conditions. The leader UAV provides essential guidance, enabling the follower UAVs to promptly adjust their velocities and positions. This dynamic coordination ensures that the UAVs can effectively avoid obstacles, maintain formation integrity, and respond promptly to changes in the leader UAV’s trajectory. This demonstrates the robustness of the control algorithm in achieving coordinated, collision-free multi-UAV formation flight.

By introducing obstacles in

Table 8. Obstacle Destination Parameters.

Serial Number	Parameter Name	Parameter Value
1	Obstacle 1	(1000, 15,500, 1000)
2	Obstacle 2	(−800, 10,000, 200)

into the simulation, the performance of the formation control algorithm can be evaluated in complex environments, and its effectiveness in dealing with potential flight obstacles can be verified. This helps to optimize the algorithm design and enhance the safety and stability of the UAV formation flight.

As shown in Figure 25, the designed leader-follower formation control algorithm allows the multi-UAV system to successfully perceive and avoid obstacles. During formation flight, the leader UAV dynamically adjusts its flight path based on the position and radius of the detected obstacles. It then communicates these adjustments to the follower UAVs, ensuring that they safely bypass obstacles while maintaining their formation. Additionally, the feedback control system, comprising the inner and outer loops, integrates obstacle feedback derived from the IAAPF. This obstacle information is processed before the motion controllers of the follower UAVs receive the desired state information, ensuring that the motion controllers account for the obstacles in their calculations. This approach allows the UAVs to adjust their flight paths and maintain a stable formation while effectively navigating around obstacles. The seamless integration of obstacle feedback into the control algorithm enhances the system’s robustness and reliability, ensuring safe and coordinated multi-UAV formation flight.

As shown in Figure 26, the virtual control signals represent the control inputs of the UAVs, specifically yaw and pitch angular velocities, corresponding to rotational movements in the horizontal and vertical planes. These signals reflect the control actions necessary for each UAV to achieve its desired positioning and orientation. From the control signal curves, it is evident that the eight UAVs exhibit some initial oscillations during the first 20 s. However, the control signals gradually stabilize, indicating that the UAVs’ attitudes are being effectively adjusted by the control system to the target state. This demonstrates the efficacy of each UAV control system in autonomously regulating its behavior for tasks, such as formation flying and obstacle avoidance. Further analysis shows that the control signals stabilize around 50 s, with no signs of prolonged oscillations or instability. Both the yaw and pitch angular velocities remain stable after this adjustment period, suggesting that the SMC employed is both stable and effective. During the initial phase, high-frequency oscillations are observed in some UAVs, particularly in the yaw angular velocity plot for UAV 1 and UAV 2. This phenomenon is likely attributed to the chattering effect inherent to the SMC. However, after this initial phase, the chattering significantly diminishes, and all UAVs’ control signals stabilize. In terms of adjustment time, UAV 1 stabilizes the quickest, within 20 s, while UAVs 2 and 3 take slightly longer (30–40 s), with the remaining UAVs reaching stability closer to 50 s. These differences in the adjustment time may result from variations in the initial conditions, control parameters, and the system’s chattering suppression mechanisms. Chattering, a typical effect in SMC, is reflected in high-frequency oscillations in the control signals, especially during the early stages of adjustment. UAV 1 and UAV 2 exhibit significant oscillations in the yaw angular velocity plot, which is indicative of rapid switching in the control inputs. Despite the presence of chattering, it diminishes after approximately 20 s, indicating that the system successfully suppresses chattering during the steady-state phase. The chattering level remains within acceptable limits, particularly for UAVs 3 through 8, which show relatively mild oscillations, further confirming the robustness of the SMC approach in managing complex UAV systems. Overshoot is more pronounced in UAV 1 and UAV 2, where the yaw angular velocity exceeds 0.3 rad/s, whereas other UAVs have smaller overshoot values. Similarly, UAV 1 shows a larger overshoot in pitch angular velocity, approaching 0.06 rad/s, while the other UAVs maintain overshoot values around 0.03 rad/s.

In conclusion, significant chattering is observed during the first 20 s, particularly in UAV 1 and UAV 2, where yaw angular velocity oscillates within a ±0.3 rad/s range, with high frequency and amplitude, reflecting the strong chattering effect of SMC. In contrast, pitch angular velocity shows milder chattering, mostly within the first 10 s, with oscillations around 0.02 rad/s, indicating less severe high-frequency oscillations. Overall, SMC effectively stabilizes the UAVs post-adjustment, with chattering greatly reduced as the system reaches a steady state, highlighting the robustness and effectiveness of SMC in coordinating multi-UAV systems.

6. Conclusions

This study aims to optimize the APF function to address its inherent limitations in multi-UAV formation control and obstacle avoidance. By introducing a segmented attractive potential field, the risk of encountering obstacles near the initial point is effectively reduced, and the obstacle avoidance path is optimized. Additionally, the integration of an SMC approach within an IAAPF-based obstacle avoidance framework significantly enhances the control and stability of multi-UAV formations. Simulation results verify that under the guidance of the improved algorithm, multi-UAV systems can successfully avoid obstacles, reach the desired velocity, and maintain formation convergence within a short period of time. Eventually, the UAVs arrived safely at the target destination.

Although our findings are promising, they are based solely on computer simulations. Due to resource limitations, integration testing with real UAVs has not yet been performed. Real-world testing is essential for validating the practical applicability and robustness of the proposed method in dynamic environments. Future work will involve extending the current IAAPF framework to 3D environments. This will include the validation of 3D trajectory planning and obstacle avoidance through numerical simulations as well as real-world implementation in UAV systems that require advanced 3D maneuvering capabilities.