Abstract
Reinforcement learning (RL) has been shown to be effective in path planning. However, it usually requires exploring a sufficient number of state–action pairs, some of which may be unsafe when deployed in practical obstacle environments. To this end, this paper proposes an end-to-end planning method based model-free RL framework with optimization, which can achieve better learning performance with a safety guarantee. Firstly, for second-order drone systems, a differentiable high-order control barrier function (HOCBF) is introduced to ensure the output of the planning algorithm falls in a safe range. Then, a safety layer based on the HOCBF is proposed, which projects RL actions into a feasible solution set to guarantee safe exploration. Finally, we conducted a simulation for drone obstacle avoidance and validated the proposed method in the simulation environment. The experimental results demonstrate a significant enhancement over the baseline approach. Specifically, the proposed method achieved a substantial reduction in the average cumulative number of collisions per drone during training compared to the baseline. Additionally, in the testing phase, the proposed method realized a 43% improvement in the task success rate relative to the MADDPG.
1. Introduction
Autonomous path planning presents a significant challenge, necessitating the agent to determine an optimal route from the initial position to the target destination while effectively avoiding obstacles [1]. Reinforcement learning (RL) has exhibited significant and encouraging results in the domain of agent path planning [2,3,4,5,6]. Meanwhile, safe control strategies are essential for agents in the real world. Since RL focuses on maximizing long-term returns, unsafe behaviors may be explored during the learning process. One of the main obstacles limiting the application of RL algorithms to real-world problems is the lack of safety guarantees, where agents using RL may make decisions based on reward signals, thus violating safety constraints. For example, a car control agent in autonomous driving may drive at high speeds for high rewards; however, this is highly unsafe in real-world deployments [7].
Recent studies have targeted the development of innovative RL algorithms, such as actor–critic, for constrained Markov decision processes (CMDPs) [8,9,10]. While these methods are valued for their broad applicability and straightforwardness, they often require a model, or aim to meet safety constraints only in a probabilistic manner [11]. Alternatively, some approaches focus on guaranteeing safety by constructing control barrier functions (CBFs) that can ensure safety. Typically, these safe controllers are devised by incorporating a safety filter into a reference controller. The combination of CBFs and model predictive control (MPC) has achieved significant results in the obstacle avoidance problem [12,13,14]. Certainly, controllers that integrate reinforcement learning with control barrier functions exist [15,16]. However, these controllers typically do not explicitly account for the action modifications by the CBF layer within the RL algorithm’s loss function, treating the CBF and RL as two separate controllers.
In this paper, we address the safety challenges during multi-drone training by proposing a new RL framework. Unlike previous RL controllers, our framework explicitly integrates the CBF-modified actions into the loss function, thereby enhancing learning efficiency and ensuring compliance with safety constraints. The primary contributions of this paper are as follows.
(1) We propose a safe learning framework based on the multi-agent deep deterministic policy gradient (MADDPG) method. This framework introduces a high-order control barrier function (HOCBF) with a relative degree of two, specifically designed for multi-drone systems. By leveraging safety constraints derived from the HOCBF, we have developed a differentiable safety layer that is integrated into the policy network, formulating a differentiable quadratic programming problem essential for safe action correction. This integration enables end-to-end learning by backpropagating the effects of optimization.
(2) We validate the effectiveness of the proposed algorithm through a series of simulation experiments. Using consistent hyperparameters and simulation environment settings, our method demonstrates a significant reduction in collision rates during training compared to the benchmark method. Moreover, it significantly improves task success rates after convergence.
2. Related Work
Reinforcement learning has increasingly been applied to path planning due to its robust adaptability and model-free nature. Q-learning algorithms are employed for path planning in unknown environments, enhancing planning capabilities in such scenarios; however, in large and complex environments, these algorithms exhibit low learning efficiency and suffer from reward sparsity issues [17]. To address this, Marc-André et al. [18] proposed a proximity-based reward system and integrated it with various optimization techniques and algorithms for path planning tasks. By assessing the performance of these methods through metrics such as the total completion rate of the maze and the average training time, they demonstrated that the combination of reward systems and optimization techniques significantly reduced training time. Amala et al. [19] presented a UAV path planning approach based on Q-learning for dynamic obstacle avoidance. This method integrated a shortest distance priority policy and was compared against algorithms like A* and Dijkstra. Their experimental results showed that the proposed method effectively decreased the distance UAVs needed to travel to reach their targets.
To address the path planning challenges of mobile robots in dynamic environments, Li et al. [20] proposed an enhanced version of the twin delayed deep deterministic policy gradient (TD3) algorithm. This improvement targeted the low success rate and slow training speed issues associated with the original TD3 algorithm in such settings. Their experimental results demonstrated that the enhanced TD3 algorithm exhibited superior performance in generating effective path plans for mobile robots within continuous action spaces. Wang et al. [21] introduced a DDPG algorithm incorporating multiple judging delays to mitigate the overestimation problem inherent in the DDPG algorithm, with added noise to enhance robustness. The simulation results demonstrated that the proposed algorithm achieved high convergence speed and stability. Significant research has been conducted on multi-UAV path planning. Westheider et al. [22] presented an innovative multi-agent information path planning method based on DRL for UAV cooperation in adaptive terrain monitoring scenarios. Their method employs a fleet of UAVs and integrates a novel network element representation to facilitate efficient path planning within a 3D workspace. Addressing the challenges of multi-UAV path planning in complex environments, Si et al. [23] developed a multi-agent DRL (MADRL) framework. This framework models the path planning problem as a partially observable Markov decision process and extends it to multi-agent scenarios using the proximal policy optimization algorithm. By meticulously designing the state observation space, action space, and reward function, this framework ensures collision-free path planning for multiple UAVs. Although reinforcement learning has achieved considerable success in path planning, many existing studies often neglect safety considerations during the training phase.
Currently, numerous methods exist for ensuring the safety of RL, including Lagrangian approaches such as proximal policy optimization with Lagrangian constraints (PPO-Lag) [24] and multi-agent PPO-lag (MAPPO-lag) [10]. A common feature of these approaches is the utilization of constrained neural networks, where a loss function incorporating both cost and value is used to refine the evaluation network. However, these methods do not ensure that all actions remain within the safe set during the training phase; safety is only guaranteed upon convergence. Additionally, balancing the weights assigned to cost and value parameters presents a significant challenge. Dalal et al. [25] proposed a safe filter for model-free reinforcement learning that involves directly adding a safety layer to the policy, constructing a quadratic programming problem to analytically resolve the correction formula for each action. Sheebaelhamd et al. [26] extended this approach to a multi-agent system with their soft-MADDPG framework, addressing infeasibility issues through soft constraints. The experiments demonstrate that this soft formulation significantly reduces constraint violations, ensuring safety even during the learning process. However, the constraints for this safety layer are derived from a constraint network obtained through pre-training, which requires violating constraints during training, contrary to the original intention of safety. Elsayed-Aly et al. [27] proposed a centralized shielding framework for MARL, but its practical application presents challenges. Its scalability is constrained by the centralized shielding itself, and communication limitations further restrict its applicability.
To ensure the safety of RL and enhance exploration efficiency, CBFs have been incorporated with existing model-free RL algorithms, as demonstrated in [16]. CBFs, which act as Lyapunov-like functions, extend safety guarantees [28]. The experiments in [16], conducted on an inverted pendulum and an auto-following task, show that this approach improves learning efficiency and ensures safety throughout the learning process when compared to other state-of-the-art methods. However, the modifications to the actions by the CBF layer are not explicitly included in the loss function of the RL algorithm in [16]. Instead, the CBF layer is treated as part of an unknown transformation function, which may impede learning when the agent adopts aggressive behaviors to avoid violating safety constraints. Although Refs. [15,17] explored the integration of CBFs with RL, their focus was primarily on single-agent systems. Multi-agent CBFs were introduced in [18], with different CBFs designed for each agent. Cheng et al. [29] proposed robust multi-agent CBFs to address uncertainties in both agents and their environments, ensuring safety with high probability in scenarios involving multiple uncontrolled and uncertain agents. However, despite the contributions of [18,29] to multi-agent safety, each agent is treated as an isolated entity, lacking inter-agent coordination.
The integration of CBFs with various control strategies and learning algorithms has proven to be a promising approach for enhancing the safety and reliability of dynamic systems. In this paper, we adopt a centralized training and distributed execution framework in MADRL to achieve multi-drone path planning. To address the initial safety challenges during reinforcement learning training, we integrate a distributed and differentiable high-order CBF layer with the actor network, ensuring safety constraints for each drone.
3. Problem Definition and Necessary Theory
3.1. Problem Description
As illustrated in Figure 1, the environment contains N quadcopters (depicted as blue drones), with each drone’s position denoted by , . Additionally, there are M circular obstacles (gray circles), each with a radius of and positions denoted by , . Each drone has a corresponding target point located at , . The objective for each drone is to navigate to its assigned target point while avoiding collisions with both static obstacles and other drones. The mission of an individual drone is considered complete when its distance to the target is less than a specified threshold . The overall mission is considered successful when all drones reach their designated target points without any collisions.
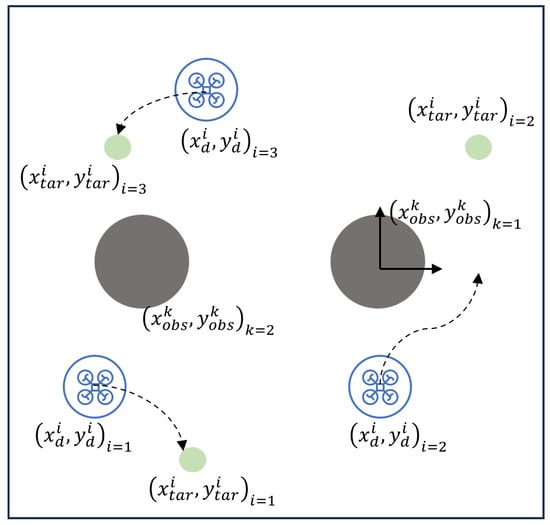
Figure 1.
The scenario of multi-drone path planning.
3.2. Drone Dynamics Model
When the drone is assumed to be flying at a constant altitude, it can be modeled as moving in a two-dimensional plane. As noted in [30], the aerodynamic force in the vertical direction can be decomposed into components along the x and y axes to control acceleration in both directions. Therefore, the dynamics of the drone are
As shown in Figure 2, where represents the position in the two-dimensional plane, denotes the force acting in the x and y directions, and denotes the velocity vector of the drone.
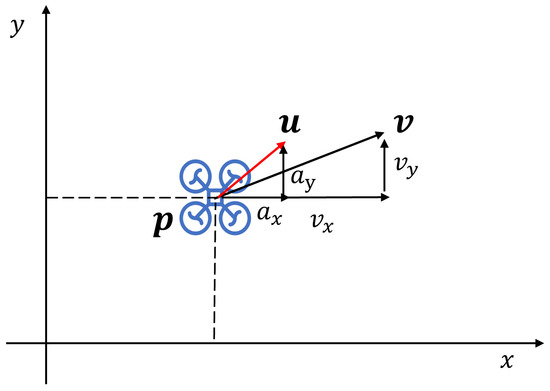
Figure 2.
Schematic of drone‘s motion.
3.3. Control Barrier Function
The control barrier function ensures the safety of the operation by defining a safety set in the state space of the system and ensuring that the system complies with specific security constraints so that the system state remains within this set. Consider an affine control system of the form
where , and are locally Lipschitz functions, and (with representing the control constraint set). The safe set is given by . If the time derivative of satisfies [28]
where is a class function. This ensures that if the system starts within the safe set, it will remain there at all future times. In the environment shown in Figure 1, we require that the drone does not collide with friends and obstacles. Take obstacles as an example, it is required that at all times the distance between the drone and the obstacle is greater than a safe distance (constant ), i.e.,
Let Therefore, we can determine that the set of control inputs that ensure the drone avoids collision with obstacles constitutes the action safety set. For a dual-integrator drone system, Equation (3) can be expressed as follows:
For simplicity, we set as the identity function. As indicated by Equation (5), the control input u does not explicitly appear in the constraint, making it challenging to formulate a quadratic programming problem using the CBF constraint. Therefore, we employ higher-order CBFs to address the issue of implicit control.
For high-order CBFs, the formulation involves the derivatives of the barrier function up to the order corresponding to the system’s relative degree. For a system with the relative degree r, the higher-order CBF condition can be expressed as follows [31]:
so the higher-order CBF condition then becomes
or more generally
where This formulation ensures that the higher-order derivatives of the barrier function satisfy the required conditions to enforce safety constraints for systems with higher relative degrees. In this paper, we consider the case that is a linear function. In the given form, the HOCBF condition can be written as [31]
where is a row vector and is defined as
where . represents the i-th Lie derivative of h with respect to the vector field f, and represents the Lie derivative of with respect to g. For second-order drone systems, assuming the functions and are linear for simplicity, we can express them as follows:
Thus, the HOCBF condition is simplified to
By combining terms and expressing in matrix form, we obtain
where .
4. Proposed MADDPG-CBF Algorithm for Multi-Drone Path Planning
According to Theorem 3 in [31], when h satisfies the conditions outlined in (9), the system is forward-invariant within the safety set, and the control input u that meets the constraints ensures system safety at any time t. We incorporated the CBF constraints into the MADDPG algorithm to guarantee that the policy output from the RL process adheres to safety guarantees, and into RL in order to make the policy output network satisfy the safety constraints. It is necessary to make the process of optimizing and solving the security policy differentiable with respect to the input of the network, i.e., the effect of the secure policy on the reward function can be propagated back to the input in the reverse direction; therefore, we make use of a differentiable QP (DiffQP) [32] (in simulation, corresponding to python’s qpth package), and by combining HOCBF with DiffQP, we design the core architecture of this paper—a multi-agent safe RL architecture. A safety layer comprising HOCBF is employed to correct potentially unsafe actions of drones within the actor network. The specific action correction formula is detailed in Section 4.3.
4.1. Multi-Agent Markov Decision Process
In MADRL, the Markov decision process (MDP) for single-agent scenarios is extended to handle multiple agents interacting within a shared environment. The fundamental process is illustrated in Figure 3.
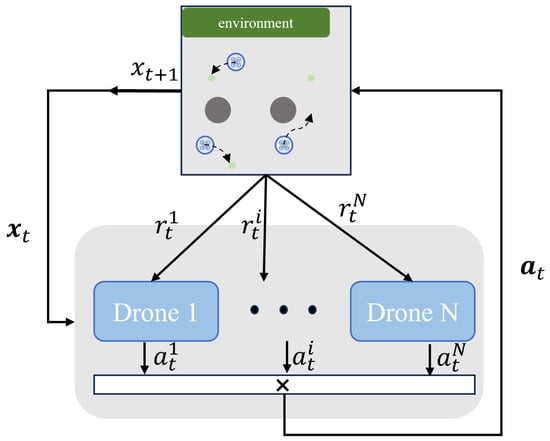
Figure 3.
Multi-agent Markov decision process.
The multi-agent MDP (MAMDP) can be expressed as a tuple , where S represents the global state space of the environment, and N is the number of agents. Each agent i has an individual action space , and the joint action space A is defined as . The state transition function represents the probability of transitioning from the current state to the next state . The reward function for the agent i is denoted as , and the discount factor for future rewards is represented by .
In an MAMDP, each agent i (for selects its action as part of a joint action Upon executing this joint action, the environment transitions from the current state to the next state and provides a reward. Each agent then updates its strategy based on the received reward and the observed state transition. This iterative process of action selection, state transition, and reward feedback continues as agents aim to maximize their cumulative return. Through repeated interactions with the environment, agents seek to refine their strategies to achieve optimal performance.
4.2. Multi-Agent Deep Deterministic Policy Gradient
MADDPG is a representative algorithm in MADRL that extends the DDPG algorithm to multi-agent systems. It efficiently handles continuous action spaces, offering advantages over stochastic strategies. The MADDPG framework employs a network architecture that combines centralized evaluation with decentralized execution. In this architecture, each agent utilizes its own actor and critic networks. In MADDPG, each agent determines its optimal policy by maximizing cumulative rewards. For agent i, this can be expressed as follows:
where represents the current state at time t, and denotes the action taken by the agent in the current state. The state transition probability distribution is denoted by and represents the reward value provided by the environment for the given state–action pair. The MADDPG algorithm employs an actor–critic method, where the Q-value network is parameterized by and the policy network is parameterized by by . Consequently, the loss function for the Q-value network can be formulated as follows:
where
The replay buffer is denoted by , and represents the parameters of the target Q-network. Consequently, the policy loss can be expressed as follows:
4.2.1. Action Space
In this paper, we consider the continuous action space of the drone, represented as a 2D velocity vector (), allowing the drones to move with variable velocities in any direction. Additionally, to ensure the mission control aligns closely with real-world conditions, as detailed in the drone dynamics model in Section 3.2, the model output is
where , denote the acceleration of the drone in the x and y directions. The corresponding velocity can be obtained through the following velocity formula:
where and represent the speed of the drone in the x and y directions, respectively, and represents the time interval.
4.2.2. State Space
The state space of the drone provides valuable insights based on the agent’s observation model, enabling the agent to perceive its environment and make informed decisions. In multi-drone path planning, the width and length of the mission scenario are set as and , respectively. The state information of the drone itself is set as
where and represent the horizontal and ordinate values of the i-th drone, respectively. is the maximum speed set for a drone. For the i-th drone, the information of other drones is
The target information obtained by it is
where and represent the horizontal and ordinate values of the target k respectively, and and represent the distance and relative azimuth vectors between the drone and all targets, respectively. The target information obtained by it is
where and represent the horizontal and ordinate values of the obstacle k, respectively. represents the distance vector between the drone and all obstacles. Finally, for the i-th UAV, its observation information is
Due to the partial observability of the problem, observations from a single drone do not fully capture the true state of the environment. To ensure the stability of MADRL, we define the observation set as the state of the training environment for all drones, where
4.2.3. Reward Function
Rational reward design is crucial for reinforcement learning. In single-agent path planning, the agent only needs to consider its relative distance to the target. However, in multi-agent path planning, each agent must account for the uncertainty introduced by other team members to achieve efficient multi-path planning with minimal cost. Therefore, designing effective reward features is critical to ensure the successful attainment of multiple goals. In this section, we design the reward function to address different environmental factors. (1) For targets, the reward function includes a distance reward and an arrival reward ; (2) for team members, it incorporates a safety reward to maintain collision-free interactions, including collision penalties and a synergy reward . (3) For obstacles, the reward function includes a collision penalty to ensure avoidance of collisions.
where denotes the negative of the Euclidean distance to the nearest target; is used to judge whether the agent completes the task or not; and denote the safe distance to friendly agents and obstacles, respectively. The reward function for agent i can be formulated as follows:
where – are constants, which are used to balance the weights among various rewards and ensure that the agent converges in a positive direction. – are all positive. In the subsequent experiments, all parameters are set to 1.
4.3. Proposed MADDPG-CBF Algorithm
In this subsection, we present the safety layer based on the differentiable CBF-QP. Combining inequality (13) for drones with a relativity of 2, CBF-QP takes the form
where is affine in u. The slack variable ensures the feasibility of the QP. The term () is a larger weighting factor used to minimize safety violations. is a gain matrix.
We use the QP solver to carry out the solution of (31), so it takes the form
where
the constraint parameters are
The HOCBF-based optimization process illustrated in Figure 4 minimally adjusts the RL policy to ensure system safety. Naively combining the actions of actor networks with CBF-QP, as discussed in [16], is problematic. Specifically, the training of the RL policy does not consider the effects of CBF-QP, and the final action performed in the environment is a modified safe action generated by the CBF layer. However, the updates in Equations (15) and (17) are generally based on potentially unsafe RL actions. This is equivalent to the safety layer being part of the transition dynamics with respect to the RL algorithm. Consequently, significant changes in the output of the safety layer often occur near unsafe states, which can complicate the learning process.
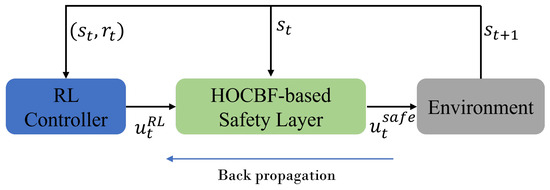
Figure 4.
Safety correction schematic. At time step t, the RL agent outputs a potentially unsafe control , which is then rendered safe by the CBF controller.
In Figure 5, the action correction procedure is distributed and embedded into the actor network of each agent to ensure individual safety, leveraging each agent’s own observation state, which ensures scalability. In order to make the safe actions more efficiently trained for the RL controller, we propose explicitly considering the output of the safety layer in the RL loss, significantly improving learning performance. We utilize a differentiable version of the safety layer to backpropagate through the QP, thereby explicitly interpreting the output of the QP in the RL loss. We employ the differentiable optimization framework introduced in [32,33], which utilizes KKT conditions and matrix operations to compute the gradient efficiently, and the computed gradient directly affects the tuning of each parameter in the optimization process, allowing the RL network to be progressively optimized and improve performance.
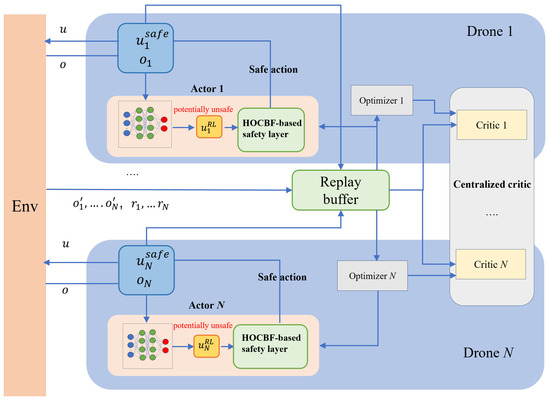
Figure 5.
A diagram of the proposed framework. The safety layer is integrated into the actor network.
Thus, we can explicitly obtain the safe operation updates in (36) and (38) and backpropagate these updates in an end-to-end manner via the CBF-QP, such that the loss of the MADDPG is given by the following equation:
where
and
where is derived from (32). In summary, the MADDPG-CBF algorithm proposed in this paper integrates a differentiable CBF layer with an actor network to ensure safety during training and directly impact the learning process. The complete MADDPG-CBF algorithm is outlined in Algorithm 1.
5. Experiment and Result Analysis
5.1. Experimental Setup
The experimental platform is a two-dimensional plane in the shape of a square, with each side measuring 2 km. There are two obstacles in the plane, each with a radius of = 0.2 km. The drone has a radius of 0.1 km. It is assumed that the drone and obstacles are randomly placed in the scene while ensuring that the initial distances between the drone and each obstacle exceed the safety distance. Each target point in the scene can be seen as a mass point; for each drone, in the case of no collision, when the distance between the center of mass and the target point is less than 0.01 km, this can be seen as a successful completion of the task. Table 1 lists the key parameters for the environment and drones.
| Algorithm 1 MADDPG-CBF |
|

Table 1.
The parameter settings for the agent platforms in the multi-drone environment.
In the DRL-based multi-drone framework, both the actor and critic networks utilize a two-layer perceptron architecture. The actor network, along with its target network, consists of fully connected layers with the following dimensions: . Similarly, the critic network and its target network are structured with fully connected layers of size . To observe drone movements more effectively, the environment is configured not to terminate upon collision. Instead, it only resets when the agent exceeds the maximum number of steps allowed per episode. The Adam optimizer is used to update the neural network parameters after the replay buffer accumulates the designated batch size. For a comprehensive overview of the network hyperparameters, refer to Table 2.

Table 2.
The detailed parameter settings of drone training.
5.2. Results Analysis
We evaluate the performance of the proposed algorithms using three key metrics: the average reward, the average cumulative number of collisions during the training phase, and the average cumulative number of collisions in the testing phase after convergence. We benchmark four distinct DRL strategies: MADDPG, IDDPG (where IDDPG uses distributed training), IDDPG-CBF, and MADDPG-CBF. IDDPG-CBF and MADDPG-CBF can correct potentially dangerous actions in the actor network using formula (32). In addition, we analyze the performance of the drones under unsafe initialization (UI) and safe initialization (SI).
For simplicity, we present only the average reward in the SI, as depicted in Figure 6. The average reward is computed as the mean reward of three agents. Interestingly, we observe a similar trend in all algorithms, which are not affected by constraints. Compared to IDDPG and MADDPG, both IDDPG-CBF and MADDPG-CBF achieve higher rewards at the final stage of convergence, indicating that the addition of the safety layer enhances reward acquisition. MADDPG-CBF outperforms IDDPG-CBF because centralized training enables agents to choose more optimal actions from a global perspective, resulting in greater reward feedback.
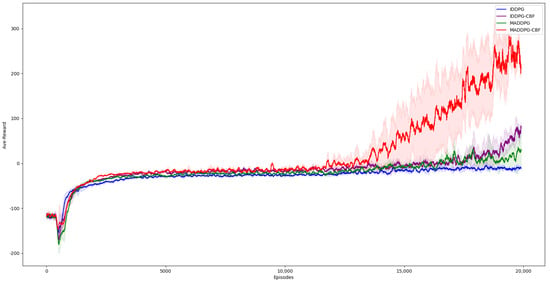
Figure 6.
An illustration of the average reward per drone during training. We note that higher rewards are obtained by adding a safety layer.
Figure 7 shows the average number of cumulative collisions per drone during the training period. As expected, a large number of collisions were observed in the MADDPG and IDDPG algorithms both in the UI and SI states, due to unsafe exploration in the early stages. In contrast, the average cumulative number of collisions in the IDDPG-CBF and MADDPG-CBF algorithms is greatly reduced and even tends to zero, indicating that incorporating CBF constraints can effectively reduce unsafe exploration, thereby validating the effectiveness of our algorithm. Figure 8 shows the average number of cumulative collisions per drone during the test simulations. It is worth noting that even during the convergence phase, IDDPG-CBF and MADDPG-CBF have far fewer collisions than their base methods.
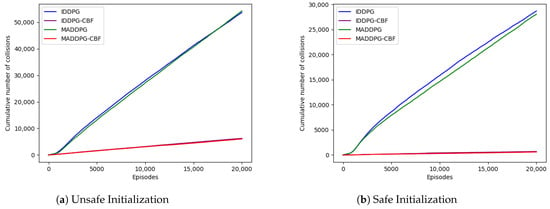
Figure 7.
An illustration of the average cumulative number of collisions per drone throughout the training period for both UI and SI.
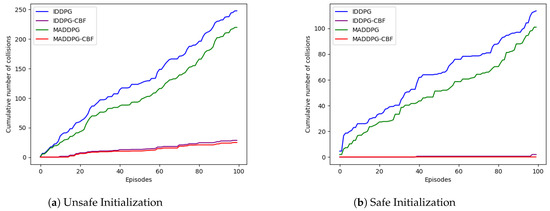
Figure 8.
An illustration of the average cumulative number of collisions per drone throughout the test period for both UI and SI.
During the testing phase, we observed the trajectory plots of each drone in SI for a particular round under the same random seed, as shown in Figure 9. It is evident that all three drones exhibit anomalous trajectories in the IDDPG and MADDPG algorithms, particularly in the folded portions of the graph. These anomalies are due to sudden changes in trajectories caused by mutual collisions between the drones. Although all drones eventually reach their target points, these anomalous trajectories indicate a failure in mission completion. Although no anomalous trajectories were observed in the IDDPG-CBF, two drones still failed to reach the target point. This is also considered a mission failure. In contrast, in the MADDPG-CBF algorithm, none of the drones displayed abnormal trajectories, effectively avoiding the risk of collisions with obstacles and other team members, and successfully reaching their target points.
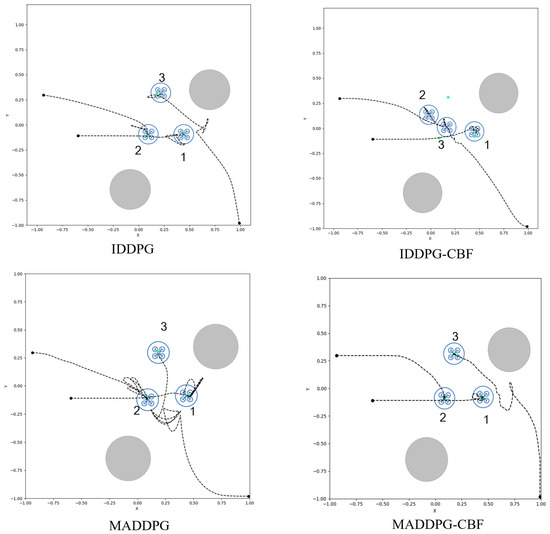
Figure 9.
Trajectory paths of drones in a specific testing round. The green dots represent the target points of each drone.
To thoroughly analyze the maneuvering decisions of the drones throughout the process, we selected drone 1 as the primary object of study. We plotted several critical metrics including the barrier functions (where , , , ), distance to the target, output actions, and positional variations during a specific round. This approach enables a deeper understanding of drone 1’s decision-making process in obstacle avoidance and target convergence, providing a clearer evaluation of its trajectory planning and control actions.
As illustrated in Figure 10, during the initial phase of the mission (0–16 s), drone 1 accelerates in the x-direction to approach the target as swiftly as possible, as depicted in Figure 10f. As the distance to the target decreases, drone 1 reduces the magnitude of acceleration in the x-direction and adjusts the y-direction acceleration to achieve a smooth and low-speed approach to the target (16–30 s). At s, drone 1 has reached the target as shown in Figure 10e. However, the proximity of drone 2 introduces a potential collision risk. In response, drone 1 adjusts its accelerations in both x- and y-directions to avoid a collision with drone 2 and subsequently returns to the target position once the risk has been mitigated. The specific changes in position and control actions during the interval from 35 s to 45 s are detailed in the schematic diagrams of Figure 10e–g. Throughout the process, drone 1 consistently maintains a significant safe distance from the two fixed obstacles. As a result, the analysis of the obstacle functions and is not extensively emphasized. We can see that it can also effectively apply safety corrections for cooperative obstacle avoidance between multiple drones when a single drone reaches a target point.
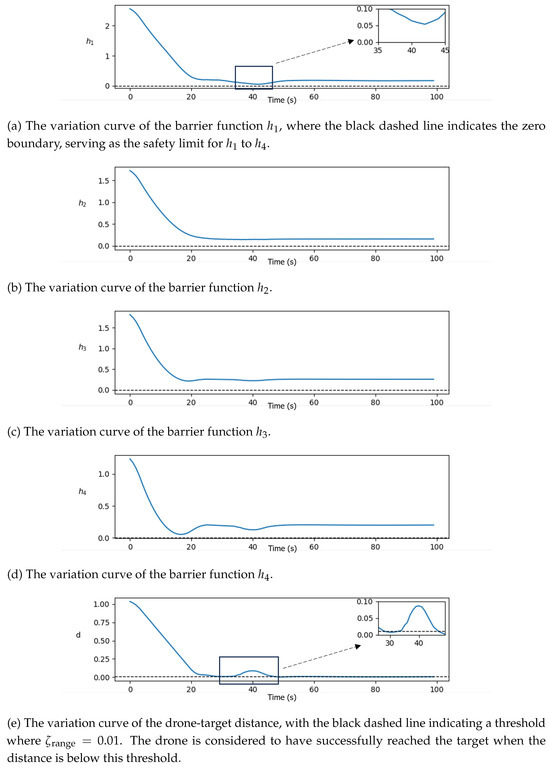
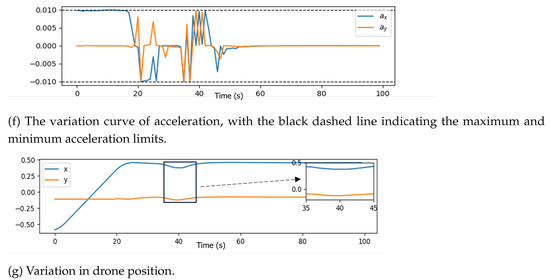
Figure 10.
Variation in control barrier functions, target distance, acceleration, and position change for drone 1.
Finally, to explore the impact of the proposed safety layer on the success rate of the task. Under SI, we conducted 100 rounds of tests. The success rates, along with their confidence intervals, are shown in Table 3. In these tests, any collision was regarded as a task failure.

Table 3.
A comparison of the success rates of the four algorithms was conducted over 100 test rounds.
Table 3 shows that the success rate of IDDPG-CBF is approximately 35% higher than DDPG without collisions, while MADDPG-CBF achieves about 43% higher success rates compared to the unconstrained MADDPG. Additionally, MADDPG-CBF outperforms IDDPG-CBF by around 11%. These results demonstrate that the proposed method significantly improves success rates over the baseline methods.
6. Conclusions
In this paper, we propose a model-free RL framework for the path planning of multiple drones in a continuous action space. This framework incorporates a safety layer based on a differentiable HOCBF to ensure safe actions. To validate the proposed method, we conducted a simulation where multiple drones navigated from an initial position to a target position while avoiding collisions and obstacles. The results demonstrate that our algorithm significantly reduces the number of collisions during training, with the average cumulative number of collisions per drone being approximately 1/800 of IDDPG and MADDPG. Additionally, the success rate of the task in the testing phase is 43% higher compared to MADDPG, with collisions being absent. These results indicate that the proposed method effectively facilitates drone path planning and obstacle avoidance, ensuring safe operation. In future work, we will extend this approach to 3D space to enhance practical applicability.
Author Contributions
Conceptualization, D.H. and C.W.; methodology, C.W. and L.S.; software, H.C.; validation, H.C.; formal analysis, C.W.; investigation, H.C. and C.W.; resources, L.S. and H.L.; data curation, C.W.; writing—original draft preparation, H.C. and C.W.; writing—review and editing, C.W. and L.D.; visualization, C.W.; supervision, L.S. and C.W.; project administration, D.H.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62303316), Science Center Program of National Natural Science Foundation of China (62188101), Fellowship of China National Postdoctoral Program for Innovative Talents (BX20240224), Oceanic Interdisciplinary Program of Shanghai Jiao Tong University (SL2022MS010) and Joint Fund of Equipment Pre-Research and Ministry of Education of China (8091B022235).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests orpersonal relationships that could have appeared to influence the work reported in this paper.
References
- Guo, Z.; Meng, D.; Chakraborty, C.; Fan, X.-R.; Bhardwaj, A.; Yu, K. Autonomous Behavioral Decision for Vehicular Agents Based on Cyber-Physical Social Intelligence. IEEE Trans. Comput. Soc. Syst. 2023, 10, 2111–2122. [Google Scholar] [CrossRef]
- Fu, G.; Gao, Y.; Liu, L.; Yang, M.; Zhu, X. UAV Mission Path Planning Based on Reinforcement Learning in Dynamic Environment. J. Funct. Spaces 2023, 2023, 9708143. [Google Scholar] [CrossRef]
- Khamidehi, B.; Sousa, E.S. Reinforcement-Learning-Aided Safe Planning for Aerial Robots to Collect Data in Dynamic Environments. IEEE Internet Things J. 2022, 9, 13901–13912. [Google Scholar] [CrossRef]
- Ding, Q.; Xu, X.; Gui, W. Path Planning Based on Reinforcement Learning with Improved APF Model for Synergistic Multi-UAVs. In Proceedings of the 2023 26th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Rio de Janeiro, Brazil, 24–26 May 2023. [Google Scholar] [CrossRef]
- Hu, J.; Yang, X.; Wang, W.; Wei, P.; Ying, L.; Liu, Y. Obstacle avoidance for uas in continuous action space using deep reinforcement learning. IEEE Access 2022, 10, 90623–90634. [Google Scholar] [CrossRef]
- Razzaghi, P.; Tabrizian, A.; Guo, W.; Chen, S.; Taye, A.; Thompson, E.; Bregeon, A.; Baheri, A.; Wei, P. A survey on reinforcement learning in aviation applications. arXiv 2022, arXiv:2211.02147. [Google Scholar] [CrossRef]
- Lefevre, S.; Carvalho, A.; Borrelli, F. A Learning-Based Framework for Velocity Control in Autonomous Driving. IEEE Trans. Autom. Sci. Eng. 2016, 13, 32–42. [Google Scholar] [CrossRef]
- Tessler, C.; Mankowitz, D.J.; Mannor, S. Reward constrained policy optimization 2018. arXiv 2018, arXiv:1805.11074. [Google Scholar]
- Achiam, J.; Held, D.; Tamar, A.; Abbeel, P. Constrained Policy Optimization. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 22–31. [Google Scholar]
- Gu, S.; Kuba, J.G.; Chen, Y.; Du, Y.; Yang, L.; Knoll, A.; Yang, Y. Safe Multi-Agent Reinforcement Learning for Multi-Robot Control. Artif. Intell. 2023, 319, 103905. [Google Scholar] [CrossRef]
- Du, D.; Han, S.; Qi, N.; Ammar, H.B.; Wang, J.; Pan, W. Reinforcement Learning for Safe Robot Control Using Control Lyapunov Barrier Functions. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, B.; Sreenath, K. Safety-Critical Model Predictive Control with Discrete-Time Control Barrier Function. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021. [Google Scholar] [CrossRef]
- Thirugnanam, A.; Zeng, J.; Sreenath, K. Safety-Critical Control and Planning for Obstacle Avoidance between Polytopes with Control Barrier Functions. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA) 2022, Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar] [CrossRef]
- Xue, H.; Lai, Y.H.; Sun, K. Human-like constraint-adaptive model predictive control with risk-tunable control barrier functions for autonomous ships. Ocean. Eng. 2024, 308, 118219. [Google Scholar] [CrossRef]
- Cohen, M.H.; Belta, C. Safe Exploration in Model-Based Reinforcement Learning Using Control Barrier Functions. Automatica 2023, 147, 110684. [Google Scholar] [CrossRef]
- Cheng, R.; Orosz, G.; Murray, R.M.; Burdick, J.W. End-to-End Safe Reinforcement Learning through Barrier Functions for Safety-Critical Continuous Control Tasks. Proc. Aaai Conf. Artif. Intell. 2019, 33, 3387–3395. [Google Scholar] [CrossRef]
- Emam, Y.; Notomista, G.; Glotfelter, P.; Kira, Z.; Egerstedt, M. Safe Reinforcement Learning Using Robust Control Barrier Functions. IEEE Robot. Autom. Lett. 2024, 1–8. [Google Scholar] [CrossRef]
- Borrmann, U.; Wang, L.; Ames, A.D.; Egerstedt, M. Control Barrier Certificates for Safe Swarm Behavior. IFAC-PapersOnLine 2015, 48, 68–73. [Google Scholar] [CrossRef]
- Sonny, A.; Yeduri, S.R.; Cenkeramaddi, L.R. Q-Learning-Based Unmanned Aerial Vehicle Path Planning with Dynamic Obstacle Avoidance. Appl. Soft Comput. 2023, 147, 110773. [Google Scholar] [CrossRef]
- Peng, L.; Donghui, C.; Yuchen, W.; Lanyong, Z.; Shiquan, Z. Path Planning of Mobile Robot Based on Improved TD3 Algorithm in Dynamic Environment. Heliyon 2024, 10, e32167. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Cao, D.; Ma, L.; Li, K.; Jia, L.; Cui, Y. Coverage Path Planning for Kiwifruit Picking Robots Based on Deep Reinforcement Learning. Comput. Electron. Agric. 2023, 205, 107593. [Google Scholar] [CrossRef]
- Westheider, J.; Rückin, J.; Popović, M. Multi-UAV Adaptive Path Planning Using Deep Reinforcement Learning. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Y.; Lu, X.; Guo, W.; Miao, H. Multi-Agent Deep Reinforcement Learning Based Decision Support Model for Resilient Community Post-Hazard Recovery. Reliab. Eng. Syst. Saf. 2024, 242, 109754. [Google Scholar] [CrossRef]
- Ray, A.; Achiam, J.; Amodei, D. Benchmarking safe exploration in deep reinforcement learning. arXiv 2019, arXiv:1910.01708. [Google Scholar]
- Dalal, G.; Dvijotham, K.; Vecerik, M.; Hester, T.; Paduraru, C.; Tassa, Y. Safe exploration in continuous action spaces. arXiv 2018, arXiv:1801.08757. [Google Scholar]
- Sheebaelhamd, Z.; Zisis, K.; Nisioti, A.; Gkouletsos, D.; Pavllo, D.; Kohler, J. Safe deep reinforcement learning for multi-agent systems with continuous action spaces. arXiv 2021, arXiv:2108.03952. [Google Scholar]
- ElSayed-Aly, I.; Bharadwaj, S.; Amato, C.; Ehlers, R.; Topcu, U.; Feng, L. Safe Multi-Agent Reinforcement Learning via Shielding. In Proceedings of the 20th International Conference on Autonomous Agents and MultiAgent Systems 2021, Virtual, 3–7 May 2021; pp. 483–491. [Google Scholar]
- Khalil, H.K. Nonlinear System; Macmillan Publishing Company: New York, NY, USA, 1992; pp. 461–483. [Google Scholar]
- Cheng, R.; Khojasteh, M.J.; Ames, A.D.; Burdick, J.W. Safe Multi-Agent Interaction through Robust Control Barrier Functions with Learned Uncertainties. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Zhang, X.; Dou, L.; Tian, B. Game of Drones: Multi-UAV Pursuit-Evasion Game with Online Motion Planning by Deep Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7900–7909. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Belta, C. High-Order Control Barrier Functions. IEEE Trans. Autom. Control. 2022, 67, 3655–3662. [Google Scholar] [CrossRef]
- Amos, B.; Kolter, J.Z. OptNet: Differentiable Optimization as a Layer in Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 136–145. [Google Scholar]
- Jiang, Y.; Wang, C.; He, Z.; Song, L. A Differentiable QP-based Learning Framework for Safety-Critical Control of Fully Actuated AUVs. In Proceedings of the 2024 3rd Conference on Fully Actuated System Theory and Applications 2024, Shenzhen, China, 10–12 May 2024; pp. 259–264. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).