Abstract
In the evolving landscape of logistics, drone technology presents a solution to the challenges posed by traditional ground-based deliveries, such as traffic congestion and unforeseen road closures. This research addresses the Truck–Drone Delivery Problem (TDDP), wherein a truck collaborates with a drone, acting as a mobile charging and storage unit. Although the Traveling Salesman Problem (TSP) can represent the TDDP, it becomes computationally burdensome when nodes are dynamically altered. Motivated by this limitation, our study’s primary objective is to devise a model that ensures swift execution without compromising the solution quality. We introduce two meta-heuristics: the Strawberry Plant, which refines the initial truck schedule, and Genetic Algorithms, which optimize the combined truck–drone schedule. Using “Dataset 1” and comparing with the Multi-Start Tabu Search (MSTS) algorithm, our model targeted costs to remain within 10% of the optimum and aimed for a 73% reduction in the execution time. Of the 45 evaluations, 37 met these cost parameters, with our model surpassing MSTS in eight scenarios. In contrast, using “Dataset 2” against the CPLEX solver, our model optimally addressed all 810 experiments, while CPLEX managed only 90 within the prescribed time. For 20-customer scenarios and more, CPLEX encountered memory limitations. Notably, when both methods achieved optimal outcomes, our model’s computational efficiency exceeded CPLEX by a significant margin. As the customer count increased, so did computational challenges, indicating the importance of refining our model’s strategies. Overall, these findings underscore our model’s superiority over established solvers like CPLEX and the economic advantages of drone-assisted delivery systems.
1. Introduction
As a result of the growth of e-commerce and accompanying parcel shipping services, logistics companies in urban areas have recognized the significance of delivering a diverse range of products through parcel distribution. Historically, surface transportation such as motorcycles, bicycles, cars, and trucks have been utilized for this purpose due to their accessibility, cost-effectiveness, and convenience. However, the ever-changing traffic conditions make land transportation a time-consuming mode of delivery, and the actions of various road users, such as pedestrians, cyclists, and vehicles, can significantly impact delivery schedules. Moreover, there are situations where land transport is not the most cost-efficient solution. For instance, letter delivery can account for anywhere between 13 and 75 percent of total delivery costs and up to 40 percent of the consumer’s final cost. Thus, optimizing this process holds significant value [1].
Given these challenges, the integration of unmanned aerial vehicles (UAVs) into delivery systems has emerged as a promising solution. Drones can bypass traffic, reduce delivery times, and access remote areas that are difficult to reach by land. Numerous prominent corporations, such as Amazon and DHL, have initiated pilot programs for package delivery systems incorporating UAV technology. Furthermore, advancements in regulations related to the control of UAVs in countries such as Canada and China are enabling businesses to streamline their delivery processes by deploying drones.
Recently, UAVs have gained much attention as a potential solution to growing transportation problems like traffic congestion. Advanced drone capabilities, including payload, speed, autonomous navigation systems, and endurance, have made their use in this market a viable option [1]. Previous research has looked at how drones could be used in a variety of fields, including medicine [2], humanitarian aid distribution [3], search and rescue [4], and transportation [5]. Recent developments in the transportation sector have shown that drone-based package delivery could be a practical use. The following are many benefits of using UAVs in package delivery services. First, drones can carry packages far more quickly than ground vehicles because they do not become stuck in traffic like cars. Drones may make direct deliveries to customers, eliminating the need for intermediaries and drastically reducing the turnaround time. Second, the use of resources like labor and power is reduced thanks to drone delivery. Third, remote places inaccessible by traditional shipping methods can benefit from drone delivery [6]. However, there are certain restrictions on using UAVs for package delivery, such as their difficulty in carrying heavy weight simultaneously and their short flying time and range on a single charge. As a result, the terrestrial and drone delivery systems have recently been synchronized. Packages can be delivered by drones or trucks, reducing costs while improving service quality, thanks to crewless aerial vehicles’ special capabilities and advantages [7].
The well-known Traveling Salesman Problem (TSP) can be employed to model the scheduling of drone and truck deliveries. This problem involves making assignment decisions to determine which vehicle, truck, or drone will serve each client and routing decisions to establish the sequence of visits to clients assigned to each vehicle. This paper presents a Multi-Visit TSP using a one-truck and one-drone (MTSP-TD) framework. A single drone can deliver shipments to multiple clients with a single flight, with the constraints of its payload capacity, flight time, and energy consumption. The depot and client nodes can conduct launch and retrieval operations. Furthermore, multiple delivery operations can be performed simultaneously at a node when the truck has an automatic flight control system. The primary objective of this research is to minimize the total time required for the truck–drone system to serve each customer.
To address these challenges, this research focuses on the Truck–Drone Delivery Problem (TDDP), where a truck collaborates with a drone, acting as a mobile charging and storage unit. This approach aims to optimize delivery schedules by combining the strengths of both trucks and drones. The study introduces two meta-heuristic techniques: the Strawberry Plant Algorithm, which refines the initial truck schedule, and Genetic Algorithms, which optimize the combined truck–drone schedule.
The literature presents various solutions to this problem from different perspectives. To resolve this issue, we turn to mathematical programming techniques like integer linear programming [8] and dynamic programming [9] for their precision and efficiency in finding optimal solutions. However, such methods can only address the issue when fewer than ten locations are involved [10]. Because of this, a great deal of study has been devoted to heuristic and meta-heuristic techniques, such as simple heuristics [10,11,12], Genetic Algorithms [1,13], simulated annealing [14], and greedy and randomized adaptive search procedure [10,15].
This paper aims to fill a critical research gap by exploring the efficacy of meta-heuristic methodologies in determining the optimal truck–drone schedules concerning delivery time and cost. By addressing this gap, the study intends to contribute to the progression of the field and offer pragmatic solutions for the logistics industry.
Utilizing a new meta-heuristic method, the “Strawberry Plant algorithm”, to determine the ideal truck–drone schedule in this new domain of parcel distribution is the primary contribution of this research. The Strawberry Plant Algorithm [16] is a meta-heuristic optimization algorithm used in various fields such as engineering [17,18], operations research, and computer science [19]. A Strawberry Plant’s participation in an optimization technique is predicated on whether its runners and roots influence whether convergence is ensured and whether the procedure leads to an optimal solution. Runners play a crucial role in global search, whereas roots concentrate on local searches because they move slowly across a domain to find the solution. Some potential benefits of using the Strawberry Plant Algorithm include the following:
- Significant benefits of employing the Strawberry Plant Algorithm are centered around its demonstrated search efficiency. This algorithm’s efficiency can be quantified by (1) the reduced computational time required to locate optimal solutions compared to traditional methods and (2) the lower number of iterations it typically necessitates to converge to an optimal solution. Its faster convergence speed and lower resource consumption showcase its robust efficiency and effectiveness in optimization tasks.
- The Strawberry Plant Algorithm has shown a propensity to find globally optimal solutions across various tested problem domains, aligning with the understanding imparted by the “No Free Lunch” theorem. This suggests the algorithm’s robustness in optimization tasks, with the caveat that, like any algorithm, its effectiveness may vary depending on the specific characteristics of the problem at hand.
- Simple and Easy to Implement: The algorithm is straightforward to implement, making it accessible for researchers and practitioners.
- Robustness: The algorithm is robust against premature convergence and can effectively escape from local optima.
- Versatility: The algorithm can be applied to many optimization problems, including complex and multi-objective optimization problems.
Research Limitation: The proposed research has certain limitations. Specifically, the maintenance cost of the automatic airport system, the charging requirements of the drones, and other technical considerations are not addressed. The research focuses on the practical feasibility and viability of implementing automatic airports. In older truck–drone scheduling systems, the process of adding or removing clients was complex and challenging. These systems’ rigid and inflexible nature made it difficult to adapt to changing client needs, leading to inefficiencies and a slow response time to changes. As a result, making adjustments to the system was time-consuming and often required manual updates, leading to reduced productivity. These limitations may impact the comprehensive evaluation of the proposed truck–drone delivery system and require further research to address these constraints and improve the system’s performance in real-world scenarios.
Key Contributions of this Study:
- Enhanced Client Flexibility: We address the complexities of dynamically adding or removing clients in previous truck–drone scheduling, ensuring adaptability in real-world applications.
- Scalable Efficacy Assessment: Through simulated TSP instances, the model’s effectiveness is rigorously assessed across diverse scales. This is further validated using “Dataset 1” and “Dataset 2”, ensuring its robustness in varied scenarios.
- Superior Computational Efficiency: Our algorithm not only outperforms the Multi-Start Tabu Search (MSTS) but also demonstrates remarkable efficiency against the general-purpose solver CPLEX, as evidenced in our comparative analysis.
- Advanced Meta-heuristic Integration: By uniquely combining the Strawberry Plant and Genetic Algorithms, our model harnesses the synergistic potential of these meta-heuristics for optimal scheduling.
- Sensitivity Analysis on Drone Integration: An analysis of drone integration into delivery systems highlights varied drone profiles by battery and weight. Results cost savings of over 55% with high-capacity drones compared to truck-only delivery, underscoring the economic advantages of drone use.
- Pioneering in Drone Mobility Research: With its innovative approach and significant findings, this study positions itself as a cornerstone reference in drone and vehicle mobility research, especially in the context of large-scale datasets and challenges posed by established solvers like CPLEX.
The following sections of this paper are organized as follows: Section 2 provides a review of pertinent literature, Section 3 introduces the mathematical model, Section 4 describes the components of the proposed algorithm, Section 5 presents the results of the experimental studies, and Section 6 offers concluding observations and implications for future research.
2. Literature Review
In recent years, there has been a growing interest in using drones for parcel delivery, particularly in addressing last-mile delivery challenges. Numerous studies have investigated the integration of drones with trucks in the Traveling Salesman Problem (TSP) framework. This literature review focuses on the combined use of drones and vehicles for parcel delivery.
The Truck–Drone Delivery Problem (TDDP) serves as a broad framework for integrating trucks and drones in delivery systems, focusing on optimizing their combined operations to enhance delivery efficiency. This problem encompasses various configurations, including different numbers of trucks and drones, and aims to leverage the strengths of both vehicles, such as using the truck as a mobile base for the drone, to optimize delivery schedules and reduce costs.
Within this broad framework, the Flying Sidekick Traveling Salesman Problem (FSTSP) is a specific variant where a truck and a drone collaborate to deliver packages. In FSTSP, the drone is launched from the truck to make a single delivery before returning, optimizing the combined route to minimize delivery time or cost. This model serves as a foundational concept for more complex problems.
The Traveling Salesman Problem with Drones (TSP-D) generalizes FSTSP by allowing the drone to operate along the same road network as the truck, focusing on optimizing delivery routes with similar constraints.
Building on these concepts, the Multi-Visit Traveling Salesman Problem with Drones (MTSP-TD) represents a more specific case where a single truck and a single drone are used, with the drone capable of making multiple deliveries in one flight. The primary objective here is to optimize the sequence of visits to minimize total delivery time, considering constraints like payload capacity and energy consumption.
Another specific case is the Multi-Visit Traveling Salesman Problem with Multiple Drones (MTSP-MD), which extends the MTSP-TD by incorporating multiple drones, each capable of serving multiple clients per flight, thereby enhancing delivery efficiency in larger networks.
These specific models, FSTSP, TSP-D, MTSP-TD, and MTSP-MD, provide detailed insights and solutions that contribute to the broader TDDP framework, addressing complex logistics challenges in both urban and remote areas.
The “Flying Sidekick Traveling Salesman Problem” (FSTSP) [11] is a pioneering study that explores the coordination of drone flights with truck routes for logistics distribution. In FSTSP, a drone can deliver one package at a time, and the problem is formulated as a mixed-integer linear program (MILP), solved using a heuristic approach based on the “Truck First, Drone Second” principle. This method iteratively relocates nodes to optimize the objective function, but it has been tested with only a limited number of customers.
For the first time, the authors in [10] explored a form of the FSTSP to reduce operational expenses. Two strategies can be used to solve the FSTSP based on the MILP formulation. The “cluster first-route second heuristic” is the foundation of the suggested method. Before constructing the truck’s route heuristically, they create a mathematical model that finds the most efficient route for the drone to take. They also offered an alternative heuristic strategy that prioritizes routes over clusters.
Moreover, an adaptation of FSTSP is explored in [12]. Along with the MILP formulation, the researchers proposed two solution strategies: a GRASP-based heuristic and a TSP-LS. Computational simulations involving up to 100 clients demonstrated that while the GRASP approach yielded higher solution quality than TSP-LS, it necessitated significantly more runtime. Further investigation into FSTP is presented in [18], where the authors put forth extensional restrictions to enhance the MILP model and utilized a heuristic approach grounded in simulated annealing.
The “Traveling Salesman Problem with Drones” (TSP-D) is a generalization of the FSTSP in which the drone must use the same road network as the truck. In TSP-D, the drone could be taken off and landed in the same place, but this is not allowed in FSTSP. For this reason, academics have tried exact and heuristic methods to solve the TSP-D problem. In contrast, others have provided innovative and useful route characteristics, as discussed below and summarized in Table 1. The authors of [9] presented TSP-D to cut down on logistics expenses. His research is based on the idea that a truck and a drone could use the same road network and that the drone could take off and land at the same point. In addition, the author formulated TSP-D as a MILP problem and found a solution using the “Truck First, Drone Second” method. Integer programming was used to create a model, and route-first and cluster-second heuristics were devised using dynamic programming and local search. It has been demonstrated that the proposed method can resolve more complex situations.
TSP-D is the subject of research in [15]. An “iterative technique based on a deconstruction approach” was proposed in the study to reduce delivery times. The creators initially chose the truck’s route and the drone’s assigned consumers. After that, the drone’s route is optimized by adjusting the routing and assignment decisions made in the first stage using a solved MILP model. To make better assignment and routing decisions, we begin with the truck’s shortest path and work backwards. Even worse, this heuristic method only works for medium-sized cases. A better mathematical model of TSP-D was proposed in [20]. They used branch-and-bound procedures to enhance their model with instance pre-processing, valid inequalities, and parameter scaling. Their findings show that the proposed method outperforms alternative MILP formulations in computational efficiency.
TSP-D is also solved in [21] to further reduce the total time required, which benefits both the drone and truck projects (min-time TSP-D). The authors developed a split-based hybrid genetic search for TSP-D that features dynamic population management and adaptive diversity control. The TSP-D problem has been tackled using different heuristic approaches [15,20], while other studies have provided innovative and useful route characteristics [22,23,24,25,26].
The “Vehicle Routing Problem with Drones” (VRPD) is another development of the FSTSP. A fleet of vehicles, each with its drone, makes deliveries to consumers in VRPD. In [27], the VRPD is examined, which involves several trucks, each with one drone, delivering items to clients. Also, they calculated the absolute worst-case ratios of delivery times with and without drones. Likely, the uncrewed aerial vehicle will return to the pickup truck from which it took off. As a result, it is illegal for a drone to have the kind of connectivity that would allow it to follow a convoy of vehicles. Therefore, they propose beginning with a near-optimal solution and improving it using local optimization techniques to maintain VRPD practicality. To further shorten the duration of the tour, they also use a second strategy that involves starting with an acceptable solution before adding drones.
The authors of [24] analyzed two types of drone tasks in VRPD: delivery and retrieval. After delivery, a drone can fly back to a hub or directly to the recipient. It presents a framework for effectively addressing such operational issues by modeling the problem as a scheduling issue for separate parallel machines with a sequence-dependent setup, precedence relationship, and re-entrant behavior. Multiple depots, cars, drones, and hundreds of clients scattered across an 8-mile square area are used to explain and evaluate a constraint programming technique. However, the meeting of different vehicle types was ignored in this investigation. To give a strategic analysis of VRPD, the authors in [25] used continuous approximation modeling techniques to make broad conclusions. TSP-D, FSTSP, and VRPD use one drone per truck, simplifying the synchronization problem. The drone routing problem can be addressed in O(n3) time by precomputing all possible drone flights as a three-dimensional tuple, as there is only one customer per drone trip. Two new, more difficult challenges have been proposed to broaden FSTSP: using a more sophisticated model for drone flying endurance, as shown below, it is possible to accomplish (1) multiple drones per truck and (2) several deliveries per drone trip.
Instead of using a single drone-like in TSP-D, the authors of [28] investigated the routing issue from the perspective of a vehicle and a swarm of drones; they dubbed this setup TSP-MD. The truck serves as a transport mechanism, taking the drones to designated hubs from where they can provide aerial service to paying consumers. An adaptive large neighborhood search (ALNS) technique is developed to solve TSP-MD after the GRASP is modified to address this challenge. The outcomes of several examples show that the GRASP can provide a better solution. However, the GRASP is also less effective than the ALNS in this scenario.
The publications [13,26] also explored the routing problem with many drones and a vehicle, wherein the truck releases many drones from a series of dispersed launch points along its route. The drones return to the truck just before moving to the next destination. The truck is driven to each cluster using clustering algorithms while neighboring consumers are served by uncrewed aerial vehicles. Contrarily, the TSP-MD in [27] looks at a single vehicle that can launch many UAVs, some of which can fly back to the truck. A MILP formulation is provided and tested for scenarios with as many as ten consumers. Another similar problem, the TSP with several drones, saw [28] present an adaptable large neighborhood search method (TSP-MD). In [29], the authors investigate the issue of customers receiving packages from a fleet of drones and a single delivery vehicle. These drones’ useful ranges may be increased if deployed and recovered from the vehicle. The length of time a drone can remain in the air is calculated using a model that considers the drone’s battery capacity, range, payload, and flight phases.
Using a fleet of trucks and UAVs as an extension of the FSTSP without endurance and launch/delivery limits are studied in [30]. While numerous trucks can launch and retrieve UAVs, only one UAV can be used for each customer site. For situations with up to 50 customers, they provide a MILP formulation and an insertion-based heuristic. Applications in surveillance [28,29,30,31,32,33,34,35] led to most of the research into many visits in each drone journey. In [36], a piecewise linear energy consumption function is used with heuristics to solve the multi-visit drone delivery problem with a single truck–drone team.
Conversely, ref. [37] proposed an iterative greedy search technique that utilizes a linear energy consumption function to address the issue. However, this solution only considers the scenario of one drone per vehicle. When multiple drones are associated with a single truck, the synchronization problem for multiple visits becomes more complex to model and solve. To address this, the authors introduced the k multi-visit drone routing problem (k-MVDRP) in [22], which is suitable for several drones operating from a single truck. A key requirement of this model is that after launching the drones, the vehicle cannot stop at any other nodes on the way to the retrieval node; it must proceed directly there. This stipulation simplifies the synchronization problem, allowing each drone flight’s viability to be evaluated independently. In [38], the authors enforce a drone flight endurance model based on the maximum length of a drone route and limit each customer node to at most one launching or retrieval operation. This is achieved by formulating the two-echelon vehicle routing problem with drones (2EVRPD), which involves multiple visits and multiple drones per truck. Consequently, additional clients must be assigned to the truck route as collection or launch nodes as more drone trips are generated. This approach, however, contradicts the original intent of shortening the makespan by increasing the number of concurrent drone deliveries.
A Multi-Visit Traveling Salesman Problem with Multiple Drones (MTSP-MD) is presented by Zhihao Luoac et al. in [38], in which each drone may deliver packages to many clients in a single flight. All drones are constrained by the maximum cargo capacity restrictions and energy consumption restrictions based on the flight time and payload. An automated flight control system aboard the truck facilitates the launch and recovery activities at the depot and any client node, while multiple delivery operations can be executed concurrently at a node. The goal was to reduce the latest time (also known as makespan) needed for the truck and drones to service every customer. The MTSP-MD problem is a composite of three sub-problems: (1) a drone routing problem with payload and flight constraints, (2) a TSP with precedence constraints, and (3) a synchronization challenge between the truck route and multiple drone schedules. For the MTSP-MD problem, they created a mixed-integer linear programming (MILP) model that can be solved on a small scale by commercially available solvers and is used to analyze the problem’s special characteristics. Larger instances are solved using a two-level feasibility evaluation process, swap neighborhood structures, and a Multi-Start Tabu Search (MSTS) heuristic (CPM). The suggested algorithm’s effectiveness was confirmed on freshly created instances that were expanded from Solomon’s samples. Experimental findings show considerable cost savings when considering several trips, multiple drones, and other factors.
In their study [39], Kazuki Satoh and Hiroshi Morita put forth a unique solution to tackle two specific problems: the Flying Sidekick Traveling Salesman Problem (FSTSP) and the Parallel Drone Scheduling Traveling Salesman Problem (PDSTSP). They undertook numerical tests using their proposed heuristic, involving a single drone and a truck, contrasting the findings with preceding studies. Their innovative algorithm demonstrated reduced computational complexity and increased precision compared to conventional methods. The research indicated that the FSTSP displayed shorter delivery durations when the proportion of delivery destinations close to the distribution hub was less than 0.4. At the same time, the PDSTSP was more effective when this ratio was above 0.4. However, several variables, including the location of the distribution center, the drone speed, and the maximum flight distance, may affect the results. Thus, more extensive experimentation is necessary for a more comprehensive understanding of these influencing factors.
In their work [40], Zhang, S. et al. developed a three-part process to minimize the delivery distance of trucks and drones and reduce the number of required drone dispatches. They initially used the scalable K-means++ algorithm for clustering customer points, ensuring each point is within the drone’s reach. Next, they optimized the truck’s driving route using the classic TSP model based on the clustering results. Finally, they established a simultaneous pickup and delivery model for the drone fleet, considering constraints on capacity and mileage. The developed heuristics were comparable to the optimal solution for small problem instances and showed efficient performance for larger problem instances, reducing execution times.
Ho Young Jeong and Seokcheon Lee [38] proposed DRP-T, a novel version of a hybrid delivery system. Their system maximizes drone usage by enabling multiple trips and incorporating additional launch locations to minimize truck movements. The authors proposed a specific MILP model for DRP-T. However, due to the problem’s complexity, the generation of timely delivery schedules becomes challenging. They suggested a heuristic algorithm named MACH to address this issue, offering optimized results while maintaining a reasonable computational time.
In their study [41], M. E. Bruni and colleagues investigated the drone delivery problem, focusing on tactical decision-making in last-mile drone deliveries, considering their connection to operational plans. The problem involves strategically selecting a subset of Fulfillment Centers (FCs) for launching and retrieving drones and determining the optimal number of drones to deploy. The researchers integrated a non-linear and load-dependent energy consumption function into the definition of a load-indexed layered network, leading to the development of a computationally efficient MILP capable of efficiently solving instances with 50 and 75 customers.
The Strawberry Algorithm (SBA) is a nature-inspired optimization technique based on the propagation process of a strawberry plant. In this algorithm, the plant gathers resources such as water through runners and roots, much like how runner branches in a strawberry plant are connected to the parent plant (Mother plant) on one side while the other side is free to explore. This dual mechanism allows the plant to perform both global searches via runners and local searches via roots to locate resources. SBA adopts this concept, integrating both global and local searches into the optimization process [16].
The SBA has demonstrated its efficacy in optimizing complex combinatorial problems like the TSP, including optimizing linear equations [1], drone placement [18], software effort estimation [1], energy management in smart grids [42], and more. In software engineering [19], the SBA was successfully applied to optimize the Constructive Cost Model (COCOMO), resulting in a significant reduction in the Mean Magnitude of Relative Error (MMRE) by 23.8% when estimating project effort. In [1], the SBA was shown to outperform the Genetic Algorithm in terms of efficiency and speed when finding the roots of linear equations. Additionally, in [18], the SBA’s superiority over Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) in optimizing drone placement was highlighted, particularly in reducing the number of drones and improving convergence and computation time. In the context of smart grids, the SBA was employed in an Energy Management Controller (EMC) to minimize electricity costs and reduce the Peak-to-Average Ratio (PAR), proving more effective than Enhanced Differential Evolution (EDE) in cost reduction [1].
The success of the Strawberry Algorithm (SBA) in various optimization tasks demonstrates its broad applicability and effectiveness. Its proven capabilities in improving efficiency and performance across different domains underscore its potential for tackling complex, real-world challenges. In this study, the SBA’s application to the Truck–Drone Delivery Problem (TDDP) reinforces its role as a versatile and powerful tool, capable of addressing a wide range of dynamic and multifaceted optimization problems.
Research Gap: The domain of truck–drone scheduling has garnered substantial interest in recent years due to the increasing urgency to enhance delivery times and cut costs in the logistics industry. Despite advancements in this sphere, a vital element remains unresolved: the degree to which meta-heuristic approaches can yield the optimal truck–drone schedule in relation to the delivery time and cost. While existing models can unearth the ideal schedule, the task of doing so is strenuous and time-consuming, making them ill suited for dynamic systems where nodes are consistently added and removed. In earlier truck–drone scheduling systems, alterations such as client additions or removals presented notable challenges. These systems were not developed to adapt to fluctuating requirements swiftly, rendering the process of implementing changes slow and arduous. This rigidity often led to inefficiencies and decreased productivity, as manual adjustments were frequently necessary. This shortcoming underscores a critical research gap demanding further exploration. To bridge this gap, the present study delves into the Truck–Drone Delivery Problem (TDDP), which aims to ameliorate delivery times and costs by merging a conventional delivery truck with a drone. The study endeavors to ascertain the efficacy of employing meta-heuristic methodologies in determining the optimal truck–drone schedule regarding delivery time and cost. By addressing this research gap, the study intends to contribute to the progression of the field and proffer pragmatic solutions for the logistics industry.

Table 1.
The literature related to the truck and drone parcel delivery problem.
Table 1.
The literature related to the truck and drone parcel delivery problem.
| Ref. | Problem | Objective | Drone Capacity | Algorithm | No. of Trucks and Drones | Solved Instances |
|---|---|---|---|---|---|---|
| [9] | TSP-D | Minimizing the logistic costs | One customer | Dynamic programming and local search | One truck and one drone | 10 customers |
| [11] | FSTSP | Minimizing returning time of trucks | One customer | Heuristic approach | One truck and one drone | 10 customers |
| [1] | FSTSP | Minimizing the operational costs | One customer | Simulated Annealing | One truck and one drone | 200 customers |
| [10] | FSTSP | Minimizing the operational costs | One customer | GRASP and TSP-LS | One truck and one drone | 100 customers |
| [15] | TSP-D | Minimizing the delivery completion time | One customer | An iterative heuristic algorithm based on a decomposition approach | One truck and one drone | 20 customers |
| [20] | TSP-D | Minimizing the duration of the joint tour. | One customer | A heuristic branch-and-bound algorithm | One truck and one drone | 24 customers |
| [22] | k-MVDRP | Minimizing the total route completion time | Many customers | Heuristic solution approach called Route, Transform, Shortest Path (RTS) | Many drones on one truck | 100 customers |
| [23] | VRPD | Minimize the completion time to deliver all packages and return all vehicles to the central depot. (Minimize the maximum duration route) | One customer | Local optimization procedures | Multiple trucks and one drone per truck | --- |
| [24] | VRAD | Minimizing the time required to service all customers by either the truck or the drone and return both vehicles to the depot | Many customers | Exact approach (constraint programming) | Multiple trucks and multiple drones per truck | 100 customers |
| [27] | TSP-MD | Minimizing total cost | One customer | An adaptive large neighborhood search (ALNS) heuristic | Many drones on one truck | 10 customers |
| [32] | TSP-MD | Minimizing the arrival time of both trucks and drones at the depot after completing the deliveries | One customer | Insertion heuristic approach | Multiple trucks and multiple drones per truck | 50 customers |
| [36] | mVRPD | Minimizing the logistics cost | Many customers | Exact algorithm (a branch-and-price algorithm) | One truck and one drone | 15 customers |
| [37] | 2EVRPD | Minimizing the total truck arrival time of truck at the depot | Many customers | Heuristic solution approach | Multiple trucks and multiple drones | 100 customers |
| [38] | MTSP-MD | Minimize the latest time required by the truck and drones to serve all customers | Many customers | Heuristic approach | One truck and multiple drones | Up to 100 customers |
| [39] | FSTSP and PDSTSP | Minimize the delivery time | Many customers | Heuristic | One truck and one drone | Up to 40 customers |
| [40] | MDVRPSPD | Minimize the distance traveled by drones and vehicles and the total number of drones used | Many customers | K-means++, TSP and tabu search algorithms | One truck and multiple drones | Up to 50 customers |
| [38] | DRP-T | Reduce computation time | Many customers | Memetic Algorithm with Constructive Heuristic (MACH) | One truck and multiple drones | Up to 100 customers |
| [41] | DRP-SD | Minimizing the total cost | Mixed Integer Linear Programming model (MILP) | Multiple drones | Up to 75 customers | |
| This paper | MTSP-TD | Minimizing the execution time it takes to find a reasonable truck drone schedule to deliver all of the parcels. | Many customers | Strawberry and GA | One truck and multiple drones | Up to 100 customers |
3. Mathematical Model
The suggested MTSP-TD model represents the parcel delivery problem using the TSP model. As seen in Figure 1, it can be represented by the graph, which represents the set of vertices or nodes and the set of arcs or connections between the nodes. The parcel positions or the set of clients are represented by the 0 and n + 1 nodes, denoting the starting and ending nodes (depot). The parcel delivery problem begins with the vehicle at the depot that transports both drones and packages. The solid arcs indicate truck routes, as shown in Figure 1a,b, and the dashed line routes indicate drone paths, as shown in Figure 1b. The primary objective of this research is to determine the optimal truck–drone schedule, which is contingent on a set of restrictions that we will discuss in detail in the following sections. The variables utilized in our mathematical model are provided in Table 2.
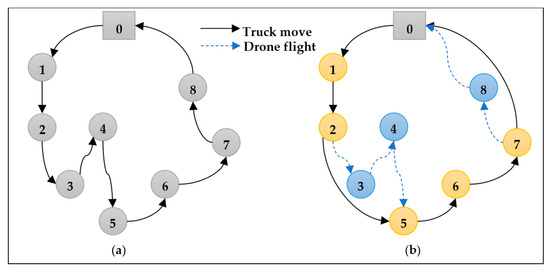
Figure 1.
(a) TSP route without drone support. (b) TSP route with drone-assisted delivery.

Table 2.
Parameters description.
3.1. The Precedence Constraints
The parcel delivery issue under investigation is formally formulated as a Traveling Salesman Problem (TSP), which aims to determine the optimal truck–drone schedules. In this problem, each client or node must be served exactly once, with the depot as both the starting and ending points. Furthermore, it is assumed that the truck directly serves the customers it visits, and only one truck is utilized in this study.
The drone and truck are identified by superscripts “D” and “T”, respectively. Only one truck or one of the drones should serve the customer i ∈ N. The set of customers who are served by the truck is denoted by , where ⊆ N. The other customers, excluding , denoted by represent the customers who are served by the drones. The truck and drone nodes are those served by trucks and drones, respectively.
The Euclidean distance represents the weight on the arc (i, j) (), where i and j represent two nodes. The truck can ship all packages and drones on board and has no restriction on its travel distance in this paper. Drones can be launched from a vehicle at the depot or from a customer node carrying many packages simultaneously to serve numerous customers, and this is contingent upon the capacity, energy, and time synchronization restrictions that will be detailed later.
3.2. The Capacity Constraints
In this study, multiple shipments can be carried concurrently by drones launched from either the depot or a customer node. Each drone journey consists of three components: a launch node, a set of clients served by the drone, and a retrieval node. During the delivery process, when a drone is not in use, it is transported by truck to the next target node that is farther away from the main road. It should be noted that the drones cannot be recharged at the launch node.
The capacity constraints are divided into two parts: the maximum capacity that the drone can carry, which is dependent on the drone’s design and kind, and the parcel capacity that must be delivered. The drone has its self-weight and its maximum capability for the combined weight of all carried packages for each trip (excluding the drone’s self-weight). Thus, the drone can have multiple packages per trip, whereas if the parcel package weight exceeds the drone’s available capacity, this node must be served by truck.
The suggested model monitors payload modifications throughout each drone flight concerning capacity restrictions. The whole number of payloads that the drone must carry in drone trip k ∈ K is determined by applying the following equation:
where is the parcel weight of customer i and is the set of customers served by the drone in drone trip k, and it must not exceed the available (or maximum) drone capacity.
3.3. The Energy Endurance Constraints
The maximum battery capacity (B) is a crucial constraint to consider during each drone trip. Upon returning to the truck, the drone’s battery must be replaced with a fully charged battery for the next flight. It is assumed that the replacement time is negligible and can be ignored in the analysis.
Several variables, including flight speed, self-weight, and total payload, are connected with the energy consumption rate of the drone in this research. The drone and vehicle speeds are assumed to be consistent with their average speeds, accounting for typical variations in real-world conditions. It is proposed that drones maintain an average speed during flight. A parameter φ is presented to show the energy consumption rate per weight and time unit. Hence, the energy consumption for a drone flight along an arc (i, j) ∈ relies on the flight time in addition to the whole weight of the parcels and drone:
where represents the total payload of the drone when it departs node i and is the drone travel time between nodes i and j summarizes the abbreviations.
If the drone reaches the pickup location before the truck, it must hover until it arrives. The drone consumes energy when serving a consumer or hovering above the retrieval node. Drones that hover have no payload because they can only hover at the spot where they are retrieved after their missions. When a drone delivers a package to a customer, its total weight equals the drone’s weight plus the payload it carries when it is about to depart. Therefore, the energy consumption when the drone is hovering and the actual energy consumption for serving customer i ∈ N can be simplified into the following:
where describes the time duration of the drone for hovering and is the drone service time for node i.
The drone should hover and wait for time units while consuming units of energy if the drone arrives at the retrieval node before the truck, where is the time when the truck arrives at the node i ∈ N and is the time the truck launches from the node i ∈ N. Both and must be greater than zero. The total energy consumption must not exceed the total available energy .
The energy model for the drone is based on the time spent in operation, including flight and hover times, reflecting the proportional relationship between time and energy consumption. This model was selected for its simplicity and direct correlation with time, a critical factor in drone operations.
The algorithms are designed to be adaptable, allowing for any proportional energy model to be applied without requiring changes to the algorithmic structure. This ensures robustness across different scenarios and makes it easy to adjust model parameters for various operational conditions or technological updates.
3.4. The Time Constraints
Vehicles and drones travel at various speeds, which results in varied transit durations. and are the travel times for the drones and the truck to traverse arc (i, j) ∈ V. The travel times are estimated by dividing the Euclidean distance () of arc (i, j) by the travel speeds of the truck or the drones, respectively. Loading, takeoff, and landing times are neglected and therefore assumed zero in this research. If the drone arrives at the retrieval node before the truck, it must hover until the truck arrives. As mentioned in Section 3.3, the hover time is presented by .
3.5. The Objective Function
The MTSP-TD aims to determine the shortest delivery path so that all clients can be supplied either by the truck or the drone. The objective is to minimize the maximum of two key time variables: the drone’s arrival time and the truck’s arrival time at the depot after completing all deliveries. This can be mathematically represented as
Here, denotes the time at which the drone arrives back at the depot and denotes the time at which the truck arrives back at the depot. The node (n + 1) represents the depot, which is indexed as the final node in the sequence of deliveries. For example, if there are eight customer nodes, the depot will be indexed as node 0 at the start and as node 9 (or n + 1) at the end of the route. The goal is to minimize the overall completion time of the delivery operation, taking into account both the truck and the drone.
4. Proposed Model
The suggested model is introduced in this section, and Figure 2 depicts the model’s general layout. Beginning with a formulation of the TSP, the statement of the problem includes the following:
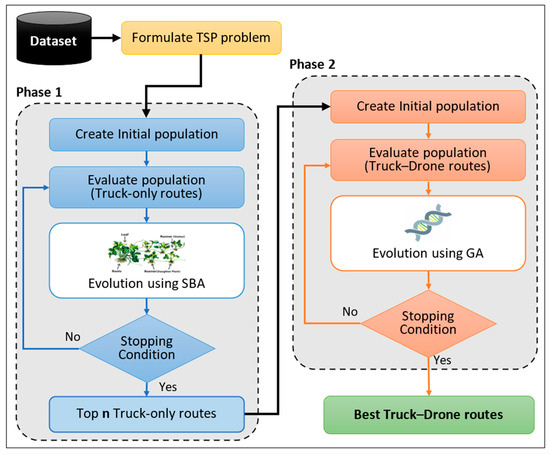
Figure 2.
The proposed model.
- Create the TSP Node (City) Network: The network is constructed by defining a list of nodes based on their location (x, y), service time, and cargo weight.
- Generate the Adjacency Matrix: This matrix represents the relationships between nodes (cities) and is created by calculating the Euclidean distance between each pair of nodes.
- Compile the Truck List: A list of available trucks is compiled, including information about each truck, such as its speed. In this paper, only one truck is used.
- Develop the Drone List: A list of available drones is generated, comprising information about each drone’s profile (L, M, or H). For the purposes of this study, only one drone is utilized.
The objective of the proposed model is to determine the most efficient truck–drone routes for servicing all nodes to minimize the required time. The model consists of two primary phases, each with a specific purpose. The first phase focuses on determining the optimal routes for the truck to visit all nodes in the shortest amount of time possible. The second phase aims to improve upon the results of phase one by incorporating the use of drones, considering energy and capacity constraints and time limits. The model employs two meta-heuristic techniques to achieve its goals. The first technique generates the optimal initial truck schedule with a specified threshold, while the second algorithm generates the optimal truck–drone schedules.
Using two-fold algorithms in this model allows for a more comprehensive and efficient search for the optimal truck–drone routes. By utilizing two different heuristics, the model can take advantage of the strengths of each technique and generate a more optimized solution. One heuristic may perform well in generating an initial solution quickly, while the other may be more effective in fine-tuning and improving upon that solution. The model can achieve a better overall solution by combining these two techniques compared to using just one heuristic. The specific order in which the heuristics are applied may also impact the final solution, so it may be necessary to try different combinations to determine the best approach.
Starting the optimization process with an initial solution generated by the first heuristic reduces the search space. It allows the second heuristic to focus on refining a more feasible solution rather than starting from scratch. This can lead to faster convergence to the optimal solution and make the optimization process more efficient. In other words, starting from a “ripe” solution can allow the second heuristic to build upon a solid foundation and improve upon it, rather than starting from scratch and searching for a solution from a much larger and less defined space. This two-fold approach can provide a more balanced and effective optimization process, leading to improved solutions.
In the study, the use of Plant Strawberry as the first meta-heuristic in the two-fold optimization process was chosen as it has been shown to provide a fast execution time while still producing a reasonable solution. The selection of the Plant Strawberry Algorithm as the initial method was influenced by its capacity to optimize the preliminary truck schedule effectively. This establishes a robust foundation for the subsequent use of the Genetic Algorithms meta-heuristic, further refining the truck–drone schedule.
4.1. Phase 1: Finding the Best n Truck-Only Routes
4.1.1. Creating the Initial Population
Phase 1 of the model commences with the generation of the initial truck-only schedule population. To generate the initial population of truck-only schedules, a random or heuristic-based approach is employed to create diverse sequences of nodes. Each solution in this population adheres to the following constraints:
- A unique identifier represents each node and must not be repeated within the solution.
- The depot node is represented by two separate identifier values, appearing as the first and final nodes in the solution.
For instance, consider the solution [0, 5, 3, 1, 2, 4, 6, 8, 7, 9]. It is a valid solution for a TSP involving eight nodes to be served. The node numbers ‘0’ and ‘9’ represent the depot node. Thus, the nodes numbered 1 to 8 correspond to the nodes to be served. Based on this solution, the truck commences at the depot node ‘0’ and then visits nodes in the following order: 5 → 3 → 1 → 2 → 4 → 6 → 8 → 7, ultimately returning to the depot node ‘9’.
4.1.2. Evaluation of Population
Each solution should be evaluated to find its cost. The cost is the sum of time required to travel from one node to another while serving all nodes by truck. The traveling time is calculated by knowing the distance between the two nodes (according to the Adjacency Matrix) and the truck’s speed.
where is the time required for the truck to move from node ‘0’ to the last node ‘n’ and serve all the in-between nodes.
4.1.3. Evolution Using the Strawberry Plant Algorithm (SBA)
The evolution of the initial population in the optimization process is guided by the Strawberry Algorithm (SBA) [38]. The SBA is a naturally inspired algorithm modeled after the propagation mechanism of a strawberry plant. In this algorithm, the plant obtains resources like water through runners and roots, just as the runner branches in a strawberry plant are attached to the parent plant (Mother plant) on one side and free to move on the other, enabling the plant to perform both global searches through runners and local searches through roots in the pursuit of resources. This concept of incorporating both global and local searches into the optimization process is adopted in SBA.
There are two methods to obtain the new population generation in this step. The first method is the rootMove, in which a random node (except the depot node) is selected and changes its position with another city in a small range (typically ±20% of the solution length). For example, if the solution has ten nodes, the rootMove changes the city’s position to the right or the left by a maximum of two places. The second method is the runnerMove, in which a random node (except the depot node) is selected and changes its position with another city in a large range (typically larger than ±20% and less than ±80% of the solution length). For example, if the solution has ten nodes, the runnerMove changes the city’s position to the right or the left by three to eight places. An example usage of the two approaches is shown in Figure 3. Algorithm 1 shows the steps of phase 1.
| Algorithm 1: Phase 1 |
| Initialization: 1. Load a problem from the dataset with a certain number of nodes (city) and denote it as (Prob) Hint: Prob has the following static lists: NodesList, TrucksList, DronesList, and AdjacencyMatrix. 2.Generate initial population (IP) (details in Section 0) 3. set SBA parameters:
BestTruckRoutes: a list containing the best (minimum cost) evaluated truck-only routes. Steps: for t = 1 to GN foreach originalRoute in IP for i = 1 to RunnersNum runnerRoute = apply RunnerMove between nodes in originalRoute (see Figure 3) end add runnerRoute to runnerP (runners population) for i = 1 to RootsNum rootRoute = apply RootMove between nodes in originalRoute (see Figure 3) end add rootRoute to rootP (roots population) Next Combine IR and runner, rootP into conbinePopulationList Sort conbinePopulationList according to cost ascending. BestTruckRoutes = select top N routes in conbinePopulationList (minimum cost) IP = BestTruckRoutes Next |
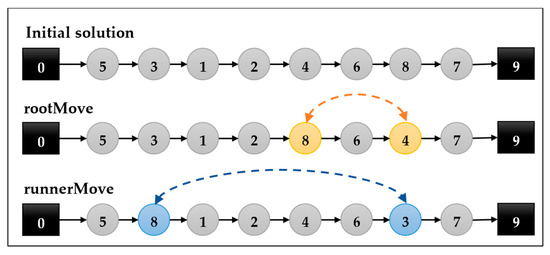
Figure 3.
Example of phase 1: evolution using SBA.
4.2. Phase 2: Finding the Best Truck–Drone Routes
4.2.1. Creating the Initial Population
Creating the initial population constitutes the first step of phase 1 in the optimization process. Each solution in the population is represented as a chromosome, with each gene corresponding to a node. In this representation, the presence of a ‘0’ signifies that the node will be serviced by the truck, while a ‘1’ indicates that the drone will be responsible for delivering to the node. Furthermore, ensuring that the first and last genes in the chromosome representation are ‘0’ guarantees that the depot node is serviced by the truck.
For example, if a chromosome [0, 0, 1, 1, 0, 0, 1, 0, 0, 0] is suggested, considering that the truck-only route from phase 1 is [0, 5, 3, 1, 2, 4, 6, 8, 7, 9], that means that nodes ’0’, ‘5’, ’2’, ‘4’, ‘8’, ‘7’, and ‘9’ are served by the truck, and the rest nodes are served by the drone, as shown in Figure 4. The flowchart of the truck–drone route simulation algorithm is presented in Figure 5.
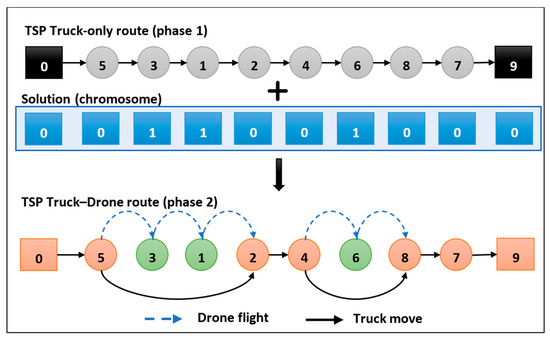
Figure 4.
Example of phase 2 solution.
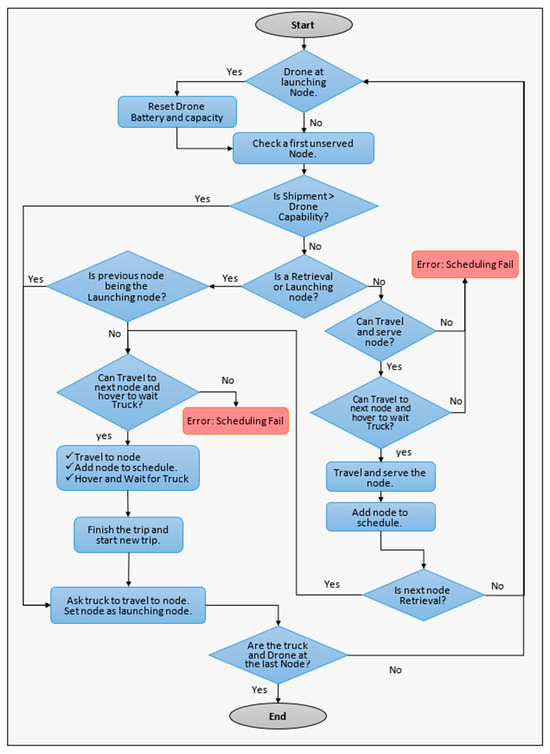
Figure 5.
Truck–drone route simulation algorithm.
4.2.2. Evaluation of Population
Each solution must undergo an evaluation to determine its associated time and energy costs. Given that the drone’s energy consumption is directly related to the time it spends in operation, as described in Equations (3) and (4), these time-based energy costs are calculated for both flight and hover operations. The solution is then checked against the drone’s energy capacity to ensure compliance with the energy constraints. Additionally, the solution must be thoroughly assessed to confirm that it adheres to all relevant capacity and time constraints. If any constraint, including energy, is violated during the evaluation process, the solution is rejected, indicated by an infinite cost value, as depicted in Figure 5. The proposed routes can comprise two types of trips, each with its cost calculation method. This concept is illustrated in Figure 6.
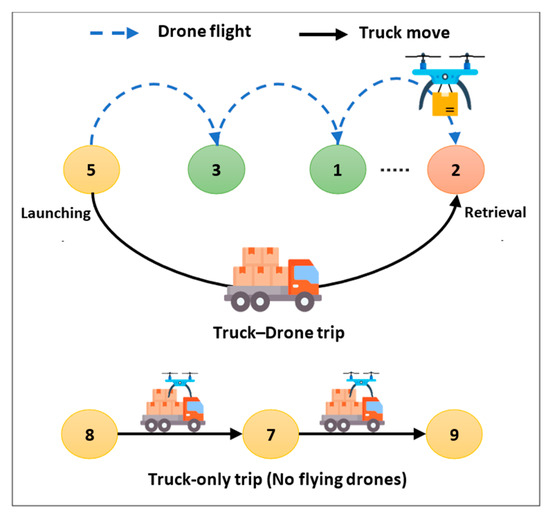
Figure 6.
Two types of trips in the truck–drone route.
- Truck–drone trip: A trip that begins at the launching node, where the drone starts to fly and serve the previously defined nodes. Simultaneously, the vehicle proceeds to the retrieval node, where it meets the drone again. This type contains two cases:
The truck trip is faster than the drone trip.
The drone trip is faster than the truck trip, and the drone should hover and wait for the truck at the retrieval node.
In both cases, the time of the longest trip is considered as the total time required to leave the truck at the launching node, move and serve the in-between nodes, and meet the truck at the retrieval node again.
where is the total time of the drone trips required to fly and serve all the customers in the drone trip between launching node ‘L’ and retrieval node ‘R’, is the time required to hover and wait to meet the truck at node ‘R’, and is the time required for the truck to move from node ‘L’ to node ‘R’.
- 2.
- Truck-only trip: A trip with no flying drone. So, the cost is simply the sum of time required to travel from one node to another and to serve the nodes by truck. During this trip, the drone is on the truck and has no jobs to perform.
4.2.3. Evolution Using GA
The final phase of the proposed model entails utilizing the results of phase 1 and the initial population to establish the optimal truck–drone path. In phase 2, the initial population of truck–drone schedules was generated in the first step. As previously stated, phase 1 resulted in “n” of the most optimal truck-only routes, each with its separate initial population in phase 2 that is evaluated independently. Upon completion of phase 2, the best combination of results from both phases is selected and deemed the ultimate and final schedules of the proposed model.
The Genetic Algorithm (GA) [43] finds the best solution in phase 2. First, the initial population goes through the steps adopted in the Genetic Algorithm, select parents → crossover → mutation, to generate the new population generation and continue to find the best solution. Algorithm 2 shows the steps of phase 2.
| Algorithm 2: Phase 2 |
| Initialization: 1. Get problem configuration (Prob) from phase 1 Hint: Prob has the following static lists: NodesList, TrucksList, DronesList, and AdjacencyMatrix. 2. Get the best N truck-only routes from phase 1 (TruckRouts) 3. Set the Genetic Algorithm parameters: NG: number of generations size: Number of solutions in the population chromosome size (number of gens): length of NodesList Pm: mutation probability Pc: crossover probability gene_space: [0, 1] binary stop_criteria: stop after 50 non-enhanced generations 4. fitness function: cost of the truck–drone route (see Section 4.2.2) Output: BestTSProute: the best truck–drone route (minimum cost). Steps: forech TRoute in TruckRouts P = Generate initial population (see Section 4.2.1) for i in NG parentsList = roulette_wheel_selection (P) (see Appendix A) Offspring = TwoPointDynamicCrossover(parentsList) (see Appendix A) Offspring_m = Mutation(Offspring) (see Appendix A) P = Offspring_m (new population) next Sort P according to cost ascending. BestTSProute = select a top route in newIP (minimum cost) Next return BestTSProute |
5. Experimental Results
This section outlines the experimental results that assess the effectiveness of the proposed model. Two datasets serve as the foundation for this evaluation: “Dataset 1”, detailed in Section 5.2, and “Dataset 2”, elaborated in Section 5.3. An overview of the implementation environment, experimental configuration, and parameter initialization is also included. This section concludes with a thorough analysis of the obtained results
5.1. General Experiments Setting
Only one profile is possessed by the vehicle (truck), maintaining a single travel speed for all instances. Three profiles are assigned to drones: “H” for high capacity, “M” for medium capacity, and “L” for low capacity. The main specifications of each drone profile are summarized in Table 3.

Table 3.
Drone profile parameters.
The environment was implemented using Python 3.10 and was tested on a machine characterized by the following specifications: Core i5 Processor 2.5 GHz/16 GB RAM, GPU: NVIDIA GeForce GTX1050 4GB. Two meta-heuristics algorithms (SBA, GA) are incorporated in the proposed model. Many hyperparameters in these algorithms need to be tuned to achieve optimal results. For comparative purposes, the values of the main hyperparameters used in the experiments are displayed in Table 4, allowing the results of the proposed model to be compared against those of other related models.

Table 4.
Meta-heuristic algorithms parameters.
5.2. Dataset 1
The dataset presented in [44] is the standard dataset used in this research. It has three collections labeled ‘C101’, ‘R101’, and ‘RC101’, each containing information about 100 nodes and a depot node. These data include the node id, the node location (x, y), the shipment (parcel) weight, and the node service time. Many sub-test cases can be formulated from these collections involving customers of varied sizes (8, 10, 25, 50, 100). The trip duration is determined by dividing the Euclidean distance between two nodes by the truck’s and drone’s respective travel speeds.
5.2.1. Implementation Environment
A key objective during the implementation of the proposed model is to design it to facilitate the testing and implementation of any algorithms or models. The implementation aims to establish a base for a general work environment to investigate the movement of drones and vehicles in similar problems. Emphasis is placed on ensuring that the implementation process supports easy experimentation and examination of various algorithms or models.
The implementation has four main entities: node, truck, drone, and problem. In addition, two main algorithms are implemented: Phase1_SBA and Phase2_GA. Different meta-heuristic algorithms can achieve the job of these implemented algorithms with simple modifications. Truck and drone entities contain the main information about the specifications (speed, battery capacity, weight capacity, …, etc.), the current location, and the history of each entity’s trips and jobs.
5.2.2. Experiments Setup and Parameters Initialization
Each experiment (test instance) has a notation representing its main setting. For example, the description “XXXX-n-R-T” means an experiment in which XXXX denotes the originally used dataset collection (i.e., C101, R101, or RC101), n is the number of nodes (Size), R is the maximum number of drones, and T represents the drone’s capacity profile. For example, in the experiment “C101-10-1-H”, the instant C101 is used with 10 nodes and one drone with an ‘H’ profile. Although only one drone is used in this paper in all experiments, implementing the proposed model considers the future work in which multiple drones can be tested.
5.2.3. Experimental Results and Discussion
This section presents a comparative study between the proposed and the MSTS models proposed in [44]. The results of MSTS are compared to a mixed integer linear program (MILP) model that is solved with IBM ILOG CPLEX 12.8.0. MSTS is an excellent model that outperforms many others, but its main drawback is its execution time is very high. In [44], the models are evaluated using two main metrics: cost and time. The time required to serve all nodes in the studied instance is referred to as the cost, while the time needed to obtain the final result from the model is referred to as time. The high execution time of the MSTS model prevents its use in dynamic real-world scenarios. So, the target of the proposed model is to find a fast model that can find a reasonable solution with a cost close to the cost of MSTS. The target was a cost no more than 10% above the MSTS cost. Table 5 summarizes the main results of the proposed model versus the MSTS model. Table 5 contains the improvement percentage in terms of time and the error in cost calculation in each case. The positive number of cost errors represents the percentage of increase in cost, and the negative number represents the cost reduction percentage. The positive number of time improvement percentages represent the enhancement in execution time in the case of using the proposed model. The improvement in execution time is, on average, 73%. The proposed model achieves the target cost in thirty-seven out of forty-five experiments and outperforms the MSTS model in eight cases in terms of cost. As noticed, there is a clear superiority of the proposed model in most cases in terms of time.

Table 5.
Results of experiments for Dataset 1.
Figure 7, the Time Comparison Plot, visually demonstrates the execution time differences between the proposed model and MSTS across various scenarios, including different dataset collections, numbers of nodes, and drone profiles. Lower time values for the proposed model indicate its superior time optimization. Figure 8, the Time Improvement Percentage Plot, shows the percentage improvement in time achieved by the proposed model compared to MSTS. Positive values on the y-axis indicate the percentage of time improvement obtained by the proposed model. These figures highlight the significant time optimization potential offered by the proposed model, emphasizing its effectiveness in reducing delivery times and enhancing overall operational efficiency in the context of truck–drone scheduling in parcel distribution.
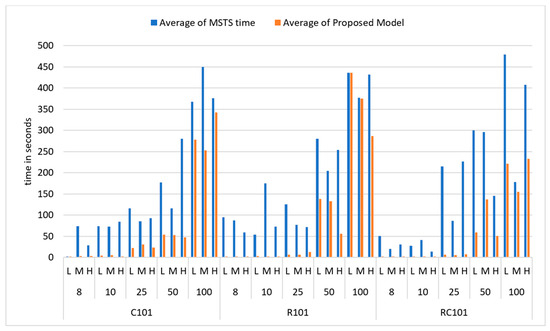
Figure 7.
Time Comparison Plot: evaluating execution times of the proposed model vs. MSTS.
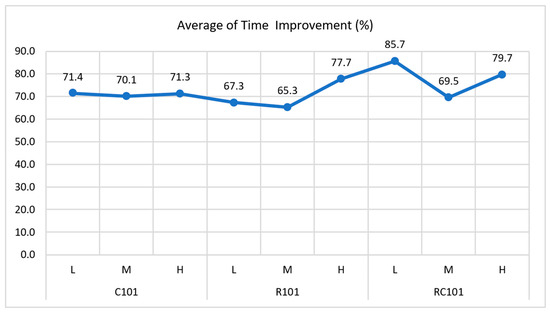
Figure 8.
Time Improvement Percentage Plot: assessing the performance gains of the proposed model in time optimization.
In Figure 9, a detailed example is presented. The figure shows the node distribution of experiment R101_10_1_M. In Figure 9a, the output of phase 1 ([0, 6, 5, 8, 7, 10, 1, 9, 3, 4, 2, 0]) that represents the best truck-only route is simulated. In Figure 9b, the output of phase 2 ([0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0]) that represents the best truck–drone route is simulated. Figure 10 presents the details of the experiment. These details show the following for the truck and the drone: current node ID (N_id), node service time (SV_T), arrival time (Arr_T), departure time (Dep_T), time to reach next node (To_nxt), drove battery when arriving node (Arr_Bat), drone battery after serving the node (Dep_Bat), drone weight (Tt_wt), and shipment weight of the node (Q).
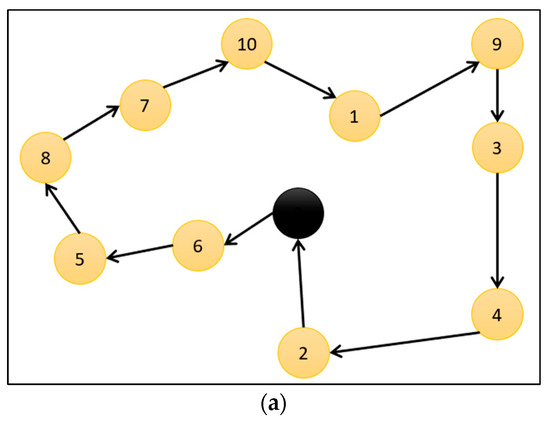
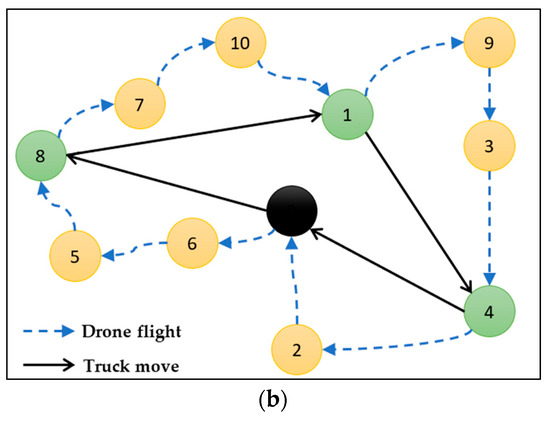
Figure 9.
Truck and drone route for instance (R101_10_1_M). (a) Phase 1: truck-only route (total cost = 273.04); (b) phase 2: truck–drone route (total cost = 146.24).
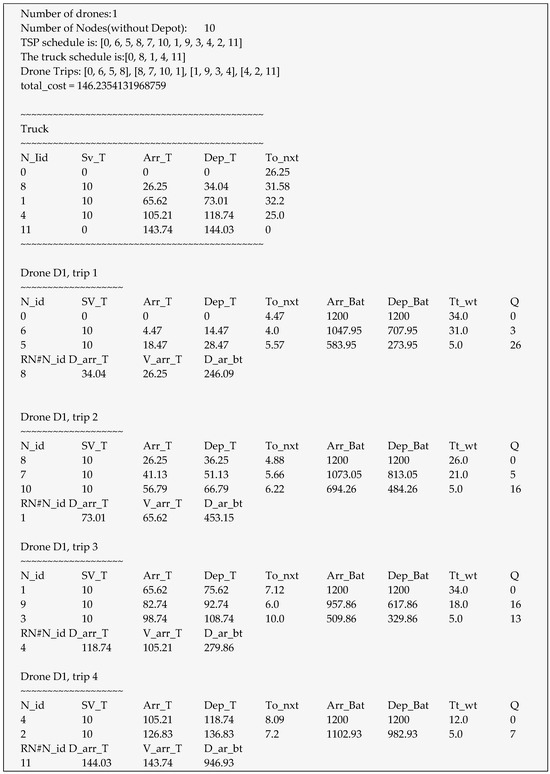
Figure 10.
Details of truck and drone route for instance (R101_10_1_M).
5.3. Dataset 2
A new dataset was created drawing upon methods from earlier research [44,45]. The CPLEX solver was then employed to build a reference model. This model was subsequently compared with our proposed model to note the differences in efficiency, accuracy, and computational needs.
5.3.1. Instance Generation
While the benchmark dataset from Section 5.2 has not been widely adopted in the research community, a need for a new dataset was identified for comprehensive analysis and validation. Based on techniques from prior studies [1,45], this new dataset was formulated. It spans locations within a 15-square-kilometer area and is divided into three distinct configurations:
Type 1: Locations for both the depot and customer sites were randomly selected from a grid marked by coordinates {0, 0.5, 1, 1.5, …, 15}.
Type 2: Locations for customers were chosen at random from the aforementioned grid, while the position of the depot was determined by averaging the coordinates of the customer sites.
Type 3: Coordinates for customer locations were derived using specific mathematical formulas, with the depot consistently centered.
Different sizes, represented by n ∈ {10, 20, 30, 35, 40, 45}, were established for each type. Each size yielded three distinct datasets. Within every dataset, there were (n + 1) nodes that the depot included. It was ensured that the depot consistently had a shipment weight of 0, while the customers were assigned weights from the list {10, 20, 25, 35, 40, 45, 50}. Based on a designated value θ, only a subset of customers was allocated non-zero weights. Collectively, this methodological approach led to the development of 270 unique dataset instances primed for a comprehensive analysis within this study.
5.3.2. CPLEX-Based MILP Model Implementation
Mixed-integer linear programming (MILP) problems encompass both continuous and integer variables, increasing in complexity with size. The use of IBM CPLEX v20.1’s Python API further intensifies this challenge due to its reliance on the branch-and-bound method, which segments the problem based on integer variables, potentially expanding the problem’s scope with each addition. Addressing such problems demands robust computational resources, particularly for those with extensive constraints or large datasets. Solutions can vary in derivation time, from seconds to days, based on the problem’s intricacy. Optimal solver usage, deep problem understanding, and solver setting modifications can enhance the solution speed. In the conducted experiments, a solver time constraint was set to maintain consistent operation durations. Algorithm 3 offers a pseudocode representation of the CPLEX Python API’s application for MILP problems.
| Algorithm 3: Pseudocode for the MILP Model of Truck–Drone Delivery Using CPLEX |
Initialization:
Indicate that no feasible solution was found. |
5.3.3. Experiments Setup
For files in a dataset, a systematic and descriptive naming convention was utilized, ensuring clarity in identification. In the format “TypeX_NodesY_ThetaZ_InstanceW”, each segment provides specific details. “X” denotes the configuration type, “Y” indicates the dataset size, “ThetaZ” signifies the θ value, and “W” represents the instance id of this combination. Through this methodology, each file was designed for easy identification, promoting efficient analysis. For example, the file “Type1_Nodes10_Theta0.1_Instance1” indicates the first configuration where locations were randomly chosen, a dataset size of 10 nodes, a θ value of 0.1, and it is the first instance of this combination. Furthermore, with the creation of 270 unique dataset instances and the introduction of three distinct drone profiles, a total of 810 different experiments were derived.
5.3.4. Experimental Results and Discussion
In this section, the performance of the proposed model is evaluated by contrasting it with the results obtained from solving the MILP using CPLEX 12.8.0. Experiments were conducted on all instances. A maximum time limit of 7200 s was allocated for instances with 10 to 35 customers, while 10,800 s was designated for instances with 40 and 45 customers [45]. Table 6 presents the results, where “Av. Cost” refers to the average value of the cost for different instances and “Av. Time” ” refers to the average value of the cost for different instances, and “L.M,H” refers to different drones’ profiles used in these experiments. The results clearly demonstrate the superiority of the proposed model over CPLEX within the designated time frames. Notably, only 90 out of the 810 experiments were optimally solved by CPLEX within the given time constraints. For instances with 20 customers or more, CPLEX was unable to find a feasible solution due to memory limitations. In the instances where CPLEX did succeed in optimization, the maximum gap between the results of the proposed model and CPLEX was +2.11%. On the other hand, the proposed model optimally solved all 810 experiments within the set time limit. Furthermore, when both methods optimally addressed instances, the proposed model reduced computational time by an average of three orders of magnitude in comparison to CPLEX. As anticipated, it was observed that the problem’s complexity augmented with an increasing number of customers. This led to a notable surge in average computational time, and a higher number of instances remained unresolved within the time constraints. Thus, devising strategies to adeptly address the pricing problem could bolster the performance of the proposed model. Collectively, these findings underscore the proposed model’s dominance over the general-purpose solver CPLEX, particularly for large-scale instances.

Table 6.
Results of experiments for Dataset 2.
5.3.5. Sensitivity Analysis
The integration of drones into delivery systems and its subsequent impact is critically examined in this section, with a particular focus on different drone profiles based on battery and weight capacities. Table 7 and Figure 11 together provide a comprehensive view, showcasing the costs associated with truck-only delivery and truck–drone delivery across varying numbers of nodes and θ values.

Table 7.
The costs associated with truck–drone delivery and truck-only delivery.
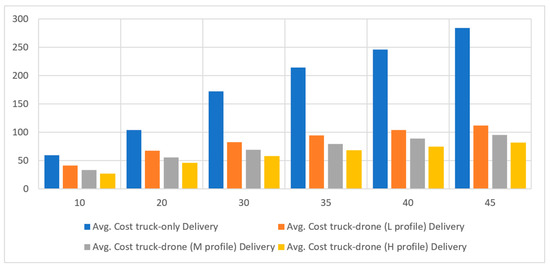
Figure 11.
Comparison of average delivery costs: truck-only vs. truck–drone delivery across different drone profiles and node sizes.
Drone Profile Analysis: Battery and Weight Capacities
As visualized in Figure 11 and detailed in Table 7, there is a consistent decrease in the cost of truck–drone delivery as we move from the “L” (Low capacity) drone profile to the “H” (High capacity) profile across all node sizes and θ values. For instance, with a node size of 10, the transition from “L” to “H” profiles results in cost reductions ranging from approximately 15% to 20%. This trend in cost savings becomes even more significant for larger node sizes. To illustrate, for a node size of 45 with a θ value of 0.1, the cost difference between using “L” and “H” profiles is nearly 30%.
Advantages of Integrating Drones in Delivery Systems
Figure 11 further emphasizes the significant cost savings when comparing truck-only delivery to truck–drone delivery. A notable example from Table 7 is the scenario with a node size of 10 and θ value of 0.1: The truck-only delivery cost stands at 63.55, whereas the truck–drone delivery, when utilizing the “H” profile, is at 27.73. This represents a savings of over 55%. Such cost benefits, evident across all node sizes and θ values, highlight the substantial economic advantages of incorporating drones into delivery systems.
6. Conclusions and Future Work
The Truck–Drone Delivery Problem (TDDP) was addressed in this research, focusing on the integration of a conventional delivery truck with a drone to optimize delivery efficiency and reduce costs. In this hybrid delivery system, coordination between the delivery truck and the drone was essential. The Traveling Salesman Problem (TSP) was used to model the truck–drone delivery system.
In our pursuit to address the TDDP, we employed two meta-heuristics: the Strawberry Plant and Genetic Algorithms. The Strawberry Plant Algorithm was pivotal in carving out an initial truck schedule that was both efficient and feasible. This initial schedule served as a foundation upon which the Genetic Algorithm further optimized the combined truck–drone itinerary. Our rigorous evaluations were two-fold. Firstly, using Dataset 1, we juxtaposed our model against the well-regarded MSTS algorithm. The results were illuminating: Our model not only outperformed the MSTS algorithm in eight out of forty-five instances but also closely mirrored the optimal solution in the majority of the other scenarios. This was achieved without a significant surge in execution time, underscoring the efficiency of our approach. Secondly, with the introduction of Dataset 2, our model’s versatility was put to the test. It demonstrated remarkable adaptability, especially when benchmarked against the general-purpose solver CPLEX in large-scale instances. The model consistently showcased its prowess, emphasizing its potential as a robust solution for the TDDP.
This area presents an abundance of options for future investigation. For instance, the proposed algorithm can be expanded to permit the concurrent operation of numerous trucks, which may allow deployed drones to be retrieved by a truck with excess capacity. Developing more efficient heuristic approaches and incorporating more real-world factors are further avenues for development. New theoretical limits on characteristics such as drone multi-visits and critical path scheduling with complex synchronization restrictions may be useful for evaluating the performance of heuristic techniques for large-scale challenges. Additional research could investigate multi-objective optimization or total cost minimization by eliminating suboptimal single drone flights. Considering the stochastic demand of customers and developing a model to simultaneously optimize several objectives, such as customer satisfaction and the lowest delivery time, will constitute significant future research.
Author Contributions
All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by T.A.F., M.A.F., M.A.E., A.E.H. and H.A. The first draft of the manuscript was written by T.A.F., M.A.F., H.A. and M.A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Graduate Studies and Scientific Research, Taif University. The article processing charge (APC) was funded by Tamer Ahmed Farrag.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The implementation of our work has been made available for the research community and interested parties. The complete source code, along with related materials, is provided at the following GitHub repository: [https://github.com/tfarrag2000/TSP_truck_drones accessed on 9 September 2024]. It is hoped that researchers and practitioners will be inspired to utilize, adapt, and expand upon this codebase to suit their specific needs and contributions.
Acknowledgments
The authors would like to acknowledge Deanship of Graduate Studies and Scientific Research, Taif University for funding this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, we provide detailed explanations of certain methods used in Algorithm 2, such as Roulette_wheel_selection(), TwoPointDynamicCrossover(), and Mutation().
Appendix A.1. Roulette Wheel Selection
Roulette wheel selection was proposed by Holland [46]. In the roulette wheel selection method, individuals are chosen based on probabilities that are directly proportional to their fitness values. This selection process can be visualized as a roulette wheel where each individual occupies a segment of the wheel, with the segment size corresponding to the individual’s fitness. Individuals with higher fitness values have larger segments, thus increasing their likelihood of being selected. Conversely, individuals with lower fitness values have smaller segments. The total circumference of the wheel equals the sum of all individuals’ fitness values. When the wheel is spun, the pointer will most likely land on a larger segment, but every segment has a chance of being selected, proportional to its size. This ensures that individuals with higher fitness are selected more frequently, aligning with the principle of “survival of the fittest”. The probability ( of selection for an individual () with fitness value () is defined as follows:
Appendix A.2. Two-Point Crossover
Crossover is performed by selecting a random point on the chromosome where the exchange of genetic material between parents occurs. This process creates a new offspring based on the chosen exchange point. In a two-point crossover, two points are chosen on the parent chromosomes, and the genes between these points are swapped to produce two offspring. The crossover operation prevents the exact replication of parent chromosomes in the offspring, ensuring that the new generation inherits beneficial traits from the parents while introducing diversity. As illustrated in Figure A1, this mechanism promotes significant changes in the solutions. The flexibility of the crossover operator enables the algorithm to continuously explore for the global optimal solution while minimizing the risk of becoming trapped in local optima.
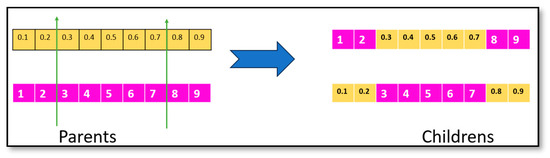
Figure A1.
Two-Point Crossover.
Appendix A.3. Mutation()
The mutation operator [47] introduces changes to one or more genes within the population to enhance population diversity. Its primary objective is to prevent premature convergence, which occurs when the algorithm becomes stuck in a local minimum and fails to explore other potential solutions. Mutation achieves this by altering genes to another value inside the boundary of the search space based on a specified genetic parameter known as the mutation probability, Pm. This probability determines the likelihood of a gene undergoing mutation, thereby contributing to the exploration of new and potentially better solutions within the search space.
References
- Lee, J. Optimization of a modular drone delivery system. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; pp. 1–8. [Google Scholar]
- Hiebert, B.; Nouvet, E.; Jeyabalan, V.; Donelle, L. The application of drones in healthcare and health-related services in north America: A scoping review. Drones 2020, 4, 30. [Google Scholar] [CrossRef]
- Shavarani, S.M. Multi-level facility location-allocation problem for post-disaster humanitarian relief distribution: A case study. J. Humanit. Logist. Supply Chain Manag. 2019, 9, 70–81. [Google Scholar] [CrossRef]
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Dung, N.D. Developing models for managing drones in the transportation system in smart cities. Electr. Control Commun. Eng. 2019, 15, 71–78. [Google Scholar] [CrossRef]
- Sawadsitang, S.; Niyato, D.; Tan, P.-S.; Wang, P. Joint ground and aerial package delivery services: A stochastic optimization approach. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2241–2254. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized truck and drone routing in package delivery logistics. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5772–5782. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization approaches for the traveling salesman problem with drone. Transp. Sci. 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Bouman, P.; Agatz, N.; Schmidt, M. Dynamic programming approaches for the traveling salesman problem with drone. Networks 2018, 72, 528–542. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Ha, M.H. Heuristic methods for the traveling salesman problem with drone. arXiv 2015, arXiv:1509.08764. [Google Scholar]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transp. Res. Part C Emerg. Technol. 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the min-cost traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Ferrandez, S.M.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374–388. [Google Scholar] [CrossRef]
- AlMuhaideb, S.; Alhussan, T.; Alamri, S.; Altwaijry, Y.; Aljarbou, L.; Alrayes, H. Optimization of Truck-Drone Parcel Delivery Using Metaheuristics. Appl. Sci. 2021, 11, 6443. [Google Scholar] [CrossRef]
- Yurek, E.E.; Ozmutlu, H.C. A decomposition-based iterative optimization algorithm for traveling salesman problem with drone. Transp. Res. Part C Emerg. Technol. 2018, 91, 249–262. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F. A numerical optimization algorithm inspired by the strawberry plant. arXiv 2014, arXiv:1407.7399. [Google Scholar]
- Shahzad, M.; Akram, W.; Arif, M.; Khan, U.; Ullah, B. Optimal siting and sizing of distributed generators by strawberry plant propagation algorithm. Energies 2021, 14, 1744. [Google Scholar] [CrossRef]
- Farrag, T.A.; Farag, M.A.; Rizk-Allah, R.M.; Hassanien, A.E.; Elhosseini, M.A. An improved parallel processing-based strawberry optimization algorithm for drone placement. Telecommun. Syst. 2023, 82, 245–275. [Google Scholar] [CrossRef]
- Khan, M.S.; Hassan, C.A.U.; Shah, M.A.; Shamim, A. Software cost and effort estimation using a new optimization algorithm inspired by strawberry plant. In Proceedings of the 2018 24th International Conference on Automation and Computing (ICAC), Newcastle Upon Tyne, UK, 6–7 September 2018; pp. 1–6. [Google Scholar]
- El-Adle, A.M.; Ghoniem, A.; Haouari, M. Parcel delivery by vehicle and drone. J. Oper. Res. Soc. 2021, 72, 398–416. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. A hybrid genetic algorithm for the traveling salesman problem with drone. J. Heuristics 2019, 26, 219–247. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B. Multi-visit drone routing problem. Comput. Oper. Res. 2020, 113, 104802. [Google Scholar] [CrossRef]
- Poikonen, S.; Wang, X.; Golden, B. The vehicle routing problem with drones: Extended models and connections. Networks 2017, 70, 34–43. [Google Scholar] [CrossRef]
- Ham, A.M. Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming. Transp. Res. Part C Emerg. Technol. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Campbell, J.F.; Sweeney, D.; Zhang, J. Strategic design for delivery with trucks and drones. Supply Chain Anal. Rep. SCMA 2017, 47–55. Available online: https://www.villagereach.org/wp-content/uploads/2018/07/StrategicDesignforDeliverywithDronesandTrucks_4-17-17_SCMA-2017-0201.pdf (accessed on 9 September 2024).
- Chang, Y.S.; Lee, H.J. Optimal delivery routing with wider drone-delivery areas along a shorter truck-route. Expert Syst. Appl. 2018, 104, 307–317. [Google Scholar] [CrossRef]
- Yoon, J.J. The Traveling Salesman Problem with Multiple Drones: An Optimization Model for Last-Mile Delivery. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Tu, P.A.; Dat, N.T.; Dung, P.Q. Traveling salesman problem with multiple drones. In Proceedings of the Ninth International Symposium on Information and Communication Technology, Danang City, Vietnam, 6–7 December 2018; pp. 46–53. [Google Scholar]
- Raj, R.; Murray, C. The multiple flying sidekicks traveling salesman problem with variable drone speeds. Transp. Res. Part C Emerg. Technol. 2020, 120, 102813. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Ventresca, M.; Moshref-Javadi, M.; Lee, S.; Tanchoco, J.M.A.; Brunese, P.A. Multiple traveling salesman problem with drones: Mathematical model and heuristic approach. Comput. Ind. Eng. 2019, 129, 14–30. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J. A Two-echelon cooperated routing problem for a ground vehicle and its carried unmanned aerial vehicle. Sensors 2017, 17, 1144. [Google Scholar] [CrossRef]
- Carlsson, J.G.; Song, S. Coordinated logistics with a truck and a drone. Manag. Sci. 2018, 64, 4052–4069. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J.; Wang, Q.; Zhou, T.; Liu, Y. The mathematical modeling of the two-echelon ground vehicle and its mounted unmanned aerial vehicle cooperated routing problem. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1163–1170. [Google Scholar]
- Liu, Y.; Luo, Z.; Liu, Z.; Shi, J.; Cheng, G. Cooperative routing problem for ground vehicle and unmanned aerial vehicle: The application on intelligence, surveillance, and reconnaissance missions. IEEE Access 2019, 7, 63504–63518. [Google Scholar] [CrossRef]
- Campbell, J.F.; Corberán, Á.; Plana, I.; Sanchis, J.M. Drone arc routing problems. Networks 2018, 72, 543–559. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.-B. Vehicle routing problem with drones. Transp. Res. Part B Methodol. 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Lee, S. Drone routing problem with truck: Optimization and quantitative analysis. Expert Syst. Appl. 2023, 227, 120260. [Google Scholar] [CrossRef]
- Kitjacharoenchai, P.; Min, B.-C.; Lee, S. Two echelon vehicle routing problem with drones in last mile delivery. Int. J. Prod. Econ. 2020, 225, 107598. [Google Scholar] [CrossRef]
- Satoh, K.; Morita, H. Determining the optimal parcel delivery method using one drone and one truck. Int. J. Math. Oper. Res. 2023, 24, 451. [Google Scholar] [CrossRef]
- Zhang, S.; Li, L. The Multi-visits Drone-Vehicle Routing Problem with Simultaneous Pickup and Delivery Service. J. Oper. Res. Soc. China 2023, 1, 1–31. [Google Scholar] [CrossRef]
- Bruni, M.E.; Khodaparasti, S.; Perboli, G. Energy Efficient UAV-Based Last-Mile Delivery: A Tactical-Operational Model with Shared Depots and Non-Linear Energy Consumption. IEEE Access 2023, 11, 18560–18570. [Google Scholar] [CrossRef]
- Khan, M.S.; Anwar ul Hassan, C.H.; Sadiq, H.A.; Ali, I.; Rauf, A.; Javaid, N. A new meta-heuristic optimization algorithm inspired from strawberry plant for demand side management in smart grid. In Advances in Intelligent Networking and Collaborative Systems, Proceedings of the 9th International Conference on Intelligent Networking and Collaborative Systems (INCoS-2017), Toronto, Canada, 24–26 August 2017; Springer International Publishing: Cham, Switzerland, 2018; pp. 143–154. [Google Scholar]
- Hussain, Q.H.; AL Wahab, A.A.A.; Aref, G.E. Using Strawberry algorithm to solve general mathematical model. AIP Conf. Proc. 2022, 2394, 070018. [Google Scholar]
- Konidala, S.R. Strawberry algorithm and its newly evolved variant for pattern nulling in an antenna array. RAIRO Oper. Res. 2021, 55, S1089–S1111. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Schoenauer, M. Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 1996, 4, 1–32. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and ArtiFcial Systems: An Introductory Analysis with Applications to Biology, Control, and ArtiFcial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).