TriNet: Exploring More Affordable and Generalisable Remote Phenotyping with Explainable Deep Models

Abstract

In this study, we propose a scalable deep learning approach to automated phenotyping using UAV multispectral imagery, exemplified by yellow rust detection in winter wheat. We adopt a high-granularity scoring method (1 to 9 scale) to align with international standards and plant breeders’ needs. Using a lower spatial resolution (60 m flight height at 2.5 cm GSD), we reduce the data volume by a factor of 3.4, making large-scale phenotyping faster and more cost-effective while obtaining results comparable to those of the state-of-the-art. Our model incorporates explainability components to optimise spectral bands and flight schedules, achieving top-three accuracies of 0.87 for validation and 0.67 and 0.70 on two separate test sets. We demonstrate that a minimal set of bands (EVI, Red, and GNDVI) can achieve results comparable to more complex setups, highlighting the potential for cost-effective solutions. Additionally, we show that high performance can be maintained with fewer time steps, reducing operational complexity. Our interpretable model components improve performance through regularisation and provide actionable insights for agronomists and plant breeders. This scalable and explainable approach offers an efficient solution for yellow rust phenotyping and can be adapted for other phenotypes and species, with future work focusing on optimising the balance between spatial, spectral, and temporal resolutions.

1. Introduction

Amid growing concerns over food security and the stagnation of global crop production [1], there is a pressing need to enhance the scalability of agricultural innovations, particularly in the realm of plant phenotyping. As wheat is a staple crop consumed globally, improving the resilience and yield of winter wheat (Triticum aestivum L.) through advanced breeding techniques is vital for ensuring food security [2]. To this end, remote phenotyping, which utilises non-destructive sensors and cameras to measure plant characteristics, has emerged as a pivotal technology. It offers a more scalable alternative to traditional, labour-intensive methods of genotype selection [3].

Focusing on the scalability of automatic phenotyping systems, this paper studies the case of yellow rust, or stripe rust-affected (Puccinia striiformis) [4] winter wheat, to explore the effectiveness of these technologies in a multi-temporal setup. Numerous countries worldwide have experienced large-scale yellow rust epidemics in the past [5,6,7]. In 1950 and 1964, devastating yellow rust epidemics in China resulted in estimated yield losses of 6.0 and 3.2 million tons, respectively [6]. Ref. [7] reported a severe yellow rust epidemic in Central and West Asia with yield losses ranging from 20% to 70% across countries. In the 1960s and 1970s, around 10% of Europe’s yield was lost due to yellow rust [8]. The most recent significant outbreak identified occurred in the United States in 2016 with average losses of 5.61% across the country, resulting in a total loss of approximately 3.5 million tons [7]. Multiple approaches can mitigate yield losses caused by yellow rust, including the development and use of resistant cultivars [9]. Since new yellow rust races continuously emerge, posing a threat to existing resistant cultivars [9], this approach requires their continued renewal. This underscores the need for ongoing yellow rust resistance testing and the development of new resistant cultivars and justifies the need for efficient phenotyping strategies for the foreseeable future.

In the realm of agricultural research, the integration of cutting-edge technologies has become pivotal in combating crop diseases such as yellow rust. One promising avenue involves harnessing machine learning (ML) to analyse multispectral imaging data sourced from UAV flights or other platforms [10]. UAVs are particularly helpful, since they can cover large areas of agricultural fields and carry different types of multispectral and hyperspectral sensors [11,12]. This synergy between remote sensing and ML promises powerful solutions to detect yellow rust susceptibility or resistance [13]. Several groups have proposed approaches for yellow rust monitoring.

Table 1. Synthesis of past studies on yellow rust prediction.

Study	Key Findings	Accuracy	UAV	Target Class #
[14]	Demonstrated the superiority of deep learning with a multi-layered perceptron (MLP), achieving 99% accuracy in single leaf detection.	99%	No	2 classes
[15]	Utilised a deep convolutional neural network (DCNN) for wheat rust disease classification, achieving 97.16% accuracy in distinguishing between healthy and diseased plants at the leaf level.	97.16%	No	2 classes
[16]	Processed phenocart-acquired data to predict yellow rust infection, revealing considerable infection and exploring the influence of different time steps on prediction.	61%	No	2 classes
[17]	Introduced a C-DenseNet architecture for wheat stripe rust disease grading, achieving a test accuracy of 97.99%. The dataset classifies leaf images with six levels of stripe rust infection.	97.99%	No	6 Classes
[18]	RustNet, based on ResNet-18, achieved accuracies between 79% and 86% on low-height flights.	86%	Yes	2 classes
[19]	Used hyperspectral data at 30 m altitude to forecast yellow rust presence, achieving higher accuracy with a deep convolutional neural network (DCNN) compared to basic methods.	85%	Yes	3 Classes
[20]	Explored a similar setup as in this study for spring wheat, emphasising the incorporation of temporal information in a 3D-CNN and achieving detection accuracy of 79% for spectral-spatio-temporal fused data.	79%	Yes	3 Classes

presents an overview of the most important ones.

We differentiate ourselves from these studies in three key scalability aspects:

• Most of these studies gather the measurements used for phenotyping using phenocarts or handheld devices. We use UAV imagery, a more scalable solution which can be easily applied to new fields.
• All of these studies consider high- to very high-resolution data, with non-UAV studies acquiring data at very close range and UAV flights going up to 30 m of altitude. We want to favour lower volumes of data and faster acquisition with regular and standardised flights from an altitude of 60 m at high accuracy using fixed ground control points (GCP).
• None of these studies adhere to the agricultural standards of disease scoring; instead, they only distinguish between two or three classes most of the time.

In the following paragraphs, we study these current trends and their drawbacks in more detail.

In terms of time and hardware needed, refs. [14,15,16,17] use phenocart and images acquired by handheld devices to make the predictions. Although this presents an inherently easier machine learning problem [14], we prefer the UAV solution, which merely requires flying a drone over the field. This is non-intrusive [21] (i.e., it does not require adapting the field to the phenotyping method) and requires little time from the perspective of the human operator. To leverage this, in [18,19,20], UAVs are employed for yellow rust monitoring. Nevertheless, those approaches have several drawbacks.

Flying a drone can be a time-comsuming endeavour if the target resolution is high. High spatial-resolution images are very rich and can be exploited by deep learning convolutional modules to extract image patterns, textures, and more general spatial components [22]. When using high spatial resolutions, the yellow rust pustules are visible, and a deep vision model can identify them [14]. However, this leads to larger data volumes, which implies higher hardware requirements. It also significantly increases the flight time, which in turn may lead to the necessity of changing the drone’s batteries more often. Ref. [18] uses a drone hovering 1.2 m above the canopies, leading to extremely high data throughputs. Ref. [20] operates at a more efficient altitude of 20 m, but this remains insufficient to efficiently capture large areas. Finally, ref. [19] uses a hyperspectral camera and flies at an altitude of 30 m, but although hyperspectral cameras provide very rich data, they are particularly expensive. In our research, we adopt a much higher flight altitude of 60 m and include more spectral bands (RGB, Red Edge, and NIR) to assess how spectral resolution [23] can counteract this lack of spatial resolution. We also try to develop a model that, through the usage of fewer spectral bands and indices as well as less frequent UAV acquisition, can yield good performance and further scale remote phenotyping. However, in contrast to [19], we do so conservatively and attempt to study which bands contribute the most for future optimisation.

The results present in the literature, reported in Table 1, appear solid, with accuracies as high as 99% on the binary healthy/unhealthy regression problem [14] and 97.99% on the six class problem [17]. However, it is important to note that while many approaches focus on the binary healthy/unhealthy problem in yellow rust prediction, this scale is often insufficient for breeding operations. In our study, we scored yellow rust following the official Austrian national variety testing agency AGES (Austrian Agency for Health and Food Safety GmbH) on a scale from 1 to 9. The Federal Plant Variety Office in Germany also uses a comparable scoring system from 1 to 9 for yellow rust disease occurrence. Various other methodologies exist for measuring or scoring yellow rust damage, including evaluating percent rust severity using the modified Cobb Scale [24], scoring host reaction type [25], and flag leaf infection scoring [26]. For instance, ref. [27] uses continuous disease scoring from 1 to 12 throughout the season to evaluate the area under the disease progression curve. These scoring scales are designed in the context of plant breeding to be useful in a variety of situations, comparable to international standards and results and from one dataset to another. In contrast, the number of target classes used in the literature is extremely coarse, which makes it hard to validate, generalise, and share across different domains.

Our proposed approach, TriNet, consists of a sophisticated architecture designed to tackle the challenges of yellow rust prediction. TriNet comprises three components—a spatial, a temporal, and a spectral processor—which disentangle the three dimensions of our data and allow us to design built-in interpretability in each of them. TriNet maintains performance levels comparable to the state-of-the-art, despite the difficulties introduced by higher operational flight heights and thus lower spatial resolutions. Furthermore, TriNet generates interpretable insights through the importance of attention weights. This facilitate more informed breeding decisions. We leverage domain knowledge during model training thanks to the interpretability offered by attention weights present in the spatial, temporal, and spectral processors, which we hope to be a promising avenue for fostering the development of more robust and generalisable models.

In this study, we claim the following contributions:

• We achieve promising results in terms of top-two accuracy for yellow rust detection using UAV-captured images taken from a height of 60 m (see Section 3.2).
• We introduce a modular deep learning model with its performance validated through an ablation study. The ablation is applied to the architectural elements as well as the spectral components and the time steps (see Section 3.3 and Section 3.5).
• We demonstrate the interpretability of our model by showing that it can offer valuable insights for the breeding community, showcasing its ability to select important bands and time steps (see Section 3.4) in particular. We believe these results to be an important step forward for scalability in remote phenotyping.

2. Materials and Methods

2.1. Study Area and Experiments

We study the growth and development of yellow rust in winter wheat in Obersiebenbrunn, Austria. The agricultural research facility in Obersiebenbrunn is overseen by the plant breeding organisation Saatzucht Edelhof [28].

The experiments were performed during the 2022/23 season in chernozem soil. The mean annual temperature was 10.4 °C, and the mean annual precipitation was 550 mm. Plots of winter wheat genotypes at various stages in the breeding processes were established with 380 germinable seeds m⁻². Exceptions were the experiments WW6 and WW606, which consisted of four commercial cultivars (Activus, Ekonom, Ernestus, and WPB Calgary) in four different sowing densities (180, 280, 380, and 480 germinable seeds per square metre) in one replication for both WW6 and WW606, respectively. The pre-crop of the field was sunflower. The seedbed was prepared using a tine cultivator to a depth of 20 cm. Sowing was performed on 18 October 2022 with a plot drill seeder at a depth of 4 cm. Fertilisation as well as the control of weeds and insects were conducted in accordance with good agricultural practice. No fungicides were applied.

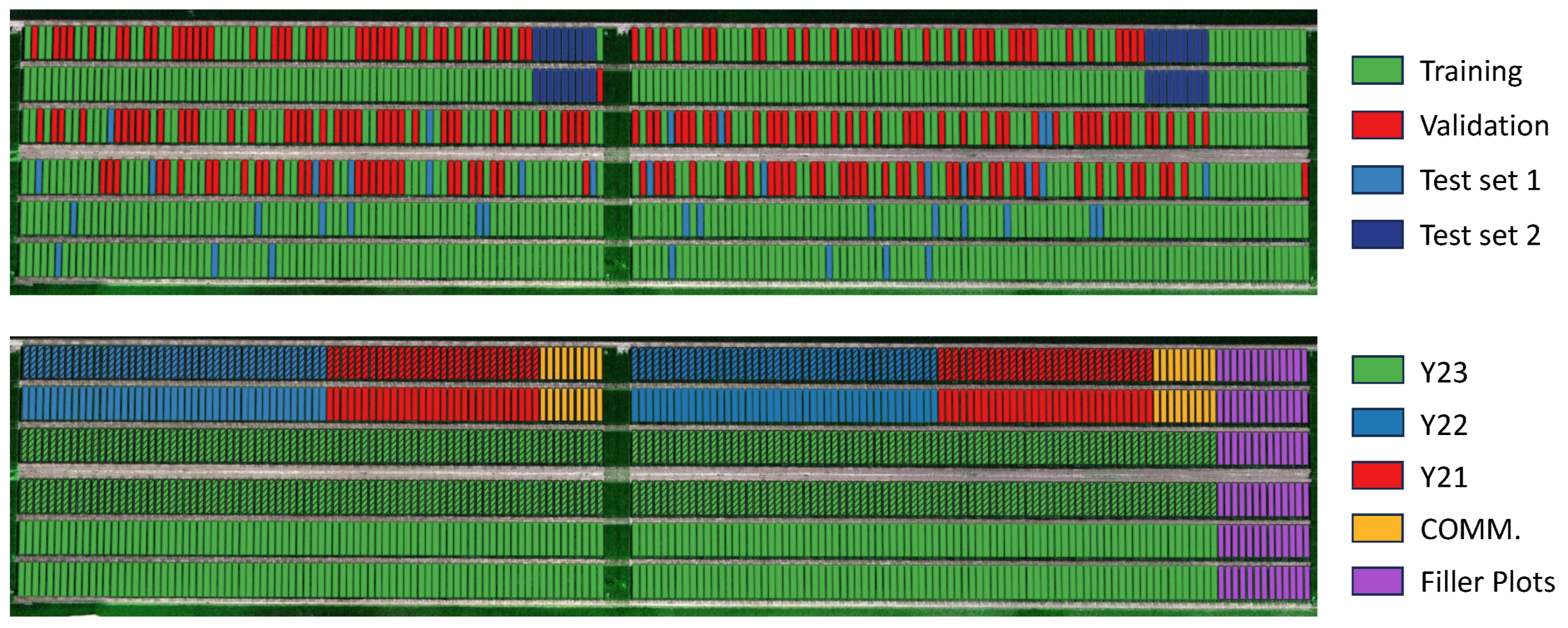
The field was organised into 1064 experimental plots where the experiments were conducted (Figure 1). To identify each plot, we use the notation system Y-G-R structured as follows:

• Y represents the year in which the genotype reached the stage of experimental yield trials in the breeding process. The experiments, however, also include check cultivars, which are genotypes that are already on the market and used to compare the performance of genotypes in development to the current cultivars on the market. These commercial cultivars are denoted as “COMM”.
• G denotes the name of the genotype planted in the plot.
• R signifies whether the plot serves as a replication for statistical robustness. It is followed by a numerical value (R1 or R2) to distinguish between different replication instances.

For instance, a plot identified as Y[21]-G[SE 001-21 WW]-R[2] indicates that the seed genotype SE 001-21 WW was selected in the year 2021 (Y21), and out of our two replicated plots with these characteristics, this is the second one (R2). A total of 168 plots of the fields were sown with commercially available genotypes, and 36 of these were treated as a control group and were assigned the identifier “COMM”. This metadata is used to determine relevant data splits for machine learning in Section 2.3. To visualise the distribution of these traits, please consult Figure 2.

As previously stated, yellow rust was scored in this study according to the official Austrian national variety testing agency AGES (Austrian Agency for Health and Food Safety GmbH). Therefore, yellow rust severity was scored on a scale from 1 to 9. The individual scale levels from 1 to 9 were defined as follows: 1, no stripe rust occurrence; 2, very low or low occurrence (only individual pustules); 3, low occurrence (many plants with few symptoms or few plants with medium symptoms); 4, low to medium occurrence; 5, medium occurrence (many plants with medium symptoms or few plants with many symptoms); 6, medium to high occurrence; 7, high occurrence (all plants with medium symptoms or many plants with many symptoms); 8, high to very high occurrence; 9, very high occurrence (almost all leaf and stem areas are covered in pustules).

2.2. Sensor and Data Acquisition

For this study, we acquired a time series of multispectral data with a UAV. This drone platform is well-suited for its capacity to carry substantial payloads, including a multispectral camera. The camera utilised in our study was the Altum-PT model [29], weighing 0.5 kg, capable of capturing RGB, Red Edge, NIR, LWIR, and panchromatic bands. For the sensor specifics, see

Table 2. Spectral Bands of Altum-PT Camera.

Band	Center (nm)	Bandwidth (nm)
Blue	475.0	32.0
Green	560.0	27.0
Red	668.0	16.0
Panchromatic	634.5	463.0
Red edge	717.0	12.0
Near-IR	842.0	57.0
LWIR	$10.5\times 10.5^3$	$6.0\times {10}^3$

.

The UAV maintains a flight altitude of 60 m, resulting in a ground sampling distance (GSD) of 2.5 cm for the multispectral bands, 16.7 cm for the LWIR band, and 1.2 cm for the panchromatic band. This GSD is larger than most existing UAV-based yellow rust monitoring approaches. For instance, in [19], the flight altitude is 30 m (~2 cm GSD); in [18], it is 1.2 m (0.5 mm GSD); and in [20], the height is 20 m (1 cm GSD). In our study, we contribute to investigating the trade-off between model performance and GSD by choosing a higher flight altitude. Specifically, we choose a GSD of 2.5 cm. While being much higher than that used in competing studies to assess the possibility of performing phenotyping from this height, this GSD closely matches the size of wheat flag leaves, which are pivotal for evaluating wheat plants [30]. Therefore, this seems to be a good starting point to evaluate the potential of higher-altitude flights in wheat phenotyping.

To thoroughly understand the potential of this lower GSD for remote phenotyping, we performed a rich multispectral and multi-temporal acquisition paired with expert-assessed yellow rust disease scores. Throughout the winter wheat growth period, we conducted a total of 7 flight missions from March to June to gather data in our test fields. The specific dates are reported in Appendix A 

Table A1. Dates of data acquisition and growth stages of winter wheat.

Date of the Flight	Growth Stage
22 March 2023	Stem Elongation
18 April 2023	Stem Elongation
27 April 2023	Booting
15 May 2023	Heading
24 May 2023	Flowering
5 June 2023	Milk Development
14 June 2023	Dough Development

.

During each flight, our drone captured approximately 320 multispectral images following a predefined path covering 282 × 57 m of the entire experimental field with an overlap of at least 6 images per pixel. These images were subsequently orthorectified, radiometrically calibrated, and stitched together, as comprehensively detailed in [31]. All flight campaigns were conducted around noon to ensure consistent lighting conditions. We performed radiometric calibration using a two-step approach: pre-flight calibration with a reflectance panel for each band and in-flight correction using a downwelling light sensor (DLS) to account for varying ambient light. The data were processed using Pix4Dmapper, which also addressed potential spectral mixing issues. The combination of standardised calibration, consistent flight patterns, and high image overlap helped to minimise radiometric and geometric distortions in the final dataset.

One important feature of our data acquisition was the use of ground control points (GCPs), as in [32], to enhance the geolocalisation of the UAV’s images. The outcome of this process was a tensor comprising 7 spectral channels and covering the entire field. However, this reflectance map is not readily usable as a machine-learning dataset. As a reference, the size of the acquired data in our setup with an operational height of 60 m is 1.74 GB, while it is 5.96 GB when flying at 20 m. This large difference in data volume significantly speeds up the preprocessing to obtain the reflectance maps using pix4D (by a time factor of 4).

Four external points of known geolocation delineate the boundaries of each plot. As described in [31], these points serve as reference coordinates to resample the plot quadrilateral into a rectangular matrix of reflectance values using a homography transformation to eliminate the effect of geographic raster grid alignment. In Figure 3, we present a diagram illustrating the transition from the larger reflectance map to the resampled plot.

In our case, we used bicubic resampling to reconstruct the pixel values in our final plot data. During this procedure, we maintained high absolute geolocation accuracy through the use of GCPs. Rectangular images with no borders around the fields are easier to use in the context of deep learning, particularly because the flip augmentations follow the axes of symmetry of the fields. This was particularly significant as we were, among other things, interested in measuring the intensity of border effects on the chosen phenotype. This procedure was applied to each of the drone flights. The result was a tensor with the following dimensions:

• Plot Number (length 1025): Denoted as p; a unique identifier assigned to each experimental plot within the research facility.
• Time Dimension (length 7): Denoted as t; the date when the multispectral images were captured.
• Spectral Dimension (length 7): Denoted as $sc$; the spectral bands recorded by our camera plus the panchromatic band.
• Spatial Dimensions: Collectively denoted as $st$:

  –

  Height Dimension (length 64): Denoted as h; the height of one plot in pixels.

  –

  Width Dimension (length 372): Denoted as w; the length of one plot in pixels.

2.3. Dataset Preparation

We added several spectral indices tailored to describe specific plant physiological parameters [33]. These indices have been shown to effectively describe wheat plants’ health and growth status [34]. In general, spectral indices elicit more information from the data than raw spectral bands, and they have long been used in plant science as high-quality features. We selected a total of 13 indices, and we report them in

Table 3. Vegetation indices with corresponding equations and sources.

Index	Equation	Full Name	Source
NDVI	${\displaystyle \frac{NIR-Red}{NIR+Red}}$	Normalised Difference Vegetation Index	[35,36,37]
SAVI	${\displaystyle \frac{NIR-Red}{(NIR+Red+0.5)·1.5}}$	Soil Adjusted Vegetation Index	[38]
OSAVI	${\displaystyle \frac{1.16·(NIR-Red)}{NIR+Red+0.16}}$	Optimised Soil Adjusted Vegetation Index	[39]
EVI	${\displaystyle \frac{5·(NIR-Red)}{2·(NIR+6·Red-7.5·Blue+1)}}$	Enhanced Vegetation Index	[40]
GNDVI	${\displaystyle \frac{NIR-Green}{NIR+Green}}$	Green Normalised Difference Vegetation Index	[41]
GOSAVI	${\displaystyle \frac{NIR-Green}{NIR+Green+0.16}}$	Green-Optimised Soil Adjusted Vegetation Index	[42]
NDRE	${\displaystyle \frac{NIR-RE}{NIR+RE}}$	Normalised Difference Red Edge	[43]
CCCI	${\displaystyle \frac{NDRE-NDR{E}_{min}}{NDR{E}_{max}-NDR{E}_{min}}}$	Canopy Chlorophyll Content Index	[44]
GCI	${\displaystyle \frac{NIR}{Green}}-1$	Green Chlorophyll Index	[45]
PSSRa	${\displaystyle \frac{NIR}{Red}}$	Pigment Specific Simple Ratio	[46,47]
GLI	${\displaystyle \frac{(Green-Red)+(Green-Blue)}{2·Green+Blue+Green}}$	Green Leaf Index	[45]
MCARI	$[(RE-Red)-0.2·(RE-Green)]·{\displaystyle \frac{RE}{Red}}$	Modified Chlorophyll Absorption in Reflectance Index	[48]
RDVI	${\displaystyle \frac{NIR-Red}{\sqrt{NIR+Red}}}$	Renormalised difference vegetation index	[49]

.

These 13 indices, which constitute information regarding the physiology of the plant, were computed and then added as new channels to the dataset tensor, resulting in 20 channels. Introducing domain-motivated features in the form of those spectral indices acted as an inductive bias to converge to better results despite our comparatively low data regime. In other words, they constituted already valuable information that the model did not need to learn to derive from the input data, and they guided the model towards a solution that made use of these specific characteristics of the input bands.

We then divided the dataset into four distinct sets: training, validation, and two test sets used to evaluate different characteristics of our models. This split was based upon the operational division employed by agronomers, as visible in Figure 2. In 

Table 4. Description of our data splits for machine learning. In test set 1, $\widehat{X}$ stands for genotypes not previously selected. There is no overlap between breeds/genotypes represented by $\widehat{X}$ and X. COMM. refers to commercially available genotypes.

Split	Cardinality	Identifiers
Train	726	Y[20/21/22]-G[X]-R[1], Y[20/21/22]-G[X]-R[2]
Validation	222	Y[20/21/22]-G[X]-R[2]
Test 1	41	Y[20/21/22]-G[$\widehat{X}$]-R[1], Y[20/21/22]-G[$\widehat{X}$]-R[2]
Test 2	36	COMM.

, we present a summary.

• Test Set 1: This set comprised 10 genotypes chosen from the breeds initially selected in 2023, 2022, and 2021. This test set aimed to match the distribution of the training and validation sets. To ensure a comprehensive evaluation despite our unbalanced labels, we maintained similar class distributions across training, validation, and test set 1. This set tests our model’s overall generalisation capabilities.
• Test Set 2: This test set included plots whose genotypes were commercially available. Its primary function was to act as a control group, assessing the algorithm’s ability to generalise to genotypes selected in previous years by different wheat breeding companies. However, it is worth noting that this dataset was unbalanced, with a predominance of low disease scores.
• Validation: This set was composed of 54% of replication 2 of the remaining plots, totalling 222 time-series. This set served as a set to validate the training results, comparing model trained with different architectures and hyperparameters and fine-tuning the hyperparameters.
• Training: The remaining experiments composed the training set. This set had 726 time series of multispectral images.

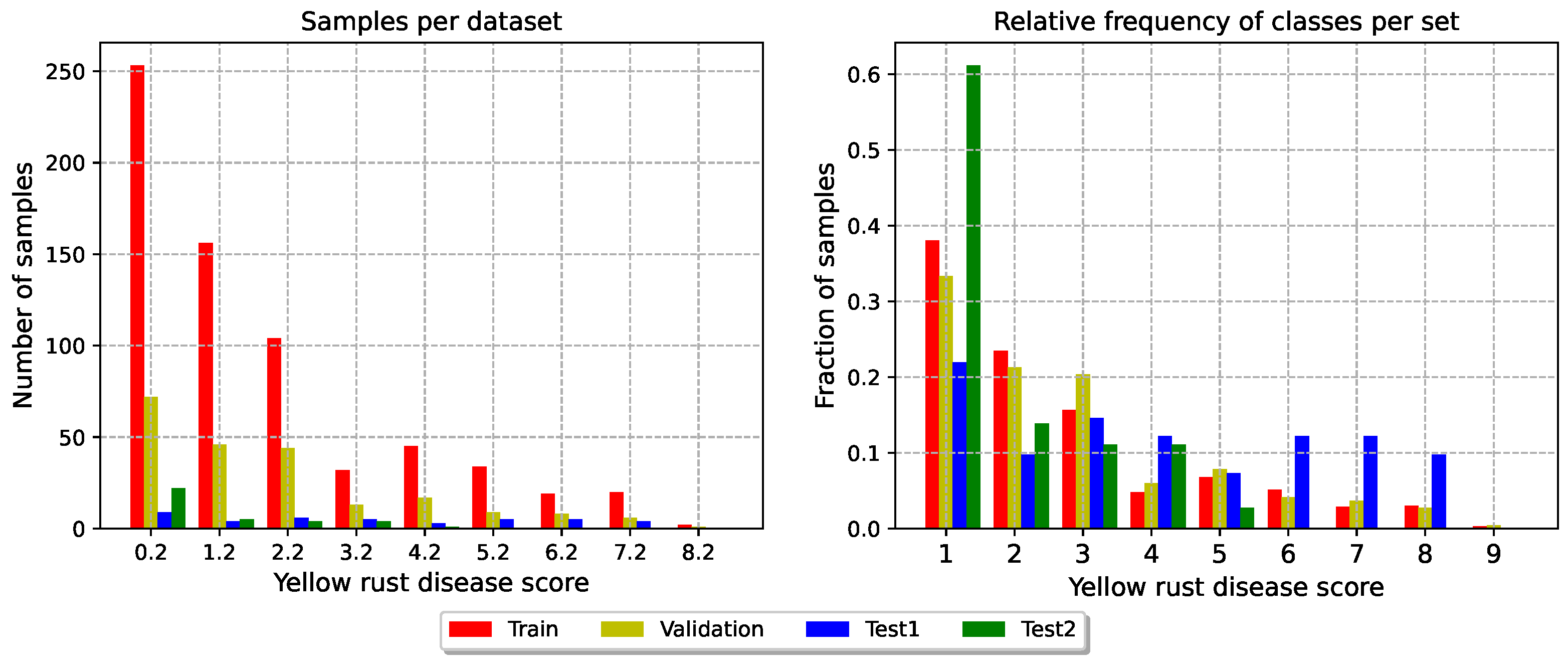
This split provides a robust setup for various machine-learning experiments. Figure 4 provides a visualisation of the distribution of the targets in the four sets.

2.4. TriNet Architecture

In this study, we propose TriNet, a deep learning model designed to solve the task of remote phenotyping of yellow rust while providing insights to make acquisition operations more resource efficient in the future. For example, we hope to learn which bands are the most impactful for the performance or at which time steps it is the most important to acquire data. TriNet consists of three distinct stages which each independently process one of the problem’s dimensions: the spectral processor, the spatial processor, and the time processor. A schematic representation illustrating the various parts can be found in Figure 5.

• Spectral Processing Stage: The model dynamically identifies the most pertinent spectral bands and vegetation indices during training.
• Spatial Processing Stage: The model’s feature extractor extracts patterns from the image data. Then, it collapses the two spatial dimensions, width and height, by averaging the features, facilitating the processing of the time dimension.
• Time Processing Stage: The model captures and exploits temporal dependencies within the time series data, trying to make use of different kinds of information from different growth stages.

2.4.1. Attention Layers in TriNet

Each of these stages harnesses the concept of attention, originally introduced in [50] in the context of machine learning. Different kinds of attention were used across the literature until self- and cross-attention, in which attention weights are derived from the input data itself, became the main components of some of the most powerful known models in natural language processing [51] and computer vision [52]. Attention mechanisms were initially applied to neural networks as essential components, enabling the adaptive and dynamic processing of spatial features and patterns, while also serving as interpretable elements that provided insights into the model’s inner workings. In our implementation, we focus on the interpretability of attention layers and therefore use the simpler original attention from [50] with one or several attention heads.

Single-head attention essentially computes a weighted average of input features along a given dimension, with the weights indicating the relative importance of each feature. By extension, multi-head attention generates multiple feature-weighted averages by applying independent sets of weights. Our aim is to select generally better spectral bands or time steps for yellow rust remote phenotyping, as well as to understand the impact of the relative location inside the plot when monitoring yellow rust. Therefore, constant learned attention weights are the tool of choice for our purpose, as opposed to self-attention, for example.

Mathematically, we can write an attention function with h heads operating on dimension k as a parametric function ${\mathcal{A}}_k^h(X:W)$, where $X\in {\mathbb{R}}^{|d_1|\times ...\times |d_D|}$ is a tensor with D dimensions, and $W\in {\mathbb{R}}^{h\times |d_k|}$ can be seen as h vectors of one weight per element in X along its $k^{\mathrm{th}}$ dimension. With a single head, $\mathcal{A}$ will collapse X’s $k^{\mathrm{th}}$ dimension, giving as output a tensor $Y\in {\mathbb{R}}^{|d_1|\times ...\times |d_{k-1}|\times |d_{k+1}|\times ...\times |d_D|}$. If we denote as $X_{d_k=i}$ the tensor slice corresponding to the $i^{\mathrm{th}}$ element of X along the $k^{\mathrm{th}}$ dimension, then single-head attention can be written as

$$Y={\mathcal{A}}_k^1(X:w)=\sum _{i=1}^{|d_k|}{X}_{d_k=i}·\mathrm{softmax}{\left(w\right)}_i$$

where w, in the single-headed case, is simply a vector of $|d_k|$ elements, and softmax is the softmax function [53] (such that the weights used for averaging are positive and sum to 1). From this, the general h-heads case gives as output a tensor ${\mathcal{A}}_k^h(X:W)=Y\in {\mathbb{R}}^{|d_1|\times ...\times |d_{k-1}|\times h\times |d_{k+1}|\times ...\times |d_D|}$, where the $j^{\mathrm{th}}$ element along the $k^{\mathrm{th}}$ dimension is the output of the $j^{\mathrm{th}}$ head and can be written as

$$Y_{d_k=j}=\sum _{i=1}^{|d_k|}{X}_{d_k=i}·\mathrm{softmax}{\left(W_j\right)}_i$$

In what follows, we typically refer to dimensions by name instead of by index; for example, ${\mathcal{A}}_{sc}^h\left(X\right)$ is an h-heads attention along the spectral dimension of a plot denoted as X.

2.4.2. Spectral Processor

Let our input plot $X_{in}$ be a tensor with dimensions [t, sc, h, w]. Our spectral processor (see Figure 5) selects the bands and spectral indices to use in the subsequent processors. We seek to both to better understand the contributions of our bands and indices and to minimise the complexity of the following spatial processor (see Section 2.4.3). Therefore, in this processor, we have a strong incentive to aggressively select as few bands as possible so long as it does not degrade the model’s performance. Reusing the formalism established in Section 2.4.1, this processor can simply be written as one h-heads attention layer, with h being the number of spectral bands and indices we want to keep in the output $X_{sc}$:

$$X_{sc}={\mathcal{A}}_{sc}^h(X_{in}:W_{sc})$$

(1)

The output $X_{sc}$ still has dimensions [t, sc, h, and w], but now, the $sc$ dimension contains h composite bands each created from performing attention on the input bands and indices.

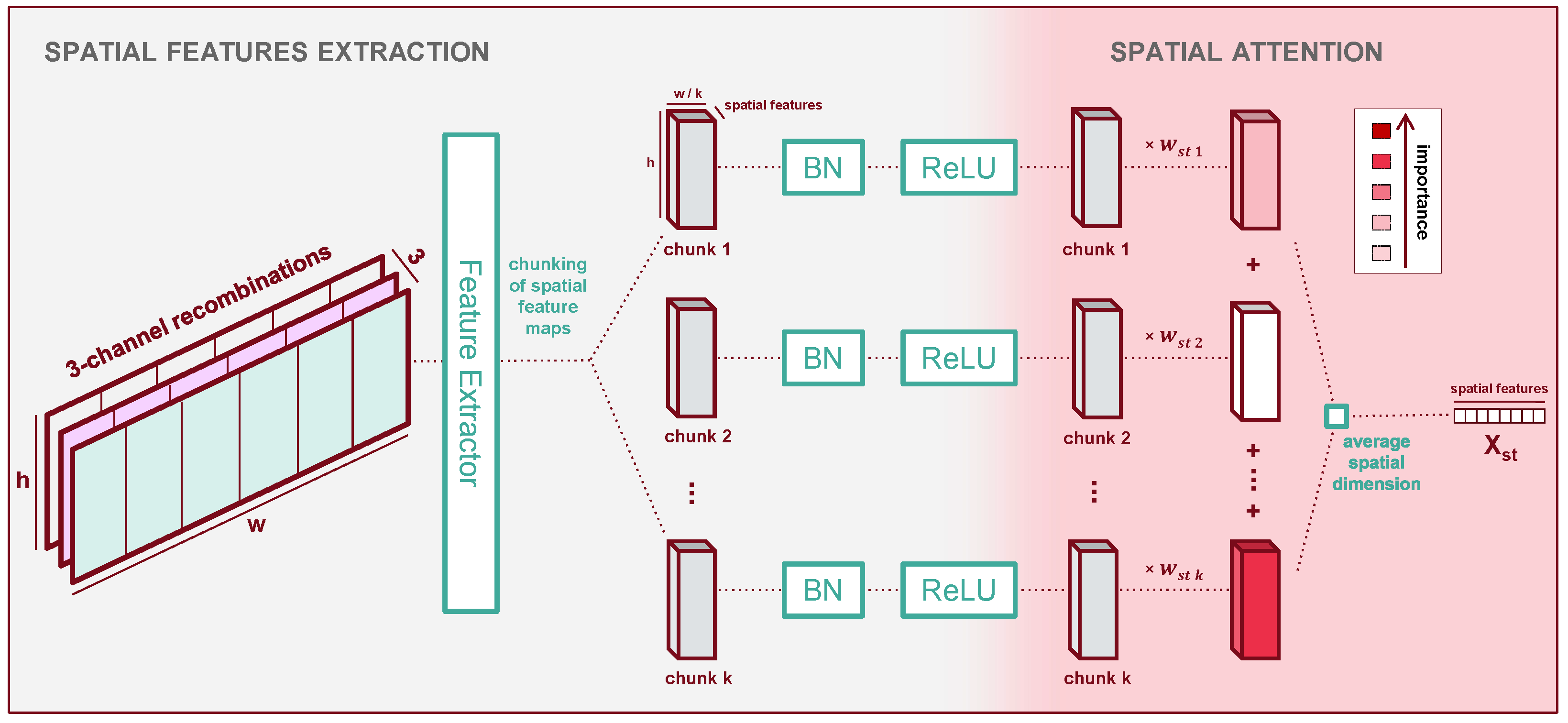
2.4.3. Spatial Processor

The spatial processor consists of three parts, as shown in Figure 6: first spatial processing, then chunking the plot along its width into several areas, then spatial attention between those areas.

In this module’s first section, we extract the spatial features which we then use as predictors for the presence of yellow rust in subsequent steps. We design our spatial feature extractor based on several key hypotheses:

• Our UAV observations have a relatively low resolution at which individual plants are not always discernible. Therefore, we hypothesise that the features should focus on local texture and intensities rather than shapes and higher-level representations.
• Although yellow rust’s outburst and propagation may depend on long-range factors and interactions within the plots, measuring the presence of yellow rust is a local operation which only requires a limited receptive field.
• As we care more about local information on textural cues (i.e., high-frequency components), essentially computing statistics on local patterns, a generically-trained feature extractor might suffice. In addition, because of this generality, the same feature extractor might work for all input band composites in the spectral processor’s output.

To make use of these hypotheses, we choose a pre-trained deep feature extractor denoted $FE$, which we keep frozen. Early experiments with non-pre-trained feature extractors do not converge, which we interpret as indicating that our dataset is too small to train the significant number of parameters they contain. In this study, we use ResNet-34 [54] as our feature extractor. ResNet-34 was proven to be efficient in predicting yellow rust in other studies using low altitude UAV images [19,55] or mobile platforms [56]. We experiment with various shallow subsets among the first layers of ResNet-34 in order to avoid higher-level representations in line with our hypotheses. Finally, since ResNet-34 is pre-trained on RGB images, it expects 3 channels. Therefore, we use a function denoted as $rec$ to recombine our input channels into groups of three to satisfy this requirement. More details are given in Appendix C. The extracted feature maps from each group of three input channels are then concatenated back together.

In the second part of the spatial processor, the plot’s feature maps are chunked along the width dimension. This allows us to apply attention to different locations in a plot. At a glance, this might not seem intuitive, because it would seem more natural to consider each plot chunk equally to evaluate the average health. Although it introduces additional parameters and sparsity to the model, which might make it harder to train, allowing the model to focus unequally on different chunks allows us to verify this assumption:

• If some spatial chunks of the plot contain biases (e.g., border effects or score measurement biases), then the model might learn unequal weights;
• if no such biases exist, then we expect the model to attend equally to all chunks.

The result of our chunking is a tensor of dimensions [t, sc, ck, w, and h], where a new dimension $ck$ stores the chunks, and the new width along dimension w is the width of the features maps divided by the number of chunks. This chunking operation is denoted as $chunk$. We post-process the chunks with batch normalisation (denoted $BN$) and a ReLU activation (denoted $ReLU$), following standard techniques in image recognition [57]. The use of batch normalisation in the latent space of deep architectures has been shown to facilitate convergence across a wide variety of tasks. The third part of the spatial processor then applies attention to the chunks.

Now that a potential bias in the chunk location has been accounted for, we assume that the plot’s overall health is the average of the local health over all locations. Therefore, we collapse the spatial dimension of our data by averaging all features—our predictors for the plot’s health—across their spatial dimension. We call this operation $mea{n}_{st}$.

At each time step, we obtain a vector of global features describing the plot’s spatial and spectral dimensions. Using the notations presented throughout this section, we get the expression of the output $X_{st}$ of the spatial processor concerning the output $X_{sc}$ of the previous spectral processor:

$$X_{st}=mea{n}_{st}\left({\mathcal{A}}_{ck}^1(ReLU\left(BN\left(chunk\left(FE\left(rec\left(X_{sc}\right)\right)\right)\right)\right):w_{st})\right)$$

(2)

The output $X_{st}$ has the dimensions [t, f], with f being the dimension of the new spatial features.

2.4.4. Feature Selection

Since we use a generically trained feature extractor, it is reasonable to assume that most of the extracted features do not correlate well with the presence of yellow rust. A natural step to take before processing the plot data along its time dimension is to further select from $X_{st}$ the features useful for the task at hand. We use a single fully connected layer, which we denote as $LASSO$ because of its L1-regularised weights, as a selection layer with a slightly higher expressive power than an attention layer due to its fully connected nature. L1 regularisation guides the weights towards sparser solutions, meaning that the weights will tend to collapse to zero unless this decreases performance, hence selectively passing only useful information to the next layer. It is also followed by an additional rectified linear unit ($ReLU$). Here, and in general, we add such $ReLU$ layers as non-linear components that also introduce sparsity by setting negative activations to zero and thus reducing the number of active features. The output $X_f$ has the same dimensions as $X_{st}$ but contains a smaller number $n_f$ of extracted features for each time step.

$$X_f=ReLU\left(LASSO\left(X_{st}\right)\right)$$

2.4.5. Time Processor

The last dimension of our data—time—is processed by our time processor. The spatial features at each time step are first processed together by $l_{LSTM}$ layers of long short-term memory [58] cells with $n_{LSTM}$ neurons, which we collectively denote as $LSTM$. Long short-term memory cells have long been used as an architectural component in deep architectures to process time series data differentiably [59]. The features in the output of this layer finally encode the information in the three spectral, spatial, and temporal dimensions. The long short-term memory layers are followed by another, $ReLU$, and a single-head attention on the t dimension. Intuitively, we want the model to learn which flight dates contribute the most to detecting yellow rust, hence the use of attention once again. The output $X_t$ is a simple vector containing rich features encoding all the dimensions of the input data and is obtained as shown in Equation (3). The importance of how much a single time step contributes to the regression problem is represented by the magnitude of the weight $w_t$, with t being associated with one of the dates reported in Table A1.

$$X_t={\mathcal{A}}_t^1(ReLU\left(LSTM\left(X_f\right)\right):w_t)$$

(3)

2.4.6. Regression Head

We compute our regression outputs $X_{out}$ with $l_{head}$ fully connected layers with $n_{head}$ neurons and $ReLU$ layers as activations followed by a fully connected layer with a single neuron and no activation. These layers are collectively denoted as $head$, which yields the final output of our model.

$$X_{out}=head\left(X_t\right)$$

2.4.7. Loss Function

We train TriNet using the mean squared error, denoted as $MSE$, between the predicted yellow rust score (between 1 and 9) and the score obtained during our expert scoring (see Section 2.1).

We also regularise some weights with different loss functions in order to encourage the model to exhibit specific behaviours. As explained in Section 2.4.4, we want the feature selector to aggressively select which features to keep for the subsequent steps. The rationale behind this is that ResNet generates a high number of channels in its output, and not all of them contribute to the model’s output. By introducing this generalisation, we nudge the model into the direction of excluding those channels. For this purpose, the weights $W_f$ of our $LASSO$ layer are regularised by their $L_1$ norm as in standard Lasso [60].

In this study, one of our main goals is to analyse which bands, indices, and time steps are the most influential in order to simplify future studies. Therefore, we also add entropy losses to all our attention weights. Intuitively, minimising entropy means favouring sparser attention weights, or in other words, more selective attention layers. For attention weights w, we consider the entropy $\mathcal{H}$

$$\mathcal{H}\left(w\right)=-\sum _{i=1}^{\left|w\right|}\mathrm{softmax}{\left(w\right)}_{i}log\mathrm{softmax}{\left(w\right)}_i$$

We apply entropy to the weights $W_{sc}$ of each head in Equation (1), the weights $w_{st}$ in Equation (2), and the weights $w_t$ in Equation (3).

To each additional loss, we assign a scalar $\gamma$ to serve as a regularisation term, leading to the loss function

$$\begin{array}{cc}\hfill \mathcal{L}(\mathrm{TriNet},X_{in},y)=& MSE(\mathrm{TriNet}\left(X_{in}\right),y)\hfill \\ & +{\gamma }_f\left|\right|W_f{\left|\right|}_1+{\displaystyle \frac{{\gamma }_{sc}}{h}}\sum _i^h\mathcal{H}\left(W_{sc,i}\right)+{\gamma }_{st}\mathcal{H}\left(w_{st}\right)+{\gamma }_t\mathcal{H}\left(w_t\right)\hfill \end{array}$$

with TriNet being our model, $X_{in}$ being the input data, and y being the associated ground truth score.

3. Results

We conducted extensive experiments using our proposed TriNet architecture for our two main purposes:

• Training a state-of-the-art model for yellow rust phenotyping at a 60 m flight height (see Section 3.2);
• Gaining insights into efficient operational choices for yellow rust remote phenotyping (see Section 3.4).

3.1. Metrics

We evaluated TriNet using a set of carefully chosen metrics. Our model outputs a single number which is a regression over the possible scores (between 1 and 9). Therefore, traditional regression metrics (in our case, $MSE$ and $MAD$) naturally make sense for comparing our results. However, they do not constitute the best way to assess the practical usability of our model because we want to develop a tool usable and interpretable by breeders and agronomists. Since, in the field, several classification scales are used, we transformed the regression problem into a classification one by considering each integer as an ordered class. As a consequence, we also proposed to use classification metrics and further report the top-k accuracy metric. In our case, we assumed the top-k predicted classes to be the k closest classes to the predicted score. For example, if we predicted $2.7$, then the top 3 classes would be 3, 2, and 4 from the closest to the furthest. Top-k accuracy therefore describes the percentage of samples in a set for which the correct class is among the k closest classes.

Classification metrics are useful to plant breeders because they need to know approximately which class a certain field is classified as and group several classes together to make decisions [61]. These groups of classes can vary based on the application and the breeders; hence, the entire scale from 1 to 9 is generally necessary. Therefore, we need metrics to inform on the capacity of the model to give accurate scores but also metrics to inform on its capacity to give approximate scores at different resolutions. This is also useful for fairer comparisons to existing literature with fewer classes. The class groups used to obtain a certain binary or ternary score are unknown, and we therefore choose top-k accuracy metrics as a good compromise.

We generally report top-3 accuracy as our metric of choice from an interpretability perspective, which corresponds to being within one class of the correct class. We also report top-1 and top-2 accuracy for completeness. We hope to give the reader a better intuition of how to compare this model to the two-class or three-class formulations usually present in yellow rust monitoring literature [14,15,16,18]. We chose this because comparing results between a 2-class and a nine-class problem presents significant challenges. Simplifying a nine-class problem by grouping classes into two broad categories is inherently imprecise. It raises the issue of how to appropriately group these classes and overlooks their natural ordering. For example, if classes 1 to 4 are grouped into a “negative” category, then a predicted class of 5 or 9 would be incorrectly classified as equally significant true positives, which is a poor representation of reality.

Top-k accuracy offers a more nuanced solution. This classification metric accounts for how close the model’s prediction is to the actual score, thereby providing insight into how a nine-class problem might be translated into various two-class or three-class versions without arbitrarily deciding on specific groupings. It also accounts for the class ordering in a finer way than binary or ternary classification does.

In a binary classification framework with a threshold (e.g., class 3; see [62]), the ordering plays a critical role. Binary classification checks whether the true value exceeds a certain threshold, effectively utilising the ordered nature of the classes. Thus, the inherent order in the regression problem facilitates a comparison of top-k accuracy, which measures the closeness of a prediction to the true value, with binary classification, which determines whether the true value surpasses a specified threshold. This approach provides a method to compare our regression study’s performance with other studies in the literature, bridging the gap between multi-class and binary classification analyses.

3.2. Base Model

First, we optimised TriNet to obtain the best phenotyping quality possible at our operating height. We report the model that achieves the highest validation $R_2$ score during our extensive experimentation. The model presents the following values:

• We used $h=3$ as our number of heads in the spectral attention layer;
• The number of pretrained modules was $l_{FE}=1$ in our feature extractor (a module in ResNet consists of all the layers before a max pooling operation, including this max pooling operation);
• We used a $k=1$ chunk in our spatial processor (meaning we do not chunk the data spatially);
• The number of output channels was $n_f=64$ for our feature selector;
• The number of LSTM layers was $l_{LSTM}=3$, and the size of their internal layers was $n_{LSTM}=32$;
• The number of hidden layers was $l_{head}=2$, and their number of neurons was $n_{head}=256$ in the regression head;
• The loss components were ${\gamma }_{sc}=0$, ${\gamma }_f=0.001$, and ${\gamma }_t=0.00063$;
• The learning rate was $lr=0.01$, multiplied by $0.1$ every 30 epoch for 200 epochs, with a batch size of 16. We also applied a dropout of $0.2$ on the $head$’s hidden layers and the LSTM’s weights. We used a weight decay of $0.0001$ and clip gradients of norm above 1.

In addition, we noticed that using statistics tracked during training at inference time in batch normalisation layers reduced the performance significantly, and therefore, we used online-calculated statistics contrary to popular convention. We interpreted this as the model needing precise statistics to perform regression, contrary to when performing a discrete task such as classification. This problem was further exacerbated by the small size of the training dataset, since the running means were not good descriptors for each possible subset of data.

Two parameters are of particular note here. First, using no chunks seemed better than using chunks for spatial processing. This would imply that training additional per-chunk weights is an unnecessary overhead for the model and that all locations within a plot should be considered equally. We will come back on this conclusion in future sections. Second, our base model was achieved without any regularisation for the attention weights selecting the bands. As we will see, using bands selected that way is still conclusive, although a stronger regularisation would have lead to a clearer selection.

With these parameters, we obtained our best results for yellow rust phenotyping at 60 m of altitude with scores from 1 to 9. We report our results in

Table 5. The mean square error (MSE), the mean absolute deviation (MAD), and some top-k accuracy results from all sets for our base model. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
Train	0.91 [0.71,1.15]	0.75 [0.68,0.83]	0.44 [0.38,0.51]	0.74 [0.68,0.80]	0.90 [0.86,0.94]
Validation	1.33 [0.82,2.01]	0.88 [0.73,1.07]	0.38 [0.26,0.50]	0.69 [0.59,0.81]	0.87 [0.78,0.94]
Test 1	2.38 [0.74,4.89]	1.16 [0.63,1.77]	0.35 [0.12,0.65]	0.59 [0.30,0.83]	0.76 [0.52,0.95]
Test 2	2.84 [0.77,6.18]	1.24 [0.71,2.00]	0.33 [0.08,0.62]	0.61 [0.32,0.88]	0.72 [0.44,0.94]

with a 90% confidence interval obtained via bootstrapping with 100,000 resamplings of sizes equal to the original dataset size. All of the confidence intervals in this paper are reported this way.

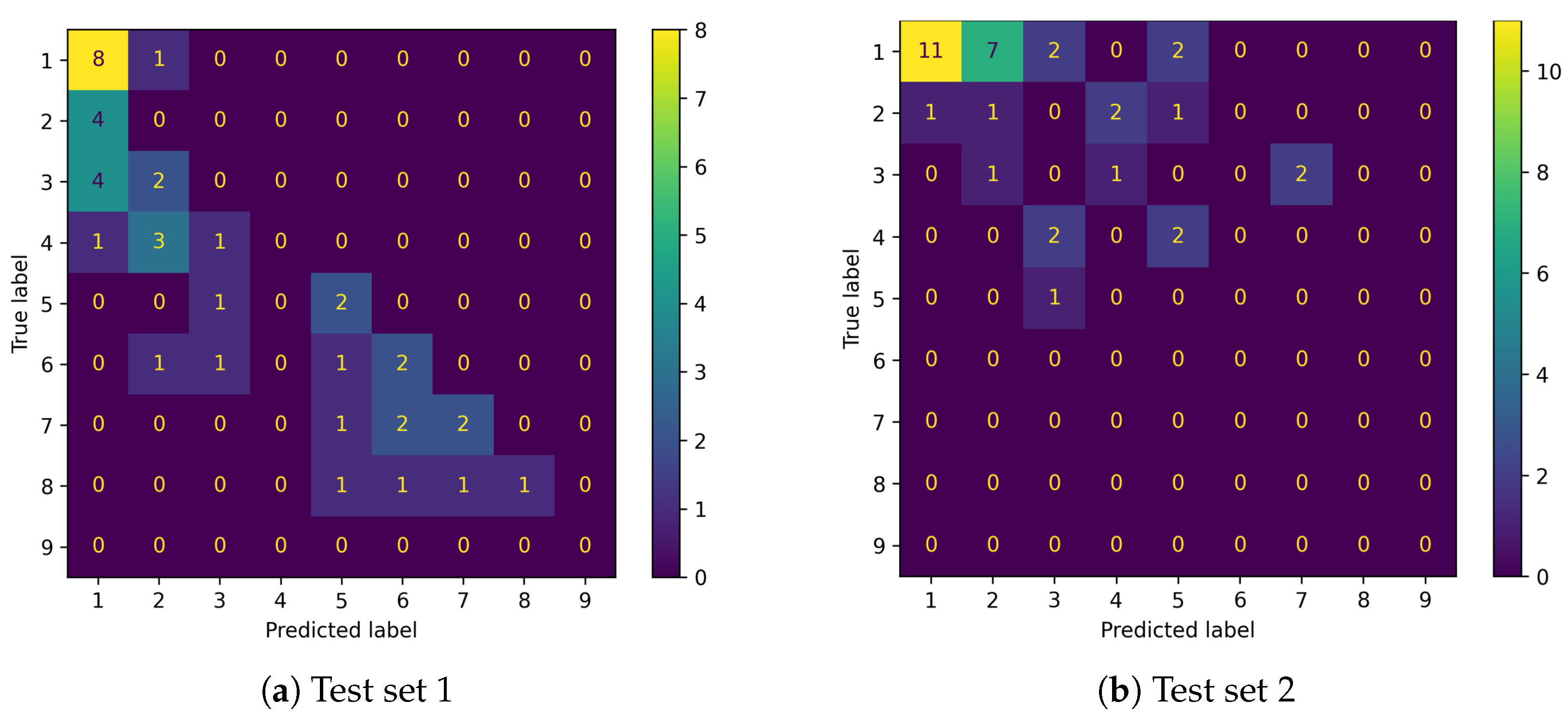
To provide a a finer understanding of these results, we also report confusion matrices by assigning each predicted score to the closest integer in order to obtain classes.

The first test set yielded satisfactory results. The points were mostly aligned along the main diagonal of the confusion matrix. The main issue is that the model tends to overall underestimate the yellow rust gravity, as evident from the lower triangular part of Figure 7a. This issue probably arises from the scarcity of heavily diseased plots in the training dataset, with only three plots having a disease score of 9 (see Figure 4). Conversely, the model struggles to generalise on the second test set. In particular, lower classes are often overrepresented, as visible in the upper triangular area in Figure 7b. This hinders the capability of the model to yield good results.

3.3. Architectural Ablation Study

In this section, we perform an ablation study to support the architectural choices made in our base model. We are interested in testing for the following components, which we ablate in

Table A3. Results obtained with variants of the base model. Each line shows an independent variant obtained by modifying the base model as described in Section 3.3. Since the test sets are small, the confidence interval with a 90% coverage probability is large. Therefore, no statistically solid insight can be extracted from these test sets. Further work ought to tackle this issue. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
Base model	Test 1	2.51 [1.04,4.64]	1.23 [0.75,1.80]	0.31 [0.07,0.57]	0.52 [0.24,0.79]	0.67 [0.42,0.88]
	Test 2	2.69 [0.75,5.73]	1.20 [0.67,1.87]	0.35 [0.08,0.62]	0.54 [0.24,0.81]	0.70 [0.41,0.95]
no heads	Test 1	2.40 [0.88,4.52]	1.19 [0.68,1.74]	0.31 [0.10,0.56]	0.54 [0.26,0.79]	0.73 [0.47,0.93]
	Test 2	1.97 [0.72,3.57]	1.10 [0.63,1.67]	0.39 [0.14,0.68]	0.61 [0.33,0.89]	0.66 [0.38,0.90]
RGB only	Test 1	2.50 [0.87,5.06]	1.23 [0.75,1.78]	0.24 [0.04,0.48]	0.49 [0.22,0.76]	0.73 [0.49,0.93]
	Test 2	1.34 [0.55,2.46]	0.96 [0.64,1.36]	0.25 [0.03,0.50]	0.61 [0.33,0.89]	0.80 [0.57,1.00]
no feature selection	Test 1	2.38 [0.96,4.63]	1.22 [0.78,1.75]	0.32 [0.10,0.58]	0.51 [0.24,0.76]	0.76 [0.51,0.95]
	Test 2	2.15 [0.84,4.51]	1.07 [0.64,1.72]	0.42 [0.14,0.69]	0.64 [0.36,0.89]	0.72 [0.44,0.94]
time average	Test 1	2.73 [0.93,5.34]	1.26 [0.75,1.87]	0.37 [0.13,0.63]	0.48 [0.23,0.76]	0.71 [0.44,0.93]
	Test 2	1.57 [0.71,2.80]	1.07 [0.72,1.47]	0.22 [0.03,0.49]	0.53 [0.25,0.81]	0.78 [0.53,0.97]
time concatenation	Test 1	2.58 [0.66,5.75]	1.16 [0.64,1.76]	0.34 [0.10,0.60]	0.56 [0.28,0.82]	0.82 [0.61,0.98]
	Test 2	1.69 [0.61,3.11]	1.02 [0.62,1.47]	0.27 [0.04,0.54]	0.61 [0.32,0.87]	0.77 [0.51,0.98]

and

Table 6. Results obtained with variants of the base model. Each line shows an independent variant obtained by modifying the base model as described in Section 3.3. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
base model	Validation	1.20 [0.74,1.83]	0.84 [0.69,1.00]	0.38 [0.27,0.50]	0.74 [0.63,0.84]	0.87 [0.79,0.94]
no heads	Validation	1.52 [0.88,2.41]	0.93 [0.76,1.19]	0.35 [0.25,0.46]	0.68 [0.57,0.78]	0.85 [0.76,0.93]
RGB only	Validation	1.38 [0.90,2.00]	0.90 [0.73,1.09]	0.36 [0.25,0.47]	0.71 [0.60,0.81]	0.86 [0.78,0.93]
no feature selector	Validation	1.48 [0.95,2.12]	0.93 [0.74,1.12]	0.37 [0.26,0.47]	0.68 [0.56,0.79]	0.82 [0.73,0.90]
time average	Validation	1.44 [0.90,2.07]	0.92 [0.76,1.10]	0.34 [0.25,0.46]	0.67 [0.56,0.78]	0.83 [0.74,0.91]
time concatenation	Validation	1.64 [0.97,2.47]	0.96 [0.77,1.17]	0.35 [0.24,0.46]	0.68 [0.56,0.78]	0.82 [0.71,0.90]

:

• Spectral Attention: In the line “no heads”, we removed the spectral selection and simply fed all bands and indices directly to the spatial processor. We also report the results of feeding only RGB directly to the spatial processor in the line “RGB only”.
• Chunk Attention: In the line “with chunking”, we performed chunking along the width in the spatial processor and the associated spatial attention with three chunks.
• Feature Selection: In the line “no feature selector”, we removed the feature selector layer and fed the concatenated features from the chunk attention directly to the LSTM.
• Time Attention: In the line “time average”, we replaced time attention with an average of all the outputs of the LSTM along the time dimension. In the line “time concatenation”, we replaced time attention with a concatenation of all the outputs of the LSTM along the time dimension.

Each of the above investigations was conducted independently by removing the corresponding component from the base model, all other things being equal. We report our results in Table 6.

As shown in Table 6, the architecture of the base model demonstrated superior—although not in a statistically significant way with regards to our validation set—performance compared to its variants across all examined metrics. Notable observations include:

• Overall Performance: The base model consistently, though not statistically significantly, outperformed all ablated variants in terms of all the considered metrics, as visible in Table 6. This result requires confirmation from future validation experiments, since the test results did not prove to be statistically descriptive, being too small (see Table A3).
• Impact of Spatial Attention: Extensive experimentation revealed that the inclusion of the spatial attention mechanism resulted in slightly worse performance compared to its absence. Despite this, the additional robustness and interpretability introduced by the spatial attention might justify minor performance drops.
• RGB Performance: It is striking that the RBG solution presented comparable results to the multispectral solution. The main advantage is that RGB solutions are economically more viable than MS approaches.

This ablation study highlights the contribution of each component to the regression problem, emphasising the importance of the overall model architecture in achieving optimal performance.

3.4. Producing Insights for Remote Phenotyping Practices

One of our main goals in this study was not only to develop a phenotype-agnostic model and to optimise it for yellow rust phenotyping, but also to pave the way for more usable and scalable research and solutions for remote phenotyping. For this reason, the TriNet architecture incorporated several components chosen for their explainability. Although it is generally true that restricting deep architectures in order to be explainable can hinder their capabilities, in many cases, this can serve as a powerful inductive bias and actually improve the results as explained in [63]. In plant breeding, works such as [64,65,66] have successfully used explainable components as inductive biases to facilitate training. In our case, we have shown in Section 3.3 that attention on spatial chunks reduces the model’s performance but that our other explainable components have a positive impact.

In this section, we train a new model with different parameters to optimise the insights we can gain from the model, as opposed to optimising for the model’s performance. In practice, because our base model already uses our other interpretability modules, this simply amounts to turning the spatial chunking back on and running the model with $k=3$ chunks in our spatial processor.

The obtained model’s results can be found in

Table 7. The mean square error (MSE), the mean absolute deviation (MAD), and some top-k accuracy results from all sets for our most explainable model, which we use to derive insights as explained in Section 3.4. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
Train	0.91 [0.72,1.15]	0.74 [0.67,0.83]	0.44 [0.38,0.51]	0.77 [0.71,0.82]	0.90 [0.86,0.94]
Validation	1.45 [0.93,2.10]	0.91 [0.74,1.10]	0.38 [0.26,0.49]	0.67 [0.57,0.78]	0.84 [0.74,0.92]
Test 1	2.51 [0.99,4.81]	1.23 [0.78,1.79]	0.31 [0.08,0.60]	0.52 [0.26,0.79]	0.67 [0.40,0.89]
Test 2	2.69 [0.69,5.59]	1.20 [0.68,1.91]	0.35 [0.11,0.64]	0.54 [0.27,0.81]	0.70 [0.43,0.93]

.

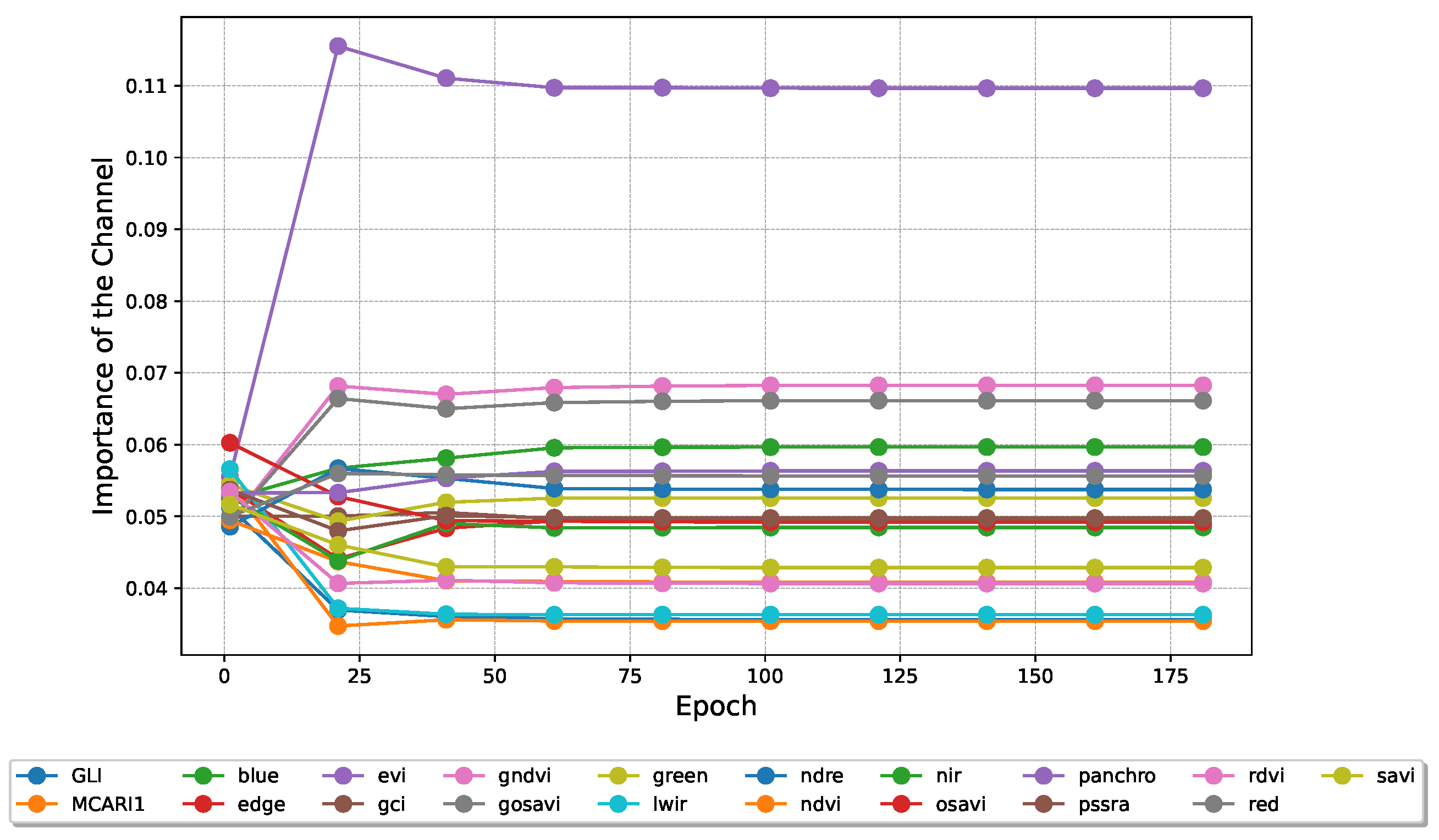
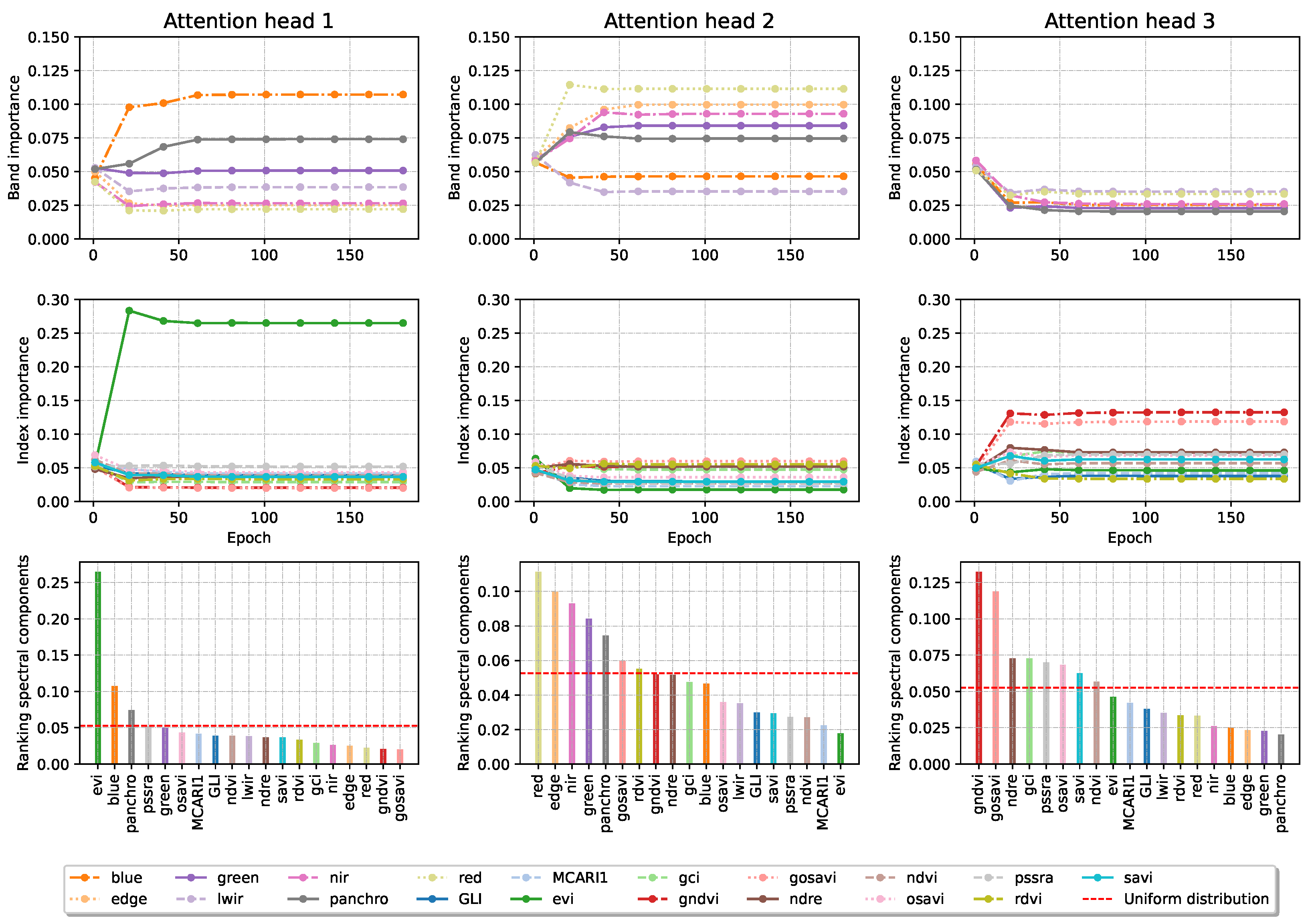
The information in the three heads can be recombined to obtain a ranking of the most important channels in the input images. This is commenced considering the average of the different channels across the three heads. Figure 8 presents the channels’ aggregate importance.

We show in Figure 9 and Figure 10 how the attention weights of the two layers of interest behave as the training progresses. The model selects the EVI, GNDVI and Red bands and indices, which we further validate in Section 3.5 and comment on in Section 4.2. In terms of time steps, it selects the sixth, seventh, and fifth time steps. For example, the fourth UAV acquisition could likely have been omitted in a lower-resource project. This does not mean that the acquisition was incorrectly performed, but rather, in our interpretation, that it contains redundant information already captured by other flights. We further validate these intuitions in Section 3.5 and comment on them in Section 4.3.

In the next section, we verify that these indices and time steps are indeed good predictors for yellow rust phenotyping, therefore proving the capacity of our interpretable components to yield actionable insights.

3.5. Insights Validation

In this section, we conduct experiments to validate the insights indicated in Section 3.4. There are two main insights we want to validate: the model’s selected bands and indices and the model’s selected time step.

To validate the selected bands, we propose to train a model without a spectral processor, taking the bands selected automatically by TriNet as input to the spatial processor. We then compare this model with models using random selections of bands instead, thereby showing that our explainable layer has converged to a sensible choice without explicit intervention. These results can be found in

Table 8. The results obtained with variants of the base model on the validation data. Line 1 is the base model presented in Table 5. Line 2 is the same architecture using only the best three selected bands and indices: EVI, Red, and GNDVI. Line 3 is the same architecture using only the Red, Green, and Blue bands. Lines 4, 5, and 6 show the 5th, 50th, and 95th percentiles of 30 independent models trained on random sets of three bands. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
base model	Validation	1.20 [0.74,1.83]	0.84 [0.69,1.00]	0.38 [0.27,0.50]	0.74 [0.63,0.84]	0.87 [0.79,0.94]
EVI, red, GNDVI	Validation	1.45 [0.91,2.05]	0.91 [0.74,1.11]	0.38 [0.27,0.50]	0.67 [0.55,0.78]	0.84 [0.75,0.92]
RGB only	Validation	1.50 [0.94,2.38]	0.92 [0.75,1.12]	0.37 [0.26,0.48]	0.68 [0.57,0.78]	0.84 [0.75,0.92]
5th percentile	Validation	3.49 [1.54,6.63]	1.50 [0.94,2.13]	0.18 [0.01,0.41]	0.37 [0.13,0.63]	0.58 [0.33,0.84]
50th percentile	Validation	2.93 [1.17,5.62]	1.33 [0.81,1.93]	0.29 [0.07,0.55]	0.45 [0.20,0.70]	0.67 [0.40,0.88]
95th percentile	Validation	2.54 [0.92,4.81]	1.23 [0.72,1.80]	0.36 [0.12,0.63]	0.52 [0.26,0.79]	0.71 [0.47,0.93]

.

Our results indicate that the selected bands achieve performances comparable to the full model within a 90% confidence interval. Notably, the model using our selected bands and time steps outperforms random selections in key metrics, including top-3 accuracy, where it surpasses 29 out of 30 random experiments. We provide further discussion on these findings in Section 4.2.

To validate the selected time steps, we propose to train a model, without temporal processor, taking as input the time step selected by TriNet. We then compare it with models using random time steps instead, thereby showing that our explainable layer has converged to a sensible choice without explicit intervention. These results can be found in

Table 9. The results obtained with variants of the base model on the validation data. Line 1 is the base model presented in Table 5. Line 2 is the same architecture using only the best three selected time steps: 5, 6, and 7. Lines 3, 4, and 5 show the 5th, 50th, and 95th percentiles of 30 independent models trained on random sets of three time steps. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
base model	Validation	1.20 [0.74,1.83]	0.84 [0.69,1.00]	0.38 [0.27,0.50]	0.74 [0.63,0.84]	0.87 [0.79,0.94]
Time steps 6 & 7	Validation	1.37 [0.89,2.00]	0.90 [0.73,1.09]	0.33 [0.22,0.44]	0.66 [0.55,0.78]	0.83 [0.74,0.91]
5th percentile	Validation	1.52 [1.24,1.84]	4.05 [2.59,5.89]	0.17 [0.09,0.27]	0.36 [0.24,0.47]	0.63 [0.51,0.74]
50th percentile	Validation	1.12 [0.92,1.36]	2.21 [1.41,3.23]	0.23 [0.13,0.33]	0.58 [0.46,0.69]	0.77 [0.67,0.86]
95th percentile	Validation	1.06 [0.83,1.26]	1.89 [1.14,2.74]	0.33 [0.23,0.45]	0.63 [0.52,0.74]	0.81 [0.72,0.89]

for the validation set and in

Table A4. The results obtained with variants of the base model. Line 1 is the base model presented in Table 5. Line 2 is the same architecture using only the two best selected time steps: 6 and 7. Lines 3, 4, and 5 show the 5th, 50th, and 95th percentiles of 39 independent models trained on random sets of three bands. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
Base model	Test 1	2.51 [1.04,4.64]	1.23 [0.75,1.80]	0.31 [0.07,0.57]	0.52 [0.24,0.79]	0.67 [0.42,0.88]
	Test 2	2.69 [0.75,5.73]	1.20 [0.67,1.87]	0.35 [0.08,0.62]	0.54 [0.24,0.81]	0.70 [0.41,0.95]
Timestep 6 and 7	Test 1	3.03 [1.33,5.47]	1.39 [0.86,1.92]	0.24 [0.05,0.50]	0.45 [0.21,0.73]	0.67 [0.42,0.90]
	Test 2	2.40 [0.86,4.43]	1.22 [0.73,1.81]	0.11 [0.00,0.30]	0.59 [0.32,0.86]	0.70 [0.43,0.92]
5th percentile	Test 1	7.59 [3.34,13.33]	2.21 [1.43,3.07]	0.10 [0.00,0.26]	0.22 [0.05,0.45]	0.45 [0.20,0.71]
	Test 2	2.44 [1.14,5.52]	1.25 [0.87,1.82]	0.08 [0.00,0.27]	0.22 [0.03,0.47]	0.68 [0.41,0.92]
50th percentile	Test 1	3.25 [1.18,6.58]	1.41 [0.89,2.06]	0.17 [0.01,0.38]	0.46 [0.21,0.73]	0.64 [0.37,0.87]
	Test 2	1.63 [0.61,2.96]	1.04 [0.67,1.50]	0.14 [0.00,0.35]	0.59 [0.32,0.86]	0.78 [0.54,0.97]
95th percentile	Test 1	2.30 [0.77,4.70]	1.15 [0.71,1.75]	0.33 [0.09,0.59]	0.52 [0.27,0.79]	0.71 [0.45,0.94]
	Test 2	1.23 [0.42,2.11]	0.88 [0.54,1.29]	0.35 [0.09,0.62]	0.75 [0.47,0.94]	0.86 [0.65,1.00]

for the two test sets.

Our results indicate that the selected time steps achieve a performance comparable to the full model within a 90% confidence interval, with a top-3 accuracy of 0.83. In Table 9, we also present a comparison with a random subset of UAV acquisition dates composing the training dataset. When it comes to our metric of choice, top-3 accuracy, the selected time steps perform better than 39 out of 39 random experiments. We comment on these results further in Section 4.3.

4. Discussion

In our study, we proposed to improve the scalability of automated phenotyping via multispectral imagery captured by a UAV. Given its importance in agriculture, we chose yellow rust as the phenotype to tackle (see Section 1). Still, the model can also be applied with different phenotypes as the target. We approach this problem from several angles:

• The recommended scoring methods have a high granularity from 1 to 9, contrary to most existing published methods. This higher granularity is an advantage for scaling algorithms to different purposes (which might need different target resolutions) or different countries (which might employ different scales); therefore, we stick to this more expressive scale for our ground truth targets;
• Current methods often achieve very high phenotyping performance by using very small GSDs. We propose to make them more scalable by analysing the performance of algorithms working from 60 m-high data and a GSD of 2.5 cm for the multispectral bands;
• Some methods, including ours, use time series or a large variety of spectral bands, which require more resources to deploy. We train our model to contain explainability components in order to optimise the number of bands and flights we need;
• We endeavour to make models more explainable in order to make them more robust and reliable, and we explore the trade-offs with model performance that this sometimes presents.

In the section that follows, we analyse these objectives and discuss our contributions with respect to the state of the art.

4.1. Using Low Spatial Resolution and High Target Resolution

The approach proposed in this paper aims to achieve greater scalability in remote phenotyping across multiple aspects. At the proposed flight height, a flight to capture all of our 1025 test fields takes around 7 min, which can be achieved without changing the battery, and the resulting data after the preparation process described take up under 6 GB of disk space. These numbers are unfortunately not reported in prior literature, preventing us from an in-depth analysis. Given the differences in GSD, we can nevertheless assume that our setup requires much less storage space and computing power for processing per square metre of field. Similarly, we assume that flights at lower altitudes would require higher flight times for equivalent area sizes with a more than proportional increase due to the need to ensure sufficient overlap for photogrammetric reconstruction and the need to change batteries more frequently (a very time-consuming operation).

We also claim that the existing literature is very hard to compare to due to the lack of granularity in the target definitions they use, which is at odds with existing standards in the field, such as those provided by the AGES, the Federal Plant Variety Office in Germany, or the Cobb scale. Collapsing detailed measurement scales to two or three classes makes the reported results ambiguous and difficult to generalise, reuse, reproduce, and validate. It is also at odds with the needs of plant breeders, who consequently cannot fully leverage the potential of these new technologies.

We finally report classification accuracies for phenotyping performed at an altitude of 60 m, corresponding to 2.5 cm/pixel. We also use the more robust scale provided by the AGES and accordingly, score yellow rust between 1 and 9. We show that this more scalable setup, although more challenging from an ML perspective, still achieves promising results. Specifically, we achieve 38% accuracy out of nine classes for the validation dataset and 33% and 35%, respectively, on test set 1 and test set 2 (see Table 5). When using more practically oriented metrics which better reflect the plant breeders’ needs and are easier to compare with the two- or three-class case, our results further jump to 0.74% for the validation score and 0.55% and 0.57%, respectively, for test set 1 and 2 for top-2 accuracy, and 0.87% for validation and 0.67% and 0.70%, respectively, for test set 1 and test set 2 for top-3 accuracy. The scores on the test set are generally lower, which we attribute to a general lack of data, which posed serious challenges to the generalisation capabilities of the model. Nevertheless, in the context of plant breed selection, a top-3 accuracy in the range of 0.7 proves to be sufficient, especially in early trials of breed selection, when time is the limiting factor of this application. New iterations of these experiments with additional data are an interesting avenue for future research.

Despite the potential loss of fine details with lower spatial resolution, we developed robust algorithms to extract meaningful features from coarser data. To ensure the impact of our architectural choices on our results, we conducted an architectural ablation study, evaluating various model variants. This study systematically analysed the impact of different components on performance, incorporating explainability components to optimise the number of spectral bands and flights while maintaining high target resolution. Our ablation study results, summarised in Table A3 and Table 6, indicate that all modified variants perform worse than our chosen model.

These findings confirm that our base model, even with lower spatial resolution and higher target resolution, maintains high accuracy and robustness, making it more suitable for large-scale deployment. This ensures that our phenotyping algorithms are adaptable by design to different agricultural practices and setups, providing a scalable, efficient solution for yellow rust phenotyping. However, in this study, we do compensate for our lack of spatial resolution with increased spectral and temporal resolution. In the next sections, we analyse our results in terms of spectral and temporal efficiency and suggest future directions to find optimal trade-offs between the three dimensions.

4.2. Optimising Bands for Cheaper Cameras and Drones

An argument can be made for reducing the cost of cameras and drones, thereby enhancing scalability, based on the decent results being achievable using only RGB imaging. Our study demonstrates that the “RGB only” variant performs competitively, achieving a top-3 accuracy ranging from 0.73 to 0.80 across different tests. This level of accuracy is comparable to two- and three-class studies in the literature, where similar methods have shown effective performance in distinguishing between classes.

TriNet uses 5 multispectral bands, the panchromatic and LWIR band, as well as 13 indices as input to compute yellow rust scores, which is significantly more than a simple RGB input. However, our model is designed to select the most useful bands and indices at an early stage and in an interpretable manner. In Table 8, we show that training a model with the selected bands and indices as input ($EVI$, $Red$, and $GNDVI$) reaches a top-3 accuracy of 0.84% on the validation and 0.66% and 0.71%, respectively, on test set 1 and 2 (see

Table A5. Results obtained with variants of the base model. Line 1 is the base model presented in Table 5. Line 2 is the same architecture using only the three best selected bands and indices: EVI, Red, and GNDVI. Line 3 is the same architecture using only the Red, Green, and Blue bands. Lines 4, 5, and 6 show the 5th, 50th, and 95th percentiles of 30 independent models trained on random sets of three bands. The MSE and MAD range from ∞ to 0, while the other three metrics from 0 to 1. The confidence intervals with a 90% coverage probability are presented in italics.

Variant	Data Split	MSE ${\downarrow }_0^{+\mathit{\infty }}$	MAD ${\downarrow }_0^{+\mathit{\infty }}$	Top-1 Accuracy ${\uparrow }_0^1$	Top-2 Accuracy ${\uparrow }_0^1$	Top-3 Accuracy ${\uparrow }_0^1$
Base model	Test 1	2.51 [1.04,4.64]	1.23 [0.75,1.80]	0.31 [0.07,0.57]	0.52 [0.24,0.79]	0.67 [0.42,0.88]
	Test 2	2.69 [0.75,5.73]	1.20 [0.67,1.87]	0.35 [0.08,0.62]	0.54 [0.24,0.81]	0.70 [0.41,0.95]
EVI, Red, GNDVI	Test 1	2.51 [0.95,4.87]	1.23 [0.74,1.81]	0.31 [0.10,0.56]	0.52 [0.26,0.81)	0.67 [0.42,0.88]
	Test 2	1.20 [0.66,1.90]	2.69 [0.69,5.62]	0.35 [0.09,0.64]	0.54 [0.26,0.81]	0.70 [0.43,0.95]
RGB only	Test 1	2.93 [1.17,5.62]	1.33 [0.81,1.93]	0.24 [0.04,0.48]	0.49 [0.22,0.76]	0.73 [0.49,0.93]
	Test 2	1.72 [0.56,3.74]	1.05 [0.61,1.52]	0.25 [0.03,0.50]	0.61 [0.33,0.89]	0.80 [0.57,1.00]
5th percentile	Test 1	2.30 [0.77,4.70]	1.15 [0.71,1.75]	0.10 [0.00,0.26]	0.22 [0.05,0.45]	0.45 [0.20,0.71]
	Test 2	1.23 [0.42,2.11]	0.88 [0.54,1.29]	0.08 [0.00,0.27]	0.22 [0.03,0.47]	0.68 [0.41,0.92]
50th percentile	Test 1	3.25 [1.18,6.58]	1.41 [0.89,2.06]	0.17 [0.01,0.38]	0.46 [0.21,0.73]	0.64 [0.37,0.87]
	Test 2	1.63 [0.61,2.96]	1.04 [0.67,1.50]	0.14 [0.00,0.35]	0.59 [0.32,0.86]	0.78 [0.54,0.97]
95th percentile	Test 1	7.59 [3.34,13.33]	2.21 [1.43,3.07]	0.33 [0.09,0.59]	0.52 [0.27,0.79]	0.71 [0.45,0.94]
	Test 2	2.44 [1.14,5.52]	1.25 [0.87,1.82]	0.35 [0.09,0.62]	0.75 [0.47,0.94]	0.86 [0.65,1.00]

) across our tests. This is not only better than the 95th percentile of experiments using random bands and indices, but is also on par with our base model, which has access to all bands. These indices would require RGB input as well as the $NIR$ band to be computed. Therefore, these results do not only pinpoint a minimal set of bands ($Red$, $Green$, $Blue$, and $NIR$) necessary to achieve the best results, but they also quantify the added benefit of the $NIR$ band compared to traditional RGB cameras. Moreover, the model generalises well on the validation data using only RGB data as the training input (see Table 8). This poses significant economic upsides for planning a monitoring campaign, since UAV equipped with RGB sensors only are significantly cheaper than a multispectral or hyperspectral sensor. Nevertheless, further research in this direction is necessary to assess whether this holds true only for yellow rust monitoring or if it also generalises to other phenotypes. Yellow rust can be observed in the visible band, while the NIR band provides important insights for other phenotypes, for instance, the drought stress level or chlorophyll content [67].

These results highlight the potential for cost-effective phenotyping solutions. By using accessible and affordable RGB bands, researchers can improve scalability without significantly compromising performance. For higher accuracy, adding the NIR band provides quantifiable benefits. This approach supports the broader adoption of phenotyping methods in agriculture and adapts to various operational contexts and resource constraints. Specifically, yellow rust signs are observable in the visible spectrum, but for phenotypes like water stress, the RGB spectrum alone may not suffice.

4.3. Optimising Time Steps for Easier Phenotyping Campaigns

Similarly to spectral resolution, time resolution is also an important source of cost when scaling phenotyping operations. Performing UAV flights on a regular basis can be a complex task, and the more time steps are required, the more brittle the overall process becomes. Indeed, UAVs require good weather and low wind speed, and they sometimes break and need repairs. As such, the number of time steps to acquire becomes a determining constraint for the actual deployment of remote phenotyping technologies. We therefore make it a priority to study the importance of different time steps for TriNet.

TriNet uses seven time steps that are spaced out throughout the winter wheat’s life cycle. In the same way that it is designed to select input bands and indices, it is also designed to select the importance of input time steps in an interpretable way. In Table 9, we show that the best two time steps (6 and 7) chosen by the time attention perform better than the 95th percentile of models trained with a random subsample of points, according to the top-3 accuracy. This accomplishment not only proves that the attention mechanism is effective in selecting the most meaningful dates inside the model, but also that it can be used to obtain domain information in order to schedule more effective and optimised UAV acquisition schedules. It is important to acknowledge that the last two time steps are also when yellow rust is most visible on the plants. Nevertheless, studying the importance coefficients provided by the time attention can generate insights into the exact date and developmental stage when one should begin acquiring drone data for future UAV acquisition campaigns without hindering performance.

Therefore, we show that it is possible to optimise the time steps used by TriNet to significantly reduce the resource requirements associated with organising flight campaigns.

However, the study presented here is only preliminary. Indeed, in practical scenarios, it is difficult to plan when flights will be possible and when symptoms of yellow rust will appear. More broadly, different time steps might be optimal to study different phenotypes, and those optimal time steps would also depend on the growth stage of the wheat. For a truly scalable multi-temporal phenotyping to be deployed with the current weather-dependent technologies, more work should be undertaken to train models that are able to leverage arbitrary input time steps to assess a given phenotype at arbitrary output time steps. Moreover, these models should be capable of estimating their own uncertainty when predicting a phenotype at a time step that is temporally remote from any available observation.

5. Conclusions

In this study, we address the challenge of scaling automated phenotyping using UAVs, focusing on yellow rust as the target phenotype. Our approach involves several innovative strategies to enhance scalability and performance, making our methodology applicable to various phenotypes and agricultural contexts.

First, we adopt a high granularity in situ scoring method (1 to 9 scale) to accommodate different target resolutions and standards across countries, ensuring broader applicability and better alignment with plant breeders’ needs.

Second, we demonstrate that using lower spatial resolution (60 m flight height and 2.5 cm GSD) significantly reduces the resources required for data acquisition, processing, and storage, without severely compromising the prediction accuracy when compared to the most recent approaches reported in Table 1. This setup facilitates faster data acquisitions and lower operational costs, making large-scale phenotyping more feasible. Our framework shows that such higher-altitude flights constitute a relevant design space for phenotyping practices and enable the testing of various trade-offs between spatial, spectral, and temporal resolution. We therefore pave the way for future efforts to determine the Pareto frontier between those parameters and make phenotyping more scalable.

Third, we incorporate explainability components into our models, optimising the number of spectral bands and flights required. This not only improves model robustness and reliability, but it also helps identify the most relevant features, thus simplifying the deployment process.

Our results show that our model achieves promising performance even with lower spatial resolution and a high target resolution of nine steps. Specifically, we attained top-3 accuracies of 0.87% for validation and 0.67% and 0.70% for test sets 1 and 2, respectively. These results underscore the effectiveness of our approach in balancing resource efficiency and phenotyping accuracy.

Future research should focus on further optimising the trade-offs between spatial, spectral, and temporal resolutions to enhance the applicability and efficiency of phenotyping technologies in diverse agricultural settings across various species and phenotypes. We also deem important the creation of a time-agnostic model which would be independent of a given set of acquisition dates. Another crucial direction for future research is a comprehensive study on the portability of TriNet to different phenotypes, such as the plant’s water status or yield content. Our encouraging results with yellow rust disease scoring show that the physiological status of the plant correlates with the latent space feature representation. Therefore, avenues are open to leverage transfer learning to phenotype other wheat diseases such as stripe rust and brown rust, or even different traits.