Quality and Efficiency of Coupled Iterative Coverage Path Planning for the Inspection of Large Complex 3D Structures
Abstract
1. Introduction
- A quality-guided and non-random dual sampling inspection strategy is employed to obtain the initial viewpoint set, enhancing conditions for subsequent iterative path optimization. Additionally, to accommodate narrow spaces using dual sampling methods, specific adjustments are made to the sizes of surface triangles on the structure surfaces near these spaces, along with the constraints on the feasible viewpoint space associated with each surface triangle.
- A dual-coupling strategy is proposed for CPP. Initially, viewpoint generation is integrated with path planning, continuously optimizing the viewpoint set and coverage path to lower path costs through iterations. Additionally, the objective function for iterative optimization is designed to integrate metrics including image resolution, orthogonality degree, and path length, thereby coupling coverage quality with efficiency. Particularly, the introduced weight coefficient in the objective function can be flexibly adjusted to meet the specific requirements of various inspection tasks concerning coverage quality and efficiency characteristics.
2. Problem Description
2.1. Model Description
- Three-dimensional structure model: The 3D structure model to be inspected is represented using surface triangles. Initially, this model can be rough since it will undergo cleaning, refinement, and adjustment of surface triangle size during the preprocessing step of the proposed method.
- UAV model: As an example, we consider a common rotary-wing UAV equipped with a gimbal camera. The gimbal camera is not fixed to the UAV body but can move independently, expanding the accessible space of the viewpoint.
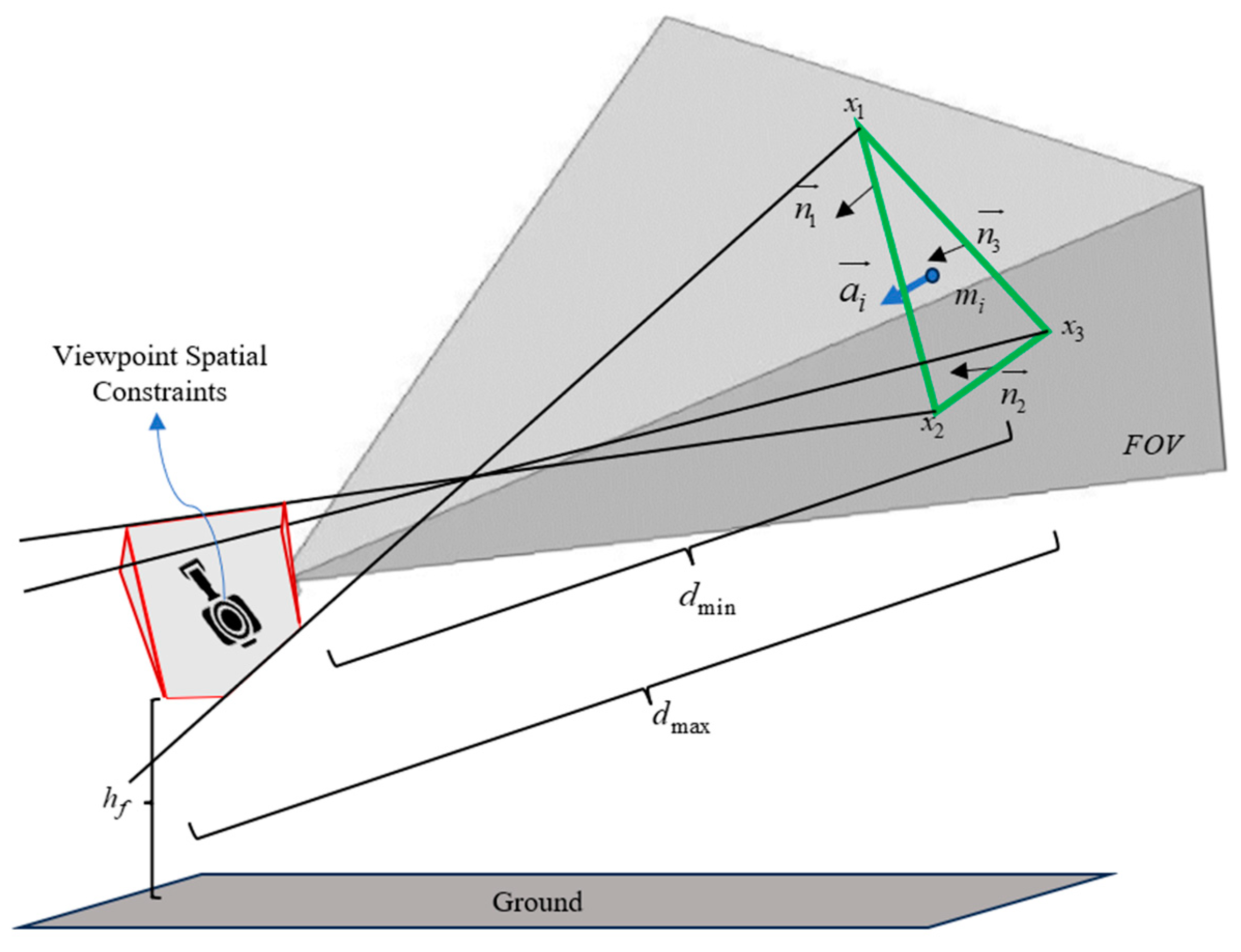
- Pan–tilt (PT) camera model: The PT camera model is defined by its frustum and orientation [29]. The shape of the frustum is determined by the corresponding field of view (FOV) as well as the minimum and maximum detecting ranges. The orientation and shutter of the PT camera are controlled by a gimbal stabilizer. Since most PT cameras do not have restrictions on yaw angles [30], we assume a yaw angle range of . As a result, the camera orientation is only restricted by the pitch angle. The PT camera is precalibrated with its radial distortion removed, and its parameters such as FOV and focal distance range are known in advance.
2.2. Definition of Inspection Quality and Inspection Efficiency
- Orthogonality degree and resolution are used to evaluate the quality of captured images. The orthogonality degree measures the deviation of the camera’s shooting direction from the normal vector direction of the surface triangle. Our goal is to align the camera’s shooting direction as closely as possible with the normal vector of the surface triangle to minimize side-angle shots and reduce image distortion. Resolution refers to the clarity of the camera’s captured surface features. For a given surface triangle and specific camera parameters, optimal view-to-surface resolution is achieved by determining the viewpoint where the projected image best fits the surface triangle. Detailed mathematical descriptions of these performance metrics will be provided later.
- Inspection Efficiency: The path distance is closely related to the efficiency of completing the task. Therefore, in this paper, the distance of the coverage path is used to represent inspection efficiency.
2.3. Problem Formulation of CPP
3. Proposed Methodology
3.1. Model Preprocessing
3.2. High-Quality Initial Path
3.2.1. Spatial Constraints Applied to Viewpoints
3.2.2. Inspection Quality-Guided Viewpoint Initialization
3.2.3. Occlusion Detection and Path Planning
3.3. Path Iterative Optimization
3.3.1. Quality-Efficiency Coupled Design
3.3.2. Viewpoint and Path Iterative Optimization
| Algorithm 1 Viewpoint and Path Iterative Optimization |
| ; ; 3. Inspection quality-guided viewpoint initialization 4. Occlusion detection and viewpoint adjustment + 1 6. end for 7. Calculate the cost matrix and solve the TSP to obtain the initial path ← 0 11. Resample viewpoints by optimizing Equation (19) under constraints in Equations (4)–(11) 12. Occlusion detection and viewpoint adjustment + 1 15. end for 16. Update the cost matrix and solve the TSP to revise the path + 1 18. end while |
4. Simulation and Evaluation
4.1. Simulation Setup
4.2. Comparative Methods and Evaluation Metric
4.2.1. Comparative Methods
4.2.2. Evaluation Metric
4.3. Results and Analysis
4.3.1. Comparative Simulation Results
4.3.2. Impact Analysis of Weight Coefficient on the Final Path
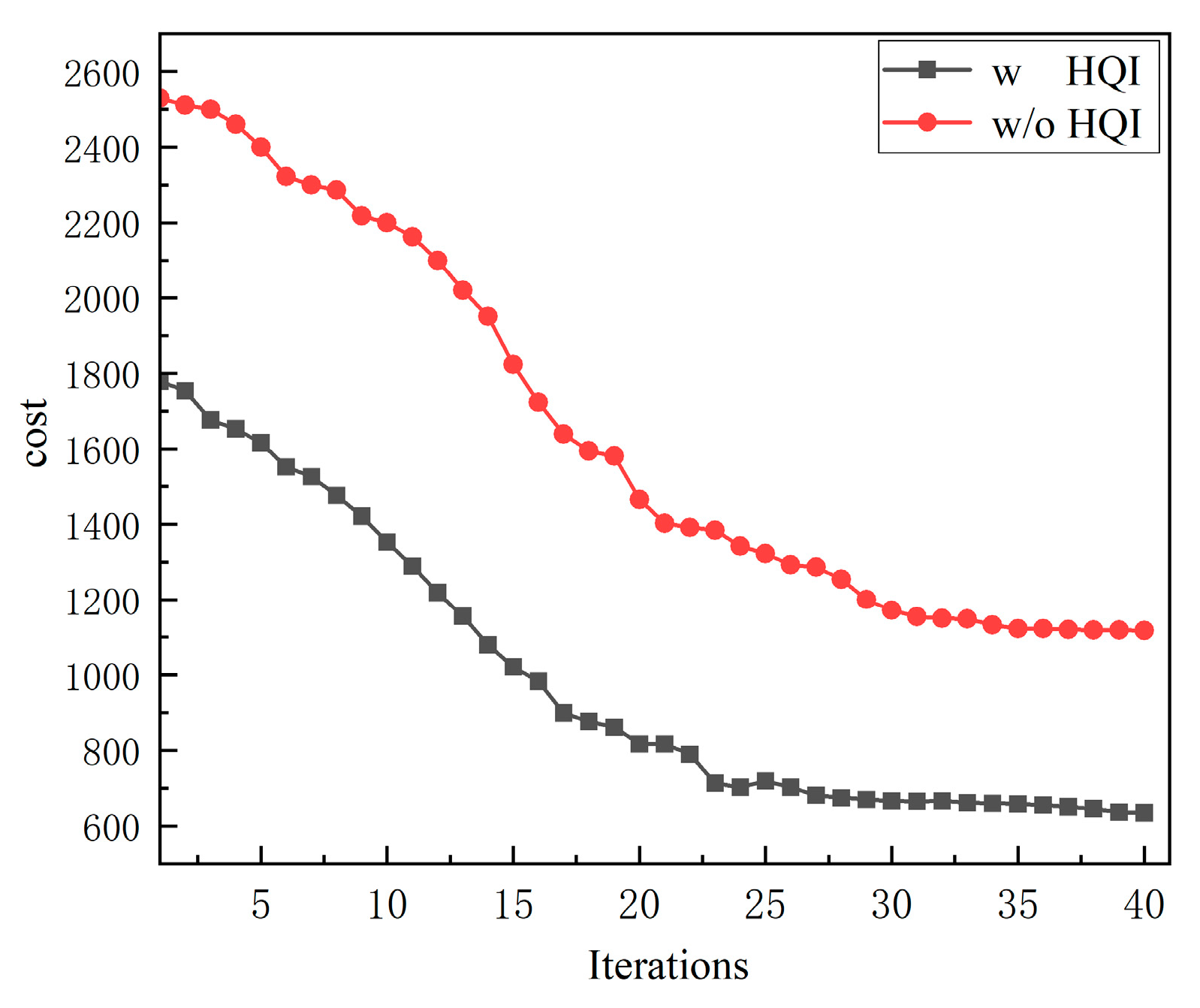
4.3.3. Impact Analysis of HQI on Total Path Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| the focal length of the camera | |
| the distance between the camera and the target surface triangle | |
| , | the length and width of the camera’s image sensor size |
| , | the length and width in the actual FOV |
| , | the maximum and minimum shooting distances between the camera and the target surface triangle |
| the height threshold for distinguishing between normal and narrow spaces | |
| , | the maximum and minimum shooting distances for the space beneath the aircraft |
| the total number of surface triangles | |
| the centroid of the i-th surface triangle | |
| , | the horizontal and vertical distances from each of the three vertices of the surface triangle to |
| the position of the viewpoint of the i-th surface triangle | |
| the coordinate vector of the three vertices of the surface triangle | |
| the normal vector of the j-th separating hyperplane | |
| the minimum incidence angle | |
| the normalized normal vector of the i-th surface triangle | |
| the minimum flight altitude of the UAV | |
| , , , | the positions of the leftmost, rightmost, top, and bottom vertices of the surface triangle |
| the minimum angle in the horizontal and vertical directions at which can cover the outermost vertices of the surface triangle | |
| , | the horizontal and vertical FOV of the camera |
| the pitch angle of the camera | |
| , | the minimum and maximum allowable values of |
| the vector transformation from to | |
| , | the optimal initial distances in narrow and normal spaces |
| , | the initialized viewpoint positions in narrow and normal spaces |
| the cost of the i-th viewpoint in the k-th iteration | |
| , | the costs of inspection quality and inspection efficiency in the k-th iteration |
| the weight coefficient | |
| the i-th viewpoint in the k-th iteration | |
| , , | the previous viewpoint and the subsequent viewpoint, and the current viewpoint of in the -th iteration |
| the iteration number |
References
- Tappe, M.; Dose, D.; Alpen, M.; Horn, J. Autonomous surface inspection of airplanes with unmanned aerial systems. In Proceedings of the 2021 7th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 4–6 February 2021; pp. 135–139. [Google Scholar]
- Maboudi, M.; Homaei, M.; Song, S.; Malihi, S.; Saadatseresht, M.; Gerke, M. A Review on Viewpoints and Path Planning for UAV-Based 3-D Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5026–5048. [Google Scholar] [CrossRef]
- Ivić, S.; Crnković, B.; Grbčić, L.; Matleković, L. Multi-UAV trajectory planning for 3D visual inspection of complex structures. Autom. Constr. 2023, 147, 104709. [Google Scholar] [CrossRef]
- Jiao, L.; Peng, Z.; Xi, L.; Ding, S.; Cui, J. Multi-Agent Coverage Path Planning via Proximity Interaction and Cooperation. IEEE Sens. J. 2022, 22, 6196–6207. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, R.; Sun, G.; Di, B.; Xiong, R. A Novel Cooperative Path Planning for Multirobot Persistent Coverage in Complex Environments. IEEE Sens. J. 2020, 20, 4485–4495. [Google Scholar] [CrossRef]
- Yuan, D.; Chang, X.; Li, Z.; He, Z. Learning Adaptive Spatial-Temporal Context-Aware Correlation Filters for UAV Tracking. ACM Trans. Multimed. Comput. Commun. Appl. 2022, 18, 1–18. [Google Scholar] [CrossRef]
- Höffmann, M.; Patel, S.; Büskens, C. Optimal Coverage Path Planning for Agricultural Vehicles with Curvature Constraints. Agriculture 2023, 13, 2112. [Google Scholar] [CrossRef]
- Pour Arab, D.; Spisser, M.; Essert, C. Complete coverage path planning for wheeled agricultural robots. J. Field Robot. 2023, 40, 1460–1503. [Google Scholar] [CrossRef]
- Silberberg, P.; Leishman, R.C. Aircraft inspection by multirotor UAV using coverage path planning. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; pp. 575–581. [Google Scholar]
- Liu, Y.; Dong, J.; Li, Y.; Gong, X.; Wang, J. A UAV-Based Aircraft Surface Defect Inspection System via External Constraints and Deep Learning. IEEE Trans. Instrum. Meas. 2022, 71, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, S.; Zhang, X.; Zhang, X.; Liu, J. Near-Optimal 3-D Visual Coverage for Quadrotor Unmanned Aerial Vehicles Under Photogrammetric Constraints. IEEE Trans. Ind. Electron. 2021, 69, 1694–1704. [Google Scholar] [CrossRef]
- Saha, A.; Kumar, L.; Sortee, S.; Dhara, B.C. An autonomous aircraft inspection system using collaborative unmanned aerial vehicles. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; pp. 1–10. [Google Scholar]
- Jing, W.; Polden, J.; Lin, W.; Shimada, K. Sampling-based view planning for 3D visual coverage task with unmanned aerial vehicle. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1808–1815. [Google Scholar]
- Englot, B.; Hover, F. Sampling-based coverage path planning for inspection of complex structures. In Proceedings of the International Conference on Automated Planning and Scheduling (ICAPS), Atibaia, Brazil, 25–29 June 2012; Volume 22, pp. 29–37. [Google Scholar]
- Englot, B.; Hover, F. Planning complex inspection tasks using redundant roadmaps. In Robotics Research: The 15th International Symposium ISRR; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 327–343. [Google Scholar]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. 1998. Available online: http://lavalle.pl/papers/Lav98c.pdf (accessed on 9 October 2020).
- Bircher, A.; Kamel, M.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Siegwart, R. Three-dimensional coverage path planning via viewpoint resampling and tour optimization for aerial robots. Auton. Robot. 2016, 40, 1059–1078. [Google Scholar] [CrossRef]
- Bircher, A.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Structural inspection path planning via iterative viewpoint resampling with application to aerial robotics. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6423–6430. [Google Scholar]
- Alexis, K.; Papachristos, C.; Siegwart, R.; Tzes, A. Uniform coverage structural inspection path-planning for micro aerial vehicles. In Proceedings of the 2015 IEEE International Symposium on Intelligent Control (ISIC), Sydney, Australia, 21–23 September 2015; pp. 59–64. [Google Scholar]
- Shang, Z.; Bradley, J.; Shen, Z. A co-optimal coverage path planning method for aerial scanning of complex structures. Expert Syst. Appl. 2020, 158, 113535. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Seneviratne, L.; Dias, J.; Cai, G. GPU accelerated coverage path planning optimized for accuracy in robotic inspection applications. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar]
- Cao, C.; Zhang, J.; Travers, M.; Choset, H. Hierarchical coverage path planning in complex 3D environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3206–3212. [Google Scholar]
- Almadhoun, R.; Taha, T.; Gan, D.; Dias, J.; Zweiri, Y.; Seneviratne, L. Coverage path planning with adaptive viewpoint sampling to construct 3D models of complex structures for the purpose of inspection. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7047–7054. [Google Scholar]
- Sun, Y.; Ma, O. Automating Aircraft Scanning for Inspection or 3D Model Creation with a UAV and Optimal Path Planning. Drones 2022, 6, 87. [Google Scholar] [CrossRef]
- Glorieux, E.; Franciosa, P.; Ceglarek, D. Coverage path planning with targetted viewpoint sampling for robotic free-form surface inspection. Robot. Comput. Manuf. 2020, 61, 101843. [Google Scholar] [CrossRef]
- Almadhoun, R.; Taha, T.; Dias, J.; Seneviratne, L.; Zweiri, Y. Coverage path planning for complex structures inspection using unmanned aerial vehicle (UAV). In Proceedings of the Intelligent Robotics and Applications: 12th International Conference, ICIRA 2019, Shenyang, China, 8–11 August 2019; Proceedings, Part V 12*; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 243–266. [Google Scholar]
- Ibrahim, A.; Golparvar-Fard, M.; El-Rayes, K. Multiobjective Optimization of Reality Capture Plans for Computer Vision–Driven Construction Monitoring with Camera-Equipped UAVs. J. Comput. Civ. Eng. 2022, 36, 04022018. [Google Scholar] [CrossRef]
- Luo, R.; Xu, J.; Zuo, H. Automated surface defects acquisition system of civil aircraft based on unmanned aerial vehicles. In Proceedings of the 2020 IEEE 2nd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Weihai, China, 14–16 October 2020; pp. 729–733. [Google Scholar]
- Cao, Y.; Cheng, X.; Mu, J. Concentrated Coverage Path Planning Algorithm of UAV Formation for Aerial Photography. IEEE Sens. J. 2022, 22, 11098–11111. [Google Scholar] [CrossRef]
- Cheng, P.; Keller, J.; Kumar, V. Time-optimal UAV trajectory planning for 3D urban structure coverage. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008; pp. 2750–2757. [Google Scholar]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Helsgaun, K. An effective implementation of the Lin–Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 2000, 126, 106–130. [Google Scholar] [CrossRef]
- Helsgaun, K. LKH-The LKH Solver. Available online: http://akira.ruc.dk/~keld/research/LKH/ (accessed on 1 November 2022).
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Chen, J.; Yu, J. An improved path planning algorithm for UAV based on RRT*. In Proceedings of the 2021 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Changsha, China, 26–28 March 2021; pp. 895–898. [Google Scholar]
- Open-Source Implementation of the SIP Algorithm as a ROS Package. Available online: https://github.com/ethzasl/StructuralInspectionPlanner (accessed on 26 June 2015).
- Open-Source Implementation of the PX4 Flight Control Software as a ROS Package. Available online: https://github.com/PX4/PX4-Autopilot (accessed on 1 June 2022).





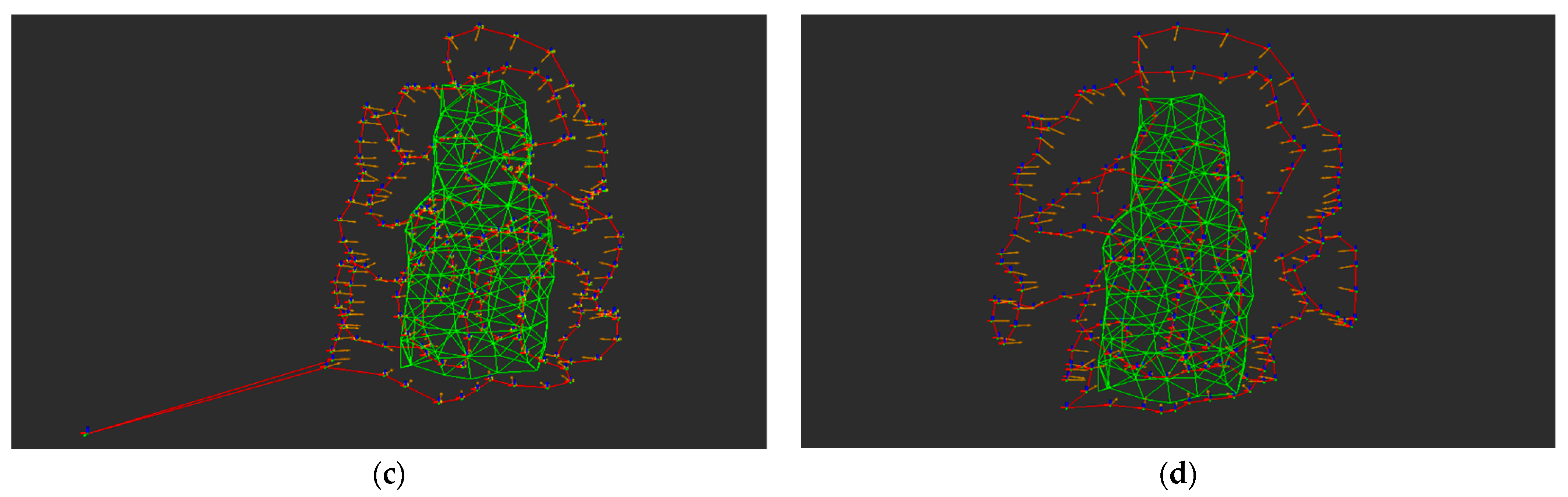

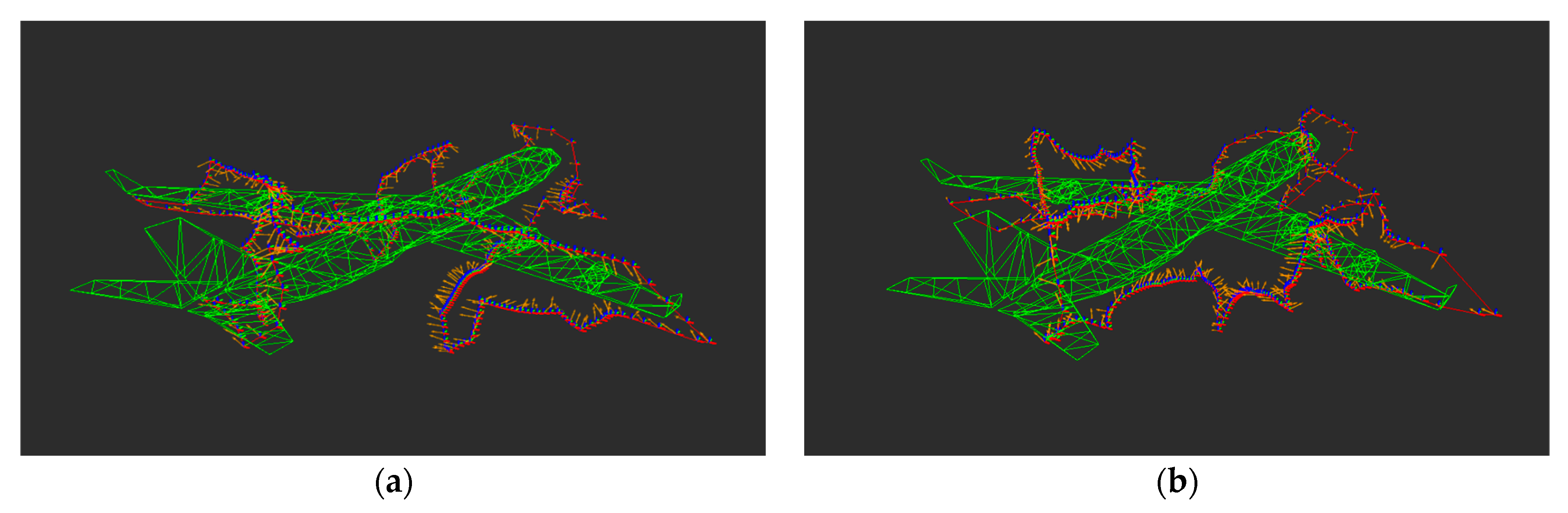



| Model |  |  |  |
| Name | Civil Aircraft | Hoa Hakanaia | Wind Turbine |
| Number of surface triangles | 435 | 225 | 720 |
| Dimensions (m) | 63.6 × 60.3 × 16.7 | 8.4 × 5.2 × 19.5 | 60.7 × 10.3 × 108.5 |
| QECI-CPP | [−90°, 80°] | [120°, 80°] | 60° | 5.2 | 0.6 | 0.5 | 3 | 2.5 | 8 | 1 | 30 | \ | \ |
| SIP | −25° | [120°, 80°] | 60° | \ | 2.5 | 8 | \ | 30 | \ | \ | |||
| CCPP | [−90°, 80°] | [120°, 80°] | 60° | \ | 2.5 | 8 | \ | 30 | 0.5 | 30 | |||
| IRRT*-LKH | [−90°, 80°] | [120°, 80°] | 60° | \ | 2.5 | 8 | \ | \ | \ | \ | |||
| QECI-CPP | [−90°, 80°] | [120°, 80°] | 60° | 0.6 | 1.5 | 7 | 1 | 30 | \ | \ |
| SIP | −25° | [120°, 80°] | 60° | \ | 1.5 | 7 | \ | 30 | \ | \ |
| CCPP | [−90°, 80°] | [120°, 80°] | 60° | \ | 1.5 | 7 | \ | 30 | 0.5 | 30 |
| IRRT*-LKH | [−90°, 80°] | [120°, 80°] | 60° | \ | 1.5 | 7 | \ | \ | \ | \ |
| QECI-CPP | [−90°, 80°] | [120°, 80°] | 60° | 0.6 | 1.5 | 13 | 1 | 30 | \ | \ |
| SIP | −25° | [120°, 80°] | 60° | \ | 1.5 | 13 | \ | 30 | \ | \ |
| CCPP | [−90°, 80°] | [120°, 80°] | 60° | \ | 1.5 | 13 | \ | 30 | 0.5 | 30 |
| IRRT*-LKH | [−90°, 80°] | [120°, 80°] | 60° | \ | 1.5 | 13 | \ | \ | \ | \ |
| Path Metrics | Civil Aircraft | Hoa Hakanaia | Wind Turbine | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QECI-CPP | SIP | CCPP | IRRT*-LKH | QECI-CPP | SIP | CCPP | IRRT*-LKH | QECI-CPP | SIP | CCPP | IRRT*-LKH | |
| Resolution | 0.94 | 0.35 | 0.92 | 0.32 | 0.96 | 0.30 | 0.93 | 0.28 | 0.91 | 0.29 | 0.90 | 0.37 |
| Orthogonality degree | 0.87 | 0.32 | 0.85 | 0.39 | 0.87 | 0.29 | 0.87 | 0.31 | 0.85 | 0.31 | 0.87 | 0.42 |
| Path distance | 593.3 | 529.8 | 721.5 | 571.6 | 223.6 | 224.7 | 358.3 | 343.8 | 568.3 | 472.4 | 671.2 | 698.5 |
| Methods | View Sampling (s) | At Each Iteration (s) | Total (s) | ||
|---|---|---|---|---|---|
| LKH Time | Cost Evaluation | Greedy Heuristic + Particles Update | |||
| QECI-CPP | 1.6 | 0.28 | 0.056 | \ | 11.3 |
| SIP | 1.9 | 0.43 | 0.066 | \ | 16.4 |
| CCPP | 15.7 | 6.39 | 0.667 | 5.58 | 427.9 |
| IRRT*-LKH | 4.2 | \ | 8.6 | ||
| Methods | View Sampling (s) | At Each Iteration (s) | Total (s) | ||
|---|---|---|---|---|---|
| LKH Time | Cost Evaluation | Greedy Heuristic + Particles Update | |||
| QECI-CPP | 0.9 | 0.15 | 0.03 | \ | 7.6 |
| SIP | 1.4 | 0.26 | 0.05 | \ | 9.3 |
| CCPP | 9.7 | 3.91 | 0.41 | 2.16 | 218.2 |
| IRRT*-LKH | 2.9 | \ | 6.1 | ||
| Methods | View Sampling (s) | At Each Iteration (s) | Total (s) | ||
|---|---|---|---|---|---|
| LKH Time | Cost Evaluation | Greedy Heuristic + Particles Update | |||
| QECI-CPP | 3.4 | 0.37 | 0.06 | \ | 34.9 |
| SIP | 4.9 | 0.63 | 0.08 | \ | 38.1 |
| CCPP | 16.8 | 8.81 | 0.83 | 12.74 | 647.5 |
| IRRT*-LKH | 4.6 | \ | 12.9 | ||
| Orthogonality Degree | Resolution | Path Distance (m) | Computation Time (s) | |
|---|---|---|---|---|
| 0 | 0.43 | 0.38 | 512.9 | 11.4 |
| 0.3 | 0.62 | 0.68 | 549.2 | 11.3 |
| 0.6 | 0.87 | 0.79 | 587.2 | 11.4 |
| 1.0 | 0.94 | 0.87 | 593.3 | 11.3 |
| 1.5 | 0.95 | 0.88 | 634.6 | 11.5 |
| 2.0 | 0.96 | 0.88 | 640.1 | 11.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Piao, M.; Li, H.; Li, Y.; Lu, B. Quality and Efficiency of Coupled Iterative Coverage Path Planning for the Inspection of Large Complex 3D Structures. Drones 2024, 8, 394. https://doi.org/10.3390/drones8080394
Liu X, Piao M, Li H, Li Y, Lu B. Quality and Efficiency of Coupled Iterative Coverage Path Planning for the Inspection of Large Complex 3D Structures. Drones. 2024; 8(8):394. https://doi.org/10.3390/drones8080394
Chicago/Turabian StyleLiu, Xiaodi, Minnan Piao, Haifeng Li, Yaohua Li, and Biao Lu. 2024. "Quality and Efficiency of Coupled Iterative Coverage Path Planning for the Inspection of Large Complex 3D Structures" Drones 8, no. 8: 394. https://doi.org/10.3390/drones8080394
APA StyleLiu, X., Piao, M., Li, H., Li, Y., & Lu, B. (2024). Quality and Efficiency of Coupled Iterative Coverage Path Planning for the Inspection of Large Complex 3D Structures. Drones, 8(8), 394. https://doi.org/10.3390/drones8080394






