Studies on V-Formation and Echelon Flight Utilizing Flapping-Wing Drones

Abstract

V-Formation and echelon formation flights can be seen used by migratory birds throughout the year and have left many scientists wondering why they choose very specific formations. Experiments and analytical studies have been completed on the topic of the formation flight of birds and have shown that migratory birds benefit aerodynamically by using these formations. However, many of these studies were completed using fixed-wing models, while migratory birds both flap and glide while in formation. This paper reports the design of and experiments with a flapping-wing model rather than only a fixed-wing model. In order to complete this study, two different approaches were used to generate a flapping-wing model. The first was a computational study using an unsteady vortex–lattice (UVLM) solver to simulate flapping bodies. The second was an experimental design using both custom-built flapping mechanisms and commercially bought flapping drones. The computations and various experimental trials confirmed that there is an aerodynamic benefit from flying in either V-formation or echelon flight while flapping. It is shown that each row of birds experiences an increase in aerodynamic performance based on positioning within the formation.

1. Introduction

The formation flight of birds is a fascinating natural phenomenon that has intrigued researchers for decades. Birds have evolved to fly in formation in order to conserve energy, improve navigation, and enhance their overall survival during migration [1]. The V-formation and echelon formation are the two most commonly observed formations, and have been shown to offer significant aerodynamic benefits, such as reduced drag and increased lift, that allow birds to fly farther and with greater ease [1,2,3,4,5,6]. The mechanisms behind these aerodynamic benefits are still not fully understood, and further research is needed to fully comprehend how birds fly in formation and how these mechanisms can be replicated in autonomous systems.

The application of formation flight techniques to autonomous systems such as drones has gained significant attention in recent years, as a way to improve their performance and capabilities. Formation flight can enhance the efficiency of drones by reducing drag, improving lift, and conserving energy, which can be crucial for their use in various applications, such as search and rescue, surveillance, and environmental monitoring [7,8,9,10,11,12,13].

It is important to note that the majority of research on formation flight has focused on fixed-wing aircraft, while the behavior of flapping-wing formation flight has received less attention. The main difference between flapping-wing and fixed-wing formation flight lies in the way lift is generated. In fixed-wing aircraft, the lift is generated by the flow of air over the wings, while in flapping-wing aircraft, the lift is generated through the wings’ movement [14,15,16]. This fundamental difference has important implications for the aerodynamic benefits of formation flight and the mechanisms behind it.

Most studies on formation flight have considered only fixed-wing aircraft, as it is easier to model and study the aerodynamic benefits in this context [7,8,9,10,11,12,13]. However, flapping-wing aircraft have unique characteristics, such as the ability to change their wing shape and frequency, that make them well suited for formation flight [14]. Despite this, there is still a lack of research on the aerodynamics of flapping-wing formation flight and its potential benefits [17].

The study of formation flight in migrating birds has been a topic of scientific speculation for many years, yet its reasons are still largely uncertain. One of the recent studies on this subject, conducted by Portugal et al., used GPS tracking to study the flight patterns of birds in migration [3]. Their work demonstrated the existence of aerodynamic benefits in bird migration and provided a foundation for further research in this area.

Subsequent studies, such as those by Hassanalian et al. [18] and Bajec et al. [19], have confirmed the benefits of V-formations and echelon formations in bird migration. These studies have used a variety of methods, including wind tunnel experiments, numerical simulations, and field observations, to provide a more complete understanding of the aerodynamic benefits of formation flight in birds.

It is important to consider the differences between studies on flapping-wing birds and fixed-wing autonomous drones when comparing their results. Flapping-wing birds exhibit unique aerodynamic properties, such as the generation of lift through the flapping of their wings, that cannot be replicated in fixed-wing autonomous drones. Additionally, the aerodynamics of flapping wings are highly complex and are not fully understood. Thus, direct comparisons between the two types of studies must be made with caution, and the differences between the two types of systems must be considered when interpreting results.

The key results from previous studies on bird migration and formation flight include the finding that birds in V-formation benefit from an upwash effect that reduces the energy required for flight). The wings of the lead bird create this upwash effect in the formation, which generates an area of low pressure behind it that lifts the wings of the following birds. This effect reduces the energy required for flight and has important implications for the optimization of bird migration [3].

In addition to the benefits of V-formation, previous studies have also found that echelon formations can reduce drag and increase stability compared with other formation types [18,19]. This reduction in drag can be attributed to the reduction in interference between the wings of the birds in the formation, which reduces the turbulence and drag experienced by each bird. The increased stability can be attributed to the improved alignment of the birds in the formation, which reduces the likelihood of wingtip vortices and other aerodynamic instabilities.

The potential applications of these formation flight techniques for autonomous drones are numerous. The use of V-formation can increase efficiency, as it reduces the energy required for flight and increases the range of the drone. This can be particularly useful in applications such as environmental monitoring, where the drone must fly long distances to reach its target. The use of echelon formations can increase stability, which can be important in applications such as search and rescue, where the drone must fly in adverse weather conditions.

This paper aims to fill the existing gap by exploring the potential of flapping-wing formation flight for autonomous drones. Through numerical simulations and experimental studies, a deeper understanding of the aerodynamics of flapping-wing formation flight can be gained, which can be applied to autonomous drones, with a specific focus on V-formations and echelon formations. This research aims to contribute to developing more efficient and capable autonomous systems by exploring the potential for formation flight to improve their performance.

V-formation flight is named simply because of the distinct ‘V’ shape that is seen when birds fly in formation. Echelon flight is very similar, but instead of a ‘V’ shape, birds fly in one diagonal line. These flight formations can be seen anywhere in the world where migratory birds pass during their migration. Wildlife refuges, particularly Bosque Del Apache in New Mexico, are great places to see them happen more often and up close. V-formation and echelon flight are typically only observed in migratory bird flocks, such as Canadian geese, cranes, or white geese like the ones seen at Bosque Del Apache Wildlife Refuge, an example of which can be seen in Figure 1 [20].

A trip to Bosque Del Apache allowed seeing various V-formations and even echelon flight formations in real time. Various photos and footage of the wildlife refuge were taken, and some important aspects of the flight formations were witnessed. There was no set number of birds that flew in formation. As few as three birds in V-formation were observed (see Figure 1b), and almost as many as thirty birds in V-formation (see Figure 1c). Also, the flight formations were not so perfectly aligned as they would be in an experiment or analytical study. In most studies, the distance from bird to bird is perfectly even on each side of the V-formation, but in nature, it is not perfect, although the birds still elect to form a V-formation or echelon formation.

It was evident that the birds were not all flapping at the same time. This could be interpreted as a phase difference between each row of birds. This is visible in Figure 1 and can be seen much more clearly in Figure 2, where it is noticeable that the second crane in the echelon flight has a different wing position than the others. The phase difference included a difference in the starting position of the wings between birds and resulted in an offset in flapping motion. For example, one bird’s wings may be flapping up while another’s are flapping down. The only information not obtained from the Bosque Del Apache Refuge footage was the flapping frequency and angle of a single bird and the V-formation or echelon formation angle. To capture information like this, a better observation position was needed. In most cases, the formations and birds were viewed at an angle that would make it difficult to accurately determine the flapping angle or formation angle.

These flight formations were a sight to see, and each carried valuable information about nature. Many formations occurred at Bosque Del Apache Refuge, proving that it was no coincidence that these birds were flying in formation, even if they were not traveling long distances. They happened so often that it would be difficult not to see or ask why these birds flew in formation. As many studies have suggested, it has to do with the aerodynamic effects experienced by the birds due to V-formation or echelon formation. It is unlikely that these birds would apply these formations so frequently without receiving significant benefits.

It is theorized that when birds fly in formation, they use a variety of flow dynamics to their advantage. Specifically, they employ the upwash and downwash effects to increase lift and reduce drag while covering long distances [18,20,21]. This allows migratory birds to travel further, increasing their chances of survival. While analysis of fixed-wing configurations in V-formation has shown improved flight performance, birds are flapping-wing bodies and thus operate differently. By studying the aerodynamics of flapping wings, a better understanding of the benefits of formation flight can be gained [14,22]. The question then becomes how to analyze data from a flapping-wing drone in a V-formation. To do this, a flapping-wing model with actuators was constructed and attached to a force-balance tool to measure the thrust force. The wings were arranged in a V-formation on the foundation to study different flow effects using lift force data obtained from experiments. The goal is to determine whether and how the upwash and downwash effect can be applied to flapping wings and whether it is advantageous for flapping-bodied creatures, such as insects, to fly in certain patterns when moving in groups. This research was divided into a computational study and an experimental study, to develop and test hypotheses about flow dynamics.

Examining flapping-wing flight is crucial due to the differences in flow dynamics compared with fixed-wing flight [23,24,25,26,27,28,29,30,31]. The production of lift and drag is distinctive, resulting in a unique correlation between the efficiency of formation patterns [32]. The generation of vortices by flapping wings alters and disrupts the flow behind the wings, which can lead to fluctuations in the lift and drag forces experienced by birds positioned behind them [33]. The testing involved the ability to adjust the frequency of the body flapping, through the motor speed. This design allowed optimization of the system by adapting the motor speed based on lift readings from the sensors. Furthermore, this testing was conducted without any additional equipment requirements, in a stable room temperature environment, where the wings were powered by turning on the motor.

However, the only disadvantage of using a motor-powered system in studying the aerodynamic effects is that the battery power is virtually infinite, thus not allowing the possibility of running a battery drain test. A battery drain experiment is a great way to test the hypothesis, because it shows whether or not the flapping bodies receive an advantageous aerodynamic effect that allows them to use less energy. So, to cover this experiment, an additional setup with limited battery power was required to test the hypothesis further. The findings of this research will have relevance for the study of micro drones [34]. Given that drones with a weight of a few grams have limited or no power supply, it is essential to make the most of flow dynamics. The success of most small drone missions is constrained by power consumption, so any decrease in lift or drag can pose challenges for the mission. Flapping wings are often used in small drones whenever possible, as they generate lift more efficiently in low Reynolds number flow conditions. Fixed-wing drones have a minimum size limitation of about 10 cm, which is not a constraint for flapping-wing models [23]. Studying the flow dynamics of small flapping drones in formation could have broad applications, as many areas of research are focused on swarm drone technologies.

The use of flapping-wing drones in drone swarms offers several benefits, particularly when compared with fixed-wing drones. One of the primary advantages is the ability to produce lift and thrust using smaller wings. This makes flapping-wing drones more suitable for use in dense environments where larger fixed-wing drones may not be able to operate effectively. Additionally, flapping-wing drones can generate lift and thrust independently, which enables them to control their position and orientation in the swarm more effectively [35,36,37].

Previous research has demonstrated the potential of flapping-wing drones in swarm applications. For example, a swarm of flapping-wing drones could be used to explore the potential for cooperative flight in a highly dense environment. The flapping-wing drones would be able to effectively navigate through obstacles and maintain formation despite the complex flow dynamics in the environment [38]. Similarly, studies have investigated the potential for flapping-wing drones to be used for search and rescue operations in urban environments [39], finding that the flapping-wing drones were able to effectively navigate through narrow spaces and fly at low altitudes, which was not possible with fixed-wing drones. Lastly, since birds in nature are not constantly flapping while in formation, it is also beneficial to analyze these setups against fixed-wing formation modeling to compare the aerodynamic effects [20]. This comparison will give insight into how different or similar are the effects between the models.

The rest of the paper is organized as follows: in Section 2, the analytical study of the V-formation using a fixed-wing model is discussed. Section 3 shows the computational studies of V-formation for flapping wings. The experimental design and results are elaborated in Section 4 and Section 5, respectively. Section 6 presents the flow visualization of flapping wings in formation flight. The summary and conclusions are given in Section 7.

2. Analytical Study

The main focus of this paper is to study V-formation effects, specifically with a flapping-wing model. However, as stated in the introduction, migratory birds use flapping and fixed-wing motions while migrating. This was also observed in person at Bosque Del Apache WildLife Refuge. So, to better understand the effects of V-formation, it was deemed beneficial also to conduct a fixed-wing model analysis using the experimental parameters in this work. More specifically, the parameters used for this analytical study were those of the commercialized flapping-wing drones described later in Section 4. The flapping drone ended up being used for the majority of the experimentation process, so it was determined that it should also be used for the analytical study. Interestingly, the results for the analytical calculations looked very similar to the experimental results. The analytical study completed in this work was based on a similar study of V-formations in Canadian geese, conducted by Mirzaeinia et al. [20]. In the study of the Canadian geese, a set of aerodynamic and theoretical equations was utilized to create the fixed-wing model and to determine how much energy each goose produced within the V-formation. The model allowed the parameters to be changed, which was useful when creating the fixed-wing model for the flapping drone. The following equations were used to determine the vortex positioning and the total amount of induced drag experienced by each bird in the V-formation. Together, they form an analytical model for a fixed-wing V-formation flight:

$$w\left(\delta x,\delta y\right)=-{\displaystyle \frac{\Gamma }{4\pi }}{\displaystyle \frac{1}{\delta x}}\{{\displaystyle \frac{\delta y+a}{\sqrt{\delta x^2+{\left(\delta y+a\right)}^2}}}-{\displaystyle \frac{\delta y-a}{\sqrt{\delta x^2+{\left(\delta y-a\right)}^2}}}\}-{\displaystyle \frac{\Gamma }{2\pi }}{\displaystyle \frac{a}{\delta y^2-a^2}}\{1-{\displaystyle \frac{\delta x}{\sqrt{\delta x^2+{\left(\delta y+a\right)}^2}}}\}$$

(1)

$$a=\left(\pi /8\right)$$

(2)

$$D_I\left(n\right)=nx{D}_{I11}+{\displaystyle \frac{4D_{I11}}{{\pi }^2}}\sum _{i=1}^{n-1}\sum _{j=i+1}^n\log \left[1-{\left({\displaystyle \frac{2a}{\left|i-j\right|\left(b+s\right)}}\right)}^2\right]$$

(3)

$$D_{Ik}=D_{I11}+{\displaystyle \frac{2D_{I11}}{{\pi }^2}}\log \prod _{j=1}^n\left[1-{\left({\displaystyle \frac{2a}{\left|k-j\right|\left(b+s\right)}}\right)}^2\right]$$

(4)

$$D.R={\displaystyle \frac{D_I\left(n\right)}{n{D}_{Ik}}}=1+{\displaystyle \frac{4}{n{\pi }^2}}\sum _{i=1}^{n-1}\sum _{j=i+1}^n\log \left[1-{\left({\displaystyle \frac{2a}{\left|i-j\right|\left(b+s\right)}}\right)}^2\right]$$

(5)

$$s_{opt}=0.5b\left(0.78-1\right)=-0.11b$$

(6)

Equation (1) is the Biot–Savart law [40] which was used to determine the vertical velocity component induced by a vortex line located at (δx, δy) away from the center of a bird’s wing. The important parameters used in this equation are w, the vertical velocity component, Γ, the strength of the vortex, and a, the half-length of the bound vortex, which is determined by Equation (2) [41]. This equation is essential for determining each bird’s upwash and downwash effects in the V-formation.

Equation (3) [42] determines the total amount of induced drag in a V-formation depending on the amount of birds n in the formation. The important parameters are D_I11, the induced drag of a bird in formation, b, the wingspan of each bird, and s, the wingtip distance between adjacent birds in the V-formation. Equation (4) [42] uses the same parameters, but instead of determining the induced drag of the whole formation, it determines the induced drag of each bird individually. Equation (5) [42] determines the ratio of induced drag of the V-formation. Lastly, Equation (6) [43] determines the optimal wingtip distance for the birds in formation to benefit the most from the upwash effects.

All of these equations were modeled in a Matlab code to generate plots to describe the amount of drag each bird experiences in the V-formation. Additionally, the code generated plots for V-formations with different flock sizing depending on a maximum value specified by the user. This was used to draw a comparison between the different flock sizes and to give insight into how the flock size affected induced drag for each bird.

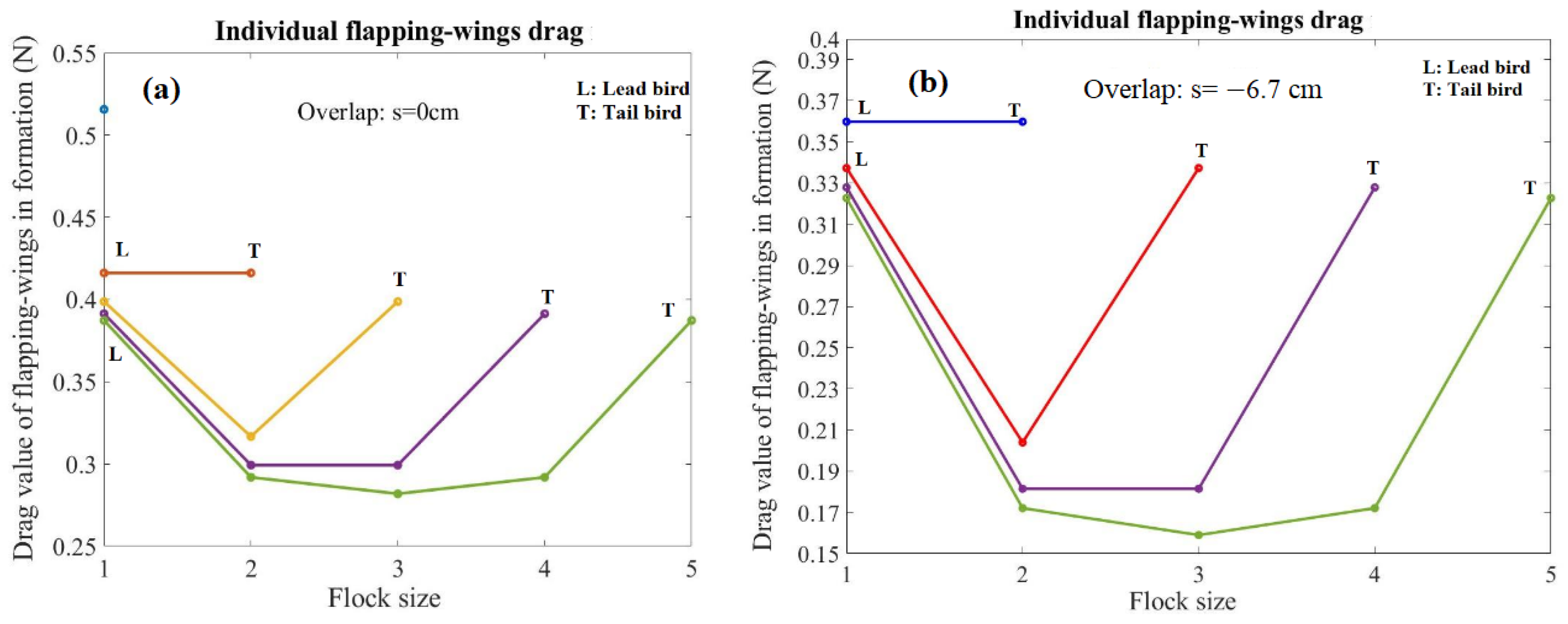
For the analysis, two different trials were run on the code. One trial was run with zero wingtip overlap, and the other was run with the optimal wingtip overlap calculated using Equation (6). The maximum flock size specified was five birds in total on one side of the V-formation. The results for this study can be seen in Figure 3a,b. From the results, it was found that the birds in the middle of the V-formation flock experienced the least amount of drag, which is what was expected from this work. The leading bird experienced the most amount drag, as did the bird at the trailing edge of the V-formation. When comparing the results between the zero wingtip overlap and the optimal overlap, it was noted that the overall drag of the V-formation reduced for any V-formation with two or more birds. From this analysis, it can be concluded benefit to using this overlap was indeed apparent. The optimal overlap plots also illustrate that there was an induced effect on the leader bird as its induced drag decreased when using the optimal overlap compared with the zero overlap. The plot that best describes the experimental setup is the plot with a flock size of three birds on each side of the V-formation. As later described in this paper, a total of five birds were used for experimentation, so this analytical study gives insight into how the experimental results may look.

3. Computational Study

Ptera software (https://www.cameronurban.com/ptera-software), an open-source unsteady vortex–lattice method (UVLM) solver, was utilized to simulate the formation flight problem. This software has been previously validated with experimental data for analyzing single ornithopters [44] and was tested for its accuracy in emulating formation flight in this study. The first step in the simulation process involved selecting a geometry to emulate. The chosen geometry for the simulation, as depicted in Figure 4, was a simple trapezoidal wing design with a 70 cm wingspan, originally intended for the experimental setup but later changed. The angle of the flapping wing was approximated to evolve sinusoidally over time with an amplitude of 15° and a period of 0.5 s. In simulations involving multiple birds, they were spaced in a V-formation. The distance between the centerline of a bird and that of the leading or trailing bird, measured in the body y-axis, was 0.5 m. The leading edge of each bird was also spaced 0.5 m in the wind x-axis from the next trailing or leading bird. The simulations assumed a 0° angle of attack, no sideslip, and that the air had a density and kinematic viscosity of 1.225 kg/m³ and 15.06 × 10⁻⁶ m²/s. The simulated results presented in this section should be considered relative to the simulated geometry and not the experimental geometry, which turned out to be considerably different from the simulation. Essentially, the simulation served as its own experiment to study V-formation flight, and the parameters did not correspond to those of the experimental setup presented in Section 4. Future work will address these differences and enable a direct comparison.

In this study, simulations with one, three, and five birds were analyzed. However, before interpreting the results for these simulations, it was important to determine the appropriate panel discretization and number of flap cycles to simulate. It is ideal to increase the number of panels and cycles to obtain convergent force values. In this study, only the number of chordwise panels was iterated, and the number of spanwise panels was adjusted automatically to ensure that the panels were on average five times longer in span than in chord. There is no clear consensus on the appropriate panel aspect ratio, so a value of five was chosen as a reasonable compromise between accuracy and simulation time. The spanwise length of the panels was varied across each wing section in a cosine distribution, placing more panels near the wing tips, roots, and section breaks where higher spanwise pressure gradients were expected. The panels were spaced uniformly in the chordwise direction, which is typically carried out with UVLM solvers. This uniform spacing allows a time step length to be chosen that makes the wake ring vortices approximately the same size as the panel wing vortices, which is necessary to govern the wake–transport equation [45].

In the convergence study, simulations for each chordwise discretization with a fixed number of flap cycles were run using two nested for loops. The number of flap cycles was then incremented, and the process was repeated. At the end of each simulation, the root-mean-square (RMS) lift and drag were computed over the final flap cycle. For example, if the simulation had one bird with X chordwise panels and Y flap cycles, the panel-based convergence criterion would be the percentage change in final-cycle RMS lift and drag (whichever was higher) from the simulation with X-1 chordwise panels and Y flap cycles. Similarly, the flap-based convergence criterion referenced the simulation with X chordwise panels and Y-1 flap cycles. The converged solution was that with X-1 chordwise panels and Y-1 flap cycles if the simulation’s chord and flap-based convergence criteria were both below 0.5%. For simulations with more than one bird, all birds had to meet the convergence criteria for the converged solution.

In this study, the drag values reported pertain to induced drag, which is the only type that can be accounted for by the inviscid UVLM solver without modification. The obtained values were plotted based on the converged number of flap cycles. Figure 5 and Figure 6 show the convergence plots for three- and five-bird simulations, respectively, displaying the RMS force values for each bird’s position. The birds are grouped by row, with the lead bird assigned to row one to reflect the symmetry of the problem. In the five-bird plots, the third-row lines heavily overlap the second-row lines, as shown in Figure 7 and Figure 8. With appropriate increases in the number of flap cycles and chordwise panels, all simulations eventually converge.

Table 1. The converged discretizations for each simulation.

Number of Birds	Number of Chordwise Panels	Number of Flap Cycles
1	8	2
3	11	3
5	11	3

indicates that the one-bird simulation required 8 chordwise panels and two flap cycles, while the three- and five-bird simulations required 11 chordwise panels and three flap-cycles.

The simulations were executed with the converged chordwise discretizations and numbers of flap cycles, and the outcomes were documented. Snapshots of individual timesteps captured for each simulation case are presented in Figure 9a–c. The final-cycle-averaged force coefficients for each simulation are outlined in

Table 2. The final-cycle-averaged force coefficients for each simulation.

Number of Birds	Row 1		Row 2		Row 3
	CL	CDi	CL	CDi	CL	CDi
1	0.012	−0.387	-	-	-	-
3	0.011	−0.384	0.007	−0.288	-	-
5	0.011	−0.385	0.007	−0.292	0.007	−0.291

. Unlike in the convergence study, the final results are expressed as arithmetic means instead of RMS values. These average values are more valuable in determining the cycle-averaged forces a bird might encounter, which could impact the amount of power it needs to exert. Additionally, the lift and induced drag were non-dimensionalized into lift and drag coefficients based on the geometry.

The simulations conducted in this study, as summarized in Table 2, demonstrated low lift coefficients and negative drag coefficients across all cases. These values were expected, given the use of uncambered wings and a zero angle of attack. However, the multi-bird simulations revealed unexpected results, in which the leader experienced the highest lift and thrust forces, with diminishing forces for the subsequent rows of birds. This finding is contrary to conventional wisdom that V-formation flight yields benefits to the birds that are following, due to the upwash generated by the leading bird(s). Various factors may have contributed to these contradictory outcomes. For example, it is possible that the wake of the leading bird did not properly influence the wings of the subsequent birds, due to the prescribed-wake model employed in the simulations and the use of zero angles of attack. Future work may involve exploring the impact of a free-wake model and/or positive angles of attack on the results. Additionally, the spacing between the birds or the phase difference between their flap cycles may also play a role, as previous research has shown that these parameters significantly affect the forces generated during V-formation flight.

4. Experimental Design and Setup

4.1. Custom-Built Flapping Wings

The purpose of creating the flapping mechanism was solely for experimentation and analysis, since the drones were not designed to fly in this experiment. As a result, a simple flapping mechanism was developed, to achieve stationary flapping motion. The flapping mechanism was modeled after a double crank system [46,47]. A 3D model of the flapping mechanism and its parts were created using Autodesk Inventor (as shown in Figure 10a). The mechanism consisted of seven primary parts, not including the gears, pins, screws, and additional equipment. These seven main parts included the base, two arm actuators, two shafts, and two wing mounts. Once fully assembled, the dimensions of the mechanism were approximately 166 mm in length, 145 mm in width, and 32 mm in depth.

The aim was to create a lightweight flapping mechanism for the purpose of measuring lift and the effects of V-shaped flight formation. PLA plastic was chosen as the material for the main parts since it is light yet strong. To prevent part failure, high-density printing was used for the shafts. The overall weight of the main components was low, but increased when additional gears, pins, and screws were added.

The modularity of the system came from the wing mounts, which were designed to accommodate different wing types. Carbon fiber rods ranging from one to three millimeters in diameter were used for the wings and attached to the mounts. However, the mounts can be swapped out for different wings. The flapping mechanism was powered by a high-torque NEMA 17 bipolar 2.1 amp extruder motor, which allowed easy control of the flapping motion. An Arduino 2560 Mega and A4988 stepper motor drive were used for logic and motor control.

The NEMA 17 stepper motor was mounted onto the 3D-printed base of the mechanism, with a 15 mm pitch diameter pinion gear attached to drive two 25 mm pitch diameter gears. Small bearings were inserted between the gears and the base to counteract axial forces that would cause the gears to slide out of place. The gears were attached to the shafts via clevis pins, which were then connected to the actuator arms. Initial test runs were successful, but problems arose once the wings were attached to the system. These issues are discussed in the following section.

The flapping mechanism was connected to an RCbenchmark (v1.2.0) Series 1520 thrust stand, which was primarily designed for testing brushless motors. However, for this experiment, the fully calibrated load cell and its software of the Series 1520 were convenient and suitable for conducting the thrust and lift analysis. The software included a built-in thrust sensor, which required only a USB connection to a computer and was able to detect data from the flapping mechanism in real time. Moreover, the load cell of the thrust stand was sensitive and able to detect even small increments of displacement. The motor mounting-part connections with the thrust stand were integrated into the base of the flapping mechanism to facilitate easy attachment to the thrust stand. The Series 1520 has also been designed to allow custom connections to be made if required, such as using a larger or custom motor mounting piece. However, one limitation of the Series 1520 is that only one sensor can be connected at a time. This became an issue for the current experiment since there were five flapping mechanisms emitting thrust data.

Before creating any design, the first thing considered was that the wings had to be designed for the intention of actual flight. Although the mechanisms in this work were not designed to fly, and there was no intention for them to fly, the wings still needed to be designed for flight so that they could properly create the aerodynamic effects experienced by birds in V-formation. The vortices and wakes that bird wings create in V-formation flight are critical to the birds in formation, so the wings used for the experimentation needed to recreate that effect. One of the first parameters chosen was the wingspan. When deciding on the wingspan of the experimental model, a typical migratory bird such as the Canadian goose was considered for inspiration. It is known that Canadian geese have a wingspan ranging from 127 to 185 cm [18], but considering how much space a V-formation with this wingspan would take, it was much too large for the laboratory space that was available. The main constraint on the wingspan was that the V-formation was planned for construction in a 13 × 13 feet drone cage. To reduce the size of the V-formation, a wingspan of 70 cm was chosen. However, the wingspan ended up being about 84.5 cm due to the extra space in between the actuators of the flapping mechanism. This wingspan was used to determine the optimal number of birds that should be used in the experiments, given the constraint of a 13 ×13 feet drone cage. It was determined that the maximum number of birds allowed was seven; however, the optimal amount was five birds. Seven birds could fit in the given drone cage space but would not allow any adjustment of the space between birds in the x-direction, which is a crucial parameter in a V-formation as it determines how the upwash and downwash of the vortices affect each bird. Using five birds instead allowed adjustment of the space in between them. A five-bird V-formation with the chosen wingspan took up about 282.5 cm of space when using the full V-formation and 141.25 cm if half of the formation was used (see Figure 11).

With the chosen wingspan, the next step was to choose a general shape. The initial shape chosen was a basic trapezoidal shape from a design cycle for micro air vehicles (MAVs) [48,49]. This design was also the wing shape used in the Ptera software computational study (see Figure 12a). With the shape chosen, the ribs of the wing then needed to be designed. Ultimately a wing with a half-wingspan of 35 cm was designed, as shown in Figure 12b.

The final step in the wing design process was to build the wings needed for all the flapping mechanisms. The wings needed a material that would be durable but also flexible. To achieve this, carbon fiber rods were acquired to build the skeleton of the wings. As stated before, two different diameters were used. The 3 mm diameter rods were used for the leading-edge spar, and 1 mm rods were used for the ribs of the wings. The material used to cover up the skeleton of the wings was mylar. In order to achieve the angles, joints were created using Inventor and then 3D printed using a resin printer, since they were very small pieces. The final assembly of the wings can be seen in Figure 13a,b.

4.2. Commercialized Flapping Wings and Analysis

The use of commercial flapping drones served two main purposes. First, it was necessary to conduct battery drain testing as the custom-built flapping mechanisms had a virtually infinite power source. Second, the commercial flapping drones were a backup for the custom-built drones because they did not fully work as intended when used for testing; more details are discussed in Section 5.

The drone selected for this work was the commercialized flapping-wing drone created by Hanvon (see Figure 14). The wingspan of the drone was about 615 mm, the length of the body about 440 mm, and the advertised speed about 5 to 7 m/s. The drone was lighter than the custom-built flapping mechanisms, and the smaller wingspan allowed much more flexible adjustment of the space in between drones. The commercial flapping-wing drones ended up being the preferred choice for conducting the tests. However, there were several downsides to using commercial drones over custom flapping mechanisms. One, of course, was the limited battery life, and another was the lack of modularity. The drones were limited to whatever wings were built for them and would require alterations if any other custom wings were to be attached to them. Another notable downside was that it was difficult to know what flapping frequency was being used while testing. A total of five flapping-wing drones were acquired for this work, and they ended up being the primary data source for the experimental results discussed later in Section 5.

To better understand the dynamics of the flapping wings, some wing analysis was conducted, and characteristic wing data were obtained. This analysis was completed using Flapsim (v1.1). This software is able to simulate the flapping dynamics of either a bird or insect wing and gives the freedom to import a wing shape. The software is ideal for experimenting and testing wing shapes and was useful in testing the wings of the flapping-wing drone. To use the software, the wing shape of the flapping drone needed to be obtained. A picture of the wing’s topside was taken and then imported to Getdata Graph Digitizer (v2.26.0.20), software used to digitize images of graphs (see Figure 15).

Table 3. Parameters for the Flapsim simulation.

Mass and Geometry
Wing Length (m):	0.305	Wing Mass (kg):	0.013
Wing Ratio (m):	0.74	Radius of Gyr. (m):	0.097
Aerodynamics
Wing cd0:	0.085	Wing cd90:	2.185
Wing cl45:	0.16	No. Induced Iter.:	20
No. Timesteps:	100	No. Elements:	10
Kinematics
Elevation Amp (deg):	35	Pron. Amp (deg):	15
Extension Amp:	0.5	Frequency (Hz.):	15
Stroke Plane (deg):	−20	Downstroke Frac.:	0.5
Hand Pron. Amp (deg):	5	Speed (m/s):	7

lists all the characteristics inputted into Flapsim.

The flapping simulation results are shown in Figure 16 and Figure 17.

In Figure 18a–d, the axial force (thrust), the normal force (lift), mechanical power, and simulated torques in the x, y, and z-directions versus time are shown, respectively.

4.3. Experimental Base Setup

The final piece of the experimental design was the foundation used to carry all of the flapping mechanisms. As seen in Figure 19, all the mechanisms or flapping wings were attached to the RCBenchmark sensor, bolted onto a wooden block that held the Arduino and breadboard. This block required another foundation to raise it up from the ground to prevent a ground effect when the wings flapped. This foundation also needed to be adjustable so that the space in between birds could be changed in both the x-direction and y-direction.

In the experimentation process, the different flapping mechanisms and flapping-wing drones were referred to as birds 10 through to 14. The schematic shown in Figure 20 describes which bird in the V-formation was which. This nomenclature was given because it was the nomenclature assigned to the RCBenchmark sensors when connected to the RCBenchmark software for the first time. When a sensor was connected, it appeared as COM10 through to COM14; so, when correlating the experiments to the software, it was decided to match the nomenclature. During the experiment, it was decided to assume that the data from one side of the V-formation would be identical to those from the other side. However, for the echelon formation tests, every bird was used to gather data.

The first experimental setup was the flapping mechanisms in V-formation. During the assembly process, it was noticed that there were some issues with axial forces causing gears to slip out of alignment. These issues were partially resolved once bearings were added to firmly hold the rods spinning the gears, but the problem occurred again when the wings were attached, because they added extra weight to the system. Nonetheless, the flapping mechanisms were still placed in a V-formation in order to test the electrical switch and to ensure that the sensors were working properly. Figure 21 shows views of the first experimental setup. Unfortunately, the test runs did not work properly. The gears continued to slip after only a few seconds, so an insignificant amount of data was captured. There are still plans to further develop these mechanisms into working conditions so that there is better control over parameters such as flapping frequency and wing shape. Luckily, the flapping-wing drones worked well and were the main source of the experimental data.

The second experimental setup was the V-formation using the flapping-wing drones without a fan to generate wind. In this experiment, there was no specific or exact measured distance between bird wingtips. The approach taken in this experimental setup was more of an approximated measurement. As stated in the introduction, in nature, birds are not perfectly aligned or uniform with each other while in formation flight. So, the distance between each bird both in the x-direction and y-direction was intentionally measured approximately by eye to see how a slightly nonuniform V-formation would perform. The system still ended up looking uniform or symmetrical, but exact measurements were not made (see Figure 22). In this experiment, a total of seven different tests were conducted, as shown in

Table 4. The tests conducted for the second experimental setup.

Order of Tests	Test Type Conducted
1	Single-bird test
2	Three-bird test, no phase difference, no wing overlap
3	Five-bird test, no phase difference, no wing overlap
4	Five-bird test, phase difference, no wing overlap
5	Five-bird test, phase difference, small wing overlap
6	Five-bird test, phase difference, large wing overlap
7	Battery drain test, phase difference, small wing overlap

.

Test 1 utilized only bird 12. All other birds were shut off to avoid any induced effect on the single bird. The purpose of this test was to measure how much thrust a single bird could generate without any drag from airflow. Test 2 utilized birds 11 through to 13. All three were turned on for each run, and data were captured for all three birds. This test was conducted with no phase difference between rows, meaning that the wings for all birds started in the same flat position. Tests 3 through to 6 were all five-bird tests. All birds were turned on for each run, but data were captured only from birds 12 through to 14 to reduce experiment time. As stated before, the wingtip space was approximated by eye. For the tests with phase difference between rows, row one had its wings completely upward, row two had its wings completely straight and flattened, and row three had its wings completely downward. For Test 7, the battery drain test, it was decided to configure the V-formation with approximated optimal conditions. The batteries for each bird were replaced with fully charged batteries before testing. All birds were turned on for this test and flapped until the batteries died.

This experimental setup was similar to the second setup; however, there were three distinct differences: a fan was introduced into the system to cause drag on the birds (see Figure 23), the space between birds in both the x and y-directions was precisely measured (see Figure 24), and only birds 12–14 were turned on while the other two on the left side of the V-formation were left off. The fan had three different speeds, low, medium and high. The highest fan speed was chosen for this experiment. The space between each bird started out at 584 mm by 584 mm. The distance was measured from the front side of each bird. A total of five tests were conducted. Each test had the measured space either decreased or increased by an increment of 76 mm, and 584 mm was chosen as the base measurement because the highest distance possible between birds in the y-direction was 660 mm. This is where the limitation of the 8020 apparatus was noticed. The total space available in the y-direction of the table was about 1448 mm. So, with the spacing between each bird set at 660 mm in the y-direction, all of the available space was taken up. Refer to

Table 5. The tests conducted for the third experimental setup.

Order of Test	Spacing Configuration (x by y)	Overlap between Wingtips
1	584 mm by 584 mm	25 mm
2	584 mm by 660 mm	25 mm
3	584 mm by 508 mm	25 mm
4	660 mm by 584 mm	−51 mm
5	580 mm by 584 mm	102 mm

for the list of tests conducted and for the overlap between wingtips, based on a 610 mm wingspan.

The negative overlap value from Test 4 indicated that there was a gap between wingtips. Not much is known about how the spacing in the y-direction affects birds aerodynamically in a V-formation. This experimental setup was a good starting point to investigate that aspect of V-formation flight, but the 8020 apparatus will need more available space in the y-direction to test larger distances and to be less constricted. Several more tests could have been conducted to obtain more spacing configuration data, but the tests were omitted to reduce testing time and also to conduct tests in a similar fashion to those conducted in the second experimental setup. Future work is likely to include the missing configuration points.

Section 2 of this paper presents a list of aerodynamic and theoretical equations to model a fixed-wing V-formation. Equation (5) in Section 2 describes an expression for optimal wingtip spacing. This equation was the basis of this experimental setup. The equation was developed assuming fixed-wing movement, but the theory was tested in this experiment to see whether it could apply to birds in flapping motion. Only two tests were conducted in this experimental setup. Both used the optimal overlap, which was 67 mm considering a 610 mm wingspan. The space configuration for optimal overlap was 543 mm between each bird in the x-direction. This space configuration was also used in the y-direction (See Figure 25). The difference between the two tests conducted was that one had the fan on at high speed while the other had the fan off.

The final experimental setup was an echelon flight formation using the flapping wings (see Figure 26). In this experiment, the fans were not used because they were not large enough to blow air equally across all of the birds. The space configuration between each bird was 543 mm by 318 mm. This configuration used the optimal overlap from the previous experimental setup. The value for the y-direction was chosen so that there was a little free space left in the y-direction of the 8020 apparatus. With this experimental setup, two tests were conducted. The first one was a regular run of the echelon flight (see Figure 27), where data were captured from each bird. The second test was a battery drain test of the echelon flight, with fully charged batteries.

Another setup was an additional small observational test of the flow visualization between two flapping drones. The system utilized a laser on a tripod and a handheld smoke machine. The tripod with the laser was positioned so that the laser pointed in between two of the birds, and the smoke machine was pointed toward the birds so that the flapping of the birds could create vortices. For this setup, the flapping drones were set to the lowest possible flapping frequency so that the vortices with the smoke were more visible. The base speed of the drones, when turned on, was too high to see the vortices with the smoke machine. A high-speed camera was also used to record all footage in slow motion for easier analysis.

5. Experimental Results

All of the data for each experiment, excluding battery drain tests, were captured via RCbenchmark software. During the data analysis, the moments where the birds sped up or slowed down were removed. The two main aspects of the data collected from each test were thrust in kilograms–force and time in seconds. These values were collected for each bird tested individually. The data for thrust were used to create an average to compare the average thrust generated for each bird. For the battery drain tests, the time at which the battery of a bird fully drained out was captured with a stopwatch.

As described before, the flapping mechanisms designed and built for this work, unfortunately, did not fully work as intended. After attaching the wings to the mechanisms, the additional weight caused the gears to slide along the axes of shafts, thus making the gears unaligned after a few seconds of flapping motion. Only two flapping mechanisms worked as intended, while the others stopped working during testing and required the gears to be re-aligned. To fix this issue, there are a few potential solutions: first, the mechanism base could be redesigned as an enclosed gearbox rather than an open one; second, thicker gears could be attached to avoid unalignment; or third, the wing size could be reduced to decrease the weight added to the mechanism. One or more of these potential solutions may be used in the future to build a more reliable system. At least some data were captured from the leader mechanism (Bird 12). The plot seen in Figure 28 shows that, at the very least, the mechanisms were able to produce a measurable thrust on the sensors. Figure 28 shows that the thrust was oscillatory, which was expected from both the flapping mechanisms and the flapping drones. Another notable observation from the flapping mechanism test is that it can be confirmed that the V-formation created its own flow. When the mechanisms were turned on, the flow being generated could be felt physically. It was also noticed that the wings on the mechanisms that failed continued to vibrate due to the flow from other mechanisms. If the mechanisms were fixed, they could prove to be a great way to test a more versatile system with more freedom of configuration.

A large portion of data was captured from the tests listed in Table 4 for the second experimental setup. Data for Test 1 were recorded to see how much thrust a single bird could generate. Figure 29 shows the cleaned-up data captured from Bird 12. As expected, the thrust came out as oscillatory. Figure 30 is a comparison of the single-bird test with and without the fan turned on. It can be seen that there was a significant difference in average thrust output between the two tests.

The next test was the three-bird test. This was conducted to see what effects could be obtained from a smaller V-formation, as seen at the Bosque Del Apache Wildlife Refuge. The results are seen in Figure 31. Although relatively small, the difference between the average thrust of each bird matched what was hypothesized in this work. Even with zero overlap and no phase difference, birds 11 and 13 both ended up having a higher average thrust output than the leader, bird 12. This effect was also seen in the five-bird test and even in the battery drain test in Figure 32a,b, respectively. In Figure 32a, tests 3–6 listed in Table 4 are congregated into a single plot to better visualize the differences between each test.

The differences in average thrust seen in Figure 32a proved that the variations in phase difference and overlap did have an effect on the thrust output by each bird in the V-formation. For example, Test 3 and Test 4 both had zero overlaps, with the key difference being the phase difference. The difference in average thrust between birds 11–13 in Test 3 was not very significant, but by applying the phase difference in Test 4, it was revealed that the average thrust output between birds 11–13 was greatly affected; the thrust output by birds 11 and 13 was significantly higher than the leading bird. The effect of overlap can be seen by comparing Tests 4–6. By increasing wingtip overlap to a small overlap, the average thrust difference between birds 11 and 13 compared with the leading and trailing birds increased slightly more, thus showing that the two middle birds outperformed the other birds a little more when going from zero overlap to a small overlap. However, a negative effect occured when the overlap went from small to large. It can be seen that for Test 6, increasing to a high overlap caused the average thrust difference between the middle birds and the leading and trailing birds to become smaller, meaning that all birds were closer to using the same amount of energy. This would be problematic in a real-life V-formation, as all birds would run out of energy at around the same time rather than extending the total amount of energy they could use.

Finally, it was interesting how Test 7, the battery drain test, resulted in a plot looking similar to that of the previous tests. Evidently, the shape of the plot was not as even as the previous tests, but this was due to a couple of factors. As stated in the previous section, only up to three birds were tested during the five-bird tests. Although all birds were flapping, only birds 12–14 were used to record data, in order to reduce experimentation time. It was assumed that the other half of the V-formation would output the same or similar results, thus making the plots look symmetrical. This was not the case for either of the battery drain tests conducted. Another reason the plot looked uneven is that as stated in the previous section, the distance between birds was not precisely measured for this specific experimental setup. Nonetheless, birds 11 and 13 outperformed both the leading and trailing birds, similarly to the previous tests. The only discrepancy was that the trailing birds in the previous tests were not able to outperform the leading bird, while in the drain test, the trailing birds did outperform the leading bird.

The results for the five-bird test with the fan on did not fully meet expectations, but some similar effects to those from previous tests were seen (see Figure 33). The results can also be explained by some flaws in the experimental setup. To begin, a comparison can be made between Tests 1–3 listed in Table 4, to see some insight into the effects of y-direction spacing in this setup. When the spacing between each bird was increased in the y-direction, the results looked very similar to the base 584 mm by 584 mm configuration and had the same general shape as the previous tests in experimental setup two. The difference in average thrust for the middle birds compared with the leading and trailing birds did increase slightly, and the overall average thrust of the system decreased. When reducing the spacing between birds in the y-direction, the results were somewhat strange. The overall average thrust of the system decreased, and the middle birds continued to outperform the leading bird, such as in the previous tests, but strangely enough, the trailing birds ended up generating a significantly higher average thrust than the middle birds and leading birds. This outcome was not expected. This outcome was also seen in Tests 4–5. For x-direction spacing, the outcomes came out looking more as expected. When increasing the x-direction to 660 mm by 584 mm, resulting in a wingtip gap of 51 mm, the average thrust difference between the middle birds and leading birds was very small, made sense because of the gap between the wingtips.

A similar result was seen when reducing the x-direction spacing to an overlap of four inches. The high overlap caused a negative effect that caused the difference in average thrust between middle birds and leading bird to reduce. Now, as with the effect seen with the trailing birds significantly outperforming the other birds, this anomaly may have occurred because of the flawed fan system used for this experimental setup. The system consisted of two circular fans placed side by side next to each other. Evidently, this was not a perfect system. Once turned on, the fans probably created a jet stream between each other which is more than likely to have caused an uneven amount of turbulent drag to be applied to the V-formation. These fans were chosen to see the effects of applied drag on the experimental setup. For better results, a future setup will require a fan system that can apply laminar and even drag across all birds tested on and needs to be wide enough to cover wider x-direction spacing. When the x-direction spacing was set to 660 mm by 584 mm, the bird at the trailing edge was not hit evenly by the fans’ airflow as the spacing caused the birds’ formation to be wider than the fans. At least there were some results that did make sense and matched up with the hypothesis.

The results for the optimal overlap test also did not come out as expected. The results of this test can be seen in Figure 34. From the plotted results, it can be seen that the leading bird seemed to be outperforming all other birds with and without the fan turned on. This outcome was definitely not expected. There are a couple of reasons why the data may have come out this way. The basis behind this setup was to test whether the optimal overlap of a fixed-wing model could also be used for a flapping model, so these results may have been caused simply because the optimal overlap of the flapping-wing model is different from that of a fixed-wing model. Another assumption as to why the results came out the way they did is the fact that the spacing in the y-direction was shorter compared with the previous tests. For this test, the spacing configuration was set to 541 mm by 541 mm. This configuration produced a wingtip overlap of 67 mm, which was the optimal overlap based on a fixed-wing model. The y-direction, however, was set to this value simply to keep the x and y spacing the same. This may have caused the results to come out the way they did. The shortest y-direction configuration used throughout all the V-formation experiments was 584 mm by 508 mm, which also gave strange results. As for all other tests on the V-formation, the y-direction spacing was between 584 mm and 660 mm. Regardless of how the results came out, this test still demonstrated an important detail about V-formation spacing; both x and y-direction spacing were critical to the performance of the overall system.

The last of the recorded data came from the echelon formation test. The results can be seen in Figure 34a,b. Before seeing how the results for the optimal overlap test came out, the echelon formation test was conducted using the same overlap as the optimal overlap test, and the results actually came out as hypothesized. As previously described in Section 4, the y-direction spacing was 318 mm, which was by far the shortest tested, due to the limited space on the 8020 table. The plot in Figure 35a shows that each subsequent bird in the flight formation had a higher average thrust than the bird in front of it, but this stopped at bird 13, which had the highest average thrust, because bird 14 had a lower average thrust. Intriguingly, the battery drain test results from Figure 35b showed a plot that looked very similar to that of Figure 35a, in a pattern where each subsequent bird ran out of power after the bird before it in the formation, but bird 14 shut off before bird 13. These results were also comparable to those of the analytical studies conducted for fixed-wing models.

6. Flow Visualization of Flapping Wings in Formation Flight

After all experiments were completed and all the data captured, the flow visualization test was conducted. This test was completed to visualize how the vortices between birds looked. A simulated view was completed with Flapsim’s Wakesim feature and can be seen in Figure 36. A view of the physical flow test with the active laser and smoke machine can be seen in Figure 37.

The fluid dynamics of flapping-wing drone flight have received increasing attention in recent years due to the potential for these systems to be used for various applications, such as search and rescue, environmental monitoring, and aerial mapping. Understanding the flow structures and vortices generated by flapping-wing drones is crucial for improving their performance and stability. One method for studying flow structures is smoke–laser visualization, which involves injecting smoke into the flow and using laser light to illuminate the flow patterns. In combination with high-speed cameras, this technique provides a unique and detailed insight into the flow structures generated by flapping-wing drones. This study examined flow dynamics in the formation flight of multiple flapping-wing drones, using a smoke–laser visualization setup. The experiment setup with the high-speed camera can be seen in Figure 37.

Figure 38 shows the results of flow visualization for a single wing flap during the down phase, generating lift. At time step 1, a vortex is observed to deform at the leading edge of the wing, within the dotted yellow circle in the images. The interaction between the wing and the fluid creates a pressure differential, which can result in the formation of a shed vortex. As time progresses, the diameter of the vortex increases, and it moves towards the trailing edge of the wing. These results suggest that the vortex plays a role in generating lift for the wing and that changes in the diameter and location of the vortex can affect the lift performance.

It is well known that vortices can have a significant impact on lift generation in flapping-wing systems. The results are supported by the general understanding of fluid flow dynamics in flapping-wing systems, but it is important to note that Figure 38 represents a 2D fluid dynamic analysis. In a full 3D analysis, the fluid dynamic landscape would be expected to be much more complex with the presence of additional flow structures that can also contribute to lift generation.

The main objective of this research was to study flight performance in formation flight and its underlying mechanisms. To accomplish this goal, it was imperative to examine the fluid dynamic interactions between the individual wings in a formation. This is due to the complex and dynamic nature of fluid flow between multiple wings, which has a significant impact on the overall flight performance. To gain a deeper understanding of these interactions, a flow visualization experiment was conducted to capture the fluid flow between two flapping wings. Figure 39 presents the results of the flow visualization experiment conducted to gain a deeper understanding of the fluid dynamic interactions between two flapping wings. The images have been postprocessed to enable easier flow observation. As shown in the figure, the two wings, wing 1 and wing 2, are depicted with wing 1 in the down phase and wing 2 in the up phase. Wing 2’s flapping motion creates a build-up of air on its top surface, pushed towards wing 1, indicated by the red dotted circle in Figure 39. This bulk of air undergoes a counter-clockwise rotation over the course of the wings’ movements and ultimately moves towards wing 1. A tip vortex is expected to form as wing 1 enters its down phase, but the rotating air reduces it, leading to increased aerodynamic efficiency. The rotating air reduces the tip vortex, resulting in increased aerodynamic efficiency for wing 1.

These results provide valuable insights into the fluid dynamic interactions between flapping wings in formation flight. The results suggest that the interactions between the wings can significantly impact the overall aerodynamics of the formation, leading to improved performance and efficiency. Further research is needed to fully understand the implications of these interactions on formation flight performance and how to optimize these interactions for improved performance.

7. Conclusions

It is interesting to see how similar the results for the analytical fixed-wing study and the flapping-wing experiment turned out to be. Although the results for each model output different units, they could still be compared because of how the units related. In the fixed-wing model, the output measured was induced drag, and it was seen that the birds in the middle of the V-formation experienced the least amount of drag while the leading and trailing birds experienced the most. For the flapping-wing results, average thrust output was measured instead of drag, and the results showed that the middle birds output the most thrust while the leading and trailing birds output the least. From these results, there was already a pattern that the middle birds seemed to be outperforming the leading and trailing birds. The two different models were more closely compared by looking at their measured outputs. Drag is the opposite of thrust, so there is less thrust with more drag. In this context, it can be seen that in the fixed-winged bird model, the middle birds experiencing less induced drag also output more thrust. Furthermore, if the plots for the fixed-wing model were to show thrust output rather than induced drag, they would appear to have the same general plot trend as that of the experimental setup. Unfortunately, though, this was not the case with the computational study. The computations using Ptera software showed the opposite effect to that seen in the fixed-wing and flapping-wing models. Using this software for V-formations was new territory for its capabilities as it was originally intended for single ornithopter design. However, the use of Ptera was not a total loss because the software showed two things. First, it showed that it could create a V-formation model; second, it revealed that even under the conditions used for the model, there was still an effect between each row of birds, whether it was beneficial or not. The computational model will require some more tweaking before it can output better results, and it has the potential to test more configurations and even for sensitivity studies on V-formation flight. Another improvement this project needs is a custom-built flapping mechanism setup. The mechanisms worked fine on their own, but once the additional weight of the wings was added, the system lost its functionality. If is more than likely that the wing size would be reduced, as this also limited the amount of space available on the 8020 apparatus. Lastly, the utilization of the flapping-wing drones for the battery drain test was instrumental in showing that, without a doubt, there are benefits to birds flying in V-formation or echelon formation. The results of the battery drain tests apply to many studies and applications involving drones. The biggest issue encountered with any drone is its limited power supply, so it would be interesting to see how a V-formation or echelon formation could be used in a real-world application to increase battery usage time.

Along with the issues mentioned above, there are plans to improve and further this work. The first piece of future work will be a more in-depth computational study with updated parameters to match what was completed in the experimental portion of this project. Running things computationally is more flexible and may allow for a closer look at the sensitivity of wingtip overlap spacing. Although a sensitivity study with the experimental setup is also planned, fine adjustment of the wingtip overlap is much easier to conduct computationally. There are several improvements needed for the experimental setup. The first is redesigning the flapping mechanisms so they function properly. The flapping mechanisms will be used in future to complete sensitivity studies regarding flapping frequency and the effect of spacing in the y-direction; however, this will require the 8020 apparatus to be extended. Additionally, with the modular design of the flapping mechanisms, further research will be conducted using several different wing shapes to determine how wing shape affects flight formation effectiveness. Lastly, birds in nature use both fixed and flapping-wing motion while in V-formation. To more accurately emulate birds in V-formation, a study on how to implement both models into one experiment or computation may be completed.