Equivalent Spatial Plane-Based Relative Pose Estimation of UAVs
Abstract
1. Introduction
2. Relative Pose Estimation Method of UAVs
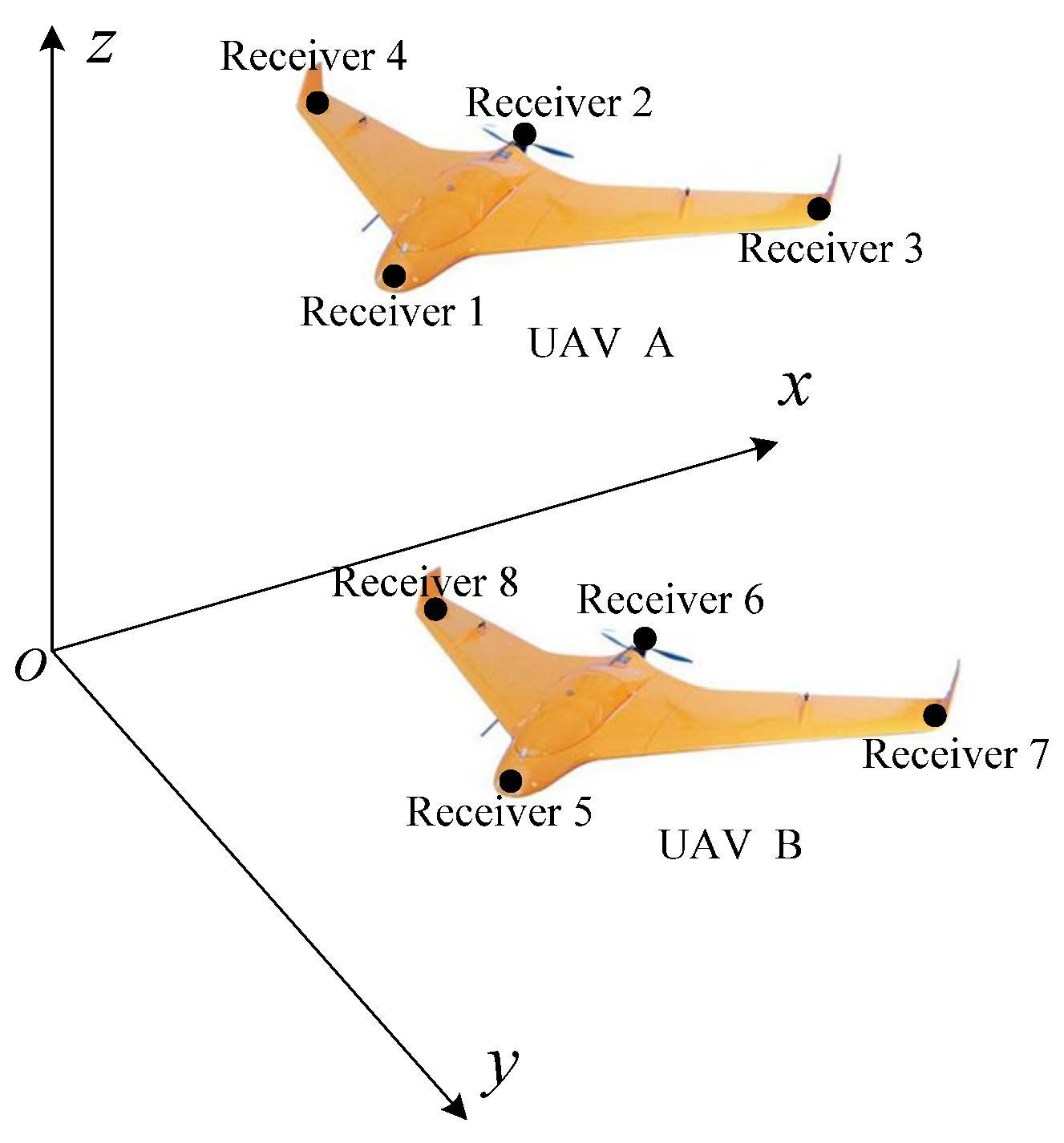
2.1. Problem Description
2.2. Determination of Spatial Equivalent Polygon Plane Equation
2.2.1. Three Points to Determine the Spatial Triangle Plane
2.2.2. Four Points to Determine the Spatial Quadrilateral Plane
2.3. Relative Pose Estimation of UAVs
2.4. Influence of Measurement Error on Estimation Results
3. Numerical Simulation and Results Analysis
3.1. Simulation Environment and Parameters
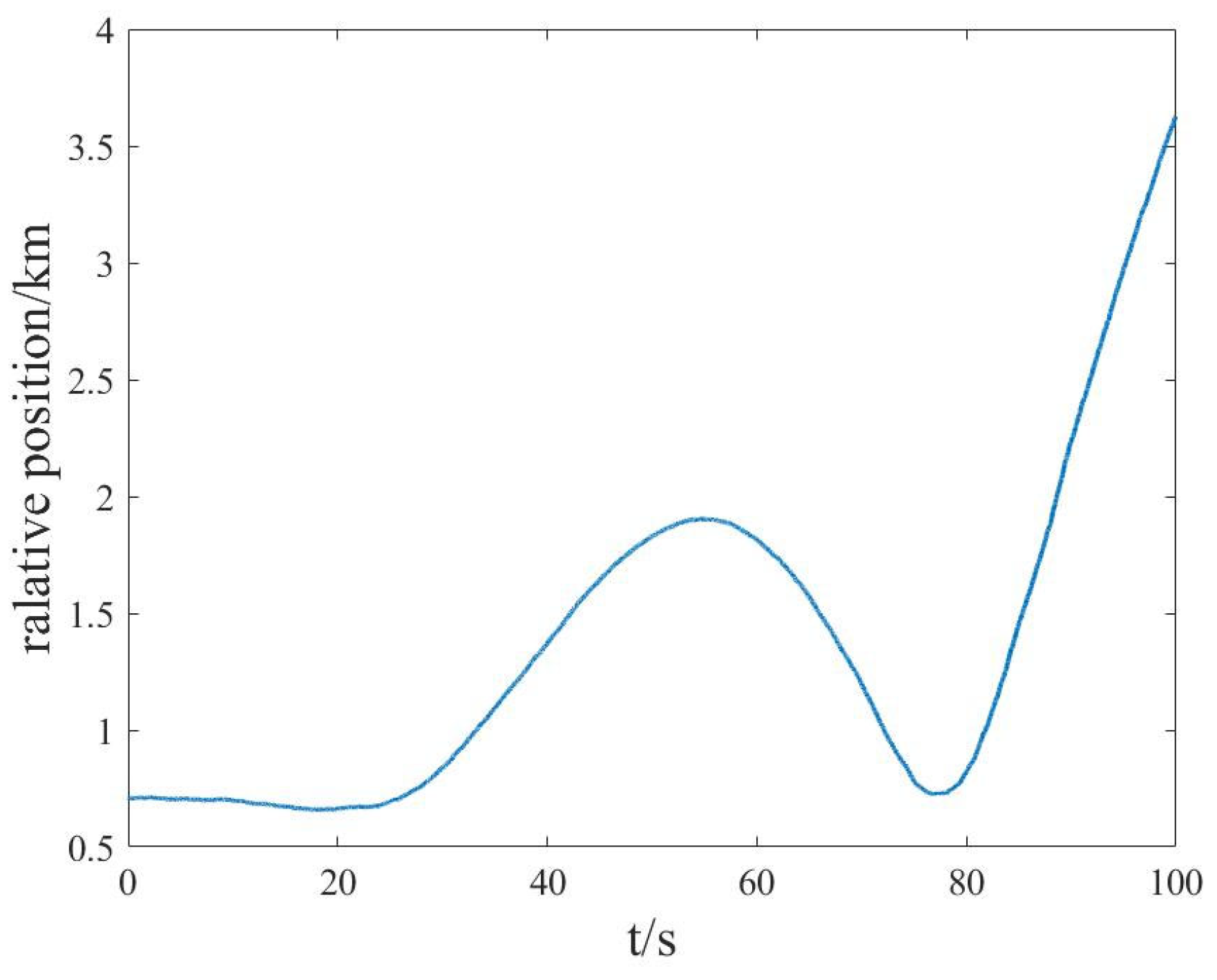
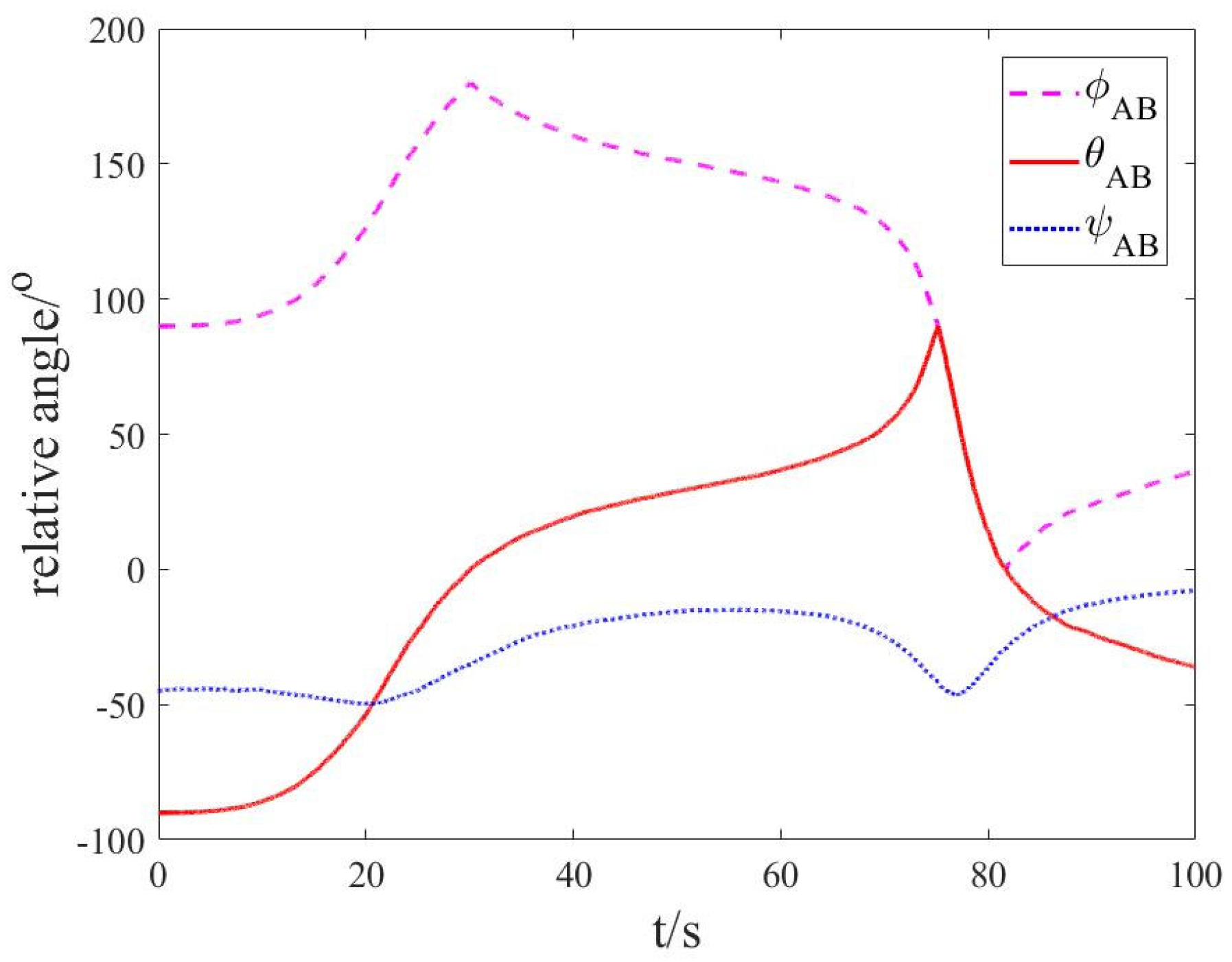
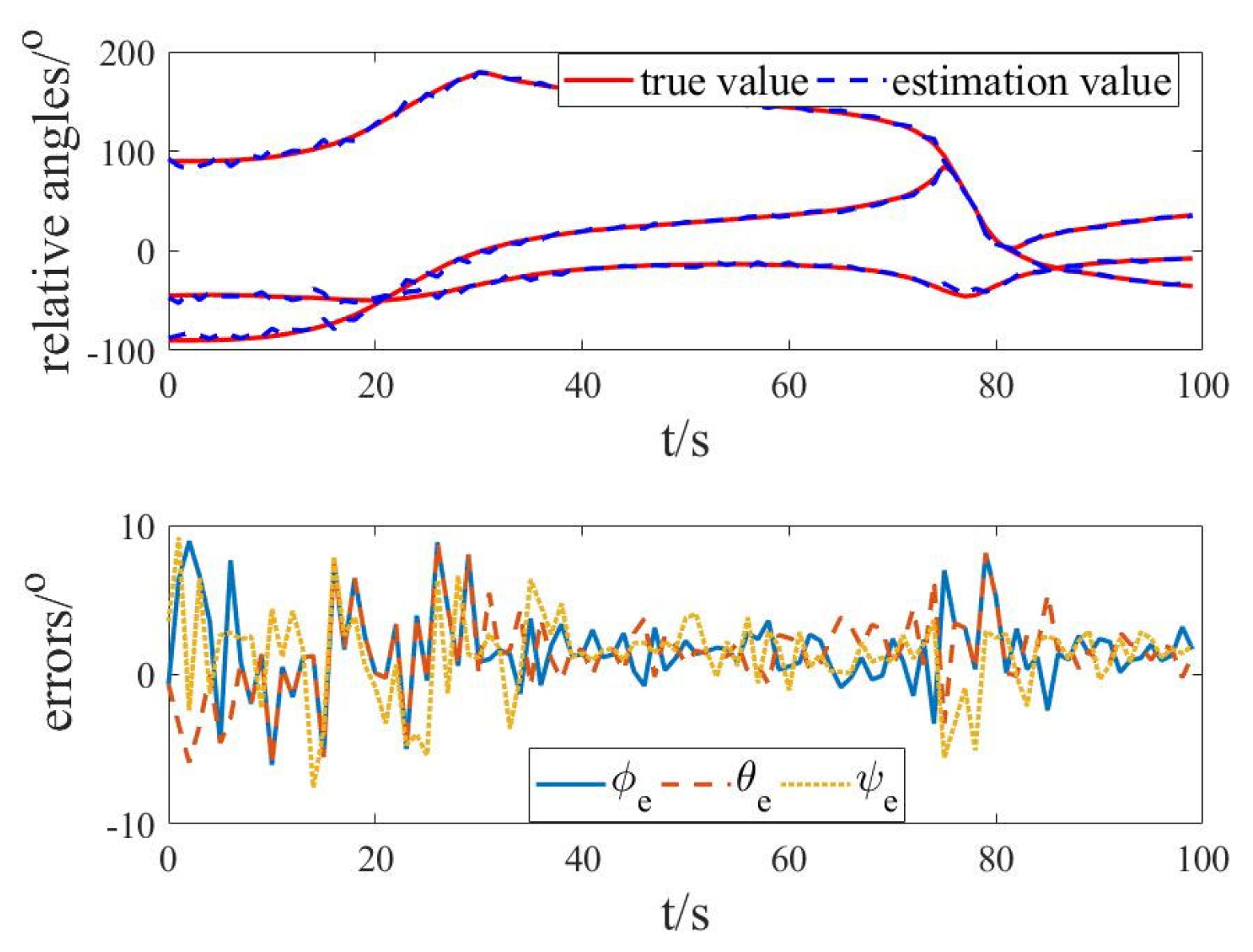
3.2. Simulation Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, X.B.; Duan, H.B.; Guo, Y.J.; Deng, Y.M. A cascade adaboost and CNN algorithm for drogue detection in UAV autonomous aerial refueling. Neurocomputing 2020, 408, 121–134. [Google Scholar] [CrossRef]
- Chao, Z.; Zhou, S.L.; Ming, L.; Zhang, W.G.; Scalia, M. UAV Formation Flight Based on Nonlinear Model Predictive Control. Math. Probl. Eng. 2012, 2012, 181–188. [Google Scholar] [CrossRef]
- de Marina, H.G.; Espinosa, F.; Santos, C. Adaptive UAV Attitude Estimation Employing Unscented Kalman Filter, FOAM and Low-Cost MEMS Sensors. Sensors 2012, 12, 9566–9585. [Google Scholar] [CrossRef] [PubMed]
- Li, J. Relative pose measurement of binocular vision based on feature circle. Optik 2019, 194, 163121. [Google Scholar] [CrossRef]
- Williamson, W.R.; Glenn, G.J.; Dang, V.T.; Speyer, J.L.; Stecko, S.M.; Takacs, J.M. Sensor fusion applied to autonomous aerial refueling. J. Guid. Control Dyn. 2009, 32, 262–275. [Google Scholar] [CrossRef]
- Gross, J.; Gu, Y.; Rhudy, M.; Chahl, J. Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements. Aerospatial 2016, 3, 14. [Google Scholar] [CrossRef]
- Korbly, R. Sensing Relative Attitudes for Automatic Docking. J. Guid. Control Dyn. 1983, 6, 213–215. [Google Scholar] [CrossRef]
- Koksal, N.; Jalalmaab, M.; Fidan, B. Adaptive Linear Quadratic Attitude Tracking Control of a Quadrotor UAV Based on IMU Sensor Data Fusion. Sensors 2018, 19, 46. [Google Scholar] [CrossRef] [PubMed]
- Li, B.R.; Mu, C.D.; Wu, B.T. Vision based close-range relative pose estimation for autonomous aerial refueling. J. Tsinghua Univ. (Sci. Technol.) 2012, 52, 1664–1669. [Google Scholar] [CrossRef]
- Campa, G.; Napolitano, M.; Fravolini, M. Simulation environment for machine vision based aerial refueling for UAVs. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 138–151. [Google Scholar] [CrossRef]
- Mammarella, M.; Campa, G.; Napolitano, M.R.; Fravolini, M.L. Comparison of point matching algorithms for the UAV aerial refueling problem. Mach. Vis. Appl. 2010, 21, 241–251. [Google Scholar] [CrossRef]
- Fravolini, M.L.; Campa, G.; Napolitano, M.R. Evaluation of machine vision algorithms for autonomous aerial refueling for unmanned aerial vehicles. J. Aerosp. Comput. Inf. Commun. 2007, 4, 968–985. [Google Scholar] [CrossRef]
- Ding, M.; Wei, L.; Wang, B. Vision-based estimation of relative pose in autonomous aerial refueling. Chin. J. Aeronaut. 2011, 6, 807–815. [Google Scholar] [CrossRef]
- Doebbler, J.; Spaeth, T.; Valasek, J.; Monda, M.J.; Schaub, H. Boom and receptacle autonomous air refueling using visual snake optical sensor. J. Guid. Control Dyn. 2009, 30, 175–1769. [Google Scholar] [CrossRef]
- Zhang, L.M.; Zhu, F.; Hao, Y.M.; Pan, W. Optimization-based non-cooperative spatialcraft pose estimation using stereo cameras during proximity operations. Appl. Opt. 2017, 56, 4522–4531. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.M.; Zhu, F.; Hao, Y.M.; Pan, W. Rectangular-structure-based pose estimation method for non-cooperative rendezvous. Appl. Opt. 2018, 57, 6164–6173. [Google Scholar] [CrossRef] [PubMed]
- Hinterstoisser, S.; Lepetit, V.; Ilic, S.; Holzer, S.; Konolige, K.; Bradski, G.; Navab, N. Technical Demonstration on Model Based Training, Detection and Pose Estimation of Texture-Less 3D Objects in Heavily Cluttered Scenes. In Proceedings of the 12th European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012; Volume 7585, pp. 593–596. [Google Scholar] [CrossRef]
- Weaver, A.D.; Veth, M.J. Image-based relative navigation for the autonomous refueling problem using predictive rendering. In Proceedings of the 2009 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; IEEE Computer Society: Piscataway, NJ, USA, 2009; pp. 1–13. [Google Scholar] [CrossRef]
- Li, G. Three-Dimensional Attitude Measurement of Complex Rigid Flying Target Based on Perspective Projection Matching. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2015. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201601&filename=1015980350.nh (accessed on 1 July 2015).
- Liebelt, J.; Schmid, C.; Schertler, K. Viewpoint-independent object class detection using 3D feature maps. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 978–986. [Google Scholar] [CrossRef]
- Teng, X.C.; Yu, Q.F.; Luo, J.; Zhang, X.H.; Wang, G. Pose Estimation for Straight Wing Aircraft Based on Consistent Line Clustering and Planes Intersection. Sensors 2019, 19, 342. [Google Scholar] [CrossRef] [PubMed]
- Williamson, W.R.; Abdel-Hafez, M.F.; Rhee, I.; Song, E.J.; Wolfe, J.D.; Chichka, D.F.; Speyer, J.L. An instrumentation system applied to formation flight. IEEE Trans. Control Syst. Technol. 2007, 15, 75–85. [Google Scholar] [CrossRef]
- Yuan, H.; Xiao, C.; Xiu, S.; Wen, Y.; Zhou, C.; Li, Q. A New Combined Vision Technique for Micro Aerial Vehicle Pose Estimation. Robotics 2017, 6, 6. [Google Scholar] [CrossRef]
- Strohmeier, M.; Montenegro, S. Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS. Electronics 2017, 6, 15. [Google Scholar] [CrossRef]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-Time Single-Frequency GPS/MEMS-IMU Attitude Determination of Lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [PubMed]
- Fosbury, A.M.; Crassidis, J.L. Relative navigation of air vehicles. J. Guid. Control Dyn. 2008, 31, 824–834. [Google Scholar] [CrossRef]
- Shao, W.; Chang, X.H.; Cui, P.Y.; Cui, H.T. Coupled feature matching and INS for small body landing navigation. J. Astronaut. 2010, 31, 1748–1755. [Google Scholar] [CrossRef]
- Wang, L.; Dong, X.M.; Zhang, Z.L. Relative pose measurement based on tightly-coupled INS/Vision. J. Chin. Inert. Technol. 2011, 19, 686–691. [Google Scholar] [CrossRef]

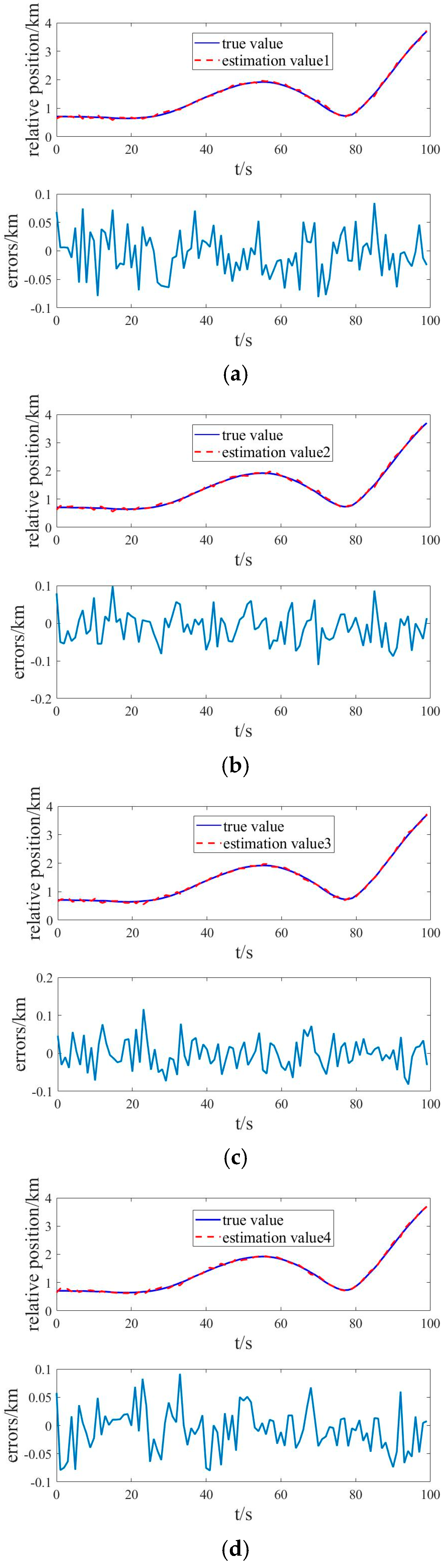




| Relative Estimation Accuracy | RMSE | |||
|---|---|---|---|---|
| Relative Position/km | φ/° | θ/° | ψ/° | |
| Estimation value 1 and true value | 0.028 | 22.5 | 2.2 | 18.9 |
| Estimation value 2 and true value | 0.031 | 25.3 | 1.9 | 20.2 |
| Estimation value 3 and true value | 0.025 | 20.8 | 1.7 | 22.3 |
| Estimation value 4 and true value | 0.009 | 3.2 | 2.8 | 3.1 |
| Estimation value 5 and true value | 0.019 | 15.7 | 1.3 | 24.7 |
| Relative Estimation Accuracy | RMSE | |||
|---|---|---|---|---|
| Relative Position/km | φ/° | θ/° | ψ/° | |
| Estimation value 1 and true value | 0.032 | 31.6 | 1.5 | 21.1 |
| Estimation value 2 and true value | 0.038 | 33.1 | 1.7 | 22.8 |
| Estimation value 3 and true value | 0.010 | 2.5 | 0.9 | 1.1 |
| Estimation value 4 and true value | 0.041 | 30.9 | 2.1 | 19.7 |
| Estimation value 5 and true value | 0.022 | 32.2 | 2.0 | 18.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Gong, S.; Chen, C.; Li, J. Equivalent Spatial Plane-Based Relative Pose Estimation of UAVs. Drones 2024, 8, 383. https://doi.org/10.3390/drones8080383
Wang H, Gong S, Chen C, Li J. Equivalent Spatial Plane-Based Relative Pose Estimation of UAVs. Drones. 2024; 8(8):383. https://doi.org/10.3390/drones8080383
Chicago/Turabian StyleWang, Hangyu, Shuangyi Gong, Chaobo Chen, and Jichao Li. 2024. "Equivalent Spatial Plane-Based Relative Pose Estimation of UAVs" Drones 8, no. 8: 383. https://doi.org/10.3390/drones8080383
APA StyleWang, H., Gong, S., Chen, C., & Li, J. (2024). Equivalent Spatial Plane-Based Relative Pose Estimation of UAVs. Drones, 8(8), 383. https://doi.org/10.3390/drones8080383






