Multi-Unmanned Aerial Vehicle Confrontation in Intelligent Air Combat: A Multi-Agent Deep Reinforcement Learning Approach ^†

Abstract

Multiple unmanned aerial vehicle (multi-UAV) confrontation is becoming an increasingly important combat mode in intelligent air combat. The confrontation highly relies on the intelligent collaboration and real-time decision-making of the UAVs. Thus, a decomposed and prioritized experience replay (PER)-based multi-agent deep deterministic policy gradient (DP-MADDPG) algorithm has been proposed in this paper for the moving and attacking decisions of UAVs. Specifically, the confrontation is formulated as a partially observable Markov game. To solve the problem, the DP-MADDPG algorithm is proposed by integrating the decomposed and PER mechanisms into the traditional MADDPG. To overcome the technical challenges of the convergence to a local optimum and a single dominant policy, the decomposed mechanism is applied to modify the MADDPG framework with local and global dual critic networks. Furthermore, to improve the convergence rate of the MADDPG training process, the PER mechanism is utilized to optimize the sampling efficiency from the experience replay buffer. Simulations have been conducted based on the Multi-agent Combat Arena (MaCA) platform, wherein the traditional MADDPG and independent learning DDPG (ILDDPG) algorithms are benchmarks. Simulation results indicate that the proposed DP-MADDPG improves the convergence rate and the convergent reward value. During confrontations against the vanilla distance-prioritized rule-empowered and intelligent ILDDPG-empowered blue parties, the DP-MADDPG-empowered red party can improve the win rate to 96% and 80.5%, respectively.

1. Introduction

In the era of intelligent air combat, multiple unmanned aerial vehicle (multi-UAV) confrontation is becoming an increasingly important combat mode in the military battlefield, which takes advantage of the efficient collaboration of UAVs to complete the confrontation mission [1,2]. In the confrontation scenario, the multiple UAVs with the capabilities of communications, sensing, and computing can collaborate with each other and complete the mission through real-time situation awareness, optimal resource allocation, and intelligent decision-making [3,4]. Therefore, to complete the multi-UAV confrontation mission, the development of intelligent decision-making algorithms is a necessity.

For the intelligent decision-making of UAVs on the battlefield, an expert system-based air combat decision-making algorithm is proposed [5], which builds a tactical rule database based on the situation of battlefields and designs maneuver decisions according to expert knowledge. However, the tactical rule database relies on expert knowledge, which leads to the low adaptability and high complexity. Falomir et al. have proposed an artificial potential field-based moving model for the UAV swarm, which enables the collaboration of multiple UAVs, while the artificial potential field may lead to the local optimum [6].

Research efforts have also been spared on the game theory-based solutions. Ha et al. have proposed a matrix game method to facilitate the UAVs with the attacking decision-making in air combat [7]. It establishes a score matrix based on the target distance, flight speed, and direction of UAVs and evaluates the decisions of each UAV in real time. However, the matrix game method can hardly be applied to the sequential decision problem. In [8], the authors proposed an auction-based attack–defense decision-making algorithm for target–attack–defense tripartite UAV swarms, wherein the swarm confrontation is modeled as the differential game. As investigated by the authors, the scalability of the tripartite UAV swarms with different scales and the distributed decision-making based on the multi-source perception could be further improved.

In terms of swarm intelligence optimization, the gray wolf optimizer (GWO) [9] has been applied to the attack–defense scenario for optimizing the success rate of a single blue-party UAV breaking through the interception of the red-party cooperative UAV swarms [10]. In [11], the pigeon intelligence optimization (PIO) [12] was improved to resolve the issue of autonomous maneuver decisions in air-to-air confrontation. However, the candidate maneuvers of UAVs are limited by the maneuver library, which cannot meet the requirements of the continuous and flexible actions of UAVs.

With the advantages of self-learning and scalability, deep reinforcement learning (DRL) algorithms have been developed for intelligent decision-making. In [13], the deep deterministic policy gradient (DDPG) [14] was improved to aid the UAV with the decision-making of the head-on attack, pursuing, fleeing, and energy-storing. However, this work focuses on the single-agent DDPG-enabled decision-making of a single UAV. Considering multiple UAVs in intelligent air combat, multi-agent DRL (MADRL) algorithms were investigated [15]. Xuan et al. [16] use the multi-agent deep deterministic policy gradient (MADDPG) algorithm [17] to enable the decision-making of UAVs, which improves the win rate of the multi-UAV confrontation. Li et al. [18] proposed a MADDPG-based confrontation algorithm, wherein a gate recurrent unit is introduced to the actor network to facilitate the decision-making of UAVs with historical decision information. Jiang et al. [19] introduce a self-attention mechanism into the MAPPDG algorithm to make it adaptable to the dynamic changes of friendly forces and enemies during the policy learning process. However, the MADRL-based confrontation algorithms still need to be improved from the perspectives of convergence and stability [20].

To resolve the issues, a decomposed and prioritized experience replay (PER)-based MADDPG (DP-MADDPG) algorithm is proposed in our work for the intelligent decision-making of UAVs in the multi-UAV confrontation scenario. Specifically, the multi-UAV confrontation system model is set up first, wherein the multi-UAV confrontation mission, UAV attack, and communications models are depicted. Subsequently, the problem of intelligent decision-making in the multi-UAV confrontation is formulated as a partially observable Markov game, wherein the real-time decisions that UAVs need to make are modeled as the actions, including the real-time acceleration, angular velocity, attacking mode, and target enemy. To resolve the problem, the DP-MADDPG algorithm is proposed, which integrates the decomposed and PER mechanisms into the traditional MADDPG. Based on the improvement of our earlier work [21], the contributions of this paper are highlighted as follows:

• The decomposed mechanism is developed to resolve the issue of data coupling among multiple UAVs, where the fundamental structure of the traditional MADDPG is modified by integrating both the local and global critic networks. With dual critic networks, UAVs can maximize both local and global rewards to resolve the local optimum and avoid a dominant decision-making policy incurred by the case of a single global critic network.
• The PER mechanism is applied to the traditional MADDPG to improve the sampling efficiency from the experience replay buffer. By using the PER, the uniform distribution of the experience samples in the experience replay buffer is crashed, and a larger sampling weight is assigned to the sample with a higher learning efficiency, so that the convergence rate can be consequently improved.
• Simulations were conducted based on the Multi-agent Combat Arena (MaCA) platform. The results indicate that the proposed DP-MADDPG improves the convergence rate and the convergent reward value compared to the traditional MADDPG and independent learning DDPG (ILDDPG). Furthermore, in the multi-UAV confrontation, as against the vanilla distance-prioritized rule-empowered and the intelligent ILDDPG-empowered blue party, the win rate of the DP-MADDPG-empowered red party was improved to 96% and 80.5%, respectively.

The rest of this paper is organized as follows. The multi-UAV confrontation system model is introduced in Section 2. The multi-UAV confrontation mission is formulated as the partially observable Markov game in Section 3. In Section 4, the DP-MADDPG algorithm for multi-UAV confrontation is proposed. The performance evaluation is conducted in Section 5. Finally, this work is summarized in Section 6.

2. Multi-UAV Confrontation System Model

The fundamental models of the multi-UAV confrontation are introduced in this section, including the multi-UAV confrontation mission, motion, and attack models.

2.1. Multi-UAV Confrontation Mission Model

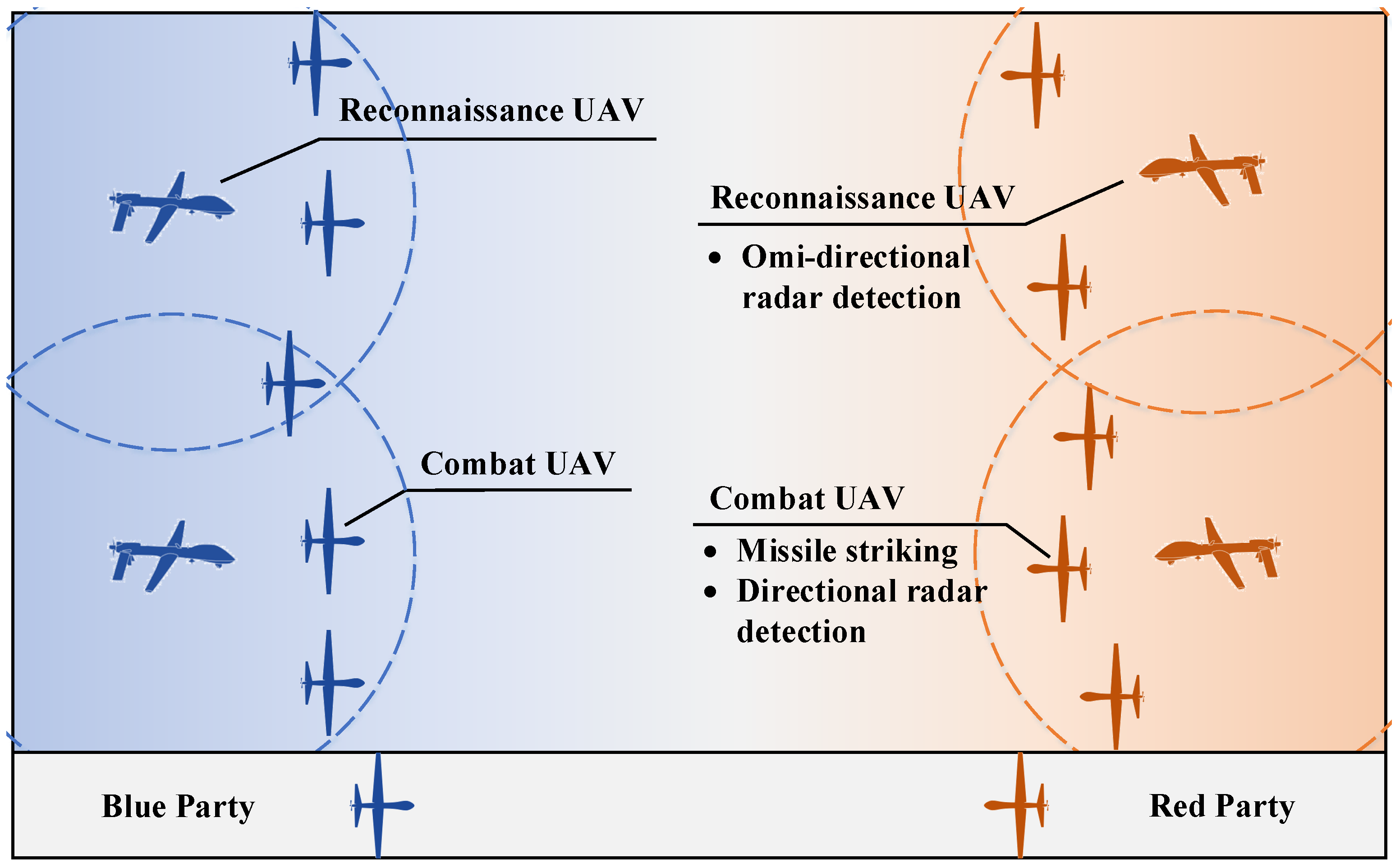
The multi-UAV confrontation is the mutual attack of UAV swarms on the battlefield, where the UAVs are intelligent agents with the capability of decision-making. It assumes that there are two parties in the scenario, namely red and blue parties, as depicted in Figure 1. Specifically, each party consists of reconnaissance UAVs and combat UAVs.

• Reconnaissance UAVs are responsible for wide-area omnidirectional detection with radars working in L and S bands and support multi-frequency switching.
• Combat UAVs have the capabilities of reconnaissance, interference, and striking. Combat UAVs are equipped with directional detection radars working in the X band and L, S, and X bands interference devices for blocking and aiming at electronic interference. They also carry a number of missiles for target striking. When a UAV runs out of missiles in the confrontation mission, it can adopt a suicide collision strategy against an enemy UAV within its attack range. Furthermore, combat UAVs have the capability of passive detection and can be applied to collaborative localization and radio source recognition.

Moreover, the UAVs are equipped with measurement devices such as the global positioning system (GPS) and inertial measurement unit (IMU) to obtain their real-time position and speed. For each UAV, the situational information of ally and enemy UAVs, including relative position, relative heading, and relative speed, is detected by the carried passive radars.

For the confrontation rule, in an allotted time, there may be multiple rounds of confrontations. If one party’s UAVs are all eliminated during the process or if it has fewer surviving UAVs in the end, then the other party is declared the winner. If both parties have the same number of surviving UAVs, the one with a larger number of remaining missiles wins.

2.2. UAV Motion Model

In this work, the multi-UAV confrontation is assumed to occur in a horizontal plane, namely, the UAVs flying at identical altitudes. Thus, the six-degree-of-freedom (6-DOF) UAV model is simplified to a 2D-plane model [20].

Based on the models in [20,22], the motion of UAV i is modeled by

$$\left\{\begin{array}{c}{x}_i(t+1)=x_i\left(t\right)+v_i\left(t\right)·cos\left({\phi }_i\left(t\right)\right)·\Delta t,\hfill \\ y_i(t+1)=y_i\left(t\right)+v_i\left(t\right)·sin\left({\phi }_i\left(t\right)\right)·\Delta t,\hfill \\ v_i(t+1)=v_i\left(t\right)+a_i\left(t\right)·\Delta t,\hfill \\ {\phi }_i(t+1)={\phi }_i\left(t\right)+{\omega }_i\left(t\right)·\Delta t,\hfill \end{array}\right.$$

(1)

where $(x_i\left(t\right),y_i\left(t\right))$ refers to the 2D coordinates in the horizontal plane at time t. ${\phi }_i\left(t\right)$ is the heading angle. $\Delta t$ is the time interval. $v_i\left(t\right)$ and ${\omega }_i\left(t\right)$ are the flying speed and angular velocity, separately. $a_i\left(t\right)$ is the acceleration.

The motion is constrained by

$$\left\{\begin{array}{c}0\le v_i\le v_{i_{max}},\hfill \\ 0\le {\varphi }_i\le 2\pi ,\hfill \\ -a_{i_{max}}\le a_i\le a_{i_{max}},\hfill \\ -{\omega }_{i_{max}}\le {\omega }_i\le {\omega }_{i_{max}},\hfill \end{array}\right.$$

(2)

where $v_{i_{max}}$, $a_{i_{max}}$, and ${\omega }_{i_{max}}$ are the upper limits of the speed, acceleration, and angular velocity.

2.3. UAV Attack Model

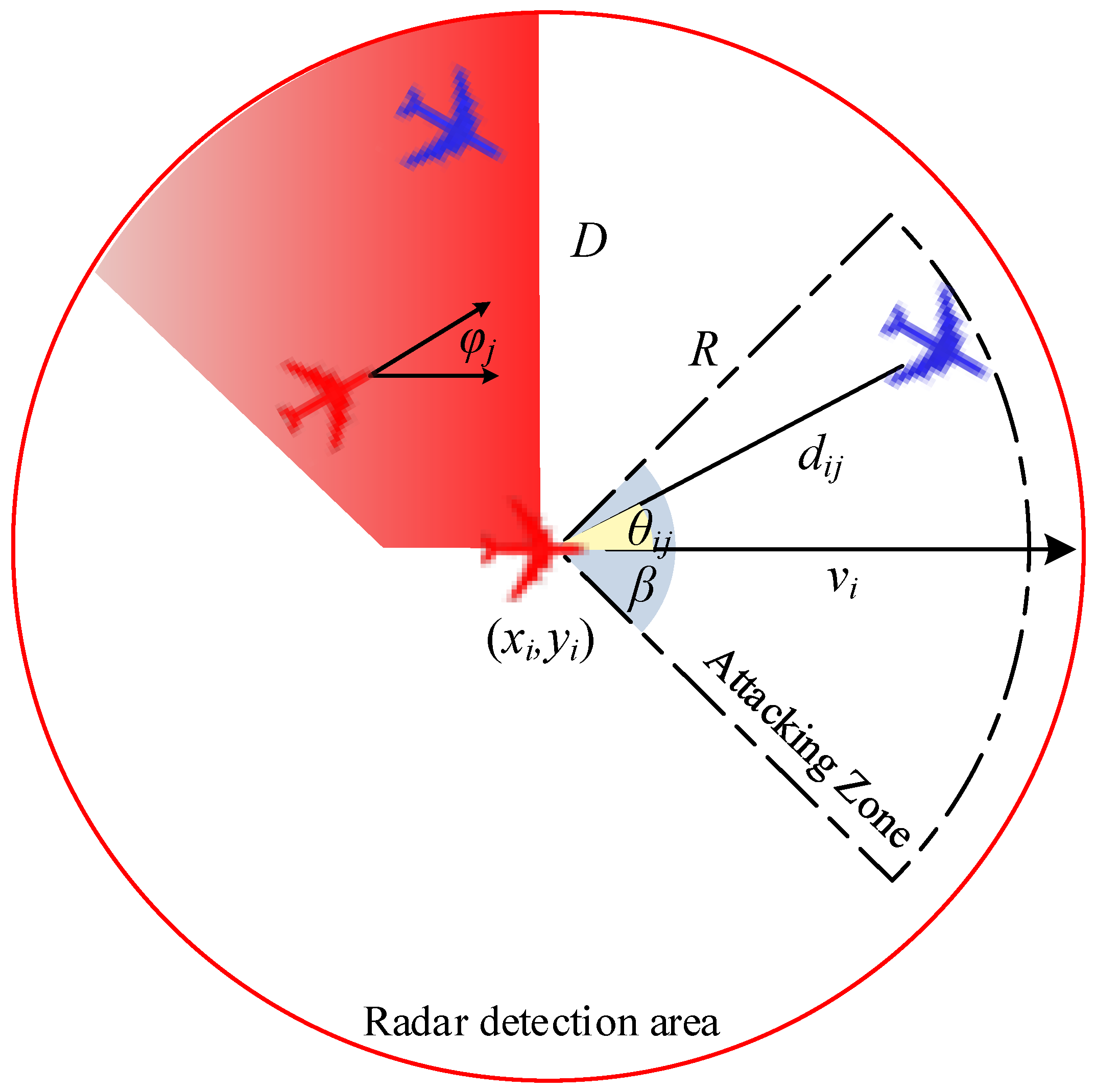
The UAV attack model is described by an attack–target pair, as shown in Figure 2. It is assumed that an attacker UAV has the capability of omnidirectional radar detection, and the detection radius is D. The attacking zone is a sector with the radius R and angle $\beta$.

The attack–target pair is denoted by ${\left[{\delta }_{ij}\left(t\right),d_{ij}\left(t\right),{\theta }_{ij}\left(t\right)\right]}^T$. Specifically, ${\delta }_{ij}$ is the relative distance vector between attacker UAV i and target UAV j at time t [22],

$${\delta }_{ij}\left(t\right)=({\delta }_{ij}^x\left(t\right),{\delta }_{ij}^y\left(t\right))=(x_j\left(t\right)-x_i\left(t\right),y_j\left(t\right)-y_i\left(t\right)).$$

(3)

$d_{ij}$ is the Euclidean distance,

$$d_{ij}\left(t\right)=\sqrt{{(x_j\left(t\right)-x_i\left(t\right))}^2+{(y_j\left(t\right)-y_i\left(t\right))}^2}.$$

(4)

${\theta }_{ij}$ is the attack angle,

$${\theta }_{ij}\left(t\right)=arctan{\displaystyle \frac{{\delta }_{ij}^y\left(t\right)}{{\delta }_{ij}^x\left(t\right)}}.$$

(5)

This supposes the attacker can strike the target when the distance and angle between the attacker UAV i and the target UAV j meet the following conditions [22]:

$$\left\{\begin{array}{c}{d}_{ij}\left(t\right)<R,\hfill \\ {\theta }_{ij}\left(t\right)<{\displaystyle \frac{\beta }{2}}.\hfill \end{array}\right.$$

(6)

3. Partially Observable Markov Game Modeling

Multi-UAV confrontation is modeled as a partially observable Markov game, wherein each UAV is regarded as an intelligent agent. The Markov game of N UAVs is defined as a tuple $(N,S,A_1,\dots ,A_N,O_1,\dots ,O_N,T,R_1,\dots ,R_N,R_g)$. S is the global state. $A_i$ and $O_i$ represent the local action and observation of UAV i, respectively. T is the state transition function, $S\times A_1\times \dots \times A_N\mapsto S$. $R_i$ is the local cumulative reward of UAV i, and $R_g$ is the global cumulative reward.

3.1. Observation Space

The local observation space $O_i$ of UAV i as listed in

Table 1. Observation space of UAV.

Information	Description
	position $(x_i,y_i)$ (unit: (m, m))
	type_id (0: combat UAV, 1: reconnaissance UAV)
	speed $v_i$ (unit: m/s)
Own	ammunition M
	heading ${\phi }_i$ (unit: °)
	attacking zone $(R,\beta )$ (unit: (m, °))
	detection radius D (unit: m)
	ally_1: relative position, relative heading, relative speed, type_id
Ally	ally_2: relative position, relative heading, relative speed, type_id
	……
	enemy_1: relative position, relative heading, relative speed, type_id
Enemy	enemy_2: relative position, relative heading, relative speed, type_id
	……

includes the information of its own, friendly forces ${\left\{all{y}_i\right\}}_{i=1}^m$, and enemy ${\left\{enem{y}_j\right\}}_{j=1}^n$, where m and n are the number of ally and enemy UAVs in its detection range, respectively. A UAV’s own information includes its coordinates, speed, heading angle, type, detection radius, sector attack area, and remaining ammunition, $\{(x_i,y_i),v_i,{\phi }_i,type\_id,D,(R,\beta ),M\}$. $type\_id$ is the type of UAV, where 0 and 1 refer to combat UAV and reconnaissance UAV, respectively. The observation information of ally and enemy UAVs includes relative position, relative speed, relative heading, and type of UAVs. The global state S consists of the local observation information of all UAVs.

3.2. Action Space

For each UAV, its moving and attacking decisions are formulated as the action space as listed in

Table 2. Action space of UAV.

Action	Description
a	acceleration (continuous) (unit: m/s2)
$\omega$	angular velocity (continuous) (unit: rad/s)
$attack\_mode$	attacking (1) or not (0) (discrete)
$attack\_enemy\_id$	target enemy ID (discrete)

, which is a vector of acceleration, angular velocity, attacking mode, and target enemy ID, namely $A_i=\left[a,\omega ,attack\_mode,attack\_enemy\_id\right]$. $attack\_mode$ is a binary variable, where 1 and 0 refer to attacking or not. Although a and $\omega$ are intrinsically continuous actions, in practical applications, they are discretized to simplify the action decision. For example, the angular velocity is in the range of $\left[0,359\right]$, wherein the horizontal rightwards is 0, and the angle is increased clockwise. The change in angle is discretized with an interval of ${10}^{\circ }$. For action $n,n=1,2,\dots$, the angle adds $10n^{\circ }$ clockwise.

3.3. Reward Function

Considering the collaborative requirements and mission objectives of the multi-UAV confrontation, the local reward of each UAV and the global reward are designed according to the confrontation result of each round. The local reward of each UAV is designed as provided in

Table 3. Local reward of UAV.

Type	Event	Reward
	Legal attack action	5
	Illegal attack action	−5
	Detection of combat UAV	5
	Detection of reconnaissance UAV	10
Combat	Successful in combating combat UAV	10
	Unsuccessful in combating combat UAV	−5
	Successful in combating reconnaissance UAV	20
	Unsuccessful in combating reconnaissance UAV	−10
	Be destroyed	−10
	Detection of combat UAV	5
Reconnaissance	Detection of reconnaissance UAV	10
	Be destroyed	−20
General	Survive each round	2

, where UAVs with different roles, namely combat and reconnaissance, are considered individually [23]. The local reward is mainly determined by the impact of the UAV’s actions on the environment and avoids the problem of reward sparseness in the meantime.

The global reward is designed as listed in

Table 4. Global reward.

Event	Reward
Complete victory	200
Victory	100
Complete defeat	−200
Defeat	−100
Draw	0
Round deduction	−50

. When designing the global reward, the comprehensive impact of one round of multi-UAV confrontation inference on the environment is mainly considered to avoid the intelligent agent falling into the local optimum during the exploration process. Particularly, the round deduction in Table 4 refers to a null round where nothing happens.

4. Proposed DP-MADDPG Algorithm for Multi-UAV Confrontation

In this section, the DP-MADDPG algorithm is proposed for the multi-UAV confrontation. First of all, the process of the MADRL-based multi-UAV confrontation is provided. Subsequently, the fundamental MADDPG algorithm is analyzed. Finally, the DP-MADDPG algorithm is proposed, where the decomposed and PER mechanisms are explained in detail.

4.1. MADRL-Based Multi-UAV Confrontation

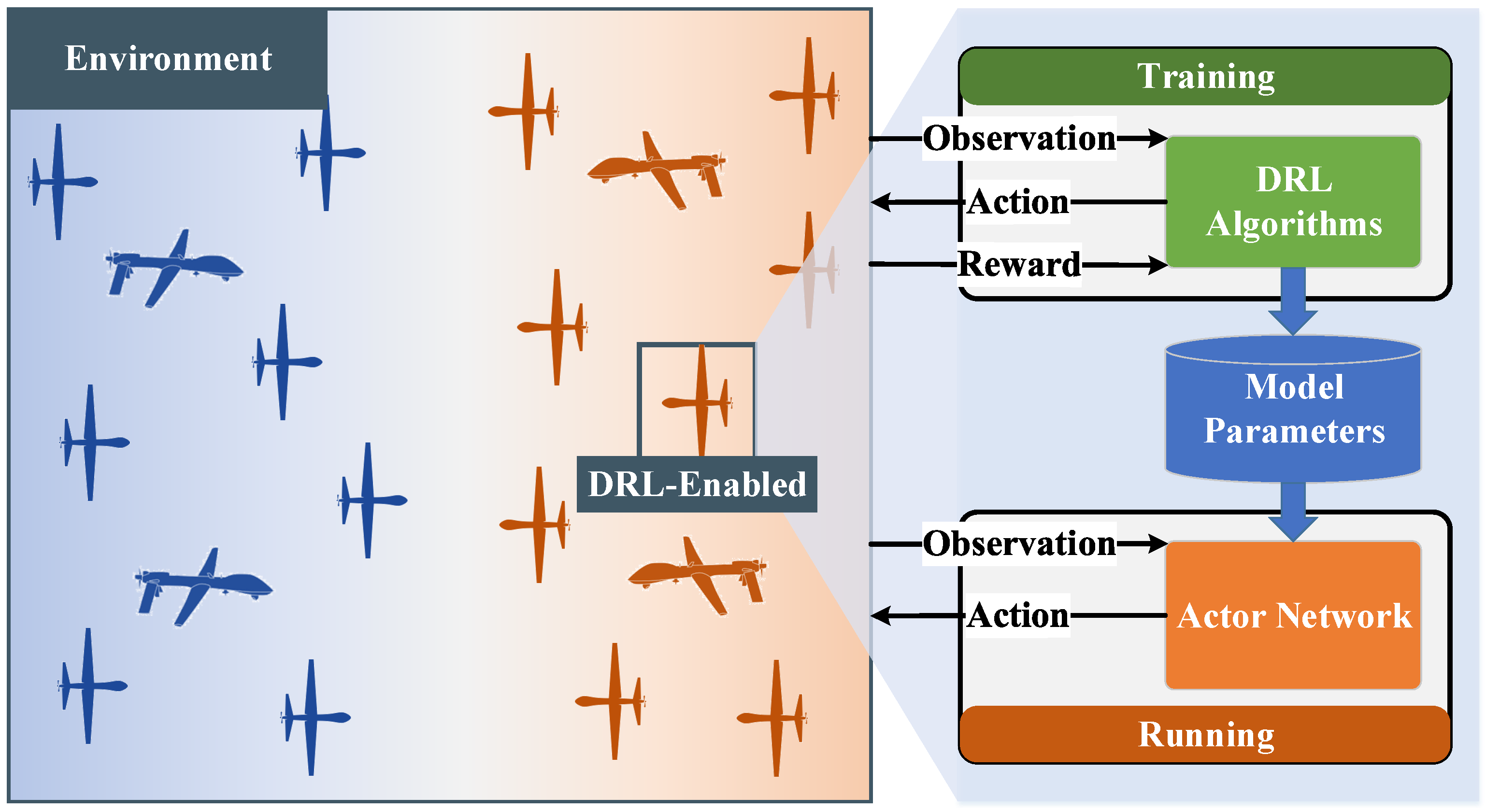
Based on modeling the multi-UAV confrontation as a partially observable Markov game, the distributed intelligent decision-making of multiple UAVs is resolved by a multi-agent DRL (MADRL) algorithm. The process of the MADRL-based multi-UAV confrontation is shown in Figure 3, which consists of two main phases, namely training and running.

4.1.1. Training

The MADRL algorithm is executed to explore the confrontation environment and train the local actor networks as the decision-making policies. At the end of the training phase, each UAV obtains a convergent actor network.

4.1.2. Running

Each UAV i determines its actions ${\mathbf{a}}_i$, including acceleration, angular velocity, attack mode, and attack target enemy ID at each time step according to its practical observations ${\mathbf{o}}_i$ and local actor network ${\mu }_i\left({\mathbf{a}}_i\right|{\mathbf{o}}_i)$.

4.2. Fundamental MADDPG Algorithm

In this work, the policy-gradient MADRL algorithm, MADDPG, is adopted as the benchmark for the following reasons. (1) MADDPG adopts the centralized training and distributed execution framework. In the centralized training, the full state of the environment can be obtained, which can help in dealing with the non-stationarity of the multi-UAV scenario. (2) By the exploitation of MADDPG, each UAV has an individual actor–critic structure, which is more flexible. Namely, each UAV has its actor network as the policy for decision-making based on the local observation and the critic network as the value function evaluating the decisions for policy optimization. (3) MADDPG is based on the deterministic policy, which is more efficient than the stochastic policy and can deal with the continuous action space.

In the confrontation scenario, it is assumed that there are N UAVs with local actor networks $\mu =\{{\mu }_1,\dots ,{\mu }_N\}$ parameterized by $\theta =\{{\theta }_1,\dots ,{\theta }_N\}$. The policy gradient for training the actor network is

$$\nabla J\left({\theta }_i\right)=E_{\mathbf{x},\mathbf{a}\sim D}\left[{\nabla }_{{\theta }_i}{\mu }_i\left({\mathbf{a}}_i\right|{\mathbf{o}}_i){\nabla }_{{\mathbf{a}}_i}{Q}_i^{\mu }(\mathbf{x},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N){|}_{{\mathbf{a}}_i={\mu }_i\left({\mathbf{o}}_i\right)}\right],$$

(7)

where ${\mathbf{o}}_i$ is the local observation of UAV i, and $\mathbf{x}=({\mathbf{o}}_1,...,{\mathbf{o}}_N)$ is the set of local observations. ${\mathbf{a}}_i$ is the local action determined by its actor network, ${\mathbf{a}}_i={\mu }_i\left({\mathbf{o}}_i\right)$. D is the experience replay buffer, $D=(\mathbf{x},\mathbf{a},\mathbf{r},{\mathbf{x}}^{\prime })$, where $\mathbf{r}$ is the set of local rewards, and ${\mathbf{x}}^{\prime }$ is the set of local observations at the next timestep. $Q_i^{\mu }$ is the critic network of UAV i with parameters ${\psi }_i$. Based on the critic network, the loss function is defined by

$$L\left({\psi }_i\right)=E_{\mathbf{x},\mathbf{a},\mathbf{r},{\mathbf{x}}^{\prime }}\left[{(Q_i^{\mu }(\mathbf{x},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N)-y_i)}^2\right],$$

(8)

and

$$y_i=r_i+\gamma Q_i^{{\mu }^{\prime }}({\mathbf{x}}^{\prime },{\mathbf{a}}_1^{\prime },\dots ,{\mathbf{a}}_N^{\prime }){|}_{{\mathbf{a}}_i^{\prime }={\mu }_i^{\prime }\left({\mathbf{o}}_i^{\prime }\right)},$$

(9)

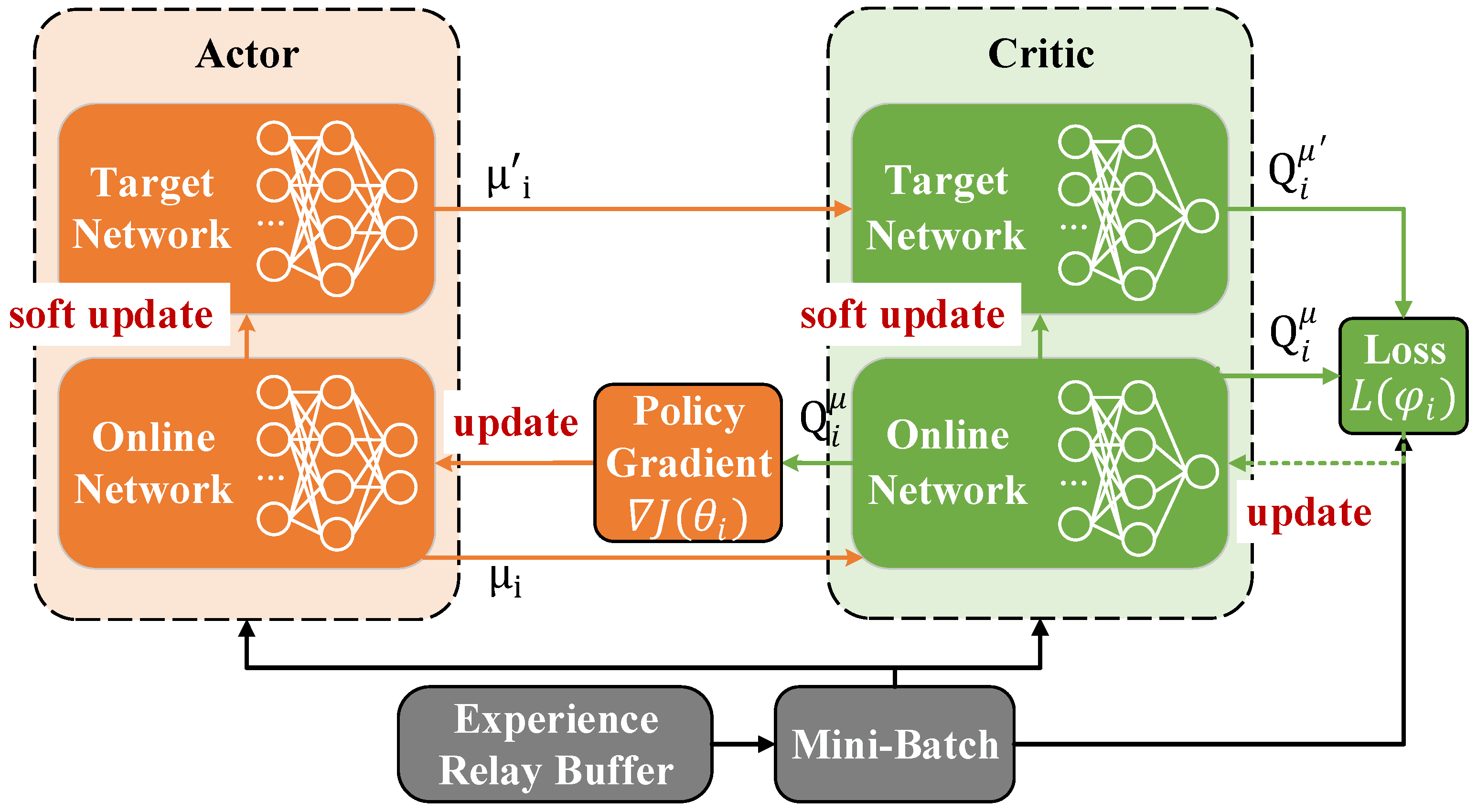
where $r_i$ is the local reward of UAV i. $\gamma$ is the discount factor. $Q_i^{{\mu }^{\prime }}$ is the target critic network with parameters ${\psi }^{\prime }$. ${\mu }_i^{\prime }$ is the target actor network with parameters ${\theta }^{\prime }$. The target networks are introduced by the double-network structure for stability, as shown in Figure 4. The parameters of the target networks are updated through soft update by

$${\theta }_i^{\prime }=\tau {\theta }_i+(1-\tau ){\theta }_i^{\prime },$$

(10)

and

$${\psi }_i^{\prime }=\tau {\psi }_i+(1-\tau ){\psi }_i^{\prime },$$

(11)

where $\tau$ is the update rate and $\tau \ll 1$.   

4.3. Proposed DP-MADDPG Algorithm

Considering the collaboration of multi-UAV confrontation, UAVs need not only real-time information exchange of the battlefield situation but also optimal cooperative decision-making for their actions. Thus, for local decision-making, the MADDPG is further improved with the decomposed and PER mechanisms.

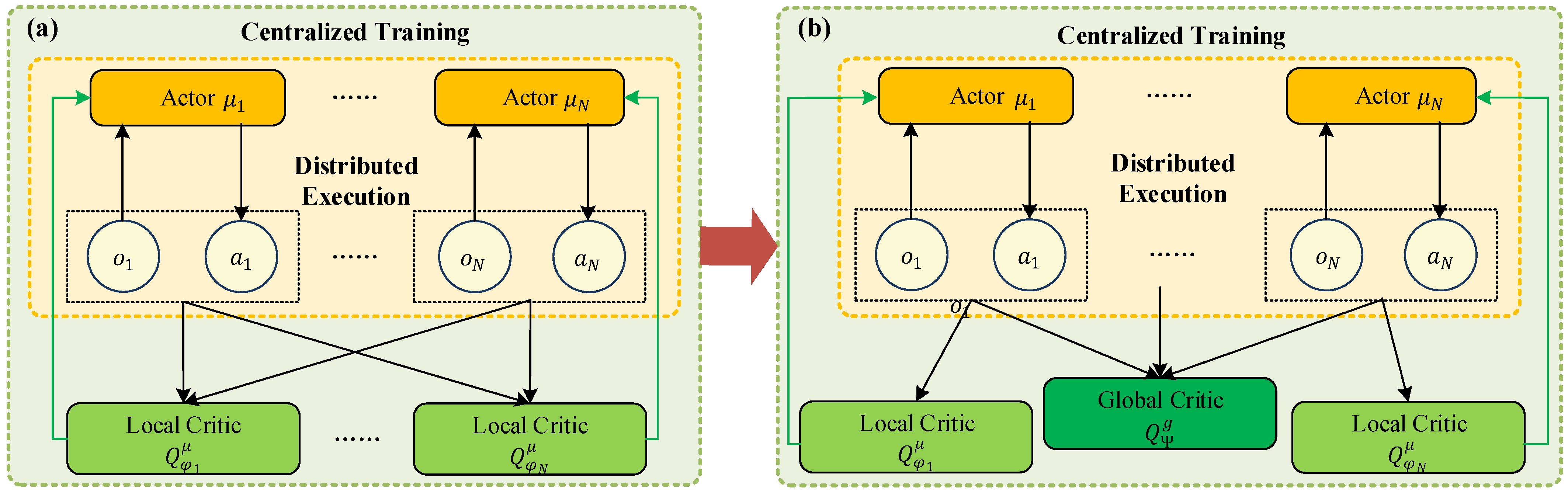
4.3.1. Decomposed Mechanism

To resolve the issue of data coupling among multiple UAVs, the decomposed mechanism is developed to modify the fundamental structure of the MADDPG, as depicted in Figure 5. In the centralized training and distributed execution framework, each UAV holds a local actor neural network as the local policy for decision-making.

For training the local policies, a local critic neural network $Q_{{\psi }_i}^{\mu }$ parameterized by ${\psi }_i$ is built for a UAV i, $i\in \left[1,N\right]$, and a global critic neural network $Q_{\Psi }^g$ is built for the environment. For UAV i, the selected actions ${\mathbf{a}}_i$ are not only passed to the global critic network $Q_{\Psi }^g(\mathbf{s},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N)$, but also to its local critic network $Q_{{\psi }_i}^{\mu }({\mathbf{o}}_i,{\mathbf{a}}_i)$. By integrating the dual critic networks into the MADDPG, UAVs can maximize both local and global rewards. On the one hand, this makes the action selections of the actor networks go in the direction of maximizing local and global rewards, and overcomes the issues of local optimum. On the other hand, it avoids the generation of a dominant decision-making policy incurred by the case of a single global critic network, which makes the method more adaptive to different environments.

Based on the modeling, the policy gradient of UAV i in DP-MADDPG is expressed as

$$\begin{array}{cc}\hfill \nabla J\left({\theta }_i\right)& =E_{{\mathbf{o}}_i,{\mathbf{a}}_i\sim D}\left[{\nabla }_{{\theta }_i}{\mu }_i\left({\mathbf{a}}_i\right|{\mathbf{o}}_i){\nabla }_{{\mathbf{a}}_i}{Q}_{{\psi }_i}^{\mu }({\mathbf{o}}_i,{\mathbf{a}}_i)\right]+\hfill \\ \hfill & E_{\mathbf{s},\mathbf{a}\sim D}\left[{\nabla }_{{\theta }_i}{\mu }_i\left({\mathbf{a}}_i\right|{\mathbf{o}}_i){\nabla }_{{\mathbf{a}}_i}{Q}_{\Psi }^g(\mathbf{s},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N)\right],\hfill \end{array}$$

(12)

where $\mathbf{s}=({\mathbf{o}}_1,\dots ,{\mathbf{o}}_N)$ is the global state that consists of the local observation information of all UAVs. ${\mathbf{a}}_i={\mu }_i\left({\mathbf{o}}_i\right)$ is the local action of UAV i determined by the local observation ${\mathbf{o}}_i$ according to the policy ${\mu }_i$. D is the experience replay buffer.

For the training of the global critic network $Q_{\Psi }^g$, the loss function is defined by

$$L(\Psi )=E_{(\mathbf{s},\mathbf{a},r_g,{\mathbf{s}}^{\prime })}\left[{(Q_{\Psi }^g(\mathbf{s},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N)-y_g)}^2\right],$$

(13)

and

$$y_g=r_g+\gamma Q_{{\Psi }^{\prime }}^g({\mathbf{s}}^{\prime },{\mathbf{a}}_1^{\prime },\dots ,{\mathbf{a}}_N^{\prime }){|}_{{\mathbf{a}}_i^{\prime }={\mu }_i^{\prime }\left({\mathbf{o}}_i^{\prime }\right)},$$

(14)

where ${\mu }^{\prime }=\{{\mu }_1^{\prime },\dots ,{\mu }_N^{\prime }\}$ are the target networks of the local actor networks parameterized by ${\theta }^{\prime }=\{{\theta }_1^{\prime },\dots ,{\theta }_N^{\prime }\}$. $r_g$ is the global reward. $\gamma$ is the discount factor. $Q_{{\Psi }^{\prime }}^g$ is the target network of the global critic network. A target network has the same structure as the main network and is periodically updated with the parameters of the main network to improve the network stability.

For the training of the local critic network $Q_{{\psi }_i}^{\mu }$, the loss function is defined by

$$L\left({\psi }_i\right)=E_{(\mathbf{o},\mathbf{a},r_l,{\mathbf{o}}^{\prime })}\left[{(Q_{{\psi }_i}^{\mu }({\mathbf{o}}_i,{\mathbf{a}}_i)-y_l^i)}^2\right],$$

(15)

and

$$y_l^i=r_l^i+\gamma Q_{{\psi }_i^{\prime }}^{{\mu }^{\prime }}({\mathbf{o}}_i^{\prime },{\mathbf{a}}_i^{\prime }){|}_{{\mathbf{a}}_i^{\prime }={\mu }_i^{\prime }\left({\mathbf{o}}_i^{\prime }\right)},$$

(16)

where $r_l^i$ is the local reward of UAV i. $\gamma$ is the discount factor. $Q_{{\psi }_i^{\prime }}^{{\mu }^{\prime }}$ is the target network of the local critic network.

4.3.2. Prioritized Experience Replay (PER) Mechanism

By using the PER mechanism, the sampling efficiency from the experience replay buffer can be dramatically improved. The principle of PER is to break the uniform distribution of the experience samples in the experience replay buffer D and assign a larger sampling weight to the sample with a higher learning efficiency. Specifically, the mechanism adopts the temporal difference (TD)-error $\delta$ to evaluate the importance of experience samples and uses random priority and TD-error-based importance sampling to grab the experience samples.

Based on the random priority, the sampling probability of an experience sample i is calculated as

$$P\left(i\right)={\displaystyle \frac{p_i^{\alpha }}{{\sum }_{k\in D}{p}_k^{\alpha }}},$$

(17)

where $\alpha$ is the amplified times of the priority and set to 0.6. $p_i=1/rank\left(i\right)$ and $rank\left(i\right)$ is the ranking of the TD-error $|{\delta }_i|$ of sample i in the experience replay buffer in a descending order. The TD-error $|{\delta }_i|$ is calculated as

$${\delta }_i=y_g^{\left(i\right)}-Q_{\Psi }^{g\left(i\right)}(\mathbf{s},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N).$$

(18)

The importance sampling weight is determined by

$${\omega }_i={({\displaystyle \frac{1}{N}}·{\displaystyle \frac{1}{P\left(i\right)}})}^{\beta },$$

(19)

where N is the size of the experience replay buffer, and $\beta$ is an adjusting factor and set to 0.4. The PER mechanism is introduced into MADDPG to grab the samples from the experience replay buffer and form the mini-batch for the neural network training. For the loss functions (13) and (15), the loss of each sample is weighted by the importance sampling weight ${\omega }_i$.

The pseudocode of the DP-MADDPG algorithm is listed in Algorithm 1.

Algorithm 1 DP-MADDPG Algorithm

1: Input: MaxEpisode, MaxStep, N  2: Initialize main and target global critic network $Q_{\psi }^g$, $Q_{{\psi }^{\prime }}^g$  3: Initialize main and target local actor network ${\mu }_{{\theta }_i}$, ${\mu }_{{\theta }_i}^{\prime }$  4: Initialize main and target local critic network $Q_{{\psi }_i}^{\mu }$, $Q_{{\psi }_i^{\prime }}^{\mu }$  5: for $episode=1,\dots ,$ MaxEpisode do  6:    Initialize the environment  7:    for $t=1,\dots ,$ MaxStep do  8:       UAV i executes action ${\mathbf{a}}_i={\mu }_{{\theta }_i}\left({\mathbf{o}}_i\right),i=1,\dots ,N$  9:       Receive global reward $r_g$ and local rewards ${\mathbf{r}}_l$, and update global state $\mathbf{s}\to {\mathbf{s}}^{\prime }$ 10:       Store $(\mathbf{s},\mathbf{a},r_g,{\mathbf{r}}_l,{\mathbf{s}}^{\prime })$ into experience replay buffer D 11:       /* Global critic network training */ 12:       S samples $({\mathbf{s}}^j,{\mathbf{a}}^j,r_g^j,{\mathbf{s}}^{\prime j})$ from D as mini-batch 13:       Calculate $y_g$ by (14) 14:       Update global critic by minimizing ${\displaystyle \frac{1}{S}}{\sum }_{j=1}^S{\omega }_S^j{(y_g-Q_{\Psi }^g(\mathbf{s},{\mathbf{a}}_1,\dots ,{\mathbf{a}}_N))}^2$ 15:       Update target global critic by $\tau \Psi +(1-\tau ){\Psi }^{\prime }\to {\Psi }^{\prime }$ 16:       /* Local actor and critic network training */ 17:       for UAV $i=1,\dots ,N$ do 18:       K samples $({\mathbf{s}}^j,{\mathbf{a}}^j,r_l^j,{\mathbf{s}}^{\prime j})$ from D as mini-batch 19:       Calculate $y_l^i$ by (16) 20:       Update local critic network by minimizing ${\displaystyle \frac{1}{K}}{\sum }_{j=1}^K{\omega }_K^j{(y_l^i-Q_{{\psi }_i}^{\mu }({\mathbf{o}}_i^j,{\mathbf{a}}_i^j))}^2$ 21:       Update actor network ${\theta }_i={\theta }_i+\nabla J\left({\theta }_i\right)$ by (12) 22:       Update target actor and critic networks by $\tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }\to {\theta }_i^{\prime }$ and $\tau {\psi }_i+(1-\tau ){\psi }_i^{\prime }\to {\psi }_i^{\prime }$ 23:       end for 24:    end for 25: end for 26: Output: Model Parameters of Actor Network ${\theta }_i$

5. Performance Evaluation

The experimental environment is set up with Win10, Intel(R) Core(TM) i7-10875H CPU, 16G RAM, and NVIDIA GeForce RTX 2060 GPU. The software framework is based on Python 3.6 and PyTorch 1.1. Based on the experimental settings in Section 5.1, the performance is analyzed from the perspectives of convergence rate and confrontation results.

5.1. Experimental Settings

The simulation platform of air combat is set up based on the MaCA released by the Key Laboratory of Cognitive and Intelligent Technology of China Electronics Technology Group Corporation [23]. The battlefield of the air combat scenario is 10 km × 10 km × 1 km. The blue and red parties both have 10 UAVs, including eight combat UAVs and two reconnaissance UAVs. Combat UAVs and reconnaissance UAVs have different radar detection ranges. The detection range of a combat UAV is 700 m × 120°, and that of a reconnaissance UAV is 2000 m × 360°. The number of missiles carried by a combat UAV is 4. The sector attack area of the attack model is (400 m, 45°). The initial speed of the UAVs is 10 m/s. 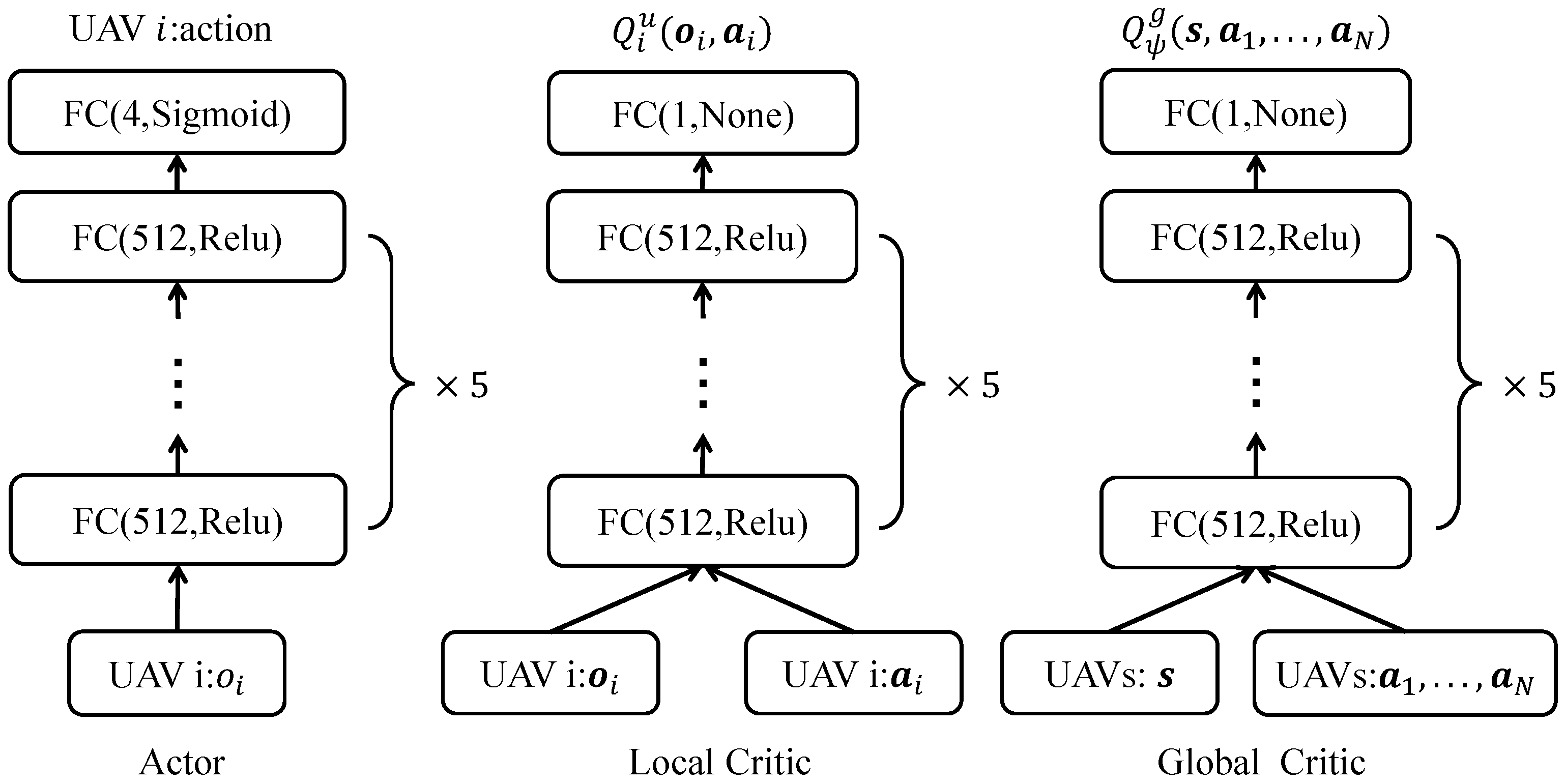The upper limits of the speed $v_{i_{max}}$, acceleration $a_{i_{max}}$, and angular velocity ${\omega }_{i_{max}}$ are 50 m/s, 5 m/s², and $\pi$/12 rad/s, respectively. The safe distance between UAVs is 20 m. It is worth noticing that the MaCA is a discrete-event simulation platform set up mainly for the multi-UAV confrontation and DRL-based strategy analysis, wherein weather conditions such as wind and rain are not considered in the current version. The network structures of the local actor network, local critic network, and global critic network are shown in Figure 6. The hyperparameter settings for the model training of DP-MADDPG are given in

Table 5. Hyperparameter settings.

Hyperparameter	Value
MaxEpisode	25,000
MaxStep	2000
Capacity of replay buffer	${10}^5$
Batch size	64
Discount factor	0.95
Soft update rate	0.01
Actor learning rate	0.001
Critic learning rate	0.001

.

5.2. Strategy Replay

To visualize the strategies learned by the UAVs, it is assumed that the red party in the multi-UAV confrontation scenario exploits the DP-MADDPG algorithm for intelligent decision-making, and the blue party adopts the fundamental distance-prioritized rule. The distance-prioritized rule refers to UAVs attacking the enemies with the nearest distances and fleeing in the opposite direction.

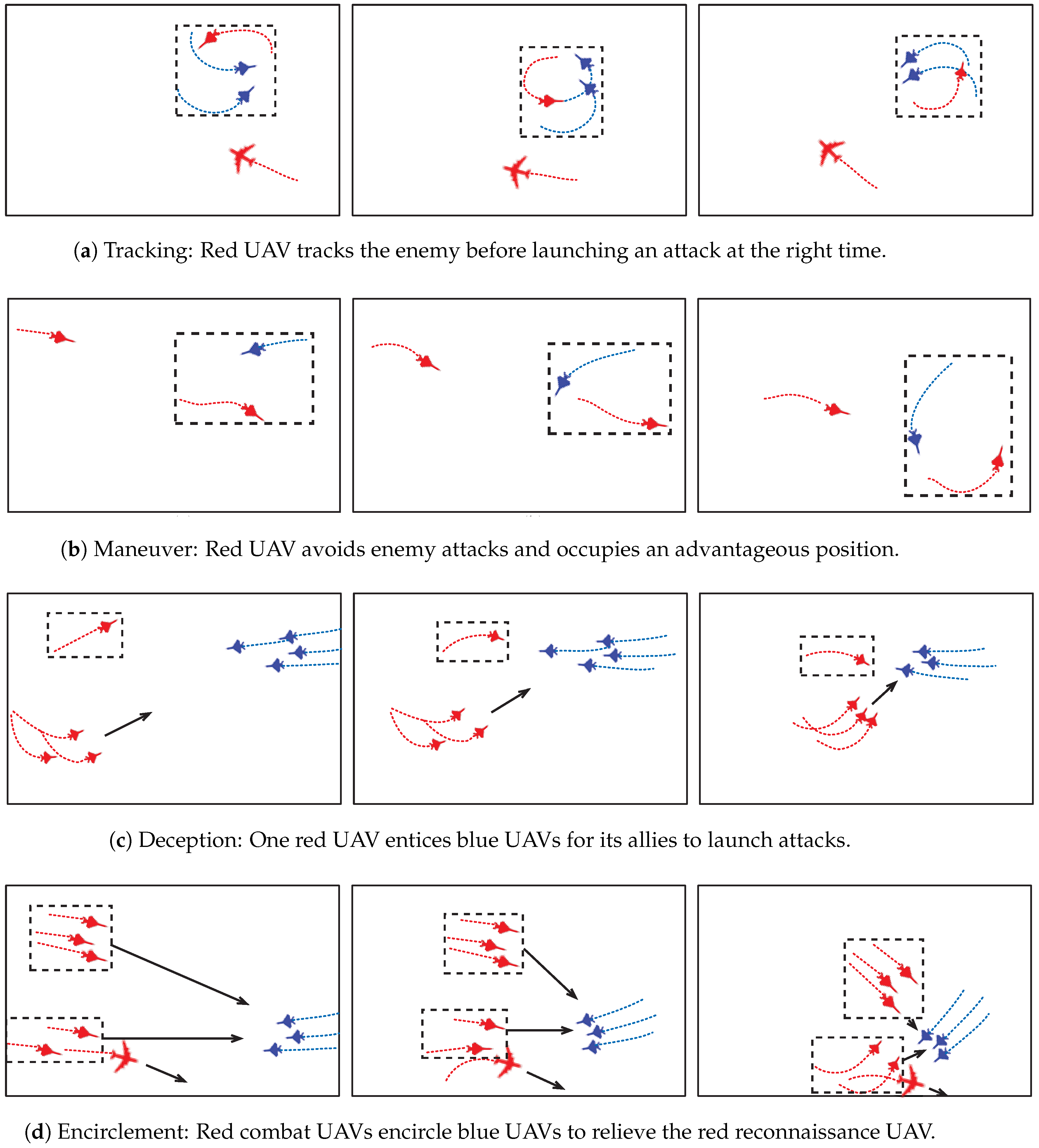
The actions of the DP-MADDPG-empowered red-party UAVs are replayed in Figure 7, which depicts the process of the UAVs in the red party gradually learning the confrontation strategies, including tracking, maneuver, deception, and encirclement.

(a) Tracking: From Figure 7a, it can be seen that the UAV in the red party has learned a tracking strategy. When an individual red UAV discovers an enemy UAV, instead of taking the initiative to attack, it adopts a tracking strategy and continuously tracks the enemy before launching an attack at the right time.

(b) Maneuver: From Figure 7b, it can be seen that a red UAV is being pursued by the blue and may be dangerous at the next moment. The red UAV promptly adopts the maneuvering strategy to avoid the enemy’s attack and occupy an advantageous position.

(c) Deception: From Figure 7c, it can be seen that a red UAV intentionally appears in the forward direction of the blue UAVs, enticing the enemies to pursue it. Its allies actively occupy the advantageous attacking positions on the left side to launch precise strikes in a way that minimizes losses.

(d) Encirclement: From Figure 7d, it can be seen that the red UAVs encircle the enemy and relieve the reconnaissance UAV from being pursued by the blue.

Thus, Figure 7 unveils that the proposed DP-MADDPG algorithm enables the UAV’s learning of effective confrontation strategies. Furthermore, Figure 7 also demonstrates the cooperative behavior of multiple UAVs in the red party.

5.3. Convergence Analysis

To evaluate the performance of the proposed DP-MADDPG algorithm, the traditional MADDPG algorithm and the independent learning DDPG (ILDDPG) are adopted as benchmarks. For ILDDPG, it refers to the case that each UAV exploits the single-agent DDPG algorithm for decision-making. It assumes that the red party in the multi-UAV confrontation scenario exploits the DRL algorithms for intelligent decision-making, including DP-MADDPG, MADDPG, and ILDDPG, and the blue party adopts the distance-prioritized rule for Case 1 and the ILDDPG for Case 2.

5.3.1. Case 1-Confrontation against Distance-Prioritized Rule

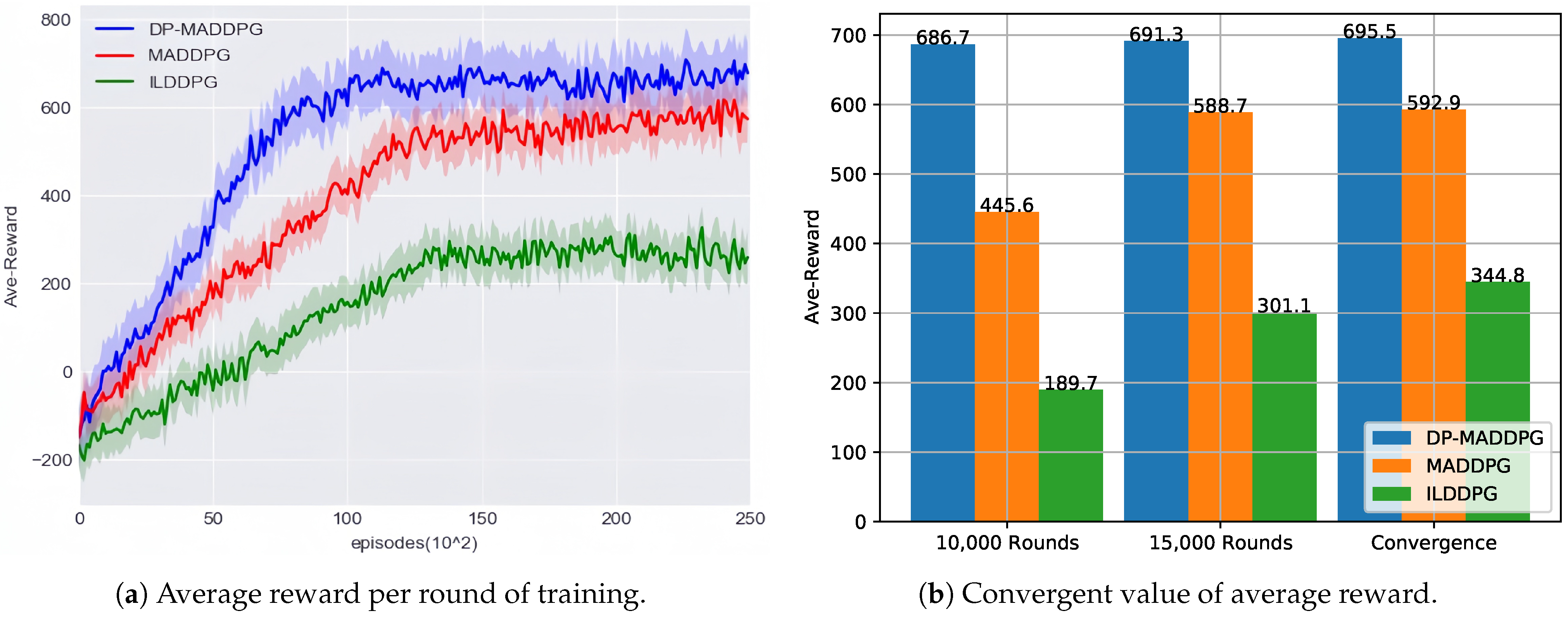
Figure 8a shows the average reward per training round, where the red party adopts the DP-MADDPG, MADDPG, and ILDDPG, respectively, and the blue party adopts the distance-prioritized rule. The total number of training rounds is 25,000. Figure 8a indicates that the proposed DP-MAPPG converges faster and finally converges to a higher value. More details about the training process are provided in Figure 8b. In the experiment, the mean value over the last 100 training rounds is regarded as the convergent reward. The reward of DP-MADDPG, MADDPG, and ILDDPG converges to 695.5, 592.9, and 344.8, respectively, which indicates that the DP-MADDPG improves the convergent reward by 17.3% and 101.7% compared to MADDPG and ILDDPG.

5.3.2. Case 2-Confrontation against ILDDPG

To further analyze the performance of the proposed DP-MADDPG algorithm, it assumes that the red party still exploits the DRL algorithms, and the blue party adopts the ILDDPG instead of the distance-prioritized rule. The average reward per training round is shown in Figure 9a. The total number of training rounds is 25,000. Details of the training process are provided in Figure 9b. The average reward of DP-MADDPG, MADDPG, and ILDDPG converges to 795.2, 711.4, and 362.8, respectively, which indicates that the DP-MADDPG improves the convergent reward by 11.8% and 119.2% compared to MADDPG and ILDDPG.

In both Case 1 and Case 2, DP-MADDPG and MADDPG converge faster to higher rewards than the ILDDPG, which indicates that collaboration is necessary for the multi-UAV confrontation. Moreover, the proposed DP-MADDPG outperforms the fundamental MADDPG. The reason is that the DP-MADDPG algorithm adopts the decomposed and PER mechanisms, which can learn the optimal strategy from the experience buffer more accurately and efficiently. From Table 3 and Table 4, the rewards are determined by the confrontation results. Thus, a higher convergent reward implies an optimal confrontation strategy leading to a higher win rate in the multi-UAV confrontation. The confrontation analysis is thus conducted in the next subsection.

5.4. Confrontation Analysis

To analyze the confrontation results, the win rate of the DRL-empowered red party is evaluated. The blue party adopts the distance-prioritized rule and the ILDDPG as well. The multi-UAV confrontation is tested 1000 times, and the rates are the average over the 1000 tests.

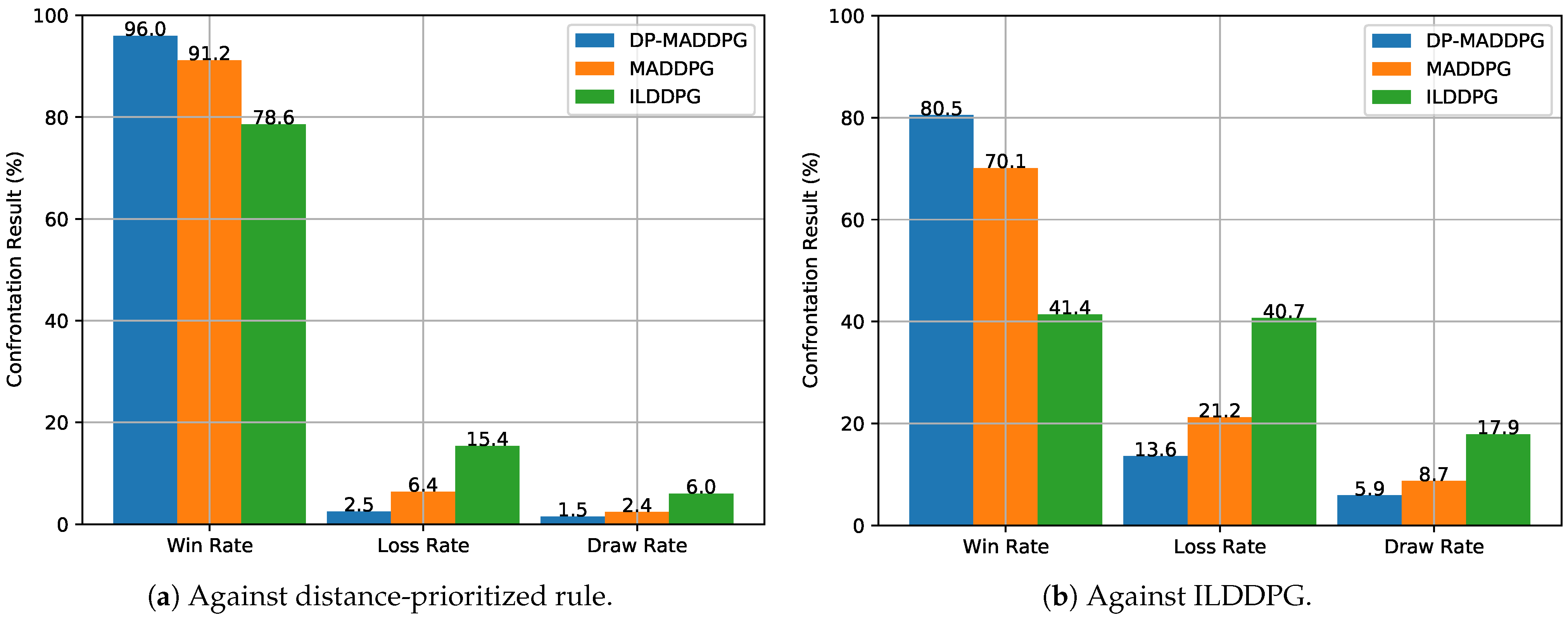
The comparison of the win rate in two different confrontation scenarios is shown in Figure 10a and Figure 10b, respectively. Figure 10a illustrates that the win rate of the proposed DP-MADDPG is 96%, which is higher than that of the MADDPG and ILDDPG with 91.2% and 78.6% in the confrontation against the distance-prioritized rule. Meanwhile, for the confrontation against the ILDDPG in Figure 10b, the win rates of the proposed DP-MADDPG, MADDPG, and ILDDPG are 80.5%, 70.1% and 41.4%, respectively.

The results in Figure 10a,b unveil that, against the distance-prioritized rule, the DRL-empowered party can achieve a higher win rate, which identifies that the DRL algorithms can optimize the decision-making. Furthermore, DP-MADDPG and MADDPG can obtain a higher win rate than ILDDPG in both scenarios. The reason for this is that ILDDPG is a single-agent DRL algorithm, wherein each UAV only has its local observation and optimizes its own policy accordingly. Meanwhile, for the multi-agent DRL algorithms, the UAVs can share the global state and optimize the cooperative policy to improve the win rate. In terms of the multi-agent DRL algorithms, the proposed DP-MADDPG outperforms the traditional MADDPG. This is because the proposed DP-MADDPG introduces the local critic network, and each UAV adopts the decomposed mechanism to maximize the global reward and local reward at the same time, which avoids the generation of unstable policies and ensures the completion of the confrontation mission of the UAVs in the red party.

5.5. Discussions and Future Work

Multi-UAV confrontation, as the main form of intelligent air combat, plays an increasingly important role on battlefields. For example, the US Air Force Laboratory released the LOCUST (LOw-Cost UAV Swarming Technology) project in 2015, planning to launch multiple UAVs to complete aerial attack and defense missions. Europe has also been studying the FCAS (Future Combat Air System) as a key instrument in ensuring European autonomy and sovereignty in defense and security. The multi-UAV confrontation relies on the cooperation of the UAV swarm, which means that UAVs with intelligent and computing capabilities cooperate to fulfill situational awareness, resource allocation, and adversarial task completion. Due to the resource constraints and the drastic changes in battlefields, intelligent decision-making is critical for multi-UAV cooperative confrontation [22]. Traditional multi-UAV cooperation and confrontation strategies meet the technical challenges of weak coordination, high computational complexity, and low accuracy, which cannot meet the real-time requirements of air combat [20]. Therefore, it is necessary to combine artificial intelligence (AI) with military technologies such as multi-UAV confrontation and design intelligent decision-making algorithms suitable for air combat.

AI technology can conduct battlefield deduction, enabling UAVs to autonomously make air combat decisions and complete adversarial missions with minimal cost. In future intelligent air combat, the critical missions in the multi-UAV confrontation include breaking through enemy defenses, carrying out precise target strikes, and intercepting incoming UAVs. The multi-UAV confrontation belongs to the tactic, and air combat decision-making is crucial for multi-UAV confrontation missions. MADRL is a kind of AI technology developed for multi-agent systems and intelligent decision-making. In this work, a MADRL algorithm, DP-MADDPG, is proposed to resolve the issues in the multi-UAV confrontation, including multi-UAV autonomous decision-making, distributed UAV swarm cooperation, and multi-UAV situation assessment. Compared to the benchmark MADDPG algorithm, the convergent rate and reward of the DP-MADDPG are improved and lead to an increased win rate of confrontation.

Nonetheless, there are still some limitations to this work. In the confrontation scenario, the effects of the aerial obstacles and interference and the weather events are not considered. In the future, research efforts will be spared to overcome these limitations and fulfill the work with more realistic confrontation scenarios. Moreover, a priori tactical rule database can be added to the framework to reduce ineffective experience exploration and improve the decision-making efficiency of multiple UAVs.

6. Conclusions

To overcome the technical challenges of intelligent decision-making in the multi-UAV confrontation, a DP-MADDPG algorithm was proposed in this paper. Specifically, the decision-making problem was formulated as a partially observable Markov game. Subsequently, the DP-MADDPG algorithm was proposed as the solution by integrating the decomposed and PER mechanisms into the traditional MADDPG. The decomposed mechanism improved the MADDPG framework with local and global dual critic networks to avoid the convergence to a local optimum and a single dominant policy. The PER mechanism optimized the sampling efficiency from the experience replay buffer. Simulation results indicate that the integration of the decomposed and PER mechanisms improved the convergence rate and the reward value of the proposed DP-MADDPG compared to MADDPG and ILDDPG. Furthermore, in the confrontation against the distance-prioritized rule-empowered blue party, the win rate of the DP-MADDPG-empowered red party improved to 96% compared to the 91.2% and 78.6% rates of MADDPG and ILDDPG. In the confrontation against the ILDDPG-empowered blue party, the win rate of the DP-MADDPG-empowered red party improved to 80.5% compared to the 70.1% and 41.4% rates of MADDPG and ILDDPG.