Multi-Type Task Assignment Algorithm for Heterogeneous UAV Cluster Based on Improved NSGA-Ⅱ

Abstract

Cluster warfare, as a disruptive technology, leverages its numerical advantage to overcome limitations such as restricted task execution types and the low resilience of single platforms, embodying a significant trend in future unmanned combat. In scenarios where only the number of known targets and their vague locations within the region are available, UAV clusters are tasked with performing missions including close-range scout, target attack, and damage assessment for each target. Consequently, taking into account constraints such as assignment, payload, task time window, task sequencing, and range, a multi-objective optimization model for task assignment was formulated. Initially, optimization objectives were set as total mission completion time, total mission revenue, and cluster damage level. Subsequently, the concept of constraint tolerance was introduced to enhance the non-dominant sorting mechanism of NSGA-II by distinguishing individuals that fail to meet constraints, thereby enabling those violating constraints with high tolerance to be retained in the next generation to participate in further evolution, thereby resolving the difficulty of achieving a convergent Pareto solution set under complex interdependent task constraints. Finally, through comparisons, the superiority of the improved NSGA-II algorithm has been verified.

1. Introduction

UAVs play a critical role in modern warfare. With the increasingly complex and dynamic nature of the battlefield, UAVs are being equipped with diverse functionalities. In addition to traditional scout and attack tasks, modern military UAVs now possess more capabilities such as a communication relay, electronic countermeasures, and damage assessment. In unmanned combat scenarios, multiple tasks may need to be executed against the same target, necessitating the collaboration of heterogeneous platforms. An efficient task assignment algorithm enables rational assignment and orderly execution of combat tasks within a UAV cluster, enhancing overall combat effectiveness and reducing the workload of operators [1].

Cluster task assignment is a combinatorial optimization problem, and various mathematical models have been proposed to address it, such as Mixed Integer Linear Programming (MILP) [2,3], Multiple Traveling Salesmen Problem (MTSP) [4,5], Network Flow Optimization (NFO) [6], Vehicle Routing Problem (VRP) [7,8], Cooperative Multiple Task Assignment Problem (CMTAP) [9,10], etc. In the context of multi-objective task assignment models, two types of algorithms are commonly used: traditional optimization algorithms and intelligent optimization algorithms. The former mainly includes weight-based methods, constraint-based methods, linear programming methods, etc. However, as the size of the problem or the number of constraints increases, the intelligent optimization algorithms, which have inherent randomness, demonstrate superior solving capability compared with the traditional ones. Intelligent optimization algorithms encompass Evolutionary Algorithms (EA) [11,12], Particle Swarm Optimization (PSO) [13,14], Genetic Algorithm (GA) [15], Ant Colony Optimization (ACO) [16,17], and others.

When solving the task assignment problem, decision-makers take into account various factors including the total time and total reward required to complete the task; the damage level of the UAV cluster and the range are also involved. This constitutes a multi-objective optimization problem. Many traditional methods attempt to transform this into a single-objective optimization problem, which goes against the nature of multi-objective optimization and conflicts with the inherent feature of uncertainty in the real-world. Traditional methods usually provide decision-makers with a single optimal solution, which heavily relies on the assigned weights for the objective function. However, it is more reasonable to present decision-makers with a set of feasible optimal solutions, considering the uncertainty involved.

Many scholars have made significant improvements to intelligent algorithms for the multi-objective optimization problem. Reference [18] proposed the Multiple Objective Particle Swarm Optimization (MOPSO) method, which utilizes Pareto dominance to determine the direction of each particle. It sets a global repository of non-dominant vectors, which could be used as the reference of other particles to guide their movements. Reference [19] introduced the Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D), which decomposes a multi-objective optimization problem into several scalar sub-problems and optimizes them simultaneously. For this algorithm, each sub-problem only utilizes information from neighboring sub-problems, which effectively reduces the computational complexity in each generation. Reference [20] proposed the Multi-Objective Particle Cluster Optimization based on Adaptive Grid Algorithms (AGA-MOPSO). It incorporates an adaptive grid algorithm for evaluating particle density estimation in non-inferior solution sets, along with the AGA-based Pareto optimal solution search technology that maintains a balance between the global and local search capabilities. Reference [21] advanced the Multi-Objective Particle Swarm Optimization algorithm based on Shared-learning and Dynamic Crowding Distance (MOPSO-SDCD), which incorporates a shared-learning factor to modify the velocity updating equation. The global and local search accuracies are both enhanced. It also maintains external files using a dynamic crowding distance sorting strategy to improve the diversity and distribution of Pareto optimal solutions. Reference [22] focused on optimizing the total flight distance and mission completion time of UAVs, while also accounting for practical constraints like heterogeneous UAV types and task execution sequences, a collaborative multi-task assignment model for heterogeneous UAVs based on multiple constraints has been developed. The Knee point-based coevolution multi-objective particle swarm optimization (KnCMPSO) algorithm has been introduced to effectively address the described model.

According to the number of task types, the cluster task assignment problems can be categorized into two classes. The first one is the class of single-type task assignment problems (each target has only one task to be executed), and the second one is the class of multi-type task assignment ones (each target has multiple tasks to be executed). This research primarily focuses on the second class. Taking the constraints of assignment, load, task time window, task order, and range into account, a multi-objective optimization model for task assignment was formulated.

In Section 2, the optimization objectives are set as follows: total task completion time, total task reward, and the level of cluster damage. In Section 3, the NSGA-II algorithm is improved. The original NSGA-II algorithm utilizes the number of constraint violations (NumVio) as a measure to determine the non-dominance relationship by comparing the magnitude of NumVio. However, when faced with a situation where there are numerous constraints with varying degrees of importance like this paper, it is easy for the population to be guided in the wrong direction, resulting in optimization failure. To address this issue, the concept of “constraint tolerance” is proposed to differentiate the impact of different constraints on the non-dominance sorting process. This allows the population to evolve towards satisfying the more important constraints first. In Section 4, simulation results are compared before and after the algorithm improvement under the same task scale, demonstrating better performance of the proposed algorithm. Additionally, the improved NSGA-II algorithm was also compared with the IMOQQPSO algorithm in the same application scenario, demonstrating the superiority of the enhanced NSGA-II algorithm. The main contributions of this paper are as follows:

• A task assignment method based on the NSGA-II algorithm is proposed to tackle the problem of multi-type task assignment with incomplete state information. Furthermore, a new encoding and decoding method specifically for this problem is designed.
• Introducing the enhancement of “constraint tolerance” in the NSGA-II algorithm addresses the challenge of converging to Pareto optimal solutions under complex and coupled task constraints. This enhancement enables task assignment results that more effectively meet complex constraint requirements.

2. Problem Description

Regarding the multi-type task assignment problem addressed, firstly, the specific attributes of three basic models in the scene are defined. Then, the constraints and objective optimization functions of the problem are described.

2.1. Basic Model Definition

2.1.1. Target Model

The symbol T_i represents target i; there are N_T targets with approximate location information. For each target T_i, where i = (1, 2, 3, …, N_T), three types of tasks (N_type = 3) need to be executed: scout, attack, and assessment. The three tasks for the same target must be performed sequentially, meaning that a target can only be attacked after it has been reconnoitered. After completing the attack task, an assessment task is required to evaluate the damage status of the target.

Table 1. Target attributes.

Model	Attribute	Symbol
Target Ti	Target number	NT
	Number of task types	Ntype
	The target location	LocaiT
	The target value	ValueiT
	Threat level	ThreatiT

presents the relevant attributes of the targets: Loca_i^T represents the position of the target. Value_i^T denotes the value of the target, indicating the reward obtained from completing all tasks related to the target. Threat_i^T represents the threat level of the target, indicating the likelihood of the target causing damage to the UAV cluster.

2.1.2. Task Model

The symbol M_k represent task k, where k = (1, 2, 3, …, N_M), and N_M = N_T × N_type represents the total number of tasks. A membership variable C_ik is used to describe the relationship between tasks and targets. If task M_k belongs to target T_i, then C_ik = i; otherwise, C_ik = 0. For tasks belonging to the same target, Type_k is used to indicate the order of the task, with Type_k ϵ {1, 2, 3}, where a smaller numerical value indicates a higher priority for execution.

Table 2. Task attributes.

Model	Attribute	Symbol
Task Mk	Number of tasks	NM
	Task resource requirements	Demandk
	Task execution timeframe	[tks, tke]
	Task duration	tdok
	Task allowable time window	[ETk, LTk]
	Task type marker	Typek
	Belonging variable	Cik

presents the detailed attributes of the tasks: Demand_k represents the resource requirement for the task, specifically the number of missiles needed to execute this task. [t_k^s, t_k^e] indicates the task execution timeframe, with t_k^s representing the start time and t_k^e representing the completion time. t_k^do represents the duration of task execution, which varies depending on the task type. [ET_k, LT_k] represent the time window constraints for the task; ET_k is the earliest allowable execution time for the task, while LT_k is the latest allowable completion time.

2.1.3. Heterogeneous UAV Model

The symbol U_j represents UAV j; there are N_U UAVs in the heterogeneous cluster. There are three types of UAV in the cluster: scout UAV, attack UAV, and scout/attack UAV. The differences between heterogeneous UAVs are mainly reflected in combat payload. The scout UAV is equipped with information scout equipment, which can perform scout and assessment tasks. Attack UAVs are equipped with limited ammunition and can perform attack tasks. Scout/attack integrated UAVs can perform scout and assessment tasks but can also carry out attack tasks.

Table 3. UAV attributes.

Model	Attribute	Symbol
UAV Uj	Number of UAVs	NU
	UAV position	PosjU
	UAV speed	VeljU
	Cost of UAV	ValuejU
	The maximum range of UAV	RangejU
	Scout UAV detection radius	DeteRadjU
	Maximum payload for attack UAVs	LjU
	The ability of Uj to carry out Mk	Pjk

presents the detailed attributes of the UAVs: Pos_j^U represents the position of the UAV. Vel_j^U represents the speed of the UAV. Value_j^U represents the cost of the UAV. Range_j^U represents the maximum range of the UAV. DeteRad_j^U represents the detection radius of a scout UAV. L_j^U represents the maximum attack payload of a UAV. P_j^k represents the ability of U_j to carry out M_k.

Based on the basic model, a variable is defined as x_jk; x_jk = 1 represents U_j to carry out M_k—that is,

$$x_{jk}=\left\{\begin{array}{l}1,U_j\mathrm{execute}{M}_k\\ 0,U_j \mathrm{d}\mathrm{o}\mathrm{e}\mathrm{s}\mathrm{n}’\mathrm{t}\mathrm{execute}{M}_k\end{array}\right.$$

(1)

2.2. Problem Constraints and Optimization Objectives

2.2.1. The Problem Constrains

All constraints can be categorized into two types: physical constraints and logical constraints. Physical constraints are limitations imposed by the capabilities of the cruise missile cluster, such as range constraints. On the other hand, Logical constraints are related to task requirements, such as task order constraints.

• Assignment constraint

Each task only needs one UAV to perform it, but one UAV can perform several tasks:

$$\forall k,{\displaystyle \sum _{j=1}^{N_V}{x}_{jk}}=1,x_{jk}\in \{1,0\}$$

(2)

2.

Payload constraint

The resources required to perform the current task shall not exceed the current load limit of the UAV:

$${\displaystyle \sum _{k=1}^{N_M}{x}_{jk}}Deman{d}_k\le L_j^U,\hspace{1em}\forall j\in N_V$$

(3)

3.

Range constraint

The flight distance of a UAV should be less than its range. In addition, the payload of one UAV may be enough to complete most of the tasks in the total task set, so if the range is not limited in the assignment process, it may lead to the situation where one UAV is over-allocated while the other UAVs have no tasks:

$$\max \left\{t_k^e{x}_{jk}+\Delta t_j^{\mathrm{back} }\right\}\cdot {Vel}_j^U<{Range}_j^U$$

(4)

4.

Time window constraint

Task execution time [t_K^s, t_K^e] should be included in the task time window [ET_K, LT_K]:

$$E{T}_k\le t_k^s<t_k^e\le L{T}_k,\hspace{0.33em}\hspace{0.33em}\forall k\in N_M$$

(5)

5.

Task order constraint

When there is a coupling relationship between tasks of the same target, execution order needs to be considered—for example, a typical task flow to a target, like “scout → attack → assess”. When M_k and M_k+n all belong to target T_i, C_ik = C_ik+n = i, and the Type_k < Type_k+n. Thus, we have

$$t_k^e\le t_{k+n}^s$$

(6)

2.2.2. The Objective Optimization Functions

In the task assignment model presented in this paper, three objective optimization functions are defined: total task completion time, total task reward, and the level of cluster damage. The distribution plan is evaluated in these three aspects.

• Total task completion time

In order to find a solution that can complete the task as soon as possible under the condition that constraints are satisfied, the objective function is as follows:

$$F_{\mathrm{time} }=\max \left\{t_k^e{x}_{jk}+\Delta t_j^{\mathrm{back} }\right\}$$

(7)

2.

Total task reward

In order to ensure that higher-value tasks have a higher success rate, the objective function of total task reward is introduced. Moreover, the objective function of total task reward is set as the remaining value of enemy targets to align with the data direction of total task completion time, as shown in the following equation:

$$F_{\mathrm{earn} }={\displaystyle \sum _{i=1}^{N_T}{Value}_i^T}\left[1-f\left(C_{\mathrm{TS} }\right){\displaystyle \prod _{j=1}^{N_V}{\displaystyle \prod _{k=1}^{N_M}{\left(P_{jk}\right)}^{C_{ik}{x}_{jk}}}}\right]/{\displaystyle \sum _{i=1}^{N_T}{Value}_i^T}$$

(8)

In the equation, f(C_TS) is the determining variable of the task order; when f(C_TS) = 0, it indicates that the task order constraint is violated. On the other hand, f(C_TS) = 1.

3.

The level of UAV cluster damage

In order to minimize the damage of UAV cluster during the task execution. Since some targets are threatening to UAVs, the objective function is related to the value of UAVs and target threat level, as shown in the following equation:

$$F_{\mathrm{loss} }={\displaystyle \sum _{j=1}^{N_V}{\displaystyle \sum _{k=1}^{N_M}{x}_{jk}}}{Value}_j^U\left[{Threat}_i^T+f\left(C_{\mathrm{TW} }\right)\left(1-{Threat}_i^T\right)\right]/{\displaystyle \sum _{j=1}^{N_V}{Value}_j^U}$$

(9)

In the equation, f(C_TW) is the determining variable of the time window; when f(C_TW) = 1, it indicates that the time window constraint is violated. On the other hand, f(C_TW) = 0.

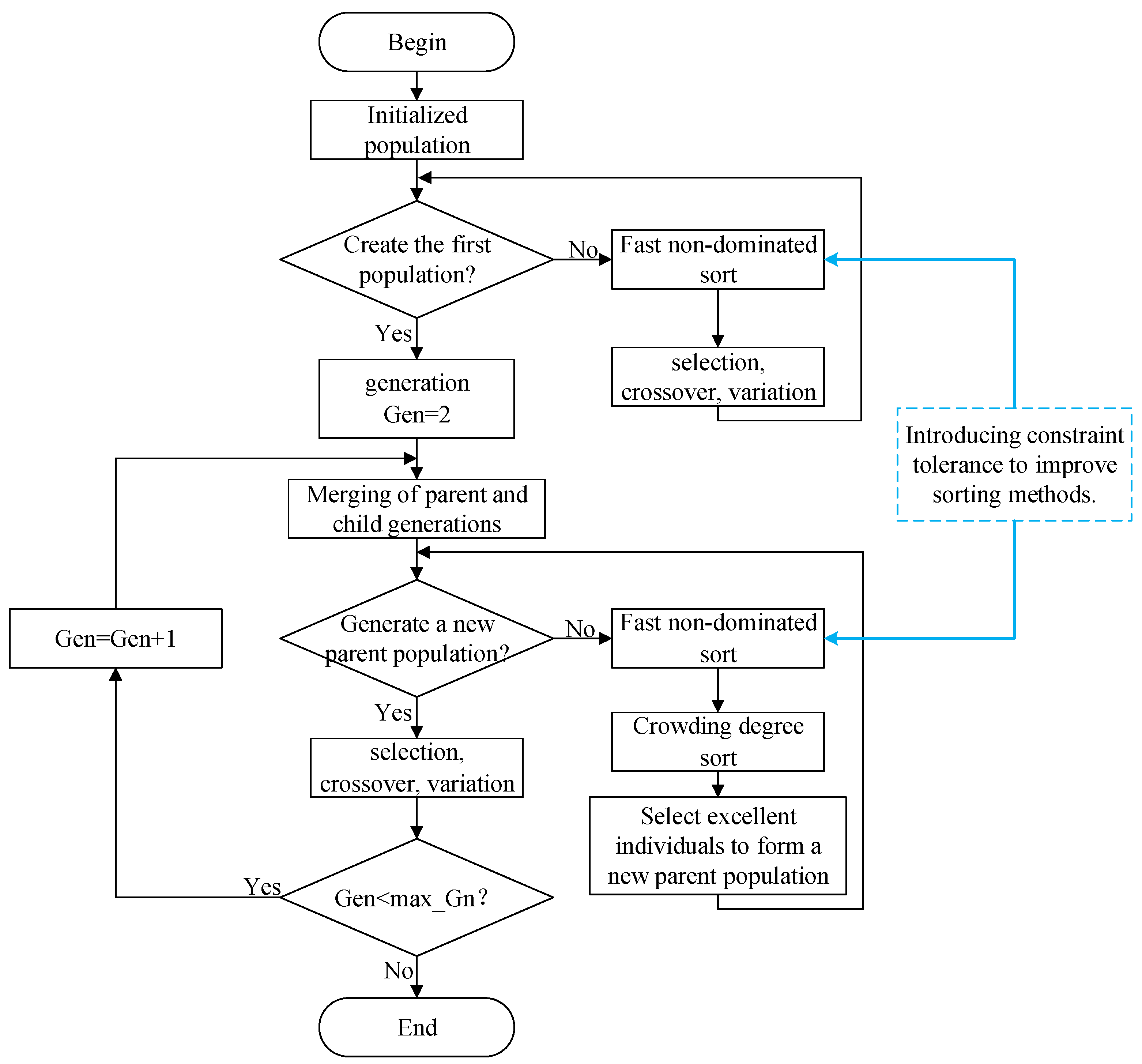
3. Improved NSGA-II Algorithm

The Non-dominated Sorting Genetic Algorithm (NSGA) was proposed by Srinivas and Deb in 1995 [23]. It is a genetic algorithm based on the concept of Pareto optimality. It performs non-dominated sorting on the population based on the dominance and non-dominance relationships among individuals. The selection operation is then performed based on the results of non-dominated sorting.

In 2002, they further proposed an improved algorithm called NSGA-II, which incorporates an elitist strategy into the non-dominated sorting genetic algorithm [24]. NSGA-II adopts a fast non-dominated sorting technique to enhance computational speed and robustness. It also introduces “crowding distance” to sort individuals within the same dominance level, promoting a more uniform distribution of non-dominated solutions in the solution space. Moreover, NSGA-II’s fast non-dominated sorting method demonstrates significant computational efficiency advantages when dealing with optimization problems with many constraints, similar to the ones discussed in this paper. The whole process of the algorithm and area for improvement are shown in Figure 1.

This section outlines the overall workflow of improving the algorithm, the specific improvement principles, and the encoding and decoding methods designed for addressing the multi-type task assignment problem for heterogeneous UAV cluster.

3.1. Improved Non-Dominated Sorting Method

Firstly, introduce the non-dominated sorting method before improvement. In the process of non-dominated sorting, two parameters need to be defined: (1) n_i represents the number of individuals in the current population that can dominate individual i, and (2) S_i represents the set of individuals in the current population that can be dominated by individual i. The steps are as follows:

① Compare the objective function values of each individual to determine n_i and S_i for all individuals in the population.

② Find the individuals in the population that are not dominated by any other individual, i.e., individuals with n_i = 0. Let k = 0, and put these individuals into set F_k.

③ For each individual in set F_k and its corresponding set S_i, for each individual l in S_i. Let n_l = n_l − 1. If n_l = 0, store this individual in set H.

④ Assign a non-dominated rank (Rank) to all individuals in set F_k and set Rank = k. Let F_k be referred to as the k^th non-dominated set.

⑤ Let k = k + 1, F_k = H, and repeat steps 2–4 until all individuals in the current population are sorted into different ranks.

Non-dominated sorting essentially involves the following steps: Firstly, select the set of individuals in the population that cannot be dominated by any other individual and name this set Rank₀. Then, temporarily exclude these individuals from the population and consider the remaining individuals to find the set of individuals that cannot be dominated by any other individual, naming it Rank₁. This process is repeated, and all individuals in the population are sorted based on the dominance relationship, resulting in non-dominated ranks for each individual. Lower rank values indicate better solutions.

When determining the dominance relationship between two solutions, the most direct approach is to compare all their objective function values. If one solution performs better than the other in all objective functions, it dominates the other solution. However, comparing all objective function values for all individuals is inefficient. In fast non-dominated sorting, the number of constraint violations (NumVio) is introduced as part of the sorting process. First, the comparison is made based on the magnitude of NumVio, where a solution with a larger NumVio is dominated by a solution with a smaller NumVio. If two solutions have the same NumVio, then the comparison is made based on the objective function values.

In the context of improving NSGA-II in this paper, the determination of NumVio for an individual solution brings in the concept of “constraint tolerance”. This means that different increments in NumVio correspond to violating constraints of different tolerance levels. For example, consider a problem with two constraints, A and B, where Constraint A has a higher tolerance level while Constraint B has a lower tolerance level. If individual solution i violates only Constraint A, then NumVio_i = 1. If it violates only Constraint B, then NumVio_i = 2. Translating this to the constraints in the problem under study in this paper, time window constraints have a higher tolerance level compared to task sequencing constraints. This means that the system can tolerate some tasks not being completed within the desired time windows but cannot tolerate tasks being executed out of order.

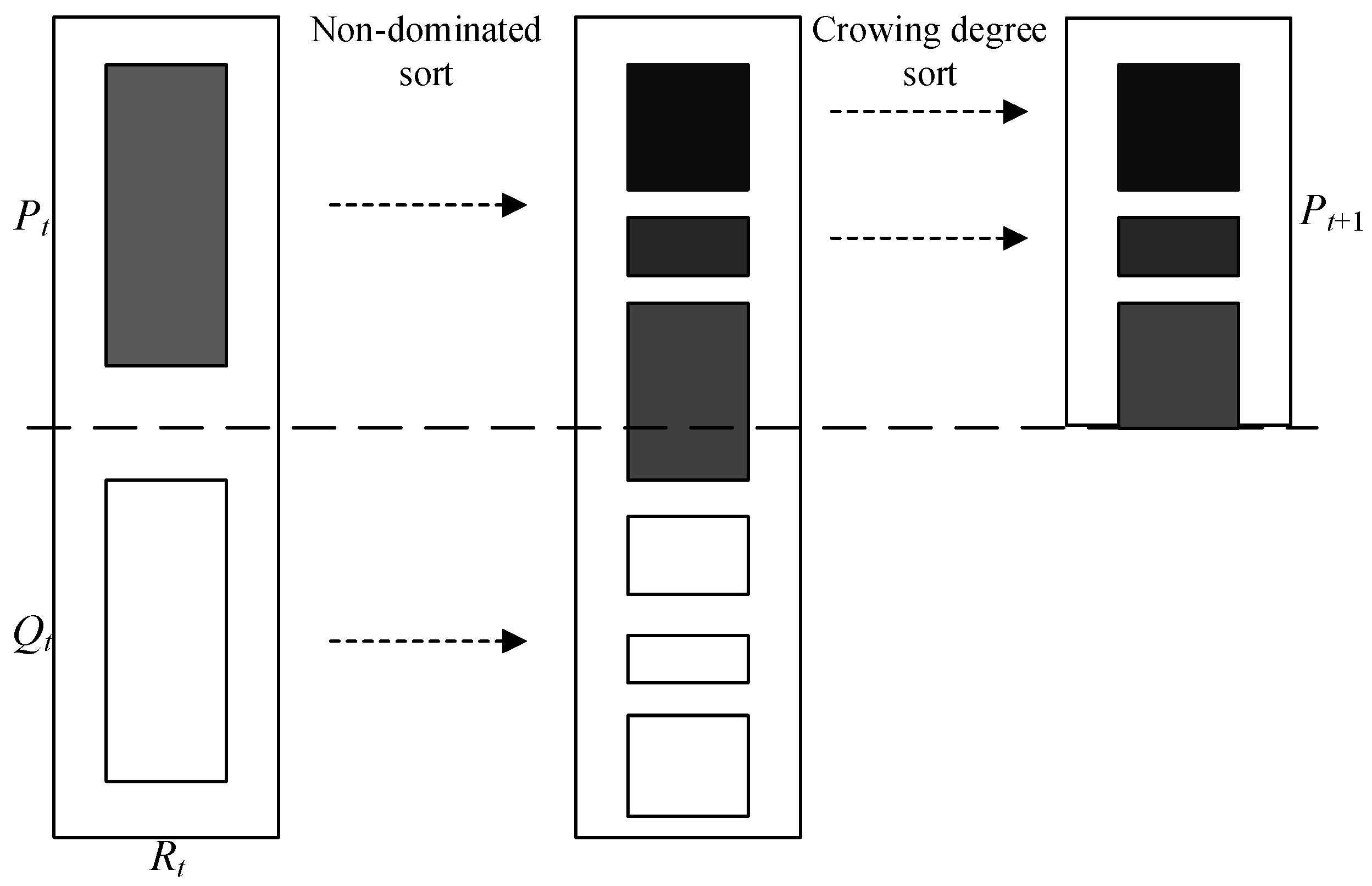
3.2. Elitist Strategy

During each iteration, the parent population P_t is used to generate the offspring population Q_t through selection, crossover, and mutation operations. The union of individuals from both the parent and offspring populations is denoted as R_t. Firstly, the merged population R_t is sorted and divided into ranks using non-dominated sorting. Then, within each rank, individuals are further sorted based on crowding distance. Finally, the top N individuals from the twice-sorted population R_t are selected as the new parent population P_t+1 for the next iteration. This process is illustrated in Figure 2. By incorporating an elitism strategy, the excellent individuals from each parent population can be preserved.

Since the population size N is fixed, the selection process first chooses the set of individuals that are not dominated by any other individual, which corresponds to Rank₀. Then, individuals in Rank1, Rank2, Rank3, and so on are selected sequentially. However, it is possible to encounter situations like the one shown in Figure 2—that is,

$$\left\{\begin{array}{l}{\displaystyle \sum _{i=0}^{n-1}Ran{k}_i<N}\\ {\displaystyle \sum _{i=0}^{n}Ran{k}_i>N}\end{array}\right.$$

(10)

To address the issue described above, it is necessary to sort individuals within the same Rank. Therefore, the concept of “crowding distance” D_i is used to evaluate the quality of individuals within the same rank. It is assumed that when two random individuals are in the same non-dominated rank, the one with a larger crowding distance is considered better than the one with a smaller crowding distance. In comparison to the NSGA algorithm that uses a sharing radius, NSGA-II incorporates the concept of crowding distance. Within the same non-dominated rank, the crowding distance is utilized to assess the density of individuals, promoting a more uniform distribution of non-dominated solutions in the solution space. This eliminates the need for setting a sensitive sharing radius parameter, leading to improved algorithm efficiency and population diversity preservation compared to the NSGA algorithm. The crowding distance is defined as the sum of differences in distances on all sub-objectives between an individual i and its neighboring individuals i−1 and i+1:

$$D_i=\left(f_{i+1,1}-f_{i-1,1}\right)+\left(f_{i-1,2}-f_{i+1,2}\right)+\dots +\left(f_{i-1,n}-f_{i+1,n}\right)$$

(11)

3.3. Individual Encoding Method and Generation Method

3.3.1. Individual Encoding and Decoding Rules

The algorithm in this paper uses the form of real number encoding to generate individuals and maps them to the task assignment scheme using multi-layer decoding. The specific coding form is as Figure 3:

Among them, the elements in the individual are all real numbers in the range of (1, N_U+1). k is the total number of tasks. Take the scene with k = 9 as an example; then, the code of an individual is as in Figure 4:

Taking the decoding of the above individual as an example, the specific process is as in Figure 5, Figure 6 and Figure 7:

Firstly, split the integer part and the decimal part of the element:

Secondly, sort the decimal elements in the second line from small to large, where the sorted number represents the task number M_k; then, according to the belonging variable of task M_k, generate line 3, and based on the type of M_k, generate line 4:

Finally, according to the original position of line 2, line 3 and line 4 are extended and line 2 is deleted. The decoding result is obtained:

Columns 2 and 6 of the above matrix represent the task list for platform 1: task 2 of T₃ and task 1 of T₁. Then, the task assignment results represented by the whole matrix are shown in

Table 4. Task assignment results of coding instance mapping.

Platform Number	Task List—Ti (Typek)
V1	3(2)→1(1)
V2	3(3)→1(3)→2(2)
V3	2(1)→1(2)→2(3)→3(1)

:

3.3.2. Individual Generation Method

Based on the number of tasks N_M, and the number of UAVs N_U, the length of the individual vector is determined as N_M and the range of values for individual elements is (1, N_U + 1). According to the aforementioned encoding and decoding rules, let x₁ = [1, 1, 1, 1, …, 1] and x₂ = (N_U + 1)∙[1, 1, 1, 1, …, 1]. All individuals in the population can be generated according to the following equation, and the population size can be set based on the requirements.

$$x=x_1+(x_2-x_1)\cdot rand(1,N_M)$$

(12)

According to the above method, most of the individuals generated in the population do not satisfy the constraints. Originally, five constraints were proposed: assignment constraint, payload constraint, task order constraint, time window constraint, and range constraint. Among them, the assignment constraint is satisfied by the encoding method. The time window and task order constraints are the most difficult to satisfy, and satisfying these two constraints is the goal of the algorithm. Therefore, it is only necessary to improve the individual generation method to satisfy the payload constraint.

The improved individual generation method for the payload constraint is “modify the integer part according to the type of task represented by decimal part”:

① For element “a. xx”, determine the sorting position k of its decimal part “0. xx”.

② By the task type of M_k, the matching relationship with the execution platform represented by the integer part “a” of the element determines how to change the value of “a”. When they do not match, the value of “a” is changed to the number of a random platform matching the task—that is, the task represented by “0. xx” is executed on a new platform. When they match, the value of “a” is not changed.

③ Put the newly formed element “a. xx” back to its original position in the individual.

4. Simulations and Comparative Analysis

4.1. Simulation Scene Setting

Consider an operational area with a range of 100 km x 100 km, which contains six enemy targets. The configuration of UAV cluster is as follows: four scout UAVs; three attack UAVs, each carrying six missiles; and two scout and attack integrated UAVs, each carrying 4 missiles. The target attributes, task attributes, and UAV attributes are shown in

Table 5. Target attributes.

Target Number	Position XT/m	ValueT	ThreatT
1	(20,000, 30,000)	200	0.10
2	(30,000, 90,000)	300	0.20
3	(45,000, 75,000)	250	0.15
4	(75,000, 50,000)	500	0.40
5	(85,000, 95,000)	400	0.30
6	(90,000, 40,000)	300	0.20

,

Table 6. Heterogeneous UAV cluster attributes.

	UAV1–4	UAV5–7	UAV8–9
Models	Scout UAV	Attack UAV	Scout and Attack UAV
RangeU/m	(30,000, 0)	(0, 75,000)	(0, 50,000)
ValueU	80	120	150
VelU/m·s−1	30	50	40
DeteRadU/m	2000	0	1500
LU	0	6	4
Scout capability	0.95	0	0.80
Attack capability	0	0.95	0.80
Assess capability	0.95	0	0.80

and

Table 7. Task attributes.

C	Type	Task Number	[ET, LT]/min	Demand	tdo
1	1	1	[0, 30]	0	180
	2	2	[30, 90]	1	20
	3	3	[95, +∞]	0	120
2	1	4	[0, 30]	0	180
	2	5	[30, 95]	1	20
	3	6	[100, +∞]	0	120
3	1	7	[0, 15]	0	180
	2	8	[15, 90]	1	20
	3	9	[95, +∞]	0	120
4	1	10	[0, 20]	0	180
	2	11	[20, 95]	2	20
	3	12	[100, +∞]	0	120
5	1	13	[0, 15]	0	180
	2	14	[15, 100]	2	20
	3	15	[105, +∞]	0	120
6	1	16	[0, 25]	0	180
	2	17	[25, 85]	1	20
	3	18	[90, +∞]	0	120

, and the entire scenario is shown in Figure 8.

4.2. Comparative Analysis before and after Algorithm Improvement

4.2.1. Simulation Results

In the case of the above scenario setting, the original NSGA-II algorithm is used for simulation calculation, and the objective function values of Pareto solution set are obtained as shown in

Table 8. Solutions of original NSGA-Ⅱ.

Solution	Total Task Completion Time/s	Total Task Reward	The Level of Cluster Damage
1	7554	0.5603	0.6929
2	7554	0.7802	0.5786
3	7554	0.9121	0.5690
4	8077	0.2745	0.8071
5	10,430	0.2745	0.6262
6	11,310	0.2745	0.6071
7	8710	0.7802	0.4833
8	9051	0.6922	0.4833
9	9322	0.5603	0.4833
10	12,390	0.5164	0.4833

:

From the results in Table 8, it can be observed that the optimal values of the three objective functions converge to a fixed value, which effectively demonstrates the convergence of the algorithm. The Gantt Chart was originally developed by Henry Laurence Gantt, an American mechanical engineer and management scientist, in 1910. It is a graphical representation that can be used as a bar chart to visualize the progress of projects, schedules, and other time-related system progress over time. In the Gantt chart, the horizontal axis represents time, and the vertical axis represents the ID of UAVs. Blocks of the same color represent tasks assigned to the same target. The length of each block along the horizontal axis represents the duration of the task. The numbers on the blocks represent the target and task identifiers. For example, “302” indicates task 02 for target 3. Figure 9, Figure 10 and Figure 11 are the Gantt charts for three of these assignments.

As can be seen from the Gantt chart above, even if the objective function of total task reward about task order is optimal—that is, the result shown in Figure 10—the task order constraint still cannot be satisfied.

Under the premise of not changing the scene settings, the improved NSGA-II algorithm, which introduces “constraint tolerance”, is used for simulation calculations. The objective function values of the solution set are shown in

Table 9. Solutions of improved NSGA-II.

Solution	Total Task Completion Time/s	Total Task Reward	The Level of Cluster Damage
1	10,180	0.3916	0.7357
2	11,380	0.2433	0.7464
3	15,110	0.2469	0.5388
4	10,490	0.4097	0.5801
5	11,340	0.2458	0.7689
6	11,250	0.2718	0.6316
7	12,580	0.3951	0.6184
8	12,660	0.3567	0.6184

, and the Gantt charts for the optimal results of the three objective functions are provided (Figure 12, Figure 13 and Figure 14).

4.2.2. Comparative Analysis of Results

From the Gantt charts of the simulation results, it can be observed that all tasks for each target were executed sequentially and satisfied all constraints. Therefore, after improving the NSGA-II algorithm, the population evolved from an initial state where no individual satisfied all constraints to a Pareto solution set that meets all constraints under the guidance of the improved algorithm.

By comparing the results before and after the improvement of the NSGA-II algorithm, the conclusion that the introduction of “constraint tolerance” effectively guides the population towards the direction of satisfying low-tolerance constraints can be obtained. As a result, a Pareto solution set with the desired effective assignments can be obtained, which outperforms the assignment results obtained by the original NSGA-II algorithm.

4.3. Compared with the IMOQPSO Algorithm

4.3.1. Simulation Results

The scene and model parameters were set the same as in reference [13], and an additional objective optimization function related to range was introduced for comparative simulation. The specific form of the objective function is shown in equation (13). The Pareto solution set obtained using the improved NSGA-II algorithm is shown in

Table 10. Solutions of improved NSGA-II in the scene of reference [13].

Solution	Total Task Completion Time/min	Total Task Reward	The Level of Cluster Damage	Range
1	144.95	0.2410	0.7939	0.5095
2	184.78	0.1857	0.7123	0.5543
3	185.10	0.2118	0.5175	0.5993
4	184.05	0.2493	0.7018	0.4639

, and the Gantt charts for the optimal results of the four objective functions are provided (Figure 15, Figure 16, Figure 17 and Figure 18).

$$F_{\mathrm{range} }={\displaystyle \sum _{j=1}^{N_U}\left[\max \left\{x_{jk}{t}_k^e\right\}-t_j^{\mathrm{go}}+\Delta t_j^{\mathrm{back}}\right]}Ve{l}_j^U/{\displaystyle \sum _{j=1}^{N_U}Rang{e}_j^U}$$

(13)

4.3.2. Comparative Analysis of Results

The simulation results in Table 10 were compared with the results from reference [13], and the comparison is presented in

Table 11. Compares the simulation solutions with the IMOQPSO algorithm.

Item	Total Task Completion Time/min	Total Task Reward	The Level of Cluster Damage	Range
IMOQPSO	114.817	0.1870	0.3350	0.4480
NSGA-Ⅱ	144.950	0.1857	0.5175	0.4639
Error	−16.2%	+7%	−54.5%	−3.5%

. From the above tables, it can be observed that the total task completion time, the level of cluster damage, and range in the task assignment results of this paper are inferior to those of the IMOQPSO algorithm in reference [13]. Only the total task reward is better than the results in reference [13]. However, each optimized result obtained by the improved NSGA-II algorithm in this paper strictly satisfies the constraints of task time windows and task sequencing.

The significant differences between the two task assignment results are total task completion time and the level of cluster damage. This is because in the task assignment results of the IMOQPSO algorithm in reference [13], the constraints of task order were not satisfied, leading to unjustifiably reduced time and damage.

The Gantt charts in Figure 19 and Figure 20 provide evidence for the optimal total time and total damage in reference [13]. In Figure 19, for target 5, the task 02 (attack) has been completed, but task 01 (scout) is still incomplete. Similarly, in Figure 20, for target 6, the task 03 (assessment) has been completed, but task 02 (attack) remains incomplete.

Based on the above comparison, it can be observed that although the IMOQPSO algorithm in reference [13] yields better optimization results for three out of the four objective functions compared to the algorithm proposed in this paper, its task assignment results involve a significant number of target tasks that are not executed in the prescribed order. In contrast, the improved NSGA-II algorithm in this paper strictly satisfies the sequencing constraints for the execution of each objective task set in all schemes. Therefore, the improved NSGA-II algorithm in this paper exhibits better capability in satisfying the sequencing constraints for task assignment problems than the IMOQPSO algorithm in reference [13]. This enables the obtained assignment results to achieve optimal values for each objective function while strictly satisfying the sequencing constraints.

5. Conclusions

This paper investigates the problem of multi-type task assignment for a cluster of heterogeneous UAVs. The NSGA-II algorithm was improved by introducing the concept of “constraint tolerance” to differentiate the impact of different constraints on the non-dominance sorting process.

In the simulation verification, both the original and improved versions of the NSGA-II algorithm were utilized to address assignment problem characterized by three optimization objectives. The results indicate that the improved NSGA-II algorithm introduces “constraint tolerance”, effectively guiding the population towards evolutionary paths that satisfy constraints under low tolerance levels. This ultimately produces a Pareto solution set where 100% of solutions satisfy all constraints, while the original NSGA-II algorithm yields assignments that violate temporal constraints.

Furthermore, both the improved NSGA-II algorithm and the IMOQPSO algorithm were employed to address assignment problems involving four optimization objective functions. The results indicate that in three objectives, the optimization outcomes of the IMOQPSO algorithm surpassed those of the improved NSGA-II algorithm. However, the assignment results of the IMOQPSO algorithm involve a considerable number of target tasks that are not executed in the prescribed order. In contrast, the optimization results of the improved NSGA-II algorithm strictly adhere to the sequencing constraints for the execution of each target task set in all assignment schemes and ultimately outperform the IMOQPSO algorithm by 7% in Total Task Reward.