A Heuristic Routing Algorithm for Heterogeneous UAVs in Time-Constrained MEC Systems

Abstract

The rapid proliferation of Internet of Things (IoT) ground devices (GDs) has created an unprecedented demand for computing resources and real-time data-processing capabilities. Integrating unmanned aerial vehicles (UAVs) into Mobile Edge Computing (MEC) emerges as a promising solution to bring computation and storage closer to the data sources. However, UAV heterogeneity and the time window constraints for task execution pose a significant challenge. This paper addresses the multiple heterogeneity UAV routing problem in MEC environments, modeling it as a multi-traveling salesman problem (MTSP) with soft time constraints. We propose a two-stage heuristic algorithm, heterogeneous multiple UAV routing (HMUR). The approach first identifies task areas (TAs) and optimal hovering positions for the UAVs and defines an effective fitness measurement to handle UAV heterogeneity. A novel scoring function further refines the path determination, prioritizing real-time task compliance to enhance Quality of Service (QoS). The simulation results demonstrate that our proposed HMUR method surpasses the existing baseline algorithms on multiple metrics, validating its effectiveness in optimizing resource scheduling in MEC environments.

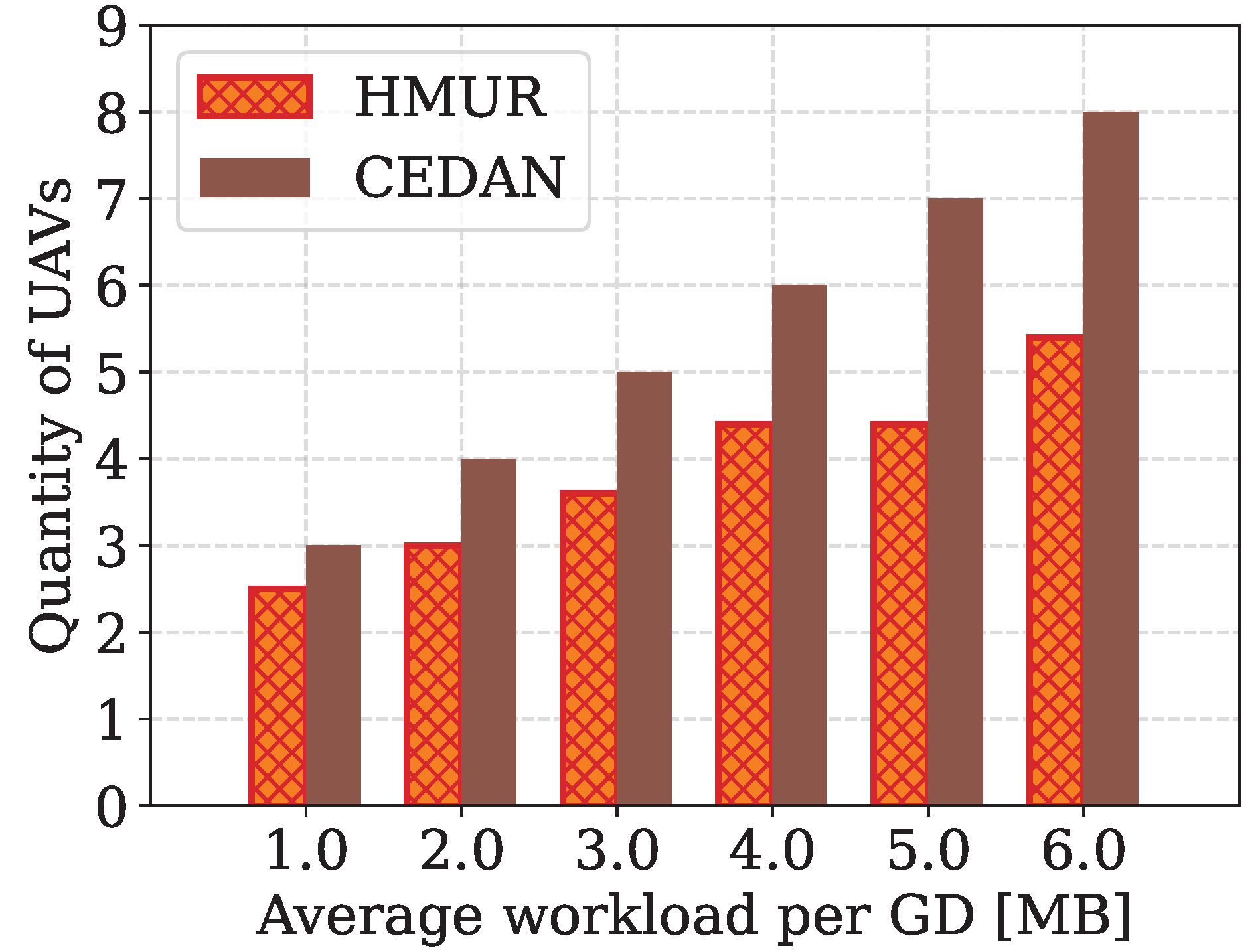
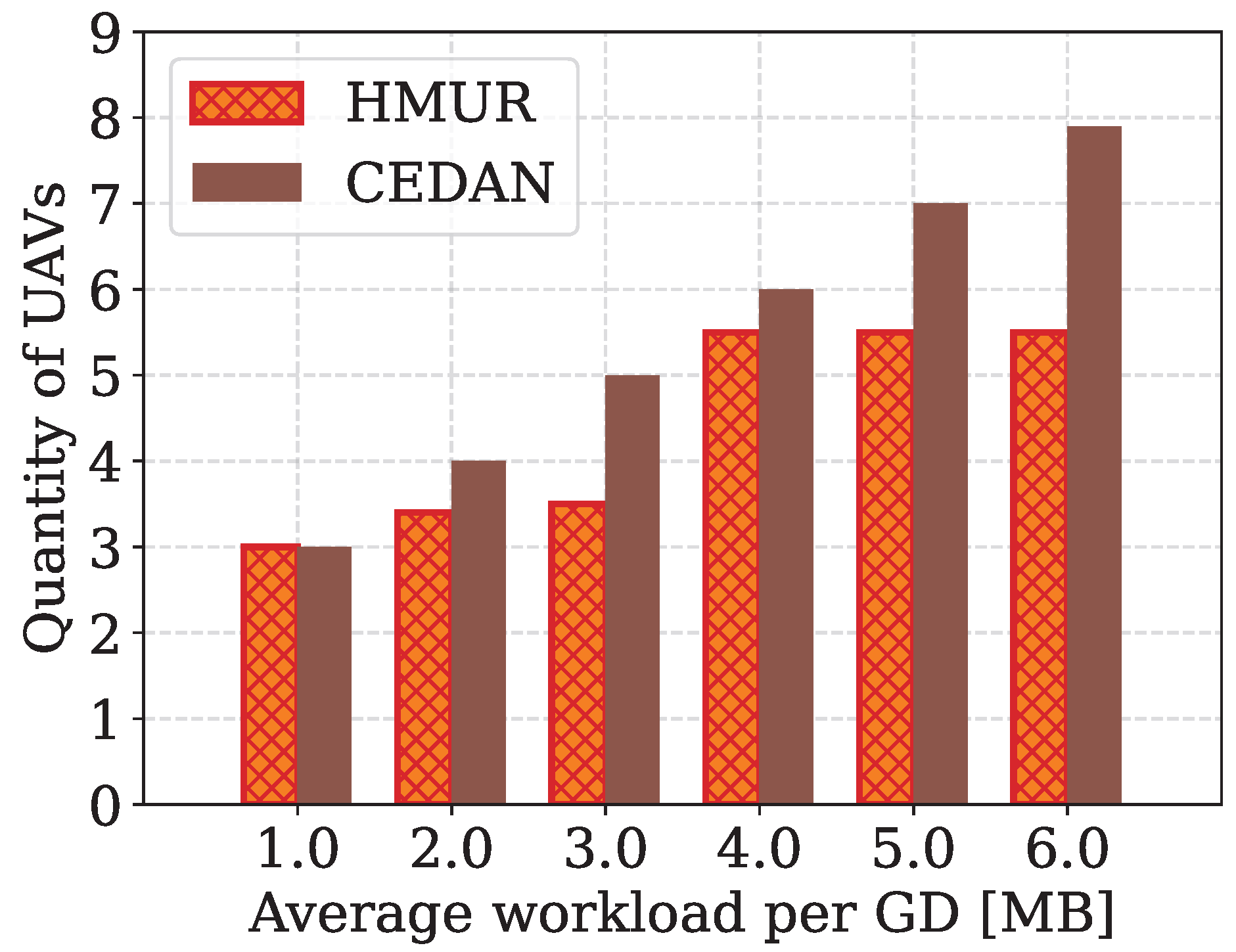
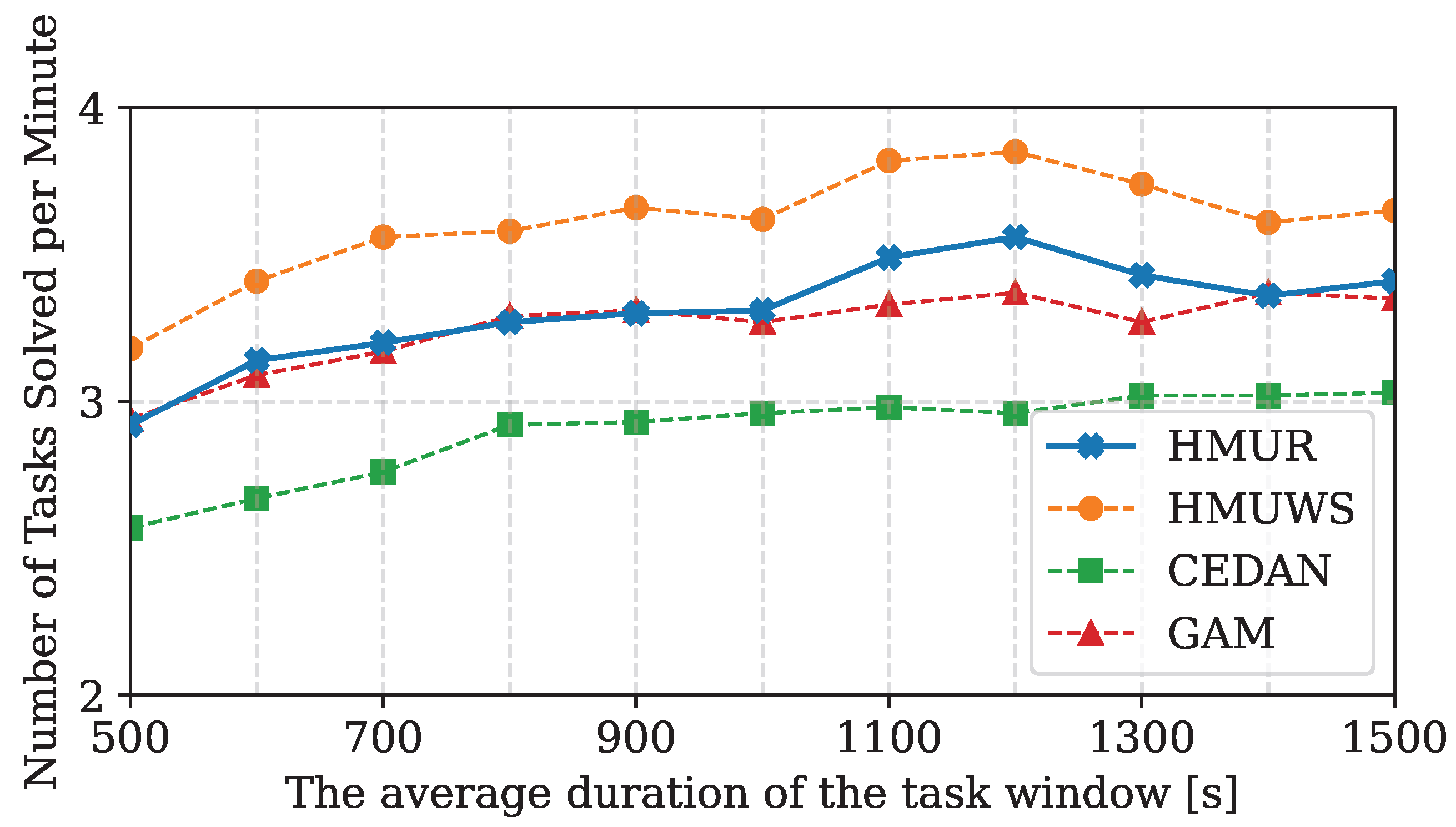
1. Introduction

Mobile Edge Computing (MEC) provides high-speed processing and large-scale distributed computing capabilities for many typical computing-intensive applications, such as automatic navigation, augmented reality, and remote control aircraft [1]. The implementation of MEC relies on dispersed large-scale IoT devices and their wireless communication. The number of global IoT devices has increased rapidly in recent years [2]. The increase in a large number of IoT devices has brought new challenges to mobile communication and service quality. At the same time, due to the limited computing power of IoT devices, additional computing resources are needed to support the effectiveness of services. In this context, UAVs have aroused significant research interest in academia due to their high maneuverability. As a result, UAV-assisted MEC has emerged as a prominent area of study [3]. Meanwhile, the short-range communication characteristics of the UAV means that it cannot transmit data over limited resources over long distances. This requires the dispatch of UAVs to IoT-device-intensive areas through task allocation, path planning, and trajectory optimization to assist in completing tasks.

This paper considers assigning multiple UAVs to multiple task clusters for auxiliary calculations, and effectively formulating UAV flight routes through a heuristic strategy. Taking into account the different flight capabilities of the UAV and the constraints of the task time window, the goal of maximizing the QoS is achieved. In this paper, we consider both the number of tasks resolved by users and the data throughput in relay communications as elements of the Quality of Service (QoS) considerations. To our best knowledge, in the MTSP, the vast majority of UAVs studied are isomorphic [2]. 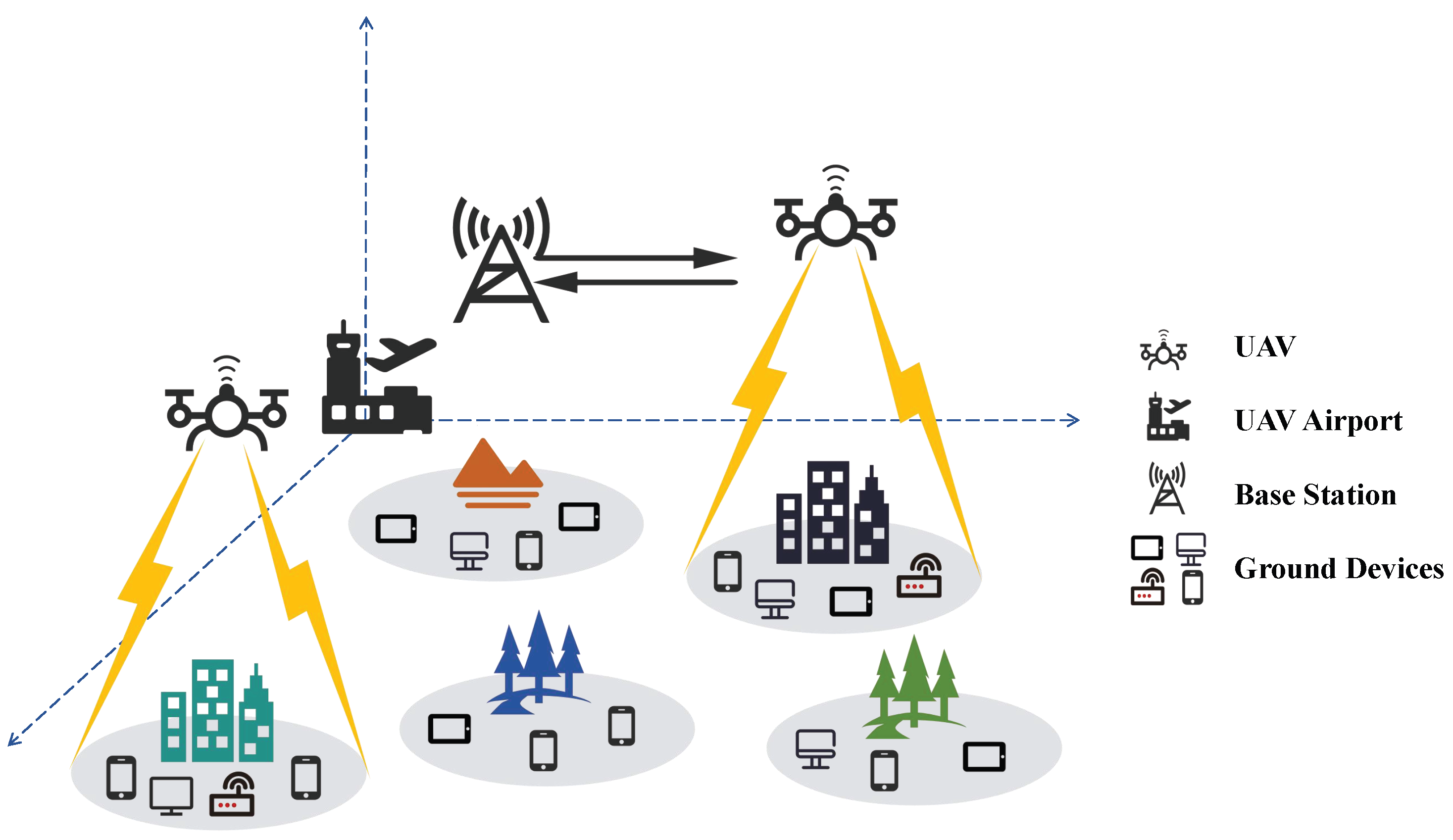However, there are many UAV manufacturers, and there is no fixed unified standard for the UAVs produced, so the heterogeneous UAV model used in this article has different flight capabilities, i.e., maximum flight coverage [4], to adapt to different UAVs produced by different manufacturers, so that various types of UAVs can be applied to our solution. Meanwhile, compared to previous studies on static environmental systems, we consider the real-time constraints of tasks generated by GDs, which means that the UAVs can only serve tasks during the open time window of the task. Real-time tasks are widely present in real environments, such as a traffic intersection having a large amount of traffic flow during specific time periods and a company’s security system needing to monitor a certain area at specific times every day. We model the UAV routing problem with the above characteristics as a heterogeneous multi-traveling salesman routing problem with soft time constraints. Based on the NP-hard characteristics of the traveling salesman problem (TSP) and the MTSP, the heterogeneous multiple traveling salesman routing problem (HMTSRP) is also NP-hard. For UAV-assisted MEC, as shown in Figure 1, the UAV departs from the airport, is deployed to a TA, that is an area where a large number of GDs are concentrated, interacts with the GD, and offloads tasks to the base station.

Providing high QoS for GDs in this model is a challenging issue: (a) A large number of dispersed GDs may make it difficult to determine the TAs, further leading to difficulties in selecting the optimal hovering position. (b) The heterogeneity of UAVs results in different flight capabilities, can lead to different results when different UAVs perform the same task combination, and significantly increase the solution space of the allocation strategy, then making the allocation of UAVs a difficult problem. (c) The time window constraint of a task defines the time it can be served, making it necessary to consider the time factor in UAV path planning. Only by scheduling the UAV to the task location within the time window can effective service be provided.

For the challenges mentioned above, we propose a heuristic UAV scheduling algorithm, referred to as HMUR, for the problem under study. The main contributions are as follows:

• The task allocation and path planning problem of heterogeneous UAVs in MEC systems is modeled as a heterogeneous MTSP with soft time constraints, which is an NP-hard problem. This article proposes a solution called HMUR, which applies a two-stage heuristic algorithm to obtain an approximate optimal solution for improving the QoS.
• Using the k-means clustering method to cluster the geographic coordinates of a large number of GDs solves the problem of too many IoT devices.
• A method for calculating the fitness between heterogeneous UAVs with different flight capabilities and different task assignments is proposed to determine UAV allocation under resource constraints.
• The time window constraint of the task is considered, and a heuristic method is used to formulate travel paths within the responsibility range of each UAV to achieve a higher QoS.

The rest of this paper is organized as follows. Section 2 reviews the existing literature on the problem under study. Section 3 proposes a modeling method for the system, and the problem is described and formulated. Section 4 introduces the HMUR algorithm proposed in this paper. Section 5 shows the experimental results, and Section 6 provides the conclusion.

2. Related Work

In a MEC environment assisted by UAVs, many studies focus on path planning, trajectory optimization, task offloading strategies, and other aspects of UAVs. In this section, we discuss the achievements of existing research and analyze the focus that can be further studied.

The integration of energy-efficient routing protocols is a critical issue in prolonging the operating time of UAVs [5]. The research focuses primarily on the following areas: Energy-Aware Routing Protocol (AODV [6]): This protocol extends the overall network lifetime by prioritizing UAVs with a higher remaining energy to transmit data. Location-Aware Routing Protocol (GPSR [7]): This protocol uses a greedy algorithm to select the node closest to the destination, thereby reducing data transmission distance and energy consumption. Cluster-Based Routing Protocol [8]: This protocol extends the lifetime of the UAV network by periodically rotating the cluster heads to balance energy consumption. Hybrid Routing Protocol (ZRP [9]): This protocol combines reactive and proactive routing mechanisms and dynamically selects the optimal routing strategy based on the distance between nodes and their energy status. Security is another critical concern in UAV-assisted MEC systems, where the integrity and confidentiality of data transmission must be maintained. Ensuring secure communication involves implementing robust encryption methods and secure communication protocols. Using advanced cryptographic techniques and secure transmission channels [10,11], the risk of data breaches and unauthorized access can be minimized.

Regarding the routing issue of a single UAV, Dariush Ebrahimi et al. [12] proposed a reinforcement learning method to enable UAVs to autonomously locate and formulate trajectories within the task area; this work improved the positioning accuracy of multiple objects while considering time and path length to reduce UAV energy consumption. Liang Zhang et al. [13] proposed an energy-efficient trajectory-optimization scheme for UAVs based on reinforcement learning; they jointly applied reinforcement learning methods to solve formulaic optimization problems, considering the average data rate, total energy consumption, and coverage fairness of IoT terminals to optimize the trajectory design of UAVs. Marceau Coupechoux et al. [14] proposed an algorithm based on the Hamilton Jacobi equation to solve the single UAV-trajectory-optimization problem. This work finds the optimal trajectory to minimize costs while considering velocity and service traffic.

Many studies on routing and trajectory optimization for multiple UAVs have received attention. Kai Wang et al. [15] proposed an iterative algorithm and made the first attempt to solve the collaborative path planning problem of multiple unmanned aerial vehicles. This work successfully transforms the problem into an integer linear programming problem by creating a new directed acyclic graph of the UAV state transition and proposes an iterative algorithm with a constant approximation ratio to solve this problem. Abhishek Bera et al. [16] modeled the multi-UAV path planning problem as a capacitated single-depot vehicle-routing problem (CSDVRP) and proposed a routing-adjustment algorithm to optimize the trajectory of the UAVs; this algorithm considers the trade-off between different activation modes of IoT devices and UAV travel time. Yejun He et al. [17] investigated a 3D multi-UAV trajectory optimization based on GDs selecting the target UAV for task computing; this algorithm theoretically derives and proves an optimal selection and uninstallation strategy for IoT devices. Hongyue Wu et al. [18] proposed an improved tabu search algorithm under the background of UAV-assisted edge computing, focusing on path planning, while effectively optimizing the number of UAVs to speed up the unloading of computing tasks. Xiaohan Qiu et al. [19] proposed an integrated host and content-centric routing mechanism that takes advantage of both mechanisms to address the issues of multi-UAV formation and integrated management. Hao Song et al. [20] modeled the UAV network using the Poisson clustering process, divided the UAV network into multiple clusters, and designed an enhanced flood routing protocol based on random network coding and clustering to achieve efficient routing management of the UAV cluster network. Anna Gaydamaka et al. [21] proposed a dynamic topology organization and maintenance method for UAV swarms and, based on this, designed advanced functions for dynamic cluster merging and separation, making it suitable for practical applications. Xutong Yang et al. [22] proposed an adaptive routing scheme based on the Bodies mobile model to complete the task of efficient unmanned aerial vehicle (UAV) networks. They developed a biologically inspired Bodies-based Social Force Model (BSFM) and designed an adaptive UAV routing scheme to improve the communication performance of the UAV network while maintaining the topology. Mohammed Gharib et al. [23] proposed a method based on linear programming modeling to address the problem of a self-organizing unmanned-aerial-vehicle-routing protocol to find the shortest path. Pengcheng Zhao et al. [24] proposed a blockchain and deep Q-network (DQN) co-evolutionary routing (BDCoER) scheme for UAV networks, which completes the path co-evolution of the entire network based on each UAV training its own DQN model.

Many works on collision avoidance in UAV routing also have achieved accomplishments. Yu-Hsin Hsu et al. [25] proposed a reinforcement learning method to help UAVs learn collision avoidance without prior knowledge of other UAV paths, while using optimization theory to find the shortest backward path for each UAV to ensure that the UAV collects data from all relevant IoT devices. Jinyu Fu et al. [26] proposed a multi-layer projection clustering algorithm for multiple UAVs, developed a straight-line flight judgment to reduce the computational complexity of obstacle avoidance, and proposed an improved adaptive window probability roadmap algorithm to plan obstacle avoidance paths.

Table 1. Summary of related work.

Related Works	Method	Number of UAVs	Heterogeneity of UAVs
[12,13]	Reinforcement Learning	one	-
[14]	Heuristic Algorithm	one	-
[15,16,17,19,20,21]	Heuristic Algorithm	Multiple	Isomorphic
[18,22]	Intelligent Algorithm	Multiple	Isomorphic
[23]	Linear Programming	Multiple	Isomorphic
[24]	Deep Learning	Multiple	Isomorphic
This paper	Heuristic Algorithm	Multiple	Heterogeneous

shows a comparison between some related work and the work of this paper. The comparison of some related works with certain features of this paper, including the methods, the number of drones, and whether the drones are heterogeneous, reveals that many studies on multiple UAVs consider UAVs that are isomorphic, with identical battery capacity, signal transmission power, CPU operating speed, and so on. To better fit the actual situation and enrich the diversity of choices, we introduce the heterogeneity of UAVs in this study and then consider routing decisions for multiple UAVs. At the same time, we consider the real-time characteristics of the task based on the static MEC environment, to be closer to the real situation of UAV-assisted MEC.

3. System Model

In our proposed algorithm, each GD possesses an auxiliary calculation task. These tasks should be offloaded to the high-computing-ability base station (BS) by choosing proper UAVs as the relay devices, so as to optimize the QoS performance metrics (i.e., the number of tasks to be solved and the amount of offloaded workload). Several essential factors are included in the process, such as the number of tasks, the amount of offloaded workload, energy consumption, and the number of dispatched UAVs. We simulated this problem by establishing the following models: (a) scenario model, (b) communication model, (c) task-assisted model, and (d) energy consumption model.

The notations to be used are listed in Notations section.

3.1. Scenario Model

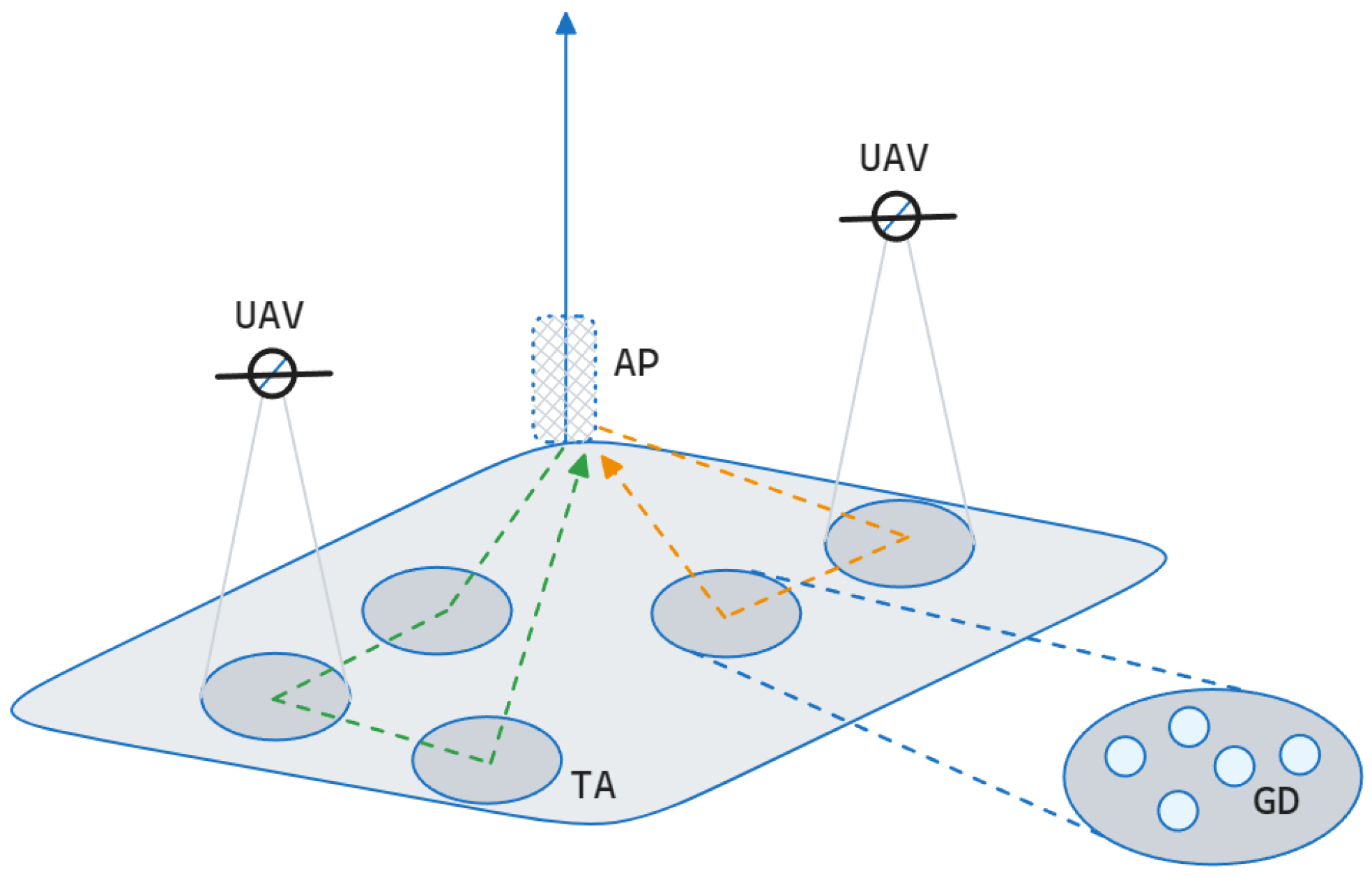
As illustrated in Figure 2, we abstracted the entire environment into two parts: the air part and the ground part; GDs are fixed in the ground part and clustered as TAs, generating tasks waiting for UAV-assisted computation; $D=\{d_1,d_2,\dots ,d_M\}$ denotes a collection of M GDs. Each GD is identified by a unique number, and a location is provided in the system. In this system, to simplify the computation, we assumed that each GD only generates one task within the same time interval, i.e., $A=\{a_1,a_2,\dots ,a_M\}$; task set A corresponds one-to-one to GD set D. Each task $a_i\in A$ is restricted by a real-time window ${\delta }_i=[{\delta }_i^{start},{\delta }_i^{end}]$ during which the task can only be performed. $L_i$ represents the workload of task $a_i$.

Due to the large number of GDs, we need to identify TAs containing several GDs in the environment as a prerequisite for dispatching UAVs, i.e., $B=\{b_1,b_2,\dots ,b_N\}$ denotes N TAs. Due to our simplified model, tasks correspond one-to-one to the GDs, and we can consider that each TA contains several tasks, i.e., $B_n=\{a_1^n,a_2^n,...,a_s^n\}$ indicates that TA $b_n$ contains a total of s tasks. For each TA, we determine a unique hover position to facilitate UAV positioning services. In addition, the BS and airport (AP) are also fixed on the ground, representing high-computing-power service base stations and UAV aprons, respectively.

In the air part, $U=\{u_1,u_2,\dots ,u_K\}$ denotes K UAVs moving in the air. In this paper, task allocation and path planning are performed on them.

3.2. Communication Model

Based on many previous studies, such as [2,3,16,27,28], we used the air-to-ground (ATG) [2] LoS channel probability model to simulate the communication between the UAV and the GD. Let $(x_k^U\left(t\right),y_k^U\left(t\right),h_k^U\left(t\right))$ and $(x_i^D,y_i^D,0)$ denote the coordinates of UAV $u_k$ and GD $d_i$ at time t; the Euclidean distance between them can be calculated as

$$d_{ik}^{DU}\left(t\right)=\sqrt{{(x_k^U\left(t\right)-x_i^D)}^2+{(y_k^U\left(t\right)-y_i^D)}^2+{\left(h_k^U\left(t\right)\right)}^2}$$

(1)

The average path loss between UAV $u_k$ and GD $d_i$ can be expressed as a probability-averaged ATG-LOS model [2,16] into

$$\overline{P{L}_{ik}}=P{r}_{ik}^{LoS}P{L}_{ik}^{LoS}+P{r}_{ik}^{NLoS}P{L}_{ik}^{NLoS}$$

(2)

where $P{L}_{ik}^{LoS}$ and $P{L}_{ik}^{NLoS}$ are the pass loss for the LoS and Non-Line of Sight (NLoS) link and $P{r}_{ik}^{LoS}$ and $P{r}_{ik}^{NLoS}$ denote the probabilities of LoS communication and NLoS communication, respectively. $P{L}_{ik}^{LoS}$ and $P{L}_{ik}^{NLoS}$ are given as

$$P{L}_{ik}^{LoS}=20{log}_{10}{\displaystyle \frac{4\pi f_c{d}_{ik}^{DU}\left(t\right)}{c}}+{\eta }_{LoS}$$

(3)

$$P{L}_{ik}^{NLoS}=20{log}_{10}{\displaystyle \frac{4\pi f_c{d}_{ik}^{DU}\left(t\right)}{c}}+{\eta }_{NLoS}$$

(4)

where $f_c$ is the carrier frequency, c is the velocity of light, and ${\eta }_{LoS}$ and ${\eta }_{NLoS}$ are the average additional loss for LoS and NLoS, respectively. $P{r}_{ik}^{LoS}$ and $P{r}_{ik}^{NLoS}$ are given as

$$P{r}_{ik}^{LoS}={(1+{\mathbf{X}}^{[-\mathbf{Y}({\theta }_{ik}-\mathbf{X})]})}^{-1}$$

(5)

$$P{r}_{ik}^{NLoS}=1-P{r}_{ik}^{LoS}$$

(6)

where $\mathbf{X}$ and $\mathbf{Y}$ are the environmental constants, depending on the environmental condition in which the system is located. ${\theta }_{ik}$ is the elevation angle between GD $d_i$ and UAV $u_k$. It is expressed in radians, as

$${\theta }_{ik}={\displaystyle \frac{180}{\pi }}arcsin{\displaystyle \frac{h_k^U\left(t\right)}{d_{ik}}}$$

(7)

Therefore, the data transfer rate (in bps) between GD $d_i$ and UAV $u_k$ is

$$R_{ik}^{DU}=B_0{log}_2(1+{\displaystyle \frac{P_i^D/\overline{P{L}_{ik}}}{{\sigma }^2}})$$

(8)

According to the orthogonal frequency-division multiple access (OFDMA) communication [2], $B^{bw}$ is the total channel bandwidth, $B_0^{bw}=B^{bw}/k_0$, $k_0$ is the number of GDs serviced simultaneously, $P_i^D$ is the transmission power of GD $d_i$, and ${\sigma }^2$ is the noise power.

Similarly, the transmission rate $R_k^{UB}$ of the offloaded data from the UAV to the BS is calculated by

$$R_k^{UB}=B_0^{bw}{log}_2(1+{\displaystyle \frac{P_k^U/\overline{P{L}_k}}{{\sigma }^2}})$$

(9)

where $P_k^U$ is the transmission power of UAV $u_k$.

3.3. Task-Assisted Model

This work considers using UAVs as mobile relay points, which means that tasks can be offloaded from UAV relays to the BS for computation. As in many previous studies [2,29,30], because its size is much smaller than the data size that must be offloaded, we ignored the delay in sending the data results from the BS back to the UAV and from the UAV back to the GD.

This work divides the working time of the entire system into several parts of a sufficiently small constant ${\delta }^t$ of equal size and considers that the UAV is stationary within a time slot. Due to our communication being divided into two parts, GD to UAV and UAV to BS, we divided a time slot into the two same parts, i.e., UAV $u_k$ assists task $a_i$ in offloading data, and we have ${\delta }_{ik}^{DU}+{\delta }_k^{UB}={\delta }^t$, where ${\delta }_{ik}^{DU}$ is the time that GD $d_i$ offloads data to UAV $u_k$. ${\delta }_k^{UB}$ is the time that UAV $u_k$ offloads data to BS. To ensure the complete processing of a portion of data within one time slot, i.e., the amount of data processed in both parts is the same, the time relationship between the two parts should meet

$${\delta }_{ik}^{DU}{R}_{ik}^{DU}\left(t\right)={\delta }_{ik}^{UB}{R}_k^{UB}\left(t\right)$$

(10)

Based on the above, there are

$${\delta }_{ik}^{DU}={\delta }^t·{\displaystyle \frac{R_k^{UB}\left(t\right)}{R_k^{UB}\left(t\right)+R_{ik}^{DU}\left(t\right)}}$$

(11)

$${\delta }_{ik}^{UB}={\delta }^t·{\displaystyle \frac{R_{ik}^{DU}\left(t\right)}{R_k^{UB}\left(t\right)+R_{ik}^{DU}\left(t\right)}}$$

(12)

At this point, the amount of data processed within one time slot, i.e., single time slot data processing speed, is represented as

$${\beta }_{ik}={\delta }^t·{\displaystyle \frac{R_{ik}^{DU}\left(t\right)R_k^{UB}\left(t\right)}{R_{ik}^{DU}\left(t\right)+R_k^{UB}\left(t\right)}}$$

(13)

The service duration of UAV $u_k$ for GD $d_i$ is $t_{ik}=L_i/{\beta }_{ik}$, where $L_i$ is the amount of data that needs to be offloaded by $d_i$. At this point, the total duration of the UAV $u_k$ hovering over TA $b_j$ is

$$t_{kj}^{hover}=\underset{d_i\in b_j}{max}{t}_{ik}$$

(14)

The total flight time of UAV $u_k$ from TA $b_p$ to TA $b_q$ is $t_{pq}^k=v_k\times D_{pq}$, where $D_{pq}$ is the Euclidean distance between TAs $b_p$ and $b_q$.

3.4. Energy Consumption Model

Due to the fact that the communication energy consumption of the UAVs is much lower than that of motion (including traveling and hovering), we ignore the communication energy consumption of the UAVs. Therefore, the energy consumption of UAV $u_k$ executing tasks along the path $r_k$ is expressed as

$$E_k^{total}=E_k^{trav}+E_k^{hover}$$

(15)

Based on the alternate fixed rotary wing UAV energy consumption calculation method [2,31] used, when UAV travels at velocity v, the unit time flight energy consumption is

$$\begin{array}{cc}\hfill P\left(\right|\left|v\right|\left|\right)& =P_0(1+{\displaystyle \frac{{3\left|\right|v\left|\right|}^2}{U_{tip}^2}})\hfill \\ \hfill & +P_i{(\sqrt{1+{\displaystyle \frac{{\left|\right|v\left|\right|}^4}{4v_0^4}}}-{\displaystyle \frac{{\left|\right|v\left|\right|}^2}{2v_0^2}})}^{{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{d}_0{\rho sA\left|\right|v\left|\right|}^3\hfill \end{array}$$

(16)

where $P_0$, $P_i$, $v_0$, $U_{tip}^2$, $d_0$, $\rho$, s, and A are the aerodynamic parameters of the UAV. Specific definitions and settings can be found in

Table 2. Parameter setting.

Parameter	Value	Definition
$f_c$	2 GHz [16]	Carrier frequency
c	$3\times {10}^8$ m/s	Velocity of light
${\eta }_{LoS}$	1 [2]	Average additional loss in LoS
${\eta }_{NLoS}$	20 [2]	Average additional loss in NLoS
$\mathbf{X}$	$10.39$ [16]	Environmental parameter
$\mathbf{Y}$	$0.05$ [16]	Environmental parameter
${\sigma }^2$	$-174$ dBm/Hz [28]	Gaussian noise
$P_0$	$158.76$ w [3]	Blade profile power in hovering status
$P_i$	$88.63$ w [3]	Induced power in hovering status
$U_{tip}$	120 m/s [3]	Tip speed of the rotor blade
$v_0$	$4.03$ [3]	Mean rotor-induced velocity in hover
$d_0$	$0.3$ [3]	Fuselage drag ratio
$\rho$	$1.225$ km/m3 [3]	Air density
s	$0.05$ [3]	Rotor solidity
A	$0.503$ m2 [3]	Rotor disc area

. Then, the total flight energy consumption of UAV $u_k$ is measured by

$$E_k={\delta }^t\sum _{n=1}^{N}P\left(\right|\left|v\right|\left|\right)$$

(17)

3.5. Problem Formulation

To optimize the QoS with the restriction of energy consumption and the number of dispatched UAVs, a soft time constraint model named HMTSRP is proposed as follows. We define

$$Y_{total}=\sum _i^A{x}_i$$

(18)

$$L_{total}=\sum _i^A{x}_i{L}_i$$

(19)

Among these, $Y_{total}$ represents the total number of serviced tasks, $L_{total}$ represents the total amount of offloaded data workload for serviced tasks, and $L_i$ represents the amount of data offloaded by task $a_i$. Boolean variable $x_i$ indicates whether task $a_i$ is served by the UAV:

$$x_i=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{a}_i\mathrm{is}\mathrm{not}\mathrm{be}\mathrm{served},\hfill \\ 1,\hfill & \mathrm{if}{a}_i\mathrm{is}\mathrm{served}.\hfill \end{array}\right.$$

(20)

Therefore, we formulate a minimization problem as

$$\begin{array}{cc}\hfill P1:max& Y_{total}\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill P2:max& L_{total}\hfill \end{array}$$

(21b)

$$\begin{array}{cc}\hfill s.t.C1:& E_k^{total}\le E_k^{max},\forall u_k\in U\hfill \end{array}$$

(21c)

$$\begin{array}{cc}\hfill C2:& q_k\left[0\right]=q_{AP},\forall u_k\in U\hfill \end{array}$$

(21d)

$$\begin{array}{cc}\hfill C3:& q_k\left[n\right]=q_{AP},\forall u_k\in U\hfill \end{array}$$

(21e)

$$\begin{array}{cc}\hfill C4:& \sum _{j=1,j\ne j^{\prime }}^{\left|\right|B\left|\right|}\varphi (b_{j^{\prime }},b_j)=1\hfill \end{array}$$

(21f)

$$\begin{array}{cc}\hfill C5:& \sum _{j^{\prime }=1,j^{\prime }\ne j}^{\left|\right|B\left|\right|}\varphi (b_{j^{\prime }},b_j)=1\hfill \end{array}$$

(21g)

(21a) and (21b) are the optimization objectives, maximizing the total number of service tasks and data offloading, subject to the following: (21c) represents the battery capacity constraint for the UAVs; (21d) and (21e) represent the starting and ending points of the UAVs, which must be the AP; among these, $q_k\left[n\right]$ is the position of UAV $u_k$ at time n and $q_{AP}$ is the location of the AP; (21f) and (21g) represent that, for all TAs, there only exist one departure and one arrival for one UAV, respectively. The definition of Boolean variable $\varphi (b_{j^{\prime }},b_j)$ is as follows:

$$\varphi (b_{j^{\prime }},b_j)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{UAV}\mathrm{selects}\mathrm{path}\mathrm{from}{b}_{j^{\prime }}\mathrm{to}{b}_j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(22)

4. Problem Analysis and Solution Approach

In order to effectively allocate tasks to BSs for computation by relaying among multiple UAVs with different capacities, a three-step algorithm named HMUR is proposed in this paper. HMUR consists of three steps: (a) TA determination: establishing TAs for related GDs and determining the optimal hover positions of UAVs; (b) UAV allocation: assigning TAs to suitable UAVs; (c) subpath determination: determining the final task execution path for each UAV.

4.1. HMUR

Algorithm 1 shows the framework of HMUR. Throughout the entire process, HMUR first applies the k-means clustering algorithm to cluster the geographic coordinates of the GD and uses its clustering center as the optimal hover location. Secondly, HMUR executes Algorithm 2 for the UAV allocation to perform tasks. Finally, HMUR executes Algorithm 3 to determine the final subpath for each UAV.

In this process, we consider using energy consumption as a constraint for task partitioning in Algorithm 2 to ensure that at least one route for the UAV to be able to complete the designated task. Meanwhile, we use the QoS as an evaluation metric in Algorithm 3 to determine the final subpath, to optimize the service QoS as much as possible within the allowable range of energy consumption.

Algorithm 1 HMUR algorithm.

Input: D, A, and U; Output: Final subpath set R; 1: k-means clustering algorithm generates B from D and determines the optimal hover position 2: Algorithm 2 determines UAV allocation for B 3: Algorithm 3 determines the final subpath set R 4: return Final subpath set R

Algorithm 2 UAV  allocation.

Input: B, U; Output: Allocation set K for UAV; 1: Generate graph G from B 2: Generate minimum spanning tree $T_{MST}$ from G 3: Generate set of odd degree vertices O from $T_{MST}$ 4: Find minimum weight matching M from O 5: Merge T and M to generate Eulerian circuit $H_{EULAR}$ 6: Generate Hamiltonian circuit $R_C$ from $H_{EULAR}$ 7: $num=0$ 8: while $num<len\left(R_C\right)$do 9:    $b_{start}=R_C\left[num\right]$ 10:    for $u_k\in U$ do 11:      Simulate travel from $b_{start}$, and generate $B_k$ 12:      Record $f_k$ 13:    end for 14:    Choose $u_{best}$ with $f_{best}$ for n TAs that it covered 15:    Generate $B_{best}$, and allocate $u_{best}$ for $B_{best}$ 16:    Add $B_{best}$ to K 17:    Remove $u_{best}$ from U 18:    $num=num+n$ 19: end while 20: return Allocation set K

Algorithm 3 Subpath  determination.

Input: U, K; Output: Final subpath set R; 1: for $B_i\in K$  do  2:   for all $b_j\in B_i$ do 3:     $visit\left[b_j\right]=0$ 4:   end for 5:   $start=AP$ 6: while $B_i\ne ⌀$ do 7:     for all  $b_j\in B_i$  do 8:        if $visit\left[b_j\right]==0$ then 9:           Calculate $S_{b_j}$ 10:       end if 11:     end for 12:    Choose TA $b_h$ with the highest $S_{b_h}$ as the target 13:    $visit\left[b_h\right]=1$ 14:    $start=b_h$ 15:    Add $b_h$ to queue $r_i$ 16:    Delete $b_h$ from $B_i$ 17:   end while 18:   if Energy consumption of $r_i$ exceeds the maximum energy consumption of $u_i$ then 19:      $r_i=$ predicted path generated by Algorithm 2 20:   end if 21:   Add $r_i$ to set R 22: end for 23: return R

4.2. TA Determination

Since there are numerous GDs in the MEC environment, it is not realistic to assign one UAV to each GD for auxiliary computation. Thus, GDs with close geographical coordinates are aggregated into TAs, which are served by UAVs within certain time periods. Under constant environmental factors, the data transmission rate is mainly related to the distance $d_{ik}^{DU}\left(t\right)$ between UAV $u_k$ and GD $d_i$. Obviously, the smaller $d_{ik}^{DU}\left(t\right)$ is, the higher the transmission rate. Therefore, in TA $b_j$, the optimal hover location is the position with the smallest distance from all GDs, and we formulate this problem as follows:

$$P2:min\sum _{d_i\in b_j}{d}_{ik}^{DU}\left(t\right)$$

(23)

The k-means clustering algorithm [16,32] is adopted here to establish clusters (i.e., TAs) and determine the cluster centers (i.e., the optimal hover positions of UAVs). The assignment of a GD to a nearby TA is iteratively updated by k-means until convergence. Then, the point with the minimum sum of distances from all the other GDs within one TA is considered as the optimal hover position.

4.3. UAV Allocation

After obtaining the TAs, each UAV will be allocated to several TAs. Let $K=\{B_1,B_2,\dots ,$$B_K\}$ be the set of allocations of K UAVs, of which each element $B_k$ represents a mapping between $u_k$ and the TA set $B_k$. Then, this paper takes the battery capacity carried by the UAV as a constraint and considers maximizing resource utilization for $u_k$ to execute tasks in $B_k$. To ensure the continuity of UAV routes, a partitioning method is proposed by adding breakpoints to a single TSP path to partition TAs. Based on the Christofides approximation algorithm [16], an advanced fitness function $f_k$ is introduced to efficiently evaluate the allocation results in TAs of different heterogeneous UAVs.

Algorithm 2 employs the Christofides algorithm to obtain an approximate solution for the traveling salesman problem (TSP). This approach utilizes a minimum spanning tree, perfect matching, an Eulerian circuit, and a Hamiltonian circuit from graph theory to provide a suboptimal solution. As mentioned in previous research [16], the performance ratio of the Christofides algorithm does not exceed 1.5 compared to the optimal solution, and it is a constructive solution that can be solved within polynomial time.

As shown in Algorithm 2, after creating a complete TSP path $R_c$ by lines 1 to 6, some breakpoints are inserted to truncate the path into several predicted paths: when UAV $u_k$ travels along $R_C$ (denoting a TA sequence) and consumes energy during flight and mission execution; when a UAV finds that its energy consumption cannot reach the next TA and then returns to the AP, it will return to the AP and represent the TAs’ path that has performed for the task as $r_k$. If $u_k$ travels along the route $r_k$, the fitness can be designed as

$$f_k=\alpha \times {\displaystyle \frac{E_k^{hover}}{E_k^{total}}}+(1-\alpha )\times {\displaystyle \frac{E_k^{total}}{E_k^{max}}}$$

(24)

where $E_k^{hover}$ represents the energy consumption of $u_k$ during task execution, $E_k^{total}$ represents the total energy consumption of this travel path, and $E_k^{max}$ represents the maximum battery capacity of $u_k$. So, the effective energy consumption rate ${\rho }_k^E=E_k^{hover}/E_k^{total}$. Due to the heterogeneity among UAVs, different UAVs executing tasks from the same route may insert virtual points into different positions (i.e., returning to the AP from different TA endpoints), resulting in different $E_k^{trav}$.

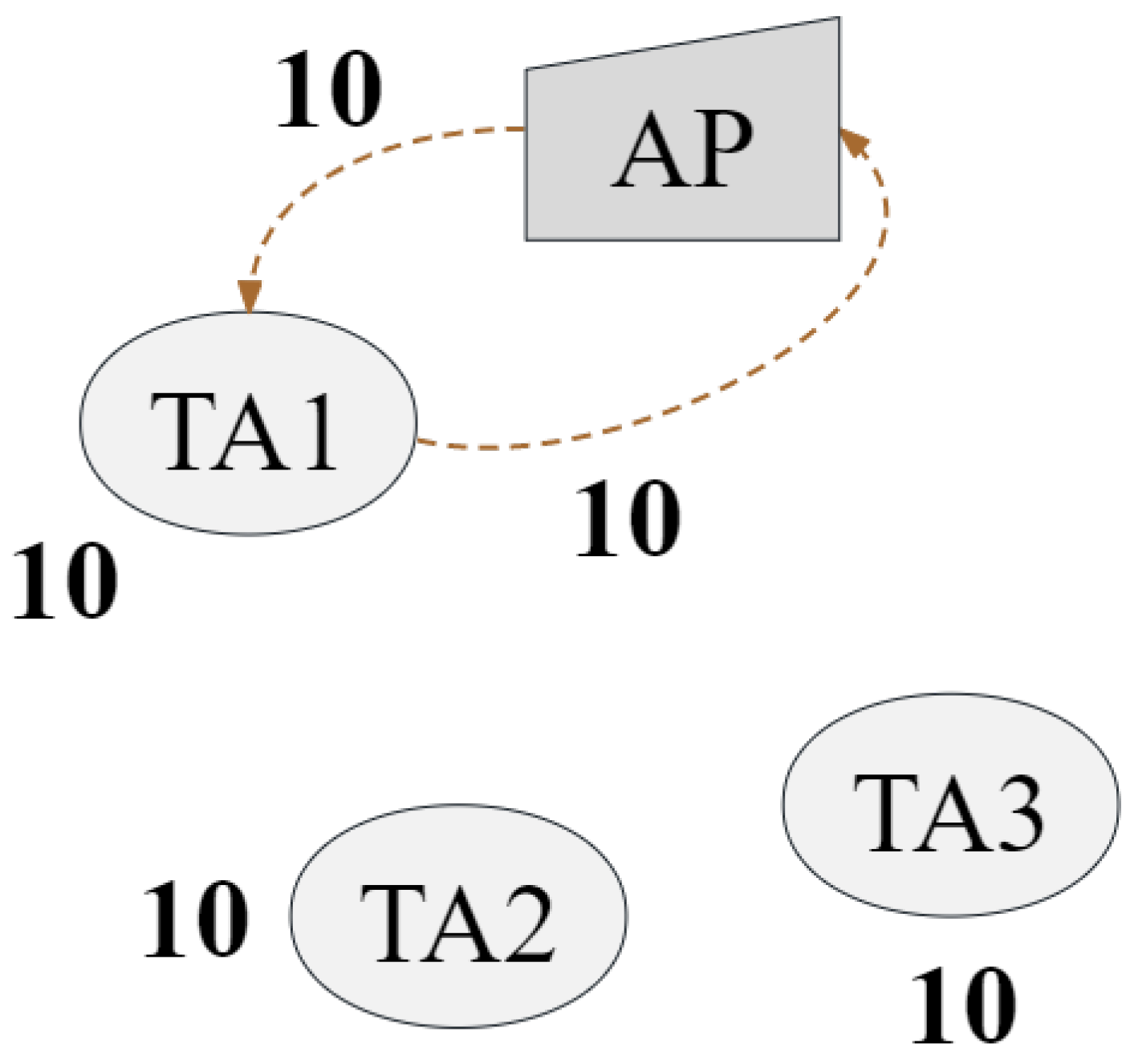
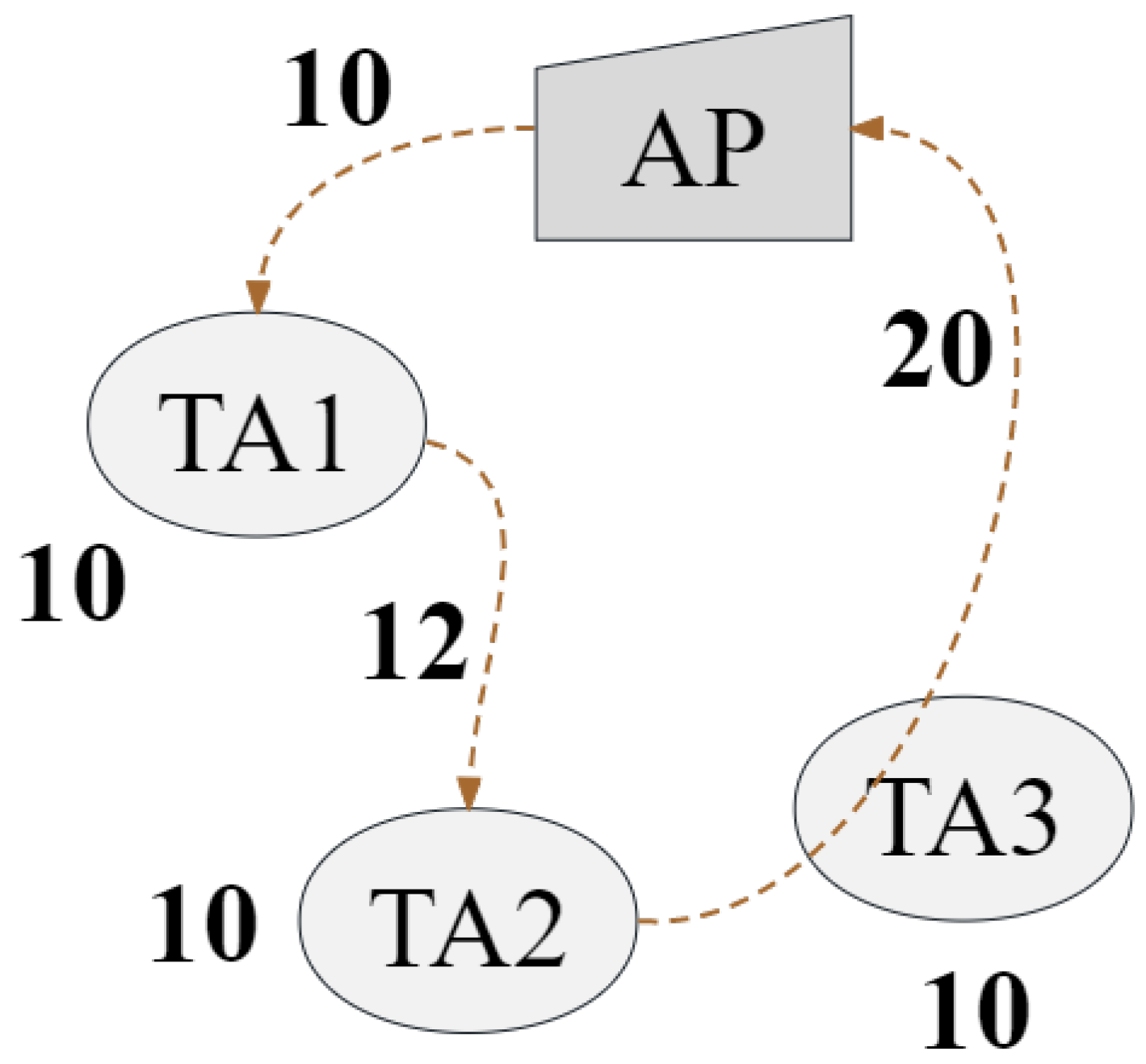
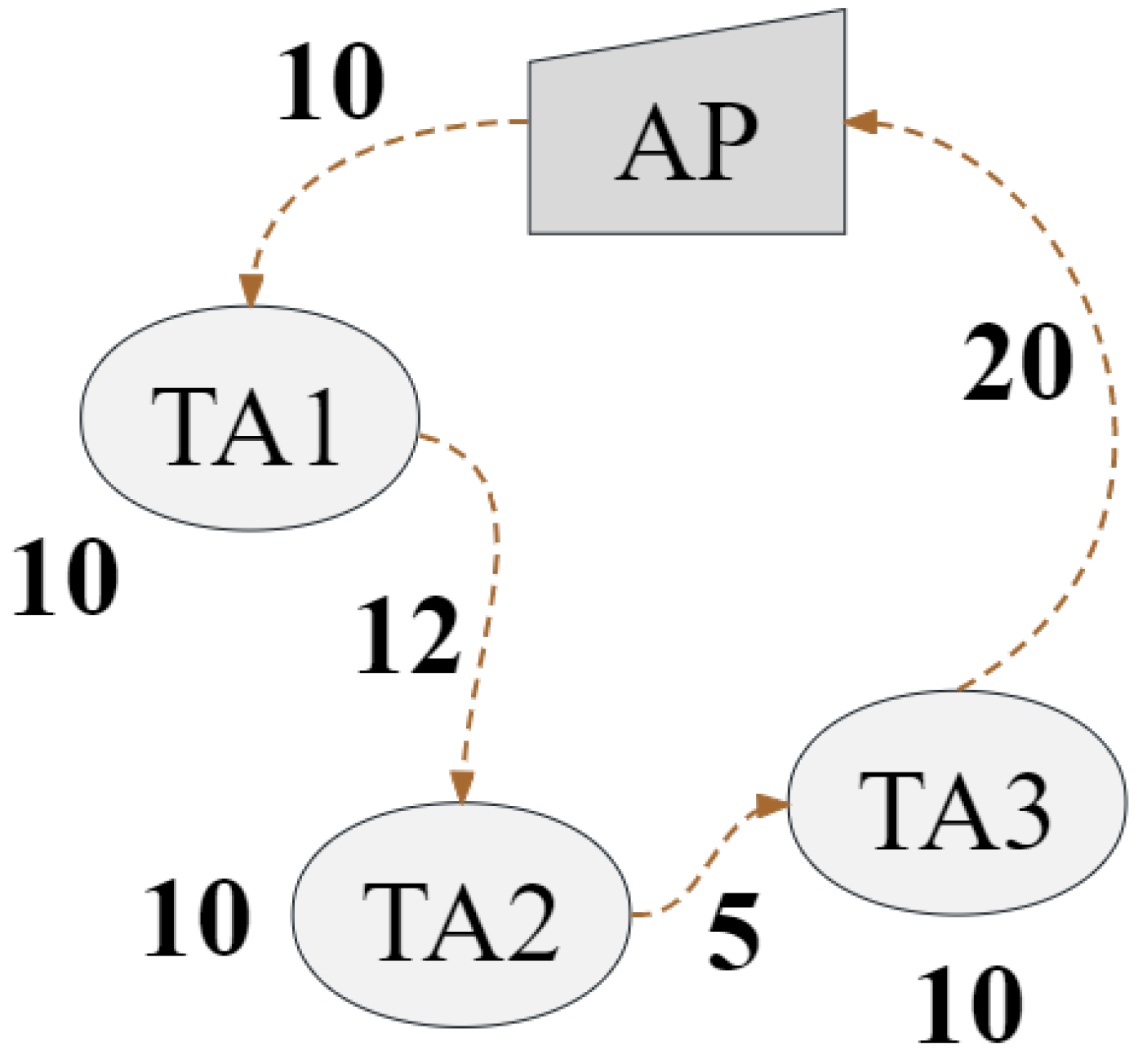
An example of Algorithm 2 is illustrated in Figure 3, Figure 4 and Figure 5. Assume that travel consumption is an integer, and temporarily assume that the hover consumption of UAV at each concerned TA is 10, i.e., the energy consumption occurring when a UAV resolves tasks at a specific TA. The UAV executes tasks in the order of $(AP-b_1\left(T{A}_1\right)-b_2\left(T{A}_2\right)-b_3\left(T{A}_3\right))$, and the energy consumption rate of each situation is ${\rho }_1^E=10/(10+10+10)=33.33\%$, ${\rho }_2^E=20/(10+10+12+10+20)=32.26\%$, and ${\rho }_3^E=30/(10+10+12+10+5+10+20)=38.96\%$, respectively. To some extent, the higher ${\rho }_k^E$, the more tasks can be solved with the same energy consumption, further indicating that we can obtain a better solution by organizing the dispatch of heterogeneous UAVs. In addition, the second item of (24) with a gravity control factor $\alpha$ is used to control the resource utilization of UAVs, aiming to maximize the utilization of the total battery resource carried by the UAV.

4.4. Subpath Determination

After obtaining the allocation set for different UAVs, HMUR determines the final task execution path for each UAV. In this section, we take into account the real-time window constraint of tasks.

We process UAV allocation options K and rearrange the routing path within the energy consumption limitation. According to the predicted results of Algorithm 2, it can be seen that, among all the tasks the UAV is responsible for, each UAV has at least one route that can complete all tasks. Specifically, in the selection of the allocation of $B_k$, the UAV $u_k$ starts from the AP, predicts the arrival time of the task points in $B_k$ that have not been traversed, and calculates the score function for the selected TA. The score function is formulated as follows:

$$S_{b_j}=Y_{b_j}^B-{log}_2{E}_{b_{j^{\prime }},b_j}^{trav}+{log}_{10}{L}_{b_j}^B$$

(25)

where $Y_{b_j}^B$ is the number of tasks that open the window upon arrival, $E_{b_{j^{\prime }},b_j}^{trav}$ is the energy consumption for flying from the previous point to $b_j$, and $L_{b_j}^B$ is total workload of data expected to be offloaded in $b_j$. The UAV selects the TA with the highest $S_{b_j}$ and travels to TA $b_j$ to complete as many tasks as possible during the window period. The optimization in this section focuses on adapting to the real-time window factor of the task, sacrificing some energy consumption to achieve greater QoS, and to some extent, neglecting energy consumption control. Therefore, during the adjustment process, there may be situations where the total energy consumption exceeds the maximum energy consumption of the UAV. In response to this situation, we abandon the path rearrangement and use the predicted path generated by Algorithm 2 as the final routing path.

This paragraph analyzes the time complexity of the algorithm to ensure the real-time applicability of the entire system. As previously mentioned, under the environment of n TAs and n UAVs, the Christofides algorithm can solve problems within polynomial time with a complexity of $O\left(n^{2}logn\right)$. Additionally, lines 8-19 of Algorithm 2 iterate through each path divided by the Christofides algorithm and traverse m UAVs in each path, with a time complexity strictly less than $O\left(mn\right)$. Moreover, after initialization, Algorithm 3 enters a double loop, which simulates the value of the UAVs reaching different TAs on each subpath, with a time complexity of $O\left(m\right)\times O\left(n\right)=O\left(mn\right)$. Consequently, HMUR can solve the problem within polynomial time.

5. Performance Evaluation

5.1. Dataset

To evaluate HMUR performance, we used real data from IoT users and BS deployments in Melbourne CBD provided by the Australian Communications and Media Authority [33]. The dataset includes a total of 816 GDs and 125 BSs available for the UAVs to offload data, In Figure 6, black dots represent geographically fixed GDs and red dots (i.e., the center of each red circle) represent the service base stations. In the clustering results of Figure 7, we retain only the abstract representation of GDs and BSs, depicting GDs in different partitions with light-colored circles of various colors and marking the clustering centers of the clustering results with red crosses. The overall distribution of the data is between geographic coordinates of latitude (−37.822, −37.808) and longitude (144.950, 144.975). Figure 6 provides a realistic map image of the scene, and Figure 7 shows the location of IoT devices and the results after clustering into TAs (the number of TAs is 50).

5.2. Benchmarks

Due to conducting experimental simulations in urban environments, set $\mathbf{X}=10.39$, $\mathbf{Y}=0.05$ [16], ${\eta }_{LoS}=1$, and ${\eta }_{NLoS}=20$ [2]. Other parameters related to aerodynamics are shown in Table 2. To better validate the effectiveness of UAV assistance, we only retained one available BS (144.966686, −37.815549) in the environment and set the AP at (144.962344, −37.815303).

The settings and definitions of the instance factors are shown in

Table 3. Factor setting.

Parameter	Value or Range of Value	Definition
$n_{GD}$	816	The number of GDs
$t_{avg}^A$	$[500,1500]$ s	Average time window of task
$n_{TA}$	$[20,60]$	The number of TAs
$L_{avg}^D$	$[1,6]$ MB	GDs’ average workload
$E_{avg}^U$	400 kJ	UAVs’ average battery capacity
$E^U$	700 kJ, 700 kJ, 600 kJ, 500 kJ, 400 kJ, 300 kJ, 200 kJ, 100 kJ, 100 kJ	Heterogeneous UAVs’ battery capacity
$\alpha$	$0.5$	Weight of fitness
$B^{bw}$	5 GHz	Bandwidth

. Among them, three essential factors are used as independent variables to analyze the performance of the algorithm, which are: (a) the number of TAs, (b) the average real-time window size of the task, and (c) the average workload generated by the GDs. Four indicators were adopted to evaluate the compared algorithms, namely (a) the total number of solved tasks, (b) the amount of offloaded workload, (c) the quantity of dispatched UAVs, and (d) the number of tasks solved by the UAVs per minute.

5.3. Performance Comparison

The architecture of this paper was written in Python 3.7, and the algorithm ran on the Ubuntu 22.04.1 LTS operating system, under an NVIDIA RTX 4090 cluster environment. To test the performance of the proposed algorithm HMUR, it was compared with the best-existing algorithms for the considered problem: CEDAN by Bera et al. [16] and the GA-based method (GAM) of Wang et al. [34]. In this paper, we set the energy payload of the UAVs in CEDAN and GAM to the average energy payload of heterogeneous UAVs in HMUR, denoted as $E_{avg}^U$. Furthermore, to evaluate the effectiveness of the subpath determination strategy (Algorithm 3), the proposed algorithm without this strategy (HMUWS) was also compared. Furthermore, in the diagram, as the task TA on the horizontal axis changes, we maintained the total number of GDs retained. Furthermore, we decreased the number of GDs included in each TA as the number of TAs increased.

The total number of solved tasks: Figure 8 shows the total number of solved tasks when varying the number of TAs. As the number of TAs increases, the number of tasks assisted by HMUR and that by the baseline algorithms both show an increasing trend, but HMUR is 73.86% higher than CEDAN and 80.22% higher than GAM, while 36.43% higher than HMUW3 (when the number of TAs is 30). Meanwhile, Figure 9 shows the numerical performance of the number of auxiliary tasks solved when the average duration of the task window changes. It reveals that the longer the duration of the task window, the more tasks the UAVs assist in solving. However, when the time window size exceeds a threshold (about 1000 s), the number of solved tasks obtained by the other three algorithms no longer increases, except that of HMUR. This is probably due to HMUR considering the soft time constraints; in each selection, HMUR tends to choose TAs with more tasks with open time windows.

The total amount of offloaded workload: It can be seen from Figure 10 that the amount of offloaded workload generated by HMUR is higher than those of the other algorithms. With an increase in the number of solved tasks, the amount of offloaded workload gradually increases for all four algorithms. In Figure 11, we vary the average duration of the task windows to obtain the value of the workload offloading. HMUR selects routes that can achieve a higher QoS by calculating the TA’s score function, thereby solving more tasks and offloading more data.

The quantity of dispatched UAVs: Figure 12, Figure 13, Figure 14 and Figure 15 shows the difference in the number of UAVs dispatched by HMUR and CEDAN when the average amount of data generated by the GDs varies. The results show that the average number of UAVs dispatched by HMUR is 25.95% (the average task window is 500 s in Figure 12), 25.19% (the average task window is 1000 s in Figure 13), 41.63% (the average task window is 1500 s in Figure 14), and 24.62% (all tasks are open in Figure 15) less than that of CEDAN. This is because HMUR considers the compatibility between heterogeneous UAVs and paths, making more rational use of the UAV resources. Moreover, since HMUR is developed by adding Algorithm 3 to the base of HMUWS, and since Algorithm 3 does not involve changes in the number of unmanned aerial vehicles, HMUWS is not considered in this context.

Number of tasks solved per minute: Figure 16 shows the time utilization of HMUR and the baseline algorithm, which we represent as the average number of tasks solved per minute. It can be seen that HMUR sacrifices some time to obtain a larger number of tasks, resulting in a decrease in time utilization. However, overall, the performance of HMUR is still acceptable.

In the above experiment, we tested the impact of system scale (number of TAs), task urgency (average duration of the task window), and task load (average workload generated by GD) on the system. The experimental results show that the number of auxiliary tasks and offloaded data increase with increasing system scale and average task window duration, while the quantity of dispatched UAVs mainly increases with the growth of the average workload generated by the GD. HMUR outperforms the other algorithms because of the following reasons: The clustering results of k-means exactly meet the requirements of the system model, that is the sum of distances between the optimal hover position and all GDs is the shortest. At the same time, in Algorithm 2, the fitness evaluates the effective energy consumption of the UAVs in executing tasks and maximizes the utilization of battery energy within the allowable range of energy consumption. Finally, in Algorithm 3, the score function considering the timeliness constraints helps the UAVs find the TA with the highest number of executable tasks at each time point, thus improving the QoS.

6. Conclusions and Future Work

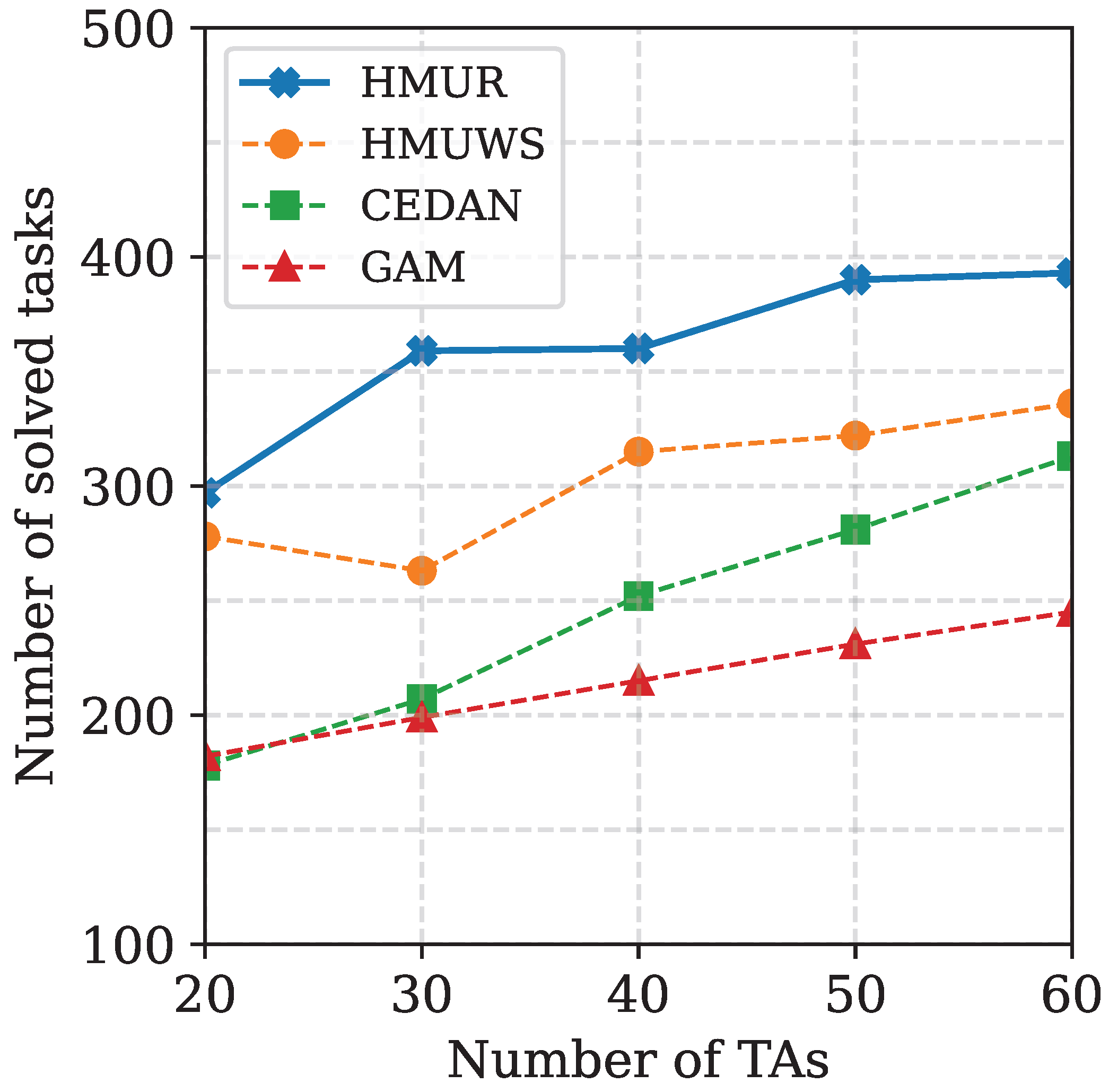
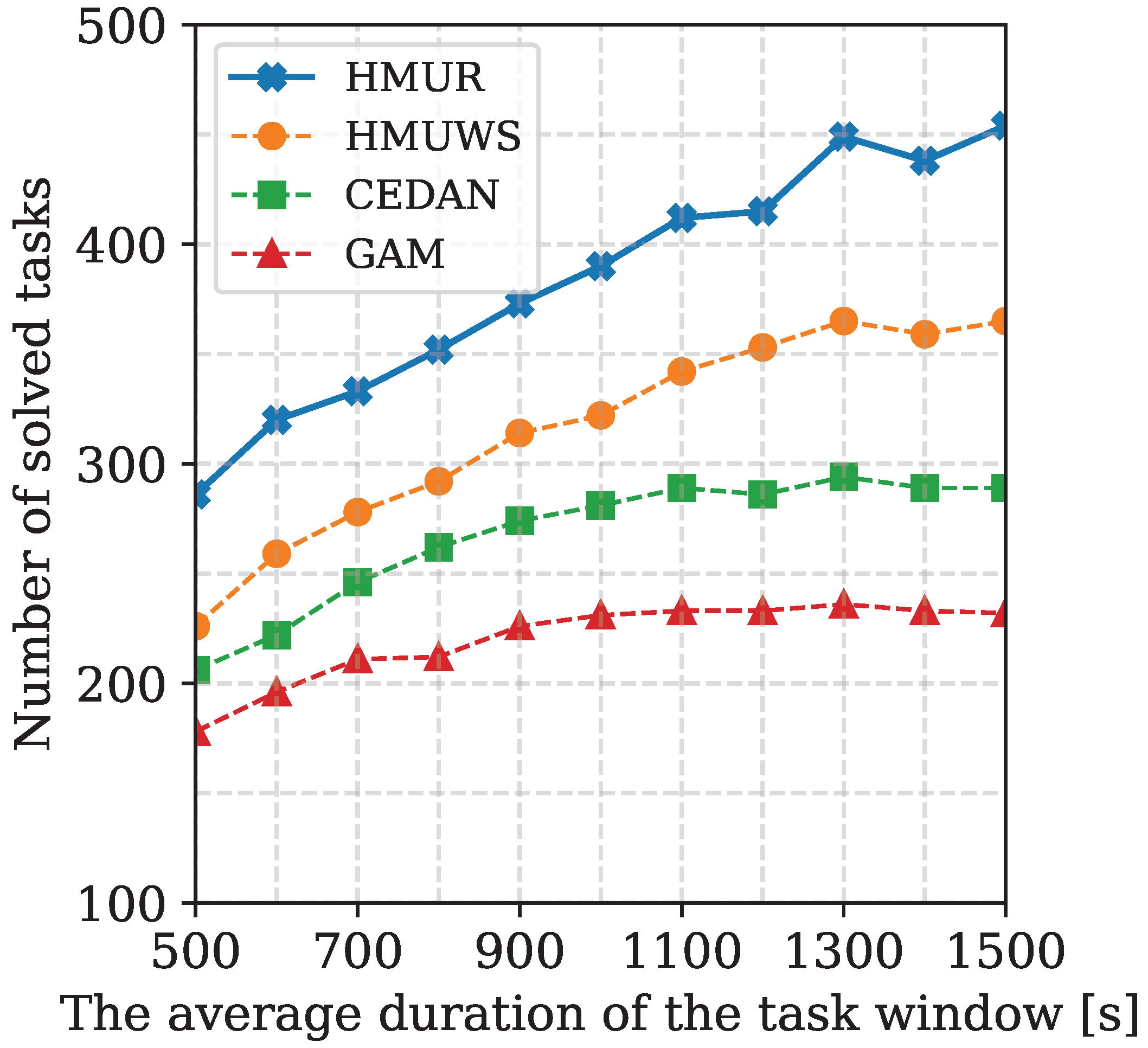
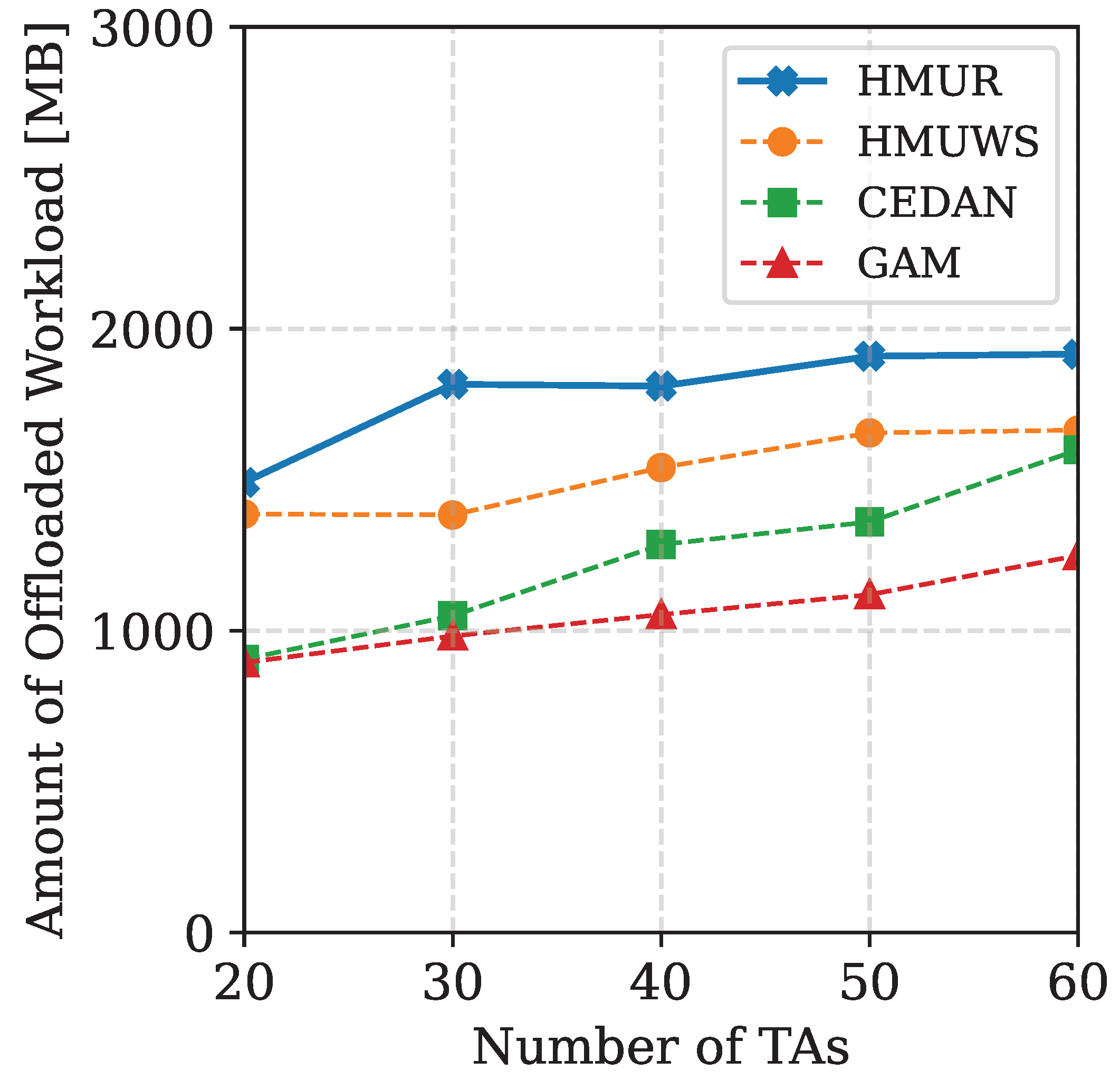
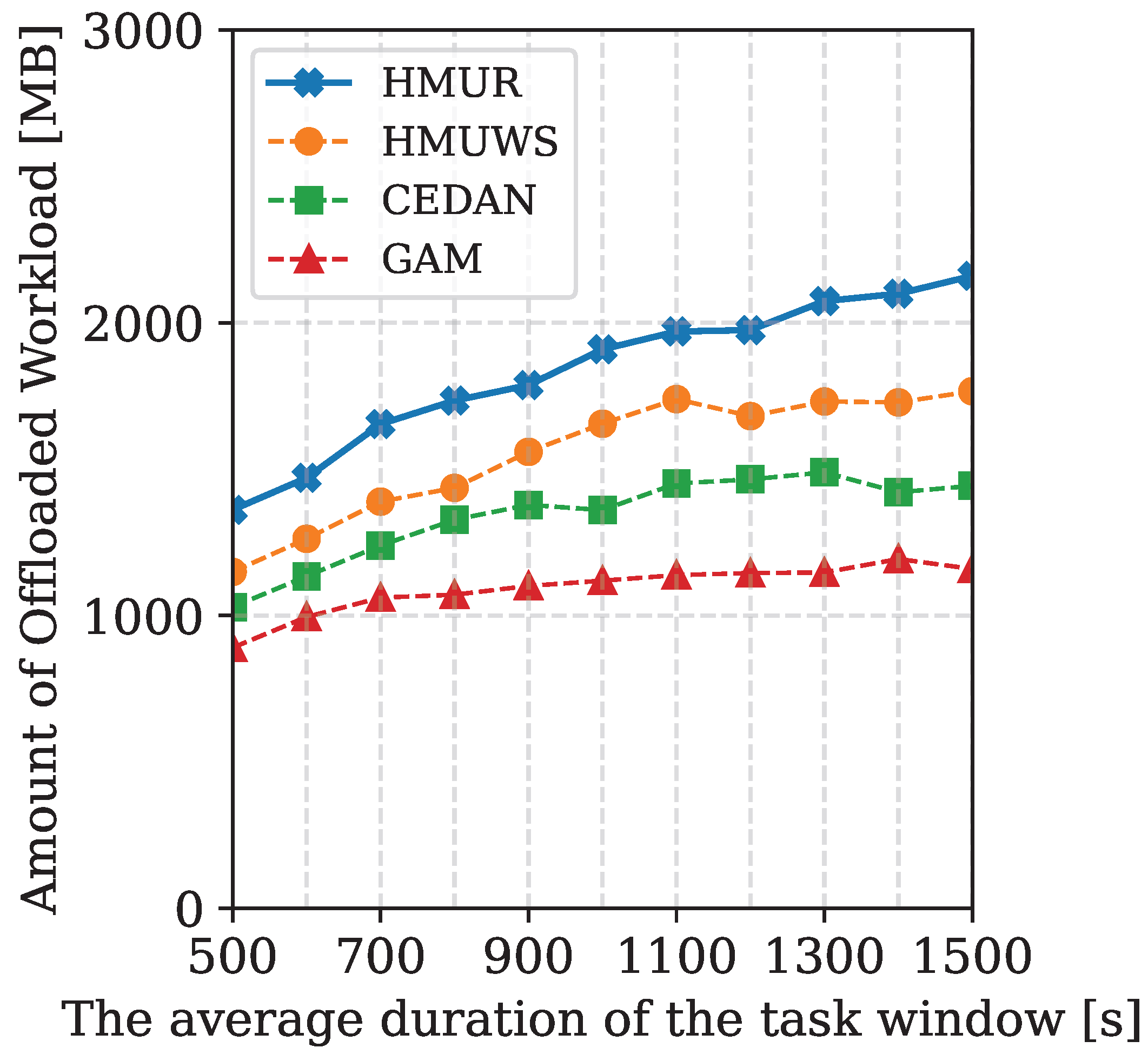
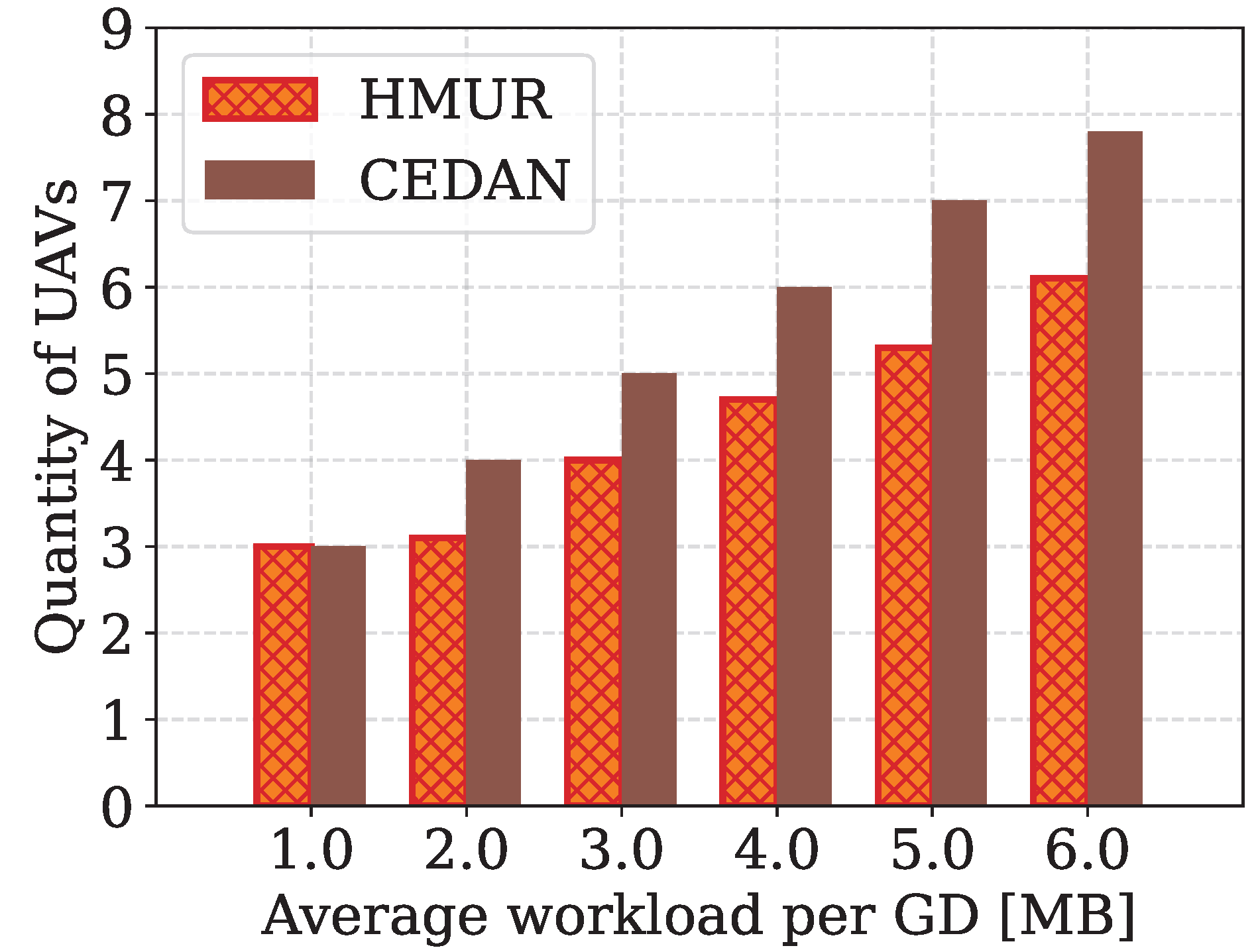
In this paper, a multi-UAV routing algorithm named HMUR is proposed for the UAV-assisted MEC problem. Instead of isomorphic UAVs as commonly considered in the literature, we also took into account the heterogeneity of UAVs and the real-time characteristics of the task. An effective fitness measurement is defined to match the UAVs and different routing paths under certain energy constraints. A score function is designed to determine the final route with the highest QoS. An extensive comparison of the proposed algorithm is performed against the best existing approaches. The experimental results show that the proposed method is superior to the best existing algorithms on multiple metrics. We demonstrated the effectiveness of the algorithm through experiments divided into four parts, which collectively evaluated the performance of the service based on the number of tasks completed, the volume of data offloaded, the efficiency of task resolution, and the number of UAVs used. The volume of data offloaded is correlated with the number of tasks completed. Through the HMUR algorithm, heterogeneous UAVs are appropriately allocated in the UAV allocation segment and tasks are reorganized in the subpath determination segment to ensure that more tasks are within their window period when the UAV reaches the task area. Furthermore, since the fitness function considers the ratios of $E_k^{hover}$ to $E_k^{total}$ (reflecting the effective energy consumption of UAVs) and $E_k^{total}$ to $E_k^{max}$ (reflecting UAV battery utilization), it ensures that the energy of each UAV is efficiently used, thereby indirectly reducing the number of UAV deployments.

Future research avenues involve the consideration of the improvement of the proposed framework. For example, more UAV attributes such as output power, battery weight, bandwidth, and flight speed can be introduced as a UAV-type selection mechanism. It also seems worthwhile to apply the proposed algorithm with some heuristic offloading solutions for further improvement. Meanwhile, future work could consider replacing FDMA with communication methods such as TDMA and LoRaWAN to achieve new effects. At the same time, we will explore the integration of machine learning techniques and reinforcement learning for routing to adaptively allocate tasks based on historical data, improving the efficiency and responsiveness of our system. Additionally, we aim to develop a user-friendly tool for easy implementation and deployment of our algorithm in various MEC environments, enhancing user adoption and practicality.