Message Passing Detectors for UAV-Based Uplink Grant-Free NOMA Systems

Abstract

Utilizing unmanned aerial vehicles (UAVs) as mobile access points or base stations has emerged as a promising solution to address the excessive traffic demands in wireless networks. This paper investigates improving the detector performance at the unmanned aerial vehicle base stations (UAV-BSs) in an uplink grant-free non-orthogonal multiple access (GF-NOMA) system by considering the activity state (AS) temporal correlation of the different user equipments (UEs) in the time domain. The Bernoulli Gaussian-Markov chain (BG-MC) probability model is used for exploiting both the sparsity and slow change characteristic of the AS of the UE. The GAMP Bernoulli Gaussian-Markov chain (GAMP-BG-MC) algorithm is proposed to improve the detector performance, which can utilize the bidirectional message passing between the neighboring time slots to fully exploit the temporally correlated AS of the UE. Furthermore, the parameters of the BG-MC model can be updated adaptively during the estimation procedure with unknown system statistics. Simulation results show that the proposed algorithm can improve the detection accuracy compared to existing methods while keeping the same order complexity.

1. Introduction

Recently, unmanned aerial vehicle (UAV) assisted communications, such as UAV base stations (UAV-BSs), have garnered significant research interest for their ability to provide rapid and widespread connectivity [1,2,3]. The UAV-BS system can offer a cost-effective and innovative solution to managing fluctuating traffic demands, especially in scenarios where traditional infrastructure-based base stations, which are expensive and slow to deploy, are not financially viable. The UAV-BS can be a data collector for sensor networks in remote or restricted areas [4]. Additionally, it can function as an emergency BS when existing ones fail due to natural disasters or become overwhelmed by sudden surges in traffic [5,6]. However, the large number of potential user equipments (UEs) makes UAV-BS communication difficult and complicated.

Currently, grant-free non-orthogonal multiple access (GF-NOMA) is a promising candidate to support UAV-BS communications. The non-orthogonal multiple access (NOMA) technique enables the system resource block to simultaneously serve multiple UEs [7,8]. At the same time, the grant-free (GF) scheme allows UEs to transmit data to the UAV-BS directly without waiting for its permission, which can decrease the access delay and reduce the control overhead for coordination [9]. In the case of applying GF-NOMA to uplink, recovering the transmitted signal through designing efficient multi-UEs detection methods is challenging, not only due to the large number of UEs present in the cell but also because they are randomly accessing the network in each access slot. However, UEs are only sporadically and randomly activated in practical massive machine-type communications (mMTC) systems, which brings sparsity of the transmitted slots in the time-frequency resource grid [10], which can be changed across different slots within a single frame [11,12]. Furthermore, once a UE is activated for performing the data transmission, it typically requires several consecutive time slots. Then, this UE will be deactivated for a certain period until the next transmission. This activation and deactivation is denoted as activity state (AS), and it exhibits a temporal correlation [13]. Consequently, to enhance the performance of the detectors in a GF-NOMA system, the existing methods incorporate not only the exploitation of sparsity but also the temporal correlation information provided by AS.

According to the literature of GF-NOMA, detectors based on message passing (MP) algorithms [12,13,14] have a better performance compared to conventional compressed sensing (CS) methods. In [12], the authors exploited the temporal correlation of the active UE and modeled it by a Markov process. The authors in [13] utilized the sparse Basianyes learing (SBL) and pattern coupled sparse Basianyes learing (PCSBL) models to formulate the slow change of the UEs AS, then proposed the SBL-based multi-UEs detection algorithms, outperforming CS methods. Then, [14] further embedded the generalized approximate message passing (GAMP) algorithm with the SBL and PCSBL models, and proposed the GAMP sparse Basianyes learing (GAMP-SBL) and the GAMP pattern coupled sparse Basianyes learing (GAMP-PCSBL) detector algorithms, which can reduce the complexity. However, the SBL and PCSBL models mainly consider the sparse structure of the UE activity. Motivated by [12], we find that the Markov chain (MC) better captures the slow change of the AS features with successive time slots and the active UE sparsity simultaneously. Furthermore, differing from [12], the hybrid message passing (HMP) rule [15] is used to update the parameters of the MC on the factor graph (FG) to improve the convergence speed.

This paper focuses on designing a high-performance MP algorithm, resulting in the GAMP-BG-MC detector algorithm for the UAV-BS-based uplink GF-NOMA system. The main contributions of this paper are summarized as follows.

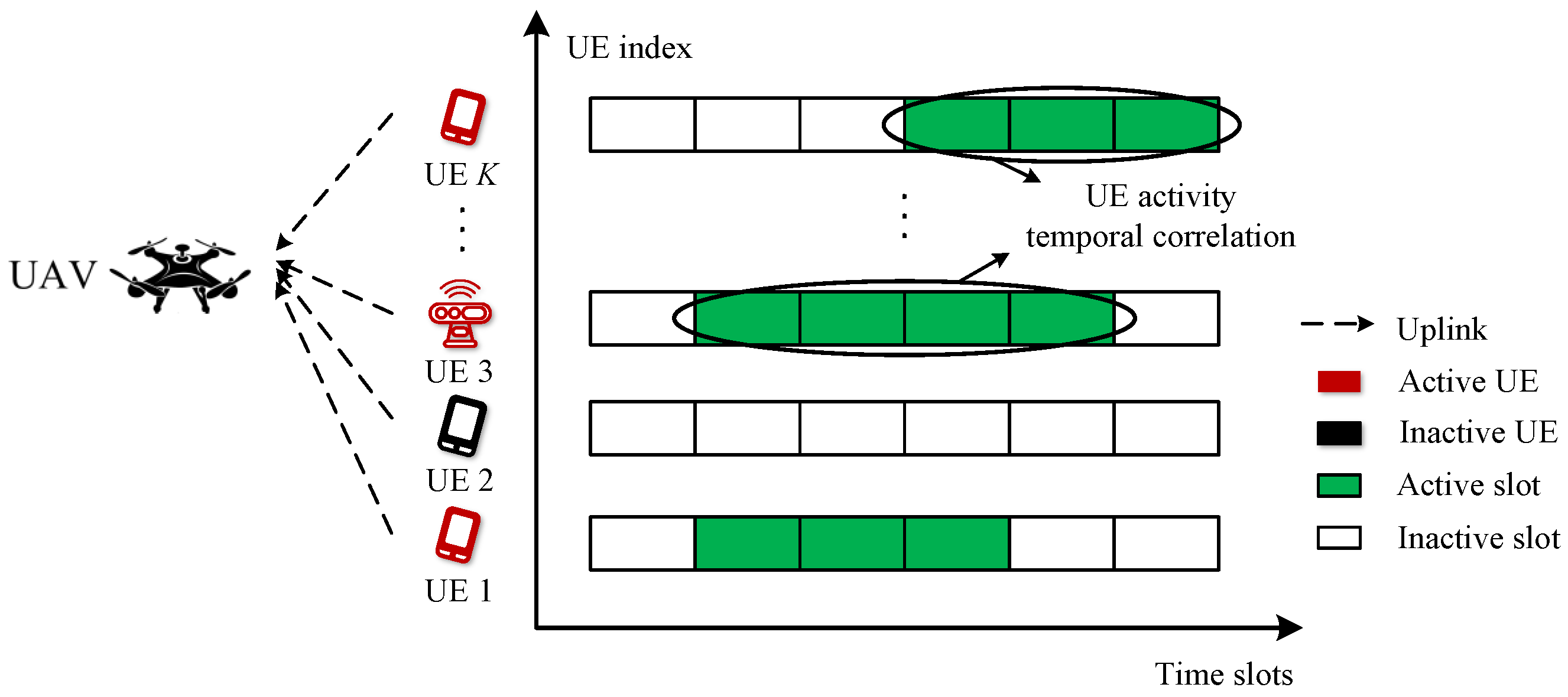
• The BG-MC model is employed to jointly exploit both the sparse structure of the active UE and the slow change feature in consecutive time slots of the AS. Indeed, the performance of the UAV-BS detector can be improved by updating the AS while considering the temporal correlation. Hence, both the forward messages from the previous slot and the backward messages from the next slot are considered in the MP algorithm at each iteration.
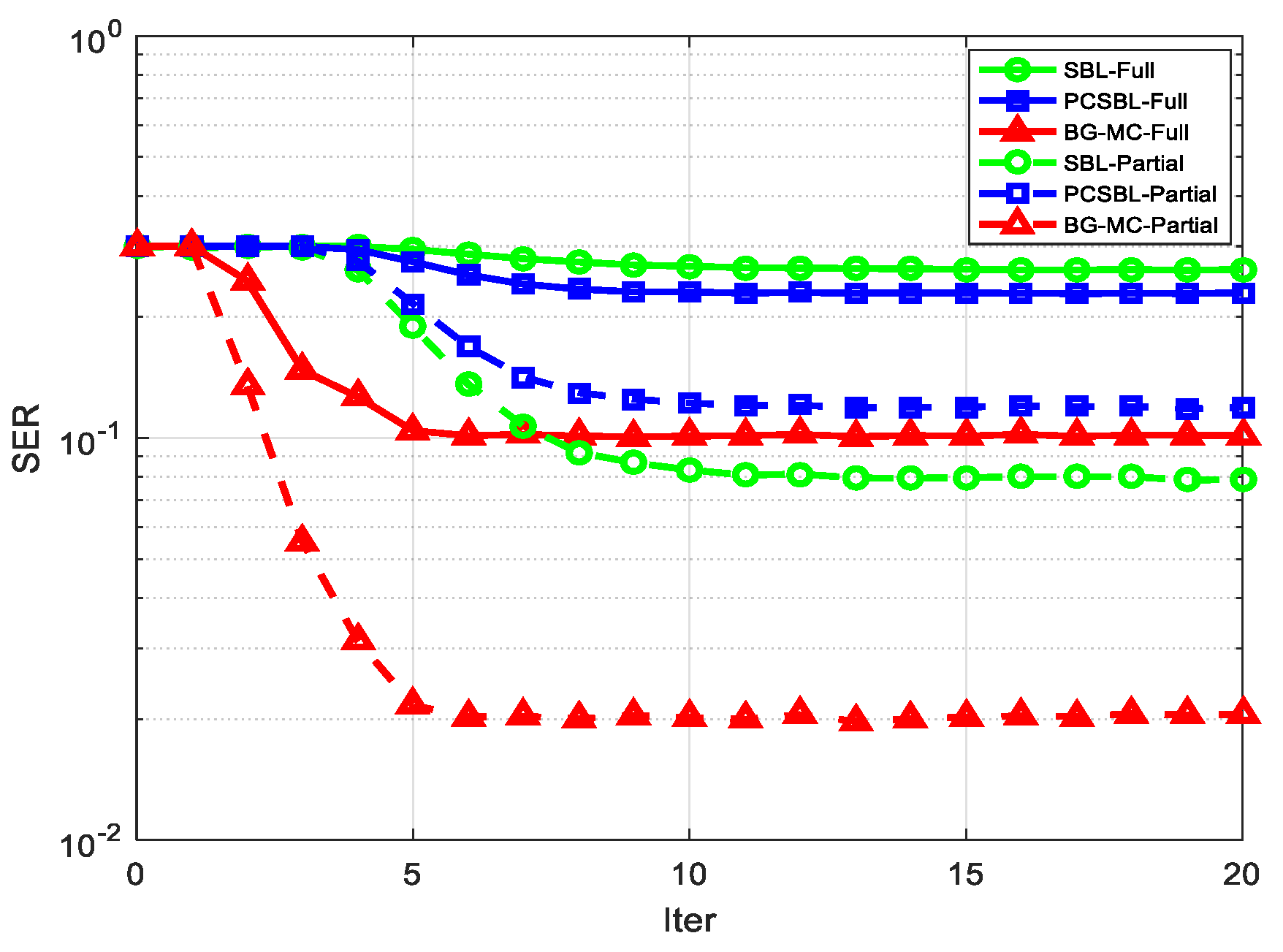
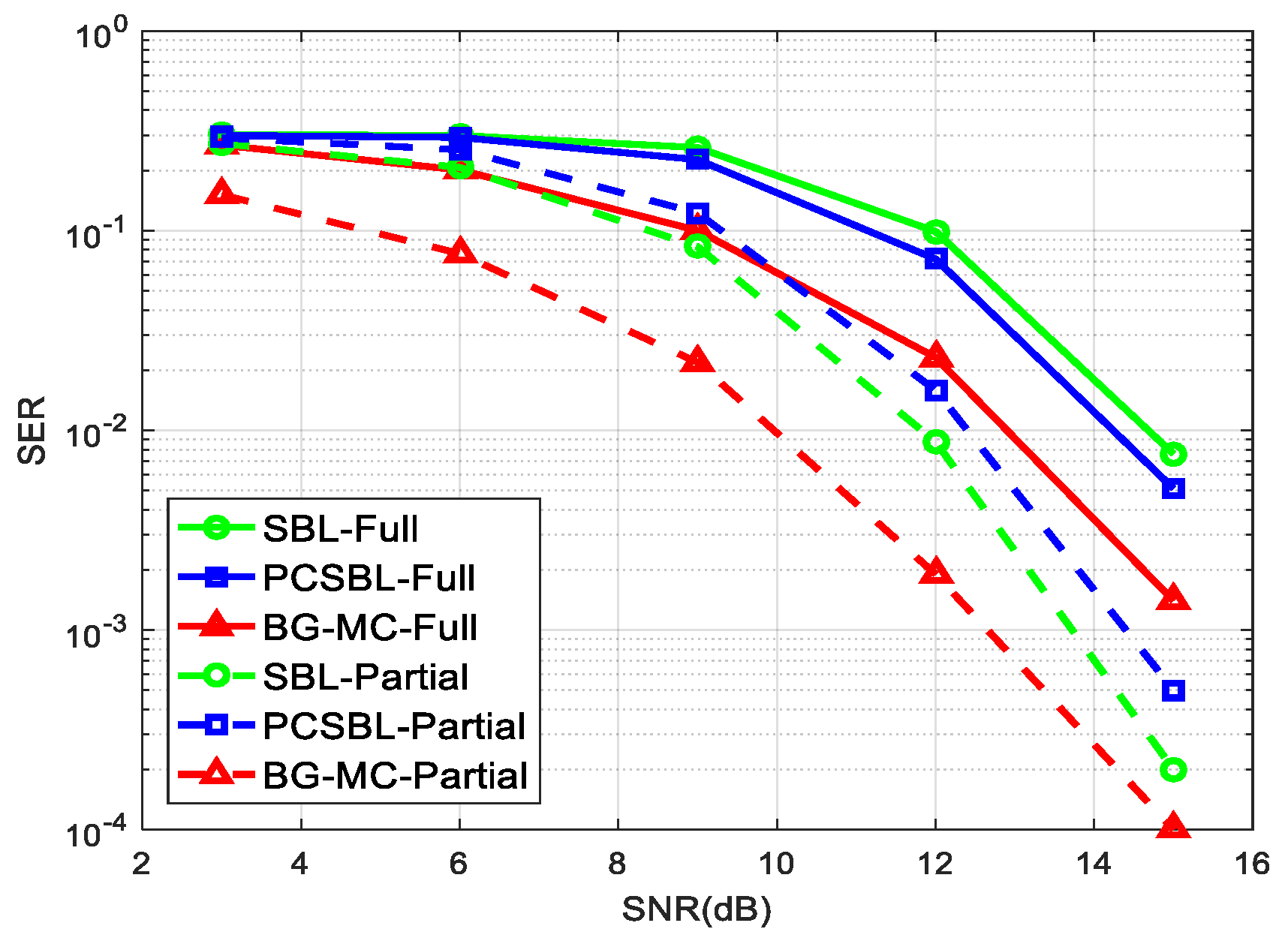
• Making use of the HMP rule, the GAMP-BG-MC algorithm is proposed to detect the UAV-BS received signal of multiple superimposed UEs. The proposed GAMP-BG-MC algorithm not only calculates the more accurate posterior probability density function (PDF) of the transmitted signal but also adaptively learns the parameters of the prior model during the estimation procedure. Simulation results show that the GAMP-BG-MC algorithm has a better signal-to-noise ratio (SNR) performance as compared to the GAMP-SBL [13,14] and the GAMP-PCSBL [14] algorithms, respectively, while keeping the complexity.

The remaining parts of this paper are organized as follows. Section 2 introduces the system model of the UAV-based uplink GF-NOMA network. Section 3 proposes the GAMP-BG-MC algorithm as the adaptive UAV-BS detector. Then, the numerical results of the proposed algorithm are given in Section 4. Finally, the conclusions of this paper are presented in Section 5.

Notation: Boldface lowercase and uppercase letters denote vectors and matrices; ${(·)}^{\mathrm{T}}$ and ${(·)}^{*}$ denote transposition and conjugation, respectively. The expectation of a function $f\left(x\right)$ w.r.t. a PDF $g\left(x\right)$ is expressed as ${〈f\left(x\right)〉}_{g\left(x\right)}$; $\mathcal{CN}(x;\mu ,v)$ denotes x following a complex Gaussian distribution with mean $\mu$ and variance v. $\delta (·)$ is the Dirac delta function.

2. System Model and Factor Graph

2.1. System Model

A typical GF-NOMA system is considered [14], where the UAV-BS is equipped with a single antenna. K potential single-antenna UEs under the service area of a UAV-BS perform GF-NOMA random access (RA), sharing the same bandwidth resource and transmitting signals to the UAV-BS, as illustrated in Figure 1. The transmission is assumed to utilize the multi-carrie code division multiple access (MC-CDMA) scheme detailed in [16], which belongs to the NOMA techniques. The MC-CDMA is a hybrid scheme combing code division multiple access (CDMA) and orthogonal frequency-division multiplexing (OFDM), making the MC-CDMA signal tolerant against frequency selective channels, inter-symbol interference (ISI), and inter-carrier interference (ICI) through the use of cyclic prefix and equalization [17]. The uplink transmission of the UEs is multiplexed over N frequency-divided subcarriers. In each time slot, the ASs of different UEs are assumed to be independent of each other, $K_a\le K$ of which are active and transmit packets to the BS. The active rate $p_a$ is used to indicate the percentage of active UEs. The active UE k sends the complex symbol $b_k$ from a predefined complex signal constellation and spreads it over the N sub-carriers. Meanwhile, the inactive UE is considered to be transmitting a zero symbol $b_k=0$. The received signal $\mathit{y}={[y_1,\cdots ,y_N]}^{\mathrm{T}}$ at the BS for the j-th time slot can be expressed as

$$\mathit{y}=\mathit{H}\mathit{b}+\mathit{w},$$

(1)

where $\mathit{H}=[{\mathit{h}}_{\mathbf{1}},\cdots ,{\mathit{h}}_{\mathit{K}}]\in {\mathbb{C}}^{N\times K}$ denotes the complex channel response matrix, representing the spread codes of K UEs over N sub-carriers. $\mathit{b}={[b_1,\cdots ,b_K]}^{\mathrm{T}}$ is the transmitted signal from K UEs. $\mathit{w}={[w_1,\cdots ,w_N]}^{\mathrm{T}}\sim \mathcal{CN}(\mathbf{0},{\lambda }^{-1}\mathit{I})$ denotes the additive white Gaussian noise (AWGN) with the variance ${\lambda }^{-1}$. The received signals $\mathit{Y}=[{\mathit{y}}_1,\cdots ,{\mathit{y}}_J]\in {\mathbb{C}}^{N\times J}$ span J continuous time slots and are represented as a multiple measurement vector (MMV) model, [14]

$$\mathit{Y}=\mathit{H}\mathit{B}+\mathit{W},$$

(2)

where $\mathit{B}=[{\mathit{b}}_1,\cdots ,{\mathit{b}}_J]\in {\mathbb{C}}^{K\times J}$ denotes the transmitted signal matrix and the noise is $\mathit{W}=[{\mathit{w}}_1,\cdots ,{\mathit{w}}_J]\in {\mathbb{C}}^{N\times J}$. In a practical mMTC scenario, the potential UEs keep their AS in some random consecutive time slots within the entire frame [10]. As shown in Figure 1, the AS of the UE exhibits a temporal correlation in the time domain, which promotes the sparse structure of signal $\mathit{B}$ in (2). The task of multi-UEs detection is to estimate the sparse transmitted signal $\mathit{B}$ from the received signal $\mathit{Y}$ with the unknown UE activity value.

2.2. Probabilistic Formulation

From (2), the hidden variable $\mathit{Z}\triangleq \mathit{H}\mathit{B}\in {\mathbb{C}}^{N\times J}$ is defined, where ${\mathit{z}}_j=\mathit{H}{\mathit{b}}_j,\forall j\in J$. Then, the detector transfer function can be written as

$$p\left(\mathit{Y}\right|\mathit{B})=p\left(\mathit{Y}\right|\mathit{Z})p\left(\mathit{Z}\right|\mathit{B})={\prod }_{j=1}^{J}p\left({\mathit{y}}_j\right|{\mathit{z}}_j)p\left({\mathit{z}}_j\right|{\mathit{b}}_j).$$

(3)

The conditional PDF $p\left({\mathit{y}}_j\right|{\mathit{z}}_j)$ can be further factorized as

$$p\left({\mathit{y}}_j\right|{\mathit{z}}_j)=\prod _{n=1}^N\underset{f_{Y,n,j}}{\underbrace{p\left(y_{n,j}\right|z_{n,j})}}=\prod _{n=1}^N\mathcal{CN}(y_{n,j};z_{n,j},{\lambda }^{-1}).$$

(4)

The hard constraint factors provided by $p\left({\mathit{z}}_j\right|{\mathit{b}}_j)$ can be concretely represented as

$$p\left({\mathit{z}}_j\right|{\mathit{b}}_j)=\prod _{n=1}^N\underset{f_{Z,n,j}}{\underbrace{p\left(z_{n,j}\right|{\mathit{b}}_j)}}=\prod _{n=1}^N\delta \left(z_{n,j}-\sum _{k=1}^K{h}_{n,k}{b}_{k,j}\right),$$

(5)

where $h_{n,k}$ denotes the element in the n-th row and k-th column of $\mathit{H}$.

For the channel prior model, the BG-MC probability model [18] is utilized, which can exploit both the block sparse structure and the slow change of the UE AS feature simultaneously. Each element $b_{k,j}$ has a conditionally independent distribution given by

$$\begin{array}{cc}\hfill p\left(\mathit{B}\right|\mathit{S},\mathit{V})& ={\prod }_{k=1}^K{\prod }_{j=1}^J\underset{f_{B,k,j}}{\underbrace{p\left(b_{j,k}\right|s_{k,j},v_{k,j})}}\hfill \\ \hfill & =\delta \left(s_{k,j}\right)\delta \left(b_{k,j}\right)+\delta (1-s_{k,j})\mathcal{CN}(b_{k,j};0,v_{k,j}^{-1}),\hfill \end{array}$$

(6)

where $s_{k,j}\in \{0,1\}$ denotes the MC state implicating if the UE is active ($s_{k,j}=1$) or inactive ($s_{k,j}=0$) at the j time slot; $v_{k,j}^{-1}$ is a non-negative hyperparameter controlling the sparsity of the transmitted signal $b_{k,j}$.

Similar to [12,18,19], the stationary first-order MC is employed to effectively capture the slow evolution of UE AS across time slots. The MC here is given by

$$p\left(\mathit{S}\right)=\prod _{k=1}^{K}p\left({\mathit{s}}_k\right)=\prod _{k=1}^K\left[\underset{f_{S_{k,1}}}{\underbrace{p\left(s_{k,1}\right)}}\prod _{j=2}^J\underset{f_{S_{k,j}}}{\underbrace{p\left(s_{k,j}\right|s_{k,j-1})}}\right],$$

(7)

with the initial probability given by $p\left(s_{k,1}\right)={\left(p_k^{10}\right)}^{s_{k,1}}{(1-p_k^{10})}^{1-s_{k,1}}$, and the transition probability is expressed as

$$p\left(s_{k,j}\right|s_{k,j-1})=\left\{\begin{array}{c}{(1-p_k^{10})}^{1-s_{k,j}}{\left(p_k^{10}\right)}^{s_{k,j}},s_{k,j-1}=0,\\ {\left(p_k^{01}\right)}^{1-s_{k,j}}{(1-p_k^{01})}^{s_{k,j}},s_{k,j-1}=1.\end{array}\right.$$

(8)

The MC is characterized by parameters $p_k^{01}\triangleq \mathrm{Pr}(s_{k,j}=0|s_{k,j-1}=1)$ and $p_k^{10}\triangleq \mathrm{Pr}(s_{k,j}=1|s_{k,j-1}=0)$ for different UEs. Differing from [12,18], the parameters $p_k^{01},p_k^{10}$ are considered as variables, with the prior given by the Beta distributions

$$\underset{f_{p_k^{01}}}{\underbrace{p\left(p_k^{01}\right)}}=\mathrm{Be}(p_k^{01};c_k,d_k),\underset{f_{p_k^{10}}}{\underbrace{p\left(p_k^{10}\right)}}=\mathrm{Be}(p_k^{10};e_k,f_k),$$

(9)

where $c_k,d_k$, and $e_k,f_k$ can control the initial values of $p_k^{01}$ and $p_k^{10}$, respectively. Meanwhile, the precision term $v_{k,j}$ can be modeled as the Gamma distribution [20], i.e.,

$$p\left(\mathit{V}\right)=\prod _{k=1}^K\prod _{j=1}^J\underset{f_{v_{k,j}}}{\underbrace{p\left(v_{k,j}\right)}}=\prod _{k=1}^K\prod _{j=1}^J\mathrm{Ga}(v_{k,j};{ϵ}_{k,j},{\eta }_{k,j}),$$

(10)

where the initial values of $v_{k,j}$ are controlled by the parameters ${ϵ}_{k,j},{\eta }_{k,j}$. The main assumptions considered in the system model are summarized in

Table 1. Main Considered Assumptions.

Assumption	Description
Transmission scheme	GF-NOMA scheme is employed for multiple UEs
Single antenna	Both UAV-BS and UEs are equipped with a single antenna
Independent UE AS	Activity states of different UEs are assumed to be independent
Channel prior model	The BG-MC probability model is utilized
GF-NOMA technique	MC-CDMA scheme, a hybrid of CDMA and OFDM, is utilized

.

2.3. Factor Graph Representation

Based on (2) and (4)–(10), the joint PDF of all unknown variables given by the observation $\mathit{Y}$ can be factorized as

$$\begin{array}{cc}\hfill & p(\mathit{B},\mathit{Z},\mathit{S},\mathit{V},{\mathit{p}}^{10},{\mathit{p}}^{01}|\mathit{Y})\hfill \\ \hfill & =p\left(\mathit{Y}\right|\mathit{Z})p\left(\mathit{Z}\right|\mathit{B})p\left(\mathit{B}\right|\mathit{S},\mathit{V},{\mathit{p}}^{10},{\mathit{p}}^{01})\hfill \\ \hfill & \propto \prod _{j=1}^J\left\{\prod _{n=1}^N{f}_{Y_{n,j}}(y_{n,j},z_{n,j})f_{Z_{n,j}}(z_{n,j},{\mathit{b}}_j)\prod _{k=1}^K{f}_{B_{k,j}}(b_{k,j},s_{k,j},v_{k,j})f_{v_{k,j}}\left(v_{k,j}\right)\right\}\hfill \\ \hfill & \prod _{k=1}^K\left\{f_{p_k^{01}}\left(p_k^{01}\right)f_{p_k^{10}}\left(p_k^{10}\right)f_{S_{k,1}}(s_{k,1},p_k^{10})\prod _{j=2}^J{f}_{S_{k,j}}(s_{k,j},s_{k,j-1},p_k^{10},p_k^{01})\right\}.\hfill \end{array}$$

(11)

The factor graph of (11) is illustrated in Figure 2. In addition, local functions and their corresponding distributions are shown in

Table 2. Functions of the factor nodes in Figure 2.

Factor	Distribution	Function
$f_{Y_{n,j}}$	$p\left(y_{n,j}\right|z_{n,j})$	$\mathcal{CN}(y_{n,j};z_{n,j},{\lambda }^{-1})$
$f_{Z_{n,j}}$	$p\left(z_{n,j}\right|{\mathit{b}}_j)$	$\delta \left(z_{n,j}-{\sum }_{k=1}^K{h}_{n,k}{b}_{k,j}\right)$
$f_{B_{k,j}}$	$p\left(b_{j,k}\right|s_{k,j},v_{k,j})$	Equation (6)
$f_{v_{k,j}}$	$p\left(v_{k,j}\right)$	$\mathrm{Ga}(v_{k,j};{ϵ}_{k,j},{\eta }_{k,j})$
$f_{S_{k,1}}$	$p\left(s_{k,1}\right|p_k^{10})$	${\left(p_k^{10}\right)}^{s_{k,1}}{(1-p_k^{10})}^{1-s_{k,1}}$
$f_{S_{k,j}}$	$p(s_{k,j},s_{k,j-1}|p_k^{10},p_k^{10})$	Equation (8)
$f_{p_k^{01}}$	$p\left(p_k^{01}\right)$	$\mathrm{Be}(p_k^{01};e_k,f_k)$
$f_{p_k^{10}}$	$p\left(p_k^{10}\right)$	$\mathrm{Be}(p_k^{10};c_k,d_k)$

. The novel MP algorithm is designed in the next Section.

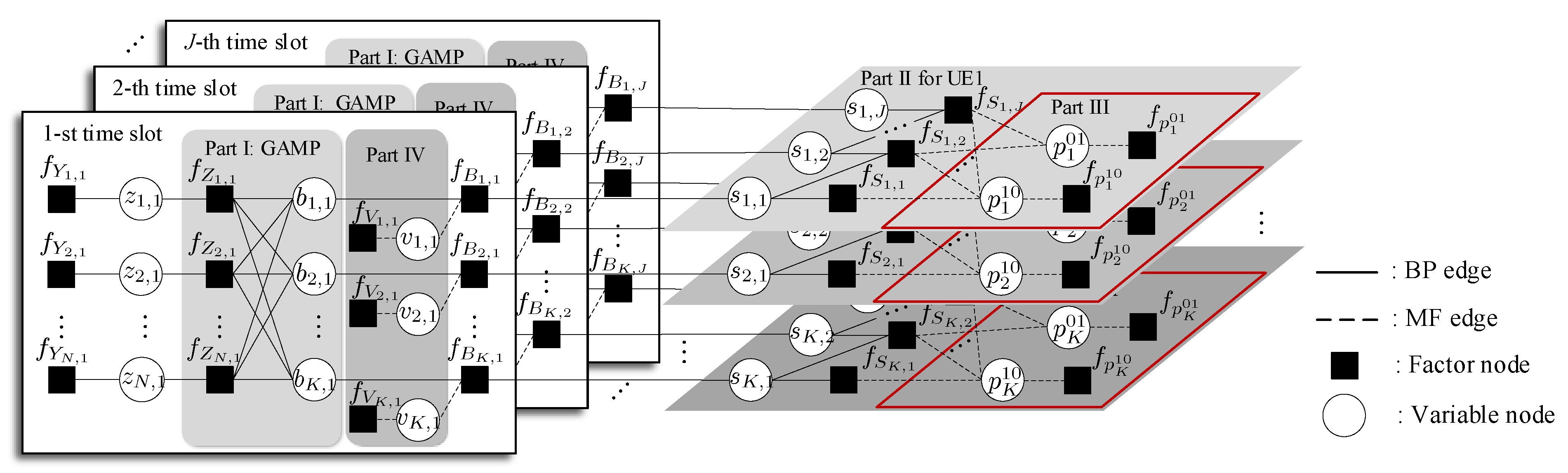
3. Adaptive UAV-BS Detector Based on the HMP Rule

In this section, the efficient GAMP algorithm is utilized to obtain the likelihood function for the signal $b_{k,j},\forall k,j$. The novel GAMP-BG-MC algorithm is proposed, which can adaptively update the parameters and obtain the accurate marginal posterior PDF.

3.1. Computation of the HMP for GAMP-BG-MC Algorithm

The probability model in (6) is implicit in the mix of linear and non-linear functional relationships, i.e., the product and summation operations among the variables as well as the updating of the Gaussian variance, while the single or combined MP rules are unavailable to calculate all the messages directly. Fortunately, the HMP rule proposed in [15] can tackle the message computation problems with the mix of linear and nonlinear models. The idea of the HMP rule [15] is that the FG groups all factor nodes into one set, ${\mathcal{A}}_{\mathrm{Hybrid}}$, while clustering all edges, $\mathcal{E}$, into two sets, ${\mathcal{E}}_{\mathrm{BP}}$ and ${\mathcal{E}}_{\mathrm{MF}}$, depicted as solid and dashed lines in Figure 2, respectively. For ${\mathcal{E}}_{\mathrm{BP}}$ edges, the messages use the equations (Equations (5) and (6) in [15]) to calculate the messages. Consequently, Equations (7)–(9) in [15] are used to calculate the messages on the ${\mathcal{E}}_{\mathrm{MF}}$. For the convenience of MP algorithm design, the factor graph is divided into four parts, as shown in Figure 2. Part I is the GAMP algorithm to calculate the likelihood function and Part II denotes the MC part for each UE in the time domain. Then, the transition probability automatic update is Part III, and Part IV is used to update the Gaussian variance. Then, the message calculation procedure will be derived separately.

3.1.1. Part I GAMP Part Messages

The GAMP algorithm is used to obtain the likelihood messages $n_{b_{k,j}\to f_{B_{k,j}}}^{\mathrm{BP}}\left(b_{k,j}\right)=\mathcal{CN}(b_{k,j};{\widehat{q}}_{k,j},v_{q_{k,j}})$ of the variable $b_{k,j}$ based on the received signal $\mathit{Y}$. The detailed scheme of the GAMP algorithm [21] is summarized in Algorithm 1. In Algorithm 1, the input message is $\mathit{Y},\mathit{H}$ and the output message $v_{q_{k,j}},{\widehat{q}}_{k,j},\forall k,j$ is obtained after one iteration. At the beginning of Algorithm 1, the belief expectation and variance of the variable $b_{k,j}$, denoted as ${\widehat{b}}_{k,j},v_{b_{k,j}}$, are first initialized. These values will be updated during the following iterations. In Algorithm 1, lines 1–2, the symbols ${\widehat{p}}_{n,j},v_{p_{n,j}}$ denote the expectation and variance of the message $m_{f_{Z_{n,j}}\to z_{n,j}}^{\mathrm{BP}}\left(b_{k,j}\right)=\mathcal{CN}(b_{k,j};{\widehat{p}}_{n,j},v_{p_{n,j}})$, respectively. In addition, $t_{n,j}$ denotes an intermediate variable, which will be updated during the iteration. Finally, Algorithm 1 outputs the message $n_{b_{k,j}\to f_{B_{k,j}}}^{\mathrm{BP}}\left(b_{k,j}\right)=\mathcal{CN}(b_{k,j};{\widehat{q}}_{k,j},v_{q_{k,j}})$, as shown in lines 4–5.

Algorithm 1: GAMP algorithm

Input: Received signal $\mathit{Y}$, channel matrix $\mathit{H}$ Output:$v_{q_{k,j}},{\widehat{q}}_{k,j},\forall k,j$ Initialize:${\widehat{b}}_{k,j}=0,v_{b_{k,j}}=1,\forall k,j;t_{n,j}=0,\forall n,j$ // $\phantom{(}$Update right output messages: $m_{f_{Z_{n,j}}\to z_{n,j}}^{\mathrm{BP}}\left(b_{k,j}\right)$$\phantom{(}$ 1  $\forall n,j$: $v_{p_{n,j}}={\sum }_{k=1}^K{\left|h_{n,k}\right|}^2{v}_{b_{k,j}}$ 2  $\forall n,j$: ${\widehat{p}}_{n,j}={\sum }_{k=1}^K{h}_{n,k}{\widehat{b}}_{k,j}-t_{n,j}{v}_{p_{n,j}}$ 3  $\forall n,j$: $t_{n,j}=\frac{y_{n,j}-{\widehat{p}}_{n,j}}{{\widehat{\lambda }}^{-1}+v_{p_{n,j}}}$ // $\phantom{(}$Update left output messages: $n_{b_{k,j}\to f_{B_{k,j}}}^{\mathrm{BP}}\left(b_{k,j}\right)$$\phantom{(}$ 4  $\forall k,j:v_{q_{k,j}}={\left({\sum }_{n=1}^N\frac{|h_{n,k}{|}^2}{{\widehat{\lambda }}^{-1}+v_{p_{n,j}}}\right)}^{-1}$ 5  $\forall k,j:{\widehat{q}}_{k,j}={\widehat{b}}_{k,j}+v_{q_{k,j}}{\sum }_{n=1}^N{h}_{n,k}^{*}{t}_{n,j}$

Based on the message $n_{b_{k,j}\to f_{B_{k,j}}}^{\mathrm{BP}}\left(b_{k,j}\right)=\mathcal{CN}(b_{k,j};{\widehat{q}}_{k,j},v_{q_{k,j}})$ is calculated by Algorithm 1. Then, we first initialize the beliefs $b\left(v_{k,j}\right)=\mathrm{Ga}(v_{k,j};{\widehat{ϵ}}_{k,j},{\widehat{\eta }}_{k,j})$, whose parameters are updated in (32). The message $m_{f_{B_{k,j}}\to s_{k,j}}^{\mathrm{BP}}\left(s_{k,j}\right)$ can be calculated by the HMP rule (Equation (5) in [15]), resulting in

$$m_{f_{B_{k,j}}\to s_{k,j}}^{\mathrm{BP}}\left(s_{k,j}\right)={\overrightarrow{\pi }}_{k,j}\delta (1-s_{k,j})+(1-{\overrightarrow{\pi }}_{k,j})\delta \left(s_{k,j}\right),$$

(12)

where the normalized parameter ${\overrightarrow{\pi }}_{k,j}$ is defined as

$$\begin{array}{cc}\hfill {\overrightarrow{\pi }}_{k,j}& =\frac{tem{p}_{k,j}}{tem{p}_{k,j}+1},\hfill \\ \hfill tem{p}_{k,j}& \triangleq \frac{{\mathrm{e}}^{\psi \left({\widehat{ϵ}}_{k,j}\right)}\mathcal{CN}({\widehat{q}}_{k,j};0,v_{q_{k,j}}+{\widehat{\eta }}_{k,j}/{\widehat{ϵ}}_{k,j})}{{\widehat{ϵ}}_{k,j}\mathcal{CN}({\widehat{q}}_{k,j};0,v_{q_{k,j}})},\hfill \\ \hfill \psi \left(x\right)& \triangleq \ln x-\frac{1}{2x}.\hfill \end{array}$$

(13)

3.1.2. Part II MC Part Messages

Firstly, the beliefs $b\left(p_k^{10}\right)=\mathrm{Be}(p_k^{10};{\widehat{e}}_k,{\widehat{f}}_k)$ and $b\left(p_k^{01}\right)=\mathrm{Be}(p_k^{01};{\widehat{c}}_k,{\widehat{d}}_k)$ can be initialized, and the parameters are updated later in (26). The MC downward messages are obtained by the HMP rule (Equations (5) and (6) in [15]) as

$$\begin{array}{c}\hfill m_{f_{S_{k,j}}\to s_{k,j}}^{\mathrm{BP}}\left(s_{k,j}\right)={\xi }_{k,j}^{\downarrow }\delta (1-s_{k,j})+(1-{\xi }_{k,j}^{\downarrow })\delta \left(s_{k,j}\right),\end{array}$$

(14)

$$\begin{array}{c}\hfill n_{s_{k,j}\to f_{S_{k,j+1}}}^{\mathrm{BP}}\left(s_{k,j}\right)={\xi }_{k,j}^{\Downarrow }\delta (1-s_{k,j})+(1-{\xi }_{k,j}^{\Downarrow })\delta \left(s_{k,j}\right),\end{array}$$

(15)

where

$$\begin{array}{cc}\hfill {\xi }_{k,1}^{\downarrow }& \triangleq \frac{\exp \left\{〈\ln p_k^{10}〉\right\}}{\exp \left\{〈\ln p_k^{10}〉\right\}+\exp \left\{〈\ln (1-p_k^{10})〉\right\}},\hfill \\ \hfill {\xi }_{k,j}^{\downarrow }& \triangleq \frac{{\xi }_{k,j-1}^{\Downarrow }{\mathrm{c}}_1+(1-{\xi }_{k,j-1}^{\Downarrow }){\mathrm{c}}_2}{{\xi }_{k,j-1}^{\Downarrow }({\mathrm{c}}_1+{\mathrm{c}}_4)+(1-{\xi }_{k,j-1}^{\Downarrow })({\mathrm{c}}_2+{\mathrm{c}}_3)},\hfill \\ \hfill {\xi }_{k,j}^{\Downarrow }& \triangleq \frac{{\xi }_{k,j}^{\downarrow }{\overrightarrow{\pi }}_{k,j}}{{\xi }_{k,j}^{\downarrow }{\overrightarrow{\pi }}_{k,j}+(1-{\xi }_{k,j}^{\downarrow })(1-{\overrightarrow{\pi }}_{k,j})},\hfill \end{array}$$

(16)

where ${\mathrm{c}}_1,{\mathrm{c}}_2,{\mathrm{c}}_3,{\mathrm{c}}_4$ denote the constants and are defined as

$$\begin{array}{c}\hfill {\mathrm{c}}_1=\exp \left\{〈\ln (1-p_k^{01})〉\right\};{\mathrm{c}}_2=\exp \left\{〈\ln p_k^{10}〉\right\},\\ \hfill {\mathrm{c}}_3=\exp \left\{〈\ln (1-p_k^{10})〉\right\};{\mathrm{c}}_4=\exp \left\{〈\ln p_k^{01}〉\right\},\end{array}$$

(17)

where ${〈\ln x〉}_{\mathrm{Be}(x;a,b)}=\psi \left(a\right)-\psi (a+b),{〈\ln (1-x)〉}_{\mathrm{Be}(x;a,b)}=\psi \left(b\right)-\psi (a+b)$.

Similarly, the MC upward messages passed between $s_{k,j}$ and $f_{S_{k,j}}$ can be computed by Equations (5) and (6) in [15], obtaining

$$\begin{array}{c}\hfill n_{s_{k,j}\to f_{S_{k,j}}}^{\mathrm{BP}}\left(s_{k,j}\right)={\xi }_{k,j}^{\Uparrow }\delta (1-s_{k,j})+(1-{\xi }_{k,j}^{\Uparrow })\delta \left(s_{k,j}\right),\end{array}$$

(18)

$$\begin{array}{c}\hfill m_{f_{S_{k,j+1}}\to s_{k,j}}^{\mathrm{BP}}\left(s_{k,j}\right)={\xi }_{k,j}^{\uparrow }\delta (1-s_{k,j})+(1-{\xi }_{k,j}^{\uparrow })\delta \left(s_{k,j}\right),\end{array}$$

(19)

where

$$\begin{array}{cc}\hfill {\xi }_{k,J}^{\Uparrow }\triangleq & {\overrightarrow{\pi }}_{k,j},{\xi }_{k,j}^{\Uparrow }\triangleq \frac{{\xi }_{k,j}^{\uparrow }{\overrightarrow{\pi }}_{k,j}}{{\xi }_{k,j}^{\uparrow }{\overrightarrow{\pi }}_{k,j}+(1-{\xi }_{k,j}^{\uparrow })(1-{\overrightarrow{\pi }}_{k,j})},\hfill \\ \hfill {\xi }_{k,j}^{\uparrow }\triangleq & \frac{{\xi }_{k,j+1}^{\Uparrow }{\mathrm{c}}_1+(1-{\xi }_{k,j+1}^{\Uparrow }){\mathrm{c}}_4}{{\xi }_{k,j+1}^{\Uparrow }({\mathrm{c}}_1+{\mathrm{c}}_2)+(1-{\xi }_{k,j+1}^{\Uparrow })({\mathrm{c}}_3+{\mathrm{c}}_4)},\hfill \end{array}$$

(20)

where ${\mathrm{c}}_1,{\mathrm{c}}_2,{\mathrm{c}}_3,{\mathrm{c}}_4$ are the same as (17). The belief $b\left(s_{k,1}\right)$ and the combined belief $b(s_{k,j},s_{k,j-1})$, $2\le j\le J$ are calculated by Equation (8) in [15], resulting in

$$b\left(s_{k,1}\right)=B_{s_{k,1}}\delta (1-s_{k,1})+(1-B_{s_{k,1}})\delta \left(s_{k,1}\right),$$

(21)

$$\begin{array}{cc}\hfill b(s_{k,j},s_{k,j-1})=& \frac{1}{{\rho }_{k,j}}[B_{k,j}^{00}\delta \left(s_{k,j-1}\right)\delta \left(s_{k,j}\right)+B_{k,j}^{01}\delta (1-s_{k,j-1})\delta \left(s_{k,j}\right),\hfill \\ \hfill & +B_{k,j}^{10}\delta \left(s_{k,j-1}\right)\delta (1-s_{k,j})+B_{k,j}^{11}\delta (1-s_{k,j-1})\delta (1-s_{k,j})],\hfill \end{array}$$

(22)

where the normalized factors are

$$B_{s_{k,1}}\triangleq \frac{{\overrightarrow{\pi }}_{k,1}{\xi }_{k,1}^{\uparrow }{\xi }_{k,1}^{\downarrow }}{{\overrightarrow{\pi }}_{k,1}{\xi }_{k,1}^{\uparrow }{\xi }_{k,1}^{\downarrow }+(1-{\overrightarrow{\pi }}_{k,1})(1-{\xi }_{k,1}^{\uparrow })(1-{\xi }_{k,1}^{\downarrow })},$$

(23)

$$\left\{\begin{array}{l}{B}_{k,j}^{00}\triangleq (1-{\xi }_{k,j-1}^{\Downarrow })(1-{\xi }_{k,j}^{\Uparrow })\exp \left\{〈\ln (1-p_k^{10})〉\right\},\\ B_{k,j}^{01}\triangleq {\xi }_{k,j-1}^{\Downarrow }(1-{\xi }_{k,j}^{\Uparrow })\exp \left\{〈\ln p_k^{01}〉\right\},\\ B_{k,j}^{10}\triangleq (1-{\xi }_{k,j-1}^{\Downarrow }){\xi }_{k,j}^{\Uparrow }\exp \left\{〈\ln p_k^{10}〉\right\},\\ B_{k,j}^{11}\triangleq {\xi }_{k,j-1}^{\Downarrow }{\xi }_{k,j}^{\Uparrow }\exp \left\{〈\ln (1-p_k^{01})〉\right\},\\ {\rho }_{k,j}\triangleq B_{k,j}^{00}+B_{k,j}^{01}+B_{k,j}^{10}+B_{k,j}^{11}.\end{array}\right.$$

(24)

3.1.3. Part III Transition Probability Update Part

The messages from $f_{S_{k,1}},f_{S_{k,j}}$ to $p_k^{10},p_k^{01}$ can be calculated by Equation (7) in [15].

$$\begin{array}{c}\hfill m_{f_{S_{k,1}}\to p_k^{10}}^{\mathrm{MF}}\left(p_k^{10}\right)\propto \mathrm{Be}(p_k^{10};B_{s_{k,1}}+1,2-B_{s_{k,1}})\\ \hfill m_{f_{S_{k,j}}\to p_k^{10}}^{\mathrm{MF}}\left(p_k^{10}\right)\propto \mathrm{Be}(p_k^{10};\frac{B_{k,j}^{10}}{{\rho }_{k,j}}+1,\frac{B_{k,j}^{00}}{{\rho }_{k,j}}+1)\\ \hfill m_{f_{S_{k,j}}\to p_k^{01}}^{\mathrm{MF}}\left(p_k^{01}\right)\propto \mathrm{Be}(p_k^{01};\frac{B_{k,j}^{01}}{{\rho }_{k,j}}+1,\frac{B_{k,j}^{11}}{{\rho }_{k,j}}+1)\end{array}$$

(25)

Given the prior messages $p\left(p_k^{10}\right)$ and $p\left(p_k^{01}\right)$, the beliefs update by $b\left(p_k^{10}\right)\propto \mathrm{Be}(p_k^{10};{\widehat{e}}_k,{\widehat{f}}_k)$ and $b\left(p_k^{01}\right)\propto \mathrm{Be}(p_k^{01};{\widehat{c}}_k,{\widehat{d}}_k)$, where the parameters are updated through

$$\begin{array}{c}\hfill {\widehat{e}}_k=B_{s_{k,1}}+e_k+\sum _{j=2}^J\frac{B_{k,j}^{10}}{{\rho }_{k,j}},{\widehat{c}}_k=c_k+\sum _{j=2}^J\frac{B_{k,j}^{01}}{{\rho }_{k,j}},\\ \hfill {\widehat{f}}_k=1-B_{s_{k,1}}+f_k+\sum _{j=2}^J\frac{B_{k,j}^{00}}{{\rho }_{k,j}},{\widehat{d}}_k=d_k+\sum _{j=2}^J\frac{B_{k,j}^{11}}{{\rho }_{k,j}},\end{array}$$

(26)

and the parameters $B_{s_{k,1}},B_{k,j}^{00},B_{k,j}^{01},B_{k,j}^{10},B_{k,j}^{11},{\rho }_{k,j}$ can be calculated in Equation (24).

3.1.4. Part IV Variance Update Part

The message going out of the MC part from $s_{k,j}$ to $f_{B_{k,j}}$ can be computed by Equation (6) in [15].

$$n_{s_{k,j}\to f_{B_{k,j}}}^{\mathrm{BP}}\left(s_{k,j}\right)={\overleftarrow{\pi }}_{k,j}\delta (1-s_{k,j})+(1-{\overleftarrow{\pi }}_{k,j})\delta \left(s_{k,j}\right),$$

(27)

where

$${\overleftarrow{\pi }}_{k,j}\triangleq \frac{{\xi }_{k,j}^{\uparrow }{\xi }_{k,j}^{\downarrow }}{{\xi }_{k,j}^{\uparrow }{\xi }_{k,j}^{\downarrow }+(1-{\xi }_{k,j}^{\uparrow })(1-{\xi }_{k,j}^{\downarrow })}.$$

(28)

To update the variance of the BG-MC channel prior distribution, the combined beliefs $b(b_{k,j},s_{k,j})$ have to be calculated first using Equation (8) in [15] as

$$\begin{array}{c}\hfill b(b_{k,j},s_{k,j})=(1-B_{b_{k,j},s_{k,j}})\delta \left(s_{k,j}\right)\delta \left(b_{k,j}\right)+B_{b_{k,j},s_{k,j}}\delta (1-s_{k,j})\mathcal{CN}(b_{k,j};{\widehat{\mu }}_{k,j},{\vartheta }_{k,j}),\end{array}$$

(29)

where

$$\begin{array}{cc}\hfill B_{b_{k,j},s_{k,j}}& \triangleq \frac{{\overleftarrow{\pi }}_{k,j}tem{p}_{k,j}}{{\overleftarrow{\pi }}_{k,j}tem{p}_{k,j}+(1-{\overleftarrow{\pi }}_{k,j})},\hfill \\ \hfill {\vartheta }_{k,j}& ={(v_{q_{k,j}}^{-1}+\frac{{\widehat{ϵ}}_{k,j}}{{\widehat{\eta }}_{k,j}})}^{-1},{\widehat{\mu }}_{k,j}=\frac{{\widehat{q}}_{k,j}}{v_{q_{k,j}}}{\vartheta }_{k,j},\hfill \end{array}$$

(30)

and the temporary variable $tem{p}_{k,j}$ is defined in (13).

Then, the message from $f_{B_{k,j}}$ to variable node $v_{k,j}$ can be computed with the HMP rule (Equation (7) in [15]) as

$$\begin{array}{c}\hfill m_{f_{B_{k,j}}\to v_{k,j}}^{\mathrm{MF}}\left(v_{k,j}\right)\propto \mathrm{Ga}(v_{k,j};B_{b_{k,j},s_{k,j}}+1,B_{b_{k,j},s_{k,j}}({\left|{\widehat{\mu }}_{k,j}\right|}^2+{\vartheta }_{k,j})).\end{array}$$

(31)

Given the prior message $m_{f_{v_{k,j}}\to v_{k,j}}^{\mathrm{MF}}\left(v_{k,j}\right)=\mathrm{Ga}(v_{k,j};{ϵ}_{k,j},{\eta }_{k,j})$, the belief $b\left(v_{k,j}\right)$ of variance variable $v_{k,j}$ can be expressed as $b\left(v_{k,j}\right)=\mathrm{Ga}(v_{k,j};{\widehat{ϵ}}_{k,j},{\widehat{\eta }}_{k,j})$, where the parameters are updated through

$$\begin{array}{cc}\hfill {\widehat{ϵ}}_{k,j}& ={ϵ}_{k,j}+B_{b_{k,j},s_{k,j}},\hfill \\ \hfill {\widehat{\eta }}_{k,j}& ={\eta }_{k,j}+B_{b_{k,j},s_{k,j}}({\left|{\widehat{\mu }}_{k,j}\right|}^2+{\vartheta }_{k,j}).\hfill \end{array}$$

(32)

With the parameters updated in (32), the message from the factor node $f_{B_{k,j}}$ to the variable node $b_{k,j}$ can be computed by the HMP rule (Equation (5) in [15]) as

$$\begin{array}{c}\hfill m_{f_{B_{k,j}}\to b_{k,j}}^{\mathrm{BP}}\left(b_{k,j}\right)=(1-{\overleftarrow{\pi }}_{k,j})\delta \left(b_{k,j}\right)+{\overleftarrow{\pi }}_{k,j}\frac{{\mathrm{e}}^{\psi \left({\widehat{ϵ}}_{k,j}\right)}}{{\widehat{ϵ}}_{k,j}}\mathcal{CN}\left(b_{k,j};0,\frac{{\widehat{ϵ}}_{k,j}}{{\widehat{\eta }}_{k,j}}\right).\end{array}$$

(33)

Finally, the belief $b\left(b_{k,j}\right)$ of the variable $b_{k,j}$ can be expressed as

$$b\left(b_{k,j}\right)=(1-B_{b_{k,j}})\delta \left(b_{k,j}\right)+B_{b_{k,j}}\mathcal{CN}(b_{k,j};{\widehat{\mu }}_{k,j},{\vartheta }_{k,j}),$$

(34)

with the parameter $B_{b_{k,j}}=B_{b_{k,j},s_{k,j}}$. Then, the algorithm outputs the mean and variance of the belief $b\left(b_{k,j}\right)$ as

$$\begin{array}{cc}\hfill {\widehat{b}}_{k,j}& ={〈b_{k,j}〉}_{b\left(b_{k,j}\right)}=B_{b_{k,j}}{\widehat{\mu }}_{k,j},\hfill \\ \hfill v_{b_{k,j}}& =B_{b_{k,j}}({\left|{\widehat{\mu }}_{k,j}\right|}^2+{\vartheta }_{k,j})-{\left|{\widehat{b}}_{k,j}\right|}^2.\hfill \end{array}$$

(35)

3.2. Message Passing Scheduling

The message passing scheme was summarized in the proposed GAMP-BG-MC algorithm, as shown in Algorithm 2. Specifically, the Part I messages are first calculated in parallel at each time slot, as shown in Section 3.1.1, which contains Algorithm 1 and the message going into the Part II. Then, the MC messages can be calculated in sequence in lines 4–7. In Part III, the parameters of $p_k^{10},p_k^{01}$ can be updated in lines 8–10. After that, the accuracy of the outgoing messages in Part IV can be improved by updating the MC part messages, again based on the updated hyperparameters $p_k^{10},p_k^{01}$. In the final step, the parameters of variance and the calculated output estimated data ${\widehat{b}}_{k,j},\forall k,j$ are updated with lines 12–15 in Part IV.

Algorithm 2: GAMP-BG-MC algorithm

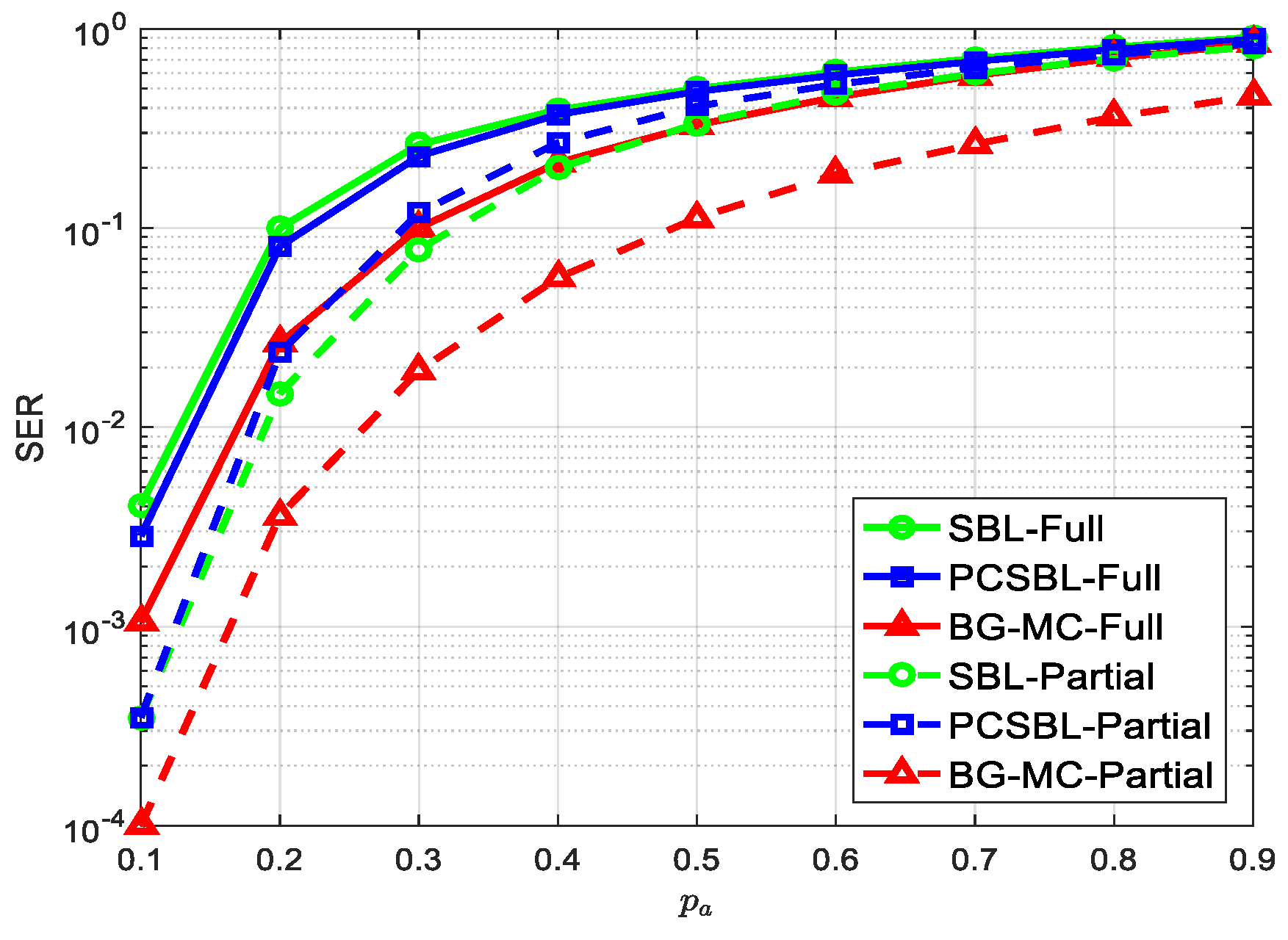
4. Simulation Results

This section compares the performance of the proposed GAMP-BG-MC algorithm. As a benchmark, we consider the state-of-the-art algorithms GAMP-SBL [13,14] and GAMP-PCSBL [14], referred to as SBL and PCSBL in the following. Referring to [14], the BPSK modulation scheme is employed in all simulations. To ensure the reproducibility of the results, the simulation setup is described as follows. The simulations were conducted using MATLAB as the programming language, utilizing its built-in functions for matrix operations and signal processing. The parameters used in the experiments are summarized in

Table 3. Parameter settings for the experiment.

Parameter Name	Value	Parameter Name	Value
UE number K	20	Spreading factor N	30
Time slots	6	Algorithm iteration T	20
Modulation scheme	BPSK	Scenarios	Partial and Full

. The experiments are conducted in two scenarios compared with the benchmark algorithms. One is the UE activity with temporal correlation, i.e., the UE will transmit the data partially during the whole frame, here denoted as “Partial”. The other is an extreme phenomenon where the UE keeps transmitting data fully to the frame, referred to as “Full”.

For the initialization, according to [15], the prior parameters are $\{{ϵ}_{k,j}={\eta }_{k,j}=1,\forall k,j\}$, $\{e_k=f_k=c_k=d_k=1,\forall k\}$, ${\xi }_{k,j}^{\Uparrow }=1/2,\forall k,j$, and the belief parameters are initialized with the same values of the priors. All the experiments are obtained by averaging $\mathrm{sim}=1000$ Monte Carlo realizations. The experiments use the symbol error rate (SER), defined as $\mathrm{SER}={\log }_{10}\left(\frac{K_{err}}{\mathrm{sim}\times K}\right)$, as a performance metric; $K_{err}$ is the number of UE whose symbol is erroneously decoded. The per-iteration complexity of the BG-MC is $\mathcal{O}\left(\right(N+1\left)KJ\right)$, and it is in the same order as the SBL and PCSBL. However, the iteration number of the BG-MC will always be small, as shown in Figure 3.

Figure 3 gives the convergence speed of the three algorithms under SNR = 9 dB, with two scenarios. The proposed BG-MC algorithm has the fastest convergence speed compared with the SBL and PCSBL algorithms in both scenarios, which demonstrates that the proposed algorithm can capture the AS correlation more accurately than the other two algorithms. Especially in the “Partial” scenario, the proposed algorithm converges faster and performs better than the comparison algorithm.

In Figure 4, the simulations compare the average SER performance as a function of the SNRs. The simulation results show that the BG-MC algorithm performs better in the two scenarios. Further, the results show that the PCSBL is better than the SBL in the second scheme and the PCSBL is efficient in characterizing the block sparse structure, while the BG-MC is more accurate, not only in the block sparse structure but also in the cluster sparse structure. The reason for this is that the BG-MC can update the statistic parameters automatically, which is suitable for the practice system.

Figure 5 shows the SER performances as a function of the UE active rate $p_a$ under SNR = 9 dB. The BG-MC algorithm outperforms the benchmark algorithms in almost all ranges of $p_a$, especially in the first scenario, which validates the effectiveness of the proposed algorithm.

5. Conclusions

This work proposed an uplink GF-NOMA message-passing detector for UAV-assisted communications. The BG-MC model was first developed to accurately characterize the slow change feature of the AS of all UEs under a GF-NOMA system. Based on the HMP rule, this work designed the GAMP-BG-MC algorithm and tested it with the two scenarios. Numerical results demonstrated that the proposed algorithm not only has a faster convergence speed but also achieves a better SER performance.

In future work, it will be interesting to investigate the impact of channel fading on the multi-user symbol detection in UAV-based GF-NOMA systems, while considering a comprehensive channel model for UAV communication and developing robust detection algorithms that can adapt to varying channel conditions in UAV communication scenarios.