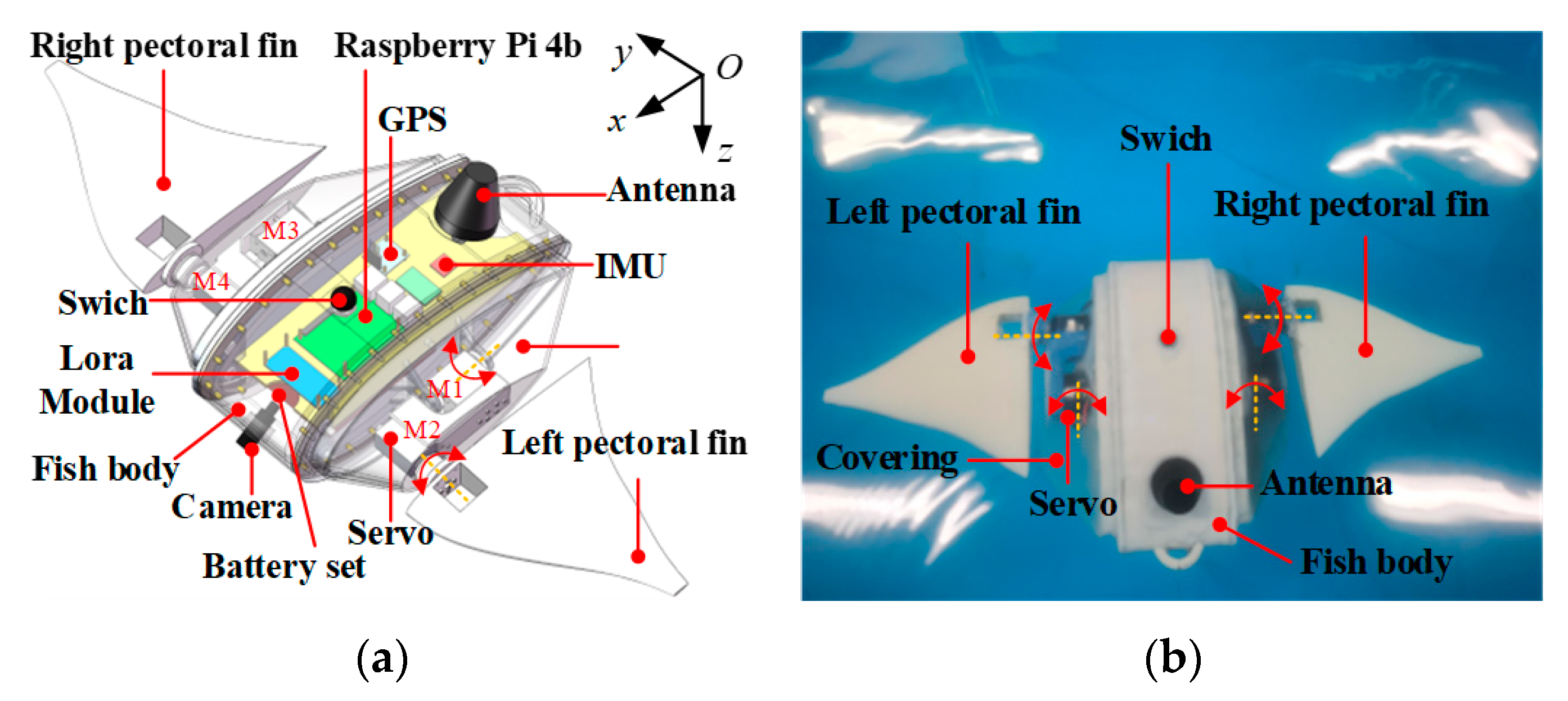
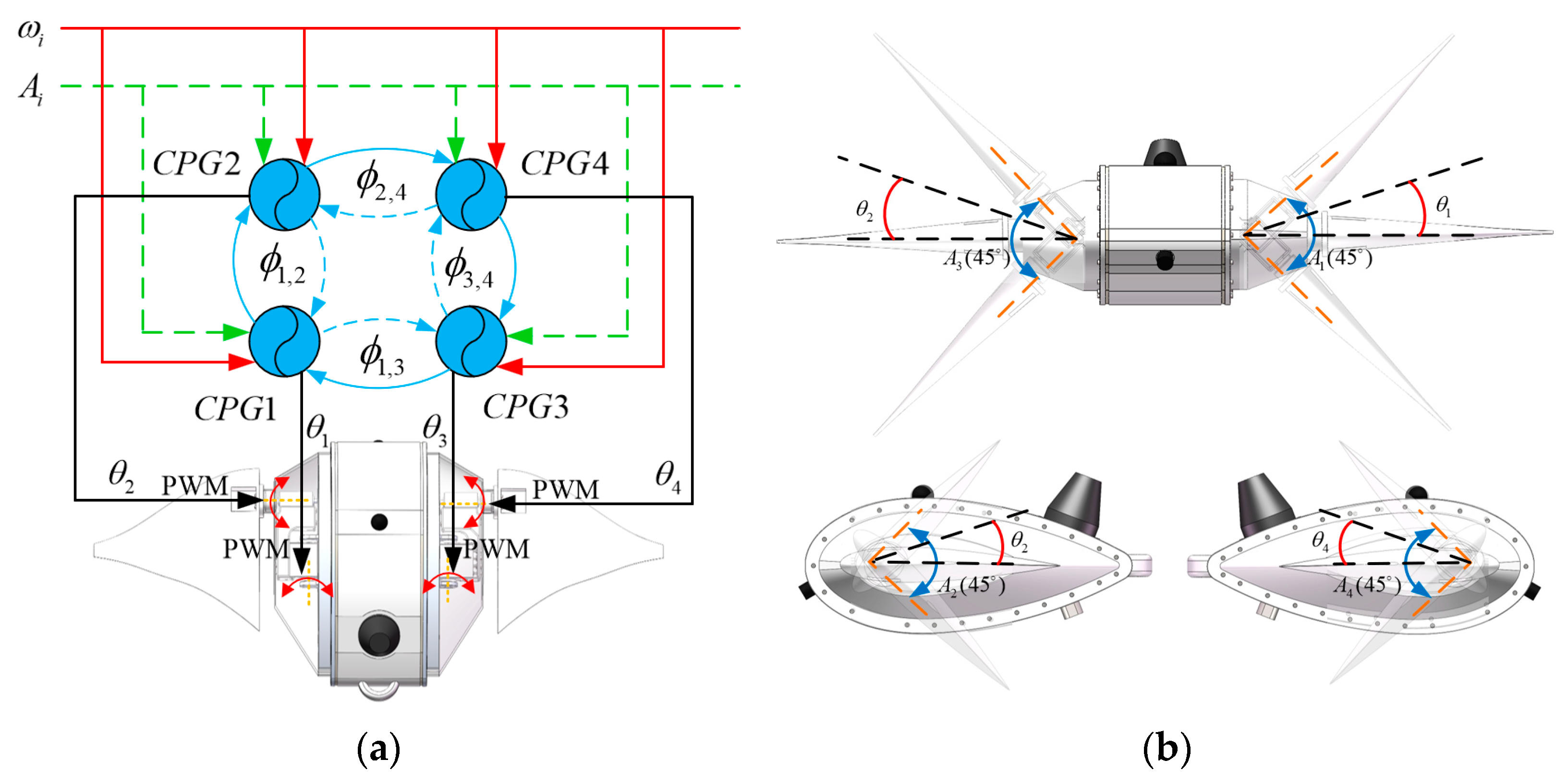
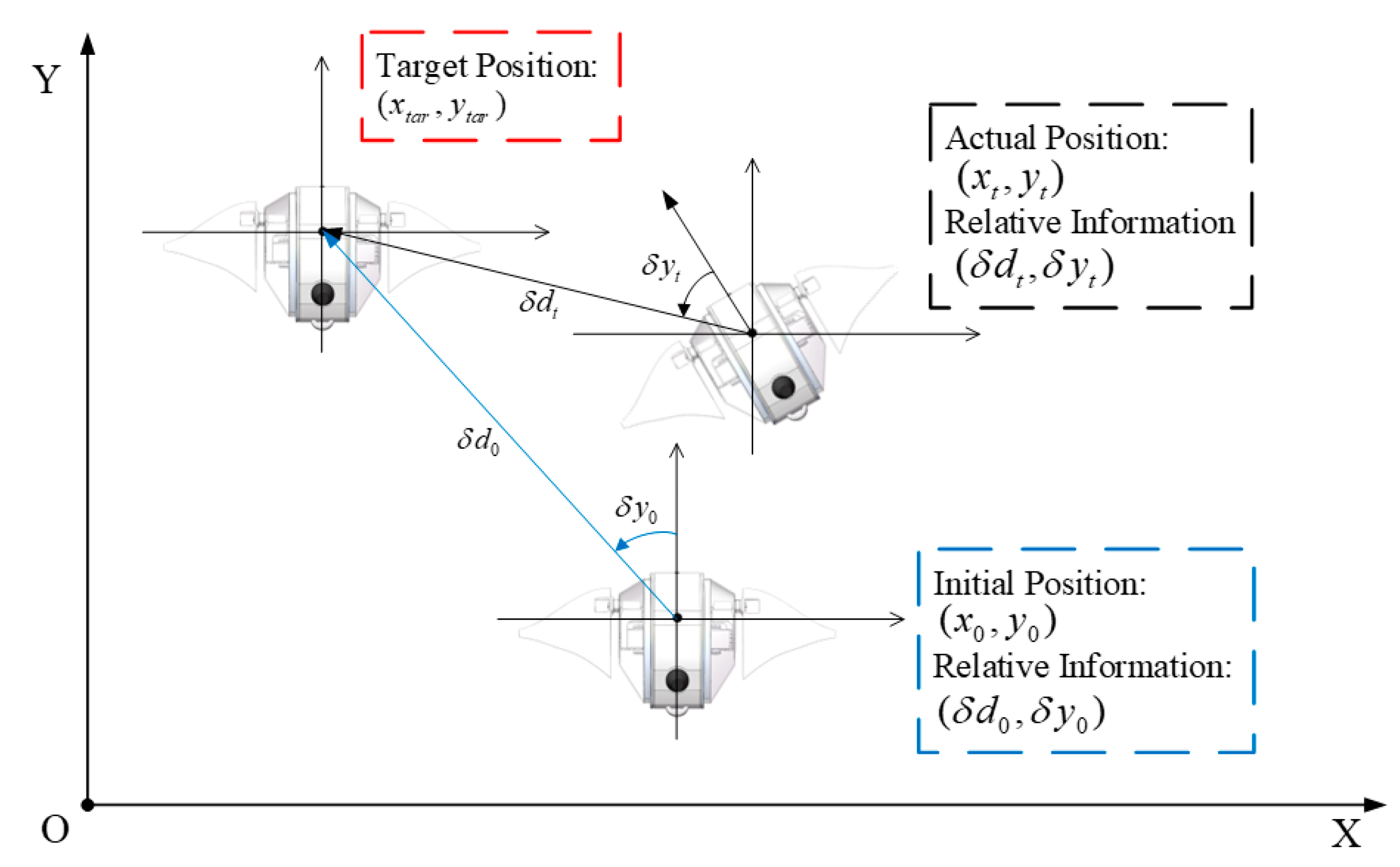
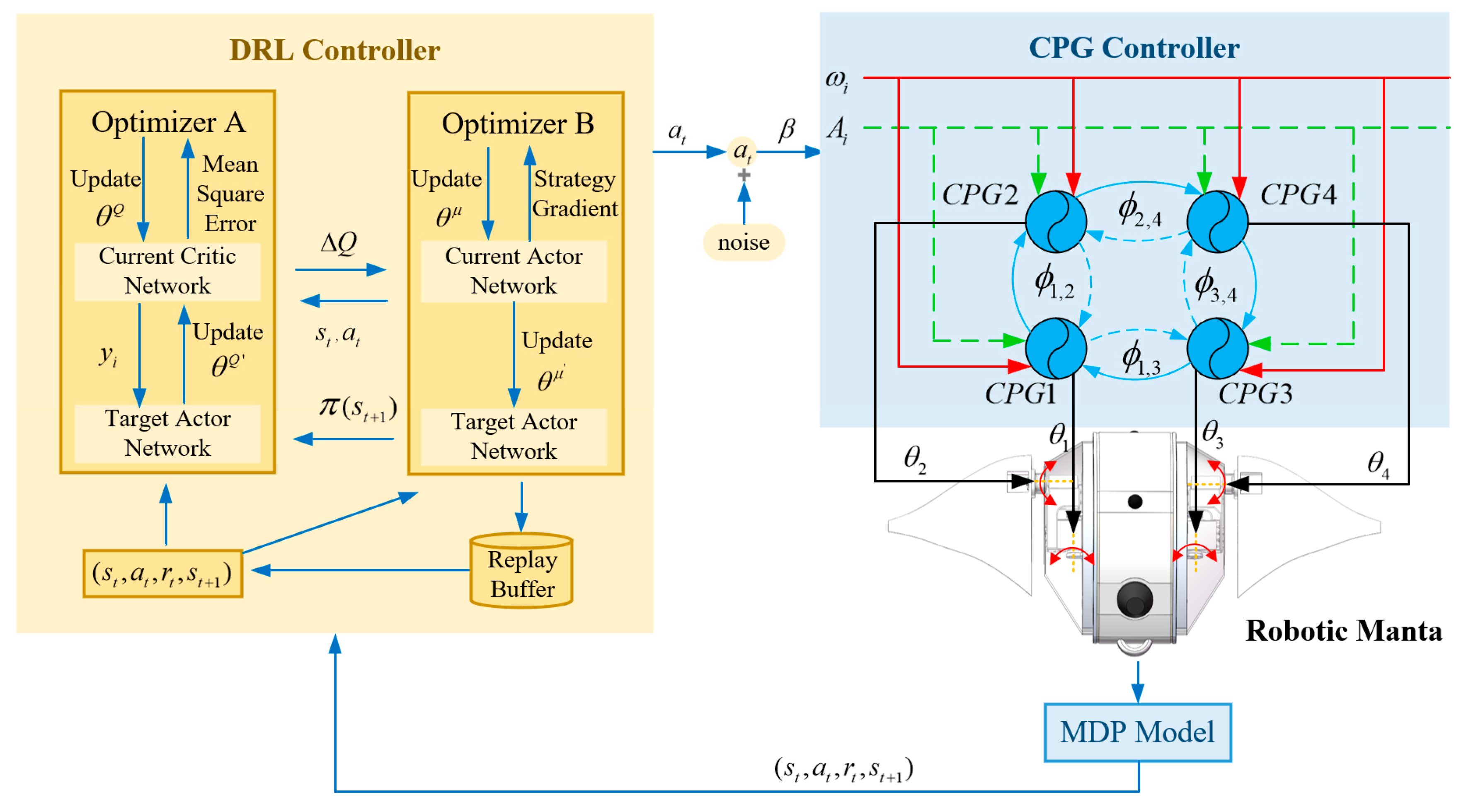
1. Introduction
The marine environment is an essential part of the Earth and contains a wealth of resources. Due to their fish-like mode of propulsion and exceptional environmental compatibility, robotic fish have been used in underwater exploration [
1,
2], environmental monitoring [
3], aquaculture [
4], and other domains [
5]. The swimming styles of robotic fish can be categorized into two groups based on their propulsion mechanisms: Body and/or Caudal Fin (BCF) propulsion and Median and/or Paired Fin (MPF) propulsion [
6]. Robotic fish utilizing BCF propulsion are noted for their high maneuverability, whereas those employing MPF propulsion are recognized for their outstanding stability at low speeds [
7]. The application of MPF propulsion, exemplified by the manta for their superior swimming efficiency, agility, and interference resistance, has garnered increasing interest from both industry and academia [
8,
9,
10,
11,
12,
13].
The mainstream swimming control strategies for robotic fish are the sinusoidal control and the Central Pattern Generator (CPG) control [
14]. The sinusoidal control can generate a diverse array of swimming gaits continuously but it cannot smoothly and naturally handle changes in swimming frequency and amplitude. CPG control orchestrates rhythmic movements by producing stable periodic signals, offering significant advantages over sinusoidal control, such as stability, robustness, smooth transition, and adjustability. Therefore, the CPG control strategy has garnered growing interest and has been extensively applied in the motion control of diverse biomimetic robotics. Hao et al. [
15] demonstrated the efficacy of the CPG control strategy by applying phase oscillators to a robotic manta. They achieved closed-loop heading control by integrating two yaw modes based on phase and amplitude differences. Chen et al. [
16] successfully realized static and moving obstacle avoidance for bionic fish using the CPG control strategy. Qiu et al. [
17] developed an asymmetric CPG and explored a passive stiffness adjustment mechanism to adapt to different swimming states of robotic fish.
The intricate and unpredictable nature of hydrodynamics in robotic fish presents significant challenges in developing precise mathematical models for their swimming control. Researchers have turned to model-free approaches to address this issue and enable autonomous swimming for robotic fishes, including Proportional Integral Derivative (PID), Active Disturbance Rejection Control (ADRC), and fuzzy control. Morgansen et al. [
18] developed a robotic fish featuring bi-articulated pectoral fins and designed a depth controller based on the PID control strategy. Wang et al. [
19] designed an MPF-type robotic fish, RobCutt, utilizing the ADRC strategy for closed-loop swimming control. Cao et al. [
20] developed a CPG algorithm combined with fuzzy control to achieve stable 3D swimming of a robot fish.
With the progression of artificial intelligence, many scholars are investigating how reinforcement learning (RL) algorithms can be utilized to enhance the autonomous movement of robotic fish. RL algorithms can learn optimal strategies directly from interactions with the environment, eliminating the necessity for predefined mathematical representations of system dynamics [
21]. This contrasts with traditional control methods that depend on precise models to forecast system behavior. Instead, RL employs a data-driven approach, enabling it to adapt and continuously enhance its performance over time. The model-free characteristic of RL allows for its application to complex dynamic systems where constructing exact models may not be feasible or practical. The advent of RL techniques has catalyzed progress in research and development within the domain of robotic fish [
22]. Zhang et al. [
23] implemented an RL algorithm as a high-level controller, complemented by a CPG control strategy as the low-level controller, for path-tracking control of a BCF-type robotic fish. However, their approach employs the Actor–Critic (A2C) algorithm, encountering limitations, including low sample efficiency and difficulties in achieving a balance between exploration and exploitation, thus reducing its practical applicability.
Deep Reinforcement Learning (DRL) is a state-of-the-art algorithmic framework that combines the principles of RL with the representational capabilities of deep learning. DRL algorithms surpass traditional RL methods in terms of generalization and learning capabilities, particularly in complex environments and under conditions of high dimensionality. Woo et al. [
24] introduced a DRL-based controller for Unmanned Surface Vehicle (USV) path tracking. However, USVs exhibit fewer complex dynamics than the intricate swimming patterns observed in robotic fish. Zhang et al. [
25] validated the robustness of the Deep Deterministic Policy Gradient (DDPG) algorithm, and their study showed the applicability of DDPG in robot control.
Although various methods have been successfully applied to numerous robotic systems, the unique morphology and kinematic properties of the robotic manta require a specialized approach.
Table 1 delineates prior studies on control strategies for robotic mantas.
Zhang et al. [
26] implemented a simple autonomous obstacle avoidance control by using infrared sensor feedback information based on the design of a simple CPG network. Zhang et al. [
10] designed a CPG controller for open-loop swimming control based on the development of a robotic manta combining rigid and soft structures. Hao et al. [
15] improved the basic swimming performance of the robotic manta by modifying the CPG model, which diversified the swimming modes. However, subsequent parameter adjustments increased the complexity of the closed-loop control strategy, making it more difficult to coordinate various parameters, leading to unstable yaw control. Zhang et al. [
27] achieved the switch between the gliding and flapping propulsion modes of the robotic manta by combining the CPG network and the fuzzy controller. However, its control accuracy and propulsion efficiency were low. He et al. [
28] achieved a smaller precision heading change control by combining the S-plane controller and the fuzzy controller. Meng et al. [
29] designed a sliding-mode fuzzy controller based on the development of a new type of robotic manta, achieving stable path-tracking control of the robotic manta. However, due to the use of a sine curve for basic swimming control, the trajectory was not smooth when the robotic manta switched swimming modes. From these studies, we find that most of the current research on the motion control of robotic mantas is focused on basic swimming control strategies. There are still many shortcomings in simultaneously improving smooth transitions between swimming modes and enhancing adaptability, autonomy, and stability in unknown environments.
This study presents a CPG–DDPG control strategy to improve the smoothness of transition in the robotic manta swimming mode, and to boost its adaptability, autonomy, and stability in unpredictable dynamic environments. The proposed control strategy integrates a CPG as the fundamental mechanism, complemented by the DDPG algorithm functioning as the advanced regulatory strategy.
The main contributions of this paper are as follows:
- (1)
We have successfully developed a robotic manta and proposed a CPG control strategy that allows for smooth transitions between different swimming modes by adjusting a single parameter, significantly reducing the difficulty of parameter adjustment in closed-loop control strategies and enhancing stability. This CPG control strategy enables us to more accurately simulate the swimming behavior of manta, thus allowing for more precise and natural control of swimming movements.
- (2)
We have put forward a CPG-based DRL control strategy to adjust the CPG control parameters of the robotic manta via the DDPG algorithm. This strategy utilizes the learning capabilities of the DDPG algorithm and the stability of the CPG model to achieve more flexible and adaptive control. By making decisions based on the current state of the robotic manta, it effectively enhances the adaptability and swimming efficiency of the robotic manta in unknown environments.
- (3)
We conducted a series of simulations and real-world prototype experiments to validate the effectiveness of the proposed CPG–DDPG control strategy in the swimming control process of the robotic manta.
The remainder of this paper is structured as follows:
Section 2 introduces the CPG model for the robotic manta swimming control.
Section 3 provides a detailed discussion of the proposed CPG-DDPG control strategy.
Section 4 describes the simulation environment and results for the robotic manta swimming task.
Section 5 details the fundamental swimming experiments and swimming task experiments conducted with the robotic manta prototype. Finally,
Section 6 summarizes the paper and outlines the contributions of the proposed CPG–DDPG control strategy.
3. Design of the CPG–DDPG Control Strategy
Swimming control of robotic mantas is a significant challenge, requiring constant changes in swimming patterns for precise maneuvering. In this paper, by combining the CPG with the DDPG, we introduce a novel CPG–DDPG control strategy. This strategy dynamically adjusts the CPG network’s parameters using the DDPG algorithm, facilitating the successful execution of the swimming task.
3.1. Control Problem and MDP Modeling of the Robotic Manta
The swimming control problem of a robotic manta can be regarded as a Markov Decision Process (MDP) [
34], defined by a tuple
, where
denotes the state space;
denotes the action space;
denotes the probability distribution of state transitions;
denotes the reward function;
is defined as the discount factor. The goal is to learn an optimal policy [
35] that maximizes the cumulative reward.
This paper models the swimming control problem of the robotic manta as an MDP task.
Figure 3 illustrates the swimming task. Imagine a robotic manta is located at a random coordinate point (initial position) at a predetermined depth, which contains 2D coordinates
and relative information
, and targets for swimming to a target position
. Here, the initial and target positions are randomly generated. Supposing the current position of the robotic manta is
, the relative position data comprise the relative distance
and the relative position angle
.
To this end, we define the state space:
where
is the time tag,
denotes the error in the actual yaw
of the robotic manta relative to the target yaw
,
denotes the relative distance,
denotes the velocity of the robotic manta, and
denotes the angular velocity of the robotic manta’s yaw.
Define the action space
:
The upper controller monitors the current state of the robotic manta and adjusts the input parameter of the CPG-based low-level controller to realize the swimming control of the robotic manta, which guides the robotic manta to swim to the target position.
The reward function
is defined as:
where
denotes the orientation reward,
denotes the position reward,
denotes the angular velocity reward,
denotes the forward velocity reward,
denotes the task completion reward,
denotes the device destruction reward,
,
,
,
,
, and
denote the weight coefficients, and
denotes the initial relative position error. When the set maximum steering speed
m/s is exceeded,
reward for overspeed is obtained.
reward is assigned when the robotic manta’s forward velocity falls below
m/s. When the robotic manta’s position in the world coordinate system falls within a cylindrical area of radius
centered on the target position, the task is considered complete; otherwise, it receives a
reward. If the robotic manta swims outside the boundaries of the maximum allowed movement area, terminate the current episode, and gain a
reward.
denotes the overall reward for the MDP task.
3.2. CPG–DDPG Strategy for Robotic Manta Swimming Control
The DDPG algorithm is not only capable of addressing continuous tasks but also discrete tasks, making it extensively utilized in robotics research. It leverages off-policy data and the Bellman equation to learn the Q-function, and it uses this Q-function to learn the policy. Furthermore, the DDPG algorithm utilizes the Actor–Critic (AC) framework, which comprises two distinct networks: the actor network , which selects actions, and the critic network , which assesses these actions by estimating their value and is used to update the weights of the action network.
The action space of the robotic manta swimming task is discrete. Therefore, this study employs the DDPG algorithm as a high-level strategy and integrates it with the CPG algorithm, thus proposing the CPG–DDPG control strategy. The CPG–DDPG control strategy is illustrated in
Figure 4 and Algorithm 1.
The DDPG algorithm serves as the decision-making core for the robotic manta, overseeing its current motion state. It processes these parameters and generates control signals β for the CPG-based motion controller. Subsequently, the CPG controller adjusts the phase differences and frequencies of its oscillators and outputs the corresponding rotation angles to the servo motors. This coordination enables the robotic manta to modulate its swimming direction and speed, facilitating navigation towards designated target points.
| Algorithm 1. CPG–DDPG |
Randomly initialize the actor network
and the critic network
with weights
and
Initialize the target network
and with weights , |
| Initialize replay buffer |
| for each episode do |
Initialize a random process N for action exploration
Receive initial observation state S0 |
| for each training step do |
Select action , according to the current policy and exploration noise
Take action at as β
Execute β to CPG controller
to 4 do |
| |
Solve for the θi
end for
Servo rotation θi
Robotic manta swimming
Observe reward rt and observe new state
Store in R
Sample a random minibatch N from R |
Update the critic network through minimizing the loss
Update the actor policy:
Update the target networks: |
| end for |
| end for |
4. Simulation
To verify the effectiveness of the proposed control strategy, this section centers on the swimming task of a robotic manta like a case study. An agent was trained in a simulation environment, and the control performance was evaluated post-training.
4.1. Simulation Setup
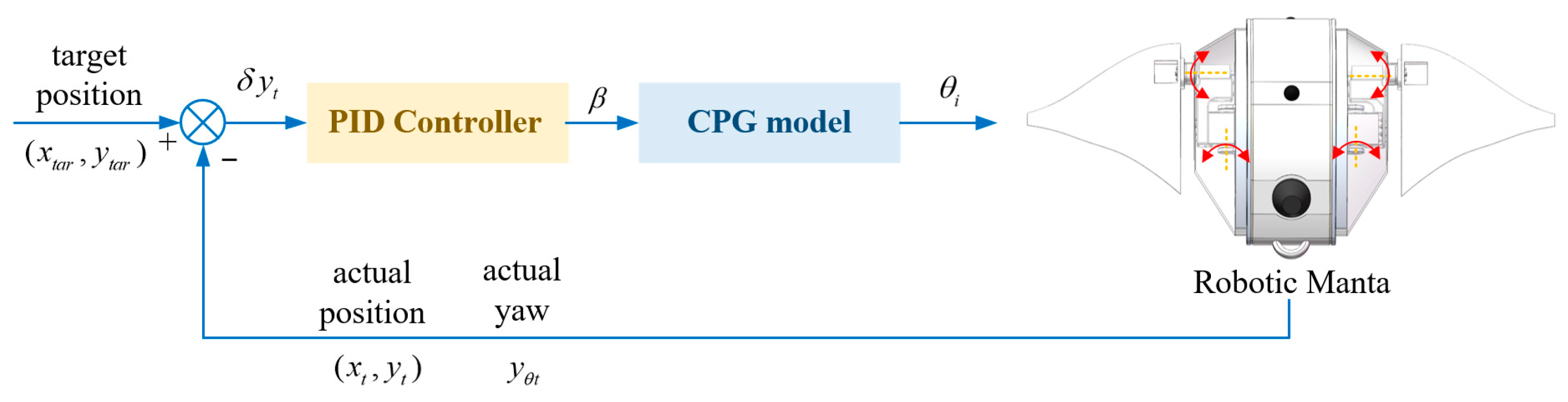
As a typical model-free closed-loop control method, the PID controller is widely used in modern control systems, while the sinusoidal motion controller is often used as a typical basic locomotion controller for robotic mantas. Therefore, in order to comprehensively evaluate the performance of the CPG–DDPG control strategy proposed in this paper in swimming control, we combine CPG with PID controllers to form the CPG–PID control strategy, combine the SIN controller with the DDPG algorithm to form a SIN–DDPG control strategy, and compare the control performance of the two strategies with the CPG–DDPG control strategy through swimming task testing in a simulation environment.
The main framework of the CPG–PID control strategy is shown in
Figure 5. The closed-loop input signal is the target position point, and the feedback signal consists of the actual position
and actual yaw angle
. The deviation signal
is used as the input for the PID controller. By applying the PID controller, the input parameters
of the CPG model are obtained, as expressed below:
where
,
, and
are the proportional, integral, and derivative coefficients of the PID controller, respectively. We conducted tests on the swimming performance of the robot under different PID parameters and optimized the control parameters. Finally, we set
,
, and
as fixed values. Consequently, the CPG outputs the steering angle
for the servo based on the input parameters
, thereby adjusting the heading of the robotic manta.
When designing the SIN–DDPG control strategy, we introduce the velocity control parameter
and the direction control parameter
in the SIN controller, which are used to adjust the swimming speed and direction of the robotic manta, respectively. The upper-level controllers of SIN–DDPG and CPG–DDPG have the same state space and reward function. The difference lies in the DDPG algorithm in SIN–DDPG, which makes decisions after observing the current state of the robotic manta and outputs two control parameters,
and
, to the SIN controller. These parameters adjust the amplitude to change the thrust generated by the pectoral fins, thereby adjusting the swimming direction and speed of the robotic manta. The SIN controller outputs the rotation angle of the servo. The specific calculation formula of the sine motion controller is as follows:
where
represents the tracking curve of the left flutter servo,
represents the tracking curve of the left rotary servo,
represents the tracking curve of the right flutter servo, and
represents the tracking curve of the right rotary servo.
denotes the velocity coefficient,
denotes the left direction coefficient, and
denotes the right direction coefficient.
The construction and training of the SIN–DDPG and CPG–DDPG control strategies relies on PyTorch, utilizing Python as the programming language. The simulation process unfolds as follows: Initially, the neural networks are established in PyTorch. Subsequently, the neural networks’ weights are continuously updated by the DDPG algorithms using the amassed training data. Once these algorithms converge, the necessary control strategies can be derived, and the weights of the neural network represent the training outcomes. The training process for this network consists of 1000 episodes, with each episode consisting of 500 training steps. The replay buffer size is set to 10,000, and the batch size is set to 62. The learning rates for both the actor and critic networks are fixed at 0.0001, with the discount factor
. Random noises are added in the training phase and used to enhance the generalization ability of the model.
Table 3 presents the hyperparameters [
36] used in the proposed SIN–DDPG and CPG–DDPG control strategies.
The simulation platforms for SIN–DDPG, CPG–DDPG, and CPG–PID control strategies all use Webots and are integrated with PyCharm to carry out collaborative simulation activities.
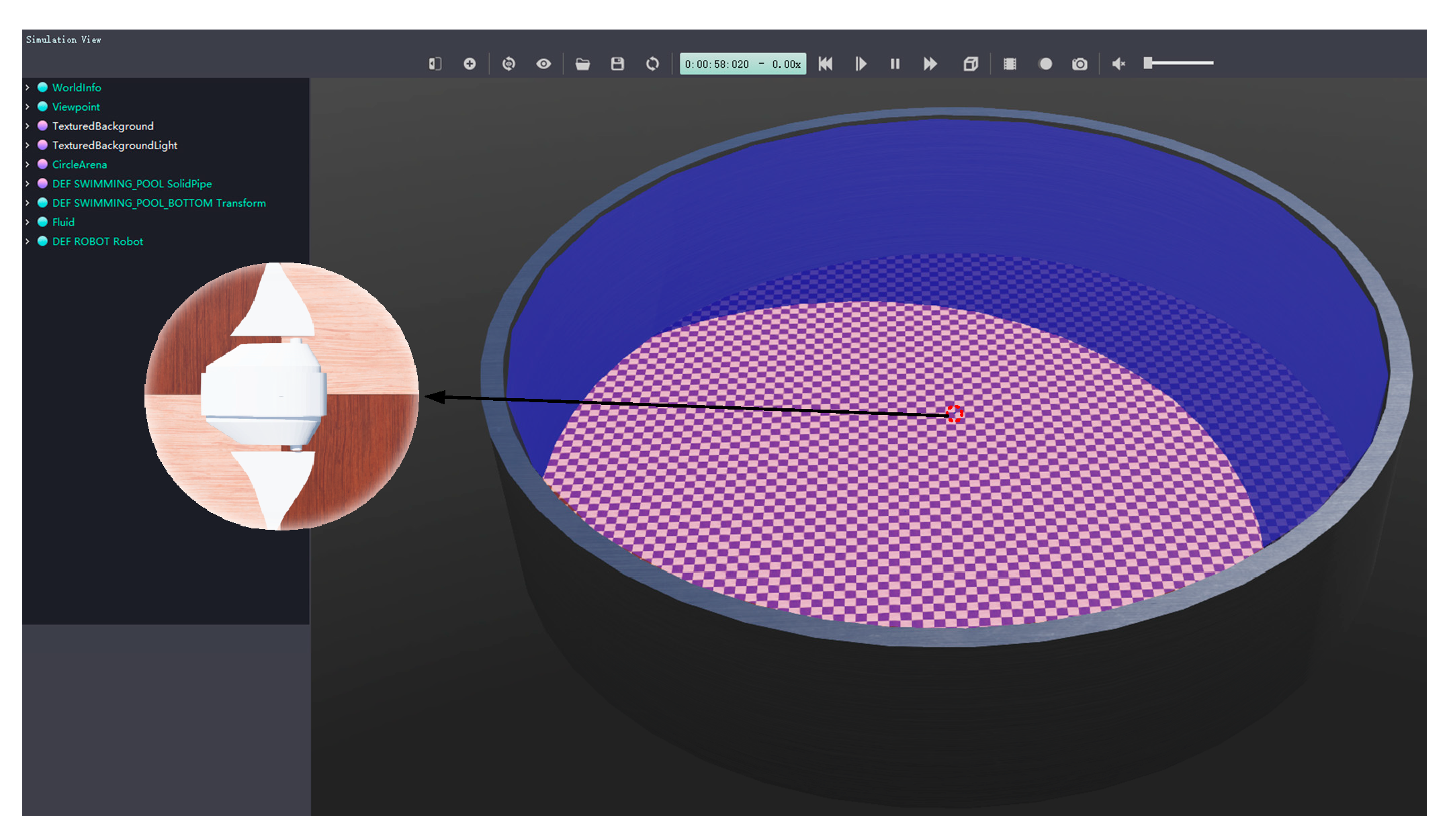
Figure 6 depicts the simulation environment of the robotic manta. The main parameters of the Webots simulation environment are shown in
Table 4.
This study compared the performance of SIN–DDPG, CPG–DDPG, and CPG–PID control strategies in simulated swimming tasks. The evaluation focused on task success rate, path length during swimming, task duration, and trajectory smoothness.
4.2. Analysis of Simulation Results
Figure 7 presents the convergence curves of the SIN–DDPG and CPG–DDPG control strategies under simulation conditions. The learning outcomes are derived from multiple training, utilizing mean and standard deviation for analysis. The results indicate that the CPG–DDPG control strategy surpasses the SIN–DDPG control strategy in terms of convergence speed and average reward value.
After training, we tested the SIN–DDPG, CPG–DDPG, and CPG–PID control strategies in a simulated environment for 100 swimming tasks, respectively. The initial coordinates were set to (4.6, 0.4) within a global coordinate system, with the destination point coordinates being randomly selected. A task was considered successful if the robotic manta reached the specified destination within 500 steps; failure was considered otherwise.
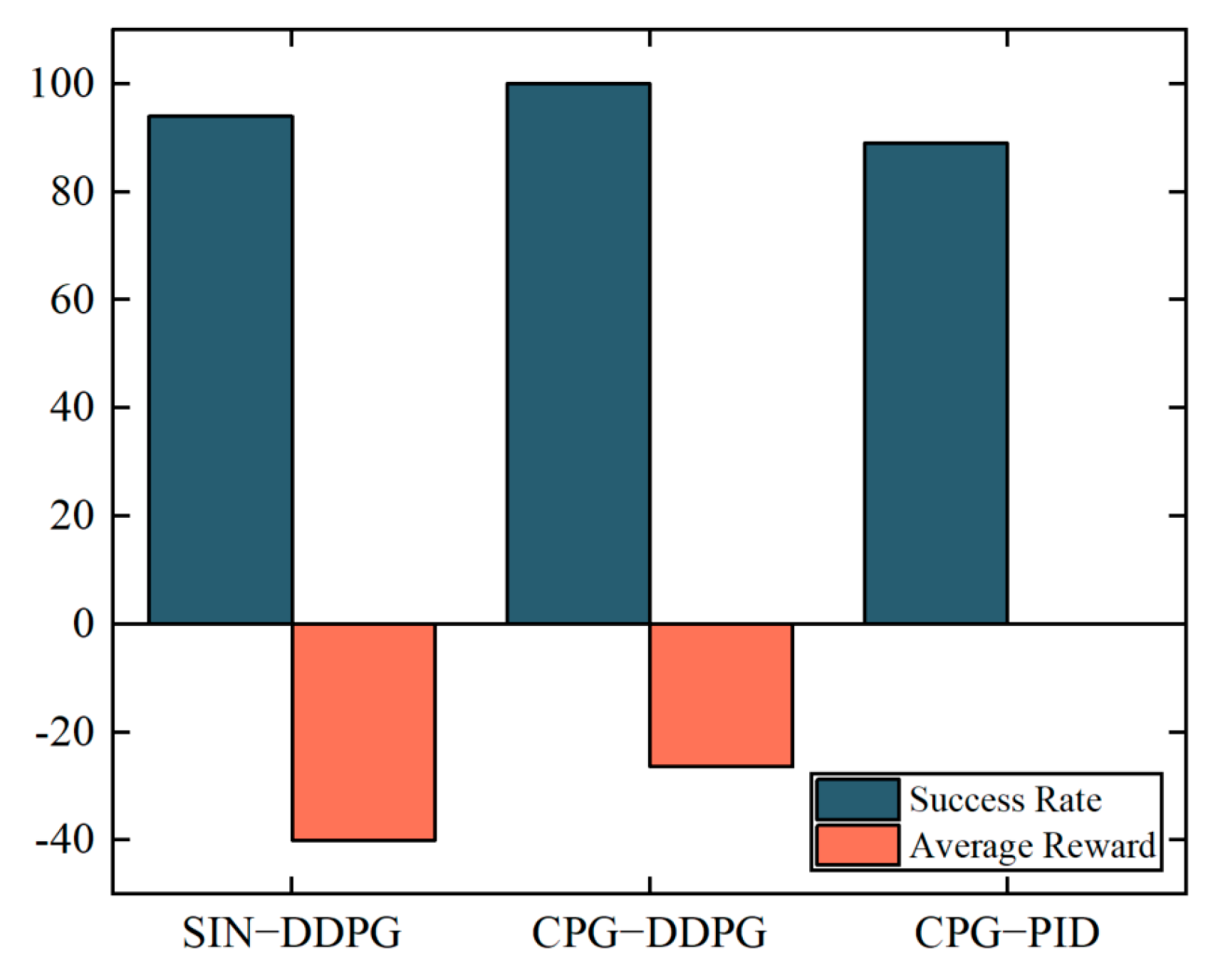
Figure 8 presents a comparison of the success rates and average rewards.
Through 100 tests, the CPG–PID control strategy successfully reached the target point 89 times, achieving a success rate of 89%. The SIN–DDPG control strategy had a success rate of 94%, with an average reward of −40. By contrast, the CPG–DDPG control strategy was the only control strategy to achieve a 100% success rate in the swimming tasks, and its average reward of −26.4 was significantly higher than that of the SIN–DDPG control strategy.
In order to further evaluate the effectiveness of the control strategies, we selected path length and time consumption as indicators. The three mentioned control strategies were employed to conduct a series of ten simulated swimming control tasks, each targeting five distinct points.
The experimental results are presented in
Table 5, where the abbreviations S–D, C–D, and C–P denote SIN–DDPG, CPG–DDPG, and CPG–PID control strategies, respectively. Analysis of the data reveals that the average path lengths for the SIN–DDPG, CPG–DDPG, and CPG–PID strategies were 16.72 m, 7.94 m, and 15.28 m, respectively. The corresponding average durations to complete the path were 166.2 s for SIN–DDPG, 37.4 s for CPG–DDPG, and 93.6 s for CPG–PID. These durations translated to average swimming speeds of 0.10 m/s for SIN–DDPG, 0.21 m/s for CPG–DDPG, and 0.17 m/s for CPG–PID. Across all five trials, each of the three control strategies successfully executed the assigned swimming control tasks.
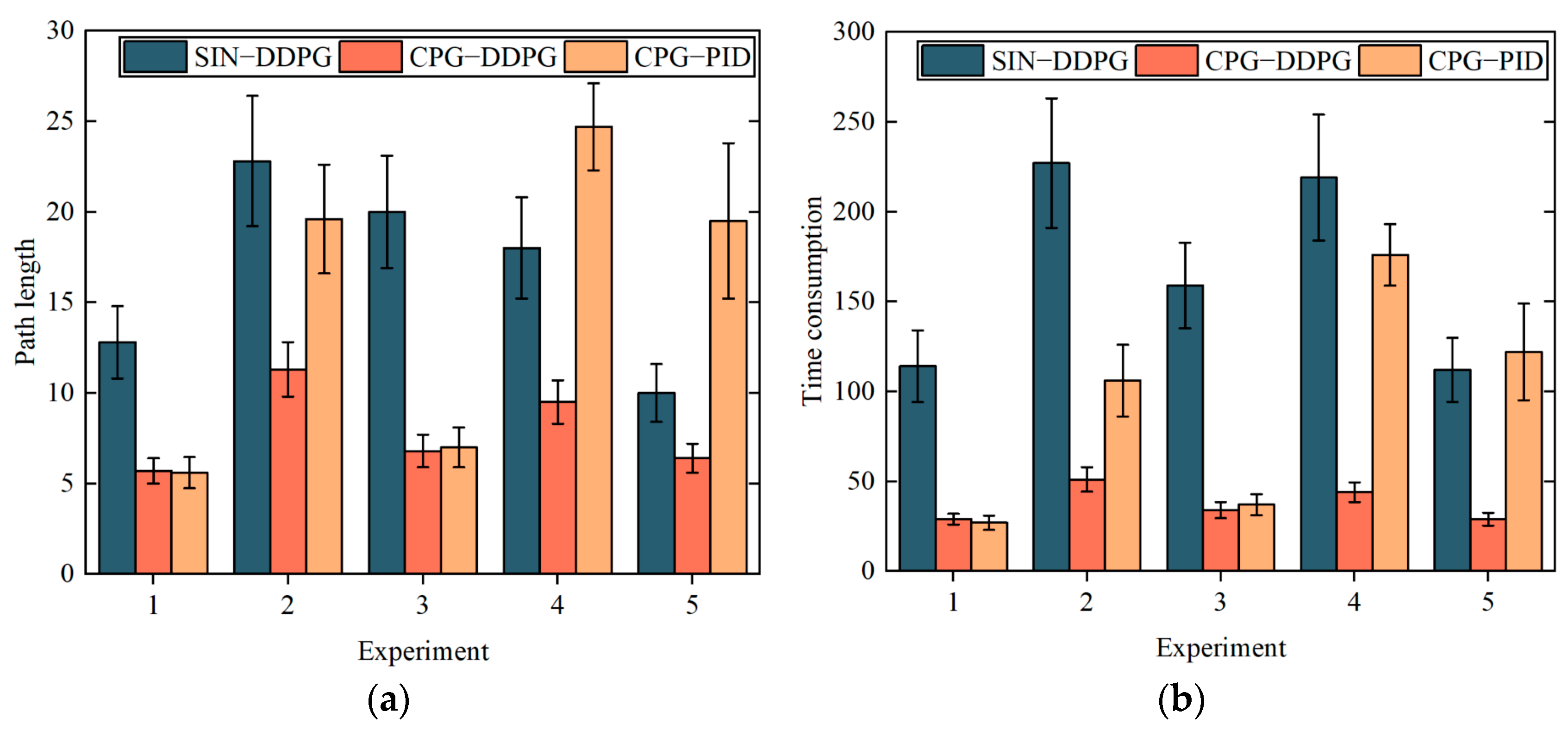
Figure 9a shows the comparison of the average path lengths of the three control strategies in the five experiments. The results indicate that the average path length of the CPG–DDPG control strategy was always less than half of the SIN–DDPG control strategy. In Experiment 1, the average path length of the CPG–DDPG control strategy slightly exceeded that of the CPG–PID control strategy. However, in the subsequent four experiments, the CPG–DDPG control strategy maintained a shorter path length. In addition, the standard deviation of the average path length for the CPG–DDPG control strategy was significantly shorter than that of the SIN–DDPG and CPG–PID control strategies.
Figure 9b compares the average time consumption of the three control strategies. Compared with the SIN–DDPG control strategy, the CPG–DDPG control strategy significantly reduced the average time consumption. Moreover, only in the first and third experiments did the average time consumption of the CPG–DDPG control strategy approach that of the CPG–PID control strategy. In the remaining three experiments, the average time consumption of the CPG–DDPG control strategy was significantly lower than the CPG–PID control strategy. Similar to the results of the average path length, the standard deviation of the average time consumption of the CPG–DDPG control strategy was still significantly lower than the other two control strategies.
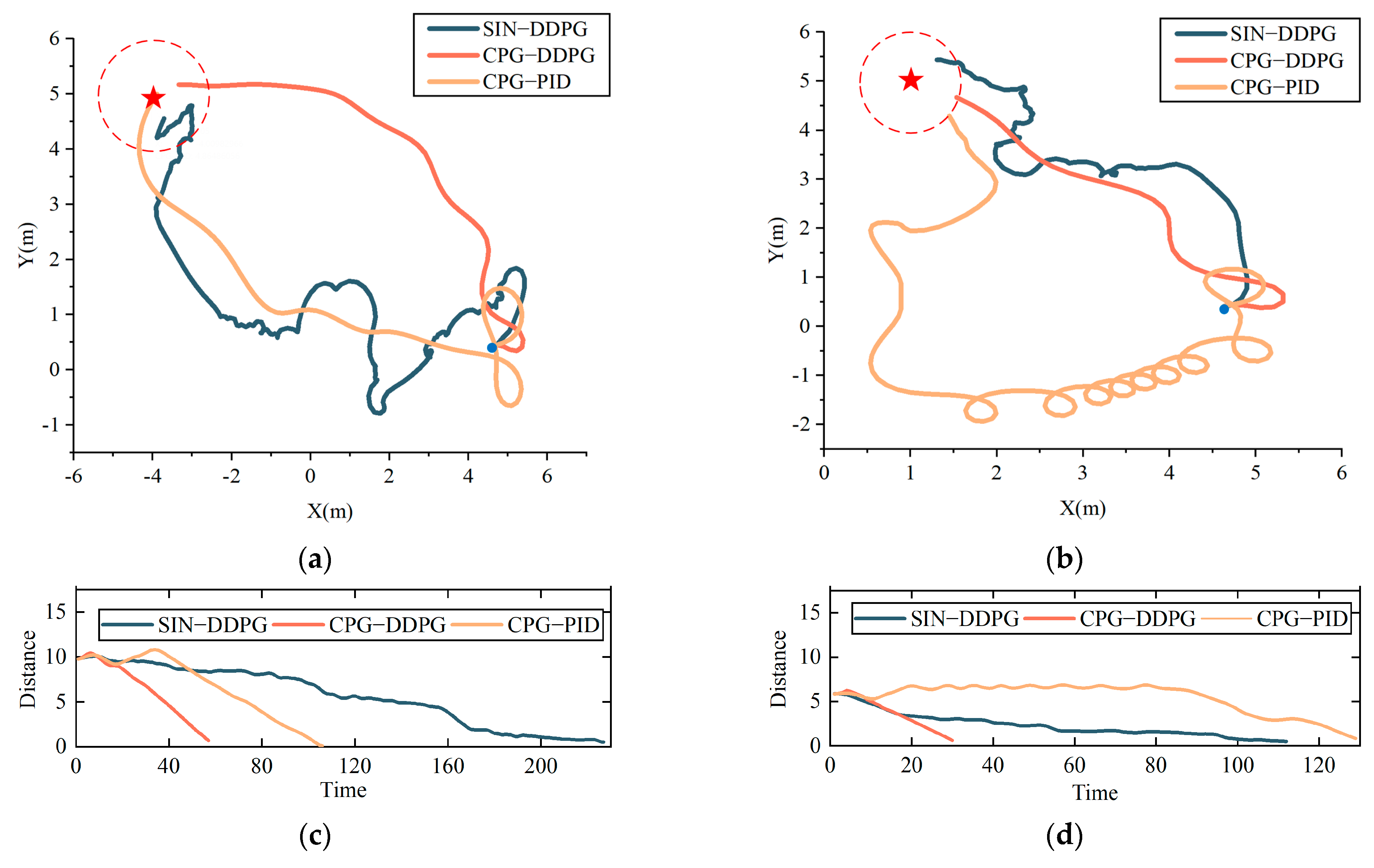
In Experiments 2 and 5, a swimming trajectory of the robotic manta was randomly selected, as shown in
Figure 10a,b, where the starting point is indicated by “•” and the end point is denoted by “★”, and the task was completed when the robotic manta swam inside the red dashed circles.
Figure 10c,d correspond to the distances between the center of the robotic manta and the target point during these two experiments, respectively. Compared with the other two control strategies, the CPG–DDPG control strategy achieved shorter and smoother trajectories due to its ability to quickly and smoothly adjust the swimming pattern of the robotic manta. It quickly corrected for heading angle errors, aligned itself with the target, and then moved quickly toward the target.
In contrast, the SIN–DDPG control strategy resulted in a longer path and a less smooth trajectory. This was due to the tendency for discontinuous acceleration and deceleration when adjusting the direction using the SIN control strategy as the base swimming control strategy. Moreover, the SIN control strategy’s high sensitivity to the coordination of two control parameters for modulating the speed and direction of the robotic manta led to less stability compared with the CPG control strategy, which smoothly transitioned between swimming modes with just a single input parameter. Consequently, the SIN–DDPG control strategy exhibited increased time consumption for the swimming task.
While the trajectory of the CPG–PID control strategy was smooth, the high sensitivity of the PID control strategy to parameter variations resulted in lower accuracy when adjusting the direction and speed of the robotic manta. This inaccuracy caused the robotic manta to swim in circles, thereby increasing the path length and time expenditure of the swimming task.
In conclusion, the CPG–DDPG control strategy outperformed the SIN–DDPG and CPG–PID control strategies in metrics such as success rate, path length, trajectory smoothness, and time consumption.
5. Experiments and Analysis
In this section, we present a series of experiments performed on the robotic manta prototype. First, we conducted open–loop experiments to evaluate the swimming ability of the prototype. Subsequently, to verify the proposed CPG–DDPG control strategy’s performance even more, we deployed the control strategy on a real–world experimental platform and compared it with the CPG–PID control strategy.
5.1. Experimental Platform
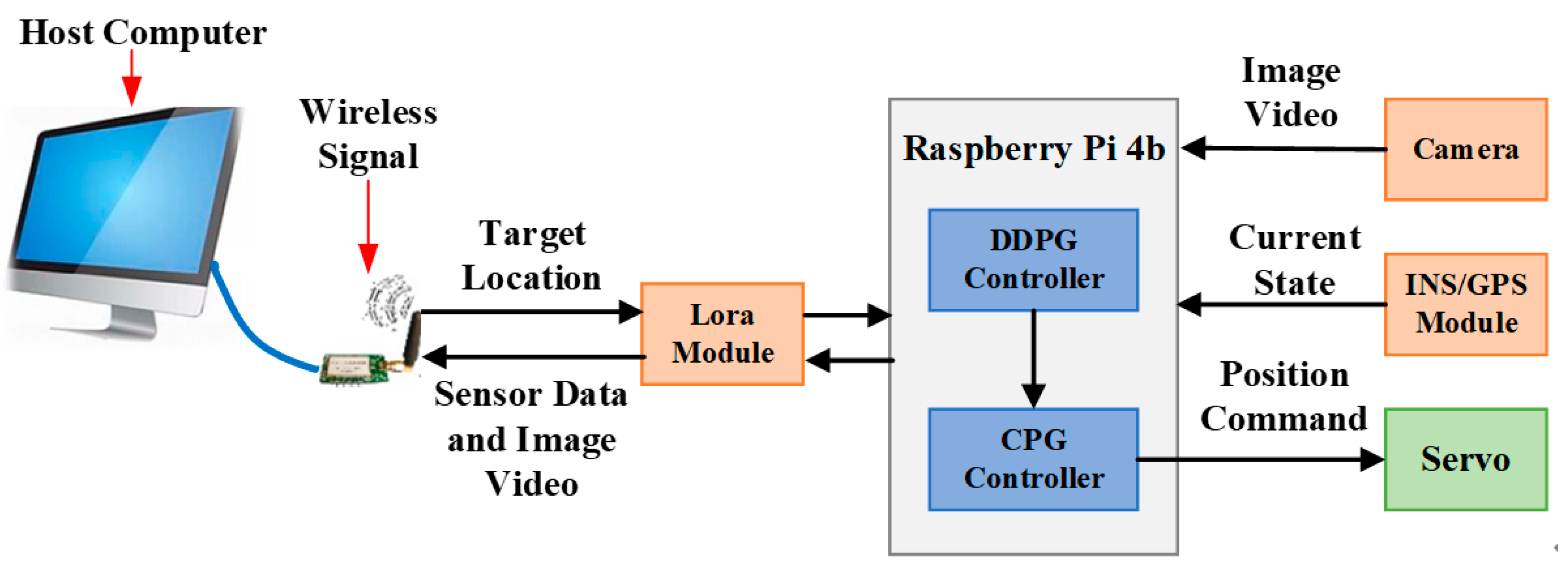
In this study, we developed an experimental platform, as shown in
Figure 11. The host computer sent task commands and other relevant data to the control center of the robotic manta via a wireless communication module. After receiving these messages, the onboard control unit adjusted the swimming modes of the robotic manta through the control strategy to complete the swimming task.
5.2. Basic Performance Test of the Robotic Manta Prototype
The low-level CPG-based swimming control strategy was validated by sending commands for different swimming modes from the host computer and observing the response of the robotic manta. As shown in
Figure 12, a straight-line swimming experiment was performed in a pool with a diameter of 1.8 m. The prototype took about 4 s to swim from one end of the pool to the other, with an average speed of 0.4 m/s.
Figure 13 depicts the experimental results of the left and right turns of the robotic manta prototype. It completed the in- situ turns with a maximum turn speed of 2 s/turn, showing excellent maneuverability.
The experimental results of surfacing and diving are presented in
Figure 14. The depth of the pool was about 0.6 m, the whole process took 2 s, and the ascent and descent speed of the robotic manta was about 0.3 m/s.
The experiments validated the feasibility of the CPG model on the robotic manta prototype, demonstrating its effectiveness across various swimming modes.
5.3. Swimming Task Experiments of the Robotic Manta Prototype
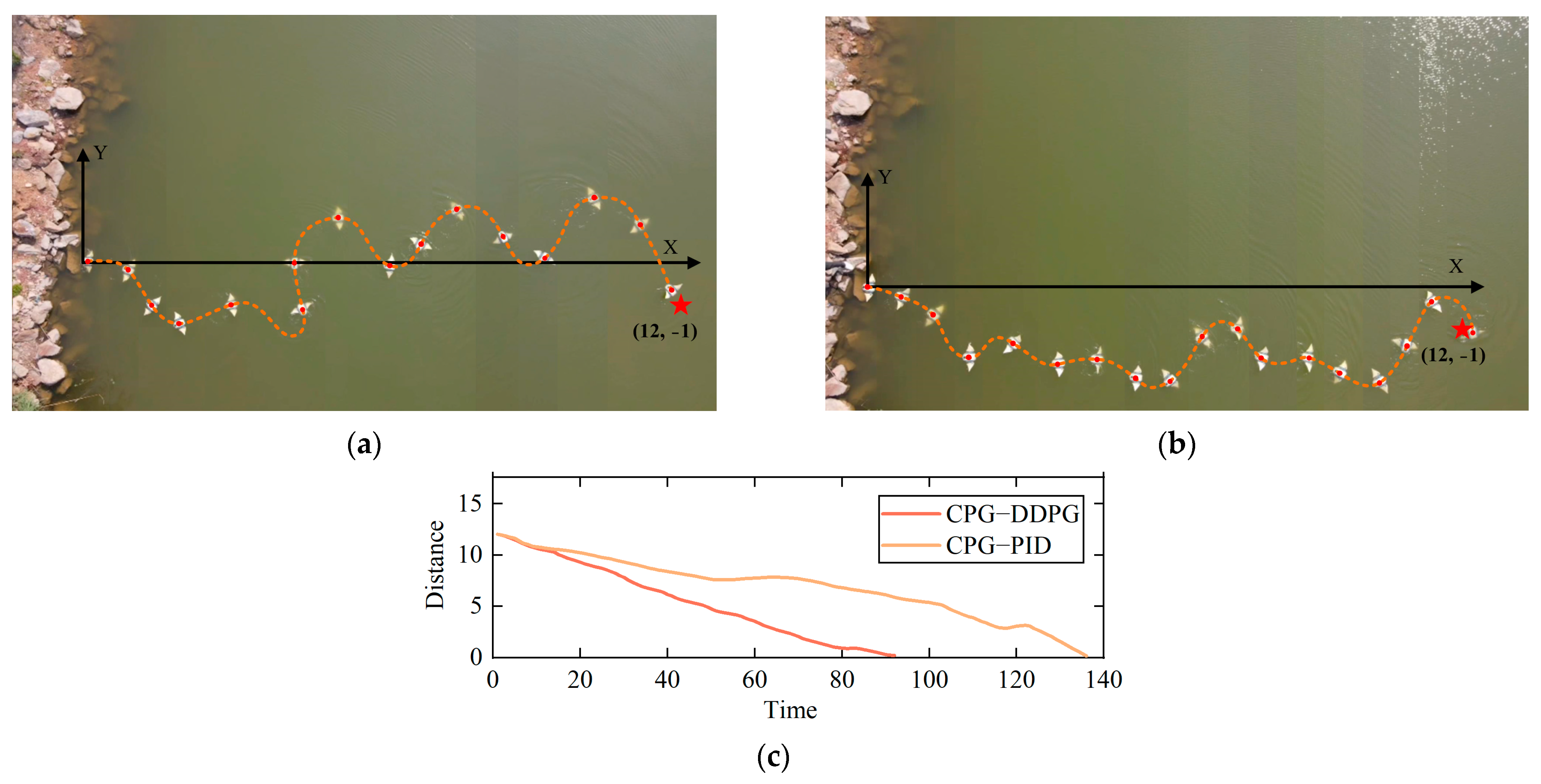
In simulation tests, we observed that the CPG–PID control strategy outperformed SIN–DDPG, despite having a slightly lower success rate. However, it showed improvements in trajectory smoothness, swimming path length, and task completion time. Considering overall performance and stability, we chose to compare the CPG–DDPG control strategy with the superior-performing CPG–PID control strategy. By controlling the robotic manta prototype to complete swimming tasks, we further assessed the performance of the two control strategies in real-world scenarios. The goal of this task was for the robotic manta to swim from the origin (0, 0) to the target position at coordinates (12, −1), covering a total distance of 12.05 m. Each control strategy was tested ten times. We used average path length and average time consumption as metrics to evaluate the experimental results. Similar to the simulation results, the CPG–DDPG control strategy resulted in shorter swimming paths and less time consumption compared with the CPG–PID control strategy. Specifically, the average swimming paths for CPG–DDPG and CPG–PID control strategies were 17.2 m and 21.3 m, respectively, with average time consumptions of 92 s and 138 s, and average swimming speeds of 0.19 m/s and 0.16 m/s.
A randomly selected swimming trajectory of the robotic manta is shown in
Figure 15a,b, where the center point of the robotic manta is indicated by a red “•”, the starting point is the origin, and the endpoint is marked with a “★”.
Figure 15c corresponds to the distances between the center of the robotic manta and the target point.
The experimental results indicate that, in the same physical world environment, the travel path of the robotic manta controlled by the CPG–DDPG control strategy was significantly shorter than that controlled by the CPG–PID control strategy.
Comparing
Figure 10 and
Figure 15 reveals the impact of simulated and real-world environments on the control performance of the robotic manta.
Figure 10 shows the trajectories of three control strategies in a simulated environment with minimal external interference, allowing for a clear evaluation of each strategy. In contrast,
Figure 15 shows the trajectories of the CPG–DDPG and CPG–PID control strategies in a real-world environment, including factors such as water flow and sensor noise. The CPG–DDPG control strategy exhibited smoother and more stable trajectories in both environments, highlighting its superior adaptability and robustness. It achieved higher precision with minimal deviation in the simulated environment and effectively resisted disturbances in the real-world environment, maintaining small deviations. Conversely, the CPG–PID control strategy was more sensitive to real-world disturbances, resulting in poorer stability and accuracy.
6. Conclusions
This paper introduces a novel control strategy for robotic manta, termed the CPG–DDPG, which integrates the DDPG algorithm with a CPG network. The CPG–DDPG control strategy consists of a low-level CPG network and a high-level DDPG algorithm, which adaptively adjusts the control parameters of the CPG network according to the actual attitude and speed of the robotic manta, and then adjusts the swimming pattern to realize the desired swimming control objectives finally. This control strategy offers stable, adaptive, and smooth modality transitions in response to environmental changes. It can be applied to multi-joint robotic fish of different types and degrees of freedom, requiring only some modifications in the CPG model section.
Simulation experiments were conducted on the swimming tasks of the robotic manta using three distinct control strategies: SIN–DDPG, CPG–DDPG, and CPG–PID. The results demonstrated that the proposed CPG–DDPG control strategy outperformed both SIN–DDPG and CPG–PID in success rate and terms of efficiency. Specifically, compared with SIN–DDPG and CPG–PID, CPG–DDPG accomplished the swimming task with 6% and 11% higher success rates and 77% and 62% higher efficiency, respectively. Additionally, the swimming trajectories under the CPG–DDPG control strategy were notably smoother than those of SIN–DDPG and CPG–PID. The results of further experiments on a robotic manta swimming task using CPG–DDPG and CPG–PID control strategies in a real-world environment show that the CPG–DDPG control strategy reduced the task consumption time by 33% compared with the CPG–PID control strategy.
Both simulation and experimental validations confirmed the superior performance of the CPG–DDPG control strategy. Compared with SIN–DDPG, CPG–DDPG more accurately simulated the swimming behavior of manta rays and provided smoother transitions between the various swimming modes. Furthermore, unlike CPG–PID, the CPG–DDPG control strategy eliminated the need for tedious parameter adjustments, and its exceptional learning ability allowed the robotic manta to navigate proficiently in unknown underwater environments. The CPG–DDPG control strategy can quickly and smoothly adjust the direction of the robotic manta to deal with deviations. For distant targets, a high-frequency swimming mode is used for rapid approach, while a low-frequency mode ensures accuracy upon arrival. This control strategy has great potential to improve the maneuverability, efficiency, stability, and adaptability of the robotic manta. However, the proposed control strategies focus solely on 2-D target point swimming control. Future research will improve the depth regulation device in hardware and combine 2-D swimming control with depth control tasks to train control strategies, ultimately achieving 3-D target point swimming control for the robotic manta.