Abstract
The issue of finite-time stability has garnered significant attention in the control systems of quadrotor aerial vehicles. However, existing techniques for achieving finite-time control often fail to consider the system’s state constraint characteristics and rarely address input quantization issues, thereby limiting their practical applicability. To address these problems, this paper proposes a finite-time adaptive neural network tracking control scheme based on a novel barrier Lyapunov function for the quadrotor unmanned aerial vehicle (UAV) system. Firstly, an adjustable boundary for the barrier Lyapunov function is introduced in the control system of a quadrotor UAV, enabling convergence of all states within finite-time constraints during trajectory tracking. Subsequently, a filter compensation signal is incorporated into the recursive design process of the controller to mitigate errors caused by filtering. Finally, a smoothing intermediate function is employed to alleviate the impact of input quantization on the quadrotor system. Experimental validation is conducted on the Quanser QDrone experimental platform to demonstrate the efficacy of the proposed control scheme.
1. Introduction
Quadrotor UAVs are widely recognized as one of the classic representatives within the realm of UAVs. They exhibit exceptional characteristics, such as a simple structure, diverse sizes, low cost, ease of operation, and robust vertical takeoff and landing capabilities. As a result, quadrotor UAVs have found extensive applications across various fields, including civil aerial photography and mapping [1,2,3], emergency detection and rescue [4,5,6], air transportation [7], power transmission line inspection [8], and pesticide spraying missions [9], among others. These diverse applications effectively showcase the advantages of quadrotor UAVs, thereby highlighting the significance of addressing control challenges in quadrotor UAV systems within the control field.
Quadrotor UAV is a typical nonlinear underactuated system. It consists of three position subsystems and three attitude subsystems coupled into a four-input and six-output system. The position subsystem needs to be controlled by adjusting the attitude subsystem. Moreover, designing a high-level trajectory tracking controller during flight missions is a challenging problem in control engineering due to inherent parameter uncertainty, unknown external interference, and the need for high flight quality and safety.
As a type of aircraft, the quadrotor UAV imposes stringent requirements on stability, accuracy, and rapidity of its controller. Ensuring the reliability and autonomy of the quadrotor aircraft during flight tasks in positional environments heavily relies on the adaptability [10] and robustness [11] of the controller. To this end, numerous researchers have proposed various control schemes. For instance, reference [12] presents an adaptive supertorsional sliding mode controller for target trajectory tracking of a quadrotor UAV, employing an adaptive supertorsional extended state observer to estimate gusts. Reference [13] mainly addresses the issue of finite-time tracking control for a quadrotor UAV in the presence of external disturbances, uncertain parameters, actuator failures, and input saturation. It introduces a composite controller aiming to achieve outstanding tracking performance, including finite-time error convergence, robust enhancement, fault tolerance, and saturation mitigation. In reference [14], a novel model-based predictive control (MPC) design is presented in this paper for a quadrotor aerial vehicle with a suspended load, achieving fast stabilization times and minimal swing angles by considering the dynamics of the hanging payload, the vehicle’s three-dimensional dynamics, and its rotation.
The above methods, despite enhancing robustness and achieving uniformly bounded tracking or finite-time error stabilization, exhibit a convergence rate that heavily relies on the presence of initialization errors and controller parameters. In the case of a large initial state, convergence may be subpar, even for specific finite-time modes, due to extended stability periods. Additionally, these methods do not take into account the system state constraints, which could potentially make them impractical. To address this issue, a state constraint control method called Barrier Lyapunov Function (BLF) has been proposed [15]. Specifically, an adaptive control method based on tan-type BLF is presented in [16] to achieve asymptotic output tracking of time-varying state-constrained strictly feedback nonlinear systems. For uncertain nonlinear systems with asymmetric time-varying full-state constraints, an adaptive neural network finite-time tracking control strategy based on time-varying asymmetric BLF (TVABLF) is proposed in [17]. Additionally, the author of [18] integrates the time-varying integral BLF (TVIBLF) into the adaptive control design, overcoming the conservative limitation of traditional BLF while respecting the full-state time-varying constraint bounds. In [19], A novel real-time adjustable barrier function is proposed to dynamically adapt the design parameters based on the tracking error. Notably, the performance of these controllers heavily relies on continuous signal transmission via wireless communication bandwidth, which may not be achievable due to the limited computing power, transmission resources, and onboard energy capacity of small quadrotor platforms.
To reduce the data transmission burden on digital platforms and improve the actuator’s execution rate, the use of quantitative control technology is prevalent in digital control systems with limited transmission bandwidth. Reference [20] employed the adaptive inversion method to investigate the stabilization problem of a nonlinear uncertain input quantization system. They introduced a hysteretic quantizer to avoid chattering and derived the criterion for selecting quantizer parameters. In [21], in order to synergistically integrate quantization output feedback control and state feedback quantization control, a compound adaptive fuzzy quantization control scheme, based on a fuzzy approximator, was employed. The authors of [22] introduced a novel quantization decomposition method to integrate the attitude quantization controller into assurance tracking. This integration reduces communication bandwidth requirements while maintaining attitude response within a given time. In reference [23], for a class of nonlinear systems with triangular structures, an improved backstepping method is proposed. This method employs a smoothing function and intermediate control law to eliminate the influence of quantization.
Inspired by the above discussion, in this paper, a finite-time adaptive state-constrained quantization control scheme is proposed to realize trajectory tracking for quadrotor UAVs. Compared with the previous studies, the novelties of this paper are summarized as follows:
- Introducing an adaptive neural network quantization controller to ensure convergence of all states within a constrained range in a finite time, maintaining them within this region and exhibiting reliable tracking performance.
- Incorporating a BLF boundary capable of online parameter adjustment in response to changing tracking errors facilitates achieving full state constraints for the quadrotor UAV and mitigates overshooting of tracking errors during transient processes.
- During recursive design of the controller, incorporating a filter compensation signal addresses filter-induced errors. Additionally, employing a smoothing function with an intermediate control law mitigates the effects of input quantization in the quadrotor UAV system.
- A finite-time adaptive neural network tracking control scheme based on a novel barrier Lyapunov function is proposed in this paper and successfully validated on a physical experimental platform.
The remainder of this paper is structured as follows: Section 2 presents the problem formulation, Section 3 provides the principal findings for the control design scheme, Section 4 delineates the experimental validation conducted to illustrate the efficacy of the proposed controller, and Section 5 culminates in the conclusion of this paper.
2. Problem Formulation and Preliminaries
2.1. System Model of Quadrotor
The structure of the quadrotor UAV is shown as Figure 1, where refers to the body frame, refers to the Earth-fixed frame, and its general dynamic model is shown in Formula (1), the derivation of which is described in reference [21].
where represent the displacement of quadrotor UAV in the directions respectively, and represent the roll angle, pitch angle, and yaw angle, respectively. on behalf of , on behalf of , g is the gravity acceleration, = 1, …, 11 are unknown, denotes the relative speed of the cross-coupled rotor and satisfies with = 1, ⋯, 4 being the rotating speed of the propeller. = 1, …, 6 denote the bounded external disturbances, = 1, …, 4 represent the aforementioned control inputs and are defined as follows:
where l is the distance from the rotor to the shaft, = 1, ⋯, 4 represents the lift force by the rotation of the four rotors, are the moment of inertia in each of the three directions.
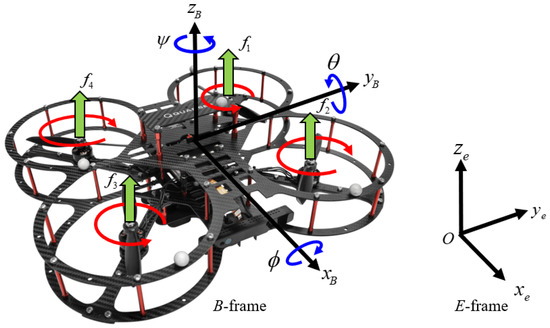
Figure 1.
The experimental environment for simulation verification.
To facilitate controller design, the above quadrotor model with input quantization characteristics is simplified, as described in (3).
where , , .
2.2. Hysteretic Quantizer
It is important to mention that using the quantized signal, which contains high-frequency components, directly for the actuator will result in a decline in control performance. Therefore, the implementation of a signal quantizer is necessary in order to compromise the communication rate. In this paper, a hysteresis quantizer (see [24,25]) is employed to minimize the occurrence of chattering phenomena. The key characteristics of the hysteresis quantizer are outlined below:
where , , , parameters satisfy . The magnitude of the dead zone for is influenced by .
The hysteretic quantizer can be decomposed into one consisting of a nonlinear part and a linear part, i.e., . The nonlinear part satisfies
2.3. Novel Barrier Lyapunov Function
The following BLF is used throughout this paper:
To enhance the performance of BLF, a novel boundary function is introduced, referring to the method introduced in reference [19]; a detailed description is given as follows:
where = 0, 1, …, 2n + 1, k = 1, 2, …, m is a constant, m is the number of adjustments. denoted as the settling time, > 0 and > 0 denote, respectively, the starting time and temporal interval of the kth adjustment. > 0 and > 0 are the configurational parameters of the boundary function, which can be adaptively tuned online based on the variation in the tracking error. The specific descriptions are as follows:
where represents the tracking error, denotes the minimum permissible value of , and a are the adjustment parameters, and .
Figure 2 shows the schematic diagram of the boundary of the novel adjustable BLF function and the boundary of the traditional exponential and constant BLF function, where
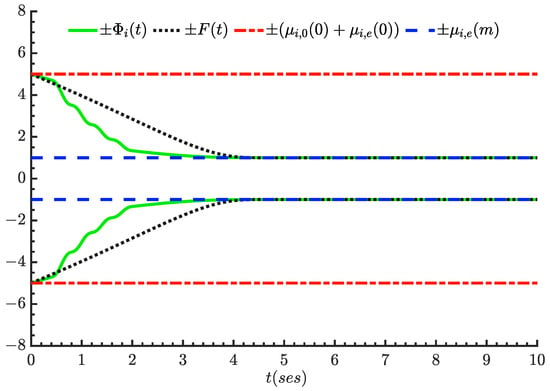
Figure 2.
The experimental environment for simulation verification.
It can be seen that the adjustable boundary used in this paper converges faster, and by introducing two adjustable parameters, the problem of excessive control signal caused by the existence of initial error can be avoided.
Remark 1.
The format of within the interval in Equation (7) is carefully designed to maintain its continuity. It can be proved that is a continuous function and satisfies . The detailed derivation process is described in reference [19].
Remark 2.
It should be noted that the novelty of this paper lies in the focused addressing of the input quantization problem specific to quadcopter aircraft, which was not covered in reference [19]. A significant contribution to UAV control design is represented by this, especially considering the limited resources of small UAV platforms.
Remark 3.
It can be obtained by deducing Equation (7) that and for . Compared with the traditional constant type and exponential type BLF, the novel BLF function boundary used in this paper has a better constraint ability on the error, and its two adjustable parameters and will be adjusted according to the size of the error, which will not cause the problem of a too large control signal caused by too small boundary parameters.
The following lemmas are required for semi-global practical finite-time stable analysis.
Lemma 1
([26]). If there exist scalars and for the system , then the Lyapunov function candidate inequality is as follows:
then the system is semi-global practical finite-time stable, that is, the solution of the system is bounded for , where and
Lemma 2
([27]). For , the the following inequality holds:
Lemma 3
([28]). The following inequality holds:
2.4. Radial Basis Function Neural Networks
In this paper, the radial basis function neural networks (RBFNNs) will be applied to approximate unknown smooth function, such that:
where Z and are the input and output of the RBFNNs, respectively, denotes the optimal weight vector, represents the basis vector function, is an approximation error with bound. A Gaussian function is chosen for the basis vector function.
where A and B are the center and width of the Gaussian function, respectively.
Lemma 4.
For any given real continuous function with being a compact set, and an arbitrary , there exists an integer , such that
where represents an optimal weight vector, which can be precisely defined as
Remark 4.
The connection between the various sections of this chapter lies in their collective contribution to the theoretical framework and methodology of our study. The system model of quadrotor provides the foundational description of our research subject, while the hysteresis quantizer serves as a key component within the system control model. The novel barrier Lyapunov function and radial basis function neural networks each offer innovative methods and technical means within control algorithms. These interconnected sections ensure the integrity and internal consistency of our study in terms of both theory and methodology.
3. Controller Design and Stability Analysis
In this section, an adaptive neural network quantization control scheme that introduces a filtered error compensation signal is designed. Furthermore, a novel BLF is employed to enforce finite-time state constraints. The graphical representation in Figure 3 depicts the block diagram of the control system.
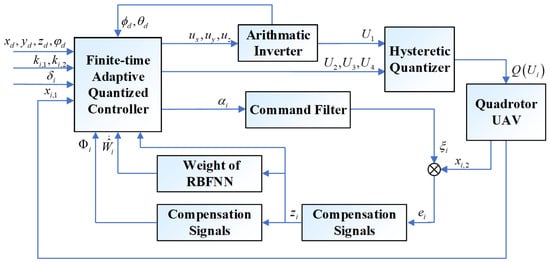
Figure 3.
The experimental environment for simulation verification.
For i = 1, …, 6, define the tracking errors as
where denote errors, denotes desired signal, and represents the output signals of the command filter, with serving as the input. For i = 1, …, 6, define the following command filter as
where serves as the input of the filter, = represents the output signals of each filter. The initial values are chosen such that (0) = (0) and (0) = 0.
A significant limitation of the conventional backstepping recursive design is the well-known issue of complexity explosion. This drawback arises from the need for repetitive differentiations of virtual controllers, which can introduce filtering errors when a command filter is utilized. In the subsequent discussion, compensation signals will be formulated to effectively eliminate errors , for i = 1, …, 6.
Define the compensation tracking errors as
where denote compensation signals.
In the approach described in this paper, the constraint is substituted with constraint , where represents a positive parameter. And the barrier Lyapunov function (6) is used in this paper. Referring to the discussion in [29], it is apparent that the error signal is bounded, and there exists a parameter so that . It should be emphasized that ensuring is necessary to achieve favorable tracking control performance. By considering , we can adjust the parameters of appropriately so that and . Finally, the constraint condition can be also guaranteed.
According to Formula (6), the Lyapunov function that constructs the first-order subsystem as
Design the virtual controller , and the adaptive law for compensating signals as
where is a positive parameter.
Taking (24) and (25) into consideration yields
Remark 5.
This paper designs a controller for a quadrotor UAV using a dynamic surface control method with a filtering compensator function. Step 1 involves designing a virtual control law for a first-order system, while Step 2 provides the actual control law for a second-order system.
Based on Lemma 4, the unknow item can be approximated as follows:
The Lyapunov function is chosen as
where is a positive parameter. , and is the estimation of .
By analyzing (30), design the intermediate control law , the adaptive law of RBFNN weights , and the adaptive law of compensation signal as follows:
It follows from (35) that
Eventually, the actual controller denoted as
where is a positive parameter, and with the form of the actual controller, it is easy to see that .
According to (5) into consideration, one has
Indeed, the above inequality holds since
It should be emphasized that, during the design process of the dual closed-loop controller, the desired roll and pitch angle trajectories are derived by incorporating the control inputs from the position subsystem and the designated reference trajectory for a specified yaw angle. Thus, decoupled control of an underactuated quadrotor system is realized.
Following Equations (46)–(48), the desired roll angle and pitch angle are prescribed as the following
and the total lift is calculated as
Remark 6.
Input quantization, a common phenomenon in practical systems due to limitations in sensor resolution or communication constraints, poses challenges for control law design. To address this, our paper utilizes the BLF method to handle constraints and introduces a smooth intermediary function to mitigate quantization errors. By combining these methods, we achieve finite-time control of a quadrotor unmanned aerial vehicle (UAV) system with both state constraints and input quantization characteristics, ensuring robustness against practical limitations.
Theorem 1.
Consider the closed-loop system (1), design virtual controllers (24), adaptive law for compensating signals (25) and (33), intermediate control function (31), actual controller (37), and adaptive law of RBFNN weights (32), then the proposed adaptive neural network-based hysteretic quantization control scheme guarantees semi-global practical finite-time stability of the closed-loop system.
Proof for Theorem 1.
According to Lemma 3, along with = 1, = , = 1 , = , = , it follows that
Similarly
Then according to Lemma 1, the system is is semi-global practical finite-time stable, that is, the solution of the system is bounded for , where 0 < < 1 and
Hence, this ends the proof. □
4. Experimental Verification
In this paper, the Quanser produced QDrone, depicted in Figure 1, serves as the experimental platform for validating the proposed scheme. The structure of the QDrone control platform, encompassing the following components, is displayed in Figure 4.
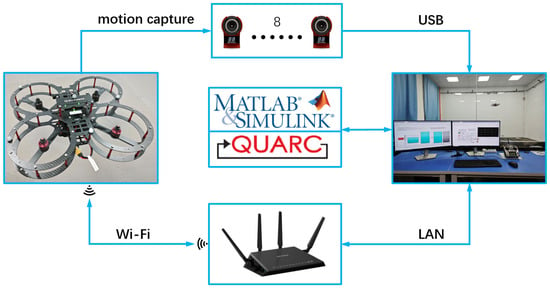
Figure 4.
The experimental environment for simulation verification.
QDrone: The UAV has dimensions of 50 cm × 50 cm × 15 cm and weighs 1200 g. It can carry a maximum load of 300 g. The power supply is a 4S 14.8 V LiPo battery with an XT60 connector. A full charge allows for a flight time of 7 to 8 min.
QuaRC: The system features real-time control software developed by Quanser (Toronto, Canada), which is fully compatible with MATLAB’s (2021a) real-time control software. The system operates in Host–Target mode, with the controller developed on MATLAB/Simulink in the Host, and then compiled and downloaded directly under Simulink to the embedded controller (target machine) of the unmanned tool, using the wireless communication protocol for real-time control.
OptiTrack: Spatial 3D localization is achieved by means of eight infrared cameras OptiTrack. The infrared positioning camera OptiTrack has a camera range of 20 m, a resolution of 1280 × 1024, a horizontal field of view of 42°–56°, a single-point tracking number of 80, a maximum of 10 simultaneous object captures, and a millisecond positioning accuracy.
The parameters of the QDrone are shown in Table 1. In the experiments, the desired trajectories of the positionare chosen as , , and . The disturbances are chosen as follows: , , , , , .

Table 1.
Quad-rotor parameters.
Remark 7.
The external disturbances represent various physical phenomena affecting the quadrotor, such as wind speed variations, air resistance changes, gravity variations, pressure changes, airflow disturbances, gyroscopic effects, and mechanical vibrations. These disturbances are incorporated into the experimental model through direct assignment to simulate real-world conditions and assess the robustness of the control strategies employed.
The controller parameters chosen for simulation are are shown in Table 2.

Table 2.
Parameters of proposed control strategy.
To comprehensively showcase the effectiveness and superiority of the control scheme proposed in this paper, a comparison is made between the results obtained from the proposed scheme and those derived from the FLS-PID method. The selection of controller parameters for the FLS-PID approach is revealed in [30].
The experimental results are displayed in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. It can be seen from Figure 5 that the quantitative control scheme proposed in this paper can achieve stable trajectory tracking of the quadrotor with state constraints. Figure 6 and Figure 7 show the tracking effect of position and Angle , respectively. Figure 8 and Figure 9 show the curves of position tracking errors , respectively. Figure 10 and Figure 11 show the curves of parameter update laws , respectively. It can be seen from the figure that the error is always within the preset range during the whole control process. Figure 12 shows the four control input signals.
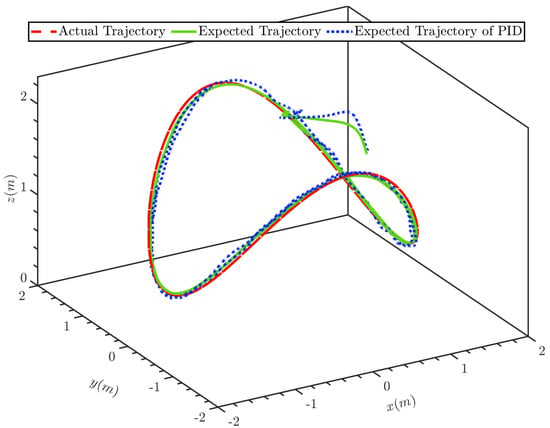
Figure 5.
Space diagram of position.
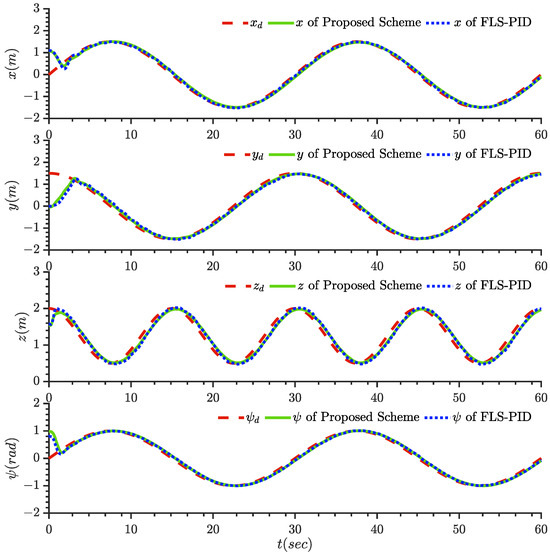
Figure 6.
Tracking performance of states .
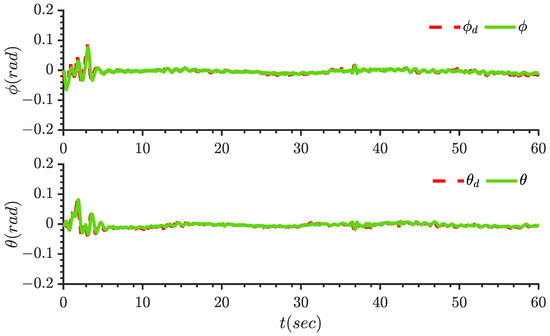
Figure 7.
Tracking performance of states , .
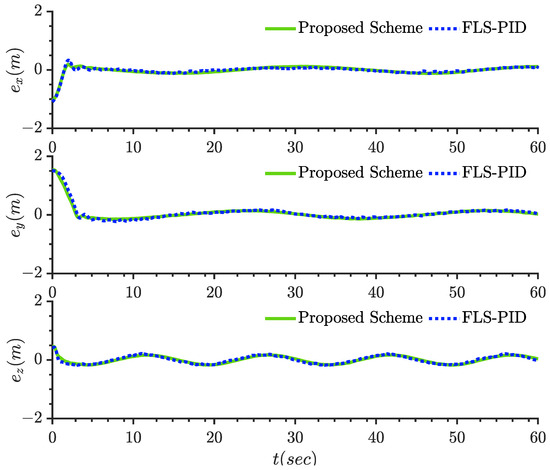
Figure 8.
Position tracking errors = 1, 2, 3.
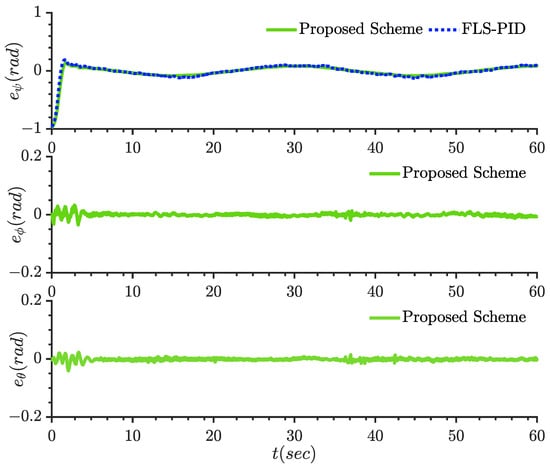
Figure 9.
Angle tracking errors = 4, 5, 6.
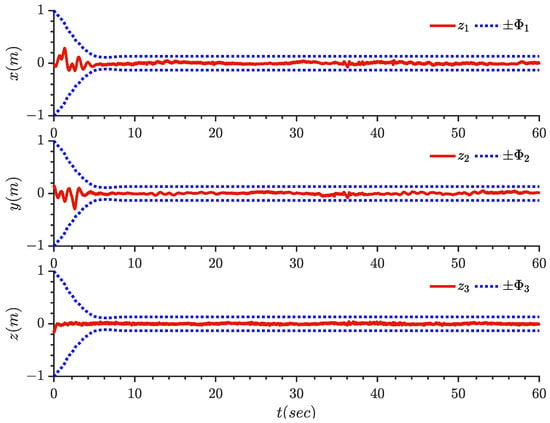
Figure 10.
Parameter update laws = 1, 2, 3.
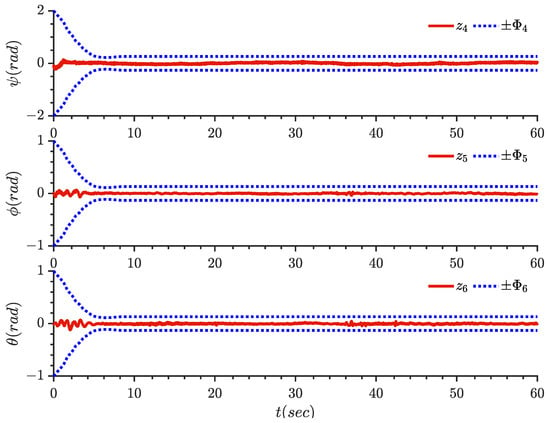
Figure 11.
Parameter update laws = 4, 5, 6.
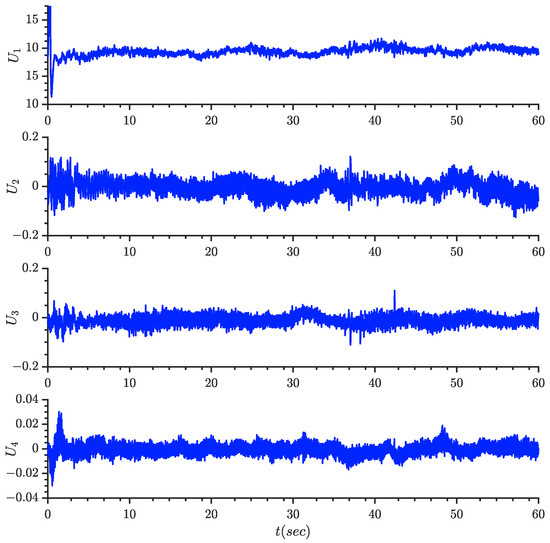
Figure 12.
Control input signals = 1, 2, 3, 4.
By examining these two figures, it is evident that the proposed scheme in this paper exhibits a smaller error margin and achieves faster convergence. To showcase the effectiveness of the control scheme designed in this study, two metrics will be introduced: the maximum value of tracking error (MVTE) and the root mean square value of tracking error (RMSVTE). Comparison results for MVTE and RMSVTE between the present control scheme and the FLS-PID scheme are outlined in Table 3, which clearly illustrates the validity of the proposed control scheme. Specifically, the MVYE in the x and y directions is reduced by about 0.03 m, the z direction is reduced by about 0.05, and the direction is reduced by about 0.01 rad.

Table 3.
Comparison of the proposed method and FLS-PID method.
It can be seen from Figure 8 and Figure 9 that the scheme proposed in this paper has a smaller error range and a faster convergence rate. In order to demonstrate the effectiveness of the control scheme designed in this study, two indicators will be introduced: maximum tracking error (MVTE) and root mean square tracking error (RMSVTE). The comparison results of MVTE and RMSVTE of this control scheme and FLS-PID scheme are shown in Table 1, the index values of the proposed scheme in the four degrees of freedom are all smaller than FLS-PID, which clearly shows the effectiveness of the proposed control scheme.
5. Conclusions
The present study addresses the issue of achieving finite-time adaptive tracking quantization control for a quadrotor UAV system based on BLF. To enhance the convergence speed of the error and reduce overshooting, a boundary function that can be adaptively tuned in real time according to the magnitude of the error is introduced to the BLF. By incorporating a smoothing function with an intermediate control law, which eliminates the impact of input quantization, an improved dynamic surface controller utilizing a filtered compensation signal is derived. Experimental validation on the Quanser Qdrone quadrotor platform demonstrates effective state-constrained tracking quantization control with superior tracking accuracy compared to alternative methods.
The method presented in this paper is applicable only when the state variable is measurable. Through experimental verification, we have discovered that the communication bandwidth redundancy can be further enhanced using the event-triggered method. Consequently, our forthcoming research will delve deeper into the control of quadrotor UAVs, focusing on output feedback and quantitative event-triggering methodologies.
Author Contributions
Conceptualization, X.Z., Y.Z. and G.Z.; methodology, X.Z. and Y.Z.; software, H.L.; validation, X.Z., G.Z. and H.L.; formal analysis, X.Z.; investigation, C.W.; resources, Y.W.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, G.Z.; visualization, H.L.; supervision, C.-Y.S.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62373092, in part by the Natural Science Foundation of Jilin Province, China under Grant 20230101240JC and in part by Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Montreal, QC H3G 1M8, Canada.
Data Availability Statement
The data used to support this study have not been made available.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, L.; Li, B.; Li, W.; BrandH, H.; Jiang, B.; Xiao, J. Concrete defects inspection and 3D mapping using CityFlyer quadrotor robot. IEEE CAA J. Autom. Sin. 2020, 7, 991–1002. [Google Scholar] [CrossRef]
- Gohari, P.S.; Mohammadi, H.; Taghvaei, S. Using chaotic maps for 3D boundary surveillance by quadrotor robot. Appl. Soft Comput. 2019, 76, 68–77. [Google Scholar] [CrossRef]
- Kanellakis, C.; Nikolakopoulos, G. Survey on computer vision for UAVs: Current developments and trends. J. Intell. Robot. Syst. 2017, 87, 141–168. [Google Scholar] [CrossRef]
- Cardona, G.A.; Ramirez-Rugeles, J.; Mojica-Nava, E.; Calderon, J.M. Visual victim detection and quadrotor-swarm coordination control in search and rescue environment. Int. J. Electr. Comput. Eng. 2021, 11, 2079. [Google Scholar] [CrossRef]
- Esfahlani, S.S. Mixed reality and remote sensing application of unmanned aerial vehicle in fire and smoke detection. J. Ind. Inf. Integr. 2019, 15, 42–49. [Google Scholar] [CrossRef]
- Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F. Fault-tolerant cooperative navigation of networked UAV swarms for forest fire monitoring. Aerosp. Sci. Technol. 2022, 123, 107494. [Google Scholar] [CrossRef]
- Villa, D.K.; Brandao, A.S.; Sarcinelli-Filho, M. A survey on load transportation using multirotor uavs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Alhassan, A.B.; Zhang, X.; Shen, H.; Xu, H. Power transmission line inspection robots: A review, trends and challenges for future research. Int. J. Electr. Power Energy Syst. 2020, 118, 105862. [Google Scholar] [CrossRef]
- Vu, N.A.; Dang, D.K.; Le Dinh, T. Electric propulsion system sizing methodology for an agriculture multicopter. Aerosp. Sci. Technol. 2019, 90, 314–326. [Google Scholar] [CrossRef]
- Zhu, G.; Li, H.; Zhang, H.; Wang, S.; Zhang, X. Adaptive dynamic surface output feedback control for a class of quadrotor aircraft with actuator faults. Assem. Autom. 2022, 42, 521–534. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S. Robust Fractional-Order Sliding Mode Tracker for Quad-Rotor UAVs: Event-Triggered Adaptive Backstepping Approach under Disturbance and Uncertainty. Aerosp. Sci. Technol. 2024, 146, 108916. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, R.; Yang, H.; Zuo, Z. Adaptive super-twisting trajectory tracking control for an unmanned aerial vehicle under gust winds. Aerosp. Sci. Technol. 2021, 115, 106833. [Google Scholar] [CrossRef]
- Liu, K.; Wang, R.; Wang, X.; Wang, X. Anti-saturation adaptive finite-time neural network based fault-tolerant tracking control for a quadrotor UAV with external disturbances. Aerosp. Sci. Technol. 2021, 115, 106790. [Google Scholar] [CrossRef]
- Urbina-Brito, N.; Guerrero-Sánchez, M.E.; Valencia-Palomo, G.; Hernández-González, O.; López-Estrada, F.R.; Hoyo-Montaño, J.A. A predictive control strategy for aerial payload transportation with an unmanned aerial vehicle. Mathematics 2021, 9, 1822. [Google Scholar] [CrossRef]
- Ngo, K.; Mahony, R.; Jiang, Z.P. Integrator Backstepping using Barrier Functions for Systems with Multiple State Constraints. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 8306–8312. [Google Scholar]
- Wang, C.; Wang, F.; Yu, J. BLF-based asymptotic tracking control for a class of time-varying full state constrained nonlinear systems. Trans. Inst. Meas. Control. 2019, 41, 3043–3052. [Google Scholar] [CrossRef]
- Hua, C.; Jiang, A.; Li, K. Adaptive neural network finite-time tracking quantized control for uncertain nonlinear systems with full-state constraints and applications to QUAVs. Neurocomputing 2021, 440, 264–274. [Google Scholar] [CrossRef]
- Liu, L.; Gao, T.; Liu, Y.J.; Tong, S.; Chen, C.P.; Ma, L. Time-varying IBLFs-based adaptive control of uncertain nonlinear systems with full state constraints. Automatica 2021, 129, 109595. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Wang, H.; Zhou, Y.; Lu, S. Finite-time adaptive tracking control for unknown nonlinear systems with a novel barrier Lyapunov function. Inf. Sci. 2020, 528, 231–245. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Yang, G. Adaptive backstepping stabilization of nonlinear uncertain systems with quantized input signal. IEEE Trans. Autom. Control 2013, 59, 460–464. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Zhu, G.; Chen, X.; Li, Z.; Wang, C.; Su, C.Y. Compound adaptive fuzzy quantized control for quadrotor and its experimental verification. IEEE Trans. Cybern. 2020, 51, 1121–1133. [Google Scholar] [CrossRef]
- Shao, X.; Xu, L.; Zhang, W. Quantized Control Capable of Appointed-Time Performances for Quadrotor Attitude Tracking: Experimental Validation. IEEE Trans. Ind. Electron. 2022, 69, 5100–5110. [Google Scholar] [CrossRef]
- Sun, K.; Karimi, H.R.; Qiu, J. Finite-time fuzzy adaptive quantized output feedback control of triangular structural systems. Inf. Sci. 2021, 557, 153–169. [Google Scholar] [CrossRef]
- Yu, X.; Lin, Y. Adaptive backstepping quantized control for a class of nonlinear systems. IEEE Trans. Autom. Control 2016, 62, 981–985. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, Y.; Huang, T.; Ma, H. Prescribed performance cooperative control for multiagent systems with input quantization. IEEE Trans. Cybern. 2019, 50, 1810–1819. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, K.; Tong, S. Finite-time adaptive fuzzy output feedback dynamic surface control for MIMO nonstrict feedback systems. IEEE Trans. Fuzzy Syst. 2018, 27, 96–110. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Sun, K.; Qiu, J.; Karimi, H.R.; Fu, Y. Event-triggered robust fuzzy adaptive finite-time control of nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. 2020, 29, 1460–1471. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command filtered adaptive backstepping. IEEE Trans. Control Syst. Technol. 2011, 20, 566–580. [Google Scholar] [CrossRef]
- Rabah, M.; Rohan, A.; Mohamed, S.A.S.; Kim, S.H. Autonomous Moving Target-Tracking for a UAV Quadcopter Based on Fuzzy-PI. IEEE Access 2019, 7, 38407–38419. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).