Multi-UAV Formation Path Planning Based on Compensation Look-Ahead Algorithm
Abstract
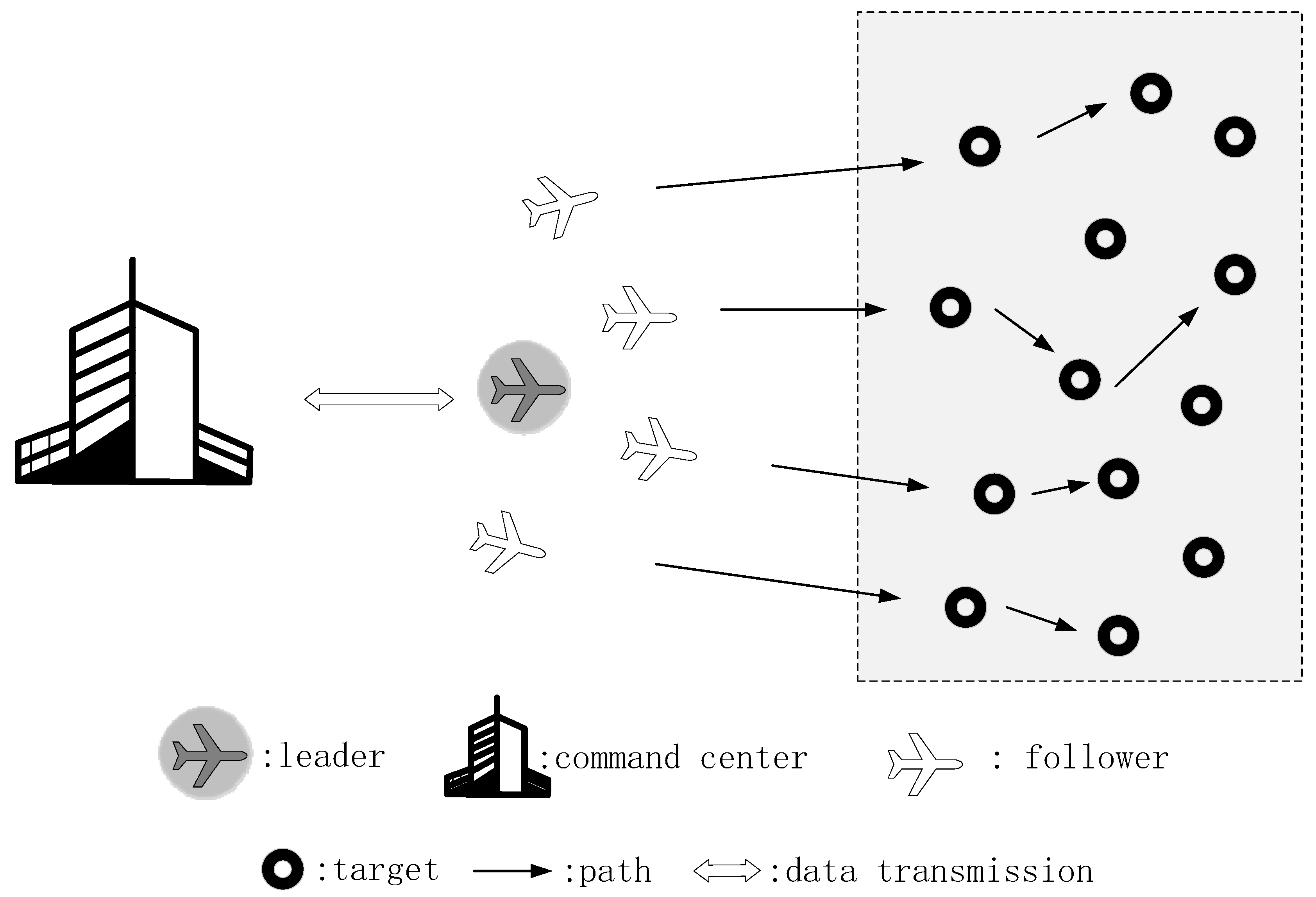
1. Introduction
2. Problem Description and Necessary Theories
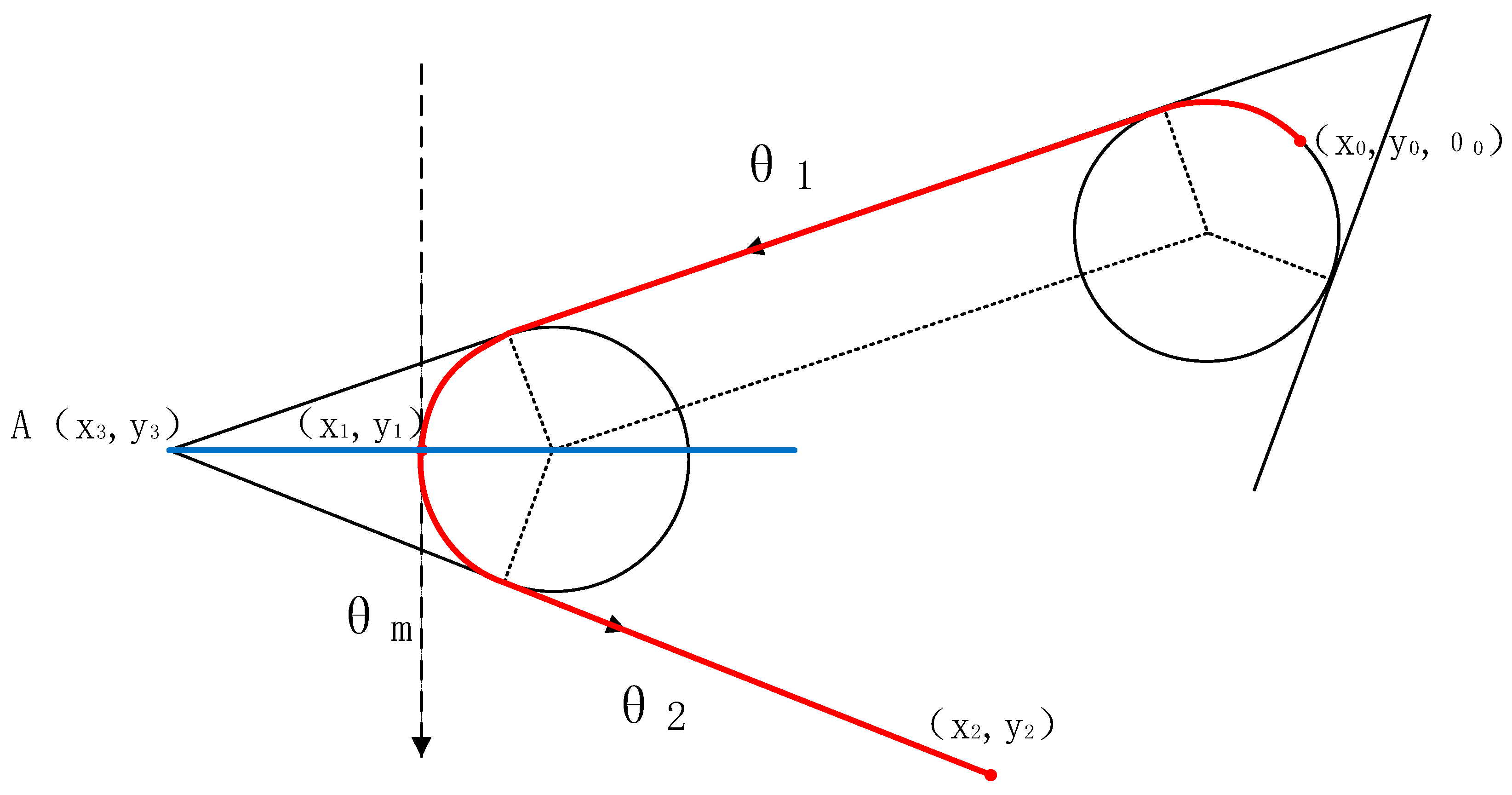
2.1. Dubins Path
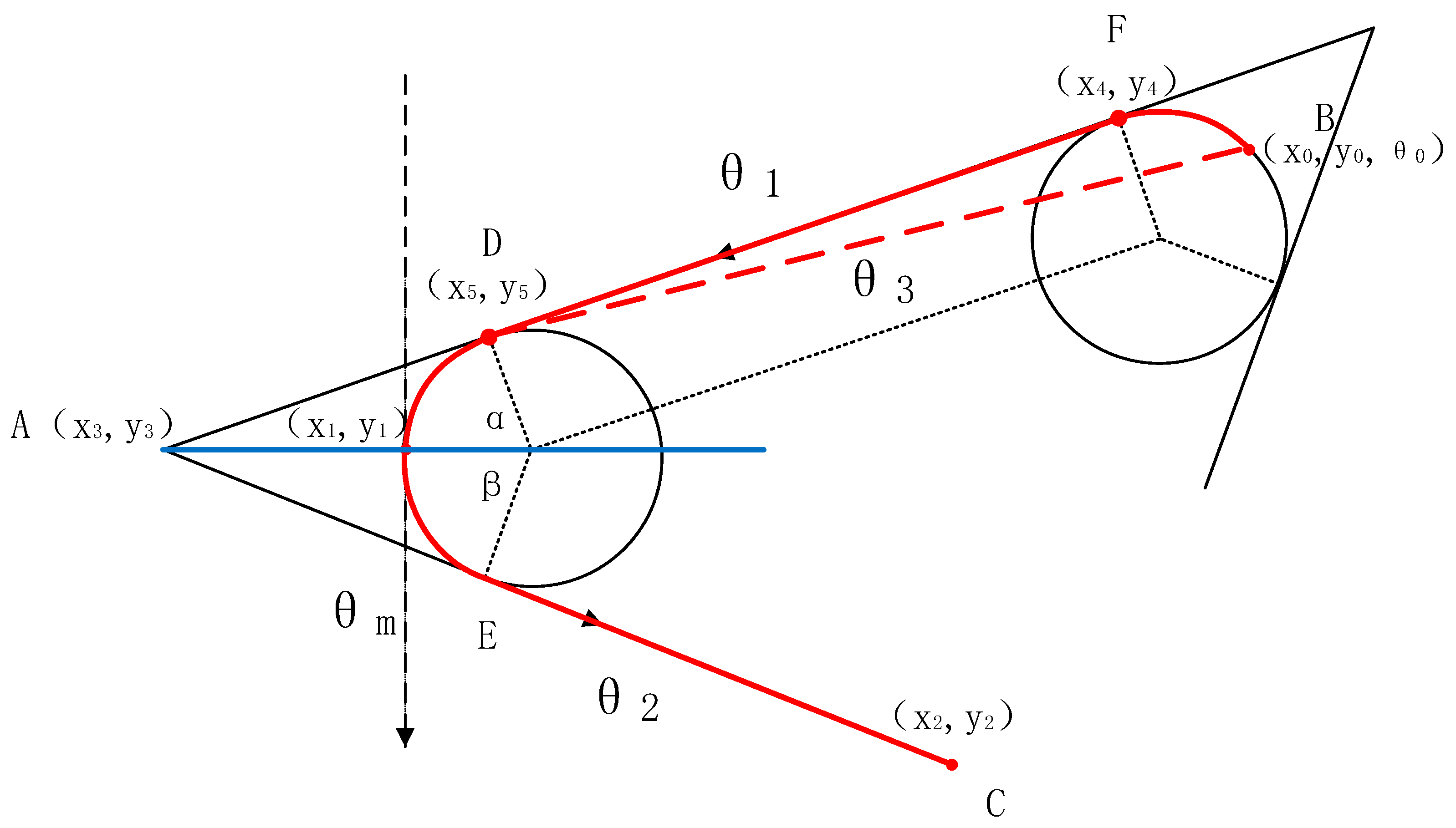
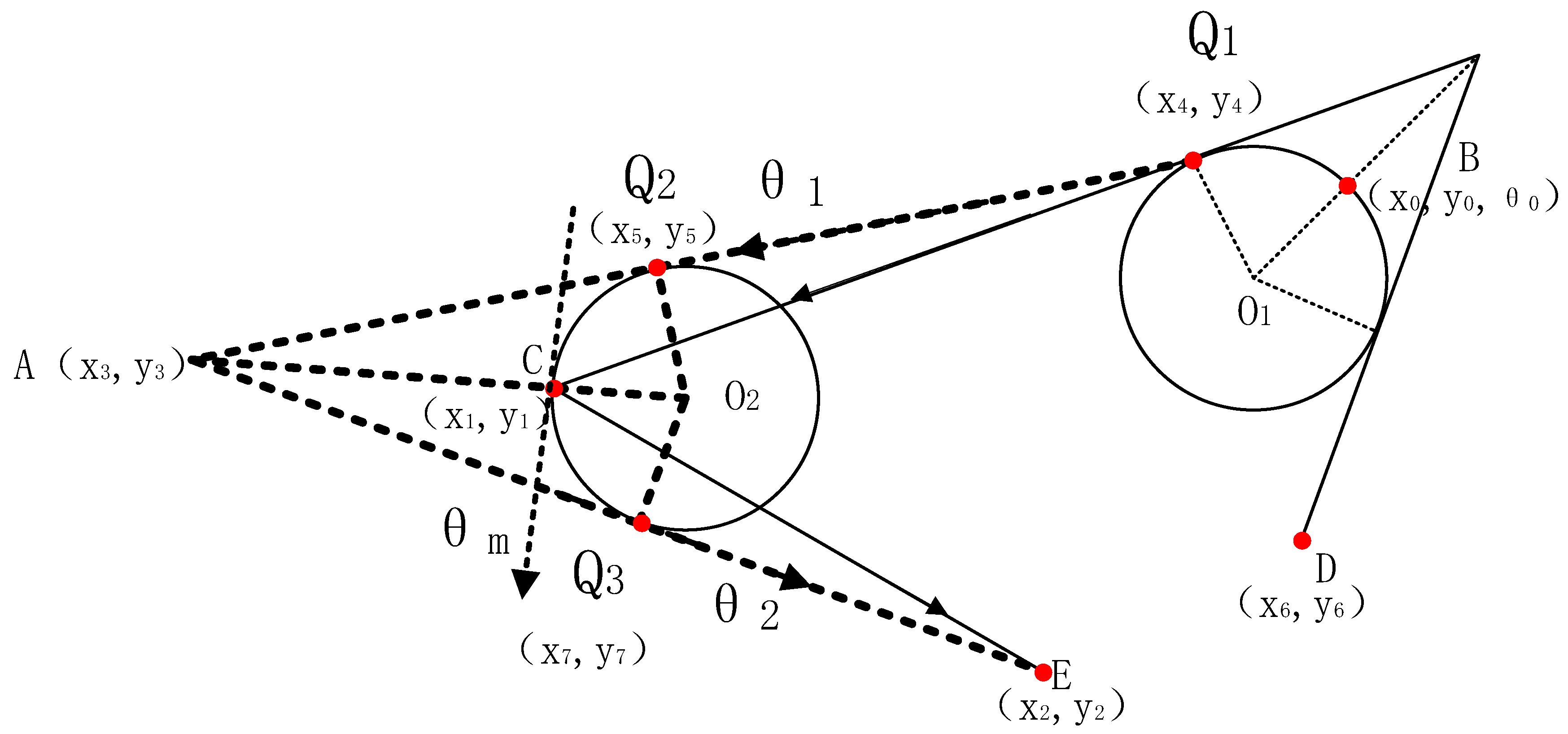
2.2. Compensatory Look-Ahead Algorithm
| Algorithm 1. Compensation look-ahead algorithm |
| Input: B Output: compensation heading angle 1: Center of circle 2: Distance from point to tangent point 3: Acquiring tangent point 4: Center of circle 5: Distance from point to tangent point 6: Distance from point to tangent point 7: Acquiring tangent point 8: Acquiring tangent point 9: Obtain compensation heading angle 10: end |
3. Model Decomposition
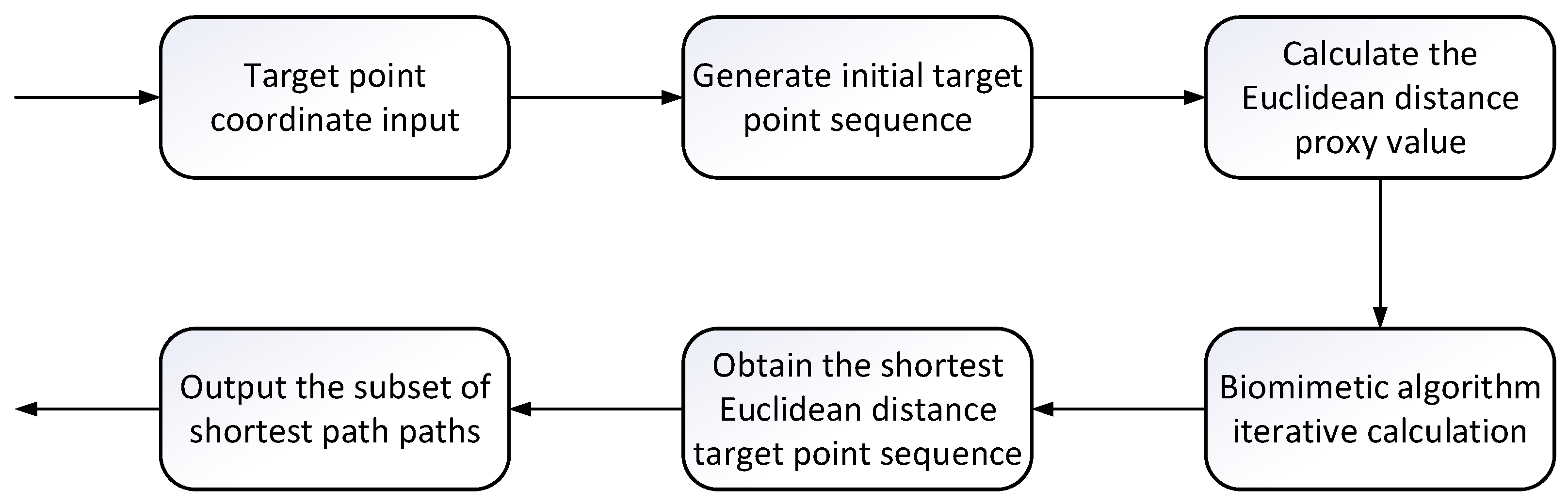
3.1. MTSP Model Based on Shortest Distance
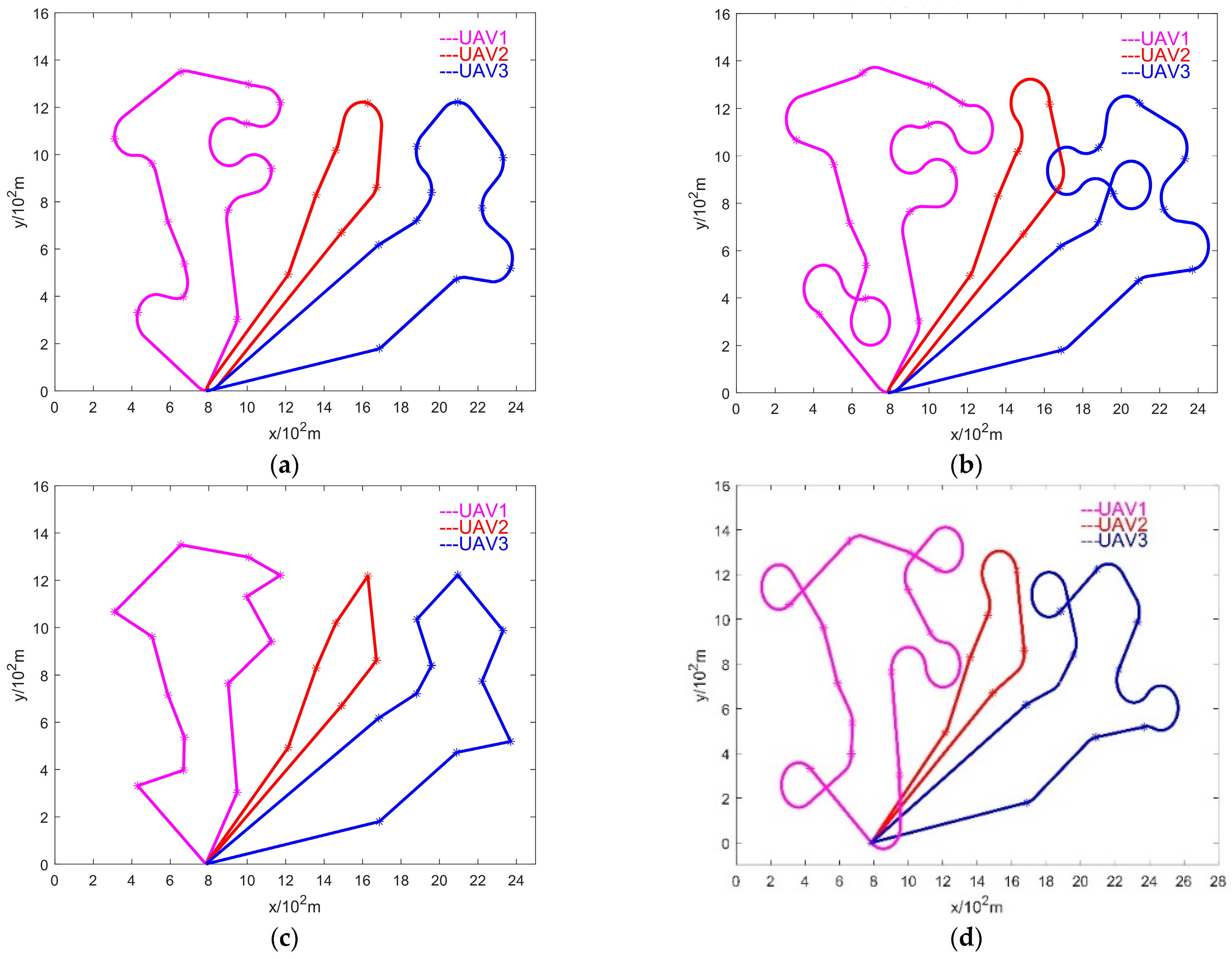
3.2. UAV Formation EDTSP Model
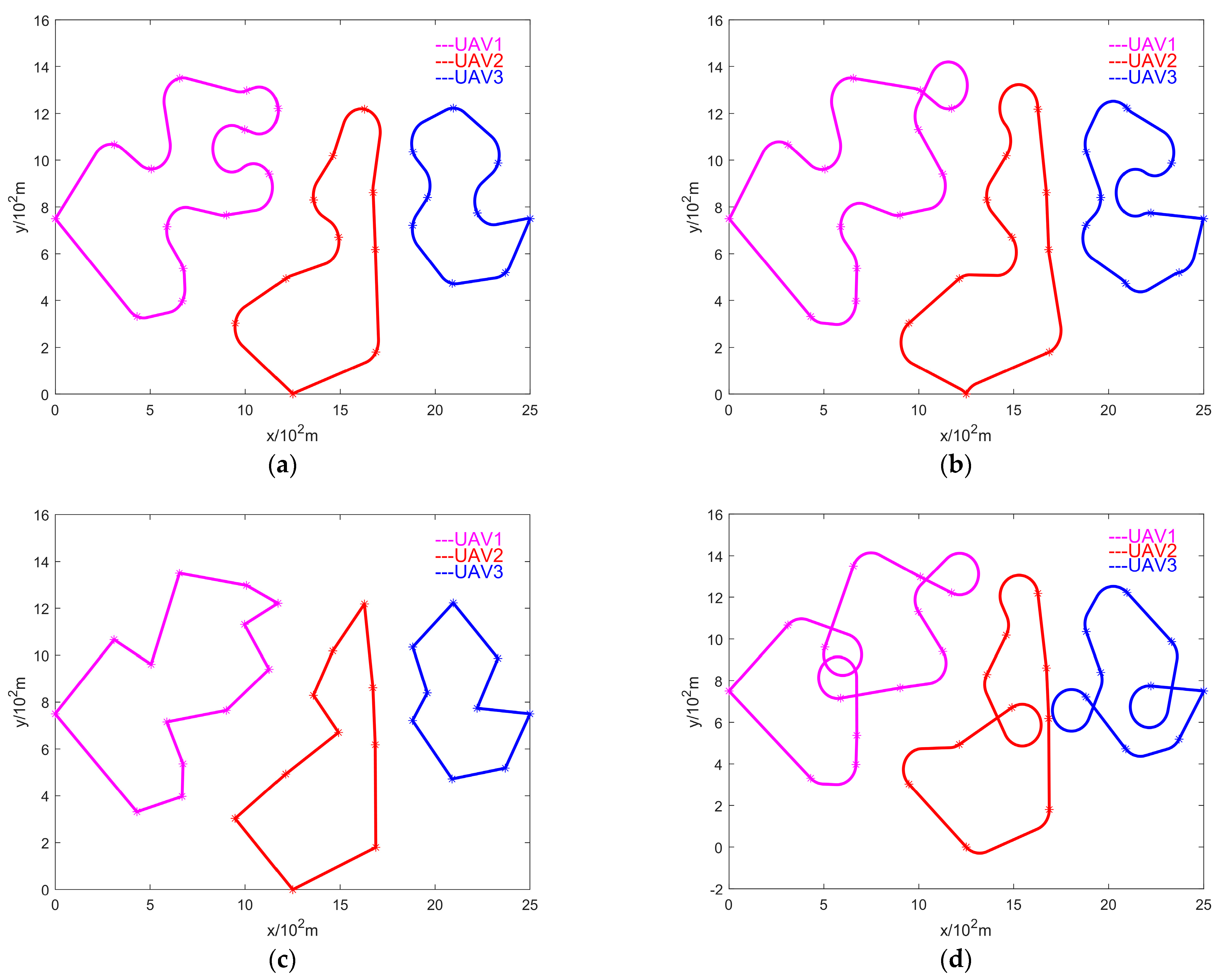
4. The Analysis of the Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richard, A.; Musa, A.A.; Bernard, E.; Jerry, A. Unmanned Aerial Vehicle (UAV) applications in coastal zone management—A review. Environ. Monit. Assess. 2021, 193, 154. [Google Scholar]
- Yang, Y.; Xiong, X.; Yan, Y. UAV Formation Trajectory Planning Algorithms: A Review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Caccia, M.; Bibuli, M.; Bono, R.; Bruzzone, G. Basic navigation, guidance and control of an unmanned surface vehicle. Auton. Robots 2008, 25, 349–365. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Khoufi, I. A Comprehensive Survey on the Multiple Travelling Salesman Problem: Applications, Approaches and Taxonomy. Comput. Sci. Rev. 2021, 40, 100369. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Y.; Xu, S.; Feng, H. Multiple UAVs cooperative formation forming control based on back-stepping-like approach. J. Syst. Eng. Electron. 2018, 29, 154–160. [Google Scholar] [CrossRef]
- Wang, X.; Shen, L.; Liu, Z.; Zhao, S.; Cong, Y.; Li, Z.; Jia, S.; Chen, H.; Yu, Y.; Chang, Y.; et al. Coordinated flight control of miniature fixed-wing UAV swarms: Methods and experiments. Sci. China Inf. Sci. 2019, 62, 212204. [Google Scholar] [CrossRef]
- Muslimov, T.; Munasypov, R.A. Consensus-based cooperative control of parallel fixed-wing UAV formations via adaptive backstepping. Aerosp. Sci. Technol. 2021, 109, 106416. [Google Scholar] [CrossRef]
- Chen, Z.; Shima, T. Relaxed Dubins Problems through Three Points. In Proceedings of the 2019 27th Mediterranean Conference on Control and Automation (MED), Akko, Israel, 1–4 July 2019. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Tian, Y.; Jiang, T. Cooperative Task Assignment of a Heterogeneous Multi-UAV System Using an Adaptive Genetic Algorithm. Electronics 2020, 9, 687. [Google Scholar] [CrossRef]
- Avla, K.; Frazzoli, E.; Bullo, F. On the point-to-point and traveling salesperson problems for Dubins’ vehicle. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; IEEE: Piscataway, NI, USA, 2005. [Google Scholar] [CrossRef]
- Xin, J.; Zhong, J.; Li, S.; Sheng, J.; Cui, Y. Greedy Mechanism Based Particle Swarm Optimization for Path Planning Problem of an Unmanned Surface Vehicle. Sensors 2019, 19, 4620. [Google Scholar] [CrossRef]
- Ma, X.; Castanon, D.A. Receding Horizon Planning for Dubins Traveling Salesman Problems. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; IEEE: Piscataway, NI, USA, 2007. [Google Scholar] [CrossRef]
- Isaiah, P.; Shima, T. Motion planning algorithms for the Dubins Travelling Salesperson Problem. Automatica 2015, 53, 247–255. [Google Scholar] [CrossRef]
- Cohen, I.; Epstein, C.; Isaiah, P.; Kuzi, S.; Shima, T. Discretization-Based and Look-Ahead Algorithms for the Dubins Traveling Salesperson Problem. IEEE Trans. Autom. Sci. Eng. 2017, 14, 383–390. [Google Scholar] [CrossRef]
- Johnson, D.S.; Mcgeoch, L.A. The Traveling Salesman Problem: A Case Study in Local Optimization. In Local Search in Combinatorial Optimization; John Wiley and Sons: London, UK, 1997. [Google Scholar]
- Savla, K.; Frazzoli, E.; Bullo, F. Traveling salesperson problems for the Dubins vehicle. IEEE Trans. Autom. Control 2008, 53, 1378–1391. [Google Scholar] [CrossRef]
- Zhu, X.; Lai, J.; Chen, S. Cooperative Location Method for Leader-Follower UAV Formation Based on Follower UAV’s Moving Vector. Sensors 2022, 22, 7125. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, J.; Xin, B.; Peng, Z. A memetic algorithm for path planning of curvature-constrained UAVs performing surveillance of multiple ground targets. Chin. J. Aeronaut. 2014, 27, 622–633. [Google Scholar] [CrossRef]
- Li, F.; Lan, Y. A drone with a combination of dual rotors and fixed wings. Acad. J. Eng. Technol. Sci. 2021, 4, 55–58. [Google Scholar]
- Drchal, J.; Faigl, J.; Vana, P. WiSM: Windowing Surrogate Model for Evaluation of Curvature-Constrained Tours with Dubins Vehicle. IEEE Trans. Cybern. 2022, 52, 1302–1311. [Google Scholar] [CrossRef] [PubMed]
- Boissonnat, D.; Bui, X.-N. Accessibility Region for a Car That Only Moves Forwards along Optimal Paths. Rapport de Recherche 2181. Ph.D. Thesis, INRIA, Le Chesnay-Rocquencourt, France, January 1994. [Google Scholar]
- Yal, C.; Markov, K.N. Dubins path via optimal control theory. Comput. Optim. Appl. 2017, 68, 719–747. [Google Scholar] [CrossRef]
- Li, L.; Shi, D.; Jin, S.; Yang, S.; Zhou, C.; Lian, Y.; Liu, H. Exact and Heuristic Multi-Robot Dubins Coverage Path Planning for Known Environments. Sensors 2023, 23, 2560. [Google Scholar] [CrossRef] [PubMed]
- Athans, M.; Falb, P.L. Optimal Control; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Shkel, A.M.; Lumelsky, V.J. Classification of the Dubins’ set. Robot. Auton. Syst. 2001, 34, 179–202. [Google Scholar] [CrossRef]
- Sussmann, H.J.; Tang, W. Shortest Paths for the Reeds-Shepp Car: A Worked Out Example of the Use of Geometric Techniques in Nonlinear Optimal Control; Report SYCON-91-10; Rutgers University: New Brunswick, NJ, USA, 1991. [Google Scholar]
- Bui, X.N.; Boissonnat, J.D.; Soueres, P.; Laumond, J.P. Shortest path synthesis for Dubins non-holonomic robot. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; IEEE: Piscataway, NI, USA, 1994. [Google Scholar] [CrossRef]
- Wenyu, C.; Meiyan, Z.; Yahong, Z. Task Assignment and Path Planning for Multiple Autonomous Underwater Vehicles Using 3D Dubins Curves. Sensors 2017, 17, 1607. [Google Scholar] [CrossRef]
- Cons, M.S.; Shima, T.; Domshlak, C. Integrating Task and Motion Planning for Unmanned Aerial Vehicles. Unmanned Syst. 2014, 2, 1938. [Google Scholar] [CrossRef]
- Carter, A.E.; Ragsdale, C.T. A new approach to solving the multiple traveling salesperson problem using genetic algorithms. Eur. J. Oper. Res. 2006, 175, 246–257. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated task assignment and path optimization for cooperating uninhabited aerial vehicles using genetic algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mischenko, E.F. The Mathematical Theory of Optimal Processes; John Wiley & Sons: Hoboken, NJ, USA, 1962. [Google Scholar]
- Noon, C.E.; Bean, J.C. A Lagrangian Based Approach for the Asymmetric Generalized Traveling Salesman Problem. Oper. Res. 1991, 39, 623632. [Google Scholar] [CrossRef]
- Yafei, D.; Quanwang, W.; Junhao, W. An improved shuffled frog-leaping algorithm for the minmax multiple traveling salesman problem. Neural Comput. Appl. 2021, 33, 17057–17069. [Google Scholar]
- Tsai, H.C.; Hong, Y.W.P.; Sheu, J.P. Completion Time Minimization for UAV-Enabled Surveillance Over Multiple Restricted Regions. IEEE Trans. Mob. Comput. 2023, 22, 6907–6920. [Google Scholar] [CrossRef]

| Compensation Look-Ahead Algorithm | 2-Opt Look-Ahead Algorithm | Alternating Algorithm | ETSP | |
|---|---|---|---|---|
| Total mileage (102 m) | 36.7695 | 42.2248 | 48.0164 | 27.6005 |
| Target Number (Total Mileage 102 m) | Compensation Look-Ahead Algorithm | 2-Opt Look-Ahead Algorithm | Alternating Algorithm | ETSP |
|---|---|---|---|---|
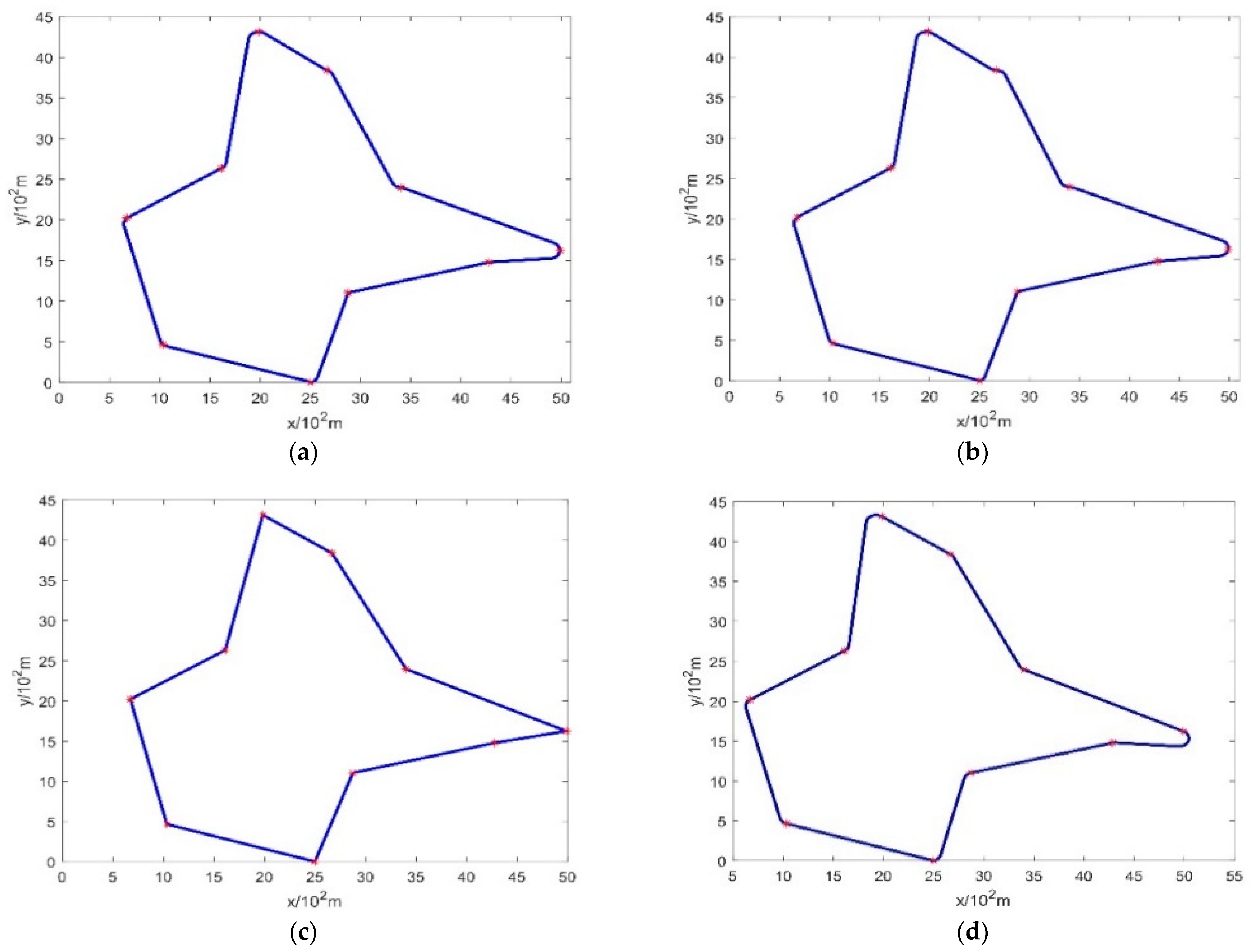
| 5 | 23.9851 | 24.8415 | 26.8562 | 22.3707 |
| 10 | 36.7695 | 42.2248 | 48.0164 | 27.6005 |
| 15 | 47.1584 | 55.5124 | 60.8612 | 35.2885 |
| 20 | 56.5147 | 64.3615 | 76.1574 | 37.7948 |
| 25 | 65.1845 | 74.6124 | 87.1451 | 41.1114 |
| Compensation Look-Ahead Algorithm | 2-Opt Look-Ahead Algorithm | Alternating Algorithm | ETSP | |
|---|---|---|---|---|
| Total mileage (102 m) | 36.7695 | 42.2248 | 48.0164 | 27.6005 |
| Compensation Look-Ahead Algorithm | 2-Opt Look-Ahead Algorithm | Alternating Algorithm | ETSP | |
|---|---|---|---|---|
| Total mileage (102 m) | 141.17 | 154.115 | 159.702 | 109.995 |
| Compensation Look-Ahead Algorithm | 2-Opt Look-Ahead Algorithm | Alternating Algorithm | ETSP | |
|---|---|---|---|---|
| Total mileage (102 m) | 114.1742 | 124.1158 | 138.4113 | 94.7549 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Sun, W.; Sun, C.; He, R. Multi-UAV Formation Path Planning Based on Compensation Look-Ahead Algorithm. Drones 2024, 8, 251. https://doi.org/10.3390/drones8060251
Sun T, Sun W, Sun C, He R. Multi-UAV Formation Path Planning Based on Compensation Look-Ahead Algorithm. Drones. 2024; 8(6):251. https://doi.org/10.3390/drones8060251
Chicago/Turabian StyleSun, Tianye, Wei Sun, Changhao Sun, and Ruofei He. 2024. "Multi-UAV Formation Path Planning Based on Compensation Look-Ahead Algorithm" Drones 8, no. 6: 251. https://doi.org/10.3390/drones8060251
APA StyleSun, T., Sun, W., Sun, C., & He, R. (2024). Multi-UAV Formation Path Planning Based on Compensation Look-Ahead Algorithm. Drones, 8(6), 251. https://doi.org/10.3390/drones8060251







