1. Introduction
Over the past decade, uncrewed aerial vehicles (UAVs) and their applications have gained increased importance and attention in various domains, such as military operations, search and rescue missions, agriculture, and surveillance [
1,
2,
3]. However, one major challenge in UAV operations is landing on a dynamic target, such as a moving vehicle or a ship. The capability to land on a moving target has numerous practical applications, including delivering supplies to moving vehicles [
4], providing aerial support to moving troops, and inspecting mobile infrastructure [
5]. In [
6,
7,
8], landing on a moving platform was tackled with several techniques that solved the problem analytically and performed well under restricted conditions and assumptions.
The robustness of autonomous UAV landings on mobile platforms hinges on the accurate localization of both the UAV and the target, adherence to a predetermined flight trajectory despite environmental disturbances like wind, and the development of a system that autonomously executes landings without external aids, such as motion capture systems or fiducial markers.
Achieving full autonomy and robustness typically requires UAV systems equipped with visual and inertial sensors. The integration of the sensors enables onboard state estimation and detection of the landing platform. Although visual-inertial odometry (VIO) and visual servoing have been extensively researched for UAV landings on moving targets, a gap remains in addressing the challenges posed by scenarios with limited observability, such as missing detection of the target due to occlusion, weather, or motion blur, which pose serious threats to the methods. In [
9], researchers formulated a visual servoing technique for the autonomous landing of UAVs on a platform capable of speeds up to 15 km/h. Of the 19 conducted trials, 17 were successful. The two unsuccessful attempts were attributed to the platform not being detected. Overcoming issues such as intermittent platform detection is essential for ensuring the safe and reliable landing of drones on mobile targets.
Equally important is addressing sensor failure. Inertial measurement units (IMUs), GPS, compasses, barometers, and other sensors that enable autonomous UAV flight are susceptible to a number of malfunctions, including magnetic field interference, turbulence-induced disconnections, or sensor malfunctions that lead to altered or missing sensor data. The literature suggests fault-tolerant methods that involve distinct modules for rapid sensor failure detection and subsequent system reconfiguration to either compensate for lost data or switch to backup systems [
10]. Nevertheless, a paucity of literature explores the occurrence of sensor failures amid the execution of landing maneuvers.
In this paper, we emphasize the significance of addressing partially observable scenarios in landing drones on moving targets and propose fusing robust policy optimization (RPO) with long short-term memory (LSTM) as an appropriate framework. Adopting an end-to-end fault-tolerant control strategy enables the UAV to address sensor failures or detection lapses by processing all fault-tolerant control stages through a unified model. Additionally, employing a learning-based control approach facilitates the training of neural networks to address a variety of fault scenarios. While existing research explores the cooperative interaction between UAVs and uncrewed ground vehicles (UGVs), our approach assumes no communication or coordination occurs during landing.
The contributions of this work with respect to prior literature are as follows: (a) We formulate an end-to-end RPO-LSTM reinforcement learning framework that tackles the challenging task of landing a UAV with missing sensor data on a moving target. (b) We validate the proposed approach through extensive simulation experiments, which include partial observability due to factors such as sensor failure or sensor noise. (c) We illustrate that adding memory to a UAV RL agent leads to higher rewards compared to conventional deep reinforcement learning algorithms, thus substantially improving system performance.
Structure
The remainder of the paper is organized as follows.
Section 2 discussed previous works on autonomous UAV landing.
Section 3 delves into the technical framework of our method and details the formulation of the UAV landing task as a POMDP and the network architecture and training.
Section 4 outlines the use of the NVIDIA Isaac Gym simulator, describes the training process, and establishes performance metrics. The results are presented to demonstrate RPO-LSTM’s performance compared to other methods under diverse partial observability scenarios.
Section 5 dissects the impact of individual components in the RPO-LSTM architecture. Finally,
Section 6 provides a conclusion to the paper, summarizing the findings and suggesting avenues for future investigation.
2. Literature Review
The challenge of landing UAVs on moving targets is an active area of research, with various approaches developed to tackle the complexities of dynamic environments and limited sensor data. Researchers seek to enable robust, fully autonomous UAV landings on diverse moving platforms. Given the multifaceted nature of the challenge, much of the literature focuses on specialized solutions for individual components. Proposed solutions aim to achieve the precise localization of both the UAV and the target, ensure robust trajectory following, or develop systems capable of autonomous landing without the need for external infrastructure.
Extensive research has been dedicated to exploring various methods for the state estimation of the UAV and UGV. Prior work utilized motion capture systems [
11], GPS [
12], or computer vision [
13] to obtain pose estimates of the UAV and UGV. Recent advancements in computer vision have enabled onboard localization and pose estimation, reducing the dependency on external infrastructure for maneuver execution. Early research by [
13,
14,
15] relied on visual fiducial systems to facilitate relative pose estimation between the drone and the target, simplifying the maneuver to just requiring a camera and a marker externally. Present-day research has pivoted toward machine learning techniques for platform detection and relative pose estimation, leading to a proliferation of visual servoing methods [
9].
The most common challenge with vision-based systems in UAV landing on a moving target is partial observability, particularly when detecting highly dynamic moving targets. Visual servoing methods, which rely on visual feedback for control, are particularly affected by partial observabilities, as they require the landing platform to be visible throughout the entire landing maneuver. Partial observability poses significant difficulties in accurately tracking the moving platform and maintaining stable and safe landing trajectories.
A diverse array of control strategies has been employed to govern UAVs during landing maneuvers. The strategies range from classical methods, such as proportional–integral–derivative (PID) [
13] and linear quadratic regulator (LQR) [
16], to contemporary approaches, like model predictive control (MPC) [
17], and even learning-based techniques, such as reinforcement learning [
18]. The methodologies are instrumental in executing robust trajectory tracking amidst uncertainties and disturbances. Nevertheless, the majority of literature that utilizes classical control methods often overlooks notable disturbances. To enhance the resilience of classical methods against disturbances and uncertainties, numerous adaptive mechanisms are required to be integrated into the control loop. The mechanisms dynamically adjust the controller parameters in response to the observed behavior of the system. In pursuit of mitigating external disturbances, some studies have turned to MPC. Notably, the work in [
17] incorporated a boundary layer sliding controller, enabling a quadcopter to land under wind conditions with speeds reaching up to 8 m/s.
Recent studies have increasingly focused on learning-based methods, especially reinforcement learning (RL), for the task of landing on moving platforms. The shift aims to address the inherent complexities associated with model-based approaches. RL-based control systems are noted for their robustness, adapting to a wide range of changes in system dynamics and unexpected disturbances, areas where static model-based controllers falter. Prior works have developed RL algorithms that are resilient to perturbations in the environment dynamics [
19,
20,
21], observations [
22,
23,
24,
25], and actions [
26]. The robust RL algorithms can learn optimal policies that maximize returns in the worst-case environments. For instance, ref. [
27] introduced a resilient RL algorithm capable of executing end-to-end, vision-based control for landing on a moving ship platform, even under windy conditions. Similarly, ref. [
18] proposed a robust RL strategy designed to accommodate variations in system dynamics while landing on a moving target. While RL is predominantly applied for robust, end-to-end control in landing scenarios, research exploring its use in managing partial observability caused by missing sensor data remains scant.
The literature addressing the issue of missing observations is sparse. Some studies, such as [
7,
12], have addressed the challenge of temporarily missing detections by employing an extended Kalman filter (EKF). The methods predict the pose of a moving target using a dynamic model that assumes constant velocity. However, the effectiveness of the approach is considerably constrained by its assumptions. Recent studies, along with the uncertainties they address, are detailed in
Table 1.
To fill the gap between optimality and control with partial observabilities, this work proposes to integrate a type of RNN, LSTM [
28], into the RPO [
29] architecture to capture long-range dependencies in sequential sensing data and handle variable-length signal sequences. The main goal is to discover missing patterns in sensing signals that have missing readings due to faulty sensors and to achieve the desired landing performance despite the partial observabilities in the environment. To highlight the significance of the memory element in addressing the issue, our research contrasts traditional methods employing an EKF with our approach and evaluates it against the baseline proximal policy optimization (PPO) algorithm as referenced in [
30]. PPO is a simple RL algorithm that is easy to implement and tune while achieving state-of-the-art performance, stability, reliability, and sample efficiency. When using RL to learn the optimal control policy with UAVs, PPO has become the preferred option. For instance, researchers deployed an RL PPO-based algorithm that enables a UAV to navigate through unknown/random environments [
31]. PPO was also used as an uncrewed traffic manager to lead autonomous uncrewed aircraft systems to their destinations while avoiding obstacles through continuous control. In [
32], a fully autonomous UAV controller was developed to steer a drone toward a moving target using PPO.
Table 1.
Comparison of control algorithms in related works and their respective uncertainties and disturbances investigated.
Table 1.
Comparison of control algorithms in related works and their respective uncertainties and disturbances investigated.
| Paper | Control Algorithm | Uncertainty/Disturbance Tackled |
|---|
| [17] | MPC | Wind |
| [27] | DDPG-RL | Wind |
| [33] | DrQv2-RL | Noisy Sensor |
| [7] | PID | Missing Platform Detection |
| [13] | PID | Wind |
| [12] | PID | Noisy Sensor |
| [34] | MPC | Wind |
| [15] | Visual Servo | Wind |
3. Methodology
The methodology section, which outlines the technical approach to address the UAV landing problem under partial observability, starts with
Section 3.1, providing a basis for MDPs and POMDPs.
Section 3.2 defines the task as a POMDP, specifying the observations, actions, and reward structure.
Section 3.3 presents the innovative actor–critic design with a unique information flow separation, along with LSTM integration for sequential data.
Section 3.4 details the RPO-based learning process, including policy updates, exploration, and LSTM training. Finally,
Section 3.5 highlights the advantages of the approach and provides an algorithm outlining the RPO-LSTM training process.
3.1. Preliminaries
The Markov decision process (MDP) is a mathematical framework for a stochastic environment in which the state of the system is observable and follows the Markov property. The MDP is defined by a 4-tuple
: state space (
S), action space (
A), transiton probability (
P), and reward (
R). However, a partially observable Markov decision process (POMDP) describes situations in which the system’s state is not entirely observable. POMDP is defined by a 6-tuple
, where
S,
A,
P, and
R are identical to the MDP but with an additional observation space (
O) and observation model (
). In a POMDP, the agent cannot directly observe the underlying state. An illustration of the MDP and POMDP as dynamic decision networks are shown in
Figure 1. One way of dealing with POMDPs is by giving memory to the agent. Recurrent reinforcement learning (RRL) is a special kind of RL that integrates RNNs into the RL framework. RNNs allow an RL agent to keep and update memory of past states and actions, allowing for a better understanding of the current state and making more informed decisions. RRL is especially useful in sequential decision-making tasks, in which the recent action depends on the previous state and action.
3.2. Problem Formulation
The objective of this paper is to formulate an innovative RL architecture for UAVs to land on a dynamic target with partial observability. The new RL architecture is grounded in the idea of integrating agent memory, enabled by LSTM, into the RPO framework. The work also evaluates the new integrative RPO-LSTM architecture as a desirable controller for a multi-rotor UAV in the presence of disturbances and uncertainties, which entails developing a control policy that maps the current state of the UAV and mobile platform to the UAV’s thrust commands to regulate its altitude and orientation for successful landing. We formulate the control problem as a POMDP where the agent must make decisions based on improper observations rather than the true state of the environment. In the following sections, observations, actions, and rewards are explained in further detail in the context of the task.
3.2.1. Observations
During each time step, the RL agent is supplied with a sequence of observations that is composed of the drone’s current state and position relative to the moving platform. The observations are contained in a vector , where d, v, , and q represent the drone’s 3D distance to the moving platform, 3D linear velocity, 3D angular velocity, and 4D quaternion, respectively.
3.2.2. Actions
Our UAV model has four control inputs: two clockwise and two counterclockwise rotors. The actor network takes in the observation vector and produces a action vector that comprises the thrust values assigned to each rotor, representing the control input. The action space is denoted as , where is the vector at time step t and represents the thrust magnitude for each rotor. The control commands vary individually for each rotor, which enables flexible and dynamic flight behaviors.
The actor network incorporates a Tanh activation function at the concluding layer to confine the range of control commands, ensuring compatibility with the physical capabilities of the UAV. Subsequently, the agent executes the derived actions in a continuous cycle until the defined goal is successfully attained.
3.2.3. Rewards
The reward function considers various aspects of the landing maneuver. The distance between the drone and the moving platform is included in the reward function. Moreover, a shaping function is employed to distinguish the significance of minimizing the position and velocity with respect to the moving platform and the generated actions. The agent learns to minimize the position relative to the moving platform and subsequently optimize its actions to produce smoother velocity references, which leads to a less aggressive movement. The reward components are described as follows.
The distance reward (
) represents the distance between the UAV and the dynamic platform, encouraging the UAV to maintain appropriate proximity:
The yaw reward (
) aims to discourage excessive yawing and promote stable heading orientation when close to the platform:
The pitch reward (
) is associated with the UAV’s pitch when near the moving platform, emphasizing the need to keep the UAV upright during close interaction:
By considering the reward components, the UAV’s behavior is effectively guided and optimized for improved performance and safety. The reward function also considers the quadcopter’s orientation during the landing process. The overall reward function is summarized by the following expression:
This multiplicative reward structure underscores the significance of the UAV’s orientation in correlation with its distance from the target. The underlying principle is that as the UAV nears the landing platform, maintaining the correct orientation becomes increasingly imperative. Conversely, when the UAV is further away, precise orientation is less crucial.
3.3. Network Architecture
To achieve the goal of successfully landing a UAV onto a moving platform under conditions of limited observability, we establish an actor–critic RL architecture. The architecture is composed of two distinct components: an actor network and a critic network. The actor, characterized by parameters
, is designed to take inputs
, which represent the UAV’s 3D distance to the moving platform, 3D linear velocity, 3D angular velocity, and the 4D quaternion, respectively. The actor then generates actions containing the thrust values of the four individual rotors, as outlined in
Section 3.2.2, guided by a policy denoted as
. On the other hand, the critic serves as an action-value evaluator, which supplies a value that gauges the effectiveness of the computed action within the given state. During the training process, the two networks are collectively optimized.
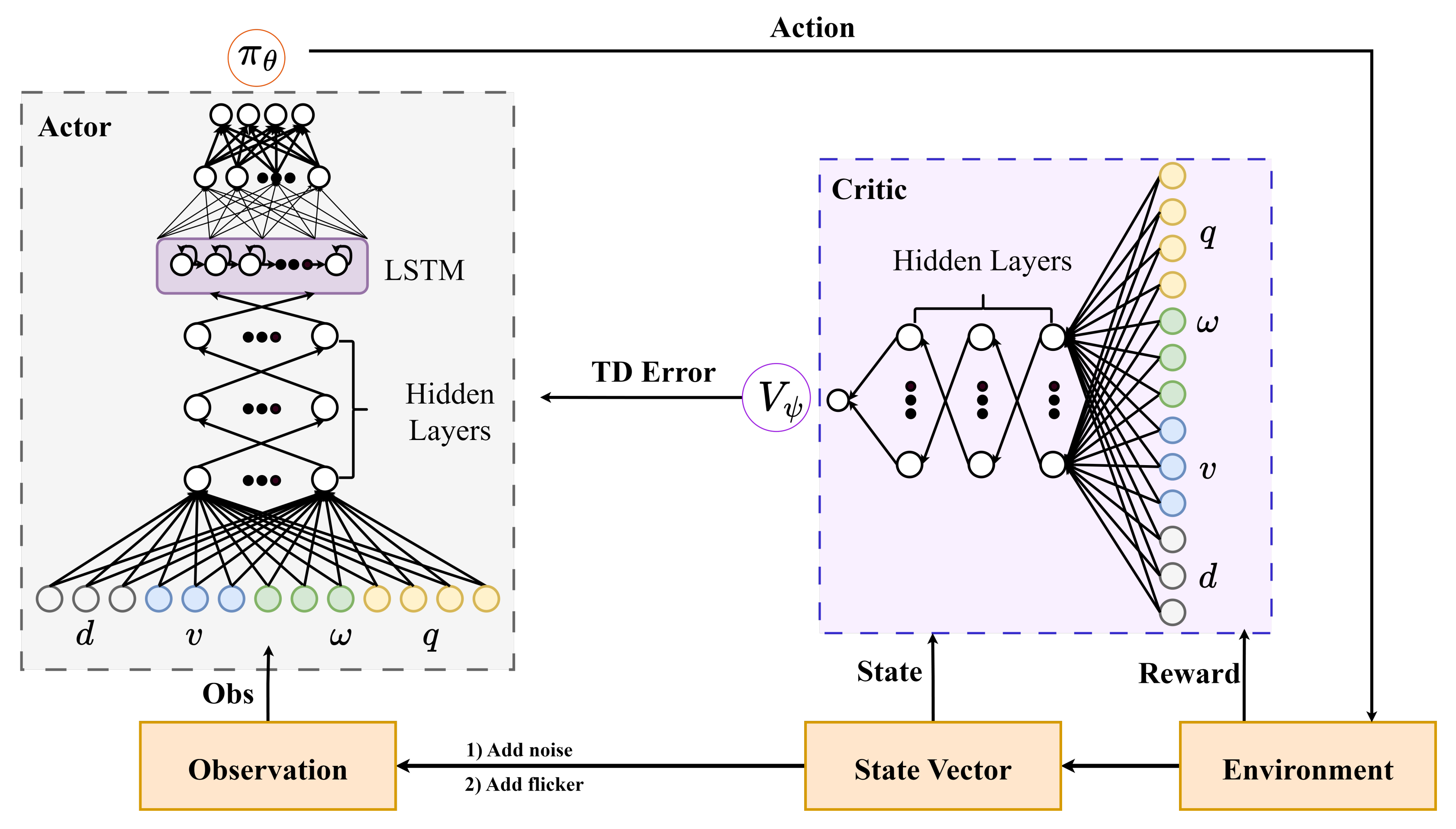
The key innovation of our architecture, as compared to the traditional actor–critic framework, is the separation of observation and state in accordance with the actor and the critic. Specifically, we feed the observations to the actor and the states to the critic during the training process. The states encapsulate accurate ground-truth information about the environment, including the UAV’s state and the states of all sensors. Conversely, the observations comprise sensor data perceived by the robot, which, in the POMDP setting, contains noise, inaccuracies, and missing information. The innovative approach of feeding the actor with the POMDP observations and the critic with states serves a distinct purpose that empowers the actor to deduce the actual states of the UAV and moving platform based on the partial observations received. The complete network architecture is shown in
Figure 2.
3.3.1. Actor
The observations taken by the actor are processed through a series of hidden layers with substantial depth. The outputs from these deep neural networks are then fed into an LSTM network, which is responsible for extracting temporal patterns within the observation and learning the policy for the precision landing task. The LSTM network maintains a memory cell that can store information across time steps, allowing the network to learn long-term dependencies and make decisions based on previous observations. The output of the LSTM network is in the form of a probability distribution over possible actions. The agent selects an optimal action to take for the UAV. The selected action is then executed in the environment, which then responds by providing a new set of observations.
3.3.2. Critic
After receiving the state from the environment, as described in
Section 3.2.1, it undergoes processing through a multi-layer perceptron (MLP). The MLP’s role is to approximate the value function associated with the states. Subsequently, the actor updates its policy based on the output of the value function provided by the critic. The value function approximated by the critic is defined as
In this equation,
represents the cumulative sum of rewards starting from time
t onward,
is the immediate reward at time step
t, and
is the discount factor, which determines the weight given to future rewards. The equation establishes a recursive relationship expressing the value function (
) as a measure of the desirability of a given state with respect to expected future rewards.
3.4. Network Training
The proposed UAV landing algorithm is an on-policy method that seeks to improve the training stability of a control policy by limiting the change made to the policy at each training epoch by avoiding having too large of a policy update. In our training of the deep reinforcement learning agent, we leverage the following policy-gradient objective function:
where
denotes the empirical return over a batch of samples,
is a stochastic policy, and
is the estimator of the advantage function at time
t. By taking the gradient ascent of the equation above, the agent takes actions that lead to higher rewards and avoids harmful actions.
The objective function of the gradient method is optimized by constraining the policy updates to ensure that the new policy is not too different from the old policy. The idea is to constrain the policy change in a small range using a clip. This new objective function, the clipped surrogate objection function, is defined as follows:
where
is the probability ratio of the policy at time
t with parameter
and the policy at time
t and
is a clipping parameter that controls the size of the update. The probability ratio function is designed as follows:
where
is the probability of taking action
in state
under policy
with parameter
and
is the probability of taking the same action under the old policy with parameter
. The ratio represents the change in the probability of taking an action under the new policy compared to the old policy.
The first term of (
7),
, replaces the logarithmic probability typically used in (
6). The ratio
is multiplied by the advantage
to obtain the left part of the new objective function. However, without a constraint, a large change in the probability of taking an action under the new policy compared to the old policy can lead to a significant policy gradient step and an excessive policy update. Therefore, this algorithm imposes a constraint that limits the size of policy updates by clipping the probability ratio to a value between
and
. This results in a clipped surrogate objective function that balances between the benefits of a large update and the risks of destabilizing the policy. The minimum between the clipped and unclipped objective is taken to make the final objective a lower bound of the unclipped objective.
The critic parameters are updated using
Here,
represents the value function’s parameter vector,
is the learning rate,
n is the number of collected samples,
is the gradient of the value function, and
is the target value at time step
t.
The actor parameters are updated using
Here,
represents the policy’s parameter vector,
is the learning rate,
n is the number of collected samples,
is the gradient of the policy,
measures the policy difference
, and
is the advantage function.
3.5. Properties of the Methodology
Traditional approaches to UAV landings on mobile platforms typically utilize a modular framework comprising distinct components for UAV state estimation, moving target estimation, trajectory planning, and UAV control, as exemplified in
Figure 3. In contrast, our method proposes an end-to-end control policy that consolidates the modules into a singular neural network. Our work not only encompasses these tasks but also extends to managing partial observabilities adeptly. To achieve end-to-end control, we synthesize existing methods into an integrated framework tailored for landing on dynamic targets under conditions of partial observability. We draw upon [
29] to enhance exploration strategies, employ LSTM networks [
28] for capturing temporal dependencies in sequential sensor data, and utilize asymmetric actor-critic methods akin to [
35] to enable the network to deduce missing information. The contribution of the methodologies to our framework is explained in subsequent sections. Algorithm 1 demonstrates how these modules are integrated and trained in unison.
3.5.1. Fostering Enhanced Exploration Strategies
The inherent stochasticity in policy gradient methods gradually diminishes during training. This leads to a reduction in the exploratory nature of the policy. To stimulate a more exploratory approach, we implemented a distribution mechanism for representing continuous actions, complementing the foundational parameterized Gaussian distribution. In our work, the policy network’s output still encompasses the Gaussian distribution’s mean and standard deviation. A key innovation is the integration of a random value into the mean , resulting in a perturbed mean . Subsequently, actions are sampled from the perturbed Gaussian distribution . Notably, the resultant distribution displays a broader shape compared to the conventional Gaussian. As a consequence, the sampled values exhibit a wider dispersion around the mean, in contrast to the tighter clustering observed in the case of the standard Gaussian distribution.
3.5.2. Capturing Long-Range Dependencies in Sequential Sensing Data
One of the key contributions of this work is the ability to deal with imperfect or flickering data under partial observability. This goal is accomplished by embedding the LSTM network into the RL actor network. LSTM is a type of RNN that is commonly used in machine-learning research for learning spatial-temporal features and sequence modeling. Unlike traditional RNNs, LSTM cells are designed to selectively retain or forget information from previous time steps as shown in
Figure 4. This allows our RL agent to effectively learn from long-term dependencies in sequential sensing data despite flickering due to faulty sensors.
Each LSTM cell is composed of several gates that control the flow of information: forget gates, input gates, and output gates. The forget gate determines which information from the previous cell state to forget, while the input gate decides which new information to add to the cell state. The output gate controls which information from the current cell state to output to the next time step. Using this gated-like structure, the RL agent can selectively transmit sequential sensing data while preserving temporal information within each cell state.
3.5.3. Learning to Infer Missing Information
By separating the flow of data into the actor and the critic in our RL framework, we leverage the privilege that the critic can tap into the state information that is not available to the actor, which can only partially observe the measurements. This encompasses noiseless observations and supplementary data into the critic network. The incorporation of these additional inputs serves a dual purpose. Firstly, it streamlines the task of acquiring accurate value estimates, as fewer aspects need to be inferred. Secondly, this streamlined learning process indirectly teaches the actor to adeptly infer the absent information, thereby enhancing its capability to handle partial observations effectively. The key link between the actor and the critic is the advantage function. The advantage of a state–action pair
quantifies how much better the chosen action is compared to the average expected value at that state. It is calculated as the difference between the actual value (or Q-value) and the predicted value (V-value) of the critic.
Fundamentally, the actor’s decision-making process is influenced by the disparity in advantage values among different actions. When an action demonstrates a substantial advantage, implying its potential for more favorable outcomes, the actor adjusts its decision strategies. This translates to an increased likelihood of selecting the advantageous action when encountering similar circumstances. Consequently, the actor concentrates on actions with higher reward potential, thereby enhancing the intelligence and efficacy of its decision-making. For our variation of RPO, the advantage is solved with a temporal difference (TD) error estimation, which is the difference between the predicted and actual output of the value function over successive time steps.
where
is the immediate reward (
4) associated with taking action
a in state
s. The
corresponds to the discount factor. The function
denotes the value function assigned to state
s formulated in (
5), while
signifies the value function assigned to the subsequent state
resulting from the execution of action
a in state
s.
| Algorithm 1 Training of RPO-LSTM |
- 1:
Initial policy parameters , initial value function parameters , LSTM hidden states - 2:
while not done do - 3:
for each environment step do - 4:
- 5:
- 6:
- 7:
- 8:
- 9:
end for - 10:
for each state and observation do - 11:
- 12:
- 13:
- 14:
- 15:
- 16:
end for - 17:
- 18:
for each update step do - 19:
Reset LSTM hidden states at the start of each episode or sequence - 20:
Sample n samples from - 21:
Update value function: - 22:
for each do - 23:
Compute target values using Temporal Difference () - 24:
end for - 25:
- 26:
Update policy: - 27:
for each do - 28:
Compute advantage using and Generalized Advantage Estimation - 29:
end for - 30:
- 31:
- 32:
Perform Backpropagation Through Time (BPTT) for LSTM update - 33:
end for - 34:
end while
|
4. Simulation Setup and Results
In this section, we provide a comprehensive overview of the simulation environments that were meticulously configured to conduct our simulation experiments. We delve into the specifics of designing the environments to replicate the conditions under which the RPO-LSTM algorithm operates to guarantee a relevant and rigorous testing ground. Additionally, we outline the training regimen of the RPO-LSTM algorithm, detailing the parameters and computational resources utilized, followed by a presentation of the experimental procedures, including the various scenarios and metrics employed to evaluate the performance of the RPO-LSTM algorithm in simulated environments.
4.1. Simulation Setup
To validate the proposed framework, we conducted experiments using the NVIDIA Isaac Gym, which is a GPU-accelerated high-fidelity physics simulator that has demonstrably facilitated successful sim-to-real transfer for various robots, as evidenced by research on drones [
36], manipulators [
37], legged robots [
38], and humanoid robots [
39]. In this simulation, we created an environment that includes both the UAV and the moving platform, which is a Clearpath Husky UGV in our case.
To train a robust UAV agent, we intentionally constructed partially observable scenarios by modifying the flow of data to the RL algorithm. Specifically, we created POMDPs consisting of an MDP version and three additional POMDP versions of the task. The MDP version had a fully observable state space, while the POMDP versions simulated different scenarios that affected the observability of the landing maneuver. The first POMDP scenario included sensor noise that gradually increased over time. The second simulated a case in which remote sensor data were lost during long-distance transmission, which we denoted as flicker; the entire 13 × 1 observations vector experienced intermittent zeroing out with varying frequency. The third scenario combined the effects of noise and flicker and created a composite challenge that reflected real-world complexities. We leveraged the Isaac Gym’s flexibility to manipulate sensor sampling rates to make the controller robust to varying sensor latencies. During training, we randomized the sampling frequency of each simulated sensor within a range of 10 Hz to 60 Hz. The approach exposed the controller to a diverse set of conditions, including those that may arise from real-world sensor delays, ensuring a more comprehensive evaluation of its performance.
4.2. Training Details
NVIDIA Isaac Gym’s parallel training capabilities make training multiple agents simultaneously using GPU acceleration possible. Using such capabilities, we trained 4098 agents in parallel, which reduced the training time to 15 min.
Figure 5 illustrates the parallel training framework in the environment. The agents were trained for a total of 500 iterations and experienced about 33 million steps in 15 min.
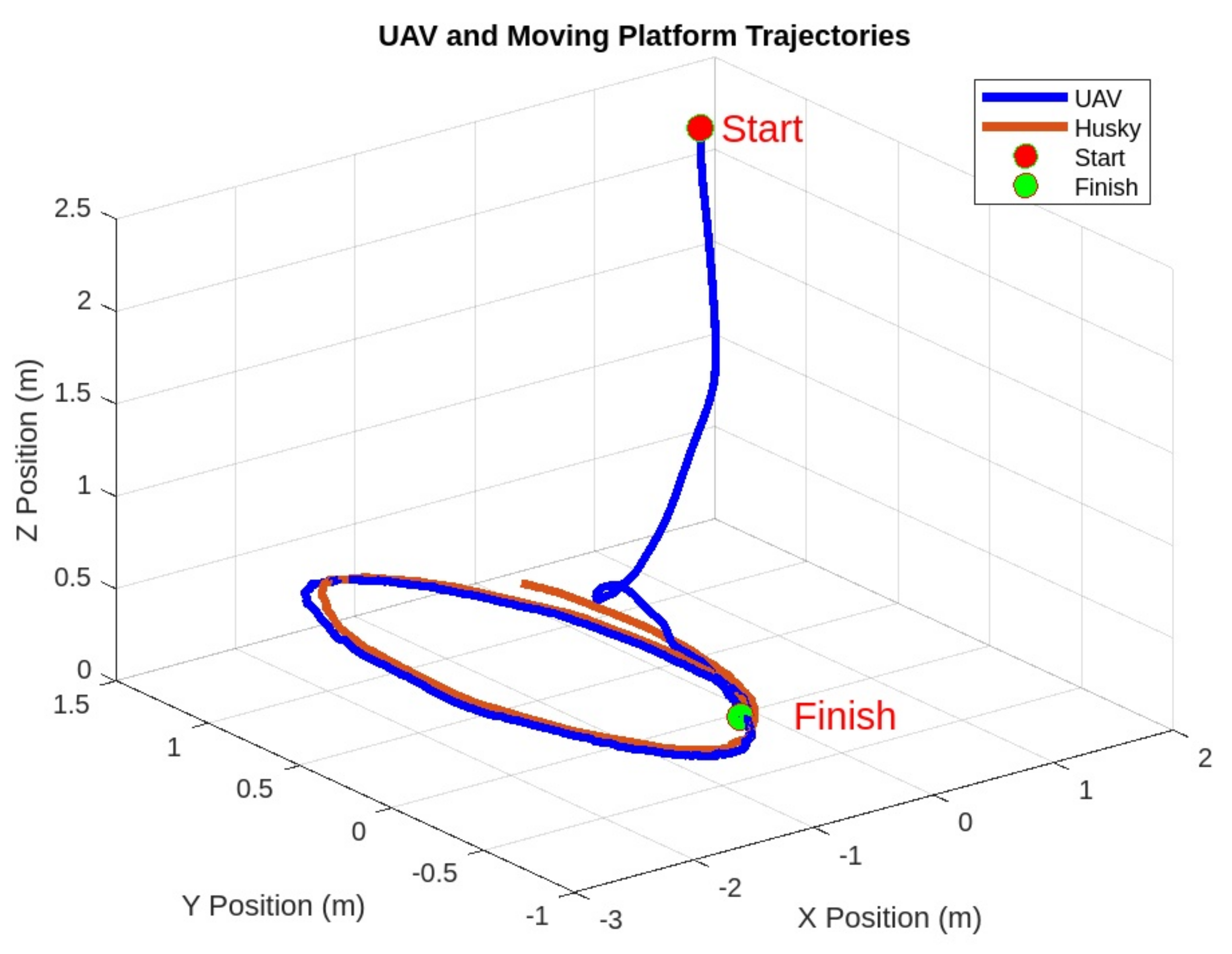
At the commencement of each episode, the initial positions of the agent and the moving platform were randomized. The UAV was positioned within a five-meter radius of the UGV. To add variability, the UGV’s trajectory was altered at the beginning of each episode, with the UGV following one of thirty predefined trajectories at speeds reaching up to 2.2 mph. A sample landing trajectory is shown in
Figure 6. During testing, the UGV was set on random trajectories that were not encountered during the training phase. The episode would reset if the UAV strayed beyond an eight-meter threshold from the moving platform or if it made contact with the ground. Of importance, no interactive communication or coordinated behavior occurred between the Husky and the UAV during landing.
During the early training epochs, the UAV agents could not fly and crashed to the ground. However, as training progressed, the agents learned to track the moving platform. The UAVs crashed into the moving platform when landing, so an orientation parameter was added to the reward function to address the issue. After the training epochs, the UAV tracked and landed on the moving platform consistently. The training rewards of the fully observed states are shown in
Figure 7. In the MDP environment, the training performance of the RPO-LSTM algorithm is comparable to that of the state-of-the-art PPO. After training, the agents were retrained with various partial observabilities, with each POMDP trained for 500 iterations. The simulation was run on a desktop PC with an Intel i7-11700K CPU, NVIDIA RTX 3060, and 64 GB of RAM.
4.3. Performance Metrics
We utilized two metrics, namely, the average training reward and successful landing rate, to assess the effectiveness of the algorithms. The evaluation framework encompasses both learning progress and task accomplishment, thereby providing comprehensive insights into the algorithms’ performance.
Average Training Reward. Employing an average training reward is a prevalent approach to evaluating machine-learning algorithms, particularly in RL contexts. The metric serves as a performance gauge, reflecting how effectively an agent learns and evolves while interacting with the environment. In our context, we computed the average rewards by evaluating Equation (
4) at intervals of 16 steps.
Successful Landing Metric. Incorporating a successful landing as a performance indicator establishes a pragmatic and direct assessment of algorithm effectiveness in executing the pivotal task. A successful landing is defined as follows:
The metric is calculated in 100 trials for each POMDP method. The dual metrics offer a comprehensive evaluation framework encapsulating the learning trajectory through rewards and ultimate fulfillment of the task through successful landings.
4.4. Results
This section presents a thorough evaluation of our proposed RPO-LSTM algorithm, tested across a spectrum of scenarios and measured against predefined metrics. We assessed our method against the established PPO algorithm, a benchmark in robotic RL, and a traditional approach that integrates the geometric Lee controller [
40] with an EKF.
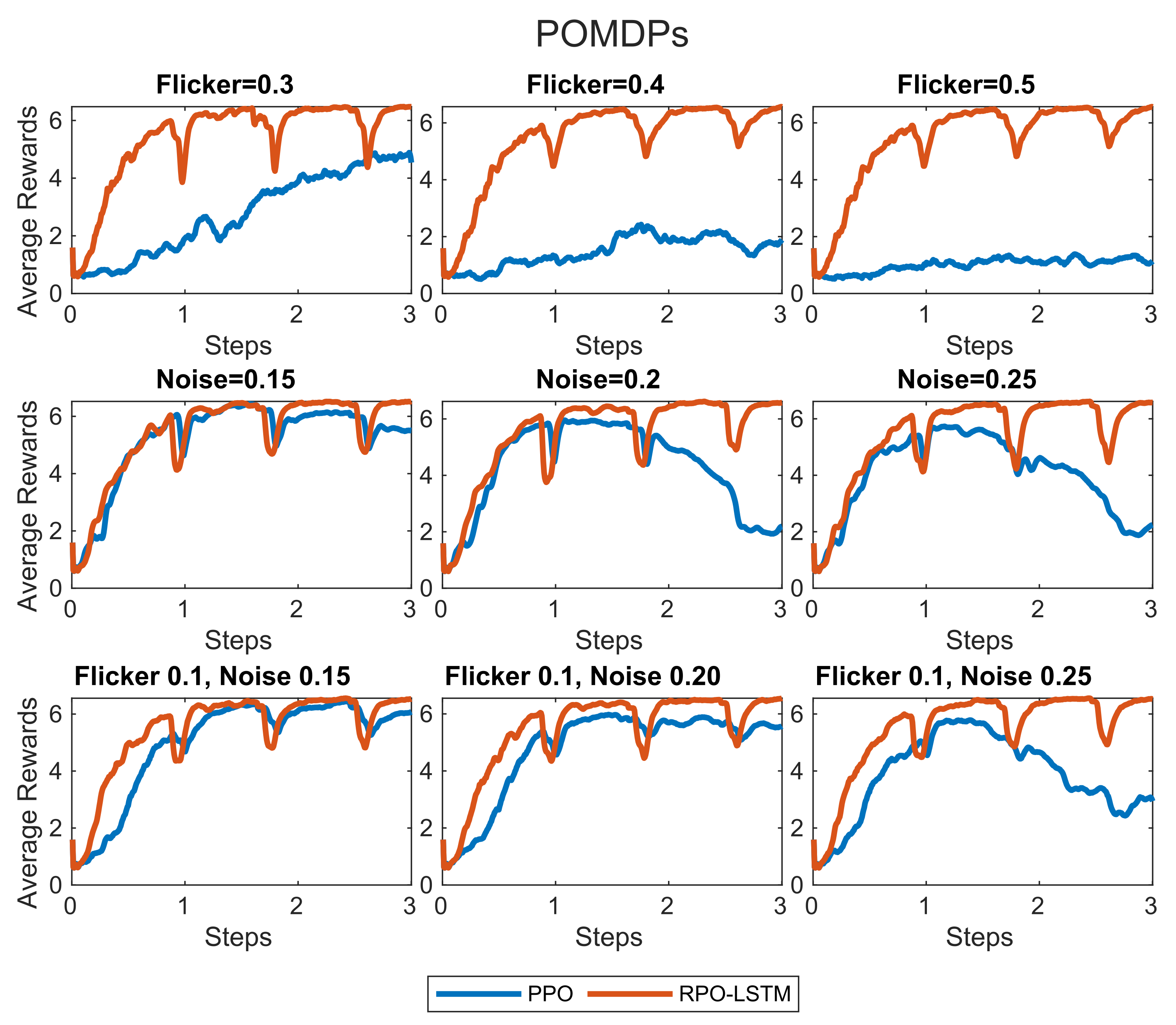
Figure 8 illustrates the comparative training rewards between our RPO-LSTM and the conventional PPO within POMDP settings. Additionally,
Table 2 details the successful landing rates of the PPO, Lee-EKF, and RPO-LSTM algorithms under various POMDP conditions, such as flickering, noise, and their combinations. The comparative analysis across the metrics consistently demonstrates the superior performance of our RPO-LSTM algorithm, which achieved a higher success rate in landings amid diverse conditions of uncertainty.
4.4.1. Comparison with PPO
The most intriguing findings and behaviors emerged within the context of flickering POMDPs. Particularly, our RPO-LSTM method demonstrated a substantial performance advantage over PPO in scenarios involving flickering conditions. Notably, with up to 50% flicker, our RPO-LSTM algorithm in a POMDP environment achieved comparable performance to the MDP counterpart (i.e., nearly perfect successful landing rate as shown in
Table 2), indicating robust adaptation in the presence of flicker. In the case of PPO, inference revealed that the UAV adeptly tracked and successfully landed on the moving platform under flicker conditions of up to 30%; beyond this threshold, its ability to execute successful landing maneuvers dramatically declined. Specifically, at 50% flickering, our RPO-LSTM method exhibited a better training performance with substantially higher rewards than the PPO method (
Figure 8). At 50% flickering, the PPO method only managed 19 successful landings out of 100 trials, while our RPO-LSTM method still maintained a 92% successful landing rate (
Table 2). Additionally, our RPO-LSTM method exhibited impressive consistency and achieved successful landings on the moving platform even under challenging conditions of up to 50% flicker.
In the context of the random noise POMDP, we intentionally introduced varying levels of noise as a means of evaluating the algorithms’ performance and adaptability. The noise levels were systematically tested across a range from a 15 to 25% noise-to-signal ratio. Notably, both the PPO and RPO-LSTM algorithms showcased remarkable resilience in effectively handling observations corrupted by noise, as seen in
Table 2. When disturbed by substantial levels of noise, our RPO-LSTM method exhibited a better ability to converge to policies that yielded reasonably effective outcomes than the state-of-the-art PPO method (middle row in
Figure 8). The results underscore RPO-LSTM’s ability to learn and adapt within the complex and noisy environments typical of the real world.
The consistent performance of both algorithms across diverse levels of random noise further accentuates their proficiency in adapting and executing successful landings in the presence of sensory noise. While both PPO and RPO-LSTM demonstrate robust performance, an intriguing distinction is evident in the recurrent architecture of RPO-LSTM, which appears to offer an inherent advantage by enabling notably higher training rewards to be maintained(
Figure 8) and success rate (
Table 2) as noise levels increase. This suggests that our RPO-LSTM’s ability to harness temporal dependencies through recurrent connections contributes to its stability in noisy conditions, allowing it to maintain accurate decision-making even amidst heightened sensory uncertainties.
Within the framework of the flicker-plus-noise POMDP, our experimentation involved maintaining a constant flicker level of 10% while varying the intensity of random noise between 15 and 25%. The approach enabled us to observe the effects of simultaneous disturbances of flicker and noise on the performance of the algorithms. Interestingly, the incorporation of flickers into noisy measurements noticeably impacted the landing performance of the PPO RL algorithm in comparison to scenarios involving random noise alone when the noise-to-signal ratio was above 20% (
Table 2). The degradation in PPO’s performance under the combination of flickers and noise suggests that the PPO algorithm’s adaptability is more challenged when multiple sources of uncertainty interact.
Overall, the flicker-plus-noise POMDP scenarios underscore the adeptness of RPO-LSTM in handling complex and multi-dimensional challenges. The integration of flickers and noise did not impede its ability to execute successful landings, as seen in
Table 2. This observation emphasizes the algorithm’s inherent adaptability and capacity to learn in complex environments with different types of uncertainties. The unwavering success rates across these diverse scenarios reflect the algorithm’s capability to navigate intricate real-world situations with great consistency. The demonstration of their potential showcases its readiness for dependable UAV autonomous landing on moving platforms under partial observability.
4.4.2. Comparison with Lee-EKF
In our comparative analysis, we juxtaposed our RPO-LSTM algorithm with a classical control method, implementing a system for UAV landing on a moving platform using Lee control and an EKF, akin to the approach described in [
41]. The Lee-EKF setup underwent the same simulation tests as the PPO and RPO-LSTM methods.
Under conditions of full observability, the Lee-EKF controller exhibited optimal performance that is attributed to the manually designed trajectory planner, fine-tuned for executing smooth and non-aggressive landing maneuvers.
However, the Lee-EKF’s efficacy significantly deteriorated in the presence of the flicker POMDP. Vulnerability to flicker effects stems from the controller’s inability to discern and disregard erroneous data. Consequently, when flicker events reset state readings to zero, the Lee-EKF erroneously acts on these nullified observations instead of dismissing them. In contrast, the RPO-LSTM demonstrated enhanced resilience in such POMDP scenarios. Through the process of reinforcement learning, it acquires the capability to identify and discard sensor data recognized as spurious. Under the flicker POMDP, the Lee-EKF managed to achieve successful landings primarily in instances when the UAV was initialized in proximity to the moving target.
As depicted in
Table 2, the performance of the Lee-EKF controller closely mirrors that of our RPO-LSTM algorithm under noisy conditions. The robustness of the Lee-EKF to noise interference is largely due to the EKF’s inherent noise-filtering capabilities, evidenced by the minimal impact on performance when the noise-to-signal ratio was increased from 15 to 25%, a testament to the EKF’s effectiveness. Both the Lee-EKF and RPO-LSTM operated consistently despite increased noise levels. The instances of failed landings primarily occurred when the UAV was initialized too close to the moving target, leading to immediate collisions. Under noisy conditions, the trajectory patterns of all tested methods remained largely unchanged compared to scenarios devoid of POMDP influences.
However, when subjected to environments compounded by flicker and noise within a POMDP framework, the RPO-LSTM algorithm’s superiority becomes evident. The Lee-EKF’s performance suffered significantly under such conditions because of its heightened susceptibility to flicker disturbances.
5. Ablation Study
In this section, we perform an ablation study to isolate the impact of key components within our RPO-LSTM architecture. Specifically, we investigate the effects of (1) enhanced exploration strategies (RPO), (2) the asymmetric actor–critic information flow (RPO+Critic), and (3) the integration of memory (RPO+LSTM). RPO+LSM indicates the integration of the LSTM network with RPO without the assymetric critic. For the ablation study, our RPO-LSTM is referred to as RPO-Full to indicate a combination of all the components. The study spans three POMDP scenarios—flicker in more than 100 maneuvers at 30%, random noise at 25%, and their combination. We present the outcomes in terms of maximum training rewards and successful landing rates in
Table 3 and
Table 4. Crucially, a consistent random seed is used for all ablations in each POMDP scenario to guarantee that performance variations are solely attributable to the specific architectural components tested rather than differences in the observed scenarios.
5.1. Effect of Exploration
RPO shows an increase in performance when compared to PPO in terms of both maximum training rewards and successful landings, which is attributed to RPO’s enhanced exploration capabilities. Examining the flight trajectories reveals that the RPO’s trajectory closely mirrors that of the PPO. Notably, both algorithms exhibit a pronounced aggressiveness in their initial descent toward the moving platform. The similarity in trajectory suggests that the primary distinction in performance arises from RPO’s ability to handle uncertainties better during exploration, rather than differences in the fundamental trajectory planning.
5.2. Effect of Asymmetric Actor–Critic
The ablation study reveals compelling insights regarding the differential impacts of providing the critic with full state information while limiting the actor to partial states. The approach resulted in significantly elevated training rewards, suggesting an efficient learning process during the training phase. However, the improvement was marginal when compared to the PPO, and it underperformed relative to the RPO in terms of successful landings. The discrepancy hints at a potential issue of overfitting, where the model is too specialized to the training environment, compromising its generalizability to new or varied conditions. Notably, a majority of unsuccessful landings occurred at the onset of the maneuver, indicating that the system’s handling of initial data loss was not as effective as that of other components in the architecture.
5.3. Effect of Adding Memory
The ablation study’s findings indicate that the inclusion of a memory component distinctly impacted the on performance metrics. Specifically, the training rewards of the RPO with memory were intermediate, falling between those of RPO+Critic and the full RPO-Full configuration. However, in terms of successful landings, RPO+LSTM surpassed RPO+Critic, suggesting an advantage in operational effectiveness. Contrary to expectations, RPO+LSTM’s performance was notably inferior to both RPO and RPO+Critic in scenarios combining flicker and noise. Interestingly, the flight trajectory associated with RPO+LSTM was observed to be the smoothest, indicating a less aggressive approach to the landing maneuver compared to the complete RPO-Full algorithm. The smoother trajectory implies a more cautious strategy, potentially prioritizing stability over the speed and assertiveness seen in other configurations.
6. Conclusions and Future Works
In this paper, we address the challenging task of landing a UAV on a dynamic target under partial observabilities. To solve this task, we developed an end-to-end RPO-LSTM reinforcement learning framework adept at managing incomplete sensor data and environmental noise through the utilization of temporal patterns and memory mechanisms. Validated in the high-fidelity simulation environment of Isaac Gym, our method demonstrated superior performance in executing landings on moving targets under conditions of partial observability. The RPO-LSTM algorithm consistently surpassed both the PPO learning-based method and the conventional Lee-EKF approach. In flicker scenarios, RPO-LSTM achieved up to 74% more successful landings than Lee-EKF and 50% more than PPO. In noisy environments, while all methods were effective, RPO-LSTM still outperformed PPO by 7% and Lee-EKF by 1%. In the compounded challenge of flicker and noise, RPO-LSTM maintained robust performance, exceeding PPO and Lee-EKF by as much as 11% and 41%, respectively.
In future work, we aim to transition our framework from simulation to real-world applications. Considering the demonstrated superiority of transformers over RNNs across various tasks, our future endeavors will focus on developing a robust reinforcement learning algorithm that harnesses the power of transformers to address this complex problem.