Abstract
We introduce a modeling framework aimed at incorporating symbolic discrete controller synthesis (DCS) into a virtual robot experimental platform. This framework involves symbolically representing the behaviors of robotic systems along with their control objectives using synchronous programming techniques. We employed DCS algorithms through the reactive synchronous environment ReaX to generate controllers that fulfill specified objectives. These resulting controllers were subsequently deployed on the virtual robot experimental platform Simscape. To demonstrate and validate our approach, we provide an implementation example involving collaborative UAV robots.
1. Introduction
Robotic systems have been growing rapidly in recent years, and the behavioral features that need to be controlled are becoming more complex. The behaviors must be controlled by ensuring that the desired system features are provided despite environmental factors such as gravity and wind. In addition, it is necessary to check the mutual constraints of the collaborative robots. In this regard, it is very important to use simulation environments before physical implementation.
Many studies have been conducted using simulation environments as a tool before physical implementation. As an example, Ref. [1] presents a groundbreaking technology for future distance education called U-Plat, providing access to a virtual robotics laboratory via the internet. Users can control simulated robots, analyze experiments, and learn the Robot Operating System (ROS) across different skill levels. Ref. [2] introduces V-REP, a versatile and scalable robot simulation framework, enabling direct integration of control techniques and simplifying simulation deployment. V-REP offers a multitude of applications, including rapid algorithm development, system verification, and factory automation simulation. Ref. [3] develops a high-level controller and navigation algorithm for ATEKS, an intelligent wheelchair, using Finite State Machine (FSM) and Kinect technology. ATEKS integrates advanced controls, affordable sensors, and open-source software (ROS, GAZEBO, and ANDROID) to meet the rising demand for wheelchairs among elderly and disabled individuals, enhancing their mobility and independence. Ref. [4] proposed a new software architecture, SIGVerse, for simulating human–robot interaction in virtual reality environments. It utilizes cloud-based VR platforms and Unity and ROS frameworks to enable synchronized interaction between avatars, showing promising feasibility for multimodal interaction applications. Ref. [5] introduced an interface between ROS and the Unity3D platform for easy simulation. Ref. [6] implemented a robust controller for quadrotor missions like automatic landing, trajectory tracking, take-off, controlling position, orientation, and motor operations within the Gazebo platform [6]. To address challenges in training for the inspection of power transmission lines on steel transmission towers, a training simulator employing virtual reality technology was developed [7]. This simulator incorporates various physical factors, including wind direction and speed, to provide a realistic training environment. The design and simulation of a four-legged robot were undertaken, incorporating PID controllers and fuzzy-logic-based controllers for motion control, implemented using the multibody dynamics approach of Simscape in MATLAB [8]. In the modeling of a 6-DOF robot, quasi-physical modeling was achieved using MATLAB/Simscape Multibody, with controllers applied to the Simscape model rather than a mathematical model or an actual robot [9]. Another method proposed the design of hardware systems for a two-wheeled self-balancing robot using software tools. The CAD model of the robot was created with SolidWorks software and imported into MATLAB, and a Simscape Multibody model of the robot was obtained for simulations. The simulations aimed to determine the angular velocity and torque requirements of the robot joints and to establish a PID controller parameters [10].
Numerous endeavors have also been undertaken to apply diverse control methodologies within simulation environments. For instance, Ref. [11] conducted research on real-time cooperative kinematic control for multiple robots operating in distributed scenarios. They introduced a dynamic-neural-network-assisted solver to manage the control scheme. In this context, the simulation environment V-REP was employed primarily to showcase the achievement of control objectives. Moreover, there exists a body of work, such as PID controller applications in the Simscape environment of MATLAB [12]. In contrast, our current research uniquely focuses on the application of the DCS technique within a virtual, experimental simulation environment. The principal strength of the DCS technique lies in its capability to generate synthesizable controllers that adhere to formal correctness standards. Unlike other control approaches that emphasize varied techniques, our research centers on seamlessly integrating the DCS technique into a virtual simulation environment, thereby ensuring the development of controllers that meet stringent formal correctness criteria.
The control theory of discrete event systems (i.e., DCS) was initially introduced as a language theory by [13]. This theory primarily focuses on synthesizing controllers for specific systems and control objectives. Subsequently, numerous modeling methodologies emerged, including automata [14], finite-state machines [13], and Petri nets [15], following the DCS paradigm. In related research, an input–output perspective was explored in [16], where systems are defined as finite-state machines or automata. Another direction was taken by [17], who proposed an automata-based synchronous language approach. However, these approaches encountered challenges stemming from the state explosion problem. To address these issues, a symbolic approach using labeled transition systems was introduced in [18]. Furthermore, the field of symbolic discrete control methods evolved, initially dealing solely with Boolean variables. Works such as [19,20,21] presented solutions based on the synthesis algorithm proposed in [22]. Subsequently, a symbolic approach catering to infinite systems was introduced in [23].
The DCS technique has been applied in various systems in the existing literature. For instance, Ref. [24] employed a safety-oriented DCS algorithm for power grids. An automata-based DCS approach was explored in [25] to address reconfigurable systems. Ref. [26] introduces the adaptation of symbolic DCS for energy-efficient multi-pocket milling in CNC machining. Additionally, the pursuit of power efficiency in hardware circuits through symbolic DCS was investigated in works such as [27,28]. Ref. [29] introduced altitude control of a quadcopter with symbolic, limited, optimal, discrete control.
Similar to its application in other domains, the utilization of DCS has extended to robotic systems, with the aim of integrating and enhancing their functionality. Ref. [30] explored the synthesis of safety controllers for collaborative robots. This study delved into modeling the manufacturing process using Markov decision processes, particularly within the context of human–robot collaboration. Pioneering contributions to the field of robotic systems control through DCS include the seminal works of [31,32]. These studies proposed a task-based model, integrated with DCS, within the robotic platform ORCCAD, an environment rooted in straightforward synchronous programming. Importantly, a symbolic approach, handling only Boolean variables, was applied to address safety properties within an excavator system. Additionally, Ref. [19] introduced the synchronous modular DCS environment BZR. This environment has the capacity to encode both automata and data-flow-based models. An illustrative example within this work demonstrates the control of robotic systems, incorporating abstracted behaviors and mutual exclusions. This body of research collectively underscores the versatility and utility of DCS in addressing diverse challenges within the domain of robotic systems, encompassing safety, task-based control, and modular approaches.
In our comprehensive literature review presented above addressing the escalating complexity of robotic systems and the concurrent development of simulation environments to mitigate installation costs, we highlight the unique challenges faced by autonomous and collaborative robots. The core of our research idea lies in focusing on the integration of the Discrete Control Systems (DCS) technique into a virtual simulation environment, specifically Simscape, emphasizing DCS’s capacity to generate synthesizable controllers adhering to formal correctness standards. The primary challenge in integrating DCS with a robotic simulation environment (e.g., Simscape) stems from DCS being an independent framework and model-checking tool. The model of a given plant is encoded within the DCS platform through pre-existing software-completed synthesis algorithms to produce a controller exhibiting desired system behaviors. Subsequently, it is compiled to generate the relevant controller. To overcome this challenge, we propose a semi-automated approach. Initially, we manually encode the desired system behaviors within the DCS platform. Subsequently, during the compilation phase, we automatically convert the obtained controller in the form of a predicate entity into codes such as C and HDL. Then, we integrate these codes (i.e., controller) into simulation environments (e.g., Simscape) and physically into microcontrollers. Autonomous systems, contending with external factors like gravity and wind, necessitate effective control mechanisms, while collaborative robots encounter intricate coordination challenges. While existing research explores various control methodologies in simulation environments, our primary goal is to seamlessly incorporate symbolic DCS into Simscape, enabling the implementation of collaborative robots to address safety and optimization challenges. The research contributions, encompassing modeling, tooling, and implementation within the proposed DCS framework, aim to fill a critical gap in the literature.
We aim to leverage the distinct advantages of DCS to integrate and enhance robotic platforms. Importantly, unlike prior endeavors, we address the novel challenge of incorporating symbolic approaches for infinite systems into robotic platforms. This endeavor fills an existing gap in the literature by introducing a novel approach that circumvents the state explosion problem while ensuring the formal correctness associated with DCS. In our research, we delve into the symbolic definitions established for governing infinite-state systems, as outlined in [23]. Our focus lies in integrating symbolic DCS into one of the extensively utilized robotic simulation environments, Simscape. Moreover, we present an implementation of collaborative robots within this framework, aiming to address their safety and optimization control challenges.
Contributions: We propose a framework for incorporating symbolic DCS into Simscape, and our contributions within this framework are as follows:
- Modeling: includes the specifications that abstract behaviors of robotic systems and their control objectives are symbolically encoded as the parallel composition of data-flow equations by the reactive synchronous language the DCS tool ReaX supports;
- Tooling: includes the incorporation and code-generation and is a semi-automated manager that comprises the encoding of abstracted behaviors of robotic systems obtained from the simulation environment and desired system specifications; ReaX-DCS compiling of constructed synchronous models and adding the synthesized controllers to the simulation platform;
- Implementation: experimentally validates our approach and guarantees the specifications of a given robotic system.
The following sections of this paper are organized as follows. Section 2 offers an outline of the robot simulation platform, Simscape. In Section 3, we furnish the requisite background on symbolic DCS. The incorporation of DCS into the virtual robotic experimental environment is detailed in Section 4. Section 4 showcases an example implementation of our collaborative robot modeling approach. Subsequently, the experimental evaluation of our approach’s effectiveness is presented in Section 5. Finally, Section 6 concludes the paper.
2. Virtual Robot Experimental Platform
Simscape enables researchers to develop models of the physical systems using the Simulink environment in MATLAB. Multibody systems can be modeled in the Simscape environment using blocks representing bodies, joints, and sensors. CAD files can be saved as XML files and can be imported, including masses, inertias, joints, constraints, and 3D geometry, into the Simscape environment. System dynamics of the model can be visualized, and control systems can be developed and tested in Simscape Multibody. Hardware-in-the-loop (HIL) applications can be carried out using the controllers developed for the model. For example, a 3D model of a robot manipulator can be created in CAD software such as Solidworks. The assembly file of the design is exported as XML files. The files are imported into the Simulink environment of MATLAB. The design is created as blocks that represent joints, links, and all assembly relations of these components. Desired motion is implemented using joints of the design that was converted to the Simscape Multibody model. Output variables of the manipulator such as position, velocity, acceleration of the links or torque, and force on the joints are obtained and visualized.
3. Background of Symbolic Discrete Controller Synthesis
We constructed a symbolic system with a set of symbols , where each symbol s in the system is denoted as . Each symbol belongs to a domain , and this mapping is denoted as . The domain set includes boolean (), numerical (), integer (), and rational () domains. Furthermore, all constants in are expressed as a symbol s. All formulae that can consist of -valued symbolic expressions are presented with the following notation:
The symbolic system we considered consists of a disjoint set of states X and inputs I. The valuation of discrete events is expressed with an assignment , where and is a -valued symbolic expression. The variable x memorizes the value based on the current state and input variables at each tick. On the other hand, s is a placeholder for the expression e in the given assignment .
Addressing symbolic control problems within these structures resembles maneuvering through a scenario akin to a game. Cases entail a successive interaction between participants: environment and supervisor. The environment allocates valuation to some input flows, whereas the supervisor tactically allocates valuation to the other variables. This interaction drives game advancement, shaping the state of the system. Central are control objectives and logical expressions including state and input variables. The core of the problem is devising a strategy for the controller to fulfill flows. Thus, the environment assigns uncontrollable flows (U), while the supervisor handles controllable flows (C). Deadlock-free structures enable consistent choices for the environment. Algorithms solving control problems should uphold this for dynamic progress and objective achievement.
Control algorithms utilized in our context are computed as fix-point calculations using binary decision diagrams. The model being controlled is constrained based on the restriction of controllable variables (C) against uncontrollable variables (U), and subsequently, the values of controllable variables are determined by the instantaneous states of uncontrollable input variables and the states (denoted by ). Below are the equations for the optimization algorithm represented as recursive functions:
where the optimal control objective involves minimizing the given objective function, denoted by , based on the ticks specified in the sequence of events. Consequently, focuses on minimizing the impact of uncontrollable variables, whereas aims to optimize controllable variables to the greatest extent possible. The safety objective () is always achieved when optimizing the objective function.
4. Incorporating Symbolic DCS to a Virtual Robot Experimental Platform
In this section, we will systematically describe how a symbolic DCS can be incorporated into a virtual robot experimentation platform using a case study.
To begin with, we will consider a case study titled “A Case for Collaborative UAV Robots”. Initially, we identify initially uncontrolled robots within the simulation platform Simscape. We model these robots using the DCS environment called ReaX along with defining control objectives that mirror desired system behaviors. Typically, these control objectives can be categorized into two groups: safety objectives like enforcing stringent rules or mutual exclusions and optimizing objectives like enhancing parameters such as range or energy efficiency.
In this phase, we transform the model of desired system behaviors based on the outcomes of safety and optimization algorithms into a synthesized controller represented as a Boolean equation. Subsequently, we integrate this synthesized controller into the robotic platform, effectively incorporating the DCS into the environment. A summary of the provided modeling framework is detailed below.
This approach systematically outlines how a symbolic DCS, represented by ReaX, can be integrated into a virtual robot experimentation platform. Through the implementation of safety and optimization algorithms, control and enhancement of robot behaviors are achieved. This, in turn, results in an augmented functionality and capabilities of the virtual experimentation platform.
4.1. Overview of Implementation: A Case for Collaborative UAV Robots
Our case study focuses on the application of the symbolic DCS approach to collaborative UAV robots. In this scenario, we begin with an initial configuration where a certain number of robots are positioned at specific waypoints. The objective is to transport loads, each with a unique color, scattered randomly across different locations of the desired arena, to corresponding targets of the same color. Throughout these operations, we aim to achieve optimization with the least range usage and highest energy efficiency, which will be facilitated by our optimization algorithm. Furthermore, to meet safety objectives within the robotic platforms, we enforce mutual exclusions among the robots. This guarantees that no robots occupy the same target simultaneously, whether they are picking up or depositing loads. The subsequent section will comprehensively outline how this scenario can be represented.
We create an artificial scenario for collaborative robots to transport loads to specified targets in the most efficient way. Each robot is initially positioned at a waypoint within the field. Then, we try to ensure that loads with different colors are transported to target points of the same color.
Our first priority is to achieve the safety objective. This includes mutual exclusion constraints in the scenario we present. In our case, mutual constraint occurs when two robots cannot be at the same target at the same time. So, our safety objective is to prevent collision situations.
Our second control objective is the optimization objective. The aim of the optimization objective is to minimize the distance traveled by robots. Meanwhile, the optimization target does not violate the collision protection provided by the safety objective. This situation is presented in Section 3. The algorithms we present not only save energy consumption and time by calculating the shortest path for robots but also meet safety objectives such as avoiding basic collisions.
The assumptions made include the consideration that all artificial implementations conducted were under ideal conditions. In other words, the experimental process was realized without accounting for environmental factors such as disturbances and noise that could occur. Within the framework, the aim is to provide principles on how to systematically model the yet uncontrolled robotic system and integrate the synthesized controller into the simulation environment. Accounting for environmental factors such as disturbances and noise is necessary for more precise measurements.
In conclusion, our case study effectively integrates symbolic DCS into a framework for collaborative robots. Through the use of our optimization algorithm, the system effectively coordinates the movement of loads and robots to achieve the lowest possible energy consumption. The integration of mutual exclusion guarantees safe operations by preventing simultaneous access to the same target location. This comprehensive approach not only enhances the efficiency of load transportation but also ensures the safety and seamless coordination of collaborative robots within the defined arena.
4.2. Models and Objectives
Achieving the desired level of dynamic response is crucial for a cluster of robots to execute a planned path successfully. This can be achieved through two fundamental methods: multibody models and differential equations, both of which can be employed to simulate the dynamic response of robots. Regardless of the preferred modeling strategy, the DCS method can be used to improve the dynamic responses of robots. In our research, we focus on collaborative robots in the form of quadcopters, a deliberate choice that lays the groundwork for more comprehensive future studies encompassing both attitude and altitude control. Our work serves as a foundational guide for more complex investigations by addressing these important aspects. Specifically, we have chosen quadcopters as our collaborative robots and intend to facilitate detailed modeling for all components, including links and joints, within a robotic system. In the following sections, we present a thorough modeling approach for the attitude and altitude control of quadcopters.
Uncontrolled System Behavior: Let us assume that the uncontrolled system behavior, or the plant, for a quadcopter is given as follows below:
where the descriptions of the symbols are shown in Table 1.

Table 1.
Descriptions of symbols in Equations (1)–(6).
Altitude Control:
The uncontrolled behaviors of the quadcopter at the z-axis are modeled as parallel data flow equations, as shown below using a simple differential calculation:
where is the velocity of the quadcopter at the z position, t, represents the time, is the uncontrollable variable, is the distance between two instants, indicates the position at the z-axis, and U, representing the trust force acting, is the controllable variable.
Upon defining an invariant, represented as below, our synthesis algorithm determines a suitable U valuation:
where L is the maximum limit for the trust force acting and T is the target for the quadcopter at the z-axis.
Attitude Control:
The uncontrolled behaviors of the quadcopter at the x-axis and y-axis are modeled as parallel data flow equations, as shown below using a simple differential calculation:
where Vs are the velocity of the quadcopter at the x and y position, t, represents the time, is the uncontrollable variable, s are the distance between two instants, Ps indicate the position at the x-axis and y-axis, and Us, represent the trust force acting, are the controllable variable.
Upon defining an invariant, represented as below, our synthesis algorithm determines suitable Us’ valuation:
where L is the maximum limit for the trust force acting and T is the target for the quadcopter.
Mutual Exclusion Control:
In this part, the modeling of mutual exclusion constraints from the perspective of safety objectives is discussed in terms of synchronous equations. In our scenario, the objective is to ensure that no quadcopters are ever simultaneously present at the same target location.
The set of quadcopters for a given system is represented as Q and the total amount of quadcopters is denoted by . Further, we associated each quadcopter with a controllable variable , where the controllable variables determine which target we will steer towards. Each target point is denoted by , which is the vector of , and the total amount of target points is denoted by . Thus, the equation for a quadcopter to be able to navigate to any target point through a controllable variable is given as follows:
A symbol of mutual exclusion constraints for Q is expressed as the EXNOR (exclusive not or) operation of positions in P excluding the AND operation of them and encoded as:
where , and ⨁ denotes the operator EXOR.
Upon defining an invariant, represented as below, our synthesis algorithm determines a suitable c valuation:
Global Safety Objective:
All of the objectives we established above fall within the scope of safety objectives, and we compile them into an invariant represented by the logic expression that is always equal to 1, denoted as .
Optimal Control:
In accordance with our optimization objectives , we formulate a cost function. Subsequently, using the optimization algorithm outlined in Section 3, we determine new valuations for controllable variables that minimize the cost function while still satisfying the safety objectives. In this context, our cost function is composed of conditional expressions that quantify the numerical distances between the positions of targets and the quadcopter. This formulation is illustrated below:
where , and denotes the distance between the quadcopter and the target.
4.3. Symbolic Control
As specified, our control objectives are categorized into two groups. Our safety objective is represented by a sigma invariant, meaning it holds true at all times (always equals 1). To achieve this, we evaluate controlled variables through the at least fix point method, ensuring that the evaluations of these variables satisfy the safety requirement. These evaluations are, in fact, outputs of the actual system. Subsequently, we construct our controller using these evaluations, ensuring that the safety objectives are consistently met. Our safety goals in our system encompass mutual exclusions, preventing robots from occupying the same position simultaneously.
Moving on to our second control objective, optimization, we treat the range as a cost function. This function is minimized while adhering to safety objectives and is evaluated over controlled variables. This approach ensures that mutual exclusions are satisfied while minimizing the range to achieve optimal efficiency. Although solving this problem can be complex, our optimization algorithm, as outlined in Section 3, provides a solution that is guaranteed to be optimal due to its use of a model-checking tool. While this process might be time-consuming in terms of execution time, it is a one-time operation performed after the modeling phase. Subsequently, the generated controller operates at runtime upon integration into the relevant environment.
Our approach is pessimistic, resembling a game where controlled variables respond optimally to the worst-case behaviors of uncontrolled variables. This analogy helps mitigate uncontrolled behaviors while maximizing controlled variable responses.
In summary, our methodology effectively addresses both safety and optimization objectives. By systematically evaluating controlled variables and constructing a controller, safety goals are perpetually met. Likewise, our optimization algorithm ensures optimal efficiency while accounting for mutual exclusions. This approach, though computationally intensive during modeling, results in a runtime controller that deals with complex scenarios through a game-like interaction between controlled and uncontrolled variables.
4.4. Incorporation
In our systematic framework for incorporation process, we present the block diagram of the system’s architecture, as depicted in Figure 1. The diagram comprises four distinct steps. The first involves a designer creating an uncontrolled design (i.e., plant). The design is both modeled in a robotic environment and the ReaX environment, the DCS tool. Additionally, the specification (i.e., desired objectives) is expressed as data flow equations within the ReaX environment, encoded in the “design.ctrln” file, as outlined in the provided model. Subsequently, employing symbolic control synthesis algorithms by means of ReaX, we generate a controller file with the “.ctrld” extension. Further, our tool, ctrl2c, converts the “.ctrld” file to C code, seamlessly integrating it with the initial design. Notably, ctrl2hdl, another proprietary tool, extends this capability to generate hardware description language (HDL) code suitable for devices like FPGAs or ASICs. Following this, the controlled design undergoes three potential processes: (i) direct deployment of the C or HDL code onto the physical system; (ii) transfer to the Simscape environment, generating desired code (e.g., MATLAB C code) for subsequent integration into the physical system; or (iii) a focus on simulation results, subjecting them to a detailed optimization process before deploying them onto the physical system, emphasizing our current emphasis on simulation refinement prior to physical implementation.
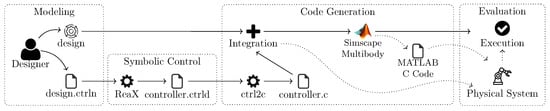
Figure 1.
Block diagram of system architecture.
In our proposed platform, the 3D models of the robots are generated using CAD software, such as Solidworks. The assembly file of a robot design is exported in XML format and subsequently imported into the Simulink environment of MATLAB. This design is automatically translated into blocks that represent the joints, links, and interconnections among these components, resulting in what is referred to as a Simscape Multibody model. To achieve desired movements, joint blocks are utilized, allowing for the simulation of the robot’s motion. Output variables, including the position, velocity, and acceleration of links, as well as torque and force on joints, can be extracted and visually presented from this Simscape Multibody model. Controllers, derived through the symbolic DCS method, are imported into the Simulink environment as C code. The integration of the symbolic DCS method to Simscape models is depicted in the block diagram presented in Figure 1.
The process of incorporation here consists of two main stages. Firstly, as depicted in the figure, the simulation platform Simscape hosts the plant, representing the initial behavior of the yet-to-be-controlled system. As explained in Section 3, this behavior is then modeled within the tool, Reax. Subsequently, the intended system reactions, that is, the control objectives, are associated with the model.
Next, employing our developed synthesis algorithms, the controller generates a Boolean predicate output. This controller is converted to C code and integrated into the robot within the Simscape environment. This integration enables the system behaviors to operate in a manner that guarantees both optimization and safety objectives. We presented the necessary steps for achieving this incorporation in previous sections within a systematic framework, supported by a case study. Consequently, the symbolic DCS has been effectively transferred into the Simscape environment.
In this process, the incorporation unfolds in a structured manner, allowing the seamless integration of the symbolic DCS approach. The simulation platform’s plant behavior is effectively linked with the Reax environment, and through a series of well-defined steps, the synthesized controller’s logic is translated into executable C code. This ensures that the system adheres to our defined optimization and safety criteria. The comprehensive approach we have delineated in previous sections offers a clear roadmap for achieving this incorporation, ultimately leading to the successful implementation of the symbolic DCS within the Simscape environment.
5. Experimental Evaluation
The role of the DCS in robotics path planning is highly significant. In Figure 2, we showcase an application of the DCS approach within the MATLAB Simscape environment. Here, a quadcopter-type UAV takes off from point H and is tasked with delivering colored boxes to matching colored circles and returning to point H, all while aiming to minimize energy consumption. This optimization is achieved by reducing the UAV’s path length. In Table 2, we compare the path lengths for randomly selected box orders, left-to-right box selection, and the DCS-optimized path.
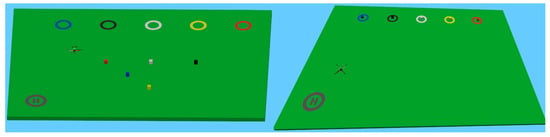
Figure 2.
UAV package delivery in Simscape.

Table 2.
Path lengths calculated with different approaches.
Figure 3 shows the package delivery process carried out by the UAV. Packages were transported and delivered according to predefined paths such as the path that is randomly generated, the path that is based on starting with the leftmost package, and the path generated with DCS. Figure 3a shows the intermediate step of the package delivery mission. The shortest path for the package delivery mission is provided by the DCS method. Figure 3b shows the trajectory of the UAV generated by the DCS method. The arrows in the figure indicate the path along which the boxes of the same color were moved.
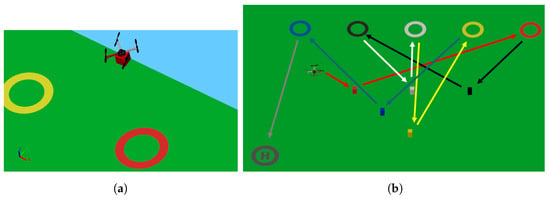
Figure 3.
Package delivery process. (a) Intermediate step for package carrying. (b) UAV trajectory.
As evident in Table 2, DCS demonstrates its efficacy by providing the shortest path at 47.5 m, underscoring its vital role in robotic path planning applications. DCS has garnered attention in various robotics studies [33], and the literature is replete with path planning research, often featuring meta-heuristic (MH) algorithms for problem-solving. MH algorithms, characterized by their stochastic nature and reliance on randomness to optimize objective functions [34], may not guarantee optimal solutions but offer faster computation than exact solution methods [35]. Notably, as the dataset size increases in path planning, MH algorithms may struggle to converge to a solution, influenced by factors like population size and maximum iteration count [36]. On the other hand, DCS shows a much superior performance, especially in path planning scenarios with a large number of waypoints (WPs).
The Vehicle Routing Problem (VRP) considers an optimization problem that aims to determine the most efficient route set starting from the same depot and ending at the same depot. In the realm of the literature, the VRP has often been tackled using Meta-Heuristic (MH) algorithms. In Table 3, we observe the application of two well-known MH algorithms, the Genetic Algorithm (GA) and Ant Colony Optimization (ACO), to find optimal routes for the VRP, considering a scenario with a single depot and ten waypoints (WPs). As depicted in Table 3, variations in population sizes and maximum iteration numbers can lead to different total path lengths. Notably, the optimal path length for this particular set of WPs stands at 197.40 m, a result achieved through the application of DCS. Smaller total path lengths translate to reduced energy consumption for robots following these generated routes, underscoring the valuable contribution of the DCS method in collaborative path-planning applications.

Table 3.
Total path lengths and computational time calculated with different approaches for VRP.
Table 3 presents the computation times required to obtain results for each MH algorithm. It is evident from Table 3 that ACO demands less computation time compared to the GA. However, these algorithms do not demonstrate a significant advantage over each other in terms of path length calculation, which is the primary focus of this study. Comparing DCS with MH algorithms is inappropriate because the DCS method does not provide a pre-calculated path. During the generation of controller path planning via DCS, dynamic selections occur in real-time. Nonetheless, the computation times, which vary depending on the state count (i.e., WP) during controller generation (solely during one compilation), are provided in Table 4.

Table 4.
Performance of the computation approach for the path planning of DCS.
The performance comparison table for the existing work and our proposed method is presented in Table 5. The test environment utilized to gather the data presented in Table 5 is Simulink/MATLAB. The test scenarios were chosen to align with those outlined in previous studies listed in Table 5. In this study, the 3D models of the robots were created using Solidworks software. The assembly files of the robot designs were exported in XML format and subsequently imported into Simulink/MATLAB. To execute path planning scenarios using DCS, waypoints were defined, and the robots navigated the path, yielding the results outlined in Table 5. To evaluate the effectiveness of the algorithms, 10 tests were conducted for each scenario listed in Table 5. The data provided for each scenario represent the optimal results obtained from these 10 tests. The Wilcoxon rank sum test was performed as the statistical test, and the obtained p-values were presented in Table 6. As a result of the Wilcoxon rank sum test, all the p-values in Table 6 were found to be less than 0.05. This outcome indicates that the MH algorithms used in this study led to significant differences, as the results of the algorithms are statistically different in all cases presented in Table 6. Therefore, the H1 hypothesis, which suggests there is a statistically significant difference between the tested MH algorithms, is accepted. As the DCS technique is a formal verification (i.e., model-checking) tool, it always guarantees the desired system properties.

Table 5.
Path lengths provided by the tested methods.

Table 6.
p-values obtained via Wilcoxon rank sum test.
The trajectory optimization of a CNC machine tool during the hole drilling process was addressed within the framework of the Traveling Salesman Problem (TSP). Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO) methods were employed to tackle the TSP. The determination of the shortest tool path was achieved by varying the population size parameter in GA, PSO, and GWO methods [37]. Notably, PSO exhibited superior performance compared to the GA, with success rates of 15%, 4%, 10%, 15%, and 0%, respectively. Surpassing even PSO, our proposed method demonstrated success rates of 27%, 33%, 23%, 15%, and 0% across all stages of the implementation process. In fact, our approach yielded results that were 16% better than the average outcomes achieved with PSO. In the realm of calculating optimal trajectories for Unmanned Aerial Vehicles (UAVs), the Vehicle Routing Problem (VRP) was addressed using the GA method. The solution to the VRP was obtained by manipulating the parameters of crossing rate and population size in the GA method, as outlined in the work by [38]. Remarkably, our approach demonstrated an 8% improvement over the mean results obtained with the GA. Furthermore, meta-heuristic methods were applied to address the path planning of a mobile robot, as reported in the work by [39]. The performance of the tested methods was compared across two distinct environments. When our proposed method was tested in these environments, it outperformed AFSA-GA, a combination of the artificial fish swarm algorithm (AFSA) and GA, by 4% and 4%, respectively.
This study primarily utilizes Simulink as the simulation environment due to its widespread usage. However, our flexible framework allows seamless integration with popular robotic simulation environments like V-REP, enhancing adaptability for future studies. The key contribution lies in leveraging the formal correctness feature of DCS, enabling the deterministic and accurate integration of safety and optimization algorithms. While there is a potential time increase during controller synthesis for a large number of states compared to metaheuristic approaches, it is essential to emphasize that the synthesized controller operates in real time post-generation.
In a range of scenarios involving collaborative robots, including mutual exclusion constraints and optimization processes, we validated the effectiveness of our technique. The results for various applications are presented in Table 5. Our verification processes rely on the foundational principle of our presented symbolic system behaving as a model-checking mechanism. Model checking, a crucial verification technique in computer science and software engineering, guarantees that a system or software model conforms to predefined properties. It proves invaluable for discovering design errors and verifying system intricacies. Model-checking involves confirming whether a system meets defined specifications, utilizing symbolic representations such as binary decision diagrams (BDDs) for efficient validation. BDDs, known for their favorable time and memory performance, maintain a unique diagram for functionally equivalent predicates. Standard temporal logic approaches for model-checking include Linear-Time Temporal Logic (LTL) and Computation Tree Logic (CTL). Ref. [40] extensively presents how CTL can be defined with symbolic approaches.
6. Conclusions & Future Works
We have introduced a systematic framework, supported by tools, to control robotic systems effectively. Utilizing the symbolic DCS approach via ReaX, we abstracted robotic behaviors and aligned them with desired control goals. Our approach automatically computes a controller and translates it into Simscape, using the language it accepts, to ensure system specifications through our tool SDCS4VREP. We have exemplified this using collaborative UAV robots, providing an illustrative case study. Our approach systematically constructs symbolic models for given robotic systems and their associated control objectives, enhancing practical applicability.
Our roadmap includes the formulation of guidelines for applying our approach to industrial manufacturing automation systems, encompassing various combinations of robotic systems and production lines. Additionally, we aim to devise a strategy that implements a task scheduling algorithm tailored for queuing systems within manufacturing contexts. Furthermore, the development of a dedicated robotic synchronous programming environment featuring symbolic control algorithms is within our plans. We also envision the application of an optimal control algorithm to different kinds of objectives. Lastly, we view the integration of DCS with stochastic models as a promising avenue to enhance human–robot collaborations.
Author Contributions
Methodology, M.Ö. and S.Ç.; Software, M.Ö. and S.Ç.; Validation, M.Ö. and S.Ç. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Erdoğmuş, A.K.; Yayan, U. Development of Virtual Robotic Laboratory and Materials for Education and Research. Bilecik Şeyh Edebali Üniversitesi Fen Bilim. Derg. 2022, 9, 514–540. [Google Scholar] [CrossRef]
- Rohmer, E.; Singh, S.P.; Freese, M. V-REP: A versatile and scalable robot simulation framework. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1321–1326. [Google Scholar]
- Özçelikörs, M.; Çoşkun, A.; Say, M.G.; Yazici, A.; Yayan, U.; Akçakoca, M. Kinect based Intelligent Wheelchair navigation with potential fields. In Proceedings of the 2014 IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA) Proceedings, Alberobello, Italy, 23–25 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 330–337. [Google Scholar]
- Mizuchi, Y.; Inamura, T. Cloud-based multimodal human–robot interaction simulator utilizing ros and unity frameworks. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 948–955. [Google Scholar]
- Babaians, E.; Tamiz, M.; Sarfi, Y.; Mogoei, A.; Mehrabi, E. Ros2unity3D: High-performance plugin to interface ros with unity3D engine. In Proceedings of the 2018 9th Conference on Artificial Intelligence and Robotics and 2nd Asia-Pacific International Symposium, Kish Island, Iran, 10 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 59–64. [Google Scholar]
- AbdulSamed, B.N.; Aldair, A.A.; Al-Mayyahi, A. Robust trajectory tracking control and obstacles avoidance algorithm for quadrotor unmanned aerial vehicle. J. Electr. Eng. Technol. 2020, 15, 855–868. [Google Scholar] [CrossRef]
- Chae, C.H.; Ko, K.H. Development of Physics-Based Virtual Training Simulator for Inspections of Steel Transmission Towers. J. Electr. Eng. Technol. 2023, 19, 1943–1953. [Google Scholar] [CrossRef]
- Aldair, A.A.; Al-Mayyahi, A.; Wang, W. Design of a stable an intelligent controller for a quadruped robot. J. Electr. Eng. Technol. 2020, 15, 817–832. [Google Scholar] [CrossRef]
- Ngoc, T.L.; Nguyen, T.L. Quasi-physical modeling of robot IRB 120 using Simscape Multibody for dynamicand control simulation. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 1949–1964. [Google Scholar]
- Mohapatra, S.; Srivastava, R.; Khera, R. Implementation of a two wheel self-balanced robot using MATLAB Simscape Multibody. In Proceedings of the 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP), Gangtok, India, 25–28 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–3. [Google Scholar]
- Liu, M.; Zhang, J.; Shang, M. Real-time Cooperative Kinematic Control for Multiple Robots in Distributed Scenarios with Dynamic Neural Networks. Neurocomputing 2021, 491, 621–632. [Google Scholar] [CrossRef]
- Ahmed, K.; Roshdy, A.A.; Ata, W.; Salem, A. PID Control of Dual Axis Inertially Stabilized Platform Simscape Multibody Model. In Proceedings of the 2022 18th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 29 December 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 1, pp. 66–73. [Google Scholar]
- Ramadge, P.; Wonham, W. The control of discrete event systems. Proc. IEEE 1989, 77, 81–98. [Google Scholar] [CrossRef]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Holloway, L.E.; Krogh, B.H.; Giua, A. A Survey of Petri Net Methods for Controlled Discrete Event Systems. Discret. Event Dyn. Syst. 1997, 7, 151–190. [Google Scholar] [CrossRef]
- Balemi, S.; Hoffmann, G.; Gyugyi, P.; Wong-Toi, H.; Franklin, G. Supervisory control of a rapid thermal multiprocessor. IEEE Trans. Autom. Control 1993, 38, 1040–1059. [Google Scholar] [CrossRef]
- Maraninchi, F.; Rémond, Y. Argos: An Automaton-Based Synchronous Language. Comput. Lang. 2001, 27, 61–92. [Google Scholar] [CrossRef]
- Altisen, K.; Clodic, A.; Maraninchi, F.; Rutten, E. Using Controller-Synthesis Techniques to Build Property-Enforcing Layers. In Proceedings of the Programming Languages and Systems, Warsaw, Poland, 7–11 April 2003; Springer: Berlin/Heidelberg, Germany, 2003; pp. 174–188. [Google Scholar]
- Delaval, G.; Rutten, É.; Marchand, H. Integrating Discrete Controller Synthesis into a Reactive Programming Language Compiler. Discret. Event Dyn. Syst. 2013, 23, 385–418. [Google Scholar] [CrossRef]
- Marchand, H.; Le Borgne, M. Partial order control of discrete event systems modelled as polynomial dynamical systems. In Proceedings of the 1998 IEEE International Conference on Control Applications (Cat. No. 98CH36104), Trieste, Italy, 4 September 1998; IEEE: Piscataway, NJ, USA, 1998; Volume 2, pp. 817–821. [Google Scholar]
- Marchand, H.; Bournai, P.; Le Borgne, M.; Le Guernic, P. Synthesis of Discrete-Event Controllers Based on the Signal Environment. Discret. Event Dyn. Syst. Theory Appl. 2000, 10, 325–346. [Google Scholar] [CrossRef]
- Dutertre, B. Spécification et Preuve de Systemes Dynamiques. Ph.D. Thesis, University of Rennes 1, Rennes, France, 1992. [Google Scholar]
- Berthier, N.; Marchand, H. Discrete Controller Synthesis for Infinite State Systems with ReaX. IFAC Proc. Vol. 2014, 47, 46–53. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.L.; Chen, Z.; Lin, F.; Wang, C.; Zhang, H. Modeling and control of discrete event systems using finite state machines with variables and their applications in power grids. Syst. Control Lett. 2012, 61, 212–222. [Google Scholar] [CrossRef]
- An, X.; Rutten, É.; Diguet, J.; Le Griguer, N.; Gamatié, A. Discrete Control for Reconfigurable FPGA-based Embedded Systems. Ifac Proc. Vol. 2013, 46, 151–156. [Google Scholar] [CrossRef]
- Çaşka, S.; Özbaltan, M. Adaptation of Symbolic Discrete Control Synthesis for Energy-Efficient Multi-Pocket Milling. Processes 2024, 12, 584. [Google Scholar] [CrossRef]
- Özbaltan, M.; Berthier, N. A Case for Symbolic Limited Optimal Discrete Control: Energy Management in Reactive Data-flow Circuits. IFAC-PapersOnLine 2020, 53, 10688–10694. [Google Scholar] [CrossRef]
- Özbaltan, M.; Berthier, N. Power-aware Scheduling of Data-flow Hardware Circuits with Symbolic Control. Arch. Control Sci. 2021, 31, 431–446. [Google Scholar] [CrossRef]
- Özbaltan, M.; Çaşka, S. Altitude control of quadcopter with symbolic limited optimal discrete control. Int. J. Dyn. Control 2023, 12, 1533–1540. [Google Scholar] [CrossRef]
- Gleirscher, M.; Calinescu, R. Safety controller synthesis for collaborative robots. In Proceedings of the 2020 25th International Conference on Engineering of Complex Computer Systems (ICECCS), Singapore, 28–31 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 83–92. [Google Scholar]
- Rutten, E. A framework for using discrete control synthesis in safe robotic programming and teleoperation. In Proceedings of the 2001 ICRA, IEEE International Conference on Robotics and Automation (Cat. No. 01CH37164), Seoul, Republic of Korea, 21–26 May 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 4, pp. 4104–4109. [Google Scholar]
- Rutten, E.; Marchand, H. Task-Level Programming for Control Systems Using Discrete Control Synthesis. Ph.D. Thesis, INRIA, Le Chesnay-Rocquencourt, France, 2002. [Google Scholar]
- Scioni, E.; Borghesani, G.; Bruyninckx, H.; Bonfè, M. Bridging the gap between Discrete Symbolic Planning and Optimization-based Robot Control. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 5075–5081. [Google Scholar]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A comparative review on mobile robot path planning: Classical or meta-heuristic methods? Annu. Rev. Control 2020, 50, 233–252. [Google Scholar] [CrossRef]
- Mac, T.T.; Copot, C.; Tranb, D.T.; De Keyser, R. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization. Appl. Soft Comput. 2017, 59, 68–76. [Google Scholar] [CrossRef]
- Çaşka, S.; Gök, K.; Gök, A. Comparison of the success of meta-heuristic algorithms in tool path planning of computer numerical control machine. Surf. Rev. Lett. 2022, 29, 2250126. [Google Scholar] [CrossRef]
- Özdemir, İ.; Çaşka, S. Calculation of The Optimum Number of Unmanned Air Vehicles Required for Surveillance Missions. Acad. Platf. J. Eng. Smart Syst. 2022, 10, 101–105. [Google Scholar] [CrossRef]
- Ma, J.; Liu, Y.; Zang, S.; Wang, L. Robot path planning based on genetic algorithm fused with continuous Bezier optimization. Comput. Intell. Neurosci. 2020, 2020, 9813040. [Google Scholar] [CrossRef] [PubMed]
- Husien, I.; Berthier, N.; Schewe, S. A hot method for synthesising cool controllers. In Proceedings of the 24th ACM SIGSOFT International SPIN Symposium on Model Checking of Software, Santa Barbara, CA, USA, 13–14 July 2017; pp. 122–131. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).