Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System
Abstract
1. Introduction
- We performed mathematical modeling to control a quadrotor system and designed a controller that combines an I-PID controller and an RBF neural network.
- To make the control system more robust, we designed an adaptive robust term that includes a reverse saturation filter.
- For the proposed controller, we designed update laws based on Lyapunov stability.
- Stability was rigorously proven by investigating the control boundness of the whole control system.
- The performance of the proposed controller was proven through simulation.
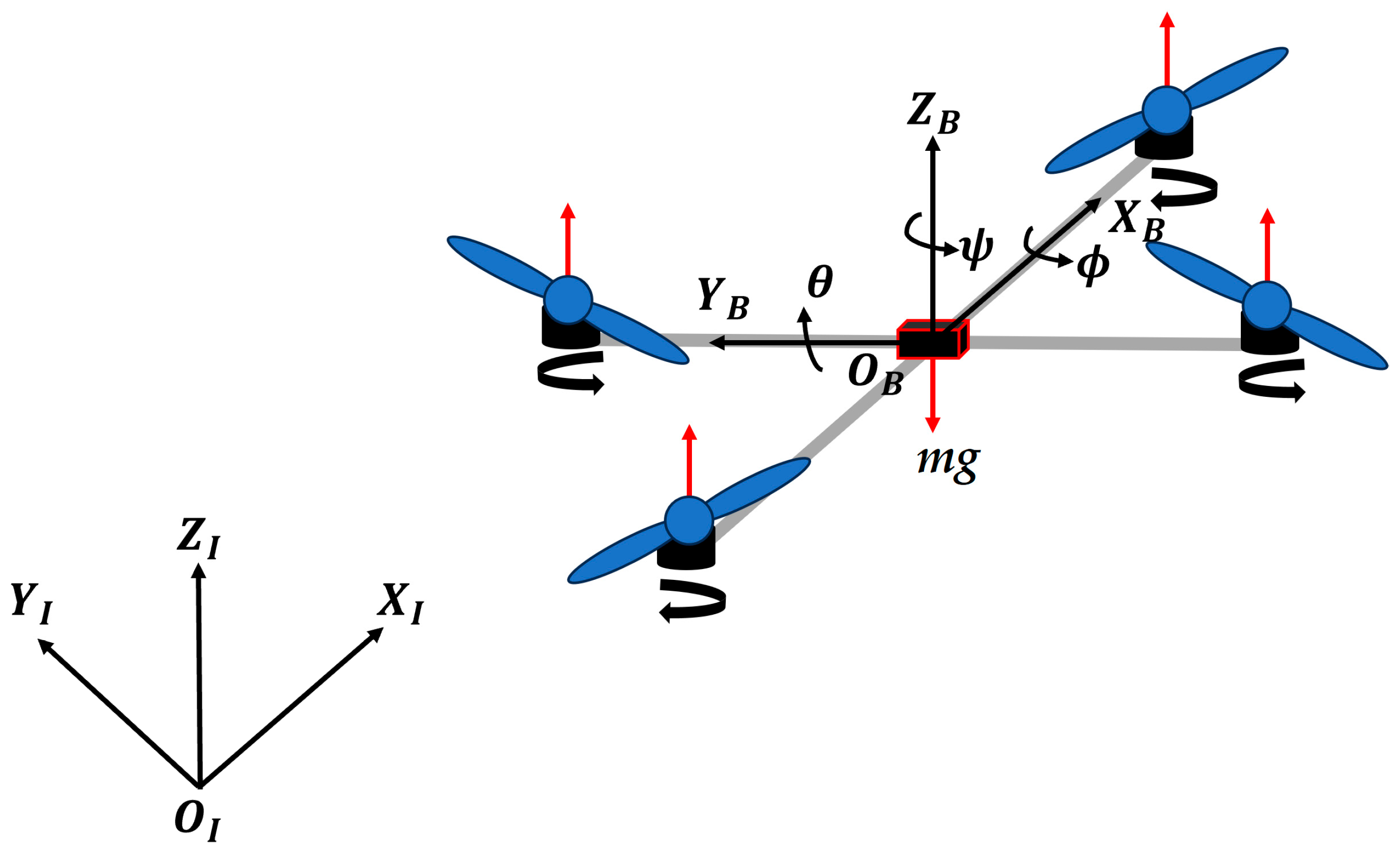
2. Dynamic Model of the Quadrotor System
3. Quadrotor Controller Design
3.1. I-PID Control
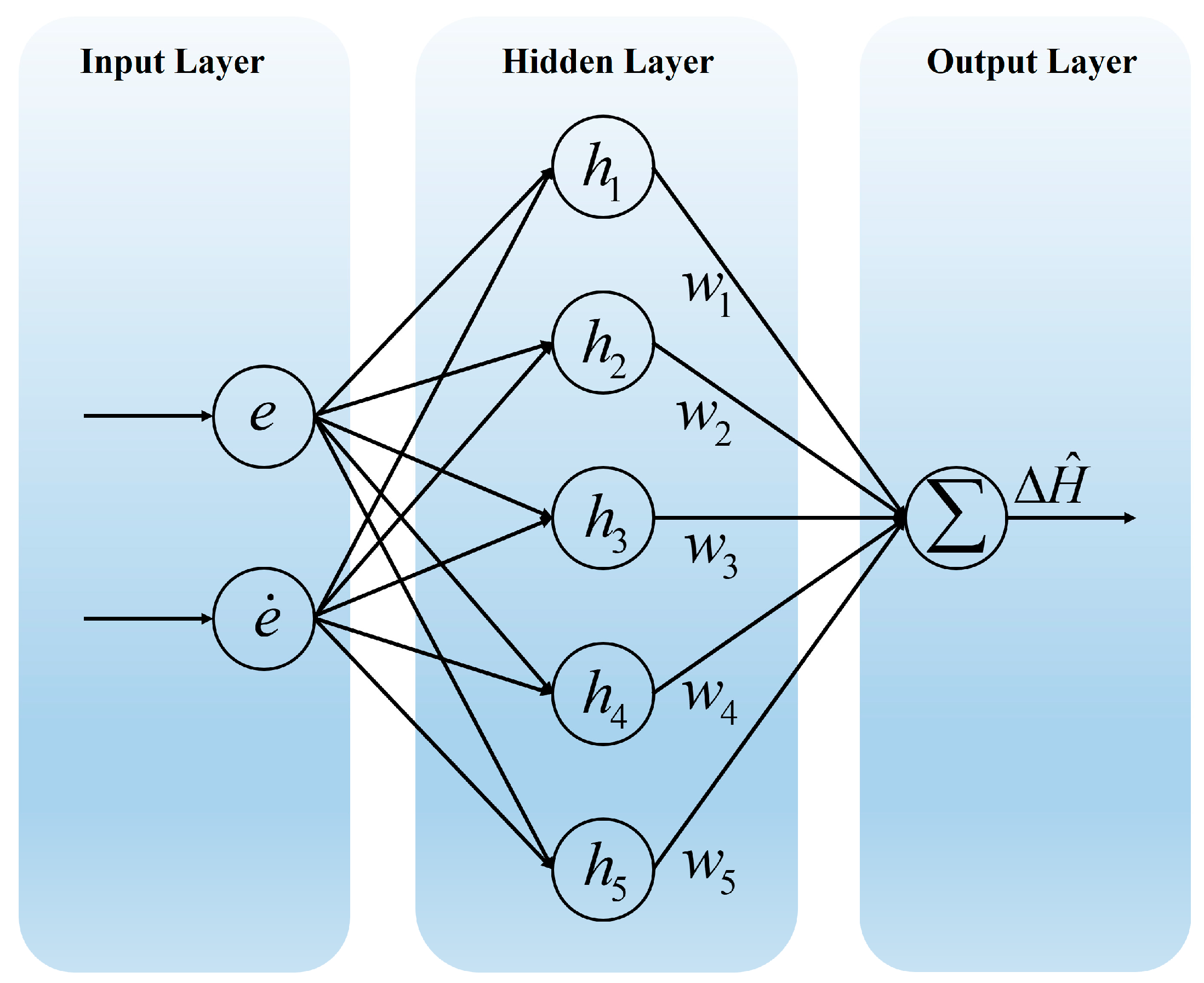
3.2. RBF Neural Network
3.3. Adaptive Robust Term
3.4. Proposed Controller Design
3.5. Stability Analysis
4. Simulation
4.1. Simulation Setup
4.2. Simulation Results
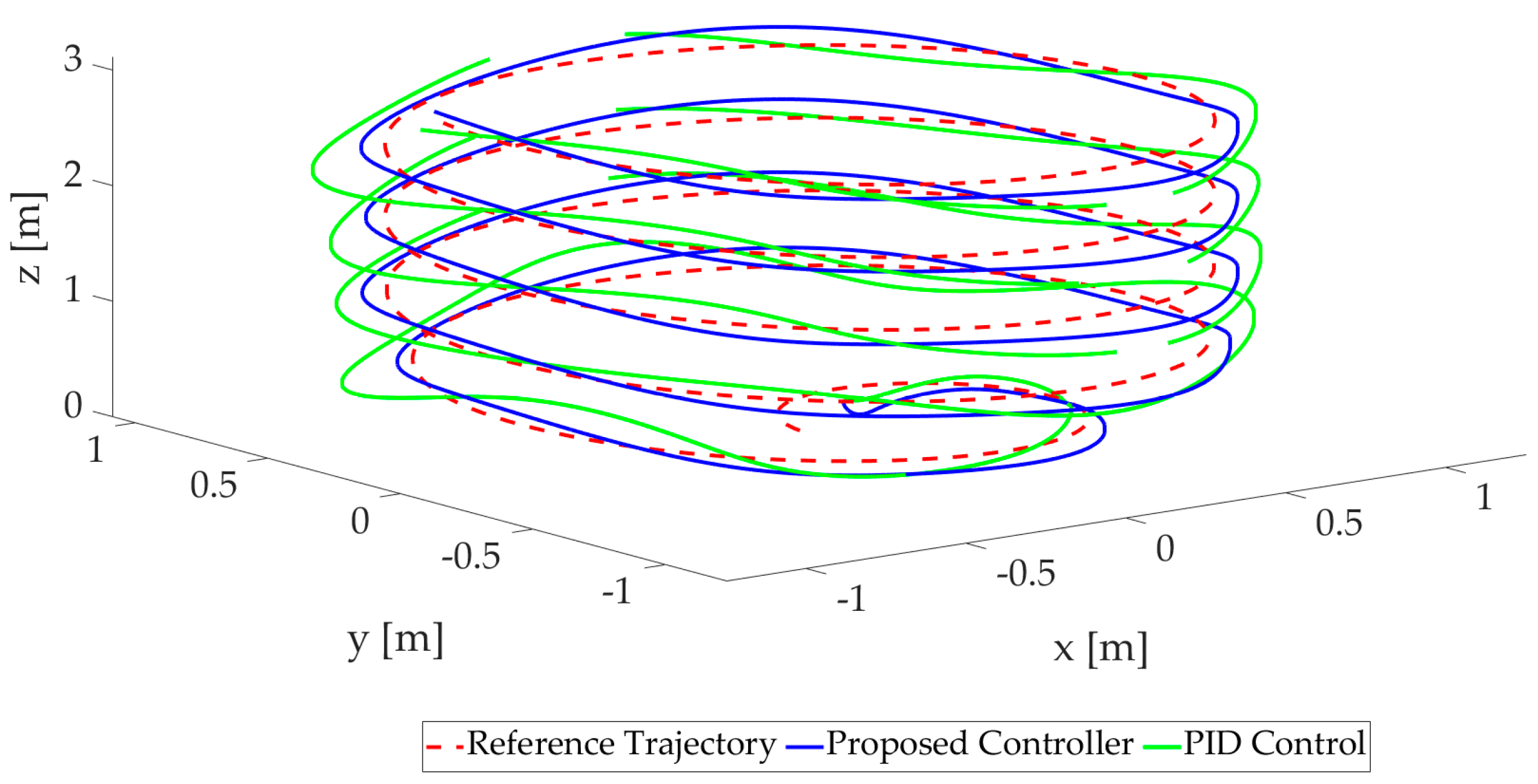
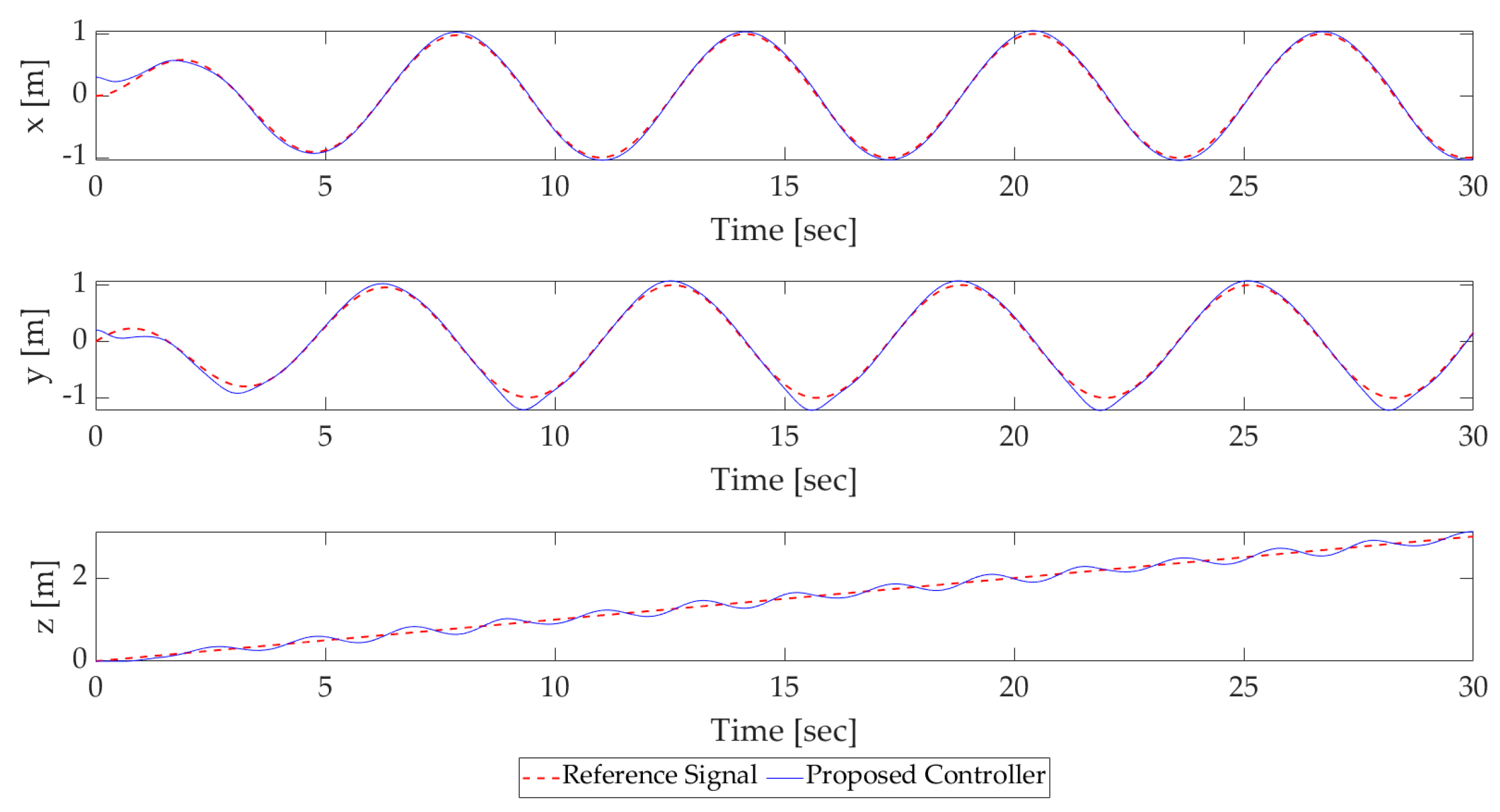
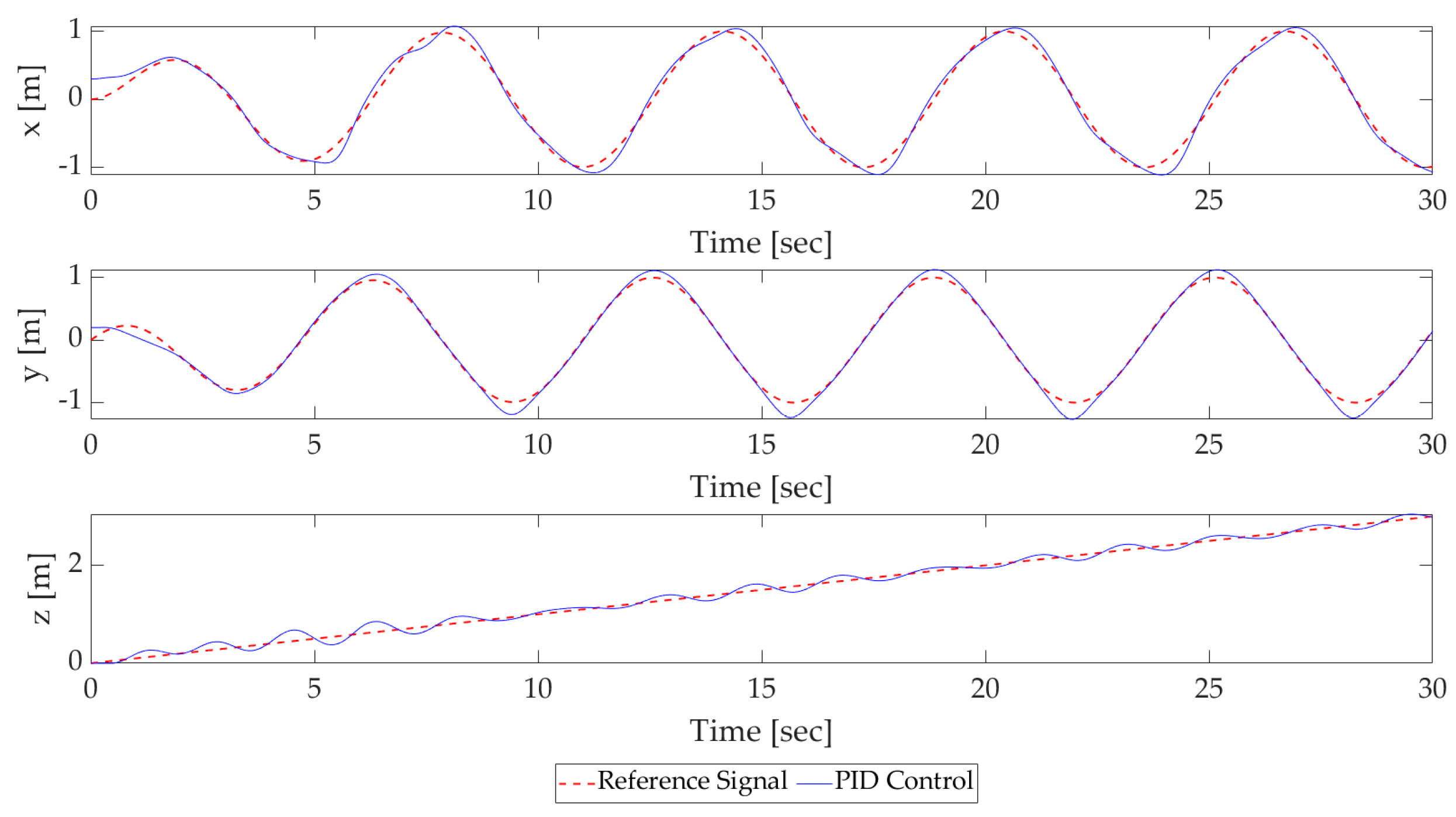
4.2.1. Position Control Simulation Results
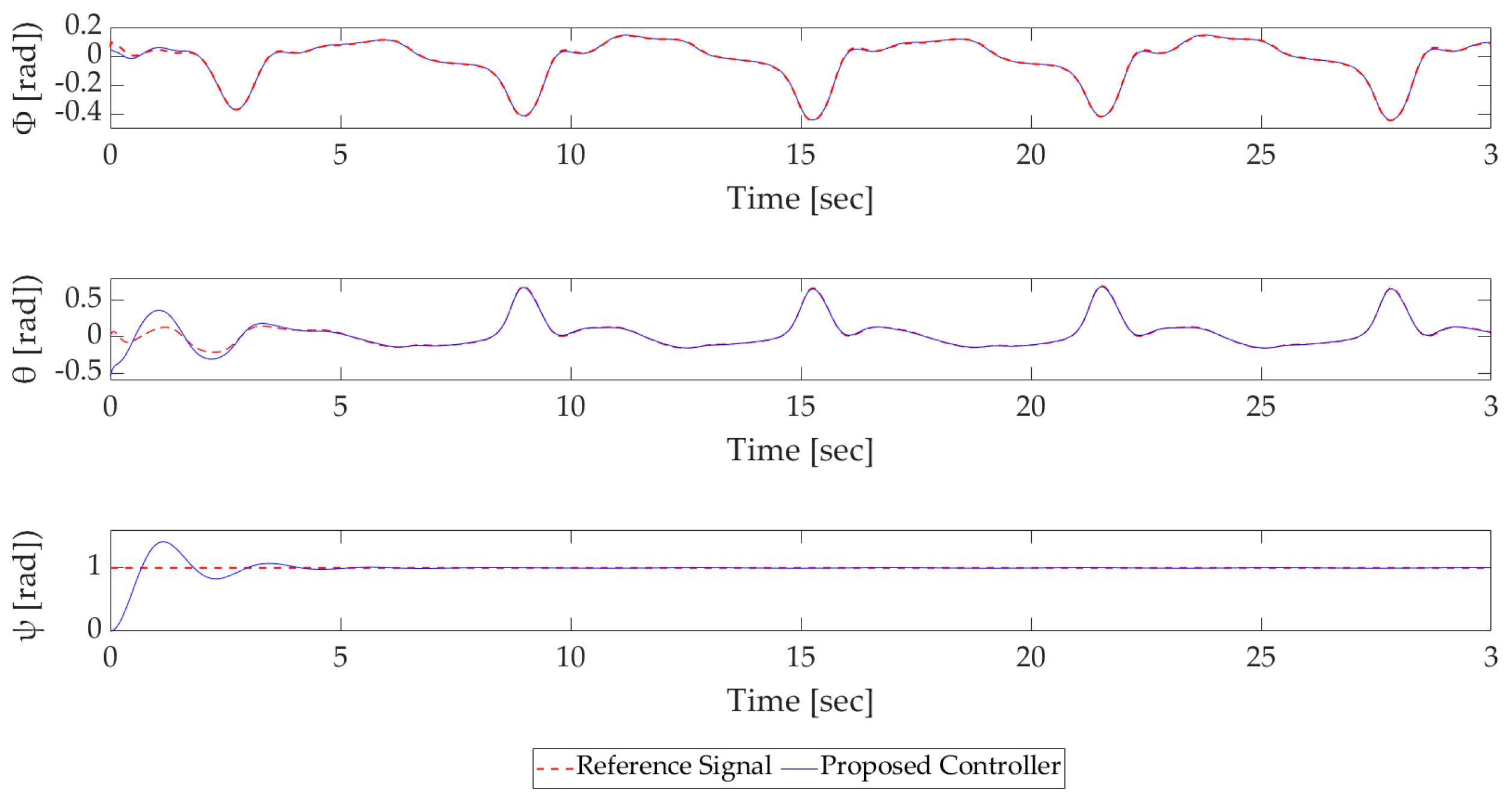
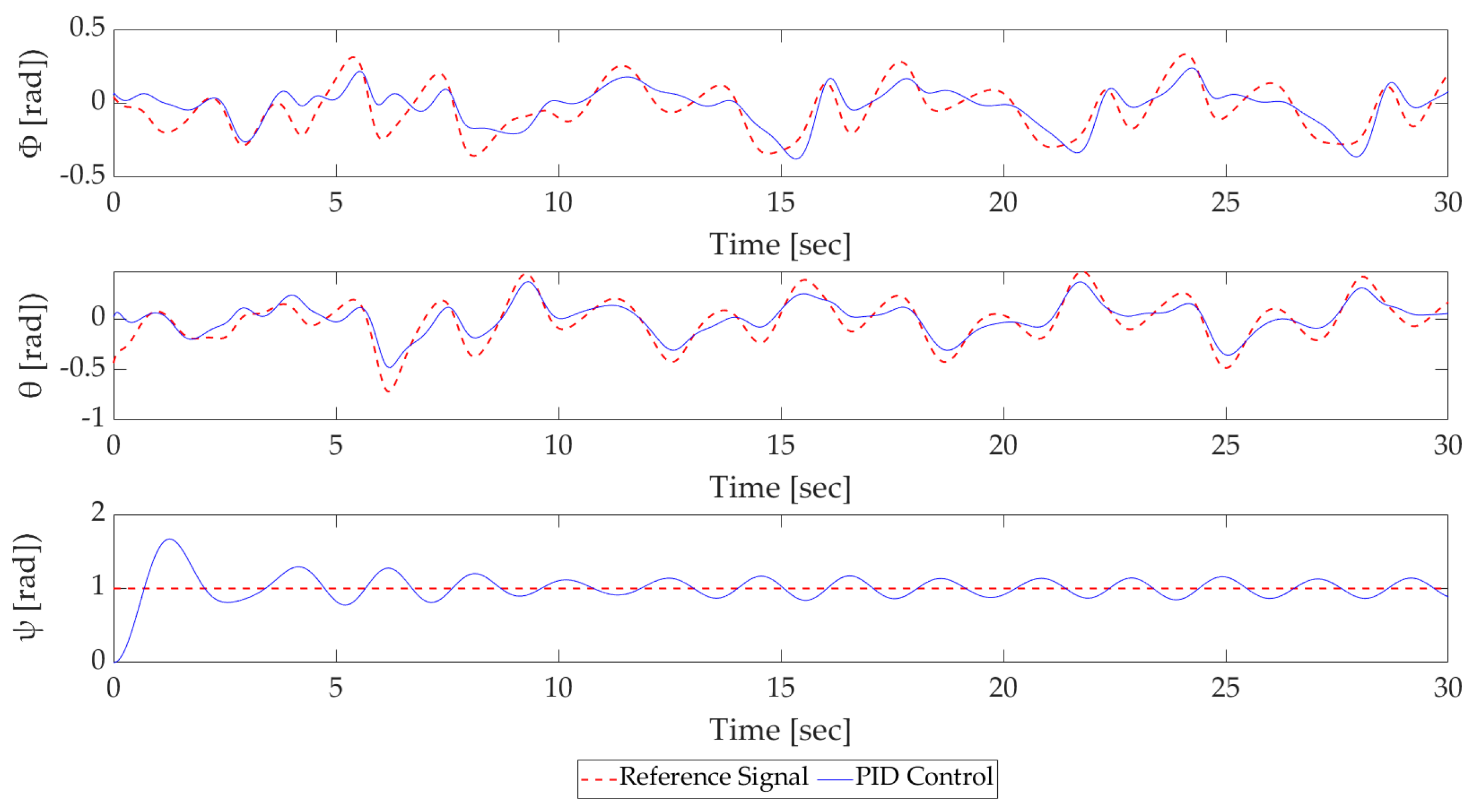
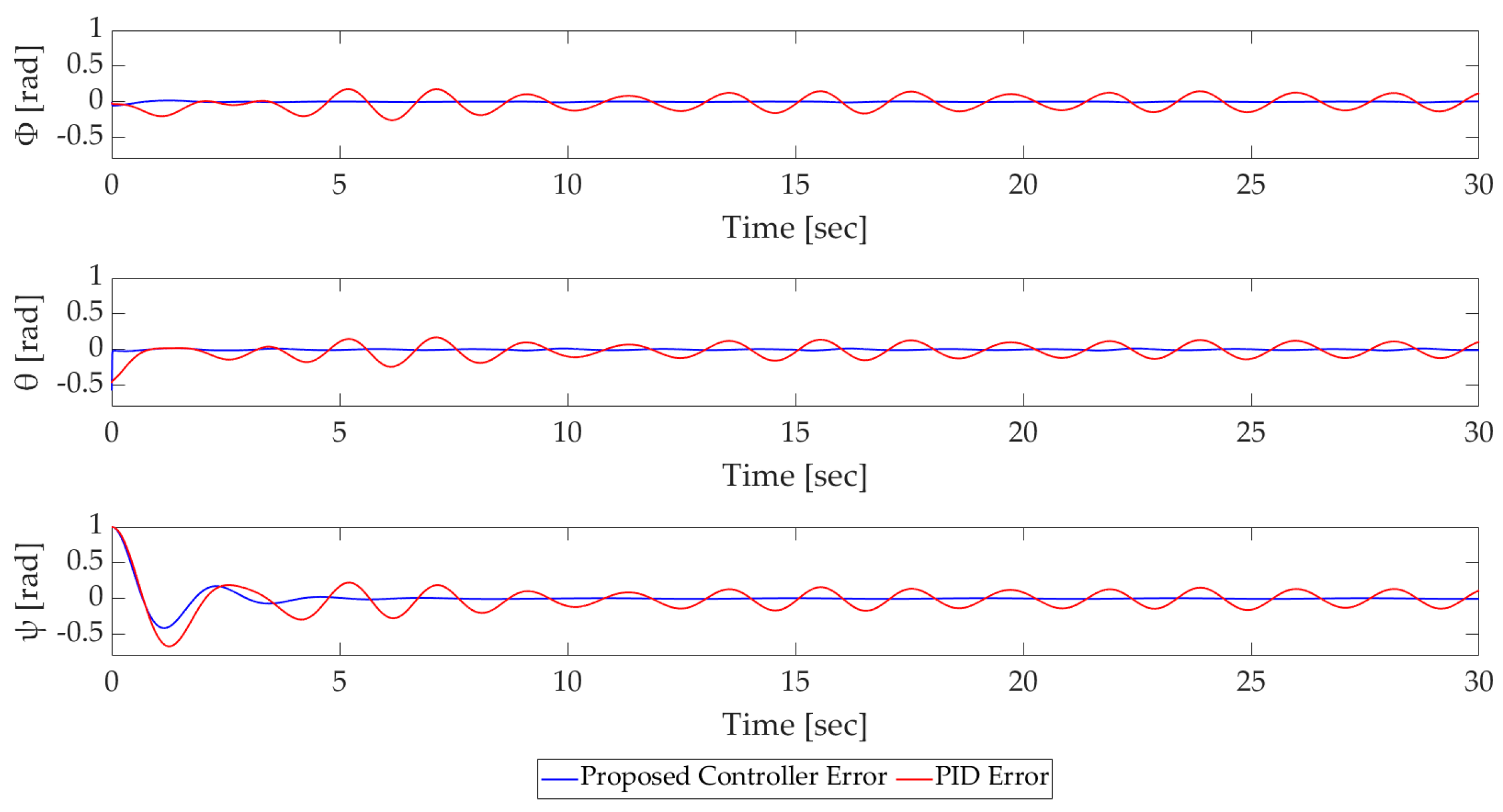
4.2.2. Attitude Control Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petrlík, M.; Báča, T.; Heřt, D.; Vrba, M.; Krajník, T.; Saska, M. A Robust UAV System for Operations in a Constrained Environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, Z. Bearing-based distributed formation control of multiple vertical take-off and landing UAVs. IEEE Trans. Control Netw. 2021, 8, 1281–1292. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H.; Song, L.; Schober, R.; Poor, H.V. Cooperative Internet of UAVs: Distributed trajectory design by multi-agent deep reinforcement learning. IEEE Trans. Commun. 2020, 68, 6807–6821. [Google Scholar] [CrossRef]
- Xu, L.; Qin, K.; Tang, F.; Shi, M.; Lin, B. UDE-Based Dynamic Surface Control for Quadrotor Drone Attitude Tracking under Non-Ideal Actuators. Drones 2023, 7, 305. [Google Scholar] [CrossRef]
- He, Z.; Hu, J.; Wang, Y.; Cong, J.; Bian, Y.; Han, L. Attitude-Tracking Control for Over-Actuated Tailless UAVs at Cruise Using Adaptive Dynamic Programming. Drones 2023, 7, 294. [Google Scholar] [CrossRef]
- Shen, Z.; Tsuchiya, T. Singular Zone in Quadrotor Yaw–Position Feedback Linearization. Drones 2022, 6, 84. [Google Scholar] [CrossRef]
- Yogi, S.C.; Tripathi, V.K.; Behera, L. Adaptive Integral Sliding Mode Control Using Fully Connected Recurrent Neural Network for Position and Attitude Control of Quadrotor. IEEE Trans. Netw. Learn. Syst. 2021, 32, 5595–5609. [Google Scholar] [CrossRef]
- Hu, M.; Ahn, H.; You, K. Finite-Time Rapid Global Sliding-Mode Control for Quadrotor Trajectory Tracking. IEEE Access 2023, 11, 22364–22375. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Yu, Y.; Sun, C. Nonlinear Robust Compensation Method for Trajectory Tracking Control of Quadrotors. IEEE Access 2019, 7, 26766–26776. [Google Scholar] [CrossRef]
- Ullah, S.; Mehmood, A.; Khan, Q.; Rehman, S.; Iqbal, J. Robust Integral Sliding Mode Control Design for Stability Enhancement of Under-actuated Quadrotor. Int. J. Control Autom. Syst. 2020, 18, 1671–1678. [Google Scholar] [CrossRef]
- Yu, G.; Reis, J.; Silvestre, C. Quad Neural Network Adaptive Control: Design and Experimental Validation. IEEE Robot. Autom. Lett. 2023, 8, 2574–2581. [Google Scholar] [CrossRef]
- Ouyang, Y.; Xue, L.; Dong, L.; Sun, C. Neural Network-Based Finite-Time Distributed Formation-Containment Control of Two Layer Quadrotor UAVs. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4836–4848. [Google Scholar] [CrossRef]
- Liu, H.; Xi, J.; Zhong, Y. Robust Attitude Stabilization for Nonlinear Quadrotor Systems with Uncertainties and Delay. IEEE Trans. Ind. Electron. 2017, 64, 5585–5595. [Google Scholar] [CrossRef]
- Tayebi, A.; McGilvray, S. Attitude stabilization of a VTOL quadrotor aircraft. IEEE Trans. Control Syst. Technol. 2006, 14, 562–571. [Google Scholar] [CrossRef]
- Alexis, K.; Nikolakopoulos, G.; Tzes, A. Switching model predictive attitude control for a quadrotor helicopter subject to atmosphere disturbance. Control Eng. Pract. 2011, 10, 1195–1207. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, X.; Zhang, W. Integrating Dynamic Event-Triggered and Sensor-Tolerant Control: Application to USV-UAVs Cooperative Formation System for Maritime Parallel Search. IEEE Trans. Intell. Transp. Syst. 2023, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, W.; Shan, Q.; Zhang, W. Cooperative Path Following Control of USV-UAVs Considering Low Design Complexity and Command Transmission Requirements. IEEE Trans. Intell. Transp. Syst. 2023, 9, 715–724. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Intelligent PID controller. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 326–331. [Google Scholar]
- Wang, J.; Mounier, H.; Cela, A.; Niculescu, S. Event-driven intelligent PID controllers with applications to motion control. In Proceedings of the 18th IFAC World Congress, Milan, Italy, 28 August–2 September 2011; pp. 10080–10085. [Google Scholar]
- Choe, Y. Optimal Tuning Strategy for 2-Degree-of-Freedom I-PID Controllers. Trans. Korean Inst. Electr. Eng. 2018, 67, 1202–1209. [Google Scholar]
- Jung, S. A Neural Network Technique of Compensating for an Inertia Model Error in a Time-delayed Controller for Robot Manipulators. Int. J. Control Autom. Syst. 2020, 18, 1863–1871. [Google Scholar] [CrossRef]
- Han, S.; Tian, Y.; Christov, N.; Wang, H. Time-delay estimation based computed torque control with robust adaptive RBF neural network compensator for a rehabilitation exoskeleton. ISA Trans. 2020, 97, 171–181. [Google Scholar] [CrossRef]
- Slama, S.; Errachdi, A.; Benrejeb, M. Neural adaptive PID and neural indirect adaptive control switch controller for nonlinear MIMO systems. Math. Probl. Eng. 2019, 2019, 7340392. [Google Scholar] [CrossRef]
- Ge, S.; Wang, C. Direct adaptive NN control of a class of nonlinear systems. IEEE Trans. Neural Netw. 2002, 15, 214–221. [Google Scholar] [CrossRef] [PubMed]
- Ong, Q.; Yin, L. Robust adaptive fault accommodation for a robot system using a radial basis function neural network. Int. J. Syst. Sci. 2010, 32, 195–204. [Google Scholar]
- Liu, J. Intelligent Control Design and MATLAB Simulation; Springer: Berlin/Heidelberg, Germany, 2018; pp. 113–233. [Google Scholar]
- Seghouane, A.; Shokouhi, N. Adaptive Learning for Robust Radial Basis Function Networks. IEEE Trans. Cybern. 2021, 51, 2847–2856. [Google Scholar] [CrossRef] [PubMed]
- Liu, J. Radial Basis Function (RBF) Neural Network Control for Mechanical Systems: Design, Analysis and Matlab Simulation; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–280. [Google Scholar]
- Kim, S.; Jin, M.; Suh, J. A Study on the Design of Error-Based Adaptive Robust RBF Neural Network Back-Stepping Controller for 2-DOF Snake Robot’s Head. IEEE Access 2023, 11, 23146–23156. [Google Scholar] [CrossRef]
- Kim, S.; Suh, J. Adaptive Robust RBF-NN Nonsingular Terminal Sliding Mode Control Scheme for Application to Snake Robot’s Head for Image Stabilization. Appl. Sci. 2023, 13, 4899. [Google Scholar] [CrossRef]
- Wan, M.; Chen, M.; Lungu, M. Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks. Drones 2023, 7, 154. [Google Scholar] [CrossRef]
- Cao, X.; Shi, P.; Li, Z.; Liu, M. Neural-network-based adaptive backstepping control with application to spacecraft attitude regulation. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4303–4313. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Peng, P.; Jiang, Z. Stable neural controller design for unknown nonlinear systems using backstepping. IEEE Trans. Neural Netw. 2000, 11, 1347–1360. [Google Scholar]
- Wang, W.; Kuo, M.; Lee, T.; Hong, C.; Leu, Y. RBF neural network adaptive backstepping controllers for MIMO nonaffine nonlinear systems. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 4946–4951. [Google Scholar]
- Zhu, J.; Cao, Z.; Zhang, T.; Yang, Y.; Yi, Y. Sufficient Condition for the Existence of the Compact Set in the RBF Neural Network Control. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3277–3282. [Google Scholar] [CrossRef]
- Bouadi, H.; Mora-Camino, F. Modeling and adaptive flight control for quadrotor trajectory tracking. J. Aircr. 2017, 55, 1–16. [Google Scholar] [CrossRef]
- Aboudonia, A.; El-Badawy, A.; Rashad, R. Disturbance observer-based feedback linearization control of an unmanned quadrotor helicopter. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 2016, 230, 877–891. [Google Scholar] [CrossRef]
- Bouadi, H.; Bouchoucha, M.; Tadjine, M. Sliding Mode Control based on Backstepping Approach for an UAV Type-Quadrotor. Int. J. Mech. Mechatron. Eng. 2007, 1, 39–44. [Google Scholar]
- Jung, S. An Impedance Force Control Approach to a Quad-Rotor System Based on an Acceleration-Based Disturbance Observer. J. Intell. Robot. Syst. 2014, 73, 175–185. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Ma, K. Model reference adaptive sliding mode control using RBF neural network for active power filter. Electr. Power Energy Syst. 2015, 73, 249–258. [Google Scholar] [CrossRef]
- Liu, Q.; Li, D.; Ouyang, Z.; Tee, K.; Ge, S. Adaptive bias RBF neural network control for a robotic manipulator. Neurocomputing 2021, 447, 213–223. [Google Scholar] [CrossRef]
- Wang, L.; Chai, T.; Zhai, L. Neural-Network-Based Terminal Sliding-Mode Control of Robotic Manipulators Including Actuator Dynamics. IEEE Trans. Ind. Electron. 2009, 56, 3296–3304. [Google Scholar] [CrossRef]
- Hwang, N.; Kim, B. Active Fault Tolerant Control of Quadrotor Based on Multiple Sliding Surface Control Method. J. KIECS 2022, 17, 59–70. [Google Scholar]



| Parameter | Description | Value |
|---|---|---|
| Mass of quadrotor | 0.5 | |
| Moment of inertia about | 0.0023 | |
| Moment of inertia about | 0.0023 | |
| Moment of inertia about | 0.0051 | |
| Distance between center of the quadrotor and the propeller | 0.17 | |
| Thrust factor | 0.00018 | |
| Total moment of inertia of motor | 0.000065 | |
| g | Acceleration of gravity | 9.81 |
| Parameter | Value |
|---|---|
| 8 | |
| 0.002 | |
| 1.6 | |
| 0.02 | |
| 0.7 | |
| 0.2 | |
| 0.5 | |
| 0.2 | |
| 0.01 | |
| 0.001 | |
| N | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-J.; Suh, J.-H. Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System. Drones 2024, 8, 179. https://doi.org/10.3390/drones8050179
Kim S-J, Suh J-H. Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System. Drones. 2024; 8(5):179. https://doi.org/10.3390/drones8050179
Chicago/Turabian StyleKim, Sung-Jae, and Jin-Ho Suh. 2024. "Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System" Drones 8, no. 5: 179. https://doi.org/10.3390/drones8050179
APA StyleKim, S.-J., & Suh, J.-H. (2024). Model-Free RBF Neural Network Intelligent-PID Control Applying Adaptive Robust Term for Quadrotor System. Drones, 8(5), 179. https://doi.org/10.3390/drones8050179







